Изобретение относится к области измерительной техники и приборостроения и может быть использовано в лазерной доплеровской локации низколетящих над водными бассейнами «объектов-невидимок» (крылатых ракет, самолетов типа Stels и др.).
11.09.2007 по Центральному телевидению подробно сообщалось о разработках в США самолета-невидимки по проекту Stels, который был использован в военной компании в Ираке и появление которого не могли зафиксировать приграничные средства ПВО в связи с особой формой этого самолета. Эта форма в нарушение законов аэродинамики позволила существенно уменьшить эффективную поверхность отражения (ЭПО) зондирующего радиоизлучения радаров ПВО и представляла собой зеркально отражающие грани корпуса, расположенные под углами к падающему излучению, что приводило к отражению последнего в направлениях, существенно не совпадающих с направлением падающего на самолет излучения радара (в основном вниз и вверх относительно вектора движения самолета). Форма самолета-невидимки напоминала форму стрелы. Один из наших ученых - Ф.Уфимцев разработал теорию дифракции электромагнитных волн для такого рода объектов и сотрудничал в США в процессе создания проекта Stels, но также предложил и способ обнаружения самолетов-невидимок, сущность которого состояла в использовании нескольких радиолокационных приемных устройств, рассредоточенных в пространстве относительно радара ПВО, с помощью которых можно принимать излучения радара, рассеянно отраженные от самолета-невидимки. Однако данный способ выражен в виде идеи возможного обнаружения, без конкретного указания на технические средства реализации способа и состав оборудования.
При использовании такого гипотетического способа обнаружения движущихся объектов-невидимок с весьма малыми величинами ЭПО применительно к задачам ВМФ, то есть в условиях работы на море (в океане), возникают трудно преодолимые препятствия, связанные с необходимостью взаимной топографической привязки группы кораблей с указанными радиолокационными приемниками рассеянно отраженного излучения радара, также размещенного на одном из кораблей данной группы, находящейся в движении. Это обстоятельство крайне затрудняет реализацию идеи Ф.Уфимцева применительно к лазерной когерентной локации низколетящих над водными бассейнами крылатых ракет или самолетов-невидимок, обнаружение которых и измерение их координат и скорости необходимо осуществлять заблаговременно.
Известно построение лазерных доплеровских локаторов с многоканальной обработкой информации на основе дисперсионных линий задержки (ДЛЗ), работающих в режиме гетеродинного приема излучений [1-7]. Использование фактора высокой когерентности излучения одночастотных газовых лазеров [8, 9], например СО2-лазеров, позволяет осуществить когерентный прием таких излучений методом фотосмешения сигнального и гетеродинного пучков, что находит применение в лазерных доплеровских локаторах. Полученные в результате фотосмешения радиосигналы разностной частоты обрабатываются в согласованных фильтрах на ДЛЗ, что позволяет повысить обнаружительную способность локаторов, то есть величину отношения сигнал/шум на входе решающего устройства [10-15]. Следует отметить, что в таких локаторах передающий тракт не включает модулирующих излучение устройств (например, электрооптических модуляторов), как это имеет место в лазерных импульсных локаторах, что обеспечивает более высокий энергетический потенциал доплеровских локаторов по сравнению с импульсными системами на единицу полезной энергии (или средней мощности) излучения лазеров.
Для обнаружения объектов в расширенной угломестной зоне Δε кругового обзора с узким мгновенным углом зрения по азимуту Δφ (то есть при «веерообразной» диаграмме излучения) в когерентных локаторах на CO2-лазерах используют фотодиодные линейки из N фоточувствительных элементов КРТ (тройные соединения Kd Hg Tl, охлаждаемые жидким азотом) с N-канальной согласованной фильтрацией с использованием ДЛЗ. При этом предельная наклонная дальность d обнаружения диффузных дифракционно-ограниченных объектов находится из решения трансцендентного уравнения
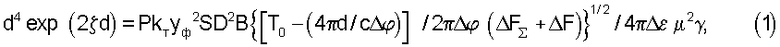
где ζ - экстинкция среды, Р - мощность излучающего лазера, kт - пропускание в излучающем и приемном трактах, уф - эффективность фотосмешения, S - эффективная поверхность отражения (ЭПО) лоцируемого объекта, D - диаметр входного зрачка (приемного объектива), µ - отношение сигнал/шум по напряжению на входе решающего устройства, γ - спектральная плотность мощности шума фотодетектора (фоточувствительного элемента КРТ), Т0 - период кругового обзора, В=τΔF - база ДЛЗ, τ - длительность импульсной характеристики ДЛЗ, ΔF - рабочая полоса частот ДЛЗ, ΔFΣ - полоса неопределенности доплеровских сдвигов частоты ΔFΣ=2Δv/λ, где Δv - разница между наибольшей и наименьшей возможных радиальных скоростей движущегося объекта, λ - длина волны лазерного излучения (λ=10,6 мкм для СО2-лазера), причем для гауссовских сигнала и шума имеем µ2=(InФ/InG)-1, где G и Ф - соответственно вероятности правильного обнаружения и ложных тревог, значениями которых обычно задаются при расчете локационной системы.
Выбор ДЛЗ существенно влияет на обнаружительные, точностные и динамические характеристики локатора, как это следует из (1). Пороговые свойства фотодетектора при когерентном приеме определяются параметрами γ и уф.
Разрешение противоречий между увеличением энергетического потенциала локатора (предельной дальности обнаружения малоразмерной цели) и упрощением процедуры измерения основных характеристик лоцируемых объектов - их высоты полета, наклонной дальности и вектора скорости (включая и параметр радиальной скорости) достигается на основе использования способа локации, известного из патента РФ №2296350 (опубл. в бюл. №9 от 27.03.2007) того же автора, который может быть использован в качестве прототипа заявляемому техническому решению.
Известный способ основан на использовании сочетания доплеровского принципа локации с триангуляционным методом местоопределения цели. Последнее достигается за счет использования бликов отраженного от цели под разными углами излучения от морской поверхности, излучение от которых поступает к локатору под разными измеряемыми углами и с доплеровскими сдвигами частоты в функции углов отражения падающего на цель зондирующего излучения от поверхности цели. По измерению углов прихода излучения от бликов морской поверхности фоточувствительной приемной матрицей и по измеренным значениям доплеровских сдвигов частоты в многоканальном блоке оптимальной фильтрации на основе гетеродинных методов приема с применением многоканальных дисперсионных линий задержки методами статистического усреднения удается реконструировать текущее местоположение цели и ее вектор скорости.
Указанный способ локации основан на зондировании дифракционно ограниченного объекта, движущегося над поверхностью моря (океана), немодулированными излучениями одночастотного лазера непрерывного действия и многоканальной когерентной обработке принимаемых излучений матричным фотоприемным устройством с определением доплеровских сдвигов частоты в переотраженном излучении и последующей многоканальной параллельной согласованной фильтрацией выделенных радиосигналов и отличается тем, что когерентному приему и обработке дополнительно и одновременно подвергают отраженные от нескольких бликов морской поверхности излучения, поступающие на фотоприемную матрицу с разных произвольно распределенных угловых направлений, определяют в соответствующих каналах, связанных с матричным фотоприемным устройством, доплеровские сдвиги частоты в принятых излучениях для переотраженных от бликов морской поверхности сигналов и соответствующие им угловые координаты на эти блики, вычисляют текущие координаты местоположения объекта и его истинную скорость, а также статистически усредняют полученные результаты вычислений всей совокупности совместных измерений указанных параметров.
Способ-прототип предполагает, что известно измеряемое доплеровское смещение частоты Δυдоп0=2vυ0/с=2v/λ зондирующего излучения в прямом отраженном от лоцируемого объекта сигнале и углы ε0 и φ0, под которыми радар «видит» напрямую данный объект (углы расположения линии наклонной дальности), где v - радиальная скорость объекта, υ0 - частота зондирующего излучения лазера. Однако в случае локации движущихся объектов-невидимок измерение прямого отраженного сигнала считается невозможным, и локация осуществляется только по совокупности бликовых переотражений от поверхности моря при рассеянии зондирующего излучения вниз-вбок от объекта локации. При этом используется иная, чем заявлено в способе-прототипе, процедура обработки принимаемых бликовых излучений.
Оптимальным по энергетическому потенциалу решением в способе-прототипе является использование многоканального тракта обработки информации на основе ДЛЗ с числом каналов, равным числу элементов фоточувствительной матрицы NЭ. При этом недостаткам такого решения является увеличенный объем оборудования, поскольку требование повышения разрешающей способности по угловым координатам, определяющее точностные характеристики локатора по определению текущих координат и скорости объекта локации, приводит к использованию в локаторе фотоприемной матрицы с весьма большим числом элементов вдоль строк и столбцов, например, матриц размером 100×100 элементов и более.
Другим недостатком известного способа является необходимость обеспечения приема прямого отраженного от объекта локации излучения, то есть в направлении зондирования, что не всегда возможно, например, при локации объекта-невидимки.
Указанные недостатки известного технического решения по способу-прототипу устранены в заявляемом способе.
Целью изобретения является существенное упрощение реализующего заявляемый способ устройства, в частности конструкции блока обработки информации с ДЛЗ, путем уменьшения более чем на один-два порядка числа каналов обработки сигналов, образующихся в элементах матричного фотоприемного устройства.
Другой целью изобретения является обеспечение возможности локации объектов-невидимок, когда отсутствует прием излучения непосредственно от объекта локации в направлении его зондирования.
Заявляемый способ может быть охарактеризован одним основным и несколькими зависимыми пунктами формулы изобретения.
1. Способ обработки информации в лазерном когерентном локаторе с матричным фотоприемником, основанный на измерении доплеровских сдвигов частоты ΔυДОПi в излучениях от морских бликов и угловых координат последних - азимутов φi и углов места εi, вычислении координат объекта локации и его скорости с последующим статистическим усреднением вычисляемых параметров за несколько смежных циклов измерений, отличающийся тем, что в NЭ=рkp элементах матричного фотоприемника образуют по два независимых выхода, которые формируют в двумерную (р=2) или трехмерную (р=3) группы, где k=1, 2, 3, … - целые числа, с n=2рk(р-1) выходными шинами в группах, к каждой из выходных шин группы параллельно подключают по r=рk соответствующих выходов строчных или столбцовых элементов матричного фотоприемника, а вычисление координат объекта локации по данным измеренных доплеровских сдвигов частоты ΔυДОП i с соответствующими им измеренными угловыми координатами - азимутом φi и углом места εi на соответствующие αi блики морской поверхности, видимые локатором в данном цикле измерения, где i=1, 2, 3, … m - число действующих бликовых излучений, осуществляют путем последовательной итерации неизвестных параметров - радиальной скорости v объекта локации в априорно ожидаемом интервале ее допустимого изменения и угла места ε0 линии наклонной дальности на объект локации, для чего в процессе указанного итеративного подбора этих параметров выбирают такие их значения v и ε0, при которых минимизируются разности между любыми парами величин, определяющих наклонную дальность до объекта локации.
2. Способ по п.1, отличающийся тем, что возникшую неопределенность выбора 2(р-1) выходных шин, соответствующих одному и тому же доплеровскому сдвигу частоты ΔυДОП i в сигнале на выходах элемента αjk матричного фотоприемника, по положению которого в матрице судят об азимуте φi и угле места εi на видимый морской блик αi, устраняют путем сравнения кодов, отображающих доплеровские сдвиги частоты, по их 2(р-1)-кратному совпадению для всех m морских бликов с заданной минимальной погрешностью.
3. Способ по п.1, отличающийся тем, что вычисление измеряемых параметров объекта локации при большом объеме вычислительных операций, связанном с процессом итерации при поиске значений v и ε0, удовлетворяющих указанному условию, производят во временном интервале, превышающем заданный цикл измерения, а затем относят полученные результаты к моменту времени исходного цикла измерений.
4. Способ по п.1, отличающийся тем, что уменьшения объема вычислительных операций при итерационном поиске значений v и ε0 в каждом последующем цикле измерений достигают путем сокращения интервала их итерационного поиска с учетом данных об этих значениях из предыдущих циклов измерений и с учетом статистического усреднения каждого из этих значений за несколько последовательных циклов измерений в предположении, что найденные значения v и ε0 являются медленно изменяющимися функциями времени в сравнении с заданным темпом следования циклов измерения.
5. Способ по п.1, отличающийся тем, что уточнение координат лоцируемого объекта осуществляют при проведении итерационного поиска значений v и ε0 совместным решением системы m уравнений хi=f(h0, ε0, φi, εi, v) для всех видимых локатором m морских бликов, то есть для i=1, 2, 3, … m, где угол рассеяния объектом зондирующего излучения относительно направления последнего равен Θi=arccos(ΔυДОП i*λ/2v), λ - длина волны лазерного излучения, h0 - известная высота над уровнем моря центральной точки приемного объектива локатора, так что координату x рассчитывают по формуле 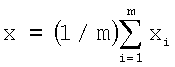 , и при этом минимизируется абсолютная величина разности любых двух значений хi с разными индексами i из их числа m.
, и при этом минимизируется абсолютная величина разности любых двух значений хi с разными индексами i из их числа m.
6. Способ по п.1, отличающийся тем, что обнаружение объекта локации и его автосопровождение осуществляют сканированием зондирующего излучения по азимуту, а диаграмму излучения выбирают веерообразной - предельно узкой по азимуту и широкой по углу места.
7. Способ по п.1, отличающийся тем, что при выполнении условия обнаружения объекта локации и его автосопровождения по азимуту, при котором линия наклонной дальности и оптическая ось приемно-передающего объектива локатора лежат в одной плоскости, местоопределение объекта локации и измерение его радиальной скорости находят вычислением, минимально по двум разным бликовым излучениям (Min m=2) в данном цикле измерения.
Достижение поставленных целей обусловлено применением триангуляционного способа местоопределения объекта, реализация которого одним локатором объясняется приемом рассредоточенных на поверхности моря бликовых излучений, образующихся при облучении морской поверхности, представляющей стохастически распределенную совокупность зеркальных отражателей, лазерным излучением, рассеянным под разными углами относительно направления зондирования корпусом объекта локации. В зависимости от угла такого рассеяния в принятых бликовых излучениях изменяются соответственно и доплеровские сдвиги частоты. Пространственное положение бликов однозначно измеряется азимутом φi и углом места εi на i-й блик при известной высоте h0 и соответствующей топографической привязке локатора. По доплеровским смещениям частоты ΔυДОП i для соответствующих морских бликов и измеряемым угловым координатам линии наклонной дальности на объект φ0 и ε0 и радиальной скорости v последнего реконструируются соответствующие углы ηi, под которыми может приходить от объекта рассеянное им излучение. Эти углы образуют коническую поверхность. По двум бликовым излучениям строится две такие поверхности, пересечение между собой которых образует кривую, на которой располагается точка корпуса объекта, из которой исходит рассеянное излучение. Использование третьей конической поверхности при рассмотрении третьего морского блика образует соответственно три указанных кривых, образующих в точках пересечения вершины криволинейного треугольника, внутри которого располагается интересующая точка корпуса объекта. При правильном выборе методом последовательных итераций значений v и ε0 площадь такого криволинейного треугольника минимизируется: в пределе такой треугольник стягивается в искомую точку. Указанная геометрическая интерпретация процедуры нахождения точек корпуса, от которых исходят рассеянные излучения и которые определяют координаты объекта локации, который, в свою очередь, рассматривается как дифракционно ограниченный, точечный по отношению к локатору, реализуется исследованием минимума разностей аналитически вычисленных отрезков хi (i-я проекция на ось х линии наклонной дальности на объект локации) для разных индексов i для m бликов в каждом цикле измерений, поскольку такие минимумы отвечают минимальным расстояниям между вершинами указанных криволинейных треугольников, то есть минимуму площади последнего.
Двумерное или трехмерное подключение элементов матричного фотоприемника к каналам обработки информации с использованием преобразования полученного с того или иного элемента матрицы сигнала в линейно-частотно-модулированный (ЛЧМ) эквивалент с последующим его усилением, спектро-временным «сжатием» в канальных дисперсионных линиях задержки (ДЛЗ), детектированием и пороговым ограничением по минимуму с заданным порогом ограничения позволяет преобразовать сигнал с доплеровским смещением частоты в короткий импульс, временное положение которого относительно строб-импульса начала цикла измерений однозначно характеризует величину указанного доплеровского смещения частоты. Это временное положение кодируется в цифровом коде и запоминается в соответствующем буферном запоминающем устройстве (БЗУ), в коде которого содержатся также код номера цикла измерений и код номера канала, по которому проводилась указанная обработка сигнала с элемента матрицы фотоприемника. Это позволяет по совокупности таких кодовых записей в данном цикле измерения реконструировать однозначно два параметра - доплеровский сдвиг частоты ΔυДОП i для сигнала с выхода соответствующего элемента матрицы и его местоположение в ней. Последнее, в свою очередь, однозначно определяет азимут φi и угол места εi на блик морской поверхности αi, видимый локатором в данном цикле измерения относительно оптической оси (оси зондирующего излучения) приемно-передающего объектива локатора (при этом считается, что центральный элемент матричного фотоприемника совмещен с указанной оптической осью).
Указанный способ подключения элементов матрицы фотоприемника к каналам обработки информации существенно уменьшает число таких каналов, то есть упрощает конструкцию реализующего заявляемый способ устройства, однако приводит к неоднозначности правильного вычисления данных об объекте локации, которая устраняется путем сравнения кодов, соответствующих измеренным доплеровским сдвигам частоты от разных бликов морской поверхности, полагая, что доплеровские сдвиги разные от разных бликов. При этом выбор двумерного р=2 или трехмерного р=3 представления групп определяется конъюнктурно. При двумерной организации группы значительно сокращается объем вычислительных операций, но растет потребное число каналов с ДЛЗ, а при трехмерной - сокращается число каналов с ДЛЗ, но несколько возрастает объем вычислительных операций из-за повышенной неопределенности, особенно при большом (более трех) числе m одновременно обрабатываемых излучений от бликов морской поверхности в данном цикле измерения.
На представленных чертежах рассматриваются отдельные положения, раскрывающие сущность заявляемого технического решения.
На фиг.1 дана схема организации двумерной группы (р=2) из NЭ=р2k элементов матричного фотоприемника 1, элементы которого αjk (для j-й строки и k-го столбца) организуются в квадратную матрицу со стороной в рk элементов. Число выходных шин сборок 2 и 3 при этом составляет n=2рk=2k+1. При такой организации элементы фотоприемной матрицы имеют по два независимых выхода сигнала. При относительно небольшом числе элементов NЭ предпочтительно применение двумерной организации группы. Так, при матрице размерностью 32×32 элемента число каналов n=64 вместо 1024.
На фиг.2 дана схема организации трехмерной группы (р=3) из NЭ=р3k элементов αjk, которая составляет куб элементов 4 со стороной такого куба р=3 элементов. Каждая из двух взаимно ортогональных граней такого куба представляет двумерные структуры 5 и 6 с числом шин в каждой по р2k=32k. Каждая такая двумерная структура определяет соответственно пару сборок 7 и 8, 9 и 10 выходных шин. При этом общее число выходных шин составляет n=2рk (р-1)=4*3k. При такой организации элементы 11 фотоприемной матрицы 12 (физически плоской конструкции) имеют по два независимых выхода сигнала, а 32k шин каждой из двумерных структур 5 и 6 соединяются с выходными шинами сборок 7-10 через промежуточные усилители 13 с двумя независимыми выходами каждый. При большом числе элементов NЭ более предпочтительной может оказаться трехмерная организация группы. Так, при матрице размерностью 729×243=19683=39 элементов, то есть при k=3, число каналов обработки n=108 вместо 19683.
На фиг.3 представлен один типовой канал обработки сигнала с выходной шины для соответствующей двумерной или трехмерной группы. Канал содержит последовательно соединенные смеситель 14, первый широкополосный усилитель 15, дисперсионную линию задержки (ДЛЗ) 16, второй широкополосный усилитель 17, компенсирующий потери сигнала в ДЛЗ, амплитудный детектор 18, ограничитель по минимуму 19 с заданным порогом ограничения и компаратор 20. Для всех n каналов обработки используется общий для них генератор линейно-частотно-модулированных колебаний (ГЛЧМ) 21, вход которого запускается от генератора строб-импульсов (ГСИ) 22, а выход ГЛЧМ подключен ко вторым входам смесителей 14 каналов. Временная задержка между моментами возникновения строб-импульса, открывающего данный цикл измерения, и нормированным импульсом с выхода компаратора 20 однозначно характеризует величину доплеровского сдвига частоты ΔυДОП i. Указанная задержка - временной интервал τзад - кодируется в буферном запоминающем устройстве (БЗУ) 23, общем для всех n каналов, и БЗУ при этом имеет соответственно n канальных входов, а также управляющий вход, связанный со вторым выходом ГСИ 22.
На фиг.4 представлены диаграммы, поясняющие работу канала обработки информации с использованием ДЛЗ. На фиг.4а указана периодическая последовательность синхроимпульсов, вырабатываемых в ГСИ 22 (фиг.3) и определяющих период цикла измерений. На фиг.4б представлена частотно-временная характеристика вырабатываемых в ГЛЧМ 21 (фиг.3) сигналов гетеродинирования, подаваемых ко вторым входам канальных смесителей 14. На фиг.4в изображено взаимодействие образующегося на выходе смесителя 14 (фиг.3) ЛЧМ-эквивалента с ДЛЗ 16. На фиг.4г показаны формируемые на выходе ДЛЗ (фиг.3) «сжатые» импульсы длительностью tимп и временная задержка τзад их появления относительно строб-импульса.
На фиг.5 изображена блок-схема БЗУ 23 (фиг.3), содержащая n многоразрядных запоминающих модулей (ЗМ) 24, 25, 26, … 27, к информационным входам которых параллельно подключен выход счетчика временных импульсов (СВИ) 28, пересчет в котором происходит от подачи на его счетный вход высокочастотных импульсов от генератора временных меток (ГВМ) 29. Запись временного кода с выхода СВИ 28 в соответствующие запоминающие модули 24, 25, 26, … 27 происходит при подаче на входы разрешения записи импульса с соответствующего канального компаратора 20 (фиг.3). Блок-схема БЗУ содержит также счетчик циклов измерения (СЦ) 30, входом соединенный со вторым выходом ГСИ 22 (фиг.3), и двухвходовые суммирующие регистры (ДСР) 31, 32, 33, … 34, перезапись кодовой информации в которые по их первым входам осуществляется в начале следующего цикла измерений от действия строб-импульса, поступающего со второго выхода ГСИ 22 (фиг.3), а вторые входы ДСР параллельно подключены к выходу СЦ 29, так что код номера цикла записывается в старшем байте регистра, а код временной задержки τзад - в младших байтах регистра. Импульс ГСИ 22 осуществляет сброс в СВИ 28 и через некоторый интервал времени задержки, организуемый элементом задержки (ЭЗ) 35, осуществляет также сброс ранее записанных кодов в соответствующих ЗМ 24, 25, 26, … 27 (для записи новых кодов времени в следующем цикле измерений). Импульсные сигналы ГСИ 22 также осуществляют фазовую синхронизацию работы ГВМ 29, частота следования импульсов в котором кратна частоте импульсов ГСИ 22 и определяет временной дискрет отсчета временной задержки τзад для каждого из действующих каналов обработки. Выход БЗУ 23 (фиг.3) образован сигналами с ГСИ 22, ДСР 31, 32, 33, … 34 и СЦ 30. Эти сигналы поступают в вычислитель измеряемых параметров объекта локации, рассмотрение конкретной структуры которого выходит за рамки рассматриваемого технического решения.
На фиг.6 дана геометрическая схема расчета местоопределения объекта локации с использованием одного (i-го) переотражающего блика на морской поверхности, положение которого задано измеряемыми на него угловыми координатами - азимутом φi и углом места εi при известной высоте h0 реперной точки локатора относительно поверхности моря (реперная точка локатора находится в центре приемно-передающего объектива). В этой схеме плоскость OABD - вертикальная в координатах x, z, плоскость ОСЕ - горизонтальная, совпадающая с поверхностью моря, в координатах x, y. В вертикальной плоскости расположены реперная точка А локатора, дифракционно-ограниченный (точечный) объект локации (точка В), линия высоты реперной точки локатора ОА=h0, объекта локации BD=Н и наклонной дальности АВ=d. В горизонтальной плоскости расположен рассматриваемый i-й блик (точка С) с измеряемыми углами φi и εi на него. Линия CG - суть перпендикуляр к линии пересечения вертикальной и горизонтальной плоскостей OD, совпадающей с осью х. По построению ОС=ОЕ, поэтому находятся углы γi и σi из соотношений tg γi=tg εi/cos φi, и σi=εi-γi. Угол при вершине В треугольника ABG, расположенного в вертикальной плоскости, обозначен как χi а угол при вершине В пространственно расположенного треугольника BCG обозначен как ψi. Поскольку треугольники ABG и BCG взаимно ортогональны, то несложным расчетом можно показать, что двугранный угол Θi между ними определяется из соотношения cos Θi=cos χi*cos ψi. При этом угол Θi является искомым углом между направлением зондирующего излучения локатора и направлением рассеянного отражения от лоцируемого объекта, определяемым по значению доплеровского смещения ΔυДОПi в принятом излучении от данного блика морской поверхности. Значение априори неизвестного угла места ε0 на невидимый объект локации и высота последнего Н над поверхностью моря определяются уравнением связи с величиной наклонной дальности d вида Н=h0+d sinε0. Проекция хi линии наклонной дальности di в i-м измерении на данной схеме отвечает отрезку OD. Число таких независимых измерений равно m, так что в результате усреднения имеем
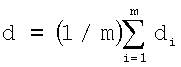
Рассматривая прямоугольный треугольник BCD (угол при его вершине D прямой), отмечаем, что линия ВС есть направление, под которым объект локации виден от данного блика морской поверхности (от точки С). При этом угол ηi наблюдения объекта локации от рассматриваемого блика является функцией измеряемых углов εi и φi и доплеровского смещения ΔυДОП i при известном значении h0 и варьируемых параметрах ε0 и v. Причем φ0=0, поскольку считается, что линия наклонной дальности на объект локации АВ лежит в вертикальной плоскости zOx, то есть при выполнении условия, что объект локации подсвечен зондирующим излучением локатора.
На фиг.7а и 7б представлена графическая интерпретация местоопределения лоцируемого объекта методом пересечения двух (и более) окружностей, расположенных в разных плоскостях. Линия пересечения этих плоскостей АВ - суть линия наклонной дальности. Точка А - реперная точка локатора с известными координатами. Точка В - точка местоположения лоцируемого объекта с априори неизвестными координатами. Точки C1 и C2 - точки расположения бликов на поверхности моря xOy, координаты которых легко вычисляются по известной высоте h0 реперной точки локатора и измеряемым азимутам φ1 и φ2 и углам места ε1 и ε2. Это позволяет вычислить координаты точки В по вычисленным углам Θ1 и Θ2 при вершине В треугольников ABC1 (фиг.7а) и АВС2 (фиг.7б) методом пересечения окружностей.
Рассмотрим операционную сущность заявляемого способа.
Как видно из фиг.1 и 2, NЭ элементов матричного фотоприемника 1, матрица которого может быть, например, прямоугольной (не обязательно квадратной) с числом строк p1 и числом столбцов р2 с элементами аjk, где j=1, 2, 3, … p1 - номера строк матрицы, k=1, 2, 3, … р2 - номера столбцов матрицы, могут быть сформированы в две различные группы - двумерную (фиг.1) или трехмерную (фиг.2), для которых соблюдается условие NЭ=рpk, где р - размерность группы, соответственно равная двум или трем. Значение целого числа k определяется из условия k=Ent[logр(р1*р2)]+δ, где δ=1 при logр(p1*р2)>Ent[logр(p1*р2)] и δ=0 при logр(p1*р2)=Ent[logp(p1*р2)]. Так, для матрицы размерностью 32×32 элементов для двумерной группы имеем k=5, а при образовании трехмерной группы k=Ent[log31024]+1=3. Однако в последнем случае имеет место значительная избыточность кубической структуры отображения элементов матрицы, поскольку 33*3=39=19683>>1024, что означает, что при таком отображении элементов матрицы проще проигнорировать ее 1024-729=295 элементов, чтобы k=2, и тогда 32·3=36=729, либо иметь размерность матрицы, например, как 27×27. В другом случае, когда матрица фотоприемника имеет размерность 100×200 элементов, для двумерной группы (р=2) имеем k=Ent[log2(2*104)]+1=15, и при этом 215=32768>>20000, так что выгоднее взять k=14 и иметь матрицу размерностью 100×163=16300 элементов. В этом примере для трехмерной группы (р=3) целесообразно выбрать k=3, что позволяет отобразить кубической структурой 19683 элемента матрицы, размерность которой следует понизить до величины 100×196 элементов. Эти примеры показывают, что при определении размерности фотоприемной матрицы p1*p2 следует исходить из следующего условия k=Ent[logp(p1*p2)], соответственно ограничивая числа p1 и р2 для получения целочисленного значения k, при котором разница рpk-p1*p2>0 и минимальна. Отметим, что выбор квадратного представления матрицы в двумерной группе или кубического в трехмерной дает минимум числа каналов обработки информации, так как квадрат определяет минимальный его полупериметр для заданной площади, а куб - минимальную его поверхность для заданного объема по сравнению соответственно с прямоугольником и параллелепипедом. Так, матрица размерностью 100×163 элементов в прямоугольном представлении определяет 100+163=263 канала обработки, а в соответствующей двумерной группе потребуется только 256 каналов обработки. Если прямоугольная матрица имеет размерность 50×326 элементов (то есть ту же площадь, как предыдущая), то число потребных для нее каналов обработки составит 376 против тех же 256 каналов при преобразовании такой матрицы в двумерную группу. При образовании трехмерной группы для матрицы размерностью 100×196 элементов кубическая структура со стороной куба в 27 элементов определяет потребность в использовании 108 каналов обработки, а параллелепипедальная того же объема с размерами сторон 27×9×81 потребует применения 126 каналов обработки, а при размерах параллелепипеда 9×9×243 число каналов возрастает уже до 270.
Если число элементов в фотоприемной матрице выбрать из условия NЭ=рkp, то общее число каналов обработки должно быть равным n=2рk(р-1). На фиг.1 представлена схема двумерной группы 1 размерностью 6х6 фотоприемных элементов, каждый из которых имеет по два независимых выхода. Выходы этих элементов соединены к шести строчным и шести столбцовым шинам, которые образуют две сборки 2 и 3 с общим числом шин, равным двенадцати (n=12). На фиг.3 представлена блок-схема трехмерной группы 4, образующий куб со сторонами из р элементов. При этом фотоприемная матрица 12 содержит 33k элементов αjk каждый из которых имеет два независимых выхода. Куб 4, образующий трехмерную группу, имеет всего 2р2k шин по р2k взаимно коллинеарных шин для каждой из его двух смежных граней. Выходы элементов матрицы соединены с взаимно ортогональными р2k шинами каждого из рk слоев куба. Каждый такой слой представляет собой двумерную группу, схема соединений которой показана на фиг.1. Поэтому к каждой из шин куба оказываются параллельно подключенными по рk соответствующих элементов матрицы 12. При этом р2k шин каждой из двух граней куба образуют две квадратные двумерные сборки 5 и 6. Каждая из этих двумерных сборок содержит р2k усилителей 13 с двумя независимыми выходами. Входы этих усилителей соединены с р2k шинами соответствующей грани куба 4, первые выходы усилителей в каждой из сборок 5 и 6 соединены с рk шинами сборок 7 и 9, а вторые - с рk шинами сборок 8 и 10, так что общее число выходных шин равно 2рk. Так, для фотоприемной матрицы 12 из 729×243 элементов имеем рk=27 и общее число шин n=4рk=108. Это позволяет более чем на два порядка снизить количество оборудования для обработки информации с 19683 фотоприемных элементов матрицы 12. Выигрыш в сокращении количества каналов обработки информации при организации трехмерной группы составляет ψ3=p2k/4.
Однако такое существенное сокращение числа каналов n обработки информации приводит к неоднозначности определения группы двух (при р=2) или четырех (при р=3) шин с одинаковыми доплеровскими смещениями частоты ΔυДОП i. Действительно, для двумерной группы (р=2) одна и та же информация от одного блика содержится в двух шинах. Если бликов m, то число действующих информационных шин равно 2 m. Чтобы из этого числа выбрать только две шины с одинаковой информацией, необходимо осуществить (2m-1) переборов, а общее число вариантов выбора m пар шин с учетом последовательно выбываемых из перебора шин (для уже найденных пар) находят по следующей формуле:
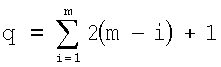
Так, при m=3 максимальное число вариантов выбора q=9, при m=4 имеем q=16, а при m=5 получаем q=25, следовательно, q=m2. Видно, что с ростом числа обрабатываемых в устройстве действующих бликов m существенно увеличивается число вычислительных операций, что следует учитывать при оценке быстродействия вычислительной среды.
В случае трехмерной группы (р=3) одна и та же информация содержится на четырех шинах из общего числа действующих шин 4m (для m бликов). Общее число вариантов m выбора m эквиинформационных четверок шин определяется по правилу
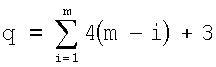
Так, при m=3 максимальное число вариантов выбора q=21, при m=4 имеем q=36, а при m=5 получаем q=55. Таким образом, при переходе от двумерной группы к трехмерной резко сокращается количество потребного оборудования для обработки информации, но при этом увеличивается число вычислительных операций, связанных с перебором вариантов (приблизительно вдвое).
Ниже будет показано, что определение координат и скорости лоцируемого объекта-невидимки возможно при измерении азимутов φi и углов места εi на несколько бликов m морской поверхности и измерении доплеровских сдвигов частоты ΔυДОП i от этих бликов (i=1, 2, 3, … m). Углы φi и εi однозначно определяются местоположением фотоэлемента αjk фотоприемной матрицы, шифруемым номерами соответствующих двух (при р=2) или четырех (при р=3) шин с одинаковыми сдвигами ΔυДОП i. Значения этих сдвигов частоты измеряют с помощью устройства, блок-схема которого для одного из n параллельно работающих каналов обработки информации представлена на фиг.3.
Схема состоит из последовательно включенных смесителя 14, первого широкополосного усилителя 15, дисперсионной линии задержки (ДЛЗ) 16, второго широкополосного (компенсирующего) усилителя 17, амплитудного детектора 18, ограничителя по минимуму 19, компаратора 20 и блока запоминающих устройств (БЗУ) 23 с n информационными входами. Ко второму входу смесителя 14 подключен выход генератора линейно-частотно-модулированных колебаний (ГЛЧМ) 21, к запускающему входу которого подключен генератор синхроимпульсов (ГСИ) 22, задающий цикл обработки информации, например, длительностью 100 мкс. Второй выход ГСИ 22 подключен к управляющему входу БЗУ 23. Элементы 21, 22 и 23 являются общими для всех n каналов обработки информации на элементах 14-20.
Работа канала обработки информации поясняется графиками на фиг.4.
На фиг.4а представлена последовательность синхроимпульсов, определяющих период цикла записи-считывания и называемых как импульсы «Цикла сброса», формируемые в ГСИ 22. На фиг.4б показан процесс периодически воспроизводимого ЛЧМ-сканинга в ГЛЧМ 21 с диапазоном изменения частоты от 80 до 130 МГц. На фиг.4в прямой жирной горизонтальной линией показан сигнал с выхода соответствующей ячейки матрицы ФПУ 12 в координатах «частота-время», например, с частотой 53 МГц (из предполагаемого возможного диапазона частот 50-60 МГц), жирной пилообразной линией изображен ЛЧМ-эквивалент, образованный на выходе смесителя 14, частота в котором изменяется от 80-53=27 МГц до 130-53=77 МГц. Параллельно пилообразному изменению частоты в ЛЧМ-эквиваленте пунктиром показаны пределы вариации последнего при изменении частоты входного сигнала в диапазоне 50-60 МГц (этот диапазон обозначен как ΔFΣ), а крайними горизонтальными пунктирными линиями указана полоса пропускания согласованного фильтра на ДЛЗ 16, в данном примере она равна 40 МГц, что позволяет получить длительность «сжатого» импульса на выходе ДЛЗ tимп=1/ΔFлз=25 нс, где ΔFлз=40 МГц - полоса частот ДЛЗ. На этом же графике пунктирными вертикальными линиями показаны границы вариации по времени возникновения импульсных откликов при изменении частоты входного сигнала в диапазоне частот доплеровских сдвигов от 50 до 60 МГц. Видно, что доплеровский сдвиг частоты преобразуется во временной сдвиг импульса-отклика относительно запускающего синхроимпульса, указанного на фиг.4а. Это обстоятельство отражено на втором графике фиг.4г, который представляет собой прямоугольный импульс с длительностью τзад, равной разности моментов времени появления импульса-отклика и предшествующего ему синхроимпульса. Отметим, что эта длительность импульса затем кодируется в многоканальном БЗУ 23.
Работа канала обработки информации связана с оценкой вероятностных характеристик обнаружения объекта локации с учетом характеристик приемного тракта.
Как известно, отношение сигнал/шум µ однозначно определяет обнаружительные вероятностные характеристики локатора [16, 17]. Так, вероятность обнаружения Робн сигнала на фоне нормального (гауссова) шума в соответствии с критерием Неймана-Пирсона определяется отношением сигнал/шум µ на входе решающего устройства с установленным в нем нормированным порогом αп=Uп/σш, где σш - среднеквадратическое напряжение шума на входе решающего устройства, Uп - пороговое напряжение, вычисляется из выражения
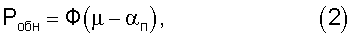
где
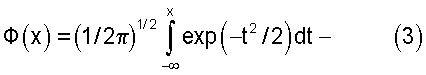
- интеграл вероятности, а вероятность ложных тревог Рлт равна

Для обычно задаваемых при расчетах локационных систем величинах вероятностей обнаружения и ложных тревог требуемое отношение сигнал/шум определяется из выражения
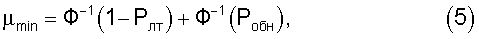
где Ф-1(x) - обратный интеграл вероятности.
Если качество ФПУ известно (величина спектральной плотности шума Gш), то на основании (5) можно рассчитать величину потребной энергии сигнала на входе ФПУ, которая достаточна для обработки в согласованном фильтре:

Вместо вероятности ложных тревог часто пользуются значением частоты ложных тревог Fлт, которая определяется выражением
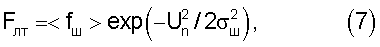
где <fш> - среднеквадратическое значение полосы шума, которое в предположении относительной узкополосности тракта имеет выражение <fш>=(f0 2+Δf2/12)1/2, причем f0 - несущая частота сигнала (или центральная частота тракта), Δf - полоса пропускания приемного тракта, по отношению к которому вычисляется полоса шума, причем из выражения (7) обычно вычисляют величину порогового напряжения Uп, которое равно:
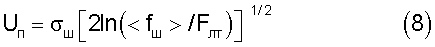
Полученное из (8) значение порогового напряжения подставляют в выражение (2) и находят вероятность обнаружения Робн для полученной величины отношения сигнал/шум на выходе согласованного фильтра µ. В зависимости от поставленных условий либо принимают решение на увеличение времени обзора в заданном телесном угле, либо, наоборот, на уменьшение этого времени или на увеличение предельной дальности обнаружения локатора (либо на увеличение точности измеряемых параметров объекта).
Работа многоканального блока запоминающих устройств (БЗУ) 23 поясняется блок-схемой на фиг.5. Схема содержит n параллельно работающих многоразрядных запоминающих модулей (ЗМ) 24, 25, 26, … 27, к информационным входам которых параллельно подключен выход счетчика временных импульсов (СВИ) 28, пересчет в котором происходит от подачи на его счетный вход высокочастотных импульсов от генератора временных меток (ГВМ) 29. Запись временного кода с выхода СВИ 28 в соответствующие запоминающие модули 24, 25, 26, … 27 происходит при подаче на входы разрешения записи импульса с соответствующего канального компаратора 20 (фиг.3). Блок-схема БЗУ содержит также счетчик циклов измерения (СЦ) 30, входом соединенный со вторым выходом ГСИ 22 (фиг.3), и двухвходовые суммирующие регистры (ДСР) 31, 32, 33, … 34, перезапись кодовой информации в которые по их первым входам осуществляется в начале следующего цикла измерений от действия строб-импульса, поступающего со второго выхода ГСИ 22 (фиг.3), а вторые входы ДСР параллельно подключены к выходу СЦ 30 так, что код номера цикла записывается в старшем байте регистра, а код временной задержки τзад - в младших байтах регистра. Импульс ГСИ 22 осуществляет сброс в СВИ 28, а через некоторый интервал времени задержки, организуемый элементом задержки (ЭЗ) 35, также сброс ранее записанных кодов в соответствующих ЗМ 24, 25, 26, … 27 (для записи новых кодов времени в следующем цикле измерений). Импульсные сигналы ГСИ 22 также осуществляют фазовую синхронизацию работы ГВМ 29, частота следования импульсов в котором кратна частоте импульсов ГСИ 22 и определяет временной дискрет отсчета временной задержки τзад для каждого из действующих каналов обработки. Выход БЗУ 23 (фиг.3) образован сигналами с ГСИ 22, ДСР 31, 32, 33, … 34 и СЦ 30. Эти сигналы поступают в вычислитель измеряемых параметров объекта локации, рассмотрение конкретной структуры которого выходит за рамки рассматриваемого технического решения.
Важно лишь отметить, что в вычислителе измеряемых параметров объекта локации осуществляются следующие операции:
- выбор m пар (при р=2) или m четверок (при р=3) шин с идентичными для них доплеровскими сдвигами частоты ΔυДОП i для m действующих в данном цикле измерения бликов методом сравнения кодов с заданной погрешностью, например ±(1-2) бита;
- определение путем дешифрации номеров шин в каждой паре (или четверке) азимутов φ1 и углов места εi на все работающие m блики;
- вычисление координат и скорости объекта локации по одному из возможных алгоритмов, включая итерационный анализ априори неизвестных параметров - азимута φ0 и угла места ε0 для линии наклонной дальности на объект локации и радиальной скорости v последнего.
Если объем вычислительных операций оказывается большим, что не позволяет его завершить в пределах данного или последующего цикла измерений, то вычисления могут производиться в течение нескольких последовательных циклов в зависимости от организации вычислительной среды и ее быстродействия, а результаты вычислений должны соотноситься во времени к рассматриваемому циклу. По мере уточнения параметров лоцируемого объекта (его координат и скорости) диапазон итерационного поиска должен автоматически сокращаться, уменьшая тем самым временные затраты на производство необходимых вычислений вплоть до интервала времени, равного времени цикла измерений.
Использование в заявляемом способе методов статистического усреднения позволяет повысить точность измерения координат и скорости движения объекта-невидимки.
На основе использования методов аналитической геометрии задача метонахождения лоцируемого объекта-невидимки, когда отсутствует прямое переизлучение от последнего вдоль линии наклонной дальности, сводится к нахождению направлений на объект локации с нескольких разнесенных в пространстве морских бликов, пересечение которых при известных координатах этих бликов происходит в точке, являющейся координатами лоцируемого объекта. Координаты бликов однозначно определяются их азимутами φi и углами места εi, а также высотой h0 реперной точки приемопередающего объектива локатора над уровнем моря, что тривиально. Более сложной задачей является определение углов ηi, под которыми объект «наблюдается» от соответствующих морских бликов. Для решения этой задачи необходимо найти углы Θi (см. фиг.6), которые определяются при рассеянном отражении лазерного излучения объектом локации и отсчитываются от направления зондирующего объект излучения (от линии наклонной дальности). Эти углы по каждому из действующих бликов однозначно зависят от измеренных значений доплеровских сдвигов частоты ΔυДОП i, поскольку известно, что ΔυДОП i=(2v/λ) cosΘi, следовательно,
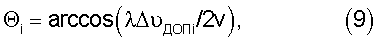
то есть угол Θi определяется по измеряемому значению доплеровского сдвига частоты и априори неизвестному значению радиальной скорости V лоцируемого объекта, значение которой требуется установить.
Высота Н полета объекта над уровнем моря также является неизвестным его параметром и выражается через априори неизвестные значения наклонной дальности d и угол места ε0 по формуле: Н=h0+d sin ε0.
Можно показать, что неизвестными параметрами рассматриваемой локационной задачи являются радиальная скорость объекта v, азимут φ0 и угол места ε0, то есть угловое положение линии наклонной дальности, а измеряемыми параметрами являются азимуты φi и углы места εi «видения» локатором m бликов, доплеровские смещения частоты ΔυДОПi в излучении с этих бликов. Однако с учетом предельно узкой диаграммы излучения в азимутальной плоскости можно считать, что блики переизлучения появляются при условии, что объект локации облучен локатором, и, следовательно, можно полагать, что величина φ0=0, либо мало отличается от этой величины. Известными константами при этом являются значение высоты h0 реперной точки локатора над уровнем моря и длина волны λ лазерного излучения. Таким образом, однозначное решение локационной задачи возможно при совместном решении системы, как минимум, трех независимых уравнений в процессе последовательного итерационного перебора неизвестных параметров v и ε0 таким образом, чтобы обеспечить минимальную ошибку местоопределения объекта в пространстве. В процессе решения системы независимых уравнений, число которых может быть выбрано равным m, но не меньшем трех, рассчитываются углы ηi, определяющие направления, под которыми «наблюдается» объект локации от соответствующих бликов. Каждый из углов ηi указывает лишь на наклон линии наблюдения относительно поверхности моря, то есть образует семейство таких одинаковых углов, то есть коническую поверхность с вершиной конуса в точке расположения на море i-го блика и высотой конуса, ортогональной поверхности моря. Совокупность двух таких разных конусов при их пересечении образует кривую второго порядка, на которой располагается точка, соответствующая координатам объекта.
При пересечении трех конических поверхностей от трех различных бликов образуются соответственно три такие кривых, которые, пересекаясь между собой, образуют фигуру в виде криволинейного треугольника, внутри которого располагается искомая точка, отвечающая координатам объекта. Задача итерационного перебора величин параметров v и ε0 сводится к минимизации площади такого криволинейного треугольника, или к минимизации расстояний между его вершинами, что по сути одно и то же. Повышение точности местоопределения объекта локации может быть достигнуто при выборе большего числа действующих бликов (m>3), хотя это и приводит к увеличению объема вычислительных операций. Получение минимума площади криволинейного треугольника приводит к установлению искомых точных значений величин v и ε0, то есть к фактическому решению локационной задачи.
Диапазон итераций параметров v и ε0 определяется конкретикой задач локации, тактико-техническими характеристиками лоцируемых объектов (в частности, априори ожидаемых скоростей их полета) и параметрами локатора (в частности, размерностью его фотоприемной матрицы). Что касается диапазона итераций параметра φ0, то он весьма мал, что определяется узконаправленным (веерообразным) излучением по азимуту, и вариация этого параметра используется практически только в целях обеспечения автосопровождения объекта по азимуту, и в расчетах можно полагать φ0=0, как это представлено на фиг.6. Диапазон вариации параметра v задается априори ожидаемым разбросом радиальных скоростей объекта, например разбросом доплеровских сдвигов частоты с полосой 10 МГц, как в рассматриваемом примере на фиг.4, с исходной дискретностью в 100 кГц, которая может изменяться в процессе уточнения этого параметра за несколько последовательных циклов измерения. Диапазон вариации параметра ε0 определяется предварительными сведениями разведданных для лоцируемого объекта (в частности, его высоты полета над поверхностью моря) и размерностью фотоприемной матрицы по ее столбцам.
Отметим, что по мере получения данных о параметрах v и ε0 диапазоны вариации этих параметров могут существенно сокращаться, что позволит решать локационную задачу за меньшее время, например в пределах одного цикла, следующего за рассматриваемым циклом. Такая возможность связана с тем, что изменение во времени этих параметров сравнительно незначительно за время одного цикла, находится за пределами инструментальной погрешности измерения величин v и ε0.
Решение локационной задачи в заявляемом техническом решении может быть существенно упрощено при соблюдении условия, что оптическая ось приемопередающего объектива локатора и линия наклонной дальности АВ на объект локации (см. фиг.6) лежат в одной плоскости, в вертикальной плоскости zOx, так что φ0=0. Это условие практически всегда выполняется, иначе от объекта не образовывались бы блики, и задача автоматического сопровождения движущегося объекта по азимуту как раз и сводится к обеспечению равенства φ0=0. При этом, как видно из фиг.6, реперная точка А локатора и точка В, определяемая координатами объекта, лежат в вертикальной плоскости. В точке С располагается на поверхности моря i-й блик, видимый локатором с азимутом φi и углом места εi с высоты ОА=h0. Этот блик расположен на расстоянии OG=h0 cos φi/tg εi вдоль оси х и на расстоянии CG=h0 sin φi/tg εi вдоль оси y. Треугольник ABC образован линией наклонной дальности на объект АВ=d и двумя линиями-направлениями с локатора на блик AC=(h0 2+CG2+OG2)1/2=h0/sin εi и от блика на объект ВС, длина которой пока не известна. Однако известно, что угол при вершине В этого треугольника ABC равен Θi и определяется из (9). Поскольку треугольник BCG перпендикулярен к вертикальной плоскости zOx, поскольку CG⊥OD и CG лежит в плоскости треугольника, то из известного соотношения cos Θi=cos χi*cos ψi можно найти из (9) значение угла ψi согласно соотношению cos ψi=cos Θi/cos χi=λ ΔυДОПi/2v cos χi, причем значение угла χi находится из рассмотрения треугольника ABG. Отметим, что по построению ОЕ=ОС=h0/tg εi и отрезок EG=ОЕ-OG=tg εi/cos φi(1-cos φi)/tg εi. Отмечаем, что tg γi=h0tg εi/h0cos φi=tg εi/cos φi и γi=εI-σi=arctg(tg εi/cos φi). Из треугольника BDG выражаем угол при его вершине G через пока неизвестную высоту Н=BD=h0+d sin ε0 так: tg(∟BGD)=Н/(OD-OG)=(h0+d sin ε0)/(d cos ε0-h0 cos φi/tg εi), откуда для углов γi и ∟BGD получаем равенства:
γi=arctg(tg εi/cos φi),
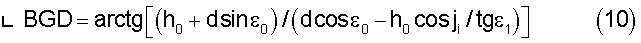
При этом угол ∟AGB при вершине G в треугольнике ABG равен
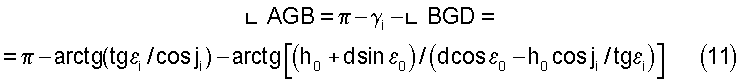
Угол при вершине А треугольника ABG, как очевидно, равен
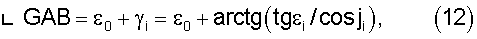
откуда находим значение искомого угла при вершине В в треугольнике ABG:
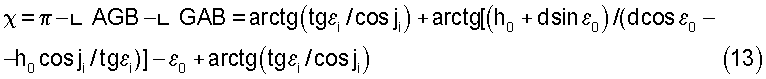
С учетом указанного ранее соотношения cos ψi=λΔυДОПi/2v cosχi из (13) находим значение угла ψi и длину стороны ВС в треугольнике BCG, которая равна
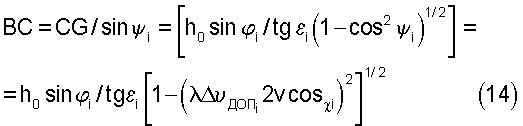
Из рассмотрения прямоугольного треугольника BCD находим значение угла ηi при вершине С по определению sin ηi=Н/ВС=(h0+d sin ε0)tg εi[1-(λ ΔυДОПi/2v cos χi)2)1/2/h0 sin φi=[1+(d/h0)sin ε0]tg εi[1-(λ ΔυДОПi/2v cos χi)2)]1/2/sin φi.
При подстановке в это выражение для sin ηi значений углов χi из выражения (13) найдем углы ηi относительно вертикалей, восстановленных из точек дислокации морских бликов, которые образуют группу m указанных ранее конических поверхностей, пересечение которых реконструирует точку в пространстве, в которой находится дифракционно ограниченный (точечный) объект локации. В это уравнение входят три неизвестные величины - ε0, V и d, из которых первые две находятся путем их последовательной итерации в заданных диапазонах, а третью ищут при совместном решении системы независимых уравнений с их числом не менее трех (m≥3). В результате получаем m значений наклонной дальности di, для которых модуль разности любой пары этих значений должен иметь минимальную возможную величину. Среднее значение наклонной дальности при этом равно
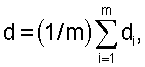
а дисперсия
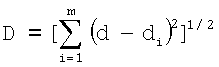
минимальна при правильном выборе варьируемых неизвестных ε0 и v.
Возможно и иное решение локационной задачи, не связанное с вычислением углов ηi и использованием методики пересекающихся конических поверхностей. Это решение, основанное на так называемом методе пересекающихся окружностей, геометрически представлено на фиг.7а и 7б. Считается, что в режиме автосопровождения лоцируемого объекта по азимуту с учетом узконаправленного зондирующего излучения в плоскости азимутов, когда возникают морские блики от рассеяния объектом лазерного облучения, реперная точка А локатора и точка В расположения объекта, то есть линия наклонной дальности АВ, лежат в вертикальной плоскости xOz. Через эти точки А и В, как известно, можно провести бесчисленное количество окружностей, а через три точки - только одну единственную. При этом различное пространственное положение этих третьих точек (C1 и C2) приводит к неколлинеарности плоскостей, в которых лежат эти окружности, а линия пересечения указанных плоскостей соответствует линии наклонной дальности на объект. Координаты точек А и C1 (А и C2) известны, а координаты точки В априори не известны и подлежат расчету. Нетрудно понять, что точка В соответствует точке пересечения окружностей, проведенных через три точки, - первая через А, В и C1, а вторая - через А, В и C2. Однако для определения координат центров этих окружностей O1 и О2, лежащих в плоскостях соответствующих треугольников ABC1 и ABC2, а также величин их радиусов r1 и r2, необходимо и достаточно определить углы Θ1 и Θ2 при вершинах В указанных треугольников, опирающиеся на хорды AC1 и АС2. Измерение этих углов, соответствующих углам между направлениями рассеяния объектом лазерного излучения на соответствующие блики морской поверхности и направлением зондирования, совпадающим с линией наклонной дальности АВ, производится на основе измерения доплеровского сдвига частоты ΔυДОП i в излучениях, принятых локатором от двух бликов.
Рассмотрим задачу определения координат центра окружности O1 (фиг.7а) и ее радиуса r1. Координаты х, y, z точек А, В и C1 следующие: А (0, 0, h0); В (х, 0, h0+x tg ε0); C1 (h0cos φ1/tg ε1, h0sin φ1/tg ε1, 0). При этом х и ε0 - априори неизвестные величины. Длина хорды AC1 равна AC1=h0/sin ε1. Центр окружности О1 лежит на перпендикуляре, проведенном из центра отрезка AC1. При известном угле Θ1 при вершине треугольника ABC1 и при условии, что точка В лежит на данной окружности, длина перпендикуляра h1 * от середины хорды AC1 - от точки F1 с координатами F1(h0cos φ1/2 tg ε1, h0sin φ1/2 tg ε1, h0/2) - равна h1 *=r1 cos Θ1, где величина радиуса окружности равна r1=h0/2 sin ε1sin Θ1.
Для соответствующей окружности на фиг.7б получаем h2 *=r2cosΘ2 и радиус r2=h0/2sin ε2sin Θ2. Пересечение этих двух окружностей происходит в точке В, координаты которой х и z вычисляются как функции х=f(h0, ε0, ε1, φ1, v) и z=g (h0, ε0, ε1, φ1, v) при вариации параметров ε0 и v, при правильном выборе которых и при числе действующих бликов m>2 расстояния между точками пересечения m окружностей вблизи точки В минимально. В последнем случае решается система m независимых уравнений при последовательно варьируемых параметрах ε0 и v, в результате чего находятся значения хi с минимальным разбросом их длин.
Данная методика интересна тем, что позволяет весьма существенно сократить диапазоны вариации параметров ε0 и v, если число действующих бликов m>2. Действительно, координаты объекта - точки В: х=f(h0, ε0, ε1, φi, v), y=0 и z=g(h0, ε0, εi, φi, v) могут быть определены решением системы из трех независимых уравнений (для m=3) без применения операции итерационного поиска параметров ε0 и v. Таким образом получают данные об этих параметрах, что и позволяет сократить диапазон итераций в последующих измерениях, одновременно уменьшая дискрет итераций, с целью увеличения точности измерения координат объекта.
Автоматическое сопровождение приемопередающего объектива локатора по азимуту обеспечивает совмещение оптической оси объектива с направлением визирования объекта локации, то есть с линией наклонной дальности АВ (фиг.6 и 7). При этом обеспечивается равенство φ0=0 (угол φ0 указывает лишь на рассогласование в азимутальной плоскости оптической оси объектива относительно оси визирования объекта, но не значение азимута на объект, отсчитываемого относительно направления на север). Вариация в малых пределах угла φ0 используется в локаторе для осуществления автоматического сопровождения объекта по азимуту по критерию максимума мощности принимаемых оптических сигналов от бликов морской поверхности. Поэтому в алгоритм решения локационной задачи не входит проведение итерации по азимуту φ0.
Рассмотрим пример построения локационной системы.
При образовании фотоприемной матрицы размерностью 181×181 элементов КРТ с диаметром элемента 0,1 мм минимальный размер матрицы составляет 18,1×18,1 мм2, а углы зрения в азимутальной Δφ и угломестной Δε плоскостях равны Δφ=Δε=0,05 рад при фокусном расстоянии приемного объектива Fпр=360 мм. При высоте реперной точки h0=30 м и при минимальной дальности наблюдения морской поверхности Lmin=500 м (т.е. при εmax=arctg(h0/Lmin)=0,06 рад) получаем εmin=εmax-Δε=0,01 рад, и максимальная дальность видения морской поверхности равна Lmax=h0/εmin=3000 м, то есть длина участка расположения видимых локатором морских бликов равна 2500 м. Ширина этого участка растет линейно по его длине от smin=Lmin*Δφ=500*0,05=25 м до smax=Lmax*Δφ=3000*0,05=150 м - в конце зоны видения на морской поверхности. Если приемный объектив локатора выполнить как трансфокатор, то можно в широких пределах варьировать длину рабочей зоны, в которой наблюдаются морские блики, а также ее положение по длине при изменении положения оптической оси приемного объектива. Так, при фокусном расстоянии Fпр=120 мм получим Δφ=Δε=0,15 рад и длину зоны видимых локатором бликов можно установить в диапазоне L=0,2…9 км с шириной зоны s=30 м … 1,35 км. Важно также отметить, что веерообразная диаграмма излучения передающим объективом локатора может быть меньше ширины обзора по углу места в приемном объективе, поскольку излучение нет необходимости направлять в сторону морской поверхности, однако оптические оси приемного и передающего объективов локатора всегда должны находиться в одной плоскости. Наконец, конфигурация расположения фоточувствительных элементов в матрице может отличаться от прямоугольной. Например, она может быть трапецеидальной, что позволит расширить зону наблюдения морской поверхности в ближней зоне, сузив ее в дальней, то есть сделать эту зону равновеликой по ширине на всей длине обзора.
Если полагать, что углы Θi находятся в диапазоне Θi≤π/3, то при работе по объектам-невидимкам, движущимся со скоростью 300 м/с на высотах 30-50 м над уровнем моря, диапазон изменения доплеровских сдвигов частоты для излучения газового СО2-лазера (λ=10,6 мкм) будет равен 8,4 МГц, то есть не превосходит указанной на фиг.4в величины ΔFΣ=10 МГц.
Всего в матрице использовано 1812=32400 элементов, что позволяет построить трехмерную группу со стороной куба в 32 элемента, что соответствует 128 каналам обработки информации на ДЛЗ. Последняя может иметь полосу частот ΔF=40 МГц и длительность импульсной характеристики τдз=50 мкс (база ДЛЗ равна В=2000), что позволяет повысить отношение сигнал/шум на входе решающего устройства в В1/2=45 раз, что компенсирует ухудшение этого отношения в 321/2=5,7 раза за счет увеличения мощности шума подключением к выходным шинам сборок 7-10 (фиг.2) тридцати двух выходов усилителей 13. «Сжатые» импульсы на выходах ДЛЗ имеют длительность tимп=25 нс, длительность цикла измерений целесообразно выбрать равной 100 мкс. При скорости лоцируемого объекта-невидимки v=300 м/с за время цикла объект проходит путь всего 3 см, что позволяет считать, что блики устойчивы в течение всего цикла. Тактовую частоту в ГВМ 29 выбирают не ниже 80 МГц, при этом коды временного положения импульса-отклика ДЛЗ должны быть 13-разрядные (младшие разряды в ДСР 31, 32, 33, … 34). Временная задержка в элементе 35 (порядка 1 мкс) обеспечивает сброс кодов в ЗМ 24, 25, 26, … 27 после того, как в начале нового цикла записанные в них данные будут переписаны в младшие разряды ДСР 31, 32, 33, … 34.
Для практического использования заявляемого способа в лазерной локации низколетящих воздушных объектов-невидимок необходимо исследовать статистику бликовых переотражений на море (в океане) в различных погодных условиях, энергетику этих оптических сигналов, преимущественные зоны на морской поверхности для приема бликовых переотражений при задании определенного класса объектов-невидимок. Кроме того, следует разработать соответствующую быстродействующую вычислительную среду для многоканальной обработки кодированных сигналов и разработать фотоприемную матрицу, например, с элементами КРТ, с низким уровнем шума и высокой плотностью размещения фотоприемных элементов в ней. В качестве лазера следует использовать мощные газовые одночастотные приборы с высокой кратковременной частотной стабильностью излучения. Также следует рекомендовать разработку многоканальных дисперсионных линий задержки в интегральном исполнении с большой базой, что позволит скомпенсировать влияние шума при параллельном включении на одну шину двумерной или трехмерной группы нескольких фотоприемных элементов матрицы. Представляет интерес разработка приемопередающего объектива локатора с трансфокацией приемного объектива и веерообразной диаграммой излучения-приема с соответствующими точными приводами управления угловым положением объективов.
Соответствующее проведение НИОКР по рассматриваемой локационной системе может быть проведено на предприятиях Министерства промышленности, связанных с разработкой оптико-электронных приборов в интересах тактических задач ВМФ России.
Литература
1. О.Ф.Меньших, Лазерный доплеровский локатор. Патент РФ №1829641.
2. О.Ф.Меньших, Обнаружитель лазерного доплеровского локатора. Патент РФ №1829640.
3. О.Ф.Меньших, Согласованный фильтр, Патент РФ №2016493.
4. О.Ф.Меньших, Устройство для анализа спектра сигналов. Патент РФ №2040798.
5. О.Ф.Меньших, Способ локации. Патент РФ №2296390.
6. Лазерная локация. Под ред. Н.Д.Устинова. - М.: Машиностроение, 1984.
7. В.В.Протопопов, Н.Д.Устинов, Инфракрасные лазерные локационные системы, М.: Воениздат, 1987.
8. Измерение спектро-частотных и корреляционных параметров и характеристик лазерного излучения. Под ред. А.Ф.Котова и Б.М.Степанова. - М.: Радио и связь, 1982.
9. Ч.Кук, М.Бернфельд, Радиолокационные сигналы, пер. с англ., под ред. В.С.Кильзона. - М.: Сов. радио, 1971.
10. Фильтры на поверхностных акустических волнах. Под ред. Г.Мэттьюза. - М.: Сов. радио, 1981, 472 с.
11. В.И.Тверской, Дисперсионно-временные методы измерения спектров радиосигналов. - М.: Сов. радио, 1974, 240 с.
12. А.А.Джек, П.М.Грант, Дж.Х.Коллинз, Те0рия проектирования и применение Фурье-процессоров на поверхностных акустических волнах, ТИИЭИР, 1980, №4, р.22-43.
13. Фильтры на поверхностных акустических волнах, технология и применение, пер. с англ. Г.Б.Звороно. Под ред. В.Б.Акпамбетова. - М.: Радио и связь, 1981.
14. Я.Д.Ширман, В.Н.Манжос, Теория и техника обработки радиолокационной информации на фоне помех. - М.: Радио и связь, 1981.
15. Ю.С.Лезин, Оптимальные фильтры и накопители импульсных сигналов. - М.: Сов. радио, 1969.
16. Б.Р.Левин, Те0ретические основы статистической радиотехники. - М.: Сов. радио, 1974, кн.1 и 2.
17. В.И.Тихонов, Оптимальный прием сигналов. - М.: Радио и связь, 1983, 320 с.
Изобретение относится к области измерительной техники и приборостроения и может быть использовано в лазерной доплеровской локации низколетящих над водными бассейнами объектов-невидимок. Техническим результатом изобретения является упрощение реализующего заявленный способ устройства, в частности конструкции блока обработки информации с дисперсионными линиями задержки (ДЛЗ), а также обеспечение возможности локации объектов-невидимок, когда отсутствует прием излучения непосредственно от объекта локации в направлении его зондирования. Способ обработки информации в лазерном когерентном локаторе с матричным фотоприемником основан на приеме лазерного излучения от бликов морской поверхности, возникающих при рассеянии зондирующего излучения объектом-невидимкой. По измерению углов прихода излучения от бликов морской поверхности фоточувствительной приемной матрицей и по измеренным значениям доплеровских сдвигов частоты в многоканальном блоке оптимальной фильтрации на основе гетеродинных методов приема с применением многоканальных дисперсионных линий задержки методами статистического усреднения реконструируется текущее местоположение объекта локации и его вектор скорости. Сокращение количества оборудования блока обработки информации достигается путем формирования двумерной или трехмерной группы из элементов матричного фотоприемника, подключаемой к каналам обработки информации. В канале обработки сигнал преобразуется в линейно-частотно-модулированный эквивалент с последующим его усилением, спектровременным «сжатием» в дисперсионной линии задержки, детектированием и пороговым ограничением по минимуму с заданным порогом ограничения, что позволяет преобразовать сигнал с доплеровским смещением частоты в короткий импульс, временное положение которого относительно строб-импульса начала цикла измерений однозначно характеризует величину указанного доплеровского смещения частоты. Это временное положение импульса кодируется в цифровом коде и запоминается в соответствующем буферном запоминающем устройстве, в коде которого содержится также код номера цикла измерений и код номера канала, по которому проводилась указанная обработка сигнала с элемента матрицы фотоприемника. По совокупности таких кодовых записей в данном цикле измерения получают информацию о доплеровских сдвигах частоты в сигналах соответствующих элементов матрицы и их местоположений в ней, что однозначно определяет азимуты и углы места на блики морской поверхности, видимые локатором в данном цикле измерения относительно оптической оси приемно-передающего объектива локатора, а также углы рассеяния зондирующего излучения объектом-невидимкой, создающим указанные блики. При выполнении условия обнаружения объекта локации и его автосопровождения по азимуту, при котором линия наклонной дальности и оптическая ось приемно-передающего объектива локатора лежат в одной плоскости, местоопределение объекта локации и измерение его радиальной скорости находят вычислением минимально по двум разным бликовым излучениям в данном цикле измерения на основе метода пересекающихся окружностей. При этом диаграмма излучения локатора является веерообразной - широкой по углу места и предельно узкой по азимуту. 6 з.п. ф-лы, 8 ил.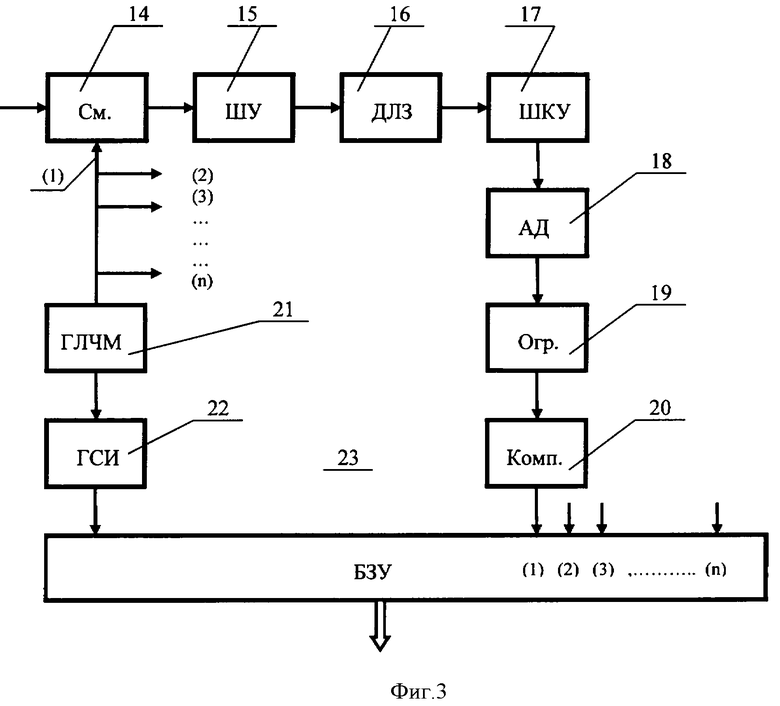
1. Способ обработки информации в лазерном когерентном локаторе с матричным фотоприемником, основанный на измерении доплеровских сдвигов частоты ΔυДОП i в излучениях от морских бликов и угловых координат последних - азимутов φi и углов места εi, вычислении координат объекта локации и его скорости с последующим статистическим усреднением вычисляемых параметров за несколько смежных циклов измерений, отличающийся тем, что в NЭ=рkp элементах матричного фотоприемника образуют по два независимых выхода, которые формируют в двумерную (р=2) или трехмерную (р=3) группы, где k=1, 2, 3, … - целые числа, с n=2pk(p-1) выходными шинами в группах, к каждой из выходных шин группы параллельно подключают по г=pk соответствующих выходов строчных или столбцовых элементов матричного фотоприемника, а вычисление координат объекта локации по данным измеренных доплеровских сдвигов частоты ΔυДОП i с соответствующими им измеренными угловыми координатами - азимутом φi, и углом места εi на соответствующие αi блики морской поверхности, видимые локатором в данном цикле измерения, где i=1, 2, 3, … m - число действующих бликовых излучений, осуществляют путем последовательной итерации неизвестных параметров - радиальной скорости V объекта локации в априорно ожидаемом интервале ее допустимого изменения и угла места εо линии наклонной дальности на объект локации, для чего в процессе указанного итеративного подбора этих параметров выбирают такие их значения v и εо, при которых минимизируются разности между любыми парами величин, определяющих наклонную дальность до объекта локации.
2. Способ по п.1, отличающийся тем, что возникшую неопределенность выбора 2(р-1) выходных шин, соответствующих одному и тому же доплеровскому сдвигу частоты ΔυДОП i в сигнале на выходах элемента αjk матричного фотоприемника, по положению которого в матрице судят об азимуте φi, и угле места εi, на видимый морской блик αi, устраняют путем сравнения кодов, отображающих доплеровские сдвиги частоты, по их 2(р-1)-кратному совпадению для всех m морских бликов с заданной минимальной погрешностью.
3. Способ по п.1, отличающийся тем, что вычисление измеряемых параметров объекта локации при большом объеме вычислительных операций, связанном с процессом итерации при поиске значений v и εo, удовлетворяющих указанному условию, производят во временном интервале, превышающем заданный цикл измерения, а затем относят полученные результаты к моменту времени исходного цикла измерений.
4. Способ по п.1, отличающийся тем, что уменьшения объема вычислительных операций при итерационном поиске значений v и εо в каждом последующем цикле измерений достигают путем сокращения интервала их итерационного поиска с учетом данных об этих значениях из предыдущих циклов измерений и с учетом статистического усреднения каждого из этих значений за несколько последовательных циклов измерений в предположении, что найденные значения v и εо являются медленно изменяющимися функциями времени в сравнении с заданным темпом следования циклов измерения.
5. Способ по п.1, отличающийся тем, что уточнение координат лоцируемого объекта осуществляют при проведении итерационного поиска значений v и εо совместным решением системы m уравнений хi=f(ho, εо, φi, εi, v) для всех видимых локатором m морских бликов, то есть для i=1, 2, 3, … m, где угол рассеяния объектом зондирующего излучения относительно направления последнего равен
Θi=arccos(ΔυДОП i·λ/2v), λ - длина волны лазерного излучения, hv - известная высота над уровнем моря центральной точки приемного объектива локатора, так что координату х рассчитывают по формуле 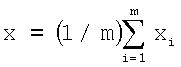 и при этом минимизируется абсолютная величина разности любых двух значений хi с разными индексами i из их числа m.
и при этом минимизируется абсолютная величина разности любых двух значений хi с разными индексами i из их числа m.
6. Способ по п.1, отличающийся тем, что обнаружение объекта локации и его автосопровождение осуществляют сканированием зондирующего излучения по азимуту, а диаграмму излучения выбирают веерообразной - предельно узкой по азимуту и широкой по углу места.
7. Способ по п.1, отличающийся тем, что при выполнении условия обнаружения объекта локации и его автосопровождения по азимуту, при котором линия наклонной дальности и оптическая ось приемно-передающего объектива локатора лежат в одной плоскости, местоопределение объекта локации и измерение его радиальной скорости находят вычислением минимально по двум разным бликовым излучениям (Min m=2) в данном цикле измерения.
| СПОСОБ ЛОКАЦИИ | 2005 |
|
RU2296350C1 |
| СПОСОБ НАВЕДЕНИЯ ИЗЛУЧЕНИЯ НА ДВИЖУЩИЙСЯ ОБЪЕКТ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1997 |
|
RU2125279C1 |
| Способ формирования радиолокационного изображения в реальном масштабе времени путем оптической корреляционной обработки сигналов и устройство для его осуществления | 1991 |
|
SU1801218A3 |
| Ротор трубогенератора | 1945 |
|
SU66539A1 |
Авторы
Даты
2009-05-10—Публикация
2007-10-29—Подача