Изобретение относится к электросвязи и вычислительной технике, в частности к области криптографической защиты электронных данных, передаваемых по телекоммуникационным сетям и сетям ЭВМ, с использованием изогений эллиптических кривых, и может быть использовано в системах передачи данных. Используемые в данном описании специфические термины поясняются в Приложении 1.
Известны системы криптографической защиты - электронной цифровой подписи (ЭЦП) электронного документа на основе эллиптических кривых [ГОСТ Р 34.10-2001. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи. Госстандарт России, М., 2001]; [ANSI X9.62. Public Key Cryptography for the Financial Services Industry, The Elliptic Curve Digital Signature Algorithm (ECDSA), 2005, http://www.comms.scitech.susx.ac.uk/fft/crypto/ecdsa.pdf], предусматривающие процессы формирования и проверки ЭЦП. Указанные стандарты ЭЦП по сути являются вариантами схем ЭЦП Эль-Гамаля [ElGamal Т.A public-key cryptosystem and a signature scheme based on discrete logarithms // IEEE Transactions on Information Theory. 1985. Vol.IT-31. P.469-472.] и Шнорра [Schnorr C.P. Efficient identification and signatures for smart cards // Advances in Cryptology - CRYPTO ′89. Lecture Notes in Computer Science. Springer-Verlag. 1990. Vol.435. P.239-252.]. Известен также способ криптографической защиты данных, заключающийся в шифровании с открытым ключом на основе эллиптических кривых [Ростовцев А.Г., Маховенко Е.Б. Теоретическая криптография, СПб, НПО «Профессионал», 2005, доступно с http://progbook.net/seti/kriptograf/1568-teoreticheskava_kriptografiya.html].
Известен способ шифрования данных с использованием изогений эллиптических кривых [Джао, Венкатесан. Использование изогений для разработки криптосистем, патент RU №2376651, патент US №7499544]. Здесь изогении рассматриваются как отображения точек одной эллиптической кривой в точки другой эллиптической кривой.
Безопасность указанных технических решений основана на сложности решения задачи дискретного логарифма на эллиптической кривой: для точек Р, Q эллиптической кривой найти целое число l такое, что P=lQ. Известно, что квантовый компьютер достаточно большой разрядности (примерно 3000 кубитов) может эффективно решать такие задачи [http://en.wikipedia.org/wiki/Elliptic_curve_cryptography]. Поэтому известные способы не обеспечивают безопасность по отношению к квантовым атакам.
Другие известные криптосистемы с открытым ключом (RSA, криптосистема на группе классов квадратичного порядка, криптосистемы на гиперэллиптических кривых [A. Menezes, P. Van Oorchot, S. Vanstone. Handbook of applied cryptography, CRC press, 1996]) также уязвимы к квантовым атакам [Ростовцев А.Г., Маховенко Е.Б. Теоретическая криптография, СПб, НПО «Профессионал», 2005]. Такие криптосистемы также уязвимы к квантовым атакам, например, для разложения составного числа может использоваться алгоритм Шора [Hughes R.J. Quantum computation. Technical report LA-UR-98-288, 1998].
Канадская фирма D-wave освоила производство квантовых компьютеров разрядности 128 кубитов [www.dwavesys.com/en/priducts-services.html] и работает над увеличением их разрядности. Таким образом, безопасность известных способов криптографической защиты информации находится под угрозой. Возникает необходимость в новых способах криптографической защиты данных, стойких по отношению к квантовым атакам.
В известных системах ЭЦП обрабатываемые данные представлены битовой строкой или набором битовых строк. Под битовой строкой (БС) понимается электромагнитный сигнал в цифровой двоичной форме, параметром которого является число битов и порядок следования нулевых и единичных значений. Битовые строки допускают операцию конкатенации, логические и арифметические операции. Криптографическая защита данных заключается в выполнении действий с БС (преобразованиях БС и выполнении операций с БС) и выполняется с помощью вычислительных устройств, например персональных компьютеров или смарт-карт [доступно с http://www.aloaha.com/press_en/elliptic-curves-and-sha-256-support.php].
Эллиптическая кривая над конечным полем из p элементов, где p - простое число, состоит из точек, заданных уравнением y2=x3+Ax+B (mod p) и точки P∞. Точки эллиптических кривых допускают операцию сложения с нулевым элементом P∞=(0, 1, 0). Полиномы деления fl(x) обращаются в 0 тогда и только тогда, когда x-координата точки порядка l является корнем этого полинома. Эллиптическая кривая характеризуется своим инвариантом j, дискриминантом Фробениуса Dc2 для целого c и соответствующим числом классов (см. Приложение 1), а также значением функции Вебера g, удовлетворяющей уравнению 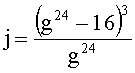
Изогения эллиптических кривых - отображение E1→E2, заданное рациональными функциями, сохраняющее неподвижным точку P∞ и переводящее сумму точек на E1 в сумму точек на E2, изогения характеризуется своей степенью (взаимно простой с p). Изогении соответствует отображение функций Вебера g(E1)→g(E2). Если изогения E1→E2 существует, то эллиптические кривые E1, E2 обладают одинаковыми дискриминантами Фробениуса.
Существуют целочисленные симметрические модулярные полиномы Фl(U, V), обращающиеся в 0, если переменные принимают значение j-инвариантов эллиптических кривых, между которыми существует изогения степени l [патент US №7623655, H04L 9/14]. Недостатком этих полиномов является большая длина коэффициентов и большое число слагаемых, что затрудняет их использование в системах защиты информации. Изогения простой нечетной степени l является изогений Элкиса, если дискриминант Фробениуса эллиптической кривой является квадратом по модулю l.
За прототип принят способ [патент RU №2376651, G09C 1/00] «Использование изогений для разработки криптосистем», дублирующий указанный выше патент US №7499544.
Существенные признаки прототипа.
Способ шифрования сообщений, содержащий: генерацию изогении, отображающей множество точек первой эллиптической кривой на вторую эллиптическую кривую, опубликование открытого ключа, соответствующего изогении, шифрование сообщения с использованием ключа, соответствующего изогении, и расшифрование зашифрованного сообщения при помощи ключа расшифрования, соответствующего изогении, при этом хотя бы один из ключей является секретным и является дуальной изогений к исходной изогении (п.1 формулы).
Способ расшифрования сообщений, содержащий опубликование открытого ключа, соответствующего изогении, отображающей множество точек первой эллиптической кривой на вторую эллиптическую кривую, и расшифрование зашифрованного сообщения при помощи ключа расшифрования, соответствующего изогении, при этом ключ расшифрования является дуальной изогений к упомянутой изогении (п.12 формулы).
Способ по п.1, дополнительно включающий формирование множества модулярных изогений без раскрытия промежуточных кривых, (п.9 формулы). При этом модулярная изогения определяется авторами на основе модулярной кривой X0(l).
Идентификационное шифрование (IBE) с использованием изогений, в котором открытым ключом является точка T∈E2 второй эллиптической кривой, а секретным ключом - точка 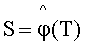
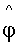
Прототип рассматривает изогению как отображение точек первой эллиптической кривой на вторую эллиптическую кривую. Здесь изогения используется для ускорения известных способов криптографической защиты данных - шифрования с открытым ключом на эллиптической кривой и вычисления спаривания Вейля/Тейта. Эти известные способы основаны на задаче вычисления дискретного логарифма на эллиптической кривой и поэтому уязвимы к квантовым атакам, следовательно, и прототип, как их ускоренная версия, не обеспечивает безопасность по отношению к квантовым атакам. Это обстоятельство является недостатком прототипа, который устраняется в заявленном способе.
Технической задачей заявляемого решения является разработка способа шифрования с открытым ключом, обеспечивающего защиту от квантовых атак.
Поставленная задача достигается тем, что обрабатываемые данные представлены функциями Вебера изогенных эллиптических кривых над конечным полем, а обработка данных заключается в отображении функций Вебера путем движения по циклам функций Вебера, при этом дискриминант Фробениуса эллиптической кривой равен произведению квадрата целого числа на число, сравнимое с 1 по модулю 8.
На фиг.1 представлен цикл функций Вебера для изогении степени l1 на фиг.2 представлен цикл функций Вебера для изогении другой степени l2.
В заявленном способе рассматривается отображение функций Вебера, которое определяется изогениями малых простых степеней l и целочисленными симметрическими полиномами Wl для функции Вебера, являющихся аналогами классических модулярных полиномов Фl для функции j. Объем памяти для хранения полинома Wl примерно в 1000 раз меньше, чем для хранения полинома Фl, за счет сокращения числа ненулевых коэффициентов и их длины. Время обработки информации с использованием полинома Фl, Wl пропорционально квадрату его длины. Поэтому скорость обработки данных с использованием функций Вебера в миллионы раз больше, чем при использовании классических модулярных полиномов.
Ниже перечислены существенные признаки предлагаемого способа.
1. Способ шифрования с защитой от квантовых атак на основе циклов функций Вебера, в котором сообщение зашифровывают с использованием открытого ключа и зашифрованное сообщение расшифровывают при помощи секретного ключа, содержащий первую эллиптическую кривую и вторую эллиптическую кривую с одинаковыми дискриминантами Фробениуса, соответствующими открытому ключу, и отображение первой эллиптической кривой во вторую эллиптическую кривую, соответствующее секретному ключу, отличающийся тем, что эллиптические кривые задают значениями функции Вебера, причем секретный ключ определяют как цепочку отображений функций Вебера, соответствующих изогениям Элкиса степеней l1, …, lk, заданную набором целых чисел N1, …, Nk, где Ni - число шагов по циклу функций Вебера для изогении степени, при этом очередное значение функции Вебера gi+1 определяют как корень симметрического полинома двух переменных при замене одной переменной на предыдущее значение функции Вебера gi, а при переходе к изогении очередной степени задают положительное направление на цикле, для этого находят полином, задающий ядро изогении, а шаги по циклу выполняют в направлении, соответствующем знаку числа Ni.
2. Способ по п.1, отличающийся тем, что дискриминант Фробениуса выбирают равным произведению квадрата целого числа на число, сравнимое с 1 по модулю 8.
3. Способ по п.1, отличающийся тем, что ядро изогении задают полиномом, для которого точки ядра лежат в расширении минимальной степени, и по его коэффициентам находят функцию Вебера, соответствующую положительному направлению.
Принципиальное различие между прототипом и заявленным способом заключается в следующем.
- Прототип уязвим к квантовым атакам, а для заявленного способа эффективные квантовые атаки не найдены.
- В прототипе шифруемые данные представлены координатами точки эллиптической кривой, что затрудняет шифрование произвольного текста, а в заявленном способе - произвольным ненулевым элементом.
- Безопасность прототипа основана на задаче дискретного логарифмирования на эллиптической кривой, для решения которой есть эффективный квантовый алгоритм, а безопасность заявленного способа основана на задаче вычисления изогении между эллиптическими кривыми, которая в настоящее время не может быть решена на квантовом компьютере.
Указанные существенные признаки данного способа позволяют строить криптосистемы с открытым ключом по аналогии с известной криптосистемой Диффи-Хеллмана и Эль-Гамаля (см. [A. Menezes, P. Van Oorchot, S. Vanstone. Handbook of applied cryptography, CRC press, 1996]). Ha сегодняшний день не созданы эффективные алгоритмы для обычного или квантового компьютера, нарушающие безопасность предлагаемой криптосистемы. Это позволяет говорить о том, что предлагаемый способ обеспечивает стойкость по отношению к квантовым атакам.
Основой заявленного способа является процедура вычисления цепочки из N≠0 отображений простой нечетной степени l функции Вебера для первоначальной эллиптической кривой E(Fp) (целое число N может быть положительным и отрицательным), которая выполняется следующим образом.
- Для эллиптической кривой E(Fp) вычисляют значение функции Вебера g0 по модулю p. Присваивают переменной g индекс i=0 и значение g.
- Для выбора положительного направления выполняют следующие действия.
- Определяют наименьшую степень расширения nl поля Fp, в котором лежит ядро изогении степени l кривой E(Fp) и наименьшую степень расширения ml, поля, в котором лежит ядро изогении скрученной кривой.
- Находят делители полинома деления fl(x), степень которых является делителем числа 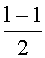
- По найденному ядру изогении вычисляют функцию Вебера g′ изогенной эллиптической кривой, задающую положительное направление.
- Если N=1, то результат: g′. Если N=-1, то выбирают тот из двух корней полинома Wl(U, g), который отличен от g′.
- Если N=±1, то находятся корни g0, g2 полинома Wl(U, g1) (mod p) и переменной g присваивается индекс 2 и значение g2.
- Если N=±2, то результат g2, иначе п.4 рекуррентно повторяется, при этом переменной g присваивается очередной индекс и вычисляется корень gi полинома Wl(U, gi-1) (mod p), пока не будет получено i=N. Результат: gN.
Если нужно вычислить цепочку отображений функций Вебера для изогений нескольких степеней l1, l2, …, lk, состоящую из Ni изогений li, то для каждой изогении выполняются указанные выше вычисления, причем в качестве начального значения g0 используется значение, найденное на предыдущем этапе.
Поскольку произведение изогений коммутативно и ассоциативно, то очередность их вычислений не влияет на результат. Например, если нужно вычислить цепочку отображений функций Вебера, заданную тремя изогениями степени l1 и двумя изогениями степени l2, то последовательности (l1, l1, l1, l2, l2), (l2, l1, l1, l2, l1), (l1, l2, l2, l1, l1) и т.п. дадут одинаковый результат.
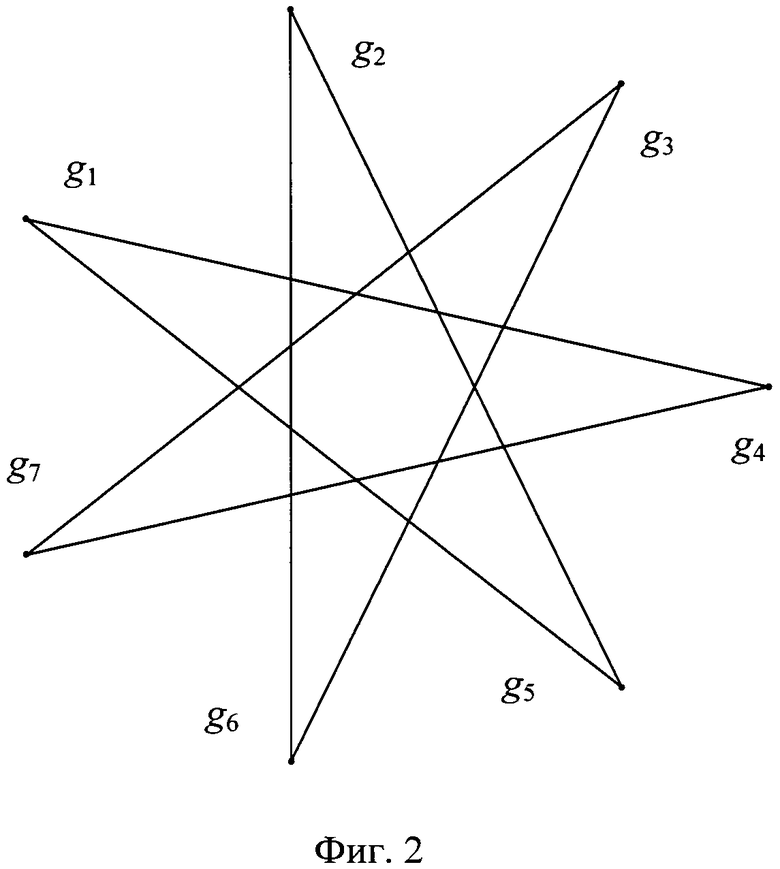
При использовании изогений степени l1 функции Вебера образуют цикл, длина которого является делителем числа классов, например для h=7 (см. фиг.1).
Зададим положительное направление g1→g2 по часовой стрелке, тогда отрицательное направление g1→g7 соответствует дуальной изогении.
При использовании изогении другой степени l2 функции Вебера тоже образуют цикл, но вершины соединяются в другом порядке (см. фиг.2).
Зададим положительное направление отображением g1→g4. Тогда один шаг изогении степени l2 соответствует трем шагам изогении степени l1, а один шаг изогении степени l1 - пяти шагам изогении степени l2. При совмещении циклов, задаваемых изогениями степенями l1 и l2, получаем звезду.
Таким образом, используемые циклы функций Вебера задают звезду. Если число классов очень велико (что имеет место в криптографии), то число вершин звезды оказывается необозримым. При этом длина шага на звезде для изогении одной степени по сравнению с другой степенью является трудновычислимой.
Ключевой обмен при использовании изогении строится по аналогии с системой Диффи-Хеллмана. Два пользователя A, B договариваются об использовании первоначальной эллиптической кривой E(Fp), для которой число классов дискриминанта Фробениуса велико. Кроме того, оба пользователя имеют библиотеку модулярных полиномов {W1, …, Wk} для функции Вебера, состоящую из полиномов Wl для простых нечетных l, по модулю которых дискриминант Фробениуса D является квадратом, библиотеку полиномов деления fl для тех же l для каждой из k изогении, при этом для изогении каждой степени определена степень полинома, задающего ядро. Если в разложении полинома деления есть несколько полиномов одинаковой степени, то положительное направление задается тем ядром, для которого y-координата лежит в поле минимальной степени расширения.
Для установления сеансового ключа пользователь А выбирает малые целые случайные числа {Nl, …, Nk} по числу модулярных полиномов своей библиотеки. В качестве первоначального значения пользователь А использует значение функции Вебера g0 исходной эллиптической кривой. Он вычисляет цепочку описанным выше способом и посылает результат gA пользователю B.
Пользователь B выбирает независимо случайные числа {M1, …, Mk}, вычисляет цепочку изогений для начального значения g0 и результат gB посылает пользователю A.
Пользователь A, используя в качестве начального значения gB, вычисляет цепочку изогений длин {N1, …, Nk}, эквивалентную цепочке {M1+N1, …, Mk+Nk} для начального значения g0 и получает результат gAB. Пользователь B, используя в качестве начального значения gA, вычисляет цепочку изогений длин {M1, …, Mk}, эквивалентную цепочке {N1+М1, …, Nk+Mk} для начального значения g0 и получает тот же результат gAB. Оба пользователя используют найденное значение gAB в качестве сеансового ключа.
Шифрование с открытым ключом выполняется следующим образом. Открытым ключом являются эллиптическая кривая E(Fp) со значением функции Вебера g0, набор изогений {l1, …, lk}, значение функции Вебера 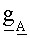
Для зашифрования текста m с помощью открытого ключа отправитель генерирует случайную цепочку длин изогений {M1, …, Mk}, вычисляет цепочку этих изогений для начального значения g0, получает значение gB, вычисляет цепочку этих же изогений для начального значения gA, получает результат gAB, вычисляет значение s≡m*gAB (mod p). Зашифрованным текстом является пара (gB, s).
Для расшифрования зашифрованного текста владелец секретного ключа вычисляет цепочку изогений степеней {N1, …, Nk} для начального значения gB и получает gAB. Затем он вычисляет m≡s*gAB -1 (mod p).
Заявленный способ позволяет выполнять аутентификацию сообщений по схеме без диалоговых доказательств с нулевым разглашением знаний.
Для вычисления коэффициентов изогенного образа эллиптической кривой можно использовать многочисленные известные алгоритмы разложения на множители. Например, произведение линейных делителей полинома F(U) равно наибольшему общему делителю полиномов: GCD(F(U), Up-U) и быстро вычисляется алгоритмом Евклида [A. Menezes, P. Van Oorchot, S. Vanstone. Handbook of applied cryptography, CRC press, 1996].
Полиномы деления fl(x) и модулярные полиномы Wl(U, V) для функций Вебера вычислимы, например, [math.mit.edu/~drew/WeberModPolys.htm]. Так, модулярные полиномы Wl для изогений степени l=5, 7, 11, 13, 17, 29 имеют вид:
W5=U6+V6-U5V5+4UV;
W7=U8+V8-U7V7+7U4V4-8UV;
W11=U12+V12-U11V11+11U9V9-44U7V7+88U5V5-88U3V3+32UV;
W13=U14+V14-U13V13+13U12V2+13U2V12+52U10V4+52U4V10+78U8V6+78U6V8+64UV;
W17=U18+V18-U17V17+17U16V10+17U10V16-34U15V3-34U3V15+34U13V13+119U12V6+119U6V12+340U9V9+272U8V2+272U2V8+544U5V5-256UV;
W29=U30+V30-U29V29+29U29V5+29U5V29+261U28V10+261U10V28+783U27V15+783U15V27+667U27V20+667U20V27-116U25V-116UV2+203U25V25+5365U24V6+5365U6V24-5713U22V16-5713U16V22-1334U21V21+4716U20V2+4716U2V20+37642U18V12+37642U12V18+12470U17V17-50112U15V3-50112U3V15-91408U14V8-91408U8V14-49880U13V13+170752U10V4+170752U4V10+85376U9V9-207872U5V5+16384UV
Направление на цикле изогении задается следующим упрощением формул Велу. Пусть исходная эллиптическая кривая задана уравнением y2=x3+Ax+B, а ее образ для изогении степени l задан уравнением y2=x3+A1x+B1. x-координаты точек ядра изогении степени l - задаются делителем степени 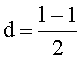
hl(x)=xd+c1xd-1+c2xd-2+ c3xd-3+…+cd
Коэффициенты A1, B1 изогенного образа эллиптической кривой равны:
A1≡-A(10d-1)-30(c1 2+2c2) (mod p);
B1≡-B(28d-1)+70(с1 3+3c1c2+3c3)+42Ac1 (mod p).
Положительное направление на цикле изогении можно задавать иначе, например, выбором одного из двух возможных значений отображения Фробениуса для заданного ядра изогении [Elkies N. Elliptic and modular curves over finite fields and related computational issues. Computational Perspectives on Number Theory: Proceedings of a Conference in Honor of A.O.L. Atkin (D.A. Buell and J.T. Teitelbaum, eds.; AMS/International Press, 1998), p.21-76]. Эти значения одинаковы для всех изогенных эллиптических кривых и могут быть определены заранее (входить в состав программного обеспечения, реализующего криптосистему).
Для практических приложений число классов h должно быть достаточно большим, чтобы перебор всех изогенных эллиптических кривых был невозможен, например h>2256. Для этого числа p, D должны иметь длину примерно 500-550 бит.
Число используемых изогении k и максимальная длина Nmax изогений каждой длины оценивается из условия, что почти каждое значение функции Вебера из h возможных значений можно получить, меняя длины цепочек. Если число используемых степеней изогении k=1, то Nmax=h/2, если k=2, то 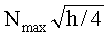
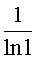
Рассмотрим примеры реализации заявленного способа для небольших чисел p.
Пример 1. Циклы функций Вебера. Исходная эллиптическая кривая задана уравнением y2=x3+x+3 (mod 971) и имеет параметры D=-2588, j=42,число классов h=23, функция Вебера равна g=466.
Дискриминант D является ненулевым квадратом по модулю l=7, 13, 17. Используем полиномы W7, W13, W17.
Для изогении степени 7 модулярный полином W7(U, g) имеет два корня по модулю p: 92 и 881. Подставляем значение 881, полином W7(U, 881) имеет два корня: 466, соответствующий предыдущему значению, и 701 - новый элемент цикла. Продолжаем эту процедуру далее и получаем цикл функций Вебера степени 7 длины h для направления, заданного корнем 881: (466, 881, 701, 120, 300, 397, 952, 108, 697, 140, 411, 839, 812, 903, 171, 374, 639, 963, 459, 613, 545, 71, 92).
Для изогении степени 13 модулярный полином W13(U, g) имеет два корня по модулю p: 300 и 613. Строим цикл функций Вебера длины h для направления, заданного корнем 613. Получаем цикл (466, 613, 374, 839, 108, 120, 92, 459, 171, 411, 952, 701, 71, 963, 903, 140, 397, 881, 545, 639, 812, 697, 300).
Для изогении степени 17 модулярный полином W17(U, g) имеет два корня по модулю p: 545 и 120. Строим цикл изогений степени 17 длины h для направления, заданного корнем 545. Получаем (466, 545, 963, 171, 839, 697, 397, 701, 92, 613, 639, 903, 411, 108, 300, 881, 71, 459, 374, 812, 140, 952, 120).
Пример 2. Определение положительного направления на цикле изогений. Исходная эллиптическая кривая задана уравнением y2=x3+x+1 (mod 1187), имеет значение следа T=-12, дискриминант отображения Фробениуса Dπ=4D где D=-1151, значение функции Вебера g0=123. Дискриминант D является квадратом по модулю простых чисел l1=5, l2=7, l3=11, l4=29. Эти простые числа задают степени используемых изогений.
Уравнение отображения Фробениуса π2-Tπ+p=0 имеет корни 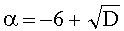
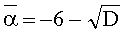
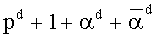
Задаем положительное направление на цикле изогении. Для изогении степени 5 модулярный полином W5(U, g0) имеет два корня: 487 и 486. Находим h2(x)=GCD(xp-x,f5(x))=645+74x+x2 (это произведение двух линейных полиномов), отсюда A1=223, B1=348, функция Вебера имеет два противоположных значения 487 и 700, первое из них совпадает с одним из корней полинома W5(U, g0). Положительное направление на цикле изогений для изогении степени 5 задается значением g=487, а отрицательное направление - другим корнем полинома W5(U, g0): g=486.
Для изогении степени 7 полином W7(U, g0) имеет два корня: 529 и 576. Для задания положительного направления находим h3(x)=GCD(xp-x,f5(x))=63+374x+1121x2+x3 (это произведение трех линейных полиномов), отсюда A1=935, B1=568, функция Вебера имеет два противоположных значения 576 и 611, первое из них совпадает с одним из корней полинома Вебера. Положительное направление на цикле изогении для изогении степени 5 задается значением g=576, а отрицательное направление - другим корнем полинома Вебера g=529.
Для изогении степени 11 полином W11(U, g0) имеет два корня: 227 и 84. Полином деления f11(x) имеет два неприводимых делителя степени 5, найденные как 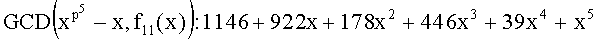
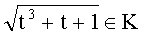
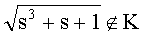
Для изогении степени 29 полином W29(U, g0) имеет два корня: 314 и 165. Для задания положительного направления находим делитель степени 14 полинома f29(x):h14(x)=668+657x+1140x2+256x3+131x4+841x5+483x6+484x7+667x8+987x9+48x10+743x11+978x12+1079x13+x14 (это произведение двух неприводимых полиномов степени 7), отсюда A1=623, B1=1128, функция Вебера имеет два противоположных значения 165 и 1022, первое из них совпадает с одним из корней полинома Вебера.
Объяснение терминов, используемых в описании и формуле изобретения.
Запись a≡b (mod p) означает, что a-b делится на p.
Конечное поле Fp из p элементов, где число p - простое множество {0, 1, …, p-1}. Сложение и умножение в конечном поле выполняются по модулю p и обозначается a+b (mod p), ab (mod p) (см. [Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра. - М.: Гелиос-АРВ, 2003]), например, 3+4≡0 (mod 7), 3·4≡5 (mod 7). Для любого ненулевого элемента a существует обратный элемент a-1 такой, что aa-1=1. Элемент a-1 может быть найден расширенным алгоритмом Евклида. Конечное поле Fp допускает конечные расширения, получаемые присоединением корней неприводимых полиномов. Степень расширения равна степени неприводимого полинома, корень которого присоединяется. Если t - корень неприводимого полинома f степени d, то остальные корни равны tp(mod f(t)), 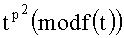
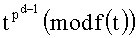
Проективная плоскость - множество точек, представленных ненулевыми тройками (X, Y, Z), X, Y, Z∈Fp, с учетом эквивалентности (X, Y, Z)=(cX, cY, cZ) для любого c≠0. Множество точек проективной плоскости вида (X, Y, 0) определяет бесконечно удаленную прямую. Остальные точки проективной плоскости с учетом эквивалентности однозначно представимы в виде пар (x, y)=(x, y, 1), где x=XZ-1, y=YZ-1.
Поскольку хотя бы одна из координат любой точки проективной плоскости отлична от 0, эта точка эквивалентна точке, у которой соответствующая ненулевая координата равна 1.
Эллиптическая кривая E(Fp) над полем из p>3 элементов состоит из точек проективной плоскости, удовлетворяющих однородному кубическому уравнению f(X, Y, Z)=0, причем ни в одной точке кривой все три частных производных полинома f не обращаются в 0 одновременно. Например, уравнение в форме Вейерштрасса Y2Z=X3+AXZ2+BZ3, где A, B∈Fp, 4A3+27B2≠0 (mod p).
Точки эллиптической кривой допускают сложение: P1+P2=P3 для любых P1 P2, причем P1+P2=P2+P1, P1+(P2+P3)=(P1+P2)+P3 для любых P1, P, P3. Если эллиптическая кривая задана уравнением в форме Вейерштрасса, то нулевым элементом по сложению является точка P∞=(0, 1, 0). Все остальные точки удовлетворяют уравнению y2=x3+Ax+B, x=X/Z, y=Y/Z. Противоположной к точке (x, y) является точка (x, -y).
На эллиптической кривой E(Fp) действует отображение Фробениуса π(X, Y, Z)=(Xp, Yp, Zp), отображающее кривую в себя, при этом π(P1+P2)=π(P1)+π(P2). Отображение Фробениуса удовлетворяет уравнению π2-Tπ+p=0 с дискриминантом Dπ=T2-4p<0, где 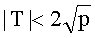
Если α, 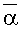
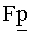
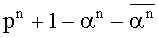
Изоморфизм эллиптических кривых задается обратимой линейной заменой переменных. Эллиптическая кривая с точностью до изоморфизма над алгебраически замкнутым полем характеризуется своим j-инвариантом [Silverman J. The arithmetic of elliptic curves. - Springer-Verlag, 1986]. Если эллиптическая кривая задана уравнением в форме Вейерштрасса, то 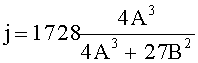
Инвариант эллиптической кривой E(Fp) с дискриминантом Dπ равен приведенному по модулю p значению модулярной функции j(τ) комплексной переменной τ для некоторого значения τ, связанного с уравнением кривой. Существует функция Вебера g(τ), связанная с функцией j соотношением 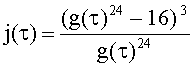
Если две эллиптические кривые в форме Вейерштрасса E1(Fp), E2(Fp), обладающие инвариантами j1, j2 соответственно, имеют одинаковое число точек над полем Fp или его квадратичным расширением, то существует изогения - отображение первой кривой во вторую и обратно, заданное дробями полиномов с коэффициентами из Fp. Число неизоморфных эллиптических кривых, обладающих одинаковым числом точек, называется числом классов дискриминанта Dπ и по порядку величины близко к 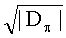
Ядро изогении φ: E1→E2 - точки кривой E1, рассматриваемой над алгебраически замкнутым полем, отображающиеся в нулевой элемент кривой E2, конечно. Изогения полностью определяется своим ядром. Число точек ядра называется также степенью изогении φ: E1→E2. Дуальная изогения 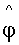
Изогении допускают умножение, степень произведения изогений равна произведению степеней исходных изогений, поэтому достаточно рассматривать только изогении простых степеней. Произведение изогений коммутативно и ассоциативно: φ1φ2=φ2φ1, φ1(φ2φ3)=(φ1φ2)φ3.
Изогения может быть вычислена по формулам Велу [Velu J. Isogenies entre courbes elliptiques. C.R. Acad. Sc. Paris, 273 (1971), 238-241]. Пусть E1(Fp):y2=x3+Ax+B; E2(Fp):ν2=u3+A1u+B1, и (xR,yR)∈E1(Fp) - точка нечетного порядка l. Для точки Q из ядра изогении положим
sQ=4xQ 3+4AxQ+4В, tQ=6xQ 2+4A.
Кривая E2(Fp) задается коэффициентами
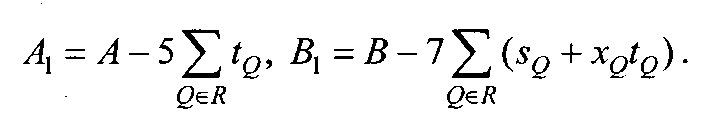
Ядро изогении простой нечетной степени l для эллиптической кривой в форме Вейерштрасса состоит из l2 точек порядка l, x-координаты которых являются корнями полиномов деления fl(x) степени (l2-1)/2.
Полиномы деления определяются рекуррентно [J. Silverman. The arithmetic of elliptic curves. - Springer-Verlag, 1986]:
ψ0=0, ψ1=1, ψ2=2y,
ψ3=3x4+6Ax2+12Bx-A2,
ψ4=4y(x6+5Ax4+20Bx2-5A2x2-4ABx-8B2-A3),
2yψ2n=ψn(ψn+2ψn-1 2-ψn-2ψn-1 2), n>2,
ψ2n+1=ψn+2ψn 3-ψn+1 3ψn-1, n<1,
fn(x)=ψn(x, y),
если n нечетное, и
fn(x)=ψn(x, y)/y,
если n четное.
Полиномы fl раскладываются на множители. Координаты точек ядра изогении степени l являются корнями одного и того же неприводимого делителя полинома деления fl(x).
Существует алгоритм Чуфа для вычисления числа точек эллиптической кривой над конечным полем и его улучшение Элкиса [N. Elkies. Elliptic and modular curves over finite fields and related issuses // Proceedings of a conference in honor of A.O.L. Atkin, AMS international press, 1998, pp.21-76]. Изогения Элкиса - изогения, по модулю степени которой дискриминант Фробениуса является квадратом. Для изогении Элкиса степени l характеристический полином отображения Фробениуса раскладывается на линейные множители по модулю l. Дуальные изогении соответствуют различным корням полинома отображения Фробениуса по модулю l.
Для изогении Элкиса степени l и кривой E0 с инвариантом j0 существует ровно два изогенных образа, соответствующие двум дуальным изогениям (для исходной и скрученной кривой). При этом существует целочисленный симметрический модулярный полином Фl(U, V), такой, что Фl(U, j0) (mod p) имеет два корня, соответствующие двум дуальным изогениям. Обозначим один из корней через j1. Тогда можно построить цикл изогений степени l вида j0→j1→…→j0. Длина цикла является делителем числа классов. При изменении степени изогении цикл состоит из тех же j-инвариантов, но переставленных. Множество точек (U, V), таких, что Фl(U, V)=0, называется классической модулярной кривой X0(l).
На практике если D≡1 (mod 8), то вместо полиномов Фl удобнее рассматривать полиномы Wl для функции Вебера g, удовлетворяющей уравнению 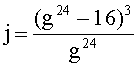
Квантовая атака основана на вычислении секретного ключа с помощью квантового компьютера.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИСПОЛЬЗОВАНИЕ ИЗОГЕНИЙ ДЛЯ РАЗРАБОТКИ КРИПТОСИСТЕМ | 2004 |
|
RU2376651C2 |
| ПРОТОКОЛ СОГЛАСОВАНИЯ КЛЮЧЕЙ НА ОСНОВЕ ИЗОГЕНИИ ЭЛЛИПТИЧЕСКИХ КРИВЫХ | 2018 |
|
RU2728519C1 |
| МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2586575C1 |
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| КРИПТОГРАФИЯ С ПАРАМЕТРИЗАЦИЕЙ НА ЭЛЛИПТИЧЕСКОЙ КРИВОЙ | 2010 |
|
RU2533087C2 |
| СПОСОБ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ НА ОСНОВЕ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ | 2010 |
|
RU2457625C1 |
| Способ защиты информации в облачных вычислениях с использованием гомоморфного шифрования | 2017 |
|
RU2691874C2 |
| УСТРОЙСТВО СПЕКТРАЛЬНОГО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ | 2005 |
|
RU2301441C2 |
| СПОСОБ ПОРОГОВОЙ ГЕНЕРАЦИИ КЛЮЧЕЙ ДЛЯ СИСТЕМЫ ЗАЩИТЫ ИНФОРМАЦИИ НА ОСНОВЕ ИДЕНТИФИКАЦИОННЫХ ДАННЫХ | 2010 |
|
RU2452111C1 |
| СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2392736C1 |
Изобретение относится к области криптографической защиты электронных данных, передаваемых по телекоммуникационным сетям и сетям ЭВМ. Технический результат - защита от квантовых атак. Способ шифрования с защитой от квантовых атак на основе циклов функций Вебера использует циклы функций Вебера для эллиптических кривых на число, сравнимое с 1 по модулю 8, а циклы определяются изогениями Элкиса малых степеней. Очередное значение функции Вебера находится как корень целочисленного симметрического полинома. Секретным ключом является список целых чисел (N1, …, Nk), где Ni - число шагов, выполняемых по циклу функций Вебера для изогении Элкиса степени li, открытым ключом является значение функции Вебера последней изогении. При первом вычислении функции Вебера для изогении степени l задается положительное направление на цикле. Для этого выбирается ядро изогении как делитель степени (l-1)/2 l-го полинома деления, определяющий минимальную степень расширения, в котором лежат точки ядра и по трем старшим коэффициентам полинома, задающего ядро, вычисляются коэффициенты изогенного образа эллиптической кривой. Шаги по циклу выполняются в соответствии со знаком числа Ni. 2 з.п. ф-лы, 2 ил.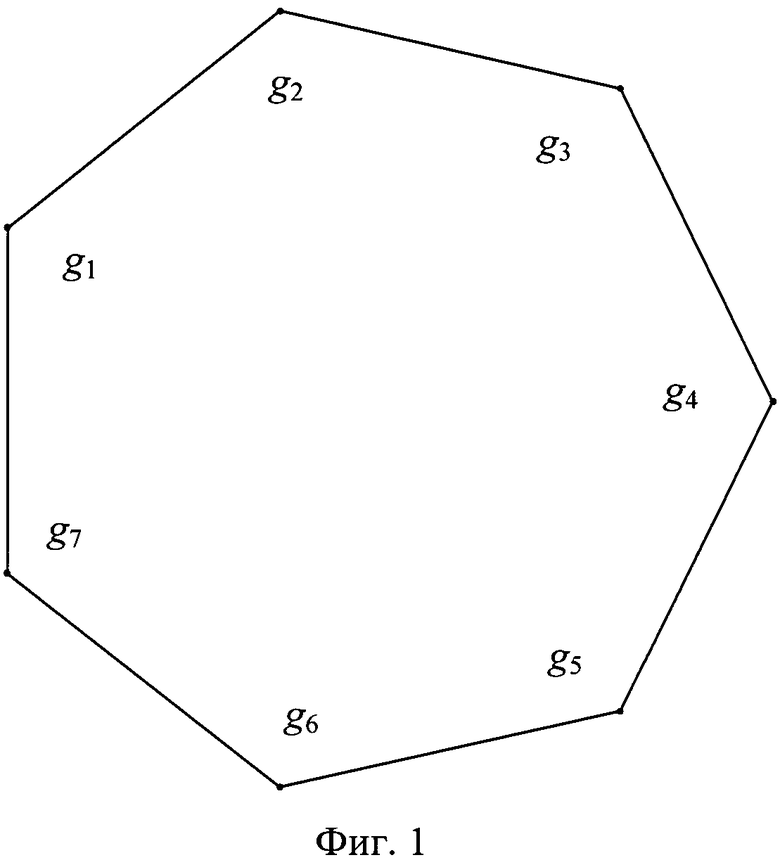
1. Способ шифрования с защитой от квантовых атак на основе циклов функций Вебера, в котором сообщение зашифровывают с использованием открытого ключа и зашифрованное сообщение расшифровывают при помощи секретного ключа, содержащий первую эллиптическую кривую и вторую эллиптическую кривую с одинаковыми дискриминантами Фробениуса, соответствующие открытому ключу, и отображение первой эллиптической кривой во вторую эллиптическую кривую, соответствующее секретному ключу, отличающийся тем, что эллиптические кривые задают значениями функции Вебера, причем секретный ключ определяют как цепочку отображений функций Вебера, соответствующих изогениям Элкиса степеней l1, …, lk, заданную набором целых чисел N1, …, Nk, где Ni - число шагов по циклу функций Вебера для изогении степени li, при этом очередное значение функции Вебера gi+1 определяют как корень симметрического полинома двух переменных при замене одной переменной на предыдущее значение функции Вебера gi, а при переходе к изогении очередной степени задают положительное направление на цикле, для этого находят полином, задающий ядро изогении, а шаги по циклу выполняют в направлении, соответствующем знаку числа Ni.
2. Способ по п.1, отличающийся тем, что дискриминант Фробениуса выбирают равным произведению квадрата целого числа на число, сравнимое с 1 по модулю 8.
3. Способ по п.1, отличающийся тем, что ядро изогении задают полиномом, для которого точки ядра которого лежат в расширении минимальной степени, и по его коэффициентам находят функцию Вебера, соответствующую положительному направлению.
| СПОСОБ ХРАНЕНИЯ И ИСПОЛЬЗОВАНИЯ КРИПТОГРАФИЧЕСКОГО КЛЮЧА | 2008 |
|
RU2417410C2 |
| ИСПОЛЬЗОВАНИЕ ИЗОГЕНИЙ ДЛЯ РАЗРАБОТКИ КРИПТОСИСТЕМ | 2004 |
|
RU2376651C2 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| US 7499544 B2, 03.03.2009 | |||
| US 7209555 B2, 24.04.2007 | |||
Авторы
Даты
2015-02-20—Публикация
2013-11-20—Подача