Настоящее изобретение касается шифрования сообщений на основе использования точек на эллиптической кривой, а более конкретно, упомянутого использования в области алгоритмов типа ЕКЕ (обмен зашифрованными ключами).
Способы аутентификации с помощью пароля основаны на использовании алгоритма типа ЕКЕ. Этот тип алгоритмов показан на фиг.1.
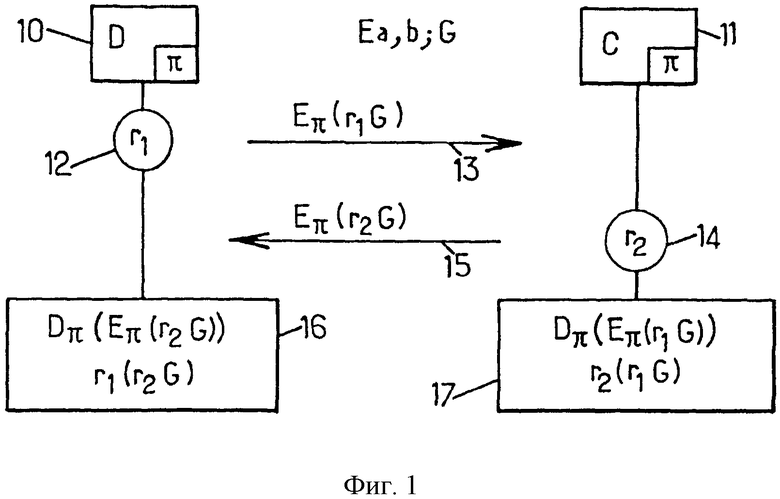
Устройство D10 хочет пройти аутентификацию на основе пароля π у контроллера C11. Каждый из этих объектов знает пароль π. Более того, предположим, что общедоступными параметрами является эллиптическая кривая Ea,b и генератор G множества точек на эллиптической кривой. Эллиптическая кривая удовлетворяет следующему уравнению:
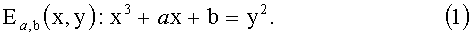
На этапе 12 устройство D10 генерирует случайное число r1. Далее оно передает это случайное число в форме точки на эллиптической кривой контроллеру 11. Для этого оно определяет некоторое передаваемое значение V, удовлетворяющее выражению:
V=r1.G.
Далее этот результат зашифровывается с помощью пароля в виде Eπ(r1.G), при этом Eπ - функция шифрования с паролем.
Далее устройство посылает сообщение 13 контроллеру, содержащее значение Eπ(r1.G).
При получении сообщения 13 контроллер 11 в свою очередь на этапе 14 генерирует случайное число r2. Далее он преобразует это число в форму точки на эллиптической кривой и передает устройству 10 сообщение 15, содержащее результат:
Eπ(r2.G).
После этого обмена случайными числами r1 и r2 в зашифрованной форме устройство 10 на этапе 16 восстанавливает случайное число r2, сгенерированное контроллером, что делается посредством дешифрования с использованием функции Dπ расшифрования с паролем; информация, содержащаяся в сообщении 15:
r2.G=DπEπ(r2.G),
а контроллер 11 на этапе 17 восстанавливает случайное число r1, сгенерированное устройством 10, что делается посредством дешифрования информации, содержащейся в сообщении 13:
r1.G=DπEπ(r1.G).
Таким образом, после защищенного обмена сообщениями каждый объект может вычислить общий ключ K:
K=r1.r2.G.
Алгоритм этого типа предназначен для обмена значениями в виде, зашифрованном с помощью пароля или ключа, полученного по паролю. Тем не менее, надо заметить, что в соответствии с классическим представлением эллиптической кривой, удовлетворяющей уравнению (1) в конечном поле Fq, описанный со ссылкой на фиг.1 обмен сообщениями позволяет потенциальному нарушителю получить информацию, касающуюся пароля π. Фактически описанный выше обмен случайными числами в зашифрованной форме с помощью сообщений 13 и 15 дает лишнюю информации, которая может позволить взломать секретность пароля. Более конкретно, при каждом перехвате нарушитель может проверять пароль на предмет расшифровывания информации, которой обмениваются в сообщениях 13 и 15. Далее для него возможны два случая. В первом случае расшифрованная информация соответствует точке на кривой и соответственно пароль правильный. Во втором случае расшифрованная информация не соответствует точке на эллиптической кривой и соответственно пароль не найден. Путем увеличения количества перехватов и отдельных паролей таким образом возможно найти пароль, принадлежащий конечному множеству элементов.
Настоящее изобретение предназначено для улучшения ситуации.
Согласно первому аспекту настоящего изобретения предложен способ проверки устройства с помощью контроллера на основе пароля;
способ включает в себя следующие этапы, осуществляемые в устройстве или контроллере:
/1/ на основе случайного числа r1 определяют точку P(X,Y) на эллиптической кривой в конечном поле Fq, при этом q - целое число и кривая задается уравнением:
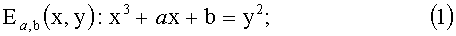
/2/ получают первый и второй параметры k и k′, такие, что
P=F(k,k′),
где F - сюръективная функция FqxFq′ в Fq;
/3/ получают первый и второй параметры в зашифрованном виде посредством шифрования в виде функции, зависящей от пароля; и
/4/ передают упомянутые первый и второй параметры контроллеру;
при этом функция F такова, что независимо от входных элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой и входные элементы не удовлетворяют уравнению (1).
Благодаря таким конструкциям возможно избежать описанных выше атак, характерных для существующего уровня техники. Фактически при этих условиях больше невозможно проверять пароль путем определения, соответствует ли полученный результат некоторой точке (X,Y) на эллиптической кривой Ea,b, так как на выходе функция F всегда дает точку на эллиптической кривой, независимо от входных параметров, хотя входные параметры не удовлетворяют классическому выражению эллиптической кривой. Следовательно, предусматривается другое представление точки на эллиптической кривой, с использованием этой сюръективной функции F, чтобы не давать никакой информации потенциальному нарушителю, которая могла быть позволить ему установить используемый пароль.
Чтобы определить упомянутую функцию F, позволяющую представить точку P(X,Y) на эллиптической кривой в соответствии с некоторой параметризацией, отличной от уравнения (1), возможно использовать в качестве основы обратимую функцию fa,b, обратная функция 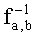
Функция F может быть записана в следующем виде:
F(k,k′)=f(k′)+fa,b(k),
где fa,b - обратимая функция, основанная на коэффициентах а и b эллиптической кривой, на вход которой подают входной параметр и на выходе получают точку эллиптической кривой;
при этом f′ - функция генерации точки на эллиптической кривой, зависящая от параметра; и
на этапе /2/ параметры k и k′ получают в ходе следующих этапов:
- случайно генерируют значение параметра k′;
- вычисляют значение f′(k′);
- определяют значение параметра k из следующего выражения:
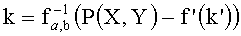 .
.
Благодаря объединению функции f′, которая позволяет генерировать точку на эллиптической кривой на основе параметра k′, принимающего случайное значение, и обратимой функции fa,b, основанной на коэффициентах а и b эллиптической кривой, возможно получить функцию F, которая дает возможность получить параметризацию точки на кривой и одновременно исключить реализацию описанных атак.
В частности, функция f может быть записана следующим образом:
f′(k′)=k′.G,
где G - генератор множества точек на эллиптической кривой; а
значение параметра k определяют из следующего выражения:
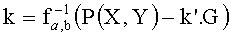 .
.
В таких условиях функцию F можно записать так:
F(k,k′)=fa,b(k)+k′.G,
В качестве альтернативы функцию f′ можно записать следующим образом:
f′(k′)=fa,b(k′)
и
значение параметра к определяют из следующего выражения:
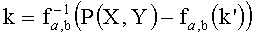 .
.
В таких условиях функцию F можно записать так:
F(k,k′)=fa,b(k)+fa,b(k′).
Таким образом, в общем для параметризации точки P(X,Y) на кривой в соответствии с настоящим изобретением первый этап предполагает получение точки на кривой для некоторого значения параметра k′. Далее определяют точку на кривой, которая соответствует вычитанию из представляемой точки Р(Х,Y) точки, полученной на первом этапе. Далее получают другую точку на эллиптической кривой. После этого функцию, обратную к функции fa,b, применяют к этой точке и получают значение параметра k. Таким образом, точку Р представляют в виде пары параметров k и k′, которые не удовлетворяют уравнению (1).
В одном варианте осуществления настоящего изобретения функция F содержит по меньшей мере одну обратимую функцию fa,b, такую, что
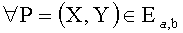 ,
, 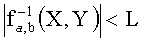
где L является целым числом, значение которого сравнительно мало по сравнению с количеством точек на эллиптической кривой (1).
Тот факт, что функция F содержит fa,b, означает, что применение функции F к первому и второму параметрам соответствует применению этой функции fa,b, по меньшей мере, или к первому параметру, или ко второму параметру. Таким образом, мы можем предусмотреть, с одной стороны, генерацию точки на кривой на основе первого параметра и, с другой стороны, применение функции, обратной для функции fa,b, с целью получения второго параметра. Следуя этой процедуре, точку на эллиптической кривой можно представить в соответствии с этими двумя параметрами.
Таким образом, применение функции F к первому и второму параметрам может соответствовать применению по меньшей мере к одному из двух параметров функции fa,b, такой, что
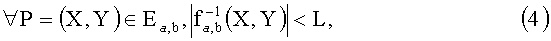
где L является целым числом, значение которого сравнительно мало по сравнению с количеством точек на эллиптической кривой (1).
Другими словами, рассматриваемая здесь функция fa,b содержит прообраз, соответствующий множеству точек Р на эллиптической кривой Еa,b и ограниченный достаточно небольшим максимальным значением по сравнению с количеством точек на эллиптической кривой. Фактически, если бы это было не так, то было бы возможно обратить функцию fa,b просто произвольно выбирая число. В этом контексте можно рассматривать, например, что L меньше произведения 1/280 и количества точек на кривой.
Благодаря использованию обратимой функции, удовлетворяющей условиям (4), легко получить функцию F для представления точки на кривой с помощью параметров k и k′, которые не позволяют реализовывать описанную выше атаку на пароль, использованный для шифрования этих параметров.
В одном варианте осуществления настоящего изобретения функция fa,b устанавливает соответствие пары параметров (x, y) параметру и так что х является единственным решением следующего уравнения:
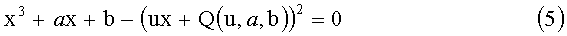
а y удовлетворяет:
y=u.x+Q(u,a,b).
Это уравнение (5), полученное заменой у в уравнении (1) на элемент ux+Q(u,a,b). Элемент ux+Q(u,a,b) является рациональной дробью, зависящей от переменных и a, и b.
Тот факт, что это уравнение (5) имеет только один корень, эквивалентно тому, что дискриминант, обозначаемый как Δ(u,а,b), следующего многочлена не является квадратом при любом параметре u:
х3+aх+b-(ux+Q(u,a,b))2.
Для q=2 mod 3 можно записать
Δ(u, a, b)=-3R(u, а, b)2,
где R - рациональная дробь.
Фактически для q=2 mod 3, -3 не является квадратом и, следовательно, -3R(u,a,b)2 никогда не является квадратом многочлена.
Так как уравнение (5) только допускает наличие единственного корня, то следующий элемент является многочленом степени 1:
gcd(x3+ax+b-(ux+Q(u,a,b))2,XP-X),
где gcd - наибольший общий делитель.
Корень этого многочлена, обозначаемый как XP, является абсциссой точки на эллиптической кривой. Наконец, точка с абсциссой XP и ординатой u.XP+Q(u,a,b) является точкой на кривой.
В одном примере в качестве рациональной дроби Q(u,a,b) можно рассмотреть следующую дробь:
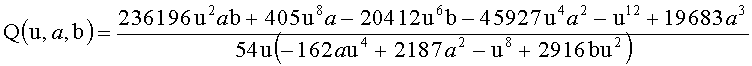
В одном варианте осуществления изобретения целесообразно следующим образом определить функцию fa,b в Fq, где q равна 2 mod 3. Она сопоставляет паре параметров (x, y) параметр u так, что
х=(ν2-b-u6/27)1/3+u2/3
и
y=u.x+ν,
где 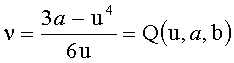
и где fa,b(0)=0.
Такая функция обратима. Таким образом, для P(X,Y) на эллиптической кривой прообраз точки для функции fa,b представляет собой решение следующего уравнения:
u4-6u2х+6uy-3a=0.
Итак, степенное уравнение такого типа может быть легко обращено.
Более того, множество прообразов точек Р для этой функции fa,b ограничено L, которое мало по сравнению с количеством точек на эллиптической кривой.
Таким образом, эта функция удовлетворяет определенным ранее характеристикам.
Также можно рассмотреть функцию F, основанную на использовании функции fa,b, которая определена на основе многочленов, удовлетворяющих равенству Скальба.
Заметим, что многочлены, удовлетворяющие равенству Скальба, определены в документе «Рациональные точки на определенных гиперэллиптических кривых над конечными полями» («Rational points on certain hyperelliptic curves over finite fields»), автор Масие Улас (Macie Ulas), 11 июня 2007 года. Эти функции являются обратимыми. Фактически заданные многочлены X1(k), X2(k), X3(k) и U(k) удовлетворяют равенству Скальба, если удовлетворяют уравнению:
f(X1(k)).f(X2(k)).f(X3(k))=U(k)2,
где f - многочлен, который определяет эллиптическую кривую Ea,b.
Более конкретно f удовлетворяет уравнению:
f(x)=y2,
где x и y являются элементами 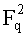
fa,b(k) определяют как точку P=(Xi(k), f(Xi(k))1/2), где i такое, что f(Xi(k)) является квадратом в Fq. Таким образом, чтобы обратить функцию fa,b, при заданной точке P=(X,Y), вычисляют решения ks трех степенных уравнений:
X1(ks)-X=0
X2(ks)-X=0
X3(ks)-X=0.
Каждое из этих решений является прообразом точки Р для функции fa,b.
В случае, когда F(k,k′) записана как:
F(k,k′)=fa,b(k)+fa,b(k′).
Для равномерного распределения входных значений мы можем получить равномерное распределение точек, выходных значений fa,b, что целесообразно. В этом случае, если входные значения определяют случайно, то выходные значения также имеют некоторое случайное распределение.
Благодаря этой процедуре возможно исключить атаки, основанные на статистическом анализе значений, используемых в качестве параметра, что могло бы дать некоторую информацию. Фактически в случае, когда обращение этой функции fa,b для точки Р на эллиптической кривой соответствует нескольким значениями входного параметра этой обратной функции, возможно, что в соответствии с законом распределения некоторые из этих значений будут повторяться чаще других. Таким образом, если нарушитель знает этот закон распределения, благодаря проверке пароля для информации, которой обмениваются, он может решить, соответствуют или нет значения параметра, которыми обмениваются, этому распределению. Таким образом, он может установить, является или нет правильным проверяемый пароль.
Для того чтобы исключить атаки такого типа, целесообразно использовать такой алгоритм, как алгоритм, который описан ниже.
Через D обозначим множество точек на эллиптической кривой Ea,b, у которых существует точно i прообразов для функции fa,b. В описанном ниже примере определено пять множеств: D1, D2, D3, D4 и D5.
Через GEN обозначим функцию, которая генерирует случайно и равновероятно распределенные точки на эллиптической кривой. Пусть 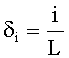
Для t от 0 до T-1, где T - целое число:
- генерируют точку Pt с помощью функции GEN;
- если Pt является элементом D0, то переходят на начало;
- если Pt является элементом Di, то
- выбирают случайное число b, находящееся между 0 и 1 и удовлетворяющее равенству:
Pr(b=0)=δi,
- если b равно 1, то переходят на этап (1);
- в ином случае
- случайно выбирают элемент и из множества 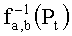
- возвращают u.
Заметим, что для получения вероятности успеха, равной 1-1/2k, достаточно, чтобы T равнялось многочлену, вычисленному в точке k степени 1, другими словами, чтобы T было кратно k.
Более того, могут быть применены следующие этапы:
- получают сообщение, содержащее первый и второй параметры, зашифрованные с помощью пароля;
- расшифровывают первый и второй параметры и получают параметры р и р′; и
- вычисляют общее секретное значение K с помощью контроллера и в соответствии со следующим выражением:
K=r1.F(p,p′),
где r1 - случайное число, используемое на этапе /1/.
Таким образом, устройство и контроллер наконец могут получить в свое распоряжение общий ключ без обмена информацией, ставящей под угрозу секретность пароля.
Согласно второму аспекту настоящего изобретения предложено электронное устройство, содержащее средство, подходящее для реализации способа проверки, который соответствует первому аспекту настоящего изобретения.
Согласно третьему аспекту настоящего изобретения предложена система проверки с паролем, содержащая первое электронное устройство, соответствующее второму аспекту и выполняющее функцию контроллера, и второе электронное устройство, соответствующее второму аспекту и выполняющее функцию проверяемого устройства.
Другие аспекты, цели и достоинства изобретения будут ясны после прочтения описания одного из вариантов осуществления изобретения. Изобретение будет лучше понятно из следующих фигур:
фиг.1 - уже описанный вид, иллюстрирующий основные этапы способа проверки, который соответствует существующему уровню техники;
фиг.2 - вид, на котором показаны основные этапы способа проверки, который соответствует одному варианту осуществления настоящего изобретения;
фиг.3 - вид, на котором показана реализация способа проверки, реализуемого между устройством и контроллером в соответствии с одним вариантом осуществления настоящего изобретения; и
фиг.4 - вид, на котором показано устройство и контроллер в соответствии с одним вариантом осуществления настоящего изобретения.
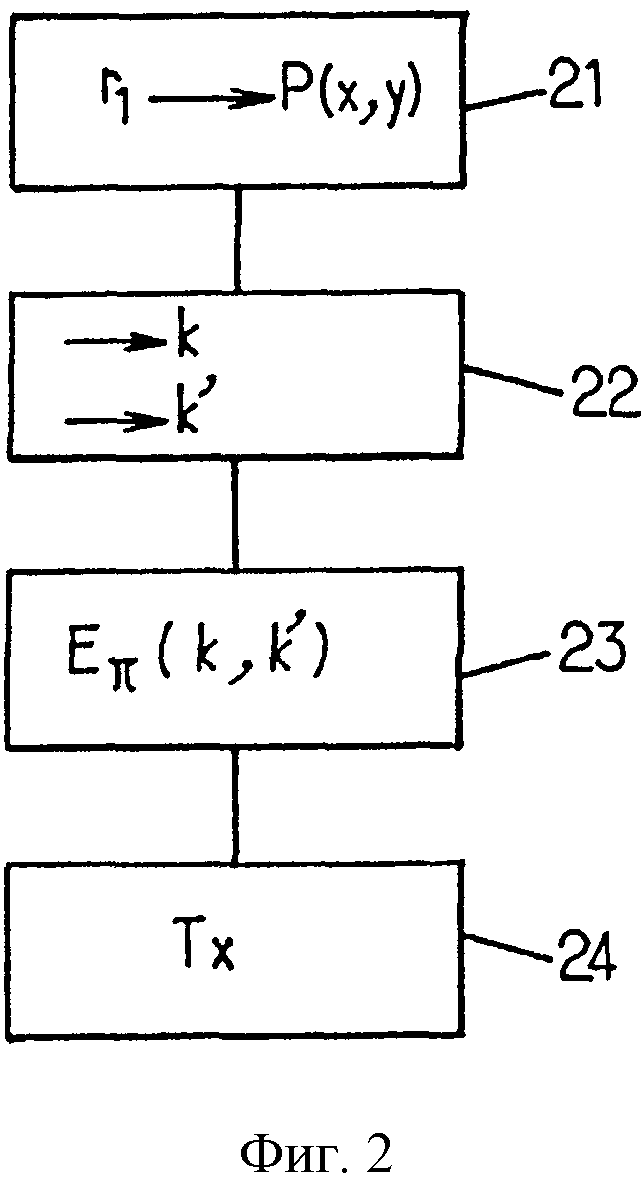
На фиг.2 показаны основные этапы способа проверки, который соответствует одному варианту осуществления настоящего изобретения.
На этапе 21 точку P=(X,Y) на эллиптической кривой в конечном поле Fq, где q - целое число, определяют на основе случайного числа r1. Далее на этапе 22 так получают первый и второй параметры k и k′, что
P=F(k,k′),
где F - сюръективная функция из FqxFq′ в Fq.
Полученные таким образом параметры дают возможность так представить точку Р, чтобы защитить секретность пароля при обмене сообщениями между устройством и контроллером.
На этапе 23 первый и второй параметры зашифровывают с помощью пароля π и, таким образом, получают их зашифрованный вид Eπ(k, k′).
В этой форме на этапе 24 целесообразно передать случайное значение r1 от устройства к контроллеру или от контроллера к проверяемому устройству с целью генерации общего секретного ключа.
Функция F такова, что независимо от элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой и элементы z и z′ не удовлетворяют уравнению (1).
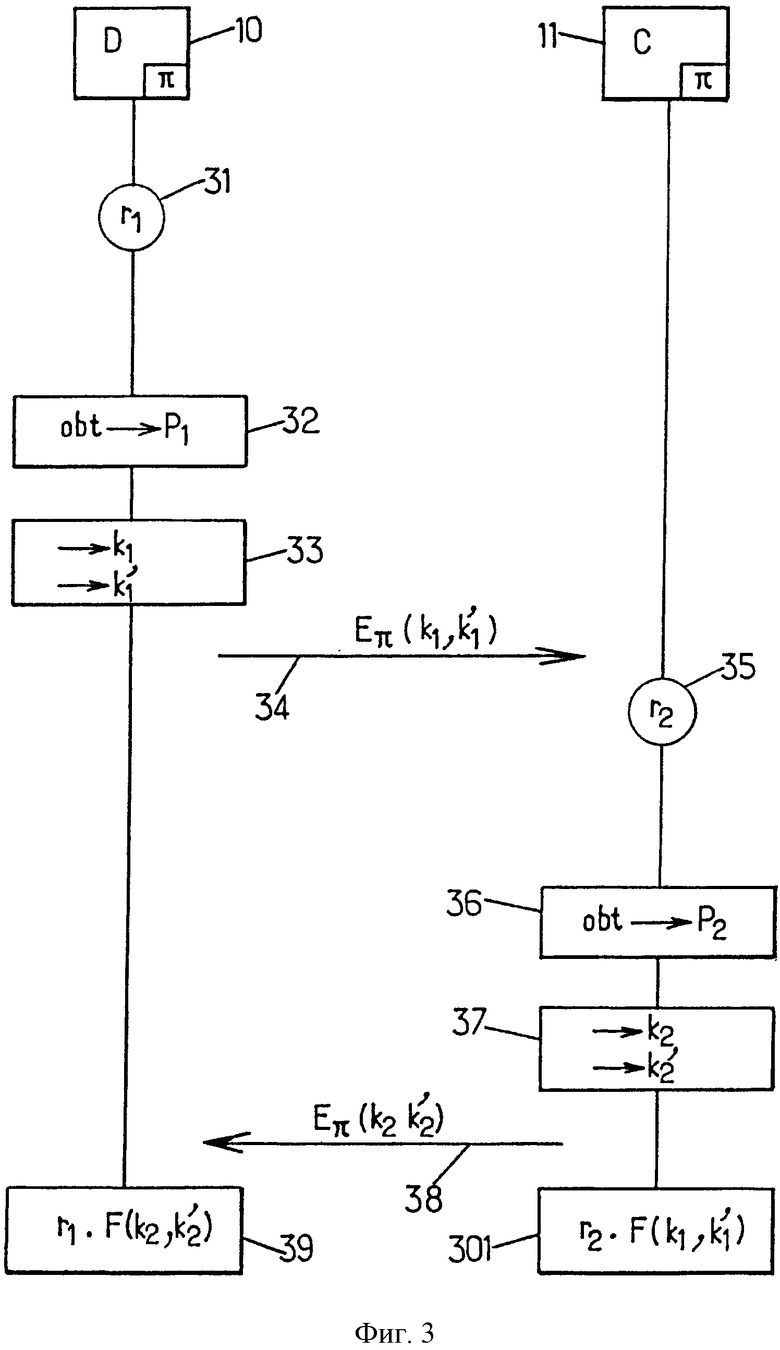
На фиг.3 показан обмен сообщениями между проверяемым устройством 10 и контроллером 11 в соответствии с одним вариантом осуществления настоящего изобретения.
Проверяемое устройство D10 сначала на этапе 31 генерирует случайное число r1. Если мощность множества точек на эллиптической кривой является целым числом N, то число r1 может быть случайным числом из следующего множества значений: [0, N-1].
Далее, с учетом этого случайного числа с использованием генератора G генерируют точку P=(X,Y) на эллиптической кривой Ea,b. Упомянутый генератор обладает следующим свойством: для любой точки Р на эллиптической кривой существует значение h, такое, что:
P=h.G.
Таким образом, точку P1 получают следующим образом:
P1=r1.G.
Далее на этапе 33 определяют значения параметров k1 и 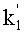
Для определения этих параметров k1 и 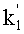
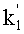
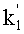
Далее получают значение параметра k1 путем применения обратного преобразования для функции fa,b к точке, соответствующей вычитанию в группе точек на эллиптической кривой: P(X,Y)-Pk1.
Параметры k1 и 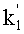
Симметричным образом на этапе 35 контроллер генерирует случайное число r2. Далее на этапе 36 он преобразует это число в точку Р2 на эллиптической кривой. Затем, как описано ранее на этапе 33, на этапе 37 контроллер получает соответствующие значения первого и второго параметров k1 и 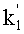
Следовательно, проверяемое устройство 10 имеет в своем распоряжении случайное число r1, числа k2 и 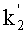
Таким образом, на этапе 39 оно восстанавливает точку P2:
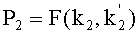
Следовательно, оно вместе с контроллером получает секретный ключ K, не давая никакой информации о пароле, при этом указанный ключ удовлетворяет равенству:
K=r1.r2.G.
Контроллер восстанавливает секретный ключ К симметричным образом на этапе 301.
Определенная выше функция F может быть записана в другой форме. В последующих разделах описаны различные представления этой точки Р, которые целесообразно дают возможность не предоставлять лишнюю информацию при обмене зашифрованными сообщениям со случайными числами.
Функция F является сюръективной функцией из FqxFq′ в Fq, такой, что:

и такой, что для любой пары чисел (k,k′) Р является точкой на эллиптической кривой, хотя k и k′ не удовлетворяют уравнению (1).
В таком контексте целесообразно, что никакой информации о пароле нельзя получить на основе обмена случайными числами, в отличие от существующего уровня техники. Фактически устройство и контроллер обмениваются в зашифрованном виде парой значений (k,k′). Но, какой бы пароль не проверял потенциальный нарушитель с целью восстановить эту пару значений, невозможно определить, является ли этот пароль правильным или нет, так как любой полученный результат соответствует точке на эллиптической кривой, хотя k и k′ не удовлетворяют уравнению (1).
Такое представление может быть основано на следующей целесообразной характеристике функции fa,b(U):
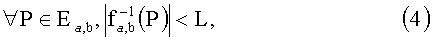 ,
,
где L - целое число.
Другими словами, размер множества прообразов этой функции ограничен величиной L, которая мала по сравнению с количеством точек на эллиптической кривой.
Рассматривая следующую функцию fa,b(u), можно целесообразно определить функцию F, которая соответствует одному варианту осуществления настоящего изобретения и которая сопоставляет паре параметров (х, u.x+v) из 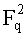
х=(ν2-b-u6/27)1/3+u2/3
и
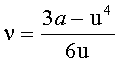 ,
,
при этом полагают fa,b(0)=0.
Функция F может быть записана следующим образом:
F(k,k′)=fa,b(k)+fa,b(k′)
или
F(k,k′)=fa,b(k)+k′.G.
Также можно считать, что fa,b является функцией, полученной из многочленов, удовлетворяющих равенству Скальба:
f(X1(k)).f(X2(k)).f(X3(k))=U(k)2,
где X1(k), X2(k), X3(k) и U(k) - многочлены, удовлетворяющие равенству Скальба, как определено, например, в документе «Рациональные точки на определенных гиперэллиптических кривых над конечными полями» («Rational points on certain hyperelliptic curves over finite fields»), автор Масие Улас, 11 июня 2007 года. Здесь через Fa,b(k) обозначаем (Xi(k),f(Xi(k))1/2), где i таково, что f(Xi(k)) является квадратом в Fq.
На фиг.4 показана система проверки, содержащая проверяемое устройство и контроллер в соответствии с одним вариантом настоящего изобретения.
В соответствии с одним вариантом настоящего изобретения такая система проверки содержит по меньшей мере одно электронное устройство, такое как проверяемое устройство 10, и устройство проверки или контроллер 11. Подобное электронное устройство, независимо от того, используется ли оно как проверяемое устройство или как контроллер, может содержать:
- блок 41 определения, предназначенный для определения точки P(X,Y) на эллиптической кривой в конечном поле Fq, где q - целое число, на основе случайного числа r1, причем эллиптическая кривая удовлетворяет уравнению:
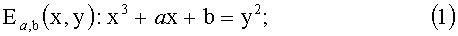
- блок 42 получения, предназначенный для получения первого и второго параметров k и k′ так, что
P=F(k,k′),
где F является сюръективной функцией из FqxFq′ в Fq;
- блок 43 шифрования, предназначенный для получения первого и второго параметров в зашифрованном виде посредством шифрования как функции от пароля; и
- блок 44 сопряжения, предназначенный для передачи упомянутых первого и второго зашифрованных параметров контроллеру,
при этом функция F такова, что независимо от входных элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой и входные элементы не удовлетворяют уравнению (1).
Функция шифрования Eπ с паролем может быть определена различным образом. Входным параметром для нее является битовая строка и выходом является битовая строка. Тем не менее, для обеспечения конфиденциальности пароля необходимо, чтобы возвращаемое значение не давало информации о пароле. Таким образом, можно различать два случая:
- или пароль используют в качестве ключа шифрования в классической функции шифрования;
- или пароль является индексом, который в базе данных указывает на значение общедоступных параметров эллиптической кривой.
В обоих случаях алгоритм шифрования может выполняться следующим образом с целью преобразования значения параметра k или k′ в битовую строку и может быть использован следующий способ:
Выбрать случайное число r. Далее преобразовать значение v параметра в битовую строку путем следующих вычислений:
v′=v+r.q′,
где q′ соответствует или q или N, при этом q - количество элементов в основной структуре Fq, N - количество точек на эллиптической кривой. Далее возможно представить v′ в виде битовой строки.
В случае, когда пароль π является индексом, v′ представляет собой зашифрованное с помощью пароля значение v, так как только человек, знающий общедоступные параметры (q или N), может найти значение v.
В случае, когда пароль используют как ключ шифрования в классической функции шифрования, достаточно зашифровать v′ с использованием функции шифрования Eπ.
Таким образом, на приемной стороне в первом случае v может быть восстановлено путем вычисления v′′ mod q′. Во втором случае необходимо расшифровать посланную битовую строку с помощью функции расшифрования, чтобы найти v′ и наконец иметь возможность вычислить v посредством вычисления v′ mod N.
Целесообразно, что настоящее изобретение может быть реализовано в криптографическом преобразовании любого типа, в котором используют эллиптические кривые. Оно может быть особенно полезно в протоколах аутентификации пароля, таких как «Установка соединения с аутентификацией пароля». В этом случае оно позволяет улучшить эффективность вычисления, не давая возможности проводить атаку, связанную со временем выполнения криптографического преобразования.
Также настоящее изобретение может быть применено для протоколов сохранения конфиденциальности, таких как протоколы, используемые для проверки электронных документов удостоверения личности, таких как электронные паспорта. Фактически перехват для представленного протокола в отличие от уровня техники не позволяет находить общедоступные параметры используемой эллиптической кривой.
| название | год | авторы | номер документа |
|---|---|---|---|
| КРИПТОГРАФИЯ НА УПРОЩЕННОЙ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ | 2010 |
|
RU2574826C2 |
| КРИПТОГРАФИЯ НА ЭЛЛИПТИЧЕСКОЙ КРИВОЙ | 2010 |
|
RU2520379C2 |
| КОДИРОВАНИЕ ТОЧЕК ЭЛЛИПТИЧЕСКОЙ КРИВОЙ | 2010 |
|
RU2533693C2 |
| ИСПОЛЬЗОВАНИЕ ИЗОГЕНИЙ ДЛЯ РАЗРАБОТКИ КРИПТОСИСТЕМ | 2004 |
|
RU2376651C2 |
| СПОСОБ ШИФРОВАНИЯ С ЗАЩИТОЙ ОТ КВАНТОВЫХ АТАК НА ОСНОВЕ ЦИКЛОВ ФУНКЦИЙ ВЕБЕРА | 2013 |
|
RU2541938C1 |
| СПОСОБ КРИПТОЗАЩИТЫ СИСТЕМЫ ТЕЛЕКОММУНИКАЦИОННЫХ ТЕХНОЛОГИЙ | 1995 |
|
RU2077113C1 |
| СИСТЕМА И СПОСОБ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2716740C1 |
| СИСТЕМА И СПОСОБ ДЛЯ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2721959C1 |
| NADO КРИПТОГРАФИЯ С ГЕНЕРАТОРАМИ КЛЮЧЕЙ | 2015 |
|
RU2691253C2 |
| СИСТЕМА И СПОСОБ ДЛЯ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2735439C2 |
Изобретение относится к способу, устройству и системе проверки устройства с помощью контроллера на основе пароля. Технический результат заключается в повышении безопасности за счет шифрования с параметризацией на эллиптической кривой. Способ содержит этапы, на которых на основе случайного числа r1 определяют точку P(X,Y) на эллиптической кривой в конечном поле Fq, где q - целое число, а кривая задается уравнением - 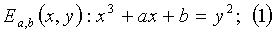 , далее получают первый и второй параметры k и k′, такие, что P=F(k,k′), где F - сюръективная функция FqxFq′ в Fq, затем получают первый и второй параметры в зашифрованном виде посредством шифрования в виде функции, зависящей от пароля, и передают упомянутые первый и второй параметры контроллеру, при этом функция F такова, что независимо от входных элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой и входные элементы не удовлетворяют уравнению (1). 3 н. и 7 з.п. ф-лы, 4 ил.
, далее получают первый и второй параметры k и k′, такие, что P=F(k,k′), где F - сюръективная функция FqxFq′ в Fq, затем получают первый и второй параметры в зашифрованном виде посредством шифрования в виде функции, зависящей от пароля, и передают упомянутые первый и второй параметры контроллеру, при этом функция F такова, что независимо от входных элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой и входные элементы не удовлетворяют уравнению (1). 3 н. и 7 з.п. ф-лы, 4 ил.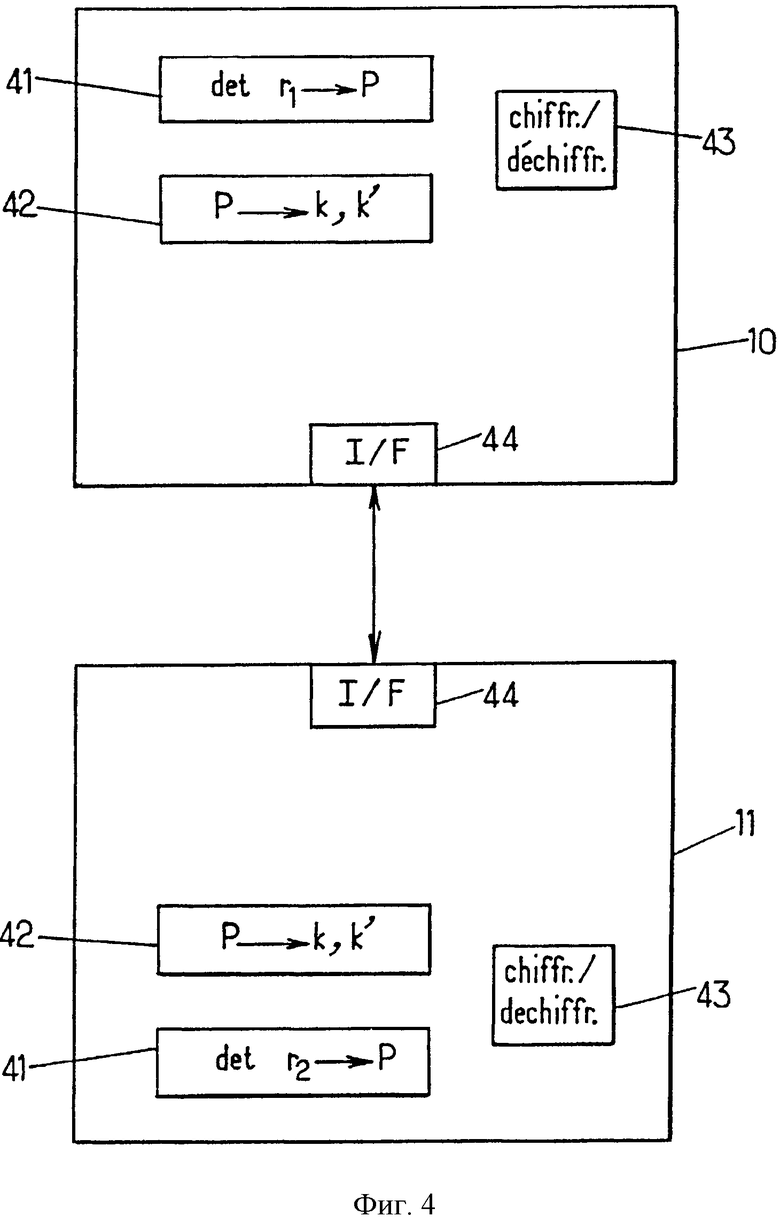
1. Способ проверки устройства (10) с помощью контроллера (11) на основе пароля (π), содержащий следующие этапы, выполненные в устройстве или контроллере:
/1/ на основе случайного числа r1 определяют точку P(X,Y) на эллиптической кривой в конечном поле Fq, где q - целое число, а кривая задается уравнением:
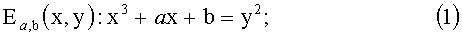
/2/ получают первый и второй параметры k и k′, такие, что
P(X,Y)=F(k,k′),
где F - сюръективная функция FqxFq′ в Fq;
/3/ получают первый и второй параметры в зашифрованном виде посредством шифрования в виде функции, зависящей от пароля; и
/4/ передают упомянутые первый и второй параметры контроллеру;
при этом функция F такова, что независимо от входных элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой и входные элементы не удовлетворяют уравнению (1).
2. Способ проверки по п.1, в котором функция F имеет вид:
F(k,k′)=f(k′)+fa,b(k),
где fa,b - обратимая функция, основанная на коэффициентах a и b эллиптической кривой, на вход которой подают входной параметр и на выходе получают точку на эллиптической кривой;
f′ - функция генерации точки на эллиптической кривой, зависящая от параметра;
причем на этапе /2/ параметры k и k′ получают в ходе следующих этапов:
случайно генерируют значение параметра k′;
вычисляют значение f′(k′);
определяют значение параметра k из следующего выражения:
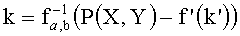 .
.
3. Способ проверки по п.2, в котором функция f′ имеет вид:
f′(k′)=k′.G,
где G - генератор множества точек на эллиптической кривой; а
значение параметра k определяют из следующего выражения:
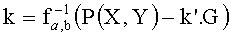 .
.
4. Способ проверки по п.2, в котором функция f′ имеет вид:
f′(k′)=fa,b(k′),
а значение параметра k определяют из следующего выражения:
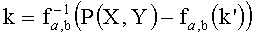
5. Способ проверки по любому из пп.1-4, в котором функция F содержит по меньшей мере одну обратимую функцию fa,b, полученную с помощью многочленов X1(k), X2(k), X3(k) и U(k), которые удовлетворяют равенству Скальба:
f(X1(k)).f(X2(k)).f(X3(k))=U(k)2,
где f - многочлен, который определяет эллиптическую кривую Ea,b.
6. Способ проверки по п.5, в котором функция fa,b сопоставляет паре параметров (x, y) в 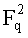
х=(ν2-b-u6/27)1/3+u2/3
и
y=u.x+ν,
где 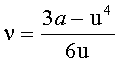 ,
,
и fa,b(0)=0.
7. Способ проверки по п.1, дополнительно включающий следующие этапы:
получают сообщение, содержащее первый и второй параметры, зашифрованные с помощью пароля;
расшифровывают первый и второй параметры и получают параметры р и р′; и
вычисляют общее секретное значение K с помощью контроллера и в соответствии со следующим выражением:
K=r1.F(p,p′),
где r1 - указанное случайное число, использованное на этапе /1/.
8. Электронное устройство в системе проверки с помощью пароля, содержащее:
блок (41) определения, выполненный с возможностью определения точки P(X,Y) на эллиптической кривой в конечном поле Fq, где q - целое число, на основе случайного числа r1, причем эллиптическая кривая удовлетворяет уравнению:
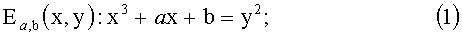
блок (42) получения, выполненный с возможностью получения первого и второго параметров k и k′, таких, что
P=F(k,k′),
где F - сюръективная функция FqxFq′ в Fq;
блок (43) шифрования, выполненный с возможностью получения первого и второго параметров в зашифрованном виде посредством шифрования в виде функции от пароля; и
блок (44) сопряжения, выполненный с возможностью передачи упомянутых первого и второго зашифрованных параметров контроллеру,
при этом функция F такова, что независимо от входных элементов z и z′ из Fq, F(z,z′) является точкой на эллиптической кривой, а входные элементы не удовлетворяют уравнению (1).
9. Электронное устройство по п.8, содержащее средство для осуществления способа проверки по п.1.
10. Система проверки с помощью пароля, содержащая по меньшей мере одно первое электронное устройство по п.8 или 9 в качестве контроллера, и второе электронное устройство по п.8 или 9 в качестве проверяемого устройства.
| US 20080165955 A1, 10.07.2008 | |||
| US 20060285682 A1, 21.12.2006 | |||
| US 6307935 B1, 23.10.2001 | |||
| ВСЕОБЪЕМЛЮЩАЯ, ОРИЕНТИРОВАННАЯ НА ПОЛЬЗОВАТЕЛЯ СЕТЕВАЯ БЕЗОПАСНОСТЬ, ОБЕСПЕЧИВАЕМАЯ ДИНАМИЧЕСКОЙ КОММУТАЦИЕЙ ДАТАГРАММ И СХЕМОЙ АУТЕНТИФИКАЦИИ И ШИФРОВАНИЯ ПО ТРЕБОВАНИЮ ЧЕРЕЗ ПЕРЕНОСНЫЕ ИНТЕЛЛЕКТУАЛЬНЫЕ НОСИТЕЛИ ИНФОРМАЦИИ | 2004 |
|
RU2308080C2 |
Авторы
Даты
2014-11-20—Публикация
2010-06-28—Подача