МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ Российский патент 2016 года по МПК G06F7/72 G06F7/57 

Предлагаемое устройство относится к вычислительной технике и может быть использовано как специализированный вычислитель - универсальный в классе логических вычислений.

Известен модулярный вычислитель систем булевых функций [1], содержащий коммутатор, входы которого являются входами устройства для подачи n булевых переменных, а выходы с (k+1) по n подключены к входам блока конъюнкций, выходы которого подключены к входам каждого из 2^k блоков памяти, выходы которых подключены к входам 2^n-k мультиплексоров, где i-й выход j-го блока памяти подключен к j-му входу i-го мультиплексора (i=1, 2, …, 2^n-k; j=1, 2, …, 2^k), управляющие входы каждого из которых соединены с k первыми входами коммутатора, а выходы подключены к входам многоместного сумматора, выходы которого являются выходами устройства выдачи результата вычисления булевых функций.

Наиболее близким по сущности технического решения заявленному устройству является арифметический вычислитель систем булевых функций [2], содержащий n входов подачи булевых переменных, коммутатор, 2^k блоков памяти хранения групп коэффициентов, n-k+1 мультиплексоров выделения группы коэффициентов, многоместный сумматор, d выходов выдачи значений булевых функций, причем информационные входы коммутатора являются входами подачи булевых переменных устройства, а выходы с (k+1)-го по n-й подключены к информационным входам каждого из 2^k блоков памяти хранения коэффициентов, выходы которых подключены к информационным входам каждого из (n-k+1) мультиплексоров выбора группы коэффициентов, где i-й выход j-го блока памяти подключен к j-му входу i-го мультиплексора (i=1, 2, …, n-k+1; j=1, 2, …, 2^k), управляющие входы каждого из которых соединены с k первыми выходами коммутатора, а выходы подключены к многоместному сумматору, d мультиплексоров выделения информационного разряда, многоканальный мультиплексор, 2^k блоков памяти хранения адресов информационных разрядов, управляющий вход подачи сигнала выбора булевых переменных разложения, который является управляющим входом коммутатора, а управляющий вход подачи сигнала выбора реализуемой булевой функции устройства является управляющим входом каждого из 2^k блоков памяти хранения коэффициентов и каждого из 2^k блоков памяти хранения адресов информационных разрядов, выходы каждого из которых подключены к информационным входам многоканального мультиплексора, управляющие входы которого соединены с первыми k выходами коммутатора, а выходы с 1-го по d-й подключены к адресным входам d мультиплексоров выделения информационного разряда соответственно, информационные входы каждого из которых соединены с выходами многоместного сумматора, а выходы являются выходами выдачи значений булевых функций устройства.

Недостатком известного устройства является большие объемы оборудования (в частности, большая размерность разрядной сетки арифметического вычислителя систем булевых функций).

Цель изобретения - уменьшение объемов оборудования (уменьшение разрядной сетки вычислителя).

Поставленная цель достигается тем, что в модулярный полиномиальный вычислитель систем булевых функций, содержащий коммутатор, информационные входы которого являются n входами подачи булевых переменных устройства, управляющие входы которого подключены к управляющему входу устройства подачи значения количества переменных разложения, 2^k блоков памяти хранения значений коэффициентов полиномов разложения, управляющие входы которых подключены к управляющему входу устройства подачи значений коэффициентов, информационные выходы которых подключены к информационным входам многоканального мультиплексора выделения группы коэффициентов, управляющие входы которого подключены к k первым выходам коммутатора, введены 2^n-k блоков памяти хранения значений вычетов возведения переменной в i-тую степень (i=0, 1, …, 2^n-k-1) по модулю Р, управляющие входы которых подключены к управляющему входу устройства подачи значений вычетов возведения переменной в i-тую степень по модулю Р, информационные выходы которых подключены к информационным входам многоканального мультиплексора выделения группы вычетов, управляющие входы которого подключены к n-k вторым информационным выходам коммутатора, 2^n-k умножителей по модулю Р, где входы j-го умножителя по модулю Р подключены к j-м информационным выходам многоканального мультиплексора выделения группы коэффициентов и многоканального мультиплексора выделения группы вычетов (j=1, 2, …, 2^n-k), выходы которых подключены к входам сумматора по модулю Р, d выходов которого являются d выходами устройства выдачи значений булевых функций.

Для представления системы булевых функций (СБФ) f₁, …, f_d интерполяционным полиномом интерпретируем значения наборов переменных СБФ и значения функций на этих наборах как записи чисел в двоичной системе счисления и затем в десятичной:

В результате данной интерпретации получим функцию F(X), область значения и область определения которой {0, 1, …, s-1}, где s=2ⁿ.

Значения аргумента X являются равноудаленными узлами интерполирования, что обеспечивает возможность применения различных способов интерполяции к интерпретированной форме записи СБФ.

Воспользуемся методом интерполяции Лагранжа для представления F(X) степенным полиномом:

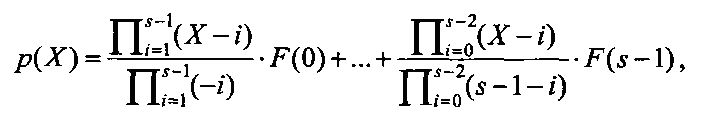
или

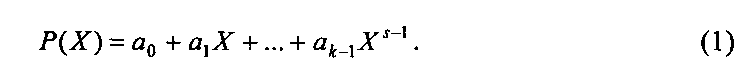
а _i - коэффициенты полинома, (i=0, 1, …, s-1), s=2ⁿ.

Пример 1. Рассмотрим представление СБФ интерполяционным полиномом, заданной таблицей истинности:

В десятичном виде таблица истинности примет вид:

Построение ИП методом Лагранжа:

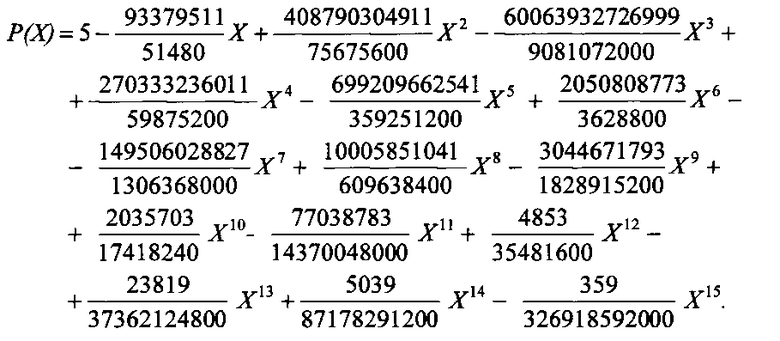
Вычисление значений СБФ:

Пусть Х=11 (x₁=1, х₂=0, х₃=1, х₄=1), тогда:

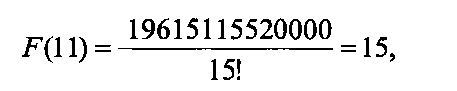
и соответственно получаем значения f₁=1, f₂=1, f₃=1, f₄=1.

Рассмотрим представление СБФ в модулярной интерполяционной полиномиальной форме представления системы булевых функций.

Так как

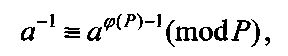
где М - простое число, φ(М) - функция Эйлера, то интерполяционный полином (1) примет вид:

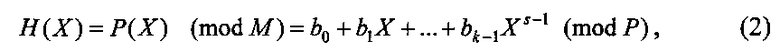
где b_i≡a _i (mod Р), i=0, 1, …, s-1, P - простое число, P>s.

Достоинством модулярной интерполяционной полиномиальной формы представления СБФ является значительное уменьшение коэффициентов. Рассмотрим СБФ из примера 1.

Пример 2. Представим полином P(Х) по модулю 17:

Z(X)=P(X) (mod 17),

Z(X)=5+11X+7X²+16Х³+11X⁴+X⁵+16Х⁶+15Х⁷+4Х⁹+12Х¹⁰+5X¹¹+9Х¹²+15Х¹³+14Х¹⁴+8Х¹⁵ (mod 17).

Полученный эффект:

- переход к целочисленным положительным значениям коэффициентов;

- среднее уменьшение коэффициентов в 250 раз.

Рассмотрим разложение интерполяционной полиномиальной формы представления системы булевых функций по булевым переменным.

Пример 3. Рассмотрим таблицу истинности системы булевых функций F(x₁, x₂, x₃):

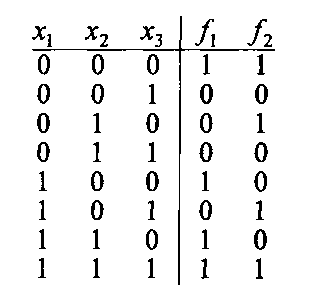
и интерпретируем ее следующим образом:

и соответственно в десятеричной системе счисления:

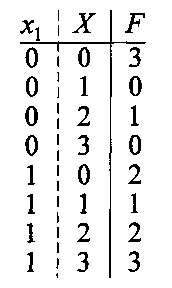
Построим интерполяционные полиномы для x₁=0 и x₁=1:

Н(х₁=0, X)=5Х²-X³-7X+3;

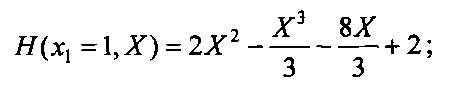
и соответственно модулярная форма примет вид:

H(x₁=0, X)(mod 5)=4Х³+3Х+3 (mod 5);

H(x₁=1, Х)(mod 5)=3Х³+2Х²+4Х+2 (mod 5).

Пусть х₁=1, X=2 (х₂=1, х₃=0):

H(x₁=1, X=2)(mod 5)=3·2³+2·2²+4·2+2 (mod 5)=2=(10)₂, тогда значения f₁=1, f₂=0.

Общий вид разложения модулярной интерполяционной формы представления СБФ по одной переменной примет вид:

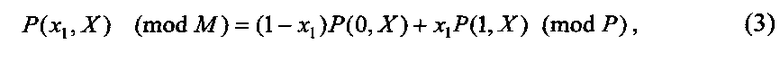
где

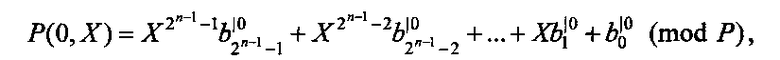
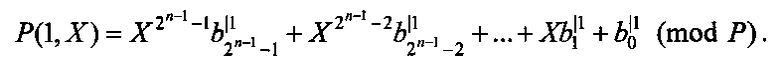
Общий вид разложения модулярной интерполяционной формы представления СБФ по k переменным примет вид:

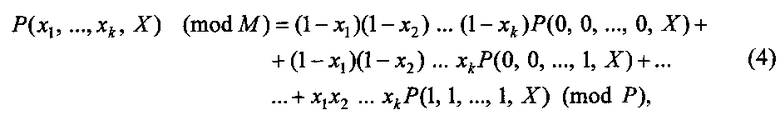
где

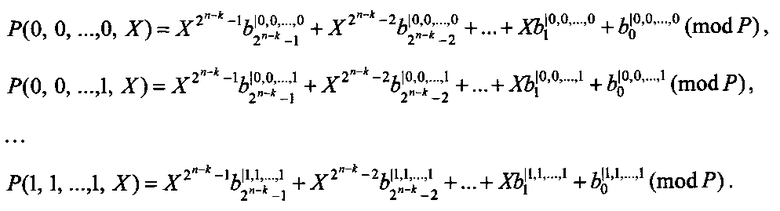
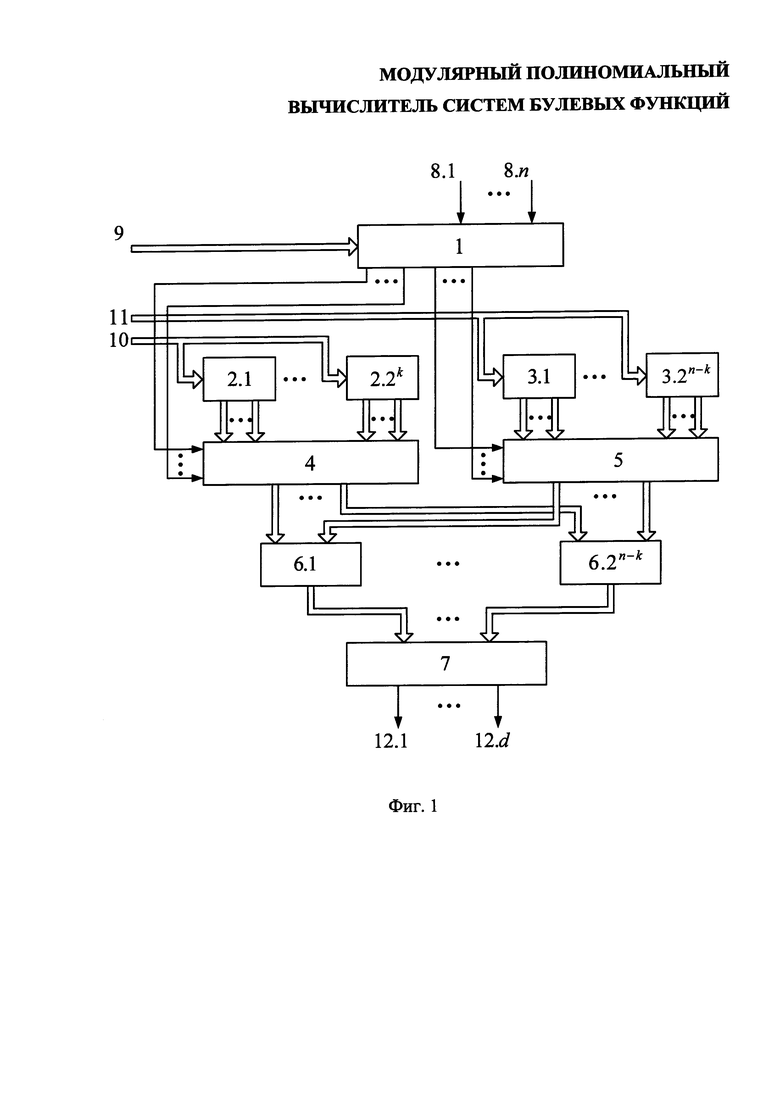
Структурная схема предлагаемого устройства представлена на фиг. 1, которое содержит коммутатор 1, блоки памяти 2.1, …, 2.2^k, блоки памяти 3.1, …, 3.2^k, многоканальный мультиплексор 4, многоканальный мультиплексор 5, умножители по модулю P 6.1, …, 6.2^n-k [3], сумматор по модулю Р 7 [4], входы устройства 8.1, …, 8.n подачи значений булевых переменных х₁, х₂, …, х_n, управляющий вход устройства 9 подачи значения количества переменных разложения, управляющий вход устройства 10 подачи значений коэффициентов, управляющий вход устройства 11 подачи значений вычетов возведения переменной в i-тую степень по модулю P, 12.1, …, 12.d выходы устройства выдачи значений булевых функций f₁, …, f_d.

Входы устройства 8.1, …, 8.n подачи булевых переменных х₁, х₂, …, х_n являются информационными входами коммутатора 1, управляющий вход которого подключен к управляющему входу устройства 9 подачи значения количества переменных разложения, управляющие входы блоков памяти 2.1, …, 2.2^k хранения значений коэффициентов разложения: 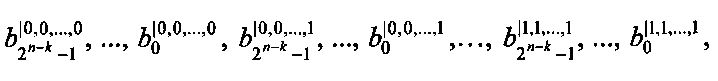подключены к управляющему входу устройства 10 подачи значений коэффициентов, управляющие входы блоков памяти 3.1, …, 3.2^k хранения значений вычетов возведения переменной X в i-ю степень по модулю Р: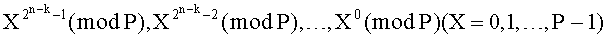 $$X^{2^{n-k}-1}(\mathrm{mod}P),X^{2^{n-k}-2}(\mathrm{mod}P),\dots ,X^0(\mathrm{mod}P)(X=\mathrm{0,}\mathrm{1,}\dots ,P-1)$$ подключены к управляющему входу устройства 11 подачи значений вычетов возведения переменной X в i-ю степень по модулю Р, управляющие входы многоканального мультиплексора 4 выделения группы коэффициентов подключены к k первым выходам коммутатора 1, где 1-й управляющий вход многоканального мультиплексора 4 подключен к 1-му входу коммутатора 1 и так далее и k-тый управляющий вход многоканального мультиплексора 4 подключен к k-му выходу коммутатора 1, а информационные входы подключены к выходам блоков памяти 2.1, …, 2.2^k, где 1-е 2^n-k информационных входов многоканального мультиплексора 4 подключены соответственно к 2^n-k выходам блока памяти 2.1 и так далее и 2^k-е 2^n-k информационных входов многоканального мультиплексора 4 подключены соответственно к 2^n-k выходам блока памяти 2.2^k, управляющие входы многоканального мультиплексора 5 выделения группы вычетов подключены к n-k вторым выходам коммутатора 1, где k+1-й управляющий вход многоканального мультиплексора 5 подключен к k+1-му входу коммутатора 1 и так далее и n-й управляющий вход многоканального мультиплексора 5 подключен к n-му выходу коммутатора 1, а информационные входы подключены к выходам блоков памяти 3.1, …, 3.2^k, где 1-е 2^n-k информационных входов многоканального мультиплексора 5 подключены соответственно к 2^n-k выходам блока памяти 3.1 и так далее и 2^k-е 2^n-k информационных входов многоканального мультиплексора 5 подключены соответственно к 2^n-k выходам блока памяти 3.2^k, входы умножителей 6.1, …, 6.2^n-k по модулю Р подключены к информационным выходам многоканального мультиплексора 4 и многоканального мультиплексора 5, где 1-й вход умножителя 6.1 подключен к 1-му информационному выходу многоканального мультиплексора 4 и 2-й вход умножителя 6.1 подключен к первому информационному выходу многоканального мультиплексора 5 и так далее и 1-й вход умножителя 6.2^n-k подключен к 2^n-k-му информационному выходу многоканального мультиплексора 4 и 2-й вход умножителя 6.2^n-k подключен к 2^n-k информационному выходу многоканального мультиплексора 5, а выходы подключены к входам сумматора 7 по моду P, где выход умножителя 6.1 подключен к 1-му входу сумматора 7 и так далее и выход умножителя 6.2^n-k подключен к 2^n-k-му входу сумматора 7, выходы сумматора 7 являются выходами выдачи значений булевых функций f₁, …, f_d устройства.

Работа модулярного полиномиального вычислителя систем булевых функций осуществляется следующим образом. В исходном состоянии с помощью управляющего сигнала, поступающего с управляющего входа устройства 10 подачи значений коэффициентов на управляющие входы блоков памяти 2.1, …, 2.2^k, осуществляется запись значений групп коэффициентов полиномов разложения 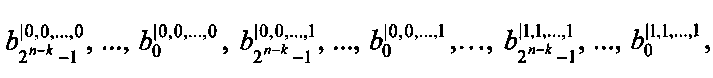и с помощью управляющего сигнала, поступающего с управляющего входа устройства 11 подачи значений вычетов возведения переменной в i-тую степень по модулю P на управляющие входы блоков памяти 3.1, …, 3.2^k хранения значений вычетов возведения переменной в i-тую степень по модулю Р, осуществляется запись предвычисленных значений переменной X по модулю Р: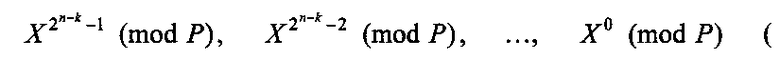 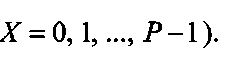В момент времени, соответствующий началу преобразования, на входы 8.1, …, 8.n коммутатора 1 поступают значения булевых переменных х₁, х₂, …, х_n. В коммутаторе 1 под воздействием управляющего сигнала, поступающего на его управляющий вход с управляющего входа устройства 9 подачи значения количества переменных разложения, выделяются переменные разложения с 1-й по k-тую, которые поступают на управляющие входы многоканального мультиплексора 4 выделения группы коэффициентов, который обеспечивает выделение группы коэффициентов из блоков памяти 2.1, …, 2.2^k в соответствии со значением переменных разложения х₁, х₂, …, х_k, где значениям переменных разложения х₁=0, х₂=0, х_k=0 соответствует группа коэффициентов 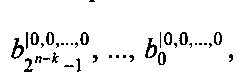и так далее и х₁=1, х₂=1, …, x_k=1 соответствует группа коэффициентов 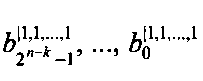. Остальные n-k значений булевых переменных поступают на управляющие входы многоканального мультиплексора 5 выделения группы вычетов, который обеспечивает выделение группы вычетов возведения переменной X=(x_n-kx_n-k+1x_n)₂ в степени 2^n-k, 2^n-k-1, …, 1, 0 в соответствии со значениями переменных x_n-k, x_n-k+1, …, х_n, значениям переменных х_n-k=0, х_n-k+1=0, …, х_n=0 соответствует группа вычетов

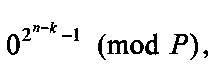
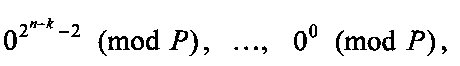и так далее и значениям переменных х_n-k=1, х_n-k+1=1, …, х_n=1 соответствует группа вычетов 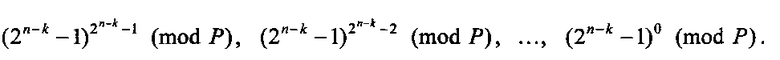Из многоканального мультиплексора 4 поступает группа коэффициентов разложения на 1-е входы умножителей 6.1, …, 6.2^n-k по модулю P, где на 1-й вход умножителя 6.1 по модулю Р поступает коэффициент 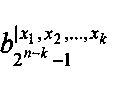и так далее и на 1-й вход умножителя 6.2^n-k по модулю Р поступает коэффициент 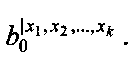Из многоканального мультиплексора 5 поступает группа вычетов возведения переменной X в i-тую степень i=(х_n-kх_n-k+1х_n)₂ на 2-е входы умножителей 6.1, …, 6.2^n-k по модулю Р, где на 2-й вход умножителя 6.1 по модулю Р поступает значение вычета 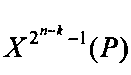и так далее и на 2-й вход умножителя 6.2^n-k по модулю Р поступает значение вычета Х⁰(Р). После преобразований в умножителях 6.1, …, 6.2^n-k значения вычислений поступают на входы сумматора 7 по модулю P, где после преобразований результат поступает на выходы устройства 12.1, …, 12.d выдачи значений булевых функций f₁, …, f_d, где младший разряд двоичного представления результата вычисления сумматора 7 соответствует значению f_d и подается на выход 12.d и так далее и старший разряд двоичного представления результата вычисления сумматора 7 соответствует значению f₁ и подается на выход 12.1.

Таким образом, технический эффект достигается за счет реализации вычислений безызбыточной полиномиальной формы представления системы булевых функций в конечном поле GF(P) аппаратными средствами умножителей по модулю Р и сумматора по модулю Р, что обеспечивает сокращение разрядной сетки вычислительных устройств и объемов памяти в L раз, где, в случае прототипа, L - количество избыточных булевых функций, необходимых для вычисления булевой функции в линейной числовой форме.

Литература

1. RU №2373564, 2009.

2. RU №2461868, 2012.

3. RU №1820377, 1993.

4. RU №2299461, 2007.

Изобретение относится к вычислительной технике и может быть использовано как специализированный вычислитель - универсальный в классе логических вычислений. Техническим результатом является уменьшение объемов оборудования. Устройство содержит коммутатор, 2^k блоков памяти хранения значений коэффициентов полиномов разложения, 2^n-k блоков памяти хранения значений вычетов возведения переменной в i-тую степень (i=0, 1, …, 2^n-k-1) по модулю Р, многоканальный мультиплексор выделения группы коэффициентов, многоканальный мультиплексор выделения группы вычетов, 2^n-k умножителей по модулю Ρ, сумматор по модулю Ρ, n входов подачи булевых переменных устройства, управляющий вход устройства подачи значения количества переменных разложения, управляющий вход устройства подачи значений коэффициентов, управляющий вход устройства подачи значений вычетов возведения переменной в i-тую степень по модулю Р, d выходов устройства выдачи значений булевых функций. 1 ил.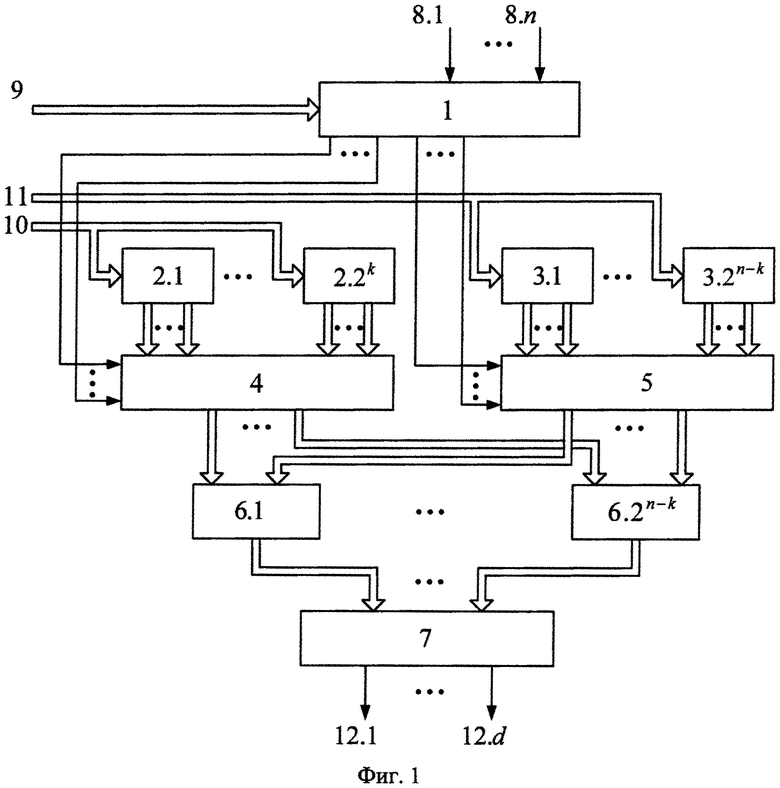

Модулярный полиномиальный вычислитель систем булевых функций, содержащий коммутатор, информационные входы которого являются n входами подачи булевых переменных устройства, управляющие входы которого подключены к управляющему входу устройства подачи значения количества переменных разложения, 2^k блоков памяти хранения значений коэффициентов полиномов разложения, управляющие входы которых подключены к управляющему входу устройства подачи значений коэффициентов, информационные выходы которых подключены к информационным входам многоканального мультиплексора выделения группы коэффициентов, управляющие входы которого подключены к k первым выходам коммутатора, отличающийся тем, что введены 2^n-k блоков памяти хранения значений вычетов возведения переменной в i-тую степень, где i=0,1,…,2^n-k-1 по модулю Р, управляющие входы которых подключены к управляющему входу устройства подачи значений вычетов возведения переменной в i-тую степень по модулю Ρ, информационные выходы которых подключены к информационным входам многоканального мультиплексора выделения группы вычетов, управляющие входы которого подключены к n-k вторым информационным выходам коммутатора, 2^n-k умножителей по модулю Р, где входы j-го умножителя по модулю Ρ подключены к j-м информационным выходам многоканального мультиплексора выделения группы коэффициентов и многоканального мультиплексора выделения группы вычетов, где j=1, 2,…,2^n-k, выходы которых подключены к входам сумматора по модулю Ρ, d выходов которого являются d выходами устройства выдачи значений булевых функций.