Изобретение относится к способам создания широкополосных случайных процессов с заданными собственными и взаимными спектральными плотностями мощности и может быть использовано в приборостроении, машиностроении, вычислительной технике для создания, в частности, многоканальных автоматических систем, в испытаниях на вибростойкость к воздействиям случайной вибрации и т.д.
Известен («Автоматическое управление вибрационными испытаниями», Библиотека по автоматике, выпуск 579, Москва, Энергия, 1978 г.) способ формирования по заданной спектральной плотности случайного сигнала в форме разложения Райса-Пирсона со случайной на каждой гармонике фазой, равномерно распределенной в диапазоне [-π, π], и выполнения процедуры обратного быстрого преобразования Фурье (ОБПФ).
Сформированные таким способом случайные сигналы являются независимыми, что в некоторых случаях является недостатком.
Предлагаемым изобретением решается задача генерирования двух случайных сигналов x(t) и y(t) с заданной функцией когерентности γху(f).
Для достижения названного технического результата предлагается способ формирования коррелированных случайных сигналов, включающий формирование во временной области по заданным спектральным плотностям Sx(f) и Sy(f) стационарных случайных сигналов x(t), y(t) в форме разложения Райса-Пирсона со случайными на каждой гармонике f1 фазами Θi и Ωi, определяемыми методом случайной выборки случайной величины, одна из которых - Θi для сигнала x(t) равномерно распределена в диапазоне [-π, π], а другая - Ωi для второго сигнала y(t) определяется как сумма Ωi=Θi+Δφi случайной величины Θi и случайной величины Δφi, равномерно распределенной в диапазоне [-φi, φi], границы которого определяются через взаимную спектральную плотность Sxy(f) случайных сигналов x(t) и y(t) из решения уравнения:
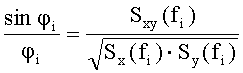
и выполнения процедуры ОБПФ.
Отличительным признаком предлагаемого способа является то, что случайные фазы Θi одного сигнала x(t) определяются на каждой гармонике fi методом случайной выборки случайной величины, равномерно распределенной в диапазоне [-π, π], а случайные фазы Ωi второго сигнала y(t) определяются на каждой гармонике fi как сумма Ωi=Θi+Δφi случайной величины Ωi, равномерно распределенной в диапазоне [-π, π], и случайной величины Δφi, равномерно распределенной в диапазоне [-φi, φi], границы которого определяются через взаимную спектральную плотность Ssy(f) случайных сигналов x(t) и y(t) из решения уравнения:
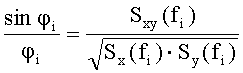
Благодаря наличию указанного отличительного признака в совокупности с известными приобретается возможность формирования двух случайных сигналов x(t) и y(t) с заданной функцией когерентности γху(f).
В результате поиска по источникам патентной и научно-технической информации, решений, содержащих аналогичные признаки, не обнаружено.
Таким образом, можно сделать заключение о том, что предложенный способ неизвестен на уровне техники и, следовательно, соответствует критерию «патентоспособности».
Предложенный способ может найти применение везде, где возникает необходимость в случайных взаимно коррелированных сигналах с заданным уровнем когерентности, что позволяет сделать вывод о соответствии критерию «Промышленная применимость».
Способ реализуется следующим образом: в заданном спектральной плотностью Sx(f) диапазоне частот с шагом Δf выбирают дискретный ряд частот fi=i Δf. В каждом частотном диапазоне fi<f<fi+1 по заданной спектральной плотности Sx(f) определяют амплитуды гармоник 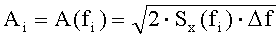
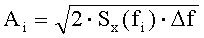
По заданной спектральной плотности Sy(f) в каждом частотном диапазоне fi<f<fi+1 определяют амплитуды гармоник 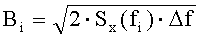
На каждой гармонике fi по заданным в частотной области спектрам амплитуд Sx(f), Sy(f) и взаимной спектральной плотности мощности Sxy(f) случайных сигналов x(f) и y(t) вычисляют функции когерентности:
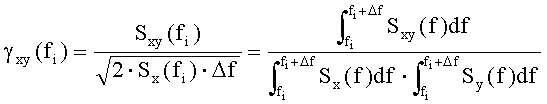
и диапазон {±φi} случайных фаз Δφi:
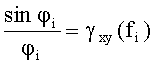
Из случайной, равномерно распределенной в диапазоне [-φi, φi] величины по случайному закону выбирают фазы Δφi. Вычисляют фазы Ωi=Θi+Δφi гармоник сигнала y(f). Формируют блок комплексных амплитуд {Re(fi), Im(fi)}:
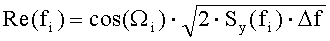
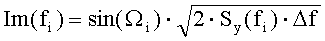
выполняют процедуры ОБПФ и получают во временной области однокомпонентный сигнал y(iΔt) в форме разложения Райса-Пирсона, длиной T=1/Δf, содержащего N точек с периодом дискретизации Δt [сек] и случайными амплитудами Bi (i=0, 1, …, N-1), распределенными по нормальному закону Гаусса, коррелированный с сигналом x(iΔt с заданной функцией когерентности γxy(fi).
В качестве иллюстрации на фигуре 1 приведены примеры взаимосвязанных сигналов (2-20 Гц, белый шум, lg скз) с когерентностью 0,9; 0,7; 0,5 и 0,0 соответственно, полученные предложенным способом.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГЕНЕРАТОР КОРРЕЛИРОВАННЫХ СЛУЧАЙНЫХ СИГНАЛОВ | 2013 |
|
RU2546580C2 |
| СПОСОБ НАПРАВЛЕННОГО ИНЕРЦИОННОГО ВИБРОВОЗБУЖДЕНИЯ И ДЕБАЛАНСНЫЙ ВИБРОВОЗБУДИТЕЛЬ НАПРАВЛЕННОГО ДЕЙСТВИЯ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2528715C1 |
| СПОСОБ ИМИТАЦИИ РАДИОЛОКАЦИОННОЙ ЦЕЛИ С НЕЛИНЕЙНЫМИ ЭЛЕКТРИЧЕСКИМИ СВОЙСТВАМИ | 2011 |
|
RU2507534C2 |
| ЭТАЛОННОЕ РАБОЧЕЕ МЕСТО АБСОЛЮТНОЙ ПРЕЦИЗИОННОЙ КАЛИБРОВКИ ЗАПАЗДЫВАНИЯ ОГИБАЮЩИХ ЛИТЕРНЫХ ЧАСТОТ В ПРИЕМНИКЕ СИГНАЛОВ ГЛОНАСС | 2011 |
|
RU2525853C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УРОВНЯ МОРЯ | 2011 |
|
RU2452984C1 |
| СПОСОБ ИМИТАЦИИ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ РАДИОЛОКАЦИОННЫХ СИСТЕМ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2015 |
|
RU2586966C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ОШИБКИ НА БИТ ПО ФЛУКТУАЦИЯМ ФАЗЫ ИНФОРМАЦИОННЫХ СИГНАЛОВ | 2012 |
|
RU2526283C2 |
| АКУСТИЧЕСКИЙ СПОСОБ ОБНАРУЖЕНИЯ НЕИСПРАВНОСТИ РЕЛЬСОВОГО ПУТИ | 2012 |
|
RU2511644C1 |
| СПОСОБ СЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ И ЭХОЛОТ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2573626C1 |
| СПОСОБ ОБНАРУЖЕНИЯ, ОПРЕДЕЛЕНИЯ КООРДИНАТ И СОПРОВОЖДЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ | 2014 |
|
RU2564385C1 |
Изобретение относится к способам создания широкополосных случайных процессов с заданными собственными и взаимными спектральными плотностями мощности и может быть использовано в приборостроении, машиностроении, вычислительной технике для создания, в частности, многоканальных автоматических систем, в испытаниях на вибростойкость к воздействиям случайной вибрации. Техническим результатом является генерирование двух случайных сигналов с заданной функцией когерентности. Способ включает формирование во временной области по заданным спектральным плотностям Sx(f)
и Sy(f)
стационарных случайных сигналов x(f),
y(t)
в форме разложения Райса-Пирсона со случайными на каждой гармонике fi
фазами Θi и Ωi, определяемыми методом случайной выборки случайной величины, одна из которых - Θi для сигнала x(t)
равномерно распределена в диапазоне [-π, π], а другая - Ωi для второго сигнала y(t)
определяется как сумма Ωi=Θi+Δφi случайной величины Θi и случайной величины Δφi,
равномерно распределенной в диапазоне [-φi, φi],
границы которого определяются через взаимную спектральную плотность Sxy(f) случайных сигналов x(t)
и y(t). 1 ил.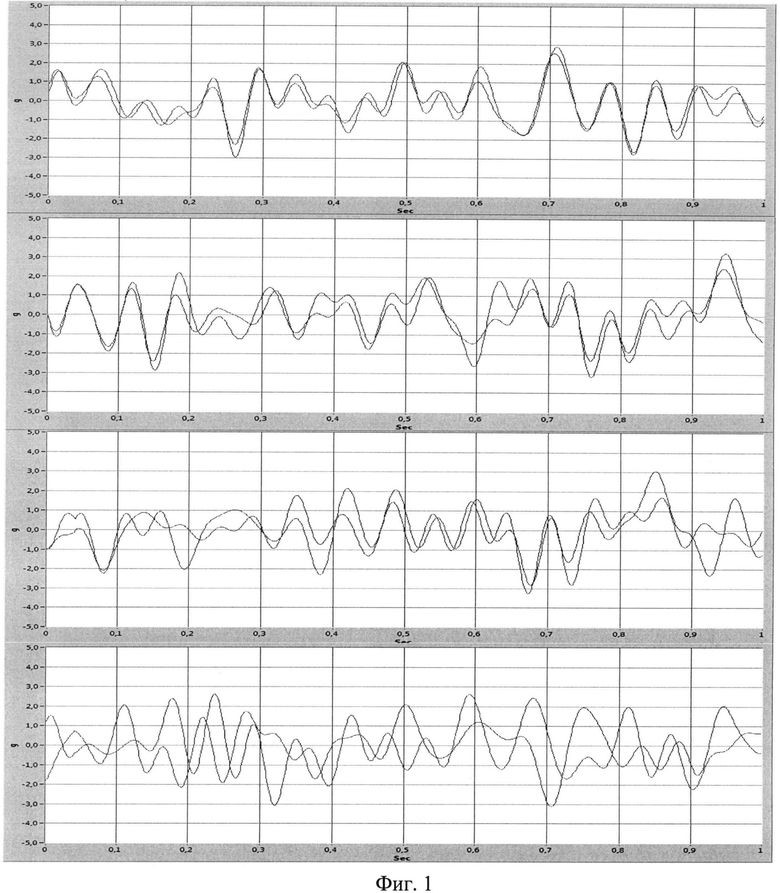
Способ формирования коррелированных случайных сигналов, включающий формирование во временной области по заданным спектральным плотностям Sx(f) и
Sy(f)
стационарных случайных сигналов x(t), y(t)
в форме разложения Райса-Пирсона со случайными на каждой гармонике fi
фазами Θi и Ωi, отличающийся тем, что случайные фазы Θi одного сигнала x(t)
определяются на каждой гармонике fi
методом случайной выборки случайной величины, равномерно распределенной в диапазоне [-π,
π], а случайные фазы Ωi второго сигнала y(t)
определяются на каждой гармонике fi
как сумма Ωi=Θi+Δφi, случайной величины Θi, равномерно распределенной в диапазоне [-π, π], и случайной величины ΔφI,
равномерно распределенной в диапазоне [-φ,
φi],
границы которого определяются через взаимную спектральную плотность Sxy(f)
случайных сигналов x(t)
и y(t)
из решения уравнения:
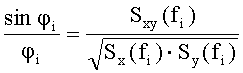 .
.
| ГЕТМАНОВ А.Г | |||
| и др | |||
| АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ВИБРАЦИОННЫМИ ИСПЫТАНИЯМИ, Москва, Энергия, 1978, с | |||
| Способ размножения копий рисунков, текста и т.п. | 1921 |
|
SU89A1 |
| Генератор случайного процесса | 1982 |
|
SU1068936A1 |
| Формирователь случайных сигналов | 1987 |
|
SU1483587A1 |
| ГЕНЕРАТОР СЛУЧАЙНЫХ СИГНАЛОВ | 2000 |
|
RU2201649C2 |
| US 6337643 B1, 08.01.2002 | |||
Авторы
Даты
2015-04-10—Публикация
2013-04-11—Подача