Изобретение относится к физике материального контактного взаимодействия, конкретно к способу установления предельного состояния деформируемой сжимающей и растягивающей нагрузкой материальной среды.
Известен способ установления предельного состояния деформируемой структурно-устойчивой материальной среды по закону Ш. Кулона, заключающийся в том, что образцы материальной среды с ненарушенной структурой, отобранные из массива с глубины h, с удельный весом γ, выдерживают в условиях компрессии под гравитационным (бытовым) давлением pб=γh, выдержанные под давлением pб образцы нагружают в условиях компрессии возрастающими ступенями сжимающего давления pi, на каждой ступени давления pi при стабилизации осадки образца производят его поступательный сдвиг при максимальном тангенциальном напряжении τi, строят прямолинейный график зависимости Ш. Кулона τi=pi·tgφстр+cстр, по углу наклона которого рассчитывают угол φстр внутреннего трения и определяют удельное сцепление cстр среды на оси τi графика при нулевом сжимающем давлении p=0 [1].
Недостатком известного способа установления предельного состояния материальной среды по закону Ш. Кулона является ограниченная применимость графика τi=pi·tgφстр+cстр растяжений только несжимаемых (безпористых) структурно-устойчивых материальных сред.
Наиболее близким к предлагаемому является способ установления предельного состояния сжимаемой (пористой) грунтовой материальной среды под штампом лопастного сдвигомера-прессиометра Л.С. Амаряна методом поступательного среза в скважине, заключающийся в том, что бурят скважину и погружают через нее на глубину h грунтового массива распорные штампы рабочего наконечника, создают через штампы на грунт ступени горизонтального сжимающего давления pi, срезают обжатые ступенью давления рi стенки скважины поперечными грунтозацепами штампов при поступательном их извлечении с рабочим наконечником из скважины и замеряют соответствующие ступеням pi тангенциальные срезающие напряжения τi, отличающийся тем, что график испытаний τi=ƒ(pi) линеаризируют прямой, которая отсекает при давлении p=0 на оси τi величину удельного сцепления c-cстр, по углу наклона прямой графика испытаний определяют угол φ=φстр внутреннего трения грунта [2].
Недостатком известного способа установления предельного состояния грунтов методом поступательного среза является низкая точность определения параметров прочности грунта φ=φстр и c=cстр с ненарушенной структурой из-за криволинейности графика τi=ƒ(pi), представляющего зависимость для тангенциального срезающего напряжения τстр=p·tgφстр+cстр. Определяемые параметры прочности φстр и cстр в массиве не соответствуют результатам лабораторных испытаний грунтов на сдвиговых приборах, поэтому метод поступательного среза грунтов не получил широкого распространения в практике инженерных изысканий, в то время, как именно он является более достоверным по сравнению с данными лабораторных испытаний в условиях компрессии. Показатели прочности (φн и cн) нарушенной структуры грунта при давлениях сверх бытового p>pб в большей мере интересуют проектировщиков для расчета оснований под реальными сооружениями. Таким образом, графики тангенциальных срезающих напряжений τн=p·tgφн+cн и предельного состояния именно нарушенной структуры грунта под сооружениями, получаемые при его поступательном сдвиге в скважине, реально отражают работу рассматриваемых проектировщиками оснований сооружений.
В изобретении поставлена задача определения границ предельного состояния материальной связной среды с нарушенной структурной прочностью, характерной под активно воздействующей внешней нагрузкой, превосходящей структурную прочность среды, и установления закономерности предельного состояния связной среды за пределами ее структурной прочности и закона Ш. Кулона при давлениях pi свыше гравитационного (бытового) рб, т.е. pi>рб.
Решение поставленной задачи позволяет достичь технический результат по способу установления предельного состояния деформируемой материальной среды, заключающемуся в том, что по данным сдвига нагруженной ступенями нормального давления pi материальной среды на глубине h соответствующей тангенциальной нагрузкой τi, строят график зависимости τi=ƒ(pi), график линеаризируют прямой до пересечения с осью τi и осью pi, на оси τi устанавливают величину удельного сцепления с=сстр структурированной среды, на оси pi устанавливают величину противодавления связности среды -ре= -сстр·ctgφстр и определяют угол φ=φстр внутреннего трения структурированной среды в соответствие с законом Ш. Кулона τi=pi·tgφстр+сстр, который достигается тем, что закон Ш. Кулона τстр=pi·tgφстр+сстр устанавливают в интервале нормального давления -(ре)≤pi≤(+рб), где рб=(γстр·h-сстр)ctgφстр - гравитационное (бытовое) давление для структурированной среды с удельным весом γстр, при давлении pi>рб предельное состояние материальной среды рассматривают с нарушенной структурой и описывают зависимостью τн=рн·tgφн+сн, где рн - ступени давления нарушения структурной прочности среды (рн≥рб) с удельным весом γн, 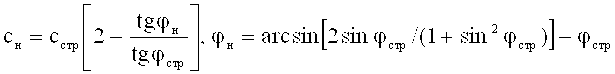
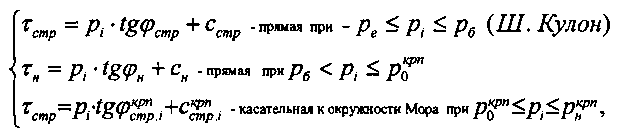
где 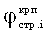
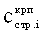
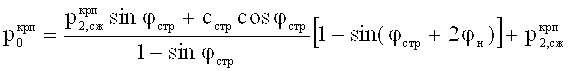
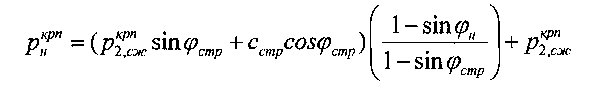 - предельно критическое разрушающее давление под упругим ядром уплотнения среды,
- предельно критическое разрушающее давление под упругим ядром уплотнения среды,
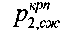 - разрушающее предельно критическое для среды давление под краями штампа,
- разрушающее предельно критическое для среды давление под краями штампа,
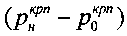 - интервал давлений структурной прочности среды в упругом ядре уплотнения под штампом при удельном весе среды в ядре γя>>γстр.
- интервал давлений структурной прочности среды в упругом ядре уплотнения под штампом при удельном весе среды в ядре γя>>γстр.
Линеаризация графика Ш. Кулона τi=ƒ(pi) при давлениях pi>pб оправдана, так как прямая графика определяет на оси τi минимальное значение удельного сцепления cmin=cн, что устраивает проектировщиков в процессе введения коэффициентов запаса прочности оснований и конструкций сооружений.
Величина гравитационного давления для массива связной среды определена законом Ш. Кулона τ=p·tgφ°+c, откуда 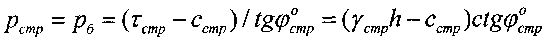
где γстр=γстр·h - тангенциальное напряжение, γстр - удельный вес материальной среды в массиве естественного природного сложения [1].
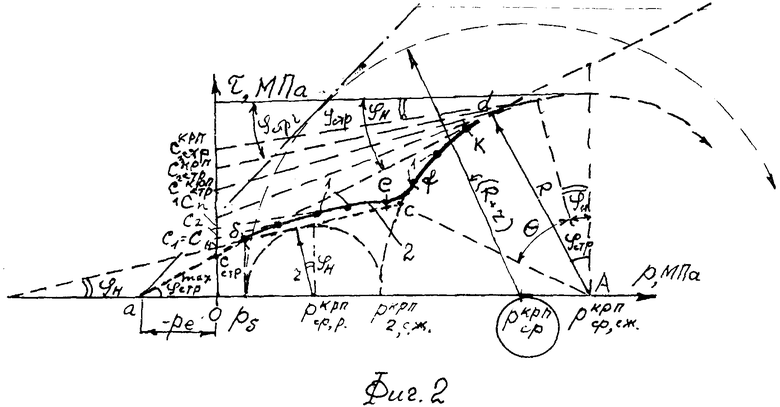
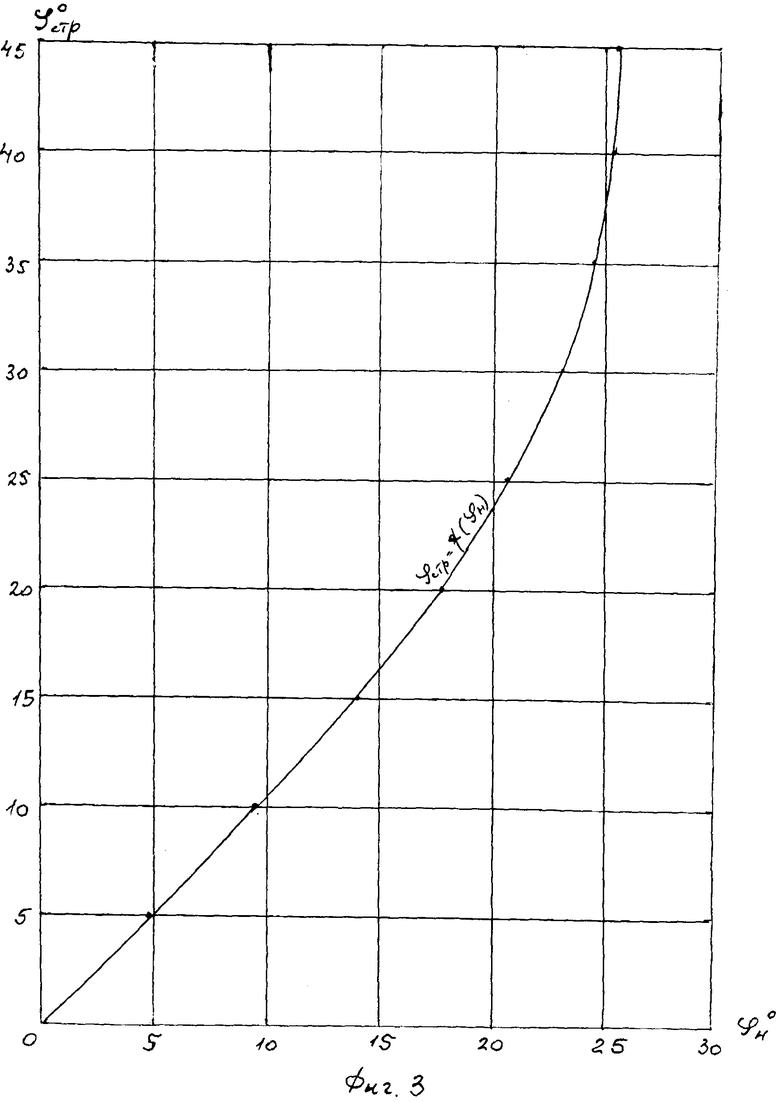
Изобретение поясняется графическими материалами, где на фиг. 1 представлены графики предельного состояния материальной среды в структурированном (Ш. Кулон) и нарушенном состоянии при растяжении-сжатии; на фиг. 2 - график (жирная линия) результатов испытаний суглинка на поступательный сдвиг в скважине лопастным прессиометром ЛПМ-12С проф. Л.С. Амаряна; фиг. 3 - график зависимости φн=ƒ(φстр).
Способ установления предельного состояния связной материальной среды реализуется следующим образом. На заданной глубине h массива среды определяют ее удельный вес γстр по образцам, отобранным в пробуренной скважине. Стандартным методом [3] исследования связной материальной среды - поступательного среза в скважине лопастным прессиометром-сдвигометром определяют величину тангенциального напряжения τстр при срезе стенок скважины, обжатых возрастающими ступенями нормального давления pстр (фиг. 2). За первую ступень давления принимают величину давления, близкую к бытовому давлению, но отличную от нуля. За последнюю ступень давления принимают давление, при дальнейшем увеличении которого происходит разрушение стенок скважины под проваливающимся штампом прессиометра-сдвигометра. По данным pстр и τстр строят график (фиг. 2) зависимости τi=ƒ(pi) - кривая б, е, c, f, к. Лианизируя участок графика «б е» до пересечения прямой с осями «о τ» и «о p» координат графика, определяют величину угла φн внутреннего трения и удельного сцепления cн среды с нарушенной структурой. По точкам на дуге «с к» строят окружность радиусом R (фиг. 2) с центром в точке А, отсекающей на оси «о р» значение разрушающего предельно критического давления 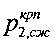 под краями штампа и пересекающейся с прямой «б е» в точке «с» (фиг. 2), соответствующей предельно критическому давлению
под краями штампа и пересекающейся с прямой «б е» в точке «с» (фиг. 2), соответствующей предельно критическому давлению 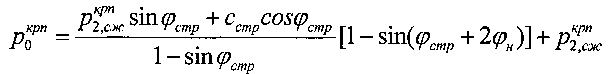 вблизи краев штампа (фиг. 1). Проводят касательную линию к дуге «с к» окружности радиусом R, проходящую через точку «б», соответствующую тангенциальному напряжению τ=γстр·h при бытовом давлении
вблизи краев штампа (фиг. 1). Проводят касательную линию к дуге «с к» окружности радиусом R, проходящую через точку «б», соответствующую тангенциальному напряжению τ=γстр·h при бытовом давлении 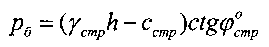 , равном предельно критическому разрушающему давлению
, равном предельно критическому разрушающему давлению 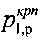 за краями штампа у краев воронки сжатия-растяжения среды, отсекаемому на оси «о p» дугой окружности радиусом r (фиг. 1).
за краями штампа у краев воронки сжатия-растяжения среды, отсекаемому на оси «о p» дугой окружности радиусом r (фиг. 1).
Через точку «б» проводят (фиг. 1, 2) прямую, касательную к окружности радиусом R в точке d и отсекающую на оси «о τ» величину удельного сцепления cстр структурированной среды, а на оси «о p» в точке «a» - величину давления связной среды 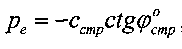 , где угол наклона касательной прямой «a d» к оси «о p», равный углу
, где угол наклона касательной прямой «a d» к оси «о p», равный углу 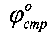 внутреннего трения структурированной среды. Из геометрических соотношений графика τ=ƒ(p) предельного состояния среды (фиг. 1, 2) [4] получают значения величин: гравитационного давления
внутреннего трения структурированной среды. Из геометрических соотношений графика τ=ƒ(p) предельного состояния среды (фиг. 1, 2) [4] получают значения величин: гравитационного давления 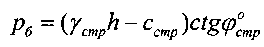 ; давления в точке «с» пересечения прямой «б с» графика с дугой окружности радиусом R
; давления в точке «с» пересечения прямой «б с» графика с дугой окружности радиусом R
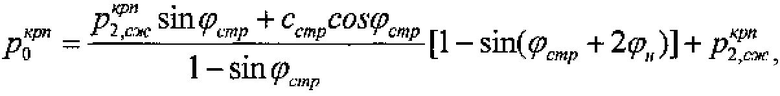
где 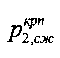 - разрушающее предельно критическое для среды давление под краями штампа,
- разрушающее предельно критическое для среды давление под краями штампа, 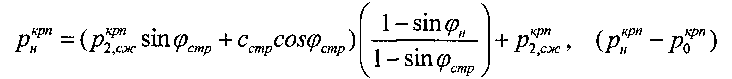 - интервал давления структурированной прочности среды в упругом ядре уплотнения под штампом при удельном весе среды в ядре γя>>γстр; зависимостей [4]
- интервал давления структурированной прочности среды в упругом ядре уплотнения под штампом при удельном весе среды в ядре γя>>γстр; зависимостей [4] 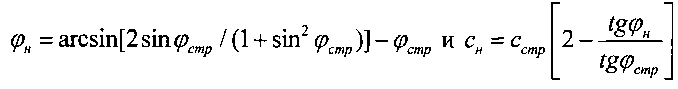
При давлениях 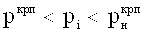
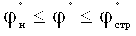
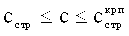
Пример реализации способа. Результаты 10 испытаний суглинков пос. Икша Московской области (1980 г. ) на сжатие и сдвиг в скважинах лопастным прессиометром-сдвигомером были обработаны в соответствии с тарировочными данными и построены графики предельного состояния материальной среды (фиг. 1). На фиг. 2 представлен результат обработки опытных данных, полученных сдвигомером-прессиометром, в виде обведенных точек 1 (б, e, f, к) типового криволинейного графика 2 зависимости τi=ƒ(pi). Опыты начинались при обжатии суглинка штампами в скважине бытовым давлением рб≈0,02 МПа с глубины 1 м. По данным параллельных испытаний отобранных из скважины образцов суглинка его физические характеристики имели значения: сстр=0,02МПа, φстр=23°, γ=0,019 кг/см3.
После построения графика (б, e, f, к) его аппроксимируют прямой «б с» и окружностью с центром в точке А и радиусом R (фиг. 2) получают дугу окружности «c, f, к, d», пересекающуюся с прямой графика в точке «с». Продолжение прямой графика «с, б» с осью τ при р=0 дает отсечку удельного сцепления с=сн=0,023 МПа, а угол ее наклона к оси pi - значение угла φ=φн=19,7° внутреннего трения суглинка нарушенной структуры в интервале упруго-пластического состояния среды 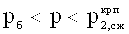

Предложенный способ установления предельного состояния растяжения-сжатия связной материальной среды, характеризующийся физическими параметрами - углом внутреннего трения и удельным сцеплением, впервые устанавливает рамки применимости закона Ш. Кулона к чисто упругим материалам и расширяет возможности изучения предельного напряженно-деформированного состояния среды под нагрузкой в фазах упруго-пластических деформаций до полного ее разрушения. Впервые предельное состояние деформируемой среды определяется как под плоским, так и под сферическим штампом [5] (по окружности Мора радиусом (r+R), по удельному эквивалентному сцеплению - cэ, по углу θ внутреннего трения - фиг. 1 и фиг. 2).
Источники информации
1. Цитович Н.А. Механика грунтов (краткий курс): Учебник для ВУЗов. - 3-е изд., доп.- М.: Высшая школа, 1979. - С.43 - 50 (аналог), с. 48-49.
2. ГОСТ 21719-80. Грунты. Методы полевых испытаний на срез в скважинах и в массиве. - М.: Госстандарт СССР, 1980 г. - С. 16 - 17, 20 (прототип).
3. Рекомендации по испытанию грунтов методом лопастной прессиометрии / ПНИИИС.- М.: Стройиздат, 1985. - с. 28-29, 34-35.
4. Хрусталев Е.Н. Контактное взаимодействие в геомеханике. Часть I: Нсущая способность оснований сооружений. - Тверь: ТГТУ, 2004 - с. 75-77 (рис. 2.13).
5. Цитович Н.А. Механика грунтов (краткий курс): Учебник для ВУЗов. - 3-е изд., доп. - М.: Высшая школа, 1979. - С. 56-57.
Изобретение относится к физике материального контактного взаимодействия, конкретно к способу установления предельного состояния деформируемой сжимающей и растягивающей нагрузкой материальной среды. Сущность: по данным сдвига нагруженной ступенями нормального давления pi материальной среды на глубине h тангенциальной нагрузкой τi строят график зависимости τi=ƒ(pi). График линеаризируют прямой до пересечения с осью τi и осью pi, на оси τi устанавливают величину удельного сцепления структурированной среды с=сстр, на оси pi устанавливают величину противодавления связности среды -ре= -сстр·ctgφстр и определяют угол φ=φстр внутреннего трения структурированной среды. Закон Ш. Кулона τстр=pi·tgφстр+сстр устанавливают в интервале нормального давления -(ре)≤pi≤(+рб), где рб=(γстр·h-сстр)ctgφстр - гравитационное (бытовое) давление для структурированной среды с удельным весом γстр, при давлении pi>рб. Предельное состояние материальной среды рассматривают с нарушенной структурой и описывают зависимостью τн=рн·tgφн+сн, а предельное состояние материальной среды в общем виде описывают системой уравнений. Технический результат: возможность определения границ предельного состояния материальной связной среды с нарушенной структурной прочностью и установления закономерности предельного состояния связной среды за пределами ее структурной прочности и закона Ш. Кулона при давлениях pi свыше гравитационного (бытового) рб, т.е. pi>рб. 3 ил.,1 табл.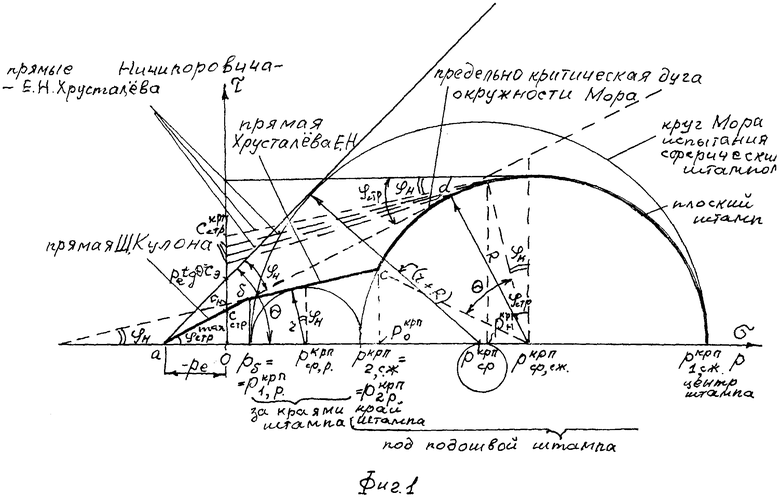
Способ установления предельного состояния деформируемой материальной среды, заключающийся в том, что по данным сдвига нагруженной ступенями нормального давления pi материальной среды на глубине h соответствующей тангенциальной нагрузкой τi строят график зависимости τi=ƒ(pi), график линеаризируют прямой до пересечения с осью τi и осью pi, на оси τi устанавливают величину удельного сцепления структурированной среды с=сстр, на оси pi устанавливают величину противодавления связности среды -ре= -сстр·ctgφстр и определяют угол φ=φстр внутреннего трения структурированной среды в соответствии с законом Ш. Кулона τi=pi·tgφстр+сстр, отличающийся тем, что закон Ш. Кулона τстр=pi·tgφстр+сстр устанавливают в интервале нормального давления -(ре)≤pi≤(+рб), где рб=(γстр·h-сстр)ctgφстр - гравитационное (бытовое) давление для структурированной среды с удельным весом γстр, при давлении pi>рб предельное состояние материальной среды рассматривают с нарушенной структурой и описывают зависимостью τн=рн·tgφн+сн, где рн - ступени давления нарушения структурной прочности среды (рн≥рб) с удельным весом γн, 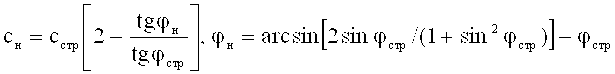
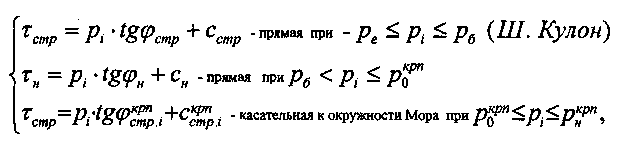
где 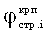
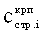
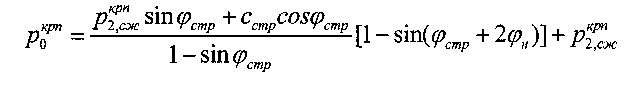 - предельно критическое давление сжатия вблизи краев штампа,
- предельно критическое давление сжатия вблизи краев штампа,
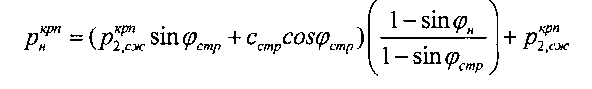 - предельно критическое разрушающее давление под упругим ядром уплотнения среды,
- предельно критическое разрушающее давление под упругим ядром уплотнения среды,
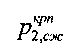 - разрушающее предельно критическое для среды давление под краями штампа,
- разрушающее предельно критическое для среды давление под краями штампа,
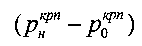 - интервал давлений структурной прочности среды в упругом ядре уплотнения под штампом при удельном весе среды в ядре γя>>γстр.
- интервал давлений структурной прочности среды в упругом ядре уплотнения под штампом при удельном весе среды в ядре γя>>γстр.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНО МАКСИМАЛЬНОЙ КОНТАКТНОЙ ПРОЧНОСТИ ГРУНТОВОГО ОСНОВАНИЯ В УСЛОВИЯХ ПЛОСКОЙ ДЕФОРМАЦИИ | 2004 |
|
RU2265824C1 |
| Способ исследования прочностных свойств грунта и устройство для его осуществления | 1987 |
|
SU1609858A1 |
| Устройство для исследования прочностных свойств грунта | 1989 |
|
SU1709015A1 |
| US 3616685 A1 02.11.1971 | |||
Авторы
Даты
2015-07-10—Публикация
2013-08-22—Подача