Изобретение относится к области физики материального контактного взаимодействия, конкретно к способу получения определяющих физических параметров удельного сцепления и угла внутреннего трения структурированной и нарушенной по структуре материальной среды.
1. Известен способ определения физических параметров - угла ϕ=ϕстр внутреннего трения и удельного сцепления С=Сстр грунтовой материальной среды в массиве с ненарушенной структурой, заключающийся в том, что из массива отбирают образцы среды с ненарушенной структурой, выдерживают их под гравитационной бытовой нагрузкой 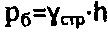 , где
, где 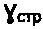 - удельный вес среды, h - глубина отбора образца из массива среды, поочередно образцы заряжают в кольцевую обойму сдвигового прибора, производят обжатие каждого из них плоским штампом возрастающей ступенью нагрузки pi и плоскостной срез обжатого образца с замером сопротивления сдвига τ, отличающийся тем, что строят график зависимости Кулона-Мора
- удельный вес среды, h - глубина отбора образца из массива среды, поочередно образцы заряжают в кольцевую обойму сдвигового прибора, производят обжатие каждого из них плоским штампом возрастающей ступенью нагрузки pi и плоскостной срез обжатого образца с замером сопротивления сдвига τ, отличающийся тем, что строят график зависимости Кулона-Мора 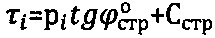 и при нулевом давлении р=0 в условиях компрессии определяют удельное сцепление Сстр и угол
и при нулевом давлении р=0 в условиях компрессии определяют удельное сцепление Сстр и угол 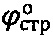 внутреннего трения среды ненарушенной структуры [1].
внутреннего трения среды ненарушенной структуры [1].
Недостатком известного способа является определение параметров 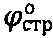 и Сстр среды ненарушенной структуры при гидростатическом бытовом давлении
и Сстр среды ненарушенной структуры при гидростатическом бытовом давлении 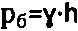 , когда связная среда обладает в массиве бытовым давлением
, когда связная среда обладает в массиве бытовым давлением 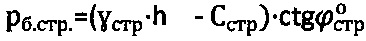 . Проектировщиков интересуют давление пригрузок р>рб. от действующих сооружений, когда требуется значение углов ϕ=ϕн и удельного сцепления С=Сн среды с нарушенной структурой. С другой стороны, испытания ненарушенных образцов среды на сдвиг в лабораториях производят в условиях компрессии, а не с поверхности полупространства массива, в связи с чем параметры ϕстр и Сстр получают искаженными, отличными от действительных.
. Проектировщиков интересуют давление пригрузок р>рб. от действующих сооружений, когда требуется значение углов ϕ=ϕн и удельного сцепления С=Сн среды с нарушенной структурой. С другой стороны, испытания ненарушенных образцов среды на сдвиг в лабораториях производят в условиях компрессии, а не с поверхности полупространства массива, в связи с чем параметры ϕстр и Сстр получают искаженными, отличными от действительных.
Известен способ определения физических параметров прочности ненарушенной структуры грунтовой материальной среды в массиве методом поступательного среза лопастным сдвигомером-прессиометром Л.С. Амаряна, заключающийся в том, что бурят вертикальную скважину в массиве среды, в скважину задавливают на заданную глубину h двутавровый рабочий наконечник сдвигомера-прессиометра с обрезанием ее боковых стенок плоскими полками, из боковых полок двутаврового наконечника выдвигают поочередно возрастающими ступенями давления pi жесткие плоские штампы с поперечными грунтозацепами, далее производят сдвиг среды на глубине h на каждой ступени давления pi>рб., выше бытового давления 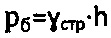 в момент стабилизации осадок среды под ступенями давления путем поступательного среза под напряжением τi - обжатой среды в скважине, по полученным данным pi и τi строят график Кулона-Мора
в момент стабилизации осадок среды под ступенями давления путем поступательного среза под напряжением τi - обжатой среды в скважине, по полученным данным pi и τi строят график Кулона-Мора 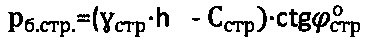 и определяют параметры прочности среды ϕ=ϕстр и С=Сстр [2, 3].
и определяют параметры прочности среды ϕ=ϕстр и С=Сстр [2, 3].
Получаемые лопастными прессиометрами-сдвигомерами параметры прочности 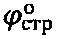 и Сстр не совпадают с лабораторными данными исследований образцов среды ϕ=ϕстр и С=Сстр ненарушенной структуры в условиях компрессионного сжатия, поэтому метод поступательного среза среды лопастными прессиометрами-сдвигомерами не получает распространения. В действительности срез среды, обжатой давлением штампов лопастных сдвигомеров-прессиометров, производится уже в нарушенном состоянии ее структуры обжимающим давлением р>рб. и параметры прочности получают по графику Кулона-Мора именно в виде ϕн и С=Сн интересующем проектировщиков.
и Сстр не совпадают с лабораторными данными исследований образцов среды ϕ=ϕстр и С=Сстр ненарушенной структуры в условиях компрессионного сжатия, поэтому метод поступательного среза среды лопастными прессиометрами-сдвигомерами не получает распространения. В действительности срез среды, обжатой давлением штампов лопастных сдвигомеров-прессиометров, производится уже в нарушенном состоянии ее структуры обжимающим давлением р>рб. и параметры прочности получают по графику Кулона-Мора именно в виде ϕн и С=Сн интересующем проектировщиков.
Наиболее близким по технической сущности к предлагаемому является способ определения физических параметров прочности нарушенной структуры грунтовой материальной среды и торфа под запроектированной нагрузкой р>рб., превышающей ее структурную прочность, заключающийся в том, что на образцах в лаборатории определяют угол ϕ=ϕстр внутреннего трения и удельного сцепления С=Сстр среды ненарушенной структуры при построении графика Кулона-Мора 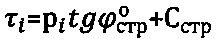 предельного состояния среды под давлением pi, где τi - напряжение сдвига среды под давлением сжатия, заключающийся в том, что моментом начала нарушения структурной прочности связной материальной среды считают достижение под штампом давления, равного бытовому давлению
предельного состояния среды под давлением pi, где τi - напряжение сдвига среды под давлением сжатия, заключающийся в том, что моментом начала нарушения структурной прочности связной материальной среды считают достижение под штампом давления, равного бытовому давлению 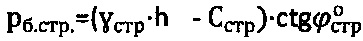 на отметке h массива ее естественного сложения, при этом угол внутреннего трения среды с нарушенной структурой определяют из выражения
на отметке h массива ее естественного сложения, при этом угол внутреннего трения среды с нарушенной структурой определяют из выражения 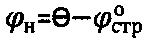 , где угол
, где угол 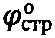 - угол внутреннего трения среды ненарушенной структуры, угол
- угол внутреннего трения среды ненарушенной структуры, угол 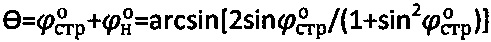 , причем удельное сцепление среды нарушенной структуры определяют как
, причем удельное сцепление среды нарушенной структуры определяют как 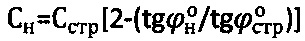 [4].
[4].
Получаемые параметры прочности 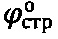 и Сстр материальной среды в массиве в структурированном состоянии при построении графика Кулона-Мора имеют низкую точность определения их величины, связанную с вероятностным методом построения графика
и Сстр материальной среды в массиве в структурированном состоянии при построении графика Кулона-Мора имеют низкую точность определения их величины, связанную с вероятностным методом построения графика 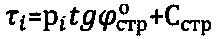 предельного состояния среды [3], что в свою очередь отражается на точности определения расчетных параметров прочности среды в нарушенном по структуре состоянии
предельного состояния среды [3], что в свою очередь отражается на точности определения расчетных параметров прочности среды в нарушенном по структуре состоянии 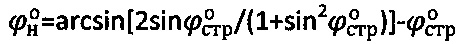 и
и 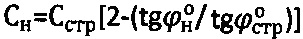 .
.
Целью предлагаемого изобретения является повышение точности определения удельного сцепления и угла внутреннего трения материальной среды в массиве в структурированном и нарушенном состоянии.
Технический результат по способу определения физических параметров прочности дисперсной материальной среды, заключающемуся в том, что определяют при лабораторном сдвиге образцов, отобранным с глубины h массива грунтовой среды ненарушенной структуры, в условиях компрессии под жестким плоским штампом расчетный угол 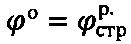 внутреннего трения и расчетное удельное сцепление
внутреннего трения и расчетное удельное сцепление 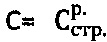 среды ненарушенной структуры при построении графика Кулона-Мора
среды ненарушенной структуры при построении графика Кулона-Мора 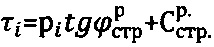 ее предельного состояния под давлением pi, где τi - напряжение сдвига среды под давлением сжатия pi, лабораторным методом по образцам определяют удельный вес
ее предельного состояния под давлением pi, где τi - напряжение сдвига среды под давлением сжатия pi, лабораторным методом по образцам определяют удельный вес  , рассчитывают главное гравитационное (бытовое) давление среды
, рассчитывают главное гравитационное (бытовое) давление среды  , где
, где 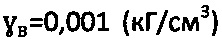 - удельный вес воды, hв - уровень воды на отметке h массива естественного сложения, и определяют расчетный угол внутреннего трения среды с нарушенной структурой
- удельный вес воды, hв - уровень воды на отметке h массива естественного сложения, и определяют расчетный угол внутреннего трения среды с нарушенной структурой 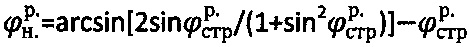 , достигается тем, что при главном гравитационном давлении рб.стр>0 на глубине
, достигается тем, что при главном гравитационном давлении рб.стр>0 на глубине 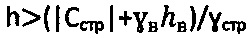 массива структурированной среды и отсутствии атмосферного давления (ратм=0) расчетное гравитационное давление среды с нарушенной структурой определяют как
массива структурированной среды и отсутствии атмосферного давления (ратм=0) расчетное гравитационное давление среды с нарушенной структурой определяют как 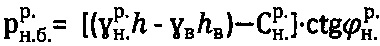 , где
, где 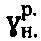 - расчетный удельный вес среды в нарушенном состоянии, а точное отрицательное значение удельного сцепления структурированной среды в массиве определяют как
- расчетный удельный вес среды в нарушенном состоянии, а точное отрицательное значение удельного сцепления структурированной среды в массиве определяют как 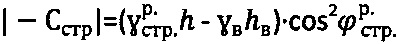 , а среды с нарушенной структурой - как
, а среды с нарушенной структурой - как 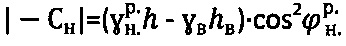 при уточнении параметров гравитационного давления среды
при уточнении параметров гравитационного давления среды  ,
, 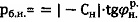 и удельного веса - как
и удельного веса - как  ,
, 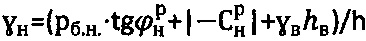 , причем при главном гравитационном давлении рб.стр.=0 на глубине
, причем при главном гравитационном давлении рб.стр.=0 на глубине 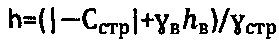 массива структурированной среды и доступе атмосферного давления ратм=1,033 (кГ/см2) величину расчетного отрицательного удельного сцепления среды определяют по зависимости
массива структурированной среды и доступе атмосферного давления ратм=1,033 (кГ/см2) величину расчетного отрицательного удельного сцепления среды определяют по зависимости 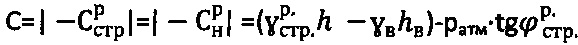 при уточнении параметров углов внутреннего трения среды
при уточнении параметров углов внутреннего трения среды 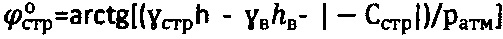 ,
, 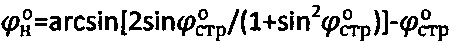 , отрицательного удельного сцепления среды
, отрицательного удельного сцепления среды 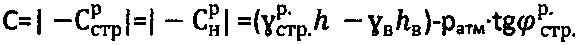 и ее удельного веса
и ее удельного веса 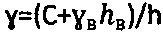 , при этом при главном бытовом давлении рб.стр<0 на глубине
, при этом при главном бытовом давлении рб.стр<0 на глубине 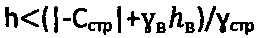 массива структурированной среды и доступе атмосферного давления ратм=1/033 (кГ/см2) величину расчетного отрицательного удельного сцепления среды определяют по зависимостям
массива структурированной среды и доступе атмосферного давления ратм=1/033 (кГ/см2) величину расчетного отрицательного удельного сцепления среды определяют по зависимостям 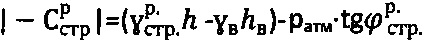 ,
, 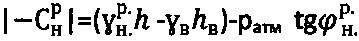 при уточненных углах внутреннего трения среды
при уточненных углах внутреннего трения среды 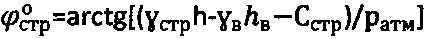 ,
, 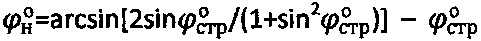 и уточняют отрицательные значения удельного сцепления среды
и уточняют отрицательные значения удельного сцепления среды 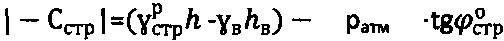 ,
, 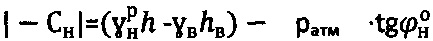 при ее уточненном удельном весе
при ее уточненном удельном весе 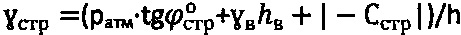 ,
, 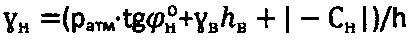 и гравитационном давлении на глубине h
и гравитационном давлении на глубине h 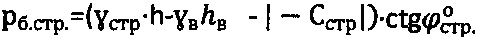 ,
, 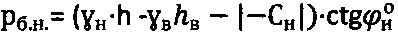 .
.
Предлагаемый способ позволяет при знании величины гравитационного давления или удельного веса среды на заданной глубине h массива и при знании угла внутреннего трения определять величину удельного сцепления среды в структурированном и нарушенном по структуре состоянии и наоборот. Предлагаемые аналитические расчетные зависимости взаимно уточняют друг друга и повышают точность определения несущей способности материальной среды под нагрузкой при достоверном определении ее параметров удельного сцепления Сстр и Сн и угла внутреннего трения 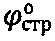 и
и 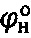 .
.
Предлагаемый способ базируется на новых закономерностях физики материального контактного взаимодействия, по которым гравитационное давление в связных средах определяется по точным зависимостям как 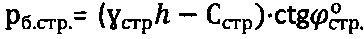 , а в обводненных грунтах как
, а в обводненных грунтах как 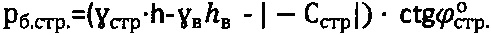 , где
, где 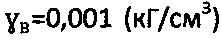 - удельный вес воды, hв - уровень воды на отметке h массива среды естественного сложения. В механике грунтов академиком Н.А. Цытовичем [1] бытовое давление в обводненных грунтовых средах определяют по зависимости
- удельный вес воды, hв - уровень воды на отметке h массива среды естественного сложения. В механике грунтов академиком Н.А. Цытовичем [1] бытовое давление в обводненных грунтовых средах определяют по зависимости 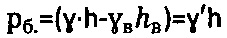 с учетом взвешивающего давления воды
с учетом взвешивающего давления воды 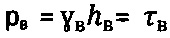 и ошибочно принимая обводненный грунт также за безсвязную среду
и ошибочно принимая обводненный грунт также за безсвязную среду  . На сегодняшний день научные положения Н.А. Цытовича для обводненной среды перенесены ошибочно на осушенную материальную среду, и уже принимают бытовое давление для осушенной среды как
. На сегодняшний день научные положения Н.А. Цытовича для обводненной среды перенесены ошибочно на осушенную материальную среду, и уже принимают бытовое давление для осушенной среды как 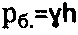 , а для обводненной среды с прежними ошибками как
, а для обводненной среды с прежними ошибками как 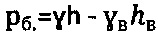 .
.
2. Известен способ определения параметров прочности материальной мерзлой грунтовой и торфяной среды, включающий ее нагружение усилием Р жесткого сферического штампа диаметром D до стабилизации осадки St, разгрузку штампа с замером мессурой его осадки  по остаточному диаметру dк лунки сжатия, определение длительного сцепления мерзлой среды как Сдл.=0,18⋅P/(πDSo) [6].
по остаточному диаметру dк лунки сжатия, определение длительного сцепления мерзлой среды как Сдл.=0,18⋅P/(πDSo) [6].
Недостатком известного способа является низкая расчетная точность параметров прочности мерзлой среды при несоответствии остаточной осадки лунки сжатия контактной осадке So сферы, взаимодействующей с мерзлой средой. Диаметр остаточной лунки сжатия соответствует только остаточным пластическим деформациям, так как упругие остаточные деформации после разгрузки сферы в лунке сжатия восстанавливаются.
Известен способ определения параметров прочности мерзлой и обычной грунтовой и торфяной среды, включающий их нагружение усилием Р жесткой сферы диаметром D с замером текущей осадки St до момента ее стабилизации во времени t, разгрузку сферы, определение ее контактной осадки So и по результатам испытании - длительного сцеплении Сдл., отличающийся тем, что усилие на сферу при испытании среды передают через динамометрический упругий элемент, сферу в среду погружают принудительно не менее трех раз на заданные глубины St1<St2<Stk, величину которых поддерживают постоянной до момента времени t стабилизации соответствующих усилий P1, P2, Pk, после чего производят разгрузку сферы с замером окружностей оставшегося на среде отпечатка диаметром dк, рассчитывают контактные осадки сферы 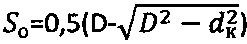 , соответствующие средним контактным давлениям рср.=Pk/[πSo(D-So)], строят график зависимости
, соответствующие средним контактным давлениям рср.=Pk/[πSo(D-So)], строят график зависимости 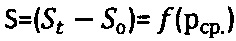 и касательные прямые линии к точкам графика, соответствующим усилиям P1, P2, Pk до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср. и соответствующих им точек пересечения касательных с осью абсцисс, строят круги напряжений Мора максимально предельного состояния среды при растяжении, и проводят к ним общую касательную прямую (maxτпр)=рср.⋅tgθ+Cэ до пересечения с осями абсцисс и ординат, с графика
и касательные прямые линии к точкам графика, соответствующим усилиям P1, P2, Pk до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср. и соответствующих им точек пересечения касательных с осью абсцисс, строят круги напряжений Мора максимально предельного состояния среды при растяжении, и проводят к ним общую касательную прямую (maxτпр)=рср.⋅tgθ+Cэ до пересечения с осями абсцисс и ординат, с графика  снимают предельный угол θ° внутреннего трения грунта [5] и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения
снимают предельный угол θ° внутреннего трения грунта [5] и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения 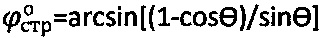 и удельное сцепление
и удельное сцепление 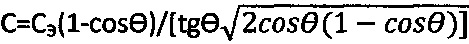 , радиусом Ro от начала координат графика
, радиусом Ro от начала координат графика 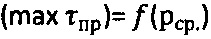 проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2⋅Ro=2⋅Сэ⋅cosθ/(1+sinθ), значению которого по графику
проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2⋅Ro=2⋅Сэ⋅cosθ/(1+sinθ), значению которого по графику 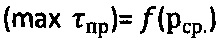 соответствует длительное сцепление
соответствует длительное сцепление 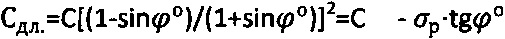 , далее через сферу к среде прикладывают постоянно возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен ψ°=arcsin(2rc/D), где
, далее через сферу к среде прикладывают постоянно возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен ψ°=arcsin(2rc/D), где 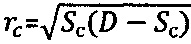 , предельный угол внутреннего трения проверяют по выражению θ=π/2-2ψ, тогда для мерзлой среды (при ϕ°=0°) длительное сцепление равно
, предельный угол внутреннего трения проверяют по выражению θ=π/2-2ψ, тогда для мерзлой среды (при ϕ°=0°) длительное сцепление равно 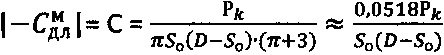 ,
,
для обычного грунта: 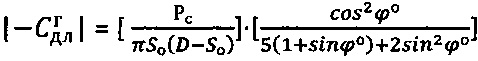 ,
,
для обычного торфа: 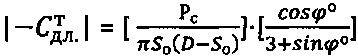 ,
,
удельное сцепление любой среды равно: 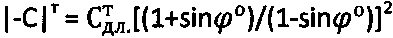 ,
,
а угол внутреннего трения 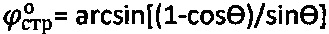 [7].
[7].
Научные положения физики материального контактного взаимодействия существенно уточняют параметры прочности материальной среды при ее испытании по известному способу давлением сферическим штампом:
1) угол ϕ° внутреннего трения среды следует относить к среде, находящейся в структурированном состоянии 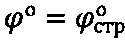 ,
,
2) угол ψ сектора полуконтакта сферы со средой равен 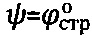 [8],
[8],
3) удельное сцепление следует относить при р>рб к среде в нарушенном состоянии С=Сн,
4) разница углов 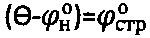 соответствует углу внутреннего трения среды в структурированном состоянии [4, 5],
соответствует углу внутреннего трения среды в структурированном состоянии [4, 5],
5) влажная среда при сцеплении воды Св,стр≈0, угле внутреннего трения 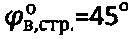 [9] в мерзлом структурированном состоянии при Св>>0 и
[9] в мерзлом структурированном состоянии при Св>>0 и  определяется предельным углом внутреннего трения льда
определяется предельным углом внутреннего трения льда 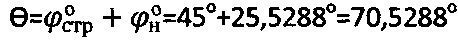 при угле внутреннего трения льда с нарушенной структурой
при угле внутреннего трения льда с нарушенной структурой 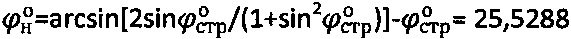 [4],
[4],
6) линии сдвигов среды на глубине массива под штампом развиваются вглубь от центра и к краям штампа при отрицательных значениях касательных напряжений (-τxy).
Поставлена цель - с позиции новых научных положений физики материального контактного взаимодействия повысить точность и достоверность определения параметров прочности материальной среды в обычном и мерзлом состоянии сферическим штампом.
Технический результат по способу определения физических параметров прочности материальной среды, включающему нагружение обычной и мерзлой грунтовой и торфяной среды усилием Р жесткого сферического штампа диаметром D с замером текущей осадки St до момента ее стабилизации во времени t, разгрузку сферы, определение ее контактной осадки So и по результатам испытаний - длительного сцепления Сдл., при этом усилие на сферу при испытании среды передают через динамометрический упругий элемент, сферу в среду погружают принудительно не менее трех раз на заданную глубину St1<St2<Stk, величину которой поддерживают постоянной до момента времени t стабилизации соответствующих усилий Pl, Р2, Pk, после чего производят разгрузку сферы с замером окружностей оставшегося на среде отпечатка диаметром dк, рассчитывают контактные осадки сферы 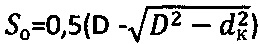 , соответствующие средним контактным давлениям рср.=Pk/[πSo(D-So)], строят график зависимости
, соответствующие средним контактным давлениям рср.=Pk/[πSo(D-So)], строят график зависимости 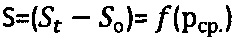 и касательные прямые линии к точкам графика, соответствующим усилиям Р1, Р2, Pk до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср. и соответствующих им точек пересечения касательных с осью абсцисс, строят круги напряжений Мора при растяжении и проводят к ним общую касательную прямую (maxτпр)=рср.⋅tgθ+Сэ до пересечения с осями абсцисс и ординат, с графика
и касательные прямые линии к точкам графика, соответствующим усилиям Р1, Р2, Pk до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср. и соответствующих им точек пересечения касательных с осью абсцисс, строят круги напряжений Мора при растяжении и проводят к ним общую касательную прямую (maxτпр)=рср.⋅tgθ+Сэ до пересечения с осями абсцисс и ординат, с графика 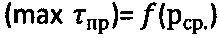 снимают предельный угол внутреннего трения среды θ и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения среды
снимают предельный угол внутреннего трения среды θ и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения среды 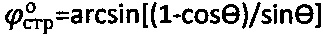 и удельное сцепление
и удельное сцепление 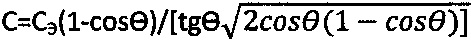 , радиусом Ro от начала координат графика
, радиусом Ro от начала координат графика 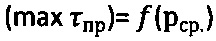 проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2⋅Ro=2⋅Сэ⋅cosθ/(1+sinθ), значению которого по графику
проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2⋅Ro=2⋅Сэ⋅cosθ/(1+sinθ), значению которого по графику 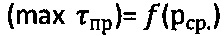 соответствует длительное сцепление
соответствует длительное сцепление  , далее через сферу к среде прикладывают постоянно возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен ψ°=arcsin(2rc/D), где
, далее через сферу к среде прикладывают постоянно возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен ψ°=arcsin(2rc/D), где 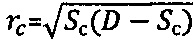 , и определяют величину длительного сцепления для мерзлой грунтовой и торфяной среды как:
, и определяют величину длительного сцепления для мерзлой грунтовой и торфяной среды как: 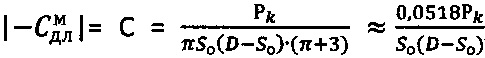 , для обычной грунтовой среды как:
, для обычной грунтовой среды как: 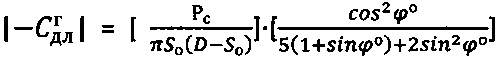 , для обычной торфяной среды - как:
, для обычной торфяной среды - как: 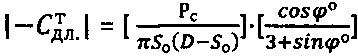 , при сцеплении
, при сцеплении  , а угол внутреннего трения среды уточняют как
, а угол внутреннего трения среды уточняют как 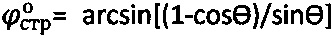 , достигается тем, что предельную осадку среды Sc под сферическим штампом принимают при угле сектора полуконтакта равным
, достигается тем, что предельную осадку среды Sc под сферическим штампом принимают при угле сектора полуконтакта равным 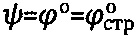 , где
, где 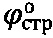 - угол внутреннего трения среды в структурированном состоянии, за мгновенное эквивалентное сцепление обычной грунтовой среды и торфа принимают величину атмосферного давления
- угол внутреннего трения среды в структурированном состоянии, за мгновенное эквивалентное сцепление обычной грунтовой среды и торфа принимают величину атмосферного давления 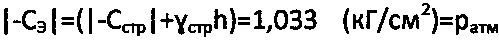 , при предельном угле внутреннего трения среды
, при предельном угле внутреннего трения среды 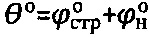 , где
, где 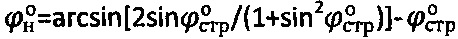 - угол внутреннего трения среды с нарушенной структурой, удельное сцепление структурированной грунтовой среды и торфа определяют как
- угол внутреннего трения среды с нарушенной структурой, удельное сцепление структурированной грунтовой среды и торфа определяют как 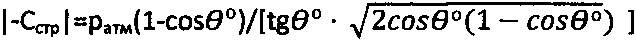 , длительное сцепление - по выражению
, длительное сцепление - по выражению 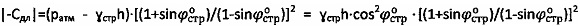 при
при 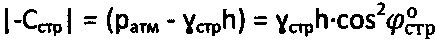 , для мерзлой и обычной грунтовой и торфяной среды структурное сцепление определяют как
, для мерзлой и обычной грунтовой и торфяной среды структурное сцепление определяют как 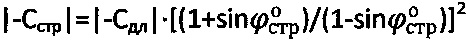 , а эквивалентное сцепление - как
, а эквивалентное сцепление - как 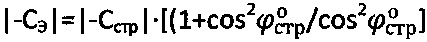 .
.
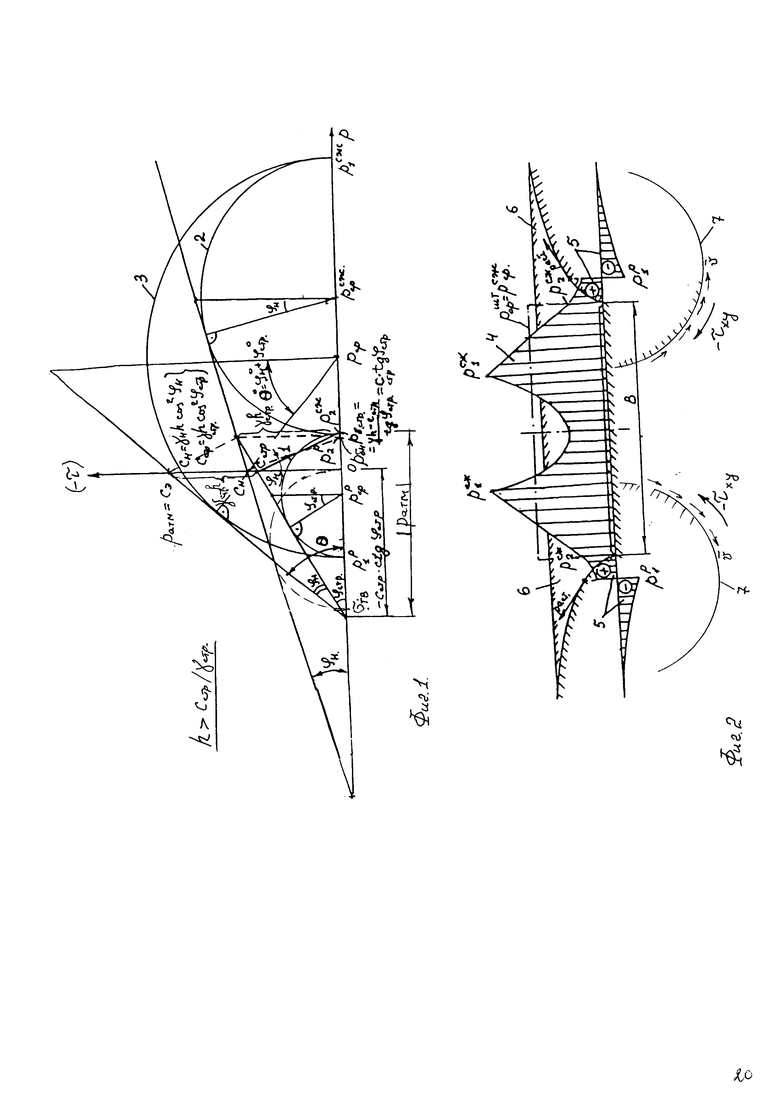
Изобретение поясняется графическими материалами, где на фиг. 1 представлены графики Кулона-Мора 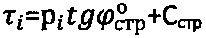 предельного состояния структурированной среды и
предельного состояния структурированной среды и 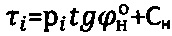 предельного состояния материальной среды с нарушенной структурой на глубине
предельного состояния материальной среды с нарушенной структурой на глубине 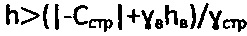 ; на фиг. 2 - эпюры контактных напряжений под и за краями штампа (на поверхности воронки сжатия); на фиг. 3 - графики предельного состояния массива материальной среды на глубине
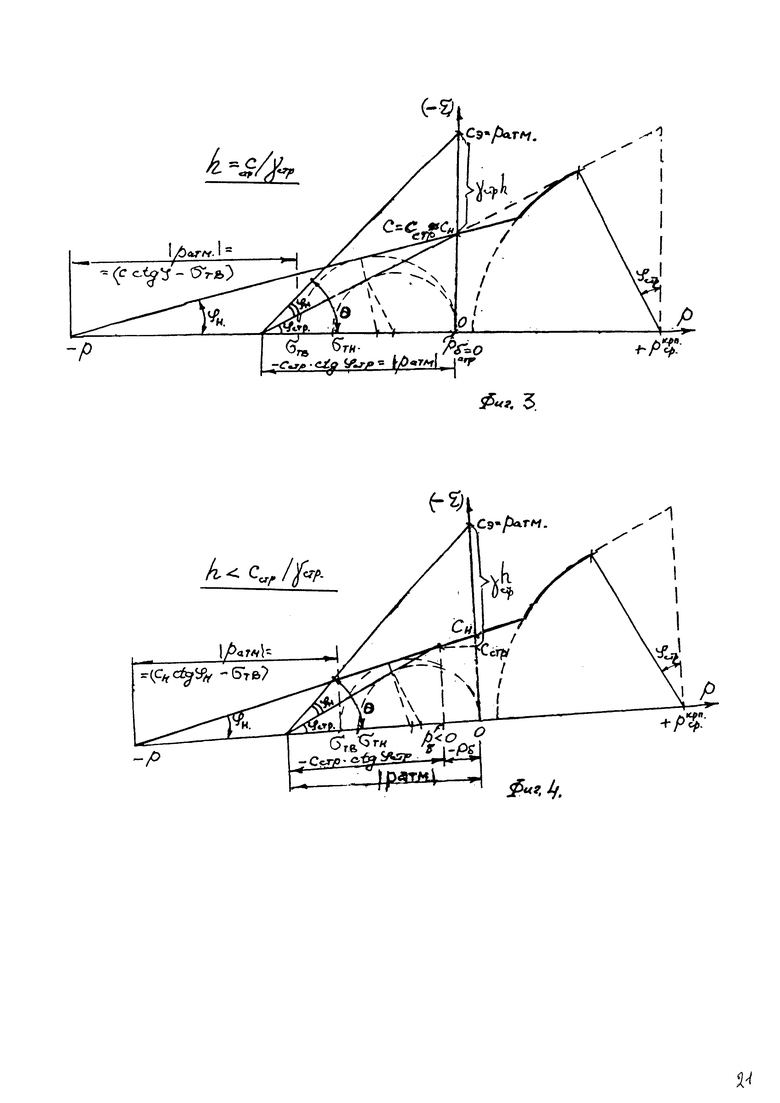
; на фиг. 2 - эпюры контактных напряжений под и за краями штампа (на поверхности воронки сжатия); на фиг. 3 - графики предельного состояния массива материальной среды на глубине 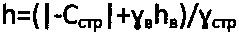 при рб=0; на фиг. 4 - графики предельного состояния массива материальной среды на глубине
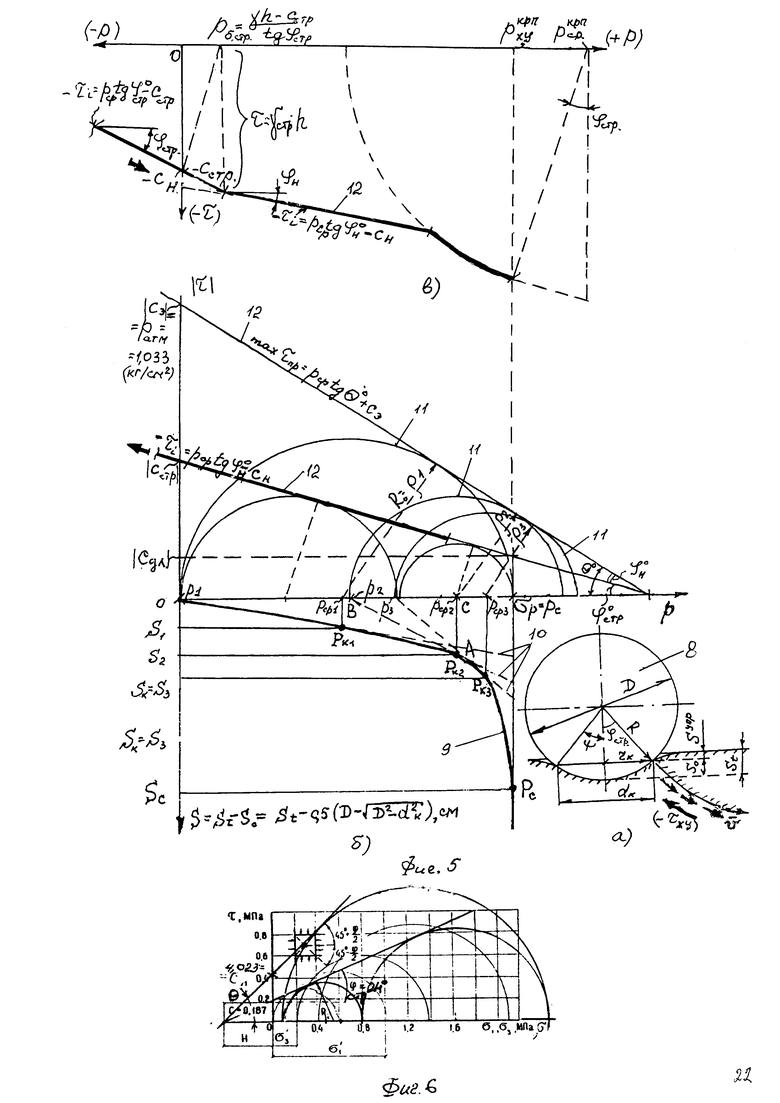
при рб=0; на фиг. 4 - графики предельного состояния массива материальной среды на глубине 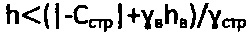 при рб<0; на фиг. 5 - графики испытания обычной и мерзлой грунтовой и торфяной среды сферическим штампом (фиг. 5, а)
при рб<0; на фиг. 5 - графики испытания обычной и мерзлой грунтовой и торфяной среды сферическим штампом (фиг. 5, а) 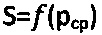 (фиг. 5, б) (maxτпр)=рср.⋅tgθ+Сэ, совмещенные с истинным графиком предельного состояния среды
(фиг. 5, б) (maxτпр)=рср.⋅tgθ+Сэ, совмещенные с истинным графиком предельного состояния среды 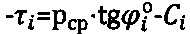 (фиг. 5, в); на фиг. 6 - круги предельных напряжений Мора и положение осредняющей прямой сдвига при трехосевом сжатии мерзлого торфа при температуре (-3°C).
(фиг. 5, в); на фиг. 6 - круги предельных напряжений Мора и положение осредняющей прямой сдвига при трехосевом сжатии мерзлого торфа при температуре (-3°C).
По способу 1 согласно известной методике определении максимальной контактной прочности обычной материальной связной среды в условиях плоской деформации [5], график поверхности полупространства выглядит в виде трех кругов Мора (фиг. 1): круга 1 предельного состояния среды под подошвой штампа, круга 2 предельного состояния среды за краями штампа и охватывающего их круга 3 Мора, суммирующего предельное напряженное состояние среды в целом (под и за пределами контакта штампа со средой в воронке сжатия). Предельное состояние среды в воронке растяжения-сжатия под и за краями штампа представлено в виде эпюр контактных напряжений (фиг. 2) с зонами сдвиговых деформаций под краями штампа (эпюра 4) и с зонами растяжения-сжатия за краями штампа (эпюра 5) в деформационной воронке 6.
Из тригонометрических соотношений графика Кулона-Мора (фиг. 1) определяем, что 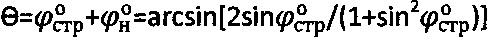 , откуда угол внутреннего трения нарушенной структуры деформируемой среды
, откуда угол внутреннего трения нарушенной структуры деформируемой среды 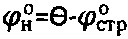 .
.
Главное гравитационное давление на глубине h структурированного массива среды с подтоплением водой на глубине hв определяют по зависимости  при действующем давлении
при действующем давлении 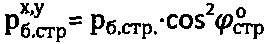 .
.
По предлагаемому способу определяют главное гравитационное давление массива среды с нарушенной структурой и удельным весом 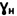 по зависимости
по зависимости 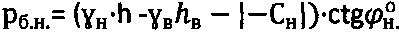 .
.
Вариант 1 реализации способа при 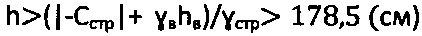 при рб.стр>0 и без доступа атмосферного давления (ратм=0) (фиг. 1).
при рб.стр>0 и без доступа атмосферного давления (ратм=0) (фиг. 1).
1) При глубине исследования h=200 см и присутствии воды с глубины hв=97 см получают расчетную величину гравитационного давления суглинка с удельным сцеплением 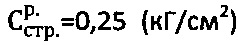 ,
, 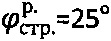 и
и 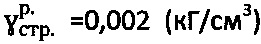 , равную
, равную 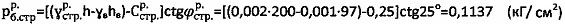 при
при 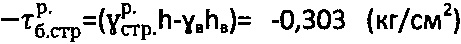 , имеющего отрицательное значение (фиг. 2) на линиях 7 сдвига
, имеющего отрицательное значение (фиг. 2) на линиях 7 сдвига 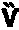 .
.
2) Величина расчетного угла 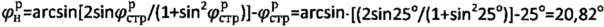 .
.
3) По предлагаемому способу величина гравитационного давления 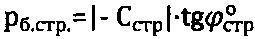 , тогда при
, тогда при 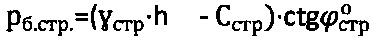 находим для обводненного массива среды
находим для обводненного массива среды  и
и 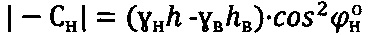 (фиг. 3).
(фиг. 3).
Для суглинка с уровнем грунтовых вод hв=97 см находят расчетные значения 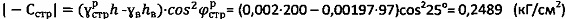 или
или 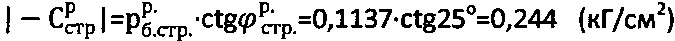 , принимают
, принимают 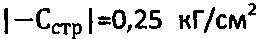 . Для суглинка с нарушенной структурой принимают
. Для суглинка с нарушенной структурой принимают 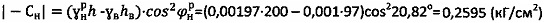 .
.
4) Находят величину главного гравитационного давления как 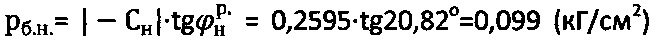 - для массива среды с нарушенной структурой.
- для массива среды с нарушенной структурой.
5) Находят значение удельного веса среды с нарушенной структурой 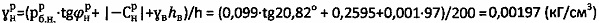 .
.
По Н.А. Цытовичу 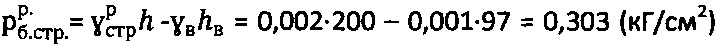 и
и 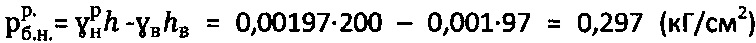 , что в 3 раза превышает расчетные значения по предлагаемым зависимостям. Окончательно принимают величины:
, что в 3 раза превышает расчетные значения по предлагаемым зависимостям. Окончательно принимают величины: 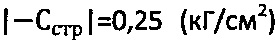 ,
, 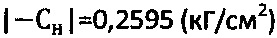 , рб.стр.=0,1137 (кГ/см2) и рб.н.=0,0099 (кГ/см2),
, рб.стр.=0,1137 (кГ/см2) и рб.н.=0,0099 (кГ/см2), 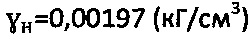 .
.
Вариант 2 реализации способа при 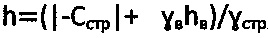 , рб.стр=0,
, рб.стр=0, 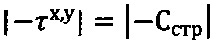 , доступе атмосферного давления ратм=1,033 (кГ/см2) (фиг. 3) и hв=0.
, доступе атмосферного давления ратм=1,033 (кГ/см2) (фиг. 3) и hв=0.
При исследовании суглинка в массиве на глубине  лабораторными методами определяют параметры:
лабораторными методами определяют параметры: 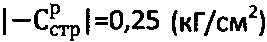 ,
, 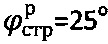 ,
, 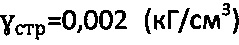 , а расчетными методами получают:
, а расчетными методами получают: 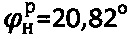 ,
, 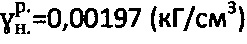 .
.
1) По предлагаемому способу величина главного гравитационного давления на глубине 125 см равна 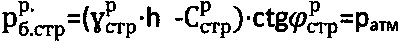 , откуда расчетная величина удельного сцепления равна
, откуда расчетная величина удельного сцепления равна 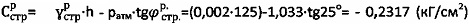 и имеет отрицательное значение, что определено знаком сжимающих приповерхностных тангенциальных напряжений (-τсж), растягивающих по вертикали вверх (y поверхности Земли) суглинок и уравновешиваемых активным напряжением τа.стр=ратм, а расчетная величина
и имеет отрицательное значение, что определено знаком сжимающих приповерхностных тангенциальных напряжений (-τсж), растягивающих по вертикали вверх (y поверхности Земли) суглинок и уравновешиваемых активным напряжением τа.стр=ратм, а расчетная величина 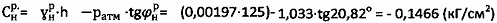 .
.
2) При удельном сцеплении Сстр=-0,2317 (кГ/см2) (определенном в лабораторных условиях со знаком «минус» с учетом растягивающих тангенциальных напряжений в натурных условиях работы массива среды (фиг. 2), уравновешиваемых всесторонним давлением атмосферы 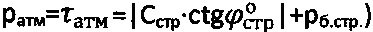 находят уточненное значение угла внутреннего трения суглинка на глубине h=125 см из выражения
находят уточненное значение угла внутреннего трения суглинка на глубине h=125 см из выражения 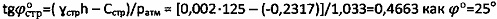 .
.
3) Уточненное значение угла 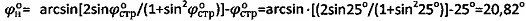 .
.
4) Точное значение удельного сцепления суглинка находим как 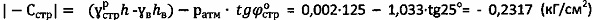 .
.
5) При 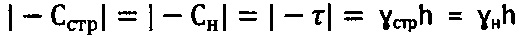 и рб=0 находят значение удельного веса суглинка как
и рб=0 находят значение удельного веса суглинка как 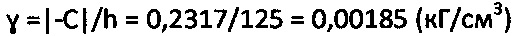 .
.
6) Величина гравитационного давления в массиве составляет 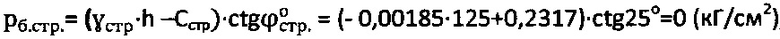 ,
, 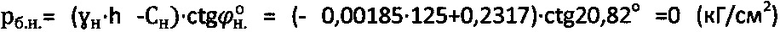 при отрицательных тангенциальных напряжениях
при отрицательных тангенциальных напряжениях 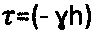 .
.
Величину активных сжимающих давлений определяют как ра.стр.=ра.н.=ратм+рб.=1,033+0=1,033 (кГ/см2).
Вариант 3 реализации способа при 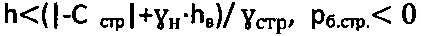 и доступе атмосферного давления ратм=1,033 (кГ/см2) (фиг. 4) и hв=0.
и доступе атмосферного давления ратм=1,033 (кГ/см2) (фиг. 4) и hв=0.
При исследовании суглинка в массиве на глубине  лабораторными методами в компрессионных условиях определяют параметры
лабораторными методами в компрессионных условиях определяют параметры 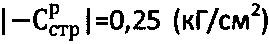 ,
, 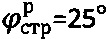 ,
, 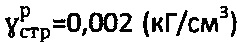 , а расчетными методами получают:
, а расчетными методами получают: 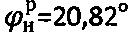 при
при 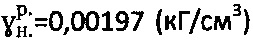 .
.
1) По предлагаемому способу величина расчетного удельного сцепления равна 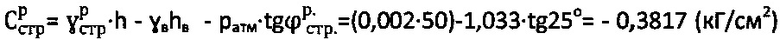 для растягиваемого по вертикали (и сжимаемого по горизонтали) суглинка при величине активного тангенциального напряжения τа,стр=1,033-0,3817=0,6513 (кГ/см2).
для растягиваемого по вертикали (и сжимаемого по горизонтали) суглинка при величине активного тангенциального напряжения τа,стр=1,033-0,3817=0,6513 (кГ/см2).
Величина 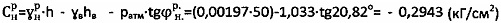 .
.
2) Уточняют значение угла 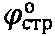 по зависимости
по зависимости 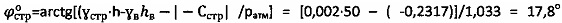 и угла
и угла 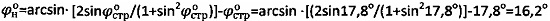 .
.
3) Точные значения удельного сцепления находят как
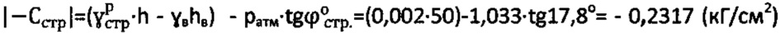 и
и 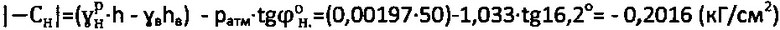 .
.
4) Уточняют удельный вес суглинка как
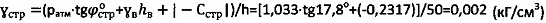 и
и 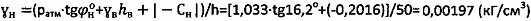 .
.
5) Величину гравитационного давления определяют как
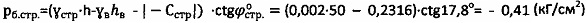 и
и 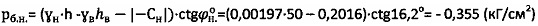 .
.
Величину активного сжимающего давления определяют как ра,стр=ратм+рб.стр=1,033-0,41=0,623 (кг/см2) и ра,н=ратм+рб.н=1,033-0,355=0,678 (кГ/см2).
По способу 2 определение параметров прочности среды производят следующим образом. На поверхность материальной среды (фиг. 5) устанавливают сферический штамп диаметром D. С помощью винтового домкрата производят сжатие динамометрической пружины и передачу возрастающего усилия Р сжатия пружины на сферический штамп 8 (фиг. 5, а) до тех пор, пока заданная осадка штампа не консолидируется до постоянной принятой величины St1=const, выдержанной во времени t. Осадку St1 и соответствующее усилие на штамп 8 фиксируют путем перевода деформации пружины 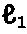 по тарировочному графику в усилие P1. Для повышения точности определения прочностных характеристик среды назначают последовательно осадки штампа St2>St1, St3>St2, стабилизированным значениям которых соответствуют усилия Р2 и Р3 на штамп 8. Погружение сферы в среду производят на заданные величины ее осадок не менее трех раз. После каждого опыта производят замер диаметра поверхности погруженной в среду сферы dк и определяют ее контактную осадку
по тарировочному графику в усилие P1. Для повышения точности определения прочностных характеристик среды назначают последовательно осадки штампа St2>St1, St3>St2, стабилизированным значениям которых соответствуют усилия Р2 и Р3 на штамп 8. Погружение сферы в среду производят на заданные величины ее осадок не менее трех раз. После каждого опыта производят замер диаметра поверхности погруженной в среду сферы dк и определяют ее контактную осадку 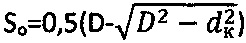 .
.
В прямоугольной системе координат строят график 9 (фиг. 5, б) зависимости 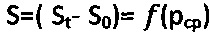 , где среднее давление в зоне контакта сферы с основанием определяют по выражению
, где среднее давление в зоне контакта сферы с основанием определяют по выражению 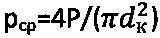 (фиг. 5, а).
(фиг. 5, а).
Через точки Рк1, Рк2 и Рк3 графика 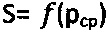 проводят касательные прямые линии 10 до пересечения с осью абсцисс и радиусами ρ1, ρ2, ρ3, равными разнице значений рср и точек пересечения касательных с осью абсцисс, строят круги 11 Мора максимального предельного состояния основания при растяжении. К кругам Мора проводят касательную прямую линию 12 зависимости (maxτпр)=рср.⋅tgθ+Сэ, с помощью которой с графика снимают предельный угол
проводят касательные прямые линии 10 до пересечения с осью абсцисс и радиусами ρ1, ρ2, ρ3, равными разнице значений рср и точек пересечения касательных с осью абсцисс, строят круги 11 Мора максимального предельного состояния основания при растяжении. К кругам Мора проводят касательную прямую линию 12 зависимости (maxτпр)=рср.⋅tgθ+Сэ, с помощью которой с графика снимают предельный угол 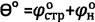 внутреннего трения, по оси ординат отмеряют мгновенное эквивалентное сцепление Сэ и рассчитывают значение угла внутреннего трения обычной или мерзлой грунтовой или торфяной среды ϕ=arcsin[(1-cosθ°/sinθ°)] и величину удельного сцепления
внутреннего трения, по оси ординат отмеряют мгновенное эквивалентное сцепление Сэ и рассчитывают значение угла внутреннего трения обычной или мерзлой грунтовой или торфяной среды ϕ=arcsin[(1-cosθ°/sinθ°)] и величину удельного сцепления  .
.
Длительное сцепление среды определяют как
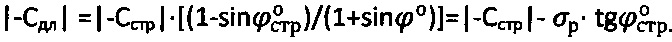 ,
,
где σp=2Cэ⋅cosθ/(1+sinθ) - предельное напряжение на растяжение. Далее через сферу к среде прикладывают постоянно вырастающее усилие Рс>Рк до момента стабилизации его предельной величины P-const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен 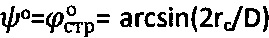 , где
, где 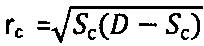 . Определяют предельный угол внутреннего трения среды
. Определяют предельный угол внутреннего трения среды 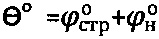 , где
, где 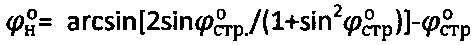 - угол внутреннего трения среды с нарушенной структурой.
- угол внутреннего трения среды с нарушенной структурой.
Для обычной мерзлой грунтовой и торфяной среды удельного сцепления 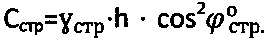 , а эквивалентное сцепление равно
, а эквивалентное сцепление равно 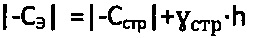 (фиг. 1), тогда получают величину
(фиг. 1), тогда получают величину 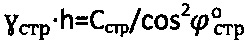 и эквивалентного сцепления
и эквивалентного сцепления 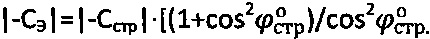 . Величину структурного сцепления определяют как
. Величину структурного сцепления определяют как 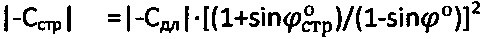 при эквивалентном сцеплении
при эквивалентном сцеплении 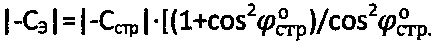 .
.
При этом длительное сцепление для мерзлой грунтовой или торфяной среды определяют как 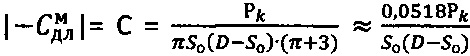 , для обычного грунта -
, для обычного грунта - 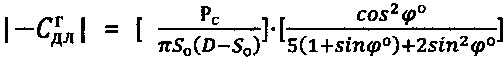 , для обычного торфа -
, для обычного торфа - 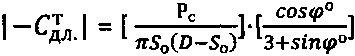 , при величине удельного сцепления
, при величине удельного сцепления 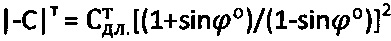 .
.
Пример 1 реализации способа. Стальной шарик диаметром D=22 мм вдавливают в мерзлый торф постоянно возрастающей нагрузкой до момента ее стабилизации Pc=const, при этом диаметр отпечатка составляет dк=8,95 мм при зафиксированной осадке шарика St=1,74 мм. Угол полуконтакта шарика с мерзлым торфом составил при температуре (-3°C) 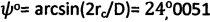 , что соответствует углу внутреннего трения мерзлого торфа
, что соответствует углу внутреннего трения мерзлого торфа 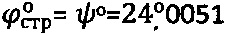 в структурированном состоянии и углу
в структурированном состоянии и углу  в нарушенном состоянии при контактной осадке сферы
в нарушенном состоянии при контактной осадке сферы 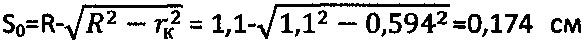 . Предельный угол внутреннего трения мерзлого торфа равен
. Предельный угол внутреннего трения мерзлого торфа равен 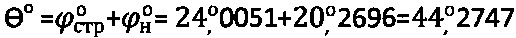 .
.
Удельный вес мерзлого торфа составляет 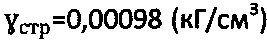 на глубине массива h=100 см. Далее шарик погружают в мерзлый торф на глубину St=0,62 мм до стабилизации усилия Рк=24,95Н=2,5473 кГ. Нагрузку снимают и замеряют диаметр dк=7,11 мм шаровой поверхности. Рассчитывают значение контактной осадки шарика
на глубине массива h=100 см. Далее шарик погружают в мерзлый торф на глубину St=0,62 мм до стабилизации усилия Рк=24,95Н=2,5473 кГ. Нагрузку снимают и замеряют диаметр dк=7,11 мм шаровой поверхности. Рассчитывают значение контактной осадки шарика 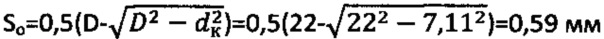 .
.
Длительное сцепление мерзлого торфа равно 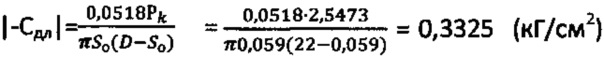 . При
. При 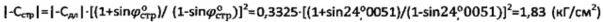 величина эквивалентного сцепления будет равна
величина эквивалентного сцепления будет равна 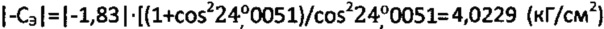 , что соответствует данным трехосных испытаний торфяной среды при температуре (-3°C) [10].
, что соответствует данным трехосных испытаний торфяной среды при температуре (-3°C) [10].
Предельное напряжение на растяжение
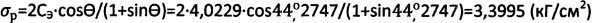 .
.
Полученные данные полностью соответствуют результатам испытания образцов мерзлого торфа в приборах трехосного сжатия-растяжения (фиг. 6) [10].
Пример 2 реализации способа. Сферу диаметром D=200 мм вдавливают в обычный суглинок 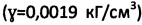 на глубины St1=0,131 см, St2=0,269 см, St3=0,842 см и фиксируют соответствующие им стабилизированные значения усилий вдавливания через динамический упругий элемент P1=26,9 Н, Р2=99,5 Н и Р3=481,0 Н. После разгрузки сферы замеряют соответствующие диаметры dк1=3,65 см, dк2=3,96 см, dк3=7,62 см отпечатков сфер при соответствующих давлениях в площади контакта рср1=0,04771 МПа, рср2=0,08 МПа, рср3=0,10605 МПа. Контактные осадки сферы составили: S01=0,09 см, S02=0,20 см, S03=0,092 см. В прямоугольных координатах строят график зависимости
на глубины St1=0,131 см, St2=0,269 см, St3=0,842 см и фиксируют соответствующие им стабилизированные значения усилий вдавливания через динамический упругий элемент P1=26,9 Н, Р2=99,5 Н и Р3=481,0 Н. После разгрузки сферы замеряют соответствующие диаметры dк1=3,65 см, dк2=3,96 см, dк3=7,62 см отпечатков сфер при соответствующих давлениях в площади контакта рср1=0,04771 МПа, рср2=0,08 МПа, рср3=0,10605 МПа. Контактные осадки сферы составили: S01=0,09 см, S02=0,20 см, S03=0,092 см. В прямоугольных координатах строят график зависимости 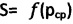 (фиг. 5), к точкам которого, соответствующим усилиям Рк1, Рк2, Рк3, проводят касательные линии до пересечения с осью абсцисс в точках р1, р2, р3 и радиусами ρ1=pcp1-р1, ρ2=рср2-р2, ρ3=рср3-р3, строят круги максимально предельных напряжений Мора, к которым проводят прямую (maxτпр)=рср.⋅tgθ+Cэ, отсекающую на оси ординат замеряемое значение мгновенного эквивалентного сцепления Сэ=1,033 (кГ/см2)=ратм, и измеряют угол между прямой и осью абсцисс θс=44,3°. Угол внутреннего трения находят как ϕ=arcsin[(1-cosθ)/sinθ]=arcsin[(1-cos44,3°)/sin44,3°]=24,0212°, ϕн=θ-ϕстр=44/3°-24,0212°=20,2788°, а величину удельного сцепления - как
(фиг. 5), к точкам которого, соответствующим усилиям Рк1, Рк2, Рк3, проводят касательные линии до пересечения с осью абсцисс в точках р1, р2, р3 и радиусами ρ1=pcp1-р1, ρ2=рср2-р2, ρ3=рср3-р3, строят круги максимально предельных напряжений Мора, к которым проводят прямую (maxτпр)=рср.⋅tgθ+Cэ, отсекающую на оси ординат замеряемое значение мгновенного эквивалентного сцепления Сэ=1,033 (кГ/см2)=ратм, и измеряют угол между прямой и осью абсцисс θс=44,3°. Угол внутреннего трения находят как ϕ=arcsin[(1-cosθ)/sinθ]=arcsin[(1-cos44,3°)/sin44,3°]=24,0212°, ϕн=θ-ϕстр=44/3°-24,0212°=20,2788°, а величину удельного сцепления - как 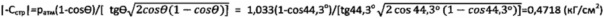 .
.
Величину длительного сцепления определяют по выражению 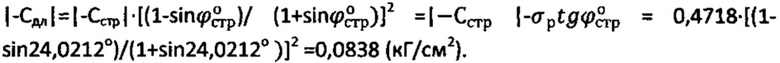
Предлагаемое изобретение существенно повышает точность определения прочностных характеристик материальной среды на базе новых теоретических положений физики материального контактного взаимодействия.
Источники информации, принятые во внимание при составлении заявочных материалов:
1. Цитович Н.А. Механика грунтов (краткий курс): Учебники для ВУЗов. - 3-е изд., доп. - М.: Высшая школа, 1979. - с. 41-48, с. 107.
2. Амарян Л.С. Свойства слабых грунтов и методы их изучения. - М.: «Недра», 1990. - с. 57-59.
3. Ingineering, №9, 2012. ГОСТ 21719-80. Грунты. Методы полевых испытаний на срез в скважинах и в массиве. - М.: Госстандарт СССР. - с. 16-17, 20.
4. Патент РФ №2537725 «Способ определения физических параметров прочности нарушенной структуры материальной среды» / Хрусталев Е.Н., Б.И. №1 за 10.01.2015 г.
5. Патент РФ №2265824, G01N 8/24. Б.И. №34 от 10.12.2005 г.
6. Роман Л.Т., Веретехина Э.Г. Определение деформационных характеристик мерзлых грунтов вдавливанием шарового штампа / Основания, фундаменты и механика грунтов. - 2004. - №2. С. 21-24.
7. Патент РФ №2345360 «Способ определения механических характеристик грунтового, торфяного и мерзлого основания» / Хрусталев Е.Н., Б.И. №3 за 27.01.2009 г.
8. Патент РФ №2536427 «Способ повышения проходимости движителя военной техники и устройство движителя военной техники» / Хрусталев Е.Н., Б.И. №35 от 20.12.2014 г.
9. Патент РФ №2539905 «Способ определения физических параметров воды» / Хрусталев Е.Н., Б.И. №3 от 27.01.2015 г.
10. Миронов В.А. Проектирование оснований и фундаментов сооружений в сложных инженерно-геологических условиях: Учебное пособие - Калинин: Калининский гос. университет, 1988. - С. 44 (рис. 26).
Изобретение относится к области физики материального контактного взаимодействия, а именно к способам определения удельного сцепления и угла внутреннего трения материальной связной среды, воспринимающей давление свыше гравитационного.
Способ 1 определения физических параметров прочности материальной среды плоским жестким штампом заключается в установлении при лабораторном сдвиге образцов, например, грунта и торфа ненарушенной структуры в условиях компрессии угла 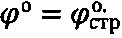 внутреннего трения и удельного сцепления С=Сстр среды при построении графика Кулона-Мора
внутреннего трения и удельного сцепления С=Сстр среды при построении графика Кулона-Мора 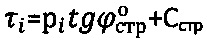 предельного состояния среды под давлением pi, где τi - напряжение сдвига среды под давлением сжатия pi, определении расчетного удельного веса среды ненарушенной и нарушенной структуры
предельного состояния среды под давлением pi, где τi - напряжение сдвига среды под давлением сжатия pi, определении расчетного удельного веса среды ненарушенной и нарушенной структуры 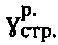 и
и 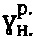 , ее расчетного угла внутреннего трения с нарушенной структурой
, ее расчетного угла внутреннего трения с нарушенной структурой 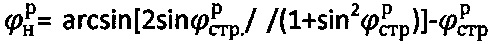 , расчетного бытового давления
, расчетного бытового давления  ,
, 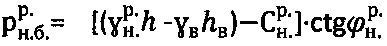 на глубине h, определении уточненного значения:
на глубине h, определении уточненного значения:
1) удельного сцепления подтопленной среды 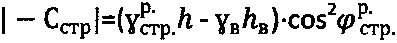 ,
, 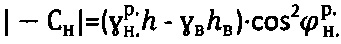 , гравитационного давления
, гравитационного давления  ,
, 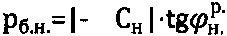 , удельного веса
, удельного веса 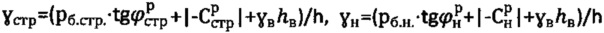 при
при 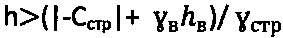 , рб>0 и отсутствии атмосферного давления;
, рб>0 и отсутствии атмосферного давления;
2) удельного сцепления среды 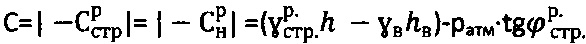 при уточненных значениях
при уточненных значениях 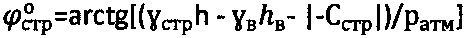 ,
, 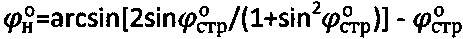 ,
,
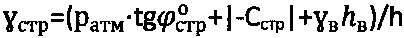 ,
, 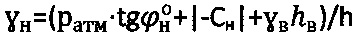 - при
- при 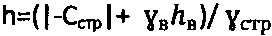 , рб=0 и доступе атмосферного давления ратм=1,033 (кГ/см2);
, рб=0 и доступе атмосферного давления ратм=1,033 (кГ/см2);
3) удельного сцепления среды 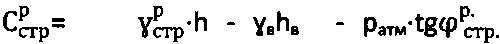 ,
, 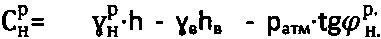 и уточняют значения: удельного веса среды
и уточняют значения: удельного веса среды 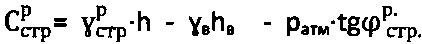 ,
, 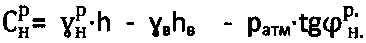 и уточняют значения удельного веса среды
и уточняют значения удельного веса среды 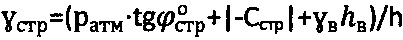 ,
,  и гравитационного давления
и гравитационного давления 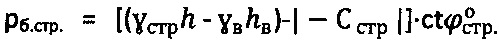 ,
, 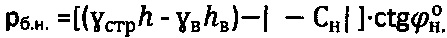 , рб.<0 и доступе атмосферного давления ратм=1,033 (кГ/см2).
, рб.<0 и доступе атмосферного давления ратм=1,033 (кГ/см2).
Способ 2 определения физических параметров прочности материальной среды сферическим штампом включает нагружение сухой среды усилием Р диаметром D с замером текущей осадки St до момента ее стабилизации во времени t, разгрузку сферы, определение ее контактной осадки So и по результатам испытаний - длительного сцепления Сдл, сферу в среду погружают не менее трех раз через динамометрический упругий элемент на заданную глубину St1<St2<Stk, величину которых поддерживают постоянной во времени t стабилизации соответствующих усилий P1, P2, Pk, после чего сферу разгружают с замером диаметра отпечатка диаметром dk. Далее рассчитывают осадки сферы  при давлениях рср=Pk/[πSo(D-So)], строят график
при давлениях рср=Pk/[πSo(D-So)], строят график 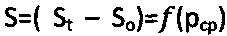 и касательные прямые к точкам графика, соответствующим усилиям P1, P2, Pk до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср и соответствующих им точек пересечения касательных с осью абсцисс, строят круги Мора и проводят к ним касательную прямую (maxτпр)=рср.⋅tgθ+Сэ до пересечения с осями абсцисс и ординат, с графика
и касательные прямые к точкам графика, соответствующим усилиям P1, P2, Pk до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср и соответствующих им точек пересечения касательных с осью абсцисс, строят круги Мора и проводят к ним касательную прямую (maxτпр)=рср.⋅tgθ+Сэ до пересечения с осями абсцисс и ординат, с графика 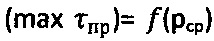 снимают предельный угол θ внутреннего трения грунта и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения среды в структурированном состоянии
снимают предельный угол θ внутреннего трения грунта и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения среды в структурированном состоянии 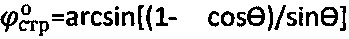 и удельное сцепление
и удельное сцепление  , радиусом Ro от начала координат графика
, радиусом Ro от начала координат графика 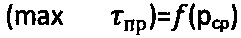 проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2Ro=2Сэ⋅cosθ/(1+sinθ), значению которого соответствует длительное сцепление
проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2Ro=2Сэ⋅cosθ/(1+sinθ), значению которого соответствует длительное сцепление 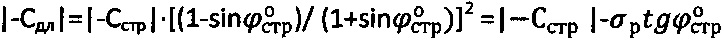 .
.
Далее через сферу к среде прикладывают возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему осадки Sc среды, при которой угол сектора полуконтакта сферы со средой 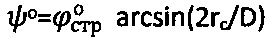 , где
, где 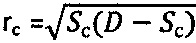 , и определяют величину длительного сцепления для мерзлой среды - как
, и определяют величину длительного сцепления для мерзлой среды - как 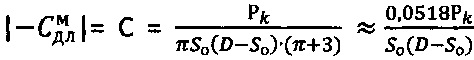 , для обычной грунтовой среды - как
, для обычной грунтовой среды - как  ,
,
для торфяной среды - как: 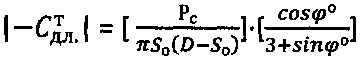 при сцеплении
при сцеплении 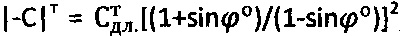 , а угол внутреннего трения среды уточняют как
, а угол внутреннего трения среды уточняют как 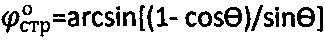 .
.
За мгновенное эквивалентное сцепление грунтовой среды и торфа принимают величину атмосферного давления 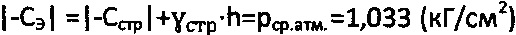 при предельном угле внутреннего трения среды
при предельном угле внутреннего трения среды 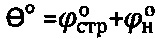 , где
, где 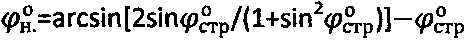 - угол внутреннего трения среды с нарушенной структурой, удельное сцепление структурированной грунтовой среды и торфа определяют как
- угол внутреннего трения среды с нарушенной структурой, удельное сцепление структурированной грунтовой среды и торфа определяют как 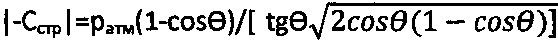 , а величину длительного сцепления - по выражению
, а величину длительного сцепления - по выражению 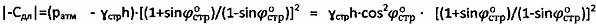 при
при 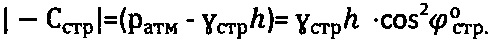 , для мерзлой и обычной грунтовой среды и торфа структурное сцепление определяют как
, для мерзлой и обычной грунтовой среды и торфа структурное сцепление определяют как 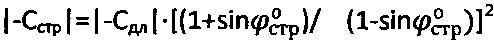 , а эквивалентное сцепление как
, а эквивалентное сцепление как 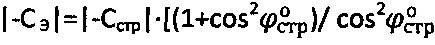 .
.
Технический результат - получение при угле 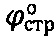 внутреннего трения достоверных значений параметров удельного сцепления материальной среды в сухом и обводненном состоянии в структурированном и нарушенном состоянии, уточняющих величину гравитационного давления среды рстр.б., рн.б. и ее удельного веса
внутреннего трения достоверных значений параметров удельного сцепления материальной среды в сухом и обводненном состоянии в структурированном и нарушенном состоянии, уточняющих величину гравитационного давления среды рстр.б., рн.б. и ее удельного веса  ,
, 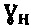 . 2 н. и 2 з.п. ф-лы, 6 ил.
. 2 н. и 2 з.п. ф-лы, 6 ил.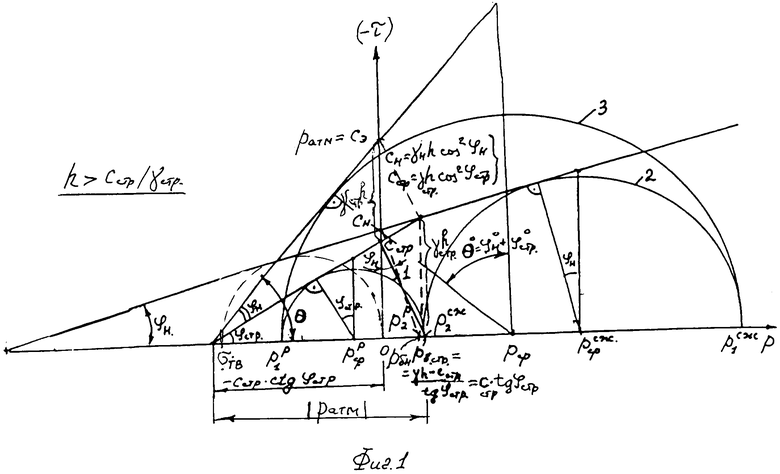
1. Способ определения физических параметров прочности материальной среды, заключающийся в том, что определяют при лабораторном сдвиге образцов, отобранных с глубины h массива грунтовой среды ненарушенной структуры, в условиях компрессии расчетный угол 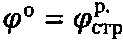 внутреннего трения и расчетное удельное сцепление
внутреннего трения и расчетное удельное сцепление 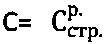 среды ненарушенной структуры при построении графика Кулона-Мора
среды ненарушенной структуры при построении графика Кулона-Мора 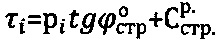 предельного состояния среды под давлением pi, где τi - напряжение сдвига среды под давлением сжатия pi, лабораторным методом по образцам определяют удельный вес исследуемой среды в структурированном состоянии
предельного состояния среды под давлением pi, где τi - напряжение сдвига среды под давлением сжатия pi, лабораторным методом по образцам определяют удельный вес исследуемой среды в структурированном состоянии 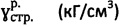 , рассчитывают главное бытовое давление структурированной среды как
, рассчитывают главное бытовое давление структурированной среды как  , где
, где 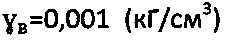 - удельный вес воды, hв - уровень воды на отметке h массива естественного сложения, определяют расчетный угол внутреннего трения среды с нарушенной структурой как
- удельный вес воды, hв - уровень воды на отметке h массива естественного сложения, определяют расчетный угол внутреннего трения среды с нарушенной структурой как 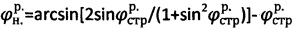 , отличающийся тем, что при главном бытовом давлении pб.стр.>0 на глубине
, отличающийся тем, что при главном бытовом давлении pб.стр.>0 на глубине 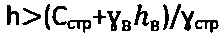 массива структурированной среды и отсутствии атмосферного давления ратм=0 расчетное бытовое давление материальной среды с нарушенной структурой определяют как
массива структурированной среды и отсутствии атмосферного давления ратм=0 расчетное бытовое давление материальной среды с нарушенной структурой определяют как 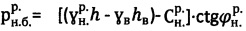 , где
, где  - расчетный удельный вес среды в нарушенном состоянии, а точное значение удельного сцепления структурированной среды определяют как
- расчетный удельный вес среды в нарушенном состоянии, а точное значение удельного сцепления структурированной среды определяют как 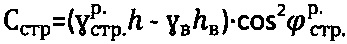 , среды с нарушенной структурой как
, среды с нарушенной структурой как 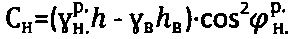 при уточнении параметров гравитационного давления среды в виде
при уточнении параметров гравитационного давления среды в виде  , удельного веса среды в виде
, удельного веса среды в виде 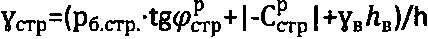 ,
, 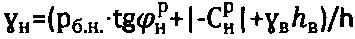 .
.
2. Способ по п. 1, отличающийся тем, что при главном бытовом давлении pб.стр.=0 на глубине 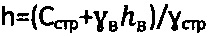 массива структурированной сухой среды и доступе атмосферного давления ратм=1,033 (кГ/см2) величину расчетного удельного сцепления среды определяют по зависимостям
массива структурированной сухой среды и доступе атмосферного давления ратм=1,033 (кГ/см2) величину расчетного удельного сцепления среды определяют по зависимостям 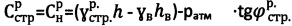 , уточняют значения углов внутреннего трения среды
, уточняют значения углов внутреннего трения среды  ,
, 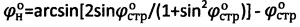 , устанавливают значения точного удельного сцепления среды как
, устанавливают значения точного удельного сцепления среды как 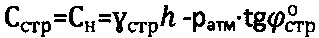 и уточняют удельный вес среды как
и уточняют удельный вес среды как 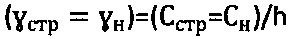 .
.
3. Способ по п. 1, отличающийся тем, что при главном бытовом давлении pб.стр<0 на глубине 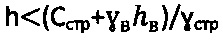 массива структурированной сухой среды и доступе атмосферного давления ратм=1,033 (кГ/см2) величину расчетного удельного сцепления среды определяют по зависимостям
массива структурированной сухой среды и доступе атмосферного давления ратм=1,033 (кГ/см2) величину расчетного удельного сцепления среды определяют по зависимостям 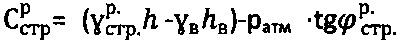 ,
, 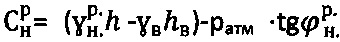 , уточняют значения углов внутреннего трения среды
, уточняют значения углов внутреннего трения среды 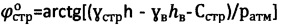 ,
, 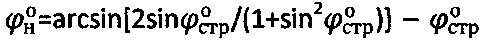 , устанавливают значения уточненного удельного сцепления среды как
, устанавливают значения уточненного удельного сцепления среды как 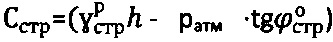 ,
, 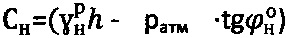 , уточняют значения удельного веса среды как
, уточняют значения удельного веса среды как 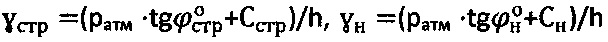 и гравитационного давления на глубине h по зависимостям
и гравитационного давления на глубине h по зависимостям 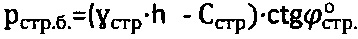 ,
, 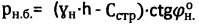
4. Способ определения физических параметров прочности материальной среды, включающий нагружение обычной и мерзлой грунтовой и торфяной среды усилием Р жесткого сферического штампа диаметром D с замером текущей осадки St до момента ее стабилизации во времени t, разгрузку сферы, определение ее контактной осадки So и по результатам испытаниий - длительного сцепления Сдл., при этом усилие на сферу при испытании среды передают через динамометрический упругий элемент, сферу в среду погружают принудительно не менее трех раз на заданную глубину St1<St2<Stk, величину которой поддерживают постоянной до момента времени t стабилизации соответствующих усилий P1, P2, Pk, после чего производят разгрузку сферы с замером окружностей оставшегося на среде отпечатка диаметром dк, рассчитывают контактные осадки сферы 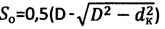 , соответствующие средним контактным давлениям рср.=Pk/[πSo(D-So)], строят график зависимости
, соответствующие средним контактным давлениям рср.=Pk/[πSo(D-So)], строят график зависимости 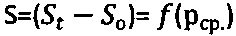 и касательные прямые линии к точкам графика, соответствующим усилиям P1, P2, Pk, до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср. и соответствующих им точек пересечения касательных с осью абсцисс, строят круги напряжений Мора при растяжении и проводят к ним общую касательную прямую (maxτпр)=рср.⋅tgθ+Сэ до пересечения с осями абсцисс и ординат, с графика
и касательные прямые линии к точкам графика, соответствующим усилиям P1, P2, Pk, до пересечения с осью абсцисс; радиусами ρ, равными разнице значений рср. и соответствующих им точек пересечения касательных с осью абсцисс, строят круги напряжений Мора при растяжении и проводят к ним общую касательную прямую (maxτпр)=рср.⋅tgθ+Сэ до пересечения с осями абсцисс и ординат, с графика 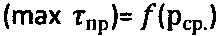 снимают предельный угол внутреннего трения среды θ и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения среды
снимают предельный угол внутреннего трения среды θ и отмеряют мгновенное эквивалентное сцепление Сэ, рассчитывают угол внутреннего трения среды 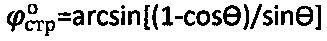 и удельное сцепление
и удельное сцепление
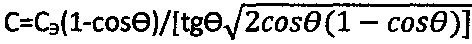 , радиусом Ro от начала координат графика
, радиусом Ro от начала координат графика 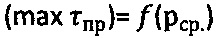 проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2⋅Ro=2⋅Cэ⋅cosθ/(1+sinθ), значению которого по графику
проводят полуокружность, соприкасающуюся с ним и отсекающую на оси абсцисс точку, соответствующую предельному напряжению на растяжение σp=2⋅Ro=2⋅Cэ⋅cosθ/(1+sinθ), значению которого по графику 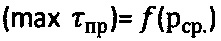 соответствует длительное сцепление
соответствует длительное сцепление 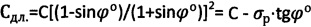 , далее через сферу к среде прикладывают постоянно возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен ψ°=arcsin(2rc/D), где
, далее через сферу к среде прикладывают постоянно возрастающее усилие Рс>Pk до момента стабилизации его предельной величины Pc=const при регистрации соответствующей ему общей осадки Sc среды, при которой угол сектора полуконтакта сферы со средой равен ψ°=arcsin(2rc/D), где 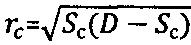 , и определяют величину длительного сцепления для мерзлой грунтовой и торфяной среды как
, и определяют величину длительного сцепления для мерзлой грунтовой и торфяной среды как 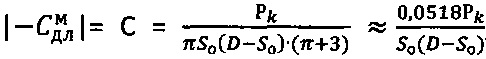 , для обычной грунтовой среды как
, для обычной грунтовой среды как 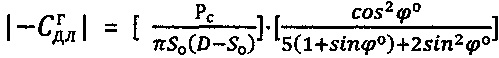 , для обычной торфяной среды как
, для обычной торфяной среды как  , при сцеплении
, при сцеплении 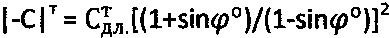 , а угол внутреннего трения среды уточняют как
, а угол внутреннего трения среды уточняют как 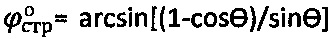 , отличающийся тем, что предельную осадку среды Sc под сферическим штампом принимают при угле сектора полуконтакта равном
, отличающийся тем, что предельную осадку среды Sc под сферическим штампом принимают при угле сектора полуконтакта равном 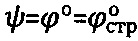 , где
, где 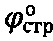 - угол внутреннего трения среды в структурированном состоянии, за мгновенное эквивалентное сцепление обычной грунтовой среды и торфа принимают величину атмосферного давления
- угол внутреннего трения среды в структурированном состоянии, за мгновенное эквивалентное сцепление обычной грунтовой среды и торфа принимают величину атмосферного давления 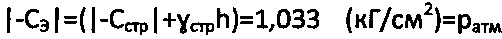 , при предельном угле внутреннего трения среды
, при предельном угле внутреннего трения среды  , где
, где 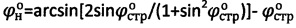 - угол внутреннего трения среды с нарушенной структурой, удельное сцепление структурированной грунтовой среды и торфа определяют как
- угол внутреннего трения среды с нарушенной структурой, удельное сцепление структурированной грунтовой среды и торфа определяют как 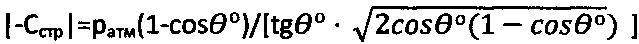 , длительное сцепление - по выражению
, длительное сцепление - по выражению 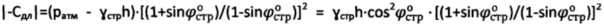 при
при 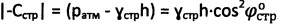 , для мерзлой и обычной грунтовой и торфяной среды структурное сцепление определяют как
, для мерзлой и обычной грунтовой и торфяной среды структурное сцепление определяют как 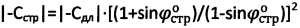 , а эквивалентное сцепление как
, а эквивалентное сцепление как 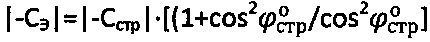 .
.
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ПРОЧНОСТИ НАРУШЕННОЙ СТРУКТУРЫ МАТЕРИАЛЬНОЙ СРЕДЫ | 2013 |
|
RU2537725C1 |
| ГОСТ 20276-99.Грунты | |||
| Методы полевого определения характеристик прочности и деформируемости | |||
| - М.: МИТКС, Госстрой России, 1999 | |||
| Устройство для выпрямления опрокинувшихся на бок и затонувших у берега судов | 1922 |
|
SU85A1 |
| Хрусталев Е.Н | |||
| Контактное взаимодействие в геомеханике | |||
| ч | |||
| I: Несущая способность оснований сооружений | |||
| - Тверь, ТГТУ, "Золотая буква", 2004 | |||
| - С | |||
| Аппарат, предназначенный для летания | 0 |
|
SU76A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ГРУНТОВОГО, ТОРФЯНОГО И МЕРЗЛОГО ОСНОВАНИЙ | 2007 |
|
RU2345360C2 |
Авторы
Даты
2017-04-05—Публикация
2015-11-05—Подача