СПОСОБ ПОСТРОЕНИЯ ОПТИМАЛЬНОЙ АЭРОДИНАМИЧЕСКОЙ ПОВЕРХНОСТИ ГИПЕРЗВУКОВОГО ЛЕТАТЕЛЬНОГО АППАРАТА Российский патент 2015 года по МПК B64F5/00 G06F17/50 

Заявляемое изобретение относится к ракетно-космической технике и может быть использовано для определения оптимальной формы поверхности гиперзвукового летательного аппарата, предназначенного для спасения экипажа с борта космической станции, терпящей аварию.

Известно построение поверхности гиперзвукового планирующего летательного аппарата с использованием в качестве критерия оптимальности формы - условие максимума для аэродинамического качества синтезируемого изделия (K→max), что является определенным ограничением из-за неучета уклонения [1].

Ближайшим решением к заявляемому является способ построения оптимальной аэродинамической поверхности гиперзвукового летательного аппарата, заключающийся в воздействии с использованием критерия оптимизации, связанного с максимизацией аэродинамического коэффициента лобового сопротивления [2].

Недостатком известного решения являются ограниченные возможности способа вследствие невозможности обеспечения оптимального уклонения от столкновения.

Задача заключается в предложении определения критериев уклонения от столкновения и способа построения оптимальной поверхности гиперзвукового летательного аппарата для обеспечения оптимального уклонения от столкновения.

Решение поставленной задачи обеспечивается тем, что в способе построения оптимальной аэродинамической поверхности гиперзвукового летательного аппарата, включающем воздействие на его поверхность с использованием критерия оптимизации, в качестве критерия оптимизации используют отношение степеней коэффициентов подъемной силы и силы лобового сопротивления 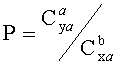$$P=\raisebox{1ex}{$C_{ya}^a$}\!\left/ \!\raisebox{-1ex}{$C_{xa}^b$}\right.$$ , по которому формируют оптимальную поверхность летательного аппарата для решения задачи уклонения от столкновения, с использованием численных методов решения полных уравнений Навье-Стокса, для чего определяют рациональное расположение несущих поверхностей и форму носовой части аппарата с минимальными тепловыми нагрузками, где

P - отношение степеней коэффициентов подъемной силы и силы лобового сопротивления, характеризующее показатель эффективности, полученный в результате численного решения дифференциальной игры качества,

$$C_{ya}^a$$ - коэффициент подъемной силы, определяемый как отношение подъемной силы к скоростному напору и характерной площади,

$$C_{xa}^b$$ - коэффициент силы лобового сопротивления, определяемый как отношение силы лобового сопротивления к скоростному напору и характерной площади.

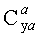
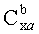
Изобретение поясняется следующим примером.

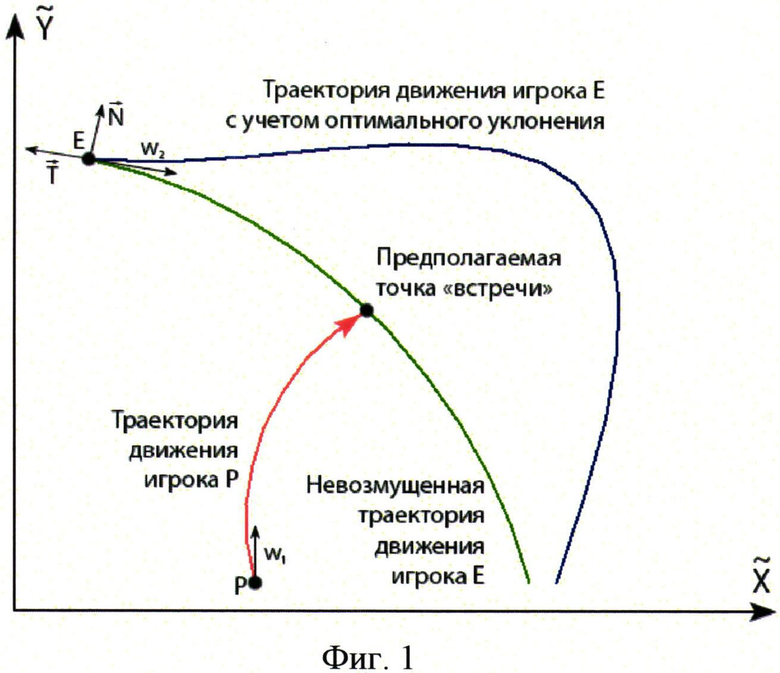
Схема конфликтной ситуации об избежании столкновения двух летательных аппаратов (двух игроков с противоположными (антагонистическими) интересами) представлена на фиг.1. Игрок Р стремится сблизиться с игроком Е на минимальное расстояние, игрок Е стремится максимизировать минимальное расстояние. Игра заканчивается победой Р в случае, если отрезок РЕ окажется менее величины l, и поражением Р, если игрок Е пройдет область сближения на расстояние более l.

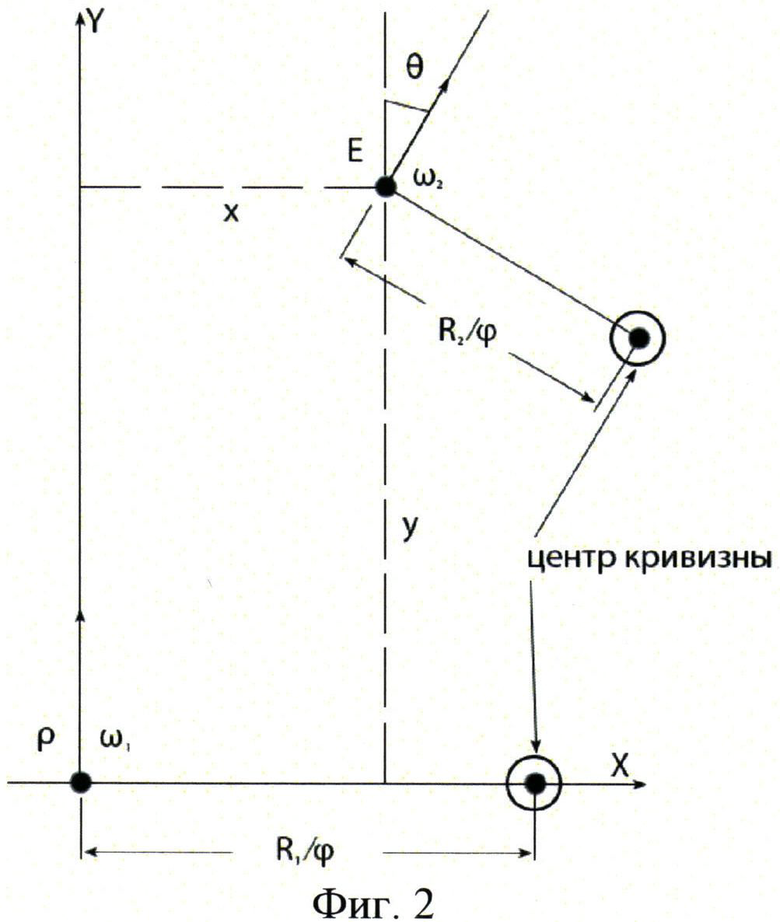
Дифференциальная игра качества решалась численно в связанной в игроком Р системе координат при условии превосходства игрока Е в скорости и первоначальном расположении игроков на встречных курсах. Схематизация дифференциальной игры в системе координат, связанной с минимизирующим игроком, представлена на фиг.2. Маневренные возможности игрока Е были ограничены величиной минимального радиуса разворота (значением коэффициента подъемной силы), а его скорость уменьшалась по квадратичному закону с коэффициентом пропорциональности, связанным с аэродинамическим коэффициентом лобового сопротивления.

В отмеченной постановке дифференциальная игра была описана системой обыкновенных дифференциальных уравнений:

,

,

,

,

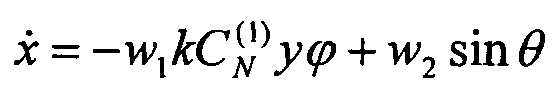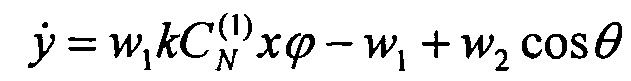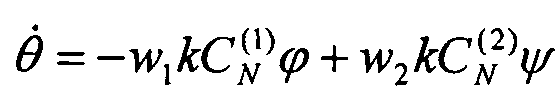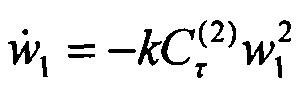где x и y - геометрические координаты (уклоняющегося игрока Е в системе координат, связанной с игроком Р);

w₁ и w₂ - скорости игроков Р и Е;

R₁ и R₂ - минимальные радиусы кривизны траекторий Р и Е;

θ - ориентация вектора скорости (w₂) уклоняющегося игрока Е;

φ и ψ - параметры управления движением игроков Р и Е, -1≤φ, ψ≤1;

$$C_N^{(1)}$$ , $$C_N^{(2)}$$ - коэффициенты нормальных сил игроков Р и Е;

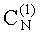
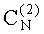
k - масштабирующий коэффициент для выделения безразмерных аэродинамических коэффициентов, учитывающих высоту полета, массу игроков и их характерную площадь;

$$C_{\tau }^{(2)}$$ - коэффициент тангенциальной силы игрока Е,

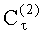
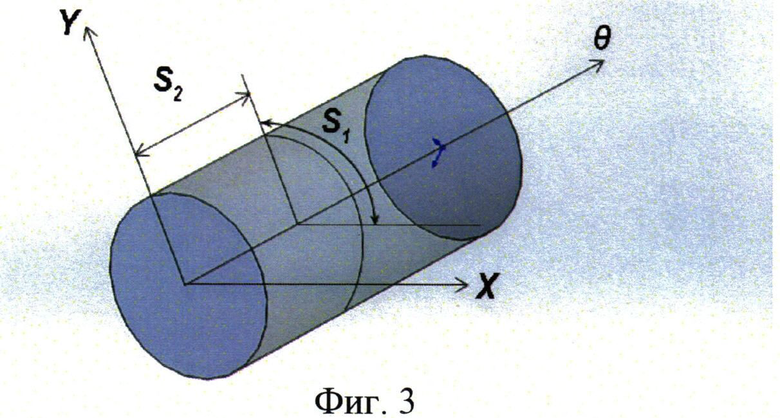
с начальными условиями на терминальной поверхности в точке ее касания поверхностью барьера, изображенными на фиг.3.

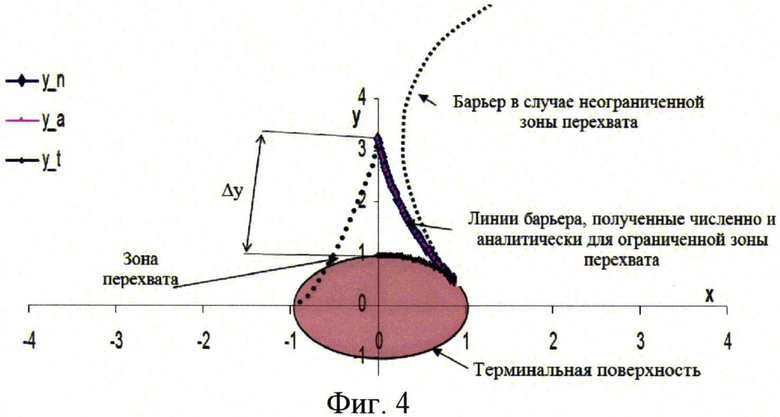
Задача решалась численно методами Эйлера и Рунге-Кутта, достоверность результатов подтверждена сходимостью процессов по математическому времени (по числу итераций) и по сетке управляющих параметров. В качестве самостоятельного теста было рассмотрено сравнение численного и аналитического решения задачи о «шофере-убийце», предложенной Р. Айзексом [3], как показано на фиг.4.

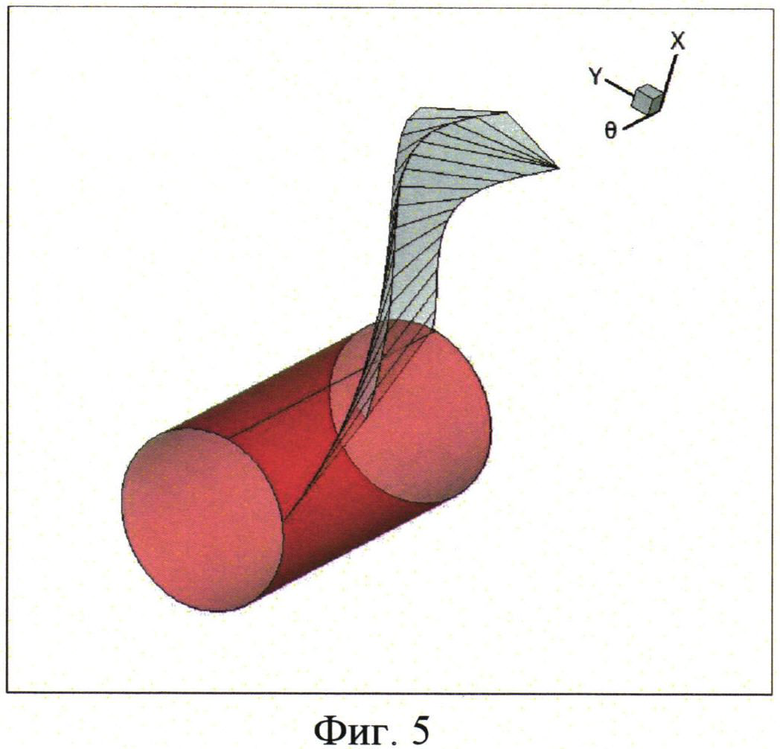
Численные расчеты заканчивались в контрольной точке - пересечение барьером плоскости симметрии дифференциальной игры, соответствующей точке начала маневрирования и, соответственно, некой линейной меры оптимального уклонения. Терминальная поверхность и поверхности барьеров 4-хмерного фазового пространства представлены на фиг.5.

Аппроксимация результатов параметрических исследований и их дальнейший анализ позволил установить закон степеней для показателя эффективности аэродинамической компоновки гиперзвукового летательного аппарата: 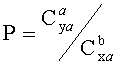$$P=\raisebox{1ex}{$C_{ya}^a$}\!\left/ \!\raisebox{-1ex}{$C_{xa}^b$}\right.$$ .

Поверхность гиперзвукового летательного аппарата оптимальной формы была построена численно методом локальных вариаций с целевой функцией: P→max и начальной формой поверхности летательного аппарата в виде затупленного по сфере конуса ограниченной длины и миделевого сечения и структурированной сеткой четырехугольных ячеек на его поверхности, показанной на фиг.6.

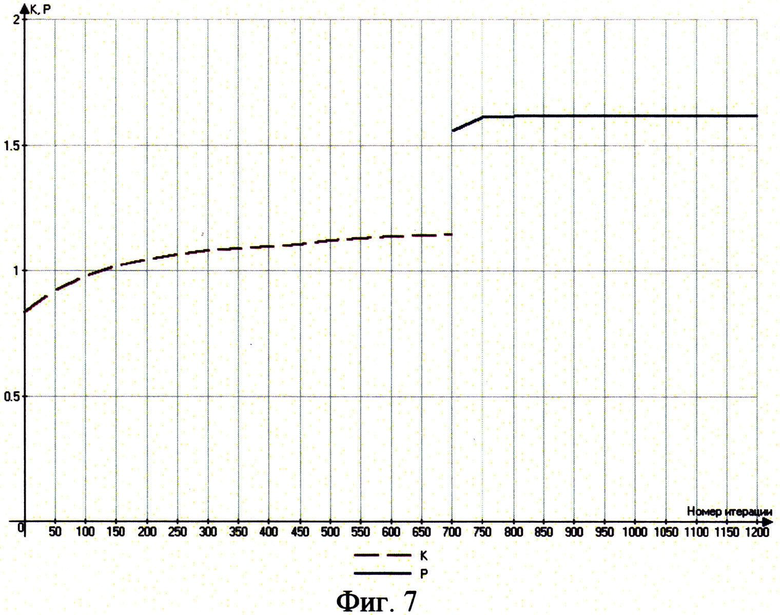
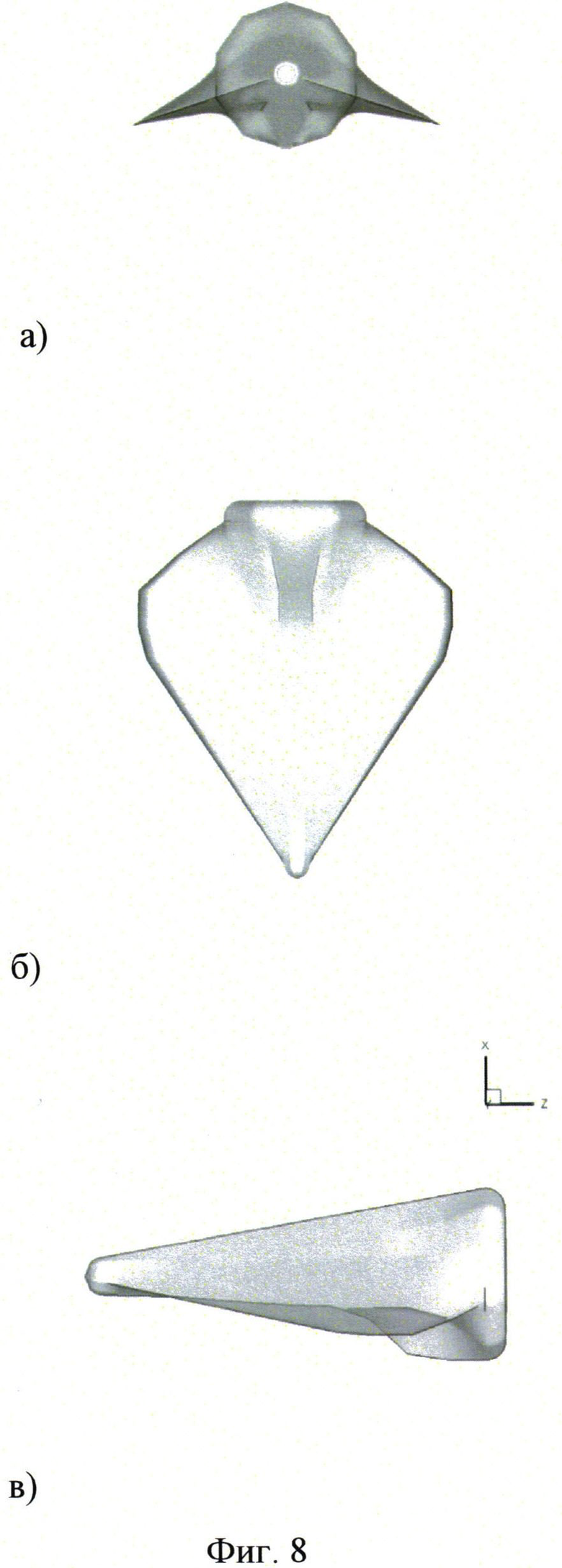
Численное решение вариационной задачи о построении оптимальной поверхности летательного аппарата было получено за 3000 итераций, зависимость соответствующего показателя эффективности показана на фиг.7. Значение показателя эффективности Р для оптимальной компоновки при ограничениях на форму носка и донного среза, длину аппарата и размеры отсеков для полезной нагрузки составило 1,5, а его форма приведена на фиг.8 (а - вид спереди, б - вид сверху, в - вид сбоку).

Представленная на фиг.8 форма летательного аппарата содержит технические решения по ограничению максимальных тепловых нагрузок, технологичность сборки с разгонным носителем, а также возможность использования критических CALS-технологий. Форма крылатого гиперзвукового летательного аппарата была получена при постоянстве внутренних объемов с полезной нагрузкой, неизменности носовой и кормовой частей летательного аппарата. Фиксированная форма носовой части позволяла обеспечивать необходимый балансировочный угол атаки, а кормовая часть была унифицирована для расположения на разгонной ступени РН.

Таким образом, заявленное изобретение позволяет решить задачу определения оптимальной формы уклоняющегося гиперзвукового летательного аппарата, который может обеспечить спасение экипажа с борта космической станции, терпящей аварию, а также решение задачи избежания столкновения воздушных судов скоростной гражданской авиации.

Список литературы

1. Фофонов Д.М. Оптимизация аэродинамической компоновки гиперзвуковых летательных аппаратов. // Космонавтика и ракетостроение. - 2010. - 17 с.

2. Петров К.П. Аэродинамика транспортных космических систем. - М.: Эдиториал УРСС, 2000. - 368 с.

3. Айзекс Р. Дифференциальные игры. - М.: Мир, 1967. - 315 с.

Изобретение относится к области летательных аппаратов. Способ построения оптимальной аэродинамической поверхности гиперзвукового летательного аппарата включает воздействие на поверхность летательного аппарата с использованием критерия оптимизации. В качестве критерия оптимизации используют отношение степеней коэффициентов подъемной силы и силы лобового сопротивления, по которому формируют оптимальную поверхность летательного аппарата для решения задачи уклонения от столкновения с использованием численных методов решения полных уравнений Навье-Стокса. При этом определяют рациональное расположение несущих поверхностей и форму носовой части аппарата с минимальными тепловыми нагрузками. Изобретение направлено на оптимизацию уклонения от столкновения. 8 ил.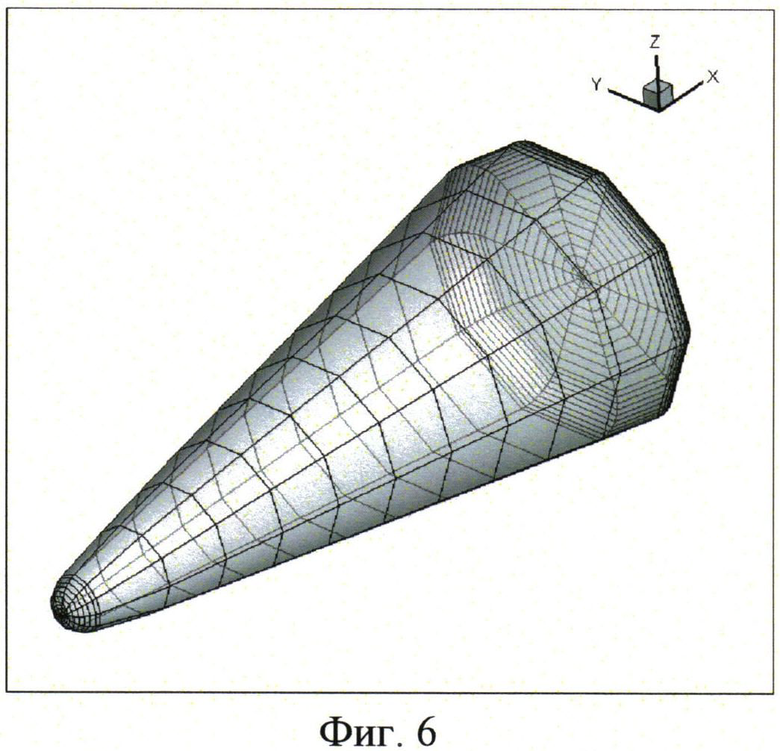

Способ построения оптимальной аэродинамической поверхности гиперзвукового летательного аппарата, включающий воздействие на его поверхность с использованием критерия оптимизации, отличающийся тем, что в качестве критерия оптимизации используют отношение степеней коэффициентов подъемной силы и силы лобового сопротивления 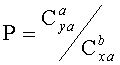, по которому формируют оптимальную поверхность летательного аппарата для решения задачи уклонения от столкновения, с использованием численных методов решения полных уравнений Навье-Стокса, для чего определяют рациональное расположение несущих поверхностей и форму носовой части аппарата с минимальными тепловыми нагрузками, где
Р - отношение степеней коэффициентов подъемной силы и силы лобового сопротивления, характеризующее показатель эффективности, полученный в результате численного решения дифференциальной игры качества,
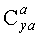- коэффициент подъемной силы, определяемый как отношение подъемной силы к скоростному напору и характерной площади,
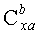- коэффициент силы лобового сопротивления, определяемый как отношение силы лобового сопротивления к скоростному напору и характерной площади.