Предлагаемое изобретение относится к области точного приборостроения и может быть использовано при создании таких средств измерения угловой скорости вращения объектов, как гироскопы.
Способ измерения частоты вращения гироскопов, основанный [Панов М.Ф., Соломонов А.В., Филатов Ю.В. Физические основы интегральной оптики. - М.: изд. Радиоэлектроника. 2010. - 432 с., Бычков СИ., Лукьянов Д.П., Бакаляр А.И. Лазерный гироскоп. - М.: Сов. радио. 1975. - 424 с.] на применении так называемого «оптического вихревого эффекта Саньяка», проявляющегося в изменении времени обхода электромагнитным (ЭМ) полем замкнутого контура L во внутренней полости при вращении последнего относительно инерциальной системы отсчета. Считается, что в таком интерферометре ЭМ-поле, распространяясь в двух противоположных - относительно направления вращения - направлениях, испытывает разный набег фазы, а разность фаз пропорциональна частоте вращения Ω. Интерференционная картина сдвигается, величина этого сдвига используется для измерения скорости (частоты) вращения с помощью частотомера и решающего устройства (фотопластины, фотоприемника и др.).
Фазовый сдвиг во вращающихся интерферометрах вычисляется на основе разного рода допущений. В ряде работ, например, в [Лауэ М. К опыту Ф.Харреса. // В кн. Статьи и речи. - М. Изд. Наука, пер. с нем. 1969. С.367] и во многих других, допускается возможность существования скорости распространения ЭМ-поля большей скорости света с, в других работах вычисления производятся на основе электродинамики классической физики. Но результаты вычислений одинаковы - они получены еще Максом Лауэ: расчетное соотношение для разности времен прохождения ЭМ-полями путей по направлению движения часовой стрелки и против движения часовой стрелки Δt=8πFS/c2, где F=Ω/2π - число оборотов интерферометра в секунду, S - площадь, ограниченная «путями распространения ЭМ-поля». Разность фаз ЭМ-полей при этом за счет разности хода вычисляется по формуле

где ω0 и λ0 - частота и длина волны тока излучающего источника.
Но А.Зоммерфельд [Зоммерфельд А. Оптика / А.Зоммерфельд. - М.: Изд. ИЛ. - 1953. - 486 с.], а потом и М.Лауэ [Лауэ М. К опыту Ф.Харреса. // В кн. Статьи и речи. - М. Изд. Наука, пер. с нем. 1969. С.367] показали, что для вычисления разности фаз ΔФ необходимо поставить и решить граничную задачу в неинерциальной системе отсчета, поскольку на ЭМ-поле во вращающемся интерферометре или резонаторе воздействуют гравитационные силы.
Попытки строгих постановки и решения этой задачи предприняты в многочисленных работах (см. библиографию в [Бычков СИ., Лукьянов Д.П., Бакаляр А.И. Лазерный гироскоп. - М.: Сов.радио. 1975. - 424 с., Лауэ М. К опыту Ф.Харреса. // В кн. Статьи и речи. - М. Изд. Наука, пер. с нем. 1969. С.367, Post E.J., Vildiz A., Cavity Resonances in Accelerated Systems. // Physical Review Letters. 1965. V.15, №5, pp.177-178., Хромых A.M. Кольцевой генератор во вращающейся системе отсчета. // ЖЭТФ. 1966. Т.50. Вып.1. С.281-282., Andersson Y.L., Ryon J.W. Electromagnetic Radiation in Accelerated Systems. // Physical Review. 1969. V.181.№5. P.1765-1775, Белоногов A.M. Электромагнитные колебания в объемном резонаторе во вращающейся системе отсчета // ЖТФ. 1969. Т.39, вып.7. С.1170-1176]). Но при этом применялась или нековариантная формулировка уравнений Максвелла, или в материальных, или в дифференциальных уравнениях делались упрощающие допущения, что приводило к решениям, эквивалентным, по существу, решениям классической электродинамики. Поэтому расчеты радиоэлектронных гироскопов основаны на приближенных представлениях об ЭМ-поле.
В соответствии с выражением (1) считается, что в случае резонатора «изменение его периметра» при вращении приведет к изменению «частот настройки» для «встречных волн», разность частот

где λ=4πc/(ω1+ω2) - средняя длина волны, ω1 и ω2 - частоты настройки вращающегося кольцевого резонатора для «волн», распространяющихся в направлении вращения и против последнего.
Из решения задачи о возможности распространения ЭМ-поля во вращающемся резонаторе на основе ряда допущений получена разность частот («расщепление» частот) встречных волн Δω=2(Ωcℵ), где Ω и cℵ - векторы частоты вращения и коэффициента «расщепления собственных частот». «Расчет последнего представляет большие трудности и может быть произведен только на основе ряда упрощений» [Бычков СИ., Лукьянов Д.П., Бакаляр А.И. Лазерный гироскоп. - М.: Сов. радио. 1975. - 424 с.].
Эти упрощения использованы при расчетах параметров ЭМ-полей, например, в патентах «Волоконно-оптический тахометр» (патент РФ №2275642), «Волоконно-оптический тахометр» (патент РФ №2297006), «Твердотельный лазерный гироскоп с механически активируемой усиливающей средой» (патент РФ №2437062), «Лазерный гироскоп» (патент РФ №2364837), «Волоконно-оптический гироскоп» (патент РФ №2283475).
Из основных расчетных выражений (1) и (1а) следуют выводы: отношение площади интерферометра к длине волны источника ЭМ-поля должно быть большим для того, чтобы разность фаз ДФ была измеряемой величиной. Это означает, что, во-первых, ЭМ-поле должно использоваться только оптического диапазона длин волн, а во-вторых, вращающиеся интерферометры должны работать при этом в многомодовом режиме. Частота вращения при этом измеряется с помощью измерителя разности фаз и решающего устройства по разности фаз ΔФ, т.е. косвенным способом.
Известен радиолокационный способ измерения скорости вращения объекта (Петров Б.М. «Радиолокационный способ измерения скорости вращения», авторское свидетельство №278269), в котором контролируемый объект облучается ЭМ-полем. Рассеянное (отраженное, вторичное) ЭМ-поле за счет модуляции поля при вращении объекта имеет дискретный спектр частот, спектральные составляющие которого в общем случае сдвинуты по оси частот на частоту вращения. Вычисляя разность частот между соседними спектральными составляющими, можно определить частоту вращения.
Ниже для обоснования предлагаемого нового резонансного (радиоэлектронного) способа измерения частоты вращения объекта по внутреннему электромагнитному полю в полости этого объекта даны на основе ковариантных уравнений электродинамики строгие постановки и решения граничных задач о возможности существования полей колебаний электрического и магнитного типов во вращающемся шаровом резонаторе. Приведен анализ результатов решения. Приведены и основные результаты строгого решения граничной задачи о возможности существования поля электрического типа колебаний в коаксиальном резонаторе гироскопа.
Электромагнитные колебания во вращающемся шаровом резонаторе
Постановка граничных задач. Введем в свободное пространство инерциальную (декартову) систему отсчета K'(x',y' z',ict)=K'(R',θ',φ',ict)=K'(xj'), где i - мнимая единица, t - время, xj'=(x1',x2',х3',x0'), xj'=(R',θ',φ') - сферические координаты (α'=1',2',3'), и покоящуюся в ней точку наблюдения P'(xj',ict). Шаровой резонатор, образованный металлической сферической оболочкой радиуса а проводимости σ1, пространство внутри которой заполнено изотропной однородной линейной средой без джоулевых потерь и гистерезиса с диэлектрической ε=ε0ε' и магнитной µ=µ0µ' проницаемостями, где ε0 и µ0 - электрическая и магнитная постоянные, вращается относительно точки P' с постоянной угловой частотой Ω. Введем жесткую вращающуюся систему отсчета K(R,θ,φ,t)=K(xj,t). Начала сферических систем координат поместим в центре шара, а полярную ось (θ=θ'=0) направим вдоль оси вращения. Обозначим через P(pα,t), где pα=pα(x1,x2,x3)=pα(R, θ,φ), покоящуюся в системе отсчета K точку наблюдения ЭМ-поля. При этом R'=R,θ'=θ,φ'=φ+Ωt. Параметры σ1,ε,µ. и a считаем измеренными в системе отсчета K. Полагаем, что область сторонних источников, возбуждающих ЭМ-поле на частоте ω0(λ0 - длина волны), измеренной во времени t, выведена из объема резонатора.
Необходимо рассмотреть возможность существования ЭМ-поля в объеме вращающегося резонатора.
Уравнения Максвелла в резонаторе в системе отсчета K однородны и могут быть записаны в соответствии с [Петров Б.М. Прикладная электродинамика вращающихся тел. - М.: Горячая линия - Телеком, 2009. - 288 с.] в трехмерной форме для ковариантного вектора напряженности электрического поля Eα=(E1,E2,E3)=(ER,REθ,RsinθEφ)=E, для напряженности магнитного поля - контравариантной бивекторной плотности веса 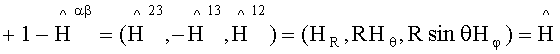 , для электрической индукции - контравариантной векторной плотности веса
, для электрической индукции - контравариантной векторной плотности веса 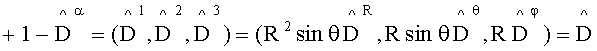 , для ковариантного бивектора магнитной индукции Bαβ=(B23,-B13,B12)=(R2sinθBθφ,-RsinθBRφ,RBRθ)=B:
, для ковариантного бивектора магнитной индукции Bαβ=(B23,-B13,B12)=(R2sinθBθφ,-RsinθBRφ,RBRθ)=B:

где компоненты напряженностей полей и индукций входят в дуальных формах.
В системе отсчета K ЭМ-поле, удовлетворяющее уравнениям (2), с помощью материальных уравнений, полученных в [Петров Б.М. Прикладная электродинамика вращающихся тел. - М.: Горячая линия - Телеком, 2009. - 288 с.], и вспомогательных функций vэ и vм, которые имеют смысл электрического и магнитного потенциалов Дебая в неинерциальной системе отсчета и которые удовлетворяют волновому уравнению
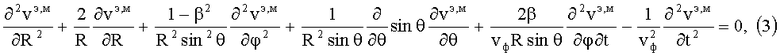
где β=ΩRsinθ/vф, vф=(εµ)-1/2, разделяется на ЭМ-поле колебаний электрического типа (E-колебаний), когда радиальная компонента бивектора магнитной индукции Bθφ=0, или BR=0, и на ЭМ-поле колебаний магнитного типа (H-колебаний), когда радиальная компонента векторной плотности электрической индукции 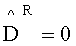 . При этом в случае E-колебаний для компонент ЭМ-поля получаем
. При этом в случае E-колебаний для компонент ЭМ-поля получаем
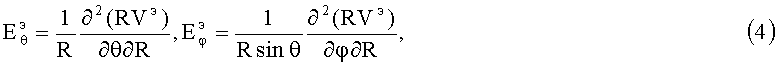
 ;
;
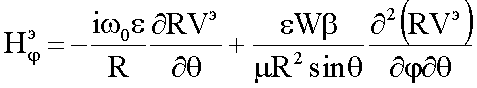 ;
;

 ,
,
где радиальная компонента  по (5) отличается от нуля и пропорциональна коэффициенту β и обратно пропорциональна характеристическому сопротивлению W=(µ/ε)1/2.
по (5) отличается от нуля и пропорциональна коэффициенту β и обратно пропорциональна характеристическому сопротивлению W=(µ/ε)1/2.
В случае Н-колебаний для компонент ЭМ-поля получаем при Bθφ=0:
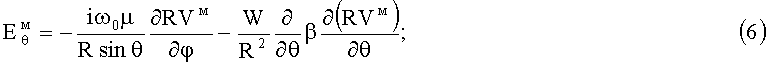
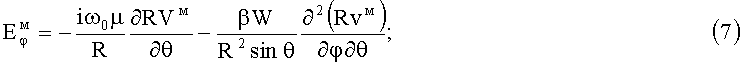
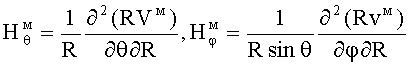 ;
;

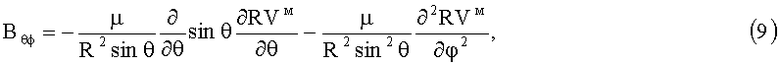
где радиальная компонента 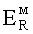 по (8) отличается от нуля и пропорциональна коэффициенту β и W.
по (8) отличается от нуля и пропорциональна коэффициенту β и W.
В математической модели считаем проводимость металлической оболочки σ1 идеальной. Тогда на поверхности оболочки в случае Е-волн касательные к оболочке компоненты 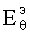 и
и 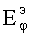 должны обращаться в нуль, т.е.
должны обращаться в нуль, т.е. 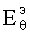 =
=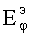 =0 при R=a. Значит, в соответствии с (4) необходимо выполнение условия для электрического потенциала Дебая
=0 при R=a. Значит, в соответствии с (4) необходимо выполнение условия для электрического потенциала Дебая

При этом нормальная к поверхности оболочки составляющая 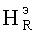 при R=a тоже обращается в нуль, т.е. удовлетворяются граничные условия и для магнитного поля.
при R=a тоже обращается в нуль, т.е. удовлетворяются граничные условия и для магнитного поля.
В случае колебаний магнитного типа компоненты  и
и 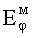 при R=a должны обращаться в нуль. Значит, в соответствии с (6) и (7) необходимо выполнение граничного условия для магнитного потенциала Дебая
при R=a должны обращаться в нуль. Значит, в соответствии с (6) и (7) необходимо выполнение граничного условия для магнитного потенциала Дебая

При этом нормальная к поверхности оболочки составляющая 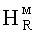 при R=a тоже обращается в нуль, т.е. удовлетворяются граничные условия и для магнитного поля.
при R=a тоже обращается в нуль, т.е. удовлетворяются граничные условия и для магнитного поля.
Решение граничной задачи для ЭМ-поля E-колебаний
Характеристическим решением уравнения (3) во вращающейся системе отсчета со сферическими координатами, конечным при θ=0 и θ=π, является пространственная гармоника
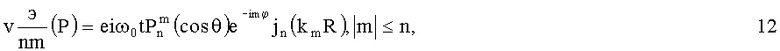
где 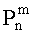 (соsθ) - присоединенные полиномы Лежандра, определенные по [Гобсон Е.В. Теория сферических и сфероидальных функций. М.: Изд. ИЛ. 1952. - с.92], jn(kmR) - сферические функции Бесселя, km=k0+mΩ/vф, k0=ω0/vф, n и m - целые числа.
(соsθ) - присоединенные полиномы Лежандра, определенные по [Гобсон Е.В. Теория сферических и сфероидальных функций. М.: Изд. ИЛ. 1952. - с.92], jn(kmR) - сферические функции Бесселя, km=k0+mΩ/vф, k0=ω0/vф, n и m - целые числа.
Подставляя (12) в граничное условие (10), получаем
 , или
, или 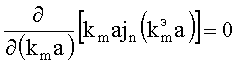
Решениями этого дисперсионного уравнения являются корни 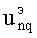 , где q=1, 2, 3,… При этом
, где q=1, 2, 3,… При этом 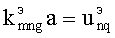 , т.е. собственными (резонансными) частотами вращающегося резонатора являются
, т.е. собственными (резонансными) частотами вращающегося резонатора являются
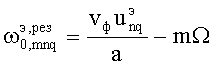 ,
, 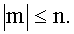
Для зональной гармоники, когда m=0, собственные частоты вращающегося резонатора 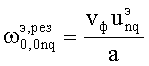 совпадают с собственными частотами «неподвижного» резонатора (при Ω=0). Поэтому зональная гармоника ЭМ-поля информации о частоте вращения не несет.
совпадают с собственными частотами «неподвижного» резонатора (при Ω=0). Поэтому зональная гармоника ЭМ-поля информации о частоте вращения не несет.
Имеем 
Существование ЭМ-поля Emnq-колебаний возможно только на дискретных частотах (13). Поэтому

На заданной резонансной частоте 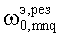 компоненты ЭМ-поля Emnq-колебаний получаются с помощью выражений (4), (5) и (14).
компоненты ЭМ-поля Emnq-колебаний получаются с помощью выражений (4), (5) и (14).
Решение граничной задачи для ЭМ-поля H-колебаний
Характеристическим решением уравнения (3) в системе отсчета K со сферическими координатами является пространственная гармоника
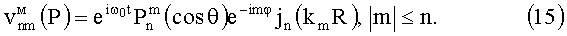
Удовлетворяя граничному условию (11), получаем дисперсионное уравнение
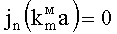 ,
,
решениями которого являются корни  , где q=1, 2, 3,…, т.е. собственными частотами вращающегося резонатора являются
, где q=1, 2, 3,…, т.е. собственными частотами вращающегося резонатора являются

Существование ЭМ-поля Hmnq-колебаний возможно только на этих дискретных частотах. Из (15) имеем пространственную гармонику потенциала Дебая Hmnq-колебаний:
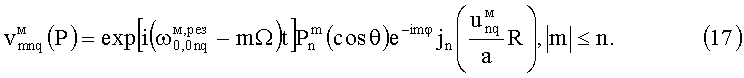
На заданной резонансной частоте 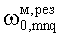 компоненты ЭМ-поля Hmnq-колебаний получаются с помощью выражений (6)-(9) и (17).
компоненты ЭМ-поля Hmnq-колебаний получаются с помощью выражений (6)-(9) и (17).
Анализ ЭМ-полей Emnq- и Hmnq-колебаний. Назовем  собственными частотами «неподвижного» резонатора,
собственными частотами «неподвижного» резонатора, 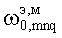 - собственными частотами вращающегося резонатора. В соответствии с (13) и (16) для тессеральных гармоник с m<о имеем
- собственными частотами вращающегося резонатора. В соответствии с (13) и (16) для тессеральных гармоник с m<о имеем  >
> , а для тессеральных гармоник с m>0
, а для тессеральных гармоник с m>0  <
< . Из выражений (13) и (16) следует: каждое собственное значение частоты «неподвижного» резонатора «расщепляется» на 2n собственных частот во вращающемся резонаторе. Происходит это из-за влияния на ЭМ-поле тессеральных гармоник, распространяющихся по направлению вращения и против этого направления, сил Кориолиса разных знаков. Среда, заполняющая вращающийся резонатор, становится анизотропной средой для распространяющегося ЭМ-поля.
. Из выражений (13) и (16) следует: каждое собственное значение частоты «неподвижного» резонатора «расщепляется» на 2n собственных частот во вращающемся резонаторе. Происходит это из-за влияния на ЭМ-поле тессеральных гармоник, распространяющихся по направлению вращения и против этого направления, сил Кориолиса разных знаков. Среда, заполняющая вращающийся резонатор, становится анизотропной средой для распространяющегося ЭМ-поля.
Если «неподвижный» резонатор настроен на ЭМ-поле H011-колебания, то 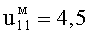 ,
, 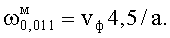 . Тогда имеем две собственные частоты вращающегося резонатора
. Тогда имеем две собственные частоты вращающегося резонатора  и
и  . Разность «расщепления» резонансных частот вращающегося резонатора
. Разность «расщепления» резонансных частот вращающегося резонатора
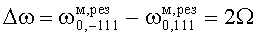 .
.
Для «неподвижного» резонатора, рассчитанного на применение ЭМ-поля H012-колебания, имеем 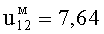 ,
,  . Тогда получаем две собственные частоты вращения:
. Тогда получаем две собственные частоты вращения:  и
и  . Разность «расщепления» резонансных частот вращающегося резонатора Δω=2Ω.
. Разность «расщепления» резонансных частот вращающегося резонатора Δω=2Ω.
Пусть резонатор настроен на ЭМ-поле H021-колебания. При этом 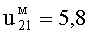 ,
, 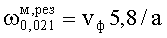 . Имеем 4 собственные частоты вращающегося резонатора:
. Имеем 4 собственные частоты вращающегося резонатора: 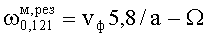 ,
, 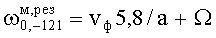 и
и 
 . Разность «расщепления» крайних резонансных частот вращающегося резонатора равна 4Ω.
. Разность «расщепления» крайних резонансных частот вращающегося резонатора равна 4Ω.
Если резонатор рассчитан на применение ЭМ-поля E011-колебания, то  ,
,  . Имеем две собственные частоты вращающегося резонатора:
. Имеем две собственные частоты вращающегося резонатора: 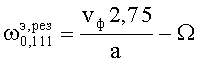 и
и  . Разность «расщепления» резонансных частот вращающегося резонатора равна 2Ω.
. Разность «расщепления» резонансных частот вращающегося резонатора равна 2Ω.
Частота 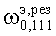 является наименьшей из всех возможных собственных
является наименьшей из всех возможных собственных
частот вращающегося резонатора. Поэтому E111-колебание вращающегося резонатора, несущее информацию о частоте вращения, назовем основным. Остальные типы Emnq- и Hmnq-колебаний вращающегося резонатора назовем высшими типами (модами).
В случае основного типа E111-колебания компоненты ЭМ-поля, отличающиеся от нуля, получим из (4), (5) и (14). Поскольку 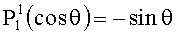 , то
, то
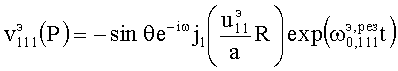 ,
,

где A - постоянный коэффициент.
Рассмотрим случай, когда электрический радиус вращающегося резонатора такой, что в нем существуют, наряду с основным, высшие типы колебаний (многомодовый режим). При этом число типов колебаний с m>0 определяется приближенно величиной mмакс≈νNk0a, а число типов колебаний с m<0 - величиной mмин≈-νNk0a, где νN - коэффициент, зависящий от k0a и чувствительности измерительной аппаратуры [Петров Б.М. Прикладная электродинамика вращающихся тел. - М: Горячая линия - Телеком, 2009. - 288 с/]. Тогда разность «расщепления» всех возможных собственных частот вращающегося резонатора Δω≈νN2k0aΩ. Если приближенно считать, что «время обхода» контура L=2πa «лучом» равно τ=L/vф, то разность фаз за счет разности хода «лучей», распространяющихся по направлению вращения резонатора и против этого направления
Δф=Δωτ=νN8πSΩ/λ0vф, S=πa2,
что отличается от (1) коэффициентом νN>1, который определяется приближенно.
Выводы. Поставленные граничные задачи о возможности существования ЭМ-полей электрических и магнитных колебаний впервые решены строго на основе электродинамики общей теории относительности. Показано, что в ЭМ-поле вращающегося резонатора не существует «вихревых эффектов» или изменений частоты ЭМ-поля; вращение приводит к проявлению (возникновению) новых резонансных частот, сдвинутых на частоту вращения относительно друг друга. Это явление - эффект проявления собственных частот вещества во вращающемся резонаторе под влиянием гравитационного поля - подобно явлениям Штарка и Зеемана; для измерения частоты вращения возможно применение по конструктивным соображениям ЭМ-поля диапазона радиочастот.
Электромагнитные колебания во вращающемся коаксиальном резонаторе
Постановка граничной задачи. Введем в свободное пространство инерциальную (декартову) систему отсчета K'(x',y',z',ict)=K'(r',φ',z',ict)=K'(xj'), где i - мнимая единица, t - время; xj'=(x1',x2',x3',x0')xα'=(r',φ',z') - цилиндрические координаты (α=1, 2, 3), и покоящуюся в ней точку наблюдения P'(xα',ict). Внутри металлической цилиндрической трубы радиуса a, длины l расположен коаксиально металлический цилиндр радиуса b, длины l. Ось z' направлена вдоль осей коаксиальных цилиндров. В поперечных сечениях при z'=0 и z'=l расположены металлические плоские торцы. Коаксиальные цилиндры с торцами вращаются относительно точки P' с постоянной угловой частотой Ω=2πF. Введем жесткую вращающуюся систему отсчета K(r,φ,z,t)=K(xα,t) с осью z, направленной вдоль осей цилиндров. Тогда ось z=z' является осью вращения. Обозначим через P(pα,t), где pα=pα(r,φ,z), покоящуюся в системе отсчета K точку наблюдения ЭМ-поля. Пространство между коаксиальными цилиндрами заполнено изотропной однородной линейной средой без джоулевых потерь и гистерезиса с диэлектрической ε=ε0ε' и магнитной µ=µ0µ' проницаемостями, где ε0 и µ0 - электрическая и магнитная постоянные. Если xα=α(r,φ,z) - цилиндрические координаты, то r'=r,φ'=φ+Ωt,z'=z. Параметры ε,µ,a,b считаем измеренными в системе отсчета К. Полагаем, что область сторонних источников, возбуждающих ЭМ-поле на частоте ω0 (длина волны λ0), измеренной во времени t, выведена из объема, образованного коаксиальными цилиндрами и торцами (объема резонатора). Тогда необходимо рассмотреть возможность существования ЭМ-поля в объеме вращающегося резонатора.
Уравнения Максвелла в резонаторе в системе отсчета K однородны и могут быть записаны в соответствии с [Петров Б.М. Прикладная электродинамика вращающихся тел. - М.: Горячая линия - Телеком, 2009. - 288 с/] в трехмерной форме для ковариантного вектора напряженности электрического поля Eα=(E1,E2,E3)=E, для контравариантной векторной плотности веса +1 - напряженности магнитного поля 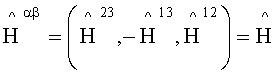 , для контравариантной плотности веса +1 - электрической индукции
, для контравариантной плотности веса +1 - электрической индукции 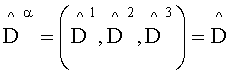 , для ковариантного бивектора магнитной индукции Bαβ=(B23,-В13,B12)=B:
, для ковариантного бивектора магнитной индукции Bαβ=(B23,-В13,B12)=B:

ЭМ-поле в системе отсчета K, удовлетворяющее (18), с помощью электрического Vэ и магнитного Vм потенциалов Дебая, являющихся
решениями волнового уравнения
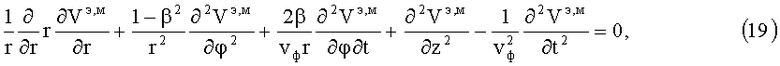
где 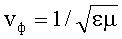 , β=Ωr/vф, разделяется на ЭМ-поле волн электрического типа (Е-волн), когда продольная компонента бивектора магнитной индукции Brφ=r-1B12,B12=0, и на ЭМ-поле волн магнитного типа (H-волн), когда продольная компонента векторной плотности электрической индукции
, β=Ωr/vф, разделяется на ЭМ-поле волн электрического типа (Е-волн), когда продольная компонента бивектора магнитной индукции Brφ=r-1B12,B12=0, и на ЭМ-поле волн магнитного типа (H-волн), когда продольная компонента векторной плотности электрической индукции  . При этом для Е-волн, если обозначить
. При этом для Е-волн, если обозначить  , то
, то
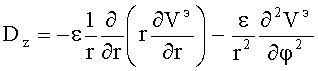 ;
;  ;
;
 ;
; 
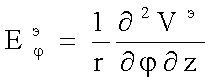 ;
;  ;
; 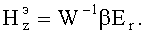
В математической модели считаем проводимость стенок цилиндров и торцов идеальной. Тогда на поверхностях цилиндров и на торцах для ЭМ-поля E-волн должны выполняться граничные условия
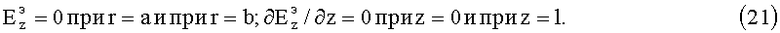
Таким образом, для ЭМ-поля E-колебаний необходимо найти решение уравнений (18) при граничных условиях (21).
Решение задачи для ЭМ-поля E-колебаний. Потенциал Дебая Vэ, являющийся решением уравнения (19), полученного из уравнений Максвелла (18), представляется при z≥0 линейной комбинацией элементарных цилиндрических волн

где 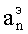 - коэффициенты,
- коэффициенты,  , kn=ωn/vф, ωn=ω0+nΩ;
, kn=ωn/vф, ωn=ω0+nΩ;  ; Zn(χr) - цилиндрическая функция аргумента χr, порядка n. Так как ЭМ-поле ищется в полости при b≤r≤a, то начало координат из рассмотрения исключается, поскольку ЭМ-поле в проводнике идеальной проводимости отсутствует. Тогда при b≤r≤a, z≥0 по (22) имеем
; Zn(χr) - цилиндрическая функция аргумента χr, порядка n. Так как ЭМ-поле ищется в полости при b≤r≤a, то начало координат из рассмотрения исключается, поскольку ЭМ-поле в проводнике идеальной проводимости отсутствует. Тогда при b≤r≤a, z≥0 по (22) имеем
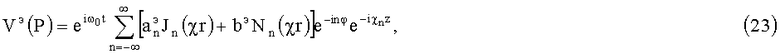
где aэ, bэ - коэффициенты, Jn(χr) и Nn(χr) - функции Бесселя и Неймана.
Для того чтобы выразить составляющую  в (20), подставим значения Dz и
в (20), подставим значения Dz и  в общее выражение
в общее выражение  . Используя волновое уравнение (19) для потенциала Vэ, получаем
. Используя волновое уравнение (19) для потенциала Vэ, получаем
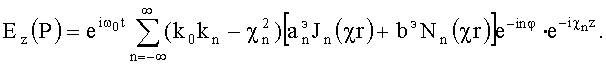
Из первого граничного условия (21) при r=a имеем, оставляя множители, зависящие от a,  . Из второго граничного условия (21) при r=b имеем, оставляя множители, зависящие от b, a
эJn(χb)+bэNn(χb)=0. Чтобы ЭМ-поле существовало в полости (отличалось от нуля), необходимо, чтобы в системе двух последних уравнений коэффициенты
. Из второго граничного условия (21) при r=b имеем, оставляя множители, зависящие от b, a
эJn(χb)+bэNn(χb)=0. Чтобы ЭМ-поле существовало в полости (отличалось от нуля), необходимо, чтобы в системе двух последних уравнений коэффициенты  ,
,  не равнялись нулю. Они не равны нулю только, если определитель из функций Бесселя и Неймана равен нулю, т.е.
не равнялись нулю. Они не равны нулю только, если определитель из функций Бесселя и Неймана равен нулю, т.е.
Jn(χa)Nn(χb)-Jn(χb)Nn(χa)=0.
Корни  этого дисперсионного уравнения определяют поперечные коэффициенты распространения
этого дисперсионного уравнения определяют поперечные коэффициенты распространения 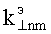 азимутальных гармоник ЭМ-поля. Обозначим a=ζb, где ζ>1. Тогда имеем
азимутальных гармоник ЭМ-поля. Обозначим a=ζb, где ζ>1. Тогда имеем
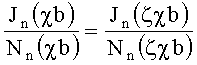 .
.
Корнями этого уравнения, например, при ζ=1,2 являются значения 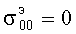 ,
,  ,
, 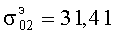 ,
, 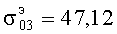 ,
,  и т.д.; при n=1 корнями являются числа
и т.д.; при n=1 корнями являются числа 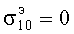 ,
, 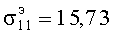 ,
, 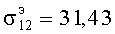 ,
, 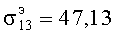 ,
,  и т.д. [Янке Е., Эмде Ф., Леш Ф. Специальные функции. Изд. 2-е. - М.: Наука. 1968. - 344 с/]. Если использовать асимптотические выражения цилиндрических функций в этом уравнении при χb>>|n|, то получим значения корней
и т.д. [Янке Е., Эмде Ф., Леш Ф. Специальные функции. Изд. 2-е. - М.: Наука. 1968. - 344 с/]. Если использовать асимптотические выражения цилиндрических функций в этом уравнении при χb>>|n|, то получим значения корней

Эти значения мало отличаются от строгого решения уравнения.
Таким образом, 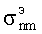 , по крайней мере, при малых n и m можно вычислять по (24). При этом поперечный коэффициент распространения
, по крайней мере, при малых n и m можно вычислять по (24). При этом поперечный коэффициент распространения  почти не зависит от номера азимутальной гармоники. При m=0 необходимы дополнительные исследования, так как при
почти не зависит от номера азимутальной гармоники. При m=0 необходимы дополнительные исследования, так как при 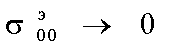

Решение уравнения (19), удовлетворяющее граничным условиям при r=b и r=a, в соответствии с (23) теперь можно представить в виде
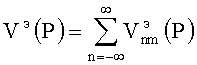 ,
,
где
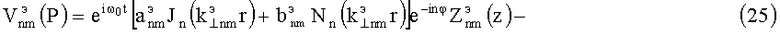
пространственная гармоника потенциала Дебая, a  - искомая функция такая, что
- искомая функция такая, что 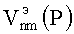 должна удовлетворять волновому уравнению и
должна удовлетворять волновому уравнению и
граничным условиям при z=0 и z=l.
Для определения функции  подставим (25) в (19) и учтем, что
подставим (25) в (19) и учтем, что  удовлетворяет уравнению Бесселя. Получаем
удовлетворяет уравнению Бесселя. Получаем
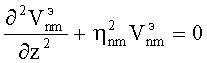 ,
,
где  .
.
Подставим в это выражение значение  из (25). Сокращая множители, не зависящие от z, имеем обыкновенное дифференциальное уравнение для искомой функции
из (25). Сокращая множители, не зависящие от z, имеем обыкновенное дифференциальное уравнение для искомой функции 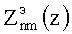 :
:
 ,
,
общим решением которого является
 ,
,
где gnm, 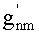 - амплитуды бегущих волн.
- амплитуды бегущих волн.
Сформулируем граничные условия для функции 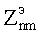
Пространственная гармоника продольной составляющей 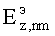 с помощью (19) и (20) выражается через
с помощью (19) и (20) выражается через  следующим образом
следующим образом
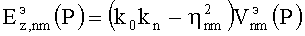 ,
,
поэтому граничное условие на торцах выполняется, если
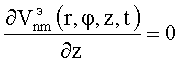 при z=0 и z=l.
при z=0 и z=l.
Значит, функция 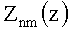 должна удовлетворять граничным условиям
должна удовлетворять граничным условиям 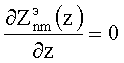 при z=0, z=l. Поэтому
при z=0, z=l. Поэтому

Таким образом, пространственной азимутальной гармоникой потенциала Дебая для ЭМ-поля колебаний электрического типа является
 ,
,
где 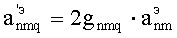 ,
, 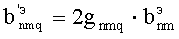 - коэффициенты.
- коэффициенты.
Решением граничной задачи по определению ЭМ-поля E-колебаний вращающегося резонатора является потенциал Дебая

совместно с выражениями (20).
Собственные частоты Enmq-колебаний. Подставим (26) в волновое уравнение (29), выполняя дифференциальные операции, получаем
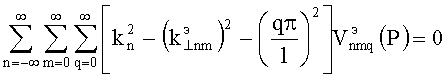 .
.
Для существования ЭМ-поля в резонаторе необходимо, чтобы выражение в квадратных скобках равнялось нулю 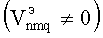 . При этом
. При этом
 ,
,
т.е.
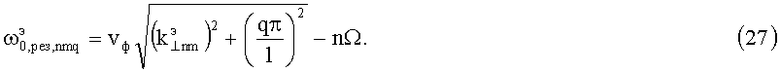
Рассмотрим первый случай, когда задана частота вращения Ω. Тогда для пространственных гармоник, распространяющихся в направлении увеличения координаты φ (в положительном направлении), для ЭМ-поля E|n|mq-колебаний, резонансной (собственной) частотой является
 ,
,
где 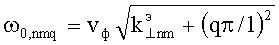 - собственная частота «неподвижного» резонатора.
- собственная частота «неподвижного» резонатора.
Для пространственных гармоник, распространяющихся в противоположном направлении (в отрицательном направлении), т.е. для поля E-|n|mq - колебаний, резонансной (собственной) частотой является
 .
.
Таким образом, разность резонансных частот E-|n|mq - и E|n|mq- колебаний («расщепление» частот)

В этом выражении n определяет тип колебания «неподвижного» резонатора. Если применить для измерения частоты вращения E0mq-колебания, то n=0 и расщепление частот не происходит:  . Значит, на основном или E010-, или T1-колебании «неподвижного» коаксиального резонатора измерения частоты вращения произвести невозможно. Учитывая асимптотические свойства цилиндрических функций в (26), получаем, что при k0b>>1 и малых q в многомодовом режиме минимальное значение |n|мин=νNk0b, максимальное значение
. Значит, на основном или E010-, или T1-колебании «неподвижного» коаксиального резонатора измерения частоты вращения произвести невозможно. Учитывая асимптотические свойства цилиндрических функций в (26), получаем, что при k0b>>1 и малых q в многомодовом режиме минимальное значение |n|мин=νNk0b, максимальное значение  , где коэффициенты νN>1,
, где коэффициенты νN>1,  определены в [Петров Б.М. Прикладная электродинамика вращающихся тел. - М.: Горячая линия - Телеком, 2009. - 288 с.]. Тогда расщепление частот по (28)
определены в [Петров Б.М. Прикладная электродинамика вращающихся тел. - М.: Горячая линия - Телеком, 2009. - 288 с.]. Тогда расщепление частот по (28)
 ,
,
что при b=0 и только при  совпадает с выражением (1).
совпадает с выражением (1).
Таким образом, во вращающемся коаксиальном резонаторе могут существовать E-|n|mq- и E|n|mq-колебания, им соответствуют две собственные частоты, зависящие как и в «неподвижном» резонаторе, от электродинамических параметров заполняющего резонатор вещества, электрических размеров и частоты вращения резонатора. Во вращающемся резонаторе происходит «расщепление» собственных частот.
Рассмотрим второй случай, соответствующий измерению частот 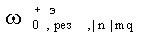 и
и 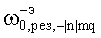 . При этом для E|n|mq-колебаний с положительным индексом резонансная частота вращения в соответствии с (27)
. При этом для E|n|mq-колебаний с положительным индексом резонансная частота вращения в соответствии с (27)
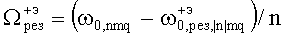 ,
,
а для E-|n|mq-колебаний с отрицательным индексом резонансная частота вращения
 .
.
Выводы
Таким образом, строгие постановка и решение граничных, задач о возможности существования ЭМ-поля во вращающейся полости показывают, что каждая из собственных (резонансных) частот ее определяется суммой собственной частоты «покоящейся»полости и частоты вращения, умноженной на целое число, зависящее от типа ЭМ-колебания. Поэтому измерить частоту вращения полости можно как разность между частотой вращения и резонансной частотой «покоящейся» полости на заданном типе ЭМ-колебания; эта разность делится на зависящее от заданного типа ЭМ-колебания целое число.
Техническим результатом заявляемого резонансного способа измерения частоты вращения объекта является возможность миниатюризации линейных размеров вращающейся полости с одновременным увеличением точности измерения частоты вращения за счет использования разных резонансных свойств ЭМ-поля в одной и той же вращающейся и «покоящейся» полости.
Заявляемый способ дает возможность использовать одномодовый режим и, значит, выбрать собственную частоту из частот радиодиапазона. При этом точность измерения частоты вращения определяется хорошо разработанными радиотехническими методами измерения частоты, а способ измерения является прямым.
Способ измерения частоты вращения полости, основанный на «оптическом вихревом эффекте Саньяка», т.е. приближенной формуле (1) или на приближенной формуле (1а), не учитывает физических явлений во вращающейся полости, является принципиально приближенным, так как измеряется разность фаз, а не частота вращения, поэтому он является косвенным.
По заявляемому резонансному способу измерения частоты вращения геометрические размеры полости на заданном типе ЭМ-колебания могут не превышать значения длины волны источника ЭМ-поля. Например, при шаровой форме резонатора в случае выбора основного колебания (E111-колебания) собственная частота «покоящегося» резонатора 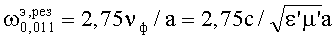 , а собственная частота вращающегося резонатора
, а собственная частота вращающегося резонатора 
 .
.
Тогда радиус резонатора  .
.
На частоте 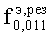 =10 ГГц (трехсантиметровый диапазон длин волн) a=1,31 см при ε'=µ'=1.
=10 ГГц (трехсантиметровый диапазон длин волн) a=1,31 см при ε'=µ'=1.
Применением магнитодиэлектрика (ε'>1 или µ>1), заполняющего резонатор, можно уменьшить радиус резонатора.
Таким образом, выбором частоты «неподвижного» резонатора и параметров магнитодиэлектрика можно выполнить миниатюризацию резонатора.
При применении формулы (1) для лазера с λ0=436·10-9м и радиусе резонатора a=1,31 см (ε'=µ'=1) получаем разность фаз ΔФ=1,03·10-4Ω, которую измерить трудно при любой частоте вращения.
Таким образом, способ измерения частоты вращения, основанный на «оптическом вихревом эффекте Саньяка», предполагающий обязательное применение длин волн оптического диапазона и многоводовый режим вращающейся полости, не позволяет выполнить миниатюризацию полости и повысить точность измерения частоты вращения.
Во вращающейся полости при монохроматическом источнике ЭМ-поля дискретная спектральная структура ЭМ-поля отсутствует, поэтому достичь основного технического результата - измерения частоты вращения полости радиолокационным способом нельзя.
Заявляемый способ поясняется следующим образом: для измерения частоты вращения полости надо измерить только резонансную частоту вращения вращающейся полости, так как резонансная частота «покоящейся» полости задана при расчете резонатора. Затем надо вычислить разность между измеренной резонансной частотой вращения и резонансной частотой «покоя» и разделить ее (разность) на постоянное целое число, определяемое заданным типом ЭМ-колебания.
Для достижения технического результата в резонансном способе измерения частоты вращения объекта измеряемую частоту вращения определяют как разность между собственной частотой вращения полости на выбранном типе электромагнитного колебания и собственной частотой «неподвижной» полости на том же типе колебания, деленную на постоянное число, определяемое выбранным при расчете полости типом колебания, а направление вращения определяют знаком этой разности.
Для достижения технического результата устройство, реализующее резонансный способ измерения частоты вращения объекта, содержит монохроматический автогенератор перестраиваемой частоты, зонд-возбудитель, детектор электромагнитного поля, устройство перестройки частоты автогенератора, частотомер и решающее устройство, которое вычисляет частоту вращения как разность между резонансной частотой вращения полости и резонансной частотой «неподвижной» полости, деленную на постоянное число, определяемое выбранным при расчете полости типом электромагнитного колебания, а направление вращения определяется знаком этой разности.
Резонансный способ измерения частоты вращения объекта реализует предлагаемое устройство, заявляемое в качестве изобретения. Устройство поясняется фигурой 1, где:
1 - резонатор;
2 - автогенератор монохроматического ЭМ-поля;
3 - устройство перестройки частоты автогенератора;
4 - зонд-возбудитель ЭМ-поля;
5 - детектор ЭМ-поля;
6 - решающее устройство;
7 - частотомер.
Рассмотрим работу устройства, реализующего резонансный способ определения частоты вращения объекта. В состоянии «покоя» (Ω=0) резонатора автогенератор (2) возбуждает ЭМ-поле в резонаторе (1) с помощью электрического или магнитного зондов, или дифракционной связи (4). Если частота ω0 автогенератора (2) отличается от резонансной частоты «покоя» полости (1), то с детектора ЭМ- поля (5) на решающее устройство (6) поступает напряжение, близкое к нулевому, что является информацией об отсутствии резонанса. Решающее устройство (6) подает сигнал на устройство перестройки частоты (3) автогенератора (2), которое перестраивает частоту автогенератора до тех пор, пока показания детектора ЭМ-поля (5) не станут максимальными, что указывает на наличие резонанса. Частота автогенератора измеряется частотомером (7) и записывается в решающем устройстве (6).
При вращении полости (1) резонансная частота вращения отличается от резонансной частоты «покоя» полости, поэтому резонанс ЭМ-поля отсутствует, на детекторе (5) напряжение становится близким к нулю. На решающее устройство (6) поступает сигнал об отсутствии резонанса. Решающее устройство (6) подает сигнал на устройство перестройки частоты (3) автогенератора (2), которое перестраивает частоту автогенератора до тех пор, пока показания ЭМ-поля (5) не станут максимальными. При этом частота автогенератора (2) измеряется частотомером (7) и записывается в решающее устройство (6). В решающем устройстве (6) вычисляется разность между записанными частотой «покоя» полости и частотой вращения. Разность делится на целое положительное число, определяемое выбранным при расчете полости типом ЭМ-колебания.
Таким образом, применение заявляемого способа измерения частоты вращения объекта и устройства, реализующее этот способ, значительно улучшает точность и весогабаритные характеристики гироскопических приборов, что позволяет создать миниатюрные индикаторы углового движения на летательных аппаратах, надводных и подводных объектах.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОДНОВОЛНОВЫЙ СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ИНТЕРФЕРОМЕТРА | 2014 |
|
RU2554316C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ЖЕЛЕЗА, ВОССТАНОВЛЕНИЯ КРЕМНИЯ И ВОССТАНОВЛЕНИЯ ДИОКСИДА ТИТАНА ДО МЕТАЛЛИЧЕСКОГО ТИТАНА ПУТЁМ ГЕНЕРАЦИИ ЭЛЕКТРОМАГНИТНЫХ ВЗАИМОДЕЙСТВИЙ ЧАСТИЦ SiO, КРЕМНИЙСОДЕРЖАЩЕГО ГАЗА, ЧАСТИЦ FeTiО И МАГНИТНЫХ ВОЛН | 2012 |
|
RU2561081C2 |
| ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ВИБРАЦИОННЫЙ ГИРОСКОП (ВАРИАНТЫ) | 2010 |
|
RU2426072C1 |
| ЛАМПА СТОЯЧЕЙ ВОЛНЫ | 1998 |
|
RU2163415C2 |
| Способ измерения собственной добротности диэлектрического резонатора | 2020 |
|
RU2739937C1 |
| СПОСОБ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИИ ФЕРРОМАГНИТНЫХ ЧАСТИЦ В ЖИДКОСТИ | 1995 |
|
RU2084887C1 |
| СПОСОБ ОТБРАКОВКИ КОЛЬЦЕВЫХ РЕЗОНАТОРОВ ЛАЗЕРНЫХ ГИРОСКОПОВ | 2014 |
|
RU2570096C1 |
| СИРЕНА ВСТРЕЧНЫХ РЕЗОНАНСНЫХ ВОЛН | 2007 |
|
RU2344001C9 |
| Микроволновой СВЧ излучатель | 2023 |
|
RU2813641C1 |
| Расходомер постоянного перепада давления типа ротаметра с дистанционной передачей величины расхода | 2023 |
|
RU2805029C1 |
Изобретение относится к области точного приборостроения и может быть использовано при создании таких средств измерения угловой скорости вращения объектов, как гироскопы. В резонансном способе измерения частоты вращения объекта измеряемую частоту вращения определяют как разность между собственной частотой вращения полости на выбранном типе электромагнитного колебания и собственной частотой «неподвижной» полости на том же типе колебания, деленную на постоянное число, определяемое выбранным при расчете полости типом колебания, а направление вращения определяют знаком этой разности. Устройство, реализующее резонансный способ измерения частоты вращения объекта, содержит монохроматический автогенератор перестраиваемой частоты, зонд-возбудитель, детектор электромагнитного поля, устройство перестройки частоты автогенератора, частотомер и решающее устройство, которое вычисляет частоту вращения как разность между резонансной частотой вращения полости и резонансной частотой «неподвижной» полости, деленную на постоянное число, определяемое выбранным при расчете полости типом электромагнитного колебания, а направление вращения определяет знаком этой разности. 2 н.п. ф-лы, 1 ил.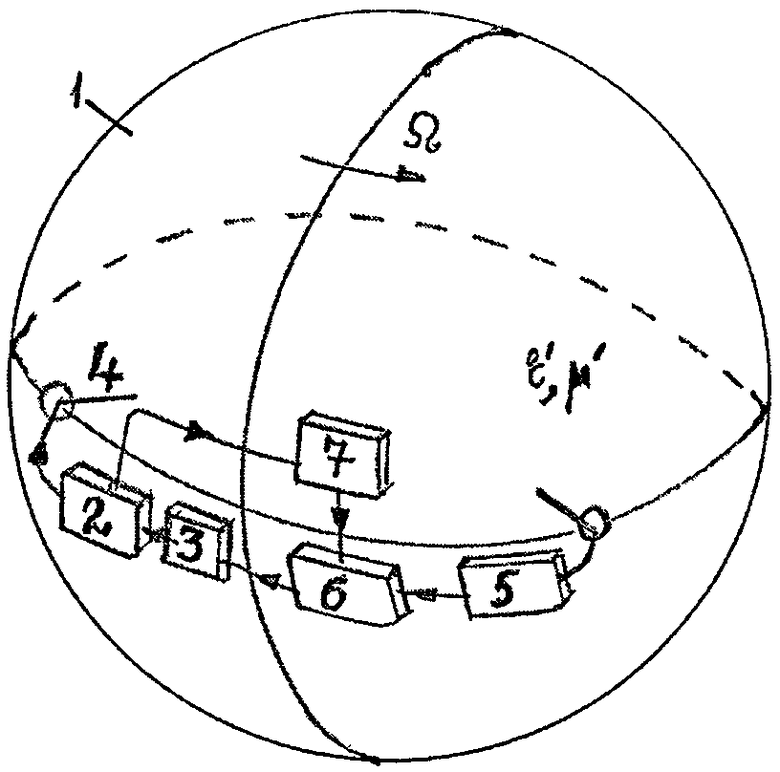
1. Резонансный способ измерения частоты вращения объекта, отличающийся тем, что измеряемую частоту вращения определяют как разность между собственной частотой вращения полости на выбранном типе электромагнитного колебания и собственной частотой «неподвижной» полости на том же типе колебания, деленную на постоянное число, определяемое выбранным при расчете полости типом колебания, а направление вращения определяют знаком этой разности.
2. Устройство, реализующее резонансный способ измерения частоты вращения объекта, отличающееся тем, что оно содержит монохроматический автогенератор перестраиваемой частоты, зонд-возбудитель, детектор электромагнитного поля, устройство перестройки частоты автогенератора, частотомер и решающее устройство, которое вычисляет частоту вращения как разность между резонансной частотой вращения полости и резонансной частотой «неподвижной» полости, деленную на постоянное число, определяемое выбранным при расчете полости типом электромагнитного колебания, а направление вращения определяется знаком этой разности.
| ВОЛОКОННО-ОПТИЧЕСКИЙ ГИРОСКОП | 2005 |
|
RU2283475C1 |
| ВОЛОКОННО-ОПТИЧЕСКИЙ ТАХОМЕТР | 2004 |
|
RU2275642C2 |
| ВОЛОКОННО-ОПТИЧЕСКИЙ ТАХОМЕТР | 2005 |
|
RU2297006C2 |
| JP 0061017015 A, 25.01.1986 | |||
| ТВЕРДОТЕЛЬНЫЙ ЛАЗЕРНЫЙ ГИРОСКОП С МЕХАНИЧЕСКИ АКТИВИРУЕМОЙ УСИЛИВАЮЩЕЙ СРЕДОЙ | 2007 |
|
RU2437062C2 |
| US 5367528 A1, 22.11.1994 | |||
Авторы
Даты
2015-09-10—Публикация
2013-04-10—Подача