Изобретение относится к области «Физики материального контактного взаимодействия», конкретно к способу определения упругой и общей деформации сжимаемой материальной среды под внешним давлением в массиве.
Известен способ определения начальной упругой деформации однородной грунтовой материальной среды в массиве под избыточным давлением p (кГ/см2), заключающийся в том, что упругую деформацию грунта в массиве рассчитывают по зависимости теории упругости  , где ω - коэффициент формы и жесткости штампа шириной в (см) или диаметром d (см), νстр - коэффициент (Пуассона) общей относительной поперечной упругой деформации среды в массиве, Eупр (кГ/см2) - модуль упругости грунтовой среды, p≤pб, где pб (кГ/см2) - гравитационное (бытовое) давление среды в массиве [1].
, где ω - коэффициент формы и жесткости штампа шириной в (см) или диаметром d (см), νстр - коэффициент (Пуассона) общей относительной поперечной упругой деформации среды в массиве, Eупр (кГ/см2) - модуль упругости грунтовой среды, p≤pб, где pб (кГ/см2) - гравитационное (бытовое) давление среды в массиве [1].
Упругие деформации грунта мало интересуют проектировщиков сооружений, создающих на грунтовое основание давления, значительно превышающие его структурную прочность, характеризующую упругость деформируемой среды.
Известен способ определения замедленной деформации однородной упруговязкопластичной грунтовой среды под избыточным давлением p (кГ/см2), заключающийся в том, что общую упруговязкопластическую деформацию среды в массиве рассчитывают по зависимости 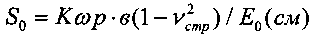 , где ω - коэффициент формы и жесткости опытного штампа шириной в (см) или диаметром d (см), νстр - коэффициент Пуассона структурированной среды, E0 (кГ/см2) - модуль общей деформации среды, К - корректирующий коэффициент [2, 3].
, где ω - коэффициент формы и жесткости опытного штампа шириной в (см) или диаметром d (см), νстр - коэффициент Пуассона структурированной среды, E0 (кГ/см2) - модуль общей деформации среды, К - корректирующий коэффициент [2, 3].
Предлагаемая зависимость позволяет определять деформируемость среды в условиях только компрессионного сжатия. Коэффициент Пуассона среды в нарушенном состоянии аналитическими зависимостями не определен. Корректирующий коэффициент К различен для различных условий работы штампа (массив, поверхность полупространства, вертикальная и горизонтальная сжимаемость среды в массиве и др). Выражение (1-ν2) получено путем математического решения упругопластической задачи «Механики деформируемого твердого тела» [4]. Коэффициент ω не имеет аналитического выражения и его устанавливают с весьма приближенным значением. Давление p принимают равным значению разности давлений на условно линейном участке зависимости S=f(pср), не имеющем четко установленных границ. Таким образом, величины расчетных деформаций массива грунтовой среды являются весьма приближенными и уточняются через корректирующий коэффициент К.
Известен способ определения замедленной деформации однородного верхнего слоя (i=1) упруговязкопластичной грунтовой среды под избыточным давлением p (кГ/см2) штампа, заключающийся в том, что определяют толщину H (см) верхнего деформируемого слоя грунта, модуль его общей деформации E0 (кГ/см2), σz - среднее значение осевого нормального вертикального напряжения на верхний слой грунта, а деформацию слоя грунта под напряжением σz определяют как S0=βσzH/E0 (см), где β≈0,8=(1+ν)(1-2ν)/(1-ν) - коэффициент [3].
Недостатком известного способа определения деформации грунтовой среды под нагрузкой p является необходимость сложного определения: достоверного распределения контактного напряжения σz под штампом, толщины деформируемого слоя h грунта под штампом, точного значения коэффициента β в связи с отсутствием истинных значений коэффициента ν Пуассона грунтовой среды. Напряжения σz распространяются под штампом в массиве на глубину Ha (см) активно сжимаемого слоя грунта, величина которого может оказаться меньше величины H слоя самого грунта, поэтому деформация S0 оказывается завышенной, и существует необходимость в определении истинного значения величины активно сжимаемой толщины Ha среды.
Технический результат по способу определения деформации материальной среды под давлением, заключающемуся в том, что на глубине h массива среды предусматривают ее деформацию давлением p в выработке через жесткий плоский штамп, определяют модуль общей и упругой деформации среды E0 (кГ/см2), Eупр (кГ/см2), устанавливают величину однородной толщи среды под штампом шириной в (см) или диаметром d (см), достигается тем, что на глубине h структурированной среды определяют ее угол 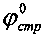 внутреннего трения и cстр (кГ/см2) - удельное сцепление, рассчитывают угол внутреннего трения среды с нарушенной структурой как
внутреннего трения и cстр (кГ/см2) - удельное сцепление, рассчитывают угол внутреннего трения среды с нарушенной структурой как 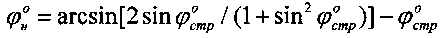 и ее удельное сцепление -
и ее удельное сцепление - 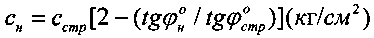 , определяют величину активно сжимаемой толщи материальной среды под штампом по зависимостям
, определяют величину активно сжимаемой толщи материальной среды под штампом по зависимостям 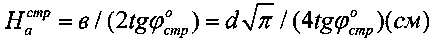 - для упругой структурированной среды и
- для упругой структурированной среды и 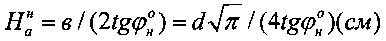 - для среды с нарушенной структурой, где d (см) - диаметр круглого штампа эквивалентного прямоугольному в×l (см×см) со стороной в<l, величину упругой деформации разуплотненной среды в выработке под давлением штампа
- для среды с нарушенной структурой, где d (см) - диаметр круглого штампа эквивалентного прямоугольному в×l (см×см) со стороной в<l, величину упругой деформации разуплотненной среды в выработке под давлением штампа 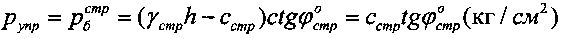 рассчитывают по зависимости
рассчитывают по зависимости 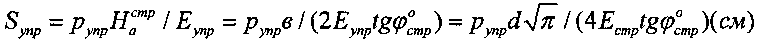 , а величину активной осадки материальной среды под избыточным давлением p (кГ/см2) штампа в массиве определяют по зависимости
, а величину активной осадки материальной среды под избыточным давлением p (кГ/см2) штампа в массиве определяют по зависимости 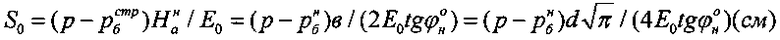 .
.
Изобретение поясняется графическими материалами, где на фиг. 1 представлена схема развития эпюры предельных напряжений σпр под центром штампа шириной в в массиве материальной сжимаемой среды на глубине h.
Интегрирование уравнений М. Фламана [5] позволяет получить для напряжений в произвольной точке A массива (фиг. 1) деформируемой жестким штампом 1 среды 2 выражение σz=[p/(0,5π)]·[α-sinαcos(α1+α2)] (кГ/см2), где α° - угол видимости подошвы штампа из точки A массива среды, 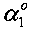 и
и 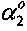 - углы, составленные лучами видимости краев подошвы штампа из точки A с поверхностью деформируемого полупространства среды на глубине h от дневной поверхности. Максимум вертикальных напряжений
- углы, составленные лучами видимости краев подошвы штампа из точки A с поверхностью деформируемого полупространства среды на глубине h от дневной поверхности. Максимум вертикальных напряжений 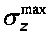 получают под центром штампа при α1=π-α2=π/2-α/2, откуда
получают под центром штампа при α1=π-α2=π/2-α/2, откуда 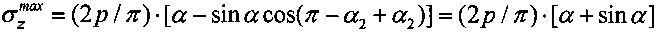 .
.
Равномерное распределение среднего давления p под штампом проявляется только при угле α°=φ°, где 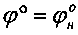 - угол внутреннего трения среды в нарушенном состоянии и
- угол внутреннего трения среды в нарушенном состоянии и 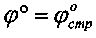 - для структурированной среды. Тогда σz=(2pср/π)·[2φ°+sin2φ°] (кГ/см2).
- для структурированной среды. Тогда σz=(2pср/π)·[2φ°+sin2φ°] (кГ/см2).
Максимальное вертикальное напряжение под центром штампа получают, приравнивая первую производную полученного выражения для σz нулю, а именно (σz)′=(2pср/π)·[2+2cos2φ°]=0, что выполняется при cos2φ°=-1, 2φ°=π или φ°=45°, то есть в идеально чистых песках. При α°=2φ° максимальная глубина распространения вертикальных напряжений вглубь материального массива под подошвой штампа составляет величину при ширине в (см) штампа, равную активно сжимаемой толщи массива среды Ha=в/(2tgφ°). При 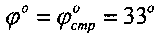 и в=100 см величина
и в=100 см величина 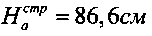 , при
, при 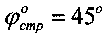 получаем
получаем 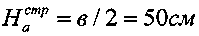 . При
. При 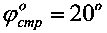 получаем
получаем 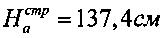 , при
, при 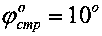 получаем
получаем 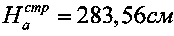 .
.
Величина общей деформации сжимаемой плоским жестким штампом материальной среды с модулем общей деформации E0 (кГ/см2) составляет 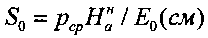 , величина упругой деформации разуплотненной в шурфе среды
, величина упругой деформации разуплотненной в шурфе среды 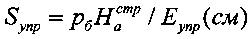 .
.
Пример 1 реализации способа. Определим осадку S0 под давлением p=2,5 (кГ/см2) суглинка в открытом шурфе-дудке на глубине h=210 см массива среды под жестким плоским круглым штампом площадью F=2500 см2 и диаметром d=56,42 см.
Угол внутреннего трения структурированного суглинка 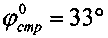 , его удельное сцепление cстр=0,16 (кГ/см2), удельный вес γстр=0,0022 (кГ/см3), модуль упругости Eупр=Eстр=180 (кГ/см2), модуль общей деформации E0=60 (кГ/см2).
, его удельное сцепление cстр=0,16 (кГ/см2), удельный вес γстр=0,0022 (кГ/см3), модуль упругости Eупр=Eстр=180 (кГ/см2), модуль общей деформации E0=60 (кГ/см2).
Определяем физический показатель суглинка в нарушенном состоянии: 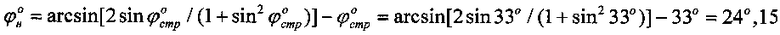 ;
; 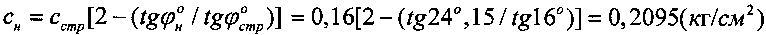 .
.
Величина активно сжимаемой толщи суглинка под штампом равна 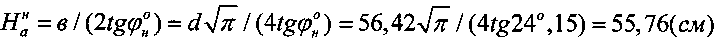 .
.
Упругая осадка разуплотненного в шурфе-дудке суглинка под давлением штампа, равным бытовому гравитационному давлению на глубине h=210 см 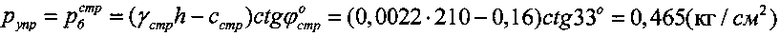 , составляет величину
, составляет величину 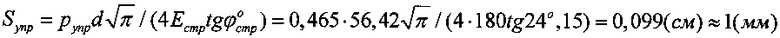 .
.
Осадка суглинка под штампом при давлении p=2,5 (кГ/см2) составляет величину 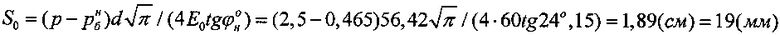 .
.
Пример 2 реализации способа. Определим общую осадку квадратного фундамента со стороной в=300 (см) с поверхности полупространства под давлением p=2,5 (кГ/см2), установленном на суглинке с показателями: 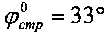 , cстр=0,16 (кГ/см2),
, cстр=0,16 (кГ/см2), 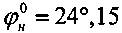 , cн=0,2095 (кГ/см2), γстр=0,0022 (кГ/см3), Eупр=180 (кГ/см2), E0=60 (кГ/см2).
, cн=0,2095 (кГ/см2), γстр=0,0022 (кГ/см3), Eупр=180 (кГ/см2), E0=60 (кГ/см2).
Величина упруго растянутой толщи суглинка под поверхностью полупространства равна ha=cстр/γстр=0,16/0,0022=72,73 см. На глубине ha бытовое гравитационное давление 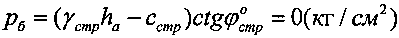 , осадка суглинка S0=0 (см). Давление вертикального растяжения поверхности полупространства равно
, осадка суглинка S0=0 (см). Давление вертикального растяжения поверхности полупространства равно 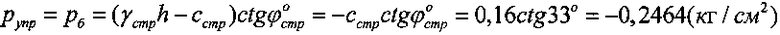 .
.
Упругая осадка суглинка под фундаментом с поверхности полупространства составляет величину 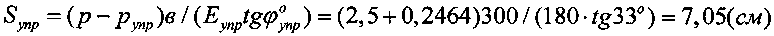 . Напряжение на глубине 72,73 см под нагруженным фундаментом составляет величину
. Напряжение на глубине 72,73 см под нагруженным фундаментом составляет величину 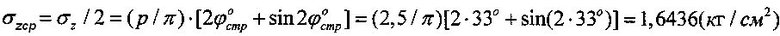 .
.
Осадка суглинка в массиве под напряжением σzcp=1,6436 (кГ/см2) составляет величину 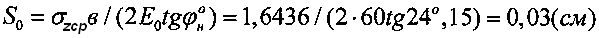 при величине активно сжимаемой толщи суглинка в массиве
при величине активно сжимаемой толщи суглинка в массиве 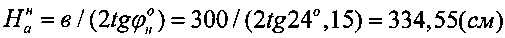 .
.
Общая деформация суглинка под фундаментом равна S=S0+Sупр=0,03+7,05=7,08 (см).
Впервые определена глубина Ha активно сжимаемой толщи материальной среды и ее величина упругой и общей деформации, совпадающая с реальными осадками среды под избыточным внешним давлением.
Источники информации
1. Цитович Н.А. Механика грунтов (краткий курс): Учебник для вузов. - 3-е изд., доп. - М.: Высшая школа, 1979. - С. 167.
2. Цитович Н.А. Механика грунтов (краткий курс): Учебник для вузов. - 3-е изд., доп. - М.: Высшая школа, 1979. - С. 168.
3. Гольдштейн М.Н., Кушнер С.Г., Шевченко М.И. Расчеты осадок и прочности оснований зданий и сооружений - Киев: «Будивельник», 1977. - С. 82, 83-84, 85-93.
4. Тимошенко С.П., Гудьер. Дж. Теория упругости: Пер. с англ. / Под ред. Г.С. Шапиро - 2-е изд. - М.: Наука. Гл. редакция физ.-мат. лит-ры, 1979. - С. 410.
5. Хрусталев Е.Н. Контактное взаимодействие в геомеханике. Часть II: Напряжения и деформации оснований сооружений: Монография. - Тверь: Научная книга, 2007. - С. 62-68.
Изобретение относится к области «Физики материального контактного взаимодействия», конкретно к способу определения упругой и общей деформации сжимаемой материальной среды в массиве. Способ заключается в том, что на глубине h массива среды предусматривают ее деформацию давлением p в выработке через жесткий плоский штамп, определяют модуль общей и упругой деформации среды E0 (кГ/см2), Eупр (кГ/см2), устанавливают величину однородной толщи среды под штампом шириной в (см) или диаметром d (см), при этом на глубине h структурированной среды определяют ее угол 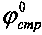 внутреннего трения и cстр (кГ/см2) - удельное сцепление, рассчитывают угол внутреннего трения среды с нарушенной структурой как
внутреннего трения и cстр (кГ/см2) - удельное сцепление, рассчитывают угол внутреннего трения среды с нарушенной структурой как 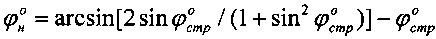
и ее удельное сцепление - 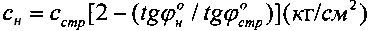 ,
,
определяют величину активно сжимаемой толщи материальной среды под штампом по зависимостям
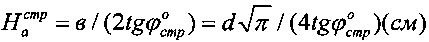 - для упругой структурированной среды и
- для упругой структурированной среды и 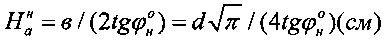 - для среды с нарушенной структурой, где d (см) - диаметр круглого штампа эквивалентного прямоугольному в×l (см×см) со стороной в<l, величину упругой деформации разуплотненной среды в выработке под давлением штампа
- для среды с нарушенной структурой, где d (см) - диаметр круглого штампа эквивалентного прямоугольному в×l (см×см) со стороной в<l, величину упругой деформации разуплотненной среды в выработке под давлением штампа 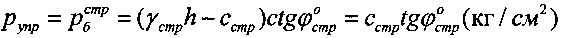 рассчитывают по зависимости
рассчитывают по зависимости 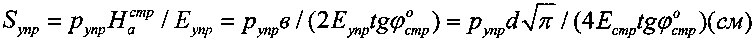 , а величину активной осадки материальной среды под избыточным давлением p (кГ/см2) штампа в массиве определяют по зависимости
, а величину активной осадки материальной среды под избыточным давлением p (кГ/см2) штампа в массиве определяют по зависимости 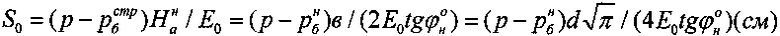 . Технический результат - упрощение способа определения упругой и общей деформации сжимаемой материальной среды в массиве. 1 ил.
. Технический результат - упрощение способа определения упругой и общей деформации сжимаемой материальной среды в массиве. 1 ил.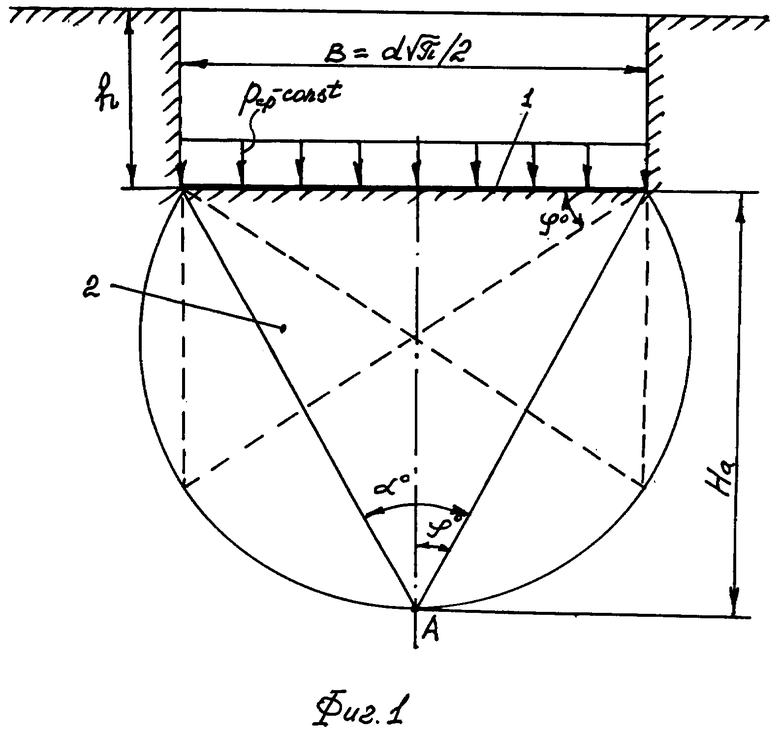
Способ определения деформации материальной среды под давлением, заключающийся в
том, что на глубине h массива среды предусматривают ее деформацию давлением p в выработке через жесткий плоский штамп, определяют модуль общей и упругой деформации среды Е0 (кГ/см2), Еупр (кГ/см2), устанавливают величину однородной толщи среды под штампом шириной в (см) или диаметром d (см), отличающийся тем, что на глубине h структурированной среды определяют ее угол 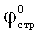
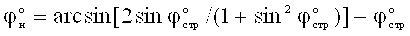
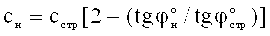
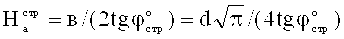
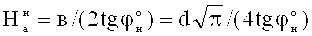
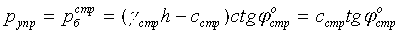
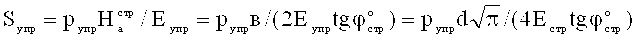
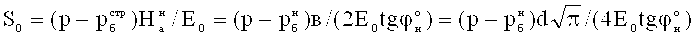
| RU 2007108224 A, 10.09.2008 | |||
| Хрусталев Е.Н | |||
| Исследования сжимаемости слабых грунтов методом лопастной прессиометрии и результаты его внедрения в практику инженерных изысканий / Автореферат диссертации на соискание уч | |||
| степени к | |||
| техн | |||
| н | |||
| - ПНИИИС Госстроя СССР, 1981 | |||
| - С | |||
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
| Зиангиров Р.С., Роот П.Э | |||
| и др | |||
| Практикум по механике грунтов | |||
| - М.: Изд-во МГУ, 1984 | |||
| - С | |||
| Видоизменение прибора для получения стереоскопических впечатлений от двух изображений различного масштаба | 1919 |
|
SU54A1 |
| Зонд-прессиометр | 1977 |
|
SU631586A1 |
Авторы
Даты
2015-11-27—Публикация
2014-08-27—Подача