ПЕРЕКРЕСТНАЯ ССЫЛКА НА РОДСТВЕННУЮ ЗАЯВКУ
Эта заявка испрашивает приоритет по предварительной патентной заявке США 61/564,669, поданной 29 ноября, 2011, озаглавленной METHODS FOR APPROXIMATING HESSIAN TIMES VECTOR OPERATION IN FULL WAVEFIELD INVERSION, полнота которой включается сюда по ссылке.
ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Это изобретение относится, в общем, к области геофизической разведки и, более конкретно, к обработке сейсмических данных. Конкретно, изобретение является способом для более быстрой оценки величины, известной как умножение гессиана на вектор, которая возникает в некоторых способах для численного решения дифференциальных уравнений в частных производных, например итеративной инверсии сейсмических данных, чтобы выводить упругие свойства среды, при использовании прямого моделирования синтетических данных посредством решения волнового уравнения в среде модели.
УРОВЕНЬ ТЕХНИКИ
Полная инверсия волнового поля (FWI) в обработке сейсмической разведки полагается на вычисление градиента целевой функции по отношению к параметрам модели недр [9]. Градиент целевой функции используется, чтобы вычислять обновление для модели. Целевая функция 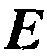 обычно задается как
обычно задается как 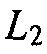 , норма как
, норма как
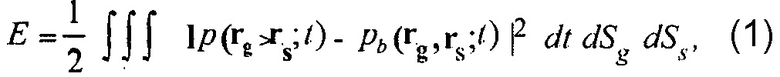
где 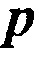 и
и 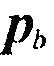 являются измеренным давлением, т.е. сейсмической амплитудой, и смоделированным давлением в фоновой модели недр в местоположении приемника
являются измеренным давлением, т.е. сейсмической амплитудой, и смоделированным давлением в фоновой модели недр в местоположении приемника 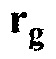 для взрыва, расположенного в
для взрыва, расположенного в 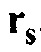 . В обработках итеративной инверсии фоновая среда является обычно средой, результирующей из предыдущего цикла инверсии. В обработках неитеративной инверсии или миграциях фоновая среда обычно выводится с использованием стандартных способов сейсмической обработки, таких как анализ скорости миграции. Целевая функция интегрируется по всему времени
. В обработках итеративной инверсии фоновая среда является обычно средой, результирующей из предыдущего цикла инверсии. В обработках неитеративной инверсии или миграциях фоновая среда обычно выводится с использованием стандартных способов сейсмической обработки, таких как анализ скорости миграции. Целевая функция интегрируется по всему времени 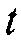 , и поверхностям
, и поверхностям 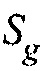 и
и 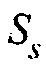 , которые определяются распределением приемников и взрывов. Мы определяем
, которые определяются распределением приемников и взрывов. Мы определяем 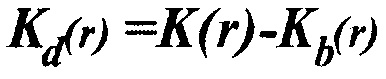 и
и  , где
, где 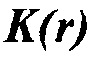 и
и 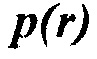 являются истинными модулем объемной упругости и плотностью и
являются истинными модулем объемной упругости и плотностью и 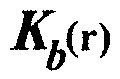 и
и 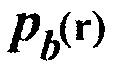 являются модулем объемной упругости и плотностью фоновой модели в подземном местоположении
являются модулем объемной упругости и плотностью фоновой модели в подземном местоположении 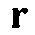 (модуль объемной упругости используется здесь в качестве примера, но вместо этого могут использоваться любые из 21 упругих констант). Мы также определяем разность между измеренным и смоделированным давлением как
(модуль объемной упругости используется здесь в качестве примера, но вместо этого могут использоваться любые из 21 упругих констант). Мы также определяем разность между измеренным и смоделированным давлением как 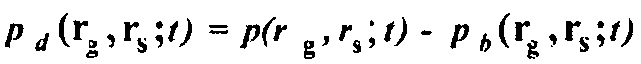 .
.
Измеренное давление 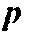 удовлетворяет волновому уравнению
удовлетворяет волновому уравнению
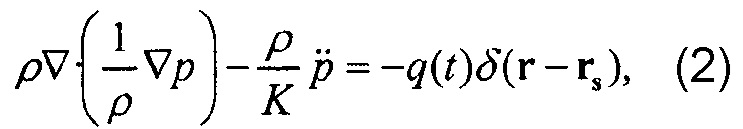
где 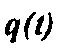 является формой импульса источника. Можно показать, что градиент целевой функции
является формой импульса источника. Можно показать, что градиент целевой функции 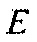 по отношению к модулю объемной упругости
по отношению к модулю объемной упругости 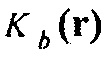 , например, задается как
, например, задается как
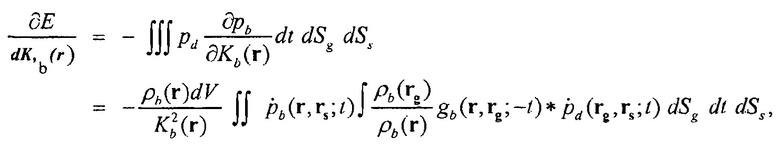 (3)
(3)
где 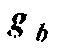 является функцией Грина в фоновой среде, и
является функцией Грина в фоновой среде, и 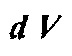 является бесконечно малым объемом вокруг
является бесконечно малым объемом вокруг 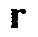 [9, 3]. Уравнения для градиентов других параметров среды недр в общих упругих случаях могут быть найдены в источниках [10, 6, 1]. Можно затем выполнять полную инверсию волнового поля посредством минимизации значения целевой функции
[9, 3]. Уравнения для градиентов других параметров среды недр в общих упругих случаях могут быть найдены в источниках [10, 6, 1]. Можно затем выполнять полную инверсию волнового поля посредством минимизации значения целевой функции 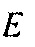 итеративным способом, с использованием градиентных уравнений для параметров среды, таких как в Уравнении 3.
итеративным способом, с использованием градиентных уравнений для параметров среды, таких как в Уравнении 3.
Скорость сходимости полной инверсии волнового поля может быть улучшена, когда в обработке инверсии используется информация о гессиане целевой функции 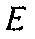 [7, 5]. Гессиан является матрицей вторых частных производных функции. Гессиан (по отношению к модулю объемной упругости физического свойства) целевой функции E в Уравнении 1 задается как
[7, 5]. Гессиан является матрицей вторых частных производных функции. Гессиан (по отношению к модулю объемной упругости физического свойства) целевой функции E в Уравнении 1 задается как
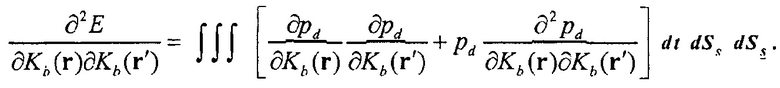 (4)
(4)
Второй член на правой стороне является членом, ответственным за многократное рассеяние, и часто игнорируется вследствие трудности в вычислении [11]. Посредством отбрасывания этого второго члена получают уравнение для гессиана Гаусса-Ньютона,
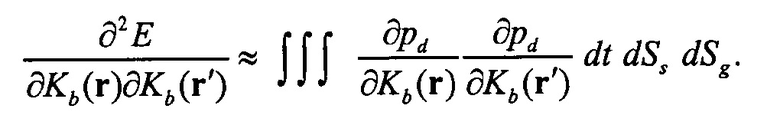 (5)
(5)
Как только матрица Гессе вычисляется, обновление параметров среды, требуемое для минимизации 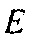 , может получаться посредством умножения обращения матрицы Гессе и градиента с использованием способа Ньютона [5]
, может получаться посредством умножения обращения матрицы Гессе и градиента с использованием способа Ньютона [5]
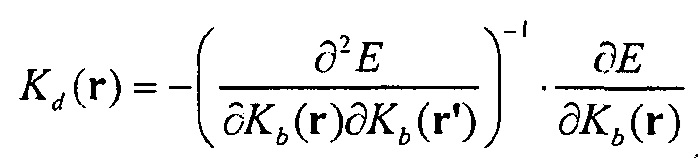
Прямое вычисление обращения матрицы Гессе, однако, часто требует чрезмерно большого пространства памяти в полной инверсии волнового поля, и, таким образом, обращение гессиана вычисляется итеративно с использованием метода сопряженных градиентов (CG). Эта итеративная схема часто упоминается как способ Ньютона-CG, которая может использоваться либо для полного гессиана из уравнения 4, либо для гессиана Гаусса-Ньютона из уравнения 5. Пример этого способа Ньютона-CG может быть найден в Алгоритме 7.1 из источника [5], который воспроизводится ниже. Для удобства обозначений мы используем 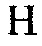 для матрицы Гессе и
для матрицы Гессе и 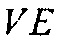 для вектора градиента.
для вектора градиента.
1. Определить допустимое отклонение 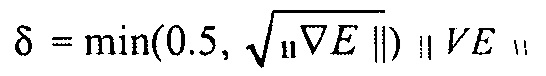
2. Установить 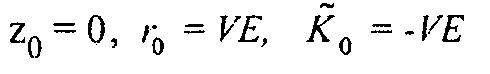
3. Для j=0, 1, 2,
a. Если 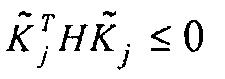
i. Если j=0
1. Возвратить 
ii. Иначе
1. Возвратить 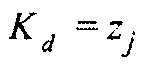
b. Установить 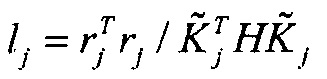
c. Установить 
d. Установить 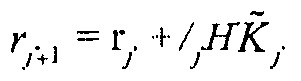
e. Если 
i. Возвратить 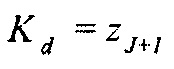
f. Установить 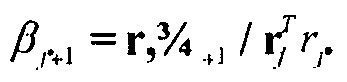
g. Установить 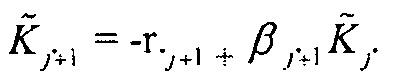
4. Выполнить линейный поиск с использованием 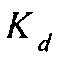 в качестве направления поиска для обновления параметров среды, начиная с размера шага, равного 1, если возможно.
в качестве направления поиска для обновления параметров среды, начиная с размера шага, равного 1, если возможно.
Вышеописанный алгоритм требует повторяющегося вычисления умножения гессиана на вектор 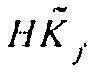 в цикле, где
в цикле, где 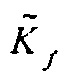 для j=0 устанавливается как взятый со знаком минус градиент. Значение
для j=0 устанавливается как взятый со знаком минус градиент. Значение 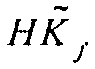 затем используется, чтобы обновлять
затем используется, чтобы обновлять 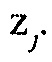 , которое в конечном счете становится умножением обращения гессиана на градиент
, которое в конечном счете становится умножением обращения гессиана на градиент 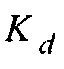 в 3.a.ii.1 или 3.e.i.
в 3.a.ii.1 или 3.e.i.
Способ Ньютона-CG требует вычисления умножения (т.е. произведения) матрицы Гессе на вектор возмущения среды 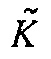 , который может упоминаться в дальнейшем в этом документе как "умножение гессиана (Гаусса-Ньютона) на вектор",
, который может упоминаться в дальнейшем в этом документе как "умножение гессиана (Гаусса-Ньютона) на вектор",
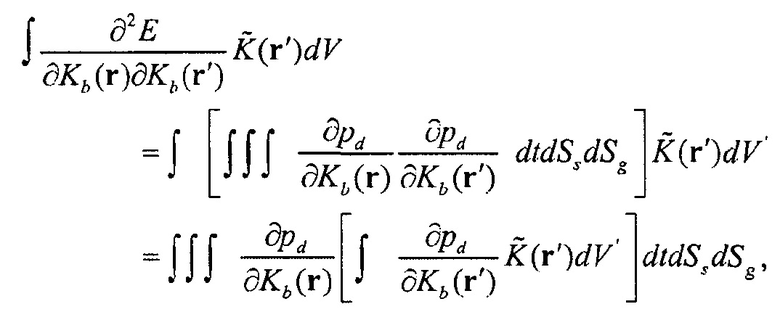 (6)
(6)
где гессиан аппроксимирован как гессиан Гаусса-Ньютона. Например, в оценке параметров модели физических свойств посредством итеративной инверсии геофизических данных вектор возмущения среды обычно исходно является градиентом (в пространстве параметров модели) целевой функции. По мере осуществления итераций этот вектор постепенно отклоняется от градиента и теряет физический смысл как таковой. Для уравнения (6) может быть найдено численное значение посредством выполнения двух вычислений распространения прямой волны и двух вычислений распространения обратной волны. Настоящее изобретение является способом, который обеспечивает возможность находить численное значение этого уравнения посредством выполнения только одного вычисления распространения прямой волны (одного прямого решения дифференциального уравнения в частных производных, такого как волновое уравнение) и одного вычисления распространения обратной волны (т.е. одного вычисления градиента целевой функции), что дает результатом ценную экономию машинного времени.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
В одном варианте осуществления изобретение является способом для определения дискретной модели физических свойств области недр, которая может упоминаться как "модель", посредством итеративного инвертирования измеренных геофизических данных, полученных из области недр, при этом способ содержит использование матрицы Гессе целевой функции, которая затем умножается на вектор, что называется "умножение гессиана на вектор", чтобы определять обновление для модели, при этом умножение гессиана на вектор аппроксимируется с использованием компьютера, с помощью одиночного смоделированного распространения прямой волны и одиночного вычисления градиента целевой функции в модифицированной модели недр.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Настоящее изобретение и его преимущества будут лучше пониматься с использованием ссылки на последующее подробное описание и прилагаемые чертежи, на которых
Фиг. 1 является графиком, сравнивающим скорость сходимости полной инверсии волновой формы с использованием представленного нового способа по сравнению с традиционным способом для оценки умножения гессиана на вектор, в тестовом примере, использующем модели из фиг. 3A и 3B;
Фиг. 2 является блок-схемой последовательности операций, показывающей базовые этапы в одном варианте осуществления представленного нового способа; и
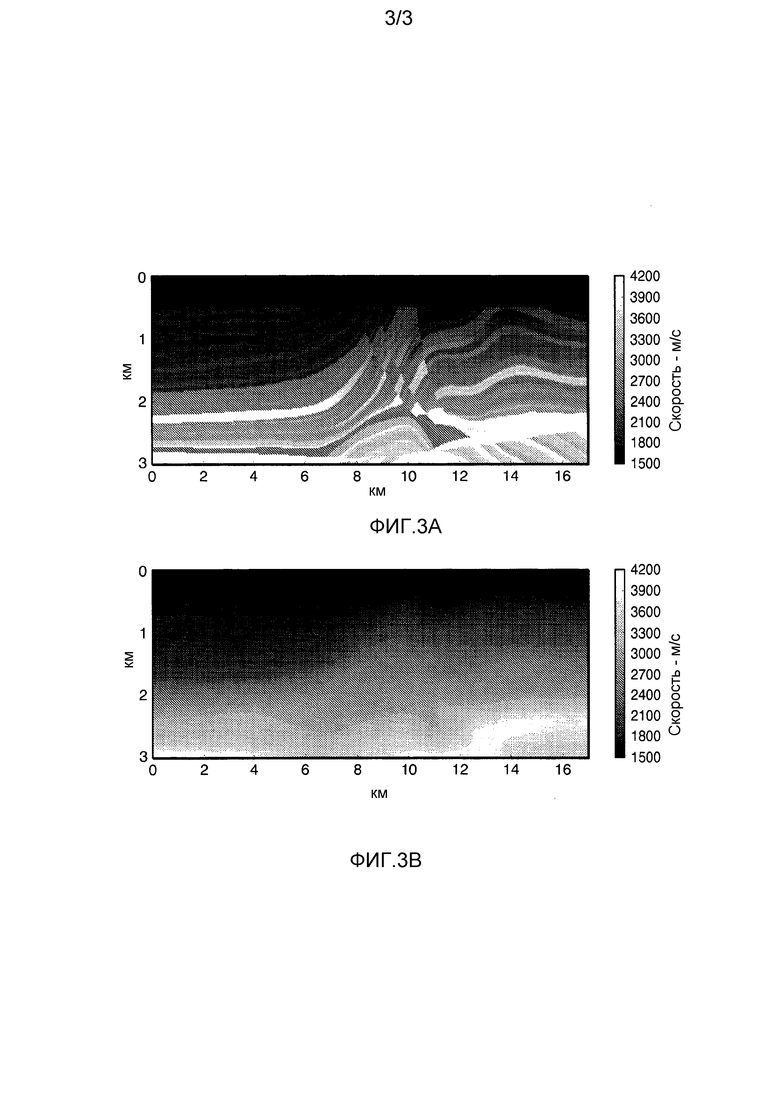
Фиг. 3A показывает "истинную" модель распределения скоростей в разрезе для генерирования сейсмических данных в синтетическом тестовом примере представленного нового способа, и
Фиг. 3B показывает начальную модель распределения скоростей, используемую в итеративной полной инверсии волнового поля, применяющей способ настоящего изобретения.
Изобретение будет описываться в соединении с иллюстративными вариантами осуществления. Однако до той степени, что последующее подробное описание является специальным для конкретного варианта осуществления или конкретного использования изобретения, предполагается, что оно является только иллюстративным, и не должно толковаться как ограничивающее объем изобретения. Наоборот, предполагается, что оно охватывает все альтернативы, модификации и эквиваленты, которые могут содержаться в пределах объема изобретения, как определено посредством прилагаемой формулы изобретения. Специалисты в данной области техники должны легко понять, что все практические применения представленного нового способа выполняются с использованием компьютера, запрограммированного согласно раскрытию отсюда.
Подробное описание иллюстративных вариантов осуществления
Пусть
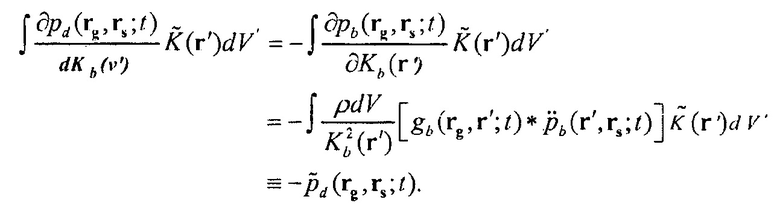 (7)
(7)
Можно заметить, что Уравнение 7 является уравнением для рассеянного поля Борна 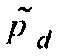 , где
, где  ведет себя как распределение рассеивателей в фоновой среде с модулем объемной упругости
ведет себя как распределение рассеивателей в фоновой среде с модулем объемной упругости 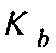 . Умножение гессиана Гаусса-Ньютона на вектор может быть представлено как
. Умножение гессиана Гаусса-Ньютона на вектор может быть представлено как
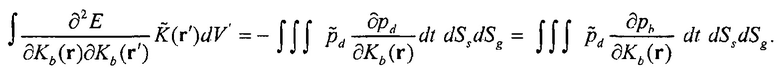 (8)
(8)
Поэтому вычисление умножения гессиана Гаусса-Ньютона на вектор эквивалентно вычислению градиента с использованием искусственного остатка 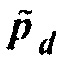 . Как упомянуто выше, искусственный остаток
. Как упомянуто выше, искусственный остаток 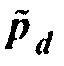 вычисляется с использованием Борновского приближения в фоновой модели с рассеивателями
вычисляется с использованием Борновского приближения в фоновой модели с рассеивателями 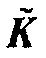 . Если волновое уравнение является линейным, так что Борновское приближение является точным, и если
. Если волновое уравнение является линейным, так что Борновское приближение является точным, и если 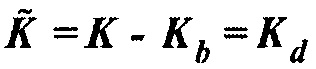 , то искусственный остаток
, то искусственный остаток 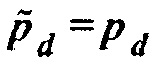 . Поэтому взятое со знаком минус умножение гессиана на вектор выше должно быть равным градиенту в этом случае.
. Поэтому взятое со знаком минус умножение гессиана на вектор выше должно быть равным градиенту в этом случае.
Можно отметить, что рассеянное поле Борна 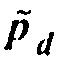 в Уравнении 7 может быть аппроксимировано как
в Уравнении 7 может быть аппроксимировано как
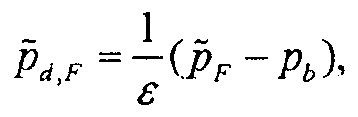 (9)
(9)
где 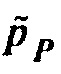 является решением волнового уравнения
является решением волнового уравнения
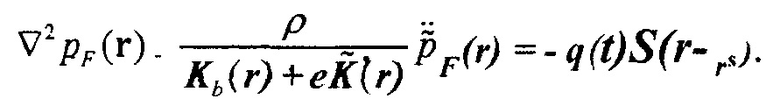 (10)
(10)
Если 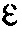 в Уравнении 10 является достаточно малым,
в Уравнении 10 является достаточно малым,  должно быть приблизительно равным сумме
должно быть приблизительно равным сумме 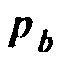 и рассеянного поля Борна вследствие
и рассеянного поля Борна вследствие 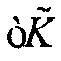 . Так как амплитуда рассеяния Борна является линейной по отношению к возмущению свойств среды рассеивателей,
. Так как амплитуда рассеяния Борна является линейной по отношению к возмущению свойств среды рассеивателей, 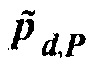 в Уравнении 9 должно быть приблизительно равным
в Уравнении 9 должно быть приблизительно равным  в Уравнении 7.
в Уравнении 7.
Операция умножения гессиана на вектор может быть аппроксимирована как
 (11)
(11)
Уравнение выше показывает, что можно вычислить умножение гессиана на вектор посредством (1) создания новой модели недр 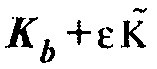 , (2) вычисления принятого поля
, (2) вычисления принятого поля  в новой модели недр, (3) вычисления градиента в фоновой модели
в новой модели недр, (3) вычисления градиента в фоновой модели 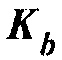 посредством трактовки
посредством трактовки 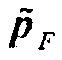 как измерения поля, и (4) масштабирования градиента посредством lis. Так как эти операции используют только вычисление распространения прямой волны и градиента, этот способ устраняет необходимость реализации операторов умножения гессиана на вектор, т.е. устраняет необходимость осуществления компьютерной программы, которая вычисляет умножение гессиана на вектор. Вместо этого можно повторно использовать уже существующие процедуры вычисления прямого распространения и градиента, чтобы получить умножение гессиана на вектор. Конечно, это преимущество исчезает, если операция умножения гессиана на вектор уже реализована. Дополнительно, операция, здесь раскрытая, требует приблизительно 3,5 волновых распространений по сравнению с 4 волновыми распространениями в Уравнении 6 и, таким образом, вычислительно является более эффективной.
как измерения поля, и (4) масштабирования градиента посредством lis. Так как эти операции используют только вычисление распространения прямой волны и градиента, этот способ устраняет необходимость реализации операторов умножения гессиана на вектор, т.е. устраняет необходимость осуществления компьютерной программы, которая вычисляет умножение гессиана на вектор. Вместо этого можно повторно использовать уже существующие процедуры вычисления прямого распространения и градиента, чтобы получить умножение гессиана на вектор. Конечно, это преимущество исчезает, если операция умножения гессиана на вектор уже реализована. Дополнительно, операция, здесь раскрытая, требует приблизительно 3,5 волновых распространений по сравнению с 4 волновыми распространениями в Уравнении 6 и, таким образом, вычислительно является более эффективной.
Можно дополнительно улучшить сходимость к минимумам посредством увеличения значения 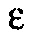 в Уравнении 10. Когда значение
в Уравнении 10. Когда значение  увеличивается, рассеянное поле
увеличивается, рассеянное поле 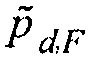 в Уравнении 9 отходит от рассеянного поля Борна, и оно включает в себя нелинейные эффекты, такие как многократное рассеяние, изменение времени прохождения и нелинейное масштабирование амплитуды по отношению к
в Уравнении 9 отходит от рассеянного поля Борна, и оно включает в себя нелинейные эффекты, такие как многократное рассеяние, изменение времени прохождения и нелинейное масштабирование амплитуды по отношению к 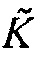 . Одним специальным случаем большого значения
. Одним специальным случаем большого значения 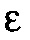 является, когда
является, когда  , и
, и 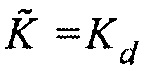 . В этом случае волновое уравнение 10 является волновым уравнением для истинной среды недр и, таким образом,
. В этом случае волновое уравнение 10 является волновым уравнением для истинной среды недр и, таким образом, 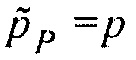 . Умножение гессиана на вектор в Уравнении 11 является тогда в точности равным градиенту, что никогда не достигается в Уравнении 6, даже когда
. Умножение гессиана на вектор в Уравнении 11 является тогда в точности равным градиенту, что никогда не достигается в Уравнении 6, даже когда 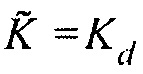 , вследствие отброшенных членов более высокого порядка в Уравнении 6.
, вследствие отброшенных членов более высокого порядка в Уравнении 6.
Для практических целей мы можем определить 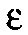 как
как
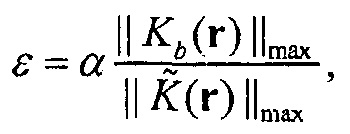 (12)
(12)
где 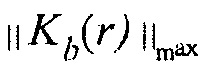 и
и 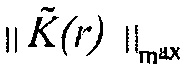 являются максимальными абсолютными значениями
являются максимальными абсолютными значениями 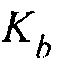 и
и 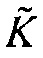 в пространстве соответственно. Параметр
в пространстве соответственно. Параметр 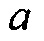 тогда представляет приблизительное дробное изменение
тогда представляет приблизительное дробное изменение 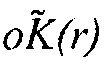 в Уравнении 10 по отношению к
в Уравнении 10 по отношению к 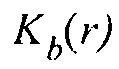 . Таким образом,
. Таким образом, 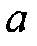 представляет отношение модуля вектора, подлежащего добавлению к модели, к модулю вектора модели, где параметры среды модели являются компонентами вектора модели в пространстве модели. Затем можно выбирать значение
представляет отношение модуля вектора, подлежащего добавлению к модели, к модулю вектора модели, где параметры среды модели являются компонентами вектора модели в пространстве модели. Затем можно выбирать значение 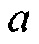 , чтобы управлять поведением умножения гессиана на вектор в Уравнении 11. Когда значение
, чтобы управлять поведением умножения гессиана на вектор в Уравнении 11. Когда значение 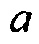 является довольно маленьким, порядка 0,01, оператор гессиана в Уравнении 11 имитирует поведение гессиана Гаусса-Ньютона в Уравнении 5. Когда значение
является довольно маленьким, порядка 0,01, оператор гессиана в Уравнении 11 имитирует поведение гессиана Гаусса-Ньютона в Уравнении 5. Когда значение 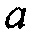 является относительно большим и достигает порядка 0,1, с другой стороны, оператор гессиана в Уравнении 11 начинает включать в себя эффект нелинейности и многократного рассеяния, и, таким образом, ведет себя аналогично Уравнению 4.
является относительно большим и достигает порядка 0,1, с другой стороны, оператор гессиана в Уравнении 11 начинает включать в себя эффект нелинейности и многократного рассеяния, и, таким образом, ведет себя аналогично Уравнению 4.
В то время как уравнение выше было выведено специально для модуля объемной упругости 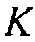 , этот способ может применяться для вычисления умножения гессиана на вектор любых общих упругих параметров, таких как плотность
, этот способ может применяться для вычисления умножения гессиана на вектор любых общих упругих параметров, таких как плотность 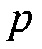 или любая из 21 константы упругой деформации
или любая из 21 константы упругой деформации  . Пусть
. Пусть 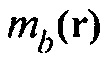 и
и 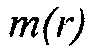 будут свойствами фоновой среды и вектором умножения любого из этих упругих параметров. Тогда умножение гессиана на вектор любого из этих свойств может быть вычислено как
будут свойствами фоновой среды и вектором умножения любого из этих упругих параметров. Тогда умножение гессиана на вектор любого из этих свойств может быть вычислено как
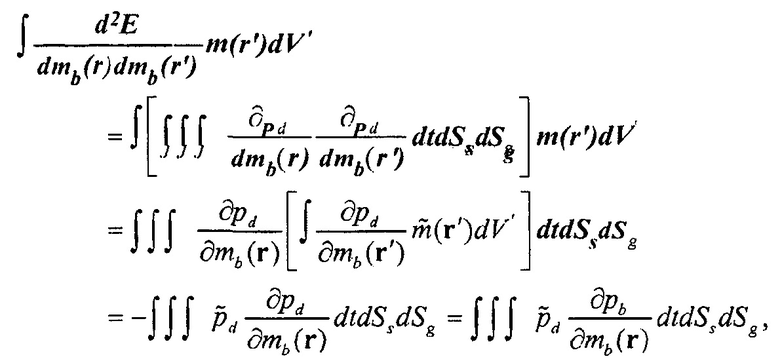 (13)
(13)
где 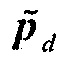 теперь может вычисляться с использованием такого же способа, как способ в Уравнениях 9 и 10. Отметим, что этот вывод является, в общем, применимым к любому типу целевых функций, таких как целевая функция
теперь может вычисляться с использованием такого же способа, как способ в Уравнениях 9 и 10. Отметим, что этот вывод является, в общем, применимым к любому типу целевых функций, таких как целевая функция  , заданная в Уравнении 1, или целевая функция взаимной корреляции в источнике 8. Отметим также, что способ, здесь представленный, является специальным случаем оптимизационных задач с ограничениями в виде PDE (дифференциальных уравнений в частных производных), и, таким образом, способ является, в общем, применимым к любым оптимизационным задачам с ограничениями в виде PDE, где необходимо вычислять умножение гессиана на вектор. Например, этот способ также может применяться к задачам, относящимся к распространению электромагнитных волн.
, заданная в Уравнении 1, или целевая функция взаимной корреляции в источнике 8. Отметим также, что способ, здесь представленный, является специальным случаем оптимизационных задач с ограничениями в виде PDE (дифференциальных уравнений в частных производных), и, таким образом, способ является, в общем, применимым к любым оптимизационным задачам с ограничениями в виде PDE, где необходимо вычислять умножение гессиана на вектор. Например, этот способ также может применяться к задачам, относящимся к распространению электромагнитных волн.
Ниже представлена процедура настоящего изобретения, как она применяется к, например, определению обновления модели в способе для оценки параметров физического свойств посредством инверсии данных с использованием градиента целевой функции, с этапами, как показано в блок-схеме последовательности операций из фиг. 2:
Этап 21. Сформировать многокомпонентный вектор, чьи компоненты относятся к значениям выбранного физического свойства в отдельных ячейках в модели недр согласно текущей модели 20 недр этого свойства (для настоящего примера вектор обычно является градиентом целевой функции, но в общем приложении заявляемого способа он является любым вектором, который позже подлежит умножению на гессиан);
Этап 22. Масштабировать вектор посредством малой скалярной константы  , т.е. посредством умножения на
, т.е. посредством умножения на 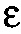 ;
;
Этап 23. Добавить масштабированный вектор к текущей модели недр;
Этап 24. Осуществить прямое распространение волновых полей в новой модели, чтобы вычислить синтетический сейсмический набор данных;
Этап 25. Вычислить градиент целевой функции, измеряющей несоответствие (обычно выбранную норму остатка данных) между прямо смоделированными данными с использованием текущей модели недр и "измеренными" данными, где синтетический сейсмический набор данных из этапа 24 трактуется как измеренные данные в целях этого этапа;
Этап 26. Разделить градиент из этапа 25 на скалярную константу 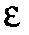 из этапа 22,
из этапа 22,
Этап 27. Использовать этот масштабированный градиент в качестве оценки умножения гессиана на вектор в процедурах оптимизации, которые требуют вычисления этого умножения гессиана на вектор.
Затем, этапы 21 по 27 могут повторяться итеративно, с использованием алгоритма Ньютона-CG, например, чтобы получать умножение обращения гессиана на градиент целевой функции, что дает обновление модели (параметров среды). Здесь, целевая функция измеряет несоответствие между фактическими измеренными полевыми данными и данными, смоделированными из текущей модели.
Суммирование на этапе 23 выполняется, ячейка за ячейкой, в дискретной модели свойств недр. Например, для применения к оценке параметров модели посредством инверсии геофизических данных обычно начинают с "вектора", который является многомерным градиентом целевой функции по отношению к каждому параметру модели. Таким образом, градиент целевой функции является вектором с таким количеством компонент, как количество того, сколько имеется ячеек в модели, умноженное на количество параметров недр, таких как модуль объемной упругости или плотность. Для каждой ячейки соответствующий компонент вектора, после масштабирования, добавляется к значению модели, иногда называемому параметр, для этой ячейки.
Способ из этапов 21-27 может использоваться в итеративном решении любого дифференциального уравнения в частных производных, включающего в себя операцию умножения гессиана на вектор.
ПРИМЕР
В качестве иллюстративного примера мы используем модель Мармуси II [4], показанную на фиг. 3A. Она является "истинной" моделью, которая использовалась, чтобы генерировать синтетические данные, о которых предполагалось, что они являются измеренными данными в целях этого примера. Начальная модель для полной инверсии волнового поля дана на фиг. 3B. Инверсия выполнялась посредством способа кодированного одновременного источника, описанного в источнике [2], который описывает модель Мармуси II и содержит два чертежа, воспроизведенных здесь. Результат инверсии, использующий способ Ньютона в качестве функции времени вычисления, показан на фиг. 1. Сплошная линия является результатом, использующим гессиан Гаусса-Ньютона, пунктирная линия является результатом, использующим настоящее изобретение, где 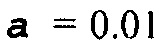 в уравнении (12), и точечная линия является результатом, использующим настоящее изобретение, где
в уравнении (12), и точечная линия является результатом, использующим настоящее изобретение, где  . Другими словами, сплошная линия использует умножение гессиана Гаусса-Ньютона на вектор в уравнении (8) с обращением, вычисленным посредством способа C-G, без преимущества настоящего изобретения, тогда как две прерывистые линии используют умножение гессиана на вектор в уравнении (11) с обращением, вычисленным посредством способа C-G, с преимуществом настоящего изобретения. Сходимость полной инверсии волновой формы показана как функция времени вычисления. Как время вычисления, так и соответствие модели нормализованы к 1. Соответствие модели определяется как RMS ошибка по скорости между инвертированной и истинной моделью, как определено в источнике [2]. Точки на линиях отмечают время для 1 итерации способа Ньютона.
. Другими словами, сплошная линия использует умножение гессиана Гаусса-Ньютона на вектор в уравнении (8) с обращением, вычисленным посредством способа C-G, без преимущества настоящего изобретения, тогда как две прерывистые линии используют умножение гессиана на вектор в уравнении (11) с обращением, вычисленным посредством способа C-G, с преимуществом настоящего изобретения. Сходимость полной инверсии волновой формы показана как функция времени вычисления. Как время вычисления, так и соответствие модели нормализованы к 1. Соответствие модели определяется как RMS ошибка по скорости между инвертированной и истинной моделью, как определено в источнике [2]. Точки на линиях отмечают время для 1 итерации способа Ньютона.
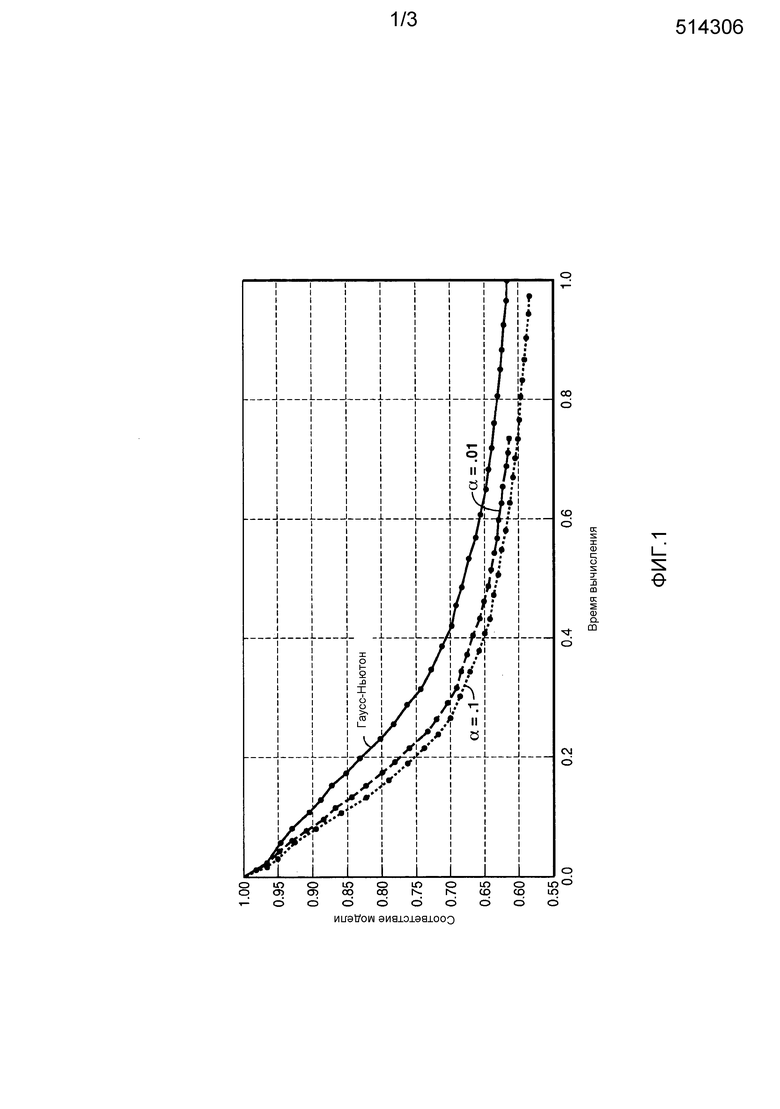
Из фиг. 1 можно видеть, что настоящее изобретение дает приблизительно 40% увеличение скорости в сходимости по сравнению с результатом, использующим гессиан Гаусса-Ньютона, когда 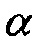 =0,01. Можно дополнительно улучшить сходимость посредством увеличения значения
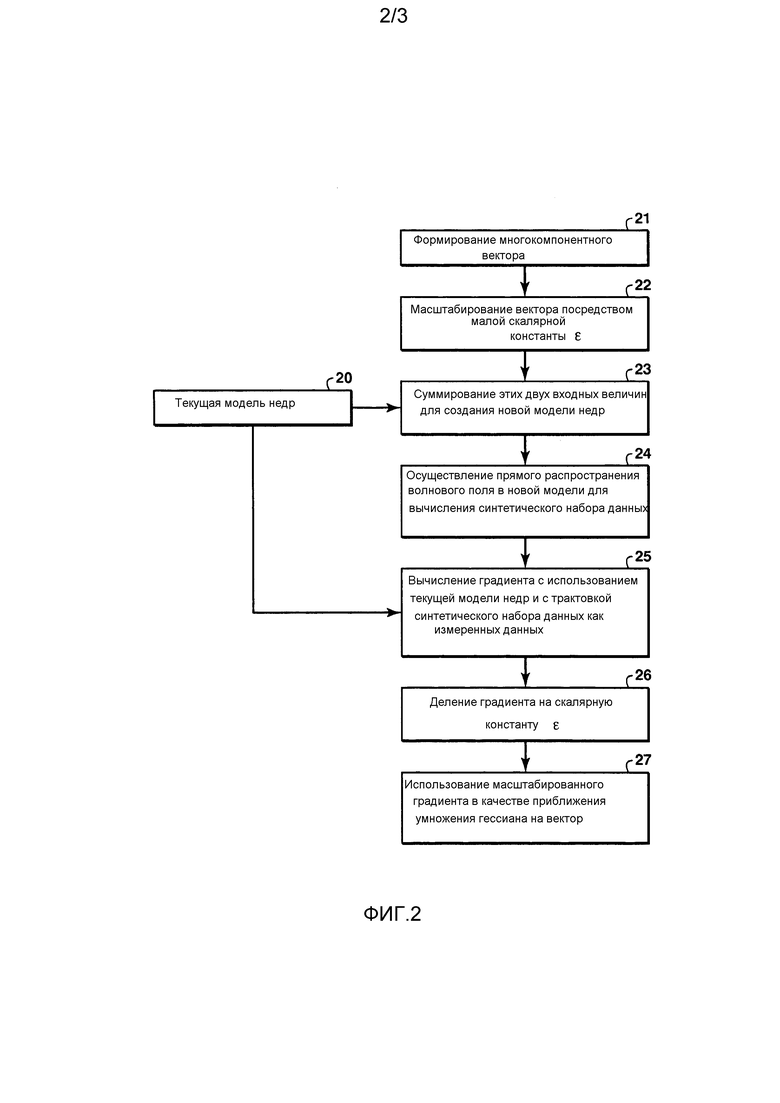
=0,01. Можно дополнительно улучшить сходимость посредством увеличения значения 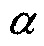 до 0,1, так что больше нелинейных эффектов включаются в аппроксимацию умножения гессиана на вектор. Однако, если значение альфа дополнительно увеличивается, новая модель на Этапе 23 выше может быть нефизической, с результатом, что невозможно даже иметь возможность вычислить прямое волновое поле на этапе 24. Например, скорость новой модели суммирования может становиться отрицательной.
до 0,1, так что больше нелинейных эффектов включаются в аппроксимацию умножения гессиана на вектор. Однако, если значение альфа дополнительно увеличивается, новая модель на Этапе 23 выше может быть нефизической, с результатом, что невозможно даже иметь возможность вычислить прямое волновое поле на этапе 24. Например, скорость новой модели суммирования может становиться отрицательной.
Вышеизложенное применение направлено на конкретные варианты осуществления настоящего изобретения для цели его иллюстрации. Должно быть ясно, однако, специалисту в данной области техники, что являются возможными многие модификации и изменения в вариантах осуществления, здесь описанных. Предполагается, что все такие модификации и изменения находятся в пределах объема настоящего изобретения, как определено в прилагаемой формуле изобретения.
ИСТОЧНИКИ ИНФОРМАЦИИ
[1] A. Baumstein, J.E. Anderson, D. Hinkley, and J.R. Krebs, "Scaling of the objective function gradient for full wavefield inversion," 79th SEG Annual International Meeting, Expanded Abstract, (2009).
[2] J.R. Krebs, J.E. Anderson, D. Hinkley, R. Neelamani, S. Lee, A. Baumstein, and M.-D. Lacasse, "Fast full-wavefield seismic inversion using encoded sources," Geophysics, 74:WCC177-188, (2009).
[3] S. Lee, J.R. Krebs, J.E. Anderson, A. Baumstein, and D. Hinkley, "Methods for subsurface parameter estimation in full wavefield inversion and reverse-time migration," 80th SEG Annual International Meeting, Expanded Abstract, (2010).
[4] G.S. Martin, R. Wiley, K.J. Marfurt, "Marmousi2: An elastic upgrade for Marmousi," The Leading Edge 25, 156-166, (2006).
[5] J. Nocedal and S.J. Wright, Numerical Optimization, Springer, Chap. 7.1, New York, 2nd edition, (2006).
[6] R.E. Plessix, "A review of the adjoin-state method for computing the gradient of a functional with geophysical applications," Geophys. J. Int., 167:495-503, (2006).
[7] R.G. Pratt, C. Shin, and G.J. Hicks, "Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion," Geophys. J. Int., 133:341-362, (1998).
[8] P. Routh, J. Krebs, S. Lazaratos, A. Baumstein, S. Lee, Y.H. Cha, I. Chikichev, N. Downey, D. Hinkley, and J. Anderson, "Encoded simultaneous source full-wavefield inversion for spectrally shaped marine streamer data," 81st SEG Annual International Meeting, Expanded Abstract, (2011).
[9] A. Tarantola, "Inversion of seismic reflection data in the acoustic approximation," Geophysics, 49:1259-1266, (1984).
[10] A. Tarantola, "A strategy for nonlinear elastic inversion of seismic reflection data," Geophysics, 51:1893-1903, (1986).
[11] A. Tarantola, "Inverse Problem Theory and Methods for Model Parameter Estimation," SIAM (2005).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ГЕОЛОГИЧЕСКОЙ СРЕДЫ ПРИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ И ОБРАТНОЙ МИГРАЦИИ ВО ВРЕМЕННОЙ ОБЛАСТИ | 2011 |
|
RU2545487C2 |
| ЭФФЕКТИВНЫЕ СПОСОБЫ ЛИНЕЙНОГО ПОИСКА ПРИ МНОГОПАРАМЕТРИЧЕСКОЙ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ | 2015 |
|
RU2649214C1 |
| ИНВЕРСИЯ ОДНОВРЕМЕННЫХ ИСТОЧНИКОВ ДЛЯ ДАННЫХ СЕЙСМОПРИЕМНОЙ КОСЫ С ВЗАИМНОКОРРЕЛЯЦИОННОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ | 2011 |
|
RU2587498C2 |
| ОРТОГОНАЛЬНОЕ КОДИРОВАНИЕ ИСТОЧНИКА И ПРИЕМНИКА | 2013 |
|
RU2612896C2 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ С КОМПЕНСАЦИЕЙ ПОКАЗАТЕЛЯ КАЧЕСТВА | 2016 |
|
RU2693495C1 |
| КОДИРОВАНИЕ ОДНОВРЕМЕННЫХ ИСТОЧНИКОВ И РАЗДЕЛЕНИЕ ИСТОЧНИКОВ В КАЧЕСТВЕ ПРАКТИЧЕСКОГО РЕШЕНИЯ ПО ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ | 2011 |
|
RU2582480C2 |
| ГИБРИДНЫЙ СПОСОБ ДЛЯ ПОЛНОВОЛНОВОЙ ИНВЕРСИИ С ИСПОЛЬЗОВАНИЕМ СПОСОБА ОДНОВРЕМЕННЫХ И ПОСЛЕДОВАТЕЛЬНЫХ ИСТОЧНИКОВ | 2011 |
|
RU2570827C2 |
| СКОРОСТЬ СХОДИМОСТИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ ПРИ ИСПОЛЬЗОВАНИИ ФОРМИРОВАНИЯ СПЕКТРА | 2012 |
|
RU2577387C2 |
| ИТЕРАТИВНАЯ ИНВЕРСИЯ ДАННЫХ ОТ ОДНОВРЕМЕННЫХ ГЕОФИЗИЧЕСКИХ ИСТОЧНИКОВ | 2007 |
|
RU2435215C2 |
| СНИЖЕНИЕ АРТЕФАКТОВ ПРИ ИТЕРАЦИОННОЙ ИНВЕРСИИ ГЕОФИЗИЧЕСКИХ ДАННЫХ | 2011 |
|
RU2573174C2 |
Изобретение относится к области геофизической разведки и, более конкретно, к обработке сейсмических данных. Техническим результатом является повышение скорости оценки величины, известной как умножение гессиана на вектор, которая возникает в некоторых способах для численного решения дифференциальных уравнений в частных производных. Способ определения дискретной модели физических свойств области недр, представляющей собой модель или модель недр, посредством итеративного инвертирования измеренных геофизических данных, полученных из области недр, содержащий: аппроксимирование матрицы Гессе целевой функции, которая затем умножается на вектор, характеризующее умножение гессиана на вектор с использованием компьютера, с помощью одиночного смоделированного распространения прямой волны и одиночного вычисления градиента целевой функции, в модифицированной модели недр, причем необходимо использование только трех распространений прямой волны или обратной волны, причем это аппроксимирование основано на уравнении приближения для Борновского рассеянного поля давления 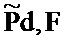
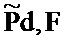
1. Способ определения дискретной модели физических свойств области недр, представляющей собой модель или модель недр, посредством итеративного инвертирования измеренных геофизических данных, полученных из области недр, содержащий:
аппроксимирование матрицы Гессе целевой функции, которая затем умножается на вектор, характеризующее умножение гессиана на вектор с использованием компьютера, с помощью одиночного смоделированного распространения прямой волны и одиночного вычисления градиента целевой функции, в модифицированной модели недр, причем необходимо использование только трех распространений прямой волны или обратной волны;
причем это аппроксимирование основано на уравнении приближения для Борновского рассеянного поля давления 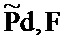
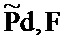
затем вычисление направления в пространстве параметров модели для обновления до текущей модели посредством умножения обращения матрицы Гессе на градиент целевой функции, причем обращение матрицы Гессе вычисляют итеративно с использованием метода сопряженных градиентов, в котором приближение умножения гессиана на вектор используется для оценки умножения матрицы Гессе на вектор возмущения среды;
выполнение линейного поиска для определения амплитуды обновления модели с использованием вычисленного направления;
добавление обновления модели к текущей модели для формирования обновленной модели и использование обновленной модели для геофизического исследования.
2. Способ по п. 1, в котором модифицированная модель недр является линейной комбинацией текущей модели недр и упомянутого вектора.
3. Способ по п. 2, в котором линейная комбинация = текущая модель недр + {(скалярная константа) × (вектор)}, при этом 0< скалярная константа ≤1.
4. Способ по п. 3, в котором скалярная константа выбирается согласно тому, будет ли матрица Гессе вычисляться точно с учетом многократного рассеяния или будет ли аппроксимироваться посредством матрицы Гессе Гаусса-Ньютона.
5. Способ по п. 4, в котором, если должна использоваться аппроксимация Гаусса-Ньютона, скалярная константа выбирается так, что {(скалярная константа) × (вектор)} равняется приблизительно 1% в величине текущей модели недр; но если матрица Гессе должна вычисляться точно, то скалярная константа выбирается так, что {(скалярная константа) × (вектор)} равняется приблизительно 10% в величине текущей модели недр.
6. Способ по п. 3, в котором вектор в первой итерации способа является градиентом целевой функции по отношению к параметрам модели, при этом целевая функция измеряет несоответствие между измеренными геофизическими данными и соответствующими синтетическими геофизическими данными, смоделированными с использованием модели, при этом упомянутое несоответствие является выбранной нормой остатка данных, при этом остаток данных равняется разности между измеренными геофизическими данными и соответствующими синтетическими геофизическими данными, смоделированными с использованием модели; при условии, что для упомянутого одиночного вычисления градиента целевой функции измеренные геофизические данные в остатке данных заменяются на синтетические данные, смоделированные с использованием модифицированной модели недр, и остаток данных делится на скалярную константу.
7. Способ по п. 1, в котором измеренные геофизические данные, которые обращаются, являются полным волновым полем сейсмических данных.
8. Способ по п. 7, в котором модель физических свойств является моделью по меньшей мере одной из группы, состоящей из 21 упругих констант, включающих в себя модуль объемной упругости; плотности; или любой комбинации двух или более из них.
9. Способ по п. 1, в котором 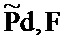
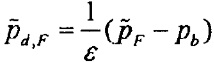 ,
,
где ε является достаточно малым значением, чем заранее заданное значение, 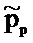
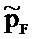
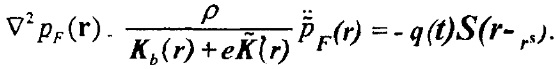
10. Способ по п. 9, в котором аппроксимация дополнительно включает в себя представление 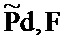

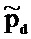
11. Способ определения дискретной модели физических свойств области недр посредством итеративного инвертирования измеренных геофизических данных, полученных из области недр, содержащий использование матрицы Гессе, соответствующей целевой функции, которая затем умножается на вектор, что характеризует "умножение гессиана на вектор", чтобы определять обновление для начальной модели, при этом умножение гессиана на вектор аппроксимируется, с использованием компьютера, с помощью одиночного смоделированного распространения прямой волны и одиночного вычисления градиента целевой функции в модифицированной модели недр, причем для аппроксимирования необходимо использование только трех распространений прямой или обратной волны, содержащий:
формирование масштабированного вектора посредством умножения вектора на число ε, где 0<ε≤1, добавление масштабированного вектора к начальной модели;
моделирование первого синтетического набора данных с использованием модели с масштабированным вектором, добавленным к ней;
формирование целевой функции, чтобы измерять несоответствие между вторым синтетическим набором данных, смоделированным с использованием начальной модели, и упомянутым первым синтетическим набором данных;
вычисление градиента сформированной целевой функции по отношению к параметрам физических свойств, деление градиента на ε и использование этого в качестве оценки умножения гессиана на вектор,
вычисление направления в пространстве параметров модели для обновления до начальной модели посредством умножения обращения матрицы Гессе на градиент целевой функции, причем обращение матрицы Гессе вычисляют итеративно с использованием метода сопряженных градиентов, в котором оценка умножения гессиана на вектор используется для оценки умножения матрицы Гессе на вектор возмущения среды;
выполнение линейного поиска для определения амплитуды обновления модели с использованием вычисленного направления;
добавление обновления модели к начальной модели для формирования обновленной модели и использование обновленной модели для геофизического исследования.
12. Способ по п. 11, в котором вектор в первой итерации итеративной инверсии является градиентом в пространстве модели целевой функции, при этом целевая функция измеряет несоответствие между измеренными геофизическими данными и соответствующими смоделированными по модели геофизическими данными.
13. Компьютерно-используемый носитель, имеющий машиночитаемый программный код, сохраненный на нем, при этом упомянутый машиночитаемый программный код выполнен с возможностью исполнения, чтобы осуществлять способ определения дискретной модели физических свойств области недр, которая характеризует модель или модель недр, посредством итеративного инвертирования измеренных геофизических данных, полученных из области недр, при этом упомянутый способ содержит:
использование матрицы Гессе целевой функции, которая затем умножается на вектор, представляющее собой "умножение гессиана на вектор", чтобы определять обновление для модели, при этом умножение гессиана на вектор аппроксимируется с помощью одиночного смоделированного распространения прямой волны и одиночного вычисления градиента целевой функции, в модифицированной модели недр, причем необходимо использование только трех распространений прямой волны или обратной волны,
причем это аппроксимирование основано на уравнении приближения для Борновского рассеянного поля давления 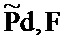
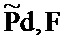
затем вычисление направления в пространстве параметров модели для обновления до текущей модели посредством умножения обращения матрицы Гессе на градиент целевой функции, причем обращение матрицы Гессе вычисляют итеративно с использованием метода сопряженных градиентов, в котором приближение умножения гессиана на вектор используется для оценки умножения матрицы Гессе на вектор возмущения среды;
выполнение линейного поиска для определения амплитуды обновления модели с использованием вычисленного направления;
добавление обновления модели к текущей модели для формирования обновленной модели и использование обновленной модели для геофизического исследования.
14. Компьютерный программный продукт по п. 13, в котором вектор в первой итерации итеративной инверсии является градиентом в пространстве модели целевой функции, при этом целевая функция измеряет несоответствие между измеренными геофизическими данными и соответствующими смоделированными по модели геофизическими данными.
| US 20110267923 A1, 03.11.2011 | |||
| US 20100142316 А1, 10.06.2010 | |||
| US 20090259447 А1, 15.10.2009 | |||
| US 20080173104 А1, 24.07.2008. |
Авторы
Даты
2017-03-15—Публикация
2012-10-26—Подача