СПОСОБ ИСПЫТАНИЯ МЕТАЛЛИЧЕСКИХ ПРЕГРАД - ОСНОВЫ ЗАЩИТНЫХ ГЕТЕРОГЕННЫХ СТРУКТУР Российский патент 2016 года по МПК G01M7/08 F41H5/00 

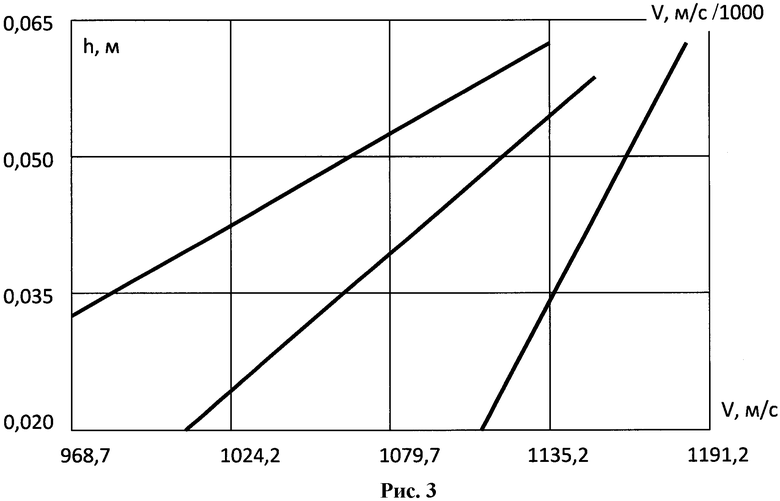
Изобретение относится к оборонной технике и предназначено для проведения испытаний лицевых металлических преград - основы гетерогенных защитных структур, путем их обстрела бойками с целью подтверждения ожидаемой V_ПСП - минимальной скорости сплошных (100%) пробитий, являющейся квантованной и соответствующей квантовым числам n=14, 15, 16, 17, 18 единиц, при которых боек калибром d проходит за стальную преграду толщиной b≈d (рис. 1a), а также с целью определения квантованных скоростей удара (V_C=V_Пn)<V_ПСП, соответствующих квантовым числам n=2, 3(1), 4,…9, на которых квантованная глубина внедрения бойка в преграду h_n увеличивается с уменьшением n от 18 до 2, достигая пробитий (h_max $$\cong$$ b) даже на V_C=V_Пn≈V_ПСП-100, м/с.

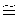
При этом малые значения глубины внедрения бойка в преграду h (рис. 1б) или h_n, соответствующие квантовым числам n=14, 15, 16, 17, 18, но получаемые на V_С≤V_ПСП, должны достигать значений b/2,08; 2,34; 2,68; 3,12; 3,73.

Рис. 1а V_ПСП>(V_C=V_Пn)≥V_ПСП Рис. 1.б (V_C=V_Пn)<<V_ПСП

По результатам экспериментальных исследований пробивного действия бойков по преградам с различными прочностными характеристиками и материалам, взятым из книги [1], было установлено, что между глубиной каверны h (при внедрении бойка в преграду) и скоростью соударения V_C (в диапазоне 500…1500 и 1500…2200 м/с) имеется линейная зависимость - (Рис. 2)

где а, b¹ - коэффициенты корреляции, определяемые по результатам экспериментов, L - длина бойка.

Рис. 2

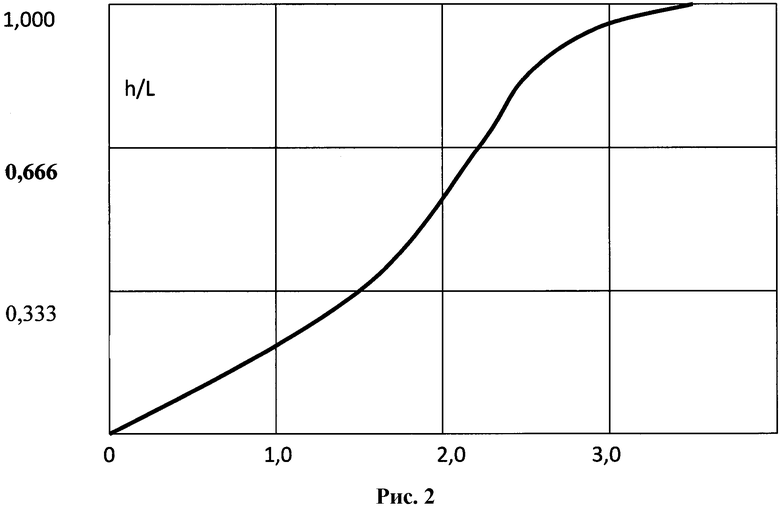
Зависимости, аналогичные (1), получены и при стрельбе удлиненными бойками по трем стальным плитам толщиной 0,08 м с различными прочностными характеристиками и под углом α=60°. Они показаны в виде Рис. 3.

Учитывая результаты испытаний, приведенные на Рис. 3, значения h, соответствующие V_ПСП, достигают 0,75 b.

В современном производстве образцов военной техники, в частности, при испытании стальных плит и оптимизации конструктивных параметров бойков, широко применяются расчетные методы оценки V_ПСП. Известны способы оценки V_ПСП как функции относительной толщины плиты, удлинения бойка, угла их встречи. Известные способы оценки V_ПСП учитывают только некоторую часть прочностных характеристик соударяемых тел и совсем не учитывают физико-химических, которые также влияют на пробиваемость стальных плит и могут в значительной степени исказить расчетное значение V_ПСП. Известен способ оценки V_ПСП, включающий выстреливание бойками по стальной плите на скоростях, близких к ожидаемой, по результатам которых устанавливают V_ПСП. Она устанавливается методом корректировки навески порохового заряда и обстрелом стальной плиты на скоростях пробития V_C>V_ПСП с последующим усреднением трех значений минимальных скоростей пробития. Причем усредненная скорость должна отличаться от максимального значения скорости, при которой h<b, не более чем на 25 м/сек. Это требование указывает на недостаточную изученность сопротивляемости стальных преград пробитию бойками на V_C≤V_ПСП.

С целью устранения этого недостатка автором получена закономерность дискретного изменения отношений кинетической энергии бойка к объему пробоины в преграде

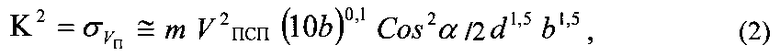
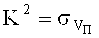
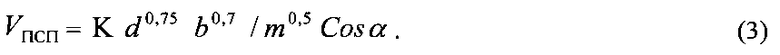
где $$K^2={\sigma }_{V_{П}}$$ - отношение кинетической энергии бойка mV² _ПСП/2 к выбитому им объему преграды d^1,5 b^1,5. При этом используется формула Жакоб де Марра [2], позволяющая одновременно учесть толщину преграды b и угол наклона ее α, диаметр d и массу бойка m при заданном значении коэффициента К, характеризующего прочность преграды, -

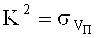
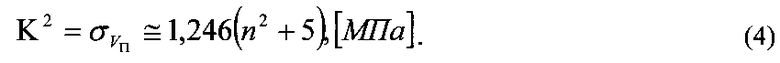
Для отечественных бойков, пробивающих бронеплиты, коэффициент К изменяется в пределах 1300, 1350, 1400, 1450, 1500, 3000. Результаты расчета автором [2] значений $$K^2={\sigma }_{V_{П}}$$ с использованием многочисленных данных полигонных испытаний бронеплит на пробитие бойками с целью определения для них V_ПСП и К позволили получить

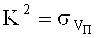
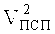
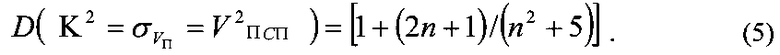
Дискретность значений $$K^2={\sigma }_{V_{П}}$$ , изменяющихся только с изменением $$V_{ПСП}^2$$ , при увеличении чисел n на единицу будет определяться следующей зависимостью [2]:

Так как значения V_ПСП являются квантованными скоростями, то с учетом зависимости (4) дискретность их будет определяться извлечением квадратного корня из этой зависимости [2]-

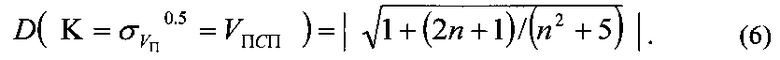
Повышает изученность явлений, происходящих на V_ПСП=V_Пn [2, 3, 4], закономерность дискретного изменения квантованных скоростей V_Пn -

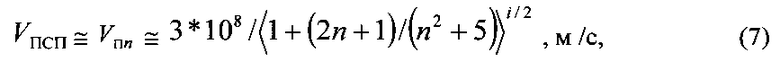
где n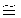 $$\cong$$ 1,2,3,…18 - квантовые числа, а i=1,2,3,…18 при каждом значении n в пределах выбранного интервала скоростей V_Н.В.<(V_C=V_Пn)≥V_ПСП.

Эта закономерность имеет два характерных свойства:

1) увеличение дискретности V_Пn с уменьшением квантового числа n до 2 и сближение между собой значений V_Пn с увеличением числа n;

2) повторяемость V_Пn, определяемых однозначными числами n, среди V_Пn, определяемых двузначными числами n.

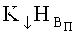
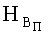
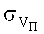
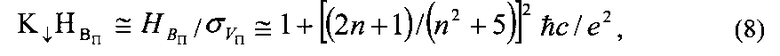
Автором [2] установлена также закономерность разупрочнения бронеплит в разрушаемом бойком объеме $$K_{\downarrow }{H}_{B_{П}}$$ , т.е. уменьшения их твердости $$H_{B_{П}}$$ до $${\sigma }_{V_{П}}$$ - значения удельного сопротивления пробитию на квантованной скорости -

где ħс/е² - обратная величина постоянной тонкой структуры атома, которой с - скорость света, е - заряд электрона, ħ - постоянная Планка, уменьшенная в 2π раз.

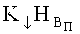
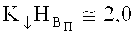
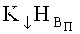
Максимальное значение $$K_{\downarrow }{H}_{B_{П}}$$ =43,5 соответствует n=2, а при n=23,7 $$K_{\downarrow }{H}_{B_{П}}\cong \mathrm{2,0}$$ . При n≥23,7 значения $$K_{\downarrow }{H}_{B_{П}}$$ уменьшаются от 2,0 до 1,0.

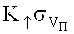
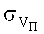
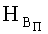
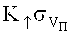
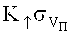
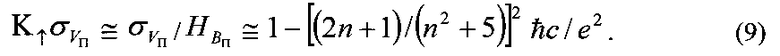
Автором [2] установлена также закономерность «упрочнения» бронеплит в разрушаемом бойком объеме $$K_{\uparrow }{\sigma }_{V_{П}}$$ , т.е. увеличения $${\sigma }_{V_{П}}$$ до $$H_{B_{П}}$$ ( $$K_{\uparrow }{\sigma }_{V_{П}}$$ - от нуля до 1,0 при n≥23,7) и увеличения отрицательных значений $$K_{\uparrow }{\sigma }_{V_{П}}$$ от - 41,5 до нуля при n≤23,7

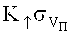
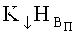
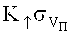
Минимальное значение $$K_{\uparrow }{\sigma }_{V_{П}}$$ =41,5 соответствует n=2. Отношение $$K_{\downarrow }{H}_{B_{П}}$$ / $$K_{\uparrow }{\sigma }_{V_{П}}$$ будет максимальным при n $$\cong$$ 23,7, а при n>23,7 и при n<23,7 будет уменьшаться, только до -1,05 при n=2 и до 1,05 при n=152.

Повышает изученность явлений, происходящих в разрушаемом бойком объеме бронеплиты на квантованных скоростях удара V_Пn, закономерность дискретного изменения квантованных значений глубины каверны h_n [2, 3, 4] -

где µ_n=[(2n+1)/(n²+5)]²137 - квантованная часть коэффициентов 1+µ_n и 1-µ_n, модуль отношения которых определяет квантованное h_n при заданном значении толщины преграды b;

n - квантовое число, практически изменяющееся в пределах 2, 3, 4,…, 18;

137 $$\cong$$ ħс/е² - обратная величина постоянной тонкой структуры атома, в которой с - скорость света, е - заряд электрона, ħ - постоянная Планка, уменьшенная в 2π раз.

Эта закономерность убедительно показывает, что увеличение дискретности V_Пn с уменьшением квантового числа n до 2 приводит к сближению значений h_n с толщиной преграды b, т.е. к увеличению пробивной способности бойков на квантованных скоростях, определяемых однозначными квантовыми числами.

Теоретическое (минимальное) преимущество значений h_n перед h_n+1 будет определяться их отношением в виде

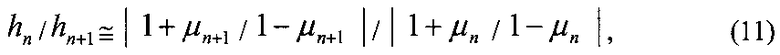
где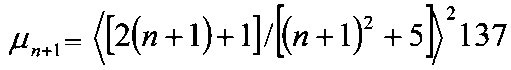

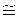
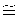
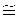
Поэтому целью настоящего изобретения является не столько подтверждение ожидаемой V_ПСП за счет получаемого линейного увеличении глубины каверны h в преграде от h $$\cong$$ 0 до h_max и получения пробитий h_max=b на V_c≥V_ПСП и на квантованных скоростях (V_c=V_Пn)<V_ПСП, являющихся следствием увеличения на этих скоростях квантованных значений глубины каверны в преграде h_n от h₁₈ $$\cong$$ b/3,73 до h₂ $$\cong$$ b/1,05, соответствующих уменьшению квантового числа n от 18 до 2. Поставленная цель при этом достигается тем, что в предлагаемом способе испытания преград, включающем выстреливание с различной начальной скоростью бойками и последующим определением

предельной скорости сквозного пробития V_ПСП=V_Пn, операцию выстреливания осуществляют не только с замером скоростей удара и глубины каверны h<b в преграде, по которым получается линейная зависимость h от V_c типа (1 и 12), но и с фиксацией пробитий h=b на V_c≥V_ПСП и на (V_c=V_Пn)<V_ПСП, соответствующих квантованным скоростям удара V_П2, V_П3, V_П4, … V_П9, их спектру при V_c=V_Пn (7)5, а также значениям h_n - их спектру (10) и зависимости (12). Значение предельной скорости сквозного пробития V_ПСП выбирается из числа полученных V_с=V_Пn при h_max=b, выше которых наблюдаются только пробития, а ниже - пробития только на V_с=V_Пn, соответствующих однозначным квантовым числам n=2, 3(1), 4,…, 9 на фоне линейной зависимости глубины каверны h от V_с типа (12).

Пример 1. По результатам экспериментальных исследований пробивного действия 23 мм бойков по 21,6 мм стальным преградам (82 удара) автором [3, 4] получена также линейная зависимость изменения малых значений глубины каверны h с увеличением скорости удара V_C от 630 м/с до V_C=V_ПСП=715 м/с

где коэффициент корреляции а=-0,051838, а коэффициент корреляции b¹=83, 92∗10^-6. Значение скорости начала внедрения 23 мм бойка в стальную преграду V_Н.В. $$\cong$$ 617,7 м/сек определяется зависимостью (12) при h=0 отношением (-а/b¹)=0,051838/83,92∗10^-6=617,7, м/сек. Значение h_mах $$\cong$$ 0,008 м зависимость (12) определяет при V_C $$\cong$$ V_ПСП, а большинство значений h не превышают h₁₈, соответствующее n $$\cong$$ 18, т.е. h₁₈ $$\cong$$ b/3,73. Зависимость (12) позволяет также определить время взаимодействия бойка с преградой τ по выражению

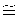
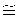
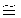
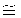
При этом установлено также резкое изменение отношения b/h от 5,4 до 1,16 на (V_C=V_Пn)<<V_ПСП. Среднеквадратическое отклонение h не превышает 0,002 м, а погрешность определения V_C составляет примерно 0,15%. При этом V_C=676 м/с соответствует V_П14=676 м/с, а на (V_C=V_Пn)<V_ПСП - наблюдается группирование пробитий на фоне каверн, глубина h которых растет при увеличении V_C по зависимости (12), достигая при V_ПСП=715 м/с величины 0,0081 м. При этом отношение b/h=0,0216/0,008 $$\cong$$ 2,7 и соответствует квантовому числу n=16, а τ=0,0081/(715- 617,7)=8,32∗10^-5, сек.

Пример 2. По результатам экспериментальных исследований пробивного действия 23 мм бойков по 20 мм (b=0,020) стальным преградам автором установлено. Среди шести непробитий на V_C=650…655 м/с получено три пробития на V_C=653…655 м/с, подтверждающих V_П2=655 м/с при b/h_n=1,05 на фоне непробитий при h=0,003 м, b/h $$\cong$$ 6,667 и τ=0,003/653-617,7=8,50∗10^-5, сек. Далее, тремя пробитиями на V_C=661…665 м/с, после которых получено четыре непробития на V_C=665…668 м/с, подтверждается V_П4=665 м/с при b/h_n $$\cong$$ 1,08 на фоне каверн при h=0,004 м, b/h $$\cong$$ 5,00 и τ=0,0042/668-617,7=8,35∗10^-5, сек. Кроме того, четырьмя пробитиями на V_C=669…674 м/с, расположенными среди шести непробитий на V_C=671…677 м/с, подтверждается V_П14=674 м/с при b/h_n $$\cong$$ 2,08 на фоне каверн при h=0,005 м, b/h $$\cong$$ 4,0 и τ=0,0048/675-617,7=8,38∗10^-5,сек. Далее четырьмя пробитиями на V_C=690…692 м/с, расположенными среди четырех непробитий на V_C=689…693 м/с, подтверждается V_П13=690 м/с при b/h_n $$\cong$$ 1,87 на фоне каверн при h=0,006 м, b/h $$\cong$$ 3,333 и τ=0,006/693- 617,7=8,00∗10^-5, сек. При этой стрельбе (23 мм бойками по 20 мм стальной плите) на V_С=695…757 м/с получены только пробития, которым предшествуют каверны с h=0,007 м, b/h $$\cong$$ 2,857, что соответствует квантовому числу n=16,45. При этом τ=0,007/700-617,7=8,51∗10^-5, сек. На V_C=638…650 м/с при этой стрельбе получены только непробития. Таким образом, в этом примере подтверждены квантованные скорости V_П2, V_П3(1), V_П4, V_П13 и V_П14, а τ является практически постоянным, имея в среднем 8,35∗10^-5, сек, а минимум - 8,00∗10^-5, сек.

Пример 3. Четырьмя пробитиями 23 мм бойков по 21,6 мм стальной плите на V_С=682…686 м/с, расположенными среди пятнадцати непробитий на V_С=683…688 м/с, подтверждаются V_П7=683 м/с и V_П8=682 м/с при b/h_n $$\cong$$ 1,21(1,27) и τ=0,006/688-617,7=8,53∗10^-5, сек на фоне каверн при h=0,006 м. Тремя пробитиями на V_C=689…693 м/с и тремя пробитиями на V_C=695…698 м/с, расположенными среди пятнадцати непробитий на V_C=689…704 м/с, подтверждаются V_П3(9)=695 м/с при b/h_n $$\cong$$ 1.06(1,35) и τ=0,007/700-617,7=8,51∗10^-5, сек на фоне каверн при h=0,007 м. Тремя пробитиями на V_C=705…706 м/с, после которых получено три непробития на V_C=706…708 м/с, подтверждаются V_П5=703 м/с при b/h_n $$\cong$$ 1,11 и τ=0,007/706-617,7=7,93∗10^-5, сек на фоне каверн при h=0,007 м. Двумя пробитиями на V_C=708…709 м/с и тремя пробитиями на V_С=712…715 м/с, выше которых имеется два непробития, подтверждаются V_П12=711 м/с при b/h_n=1,7 на фоне каверн при h=0,008 м, b/h_n=2,222 и соответствует квантовому числу n=14,56 и τ=0,008/712-617,7=8,48∗10^-5, сек. При этом h_max/(V_ПСП-V_Н.В.) $$\cong$$ τ=0,008/(717-617,7)=8,06∗10^-5, сек. Таким образом, в этом примере подтверждены квантованные скорости V_П3(9), V_П5, V_П7, V_П8 и V_П12, а отношение h/(V_C-V_Н.В.) $$\cong$$ τ является не только более постоянным, чем в примере 2, но и практически равным их значениям в примерах 1 и 2, т.е. 8,36∗10^-5, сек.

В целом, тремя примерами не только подтверждены квантованные скорости V_П2, V_П3(1), V_П4, V_П5, V_П6, V_П7, V_П8, V_П9, V_П12, V_П13, V_П14, V_П15, V_П16, V_П17, но и установлена возможность приближенного определения значения V_ПСП эмпирической зависимостью

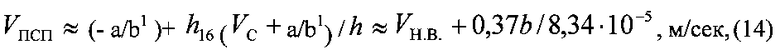
где значения толщины преграды b, квантованной глубины каверны h₁₆=0,37b и малой глубины каверны h должны быть в метрах, а время образования последней - τ=8,34·10^-5 - в сек. Зависимость (14) позволяет получить для первого примера V_ПСП $$\cong$$ 713,53, м/сек, вместо опытного значения V_ПСП $$\cong$$ 715, м/сек. Для второго примера зависимость (14) дает V_ПСП $$\cong$$ 706,43, м/сек, вместо опытного значения V_ПСП $$\cong$$ 700, м/сек. Для третьего примера зависимость (14) дает V_ПСП $$\cong$$ 713,53, м/сек, вместо опытного значения V_ПСП $$\cong$$ 717,м/сек. Среднее значение отклонения в определении V_ПСП по зависимости (14) составляет 0,07%, т.е. практически превышает погрешность определения скорости удара 0,15%.

Некоторая стабильность отношения (14) является хорошим критерием стойкости стальных преград, так как определяет наклон линии значений h к оси значений V_C при графическом представлении зависимости h от V_C, а точнее, величину тангенса угла наклона линии h к линии V_C. Для удлиненных бойков это отношение может меняться при существенном изменении прочности преград, что наглядно показывается на Рис. 3 - увеличением угла наклона линий h к оси V_C, определяющих значения V_ПСП значениями h_max.

Значения глубины внедрения h бойка в различные материалы на малых скоростях удара V_C≥V_H.B. необходимы для определения динамической твердости материалов - отношения кинетической энергии бойка в момент удара к объему вмятины в материале, максимальный диаметр которой равняется калибру бойка (прототип - патент RU 2258211) [6].

Ранее автором [5] установлено также, что скорость начала внедрения менее твердого бойка в значительно более твердую преграду V_Н.В. удовлетворительно определяется следующей зависимостью:

где 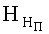$$H_{H_{П}}$$ - твердость металлической преграды, $$H_{B_{\delta }}$$ - твердость металла бойка, ρ_δ - массовая плотность металла бойка, k_П=Cos²α - коэффициент наклона преграды.

Использование предлагаемого способа испытания стальных преград обеспечивает по сравнению с существующими способами повышение точности определения пределов изменения V_ПСП=V_Пn, а также подтверждение наличия квантованных скоростей удара бойков в стальные преграды.

Применение этого способа для преград из различных металлов и их сплавов имеет целью определение пределов изменения V_ПСП=V_Пn и подтверждение наличия квантованных скоростей удара бойков в такие преграды.

При этом явлениями пробитий на (V_C=V_Пn)<<V_ПСП подтверждаются квантованные скорости V_П2, V_П3(1), V_П4, V_П5, V_П6, V_П7, V_П8, V_П9, соответствующие, прежде всего, однозначным квантовым числам.

Применение этого способа для преград из различных металлов и их сплавов имеет целью прежде всего выявление наличия квантованных скоростей удара, соответствующих однозначным квантовым числам.

Литература

1. Зухас Дж.А., Николас, Свифт Х.Ф. «Динамика удара», (перевод с английского), Москва, Мир, 1985, стр.293.

2. Толов В.В, Толов А.В. "Закономерность изменения величины и дискретности минимальных затрат кинетической энергии твердых тел на преодоление сопротивления различных сред", Описание открытия, Вестник Петровской академии наук и искусств №6, СПб, 2007 г.

3. Толов В.В., Толов А.В. Закономерности изменения величины и дискретности энергетических характеристик взаимодействия металлических тел с различными средами, Статья, Труды международного симпозиума «Надежность и Качество», Россия, Пенза, 21-31 мая, 2006 г., стр. 188.

4. Толов В.В., Толов А.В. Закономерность (определитель) дискретного уменьшения исходных физических и механических характеристик различных сред до их минимальных квантованных значений при деформировании и разрушении, Вестник Петровской Академии Наук и Искусств №7, Санкт-Петербург, 2007 г.

5. Толов В.В. Характерные скорости взаимодействия твердых тел, Статья, ЦСИФ МО, выпуск №8/118, 1976 г.

6. Дрокин П.А., Болденков В.В. Способ определения динамической твердости материалов, Патент RU 2258211, ВНИИЭФ, Москва,

Изобретение относится к оборонной технике и предназначено для проведения испытаний лицевых металлических преград - основы гетерогенных защитных структур. Способ включает выстреливание бойков со скоростью, большей скорости удара, определение и замер глубины ударного внедрения бойка диаметром d в поверхность металла h (глубина каверны). При этом скорость удара больше или меньше ожидаемой минимальной скорости сплошных пробитий. Определение предельной (минимальной) скорости сплошных пробитий, выше которой получаются сплошные пробития, а ниже - только закономерные пробития, на фоне линейной зависимости малых значений глубины каверны h от скорости удара; преимущества квантованных скоростей удара; однозначных и малых двузначных квантовых чисел n для всех скоростей, на которых получены пробития или каверны увеличенной глубины. Достигается определение наличия и преимущества квантованных скоростей удара, а также повышение точности определения минимальной скорости сплошных пробитий. 4 ил.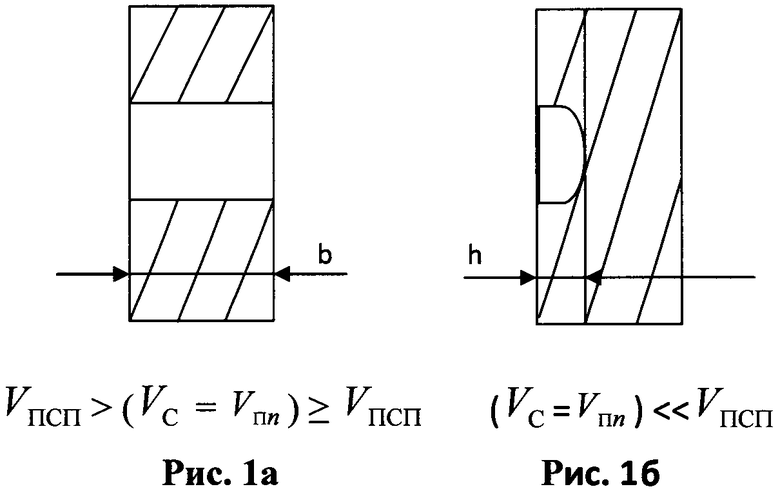

Способ испытания металлических преград - основы защитных гетерогенных структур, включающий выстреливание бойков со скоростью
V₀>V_C - скорости удара, ее определение и замер глубины ударного внедрения бойка диаметром d в поверхность металла h (глубина каверны), отличающийся более высокими скоростями удара, которые больше и меньше ожидаемой минимальной скорости сплошных (100%) пробитий V_C=V_ПCП=V_Пn, являющейся квантованной и соответствующей квантовым числам n=14, 15, 16, 17, 18, в отличие от (V_C=V_Пn)<V_ПCП, соответствующих квантовым числам n=2, 3(1), 4,…, 9, имеющий целью не столько повышение точности определения V_ПCП, сколько определение наличия и преимущества квантованных скоростей удара (V_C=V_Пn)<V_ПCП, соответствующих n - 2, 3(1), 4,…, 9, перед скоростями, соответствующими n=14, 15, 16, 17, 18, завершающийся расчетным определением:
во-первых, предельной (минимальной) скорости сплошных (100%) пробитий V_ПCП, выше которой получаются сплошные пробития, а ниже - только закономерные пробития на V_С=V_Пn, соответствующих квантовым числам n=2, 3(1), 4,…, 9, на фоне линейной зависимости (3-5) малых значений глубины каверны h от скорости удара V_C -
h=a+b¹ V_C, м,
где a, b¹ - коэффициенты корреляции, определяемые по результатам экспериментов и входящие в зависимость для определения V_ПCП -
V_ПСП≅V_Пn≅-a/b¹+h₁₆(V_C+a/b¹)/h, м/сек,
где - h₁₆ - квантованное значение глубины каверны, соответствующее квантовому числу n=16 и определяемое зависимостью
h_n≅b/|1+µ_n/1-µ_n|,
где µ_n=[(2n+1)/(n²+5)]²137 - квантованная часть коэффициентов 1+µn и 1-µ_n, модуль отношения которых определяет квантованное
h_n при заданном значении толщины преграды b;
n - квантовое число, практически изменяющееся в пределах 2, 3, 4,…, 18;
137≅ħc/e² - обратная величина постоянной тонкой структуры атома, в которой с - скорость света, е - заряд электрона, ħ - постоянная Планка, уменьшенная в 2π раз;
во-вторых, преимущества квантованных скоростей удара (V_C=V_Пn)<V_ПCП, соответствующих квантовым числам n=2, 3(1), 4,…, 9, перед скоростями (V_C=V_Пn)=V_ПCП, но соответствующими n=14, 15, 16, 17, 18, выражающегося отношением h_n/h_{14, 15, 16, 17, 18} по зависимости
h_n/h_{14, 15, 16, 17, 18}≅2,08;2,34;2,68;3,12;3,73/|1+µ_n/1-µ_n|,
где b/h₁₄≅2,08; b/h₁₅≅2,34; b/h₁₆≅2,68; b/h₁₇≅3,12; b/h₁₈≅3,73;
в-третьих, однозначных и малых двузначных квантовых чисел n для всех (V_C=V_Пn)<V_ПCП, на которых получены пробития или каверны увеличенной глубины, по следующей зависимости:
V_Пn≅3*10⁸/〈1+(2n+1)/(n²+5)〉^i/2, м/сек,
где n≅2, 3(1), 4…18 - квантовые числа, а i- 1, 2, 3,… 18 при каждом значении квантового числа n.