Предлагаемое изобретение относится к кардиологии и может быть использовано в экспериментальных и клинических исследованиях для оценки процесса распространения возбуждения в миокарде при неинвазивном способе прогнозирования атриовентрикулярных (АВ) блокад сердца.
Нарушение АВ проводимости характеризуется задержкой или прекращением проведения импульсов из предсердий через АВ узел и пучок Гиса к желудочкам [1]. Выделяют 3 степени АВ блокад. Блокада I степени характеризуется замедленным прохождением импульса от предсердий к желудочкам, что проявляется удлинением интервала между предсердными и желудочковыми сокращениями. Блокада II степени проявляется в увеличении числа сокращений предсердий по отношению к числу сокращений желудочков из-за блокированного проведения некоторых предсердных импульсов. При блокаде III степени происходит полное отсутствие координации между предсердными и желудочковыми ритмами.
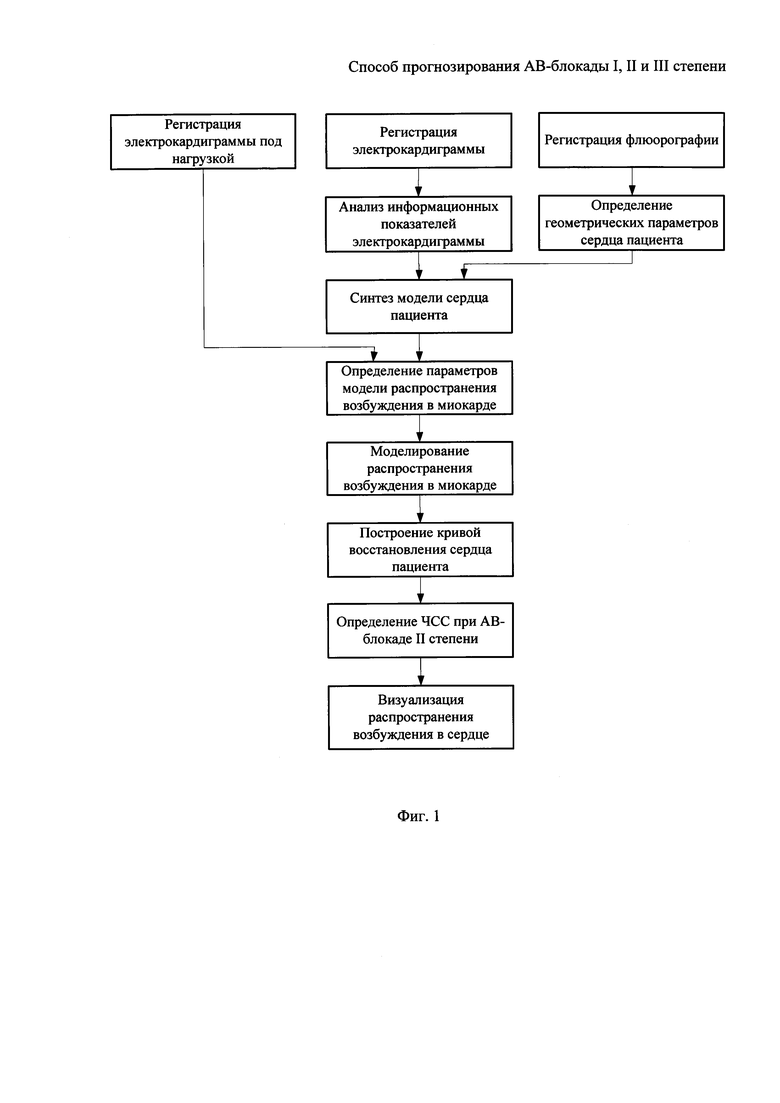
Известен способ моделирования и визуализации распространения возбуждения в миокарде, заключающийся в том, что осуществляют регистрацию электрокардиограммы (ЭКГ), регистрацию флюорографии сердца пациента, анализ информационных показателей электрокардиограммы, определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, моделирование распространения возбуждения в миокарде, затем по результатам моделирования определение частоты сердечных сокращение (ЧСС), при которой возможна АВ-блокада II степени, визуализацию распространения возбуждения в миокарде [2].
К недостаткам известного способа моделирования и визуализации распространения возбуждения в миокарде относятся
- отсутствие возможности анализа информационных показателей ЭКГ и оценки состояния сердца пациента под нагрузкой;
- отсутствие возможности прогнозирования АВ-блокад.
Наиболее близким по достигаемому результату к предполагаемому изобретению является способ прогнозирования АВ-блокады II степени [3], заключающийся в том, что осуществляют регистрацию электрокардиограммы в покое и под нагрузкой, регистрацию фронтального и левобокового флюорографических снимков сердца пациента, анализ информационных показателей электрокардиограммы путем определения длительности кардиоцикла (ts), интервала времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH), интервала времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HS), определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, определение параметров модели распространения возбуждения в миокарде, моделирование распространения возбуждения в миокарде, построение кривой восстановления сердца пациента, определение ЧСС, при которой возможна АВ-блокада II степени, визуализацию по результатам моделирования распространения возбуждения в миокарде.
К недостаткам известного способа прогнозирования АВ-блокады II степени, по мнению авторов, относятся следующие.
1. Вид кривой восстановления сердца не дает качественного описания моделируемых данных.
2. Отсутствует возможность прогнозирования АВ-блокад I и III степени.
3. Отсутствует дифференциация типов АВ-блокады II степени.
На фигуре 1 приведена схема алгоритма известного способа прогнозирования АВ-блокады II степени.
Покажем недостатки известного способа.
1. Из описания известного способа следует, что кривая восстановления сердца пациента находится путем аппроксимации результатов моделирования функцией экспоненциального вида. В качестве независимой переменной выступает интервал времени от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HS), в качестве зависимой - интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH). Экспоненциальная зависимость, являющаяся функцией аппроксимации в известном способе прогнозирования АВ-блокад II степени, предполагает неограниченное возрастание интервала SH в области малых значений HS. Последнее наблюдение не соответствует реальным физиологическим процессам, так как возрастание интервала SH ограничено сверху. Следовательно, в известном способе наблюдается противоречие между реальными параметрами распространения возбуждения в миокарде и областью значений кривой восстановления сердца, полученной после анализа результатов моделирования. При выборе регрессионной функции результатов моделирования необходимо учитывать, что рассматриваемая модель имеет точку максимума в области малых значений параметра HS. Однако при аппроксимации результатов моделирования экспоненциальной функцией невозможно определить экстремумы, так как при дифференцировании экспоненциальной функции также получается экспоненциальная функция.
Таким образом, необоснованный выбор экспоненциальной функции приводит к значительным погрешностям при построении модели и, как следствие, при прогнозировании частоты возникновения АВ-блокады.
2. Из анализа известного способа прогнозирования АВ-блокады II степени следует, что способ осуществляет прогнозирование только АВ-блокад II степени и не осуществляет прогнозирование АВ-блокад I и III степени.
Прогнозирование частот сердечных сокращений возникновения АВ-блокад крайне важно. Определение ЧСС, при которой возникает АВ-блокада II степени, позволяет оценить функциональное состояние предсердно-желудочковой проводящей системы, определить продолжительность рефрактерных периодов проводящей системы сердца [4]. Относительный рефрактерный период оценивается по максимальному интервалу сцепления между двумя последующими импульсами, при котором происходит задержка проведения импульса в АВ-узле. Такое состояние соответствует условиям возникновения АВ-блокады I степени. Эффективный рефрактерный период АВ-узла соответствует максимальному интервалу между двумя последовательными импульсами, при котором второй импульс на желудочки не проводится. Данное состояние соответствует условиям развития АВ-блокады III степени. Одним из способов определения указанных параметров является чреспищеводная электрокардиостимуляция (ЧПЭС) [4]. Однако этот метод имеет определенные недостатки, связанные с физическим дискомфортом и высокой вероятностью провокации приступа аритмии у больного. В ряде случаев, например, при заболеваниях пищевода при АВ-блокадах II и III степени, применение ЧПЭС невозможно.
Прогнозирование ЧСС, приводящей к развитию АВ-блокад, является альтернативным способом оценки функционального состояния предсердно-желудочковой проводящей системы.
Определение ЧСС, ведущей к нарушению проводимости сердца, позволяет установить безопасный для человека диапазон частоты сердцебиений и предупредить развитие тяжелых приступов аритмии. Особенно большое значение имеет определение максимальной частоты сердечных сокращений для расчета оптимального уровня физических нагрузок, что наиболее ценно в спортивной медицине. Оптимальный уровень физических нагрузок определяется индивидуально и зависит от физического состояния человека. Как правило, интенсивность физической нагрузки выражается в процентном отношении от показателя максимальной частоты сердечных сокращений - ЧСС»max. Традиционная формула вычисления максимального сердечного ритма: ЧССmax=220-«Возраст». Как записанная формула, так и многие другие подобные формулы расчета максимальной частоты сердечных сокращений являются формулами определения статистически усредненных значений максимальной ЧСС. Значение максимальной ЧСС индивидуально и зависит как от степени выносливости и тренированности человека, так и от его антропометрических параметров. Возраст, пол выступают как косвенные факторы.
Другим способом определения максимальной ЧСС являются тесты с нагрузкой. Однако существует проблема получения достоверных результатов, заключающаяся в том, что не всегда возможно дать нагрузку, соответствующую максимальной частоте сердцебиений. Кроме того, увеличение ЧСС при нагрузке может привести к развитию приступа аритмии, что является неоправданным риском для здоровья обследуемого. Решением проблемы определения максимальной частоты сердечных сокращений является прогнозирование.
Максимальной частотой сердечных сокращений, при которой сохраняется нормальная работа сердца, следует считать частоту возникновения АВ-блокады I степени, так как АВ-блокада I степени не сказывается на самочувствии человека, может быть подтверждена только на основании анализа электрокардиосигнала (ЭКС) и, в общем случае, является вариантом нормальной работы сердца [1].
Таким образом, в известном способе не осуществляется прогнозирование АВ-блокад I и III степени.
3. Из анализа известного способа следует, что способ не осуществляет дифференцирование АВ-блокад II степени, т.е., не определяется частота сердечных сокращений, при которой начинается выпадение только отдельных импульсов (АВ-блокада II степени типа Венкебах I или Венкебах II) и при которой наблюдается выпадение более половины импульсов («продвинутая» АВ-блокада II степени).
Особенность АВ-блокада II степени с периодикой Венкебаха типа I или II состоит в том, что эти типы блокад различимы только при контроле изменения длительности интервала HS. Подобный контроль возможен при условии, что после выпадения отдельного атриовентрикулярного импульса впоследствии проходит более одного атриовентрикулярного импульса, что позволяет контролировать его длительность. Термин «продвинутая АВ-блокада II степени» применяется в тех случаях, когда блокируется более двух последовательных атриовентрикулярных импульсов. При этом типе блокады установление различия длительностей двух последовательных интервалов HS невозможно [11].
Таким образом, прогнозирование АВ-блокады различной степени имеет важное диагностическое значение в клинической и спортивной медицине, и врачу необходимо предоставить инструмент для прогнозирования АВ-блокад I, II и III степени.
Изобретение направлено на расширение функциональных возможностей кардиологического исследования за счет прогнозирования АВ-блокады I, II и III степени.
Это достигается тем, что осуществляют регистрацию электрокардиограммы в покое и под нагрузкой, регистрацию фронтального и левобокового флюорографических снимков сердца пациента, анализ информационных показателей электрокардиограммы путем определения длительности кардиоцикла (ts), интервала времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH), интервала времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HS), определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, определение параметров модели распространения возбуждения в миокарде, моделирование распространения возбуждения в миокарде, построение кривой восстановления сердца пациента, определение ЧСС, при которой возможна АВ-блокада II степени, визуализацию по результатам моделирования распространения возбуждения в миокарде, дополнительно осуществляют построение кривой восстановления сердца пациента на основе распределения Вейбулла-Гнеденко с контролируемой формой по формуле
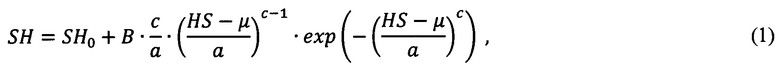
где SH0 - смещение по оси SH, равное ent[min(SH)]; с - параметр формы кривой восстановления сердца пациента, В - масштабирующий коэффициент переменной составляющей по оси SH, рассчитываемый по формуле:
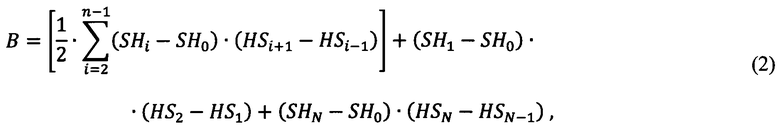
α и µ - масштабирующий коэффициент и смещение по оси HS соответственно, рассчитываемые по формулам:

где SHi, HSi - i-e значения интервалов времени SH и HS в выборке результатов моделирования распространения возбуждения в миокарде; n - количество результатов моделирования; σ(HS) - среднее квадратическое отклонение интервала времени SH в выборке результатов моделирования; HS1 и HS2 - первое и второе значение в сортированной выборке интервалов времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла,
для этого осуществляют анализ энтропии моделирования распространения возбуждения в миокарде путем
- выделения переменных составляющих результатов моделирования распространения возбуждения в миокарде для интервалов времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HSi) по формуле:

а для интервалов времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SHi) по формуле:

где SHmin - минимальный интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса;
- формирования двумерного информационно-измерительного кванта оценки энтропии,

где ΔHS и ΔSH - минимальная дискретность результатов моделирования;
- сопоставления результатов квантования результатам моделирования путем расчета вероятности соответствия информационно-измерительного кванта i-му результату по формуле:

где N - количество информационно-измерительных квантов модели, определяемое по формуле:
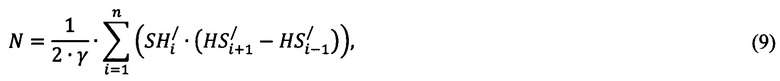
- определения энтропии распределения информационно-измерительных квантов по формуле:
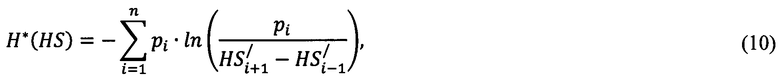
энтропии распределения параметра формы для кривой восстановления сердца пациента по формуле:

где kH(с) - коэффициент энтропии, зависящий от формы распределения,
осуществляют выбор параметра формы кривой восстановления сердца пациента (с) на основе распределения Вейбулла-Гнеденко путем установления соответствия энтропии распределения информационно-измерительных квантов (H*(HS)) и энтропии распределения параметра формы кривой восстановления сердца пациента (H(с)) для результатов моделирования по формуле:

осуществляют анализ рефрактерности миокарда на основе распределения Вейбулла-Гнеденкопо зависимости 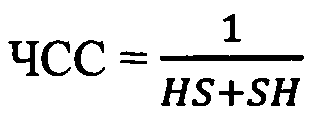 путем
путем
- определения начала развития АВ-блокады III степени в точке максимума зависимости ЧСС:

- определения начала развития «продвинутой» АВ-блокады II степени с выпадением половины импульсов в точке перегиба зависимости ЧСС при выпадении половины импульсов:

- определения начала развития АВ-блокады II степени в точке максимума скорости изменения зависимости ЧСС:

- определения начала АВ-блокады I степени в точке перегиба скорости изменения зависимости ЧСС:

Введенные действия с их связями расширяют функциональные возможности известного способа и проявляют новые свойства, которые позволяют спрогнозировать начало развития АВ-блокады I, II и III степени.
Суть предлагаемого способа заключается в улучшении аппроксимирующих свойств кривой восстановления сердца за счет выбора формы кривой. Это достигается использованием распределения Вейбулла-Гнеденко вместо экспоненциального распределения, которое включает в себя множество форм кривых (в том числе кривую экспоненциального распределения). Улучшение аппроксимирующих свойств достигается за счет корректировки параметров функции кривой восстановления сердца, отвечающих за форму кривой.
Распределение Вейбулла-Гнеденко позволяет корректировать статистическую неопределенность формы кривой восстановления сердца, и, следовательно, более точно по сравнению с экспоненциальным распределением сопоставить статистическую неопределенность формы кривой восстановления сердца и статистическую неопределенность моделируемых данных.
Кроме того, использование распределения Вейбулла-Гнеденко для аппроксимации кривой восстановления сердца позволяет анализировать рефрактерность миокарда и прогнозировать АВ-блокады I, II, III степени путем дифференцирования функции кривой восстановления сердца.
Действительно, в известном способе принятая аппроксимация кривой восстановления миокарда в виде экспоненциальной функции не может содержать решения на все возможные случаи аппроксимации результатов моделирования для прогнозирования АВ-блокады I, II, III степени, так как не позволяет дифференцировать и определять экстремумы кривой восстановления сердца. Поэтому осуществление изобретения в предлагаемом способе прогнозирования АВ-блокады I, II и III степени основано на аппроксимации результатов моделирования распределением Вейбулла-Гнеденко, включающем как экспоненциальную форму, так и другие формы распределений. Использование распределения Вейбулла-Гнеденко для аппроксимации кривой восстановления сердца позволяет дифференцировать и определять экстремумы кривой восстановления сердца.
В основе предлагаемого способа лежит модель восстановления миокарда, которая отражает изменение длительностей интервалов времени SH от момента генерации импульса в синусовом узле до начала ответного импульса в пучке Гиса. Также используемая модель восстановления миокарда отражает изменение интервалов времени HS от начала активности в пучке Гиса до момента возникновения следующего импульса с синусового узла при постепенном увеличении физической нагрузки.
Врачу необходим инструмент для прогнозирования у пациента АВ-блокады I, II и III степени. Таким инструментом является предлагаемый способ прогнозирования АВ-блокад I, II и III степени. Врач, зарегистрировав электрокардиосигнал (ЭКС) до и после нагрузки, на основе предлагаемого способа получает прогноз возникновения АВ-блокад I, II и III степени у данного пациента. Эта информация позволит врачу оценить состояние сердца пациента и организовать его лечение (аналогично знание прогноза погоды помогает человеку или теплее одеться, или взять зонт от дождя). Проверка осуществления изобретения проводилась на основе анализа ЭКС Бодина О.Н. до и после нагрузки. Совершенно очевидно, что подвергать риску состояние здоровья пациента для определения времени начала возникновения АВ-блокад I, II и III степени нельзя. Кроме того, при лечении нарушений ритма с помощью электрокардиостимуляции существуют рекомендации, согласно которым для увеличения ЧСС пациента более 250 ударов в минуту необходимо заключение медицинского консилиума [10]. Поэтому авторами предполагаемого способа для прогнозирования АВ-блокад I, II и III степени предлагается так же, как в известном способе, использовать моделирование процессов возникновения АВ-блокад, не подвергая риску здоровье пациента.
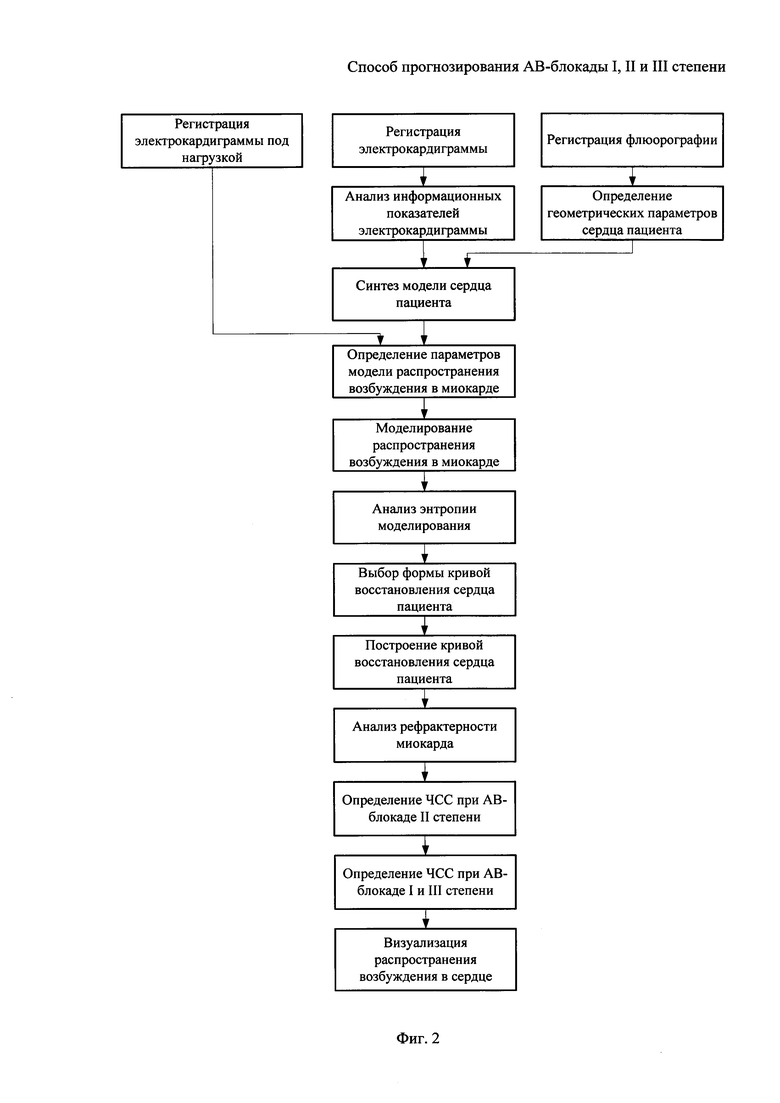
На фигуре 2 приведена схема, реализующая предлагаемый способ прогнозирования АВ-блокады I, II и III степени.
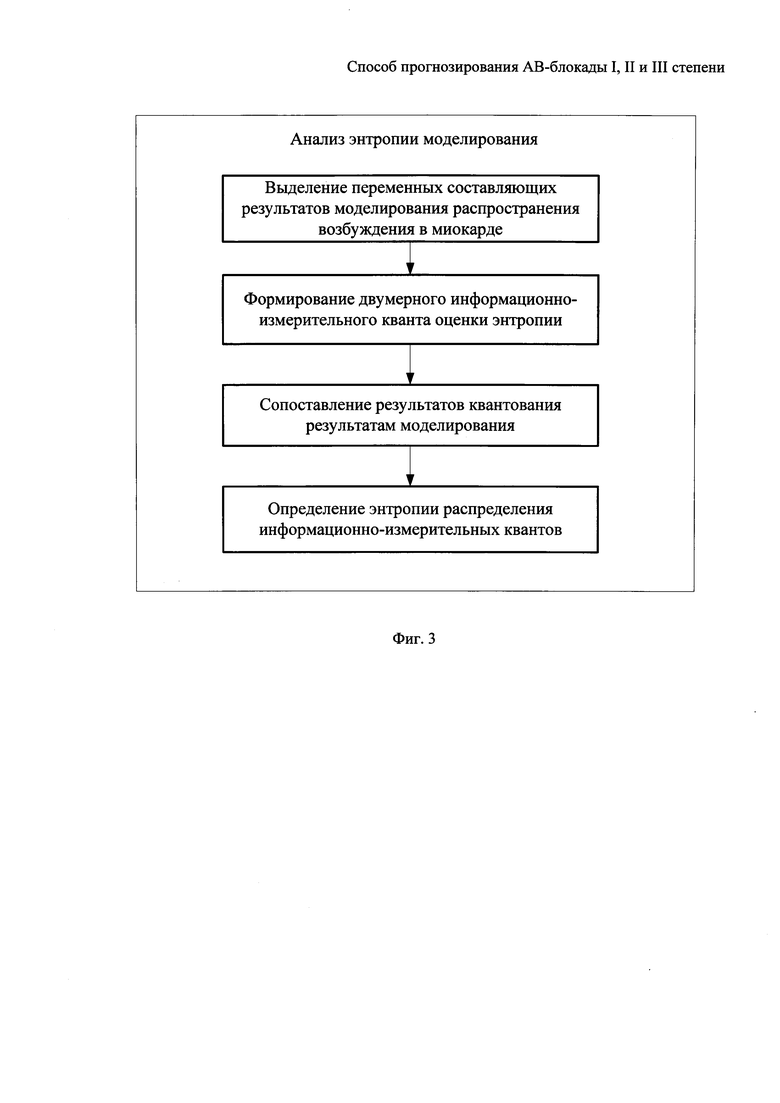
На фигуре 3 приведена схема, реализующая алгоритм анализа энтропии результатов моделирования.
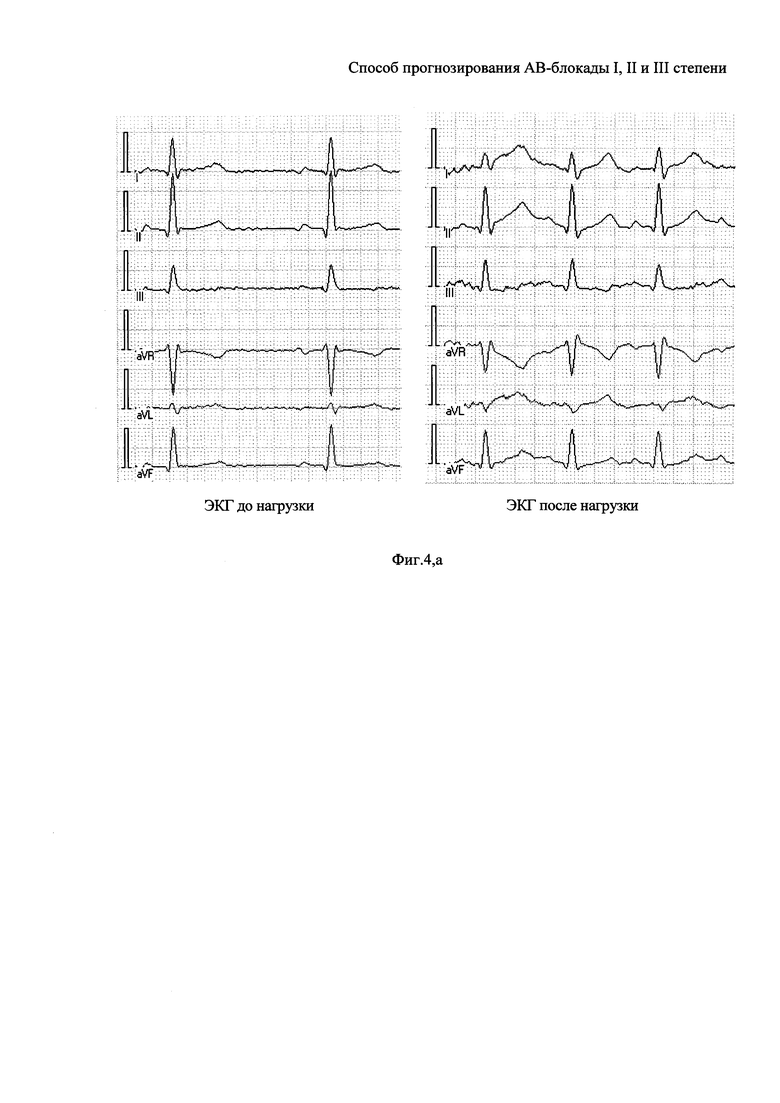
На фигуре 4, а приведена электрокардиограмма Бодина О.Н. до и после нагрузки.
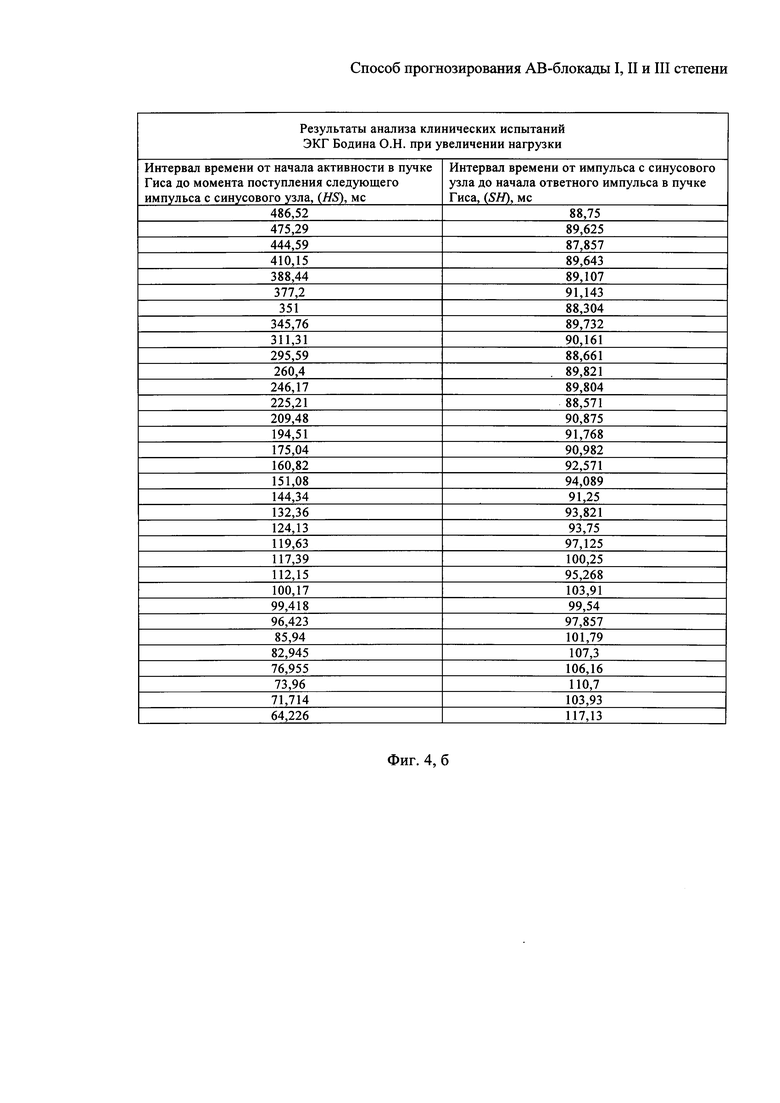
На фигуре 4, б приведена таблица результатов анализа клинических испытаний ЭКГ Бодина О.Н. при увеличении нагрузкив виде временных интервалов SH и HS.
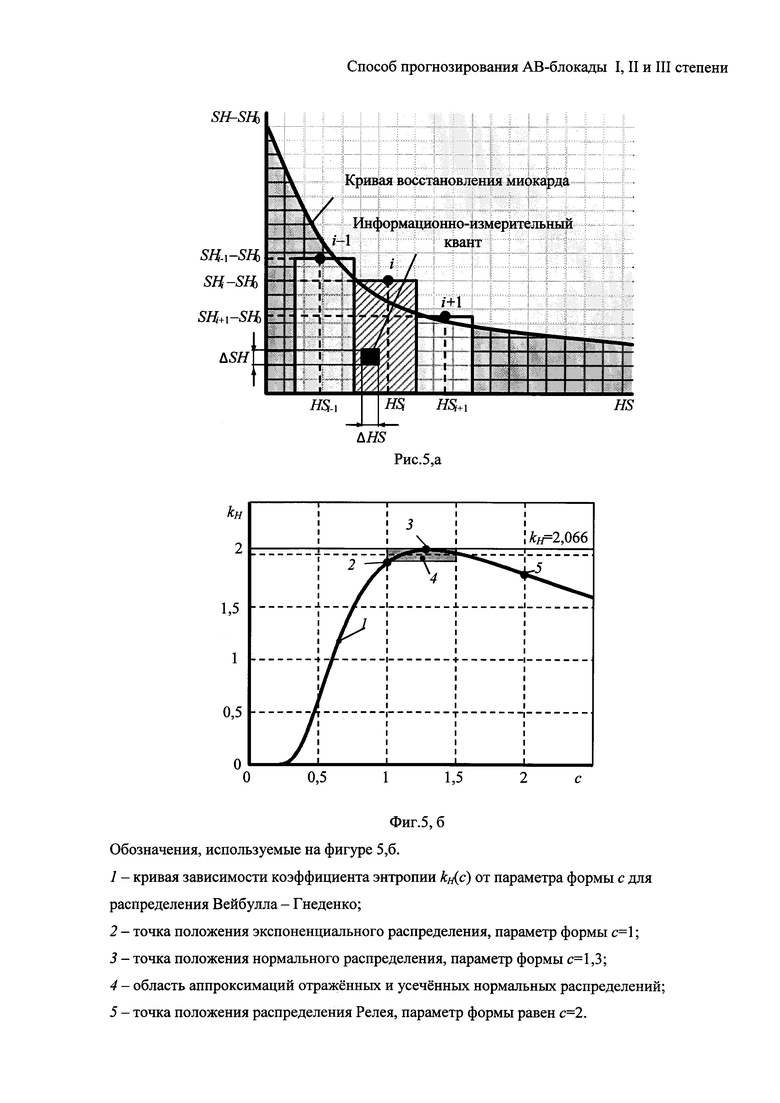
На фигуре 5, а показан пример использования информационно-измерительного кванта при построении кривой восстановления сердца.
На фигуре 5, б показана зависимость коэффициента энтропии от параметра формы (с) для распределения Вейбулла-Гнеденко.
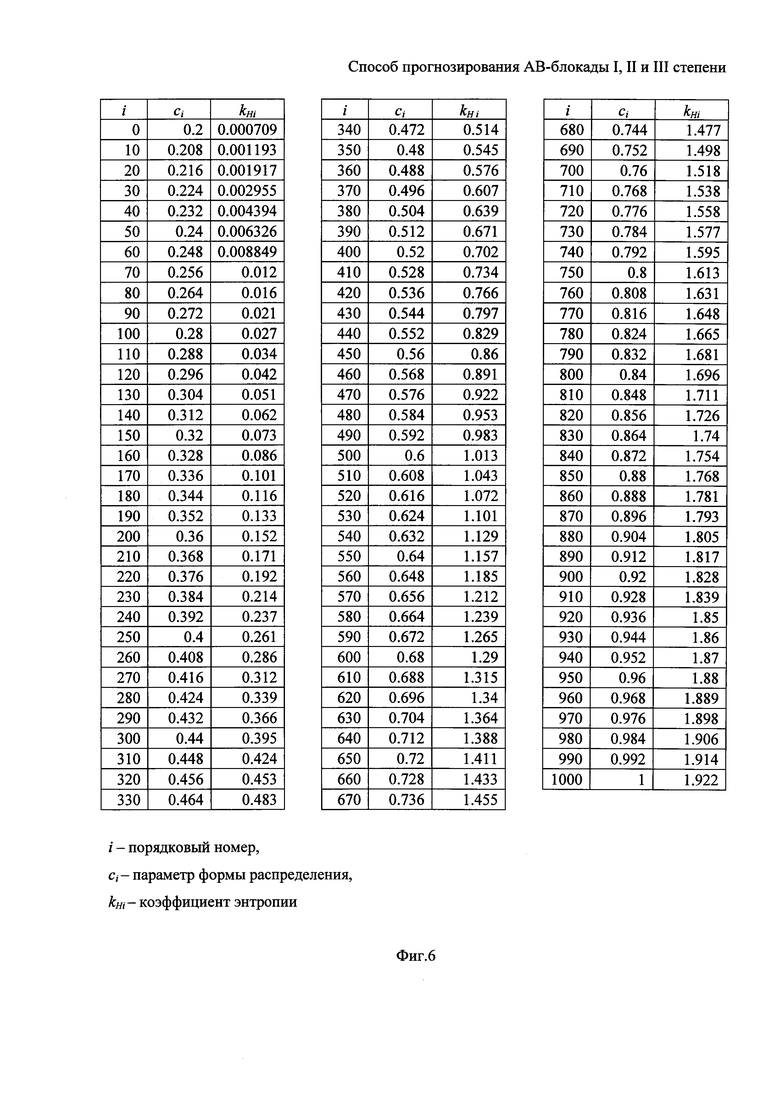
На фигуре 6 приведена таблица, связывающая коэффициент энтропии и параметр формы (с) для распределения Вейбулла-Гнеденко.
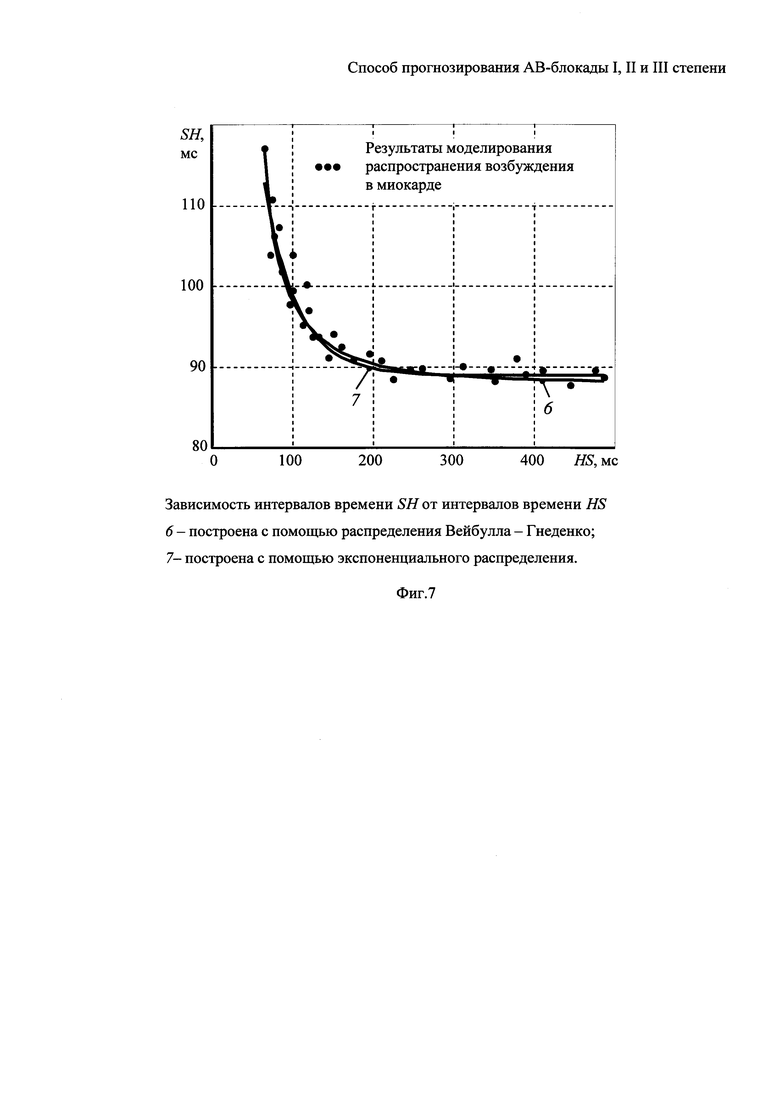
На фигуре 7 приведены кривые восстановления сердца, построенные при помощи распределения Вейбулла-Гнеденко и экспоненциального распределения.
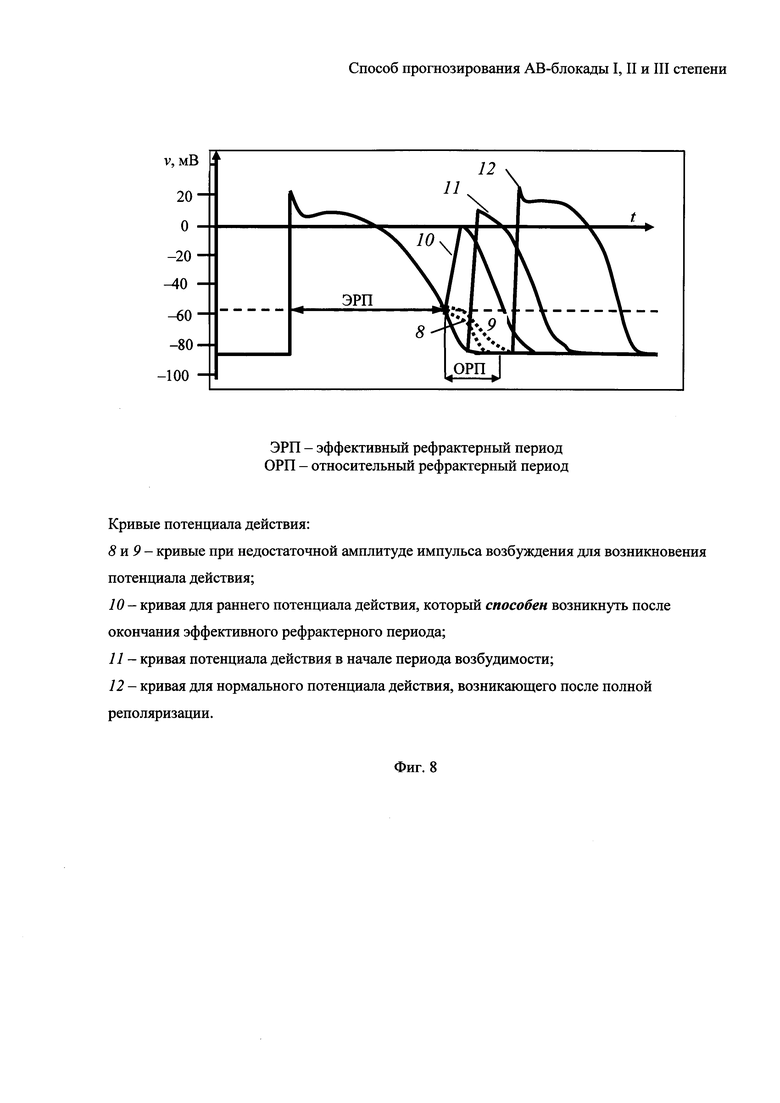
На фигуре 8 представлена зависимость распространения потенциала действия от рефрактерности возбуждаемых клеток [13].
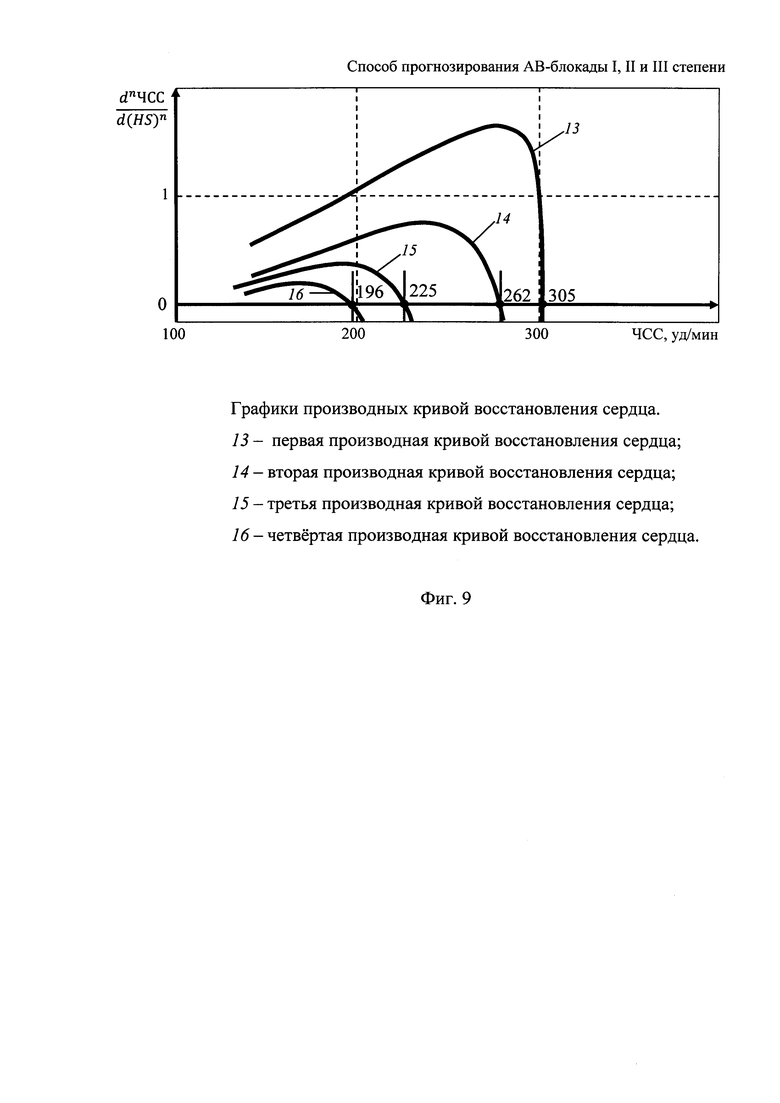
На фигуре 9 приведены графики производных кривой восстановления сердца для прогнозирования возникновения АВ-блокад, полученные по результатам анализа ЭКГ Бодина О.Н. до и после нагрузки.
Подробно рассмотрим введенные действия предлагаемого способа прогнозирования АВ-блокад.
1. Анализ энтропии моделирования распространения возбуждения в миокарде
В результате моделирования получаются значения интервалов времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HS). При этом зависимой переменной является интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH). Каждое из этих значений является независимым событием, которое несет информацию о рефрактерности клеток сердца. Появление пары независимых значений HS-SH есть случайные независимые события, появление которых при моделировании происходит с вероятностью p(HS-SH)=p(HS)·p(SH). Результаты моделирования распространения возбуждения в миокарде следует рассматривать как дискретный источник сообщений, каждое из которых в зависимости от появления несет информацию о состоянии исследуемой модели. Количество информации в сообщении тем больше, чем оно менее вероятно и более неожиданно. В связи с тем, что вероятность меньше единицы, для оценки количества информации в отдельном сообщении используется логарифм вероятности, умноженный на (-1) [8]:

Так как сообщения дискретного источника при моделировании распространения возбуждения в миокарде случайны, то количество информации также является случайной величиной, для которого существует свое распределение вероятностей, зависящее от распределения вероятностей во всем ансамбле сообщений. Для характеристики всего ансамбля сообщений используется математическое ожидание количества информации, которое принято называть энтропией дискретного источника сообщений [8]:
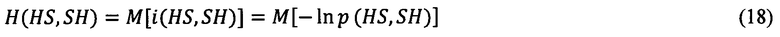
Энтропия - основная информационная характеристика источника сообщений, в качестве которой выступает моделирование распространения возбуждения в миокарде. Энтропия ансамбля сообщений, под которым понимается выборка значений HS-SH, полученная в результате моделирования распространения возбуждения в миокарде, равна среднему количеству полной информации, содержащейся в отдельном сообщении. Эта величина характеризует неупорядоченность процессов в системе, т.е. является своеобразной мерой беспорядка. Энтропия биологической системы связана с продукцией энергии и, как следствие, с продукцией энтропии внутри системы. Наблюдение за этой величиной позволяет контролировать стабильность работы системы или изменение свойств самой системы. Так как энтропия поведения системы отражается в ансамбле результатов моделирования, то необходимо сохранить энтропийные свойства (свойства внутреннего беспорядка системы) при построении регрессионной кривой восстановления миокарда, что позволит более правдоподобно отразить внутренний беспорядок биологической системы, представленной в форме модели распространения возбуждения в миокарде. В этой связи разработан алгоритмдля анализа энтропии результатов моделирования, показанный на фигуре 3. Предложенный алгоритм содержит четыре блока:
1. Выделение переменных составляющих результатов моделирования.
2. Формирование двухмерного информационно-измерительного кванта оценки энтропии.
3. Сопоставление результатов квантования результатам моделирования.
4. Определение энтропии распределения информационно-измерительных квантов.
Рассмотрим подробнее содержание каждого блока в отдельности на примере анализа энтропии результатов клинических исследований ЭКГ Бодина О.Н. до и после нагрузки, примеры которых приведены в форме характерных ЭКГ на фигуре 4, а.
Результаты анализа ЭКГ Бодина О.Н. даны на фигуре 4, б в виде таблицы, содержащей результаты моделирования интервалов времени от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HS) и интервалов времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH).
1.1. Выделение переменных составляющих результатов моделирования
При нормальном функционировании системы существует постоянная составляющая - это минимальный интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH0), который значительно больше, чем переменная составляющая, содержащая информацию об изменении рефрактерности миокарда. Энтропия неизменной части результатов моделирования стремится к нулю, т.е. отражает упорядоченные процессы в системе. Для исследования случайных процессов системы необходимо исключить постоянную составляющую из результатов моделирования. Поэтому первый этап анализа энтропии состоит в выделении переменных составляющих результатов моделирования и осуществляется путем смещения временных интервалов HS и SH. Смещение значений массива интервалов времени осуществляется по формулам (5) и (6).
Таким образом, полученные по формулам (5) и (6) переменные составляющие интервалов времени 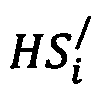 и
и 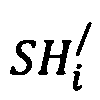 содержат характерные особенности поведения модели восстановления миокарда в области границы рефрактерности.
содержат характерные особенности поведения модели восстановления миокарда в области границы рефрактерности.
1.2. Формирование двухмерного кванта дискретизации измерений характеристик смоделированного процесса
Так как выборка результатов моделирования распространения возбуждения в миокарде представляет собой случайные величины, то задачу поиска кривой восстановления миокарда следует рассматривать как задачу статистического исследования. В качестве характеристики, отражающей статистические свойства модели, применяется мера - информационно-измерительный квант (ИИК) γ [6], построенная на произведении погрешностей двухмерного пространства координат временных интервалов ΔHS, ΔSH. Образование меры ИИК проиллюстрировано на фигуре 5, а в виде элемента площади, рассчитываемой с помощью выражения (7). Оценка меры определена по результатам моделирования как произведение минимальных приращения ΔHSmin и ΔSHmin значений сортированных рядов для интервалов HS и SH соответственно.
ИИК характеризует степень точности и статистические свойства построенной модели и представляет собой область минимальной неопределенности наблюдаемых переменных пространства HS-SH. ИИК задает ограничение возможности исследования в модели распространения возбуждения.
Таким образом, формирование двухмерного ИИК позволяет сохранить свойства неупорядоченности для результатов моделирования распространения возбуждения в миокарде.
1.3. Сопоставление результатов квантования результатам моделирования
Процедура сопоставления результатов квантования результатам моделирования необходима для определения вероятности нахождения ИИК в области пространства i-ого результата моделирования.
Вероятность соответствия ИИК i-ому результату (см. формулу (8)) получена как отношение количества информационно-измерительных квантов Ni, связанных с i-ым результатом к общему количеству N ИИК. Вероятность следует рассматривать, как вероятность обнаружения одного ИИК в совокупности квантов i-го результата моделирования.
Покажем это. Вероятности нахождения ИИК в области пространства i-ого результата моделирования, которому сопоставляется площадь пространства, ограниченного координатами HSi-1 и HSi+1 близлежащих результатов и значением i-ого результата SHi (см. фигуру 5, а), т.е.:

Тогда количество Ni ИИК модели распространения возбуждения в миокарде, связанных с i-ым результатом моделирования определяется как отношение площади пространства, сопоставленного i-му результату моделирования с помощью формулы (19) к мере информационно-измерительного кванта (7). Выражение для определения количества Ni модели распространения возбуждения в миокарде имеет вид:

Полное количество ИИК, характеризующих модель распространения возбуждения, определяется по формуле (9). Число N характеризует качество построения модели распространения возбуждения в миокарде, т.е., чем больше значение N, тем лучше точность и информативность модели распространения возбуждения в миокарде. Вероятность соответствия информационно-измерительного кванта i-ому результату (см. выражение (8)) получена, как отношение количества квантов Ni, связанных с i-ым результатом и найденных из выражения (20), к общему количеству N ИИК модели распространения возбуждения в миокарде. Вероятность pi следует рассматривать, как вероятность обнаружения одного информационно-измерительного кванта в совокупности квантов i-го дискретного сообщения источника, в качестве которого выступает моделирование распространения возбуждения в миокарде.
В соответствии с условиями нормирования вероятности обнаружения ИИК, произведение количества N ИИК на его значение γ равно площади пространства под графиком модели распространения возбуждения в миокарде

Тогда гистограмма вероятностей соответствия квантов результатам моделирования отражает свойства плотности распределения f(HSi) ИИК относительно интервала времени HSi.
Таким образом, сопоставление результатов квантования результатам моделирования позволяет получить распределение вероятности соответствия ИИК результатам моделирования. Вероятностное распределение ИИК в результатах моделирования необходимо для определения энтропии распределения ИИК.
1.4. Определение энтропии распределения информационно-измерительных квантов
Энтропия позволяет получить энтропийный потенциал (ΔHS), выражающий неопределенность исследуемой величины с сохранением ее размерности [9].
Энтропия распределения ИИК предназначена для выбора формы кривой восстановления сердца. Для расчета энтропии распределения ИИК используется формула (10). Эквивалентным в энтропийном смысле значению энтропии распределения ИИК является значение энтропийного потенциала [9]:

Энтропийный потенциал, рассчитанный с помощью выражения (22), имеет размерность временного интервала HS. Взаимосвязь энтропийного потенциала исследуемых временных интервалов HS с их разбросом (отклонением от минимального значения временного интервала HSmin) характеризуется коэффициентом энтропии kH(HS), выражающим информационные свойства распределения вероятностей и равным отношению энтропийного потенциала к стандартному отклонению к его минимальному значению:

где σHS - стандартное отклонение интервалов времени HS относительно его минимального значения HSmin:

Таким образом, определение энтропии распределения ИИК позволяет рассчитать коэффициент энтропии по результатам клинических исследований ЭКГ пациента до и после нагрузки и выбрать форму кривой восстановления сердца.
2. Выбор формы кривой восстановления сердца пациента
Выбор формы кривой восстановления сердца влияет на аппроксимирующие свойства кривой восстановления сердца. Выбор параметра формы (с) кривой восстановления сердца осуществляется путем установления соответствия энтропии распределения информационно-измерительных квантов (H*(HS)) и энтропии распределения параметра формы (с) кривой восстановления сердца пациента (H(с)) результатов моделирования по формуле (12).
Авторами в качестве регрессионной модели кривой восстановления сердца предлагается использовать распределение Вейбулла-Гнеденко. Достоинством распределения Вейбулла-Гнеденко является возможность представления множества несимметричных распределений за счет изменения формы [7]. При этом экспоненциальное распределение является частным случаем распределения Вейбулла-Гнеденко. Покажем это.
График зависимости коэффициента энтропии от параметра формы (с) кривой восстановления сердца для распределения Вейбулла-Гнеденко приведен на фигуре 5, б. Цифрами на графике обозначены:
1 - зависимость коэффициента энтропии kH(с) от параметра формы (с) для распределения Вейбулла-Гнеденко;
2 - точка соответствия экспоненциальному распределению с параметром формы с=1;
3 - точка соответствия нормальному распределению с параметром формы с=1,3;
4 - область аппроксимаций отраженных и усеченных нормальных распределений;
5 - точка соответствия распределению Релея с параметром формы с=2.
Коэффициент энтропии однозначно связан с параметрами формы (с) симметричных и несимметричных распределений. Зависимость коэффициента энтропии от параметра формы (с) для распределения Вейбулла-Гнеденко имеет вид:

Параметры формы (с) и соответствующие им коэффициенты энтропии kVG(c), рассчитанные с помощью выражения (25), представлены в форме таблицы на фигуре 6.
Таким образом, использование распределения Вейбулла-Гнеденко улучшает аппроксимацию для кривой восстановления сердца пациента. Применение кривой с контролируемой формой, построенной на основе распределения Вейбулла-Гнеденко, позволяет сохранить аппроксимирующие свойства кривой с экспоненциальной формой и добавляет принципиальную возможность анализа кривой восстановления сердца пациента за счет учета изменения электрофизиологических процессов внутри клеток сердца. Другими словами, с помощью распределения Вейбулла-Гнеденко в предлагаемом способе в отличие от известного способа появляется возможность количественной оценки ЧСС при прогнозировании возникновения АВ-блокады I, II, III степени.
Проверку адекватности использования распределения Вейбулла-Гнеденко для аппроксимации кривой восстановления сердца пациента проведем по результатам клинических исследований ЭКГ Бодина О.Н. до и после нагрузки (см. фигуру 4, а). Формулы (25) позволяют рассчитать коэффициент энтропии временных интервалов HS в ЭКГ Бодина О.Н. до и после нагрузки. Коэффициент энтропии временных интервалов HS для ЭКГ Бодина О.Н. равен kH=1,626. По коэффициенту энтропии временных интервалов HS из таблицы, приведенной на фигуре 6, выбирается значение параметра формы с=0,807.
Построение кривой восстановления сердца Бодина О.Н. на основе распределения Вейбулла-Гнеденко осуществляется по формуле (1). При подстановке данных в формулу (1) из таблицы, приведенной на фигуре 4, б, получаются следующие параметры распределения Вейбулла-Гнеденко: а=86 мс; µ=56,7 мс, SH0=87 мс, B=2125 мс2, характерные для кривой восстановления сердца Бодина О.Н.
Соответствие уравнения регрессии (1) для кривой восстановления сердца результатам анализа клинических испытаний ЭКГ Бодина О.Н. при увеличении нагрузки оценено с помощью критерия Фишера F

где R - множественный индекс корреляции; m - количество степеней свободы;

Гипотеза Н0 состоит в том, что уравнение регрессии и показатели тесноты связи статистически незначимы. При оценке критерия адекватности модели (1) для интервалов SH получены следующие значения: индекс корреляции R=0,959; индекс детерминации R2=0,919; критерий Фишера F=352,108.
Критическое значение критерия Фишера F при уровне значимости 0,05 составляет 4,28. Из сравнения следует, что полученное фактическое значение критерия много больше его критического значения. В этом случае гипотеза Н0 отвергается и делается вывод о статистической значимости и надежности уравнения (1).
На фигуре 7 даны: распределение (обозначено точками) результатов моделирования распространения возбуждения в миокарде по данным клинических исследований для ЭКГ Бодина О.Н. до и после нагрузки в пространстве интервалов времени HS-SH; зависимости 6 и 7 интервалов времени HS от интервалов времени SH, построенные по данным моделирования с помощью распределения Вейбулла-Гнеденко (зависимость 6) и с помощью экспоненциального распределения (зависимость 7). Ошибки аппроксимации для кривой восстановления сердца, построенной с помощью распределения Вейбулла-Гнеденко, составляет 
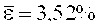
Таким образом, выбор формы кривой восстановления сердца пациента на основе распределения Вейбулла-Гнеденко обеспечивает адекватную аппроксимацию кривой восстановления сердца пациента.
3. Анализ рефрактерности миокарда
Использование кривой восстановления сердца пациента на основе распределения Вейбулла-Гнеденко обеспечивает построение регрессии с контролируемой формой и анализ рефрактерности миокарда. Рефрактерные периоды отражают способность миокарда к проведению двух последовательных импульсов. Время распространения потенциала действия в АВ-узле зависит от интервала между импульсами с синусового узла и от рефрактерности АВ-узла. Чем меньше интервал времени между двумя импульсами, тем больше вероятность замедления и прекращения проведения второго импульса вследствие относительного и абсолютного (эффективного) рефрактерного периода.
Физико-химические процессы, протекающие в миокарде, влияют на скорость восстановительных реакций, что выражается в зависимости продолжительности интервалов распространения импульсов HS и SH, определяющих развитие потенциала действия миокарда в относительный рефрактерный период. На фигуре 8 кривые 8, 9, 10, 11 и 12 показаны процессы развития потенциала действия в различные моменты относительного рефрактерного периода. При уменьшении интервала времени между импульсами к моменту поступления следующего импульса клетки АВ-узла не успевают полностью восстановиться и находятся в состоянии относительной рефрактерности, что влияет на скорость распространения потенциала действия. Кривые 8 и 9 соответствуют кривым с недостаточной амплитудой импульса возбуждения для возникновения потенциала действия.
Возможность развития потенциала действия непосредственно после окончания эффективного рефрактерного периода иллюстрирует кривая 10. Интервал времени между предыдущим импульсом потенциала действия и точкой пересечения кривой 10 с осью времени (см. фигуру 8) соответствует интервалу времени HS распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла, при котором происходит исчезновение каждого второго импульса. При этом потенциал действия распространяется медленно в результате низкой амплитуды и малой скорости деполяризации. Это соответствует началу развития «продвинутой» АВ-блокады II степени. При повышении ЧСС и уменьшении промежутка времени HS уже более половины импульсов попадают в область эффективного рефрактерного периода (см. фигуру 8), т.е. в область, когда развитие потенциала действия невозможно.
Снижение ЧСС и увеличение интервала времени HS обуславливает появление потенциала действия с малой скоростью распространения, которому соответствует кривая 11 на фигуре 8. Скорость распространения потенциала действия отлична от скорости нормального потенциала, возникающего после полной реполяризации. Эти импульсы потенциала действия определяют развитие АВ-блокады II степени типа Венкебах I или Венкебах II.
Окончание относительного рефрактерного периода связано с завершением процессов ионного обмена и восстановлением потенциала покоя миокарда. При увеличении ЧСС для распространения импульсов возбуждения в АВ-узле имеет место нормальный процесс ионного обмена. Момент времени окончания относительного рефрактерного периода соответствует максимальному периоду между импульсами, при наблюдении АВ-блокады I степени. Известно [1], что включение тока кальция (Ca2+) происходит при открытии медленных каналов, включение тока натрия Na+ и калия К+, обусловлено открытием быстрых каналов. Возникновение относительного рефрактерного периода связано с включением кальциевых каналов. Во время эффективного рефрактерного периода происходит включение Na+ и K+ каналов.
Таким образом, анализ рефрактерности миокарда показывает, что во время рефрактерного периода происходит «включение/выключение» кальциевых, натриевых и калиевых каналов, которое влияет на изменения формы кривой восстановления сердца.
Следует отметить, что семейство распределений В. Вейбулла [14] разработано для аппроксимации экспериментальных данных, где присутствуют процессы изменения структурных свойств материи. Анализ рефрактерности показывает, что при развитии АВ-блокад также происходят процессы скачкообразного изменения свойств миокарда, связанного с изменением ионных процессов.
Поэтому распределение Вейбулла-Гнеденко, выбранное в качестве основы построения кривой восстановления сердца, хорошо описывает процессы, связанные с развитием потенциала действия.
4. Определение частот сердечных сокращений при прогнозировании АВ-блокад
Использование распределения Вейбулла-Гнеденко позволяет прогнозировать частоты возникновения АВ-блокад I, II и III степени, что, в свою очередь, дает возможность врачу оценить состояние сердца пациента и организовать лечение с учетом индивидуальных особенностей сердца пациента.
Частота сердечных сокращений обратно пропорциональна периоду между импульсами ts:

Кривая восстановления сердца связывает период импульсов потенциала действия с интервалами времени HS с помощью выражения:

Зависимость ЧСС от длительности импульсов HS имеет характерные точки, т е. точки повышенного интереса, в которых изменяются свойства этой зависимости. Образование характерных точек: точек экстремума, точек перегиба, точек изменения гладкости связано с изменением процессов, происходящих внутри системы. Определение характерных точек зависимости ЧСС от длительности импульсов HS позволяет контролировать начало или окончание непрерывных процессов, происходящих внутри системы. При этом точность определения положения точек гарантируется качеством контроля параметра формы для кривой восстановления сердца, на основе которой строится зависимость ЧСС от интервалов времени HS от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла.
Такой точкой является точка максимума зависимости ЧСС. Значение этой точки равно значению первой производной зависимости ЧСС от длительности импульсов HS. В этой точке наблюдается начало срыва автоколебательных процессов, что можно рассматривать как начало развития АВ-блокады III степени.
Характерная точка перегиба зависимости ЧСС сопоставляется с выпадением половины импульсов и соответствует началу развития «продвинутой» АВ-блокады II степени. Для определения этой точки следует взять вторую производную зависимости ЧСС от длительности импульсов HS, построенную с учетом кривой восстановления миокарда.
Наличие неравновесного воздействия внутренних или внешних сил приводит к изменению кривизны функции. Быстрота изменения кривизны функции позволяет контролировать изменение этих неравновесных процессов, поэтому характерные точки быстроты изменения кривизны так же важны для анализа поведения системы.
Точка начала развития АВ-блокады II степени связана с выпадением отдельных импульсов, что отражает переключение внутренних процессов в системе. Эта точка соответствует третьей производной, взятой от зависимости ЧСС от длительности импульсов HS.
Появление начальных процессов, связанных с изменением скорости проведения импульсов, позволяет определить четвертая производная зависимости ЧСС от длительности интервалов времени HS. Эти процессы слабо выражены в системе, поэтому контроль этих процессов возможен по точке перегиба быстрота изменения кривизны функции ЧСС. Эта точка соответствует началу развития АВ-блокады I степени.
Таким образом, анализ рефрактерности по кривой восстановления сердца, построенной на основе распределения Вейбулла-Гнеденко, позволяет сделать следующие выводы:
1. В предложенном способе осуществляется прогнозирование появления частот возникновения АВ-блокад I, II и III степени. В качестве клинической реализации предложенного способа использовался электрокардиосигнал (ЭКС) Бодина О.Н., зарегистрированный до и после нагрузки. На фигуре 9 показаны графики производных функции кривой восстановления сердца Бодина О.Н., где моменты равенств производных нулю соответствуют ЧСС, при которых возникают блокады. Для исходной зависимости интервалов SH и HS были получены следующие результаты:
- -возникновению АВ-блокады III степени соответствует ЧСС 304 уд./мин.;
- возникновению АВ-блокады II степени с выпадением половины импульсов («продвинутой» АВ-блокады II степени) соответствует ЧСС 260 уд./мин.;
- возникновению АВ-блокады II степени с выпадением отдельных импульсов (АВ-блокады II степени с периодикой Венкебаха типа I или II) соответствует ЧСС 234 уд./мин.;
- возникновению АВ-блокады I степени соответствует ЧСС 200 уд./мин.
2. При использовании предложенного способа прогнозирования АВ-блокад I, II и III степени состояние здоровья пациента не подвергается опасности. При этом осуществляются:
- анализ ЭКС пациента;
- моделирование распространения возбуждения в миокарде;
- статистическая обработка результатов моделирования.
Таким образом, предложенный способ прогнозирования АВ-блокад I, II и III степени устраняет недостатки известного способа и позволяет:
1. Обеспечить построение регрессии с контролируемой формой путем аппроксимации результатов анализа ЭКС распределением Вейбулла-Гнеденко.
2. Прогнозировать возникновение АВ-блокад I и III степени. Так по результатам исследований ЭКС Бодина О.Н. появление АВ-блокады I степени прогнозируется в диапазоне ЧСС от 200 до 234 уд/мин.; АВ-блокада III степени проявляется при ЧСС, превышающих 304 уд/мин.
3. Дифференцировать прогноз возникновения АВ-блокады II степени с указанием диапазона частот появления периодики Венкебаха типа I или II и диапазона частота появления «продвинутой» АВ-блокады II степени. Так по результатам исследований ЭКС Бодина О.Н. появление АВ-блокады II с периодикой Венкебаха типа I или II прогнозируется в диапазоне ЧСС от 234 до 260 уд/мин. При превышении ЧСС более 260 уд/мин прогнозируется появление «продвинутой» АВ-блокады II степени, которая согласно [11] при повышении частоты может перейти в АВ-блокаду III степени.
Полученные результаты согласуются с известными значениями ЧСС [4, 11]. По данным [Ошибка! Неизвестный аргумент ключа.] максимальное значения ЧСС спортсменов часто достигает 200 уд./мин. Во время тренировок пиковые значения достигают 220 уд/мин. Также при проведении экспериментов, связанных с чреспищеводной электрокардиостимуляцией сердца, отмечается возможность возникновения АВ-блокады II степени при ЧСС более 200 уд./мин и при синусовой тахикардии, что не является патологическим проявлением [4].
Таким образом, прогнозируемые показатели ЧСС возникновения АВ-блокад I, II и III степени, полученные с помощью предложенного способа,лежат в диапазоне допустимых значений, известных современному здравоохранению.
При этом следует учитывать, что моделирование распространения возбуждения в миокарде для прогнозирования АВ-блокад I, II и III степени осуществляется по данным, полученным под нагрузкой, не превышающей допустимые значения, и позволяет не доводить значение ЧСС пациента до критического состояния [3].
Технико-экономический эффект, достигаемый при реализации предложенного способа, заключается в прогнозировании АВ-блокад I, II и III степени. Технический результат обеспечивается благодаря использованию распределения Вейбулла-Гнеденко для улучшения аппроксимирующих свойств кривой восстановления сердца.
Список источников информации
1. Орлов В.Н. Руководство по электрокардиографии. - М.: Медицина, 1984, 528 с.
2. Пат. 2358646 Российская Федерация. Способ моделирования и визуализации распространения возбуждения в миокарде / Бодин О.Н., Гладкова Е.А., Кузьмин А.В., Митрохина Н.Ю., Мулюкина Л.А., Строкова И.В. - №2007123430/14, заявл. 22.06.2007; опубл. 20.06.2009, Бюл. №17.
3. Пат. 2410022 Российская Федерация. Способ прогнозирования АВ-блокады II степени / Бодин О.Н., Баусова З.И., Вишнякова А.В., Востриков А.А., Гладкова Е.А., Зайцева О.А., Филькин А.В. - №2009110933/14, заявл. 25.03.2009, опубл. 27.01.2011, Бюл. №3.
4. Рахматуллов Ф.К. Чреспищеводная электрокардиостимуляция сердца и клиническая электрофизиология антиаритмических средств: монография. - Пенза: Изд-во Пенз. гос. ун-та, 2006, 112 с.
5. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. - 2-е изд., испр. - М.: ФИЗМАТЛИТ, 2012, 816 с.
6. Осадчий Е.П., Берестень М.П. Информационно-измерительный квант. // Датчики и системы, №1, 1999.
7. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - 2-е изд., перераб. и доп. - Ленинград: Издательство Энергоатомиздат. Ленингр. отделениение, 1991, 304 с.
8. Вентцель Е.С. Теория вероятности. - М.: Высш. Шк., 1998. - 576 с.
9. Лазарев В.Л. Энтропийный подход организации мониторинга и управления. - Известия РАН. Теория и системы управления. №6, 2005., С. 61-68.
10. Клинические рекомендации по проведению электрофизиологических исследований, катетерной абляциии применению имплантируемых антиаритмических устройств. МОСКВА., 2009.
11. Аритмия сердца. Механизмы, диагностика, лечение. Под редакцией В. Дж. Мандела. Москва, Медицина, 1996. Т. 2, 294 стр.
12. Вадзинский Р.Н. Справочник по вероятностным распределениям - СПб.: Наука, 2001. -295 с.
13. Основы клинической электрофизиологии сердца в норме и при патологии / http://old.smed.ru/guides/13#article
14. Weibull W. Astatistical theory of the strength of materials, Stockh., 1939.
15. Янсен Петер. ЧСС, лактат и тренировки на выносливость - Пер. с англ. - Мурманск: Издательство «Тулома», 2006. - 160 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ II СТЕПЕНИ | 2009 |
|
RU2410022C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2016 |
|
RU2615286C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ И ВИЗУАЛИЗАЦИИ РАСПРОСТРАНЕНИЯ ВОЗБУЖДЕНИЯ В МИОКАРДЕ | 2007 |
|
RU2358646C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2011 |
|
RU2489083C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ И СТЕПЕНИ ВЫРАЖЕННОСТИ КОРОНАРНОЙ НЕДОСТАТОЧНОСТИ | 1999 |
|
RU2157090C1 |
| СПОСОБ ОКАЗАНИЯ ЭКСТРЕННОЙ КАРДИОЛОГИЧЕСКОЙ ПОМОЩИ | 2016 |
|
RU2644303C1 |
| СПОСОБ ЛЕЧЕНИЯ БРАДИАРИТМИИ, ВЫЗВАННОЙ АТРИОВЕНТРИКУЛЯРНЫМИ БЛОКАДАМИ | 2009 |
|
RU2392940C1 |
| ФАРМАЦЕВТИЧЕСКАЯ КОМПОЗИЦИЯ, ПРЕПЯТСТВУЮЩАЯ РАЗВИТИЮ СИНДРОМА ПРЕДВОЗБУЖДЕНИЯ | 2011 |
|
RU2453313C1 |
| Способ выбора гемодинамически оптимальной зоны для имплантации эпикардиальных электродов для электрокардиостимуляции левого желудочка сердца у детей | 2021 |
|
RU2778617C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ЕСТЕСТВЕННОГО ТЕЧЕНИЯ ФЕНОМЕНА КОРОТКОГО ИНТЕРВАЛА PQ | 2014 |
|
RU2560776C1 |
Изобретение относится к медицине, а именно к сердечно-сосудистой диагностике. Определяют параметры модели распространения возбуждения в миокарде. На основании полученной модели осуществляют анализ энтропии моделирования распространения возбуждения в миокарде путем выделения переменных составляющих результатов моделирования распространения возбуждения в миокарде. Формирование двумерного информационно-измерительного кванта оценки энтропии, сопоставления результатов квантования результатам моделирования и определения энтропии распределения информационно-измерительных квантов. Затем осуществляют выбор формы кривой восстановления миокарда путем установления соответствия энтропии распределения информационно-измерительных квантов и энтропии распределения параметра формы кривой восстановления сердца пациента. Далее осуществляют анализ рефрактерности миокарда путем определения начала развития АВ-блокады III степени в точке максимума зависимости ЧСС. Определяют начало развития «продвинутой» АВ-блокады II степени с выпадением половины импульсов в точке перегиба зависимости ЧСС при выпадении половины импульсов. Определение начала АВ-блокады II степени в точке максимума скорости изменения зависимости ЧСС. Определение начала развития АВ-блокады I степени в точке перегиба скорости изменения зависимости ЧСС. Способ позволяет оперативно оценить возможные состояния сердечно-сосудистой системы. 9 ил.
Способ прогнозирования АВ-блокад, заключающийся в том, что осуществляют регистрацию электрокардиограммы в покое и под нагрузкой, регистрацию фронтального и левобокового флюорографических снимков сердца пациента, анализ информационных показателей электрокардиограммы путем определения длительности кардиоцикла (ts), интервала времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SH), интервала времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HS), определение по снимкам геометрических параметров сердца пациента, синтез модели сердца пациента, определение параметров модели распространения возбуждения в миокарде, моделирование распространения возбуждения в миокарде, построение кривой восстановления сердца пациента, определение частоты сердечных сокращений (ЧСС), при которой возможна АВ-блокада II степени, визуализацию по результатам моделирования распространения возбуждения в миокарде, отличающийся тем, что осуществляют построение кривой восстановления сердца пациента на основе распределения Вейбулла-Гнеденко с контролируемой формой по формуле
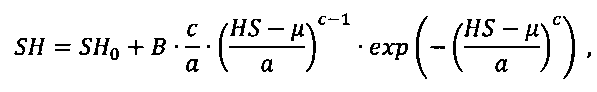
где SH0 - смещение по оси SH, равное ent[min(SH)]; с - параметр формы кривой восстановления сердца пациента, В - масштабирующий коэффициент переменной составляющей по оси SH, рассчитываемый по формуле
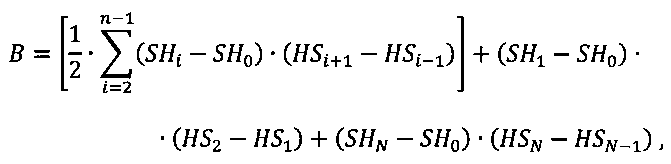
а и µ - масштабирующий коэффициент и смещение по оси HS соответственно, рассчитываемые по формулам
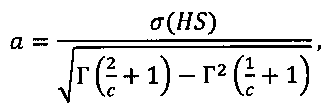
µ=2·HS1-HS2,
где SHi, HSi - i-e значения интервалов времени SH и HS в выборке результатов моделирования распространения возбуждения в миокарде; n - количество результатов моделирования; σ(HS) - среднее квадратическое отклонение интервала времени SH в выборке результатов моделирования; HS1 и HS2 - первое и второе значения в сортированной выборке интервалов времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла,
для этого осуществляют анализ энтропии моделирования распространения возбуждения в миокарде путем:
- выделения переменных составляющих результатов моделирования распространения возбуждения в миокарде для интервалов времени распространения импульсов от начала активности в пучке Гиса до момента поступления следующего импульса с синусового узла (HSi) по формуле: 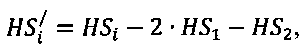 а для интервалов времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SHi) по формуле:
а для интервалов времени от импульса с синусового узла до начала ответного импульса в пучке Гиса (SHi) по формуле: 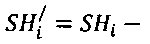
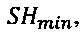 где SHmin - минимальный интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса;
где SHmin - минимальный интервал времени от импульса с синусового узла до начала ответного импульса в пучке Гиса;
- формирования двумерного информационно-измерительного кванта оценки энтропии, γ=ΔHS·ΔSH, где ΔHS и ΔSH - минимальная дискретность результатов моделирования;
- сопоставления результатов квантования результатам моделирования путем расчета вероятности соответствия информационно-измерительного кванта i-му результату по формуле 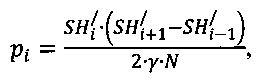 где N - количество информационно-измерительных квантов модели, определяемое по формуле
где N - количество информационно-измерительных квантов модели, определяемое по формуле 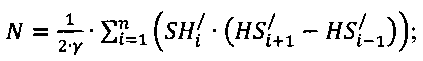
- определения энтропии распределения информационно-измерительных квантов по формуле: 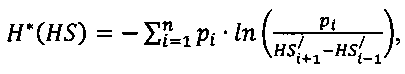 и энтропии распределения параметра формы для кривой восстановления сердца пациента по формуле:
и энтропии распределения параметра формы для кривой восстановления сердца пациента по формуле: 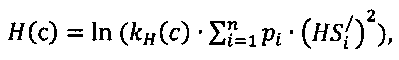 где kH(c) - коэффициент энтропии, зависящий от формы распределения,
где kH(c) - коэффициент энтропии, зависящий от формы распределения,
осуществляют выбор параметра формы кривой восстановления сердца пациента (с) на основе распределения Вейбулла-Гнеденко путем установления соответствия энтропии распределения информационно-измерительных квантов (H*(HS)) и энтропии распределения параметра формы кривой восстановления сердца пациента (H(с)) для результатов моделирования по формуле: H*(HS)=H(с),
осуществляют анализ рефрактерности миокарда на основе распределения Вейбулла-Гнеденко по зависимости 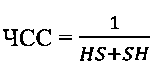 путем:
путем:
- определения начала развития АВ-блокады III степени в точке максимума зависимости ЧСС: 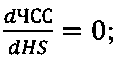
- определения начала развития «продвинутой»АВ-блокады II степени с выпадением половины импульсов в точке перегиба зависимости ЧСС при выпадении половины импульсов: 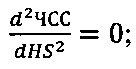
- определения начала развития АВ-блокады II степени в точке максимума скорости изменения зависимости ЧСС: 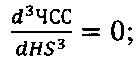
- определения начала развития АВ-блокады I степени в точке перегиба скорости изменения зависимости ЧСС: 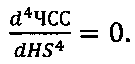
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ II СТЕПЕНИ | 2009 |
|
RU2410022C2 |
| СПОСОБ МОДЕЛИРОВАНИЯ И ВИЗУАЛИЗАЦИИ РАСПРОСТРАНЕНИЯ ВОЗБУЖДЕНИЯ В МИОКАРДЕ | 2007 |
|
RU2358646C2 |
| ТЮРИН Ю.Н | |||
| Анализ данных на компьютере, ИНФРА-М, 2003, 544 с | |||
| Рахматуллов Ф.К | |||
| Чреспищеводная электрокардиостимуляция сердца и клиническая электрофизиология антиаритмических средств: монография | |||
| - Пенза: Изд-во Пенз | |||
| гос | |||
| ун-та, 2006,112 с | |||
| ALIEV R.R | |||
| et al., Asimple model of cardiac excitation | |||
| Chaos, Soliton & Fract, 1996, N3, p.293-301, реферат. | |||
Авторы
Даты
2016-07-20—Публикация
2015-07-10—Подача