Предлагаемое изобретение относится к медицине, в частности к кардиологии, и может быть использовано как электрокардиографический способ диагностики состояния сердца.
Под основными электрофизиологическими характеристиками сердца понимаются значения дипольных моментов, потенциала и ионных токов эпикарда. Определение этих характеристик основано на решении обратной задачи электрокардиографии (ОЗ ЭКГ), а их знание расширяет функциональные возможности стандартного электрокардиографического подхода и повышает эффективность диагностики состояния сердца. Современные методы решения ОЗ ЭКГ позволяют определить дипольные моменты и потенциалы эпикарда [2, 4, 5], восстановить электрическую активность сердца (ЭАС) в опорных точках компьютерной модели сердца и построить «электрический портрет» сердца пациента [1, 3].
Известен способ неинвазивной регистрации электрофизиологических характеристик сердца [4, 13], заключающийся в том, что осуществляют регистрацию множественных электрокардиографических сигналов, измерение потенциалов, генерируемых сердцем, адаптивную пространственную интерполяцию потенциалов сердца путем разложения по пространственным сферическим функциям, расчет эпикардиального распределения потенциала, определение моментных распределений электрофизиологических характеристик на поверхности сердца, расчет электрофизиологических характеристик сердца и отображение электрофизиологических характеристик сердца.
Известен также способ неинвазивного электрофизиологического изучения сердца [1, 2, 3], заключающийся в том, что осуществляют регистрацию и обработку электрокардиосигналов (ЭКС), интерполяцию ЭКС на поверхности тела, восстановление потенциала эпикарда.
Известные способ неинвазивной регистрации электрофизиологических характеристик сердца и способ неинвазивного электрофизиологического изучения сердца основаны на регистрации множественных отведений или методе ЭКГ-картирования сердца [7], который является одним из наиболее информативных методов исследования ЭАС. ЭКГ-картирование сердца позволяет получить максимальную информацию об особенностях электрического поля сердца в любой момент деполяризации и реполяризации желудочков сердца, однако требует участия при диагностике высококвалифицированного специалиста, использования дорогостоящей аппаратуры и значительных затрат времени на проведение одного исследования. По мнению авторов предлагаемого изобретения, недостатками известных способа неинвазивной регистрации электрофизиологических характеристик сердца и способа неинвазивного электрофизиологического изучения сердца являются:
- невозможность использования в массовых профилактических обследованиях (скрининге) сердца из-за регистрации множественных электрокардиографических сигналов;
- невозможность определения составляющих ионных токов эпикарда.
Наиболее близким по достигаемому результату к предлагаемому изобретению является способ неинвазивного определения электрофизиологических характеристик сердца [5], заключающийся в том, что регистрируют электрокардиосигнал (ЭКС) и измеряют потенциалы, генерируемые сердцем, регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента, определяют по снимкам геометрические параметры сердца пациента, синтезируют компьютерную модель сердца пациента, определяют потенциалы, генерируемые сердцем на торсе пациента, определяют дипольные моменты и потенциалы эпикарда ϕ в опорных точках компьютерной модели сердца пациента, моделируют распространение волны возбуждения в эпикарде, синтезируют модельный ЭКС, сравнивают модельный ЭКС с зарегистрированным ЭКС, корректируют расчетные параметры модели распространения волны возбуждения в эпикарде путем изменения параметров при определении моментных распределений основных электрофизиологических характеристик на поверхности сердца и визуализируют электрофизиологические характеристики сердца на трехмерной модели сердца средствами компьютерной графики в наиболее удобном для восприятия виде.
На фигуре 1 приведена схема алгоритма, реализующего известный способ неинвазивного определения электрофизиологических характеристик сердца.
На фигуре 2 приведена иллюстрация функциональных возможностей известного способа неинвазивного определения электрофизиологических характеристик сердца.
Из анализа описания известного способа неинвазивного определения электрофизиологических характеристик сердца следует, что его функциональные возможности заключаются только в определении дипольных моментов и потенциалов эпикарда в опорных точках компьютерной модели сердца пациента и невозможности определения составляющих ионных токов эпикарда в опорных точках компьютерной модели сердца пациента.
Рассмотрим определение электрофизиологических характеристик сердца в известном способе неинвазивного определения электрофизиологических характеристик сердца. Физическая сущность известного способа неинвазивного определения электрофизиологических характеристик сердца заключается во взаимосвязи дипольных моментов и потенциалов эпикарда. Покажем это.
На фигуре 2,а приведена иллюстрация, на которой изображена структура биологического генератора в виде двойного слоя источников тока i-ой площадки поверхности эпикарда в опорной точке компьютерной модели сердца. Фигура 2,а иллюстрирует определение потенциала ϕ в точке M, где 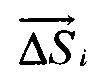 - вектор i-ой площадки поверхности эпикарда в опорной точке компьютерной модели сердца,
- вектор i-ой площадки поверхности эпикарда в опорной точке компьютерной модели сердца,  - расстояние между поверхностями двойного слоя биологического генератора.
- расстояние между поверхностями двойного слоя биологического генератора.
В известном способе для определения электрофизиологических характеристик сердца применяют систему дифференциальных уравнений Максвелла [12]. Задача электрокардиографии состоит в определении электрофизиологических характеристик сердца на основе решения системы дифференциальных уравнений Максвелла для среды, в которой условно заданы геометрические соотношения между областью генераторов тока в форме сердца и точками поверхности, где проводится измерение потенциала. Формула для расчета потенциала в такой проводящей структуре имеет вид [27]:

где r - расстояние от точки наблюдения до точек области генераторов тока, ограниченной объемом V; 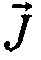 - объемная плотность дипольного момента, т.е. вектор плотности тока, созданный полем сторонних сил в неоднородном участке проводника.
- объемная плотность дипольного момента, т.е. вектор плотности тока, созданный полем сторонних сил в неоднородном участке проводника.
Объемная плотность дипольного момента равна произведению проводимости среды а на векторы напряженности поля сторонних сил 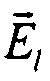 ,
,

Так как объемная плотность дипольного момента используется для количественной характеристики непрерывно распределенных дипольных источников тока в объеме пространства, где есть биологические генераторы, то произведение этой величины на площадь поверхности эпикарда, связанной с опорной точкой компьютерной модели сердца пациента, равна значению ионного тока, проходящему через эту площадь поверхности эпикарда:
 Дивергенция вектора, равного произведению скалярной функции радиуса на объемную плотность дипольного момента, равна сумме скалярного произведения вектора
Дивергенция вектора, равного произведению скалярной функции радиуса на объемную плотность дипольного момента, равна сумме скалярного произведения вектора 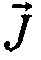 на градиент функции радиуса и произведения функции радиуса на дивергенцию вектора
на градиент функции радиуса и произведения функции радиуса на дивергенцию вектора 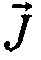

Интегрируя левую и правую часть выражения (4) по объему биологического генератора и применяя теорему Остроградского-Гаусса к его левой части, получим интегральное выражение вида:
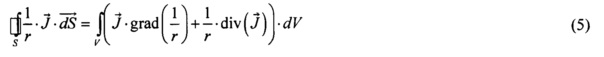
Так как на поверхности S, непосредственно соприкасающейся с эпикардом, генераторы тока отсутствуют, то вектор объемной плотности дипольного момента биологического генератора на этой поверхности будет равен нулю (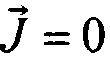 ), и, как следствие,
), и, как следствие,
интеграл по поверхности в левой части выражения (5) так же равен нулю. Тогда выделив из правой части выражения (5) интегральный сомножитель выражения (1), получим для расчета потенциала электрического поля ϕ в точке М выражение вида:

Очевидно, что для определения потенциала ϕ непосредственно на поверхности эпикарда имеют значения биологические генераторы только этой опорной точки компьютерной модели сердца пациента. В пределах отдельной площадки Si поле вектора объемной плотности дипольного момента 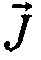 принимается однородным. В этом случае в выражении (6) модуль вектора
принимается однородным. В этом случае в выражении (6) модуль вектора 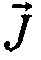 можно вынести за знак интеграла. Для плоской площадки Si эпикарда, связанной с опорной точкой, справедливо представление биологического генератора в виде двойного слоя [12, 13]. На фигуре 2,а приведена схема двойного слоя источников для определения потенциала ϕ в точке М, где
можно вынести за знак интеграла. Для плоской площадки Si эпикарда, связанной с опорной точкой, справедливо представление биологического генератора в виде двойного слоя [12, 13]. На фигуре 2,а приведена схема двойного слоя источников для определения потенциала ϕ в точке М, где 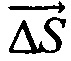 - вектор площадки поверхности эпикарда в опорной точке,
- вектор площадки поверхности эпикарда в опорной точке,  - расстояние между поверхностями двойного слоя источников. Тогда для потенциала ϕ в точке М выражение (6) примет вид:
- расстояние между поверхностями двойного слоя источников. Тогда для потенциала ϕ в точке М выражение (6) примет вид:

Интеграл по поверхности в выражении (7) равен телесному углу Ω, под которым видна площадка из точки М. Для точки, расположенной на внешней поверхности эпикарда, телесный угол, под которым видна поверхность опорной точки, равен 2π (или половине телесного угла замкнутого пространства, равного 4π). При условии 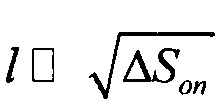 , телесный угол Ω, остается постоянным. Тогда для потенциала точки, расположенной на внешней поверхности эпикарда, справедливо выражение вида:
, телесный угол Ω, остается постоянным. Тогда для потенциала точки, расположенной на внешней поверхности эпикарда, справедливо выражение вида:

где D - значение дипольного момента площадки ΔS, связанное с опорной площадкой ΔS: D=DS⋅ΔS; DS - поверхностная плотность дипольного момента опорной точки, равная произведению объемной плотности дипольного момента 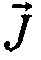 на толщину двойного слоя:
на толщину двойного слоя: 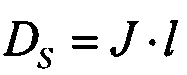 .
.
Ионный ток Iion, проходящий через площадку ΔS эпикарда в опорной точке компьютерной модели сердца равен произведению объемной плотности дипольного момента J на площадь площадки ΔS эпикарда:

Выражение (9) устанавливает зависимость между током, дипольным моментом и потенциалом эпикарда для опорной точки компьютерной модели сердца. Из выражения (9) следует, что потенциал эпикарда, дипольный момент и ионный ток для отдельной опорной точки компьютерной модели сердца имеют одинаковую форму функциональной зависимости. Очевидно, что при известной функции потенциала эпикарда известна форма функция тока через поверхность эпикарда.
Таким образом, в известном способе неинвазивного определения электрофизиологических характеристик сердца возможна оценка суммарного тока через площадку опорной точки на основе построения взаимосвязи электрофизиологических характеристик. При этом в известном способе неинвазивного определения электрофизиологических характеристик сердца не определяются составляющие ионных токов эпикарда.
Далее, в известном способе неинвазивного определения электрофизиологических характеристик сердца проверка их определения строится на основе концептуальной модели электрической активности сердца (ЭАС), предложенной Р.Р. Алиевым [16]. Отличительной особенностью концептуальной модели ЭАС является простота формального математического описания концепции явления, что делает возможным выделить качественные свойства объекта, не раскрывая его внутренней структуры. Применение концептуальных моделей направлено на описание изменения отдельного свойства объекта без описания его внутренней структуры. Такой подход не позволяет раскрыть причины изменения электрофизиологических характеристик. Главный недостаток применения концептуальной модели в известном способе определения электрофизиологических характеристик сердца состоит в отсутствии описания ионных токов, что не позволяет определить составляющие ионных токов эпикарда. Этот недостаток заложен в основе построения концептуальной модели, направленной на описание характера изменения отдельных электрофизиологических характеристик эпикарда, таких как дипольные моменты и потенциалы эпикарда, без описания причины изменения этих характеристик.
В известном способе определения электрофизиологических характеристик сердца [5] концептуальная модель Алиева-Панфилова (АП) применена для восстановления распространения трансмембранного потенциала действия (ТМПД) по поверхности эпикарда и синтеза модельного ЭКС. Используемые в модели АП значения электрофизиологических характеристик сердца (потенциалы эпикарда и дипольные моменты на поверхности эпикарда) получены при решении ОЗ ЭКГ. Двухкомпонентная концептуальная модель АП представляет собой систему двух дифференциальных уравнений параболического типа:
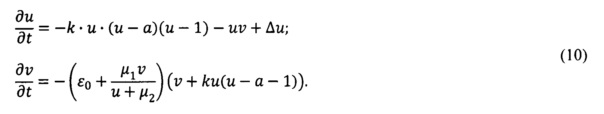
где u, v - медленная и быстрая переменные модели АП соответственно;
ε0, k, а, μ1, μ2 - параметры модели АП.
Несмотря на то, что модель АП (10) удобна для описания распространения возбуждения по поверхности миокарда, эта модель не отражает фазовых свойств развития ТМПД. На фигуре 2,6 дан пример восстановления ТМПД с помощью модели АП. Одна из характерных особенностей модели АП состоит в том, что скорость спада переднего и заднего фронтов ТМПД задаются одной и той же быстрой переменной (v), что определяет их взаимосвязанное изменение. Однако процессы развития переднего и заднего фронтов реального ТМПД отличаются и связаны с изменениями в различных структурных элементах мембраны [8, 11]. Передний фронт ТМПД определяется свойствами каналов для ионов натрия, открытие и закрытие которых происходит в течение 3-х миллисекунд. Задний фронт ТМПД характеризуется изменением проводимости мембраны для ионов калия. Скорость его изменения обусловлена работой различных по своей природе структурных элементов мембраны, регулируемых внутренними процессами в кардиомиоците. Характерная длительность заднего фронта ТМПД составляет 30…50 миллисекунд, в то время как развитие переднего фронта происходит в течение 3 миллисекунд. Очевидно, что концептуальные модели, содержащие две переменных, не пригодны для описания ионных токов для различных фаз развития ТМПД.
В известном способе определения электрофизиологических характеристик сердца [5] на основе решения ОЗ ЭКГ не содержится информация о распределении ионных токов эпикарда. Решение ОЗ ЭКГ для дипольных моментов и потенциалов эпикарда в опорных точках компьютерной модели сердца так же не содержит разделения фаз развития ТМПД и, тем более, распределения токов в различные фазы развития ТМПД.
Таким образом, несмотря на наличие информации об ионных токах, в известном способе неинвазивного определения электрофизиологических характеристик сердца отсутствует модель для описания ионных токов эпикарда, что приводит к потере важной диагностической информации.
По мнению авторов предлагаемого изобретения, определение составляющих ионных токов эпикарда является насущной потребностью кардиологии и необходимо для повышения достоверности диагностики заболевания сердца и для эффективного применения антиаритмических препаратов.
Недостатком известного способа неинвазивного определения электрофизиологических характеристик сердца является невозможность определения составляющих ионных токов эпикарда в опорных точках компьютерной модели сердца пациента.
Целью предлагаемого изобретения является расширение функциональных возможностей оценки состояния сердца посредством анализа ионных токов через поверхность эпикарда и выделения составляющей ионного тока калия временного интервала монотонной реполяризации.
Для этого в способ неинвазивного определения электрофизиологических характеристик сердца, заключающийся в том, что регистрируют электрокардиосигнал (ЭКС) и измеряют потенциалы, генерируемые сердцем, регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента, определяют по снимкам геометрические параметры сердца пациента, синтезируют компьютерную модель сердца пациента, определяют потенциалы, генерируемые сердцем на торсе пациента, определяют дипольные моменты и потенциалы эпикарда ϕ в опорных точках компьютерной модели сердца пациента, моделируют распространение волны возбуждения в эпикарде, синтезируют модельный ЭКС, сравнивают модельный ЭКС с зарегистрированным ЭКС, корректируют расчетные параметры модели распространения волны возбуждения в эпикарде путем изменения параметров при определении моментных распределений основных электрофизиологических характеристик на поверхности сердца и визуализируют электрофизиологические характеристики сердца на трехмерной модели сердца средствами компьютерной графики в наиболее удобном для восприятия виде, отличающийся тем, что дополнительно
- формируют данные для стохастической модели тока реполяризации эпикарда в опорных точках компьютерной модели сердца путем:
определения информационно-измерительного кванта (ИИК) у для выборок значений потенциала эпикарда в опорных точках компьютерной модели сердца для одного кардиоцикла: γ=Δϕ⋅Δt, где Δt - время, необходимое для получения одного отсчета; 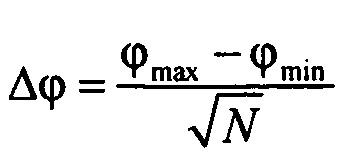 мера ИИК, ϕmax, ϕmin и N - максимальное, минимальное значение и число отсчетов в выборке значений потенциала эпикарда в опорных точках компьютерной модели сердца;
мера ИИК, ϕmax, ϕmin и N - максимальное, минимальное значение и число отсчетов в выборке значений потенциала эпикарда в опорных точках компьютерной модели сердца;
определения количества ИИК Nγ для стохастической модели тока реполяризации эпикарда 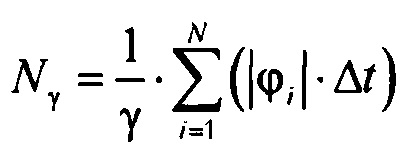 , где ϕi - i-е значение потенциала в выборке {ф} одного кардиоцикла;
, где ϕi - i-е значение потенциала в выборке {ф} одного кардиоцикла;
определения количества m ранжированных значений tp j, минимальных tmin j и максимальных tmax j границ для временных интервалов группирования ИИК
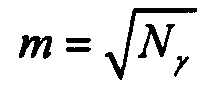 ;
;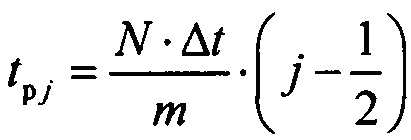 ;
;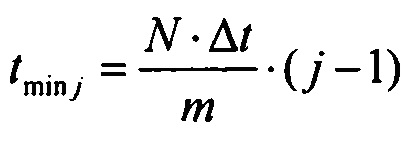 ;
; 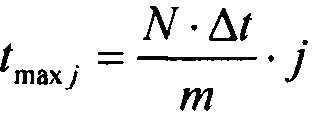
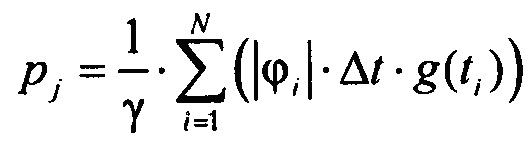 , где g(ti)=1 если tmin j<tj≤tmax j, иначе g(ti)=0,
, где g(ti)=1 если tmin j<tj≤tmax j, иначе g(ti)=0,
где j - порядковый номер временного интервала группирования ИИК;
определения распределения вероятностей ИИК 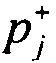 и
и 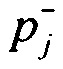 в j-м интервале группирования ИИК для положительных и отрицательных значений потенциала эпикарда в опорных точках компьютерной модели сердца пациента:
в j-м интервале группирования ИИК для положительных и отрицательных значений потенциала эпикарда в опорных точках компьютерной модели сердца пациента:
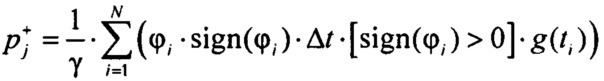 ,
,
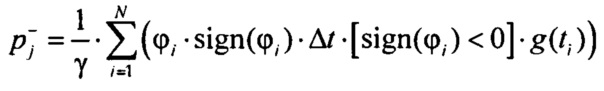 ;
;
определения разности распределений вероятностей ИИК pj в j-м интервале группирования для значений потенциала в опорных точках эпикарда компьютерной модели сердца пациента: 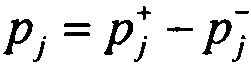 ;
;
формирования выборок отсчетов времени для положительных и отрицательных разностей распределений вероятностей ИИК t+={tj|tj∈(pj>0)}, t-={tj|tj∈(pj<0)};
выделения временного интервала фазы начальной быстрой реполяризации эпикарда в опорных точках компьютерной модели сердца пациента tнбр=min{tj|tj∈(pj<0)};
выделения временного интервала монотонной реполяризации эпикарда, включающего монотонную реполяризацию фазы плато и фазу конечной быстрой реполяризации эпикарда в опорных точках компьютерной модели сердца пациента:
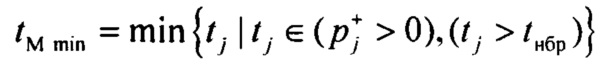 ,
, 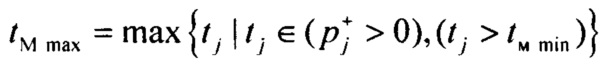 ;
;
нормирования распределения вероятности ИИК для выборок значений потенциала временного интервала монотонной реполяризации эпикарда в опорных точках компьютерной модели сердца пациента 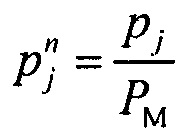 , где PM - вероятность обнаружения ИИК во временном интервале монотонной реполяризации эпикарда
, где PM - вероятность обнаружения ИИК во временном интервале монотонной реполяризации эпикарда 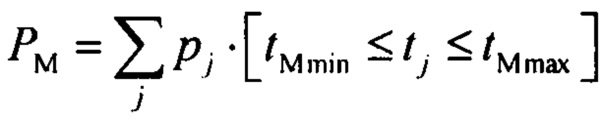 ;
;
- определяют токи калия аномального выпрямления в опорных точках компьютерной модели сердца путем:
формирования стохастической модели токов калия задержанного и аномального выпрямления 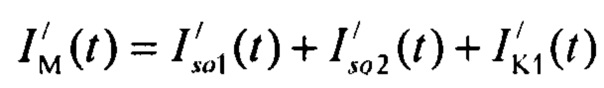 ), где
), где 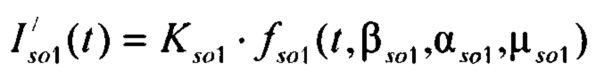 стохастическая модель Iso тока калия быстрого задержанного выпрямления;
стохастическая модель Iso тока калия быстрого задержанного выпрямления; 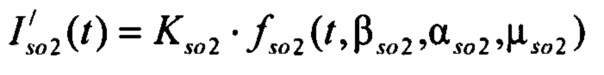 - стохастическая модель Iso тока калия медленного задержанного выпрямления;
- стохастическая модель Iso тока калия медленного задержанного выпрямления; 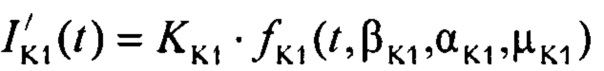 - стохастическая модель тока калия аномального выпрямления;
- стохастическая модель тока калия аномального выпрямления; 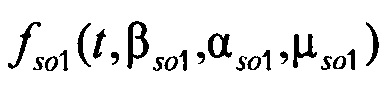 ,
, 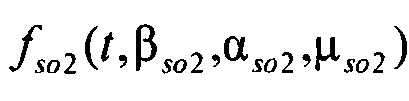 ,
, 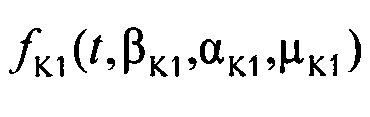 - плотности распределений ИИК для тока калия быстрого и медленного задержанного выпрямления и для тока калия аномального выпрямления соответственно; Kso1, Kso2 и KK1 - весовые коэффициенты стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления соответственно; βso1, αso1, μso1, βso2, αso2, μso2, βK1, αK1, μK1 - параметры распределений;
- плотности распределений ИИК для тока калия быстрого и медленного задержанного выпрямления и для тока калия аномального выпрямления соответственно; Kso1, Kso2 и KK1 - весовые коэффициенты стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления соответственно; βso1, αso1, μso1, βso2, αso2, μso2, βK1, αK1, μK1 - параметры распределений;
задания весовых коэффициентов стохастической модели токов калия быстрого Kso1=0,5⋅(1-KK1) и медленного Kso2=0,5⋅(1-KK1) задержанного и аномального 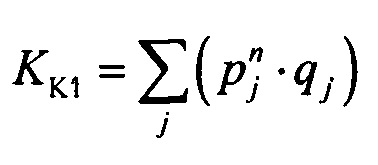 , выпрямления, где qj=1, если
, выпрямления, где qj=1, если 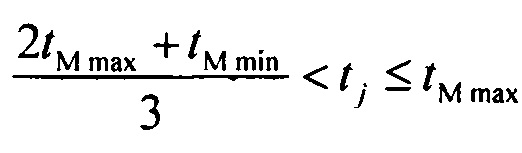 , иначе qj=0;
, иначе qj=0;
определения параметров βso1, αso1, μso1, βso2, αso2, μso2, βK1, αK1, μK1 стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления путем минимизации решения уравнения
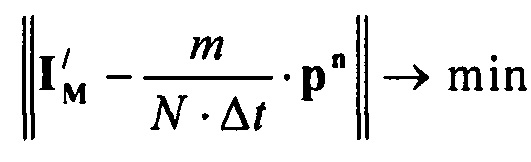
где 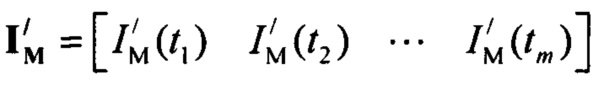 - матрица стохастической модели токов калия быстрого
- матрица стохастической модели токов калия быстрого
и медленного задержанного и аномального выпрямления; 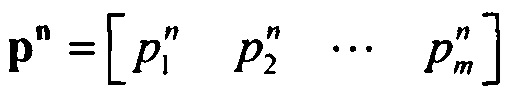 - матрица нормированных вероятностей ИИК;
- матрица нормированных вероятностей ИИК;
определения распределения вероятностей ИИК токов калия быстрого задержанного 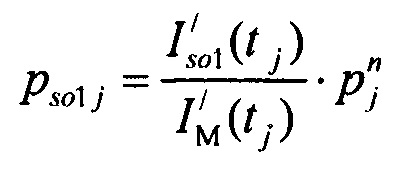 и медленного задержанного
и медленного задержанного 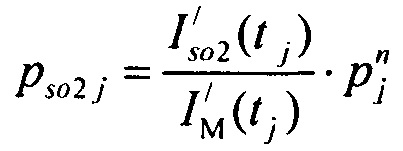 и аномального выпрямления
и аномального выпрямления 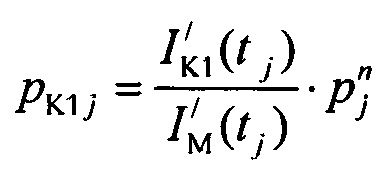 на j-м интервале группирования ИИК;
на j-м интервале группирования ИИК;
определения критерия адекватности 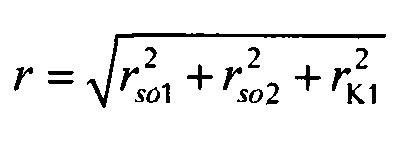 модели токов калия быстрого и медленного задержанного и аномального выпрямления в опорной точке компьютерной модели сердца пациента, где составляющие критерия вычисляют по формулам:
модели токов калия быстрого и медленного задержанного и аномального выпрямления в опорной точке компьютерной модели сердца пациента, где составляющие критерия вычисляют по формулам:
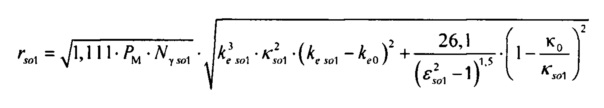 ,
,
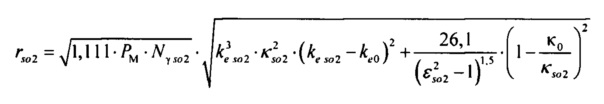 ,
,
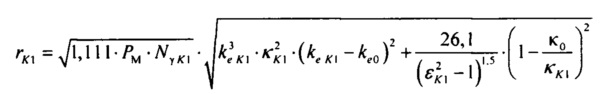 ,
,
где ke so1, κso1, ke so2, κso2, ke K1, κK1, _ коэффициенты энтропии и контрэксцесса симметричных распределений для тока калия быстрого и медленного задержанного и аномального выпрямления;
сравнения критерия r2≤3⋅ln(α-2), где α - уровень значимости принятия решения;
коррекции весовых коэффициентов стохастической модели токов калия быстрого Kso1 и медленного Kso2 задержанного и аномального KK1 выпрямления в опорных точках компьютерной модели сердца пациента;
принятия решения: «Параметры стохастической модели тока калия 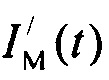 задержанного и аномального выпрямления определены корректно»;
задержанного и аномального выпрямления определены корректно»;
определения значений 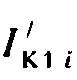 тока калия аномального выпрямления по формуле:
тока калия аномального выпрямления по формуле:
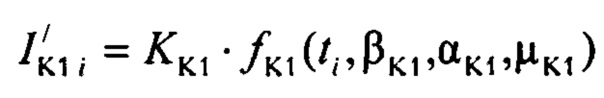
- определяют ток реполяризации эпикарда 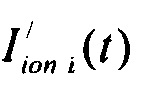 опорных точках компьютерной модели сердца пациента путем:
опорных точках компьютерной модели сердца пациента путем:
формирования стохастической модели тока 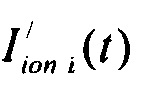 реполяризации эпикарда
реполяризации эпикарда 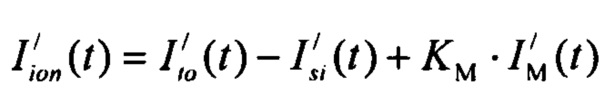 , где
, где 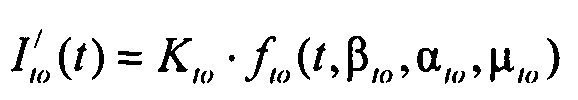 - стохастическая модель переходного транзитного тока эпикарда;
- стохастическая модель переходного транзитного тока эпикарда; 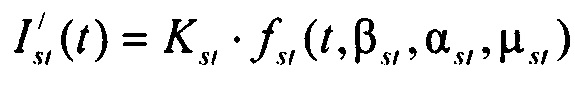 - стохастическая модель медленного деполяризующего тока кальция; Kto, Kst и KM - весовые коэффициенты стохастической модели тока реполяризации эпикарда;
- стохастическая модель медленного деполяризующего тока кальция; Kto, Kst и KM - весовые коэффициенты стохастической модели тока реполяризации эпикарда; 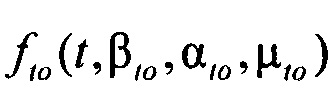 и
и 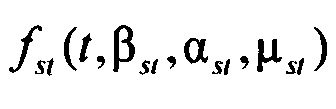 - плотности распределений ИИК для переходного транзитного тока и медленного деполяризующего тока кальция соответственно; βto, αto, μto, βst, αst, μst - параметры распределений;
- плотности распределений ИИК для переходного транзитного тока и медленного деполяризующего тока кальция соответственно; βto, αto, μto, βst, αst, μst - параметры распределений;
определения параметров стохастической модели тока 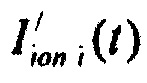 реполяризации эпикарда путем минимизации решения уравнения
реполяризации эпикарда путем минимизации решения уравнения
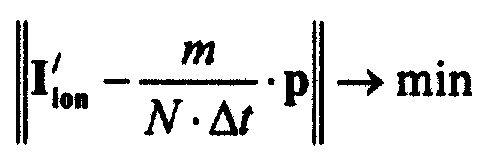 ,
,
где 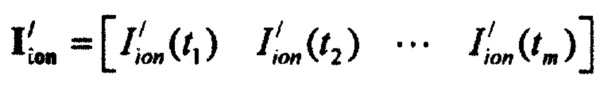 - матрица стохастической модели тока реполяризации эпикарда; р=[р, р2 … pm] - матрица разностей распределений вероятностей ИИК;
- матрица стохастической модели тока реполяризации эпикарда; р=[р, р2 … pm] - матрица разностей распределений вероятностей ИИК;
определения значения тока 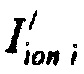 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента
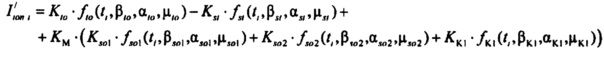 ;
;
- восстанавливают потенциал ϕmod в опорных точках эпикарда компьютерной модели сердца пациента путем:
определения коэффициента приведения потенциала эпикарда 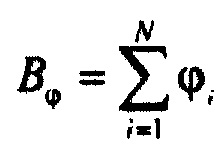 ;
;
определения коэффициента приведения тока 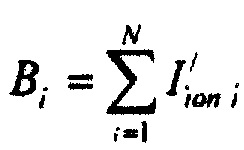 ;
;
определения значений восстановленного потенциала ϕmod i в опорных точках эпикарда компьютерной модели сердца пациента 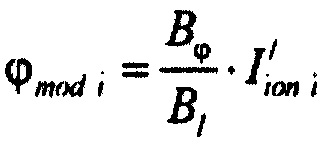 ;
;
- сравнивают восстановленный ϕmod потенциал эпикарда с потенциалом эпикарда ϕ определенном на ЭКС
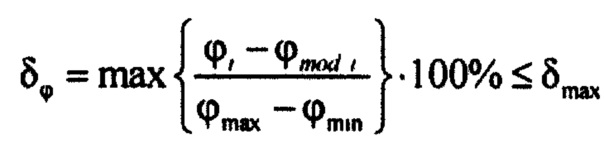 ;
;
- корректируют параметры распределений βto, αto, μto, βst, αst, μst стохастической модели тока 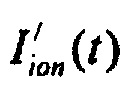 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента;
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента;
- принимают решение: «Значения тока 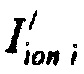 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента определены корректно».
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента определены корректно».
На фигуре 3 приведены временные диаграммы токов, формирующих трансмембранный потенциал действия (ТМПД) [17].
На фигуре 4 приведена взаимосвязь потенциала эпикарда и ТМПД кардиомиоцитов посредством ионных токов: а) при деполяризации эпикарда, б) при реполяризации эпикарда.
На фигуре 5 приведены временные диаграммы токов, формирующих ТМПД, для детальной модели Iyer-Mazhari-Winslow (IMW) [35].
На фигуре 6 приведены временные диаграммы токов, формирующих ТМПД, для детальной модели Tusscher-Noble-Noble-Panfilov (TNNP) [34]: а) желудочкового ТМПД; б) концентрации кальция; в) тока натрия; г) переходного транзитного тока; д) тока калия быстрого задержанного выпрямления; е) тока калия медленного задержанного выпрямления; ж) деполяризующего тока кальция L-типа; з) тока калия аномального выпрямления.
На фигуре 7 приведено сравнение временных диаграмм токов, формирующих ТМПД, для детальной модели Luo-Rudy (LRd) (а) и для детальной модели TNNP (б) [30].
На фигуре 8 приведено сравнение временных диаграмм токов, формирующих ТМПД, для детальной модели Priebe-Beuckelmann (РВ), для детальной модели LRd и для детальной модели TNNP [23]: а) желудочкового ТМПД; б) деполяризующего тока кальция L-типа; в) тока калия быстрого задержанного выпрямления; г) тока калия медленного задержанного выпрямления.
На фигуре 9 приведено изменение формы ТМПД при нарушении взаимодействия ионных каналов в кардиомиоците [18].
На фигуре 10 приведена таблица с перечнем причин изменения длительности ТМПД при различных синдромах [14, 15, 17, 21, 22].
На фигуре 11 приведена таблица с перечнем причин изменения формы ТМПД при синдроме Бругэда [14, 15, 17].
На фигуре 12 приведена схема алгоритма, реализующего предлагаемый способ неинвазивного определения электрофизиологических характеристик сердца.
На фигуре 13 приведена схема алгоритма формирования данных для стохастической модели тока реполяризации эпикарда в опорных точках компьютерной модели сердца.
На фигуре 14 приведена схема алгоритма определения тока калия аномального выпрямления в опорных точках компьютерной модели сердца пациента.
На фигуре 15 приведена схема алгоритма определения тока реполяризации эпикарда в опорных точках компьютерной модели сердца пациента.
На фигуре 16 приведена схема алгоритма восстановления потенциала эпикарда в опорных точках компьютерной модели сердца пациента.
На фигуре 17 приведен характерный пример потенциала эпикарда, полученного в результате восстановления электрокардиосигнала.
На фигуре 18 приведена иллюстрация формирования информационно-измерительного кванта (ИИК) по выборке потенциала эпикарда для опорной точки компьютерной модели сердца пациента.
На фигуре 19 приведена разница распределений ИИК для положительных и отрицательных значений потенциала эпикарда.
На фигуре 20 приведено представление стохастических моделей тока калия задержанного и аномального выпрямления для временного интервала монотонной реполяризации эпикарда в опорных точках компьютерной модели сердца пациента.
На фигуре 21 приведена последовательность формирования распределения вероятностей ИИК симметричной случайной величины Z для стохастической модели тока калия аномального выпрямления, где обозначено:
а) гистограмма распределения вероятностей ИИК 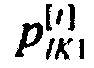 по временным интервалам группирования для стохастической модели тока калия аномального выпрямления;
по временным интервалам группирования для стохастической модели тока калия аномального выпрямления;
б) распределение вероятности ИИК 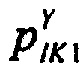 для значений случайной безразмерной величины Y, полученной путем преобразования временных отсчетов ИИК для стохастической модели тока калия аномального выпрямления;
для значений случайной безразмерной величины Y, полученной путем преобразования временных отсчетов ИИК для стохастической модели тока калия аномального выпрямления;
в) симметричное распределение вероятностей ИИК 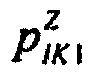 для значений случайной безразмерной величины Z для стохастической модели тока калия аномального выпрямления, полученной путем симметричного отображения вероятностей для значений случайной величины Y;
для значений случайной безразмерной величины Z для стохастической модели тока калия аномального выпрямления, полученной путем симметричного отображения вероятностей для значений случайной величины Y;
г) гистограмма распределения вероятностей ИИК 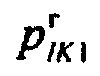 по интервалам группирования случайной величины Z для стохастической модели тока калия аномального выпрямления.
по интервалам группирования случайной величины Z для стохастической модели тока калия аномального выпрямления.
На фигуре 22 приведена последовательность формирования распределения вероятностей ИИК симметричной случайной величины Z для стохастической модели тока калия медленного задержанного выпрямления, где обозначено:
а) гистограмма распределения вероятностей ИИК 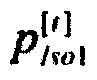 по временным интервалам группирования для стохастической модели тока калия медленного задержанного выпрямления;
по временным интервалам группирования для стохастической модели тока калия медленного задержанного выпрямления;
б) распределение вероятности ИИК 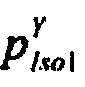 для значений случайной безразмерной величины Y, полученной путем преобразования временных отсчетов ИИК для стохастической модели тока калия медленного задержанного выпрямления;
для значений случайной безразмерной величины Y, полученной путем преобразования временных отсчетов ИИК для стохастической модели тока калия медленного задержанного выпрямления;
в) симметричное распределение вероятностей ИИК 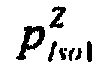 для значений случайной безразмерной величины Z для стохастической модели тока калия медленного задержанного выпрямления, полученной путем симметричного отображения вероятностей для значений случайной величины Y;
для значений случайной безразмерной величины Z для стохастической модели тока калия медленного задержанного выпрямления, полученной путем симметричного отображения вероятностей для значений случайной величины Y;
г) гистограмма распределения вероятностей ИИК 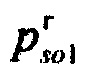 по интервалам группирования случайной величины Z для стохастической модели тока калия медленного задержанного выпрямления.
по интервалам группирования случайной величины Z для стохастической модели тока калия медленного задержанного выпрямления.
На фигуре 23 приведена последовательность формирования распределения вероятностей ИИК симметричной случайной величины Z для стохастической модели тока калия быстрого задержанного выпрямления, где обозначено:
а) гистограмма распределения вероятностей ИИК 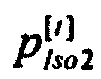 по временным интервалам группирования для стохастической модели тока калия быстрого задержанного выпрямления;
по временным интервалам группирования для стохастической модели тока калия быстрого задержанного выпрямления;
б) распределение вероятности ИИК 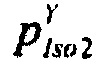 для значений случайной безразмерной величины Y, полученной путем преобразования временных отсчетов ИИК для стохастической модели тока калия быстрого задержанного выпрямления;
для значений случайной безразмерной величины Y, полученной путем преобразования временных отсчетов ИИК для стохастической модели тока калия быстрого задержанного выпрямления;
в) симметричное распределение вероятностей ИИК  для значений случайной безразмерной величины Z для стохастической модели тока калия быстрого задержанного выпрямления, полученной путем симметричного отображения вероятностей для значений случайной величины Y;
для значений случайной безразмерной величины Z для стохастической модели тока калия быстрого задержанного выпрямления, полученной путем симметричного отображения вероятностей для значений случайной величины Y;
г) гистограмма распределения вероятностей ИИК 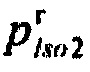 по интервалам группирования случайной величины Z для стохастической модели тока калия быстрого задержанного выпрямления.
по интервалам группирования случайной величины Z для стохастической модели тока калия быстрого задержанного выпрямления.
На фигуре 24 приведены зависимости критерия адекватности и параметров модели токов калия задержанного и аномального выпрямления от весового коэффициента K1 модели тока аномального выпрямления:
а) зависимости критерия адекватности модели тока калия задержанного и аномального выпрямления г и его составляющих 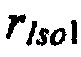 ,
, 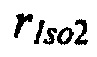 ,
, 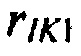 от весового коэффициента K1 модели тока аномального выпрямления;
от весового коэффициента K1 модели тока аномального выпрямления;
б) зависимость параметра формы γ модели тока калия аномального выпрямления от весового коэффициента K1 модели тока аномального выпрямления;
в) зависимость параметров масштаба 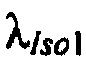 ,
, 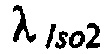 ,
,  моделей составляющих тока калия быстрого задержанного, медленного задержанного и аномального выпрямления от весового коэффициента K1 модели тока аномального выпрямления;
моделей составляющих тока калия быстрого задержанного, медленного задержанного и аномального выпрямления от весового коэффициента K1 модели тока аномального выпрямления;
г) зависимость параметров масштаба 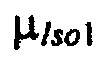 ,
, 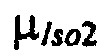 ,
, 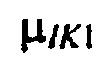 моделей составляющих тока калия быстрого задержанного, медленного задержанного и аномального выпрямления от весового коэффициента K1 модели тока аномального выпрямления.
моделей составляющих тока калия быстрого задержанного, медленного задержанного и аномального выпрямления от весового коэффициента K1 модели тока аномального выпрямления.
На фигуре 25 приведены результаты моделирования тока реполяризации эпикарда, где используются следующие обозначения: 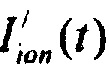 - ток реполяризации эпикарда;
- ток реполяризации эпикарда; 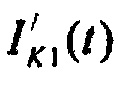 - ток аномального выпрямления;
- ток аномального выпрямления; 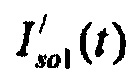 - ток быстрого задержанного выпрямления;
- ток быстрого задержанного выпрямления; 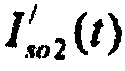 - медленного задержанного выпрямления;
- медленного задержанного выпрямления; 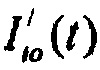 - переходной транзитный ток эпикарда;
- переходной транзитный ток эпикарда; 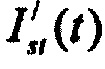 - замедленный деполяризующий ток кальция.
- замедленный деполяризующий ток кальция.
На фигуре 26 приведены графики потенциалов эпикарда: ϕ - потенциал эпикарда, полученный при решении ОЗ ЭКГ в известном способе, и ϕmod - потенциал эпикарда, восстановленный с помощью стохастической модели токов реполяризации эпикарда.
Введенные действия с их связями проявляют новые свойства, расширяющие функциональные возможности известного способа и позволяющие определить составляющие тока калия и установить причины изменения формы потенциала эпикарда. Расширение функциональных возможностей при определении электрофизиологических характеристик сердца обеспечивается путем:
- восстановления с помощью предлагаемой стохастической модели тока реполяризации эпикарда потенциала эпикарда;
- сравнения восстановленного потенциала эпикарда с потенциалом эпикарда, полученным в результате решения ОЗ ЭКГ;
- определения составляющих тока калия в случае эквивалентности сравниваемых потенциалов эпикарда;
- коррекции стохастической модели тока реполяризации эпикарда до достижения эквивалентности сравниваемых потенциалов эпикарда в случае неэквивалентности сравниваемых потенциалов эпикарда.
Суть предлагаемого изобретения заключается в определении тока калия аномального выпрямления за счет применении стохастической модели составляющих ионных токов реполяризации эпикарда при проведении электрокардиографического обследования.
Известно, что ЭАС обусловлена функционированием ионных каналов клеток миокарда - кардиомиоцитов [10]. Многие заболевания сердца связаны с дефектными изменениями функционирования ионных каналов, которые проявляются в развитии жизнеугражающих аритмий. На фигуре 3 приведена временная диаграмма составляющих токов эпикарда [17], иллюстрирующая взаимосвязь ионных токов в развитии ТМПД. Все токи в кардиомиоците разделены на входящие, деполяризующие и выходящие, реполяризующие токи. Из временных диаграмм токов, приведенных на фигуре 3, видно, что токи деполяризации состоят из двух основных составляющих: быстрый ток натрия INa и медленный деполяризующий ток кальция ICa. Токи реполяризации кардиомиоцита содержат целый комплекс составляющих: выходящие транзитные токи Ito, токи калия быстрого задержанного IKr, медленного задержанного IKs и аномального выпрямления IK1 [17].
Авторы предлагаемого изобретения убеждены в том, что знание особенностей ионных токов во время различных фаз развития ТМПД является важным диагностическим показателем. Например, для описания токов детальной модели фаза 2 плато ТМПД (см. фигуру 3) разделяется на две части. Авторы предлагаемого изобретения считают необходимым для определения токов задержанного и аномального выпрямлений объединить фазы 2 и 3 ТМПД (см. фигуру 3), и таким образом выделить временной интервал монотонной реполяризации ТМПД (см. фигуру 3). Во время монотонной реполяризации ТМПД происходят процессы управления концентрацией тока кальция, приводящие к изменению длительности ТМПД.
Отличительной особенностью предлагаемого способа в смысле получения новой диагностической информации является возможность анализа решения ОЗ ЭКГ с помощью стохастической модели тока реполяризации эпикарда, построенной с учетом характерных особенностей ионных токов во время монотонной реполяризации ТМПД. На фигуре 4 показана взаимосвязь ТМПД кардиомиоцита и потенциала эпикарда ϕ при развитии процессов деполяризации (см. фигуру 4,а) и реполяризации (см. фигуру 4,6). Во время деполяризации эпикарда происходит изменение знака и значения ТМПД, что связано с изменением избыточного заряда внутренней среды кардиомиоцита. Смена заряда происходит при распространении ТМПД от эндокарда к эпикарду. Накапливаемый в кардиомиоците заряд определяет избыточный заряд внутренней среды кардиомиоцита. Во время реполяризации происходит изменение знака ТМПД, что вызывает процесс перезарядки внутренней среды кардиомиоцита. Процессы деполяризации и реполяризации обусловлены различными ионными токами, что вызывает перемещение ионов в направлении поверхности эпикарда вследствие изменения концентраций ионов. В результате генерируется ионный ток, проходящий через эпикард и формирующий ЭКС на торсе пациента.
В связи с тем, что одни и те же ионы межклеточной среды участвуют как в образовании тока развития ТМПД, так и в образовании тока, проходящего через эпикард, то эти процессы взаимосвязаны. Наличие взаимосвязи процессов позволяет использовать схемы токов детальных моделей процесса развития ТМПД для описания процесса реполяризации эпикарда. Так как ток через эпикард образован суммарным током деполяризации и реполяризации кардиомиоцита, то его составляющие имеют случайный характер, что обуславливает необходимость использования стохастических моделей для описания ионного тока реполяризации эпикарда и образования потенциала эпикарда<р.
Для пояснения дальнейшего изложения рассмотрим детальные модели ионных токов, используемые для исследования составляющих ионных токов при развитии ТМПД. (см. фигуры 5-11). Современные детальные модели электрической активности сердца (ЭАС) созданы путем совершенствования известного формализма (модели) Ходжкина-Хаксли [24], в основе которого положены процессы управления проводимостью мембранных каналообразующих белков за счет изменения состояния потенциалозависимых частиц. При этом формальное управление поведением отдельной белковой структуры задано в виде системы дифференциальных уравнений, моделирующих состояние потенциалозависимых частиц. Наиболее известны следующие детальные модели.
1. Модель Luo-Rudy (LRd) - одна из первых детальных моделей для ТМПД, содержащая основные структурные элементы для описания проводимости через мембрану [28].
2. Модель Priebe-Beuckelmann (РВ) [31]. Эта модель разработана для изучения неправильного автоматизма и клеточных электрофизиологических последствий остановки сердца (содержит 22 переменных).
3. Модель Tusscher-Noble-Noble-Panfilov (TNNP) [34]. Эта модель, в которой применены результаты, полученные непосредственного при исследовании тканей миокарда (содержит 17 переменных состояния и 44 параметра) '
4. Модель Iyer-Mazhari-Winslow (IMW) [26, 32]. Эта модель детально описывает ионные потоки для отдельных структур мембраны, включает 67 переменных состояния и 94 параметра.
Детальные модели LRd, РВ, TNNP и IMW позволяют решить прямую задачу: при известных значениях ионных токов определить развитие ТМПД. При решении обратной задачи: определение значениях ионных токов по известной форме ТМПД возможно множество решений, зависящих от случайных воздействий. Применение детальных моделей LRd, РВ, TNNP и IMW так же ограничено из-за большого объема проводимых вычислений, что важно при рассмотрении задач распространения электрического потенциала и возникновение риентри в миокарде.
5. Упрощенная модель для ТМПД [30]. Эта модель разработана для изучения распространения ТМПД, образования риентри, рефрактерных свойств миокарда и других процессов развития аритмии вследствие изменения восстановления миокарда. Модель относится к реалистической физиологической модели и включает токи всех ионных каналов. Цель модели состоит в воспроизведении морфологической формы ТМПД и кривых возвращения к потенциалу покоя на основе результатов моделирования более сложных моделей.
Покажем определение составляющих ионных токов эпикарда в детальных моделях ионных токов. Временная диаграмма, приведенная на фигуре 5, иллюстрирует детальное моделирование составляющих ионных токов ТМПД в модели IMW [23, 35], где обозначены деполяризующие и реполяризующие токи. Также в модели IMW учтены дополнительно токи INa/Ca мембранной структуры натрий-кальциевого обменника. На фигуре 6 приведены временные диаграммы основных токов детальной модели TNNP для вентрикулярных тканей [34], из которых следует, что для построения детальной модели TNNP необходим такой же набор составляющих ионных токов. Для обеспечения качества модели важно обеспечить форму функции изменения ионных токов. Диаграммы составляющих (компонент) токов детальной модели TNNP, приведенные на фигуре 6, содержат информацию о форме изменения составляющих ионных токов во времени. На фигуре 6 приведены следующие диаграммы:
а - трансмембранного потенциала действия ϕ;
б - переходного процесса кальция Cai;
в - тока натрия INa;
г - транзитного переходного тока It0;
д - тока калия быстрого задержанного выпрямления IKr;
е - тока калия медленного задержанного выпрямления IKs;
ж - тока кальция Z-типа ICaL;
з - тока калия аномального выпрямления IK1.
Из-за большого объема проводимых вычислений использование детальных моделей LRd, РВ, TNNP и IMW затруднено при исследовании возникновения риентри в миокарде. Для изучения образования риентри при распространении ТМПД, рефрактерных свойств миокарда и других процессов развития аритмии вследствие изменения восстановления миокарда разработана упрощенная модель для ТМПД [30]. Значение построения упрощенной модели состоит в том, чтобы минимальным количеством составляющих модель ионных токов воспроизвести морфологическую форму ТМПД и кривых возвращения к потенциалу покоя. Сохранение формы кривых в упрощенной модели достигается за счет обобщения результатов более сложных детальных моделей.
В упрощенной модели токи разделены по функциональному назначению. Характер изменения токов во время активности миокарда, сгруппированных по своему функциональному назначению, даны для моделей LRd на фигуре 7, а, б и для упрощенной модели на фигуре 7, г, д [30, 28]. Из рассмотрения этих фигур следует, что в упрощенной модели все ионные токи разделены на четыре группы в соответствии с их функциональным назначением.
Первая группа - токи натрия быстрой деполяризации, направленные внутрь кардиомиоцита с быстрым окончанием процесса (быстрой инактивацией каналов проводимости).
Вторая группа - транзитные токи фазы быстрой начальной реполяризации тканей миокарда. К этой группе относятся токи, направленные наружу с быстрым окончанием процесса, из которых выделяют токи ионов калия и хлора. Функциональное назначение токов состоит в том, чтобы за малый промежуток времени перевести ТМПД в сбалансированное состояние. Эти токи хорошо аппроксимируют функции переходных процессов.
Третья группа - токи замедленной деполяризации, направленные внутрь кардиомиоцита с медленным окончанием процесса. Функциональное назначение токов состоит в том, чтобы обеспечить приток кальция и поддержание его концентрации внутри цитоплазмы для развития процессов сжатия кардиомиоцита. Эта группа токов включает в себя целый комплекс (составляющих) компонент деполяризующего тока: ток кальция L-типа, ток кальция T-типа.
Четвертая группа - токи калия реполяризации, направленные наружу, функциональное назначение которых состоит в контроле сбалансированного состояния ТМПД и изменение его длительности в зависимости от состояния кардиомиоцита: концентрации АТФ и др. ионов.
Фигура 8 содержит формы зависимостей медленных и быстрых ионных токов калия задержанного потенциала IKs и IKr, для ионного тока кальция L-типа LCaL где графики построены на основе наиболее известных детальных моделей: РВ, IMW, TNNP [23].
При нормальном функционировании ЭАС сохраняется баланс между деполяризующими и реполяризующими токами благодаря сбалансированному взаимодействию ионных каналов. Все ионные каналы находятся в одном из трех состояний: активации, инактивации и покоя. При переходе ионных каналов из состояния покоя в состояние активации происходит формирование ионного тока. Нарушение функционирования каналов отражается в изменении баланса между токами деполяризации и реполяризации кардиомиоцита и, как следствие, в изменении формы, прежде всего, длительности ТМПД [18].
На фигуре 9 даны наиболее характерные изменения формы ТМПД, обусловленные нарушением взаимодействия ионных каналов в кардиомиоците. Важный симптом нарушения работы ионных каналов связан с увеличением длительности ТМПД. Среди основных причин увеличения длительности ТМПД следует выделить:
- задержка реполяризации в результате изменения фазы плато ТМПД при условии, что время реполяризации от уровня плато до уровня полной реполяризации не изменяется;
- замедление реполяризации, при котором удлиняется 3-я фаза ТМПД от уровня плато до уровня потенциала покоя при сохранении длительности фазы «плато». При этом преобразовании ТМПД приобретает форму треугольника, которую характеризуют степенью треугольности [18, 29].
По данным исследований [18] увеличение "треугольности" ТМПД независимо от причин ее появления свидетельствует об увеличении вероятности развития аритмий. Характерный пример увеличения "треугольности" ТМПД при нарушении работы каналов проводимости дан на фигуре 9,6. Образование ТМПД треугольной формы может быть обусловлено следующими причинами: подавлением реполяризующего тока задержанного и аномального выпрямления, усилением тока Na-Ca-обменника или подавлением деполяризующего тока кальция. Электрофизиологический параметр «степень треугольности» ТМПД рассчитывается как разница длительности ТМПД на уровне 90% и 30% реполяризации [18].
Появление осцилляции длительности ТМПД (фигура 9,в) так же связано с нарушением работы каналов и повышают вероятность развития аритмии сердца. Осцилляции длительности ТМПД обусловлены развитием параметрического резонанса в тканях кардиомиоцита в результате сокращения интервала восстановления тканей. На фигуре 9,б показан пример образования осцилляции, обусловленных уменьшением диастолического интервала при повышении частоты сердечных сокращений. В этом случае кардиомиациты при нормальном ТМПД не успевают восстановиться в течение короткого диастолического интервала, что проявляется в нарушениях функционирования каналов и изменении формы (длительности) ТМПД и появлении ТМПД малой длительности. После короткого ТМПД образуется длительный интервал (ДИ), в течение которого кардиомиоцит полностью восстановится. Нормальное функционирование каналов в кардиомиоците обеспечивает развитие нормального ТМПД, после чего цикл осцилляции повторится [18].
Важность определения составляющих ионных токов при проведении электрокардиографии также подтверждается приведенными на фигурах 8 и 9 данными о симптомах генетических нарушений различных белков ионных каналов, приводящих к изменениям составляющих ионных токов и являющихся причиной развития сложных нарушений ритма сердца. В таблице 1 (см. фигуру 10) [15] приведен список генетических нарушений различных белков ионных каналов, которые влияют на токи калия замедленного и аномального выпрямления. Генетические нарушения регуляторных каналообразующих белков приводят к неправильному функционированию ионных каналов и являются причиной развития сложных нарушений ритма сердца [14, 15, 21], проявляющихся в удлинении или в уменьшении интервала Q-T ЭКС.Генетические дефекты синдрома Бругэда (см. фигуру 11) так же вызывают нарушение баланса ионных токов, что отражается в изменении длительности потенциала действия [14, 15].
Из вышеизложенного следует, что для повышения достоверности диагностики заболевания сердца необходимо определение составляющих ионных токов эпикарда. По мнению авторов предлагаемого изобретения, использование современных детальных моделей ионных токов требует неоправданно больших вычислительных затрат для определения параметров модели при проведении электрокардиографического обследования.
В основе построения современных детальных моделей лежит модель Ходжкина-Хаксли, в которой вероятностные свойства заложены в описание поведения отдельных белковых структур мембраны. Белковые ионные каналы управляются трансмембранным потенциалом действия, изменение которого в детальных моделях принимается для всех структур одинаковым. Для кардиомиоцита потенциал изменяется по поверхности мембраны и не связан с начальным состоянием потенциал зависимых частиц. Так как в формировании суммарного тока ионов через эпикард участвуют каналообразующие мембранные белки, которые находятся в различных полостях кардиомиоцита, то воздействие электрического поля на такие структуры имеет случайный характер. Применение детальных моделей для определения составляющих ионных токов, проходящих через эпикард, затруднительно из-за различия начальных фаз развития тока в различных структурах кардиомиоцита и различия состояния кардиомиоцита.
Авторы предлагаемого изобретения считают, что целесообразнее использовать вероятностные (стохастические) модели непосредственно для описания составляющих ионного тока, проходящего через эпикард. В связи с тем, что токи, формирующие ТМПД, и проходящие через эпикард, созданы одними и теми же ионами, при формировании стохастических моделей токов использованы токи детальных моделей. Использование детальных моделей для построения стохастических моделей ионных токов основано на подобии формы плотности распределения информационно-измерительного кванта (ИИК) для стохастической модели ионных токов форме изменения ионных токов реполяризации эпикарда. Поэтому для решения задачи анализа ионных токов реполяризации эпикарда использованы правила выбора наиболее подходящей (оптимальной) формы аппроксимирующего решения. При этом нарушения в организации каналообразующих белков отражаются в изменении свойств стохастической модели.
Построение стохастической модели распределения составляющих ионного тока реполяризации эпикарда заключается в выборе подходящей формы аппроксимирующей функции. Для этого предварительно по детальным моделям оценивается форма функции составляющих токов путем расчета асимметрии и эксцесса распределения ИИК функции составляющих токов, и подбирается возможная форма распределения. Затем осуществляется расчет асимметрии и эксцесса распределения ИИК для стохастической модели ионных токов по выборкам отсчетов зарегистрированного ЭКС. Сравнение параметров формы функции аппроксимации стохастических моделей ионных токов с параметрами формы ионных токов детальной модели позволяет оценить составляющие ионных токов эпикарда. Контроль изменения параметров стохастической модели ионных токов повышает достоверность оценки состояния сердца.
Рассмотрим подробно введенные действия.
Формирование данных для стохастической модели тока реполяризации эпикарда в опорных точках компьютерной модели сердца. Основная цель этого действия состоит в том, чтобы на основе отсчетов одного кардиоцикла получить выборку отсчетов, характеризующую вероятностные свойства модели токов реполяризации эпикарда. Особенность решения состоит в сравнении формы кривых и распределения отсчетов, что можно осуществить, если решение искать в виде функций распределения, площади которых равны единице. Для данных так же должно выполняться условие, что суммарное значение, используемых для моделирования значений, умноженное на время, необходимое для получения одного отсчета, должно быть равным единичной площади.
Схема развернутого алгоритма действия формирования данных для стохастической модели ионных токов реполяризации эпикарда приведена на фигуре 13. Для выполнения этапа формирования данных используется выборки значений потенциала ϕ опорных точек эпикарда. На фигуре 17 дан характерный пример распределения во времени отсчетов потенциала эпикарда для опорной точки компьютерной модели сердца пациента. Из фигуры 13 следует, что первое отличительное действие предлагаемого способа неинвазивного определения электрофизиологических характеристик сердца содержит
- определение информационно - измерительного кванта для выборки значений потенциала в опорных точках эпикарда. Формирование данных начинается с определения информационно-измерительного кванта (ИИК) - минимального математического формирования, отображающего суть вероятностных физических процессов, информация о которых содержится в выборке значений ЭКС одного кардиоцикла.
Значение ИИК γ определяют как произведение времени Δt, необходимое для получения одного отсчета на меру неопределенности Δϕ потенциала эпикарда

Взаимосвязь ИИК γ и отсчетов выборки потенциалов эпикарда, полученных при решении обратной задачи для опорной точки эпикарда, поясняет фигура 18. Для одномерной величины мера ИИК Δϕ определяется как отношение разности между максимальным ϕmax и минимальным ϕmin значениями потенциалов выборки к количеству интервалов группирования данных, которое равно корню квадратному от количества N отсчетов в выборке

Мера ИИК характеризует неопределенность расчета потенциала эпикарда, которая ограничена интервалом группирования данных. Выбор границ группирования значений «чувствителен» к грубым отсчетам. Для их исключения используется условие, что «грубым» отсчетом считается значение более 5⋅σ(ϕ). Такой подход позволяет сразу исключить из рассмотрения натриевые токи, которые определены единичным интервалом времени и значением на два порядка, превышающим СКО.
Таким образом, если за один кардиоцикл получено количество отсчетов равное 1000, то количество интервалов группирования данных будет равным 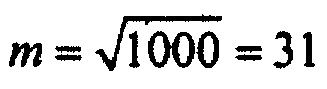 . Эта величина определяет меру кванта по оси потенциала.
. Эта величина определяет меру кванта по оси потенциала.
- определение количества ИИК для стохастической модели тока реполяризации эпикарда. Это действие алгоритма на фигуре 13 необходимо для оценки количества ИИК, содержащихся во всей выборки отсчетов потенциала эпикарда.
Выборка отсчетов содержит полное количество ИИК, равное сумме ИИК положительных и отрицательных отсчетов. Количество квантов, содержащемся в одном отсчете, равно отношению значения ϕi отсчета к мере неопределенности кванта Δϕ:

Тогда суммарное количество квантов, содержащееся в отсчетах выборки, равно отношению суммы модулей значений для всех отсчетов выборки к мере неопределенности Δϕ ИИК:

Умножая числитель и знаменатель выражения (14) на время получения одного отсчета Δt и учитывая выражение (11), получим для определения количества информационных-измерительных квантов Nγ, содержащееся во всей стохастической модели токов реполяризации эпикарда, формулу вида

- определение количества m, ранжированных значений, границ для временных интервалов группирования ИИК. Действие, состоящее в определением количества m ранжированных значений и границ для временных интервалов группирования ИИК, необходимо для формирования временных интервалов группирования квантов. Для этого определяются ранжированные значения времени tpi и границы всех временных интервалов группирования ИИК с помощью выражений:

где m - количество интервалов группирования данных, равное корню квадратному от 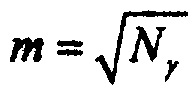 количества значений в выборке; tmin j и tmax j - минимальная и максимальная границы j-го интервала группирования данных.
количества значений в выборке; tmin j и tmax j - минимальная и максимальная границы j-го интервала группирования данных.
- определение вероятностей ИИК в j-x интервалах группирования для значений потенциала. Определение распределения вероятностей ИИК 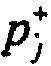 и
и 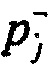 в j-м интервале группирования ИИК для положительных и отрицательных значений потенциала эпикарда в опорных точках компьютерной модели сердца пациента: необходимо для выражения значений потенциала эпикарда в единицах меры ИИК. Цель действия состоит в количественном выражении значения результата в единицах меры неопределенности результата и организации процесса усреднения значений результатов путем оценки вероятностей распределения ИИК во временных интервалах группирования потенциалов эпикарда. Для сравнения результатов используется их приведенные оценки к количеству ИИК Nγ (числу), рассчитанного для всей выборки результатов. Отношение суммарного количества мер ИИК для положительных значений результатов, попавших в j-й интервал группирования, отнесенного к количеству мер ИИК, необходимых для оценки всей выборки результатов, представляет собой вероятность
в j-м интервале группирования ИИК для положительных и отрицательных значений потенциала эпикарда в опорных точках компьютерной модели сердца пациента: необходимо для выражения значений потенциала эпикарда в единицах меры ИИК. Цель действия состоит в количественном выражении значения результата в единицах меры неопределенности результата и организации процесса усреднения значений результатов путем оценки вероятностей распределения ИИК во временных интервалах группирования потенциалов эпикарда. Для сравнения результатов используется их приведенные оценки к количеству ИИК Nγ (числу), рассчитанного для всей выборки результатов. Отношение суммарного количества мер ИИК для положительных значений результатов, попавших в j-й интервал группирования, отнесенного к количеству мер ИИК, необходимых для оценки всей выборки результатов, представляет собой вероятность 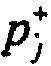 обнаружения ИИК для положительных значений потенциала эпикарда в j-м интервале группирования данных. Аналогично, отношение суммарного количества мер ИИК для отрицательных значений результатов, попавших в j-й интервал группирования, отнесенного к количеству мер ИИК всей выборки результатов представляет собой вероятность
обнаружения ИИК для положительных значений потенциала эпикарда в j-м интервале группирования данных. Аналогично, отношение суммарного количества мер ИИК для отрицательных значений результатов, попавших в j-й интервал группирования, отнесенного к количеству мер ИИК всей выборки результатов представляет собой вероятность 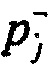 обнаружения ИИК для отрицательных значений потенциала эпикарда в j-м интервале группирования данных. Формулы для вычисления вероятностей распределения ИИК для положительных и отрицательных значений потенциала эпикарда имеют вид;
обнаружения ИИК для отрицательных значений потенциала эпикарда в j-м интервале группирования данных. Формулы для вычисления вероятностей распределения ИИК для положительных и отрицательных значений потенциала эпикарда имеют вид;
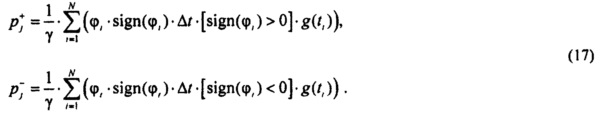
- определение разности вероятностей ИИК в интервалах группирования для значений потенциала в опорных точках компьютерной модели. Определения разности распределений вероятностей ИИК pj в j-м интервале группирования значений потенциала в опорных точках эпикарда компьютерной модели сердца пациента необходимо для получения усредненного значения потенциала, выраженного в единицах меры ИИК приведенных к полному количеству ИИК в выборке результатов. В выборке результатов присутствуют положительные или отрицательные значения. При попадании квантов в один интервал группирования результатов происходит взаимное уничтожение квантов положительных и отрицательных значений. Форму кривой изменения полезного сигнала отражает разность вероятностей ИИК для положительных 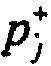 и отрицательных
и отрицательных 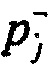 значений потенциала в интервалах группирования. Для расчета разности распределений вероятностей ИИК для положительных
значений потенциала в интервалах группирования. Для расчета разности распределений вероятностей ИИК для положительных 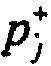 и отрицательных
и отрицательных 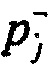 значений потенциала используется формула:
значений потенциала используется формула:

Пример разности вероятностей ИИК для опорной точки компьютерной модели дан на фигуре 19. Использование разности распределения вероятностей ИИК по интервалам группирования позволяет выделить характерные временные интервалы кардиоцикла.
- формирование выборок отсчетов времени для положительных и отрицательных разностей вероятностей. Формирование выборок отсчетов времени для положительных и отрицательных разностей распределений вероятностей ИИК необходимо для выделения временного участка монотонной реполяризации эпикарда. Для этого формируются ранжированные выборки значений времени t- и t+ для положительных pj>0 и отрицательных pj<0 разностей вероятностей согласно следующим правилам:

- выделение временного интервала фазы начальной быстрой реполяризации эпикарда в опорных точках. Выделение временного интервала фазы начальной быстрой реполяризации эпикарда в опорных точках компьютерной модели сердца пациента получают путем оценки минимального отсчета времени для выборки значений времени для отрицательных pj<0 разностей вероятностей

- выделение временного интервала монотонной реполяризации эпикарда в опорных точках. Выделения временного интервала монотонной реполяризации эпикарда, включающего интервал монотонной реполяризации фазы плато и фазу конечной быстрой реполяризации эпикарда, необходимо для определения параметров стохастической модели тока калия задержанного и аномального выпрямления. В качестве монотонного участка реполяризации выделяется область ИИК положительного знака, ограниченная с одной стороны максимальным значением времени интервала группирования ИИК с отрицательным значением, с другой стороны максимальным значением отсчета времени для положительного потенциала. Для определения границ интервалов используются выражения
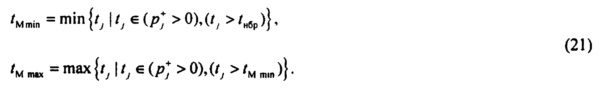
Таким образом, анализ изменения знака интервалов группирования данных является эффективным инструментом для выделения различных фаз ТМПД тканей эпикарда.
На фигуре 19 дана иллюстрация для определения временных интервалов фазы начальной быстрой реполяризации ΔTto и интервала монотонной реполяризации эпикарда ΔTK, для которых разность вероятностей обнаружения ИИК положительна (т.е. больше нуля). Временной интервал ΔTCa с отрицательной разностью вероятностей обнаружения ИИК соответствует участку поздней деполяризации тканей миокарда из-за некомпенсированных токов ионов кальция.
- нормирование вероятности распределения ИИК для потенциала временного интервала монотонной реполяризации эпикарда. Для установления формы стохастической модели тока калия задержанного и аномального выпрямления по распределению вероятности ИИК необходимо нормировать вероятности распределения ИИК для потенциала монотонной реполяризации эпикарда компьютерной модели сердца пациента. Формула для нормирования вероятности j-го интервала групирования данных имеет вид:

где PM - вероятность наблюдения меры ИИК во временном интервале монотонной реполяризации эпикарда 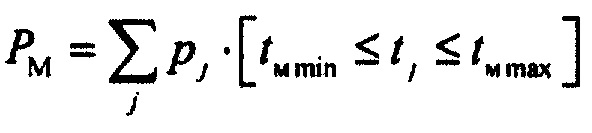 .
.
Ранжированные отсчеты времени независимы и сгруппированы в виде вектора-столбца tm, т.е. матрицы с размерностью m×1: [tm]T=[tl, …, tj, … tm]. Вектору-столбцу
временных отсчетов tm соответствует вектор нормированных вероятностей ИИК pn для интервала времени монотонной реполяризации имеет вид: 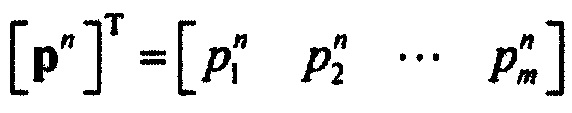 .
.
Определение тока калия аномального выпрямления в опорных точках компьютерной модели сердца. Второе отличительное действие предлагаемого способа неинвазивного определения электрофизиологических характеристик сердца состоит в определении тока калия аномального выпрямления. В связи с тем, что нормированные вероятности интервала монотонной реполяризации эпикарда содержат информацию о токах аномального выпрямления, возможно определение тока путем выделения из общего количества ИИК потенциала эпикарда только тех ИИК, появление которых обусловлено током аномального выпрямления.
Для этого предварительно на основе детальных моделей подбираются статистические распределения (нормированные функции с заданной формой) и пределы изменения параметров этих распределений для описания токов интервала монотонной реполяризации. Затем определяют параметры стохастической модели токов калия задержанного и аномального выпрямления путем минимизации разницы между моделью и нормированными вероятностями ИИК для выборок значений потенциала временного интервала монотонной реполяризации эпикарда.
Схема развернутого алгоритма действия «Определение тока калия аномального выпрямления в опорных точках компьютерной модели сердца» дана на фигуре 14. Из фигуры 14 следует, что второе отличительное действие предлагаемого способа неинвазивного определения электрофизиологических характеристик сердца содержит:
- формирование стохастической модели токов калия задержанного и аномального выпрямления. При этом общая форма стохастической модели токов калия задержанного и аномального выпрямления имеет вид:

где 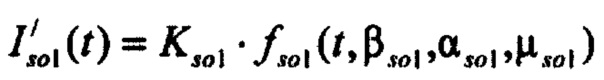 - стохастическая модель Iso тока калия быстрого задержанного выпрямления;
- стохастическая модель Iso тока калия быстрого задержанного выпрямления; 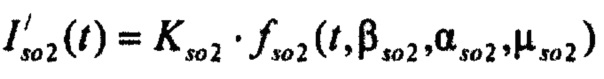 - стохастическая модель Iso тока калия медленного задержанного выпрямления;
- стохастическая модель Iso тока калия медленного задержанного выпрямления; 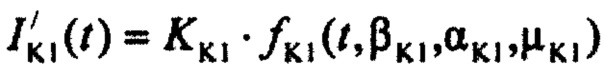 - стохастическая модель тока калия аномального выпрямления;
- стохастическая модель тока калия аномального выпрямления; 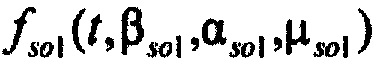 ,
, 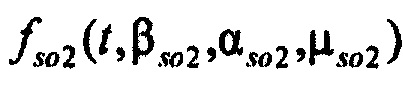 и
и 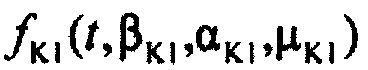 ) - плотности распределений ИИК для тока калия быстрого и медленного задержанного выпрямления и для тока калия аномального выпрямления соответственно; Kso1, Kso2 и KK1 - весовые коэффициенты стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления соответственно; βso1, αso1, μso1, βso2, αso2, μso2, βK1, αK1, μK1 - параметры распределений;
) - плотности распределений ИИК для тока калия быстрого и медленного задержанного выпрямления и для тока калия аномального выпрямления соответственно; Kso1, Kso2 и KK1 - весовые коэффициенты стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления соответственно; βso1, αso1, μso1, βso2, αso2, μso2, βK1, αK1, μK1 - параметры распределений;
Определение составляющих ионных токов осуществляется по априорно известной приближенной модели поведения ионных токов. Для ионных токов априорно известна информация, полученная с помощью детальных математических моделей TNNP [34], LRd [28], IMW [26], РВ [31]. Примеры результатов моделирования ионных токов кальция 1-типа, быстрых и медленных токов калия задержанного выпрямления с помощью известных детальных моделей РВ, IMW, TNNP даны на фигуре 8 [23]. Все основные токи детальной модели TNNP даны на фигуре 6 [34].
Авторы предлагаемого изобретения предлагают аппроксимировать формами распределения ИИК для составляющих стохастических моделей ионных токов формы ионных токов детальных моделей и определять, таким образом, составляющие ионных токов эпикарда. В качестве аппроксимации нормированных по площади медленного 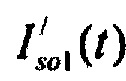 и быстрого
и быстрого 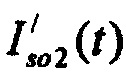 токов задержанного выпрямления используются формы стохастических моделей, построенных на основе плотностей статистических распределений
токов задержанного выпрямления используются формы стохастических моделей, построенных на основе плотностей статистических распределений 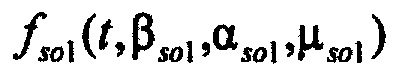 ,
, 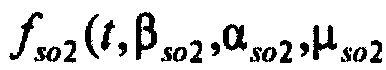 и сохраняющих возможность изменения формы.
и сохраняющих возможность изменения формы.
При выборе аппроксимирующего распределения для построения стохастической модели тока калия задержанного выпрямления 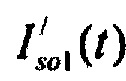 важно, чтобы временное значение положения максимума плотности распределения ИИК был больше временного значения положения для среднего значения тока калия задержанного выпрямления
важно, чтобы временное значение положения максимума плотности распределения ИИК был больше временного значения положения для среднего значения тока калия задержанного выпрямления 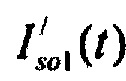 , что следует непосредственно из форм зависимостей токов задержанного выпрямления (см. фигуру 8.в).
, что следует непосредственно из форм зависимостей токов задержанного выпрямления (см. фигуру 8.в).
Следует отметить, что при построении стохастической модели токов калия задержанного и аномального выпрямления на основе сформированных данных (см. фигуру 20), большая часть токов задержанного выпрямления скомпенсирована деполяризующим током кальция L-типа ICaL. По этой причине выбор формы распределения для построения стохастической модели токов задержанного выпрямления имеет качественный характер с сохранением возможности изменения формы в широких пределах.
В работе [18] показано, что для аппроксимации тока калия аномального выпрямления предпочтительно использование распределения Вейбулла-Гнеденко с параметром формы более 2,4. В этом случае сохраняется возможность изменения формы модели, которая в общем случае имеет несимметричный вид.
- задание весовых коэффициентов стохастической модели токов задержанного и аномального выпрямления в опорных точках. Этот этап необходим для предварительной оценки соотношения между статистическим весом модели токов, из которой следует предварительная оценка весового коэффициента стохастической модели токов аномального выпрямления. Для этого оцениваются вероятность для ИИК во второй половине временного диапазона монотонной реполяризации эпикарда, и сопоставляется весовому коэффициенту KK1 стохастической модели токов аномального выпрямления. Весовые коэффициенты Kso1 и Kso2 для стохастической модели тока быстрого и медленного задержанного и аномального выпрямления задаются из выражения:
Kso1=Kso2=0,5(1-KK1).
- определение параметров стохастической модели токов задержанного и аномального выпрямления. Для этого делается подстановка в математическую модель токов задержанного и аномального выпрямления ранжированных значений времени tPj, полученных для интервалов группирования ИИК. Стохастическая модель нормирована по площади и оценивает плотность распределения ИИК (неопределенностей в выборке отсчетов) по времени. Сопоставив полученные выражения для плотностей распределения с отношениями вероятностей для соответствующих интервалов группирования ИИК, к временному интервалу группирования 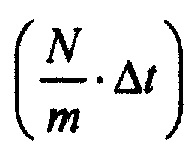 получим систему нелинейных, плохо согласованных, уравнений вида:
получим систему нелинейных, плохо согласованных, уравнений вида:
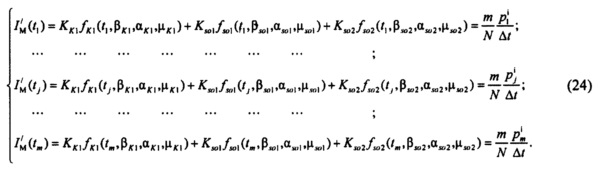
где m - количество интервалов для группирования ИИК.
Вектору-столбцу временных отсчетов tm соответствует матричная форма вектора-столбца стохастической модели 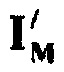 вида:
вида:
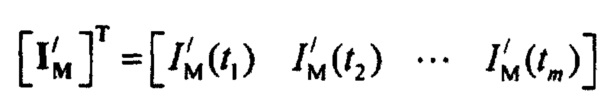 .
.
Векторная форма системы уравнений (24) имеет вид:

Компонентам стохастической модели токов калия соответствуют вероятности распределения ИИК на j-м временном интервале. Векторное уравнение (25) является плохо обусловленным, так как количество неизвестных параметров много меньше количества уравнений. Решение плохо обусловленного уравнения (25) получаем методом минимизации определителя:

В результате поиска оптимальных параметров из выражения (26) получены параметры для стохастической модели токов калия (23).
- определение вероятностей ИИК токов калия задержанного и аномального выпрямления в интервалах группирования. На фигуре 20 показана гистограмма для плотности распределения ИИК и аппроксимация 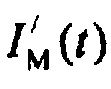 , полученная с помощью стохастической модели токов ионов калия. Из фигуры 20 наблюдается соответствие распределения и графика сглаживающей функции, полученное для интервала монотонной реполяризации. Там же даны временные зависимости и для составляющих стохастической модели тока задержанного
, полученная с помощью стохастической модели токов ионов калия. Из фигуры 20 наблюдается соответствие распределения и графика сглаживающей функции, полученное для интервала монотонной реполяризации. Там же даны временные зависимости и для составляющих стохастической модели тока задержанного 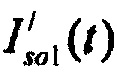 ,
, 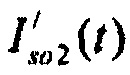 аномального
аномального 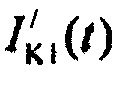 выпрямления. Для контроля формы стохастической модели токов задержанного выпрямления применена смесь двух распределений минимального значения. Составляющие тока калия быстрого и медленного задержанного выпрямления показаны пунктирными линиями
выпрямления. Для контроля формы стохастической модели токов задержанного выпрямления применена смесь двух распределений минимального значения. Составляющие тока калия быстрого и медленного задержанного выпрямления показаны пунктирными линиями 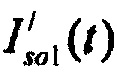 и
и 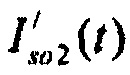 . Составляющим стохастической модели токов калия соответствуют вероятности распределения ИИК на j-м временном интервале группирования (см. фигура 20).
. Составляющим стохастической модели токов калия соответствуют вероятности распределения ИИК на j-м временном интервале группирования (см. фигура 20).
Формулы для расчета вероятностей распределения ИИК на временных интервалах группирования соответственно для стохастических моделей токов калия быстрого и медленного задержанного выпрямления pso1 j, pso2 j и аномального выпрямления pK1 j имеют вид:

Из выражения (15) следует, что вероятность распределения ИИК на временных интервалах группирования пропорциональна нормированной вероятности ИИК и отношению значения составляющей модели к значению модели на заданном интервале группирования.
- определение критерия адекватности r стохастической модели токов калия задержанного и аномального выпрямления в опорной точке эпикарда KMC.
Адекватность стохастической модели токов калия устанавливается из условия соответствия составляющих стохастической модели и полученных на ее основе гистограмм распределений отдельных компонент тока калия: 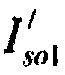 ,
, 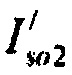 и
и 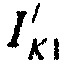 . Для анализа параметров распределения с различной формой авторами применен энтропийно-параметрический критерий проверки адекватности сглаживающего распределения выборочным данным [19], в основе которого лежит преобразование несимметричных распределений к симметричным распределениям с последующим установлением соответствия в пространстве энтропии и контрэксцессса.
. Для анализа параметров распределения с различной формой авторами применен энтропийно-параметрический критерий проверки адекватности сглаживающего распределения выборочным данным [19], в основе которого лежит преобразование несимметричных распределений к симметричным распределениям с последующим установлением соответствия в пространстве энтропии и контрэксцессса.
Формула для расчета критерия адекватности стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления в опорной точке компьютерной модели сердца пациента имеет вид:

где rso1, rso2 и rKl независимые составляющие критерия, рассчитанные для симметричных
выборок случайных величин вероятности распределения ИИК тока калия задержанного и аномального выпрямления.
Составляющие критерия вычисляют по формулам:
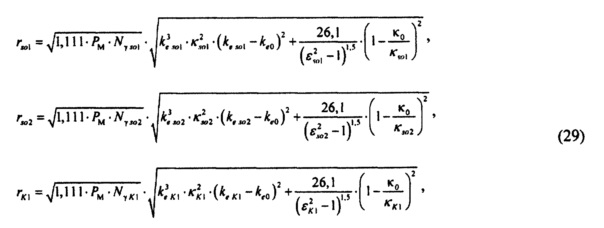
где ke so1, κso1, ke so2, κso2, ke K1, κK1, - коэффициенты энтропии и контрэксцесса симметрично распределенных случайных величин Zso1, Zso2 и ZK1 для тока калия быстрого и медленного задержанного и аномального выпрямления.
Применение критерия возможно, если задано соотношения между случайной величиной [t], распределенной по отдельной компоненте стохастической модели, и симметрично распределенной случайной величиной Z [20].
Формирование распределений вероятностей ИИК симметричных случайных величин ZK1, Zso1 и Zso2 для стохастических моделей составляющих тока калия аномального выпрямления, медленного и быстрого задержанного выпрямления даны на фигурах 21, 22 и 23, соответственно.
Распределения вероятностей ИИК симметричных случайных величин ZK1, Zso1 и Zso2 формируются на основе гистограмм распределения вероятностей ИИК 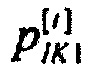 ,
, 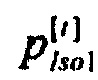 и
и 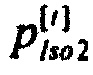 по временным интервалам группирования для стохастической модели тока калия аномального, быстрого и медленного задержанного выпрямления, которые приведены на фигурах 21а, 22а и 23а, соответственно. Для построения преобразования на основе гистограмм определяются значения элементов
по временным интервалам группирования для стохастической модели тока калия аномального, быстрого и медленного задержанного выпрямления, которые приведены на фигурах 21а, 22а и 23а, соответственно. Для построения преобразования на основе гистограмм определяются значения элементов 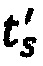 вектора-столбца временных отсчетов ts по формуле
вектора-столбца временных отсчетов ts по формуле

где m - количество интервалов группирования; ns - количество временных отсчетов вектора в одном интервале группирования ИИК; s - порядковый номер отсчета.
Вероятности распределения ИИК токов задержанного и аномального выпрямления для s-го временного отсчета рассчитываются по формулам:

Вектор-столбец временных отсчетов ts необходим для построения гистограмм вероятностей распределения ИИК по интервалам группирования. Каждому s-му временному отсчету 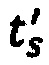 вектора-столбца временных отсчетов ts соответствует вероятность распределения ИИК для составляющих стохастической модели токов калия. Формально вероятность распределения ИИК для любого момента времени задана стохастической матрицей тока калия для 5-го отсчета времени
вектора-столбца временных отсчетов ts соответствует вероятность распределения ИИК для составляющих стохастической модели токов калия. Формально вероятность распределения ИИК для любого момента времени задана стохастической матрицей тока калия для 5-го отсчета времени 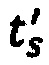 вида:
вида:
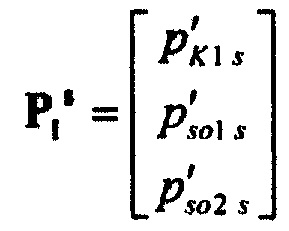 .
.
Вероятности распределения ИИК по случайным величинам отсчетов времени связаны с показательным распределением случайной величины Y с помощью следующих соотношений. Для стохастических моделей быстрого и медленного задержанного выпрямления авторами используется преобразование для распределения минимального значения случайной величины tj к случайной величине yso j, имеющей показательное распределение. Формула преобразования имеет вид:

где αso, μso - параметры масштаба и смещения распределений.
Для стохастической модели аномального выпрямления используется преобразование распределение Вейбулла-Гнеденко вида:

где αK1, μK1, βK1 - параметры масштаба, смещения и формы распределения Вейбулла-Гнеденко.
Распределения вероятностей ИИК 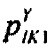 ,
, 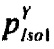 и
и 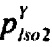 s-х значений случайных безразмерных величин YK1, Yso1 и Yso2 для стохастической модели тока калия аномального выпрямления, медленного и быстрого задержанного выпрямления приведены на фигурах 21б, 22б и 23б, соответственно.
s-х значений случайных безразмерных величин YK1, Yso1 и Yso2 для стохастической модели тока калия аномального выпрямления, медленного и быстрого задержанного выпрямления приведены на фигурах 21б, 22б и 23б, соответственно.
Отражение s-х значений случайных величин YK1, Yso1 и Yso2 относительно начала координат позволяет сформировать матрицы значений симметрично распределенных случайных безразмерных величин ZK1, Zso1 и Zso2. Так как количество значений матрицы увеличивается в 2 раза, то связанные с симметрично расположенными значениями вероятности уменьшаются так же в два раза. Симметричные распределения вероятностей ИИК 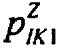 ,
, 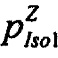 и
и 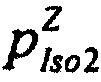 для значений случайных безразмерных величин ZK1, Zso1 и Zso2 для стохастической модели тока калия аномального выпрямления, быстрого и медленного задержанного выпрямления приведены на фигурах 21в, 22в и 23в, соответственно.
для значений случайных безразмерных величин ZK1, Zso1 и Zso2 для стохастической модели тока калия аномального выпрямления, быстрого и медленного задержанного выпрямления приведены на фигурах 21в, 22в и 23в, соответственно.
Расчет коэффициентов энтропии и контрэксцессов для симметрично распределенных случайных величин ZK1, Zso1 и Zso2 проводится по гистограммам распределения этих величин. Для построения гистограмм распределения случайных величин ZK1, Zso1 и Zso2 выделяются максимальные max[Zso1], max[Zso2], max[ZK1] и минимальные min[Zso1], min[Zso2], min[ZK1] значение для каждой случайной величины и рассчитываются интервалы группирования данных

Интервалы группирования используются для определения ранжированных значений 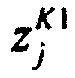 ,
, 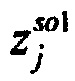 ,
, 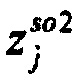 , минимальных
, минимальных 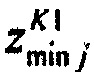 ,
, 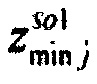 ,
, 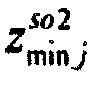 и максимальных
и максимальных 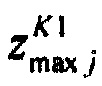 ,
, 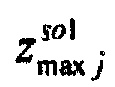 ,
, 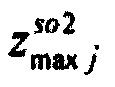 значений границ интервалов группирования данных.
значений границ интервалов группирования данных.
Распределение вероятности ИИК 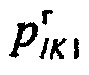 ,
, 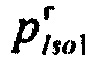 ,
, 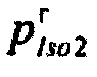 по интервалам группирования случайных величин ZK1, Zso1 и Zso2 рассчитывается по формулам:
по интервалам группирования случайных величин ZK1, Zso1 и Zso2 рассчитывается по формулам:
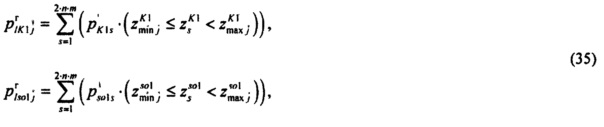
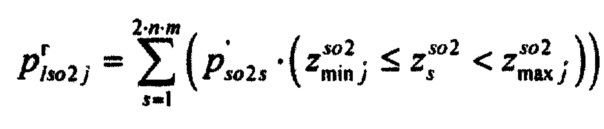
Гистограммы распределений вероятностей ИИК 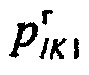 ,
, 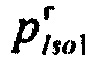 ,
, 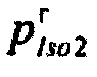 по интервалам группирования случайных величин ZK1, Zso1 и Zso2 для стохастических моделей тока калия аномального выпрямления, быстрого и медленного задержанного выпрямления приведены на фигурах 21г, 22г и 23г, соответственно.
по интервалам группирования случайных величин ZK1, Zso1 и Zso2 для стохастических моделей тока калия аномального выпрямления, быстрого и медленного задержанного выпрямления приведены на фигурах 21г, 22г и 23г, соответственно.
Для полученных распределений справедливо следующее положение: если распределение ИИК по временным интервалам группирования соответствует моделям составляющих токов калия, то случайные величины ZK1, Zso1 и Zso2 распределены в соответствии с распределением Лапласа. Тогда для установления корректности стохастической модели токов калия задержанного и аномального выпрямления достаточно, чтобы коэффициенты энтропии и контрэксцесса распределений случайных величин ZK1, Zso1 и Zso2 соответствовали коэффициенту энтропии и контерэксцесса распределения Лапласа. Для расчета коэффициентов энтропии симметрично распределенных случайных величин ZK1, Zso1 и Zso2 используются выражения:
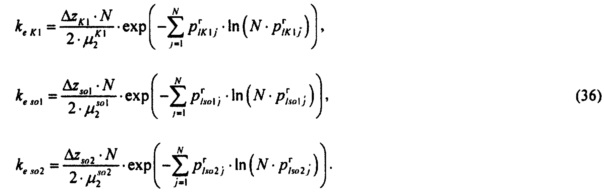
где, 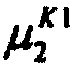 ,
, 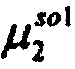 ,
, 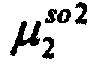 - вторые центральные моменты распределений.
- вторые центральные моменты распределений.
Для расчета контрэксцесса распределения случайных величин ZK1, Zso1 и Zso2 используются выражения:

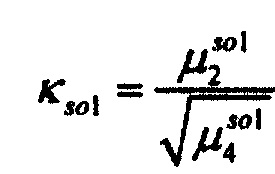 ,
,
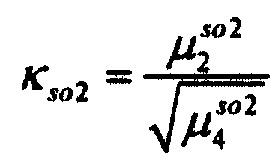 ,
,
где 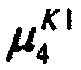 ,
, 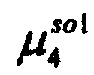 ,
, 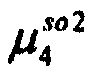 - четвертые центральные моменты распределений.
- четвертые центральные моменты распределений.
Преобразование к симметричному распределению и вычисление параметров по выражениям (36) и (37) позволяют проводить оценку соответствия гистограмм распределений для отдельных составляющих стохастических моделей тока калия в едином пространстве критерия адекватности г стохастической модели токов калия задержанного и аномального выпрямления.
- сравнение критерия адекватности с его максимальным значением. Выбор справедливой модели стохастической модели тока задержанного и аномального выпрямления выполняется на основе сравнения критерия адекватности r с максимальным значением критерия, заданного с помощью уровня значимости принятия решения α: 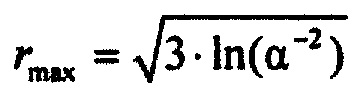 . Модель принимается справедливой, если критерий адекватности r меньше некоторого максимального значения. r≤rmax
. Модель принимается справедливой, если критерий адекватности r меньше некоторого максимального значения. r≤rmax
Изменение критерия для стохастической модели токов и ее составляющих от весового коэффициента KK1 стохастической модели тока калия аномального выпрямления приведено на фигуре 24, а, откуда можно видеть, что наиболее приемлемый результат получен при значении коэффициента, равного 0,325, при котором значение критерия равно 1,5. На фигуре 24, б показана зависимость параметра формы γ распределения вероятности ИИК для тока калия аномального выпрямления от весового коэффициента модели KK1, откуда следует, что параметр формы γ в области значений весового коэффициента модели тока калия 0,25<KK1<0,45 монотонно убывает с увеличением весового коэффициента KK1. На фигуре 24 в и г приведены зависимости параметров стохастической модели тока калия задержанного и аномального выпрямления от весового коэффициента KK1 для параметров масштаба λso1, λso2, λK1 и для параметров смещения μso, μso2, μK1 соответственно. Из приведенных зависимостей следует, что изменения параметров модели от весового коэффициента сохраняют гладкость в области изменения весового коэффициента модели 0,25<KK1<0,45.
- коррекция весовых коэффициентов стохастической модели тока калия задержанного и аномального выпрямления в опорных точках. Если критерий r больше критического значения, то проводится коррекция весовых коэффициентов стохастической модели и повторяются выполнение действия блоков, включенных в цикл из 4 - действий:
1 - определение параметров стохастической модели токов задержанного и аномального выпрямления;
2 - определение вероятности ИИК токов калия задержанного и аномального выпрямления в интервалах группирования;
3 - определение критерия адекватности стохастических моделей токов задержанного и аномального выпрямления;
4 - сравнение критерия с максимальным значением для выбора стохастической модели тока задержанного и аномального выпрямления.
- принятие решения: «Параметры стохастической модели тока калия задержанного и аномального выпрямления определены корректно». Если на этапе сравнения критерий адекватности модели меньше некоторого максимального решения, то стохастическая модель токов задержанного и аномального выпрямления адекватна распределению вероятностей ИИК. Принятие решения: «Параметры стохастической модели тока калия аномального выпрямления определены корректно» необходимо для сохранения параметров формы и масштаба стохастической модели тока аномального выпрямления для дальнейших расчетов. Так как распределение ИИК для стохастической модели тока калия аномального выпрямления полностью содержится в выборке значений потенциала эпикарда, то после выделения распределения ИИК тока калия аномального выпрямления из всей совокупности данных и построения корректной аппроксимации этой выборки, следует сохранить неизменными параметры распределения при проведении дальнейших вычислений.
- определение значений тока калия аномального выпрямления. Далее модель тока калия аномального выпрямления считается известной. Для определения параметров стохастической модели тока реполяризации эпикарда используются значения тока калия аномального выпрямления, рассчитанные по формуле 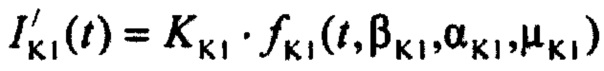 для всех значений вектора вектору временных отсчетов tm.
для всех значений вектора вектору временных отсчетов tm.
Следующим четвертым отличительным признаком предлагаемого изобретения является «Определение тока реполяризации эпикарда в опорных точках компьютерной модели сердца пациента». Схема алгоритма определения тока реполяризации эпикарда в опорных точках компьютерной модели сердца пациента приведена на фигуре 15. Входными данными для алгоритма является разность вероятностей группирования ИИК для положительных и отрицательных отсчетов.
- формирование стохастической модели токов реполяризации эпикарда. Стохастическая модель токов реполяризации эпикарда включает в себя 1ю, 2ю и 3ю фазы развития трансмембранного потенциала действия. Общая форма стохастической модели токов реполяризации эпикарда имеет вид

где 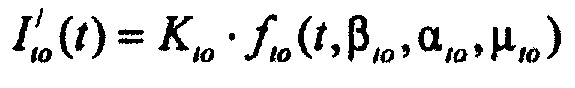 - стохастическая модель переходных транзитных токов эпикарда;
- стохастическая модель переходных транзитных токов эпикарда; 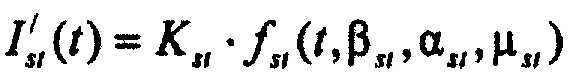 - стохастическая модель медленных деполяризующих токов кальция (отрицательный знак модели обусловлен ее деполяризующим действием); Kto, Kst и Ki - весовые коэффициенты стохастической модели токов реполяризации эпикарда;
- стохастическая модель медленных деполяризующих токов кальция (отрицательный знак модели обусловлен ее деполяризующим действием); Kto, Kst и Ki - весовые коэффициенты стохастической модели токов реполяризации эпикарда; 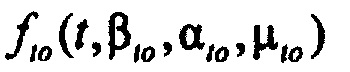 и
и 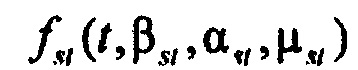 - плотности распределений ИИК для переходных транзитных токов и медленных деполяризующих токов кальция соответственно; βto, αto, μto, βst, αst, μst - параметры распределений.
- плотности распределений ИИК для переходных транзитных токов и медленных деполяризующих токов кальция соответственно; βto, αto, μto, βst, αst, μst - параметры распределений.
Использование статистических функций с контролируемой формой распределений для моделирования составляющих тока реполяризации позволяет сделать модели гибкими и учитывать изменение формы ионных токов. При этом ионные токи детальных математических моделей развития потенциала используются для оценки начальных значений и границ параметров формы стохастических моделей для составляющих ионных токов. Следует отметить, что детальные модели содержат информацию о форме токов одинакового функционального назначения. Априорная информация о токах является исходной для построения стохастической модели токов.
При построении модели токов реполяризации эпикарда используются результаты моделирования токов калия задержанного и аномального выпрямления. При этом параметры стохастической модели токов калия аномального выпрямления принимаются неизменными. Параметры стохастической модели токов калия задержанного выпрямления принимаются в качестве начальных значений моделирования. Дело в том, что ток калия задержанного выпрямления регулируют поступление кальция и, формально, большей частью оказываются скомпенсирован. В результатах эксперимента присутствуют остатки токов, восстановление которых проводится по остаточной информации.
- определение параметров стохастической модели тока реполяризации эпикарда путем. Для этого делается подстановка ранжированных значений времени tpj в стохастическую модель токов реполяризации эпикарда. Приравняв полученные выражения для плотностей распределения и отношения вероятностей для соответствующих интервалов группирования ИИК, к длительности интервалов времени группирования 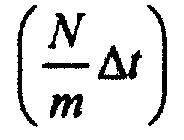 получим систему нелинейных плохо согласованных уравнений вида:
получим систему нелинейных плохо согласованных уравнений вида:

В векторной форме система уравнений (38) имеет вид:

где 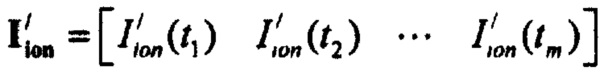 - матрица стохастической модели тока реполяризации эпикарда; р=[p1 р2 … pm] - матрица разностей вероятностей ИИК;
- матрица стохастической модели тока реполяризации эпикарда; р=[p1 р2 … pm] - матрица разностей вероятностей ИИК;
Ранжированные отсчеты времени независимы и представляют собой вектор tm размерности m. Векторное уравнение (39) является плохо обусловленным, так как количество неизвестных параметров много меньше количества уравнений. Решение плохо обусловленного уравнения (39) находим методом минимизации определителя.

В результате оптимизации выражения (40) получим параметры стохастической модели токов реполяризации эпикарда.
- определение тока реполяризации эпикарда в опорных точках компьютерной модели сердца пациента. Значения тока 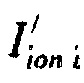 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента в моменты времени вектора tm используются для расчета коэффициента приведения тока при восстановлении модели. Формула для определения значений тока реполяризации эпикарда имеет вид
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента в моменты времени вектора tm используются для расчета коэффициента приведения тока при восстановлении модели. Формула для определения значений тока реполяризации эпикарда имеет вид
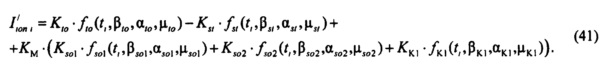
Зависимости токов от времени, полученные с помощью стохастических моделей, показаны на фигуре 25, где даны обозначения: 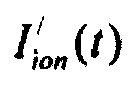 - ток реполяризации эпикарда;
- ток реполяризации эпикарда; 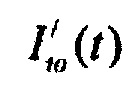 - переходный транзитный ток эпикарда;
- переходный транзитный ток эпикарда;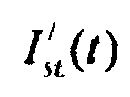 - медленный деполяризующий ток кальция;
- медленный деполяризующий ток кальция; 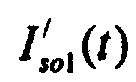 ,
, 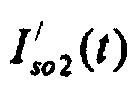 - быстрая и медленная компоненты тока калия задержанного выпрямления;
- быстрая и медленная компоненты тока калия задержанного выпрямления; 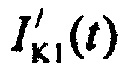 - ток калия аномального выпрямления.
- ток калия аномального выпрямления.
Следующим пятым отличительным признаком является «Восстановление потенциала в опорных точках эпикарда компьютерной модели сердца пациента». Это действие необходимо для сравнения восстановленного потенциала с потенциалом эпикарда, полученным в результате обработки ЭКС известного способа. Основные этапы процесса восстановления потенциала эпикарда иллюстрирует алгоритм на фигуре 16.
В соответствии с законом Ома для любого i-го момента времени ток через поверхность эпикарда пропорционален потенциалу эпикарда:

где Rот - сопротивление тканей тела.
Суммируя левые и правые части выражения (42) для всех отсчетов времени и учитывая неизменность сопротивления тканей организма, получим, что сумма потенциалов равна сумме токов:

Заменяя сумму потенциалов в левой части и сумму токов в правой части выражения (43) через коэффициент приведения потенциала эпикарда Bϕ и коэффициент приведения тока эпикарда В1, получим, что сопротивление среды пропорционально отношению приведенных коэффициентов для тока и потенциала.

Тогда для восстановления потенциалов эпикарда по значениям стохастической модели тока реполяризации эпикарда необходимо определить коэффициенты приведения потенциала и тока эпикарда.
- определение коэффициента приведения потенциала эпикарда. Для восстановления потенциала эпикарда определяется коэффициент приведения потенциала эпикарда, равный сумме потенциалов в опорной точке, полученных в результате обработки ЭКС.

- определение коэффициента приведения тока эпикарда. Коэффициент приведения тока, равный сумме значений рассчитанных с помощью стохастической модели токов реполяризации эпикарда в моменты отсчета времени ti по формуле

- определение значений восстановленного потенциала в опорных точках эпикарда компьютерной модели сердца. Для определения потенциала эпикарда достаточно значения тока эпикарда i-го момента времени умножить на отношение приведенного коэффициента потенциала и приведенного коэффициента тока

Значения восстановленного потенциала используются для построения «электрического портрета» сердца. Затем эти потенциалы используются при моделировании распространения возбуждения эпикарда.
Результат восстановления потенциала эпикарда приведен на фигуре 25, где обозначены ϕ - потенциал эпикарда, полученный при обработке ЭКС; ϕmod - восстановленный потенциал эпикарда с использованием стохастической модели распределения вероятностей ИИК токов реполяризации эпикарда. Из приведенных зависимостей следует их хорошее совпадение.
Затем осуществляется реализация следующего, шестого отличительного признака предлагаемого изобретения «Сравнение восстановленного и определенного по ЭКС потенциалов эпикарда». Сравнения потенциала эпикарда, определенного в результате обработки ЭКС известным способом, и потенциала эпикарда, восстановленного с использованием стохастической модели, необходимо для оценки точности моделирования.
Процесс сравнения задан с помощью формулы для максимально допустимой приведенной погрешности моделирования, равной разности между потенциалами эпикарда, восстановленного с использованием стохастической модели, и определенного по значениям ЭКС:
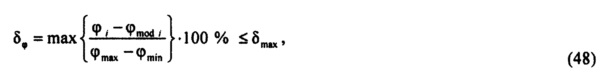
где ϕmin и ϕmax - минимальное и максимально значение потенциала эпикарда, полученные при восстановлении с помощью стохастической модели.
Сравнение потенциала ϕmod, восстановленного с помощью стохастической модели токов реполяризации эпикарда, и потенциала эпикарда ϕ, определенного по ЭКС на фигуре 12 иллюстрирует условный блок "Сравнение восстановленного и определенного по ЭКС потенциалов эпикарда".
Если при сравнении приведенная погрешность моделирования δϕ больше допустимого значения δmax, то осуществляется реализация следующего, шестого отличительного признака предлагаемого изобретения: «Коррекция параметров распределений стохастической модели тока реполяризации эпикарда». Коррекция проводится путем изменения параметров распределений βto, αto, μto, βst, αst, μst стохастической модели тока 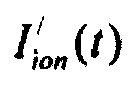 реполяризации эпикарда. Для этого изменяются начальные и граничные условия параметров при моделировании и повторяются три последних действия алгоритма: «Определение тока реполяризации эпикарда в опорных точках компьютерной модели сердца пациента», «Восстановление потенциала в опорных точках компьютерной модели сердца пациента» и «Сравнение восстановленного и определенного по ЭКС потенциала эпикарда».
реполяризации эпикарда. Для этого изменяются начальные и граничные условия параметров при моделировании и повторяются три последних действия алгоритма: «Определение тока реполяризации эпикарда в опорных точках компьютерной модели сердца пациента», «Восстановление потенциала в опорных точках компьютерной модели сердца пациента» и «Сравнение восстановленного и определенного по ЭКС потенциала эпикарда».
Принятие решения: «Значения тока реполяризации эпикарда определены корректно». Если значение приведенной погрешности δϕ, моделирования меньше принятого максимального значения осуществляется принятие решения «Значение тока реполяризации эпикарда определены корректно».
Таким образом, выявление изменения ионных токов эпикарда способствует выбору антиаритмических препаратов для эффективного лечения аритмий, применению их с минимально возможной вероятностью аритмогенного действия, разработке комплекса медицинских мероприятий по профилактике внезапной сердечной смерти и эффективному лечению жизнеугрожающих аритмий [14, 18, 21].
При таких патологических состояниях, как ишемическая болезнь сердца, гипертоническая болезнь сердца, врожденные и приобретенные пороки сердца, при гипертрофии миокарда, при электролитных и гормональных нарушениях происходит значительно снижение реполяризующих токов замедленного IKr, IKs и аномального IK1 выпрямления, что, в свою очередь, сопровождается повышением риска возникновения сложных нарушений ритма и проводимости. Таким образом, контроль токов калия аномального выпрямления в результате использования предлагаемого изобретения позволит врачу-кардиологу прогнозировать возникновение аритмий и оперативно использовать высокотехнологические кардиохирургические методы лечения.
Литература
1. Пат. 2360597 Российская Федерация. Способ определения электрической активности сердца / Бодин О.Н., Гладкова Е.А., Кузьмин А.В., Митрохина Н.Ю., Мулюкина Л.А. - МПК А61В 5/0402,2006.10.07.2009 Бюл. №19.
2. Пат. 2409313 Российская Федерация. Способ неинвазивного электрофизиологического исследования сердца / Ревишвили А.Ш., Калинин В.В., Калинин А.В. - МПК А61В 5/0402 2006, А61В 5/055 2006, А61В 6/03, 2006. 20.01.2011 Бюл. №2.
3. Пат. 2435518 Российская Федерация. Способ неинвазивного электрофизиологического исследования сердца / Ревишвили А.Ш., Калинин В.В., Калинин А.В. - МПК А61В 5/0402 2006, А61В 5/055 2006, А61В 6/03,2006. 10.12.2011 Бюл. №34.
4. Пат. 2068651 Российская Федерация. Способ неинвазивной регистрации электрофизиологических характеристик скрдца и устройство для его осуществления / Блатов И.В., Титомир Л.И. - МПК А61В 5/05,10.11.1996.
5. Пат. 2489083 Российская Федерация. Способ неинвазивного определения электрофизиологических характеристик сердца / Бодин О.Н., Кузьмин А.В., Митрохина Н.Ю., Семерич Ю.С., Рябчиков Р.В. - МПК А61В 5/0402,2006. 20.05.2013 Бюл. №14.
6. Пат. 2448643(13) Российская Федерация. Электрокардиограф с измерением координат и параметров источника электрической активности сердца / Лебедев В.В., Крамм М.Н., Жихарева Г.В., Винокуров Д.С., Филонов Д.В., Стрелков И.О.
7. Амиров Р.З. Электрокардиотопография. М.: Медицина, 1965,142 с.
8. Антонов В.Ф., Черныш A.M., Пасечник В.И. Биофизика / М.: ВЛАДОС, 2000 - 288 с.
9. Исаков И.И., Кушаковский М.С., Журавлева Н.Б. Клиническая электрокардиография. Руководство для врачей. - Л.: Медицина. 1984. - 272 с.
10. Орлов В.Н. Руководство по электрокардиографии - М.; ООО "Московское медицинское агентство", 1997., 528 стр.
11. Рубин А.Б. Биофизика / Изд. МГУ, 2004 г. 944 с.
12. Титомир Л.И. Электрический генератор сердца. М.: «Наука», 1980. 371 стр.
13. Титомир Л.И., Трунов В.Г., Айду Э.А.И. Неинвазивная электрокардиотопография // М.: Наука, 2003. - 198 с.
14. Клинические рекомендации. Диагностика и лечение нарушений ритма сердца и проводимости. Часть 1 / Голицын СП., Кролачева Е.С., Майков Е.Б., Миронов Н.Ю.. Панченко Е.П.. Соколов С.Ф., Шлевков Н.Б. Кардиологический вестник. №2. 2014. T.IX. С. 3-43.
15. Клинические рекомендации / Москва, Министерство здравоохранения РФ. 2013. - 195 с.
16. Алиев P.P. Компьютерное моделирование электрической активности сердца / Успехи физических наук, 2010. Том. 41, №3. С. 44-63.
17. Бокерия О.Л., Ахобеков А.А. Ионные каналы и их роль в развитии нарушений ритма сердца / Анналы аритмологии. 2014. - T. 11., №3. Стр. 177-184.
18. Кузьмин B.C., Розенштраух Л.В. Ионные механизмы действия аритмических препаратов III класса. Кардиология. 2010. №7. - стр. 49-61.
19. Полосин В.Г., Бодин О.Н. Энтропийно-параметрический критерий проверки адекватности модели распределения ионных токов миокарда / Информационные технологии. М.: Том 22. №1, 2016. С. 65-71.
20. Полосин В.Г., Першенков П.П. Информационный способ установления справедливости гипотез несимметричных распределений / Измерительная техника. №12, 2013 г. С. 8-10.
21. Чернова А.А., Никулина С.Ю., Гульбис А.В. Генетические аспекты врожденного синдрома удлиненного интервала QT / Рациональная Фармакотерапия в кардиологии 2012, 8(5)-С. 694.
22. Школьникова М.А., Харлап М.С., Ильдарова Р.А., Березницкая В.В., Калинин Л.А. Диагностика, стратификация риска внезапной смерти и лечение основных молекулярно-генетических вариантов синдрома удлиненного интервала QT / Кардиология. 2011. №5.
23. Bueno-Orovio A., Cherry Е.М., Fenton F.H. Minimal model for human ventricular action potentials in tissue / Journal of Theoretical Biology, 2008. Doi. 10.1016/jtbi. 2008.03.029.
24. Hodgkin A.L. and Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. / J. Physiol (Lond) 117: 500-544, 1952.
25. Hondeghem L.M., Carlsson L., Duker G. Instability and triangulation of the action potential predict serious proarrhythmia, but action potential duration prolongation is antiarrhythmic. Circulation 2001; 103: 2004-2013.
26. Iyer V., Mazhari R., Winslow R.L. A computational model of the human left ventricular epicardial myocyte. Biopsy's. 2004. V. 87. P. 1507-1525.
27. Kron L.H. The ECG field equation. - Bull. Math. Biophys., 1962, 24, №3, p. 277-278.
28. Luo C.H., Rudy Y.A.F model of the ventricular cardiac action potential // Circ. Res. 1991. V. 68. P. 1501-1526.
29. Nattel S., Maguy A., Le Bouter S., Yeh Y.H. Arrhythmogenic ion-channel remodeling in the heart: heart failure, myocardial infarction, and atrial fibrillation. Physiol Rev 2007; 87:425-456.
30. Pecaranda A., Cantalapiedra I.R., Bragard J., Echebarria B. Cardiac dynamics: a simplified model for action potential propagation / Theoretical Biology and Medical Modelling. - 2012. http://www.tbiomed.eom/content/9/1/50.
31. Priebe L., Beuckelmann D.J. Simulation study of cellular electric properties in heart failure. // Circ Res V. 82: P. 1206-1223, 1998.
32. Schilling R.J., Kadish A.H., Peters N.S. et al. Endocardial mapping of atrial fibrillation in the human right atrium using a non-contact catheter. - European Heart Journal. 2000. 21, P. 550-564.
33. Stewart P., Aslanidi O., Noble D., Noble P.J., Boyett M. R., Zhang H. Mathematical models of the electrical action potential of Purkinje fibre cells // (Philosophical Transactions of the Royal Society) Phil. Trans. R. Soc. A (2009). 367, P. 2225-2255, doi: 10.1098 / rsta.2008.0283.
34. Ten Tusscher KHWJ, Noble D., Noble P.J., Panfilov A.V. A model for human ventricular tissue/ Am. J. Physiol. Head. Circ. Physiol. 2004. V. 286. P. H1573-H1589.
35. Winslow R.L., Cortassa S., O'Rourke В., Hashambhoy Y.L., Rise J.J., Greenstein J.L. Integrative modeling of the cardiac ventricular myocyte / WIREs Systems Biology and Medicine. 2010.
ПЕРЕЧЕНЬ ПРИНЯТЫХ СОКРАЩЕНИЙ
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ I, II И III СТЕПЕНИ | 2015 |
|
RU2591839C1 |
| СПОСОБ И УСТРОЙСТВО РЕГИСТРАЦИИ МНОЖЕСТВЕННЫХ ОТВЕДЕНИЙ ЭЛЕКТРОКАРДИОСИГНАЛА | 2020 |
|
RU2764498C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2017 |
|
RU2651068C1 |
| Способ мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра | 2021 |
|
RU2758638C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2014 |
|
RU2565367C1 |
| СПОСОБ И УСТРОЙСТВО ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ОКАЗАНИИ ЭКСТРЕННОЙ КАРДИОЛОГИЧЕСКОЙ ПОМОЩИ | 2020 |
|
RU2737860C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ И ВИЗУАЛИЗАЦИИ РАСПРОСТРАНЕНИЯ ВОЗБУЖДЕНИЯ В МИОКАРДЕ | 2007 |
|
RU2358646C2 |
| СПОСОБ ОКАЗАНИЯ ЭКСТРЕННОЙ КАРДИОЛОГИЧЕСКОЙ ПОМОЩИ | 2016 |
|
RU2644303C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ СТОХАСТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2743897C1 |
| Способ контроля неопределённости стохастической системы при условной оценке центра плотности распределения | 2020 |
|
RU2746904C1 |
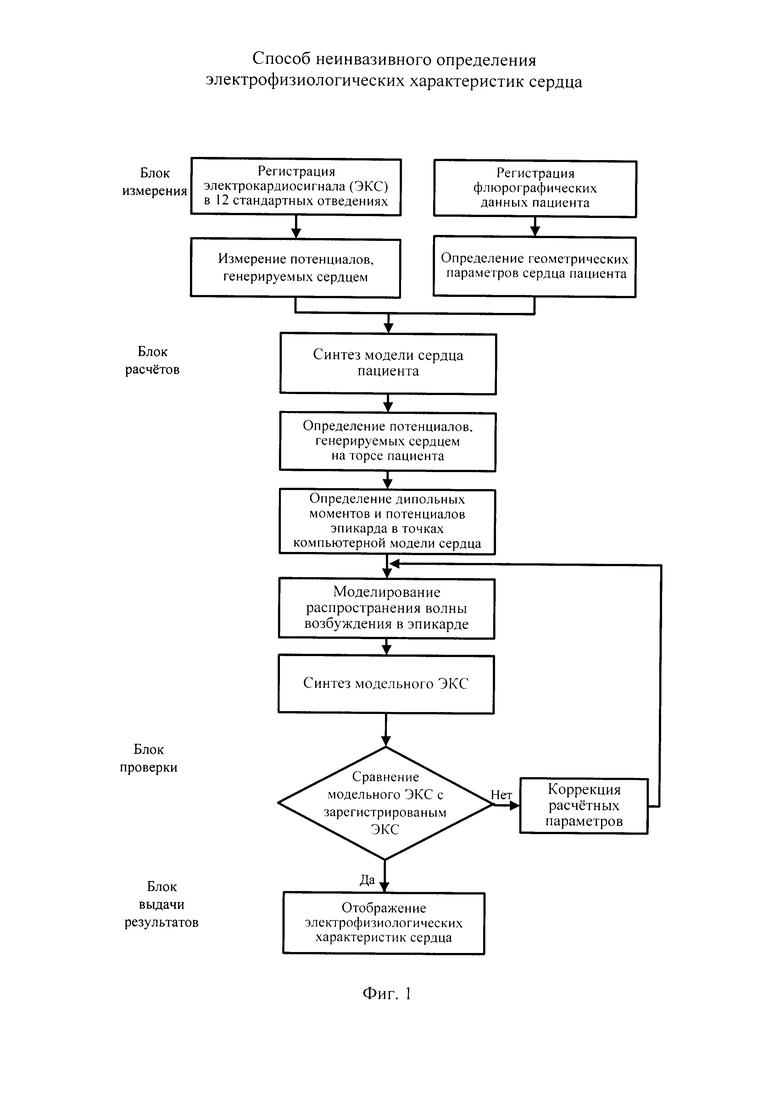
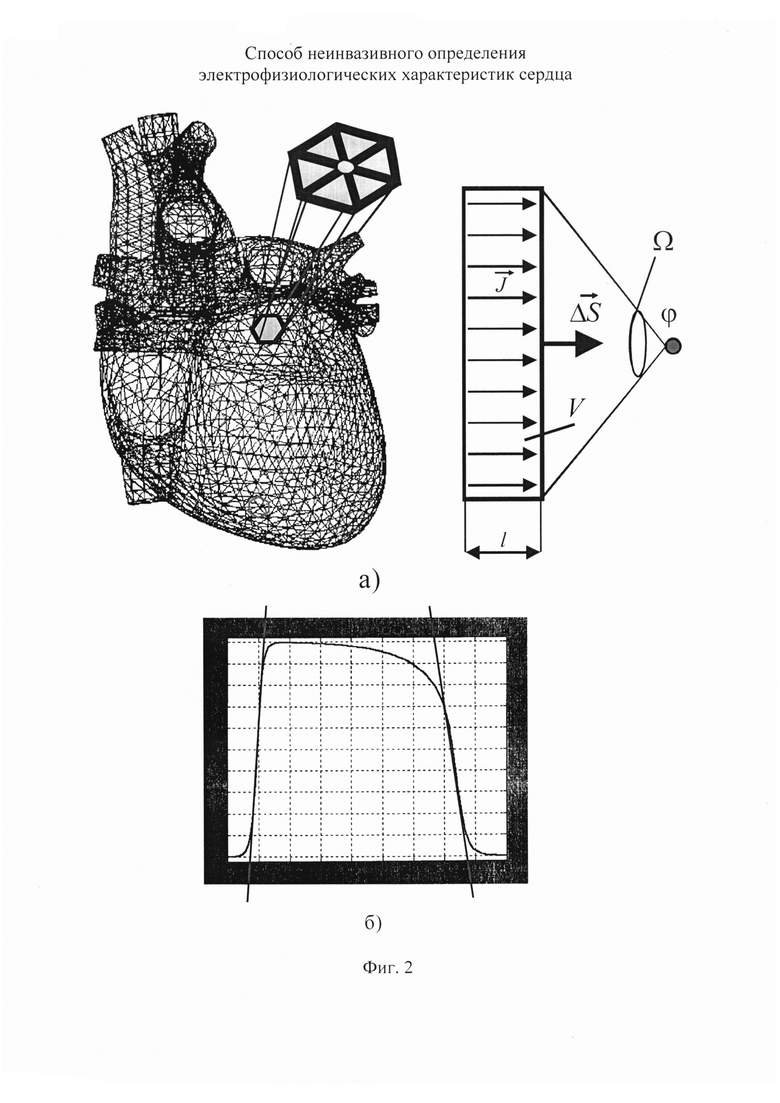
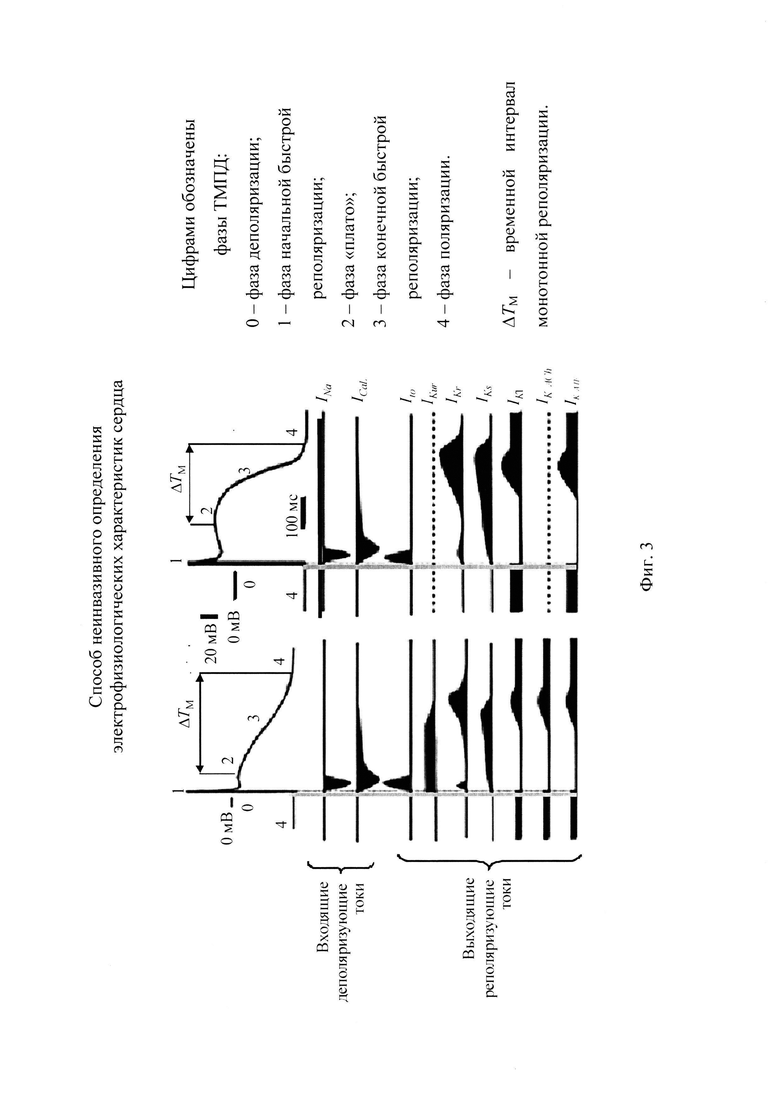
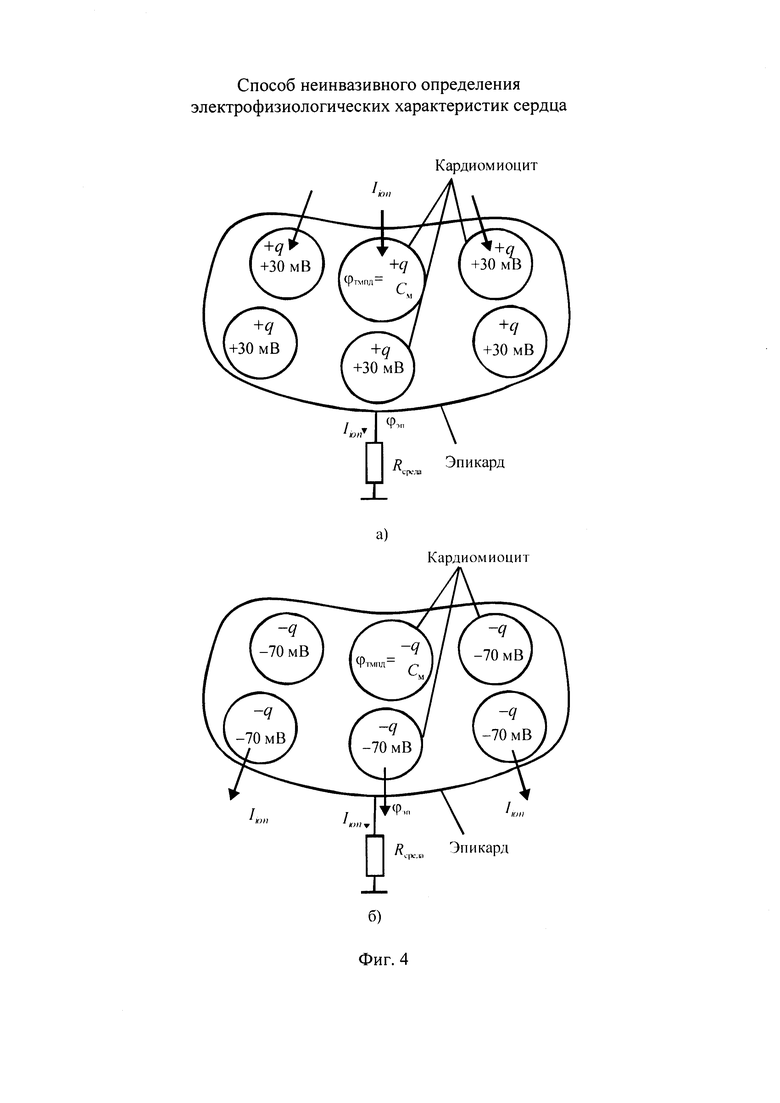
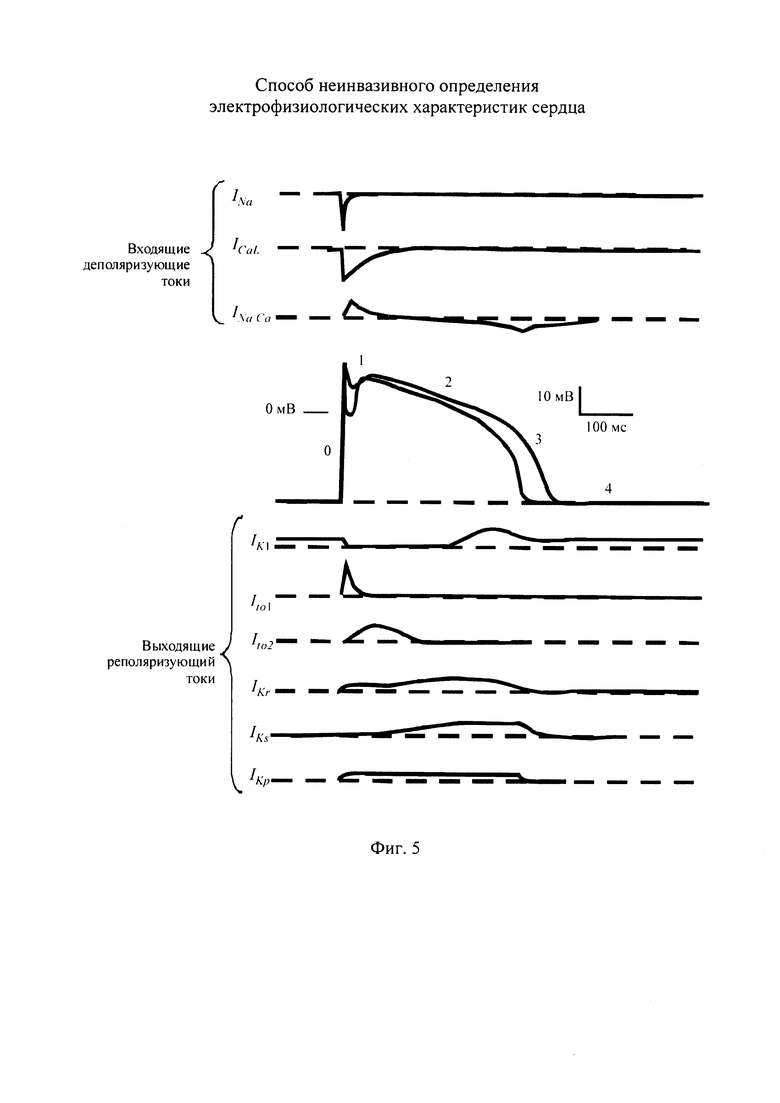
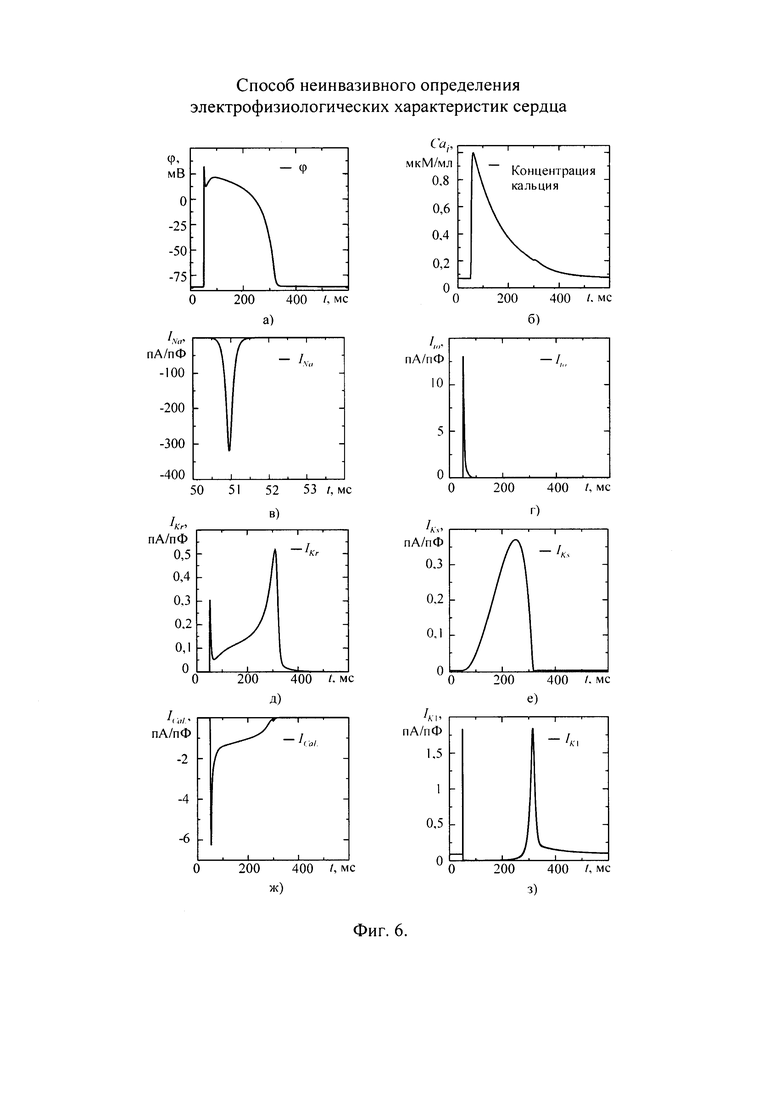
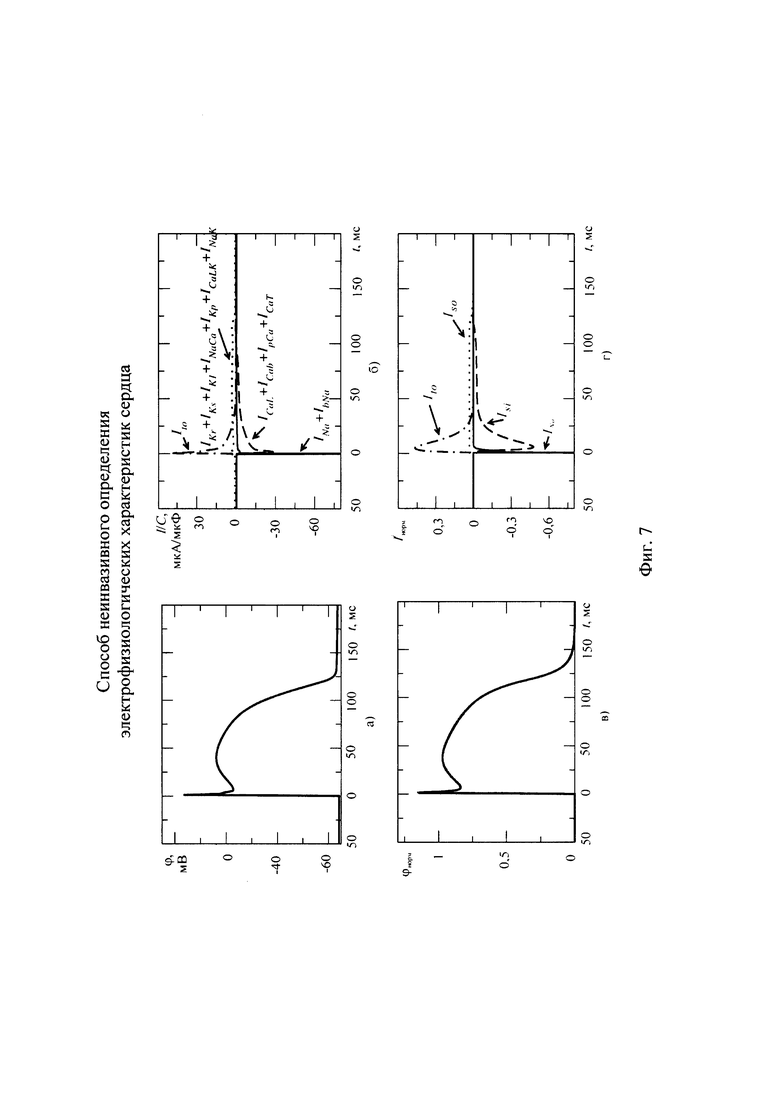
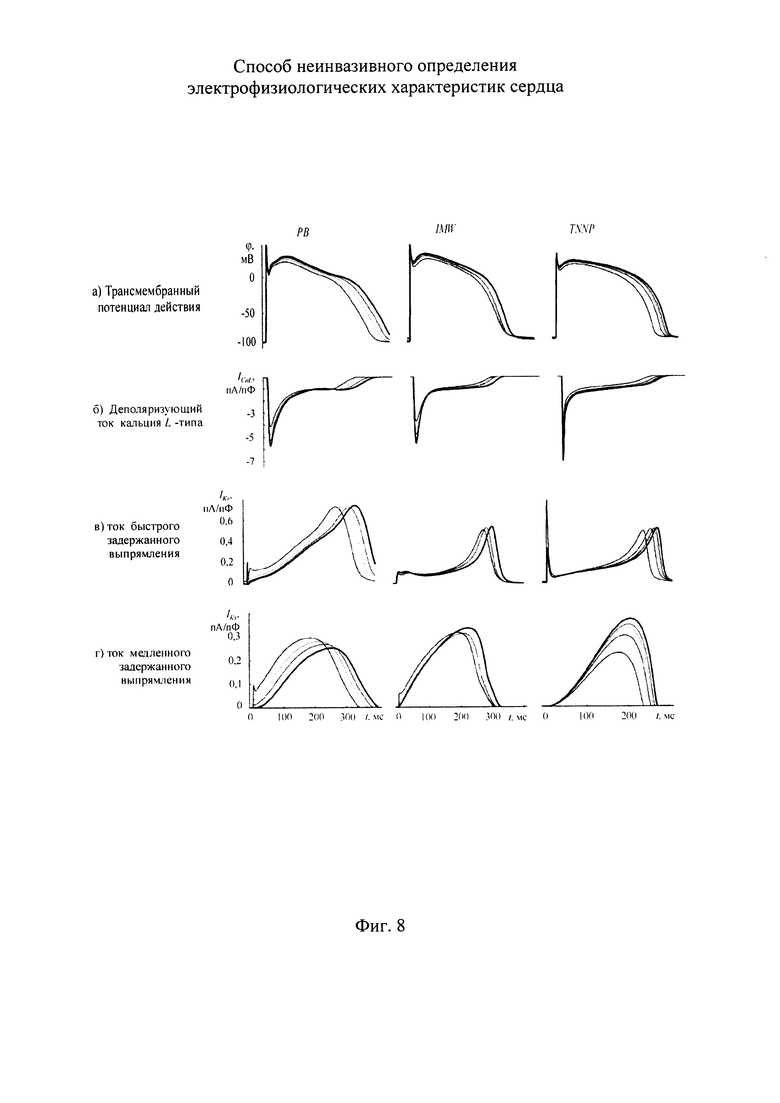
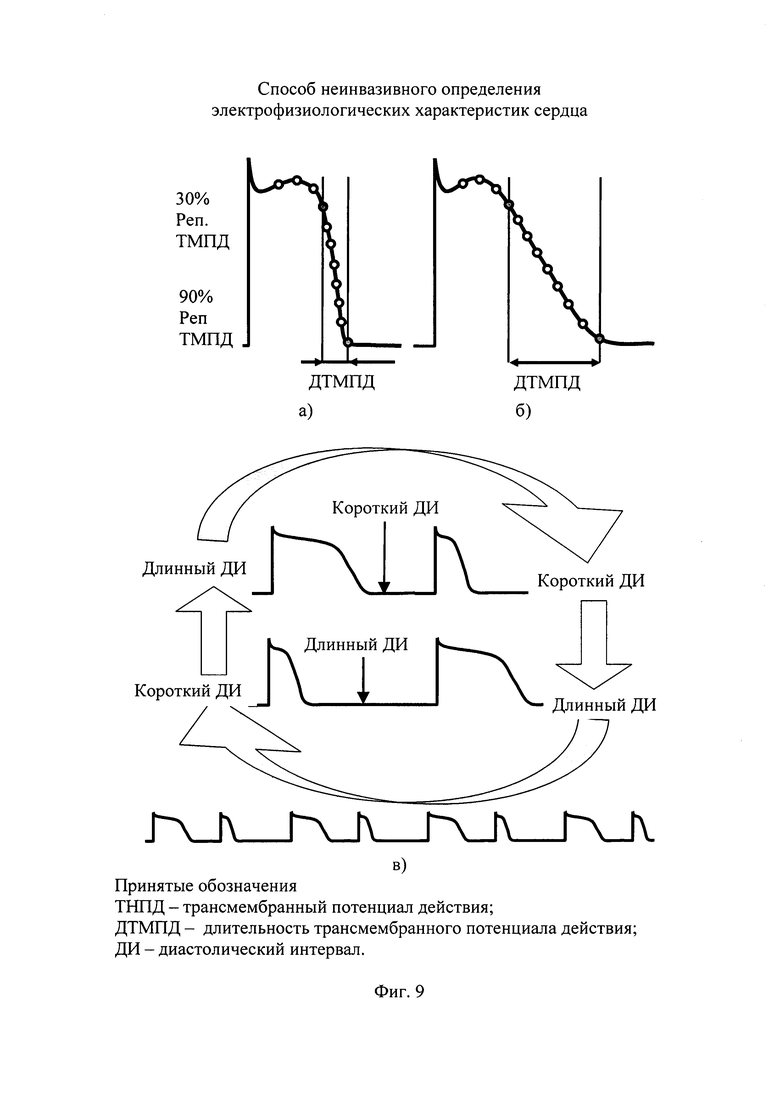
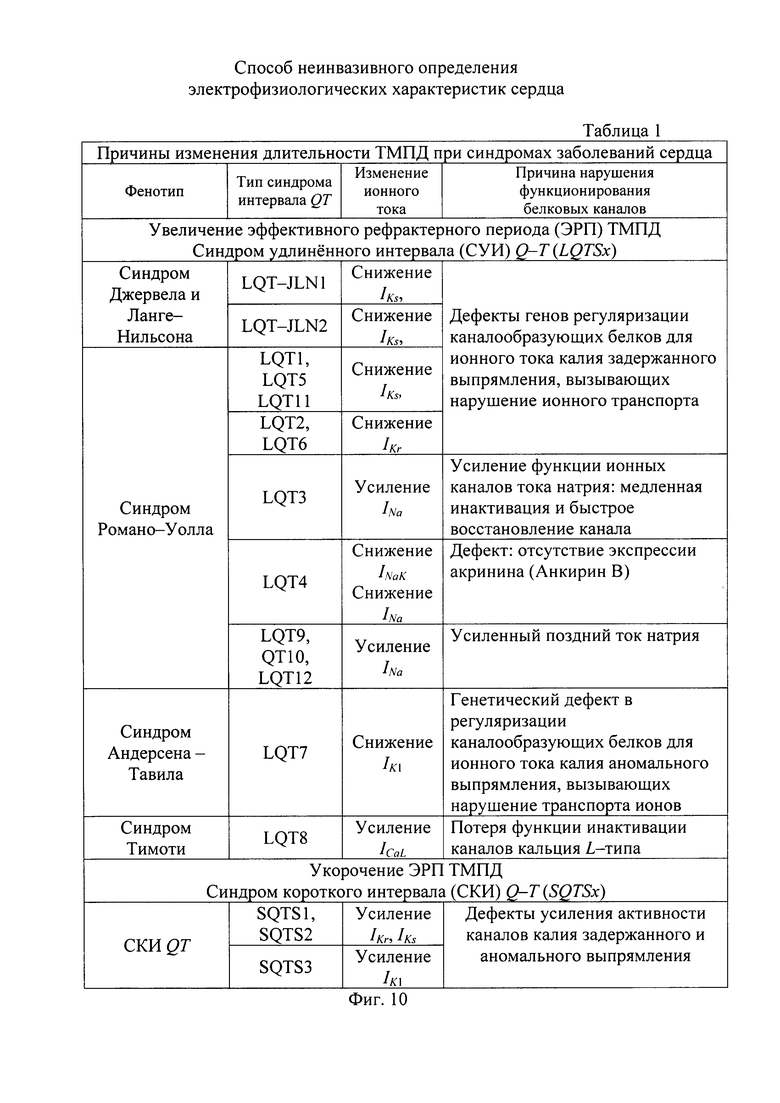
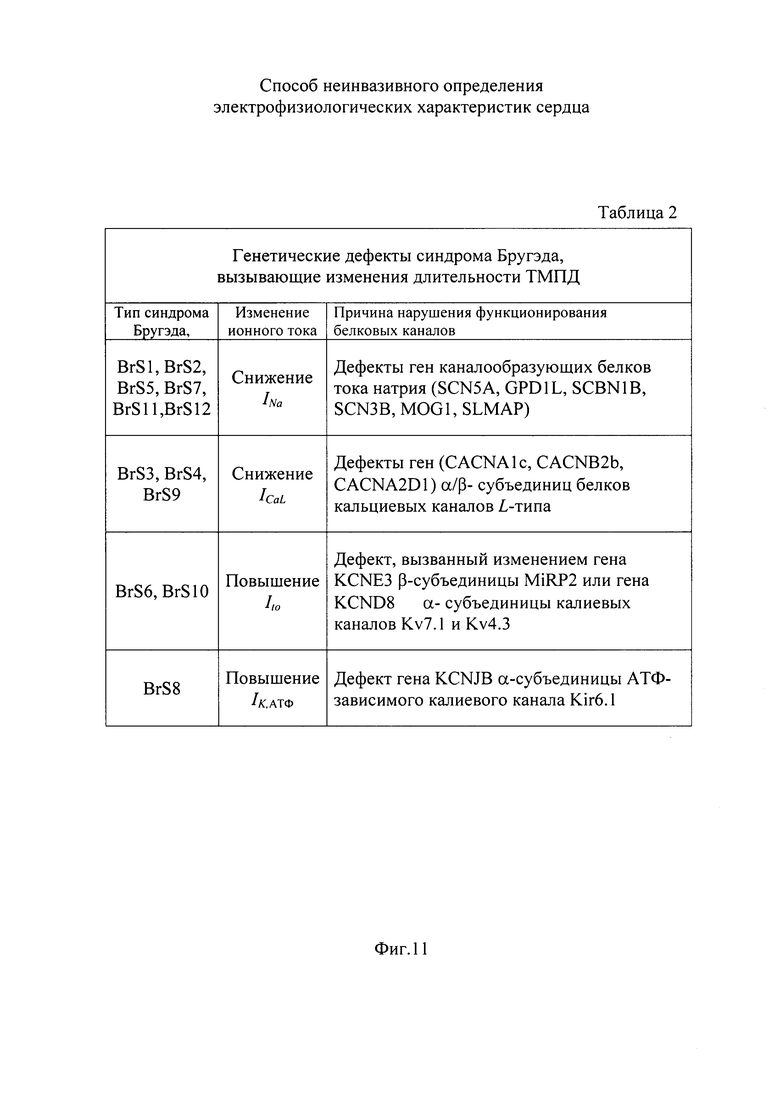
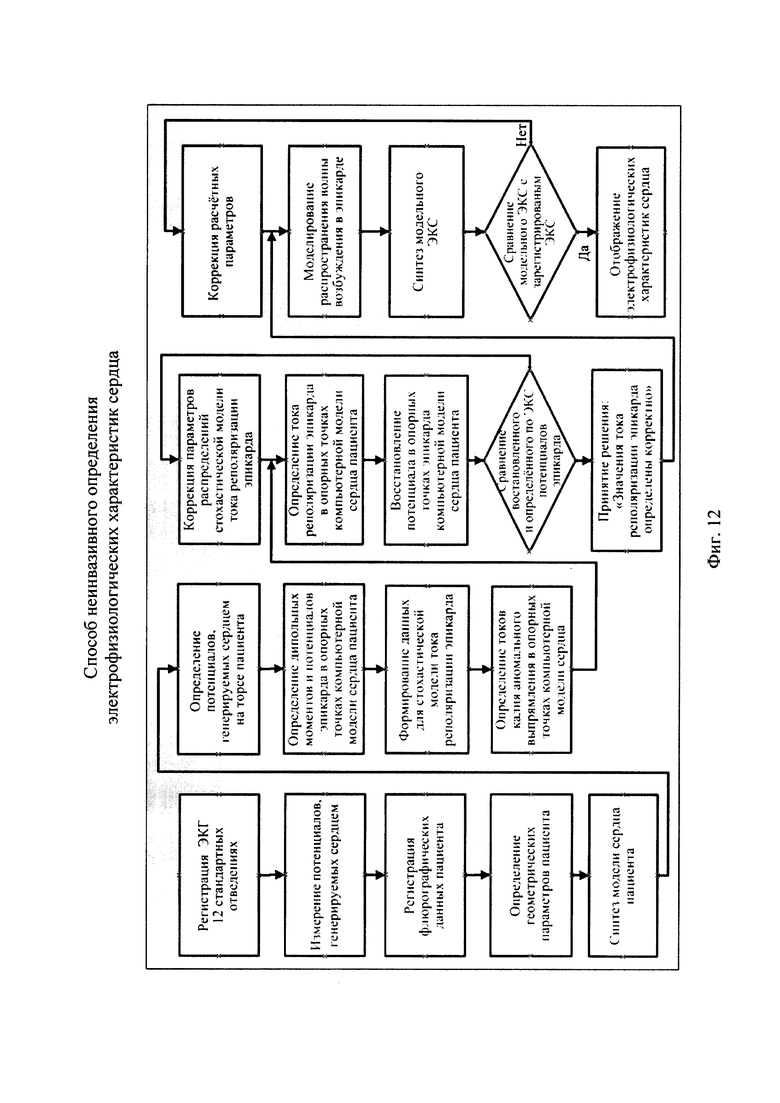

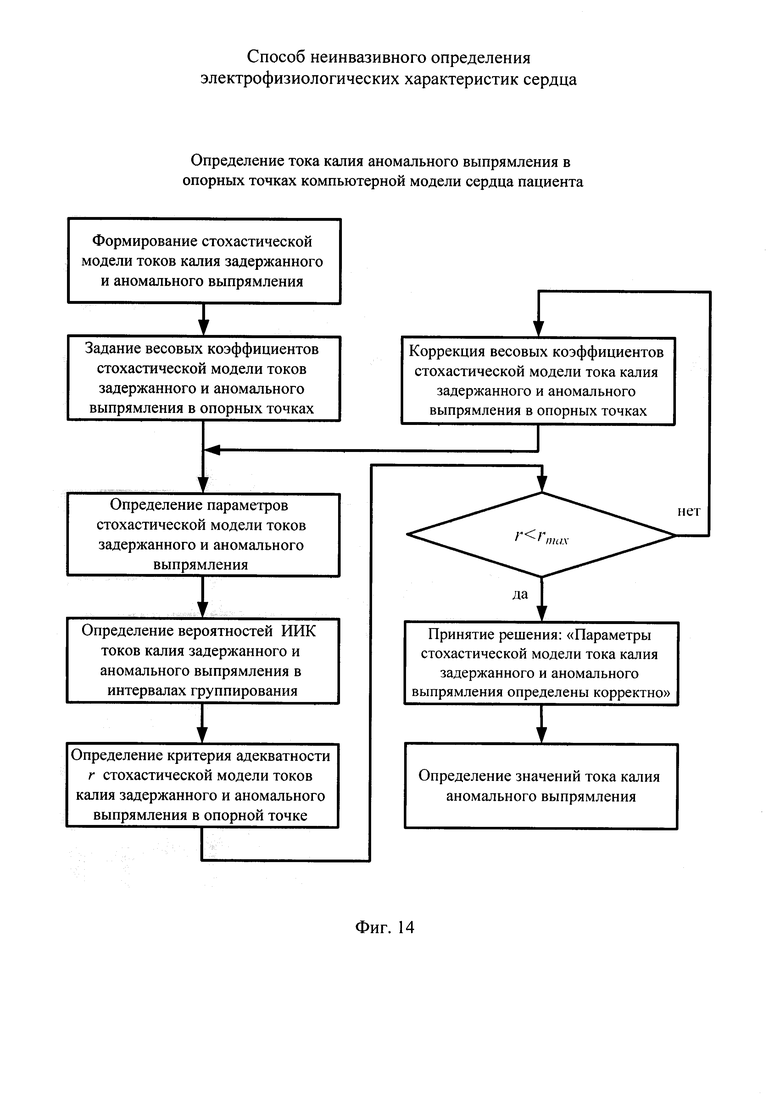
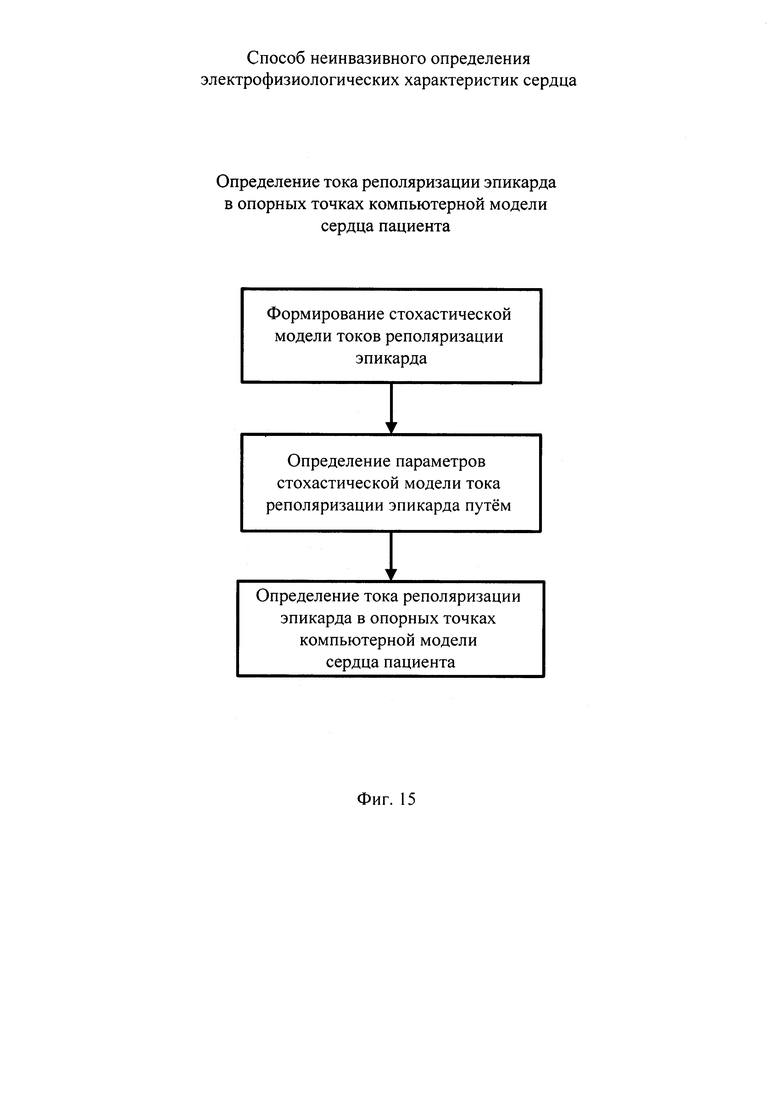
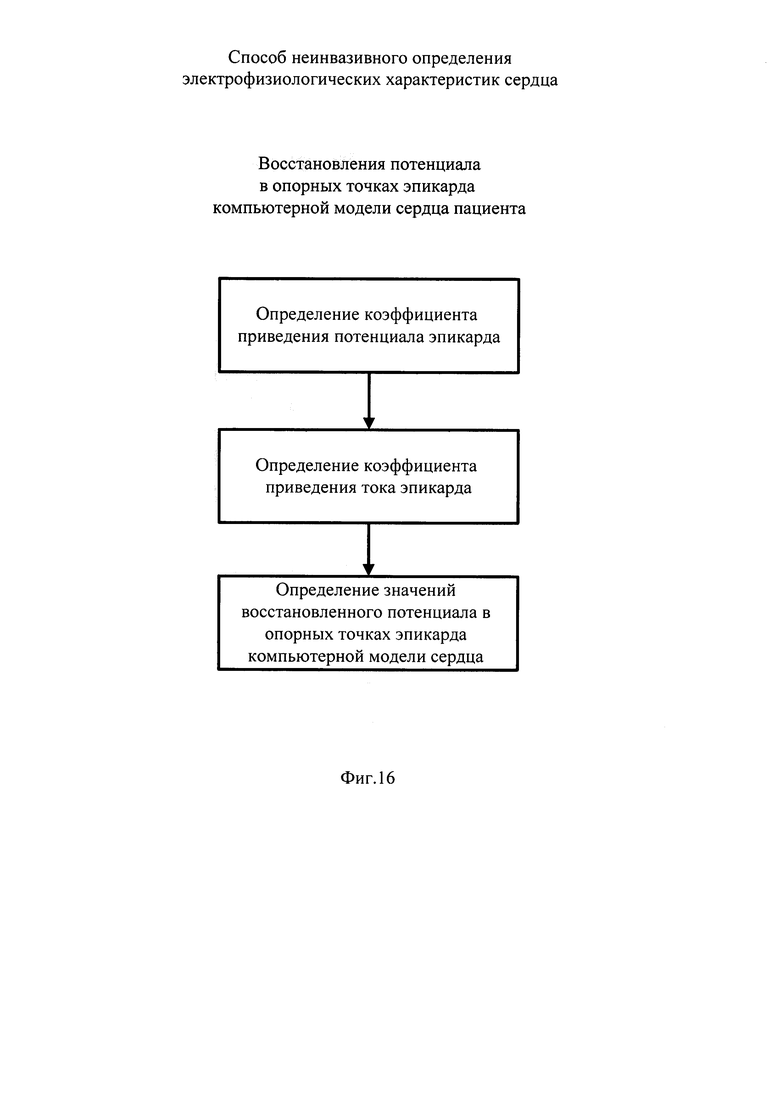
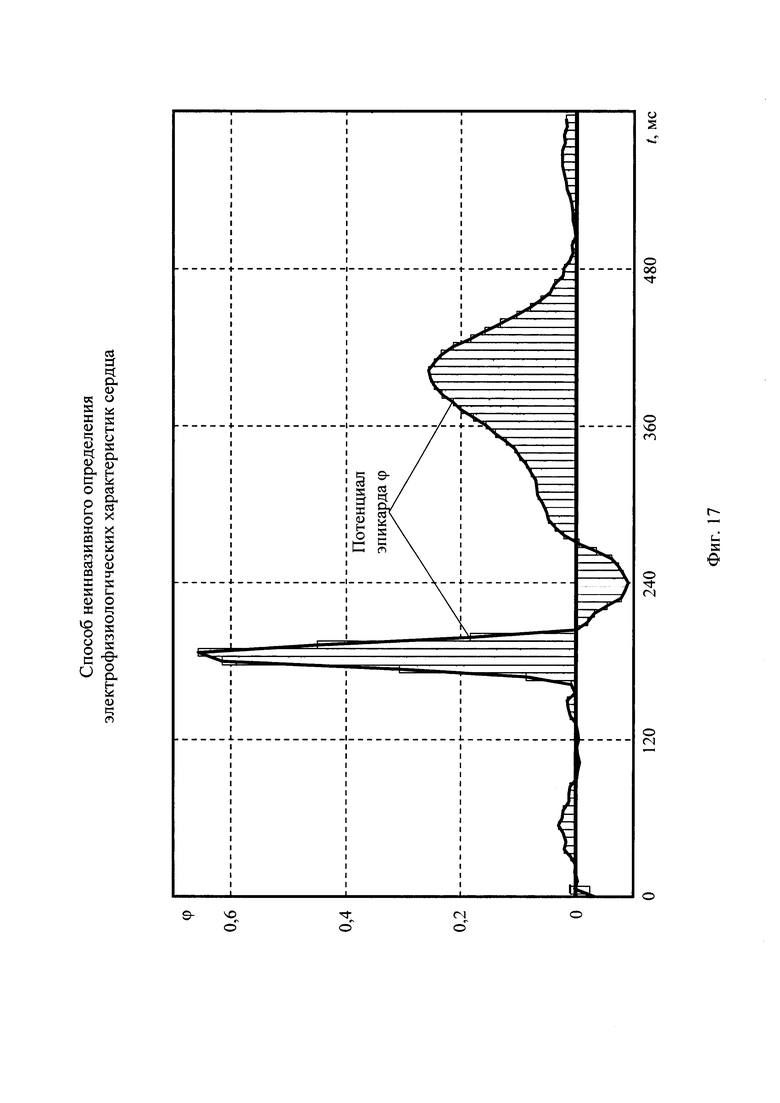
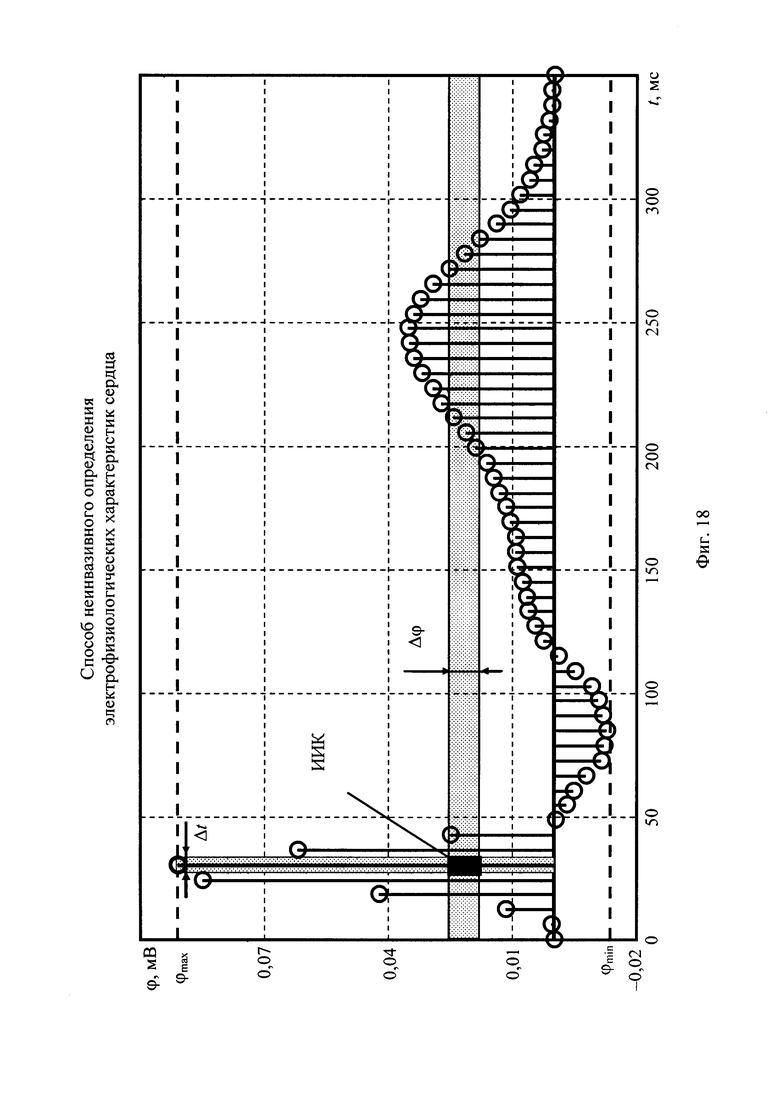
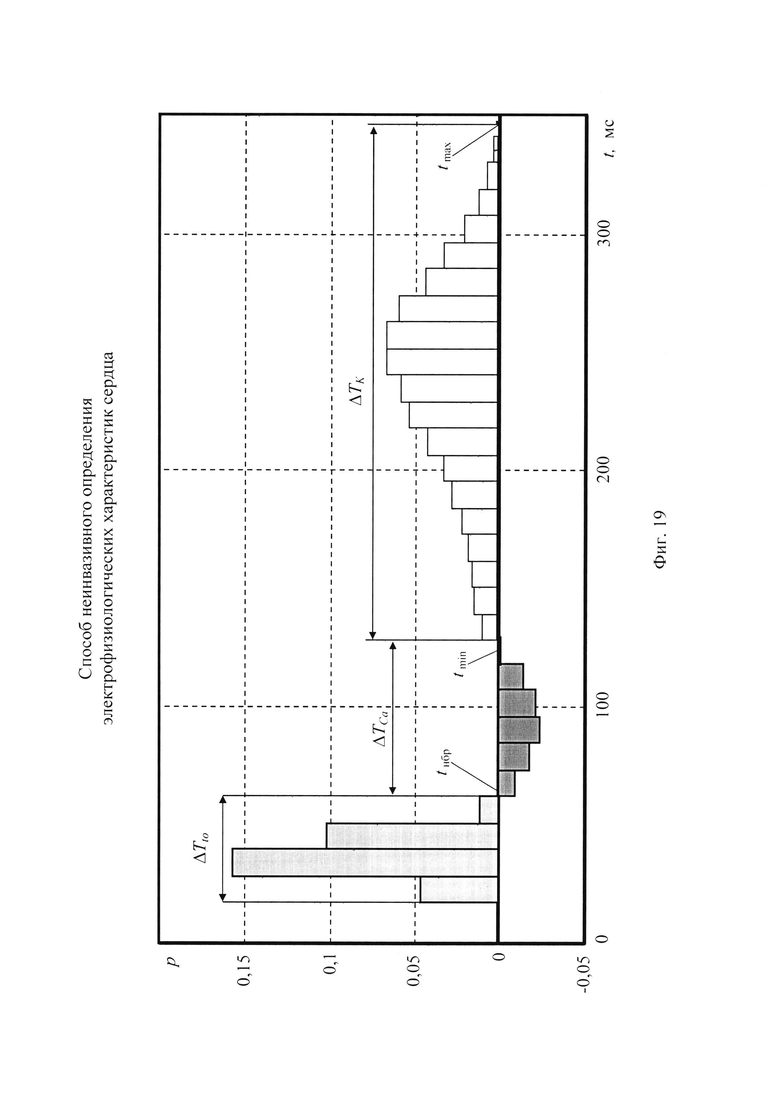
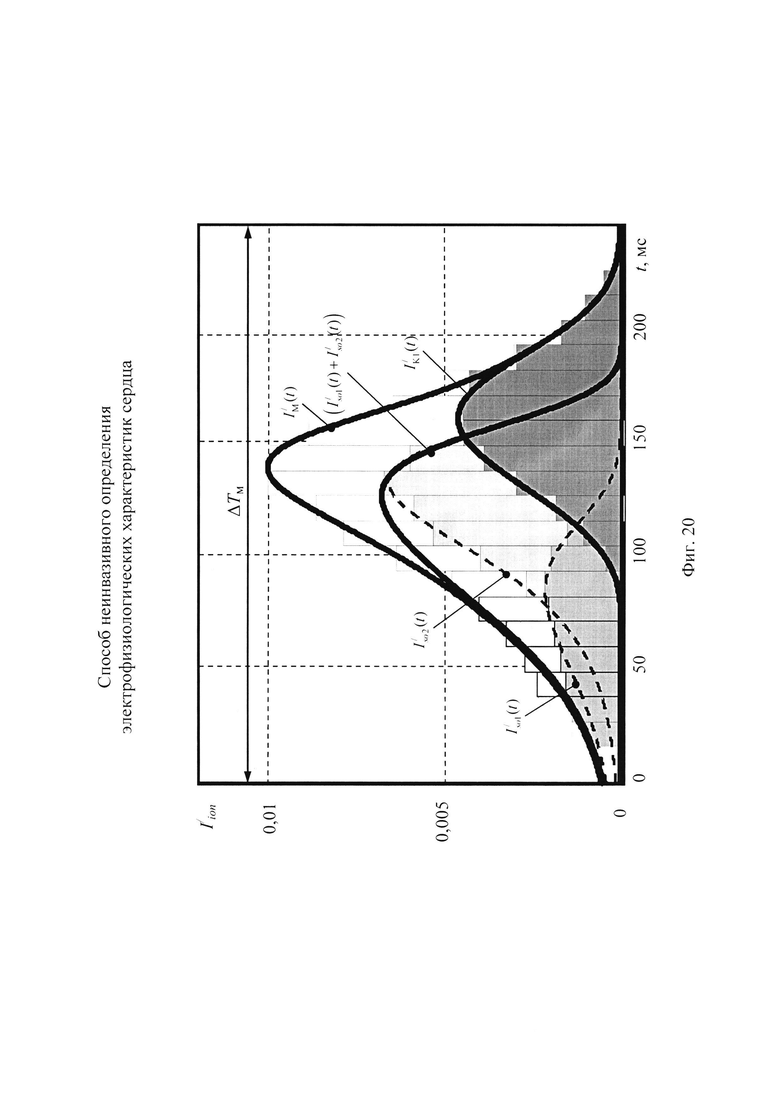
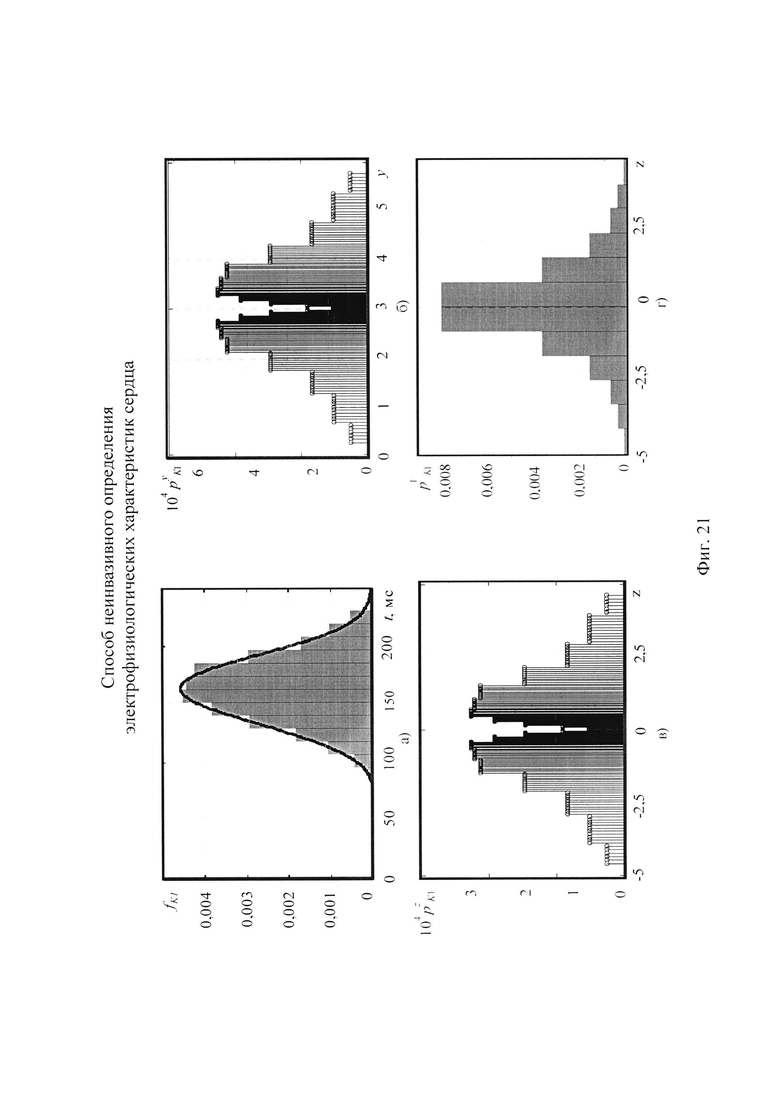
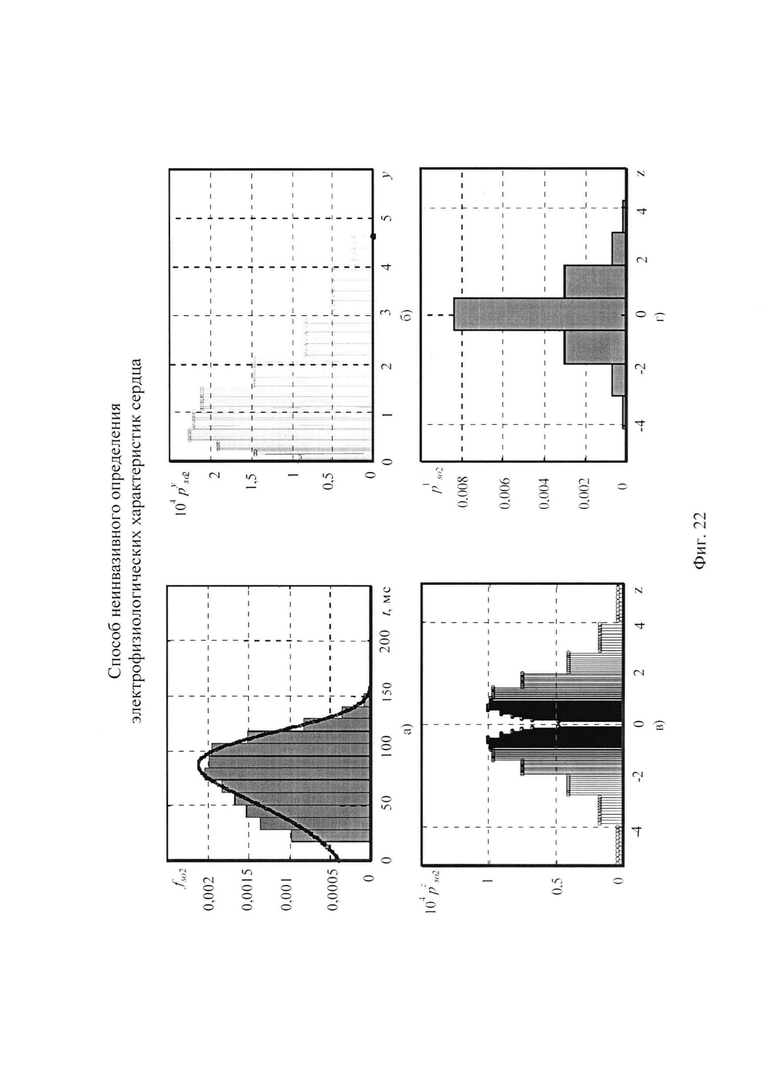
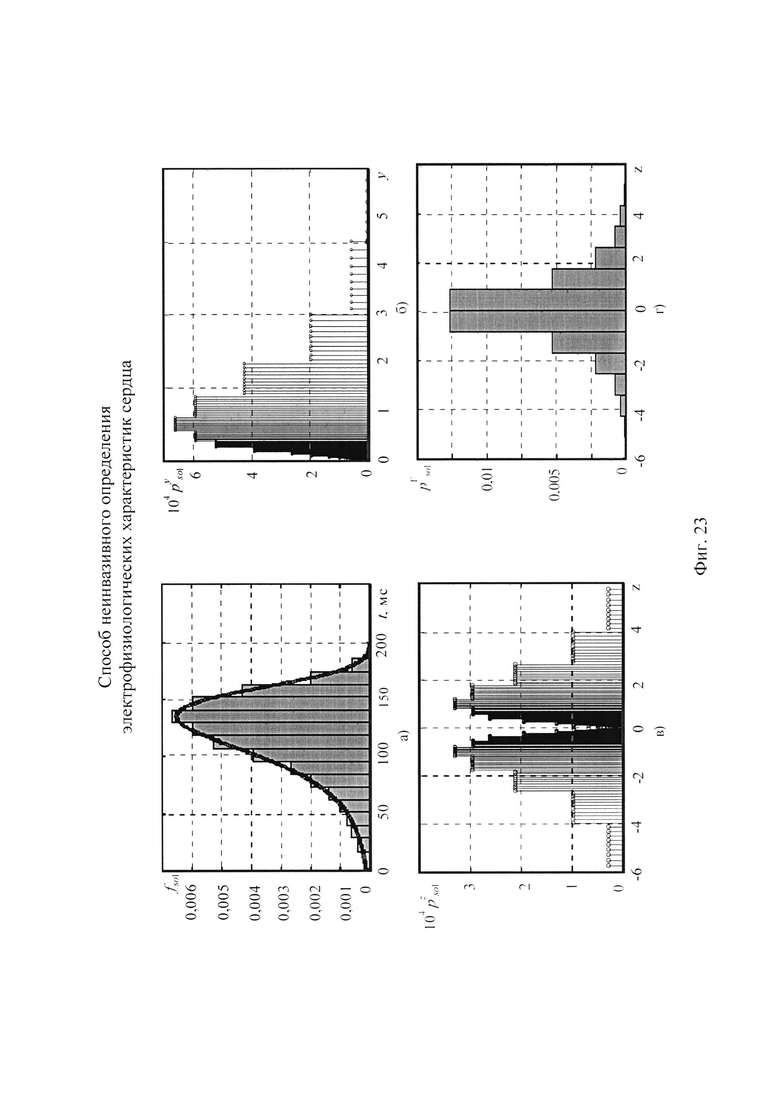
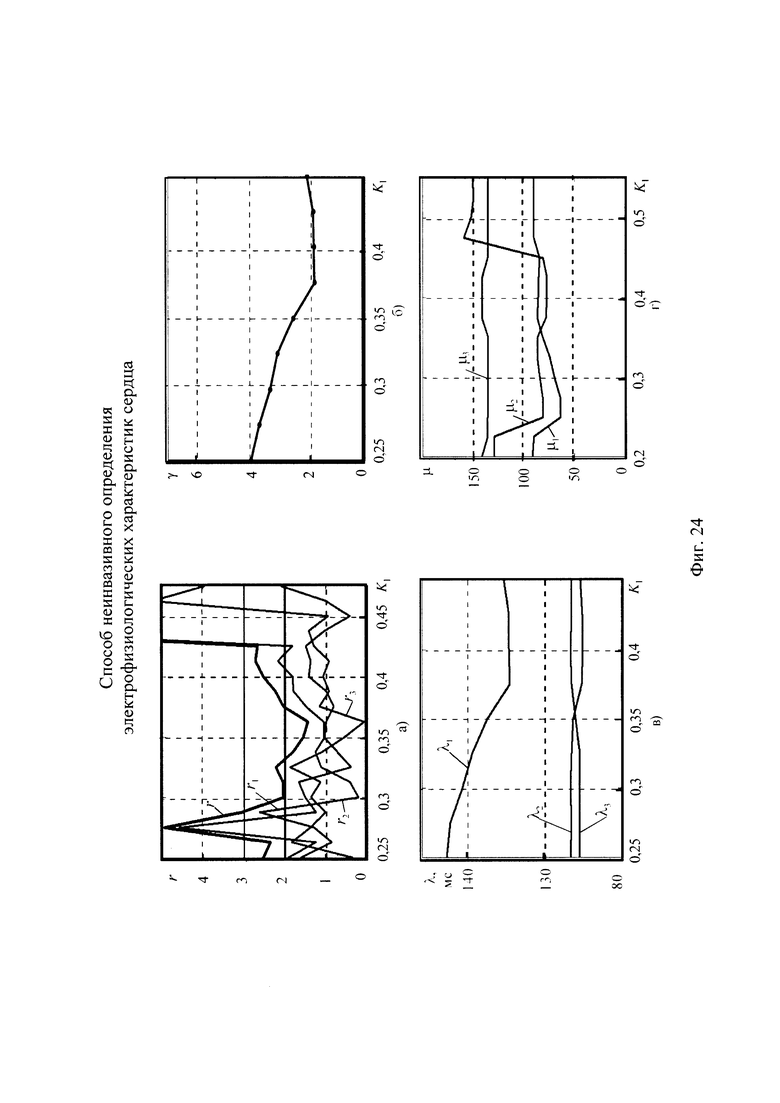
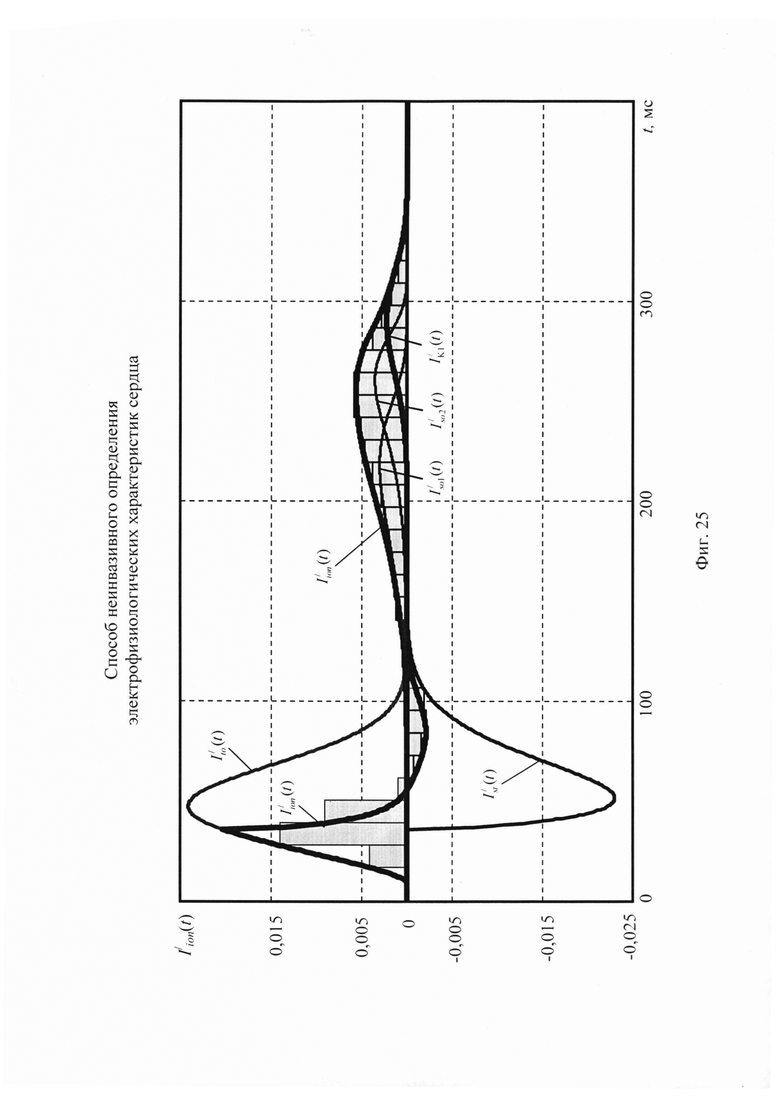
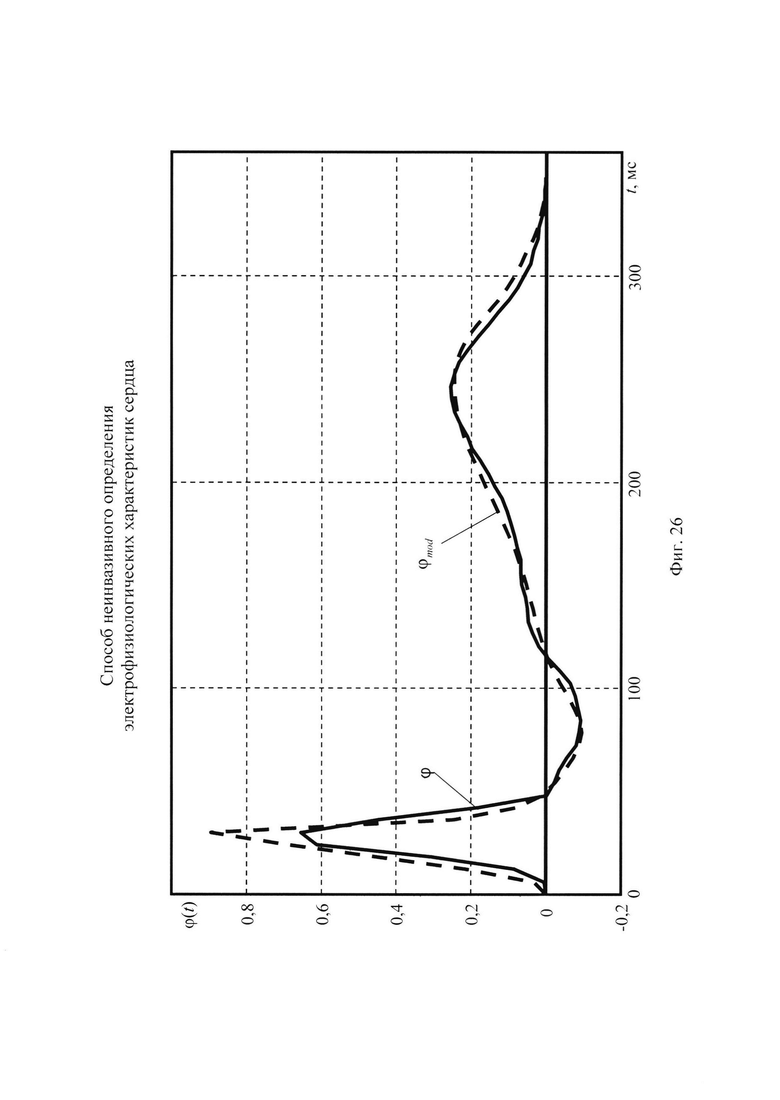
Изобретение относится к медицине, в частности к кардиологии. На основе известных детальных моделей формируется стохастическая модель тока реполяризации эпикарда и определяются ее параметры по выборкам значений потенциала эпикарда, найденного при решении обратной задачи электрокардиографии в опорных точках компьютерной модели сердца пациента. Способ позволяет расширить функциональные возможности электрокардиографического обследования, определить составляющие ионных токов по значениям потенциала эпикарда в опорных точках компьютерной модели сердца пациента. 26 ил.
Способ неинвазивного определения электрофизиологических характеристик сердца, заключающийся в том, что регистрируют электрокардиосигнал (ЭКС) и измеряют потенциалы, генерируемые сердцем, регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента, определяют по снимкам геометрические параметры сердца пациента, синтезируют компьютерную модель сердца пациента, определяют потенциалы, генерируемые сердцем на торсе пациента, определяют дипольные моменты и потенциалы эпикарда ϕ в опорных точках компьютерной модели сердца пациента, моделируют распространение волны возбуждения в эпикарде, синтезируют модельный ЭКС, сравнивают модельный ЭКС с зарегистрированным ЭКС, корректируют расчетные параметры модели распространения волны возбуждения в эпикарде путем изменения параметров при определении моментных распределений основных электрофизиологических характеристик на поверхности сердца и визуализируют электрофизиологические характеристики сердца на трехмерной модели сердца средствами компьютерной графики в наиболее удобном для восприятия виде, отличающийся тем, что дополнительно
- формируют данные для стохастической модели тока реполяризации эпикарда в опорных точках компьютерной модели сердца путем:
определения информационно-измерительного кванта (ИИК) γ для выборок значений потенциала эпикарда в опорных точках компьютерной модели сердца для одного кардиоцикла: γ=Δϕ⋅Δt, где Δt - время, необходимое для получения одного отсчета; 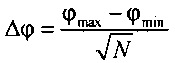 - мера ИИК, ϕmax, ϕmin и N - максимальное, минимальное значение и число отсчетов в выборке значений потенциала эпикарда в опорных точках компьютерной модели сердца;
- мера ИИК, ϕmax, ϕmin и N - максимальное, минимальное значение и число отсчетов в выборке значений потенциала эпикарда в опорных точках компьютерной модели сердца;
определения количества ИИК Nγ для стохастической модели тока реполяризации эпикарда 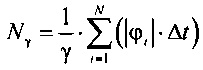 , где ϕi - i-e значение потенциала в выборке {ϕ} одного кардиоцикла;
, где ϕi - i-e значение потенциала в выборке {ϕ} одного кардиоцикла;
определения количества m ранжированных значений 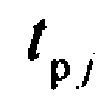 минимальных
минимальных 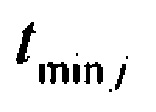 и максимальных
и максимальных 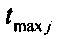 границ для временных интервалов группирования ИИК
границ для временных интервалов группирования ИИК
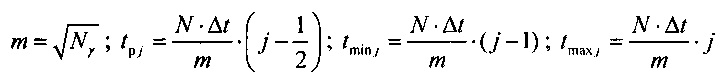
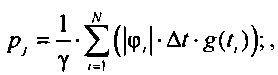 где
где 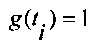 если
если 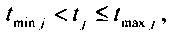 иначе
иначе 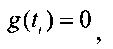
где j - порядковый номер временного интервала группирования ИИК;
определения распределения вероятностей ИИК 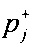 и
и 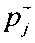 в j-м интервале группирования ИИК для положительных и отрицательных значений потенциала эпикарда в опорных точках компьютерной модели сердца пациента:
в j-м интервале группирования ИИК для положительных и отрицательных значений потенциала эпикарда в опорных точках компьютерной модели сердца пациента:
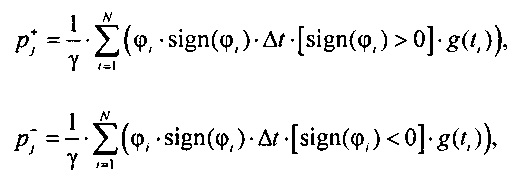
определения разности распределений вероятностей ИИК pj в j-м интервале группирования для значений потенциала в опорных точках эпикарда компьютерной модели сердца пациента: 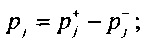
формирования выборок отсчетов времени для положительных и отрицательных разностей распределений вероятностей ИИК 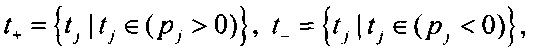
выделения временного интервала фазы начальной быстрой реполяризации эпикарда в опорных точках компьютерной модели сердца пациента 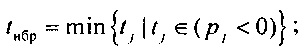
выделения временного интервала монотонной реполяризации эпикарда, включающего монотонную реполяризацию фазы плато и фазу конечной быстрой реполяризации эпикарда в опорных точках компьютерной модели сердца пациента
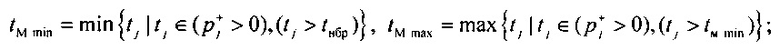
нормирования распределения вероятности ИИК для выборок значений потенциала временного интервала монотонной реполяризации эпикарда в опорных точках компьютерной модели сердца пациента 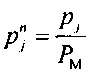 , где PM - вероятность обнаружения ИИК во временном интервале монотонной реполяризации эпикарда
, где PM - вероятность обнаружения ИИК во временном интервале монотонной реполяризации эпикарда 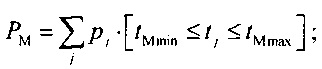
- определяют токи калия аномального выпрямления в опорных точках компьютерной модели сердца путем:
формирования стохастической модели токов калия задержанного и аномального выпрямления 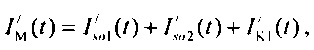 где
где 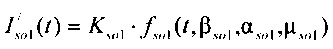 - стохастическая модель тока калия быстрого задержанного выпрямления;
- стохастическая модель тока калия быстрого задержанного выпрямления; 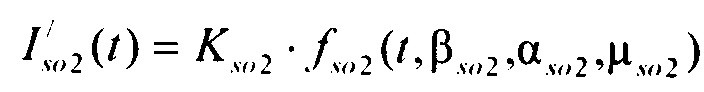 - стохастическая модель тока калия медленного задержанного выпрямления;
- стохастическая модель тока калия медленного задержанного выпрямления; 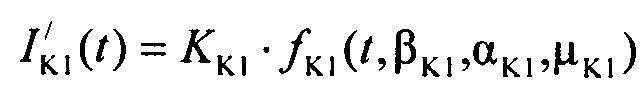 - стохастическая модель тока калия аномального выпрямления;
- стохастическая модель тока калия аномального выпрямления; 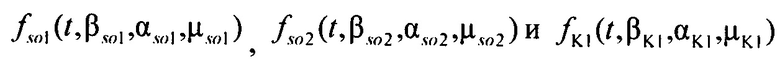 - плотности распределений ИИК для тока калия быстрого и медленного задержанного выпрямления и для тока калия аномального выпрямления соответственно;
- плотности распределений ИИК для тока калия быстрого и медленного задержанного выпрямления и для тока калия аномального выпрямления соответственно; 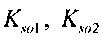 и
и 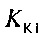 - весовые коэффициенты стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления соответственно;
- весовые коэффициенты стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления соответственно; 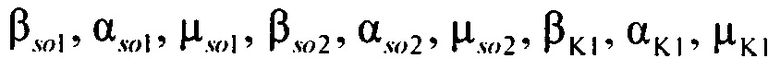 - параметры распределений;
- параметры распределений;
задания весовых коэффициентов стохастической модели токов калия быстрого 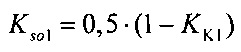 и медленного
и медленного 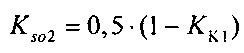 задержанного и аномального
задержанного и аномального 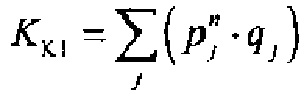 выпрямления, где qj=1, если
выпрямления, где qj=1, если 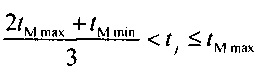 , иначе qj=0;
, иначе qj=0;
определения параметров 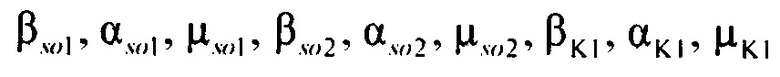 стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления путем минимизации решения уравнения
стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления путем минимизации решения уравнения
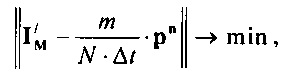
где 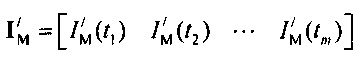 - матрица стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления;
- матрица стохастической модели токов калия быстрого и медленного задержанного и аномального выпрямления; 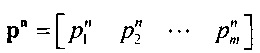 - матрица нормированных вероятностей ИИК;
- матрица нормированных вероятностей ИИК;
определения распределения вероятностей ИИК токов калия быстрого задержанного 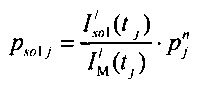 и медленного задержанного
и медленного задержанного 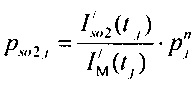 и аномального выпрямления
и аномального выпрямления 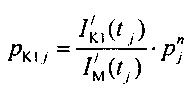 на j-м интервале группирования ИИК;
на j-м интервале группирования ИИК;
определения критерия адекватности 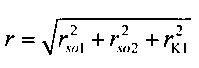 модели токов калия быстрого и медленного задержанного и аномального выпрямления в опорной точке компьютерной модели сердца пациента, где составляющие критерия вычисляют по формулам
модели токов калия быстрого и медленного задержанного и аномального выпрямления в опорной точке компьютерной модели сердца пациента, где составляющие критерия вычисляют по формулам
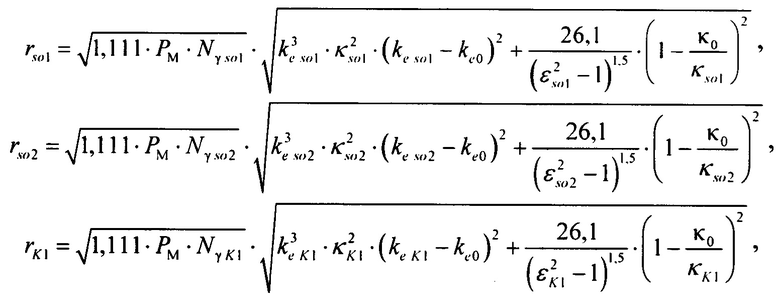
где 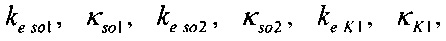 - коэффициенты энтропии и контрэксцесса симметричных распределений для тока калия быстрого и медленного задержанного и аномального выпрямления;
- коэффициенты энтропии и контрэксцесса симметричных распределений для тока калия быстрого и медленного задержанного и аномального выпрямления;
сравнения критерия r2≤3⋅ln(α-2), где α - уровень значимости принятия решения;
коррекции весовых коэффициентов стохастической модели токов калия быстрого 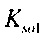 и медленного
и медленного 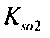 задержанного и аномального
задержанного и аномального 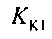 выпрямления в опорных точках компьютерной модели сердца пациента;
выпрямления в опорных точках компьютерной модели сердца пациента;
принятия решения: «Параметры стохастической модели тока калия 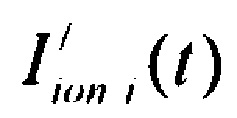 задержанного и аномального выпрямления определены корректно»;
задержанного и аномального выпрямления определены корректно»;
определения значений 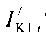 тока калия аномального выпрямления по формуле
тока калия аномального выпрямления по формуле
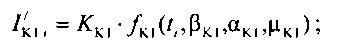
- определяют ток реполяризации эпикарда 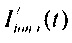 в опорных точках компьютерной модели сердца пациента путем:
в опорных точках компьютерной модели сердца пациента путем:
формирования стохастической модели тока 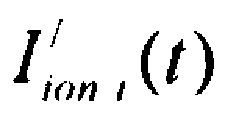 реполяризации эпикарда
реполяризации эпикарда 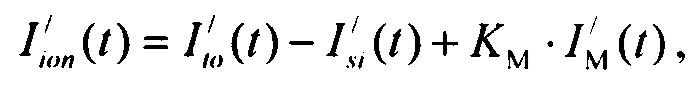 , где
, где 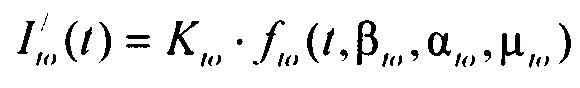 - стохастическая модель переходного транзитного тока эпикарда;
- стохастическая модель переходного транзитного тока эпикарда; 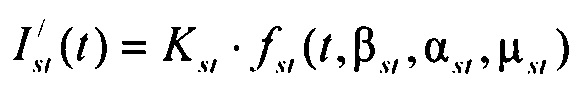 - стохастическая модель медленного деполяризующего тока кальция;
- стохастическая модель медленного деполяризующего тока кальция; 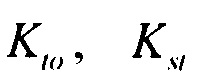 и
и 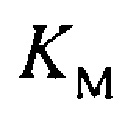 - весовые коэффициенты стохастической модели тока реполяризации эпикарда;
- весовые коэффициенты стохастической модели тока реполяризации эпикарда; 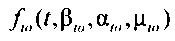 и
и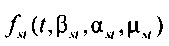 - плотности распределений ИИК для переходного транзитного тока и медленного деполяризующего тока кальция соответственно;
- плотности распределений ИИК для переходного транзитного тока и медленного деполяризующего тока кальция соответственно; 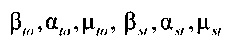 - параметры распределений;
- параметры распределений;
определения параметров стохастической модели тока 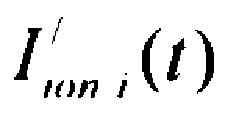 реполяризации эпикарда путем минимизации решения уравнения
реполяризации эпикарда путем минимизации решения уравнения
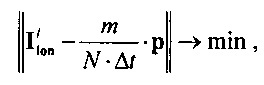
где 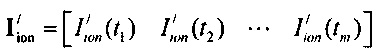 - матрица стохастической модели тока реполяризации эпикарда;
- матрица стохастической модели тока реполяризации эпикарда; 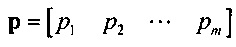 - матрица разностей распределений вероятностей ИИК;
- матрица разностей распределений вероятностей ИИК;
определения значения тока 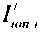 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента
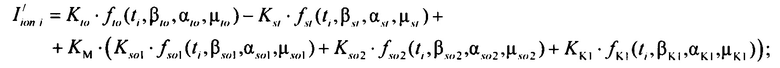
- восстанавливают потенциал ϕmod в опорных точках эпикарда компьютерной модели сердца пациента путем:
определения коэффициента приведения потенциала эпикарда 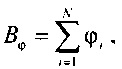
определения коэффициента приведения тока 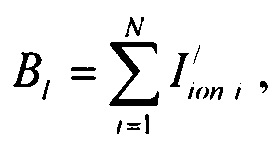
определения значений восстановленного потенциала ϕmod i, в опорных точках эпикарда компьютерной модели сердца пациента 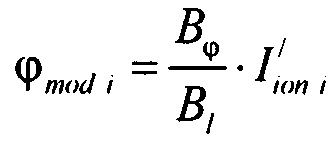
- сравнивают восстановленный ϕmod потенциал эпикарда с потенциалом эпикарда ϕ определенном на ЭКС
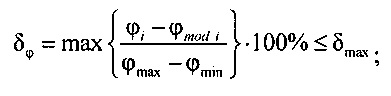
- корректируют параметры распределений 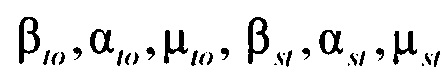 стохастической модели тока
стохастической модели тока 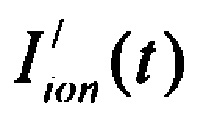 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента;
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента;
- принимают решение: «Значения тока 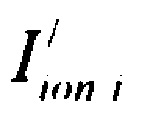 реполяризации эпикарда в опорных точках компьютерной модели сердца пациента определены корректно».
реполяризации эпикарда в опорных точках компьютерной модели сердца пациента определены корректно».
| СПОСОБ НЕИНВАЗИВНОГО ЭЛЕКТРОФИЗИОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ СЕРДЦА | 2008 |
|
RU2435518C2 |
| РЕВИШВИЛИ А.Ш | |||
| и др | |||
| Верификация новой методики неинвазивного электрофизиологического исследования сердца, основанной на решении обратной задачи электрокардиографии, Вестник аритмологии, 2008, 51, с.7-13 | |||
| ДЕНИСОВ A.M | |||
| и др | |||
| Применение метода регуляризации Тихонова для численного решения обратной задачи электрокардиографии, Вестник Московского университета, Серия 15, Вычислительная математика и кибернетика, 2008, 2, с.5-10 | |||
| Winslow R.L., Cortassa S., O'Rourke В., Hashambhoy Y.L., Rise J.J., Greenstein J.L | |||
| Integrative modeling of the cardiac ventricular myocyte / WIREs Systems Biology and Medicine | |||
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
Авторы
Даты
2017-04-04—Публикация
2016-05-25—Подача