Изобретение относится к космической технике и может быть использовано для ориентации космического аппарата (КА) при выполнение экспериментов и исследований.
Известен способ ориентации КА, включающий выставку осей КА и поддержание углового положения КА с помощью двигателей ориентации (Алексеев К.Б., Бебенин Г.Г. «Управление космическими летательными аппаратами», М.: Машиностроение, 1974).
Однако для использования данного способа необходимо расходовать рабочее тело, что приводит, кроме того, к загрязнению оптических поверхностей КА и вызывает микроускорения на борту КА.
Известен способ, включающий выставку оси КА, соответствующую минимальному моменту инерции, на центр Земли и орбитальное смещение КА (Беляев М.Ю. «Научные эксперименты на космических кораблях и орбитальных станциях», М.: Машиностроение, 1984). Данный способ используется для КА, имеющих вытянутую форму, т.е. когда момент инерции относительно продольной оси значительно меньше момента инерции относительно поперечных осей.
В этом случае обеспечивается гравитационная ориентация КА вытянутой формы, которая не требует для поддержания расхода рабочего тела и, следовательно, при этом не загрязняются оптические поверхности КА и не вызывают ускорения из-за работы двигателей управления ориентацией.
Однако вследствие неточной выставки оси КА на центр Земли появляются угловые скорости вокруг всех осей КА. Наличие угловых скоростей вокруг поперечных осей КА приводит к отклонению продольной оси аппарата от направления к центру Земли, вследствие чего ухудшается точность гравитационной ориентации КА.
Наиболее близким к предлагаемому является способ одноосной ориентации КА вытянутой формы (Патент РФ №2457159, приоритет от 30.08.2010, МПК (2006.01) B64G 1/34 - прототип), включающий выставку оси КА, соответствующей минимальному моменту инерции, на центр Земли и орбитальное смещение КА, при этом после выставки оси КА на центр Земли и орбитального смещения КА производят закрутку КА вокруг выставленной на центр Земли оси КА до требуемого момента с угловой скоростью 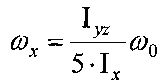 , где Iyz - среднее значение близких по величине моментов инерции КА вокруг поперечных осей КА; Iх - момент инерции КА вокруг продольной оси; ω0 - модуль абсолютной угловой скорости орбитальной системы координат.
, где Iyz - среднее значение близких по величине моментов инерции КА вокруг поперечных осей КА; Iх - момент инерции КА вокруг продольной оси; ω0 - модуль абсолютной угловой скорости орбитальной системы координат.
Способ-прототип позволяет повысить точность одноосной ориентации конкретно рассмотренного типа КА и, тем самым, снизить также микроперегрузки на КА, возникающие при раскачке и переходе КА в режим неуправляемого вращения. В общем случае вращение КА с указанной скоростью не является устойчивым для всех типов КА вытянутой формы - в общем случае со временем отклонение продольной оси КА от направления к центру Земли становится все более существенным, что приводит к «кувырканию» КА и разрушению гравитационной ориентации. Это в том числе ограничивает возможности проведения экспериментов, требующих наведения научной аппаратуры на Землю и/или низкого уровня микроускорений.
Задачей, на решение которой направлено настоящее изобретение, является повышение точности одноосной ориентации КА при выполнении экспериментов и исследований в условиях вращательного движения КА.
Технический результат предлагаемого изобретения заключается в обеспечении реализации режима гравитационной ориентации КА с закруткой на длительных временных интервалах с эволюцией угловой скорости вращения КА в сторону ускорения.
Технический результат достигается тем, что в способе одноосной ориентации КА вытянутой формы, включающем развороты КА и закрутку вокруг его продольной оси, соответствующей минимальному моменту инерции, дополнительно перед выполнением закрутки космический аппарат разворачивают до совмещения продольной оси КА с плоскостью, образованной нормалью к плоскости орбиты и радиус-вектором КА, и достижения углом между плоскостью орбиты и продольной осью КА значения 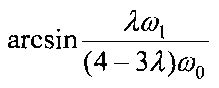 при значении угла между радиус-вектором космического аппарата и вектором, направленным из центра масс космического аппарата в центр аэродинамического давления солнечных батарей космического аппарата, >90°,
при значении угла между радиус-вектором космического аппарата и вектором, направленным из центра масс космического аппарата в центр аэродинамического давления солнечных батарей космического аппарата, >90°,
где λ - отношение минимального главного центрального момента инерции к среднему значению поперечных главных центральных моментов инерции КА,
ω0 - угловая скорость орбитального движения КА,
ω1 - абсолютная угловая скорость закрутки КА вокруг его продольной оси,
после чего выполняют закрутку КА вокруг продольной оси, при этом величину угловой скорости закрутки определяют по соотношению 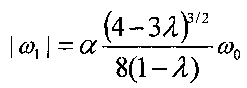 , где α>1.
, где α>1.
Поясним предложенные в способе действия.
Запишем уравнения вращательного движения КА. КА считается твердым телом, геоцентрическое движение его центра масс - кеплеровым эллиптическим. Элементы этого движения находятся по данным радиоконтроля орбиты. Для записи уравнений введем две правые декартовы системы координат - орбитальную ОХ1Х2Х3 и образованную главными центральными осями инерции КА Ох1x2x3. Точка О - центр масс КА, оси ОХ3 и ОХ1 направлены, соответственно, вдоль геоцентрического радиуса-вектора точки О и по трансверсали к орбите в этой точке. Ось Ox1 направлена вдоль продольной оси КА.
Положение системы Ох1х2х3 относительно системы ОХ1Х2Х3 будем задавать углами γ, δ и β, которые введем следующим образом. Система ОХ1Х2Х3 может быть переведена в систему Ox1x2x3 тремя последовательными поворотами: 1) на угол δ+π/2 вокруг оси ОХ2, 2) на угол β вокруг новой оси ОХ3, 3) на угол γ вокруг новой оси OX1, совпадающей с осью Ox1. Матрицу перехода от системы Ох1x2x3 к системе OX1X2X3 обозначим 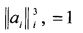 , где ai - косинус угла между осями ОХi и Oxj.
, где ai - косинус угла между осями ОХi и Oxj.
Элементы этой матрицы выражаются через введенные углы с помощью формул
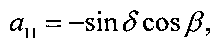
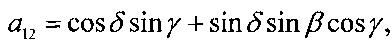
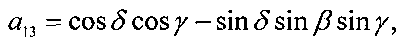
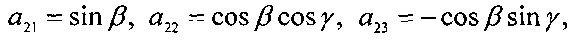
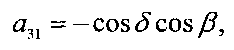
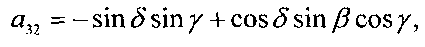
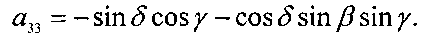
В уравнениях вращательного движения КА учитываются гравитационный и восстанавливающий аэродинамический моменты. Эти уравнения записываются в виде
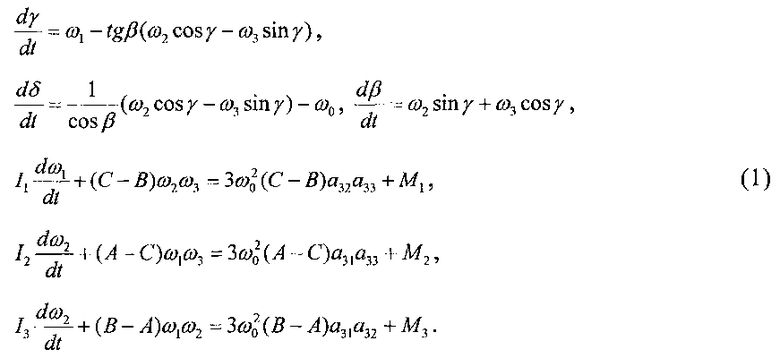
Здесь ωi (i=1, 2, 3) - компоненты абсолютной угловой скорости КА в системе координат Ox1x2x3, ω0 - угловая скорость орбитального движения КА, Ii - моменты инерции КА относительно осей Охi (главные центральные моменты инерции КА), Мl - вычисленный относительно точки О восстанавливающий аэродинамический момент, приложенный к КА.
Уравнения (1) позволяют оценить вращательные движения КА при различных условиях (Белецкий В.В. Движение искусственного спутника относительно центра масс. М., Наука, 1965; Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Издательство МГУ, 1975; Черноусько Ф.Л. Об устойчивости регулярной прецессии спутника. Прикладная математика и механика, 1963, т. 28, вып. 1, с. 155-157).
В предлагаемом способе рассматривается режим гравитационной ориентации с закруткой вытянутого вдоль продольной оси спутника. В этом режиме спутник вращается вокруг продольной оси, направленной приблизительно вдоль местной вертикали. Для применения такого режима необходимо выполнение трех условий. Во-первых, спутник должен иметь специфический центральный эллипсоид инерции: большая и средняя полуоси этого эллипсоида должны мало отличаться друг от друга и быть существенно больше (в три и более раз) малой полуоси. Во-вторых, приложенный к спутнику гравитационный момент должен существенно превышать другие действующие на спутник механические моменты. В-третьих, орбита спутника должна быть близка к круговой. Если перечисленные условия выполнены, то возможно существование движений спутника, близких так называемой конической прецессии осесимметричного твердого тела на круговой орбите с малым отклонением оси симметрии тела от местной вертикали.
В случае осесимметричного спутника на круговой орбите его продольная ось в номинальном невозмущенном режиме лежит в плоскости, проходящей через радиус-вектор центра масс и нормаль к плоскости орбиты, составляя с плоскостью орбиты угол

Здесь λ - отношение минимального главного центрального момента инерции (момент инерции КА вокруг продольной оси Ix) к среднему значению близких по величине поперечных главных центральных моментов инерции (среднее значение моментов инерции КА вокруг поперечных осей КА Iyz), ω1 - абсолютная угловая скорость закрутки КА вокруг продольной оси.
В случае λ<<1 даже при сравнительно большом отношении |ω1/ω0| угол β0 будет мал. Продольная ось спутника с неравными моментами инерции, но удовлетворяющего перечисленным выше условиям, будет совершать движение в окрестности номинального положения малые колебания.
В этом случае номинальными невозмущенными движением спутника следует считать его движения, принадлежащие двумерному интегральному многообразию уравнений движения. Это многообразие строится в виде формальных рядов по целым степеням малых параметров, характеризующих возмущения. В частности, возмущения, вызванные отличием спутника от осесимметричного, характеризуются параметром µ=(I2-I3)/I1, где I2≈I3; возмущения, вызванные эллиптичностью орбиты, характеризуются ее эксцентриситетом и т.п. Указанное интегральное многообразие параметризуется двумя перемененными. Одна из них близка угловой скорости ω1, вторая близка углу поворота спутника вокруг продольной оси. При малых параметрах, равных нулю, интегральное многообразие переходит в номинальный режим осесимметричного спутника, а его параметры в точности совпадают с ω1 и указанным углом.
Формальные ряды, представляющие интегральное многообразие, можно построить не при всех значениях ω1. Чтобы построение было возможно, величины ω0 и ω1 должны быть нерезонансными. Имеется в виду отсутствие резонансов между колебаниями продольной оси спутника в окрестности указанного выше номинального положения и вращением спутника вокруг этой оси. Вблизи резонанса амплитуда колебаний продольной оси спутника в окрестности номинального положения быстро возрастает, и режим разрушается.
Можно показать (Сарычев В.А. Вопросы ориентации искусственных спутников. - Итоги науки техники. Серия Исследования космического пространства. Т. 11. М.: ВИНИТИ, 1978; Хейл Дж. Колебания в нелинейных системах. М.: Мир, 1966; Черноусько Ф.Л. Об устойчивости регулярной прецессии спутника. Прикладная математика и механика, 1963, т. 27, №3, с. 474; Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы и теория нелинейных колебаний. М.: Физматгиз, 1963; Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1969; Хайнбокел Дж., Страбл Р.А. Периодические решения систем дифференциальных уравнений, обладающих симметрией. - Механика. 1966. №1, с. 3; Пуанкаре А. Новые методы небесной механики. Избранные труды. Т. 1 и 2. М.: Наука, 1971-1972), что при λ<<1 «резонансные» значения угловой скорости вращения КА определяемых равенствами:
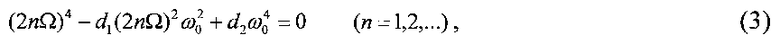
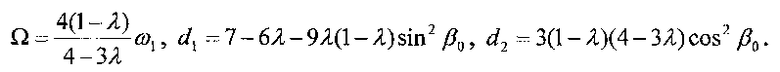
Здесь величина Ω - скорость изменения угла поворота КА вокруг продольной оси, отсчитываемого от плоскости орбиты.
С учетом (3) условие отсутствия резонансов выражается неравенствами
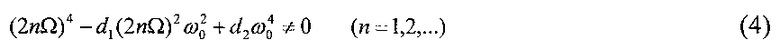
или
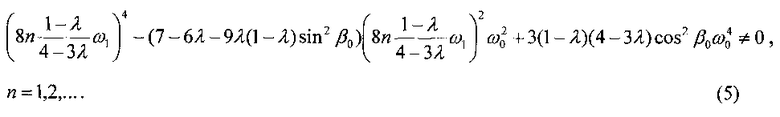
Условие отсутствия резонансов является довольно коварным. Аэродинамический момент, действующий на спутник, заставляет ω1 медленно изменяться - эволюционировать. По этой причине даже нерезонансное в начальный момент времени значение ω1 со временем может стать резонансным. Вблизи резонанса амплитуда колебаний продольной оси спутника в окрестности номинального положения быстро возрастает, и режим разрушается.
Условия (4) означают, что средняя угловая скорость вращения КА вокруг продольной оси не должна находиться в резонансе с собственными частотами колебаний этой оси по углам δ и β - углам, задающим положение продольной оси КА в орбитальной системе координат (β - угол между продольной осью КА и плоскостью орбиты, δ - угол между проекцией продольной оси КА на плоскость орбиты и направлением на Землю). Как указывалось выше, такие частоты ν определяются уравнением 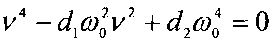 . При |β0|<<1 колебания продольной оси КА в плоскости орбиты и относительно этой плоскости с точностью до членов порядка O(β0) независимы и соответствующие им частоты приближенно равны
. При |β0|<<1 колебания продольной оси КА в плоскости орбиты и относительно этой плоскости с точностью до членов порядка O(β0) независимы и соответствующие им частоты приближенно равны 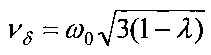 и
и 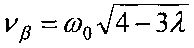 . Тогда условия (4) принимают вид
. Тогда условия (4) принимают вид
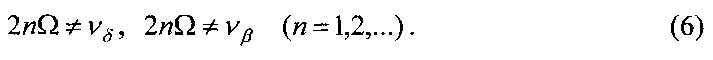
При нарушении одного из неравенств первой группы (6) имеет место резонанс между вращением КА вокруг продольной оси и колебаниями этой оси в плоскости орбиты (δ-резонанс), при нарушении одного из неравенств второй группы (6) имеет место резонанс между вращением КА вокруг продольной оси и колебаниями этой оси в направлении, перпендикулярном плоскости орбиты (β-резонанс). С учетом 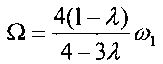 и (6) соотношения для соответствующих «резонансных» значений угловой скорости вращения спутника ω1 записываются в виде
и (6) соотношения для соответствующих «резонансных» значений угловой скорости вращения спутника ω1 записываются в виде
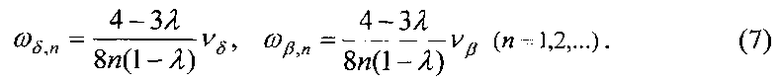
Например, для КА с характеристикой λ≈0.15 (например, транспортный грузовой корабль (ТГК) «Прогресс») величины νδ/ω0, νβ/ω0 составляют значения, соответственно, ≈1.6 и ≈1.88, а резонанс первого порядка (n=1) реализуется при значениях ωδ,1/ω0 и ωβ,1/ω0, соответственно, ≈0.83 и ≈0.98.
Считаем, что КА снабжен солнечными батареями (СБ) и что центр аэродинамического давления СБ КА расположен на продольной оси КА. Реализацию режима одноосной гравитационной ориентации КА осуществляем, принимая во внимание взаимное положение центров масс КА, Земли и центра аэродинамического давления СБ КА.
Рассматриваем ориентацию КА, в которой центр аэродинамического давления СБ КА расположен между центрами масс КА и Земли - в данной ориентации значение угла между радиус-вектором КА и вектором, направленным из центра масс КА в центр аэродинамического давления СБ КА, >90°. Тогда в процессе упомянутой выше эволюции |ω1| возрастает и если |ω1| превышает резонансные значения (7), то КА медленно раскручивается, оставаясь вблизи решения (2). В противном случае он затягивается в один из резонансов, при котором режим ориентированного движения быстро разрушается.
Таким образом, в случае, когда центр аэродинамического давления СБ КА расположен между центрами масс КА и Земли, условием длительного поддержания рассматриваемого режима гравитационной ориентации является превышение угловой скоростью закрутки спутника максимального из резонансных значений (7) 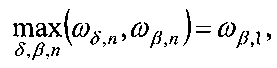 т.е. начальное значение угловой скорости вращения КА должно определяется соотношением
т.е. начальное значение угловой скорости вращения КА должно определяется соотношением
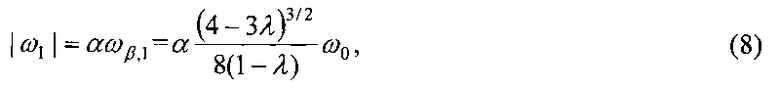
где задаваемый коэффициент α>1 определяет требуемое превышение угловой скорости закрутки КА над ее максимальным «резонансным» значением. Величина данного коэффициента определяется в том числе точностями построения требуемой ориентации и отработки импульса для закрутки КА, реализуемых системой управления КА, и требованием к длительности поддержания гравитационной ориентации.
В качестве примера приведем результаты анализа возможности реализации длительного (сотни витков) поддержания гравитационной ориентации в случае, когда центр аэродинамического давления СБ КА расположен между центрами масс КА и Земли, для КА с характеристиками λ≈0.15, ω0≈0.065°/сек при высоте орбиты порядка 400 км и длительности витка порядка 1,5 часа. Например, при требовании отклонения продольной оси КА от местной вертикали не более величины 15° в (8) можно принять α≈2÷2.6, что соответствует начальному значению угловой скорости вращения КА ω1≈0.13÷017°/сек, при которой начальное отклонение продольной оси КА от местной вертикали составляет величину β0≈5÷6°, при этом численное моделирование показывает, что длительность поддержания гравитационной ориентации до момента, когда угол между продольной осью КА и местной вертикалью достигнет и начнет превышать величину 15° (т.е. до нарушения заданного требования к точности поддержания гравитационной ориентации), составляет не менее чем сотни витков.
Опишем технический эффект предлагаемого изобретения.
Предложенный способ обеспечивает поддержание требуемых параметров ориентации КА в процессе неуправляемого вращательного движения на длительных (сотни витков) интервалах времени, а именно обеспечивает реализацию режима гравитационной ориентации КА с закруткой на длительных временных интервалах с эволюцией угловой скорости вращения КА в сторону ее ускорения.
Указанный результат достигается путем выполнения закрутки КА с предложенной угловой скоростью и из предложенной исходной ориентации, при этом предложенные параметры ориентации КА обеспечивают выполнение колебаний продольной оси КА в окрестности описанного номинального положения максимально длительное время и последующую эволюцию угловой скорости вращения КА в сторону ее ускорения.
Предложенная закрутка КА из предложенной исходной ориентации в течение длительного интервала времени «усредняет» действие угловых скоростей вокруг поперечных осей - угловые скорости вокруг поперечных осей отклоняют продольную ось КА от положения, составляющего некоторый угол с местной вертикалью, а затем, за счет вращения КА вокруг продольной оси, уменьшают это отклонение и возвращают продольную ось КА в положение, составляющее указанный угол с местной вертикалью. Вместе с тем предложенная закрутка КА вокруг продольной оси не приводит к гироскопической устойчивости этой оси в инерциальном пространстве и КА продолжает движение по орбите, сохраняя описанную одноосную ориентацию, близкую к гравитационной. При этом при реализации описанного длительного режима гравитационной ориентации с закруткой угловая скорость вращения КА изменяется в сторону ускорения (КА «раскручивается»).
В настоящее время технически все готово для реализации предложенного способа такого КА, как ТГК «Прогресс». Для реализации разворотов, закрутки и вычислений могут использоваться штатные средства системы управления ТГК «Прогресс» - система управления движением и навигацией, включая систему автономной навигации, солнечные датчики, датчики угловой скорости, двигатели ориентации, бортовой вычислитель и т.д.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2015 |
|
RU2594054C1 |
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2015 |
|
RU2594056C1 |
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2010 |
|
RU2457159C2 |
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2020 |
|
RU2764815C1 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА С НЕПОДВИЖНЫМИ ПАНЕЛЯМИ СОЛНЕЧНЫХ БАТАРЕЙ ПРИ ВЫПОЛНЕНИИ ЭКСПЕРИМЕНТОВ НА ОРБИТАХ С МАКСИМАЛЬНОЙ ДЛИТЕЛЬНОСТЬЮ ТЕНЕВОГО УЧАСТКА | 2010 |
|
RU2457158C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕНЗОРА ИНЕРЦИИ КОСМИЧЕСКОГО АППАРАТА | 2014 |
|
RU2587762C2 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА С НЕПОДВИЖНЫМИ ПАНЕЛЯМИ СОЛНЕЧНЫХ БАТАРЕЙ ПРИ ВЫПОЛНЕНИИ ЭКСПЕРИМЕНТОВ | 2014 |
|
RU2562904C1 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО АППАРАТА С НЕПОДВИЖНЫМИ ПАНЕЛЯМИ СОЛНЕЧНЫХ БАТАРЕЙ ПРИ ВЫПОЛНЕНИИ ЭКСПЕРИМЕНТОВ НА ОРБИТАХ С МАКСИМАЛЬНОЙ ДЛИТЕЛЬНОСТЬЮ ТЕНЕВОГО УЧАСТКА | 2014 |
|
RU2562903C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕНЗОРА ИНЕРЦИИ КОСМИЧЕСКОГО АППАРАТА | 2014 |
|
RU2587663C2 |
| СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО ТРАНСПОРТНОГО ГРУЗОВОГО КОРАБЛЯ С НЕПОДВИЖНЫМИ ПАНЕЛЯМИ СОЛНЕЧНЫХ БАТАРЕЙ ПРИ ПРОВЕДЕНИИ РАБОТ В УСЛОВИЯХ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ | 2013 |
|
RU2539266C2 |
Изобретение относится к управлению движением космического аппарата (КА) вокруг его центра масс. Способ включает закрутку КА вокруг оси его минимального момента инерции (продольной). Перед закруткой совмещают продольную ось КА с плоскостью, образованной нормалью к плоскости орбиты и радиус-вектором КА. Закрутку производят при достижении углом между продольной осью КА и плоскостью орбиты некоторого значения, зависящего от скорости закрутки и отношения миним. момента инерции КА к среднему значению поперечных моментов инерции. Скорость закрутки (порядка орбитальной) выбирают в зависимости от указанных угла и отношения моментов инерции КА. При этом угол между радиус-вектором КА и вектором, направленным из центра масс КА в центр аэродинамического давления солнечных батарей КА, должен быть более 90°. Технический результат изобретения состоит в реализации длительного режима гравитационной ориентации КА с закруткой, при эволюции вращения КА в сторону ускорения.
Способ одноосной ориентации космического аппарата вытянутой формы, включающий развороты космического аппарата и закрутку вокруг его продольной оси, соответствующей минимальному моменту инерции, отличающийся тем, что перед выполнением закрутки космический аппарат разворачивают до совмещения продольной оси космического аппарата с плоскостью, образованной нормалью к плоскости орбиты и радиус-вектором космического аппарата, и достижения углом между плоскостью орбиты и продольной осью космического аппарата значения
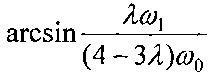 ,
,
где λ - отношение минимального главного центрального момента инерции к среднему значению поперечных главных центральных моментов инерции космического аппарата,
ω
0 - угловая скорость орбитального движения космического аппарата,
ω
1 - абсолютная угловая скорость закрутки космического аппарата вокруг его продольной оси,
при значении > 90° угла между радиус-вектором космического аппарата и вектором, направленным из центра масс космического аппарата в центр аэродинамического давления солнечных батарей космического аппарата,
после чего выполняют закрутку космического аппарата вокруг продольной оси, при этом величину угловой скорости закрутки определяют по соотношению
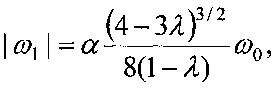
где α>1.
| СПОСОБ ОДНООСНОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА ВЫТЯНУТОЙ ФОРМЫ | 2010 |
|
RU2457159C2 |
| СПОСОБ ТРЕХОСНОЙ ГРАВИТАЦИОННОЙ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА НА ОРБИТЕ СПУТНИКА ЗЕМЛИ | 1995 |
|
RU2128607C1 |
| US 6463365 B1, 08.10.2002 | |||
| US 5474264 A1, 12.12.1995 | |||
| US 5669586 А, 23.09.1997 | |||
| US 4834325 A1, 30.05.1989 | |||
| US 5377936 A1, 03.01.1995. | |||
Авторы
Даты
2016-08-10—Публикация
2015-02-02—Подача