Настоящее изобретение относится к обработке аудиосигнала и в частности к устройству, способу и компьютерной программе для произвольных сдвигов частоты в области поддиапазонов.
Автоматизированные системы обработки данных являются неотъемлемой частью повседневной жизни в сегодняшнем обществе, которое характеризуется новыми СМИ. Системы для использования новых СМИ присутствуют почти в каждом домашнем хозяйстве в течение достаточно долгого времени. Примерами таких систем, которые передают и воспроизводят данные в цифровой форме, являются проигрыватели для видеоданных и аудиоданных, например, такие, как проигрыватели для DVD и BluRay, CD и файлов в формате mp3. Эти системы воспроизведения характеризуются воспроизведением мультимедийного контента почти без потерь. Наряду с классической телекоммуникацией, Интернет является важным порталом для связи, например, посредством VoIP. Основополагающая цифровая обработка сигналов характерна для всех упомянутых технологий. Она имеет решающее значение для качества воспроизведения и эффективности цифровых технологий.
Обработка аудиосигнала при этом получает все большее значение. В настоящее время на рынке доступно множество аудио-кодеров, которые реализуются, например, алгоритмами для цифровой обработки аудио материала для его хранения или передачи. Цель каждого способа кодирования заключается в сжатии информационного содержимого сигнала так, чтобы оно занимало по минимуму место в памяти, одновременно сохраняя наилучшее возможное качество воспроизведения. Эффективность современных аудио-кодеров главным образом зависит от требуемой в памяти места и, кроме того, от вычислительной сложности, требуемой для алгоритма.
В основном, кодер цифрового аудио представляет собой инструмент для передачи аудиосигналов в формате, подходящем для хранения или передачи. Это имеет место на передающей стороне аудио-кодера (кодировщик). Данные, произведенные таким образом, затем возвращаются к исходной форме в получателе (декодер) и, в идеальном случае, соответствуют исходным данным, за исключением постоянной задержки. Общей целью аудио-кодеров является минимизация объема данных, требуемого для представления аудиосигнала, одновременно максимизируя воспринимаемое качество воспроизведения. При разработке аудио-кодеров должен быть учтен ряд факторов, таких как, например, точность воспроизведения, скорость передачи данных и сложность. Кроме этого, задержка, прибавляемая за счет обработки сигнала (добавленная задержка), также играет важную роль (Bosi and Goldberg, 2003).
В особенности в начале применения аудиокодирования эффективность способов имела большое значение, так как память и вычислительная производительность были доступны только в очень ограниченной степени. В настоящее время это требование, кажется, имеет меньше значения. Даже домашние PC или ноутбуки в состоянии легко выполнять сложные алгоритмы в режиме реального времени, и широкополосные интернет-соединения обеспечивают достаточную ширину полосы для передачи кодированного аудиоматериала. Тем не менее, усовершенствование способов аудиокодирования имеет особое значение. В области мобильной связи и спутниковой передачи данных ширина полосы является строго ограниченной. Важным является сокращение объема передаваемых данных. Дополнительно к этому, в этой области важна эффективность используемой технологии кодирования. Базовые алгоритмы должны обладать простой структурой для того, чтобы минимизировать вычислительную производительность и потребление энергии.
Другим аспектом является качество воспроизведенных кодированных аудиосигналов. Многие аудио-кодеры уменьшают объем данных, используя сокращение ненужной части сигнала. При этом теряются части сигнала, в зависимости от скорости передачи данных. При низких скоростях передачи данных качество воспроизводимых аудиосигналов уменьшается.
Обычно различают два типа аудиокодирования, а именно, аудиокодирование с потерями и аудиокодирование без потерь. Аудиокодирование без потерь обеспечивает точное восстановление исходного сигнала на стороне получателя. Способ аудиокодирования с потерями, в отличие от этого, вызывает необратимые отклонения от исходного сигнала посредством модели субъективного восприятия (Zölzer, 2005).
Аудиокодирование без потерь основано на сокращении избыточности, содержащейся в кодируемом сигнале. Общепринятым способом здесь является, например, кодирование с линейным предсказанием (LPC) в совокупности с последующим энтропийным кодированием. Такие способы аудиокодирования позволяют точно побитно восстанавливать входной сигнал из кодированного потока битов.
Линейное предсказание использует статистические зависимости между последовательными выборками сигнала для того, чтобы предсказывать будущие значения. Это основано на том факте, что последовательные выборки более подобны друг другу, чем выборки, находящиеся на большем расстоянии друг от друга. Предсказание реализуется фильтром линейного предсказания, который оценивает текущую выборку, используя множество предыдущих выборок. Однако, далее используется не непосредственно эта оценка, которая обработана, а разность между этим значением и фактической выборкой в этом месте. Целью линейного предсказания является минимизация энергии этого сигнала ошибки с помощью оптимизированных фильтров и передача упомянутого сигнала ошибки, что требует лишь небольшой ширины полосы (Weinzierl, 2008).
После этого сигнал ошибки кодируется энтропией. Энтропия представляет собой меру среднего информационного содержания сигнала и указывает на теоретический минимум битов, требуемых для его кодирования. Типичным способом здесь является кодирование методом Хаффмана. Определенные кодовые комбинации связаны здесь с отдельными выборками, в зависимости от статистической вероятности их появления. Короткие символы связаны с часто встречающимися выборками, а редко встречающиеся значения сигнала представлены более длинными кодовыми комбинациями. В среднем, кодированный сигнал таким образом представляется наименьшим возможным количеством битов (Bosi and Goldberg, 2003).
И линейное предсказание, и энтропийное кодирование являются обратимыми, и таким образом не удаляют информацию из сигнала. При комбинировании этих двух способов из кодируемого сигнала удаляется только избыточность. Поскольку такие подходы к кодированию без потерь сильно зависят от характеристик сигнала, выгода от кодирования является сравнительно небольшой. Достигаемый уровень сжатия, то есть отношение скорости передачи битов входного сигнала и скорости передачи кодированного сигнала, находится в области между 1,5:1 и 3:1 (Weinzierl, 2008).
Аудиокодирование с потерями основано на принципе сокращения иррелевантной части информации. Для этих способов требуется модель человеческого восприятия, которая описывает психоакустические явления чувства слуха относительно времени и частотного разрешения. Таким образом, аудиокодирование с потерями также называется кодированием, адаптированным к восприятию, или психоакустическим кодированием. В области аудиокодирования все части сигнала, которые не могут быть восприняты людьми и таким образом являются неслышимыми, упоминаются как ненужные части сигнала (Zölzer, 2005). Чтобы более точно понять режим функционирования аудио кодера, адаптированного к восприятию, очень важно глубокое знание психоакустики.
Человеческий слух анализирует звуковое событие путем разложения его на группы частот. Эти группы частот представляются в шкале Барка, и в англоязычной литературе называются критическими полосами частот. Каждая из этих групп частот суммирует частотный домен, который оценивается человеческим слухом как единое целое. Таким образом, частотный домен соответствует ограниченной области на базилярной мембране. Всего с основной мембраной связано 24 критических полосы частот, ширина полосы которых увеличивается с увеличением частоты (Fastl and Zwicker, 2007). Аудио кодеры с потерями также используют эту модель групп частот для разложения широкополосных сигналов на поддиапазоны и индивидуального кодирования каждой полосы (Zölzer, 2005). Эта модель часто адаптируется, и зачастую вместо шкалы Барка используется линейное частотное деление на более чем 24 полосы.
Другой важной характеристикой слухового восприятия является частотно-зависимое ощущение громкости звуков с равными уровнями звукового давления. Из этого проистекают две особенности слуха. С одной стороны, звуки различных частот, но с равными уровнями звукового давления воспринимаются как имеющие различную громкость, с другой стороны существует частотно-зависимый порог, ниже которого звуки не могут быть восприняты (Fastl and Zwicker, 2007). Этот порог также упоминается как абсолютный порог слышимости или порог слышимости в тишине и проиллюстрирован на Фиг. 22. Из этого могут быть сделаны два вывода для аудиокодирования. Сигналы, уровни которых находятся ниже абсолютного порога слышимости, можно не обрабатывать, так как они все равно не могут быть восприняты. Кроме этого, число этапов квантизации, требуемых на полосу частот, также может быть определено по расстоянию между порогом слышимости в тишине и уровнем сигнала (Zölzer, 2005).
Экранирующие или маскирующие эффекты оказывают самое большое влияние на аудиокодирование. Различают временное и частотно-зависимое маскирование. В обоих случаях, маскирующий сигнал здесь относится к звуковому событию, которое покрывает другое звуковое событие. Таким образом, замаскированное событие становится неслышимым. При временном маскировании покрывается событие, происходящее до или после маскирующего сигнала. Премаскирование не зависит от продолжительности маскирующего сигнала и покрывает звуковые события, происходящие на интервале времени вплоть до 50 мс перед ощущением самого маскирующего сигнала (Yost, 1994). Постмаскирование, напротив, зависит от продолжительности маскирующего сигнала. Звуковые события здесь покрываются после того, как маскирующий сигнал закончился. В зависимости от продолжительности маскирующего сигнала может пройти вплоть до 200 мс, прежде чем слух снова станет способным воспринимать сигналы в диапазоне порога слышимости в тишине (Fastl and Zwicker, 2007).
На Фиг. 21 показана схематичная иллюстрация временного маскирования. В частности на Фиг. 21 схематично показаны области пре- и постмаскирования и соответствующий уровень, ниже которого сигналы маскируются. Временное маскирование может использоваться в аудиокодировании для того, чтобы скрыть побочный шум, вызванный процессом кодирования, такой как, например, шум квантизации, относительно высокоуровневых сигнальных последовательностей (переходные процессы).
Маскирующие эффекты в частотной области играют гораздо более важную роль, чем эффекты временного маскирования. Частотно-зависимое маскирование описывает изменение в пороге слышимости в тишине для отдельных звуков и узкополосного шума. Эти сигналы значительно искажают порог слышимости в тишине из-за их конкретного порога маскирования слышимости. Сигналы, уровень которых меньше, чем порог маскирования слышимости маскирующего сигнала, и которые расположены в эффективном диапазоне упомянутого порога, не могут быть восприняты (Fastl and Zwicker, 2007). Этот контекст проиллюстрирован на Фиг. 22.
На Фиг. 22 показана схематичная иллюстрация частотно-зависимого маскирования в человеческом слухе. Как показано, маскированный звук находится ниже порога маскирования слышимости маскирующего сигнала, и таким образом является неслышимым. Этот эффект используется в способах аудиокодирования с потерями. Части сигнала, находящиеся ниже частотно-зависимого порога маскирования слышимости, удаляются из сигнала и в дальнейшем не обрабатываются (Zölzer, 2005).
Общая схема типичного кодера, адаптированного к восприятию, проиллюстрирована на Фиг. 23. На Фиг. 23 показана блок-схема психоакустического аудио-кодера. Сначала сигнал PCM, подлежащий кодированию, разлагается на полосы частот аналитическим набором фильтров и подается на психоакустическую модель. Здесь зависящий от времени порог маскирования слышимости, который регулирует точность квантизации для различных полос частот, определяется описанными психоакустическими функциями слуха. Таким образом, важные полосы частот, то есть полосы частот, которые легко воспринимаются, квантуются с очень высоким разрешением, а неважные полосы частот представляются с более низким разрешением, т.е. небольшим числом бит. После этого выполняется энтропийное кодирование для уменьшения объема данных, так же, как это делается в аудиокодировании без потерь. Так как дополнительные контрольные параметры должны быть переданы аналитическим набором фильтров и психоакустической моделью, фактический поток битов устанавливается мультиплексором потока битов. Выгода от кодирования в аудио-кодерах с потерями здесь получается за счет комбинирования квантизации и энтропийного кодирования (Zölzer, 2005). В зависимости от того качества, которое должно быть достигнуто, уровень сжатия составляет от 4:1 до 50:1 (Weinzierl, 2008).
Декодер имеет сравнительно простую схему. Сначала полученный поток битов снова делится демультиплексором на сигнальные данные и контрольные параметры. После этого выполняются энтропийное декодирование и обратная квантизация. Контрольные параметры в данном случае управляют обратной квантизацией полезных данных. Сигналы поддиапазона, полученные таким образом, затем подаются на набор фильтров синтеза для того, чтобы восстановить широкополосный сигнал PCM (Zölzer, 2005). Соответствующая блок-схема психоакустического аудио декодера проиллюстрирована на Фиг. 24.
Ниже будет обсужден ряд преобразований сигнала предшествующего уровня техники. Так как квантизация во многих аудио кодерах основана на модели восприятия, которая описывает человеческое восприятие в частотной области, необходимо передавать сигнал, который также будет кодирован в частотной области. Существует большое количество преобразований с различными характеристиками, и областей их применения. Ниже будут представлены преобразования, важные для аудиокодирования, а также будет обсуждена схема набора фильтров.
Преобразование Фурье представляет собой наиболее важный способ для анализа гармонической структуры сигнала. Оно является частью анализа Фурье и названо в честь французского математика и физика Жана-Батиста-Жозефа Фурье (1768-1830), который ввел его первым. Преобразование Фурье представляет собой функцию для преобразования временного сигнала в его представление в частотной области. Оно используется, между прочим, для описания характеристик систем с линейными временными инвариантами (LTI), а также для их предсказания (Burrus and Parks, 1985). Таким образом, оно является, например, очень важным в акустике и в описании человеческого слуха. Основной процедурой преобразования Фурье является разложение временного сигнала на взвешенную сумму косинусоидальных и синусоидальных колебаний. Для апериодических непрерывных сигналов оно вычисляется следующим образом (Bosi and Goldberg, 2003):
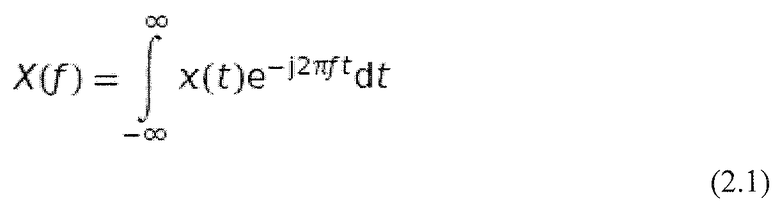 .
.
Здесь x(t) представляет собой сигнал, анализируемый во временной области, а X(ƒ) представляет собой соответствующий спектр Фурье в частотной области. Следует учесть, что результат является комплексным, хотя преобразуется вещественный сигнал. Используя соотношение Эйлера 2.2, можно показать, что вещественная часть X(ƒ) соответствует косинусоидальным членам x(t), а мнимая часть соответствует синусоидальным компонентам. Используя:
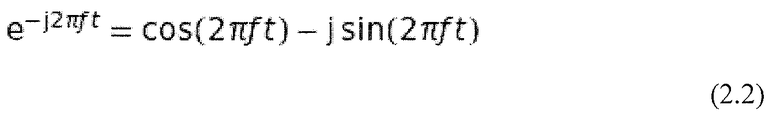
уравнение 2.1 принимает вид:
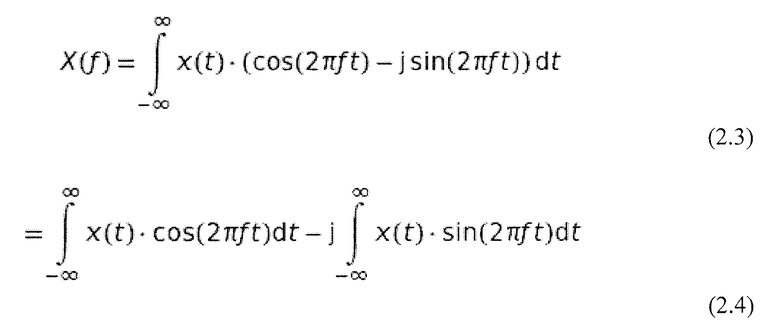
что приводит к:
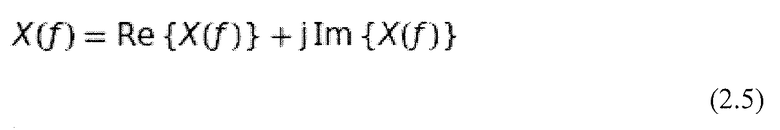 .
.
Так как синус и косинус отличаются друг от друга только их фазой, фаза сигнала может быть получена из отношения соответствующих членов. Используется следующая формула:
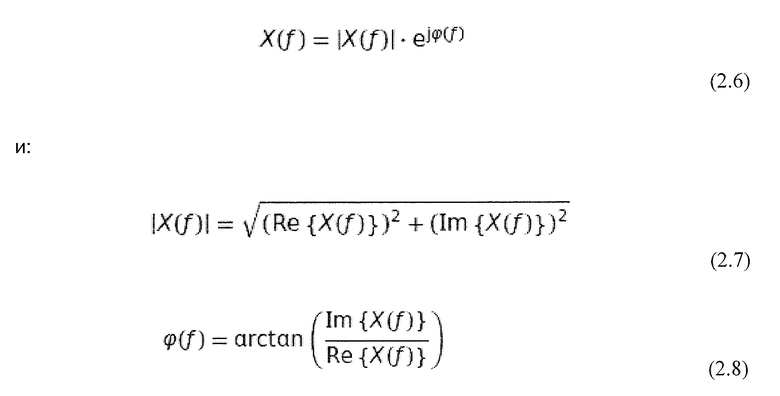 .
.
Таким образом, 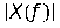 упоминается как абсолютное значение частотной характеристики, а φ(ƒ) упоминается как фазово-частотная характеристики или просто как фаза.
упоминается как абсолютное значение частотной характеристики, а φ(ƒ) упоминается как фазово-частотная характеристики или просто как фаза.
С помощью обратного преобразования Фурье (уравнение 2.9) преобразованный сигнал снова преобразуется к его исходному представлению во временной области. Следует учесть, что преобразование Фурье и обратное преобразование Фурье отличаются друг от друга постоянным коэффициентом и знаком экспоненциальной функции (Burrus and Parks, 1985).
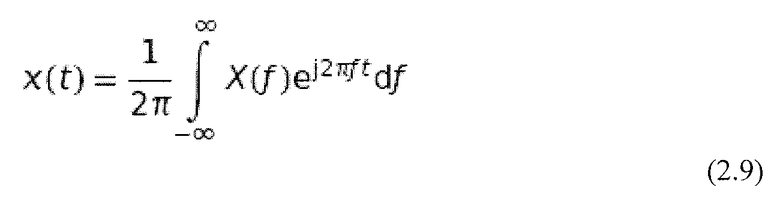 .
.
Дискретное преобразование Фурье будет обсуждено ниже более подробно.
На практике проблемы возникают в цифровых компьютерах при использовании преобразования Фурье. С одной стороны, это происходит вследствие того, что только конечное число временных значений может быть обработано, а с другой стороны частотная переменная также должна быть представлена дискретно, кроме переменной времени. Решением этих проблем является дискретное преобразование Фурье (DFT). При использовании DFT конечный дискретно-временной сигнал преобразуется в дискретный периодический спектр. Это означает, что DFT представляет собой одно из самых важных преобразований в цифровой обработке сигналов. Источником DFT является преобразование Фурье, точный вывод может быть найден в публикации (Lochmann, 1990). DFT дискретно-временного сигнала x[n] длины N определяется следующим образом (Burrus and Parks, 1985):
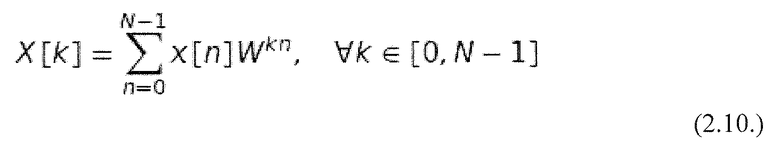 .
.
По аналогии, обратное дискретное преобразование Фурье (IDFT) выглядит следующим образом:
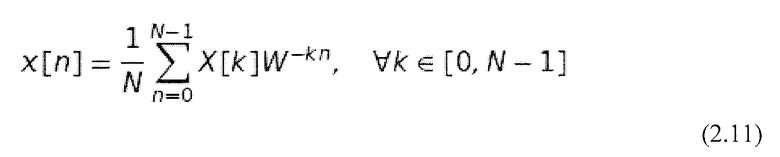
где комплексный вращающийся фазор W:

Таким образом, X[k] является дискретным периодическим спектром сигнала x[n], где 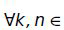
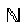 . Длина периода спектра соответствует длине преобразования N, а нормализованные частоты отображаются на интервал [0,2π].
. Длина периода спектра соответствует длине преобразования N, а нормализованные частоты отображаются на интервал [0,2π].
Для реальных входных сигналов DFT имеет важную особенность. Здесь вычисляется не N независимых частотных коэффициентов, как это имеет место в общем случае, но только их половина. Эта особенность может быть использована, например, для хранения или передачи данных. Для повторного преобразования вторая половина из N/2 значений вычисляется с использованием следующей корреляции (Rao and Yip, 2001):

Оператор * в уравнении 2,13 характеризует комплексное сопряжение. Таким образом, X(k]* является комлексно сопряженной последовательностью значений для X(k].
Вычислительная сложность DFT и IDFT составляет N2 комплексных умножений и сложений. Когда при вычислениях используются симметрии, количество необходимых шагов вычисления сокращается до 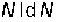 , и сложность соответствует
, и сложность соответствует 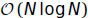 . Однако при использовании быстрых способов длина преобразования N должна соответствовать степени двух. Быстрое преобразование Фурье обычно упоминается как FFT (Kiencke and Jäkel, 2005).
. Однако при использовании быстрых способов длина преобразования N должна соответствовать степени двух. Быстрое преобразование Фурье обычно упоминается как FFT (Kiencke and Jäkel, 2005).
Дискретное преобразование Фурье не получило распространения в области сжатия данных. Большими недостатками DFT являются высокая вычислительная сложность и избыточность, содержащаяся в спектре. Хотя существуют эффективные способы для того, чтобы вычислить DFT, то есть FFT, результатом всегда будет комплексный спектр. Это означает, что N пар комплексных значений вычисляются из N значений преобразования. В дополнение к этому, только первые N/2 спектральных значений содержат новую информацию.
Дискретные синусоидальное и косинусоидальное преобразования будут обсуждены ниже.
Дискретное косинусоидальное преобразование (DCT) является решением для упомянутых выше проблем DFT. DCT представляет собой вещественное, дискретное, линейное и ортогональное преобразование. Благодаря этим особенностям оно является наиболее часто используемым преобразованием в сжатии цифровых данных (Britanak et al., 2007).
DCT представляет собой дискретное тригонометрическое преобразование. В целом различают восемь форм DCT. В зависимости от их граничного продолжения они делятся на четные и нечетные преобразования, а также на типы I, II, III и IV. Однако для цифровой обработки сигналов важны лишь четные типы DCT. Они перечислены ниже (Rao and Yio, 2001):
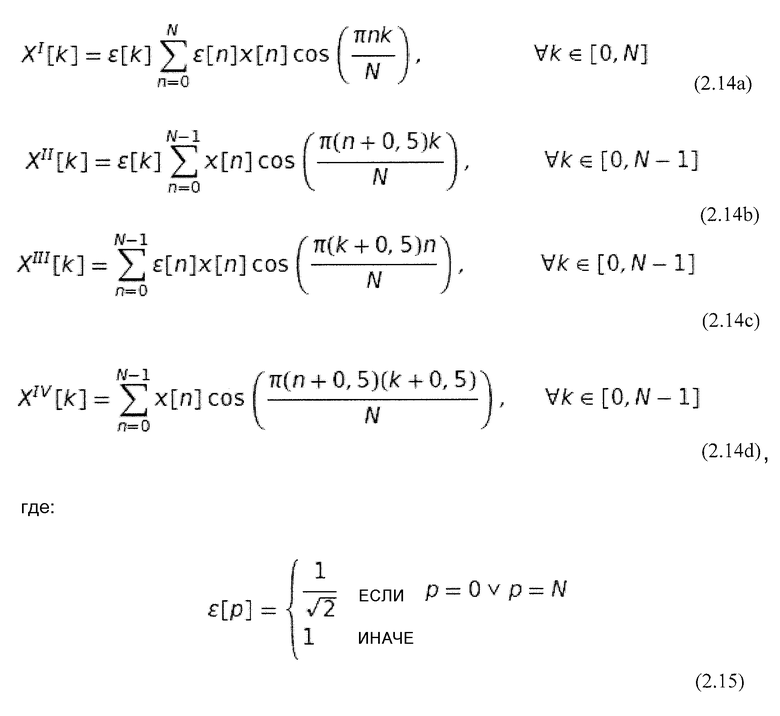
Каждая из этих форм имеет свое специальное применение в кодировании. DCT-II используется главным образом в качестве преобразования данных изображения. Литература рассматривает его как первый тип описанного DCT. Это означает, что обычно термин «DCT» относится к DCT-II (Ahmed et al., 1974). За исключением предварительного коэффициента DCT-III представляет собой обратное к DCT-II преобразование, и наоборот. Для аудиокодирования особое значение имеет преобразование DCT-IV. Оно является основой модифицированного дискретного косинусоидального преобразования.
Для того, чтобы можно было продемонстрировать важные особенности DCT, далее будет указана корреляция между DFT и DCT. Как было проиллюстрировано ранее, DFT вычисляет только N/2 независимых частотных коэффициентов из вещественных значений сигнала длины N. И наоборот, это означает, что 2N значений во временной области необходимы для того, чтобы получить N спектральных значений. Однако, если доступны только N временных значений, то сигнал должен быть подходящим образом продолжен. Симметричное расширение за счет зеркального отражения всего сигнала кажется здесь подходящим. Расширенный сигнал таким образом повторяет сам себя с длиной периода 2N. Это имеет то преимущество, что подавляется эффект побочных наводок преобразования DFT с отсеченными сигналами (Kiencke and Jäkel, 2005).
Любой вещественный сигнал x[n] длины N расширяется симметрично, давая в результате:
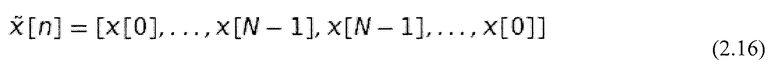
где 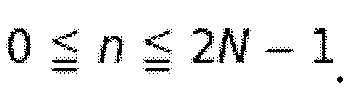 Длина
Длина 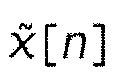 таким образом равна 2N. Затем к этому сигналу применяется DFT из уравнения 2.10 с уравнением 2.12 и конвертируется (Rao and Yip, 2001). Подробный вывод может быть найден в приложении А.1. Используются следующие формулы:
таким образом равна 2N. Затем к этому сигналу применяется DFT из уравнения 2.10 с уравнением 2.12 и конвертируется (Rao and Yip, 2001). Подробный вывод может быть найден в приложении А.1. Используются следующие формулы:
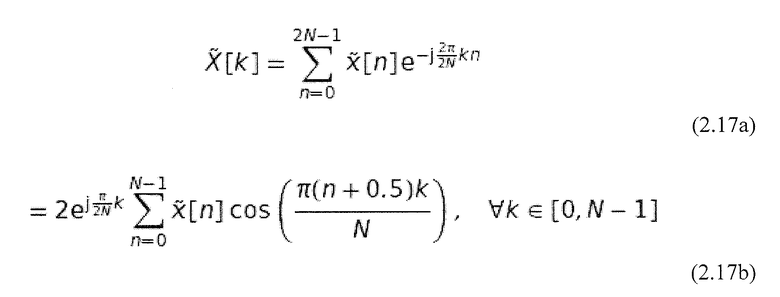
Сравнивая этот результат с DCT-II в уравнении 2.14b, можно видеть, что эти два уравнения отличаются только фазовым членом  . Так как он является независимым от сигнала и не содержит информации, им можно пренебречь при вычислении DCT (Rao and Yip, 2001). Для DCT-I можно показать подобную корреляцию, но с использованием другого продолжения сигнала x[n]. DCT-IV тогда получается из фазового вращения основной функции DCT-II. Подробный вывод этого может быть найден в публикации (Rao and Yip, 2001).
. Так как он является независимым от сигнала и не содержит информации, им можно пренебречь при вычислении DCT (Rao and Yip, 2001). Для DCT-I можно показать подобную корреляцию, но с использованием другого продолжения сигнала x[n]. DCT-IV тогда получается из фазового вращения основной функции DCT-II. Подробный вывод этого может быть найден в публикации (Rao and Yip, 2001).
Из этого результата могут быть сделаны некоторые выводы. Сначала можно заметить, что DCT, в отличие от DFT, является чисто вещественным преобразованием. Из этого следуют два преимущества. Во-первых, для вычислений не нужно выполнять никаких комплексных умножений и сложений, а во-вторых, только половина места в памяти требуется для хранения данных, так как нет никаких комплексных пар значений. Кроме того, поразительно, что DCT требует точно N значений для преобразования, т.е. для вычисления N независимых частотных коэффициентов. Все частоты находятся в интервале [0,π]. В отличие от DFT, обратилась в нуль избыточность, содержащаяся в спектре для вещественных значений входных сигналов, исчезает, и таким образом частотное разрешение становится вдвое выше. Однако недостатком является то, что спектр DCT не может быть преобразован относительно абсолютного значения (или амплитуды) и фазы. Дополнительно к этому может возникнуть такая ситуация, что частоты, которые соответствуют основным функциям DCT (см. уравнения 2.14a-2.14d), но повернуты относительно них по фазе на 90°, содержатся в сигнале. Эти частоты не формируются DCT, то есть соответствующий коэффициент DCT равен нулю. По этим причинам DCT хорошо подходит для эффективного и быстрого сжатия данных, но меньше подходит для анализа сигнала (Malvar, 1992).
Кроме дискретного косинусоидального преобразования, существует дискретное синусоидальное преобразование (DST). В целом различают восемь форм DST. Здесь важным является только DST-IV. Что касается его формы и функций, они соответствуют преобразованию DCT-IV (Rao and Yip, 2001):
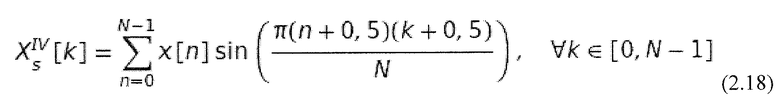
Когда сигнал преобразуется с использованием и DCT-IV, и DST-IV, комплексный спектр, сформированный комбинацией двух вещественных спектров, снова содержит информацию об абсолютном значении и фазе. Частотное разрешение здесь все еще является вдвое более высоким, чем в DFT, что означает, что частоты N отображаются на интервал [0,π] (Malvar, 1992).
Для обработки длительных аудиосигналов невозможно преобразовать сигнал в целом. С одной стороны, вычислительная сложность здесь чрезвычайно увеличивается, так как для того, чтобы вычислить DCT
требуется также
N2 вычислительных операций. С другой стороны, обработать сигнал в режиме реального времени невозможно, так как необходимо все время ожидать передачи всего потока данных до тех пор, пока сигнал не сможет быть восстановлен. Следовательно, сигнал необходимо делить на блоки. В этом случае DCT применяется как так называемое блочное преобразование (Rao and Yip, 2001). Используя индекс блока 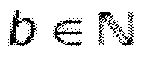 , из уравнения 2.14d получается следующее уравнение для DCT-IV:
, из уравнения 2.14d получается следующее уравнение для DCT-IV:
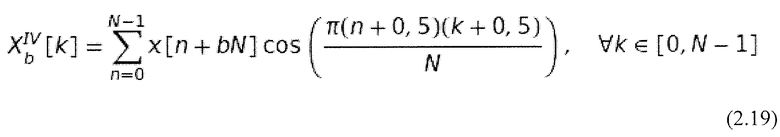
Длина сигнала x[n] соответствует bN. При блочном преобразовании возникают блочные артефакты из-за квантизации. Известным примером, где артефакты этого вида могут быть распознаны, является способ сжатия JPEG. Блочные артефакты происходят из граничных продолжений, выполняемых для периодизации. Они не соответствуют первоначально принятым сигнальным продолжениям (см. уравнение 2.16). Результатом являются скачки на границах блока, которые в частотном домене смещают энергию к высоким частотам (Malvar, 1992). Скачки в аудиосигнале могут быть восприняты как потрескивания. Человеческий слух очень чувствителен к таким артефактам. Таким образом, их следует абсолютно избежать.
Далее будет обсуждено модифицированное дискретное косинусоидальное преобразование.
Модифицированное дискретное косинусоидальное преобразование (MDCT) является центральным преобразованием для аудио сжатия. Оно используется, среди прочего, в алгоритмах mp3, AAC и Dolby Digital (ac-3). MDCT представляет собой вещественное, дискретное, линейное и ортогональное преобразование и является модификацией DCT-IV. Оно определяется следующим образом (Rao and Yip, 2001):
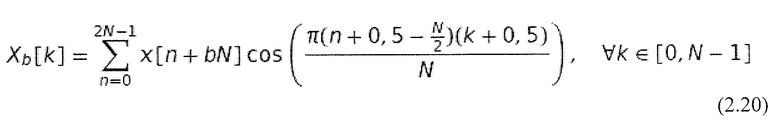
Преимуществом MDCT по сравнению с DCT-IV является то, что оно избегает блочных артефактов. Это может быть достигнуто главным образом наложением друг на друга нескольких последовательных блоков. Этот вид преобразования также известен как перекрывающееся ортогональное преобразование (LOT) (Malvar and Staelin, 1989).
Избыточность может быть снова удалена способом перекрытия - добавления (OLA). Таким образом, блоки, формирующиеся в обратном преобразовании, перекрываются до 50% и складываются, эта процедура упоминается как перекрытие - добавление.
Частотное разрешение MDCT может быть дополнительно улучшено путем взвешивания входной последовательности x[n+bN] с помощью оконной функции. В уравнении 2.20 окно соответствует прямоугольной функции, вырезающей текущий блок b из полного сигнала. В частотной области это соответствует свертке (сворачиванию) с использованием функции интегрального синуса. Плохое затухание функции интегрального синуса на границе окна может быть улучшено путем адаптации этой функции окна, и таким образом может быть достигнута увеличенная частотная селекция. Для того, чтобы преобразование MDCT было способно на качественное восстановление, оконная функция w[n] длины 2N должна выполнять условия Принсена-Брэдли (PR) (Princen et al., 1987):
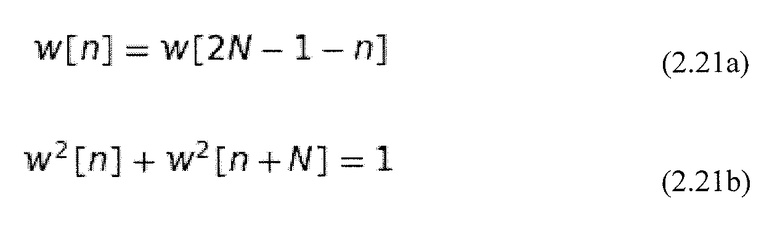 .
.
Простое окно, выполняющее эти условия и показывающее достаточное затухание на границе окна, является синусом половины волнового окна. Это используется, среди прочего, в алгоритмах mp3 и AAC, и определяется следующим образом (Malvar, 1992):
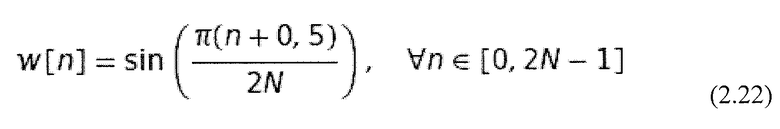
Путем вставки функции окна 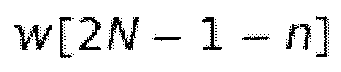 в уравнение 2.20 может быть получена другая важная функция MDCT. Результат соответствует дискретной свертке x[n+bN] использующей модулированную функцию окна
в уравнение 2.20 может быть получена другая важная функция MDCT. Результат соответствует дискретной свертке x[n+bN] использующей модулированную функцию окна 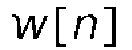 . Таким образом, поскольку
. Таким образом, поскольку 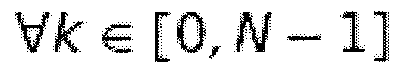 , получается следующее (Schuller and Smith, 1996):
, получается следующее (Schuller and Smith, 1996):

Таким образом, MDCT не может рассматриваться только как блочное преобразование, но также и как модулируемый набор фильтров (Malvar, 1992). Таким образом, оконная функция соответствует низкочастотному прототипному фильтру FIR, который модулируется ядром косинуса и таким образом представляет полосы частот набора фильтров. Результатом этого является то, что входная последовательность x[n+bN] разлагается точно на N поддиапазонов. В соединении с особенностью TDA MDCT выполняет предварительные условия так называемого «критически дискретизированного набора фильтров».
Такой критически дискретизированный набор фильтров проиллюстрирован на Фиг. 25. В частности, на Фиг. 25 показан критически дискретизированный набор фильтров PR с количеством полос N с системной задержкой из nd отсчетов. Такие наборы фильтров имеют особое значение для аудиокодирования, так как они описывают сигнал настолько точно и полно, насколько это возможно при самом маленьком количестве отсчетов (Rao and Yip, 2001).
Символ 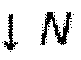 соответствует уменьшению скорости оцифровки с коэффициентом 1/N, а
соответствует уменьшению скорости оцифровки с коэффициентом 1/N, а 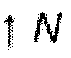 - увеличению с коэффициентом N. Сигнал после набора фильтров синтеза
- увеличению с коэффициентом N. Сигнал после набора фильтров синтеза 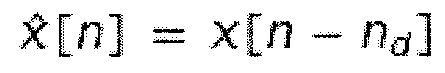 идентичен входному сигналу x[n] перед аналитическим набором фильтров, за исключением постоянной задержки из nd отсчетов. В случае MDCT,
идентичен входному сигналу x[n] перед аналитическим набором фильтров, за исключением постоянной задержки из nd отсчетов. В случае MDCT, 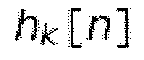 представляет собой модулированную оконную функцию
представляет собой модулированную оконную функцию 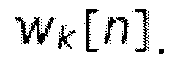 Поскольку
Поскольку  выполняет условия PR, аналитические фильтры hk идентичны фильтрам синтеза gk.
выполняет условия PR, аналитические фильтры hk идентичны фильтрам синтеза gk.
С математической точки зрения это является подходящим для того, чтобы сформулировать системы линейных уравнений, включающие в себя все преобразования, упомянутые до сих пор, в векторно-матричной системе обозначений. Сигнал x[n] длины bN представляется как вектор-столбец 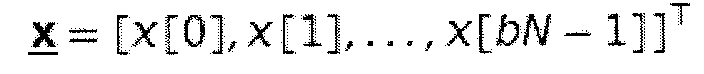 . Оператор Т здесь обозначает транспонирование. Формирование блока может быть представлено как матрица, в которой каждый столбец матрицы содержит блок x[n]:
. Оператор Т здесь обозначает транспонирование. Формирование блока может быть представлено как матрица, в которой каждый столбец матрицы содержит блок x[n]:

Правило преобразования также может быть представлено в виде матрицы. Модулированные оконные функции здесь формируют строки матрицы. При 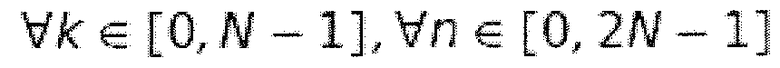 получается следующее:
получается следующее:
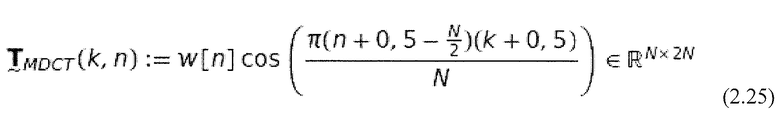 .
.
Для того, чтобы можно было вычислить MDCT 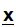 , блочная структура
, блочная структура 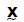 должна быть расширена 50%-ым перекрытием для TDA. Таким образом, MDCT может быть записано следующим образом:
должна быть расширена 50%-ым перекрытием для TDA. Таким образом, MDCT может быть записано следующим образом:

где:
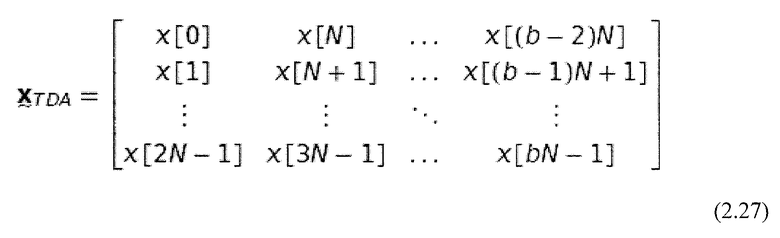
Каждый столбец 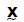 образует спектр MDCT соответствующего блока с номером b в
образует спектр MDCT соответствующего блока с номером b в 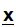 .
.
Для того, чтобы вычислить блок, эта форма MDCT требует 2N2 умножений и сложений. Однако вычислительная сложность может быть значительно уменьшена.
Таким образом, необходимо преобразовать набор фильтров, изображенный на Фиг. 25, к эквивалентному многофазному набору фильтров (см. Фиг. 26). Используя многофазное представление и z-преобразование, многоскоростные системы, такие как набор фильтров MDCT, могут быть проанализированы более широко.
Фильтр FIR h[n] всегда может быть поделен на 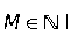 фаз, когда длина фильтра является кратной М. m-я фаза pm[n] фильтра h[n] получается путем задержки n[n] на z-m и уменьшения скорости оцифровки в М раз. (Malvar, 1992). Используется следующая формула:
фаз, когда длина фильтра является кратной М. m-я фаза pm[n] фильтра h[n] получается путем задержки n[n] на z-m и уменьшения скорости оцифровки в М раз. (Malvar, 1992). Используется следующая формула:
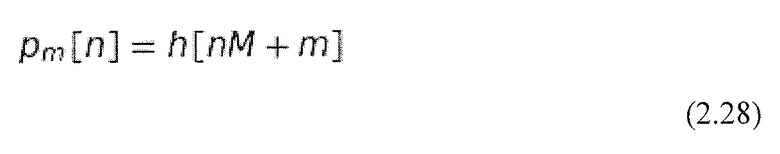
Используя разложение и z-преобразование, фильтр h[n] может быть представлен следующим образом (Malvar, 1992):
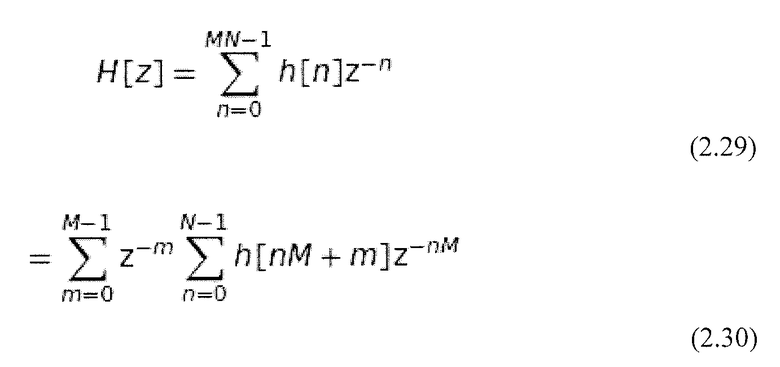
Вместо записи в виде сумм предпочтительной является векторная система обозначений. Уравнение 2.30 таким образом может быть представлено как вектор размерности N:
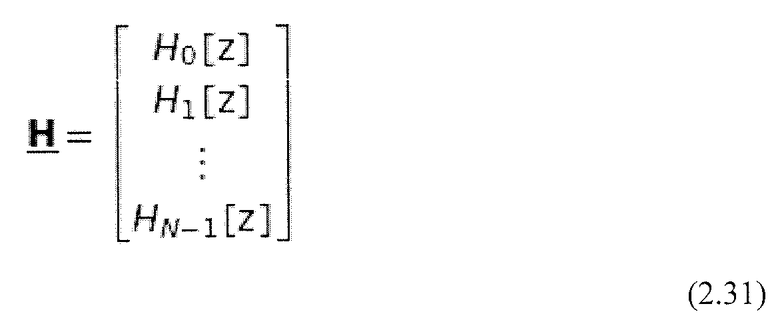
где:
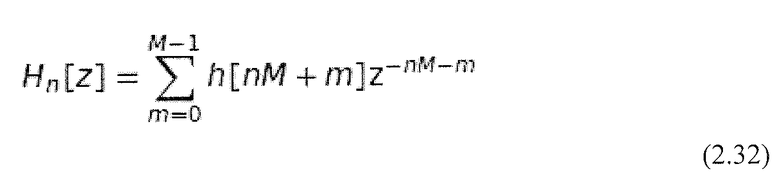
Это многофазное разложение затем может быть применено к каждому фильтру из набора фильтров MDCT. Результатом является эквивалентное многофазное представление набора фильтров, упомянутого выше, изображенное на Фиг. 26 (Schuller and Smith, 1996). Таким образом, Фиг. 26 представляет эквивалентный критически дискретизированный многофазный набор фильтров PR с количеством полос N.
Используя симметрии в ядре MDCT и особенность TDA, анализ и синтез матриц многофазных фильтров  и
и 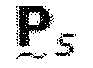 может каждый быть разделен на разреженную матрицу свертки и матрицу преобразования (Schuller and Smith, 1996). Матрицы свертки
может каждый быть разделен на разреженную матрицу свертки и матрицу преобразования (Schuller and Smith, 1996). Матрицы свертки  и
и 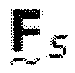 здесь имеют ромбовидную структуру с коэффициентами оконной функции
здесь имеют ромбовидную структуру с коэффициентами оконной функции 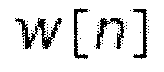 в виде полиномиалов в z-области. Они могут быть далее разложены на матрицу окна и матрицу задержки:
в виде полиномиалов в z-области. Они могут быть далее разложены на матрицу окна и матрицу задержки:

Точная форма и разбиение матриц свертки будут показаны ниже. Матрицы преобразования соответствуют матрице DCT-IV:
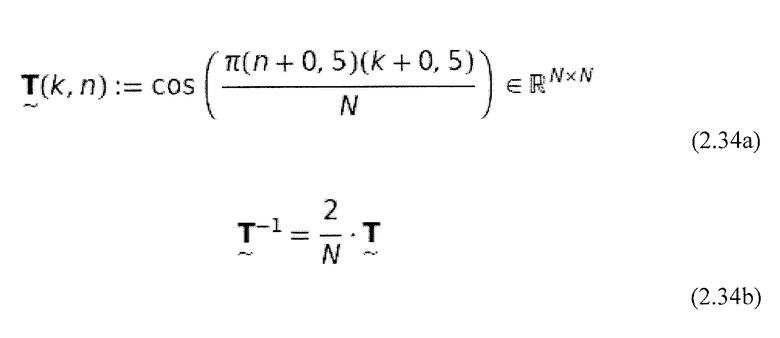
Используя эти матрицы, спектр MDCT входного сигнала, разделенного на блоки 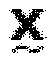 , вычисляется следующим образом (Schuller and Smith, 1996):
, вычисляется следующим образом (Schuller and Smith, 1996):

где для обратного преобразования применяется следующая формула:
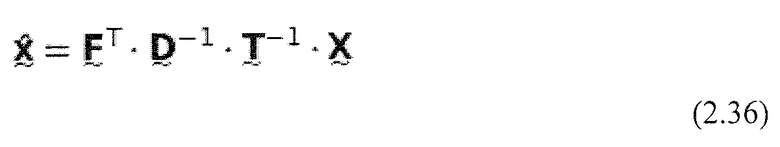
Это решение предлагает несколько преимуществ по сравнению с вычислением MDCT в соответствии с уравнением 2.26. Во-первых, формирование искажений за счет эффекта наложения во временной области может быть более легко распознано. При многофазном представлении матрицы свертки в уравнении 2.33a процесс может быть интерпретирован как переворачивающий взвешенные части сигнала блока (b-1) в текущий блок b. Путем добавления этих частей сигнала образуется TDA. Самым большим преимуществом вычисления MDCT с использованием множества фаз является значительно уменьшенная вычислительная сложность. При использовании квадратной матрицы DCT-IV и разреженной матрицы свертки вычислительная сложность уменьшается до N(N+2) умножений и сложений. Путем использования быстрых реализаций DCT, аналогично FFT, количество требуемых операций может быть сокращено вплоть до N(logN+2), и таким образом сложность может быть уменьшена до 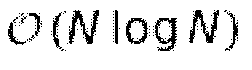 (Rao and Yip, 2001). По этим причинам в настоящем документе предполагается реализация MDCT в соответствии с многофазным подходом.
(Rao and Yip, 2001). По этим причинам в настоящем документе предполагается реализация MDCT в соответствии с многофазным подходом.
При обработке аудиосигнала может быть необходимо сдвигать сигнал низкой частоты к более высоким частотам, причем упомянутый сдвиг частоты должен быть свободно выбираемым и точным. Аудио-кодеры, которые пытаются восстановить более высокие частоты сигнала, должны сталкиваться с этой проблемой. Современные технологии аудиокодирования используют способы расширения полосы частот для более эффективного сжатия аудиоданных. Кроме психоакустических функций человеческого слуха, корреляция низкочастотных частей сигнала в высокочастотные части используется при снижении объема данных.
Несмотря на существование различных способов уменьшения скорости передачи данных при аудиокодировании, текущие аудио-кодеры достигают своих пределов, когда требуются низкие битрейты. В частности, психоакустические способы в этом случае производят нежелательные повреждения сигнала. Это может быть замечено в мешающих артефактах, таких как пропущенные высоты, размытые переходные процессы или искусственное шипение воспроизведенного аудиосигнала. Во многих случаях применения, однако, доступна только ограниченная ширина полосы передачи. Расширение полосы частот (BWE) предлагает решение для этих проблем. Обычно расширение полосы частот объединяет ряд способов, используя которые ограниченный полосой аудиосигнал может быть расширен спектрально, чтобы снова получить исходную ширину полосы. В целом различают четыре категории способов для расширения полосы частот (Larsen and Aarts, 2004). Они проиллюстрированы графически на Фиг. 27.
На Фиг. 27 показаны категории расширения полосы частот (Larsen and Aarts, 2004). На Фиг. 27 низкочастотное психоакустическое BWE показано на верхней левой части. На Фиг. 27 высокочастотное психоакустическое BWE показано на верхней правой части. Фиг. 27 показывает низкочастотное BWE на нижней левой части. В дополнение к этому, высокочастотное BWE проиллюстрировано на Фиг. 27 на нижней правой части. Энергия полосы 'a' (прерывистая линия) смещается в полосу 'b' (пунктирная линия).
Только категория III (показанная справа внизу на Фиг. 27) является полезной для аудиокодирования. При так называемом «высокочастотном BWE», частоты, присутствующие в ограниченном полосой сигнале, используются для того, чтобы восстановить высокочастотный диапазон спектра. Идея использования такого способа для расширения полосы частот аудиосигналов основана на том факте, что существует сильная корреляция между высокочастотными и низкочастотными частями сигнала. Таким образом, возможно восстановить недостающие высокие частоты по присутствующим низкочастотным частям сигнала (Larsen and Aarts, 2004). Текущие методы и способы, при использовании которых ограниченный полосой сигнал может быть расширен до его исходной ширины полосы посредством высокочастотного BWE, будут представлены ниже.
Репликация спектрального диапазона (SBR) известна из предшествующего уровня техники, как используемая, среди прочего, в HE-AAC. При репликации спектрального диапазона с помощью SBR корреляции между низкочастотными и высокочастотными частями сигнала используются для того, чтобы развернуть низкочастотный сигнал, обеспеченный кодером спектрально. Низкочастотные полосы базового набора фильтров копируются в недостающие высокочастотные полосы, и огибающая спектра адаптируется. Этот процесс копирования вызывает, в особенности при низких частотах отсечки, заметные артефакты, такие как резкость звука и нежелательные изменения в тембре. Они вызываются, главным образом, недостающим гармоническим продолжением спектра на границе между основной полосой и алгоритмически произведенными высокочастотными полосами.
Аудио-кодер SBR предшествующего уровня техники использует разложение pQMF сигнала на поддиапазоны и таким образом гарантирует высокую эффективность кодирования (Eckstrand, 2002). Это достигается путем передачи только низкочастотных полос, тогда как более высокочастотные части восстанавливаются путем использования побочной информации и сдвига частот низкочастотных полос, упомянутых ранее.
Репликация спектрального диапазона в настоящее время является наиболее широко распространенным способ для расширения полосы частот. Она используется, среди прочего, в алгоритмах HE-AAC и mp3PRO. SBR была разработана компанией Coding Technologies с целью увеличения эффективности существующих аудио-кодеров. Это достигается путем обработки кодером только частот ниже определенной граничной частоты fg. В упомянутых примерах кодеры mp3 и AAC используются в качестве базовых кодеров. Частоты выше граничной частоты описываются только несколькими параметрами. В зависимости от качества, которое должно быть достигнуто, они составляют от 5 кГц до 13 кГц. Высокочастотные части затем восстанавливаются в получателе с использованием упомянутой побочной информации и декодированного ограниченного полосой сигнала (Ekstrand, 2002).
На Фиг. 28 показана блок-схема расширенного кодера SBR. Скорость оцифровки входного сигнала уменьшается, после чего сигнал подается к фактическому кодеру. Параллельно сигнал анализируется комплексным квадратурным зеркальным набором фильтров (QMF) и выполняется вычисление энергии. Используемый QMF состоит из 64 поддиапазонов. Параметры, требуемые для оценки спектральных огибающих, могут быть получены из этого. Дополнительные параметры позволяют реагировать на специальные характеристики входного сигнала. Зная кодер SBR, это может распознавать большие различия между оригиналом и синтезируемой высокочастотной частью (HF) путем генерации высокочастотной полосы.
Когда, например, в сигнале присутствуют сильно различные отдельные звуки выше частоты среза, они описываются дополнительными параметрами и могут быть снова добавлены к восстановленному сигналу. Производимая побочная информация вставляется в выходной поток битов отдельно от фактических аудиоданных (Larsen and Aarts, 2004).
На Фиг. 29 показана блок-схема соответствующего декодера, расширенного за счет SBR. Ограниченные полосой аудиоданные декодируются декодером, и контрольные параметры извлекаются из потока битов. После этого аудиоданные снова подаются к набору фильтров QMF для того, чтобы восстановить высокочастотные части. Основная полоса копируется в пределах этого набора фильтров и вставляется выше частоты среза (см. Фиг. 30, слева).
Фиг. 30 представляет собой схематическую иллюстрацию абсолютного значения частотной характеристики. Таким образом, Фиг. 30 представляет собой схематическую иллюстрацию восстановления SBR-HF. Фиг. 30 показывает копирование и сдвиг основной полосы влево. Фиг. 30 иллюстрирует спектр после корректировки спектральной огибающей справа.
Информация, сформированная в кодере SBR, на спектральной огибающей используется для того, чтобы совместить огибающую скопированного спектра с огибающей исходного спектра. Эта адаптация выполняется с использованием переданного контрольного параметра и энергии соответствующей полосы QMF. Если особенности восстановленного спектра будут отличаться от исходных, то к сигналу дополнительно будут добавлены тональные компоненты или шум (Larsen and Aarts, 2004). Фиг. 30 показывает адаптированный восстановленный спектр справа.
Наконец, ограниченный полосой сигнал и восстановленный высокочастотный сигнал объединяются и преобразуются во временную область набором фильтров синтеза. Таким образом формируется сигнал с расширенной полосой частот, который теперь готов к воспроизведению.
В этой разновидности расширения полосы частот возникают проблемы с высокотональными сигналами сильно различной гармонической структуры. Даже если способ SBR предусматривает методы тональной адаптации спектра, они являются недостаточными для того, чтобы восстановить уничтоженную гармоническую структуру. Результатом является заметная резкость звука в сигнале (Wilde, 2009). Эти артефакты очень неприятны для слушателя. Они проистекают из процесса копирования декодера SBR. Он не учитывает гармоническую микроструктуру сигнала и просто реплицирует основную полосу. Результат показан на Фиг. 31.
На Фиг. 31 показано разрушение гармонической структуры в SBR. На Фиг. 31 показан исходный широкополосный спектр слева. На Фиг. 31 показан спектр после восстановления HF SBR справа.
Ясно видно, что гармоники смещены относительно исходного спектра в диапазоне выше частоты среза. Восстановленный спектр HF является гармоническим, но гармоническая структура смазывается дополнительной девиацией частоты 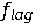 на частоте среза. Дополнительно к этому, амплитудные отношения гармонических подтонов искажаются при восстановлении огибающей. Этот эффект будет происходить со всеми гармоническими сигналами, например, с сигналами, произведенными музыкальными инструментами.
на частоте среза. Дополнительно к этому, амплитудные отношения гармонических подтонов искажаются при восстановлении огибающей. Этот эффект будет происходить со всеми гармоническими сигналами, например, с сигналами, произведенными музыкальными инструментами.
Для гармонических сигналов, таких как, например, звук трубы, SBR и эквивалентные способы расширения полосы частот создают нежелательные артефакты, такие как, например, тональная резкость и неприятный тембр, так как гармоническая структура сигнала не сохраняется полностью. Для сигналов, показывающих отличающуюся гармоническую структуру, при применении SBR возникают нежелательные артефакты, такие как резкость звука и изменения в тембре.
Вот почему были разработаны два способа расширения полосы частот во временной области, которые содержат эти структуры: управляемое фазовым вокодером гармоническое расширение полосы частот (HBE) и BWE с непрерывной модуляцией (CM), который использует специальную модуляцию боковой полосы (Nagel and Disch 2009), (Nagel et al. 2010). Благодаря непрерывной модуляции со свободно выбираемыми частотами, в частности CM-BWE достигает хорошего гармонического восстановления.
Существуют некоторые альтернативные способы расширения полосы частот, которые избегают проблемы дисгармонического спектрального продолжения. Два из этих способов будут представлены ниже. В основном эти способы заменяют генератор высокой частоты декодера SBR, изображенного на Фиг. 29, и таким образом представляют собой альтернативу простому процессу копирования. Адаптация спектральной огибающей и тональности остается неизменной. Так как входной сигнал должен находиться во временной области, этот способ также упоминается как способ расширения полосы частот во временной области.
Сначала следует упомянуть гармоническое расширение полосы частот (HBE). HBE использует фазовый вокодер для формирования высокочастотного диапазона. Спектр расширяется путем применения фазового вокодера. Как показан слева на Фиг. 32, основная полоса растягивается до максимальной частоты сигнала 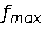 и вырезается диапазон частот от частоты среза до
и вырезается диапазон частот от частоты среза до 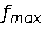 . Спектр затем составляется из упомянутой части и основной полосы (см. Фиг. 32, справа). Огибающая адаптируется как в способе SBR (Nagel and Disch 2009).
. Спектр затем составляется из упомянутой части и основной полосы (см. Фиг. 32, справа). Огибающая адаптируется как в способе SBR (Nagel and Disch 2009).
Фиг. 32 представляет собой схематическую иллюстрацию восстановления HBE-HF. Фиг. 32 слева показывает расширение основной полосы с фактором два. Фиг. 32 справа показывает спектр после адаптации спектральной огибающей.
Использование коэффициентов интегрального расширения 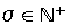 гарантирует, что частота среза fg не изменяет гармоническую структуру. Используется следующая формула:
гарантирует, что частота среза fg не изменяет гармоническую структуру. Используется следующая формула:

Недостатком является тот факт, что расстояние между подтонами в области высоких частот изменяется с коэффициентом расширения при растягивании спектра, как можно видеть на Фиг. 33. В дополнение к этому, для растягивания спектра требуются сложные вычисления. Среди них DFT с высоким разрешением, фазовая адаптация и преобразование скорости оцифровки (Dolson, 1986). Когда аудиосигнал подразделен на блоки, дополнительно необходима структура перекрытия - добавления, чтобы непрерывно продолжать фазу соседних блоков. Для высокотональных сигналов очень хорошие результаты могут быть достигнуты путем использования метода фазового вокодера, однако в перкуссионных сигналах переходные процессы размываются, и становится необходимым выполнение отдельной переходной обработки (Wilde, 2009).
На Фиг. 33 показана гармоническая структура с HBE. На Фиг. 33 слева показан исходный широкополосный спектр. Фиг. 33 справа иллюстрирует спектр после высокочастотной восстановления HBE.
Ниже будет представлена непрерывная модуляция с одной боковой полосой.
Непрерывно модулируемое расширение полосы частот (CM-BWE) является другим способом для расширения полосы частот во временной области. В этом способе основная полоса модулируется частотой fmod посредством модуляции одной боковой полосы и таким образом сдвигается к другому спектральному расположению, как проиллюстрировано на Фиг. 34. Переменная частота модуляции гарантирует, что гармоническая структура сигнала с расширенной полосой частот будет сохранена. При частотах модуляции больше, чем частота среза fg, промежуток, образующийся в спектре, должен быть заполнен шумом (Nagel et al., 2010).
На Фиг. 34 показана схематическая иллюстрация восстановления CM-BWE-HF. Фиг. 34 слева показывает модуляцию основной полосы с частотой fmod. Фиг. 34 справа показывает спектр после адаптации спектральной огибающей.
Кроме случая, проиллюстрированного на Фиг. 34, также может быть необходимо несколько раз модулировать основную полосу. В таком случае частота модуляции должна быть адаптирована для каждой модуляции, в которой выбрано ее соответствующее следующее кратное (Nagel et al., 2010). Перед модуляцией основная полоса должна быть отфильтрована фильтром НЧ в соответствии с модуляционной частотой для того, чтобы максимальная разрешенная частота сигнала fmax не была превышена после модуляции. Аналогично уже представленным способам, после этого формируется спектральная огибающая и адаптируется тональность.
На Фиг. 35 показана гармоническая структура, формирующаяся в сигнале, расширенном посредством CM-BWE. На Фиг. 35 слева показан исходный широкополосный спектр. На Фиг. 35 справа показан спектр после восстановления CM-BWE-HF. Как и в способе HBE, CM-BWE испытывает недостаток гармонического подтона в спектре. Однако, это не вызывает отрицательных эмоций, поскольку сама гармоническая структура сохраняется.
Недостатком этого способа является вычисление модуляции одной боковой полосы. Для корректного вычисления требуется аналитический сигнал, то есть сигнал, содержащий только положительные частоты. Для вычисления такого сигнала необходим преобразователь Гильберта. Преобразователь Гильберта в основном представляет собой некаузальный фильтр бесконечного ответа на импульс. Такой фильтр не может быть реализован и должен быть упрощен. Для того, чтобы, тем не менее, достичь максимально возможного затухания на границе полосы с минимальным порядком фильтра, к сигналу добавляется непренебрежимая задержка за счет каузализации фильтра (Wilde, 2009).
Однако, когда сдвиг частоты реализуется во временной области, это может быть очень сложным. Реализация сдвига в области полос частот полосового аудио-кодера по контрасту может привести к частотному разрешению, которое является слишком грубым для требуемого сдвига частоты.
Желательно минимизировать пространство памяти для требуемых цифровых данных, либо ширину полосы, требуемой для передачи упомянутых данных путем кодирования аудиосигналов. В то же самое время, воспринимаемое качество воспроизведенного аудиосигнала должно быть сопоставимым со стандартом CD (частота оцифровки 44100 Гц при глубине квантизации 16 битов). Таким образом, качество должно быть максимизировано при уменьшении скорости передачи данных.
Следовательно, задачей настоящего изобретения является предложить улучшенные концепции для свободно выбираемых сдвигов частоты в области полос частот. Задача настоящего изобретения решается устройством в соответствии с п. 1 формулы изобретения, способом в соответствии с п. 23 формулы изобретения и компьютерной программой в соответствии с п. 24 формулы изобретения.
Предлагается устройство для формирования сдвинутого по частоте аудиосигнала на основе входного аудиосигнала. Входной аудиосигнал для множества первых поддиапазонов может быть представлен здесь одним или несколькими значениями первых поддиапазонов. Это устройство включает в себя интерфейс и блок сдвига частоты. Интерфейс выполнен с возможностью получения входного аудиосигнала. Блок сдвига частоты выполнен с возможностью формирования сдвинутого по частоте аудиосигнала, который для множества вторых поддиапазонов включает в себя одно или несколько значений каждого из вторых поддиапазонов. В дополнение к этому, каждое из значений первого и второго поддиапазона включает в себя информацию об одном соответствующем фазовом угле. Блок сдвига частоты дополнительно выполнен с возможностью формирования одного из значений второго поддиапазона на основе одного из значений первого поддиапазона так, что второй фазовый угол упомянутого значения второго поддиапазона может отличаться от первого фазового угла упомянутого значения первого поддиапазона на разность фазового угла, причем разность фазового угла зависит от частотной информации, указывающей, на какую разницу частот должен быть сдвинут входной аудиосигнал для того, чтобы получить сдвинутый по частоте аудиосигнал, и разность фазового угла зависит от ширины полосы частот одного из первых поддиапазонов.
Варианты осуществления предлагают улучшенные концепции для расширения полосы частот, эти улучшенные концепции впоследствии упоминаются как «гармоническое расширение спектрального диапазона» или «HSBE». Это разработанное гармоническое расширение полосы частот в частотной области обеспечивает подавление нежелательных артефактов. Реплицированный спектр здесь модулируется так, что сохраняется исходная гармоническая структура. В отличие от других способов, HSBE может быть основан на представлении сигнала в области MDCT и таким образом обеспечивает эффективную реализацию. Гармонично корректное расширение полосы частот достигается путем процесса копирования спектральных значений с последующей модуляцией.
В соответствии с одним вариантом осуществления используется область полос частот MDCT, который обычно уже реализован в аудио кодерах. Таким образом, преобразование не приводит к дополнительной сложности или задержке.
Когда сигнал сдвигается на величину, четно кратную ширине полосы поддиапазона, в вариантах осуществления сигналы поддиапазона низких частот сдвигаются к соответствующим полосам более высокой частоты.
Когда сигнал должен быть сдвинут на нечетно кратную величину, в вариантах осуществления каждый второй отсчет сигналов поддиапазона, которые должны быть скопированы, получает обратный знак (индекс блока увеличивается в направлении времени). Таким образом, свойство устранения искажений из-за эффекта наложения набора фильтров MDCT все еще работает для сдвинутого по частоте и скопированного сигнала.
Когда сигналы нижних частот сдвигаются на величину, нецелочисленно кратную ширине полосы поддиапазона, в вариантах осуществления формируются комплексные версии поддиапазонов нижних частот, делается их копия, и они модулируются (умножаются) на комплексную экспоненциальную функцию, причем упомянутая комплексная экспоненциальная функция имеет частоту, которая соответствует разности частоты следующего целого кратного ширины полосы поддиапазона (что является дробным сдвигом ширины полосы поддиапазона). Однако это влияет на свойство компенсации искажения искажений из-за эффекта наложения набора фильтров MDCT или вообще уничтожает его.
Для того, чтобы предотвратить или уменьшить получающееся частотное искажение, выполняется подобная свертке обработка между соседними сигналами поддиапазона, в которой взвешенная версия одного сигнала поддиапазона добавляется к сигналу поддиапазона в его окружении, так, чтобы он имел обратный знак компонента искажения, и так, чтобы искажение компенсировалось или уменьшалось. В одном варианте осуществления веса выбираются так, чтобы они соответствовали требуемому дробному сдвигу частоты.
Модуляция спектра нарушает свойство TDAC алгоритма MDCT, и результатом являются компоненты искажения. Для того, чтобы устранить их, в вариантах осуществления предлагается структура фильтра FIR для устранения искажений. Импульсные ответы фильтра, требуемые для этого, оптимизируются посредством последовательного приближения и, например, сохраняются как справочная таблица.
Однако для применимости представленных здесь концепций не обязательно адаптировать процесс кодирования, то есть сжатие данных, например, путем применения психоакустической модели.
Предлагаемые концепции основаны на уже существующих способах расширения полосы частот, и улучшают их. Используя этот новый способ, становится возможным повысить качество воспроизводимого аудио материала при постоянных требованиях к памяти. Процесс кодирования здесь не затрагивается, но декодер является усовершенствованным. Разработанный способ реализует гармоническое расширение полосы частот. Он основан на репликации спектрального диапазона (SBR), которая используется в технологии HE-AAC.
Предлагаемые эффективные концепции репликации спектрального диапазона в соответствии с настоящим изобретением поддерживают гармоническую структуру исходного спектра и таким образом уменьшают описанные артефакты известной технологии SBR.
Предлагаются концепции для гармонического расширения спектрального диапазона (HSBE). Поскольку эффективность играет важную роль, будет описана базовая обработка сигналов, начиная с набора фильтров, используемого для подавления артефактов фильтров FIR.
Представленное здесь гармоническое расширение спектрального диапазона обеспечивает мощный и эффективный способ расширения ограниченного полосой спектра аудиосигнала с одновременным продолжением его гармонической структуры.
Будет показано, что необходимо учесть ряд проблем при гармоническом расширении спектрального диапазона для того, чтобы спектр продолжался гармонично корректным образом. Даже если некоторые способы для восстановления гармонической структуры спектра являются известными, полезно тем не менее разработать новые и более эффективные методы. В особенности для интегрирования в современные структуры аудио-кодеров, такие как AAC или USAC, в которых адаптация к общим условиям является совершенно обязательной.
Существенным компонентом успешного гармонического расширения спектрального диапазона является подавление образования паразитных компонентов. Именно поэтому режим функционирования и оптимизация устранения искажений, разработанного для этого, находится в фокусе настоящего документа. Было показано, что нежелательные части сигнала могут быть сильно уменьшены путем выбора подходящих фильтров FIR. Таким образом, в отличие от классического фильтрования производится свертка с использованием импульсной передаточной функции не временного сигнала, а комплексных коэффициентов MDCT/MDST. Даже если этот способ не в состоянии устранить все образующиеся компоненты искажений, достаточно устранить несколько доминирующих паразитных частей.
Кроме этого, преобразование коэффициентов MDCT в спектральные значения MDST является другим важным элементом гармонического расширения спектрального диапазона. Современные аудио-кодеры работают исключительно в области MDCT. Сигнал описывается достаточно точно в его спектральном представлении, тем не менее эта информация не является достаточной для того, чтобы реплицировать спектр с использованием HSBE. Требуемая фазовая форма может быть модифицирована только дополнительными коэффициентами MDST. В настоящем документе представлено преобразование, которое позволяет, используя постоянную задержку, вычислять неизвестные коэффициенты MDST из известных значений MDCT настолько эффективно, насколько это возможно. Кроме точного решения будет представлена подверженная ошибкам, но ресурсосберегающая альтернатива.
Модуляция спектра является важной при использовании HSBE. Это показывает, что две стадии являются полезными для эффективной репликации спектра. С одной стороны, спектр сдвигается на целое количество поддиапазонов MDCT, а с другой стороны модуляция в пределах ширины полосы поддиапазона MDCT выполняется для высокого разрешения. Для сигналов в качестве CD разрешение, достигаемое с использованием этого метода, составляет приблизительно 0,5 Гц. Это означает, что гармоническая структура спектра может быть реплицирована чрезвычайно точно.
Частота задержки, требуемая для определения модуляции, может быть, например, обеспечена кодером.
В вариантах осуществления предлагается система, устройство или способ или компьютерная программа для того, чтобы сформировать сдвинутый по частоте сигнал, в котором используется разложение поддиапазона, в котором, для сдвигов на дробную ширину полосы поддиапазона поддиапазоны умножаются на комплексную экспоненциальную функцию.
В вариантах осуществления компоненты искажения компенсируются или по меньшей мере уменьшаются путем выполнения перекрестной обработки между сигналами соседних поддиапазонов.
В соответствии с дополнительными вариантами осуществления частотный сдвиг выполняется в области полос частот системы аудиокодирования.
В вариантах осуществления частотный сдвиг используется для того, чтобы заполнить пропущенные частотные части и/или спектральные дыры частотного представления сигнала в системе аудиокодирования.
В соответствии с вариантами осуществления частотный сдвиг используется в комбинации с преобразованием скорости оцифровки для того, чтобы изменить скорость воспроизведения, оставляя высоту звука той же самой.
Например, если сначала увеличить частоту посредством частотного сдвига, а затем уменьшить скорость воспроизведения, время воспроизведения определенного количества аудиоданных станет более длительным, оставляя высоту звука той же самой. С другой стороны, если, например, сначала уменьшить частоту посредством частотного сдвига, а затем увеличить время воспроизведения некоторого количества аудиоданных, время воспроизведения станет короче при сохранении той же высоты звука.
В дополнительных вариантах осуществления эти концепции используются для тонкой подстройки музыкального сигнала. Предлагаемые концепции могут, например, особенно выгодным способом использоваться для аудио мелодии. Когда, например, должны быть реализованы только небольшие изменения высоты цифрового музыкального сигнала, то есть, например, изменения частоты, меньшие чем ширина полосы поддиапазона, например меньше, чем поддиапазон MDCT или QMF, предлагаемые концепции имеют определенное преимущество.
В соответствии с вариантами осуществления эти концепции используются для того, чтобы сформировать более высокие частоты спектра путем копирования или частотного сдвига частей спектра с меньшей частотой.
В вариантах осуществления разложение поддиапазона представляет собой модифицированное дискретное косинусоидальное преобразование (MDCT).
В дополнительных вариантах осуществления разложение поддиапазона представляет собой набор многофазных квадратурных зеркальных фильтров (QMF).
Концепции, предложенные в вышеупомянутых вариантах осуществления, могут, среди прочего, быть реализованы как система, устройство или способ или компьютерная программа.
Исполнимая реализация гармонического расширения спектрального диапазона формируется на основе предложенных и разработанных алгоритмов и функциональных принципов. Возможна реализация в реальном времени в системе математического моделирования Matlab, или на языке программирования C, или на другом языке программирования. Это означает, что предложенные концепции могут быть применены в системах реального времени. Ожидается, что качество воспроизведенного сигнала увеличит использование этих способов, как это имеет место в случае с SBR.
Анализ сложности модуляции спектра в соответствии с предложенными концепциями дает очень хорошие значения. Вычислительная сложность здесь в значительной степени зависит от преобразования MDCT-MDST.
В дополнение к этому, предлагается способ для формирования сдвинутого по частоте аудиосигнала, основанного на входном аудиосигнале, причем входной аудиосигнал для множества первых поддиапазонов может быть представлен одним или несколькими значениями первого поддиапазона.
Данный способ включает в себя:
- получение входного аудиосигнала, и
- формирование сдвинутого по частоте аудиосигнала, который для множества вторых поддиапазонов включает в себя одно или несколько значений каждого из вторых поддиапазонов,
в котором каждое из значений первого и второго поддиапазона включает в себя информацию об одном соответствующем фазовом угле, и
в котором одно из значений второго поддиапазона формируется на основе одного из значений первого поддиапазона так, что второй фазовый угол упомянутого значения второго поддиапазона может отличаться от первого фазового угла упомянутого значения первого поддиапазона на разность фазового угла, причем разность фазового угла зависит от частотной информации, указывающей, на какую разницу частот должен быть сдвинут входной аудиосигнал для того, чтобы получить сдвинутый по частоте аудиосигнал, и разность фазового угла зависит от ширины полосы частот одного из первых поддиапазонов.
В дополнение к этому предлагается компьютерная программа для выполнения вышеупомянутого способа при выполнении этой компьютерной программы на компьютере или сигнальном процессоре.
Предпочтительные варианты осуществления описаны в зависимых пунктах формулы изобретения.
Предпочтительные варианты осуществления будут описаны ниже со ссылками на чертежи, на которых показано:
Фиг. 1A - устройство для расширения полосы частот в соответствии с одним вариантом осуществления,
Фиг. 1В - устройство в соответствии с одним вариантом осуществления, причем устройство выполнено с возможностью формировать частотно-расширенный аудиосигнал,
Фиг. 2 - схематичная иллюстрация восстановления HSBE-HF в соответствии с одним вариантом осуществления,
Фиг. 3 -устройство 300 для формирования сдвинутого по частоте аудиосигнала в соответствии с одним вариантом осуществления,
Фиг. 4 - оценка матрицы преобразования MDCT-MDST в соответствии с одним вариантом осуществления,
Фиг. 5 - импульсные характеристики матрицы преобразования MDCT-MDST в соответствии с одним вариантом осуществления,
Фиг. 6 -оценка спектра MDST для белого шума,
Фиг. 7 - гармоническая структура с HSBE в соответствии с одним вариантом осуществления,
Фиг. 8 - схема расширенного восстановления HSBE-HF в соответствии с одним вариантом осуществления,
Фиг. 9 - компоненты искажений для φ=45°,
Фиг. 10 - импульсная характеристика фильтра устранения искажений в соответствии с одним вариантом осуществления для φ=90°,
Фиг. 11 - влияние фильтрации для устранения искажений на синусоидальный сигнал для φ=90° в соответствии с одним вариантом осуществления,
Фиг. 12 - перекрестную структуру для уменьшения искажений в соответствии с одним вариантом осуществления,
Фиг. 13 - адаптацию огибающей HSBE-LPC в соответствии с одним вариантом осуществления,
Фиг. 14 - сложность модуляции и фильтрации для устранения искажений в HSBE,
Фиг. 15 - сложность быстрого алгоритма MDCT/MDST,
Фиг. 16 - иллюстрация сложности алгоритма преобразования MDCT-MDST,
Фиг. 17 - остающееся возмущение в HSBE в зависимости от длины преобразования,
Фиг. 18 -сравнение HSBE и SBR,
Фиг. 19 - структура быстрого универсального преобразования DCT-III/DST-III,
Фиг. 20 - структура быстрого преобразования DCT-IV,
Фиг. 21 - схематичная иллюстрация временного маскирования,
Фиг. 22 схематичная иллюстрация частотно-зависимого маскирования для человеческого слуха,
Фиг. 23 - блок-схема психоакустического аудио-кодера,
Фиг. 24 - блок-схема психоакустического аудиодекодера,
Фиг. 25 - набор фильтров с системной задержкой nd отсчетов,
Фиг. 26 - набор многофазных фильтров,
Фиг. 27 - категории расширения полосы частот,
Фиг. 28 - блок-схема расширенного кодера SBR,
Фиг. 29 - блок-схема декодера, расширенного за счет SBR,
Фиг. 30 - схематичная иллюстрация восстановления SBR-HF,
Фиг. 31 - разрушение гармонической структуры при использовании SBR,
Фиг. 32 схематичная иллюстрация восстановления HBE-HF,
Фиг. 33 - гармоническая структура при использовании HBE,
Фиг. 34 схематическая иллюстрация восстановления CM-BWE-HF, и
Фиг. 35 гармоническая структура при использовании CM-BWE.
На Фиг. 1А показано устройство 100 для формирования сдвинутого по частоте аудиосигнала, основанного на входном аудиосигнале. Входной аудиосигнал для множества первых поддиапазонов здесь может быть представлен одним или несколькими значениями первого поддиапазона. Устройство включает в себя интерфейс 110 и блок 120 сдвига частоты. Интерфейс 110 выполнен с возможностью получения входного аудиосигнала. Блок 120 сдвига частоты выполнен с возможностью формирования сдвинутого по частоте аудиосигнала, который для множества вторых поддиапазонов включает в себя одно или несколько значений каждого из вторых поддиапазонов. В дополнение к этому, каждое из значений первого и второго поддиапазона включает в себя информацию об одном соответствующем фазовом угле. Блок 120 сдвига частоты дополнительно выполнен с возможностью формировать одно из значений второго поддиапазона на основе одного из значений первого поддиапазона так, что второй фазовый угол этого значения второго поддиапазона может отличаться от первого фазового угла этого значения первого поддиапазона на разность фазового угла, причем разность фазового угла зависит от частотной информации, указывающей, на какую разницу частот должен быть сдвинут входной аудиосигнал, то есть, например, на какую разницу частот должны быть сдвинуты значения первого поддиапазона из поддиапазонов входного аудиосигнала для того, чтобы получить сдвинутый по частоте аудиосигнал, и разность фазового угла зависит от ширины полосы частот одного из первых поддиапазонов.
В некоторых вариантах осуществления интерфейс может быть выполнен с возможностью получения частотной информации, указывающей, на какую разницу частот должны быть сдвинуты значения первого поддиапазона из поддиапазонов входного аудиосигнала.
На Фиг. 1В показано устройство 150 в соответствии с одним вариантом осуществления. Устройство 150 выполнено с возможностью формирования частотно-расширенного аудиосигнала. Устройство 150 здесь выполнено с возможностью формирования частотно-расширенного аудиосигнала путем формирования устройством 150 значений второго поддиапазона сдвинутого по частоте аудиосигнала, причем частотно-расширенный аудиосигнал включает в себя значения первого поддиапазона входного аудиосигнала и значения второго поддиапазона сдвинутого по частоте аудиосигнала.
Ниже будут представлены концепции расширения полосы частот в соответствии с вариантами осуществления, которые упоминаются как гармоническое расширение спектрального диапазона (HSBE). Это относится к концепциям, объединяющим преимущества алгоритма SBR и непрерывной модуляции одной боковой полосы. Это основано на представлении сигнала в области MDCT. Таким образом, HSBE может интегрироваться непосредственно в текущие аудио-кодеры, такие как HE-AAC или USAC, без использования дополнительного набора фильтров QMF, как это делается в алгоритме SBR. В отличие от способов временной области, необходимо вычисление DFT с высоким разрешением, не требующее анализа сигнала.
Режим работы гармонического расширения спектрального диапазона будет обсуждена ниже. Гармоническое расширение спектрального диапазона использует копию основной полосы для того, чтобы сформировать высокочастотную часть. Основная полоса реплицируется с использованием процесса копирования в высокочастотной области. В отличие от алгоритма CM-BWE, где при копировании образуется промежуток, в котором отсутствуют некоторые гармонические подтоны, сдвиг основной полосы в HSBE является расширенным. Основная полоса сначала также копируется вверх так, чтобы частота 0 Гц впоследствии находилась на частоте fg. Промежуток, образующийся при этом между последней гармоникой частоты f<fg в основной полосе и частотой fg, компенсируется путем сдвига скопированной основной полосы снова вниз, так что гармоническая структура снова становится непрерывной. Таким образом удается избежать промежутка, образующегося за счет игнорирования гармонического подтона, как в способах временной области. Процесс расширения полосы частот здесь состоит из двух частей. Одна часть реализуется путем процесса копирования в области MDCT. Низкочастотные коэффициенты MDCT реплицируются путем простого копирования. Другая часть расширения полосы частот, то есть поддержание гармонической структуры, получается за счет управления фазой. Таким образом, для этой стадии должна присутствовать фазовая информация. Гармоническое расширение спектрального диапазона в основном работает с использованием чисто вещественных коэффициентов MDCT. Это означает, что преобразование в комплексный спектр имеет место для того, чтобы изменить фазовую информацию. Это достигается за счет предлагаемого здесь преобразования MDCT-MDST.
Для того, чтобы высокие частоты основной полосы не накладывались на частоты реплицированной полосы во время адаптации, полоса высоких частот подвергается высокочастотному фильтрованию. Благодаря представлению сигнала в виде коэффициентов MDCT это фильтрование является очень простым, так как нежелательные коэффициенты могут быть просто обнулены. Однако этот тип сдвига вызывает ограничение полосы синтезируемого сигнала. Это означает, что после восстановления высокочастотного диапазона исходная максимальная частота сигнала fmax не сможет быть получена, а сможет быть получена только частота fsyn. Промежуток, образующийся между частотами fmax и fsyn, в случае необходимости может быть заполнен шумом.
Фиг. 2 представляет собой схематическую иллюстрацию процесса копирования, включая гармоническую адаптацию. Таким образом, Фиг. 2 представляет собой схематическую иллюстрацию восстановления HSBE-HF. Фиг. 2 слева показывает копирование и сдвиг основной полосы. Фиг. 2 справа показывает спектр после адаптации спектральной огибающей.
Необходимая адаптация фазы создает дополнительные паразитные компоненты в сигнале. Они подавляются фильтрацией для устранения искажений полученных комплексных значений спектра MDCT/MDST. Наконец, спектральная огибающая адаптируется к ее исходному виду подходящим способом.
На Фиг. 3 показан декодер HSBE, то есть декодер, расширенный за счет HSBE, получающегося в результате упомянутой процедуры.
На Фиг. 3 показано устройство 300 для формирования сдвинутого по частоте аудиосигнала в соответствии с одним вариантом осуществления. В одном варианте осуществления оно может быть декодером HSBE, то есть декодером, расширенным за счет HSBE.
Устройство 300 включает в себя интерфейс 310 и блок 320 сдвига частоты.
Блок 315 преобразования MDCT/MDST расположен между интерфейсом 310 и блоком 320 сдвига частоты. Дополнительно к этому устройство 300 включает в себя блок 330 фильтра. Кроме того, устройство 300 включает в себя, блок 340 преобразования синтеза, например в форме набора фильтров, а также блок 350 адаптации огибающей. Дополнительно к этому устройство 300 в варианте осуществления, изображенном на Фиг. 3, включает в себя блок для вычисления τ и φ (318).
Блок 315 преобразования MDCT/MDST может быть выполнен с возможностью получения одного или нескольких первых коэффициентов MDCT входного аудиосигнала, которые являются коэффициентами модифицированного дискретного косинусоидального преобразования входного аудиосигнала. Блок 315 преобразования MDCT/MDST может получать эти первые коэффициенты MDCT, например, от интерфейса 310.
Блок 315 преобразования MDCT/MDST выполнен с возможностью определения на основе одного или нескольких из первых коэффициентов MDCT входного аудиосигнала одного или нескольких первых коэффициентов MDST входного аудиосигнала, которые являются коэффициентами модифицированного дискретного синусоидального преобразования.
Блок 320 сдвига частоты тогда может быть выполнен с возможностью формирования значений второго поддиапазона на основе соответствующего одного из значений первого поддиапазона, каждое из которых основано на одном из первых коэффициентов MDCT и одном из первых коэффициентов MDST, который был определен на основе этого первого коэффициент MDCT.
Структура показанного устройства 300, в иллюстративных целях реализованного как декодер HSBE, зависит от реализованных алгоритмов. При использовании этого декодера в других средах может быть необходимым выполнять восстановление огибающей в частотной области. Соответствующий блок в этом случае будет находиться непосредственно перед набором фильтров синтеза MDCT/MDST. Также могут быть вставлены дополнительные компоненты, такие как адаптация тональности с использованием SBR. Однако, эти способы не оказывают влияния на общий режим функционирования гармонического расширения спектрального диапазона.
Процесс декодирования сигнала, кодированного в области MDCT в соответствии с одним вариантом осуществления, также изображен на Фиг. 3. Для того, чтобы сдвинуть некоторые части спектра в соответствии с желанием, декодированные коэффициенты MDCT сначала преобразуются в объединенное представление MDCT/MDST. Это является полезным, так как модуляция комплексного спектра будет давать большие компоненты искажений только в каждом втором поддиапазоне. Таким образом, компенсация является необходимой только в каждом втором поддиапазоне, в котором эта компенсация выполняется с использованием предложенного способа компенсации искажений.
Генератор высокой частоты сдвигает комплексные частотные входы из представления преобразования MDCT/MDST в соответствии с требуемым сдвигом, либо декодированным способом из потока битов, либо в декодере, либо с помощью внешних процессов. Используемый модуляционный член выглядит как:
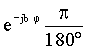
где b - индекс блока, φ - сдвиг частоты в градусах (сдвиг частоты на 180° соответствует сдвигу к центру следующего поддиапазона).
После этого будет выполняться уменьшение искажений, в котором комплексный спектр повторно преобразуется обратно во временную область и воспроизводится.
Используемый модуляционный член является комплексной экспоненциальной функцией. φ представляет собой угол в градусах, который зависит от разности частот, на которую должны быть смещены значения первого поддиапазона.
Преобразование из MDCT в MDST будет обсуждено ниже.
Модуляция одной боковой полосы для сохранения гармонической структуры частично реализуется с использованием манипулирование фазой. Для гармонического расширения спектрального диапазона фазовая характеристика имеет существенное значение. Как уже было обсуждено, HSBE обычно работает в вещественной области MDCT.
Кодер делает доступными только коэффициенты MDCT, так что для фазовой характеристики дополнительно требуются коэффициенты MDST. Преобразование коэффициентов MDCT в соответствующие коэффициенты MDST является возможным и будет обсуждено ниже.
Точное вычисление MDST будет обсуждено ниже.
Как и в DCT, в MDCT имеется соответствующая функция для вычисления синусоидальной части в сигнале: дискретное модифицированное синусоидальное преобразование (MDST). Для MDST применимы те же самые характеристики, что и для MDCT, однако оно практически не используется в аудиокодировании.
Для некоторых приложений, например, таких как HSBE, тем не менее полезно вычислять спектр MDST сигнала. Точное абсолютное значение и фазовый спектр могут быть получены путем объединения этих двух спектров (Cheng, 2004).
MDST вычисляется аналогично MDCT в уравнении 2.35. Матрица преобразования  и матрица окна
и матрица окна  имеют отличия. Матрица преобразования MDST вычисляется с использованием модуляционного ядра DST-IV (см. уравнение 2.18):
имеют отличия. Матрица преобразования MDST вычисляется с использованием модуляционного ядра DST-IV (см. уравнение 2.18):
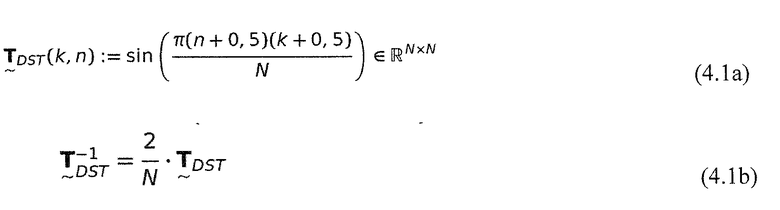
Благодаря другим свойствам симметрии и другим граничным продолжениям DST-IV по сравнению с DCT-IV, сворачивающие матрицы должны быть соответственно адаптированы. Модификацией является изменение в синусе вторых и четвертых квадрантов матрицы окна  :
:
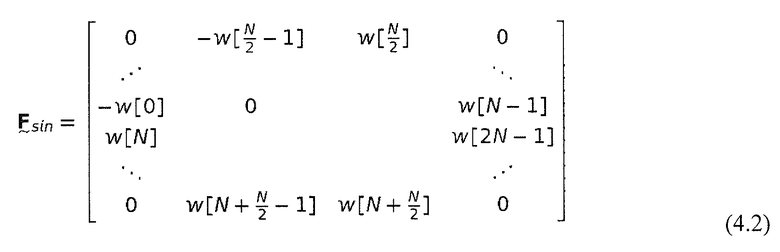
Используя эти адаптации, MDST сигнала  , поделенного на блоки, может быть вычислено следующим образом:
, поделенного на блоки, может быть вычислено следующим образом:

Для обратного преобразования применяется следующее уравнение:

Комплексная передаточная функция, вычисленная из комбинации спектров MDCT и MDST, необходима для того, чтобы управлять, например, фазовой характеристикой. Способ, реализованный для преобразования спектра MDCT в коэффициенты MDST, будет представлен ниже.
Тривиальным способом, сложным лишь в плане вычислений, является преобразование сигнала из области MDCT обратно во временную область с последующим преобразованием MDST:
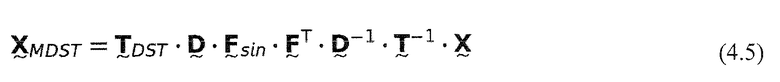
Это вычисление может быть упрощено для того, чтобы уменьшить его сложность. Таким образом, сначала многофазная матрица  определяется следующим образом:
определяется следующим образом:
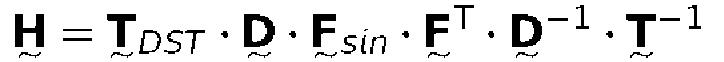 (4.6).
(4.6).
Элементы матрицы 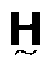 состоят каждый из многочленов третьего порядка в z. Это свойство может использоваться для того, чтобы представить
состоят каждый из многочленов третьего порядка в z. Это свойство может использоваться для того, чтобы представить  как сумму трех матриц:
как сумму трех матриц:

Эти три подматрицы 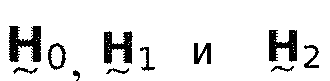 обладают характеристическими особенностями, которые приводят к эффективному вычислению. Матрица
обладают характеристическими особенностями, которые приводят к эффективному вычислению. Матрица  представляет собой слабо заполненную матрицу с элементами 0,5 и -0,5. Между матрицами
представляет собой слабо заполненную матрицу с элементами 0,5 и -0,5. Между матрицами  и
и  существует прямая связь, так что матрица
существует прямая связь, так что матрица 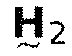 может быть получена путем отражения элементов матрицы
может быть получена путем отражения элементов матрицы  относительно ее побочной диагонали. Точная форма и подробное вычисление этих матриц будут представлены ниже. Спектр MDST блока (b-1) может быть затем вычислен следующим образом:
относительно ее побочной диагонали. Точная форма и подробное вычисление этих матриц будут представлены ниже. Спектр MDST блока (b-1) может быть затем вычислен следующим образом:
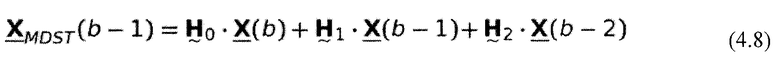
Таким образом, X(b) представляет собой b-ый столбец матрицы 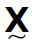 . Из этого уравнения также видно, что введена задержка на один блок для вычисления спектра MDST. Когда спектр MDST блока b присутствует, сначала спектр MDST предыдущего блока является доступным. Используя коэффициенты MDST, полученные таким образом, фазовая характеристика может быть вычислена по комплексному спектру MDCT/MDST и им можно управлять с использованием фазового вращения для поддержания гармонической структуры, как было обсуждено ранее.
. Из этого уравнения также видно, что введена задержка на один блок для вычисления спектра MDST. Когда спектр MDST блока b присутствует, сначала спектр MDST предыдущего блока является доступным. Используя коэффициенты MDST, полученные таким образом, фазовая характеристика может быть вычислена по комплексному спектру MDCT/MDST и им можно управлять с использованием фазового вращения для поддержания гармонической структуры, как было обсуждено ранее.
Упрощенное вычисление MDST будет обсуждено ниже.
Хотя в соответствии с выведенным способом вычисление MDST чрезвычайно упрощается, вычисление этого преобразования тем не менее является очень интенсивным. В дополнение к этому, большой объем памяти требуется для хранения матрицы  . Это означает, что необходимо найти дополнительное упрощение этого преобразования.
. Это означает, что необходимо найти дополнительное упрощение этого преобразования.
При более точном анализе матриц  и
и 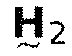 становится очевидным, что они содержат очень большое количество значений, близких к нулю. Коэффициенты с самыми большими абсолютными значениями сконцентрированы в узкой области вблизи главной диагонали матриц. Таким образом, кажется очевидным заменить остальные коэффициенты нулями для того, чтобы сэкономить таким образом как вычислительную мощность, так и память. Кроме того, значения на диагоналях являются весьма схожими. В основном они отличаются друг от друга только своими знаками. Исключительно в областях, близких к краям, находятся коэффициенты с большими значениями.
становится очевидным, что они содержат очень большое количество значений, близких к нулю. Коэффициенты с самыми большими абсолютными значениями сконцентрированы в узкой области вблизи главной диагонали матриц. Таким образом, кажется очевидным заменить остальные коэффициенты нулями для того, чтобы сэкономить таким образом как вычислительную мощность, так и память. Кроме того, значения на диагоналях являются весьма схожими. В основном они отличаются друг от друга только своими знаками. Исключительно в областях, близких к краям, находятся коэффициенты с большими значениями.
В целях упрощения предполагается, что значения ниже и выше главной диагонали являются равными, что означает, что матрица обладает осевой симметрией относительно главной диагонали. Вычисляется упрощенная матрица, значения которой берутся из центрального столбца матрицы  . Таким образом, область, включающая в себя элемент главной диагонали и любое количество дополнительных элементов ниже главной диагонали, вырезается из центрального столбца. Этот вырезаемый сектор упоминается как h[n]. Центральный столбец новой матрицы затем формируется из вектора h[n] и зеркального отражения вектора h[n] относительно основного элемента оси hij, причем остальная часть столбца состоит из нулей. Другие столбцы упрощенной матрицы формируются циклическим сдвигом этого столбца. Знак каждого второго столбца адаптируется. Используя эти способы для упрощения полностью заполненной матрицы
. Таким образом, область, включающая в себя элемент главной диагонали и любое количество дополнительных элементов ниже главной диагонали, вырезается из центрального столбца. Этот вырезаемый сектор упоминается как h[n]. Центральный столбец новой матрицы затем формируется из вектора h[n] и зеркального отражения вектора h[n] относительно основного элемента оси hij, причем остальная часть столбца состоит из нулей. Другие столбцы упрощенной матрицы формируются циклическим сдвигом этого столбца. Знак каждого второго столбца адаптируется. Используя эти способы для упрощения полностью заполненной матрицы  , можно определить слабо заполненную матрицу
, можно определить слабо заполненную матрицу  , использующую очень маленькое количество коэффициентов. Симметричная структура Теплица является особенностью этой матрицы. Она образована путем циклического сдвига обрезанной импульсной характеристики h[n], зеркально отраженного относительно главной диагонали:
, использующую очень маленькое количество коэффициентов. Симметричная структура Теплица является особенностью этой матрицы. Она образована путем циклического сдвига обрезанной импульсной характеристики h[n], зеркально отраженного относительно главной диагонали:
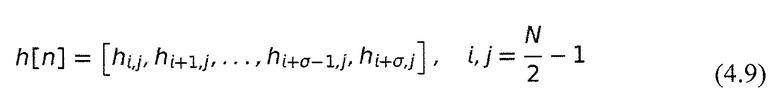
Таким образом, i представляет собой индекс строки, а j представляет собой индекс столбца матрицы  , а σ представляет собой индекс окна, определяющий длину сектора. Длина этого сектора всегда будет равна 2σ+1. Для σ=1 и N=6 структура матрицы
, а σ представляет собой индекс окна, определяющий длину сектора. Длина этого сектора всегда будет равна 2σ+1. Для σ=1 и N=6 структура матрицы  будет выглядеть следующим образом:
будет выглядеть следующим образом:

Следует учесть, что начиная с первого столбца каждый второй столбец умножается на -1. В следующих обсуждениях индекс окна σ соответствует приблизительно 10% длины преобразования N, то есть 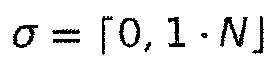 . Это означает, что требования к памяти для матрицы преобразования уменьшились до 20% благодаря зеркальному отражению значений h[n].
. Это означает, что требования к памяти для матрицы преобразования уменьшились до 20% благодаря зеркальному отражению значений h[n].
Фиг. 4 представляет оценку матрицы преобразования MDCT-MDST. Фиг. 4 слева показывает полностью заполненную матрицу преобразования  для N=64. Фиг. 4 справа показывает упрощенную матрицу преобразования
для N=64. Фиг. 4 справа показывает упрощенную матрицу преобразования  для N=64.
для N=64.
На Фиг. 4 показаны слева заполненная матрица  и, для сравнения на Фиг. 4 справа, упрощенная матрица
и, для сравнения на Фиг. 4 справа, упрощенная матрица  в симметричной структуре, аналогичной матрице Теплица. Как показано, значительная часть коэффициентов вне главной диагонали
в симметричной структуре, аналогичной матрице Теплица. Как показано, значительная часть коэффициентов вне главной диагонали  равна нулю, что вызвано упрощением.
равна нулю, что вызвано упрощением.
Фиг. 5 представляет импульсные характеристики матриц преобразования MDCT-MDST. В частности, Фиг. 5 иллюстрирует исходная импульсная характеристика 33-го столбца матрицы  (сплошная линия). Для сравнения следует дополнительно рассмотреть соответствующую импульсную характеристику, сформированную процессом копирования и зеркального отражения новой матрицы
(сплошная линия). Для сравнения следует дополнительно рассмотреть соответствующую импульсную характеристику, сформированную процессом копирования и зеркального отражения новой матрицы  . Обрезание значений производилось с использованием прямоугольного окна с индексом окна σ=6.
. Обрезание значений производилось с использованием прямоугольного окна с индексом окна σ=6.
Этот вид упрощения преобразования MDCT-MDST не обеспечивает точного спектра MDST, который формируется посредством вычисления по уравнению 4.8. Ошибка добавляется к спектру за счет выполненного упрощения матриц  и
и  . Это вызывает уменьшение отношения сигнал/шум примерно до -70 дБ, как показано на Фиг. 6. Фиг. 6 показывает оценку спектра MDST для белого шума. Ошибка оценки спектра MDST увеличивается в граничных областях спектра. Этот эффект происходит вследствие неточной оценки коэффициентов матрицы вблизи от концов главной диагонали. Полученное зеркальное отражение уменьшается высокочастотным фильтрованием алгоритма HSBE, и следовательно присутствует только на высоких частотах.
. Это вызывает уменьшение отношения сигнал/шум примерно до -70 дБ, как показано на Фиг. 6. Фиг. 6 показывает оценку спектра MDST для белого шума. Ошибка оценки спектра MDST увеличивается в граничных областях спектра. Этот эффект происходит вследствие неточной оценки коэффициентов матрицы вблизи от концов главной диагонали. Полученное зеркальное отражение уменьшается высокочастотным фильтрованием алгоритма HSBE, и следовательно присутствует только на высоких частотах.
Ниже будет обсуждена адаптация гармонической структуры спектра частот.
Преимуществом способа HSBE является поддержание гармонической структуры после расширения полосы частот. Как было уже упомянуто, это происходит за счет фазового манипулирования в комплексной области MDCT/MDST. Здесь будет рассматриваться скопированный спектральный диапазон ширины полосы B=fmax-fg. Целью является сдвиг спектра вниз так, что первая гармоника в этой полосе (например, с частотой fH,n>fg) после сдвига будет на частоте высшей гармоники в основной полосе с частотами fH,α<fg. Расстояние между частотами fH,n и fH,α упоминается как задержка частоты flag.
Адаптация гармонической структуры регулируется с использованием этой частоты. Эта частота также может быть представлена как соответствующий множитель, целочисленно или нецелочисленно кратный количеству поддиапазонов MDCT, на которое полоса частот должна быть смещена вниз. Это обеспечивает максимальную гибкость разработанного способа. После выполнения упомянутого выше условия все коэффициенты MDCT с дискретной частотой меньше чем fg обнуляются для того, чтобы основная полоса и сдвинутая полоса не накладывались друг на друга.
Фиг. 7 представляет собой схематическую иллюстрацию желаемого результата способа HSBE для тонального сигнала. Таким образом, на Фиг. 7 показана гармоническая структура в HSBE. На Фиг. 7 слева показан исходный широкополосный спектр. На Фиг. 7 справа показан спектр после восстановления HSBE HF.
Здесь сохраняется исходная гармоническая структура. Ни один гармонический подтон не пропускается при обсужденном сдвиге реплицированной высокочастотной полосы к частотам, меньшим чем частота среза fg. Сдвиг спектра таким образом может быть интерпретирован как модуляция одной боковой полосы ВЧ-отфильтрованного сигнала основной полосы с использованием модуляционной частоты fmod. Используется следующая формула:

Таким образом, следует учесть, что при частотах flag, больших чем половина ширины полосы MDCT, коэффициенты MDCT вблизи f=fmax при сдвиге обнуляются. Они могут быть заполнены шумом. Это не является необходимым, когда частота flag меньше, чем половина ширины полосы MDCT, так как при этом никакие коэффициенты MDCT не обнуляются.
Адаптация нецелочисленно кратных поддиапазонов будет обсуждена ниже.
Поддержание гармонической структуры усложняется, когда полоса MDCT включает в себя большую ширину полосы по сравнению с разностью частот последовательных подтонов гармонической структуры. При выполнении модуляции с использованием только тех частот, которые являются кратными ширине полосы MDCT, разрешение гармонического восстановления является строго ограниченным, и следовательно тонкая гармоническая структура не может быть восстановлена. Таким образом, необходимо обеспечить высокую точность модуляции, так чтобы спектр основной полосы мог модулироваться не только целочисленно кратными ширине полосы MDCT, но также и ее долями.
Используя следующий подход, становится возможным сдвигать спектр в пределах ширины полосы поддиапазона MDCT. Этот способ основан на модификации фазы комплексного спектра MDCT/MDST. Фаза здесь поворачивается на нормализованный сдвиг частоты φ, в зависимости от изменения сигнала во времени. Это временное вращение фазового угла таким образом обеспечивает очень тонкий сдвиг спектра. Используется следующая формула:
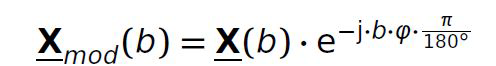 (4.12).
(4.12).
Таким образом,
X
(b) представляет собой b-й столбец комплексной матрицы 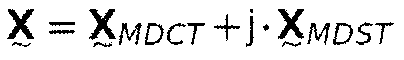 , а φ представляет собой нормализованный сдвиг частоты в градусах. Теоретически, для φ могут использоваться любые углы, но по практическим причинам диапазон значений строго ограничен и находится в пределах интервала
, а φ представляет собой нормализованный сдвиг частоты в градусах. Теоретически, для φ могут использоваться любые углы, но по практическим причинам диапазон значений строго ограничен и находится в пределах интервала  . Используя этот интервал, можно вычислить модуляции, покрывающие ширину полосы MDTC. Путем задания нормализованного сдвига частоты в обозначенном интервале спектр может быть сдвинут на половину ширины полосы MDCT как в сторону высоких частот, так и в сторону низких частот.
. Используя этот интервал, можно вычислить модуляции, покрывающие ширину полосы MDTC. Путем задания нормализованного сдвига частоты в обозначенном интервале спектр может быть сдвинут на половину ширины полосы MDCT как в сторону высоких частот, так и в сторону низких частот.
Для комплексной экспоненциальной функции 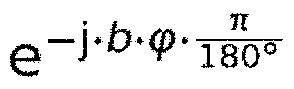 , которая зависит от b и φ, сначала может быть вычислено значение результата. φ представляет собой угол в градусах, который зависит от разности частот, на которую должны быть сдвинуты значения первого поддиапазона. Подлежащее определению значение второго поддиапазона затем может быть установлено путем умножения одного из значений первого поддиапазона в X(b) на значение результата.
, которая зависит от b и φ, сначала может быть вычислено значение результата. φ представляет собой угол в градусах, который зависит от разности частот, на которую должны быть сдвинуты значения первого поддиапазона. Подлежащее определению значение второго поддиапазона затем может быть установлено путем умножения одного из значений первого поддиапазона в X(b) на значение результата.
Далее будет обсуждена адаптация целочисленно кратных поддиапазонов.
Ограниченный диапазон значений фазового угла φ с использованием введенной модуляции позволяет сдвигать спектр самое большее на ширину полосы диапазона MDCT. Для сдвигов спектра больше чем на ширину полосы диапазона MDCT этот сдвиг делится на две части: целочисленно кратную ширине полосы диапазона MDCT и дробный остаток упомянутой ширины полосы. Сначала спектр модулируется необходимой частотой, меньшей чем ширина полосы диапазона MDCT в соответствии с уравнением 4.12, а затем спектр сдвигается на целочисленные спектральные значения.
Далее будет рассмотрен сдвиг, который соответствует точно кратному количеству ширин полосы диапазона MDCT. В этом случае имеется фазовый угол φ′, который является кратным 180°. Таким образом, сдвиг спектра на целочисленные спектральные значения MDCT может рассматриваться как особый случай способа, представленного выше для нецелочисленно кратных поддиапазонов. Оценка комплексной модуляционной функции в уравнении 4.12 дает следующие результаты. Если произведение индекса блока b и φ′ является четно кратным 180°, то результат модуляционной функции всегда будет 1, в противном случае -1. Зная это, нет необходимости оценивать функцию в уравнении 4.12 для адаптации целочисленно кратных поддиапазонов, достаточно будет простого различения таких случаев. Используется следующая формула:

где целочисленный коэффициент модуляции τ:
 .
.
Таким образом, X(b, τ: N-1) снова представляет собой b-й столбец комплексной матрицы 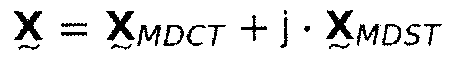 , с тем отличием, что здесь используются только элементы вектора, начиная с τ и вплоть до последнего элемента N. Это обрезание векторных элементов соответствует упомянутой выше ВЧ-фильтрации комплексного спектра MDCT/MDST.
, с тем отличием, что здесь используются только элементы вектора, начиная с τ и вплоть до последнего элемента N. Это обрезание векторных элементов соответствует упомянутой выше ВЧ-фильтрации комплексного спектра MDCT/MDST.
Для применения модуляции частота модуляции преобразуется в индекс модуляции τ и фазовый угол φ в зависимости от φlag. Сначала частота φlag нормализуется к половине частоты оцифровки fs. Затем выполняется эквивалентный сдвиг в диапазонах MDCT φlag, и индекс модуляции τ и фазовый угол φ вычисляются следующим образом:
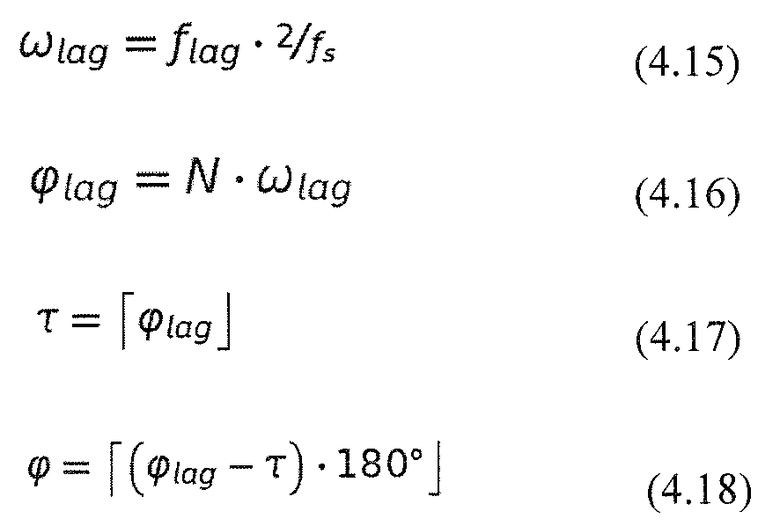
Комбинируя эти два способа, становится возможным реализовать переменные кусочные отношения. Кусочное отношение здесь представляет собой отношение максимальной возможной частоты сигнала fmax и частоты среза основной полосы fg. Кусочное отношение 2:1, например, выражает то, что устанавливается и модулируется единственная копия основной полосы (см. Фиг. 2). Кусочные отношения больше чем 2:1 имеют место при более низких или переменных скоростях передачи. Такие отношения, аналогично CM-BWE (см. выше), реализуются путем копирования и модулирования основной полосы несколько раз. Здесь также следует учитывать, что частота задержки, необходимая в данном случае, увеличивается на flag с каждой копией основной полосы, как проиллюстрировано на Фиг. 8 для кусочного отношения 2,5:1.
Фиг. 8 иллюстрирует схему расширенного восстановления HSBE-HF. На Фиг. 8 слева показано копирование и сдвиг основной полосы. На Фиг. 8 справа показан спектр после адаптации спектральной огибающей.
Далее будут описаны концепции для подавления образования паразитных компонентов. Описанные здесь концепции могут быть применены, например, в блоке 330 фильтра, изображенном на Фиг. 3.
Модуляция спектра в домене MDCT не может быть выполнена легко. Точное восстановление в обратном преобразовании MDCT больше невозможно из-за модуляции спектра. Причина этого заключается в том, что образовались компоненты искажений во временной области. Энергия этих паразитных компонентов перераспределяется при модуляции спектра. Функция TDAC преобразования MDCT этим нарушается и больше не может устранять эти компоненты при обратном преобразовании. При рассмотрении модулированного сигнала после обратного преобразования MDCT паразитные компоненты могут быть найдены в абсолютном значении частотной характеристики DFT по этой причине. При сдвиге спектра на φ=0° и τ>0 эти компоненты искажений обладают очень низкой амплитудой и расположены в первом или последнем диапазоне MDCT. В этом случае нет необходимости уменьшать эти компоненты. При коэффициентах сдвига φ≠0° амплитуда образующихся паразитных компонентов становится значительно больше. В этом случае они являются ясно слышимыми. Следовательно, эти компоненты будут обработаны.
На Фиг. 9 показаны компоненты искажений для φ=45°: yref - исходный синусоидальный тон; ymod - модулированный синусоидальный тон, включающий в себя компоненты, набор фильтров DCT-IV показан в расширенном виде для улучшенной иллюстрации.
В частности Фиг. 9 иллюстрирует абсолютное значение частотной характеристики синусоидального тона (ymod), сдвинутого на φ=45°. Частота исходного тона синуса (yref) соответствует центру 12-ого диапазона MDCT. Весь спектр модулируется одной четвертью ширины полосы диапазона MDCT в сторону высоких частот выбранным фазовым углом. Как можно заметить, наличествует восемь доминантных компонентов искажений, каждый из которых расположен в каждой второй полосе ниже и выше 12-ой полосы MDCT. Эта особенность компонентов искажений применима к любому сигналу. Причина этого состоит в том, что каждый сигнал может быть разложен на взвешенную сумму синусоидальных и косинусоидальных колебаний (см. выше). Для каждого из этих подколебаний этот особый рисунок компонентов искажений появляется при модуляции в соответствии с уравнением 4.12. Зная это, можно разработать способ, который позволял бы освобождать любой сигнал от нежелательных компонентов искажений. Таким образом, достаточно проанализировать и устранить компоненты искажений, формирующиеся при модуляции синусоидального сигнала.
Далее будут предложены концепции фильтрации для устранения искажений.
Дополнительные части сигнала формируются в частотной области путем временного наложения блоков для TDA. Они присутствуют как паразитные части в спектре сигнала с расширенной полосой частот, так как они не устраняются в обратном преобразовании сдвигом в частотной области. В преобразовании MDCT эти паразитные компоненты, распознаваемые как пики в спектре FFT (см. Фиг. 9) иллюстрируются низким затуханием на границе полосы набора фильтров DCT-IV, составляющим всего лишь приблизительно 15 дБ за счет суммы частей в нескольких из накладывающихся полос MDCT. Энергия паразитных компонентов в спектре DFT высокого разрешения таким образом может рассматриваться как суммирующая энергию нескольких полос MDCT.
Благодаря этой ассоциации предлагается фильтр для уменьшения паразитных компонентов в области MDCT. Этот фильтр основан на последовательном суммировании значений частот, взвешенных коэффициентами фильтра. Расширение фильтра центрированным значением частоты представляет область частот, в которой устраняются паразитные компоненты. Для каждого доминантного компонента искажений требуется коэффициент фильтра, который его минимизирует. Этот фильтр зависит от сдвига частоты φ. Используется следующая формула:
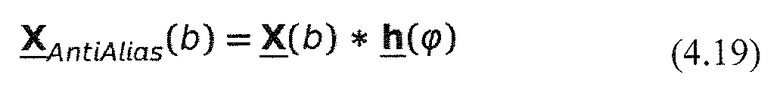 ,
,
где h(φ) представляет собой вещественный фильтр устранения искажений для определенного фазового угла φ, а X (b) представляет собой комплексный спектр MDCT/MDST. Спектр после фильтрования ( X AntiAlias(b)) здесь является более длинным, чем исходный спектр X(b). Это означает, что спектр должен быть обрезан для того, чтобы снова соответствовать длине преобразования N. Та часть спектра, где фильтр устанавливается и затухает, удаляется. Таким образом, обрезание на половину длины фильтра выполняется в начале и в конце произведения свертки в комплексной области MDCT/MDST.
На Фиг. 10 показана импульсная характеристика фильтра устранения искажений (AAF) для φ=90°. Используя пример единственного синусоидального тона, с использованием показанного фильтра можно устранить в общей сложности семь доминантных компонентов искажений. Три компонента находятся ниже частоты синусоидального тона. Эти компоненты, которые в соответствии с их положением по отношению к частоте синусоидального тона упоминаются как компоненты вплоть до третьего порядка, обрабатываются коэффициентами фильтра (отводами фильтра) 0, 2 и 4. Отводы фильтра 8, 10, 12 и 14 устраняют четыре паразитных компонента с частотами выше синусоидального тона, то есть компоненты вплоть до четвертого порядка. В целом данный фильтр включает в себя 15 коэффициентов, причем каждое второе значение равно нулю. Это соответствует вышеупомянутому наблюдению, что компоненты искажений возникают лишь в каждой второй полосе.
Таким образом, коэффициенты фильтрации, изображенного на Фиг. 10, находятся в определенном порядке. В этом порядке каждый коэффициент фильтра, который следует за ненулевым коэффициентом фильтра, имеет нулевое значение.
Используя такую структуру фильтра, можно в большинстве случаев подавить любое количество компонентов искажений. Достаточно устранить компоненты вплоть до четвертого порядка. Это обеспечивает достижение отношения сигнал/шум по меньшей мере 70 дБ, которое можно рассматривать как вполне достаточное. В дополнение к этому, компоненты искажений более высокого порядка становятся заметными только при очень больших фазовых углах φ. Ограничение на устранение паразитных компонентов вплоть до четвертого порядка таким образом представляет собой хороший компромисс между достижимым отношением сигнал/шум и вычислительной сложностью для устранения искажений.
Далее будет обсуждена оптимизация фильтров устранения искажений.
Важным компонентом описанного устранения искажений являются используемые фильтры устранения искажений. Достижимое уменьшение амплитуды отдельных паразитных компонентов решительным образом зависит от подбора подходящих коэффициентов фильтрации. Таким образом, необходимо оптимизировать эти фильтры так, чтобы было обеспечено самое высокое возможное подавление. Надежным способом здесь является численная оптимизация коэффициентов фильтрации посредством последовательного приближения.
Последовательное приближение представляет собой итеративный способ численной математики и относится к процессу приближения решаемой проблемы к точному решению шаг за шагом. Таким образом, вычислительный способ применяется повторяющимся образом, и результат одного шага используется в качестве начального значения для соответствующего следующего шага. Последовательность результатов должна быть сходящейся. Когда приемлемая ошибка для точного решения минимальна, результат определен с достаточной степенью точности (Jordan-Engeln and Reutter, 1978).
В начале процесса оптимизации аналитический сигнал модулируется с использованием уравнения 4.12 определенным фазовым углом φ. Аналитический сигнал представляет собой синусоидальный тон, по причинам, указанным выше. Частота тона идеально находится в районе одной четвертой части базовой частоты оцифровки. Преимущество этого заключается в том, что формирующиеся компоненты искажений вплоть до четвертого порядка показывают самое большое возможное расстояние до краев спектра и не интерферируют с другими паразитными компонентами. В целях оптимизации преобразование MDCT с длиной в 32 отсчета является идеальным. Остается лишь обеспечить, чтобы частота синусоидального тона соответствовала центру 16-ой полосы MDCT. Ограничение этой длиной преобразования предлагает несколько преимуществ. С одной стороны, оно позволяет сократить вычислительную сложность преобразования MDCT. С другой стороны, компоненты искажения вплоть до четвертого порядка образуются без интерференции на максимальном расстоянии друг от друга. Это имеет определенное преимущество для необходимого распознавания пиков сигнала. Распознавание пиков сигнала автоматически обнаруживает компоненты искажения, подлежащие подавлению в частотной характеристике абсолютного значения DFT с высокой разрешающей способностью.
После модуляции аналитического сигнала компоненты искажения оптимизируются один за другим в переменном порядке. Это необходимо, так как паразитные компоненты влияют друг на друга. Таким образом, порядок оптимизации - от самого слабого компонента четвертого порядка к самому доминантному компоненту первого порядка. Это гарантирует, что компоненты искажения первого порядка получат самое большое затухание. Для прямого компонента, то есть спектрального значения, для которого компоненты искажения должны быть устранены, фильтр устанавливается равным единице. Это значение не изменяется во время оптимизации.
Фактическая численная оптимизация выполняется в соответствии с принципом проиллюстрированного последовательного приближения. Таким образом, задается начальное значение того коэффициента фильтра, который будет оптимизироваться, а все другие коэффициенты, за исключением прямого компонента, остаются равными нулю. После этого комплексный спектр MDCT/MDST сворачивается с использованием этого фильтра, и частотная характеристика абсолютного значения проверяется на уменьшение соответствующего побочного компонента. Если это верно, то коэффициент фильтра будет увеличен в соответствии с заданной величиной шага. Этот способ проверки и увеличения повторяется до тех пор, пока на следующем шаге дальнейшее уменьшение этого компонента искажения не станет невозможным. После этого, следующие коэффициенты фильтрации обрабатываются точно таким же образом, причем уже оптимизированные коэффициенты фильтрации сохраняют свои оптимизированные значения.
Из-за взаимного влияния компонентов искажения имеет смысл выполнить несколько итераций этого процесса. Размер шага, на который увеличиваются коэффициенты фильтрации, уменьшается с каждой итерацией. Это означает, что качество оптимизированного фильтра увеличивается с каждым проходом. Показано, что трех итераций достаточно для оптимального набора фильтров, состоящего из одного фильтра на каждый фазовый угол. Это позволяет уменьшить компоненты искажения до уровня < -90 дБ.
Фиг. 11 иллюстрирует влияние фильтрования для устранения искажений на синусоидальный сигнал для φ=90°. XAlias представляет собой синусоидальный сигнал, модулированный величиной φ=90°; XAntiAlias представляет собой отфильтрованный сигнал, включающий в себя подавленные паразитные компоненты.
В частности на Фиг. 11 показано влияние фильтрования для устранения искажений на синусоидальный сигнал, модулированный величиной φ=90°, в частотной характеристике абсолютного значения. XAlias представляет собой спектр модулированного сигнала, а XAntiAlias представляет собой спектр модулированного сигнала, свернутого с использованием оптимизированного фильтра для соответствующего фазового угла. Пики в спектре, отмеченные значком «о», являются компонентами искажения, обнаруженными алгоритмом распознавания пиков сигнала, включая прямой компонент (четвертый распознанный пик слева). В этом примере численная оптимизация фильтров уменьшает паразитные компоненты в среднем до уровня -103 дБ.
Для каждого фазового угла в диапазоне значений установить набор фильтров достаточно лишь однажды. Для фильтрации сигнала необходимый фильтр может быть загружен из базы данных.
Например, коэффициенты фильтрации могут быть считаны из базы данных или из памяти устройства для формирования сдвинутого по частоте аудиосигнала в зависимости от фазового угла.
На Фиг. 12 показана перекрестная структура. Веса определены последовательными приближениями. Фиг. 12 таким образом показывает уменьшение искажений для поддиапазона X4 (черная линия). Этот же самый способ должен быть выполнен соответственно для всех модифицированных поддиапазонов. Для того, чтобы уменьшить компонент искажения, вызванный модуляцией X4, X4 должен быть умножен на веса w0-w4 и добавлен к сигналам поддиапазонов X0, X2, X4, X6 и X8. Следует учесть, что вес w2 всегда будет равняться 1.
И наоборот, это означает, что для того, чтобы сформировать фильтрованное значение для одного из поддиапазонов, должна быть сформирована сумма нефильтрованного значения этого поддиапазона и дополнительных слагаемых (весовой/фильтрующий коэффициент w2, который был бы применен к нефильтрованному значению этого поддиапазона, w2=1). Дополнительные слагаемые представляют собой взвешенные значения поддиапазона, а именно, одно значение поддиапазона из каждого другого поддиапазона, который уже был умножен/взвешен с помощью других весовых/фильтрующих коэффициентов.
Ниже будет описано восстановление спектральной огибающей.
Восстановление спектральной огибающей выполняется с использованием фильтрования LPC. Таким образом, тональные части сигнала удаляются в кодере фильтром линейного предсказания и передаются отдельно как коэффициенты LPC. Требуемые для этого коэффициенты фильтрации могут быть вычислены с использованием рекурсии Левинсона-Дурбина (Larsen and Aarts, 2004). Результатом является то, что основная полоса в декодере получает белую спектральную характеристику. После расширения полосы частот посредством HSBE выполняется обратное фильтрование с использованием коэффициентов LPC, и таким образом исходная спектральная огибающая снова накладывается на сигнал.
На Фиг. 13 показана адаптация огибающей HSBE-LPC. Здесь X представляет сигнал BWE перед адаптацией огибающей. XiLPC представляет собой сигнал BWE после адаптации огибающей.
В частности, на Фиг. 13 показаны частотные характеристики абсолютного значения DFT сигнала с расширенной с использованием HSBE полосой частот. Перед восстановлением спектральной огибающей сигнал X имеет упомянутую характеристику белого сигнала. После адаптации огибающей обратным фильтрованием LPC огибающая соответствует исходной спектральной характеристике. Дополнительно к этому Фиг. 13 показывает использованную передаточную функцию фильтра LPC. Нескольких коэффициентов фильтрации уже достаточно для достаточно точного описания спектральной огибающей, в этом примере используются 14 коэффициентов фильтрации LPC. Восстановление огибающей не является стандартным компонентом HSBE и может быть заменено другим способом.
Предложенные концепции будут теперь подвергнуты оценке. Здесь оценка означает как сравнение между новым способом гармонического расширения спектрального диапазона и расширением полосы частот посредством алгоритма CM-BWE, так и изучение эффективности HSBE в плане потенциалов и пределов, а также вычислительной сложности алгоритма.
Сначала будет представлено сравнение способов репликации диапазона.
Расширение полосы частот посредством непрерывной модуляции одной боковой полосы представляет собой способ, выполняемый во временной области. Это означает, что для его применения всегда будет необходим сигнал, изменяющийся во времени. Поскольку после расширения полосы частот имеют место адаптация огибающей и тональности, каждая из которых требует сигнала в спектральной области, при применении способа CM-BWE сигнал с расширенной полосой частот должен быть преобразован обратно в область частот. Это преобразование во временную область и обратно в область частот может быть опущено при гармоническом расширении спектрального диапазона, поскольку оно работает в области MDCT/MDST.
Дополнительно к этому, временной сигнал должен быть преобразован в аналитический сигнал, прежде чем применить непрерывную модуляцию одной боковой полосы. Вычисление требуемого аналитического сигнала проблематично, так как оно реализуется с использованием преобразования Гильберта. Идеальная передаточная функция преобразования Гильберта - это знаковая функция. Эта функция может быть представлена во временной области только фильтром бесконечной длины. При использовании реализуемого фильтра с конечной импульсной характеристикой идеальное преобразование Гильберта может быть только аппроксимировано. В дополнение к этому, сигнал не имеет совершенно аналитического характера после такого аппроксимированного преобразования Гильберта. Качество вычисленного псевдоаналитического сигнала таким образом зависит от длины используемого фильтра.
Применение гармонического расширения спектрального диапазона также требует дополнительного преобразования. Так как HSBE работает в частотной области, для вычисления фазовой модуляции необходим комплексный спектр. Однако перед применением расширения полосы частот в структуре декодера присутствуют только коэффициенты MDCT. Таким образом, коэффициенты MDCT должны быть преобразованы в область MDST для того, чтобы получить комплексный спектр и таким образом получить необходимую фазовую информацию. В настоящем документе это в иллюстративных целях рассматривается как реализуемое с использованием матричного умножения, сформированного путем упрощения обратного преобразования MDCT, с последующим преобразованием MDST. Как было показано, требуемая для этого вычислительная сложность может быть значительно минимизирована, причем несмотря на это может быть выполнено точное вычисление коэффициентов MDST.
Рассматривая схему частотной характеристики абсолютного значения после применения CM-BWE и HSBE, можно заметить, что часть спектра в CM-BWE должна быть заполнена белым шумом. Гармоническая структура в этой части потеряна, поскольку отдельные гармонические подтоны не могут быть здесь реплицированы. Этой проблемы не возникает при применении HSBE. Гармоническая структура продолжается без каких-либо промежутков.
Далее будет рассмотрена сложность гармонического расширения спектрального диапазона.
Эффективность нового гармонического расширения спектрального диапазона зависит от вычислительной сложности и необходимого объема памяти. Исследование этих факторов основывается на реализации алгоритма на языке программирования C. При реализации алгоритма наибольший акцент ставился на уменьшении количества шагов вычисления. Однако преобразование коэффициентов MDCT в спектральные значения MDST и фильтрование для устранения искажений находятся среди самых сложных шагов вычисления. Модуляция для формирования гармонически корректной репликации спектра является относительно легкой, поскольку сдвиг на коэффициент модуляции τ соответствует всего лишь процессу копирования, а фазовое вращение на угол φ может быть сокращено до комплексного умножения на спектральное значение. Адаптация спектральной огибающей здесь не учитывается. Поскольку она не является частью способа HSBE, которая важна для оценки, она не реализовывалась алгоритмически.
При оценке рассматриваются все относящиеся к делу машинные команды, такие как сложение (ADD), умножение (MULT) и умножение с накоплением (MAC), выполняемые при фильтровании устранения искажений. Таблица 5.1 представляет собой сводку результатов для модуляции и фильтрования спектра. Они относятся к функции local_HSBEpatching(), в которой реализованы соответствующие алгоритмы.
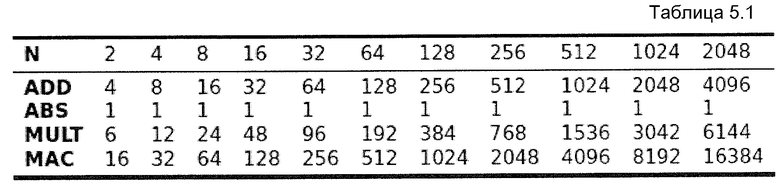
Таблица 5.1 иллюстрирует сложность модуляции HSBE и фильтрования устранения искажений. Эта таблица показывает количество соответствующих операций в зависимости от длины преобразования N. В общей сложности 10241 операция требуется для того, чтобы модулировать спектр при N=2048, среди которых 2N операций сложения и 3N операций умножения. Требуемое устранение искажений является намного более сложным. Здесь выполняется 16384 операций умножения с накоплением. Это соответствует количеству ненулевых элементов фильтра устранения искажений, умноженному на длину преобразования, то есть в данном случае на 8N (см. выше объяснения, относящиеся к сглаживающему фильтрованию). При таком результате для вычислительной сложности модуляции и AAF получается линейный контекст со сложностью  .
.
Фиг. 14 представляет собой графическую иллюстрацию этого контекста. Фиг. 14 таким образом иллюстрирует сложность модуляции HSBE и фильтрования для устранения искажений.
Центральным элементом гармонического расширения спектрального диапазона является преобразование сигнала посредством MDCT и MDST. Аналогично быстрому преобразованию Фурье, для этих преобразований также используется быстрый алгоритм. Структура базового быстрого преобразования DCT-IV дополнительно будет обсуждена ниже. Результаты оценки относятся к функции fmdcst1d(), в которой быстрое преобразование MDCT/MDST реализуется в соответствии с описанным ранее многофазным подходом. Анализ MDCT и MDST сведен в Таблицу 5.2.

При оценке этих результатов можно видеть, что в общей сложности приблизительно 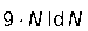 операций требуется для того, чтобы вычислить преобразование MDCT/MDST. На N умножений больше выполняется при обратном преобразовании. Причина этого заключается в том, что здесь выполняется масштабирование, требуемое для преобразования. Соответствующая оценка показана в Таблице 5.3.
операций требуется для того, чтобы вычислить преобразование MDCT/MDST. На N умножений больше выполняется при обратном преобразовании. Причина этого заключается в том, что здесь выполняется масштабирование, требуемое для преобразования. Соответствующая оценка показана в Таблице 5.3.
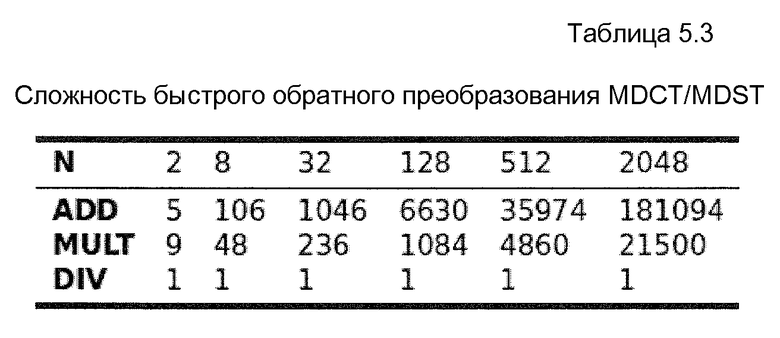
В результате сложность для прямого и обратного преобразований выглядит как  . Таким образом, реализованный алгоритм, как предполагается, выполняет требования для быстрого преобразования. Результаты этой оценки показаны на Фиг. 15.
. Таким образом, реализованный алгоритм, как предполагается, выполняет требования для быстрого преобразования. Результаты этой оценки показаны на Фиг. 15.
На Фиг. 15 показана сложность быстрого преобразования MDCT/MDST. Следует учесть, что два обратных преобразования должны быть вычислены для того, чтобы преобразовать сигнал из комплексной области MDCT/MDST во временную область. При этом количество требуемых операций удваивается.
Точное преобразование коэффициентов MDCT в спектральные значения MDST представляет собой самый сложный в вычислительном плане процесс в HSBE. Здесь образуется не только постоянная задержка на один блок, но также и самое длительное время вычислений. Даже когда требуемая сложность уменьшается представленным способом, это все равно приводит к наибольшему количеству операций, как это показано в Таблице 5.4.
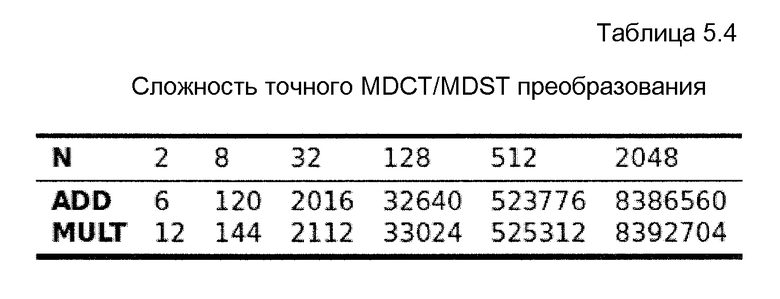
Для каждого из умножений плотных матриц  и
и  на спектральный вектор требуется в общей сложности N2 операций умножения и N(N-1) операций сложения. Слабо заполненная матрица
на спектральный вектор требуется в общей сложности N2 операций умножения и N(N-1) операций сложения. Слабо заполненная матрица
 обеспечивает эффективную реализацию, так что здесь должно быть выполнено 2N операций умножения и N операций сложения. Для точного преобразования значений MDCT в коэффициенты MDST вычисляется в общей сложности 4N2+N операций умножения и операций сложения. Для сложности реализованного алгоритма существует квадратичная зависимость от длины преобразования. Это может быть выражено как
обеспечивает эффективную реализацию, так что здесь должно быть выполнено 2N операций умножения и N операций сложения. Для точного преобразования значений MDCT в коэффициенты MDST вычисляется в общей сложности 4N2+N операций умножения и операций сложения. Для сложности реализованного алгоритма существует квадратичная зависимость от длины преобразования. Это может быть выражено как  . Упрощенный способ требует меньшего количества операций, приблизительно в
. Упрощенный способ требует меньшего количества операций, приблизительно в 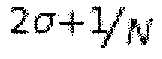 раз. Соответствующий контекст проиллюстрирован на Фиг. 16. Таким образом, Фиг. 16 показывает сложность преобразования MDCT/MDST.
раз. Соответствующий контекст проиллюстрирован на Фиг. 16. Таким образом, Фиг. 16 показывает сложность преобразования MDCT/MDST.
Кроме алгоритмической сложности, при рассмотрении эффективности важную роль играет использование памяти. В зависимости от оконечного устройства, на котором реализован аудиодекодер, доступным может быть только очень ограниченное количество памяти. Таким образом, необходимо сохранить использование оперативной памяти на максимально возможно низком уровне. Таблица 5.5 перечисляет используемые ресурсы. Описание модуля относится к исходному файлу на языке программирования C с тем же самым именем. Здесь рассматриваются только самые важные буферы, требуемые для хранения и обработки сигнальных векторов и матриц.
использование памяти преобразованием HSBE
Информация в круглых скобках содержит значения для упрощенного вычисления преобразования MDCT/MDST.
Реализация гармонического расширения спектрального диапазона основана на арифметике с плавающей точкой одинарной точности, что означает, что число с плавающей точкой представляется 32 битами. Количество, обозначенное в Таблице 5.5, относится к количеству чисел с плавающей точкой, требуемых в этом модуле. Как можно определить из таблицы, использование памяти для фактического алгоритма HSBE является сравнительно небольшим, приблизительно 109 KiB для модуляции, устранения искажений и преобразования MDCT/MDST. База данных для фильтров устранения искажений также хранится как справочная таблица и требует почти 11 KiB для общего количества коэффициентов фильтрации 2715. Решающее влияние на требования к объему памяти оказывает матрица преобразования  . Для этой матрицы используются приблизительно 16 MiB оперативной памяти. Требования к памяти матрицы
. Для этой матрицы используются приблизительно 16 MiB оперативной памяти. Требования к памяти матрицы  значительно уменьшаются за счет упрощения преобразования MDCT/MDST, представленного выше. Для примера, при
значительно уменьшаются за счет упрощения преобразования MDCT/MDST, представленного выше. Для примера, при 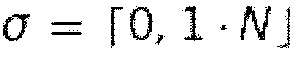 используется только приблизительно 0,8 KiB оперативной памяти.
используется только приблизительно 0,8 KiB оперативной памяти.
Используя представленную технологию, расширение полосы частот посредством предложенного в настоящем документе гармонического расширения спектрального диапазона обеспечивает гармонично корректное расширение спектра. Далее будут обсуждены потенциалы и пределы предложенных концепций.
В большинстве случаев могут быть обработаны сигналы различных длин. Однако для вычисления реализованного быстрого преобразования MDCT/MDST абсолютно необходимо, чтобы длина преобразования N была положительной целочисленной степенью числа два. Максимально возможная длина блока, аналогично AAC, ограничена числом 211, то есть 2048. При использовании HSBE также возможно изменять длину блока во время выполнения. Это, в частности, является необходимым для обработки переходных процессов в современных аудио-кодерах. Отношение сигнал/шум определяется решительно размером блока. Большие длины преобразования имеют тенденцию приводить к лучшему результату, чем очень короткие длины блока. Это вызвано компонентами искажения, образующимися из-за модуляции. Паразитные компоненты вплоть до четвертого порядка подавляются сглаживающим фильтрованием для устранения искажений, но тем не менее некоторые нежелательные компоненты остаются в сигнале. При очень коротких длинах блока эти компоненты искажения расширяются на большую ширину полосы и становятся ясно слышимыми. При больших длинах преобразования ширина полосы соответственно становится меньше, и компоненты искажения маскируются. Длина блока, равная 256, оказалась пределом в различных испытаниях. Начиная от этой длины артефакты практически не воспринимаются, как показано на Фиг. 17.
На Фиг. 17 показана интерференция при HSBE, в зависимости от длины преобразования. Фиг. 17 слева показывает спектр после обратного преобразования MDCT при N=32 и φ=90. Фиг. 17 справа показывает спектр после обратного преобразования MDCT при N=256 и φ=90.
Показаны частотные характеристики абсолютного значения синусоидального сигнала, модулированного с фазовым углом φ. Как ясно видно, при небольших размерах блока (слева на Фиг. 17), после устранения искажений ясно видны паразитные компоненты. Они находятся в диапазоне приблизительно -70 дБ и имеют решающее значение для отношения сигнал/шум. При размерах блока больше, чем 256 (справа на Фиг. 17), эти части маскируются полезным сигналом.
В целом, гармоническое расширение спектрального диапазона обеспечивает очень точное восстановление гармонической структуры сигнала. Для длины преобразования 256 и частоты оцифровки для аудиоданных, соответствующих стандарту CD 44100 Гц, разрешение разработанного способа находится в диапазоне приблизительно 0,5 Гц. Это означает, что спектр может модулироваться с точностью 0,5 Гц. При меньших частотах оцифровки или больших размерах блока разрешение возрастает, и модуляция может выполняться в еще более точных диапазонах. Результат применения HSBE к мультисинусоидальному сигналу проиллюстрирован на Фиг. 18.
На Фиг. 18 показано сравнение HSBE и SBR. «REF freq. resp.» относится к спектру исходного мультисинусоидального сигнала. «SBR freq. resp.» относится к ширине полосы сигнала, расширенной посредством SBR; «HSBE freq. resp.» относится к ширине полосы сигнала, расширенной посредством HSBE.
Как можно видеть в показанных частотных характеристиках абсолютного значения, спектр точно восстанавливается с использованием разработанного способа HSBE. После обработки ограниченного полосой сигнала с использованием HSBE (HSBE freq. resp.), спектр находится точно над исходным спектром (REF freq. resp.). Соответствующий спектр, не адаптированный гармонически (SBR freq. resp.) показан в сравнительных целях. Этот сигнал вычисляется с использованием алгоритма HSBE, но базовая частота задержки равна нулю. Это вызывает расширение полосы частот, которое в основном соответствует способу SBR. Здесь можно ясно видеть сдвиг гармонической структуры, начиная с частоты среза fg=6400 Гц и двойной этой частоты.
Вывод этого будет предоставлен ниже.
Сначала выведем преобразование DFT в DCT-II. В частности, DCT-II получается из DFT в уравнении 2.10 с использованием уравнения 2.12 (см. также Rao and Yip, 2001). Используется следующая формула:
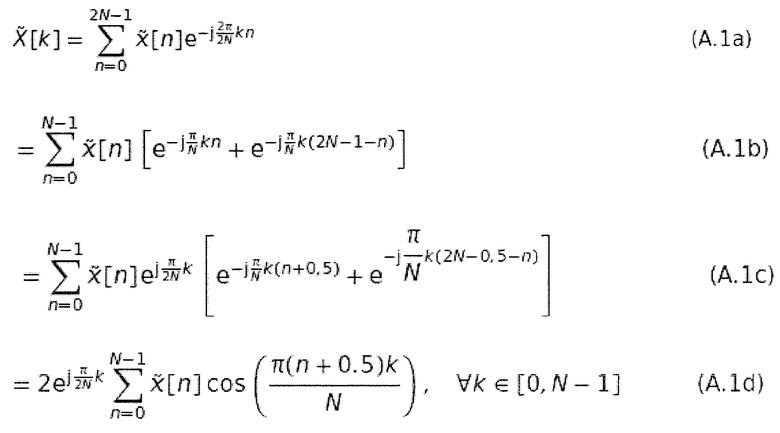 ,
,
где:
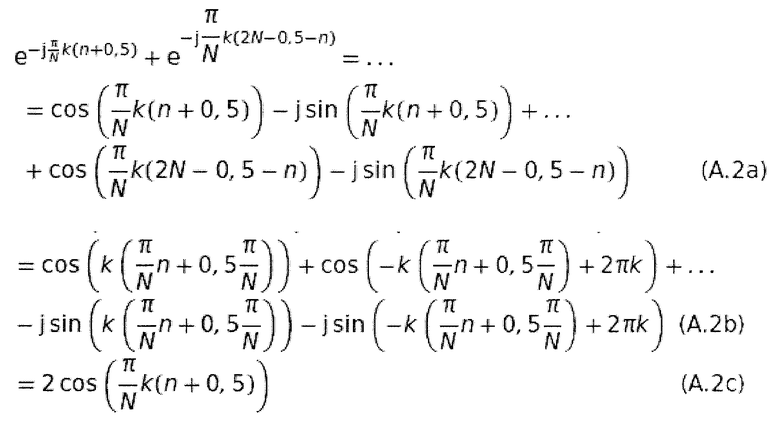 ,
,
и свойства функций синуса и косинуса:
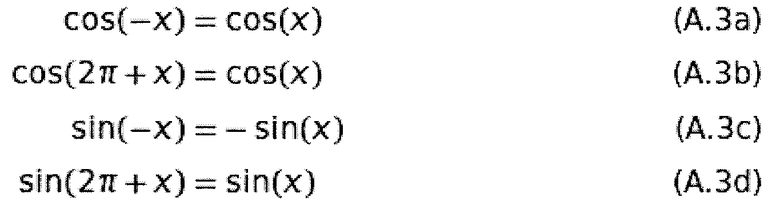 .
.
Это соединение может также использоваться для того, чтобы вычислить DCT, эффективно используя FFT (см. также Ahmed et al., 1974).
Матрицы свертки будут обсуждены ниже.
Матрицы свертки  и
и 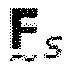 , требуемые для вычисления MCDT (см. уравнение 2.35), составлены из матрицы задержки
, требуемые для вычисления MCDT (см. уравнение 2.35), составлены из матрицы задержки  и матрицы окна
и матрицы окна 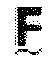 . Матрица окна содержит коэффициенты функции окна
. Матрица окна содержит коэффициенты функции окна  , расположенные в виде ромбовидной структуры. Используется следующая формула:
, расположенные в виде ромбовидной структуры. Используется следующая формула:
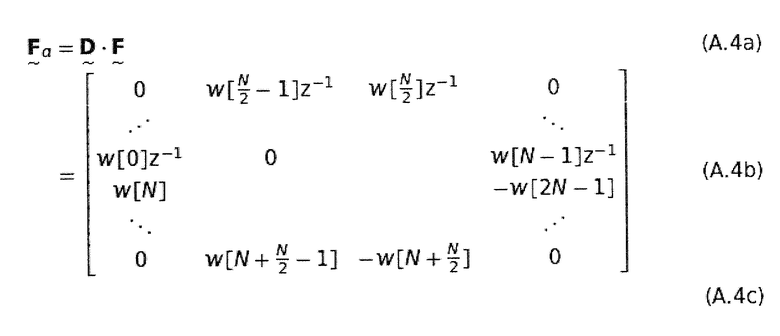
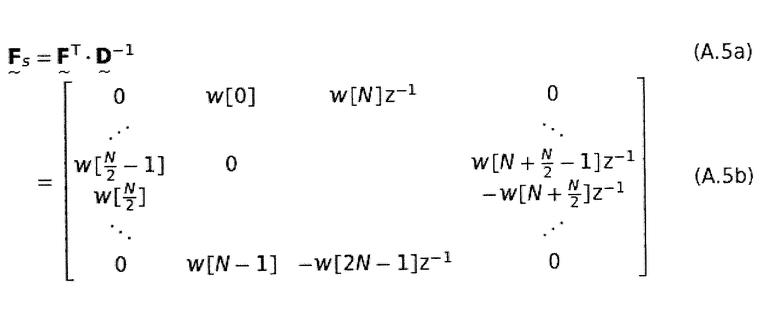 ,
,
где:
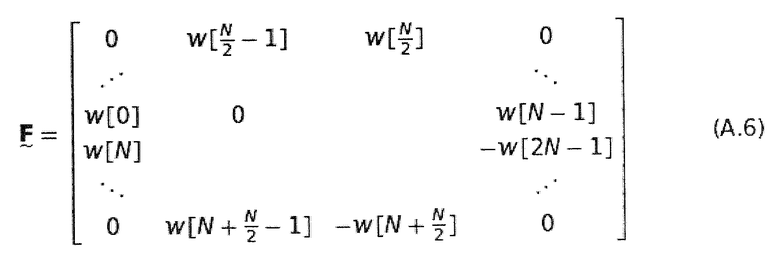
и
 .
.
Для того, чтобы сохранить обусловленность, обратная матрица задержки  была умножена на задержку z-1. Это является источником задержки набора фильтров MDCT (Schuller and Smith, 1996).
была умножена на задержку z-1. Это является источником задержки набора фильтров MDCT (Schuller and Smith, 1996).
Матрица преобразования H
Матрица преобразования  требуется для преобразования спектра MDCT в соответствующий спектр MDST. Используется следующая формула:
требуется для преобразования спектра MDCT в соответствующий спектр MDST. Используется следующая формула:
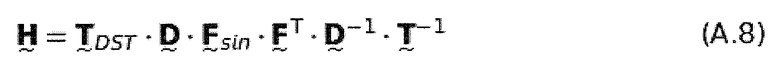 .
.
Подробное разложение будет показано с использованием примера для N=4:
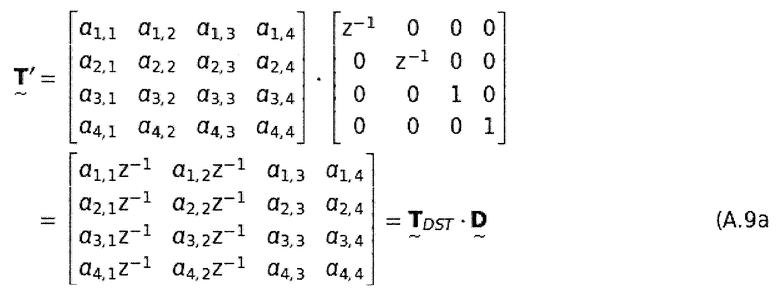
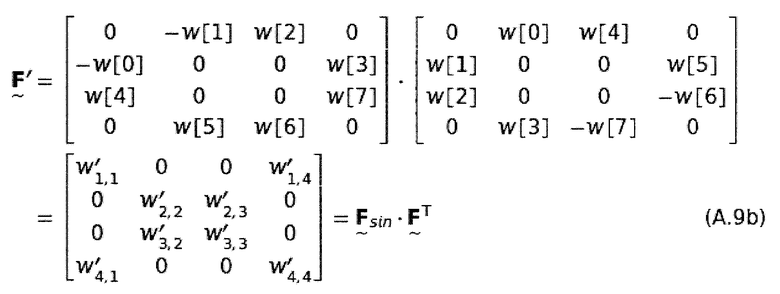
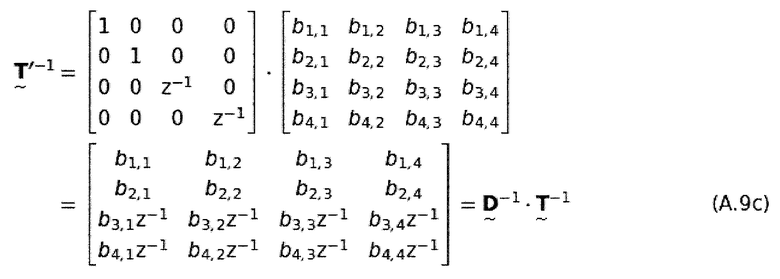 .
.
Матрицы с элементами задержки z-1 могут быть представлены как добавки к каждой из двух матриц. Получится следующее:
 .
.
Используя это разложение и матрицу  , уравнение А.8 можно выразить следующим образом:
, уравнение А.8 можно выразить следующим образом:
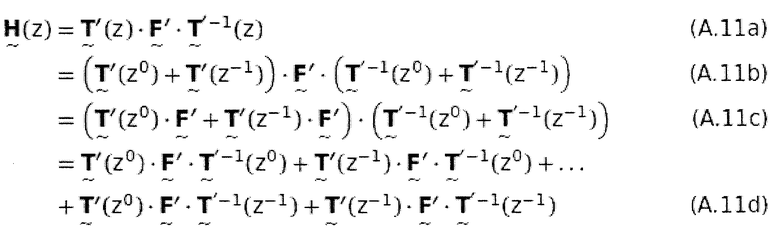 .
.
Индивидуальные члены уравнения затем заменяются с использованием их зависимости от z:
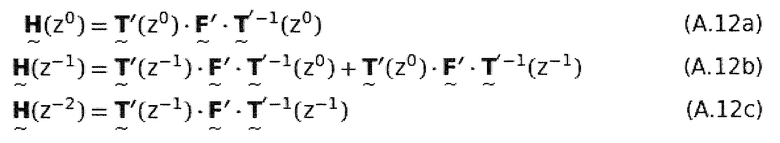
и вставляются в уравнение А.11a:
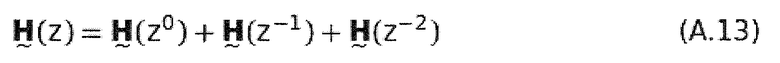 .
.
Результатом чего будет упрощенная запись уравнения 4.7:
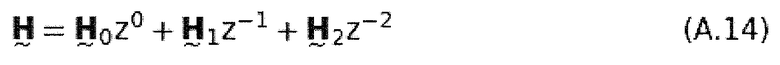 .
.
Численный анализ этих трех подматриц 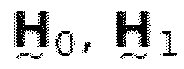 и
и 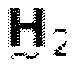 обеспечивает некоторые важные реализации, которые способствуют значительному сокращению вычислительной сложности матрицы
обеспечивает некоторые важные реализации, которые способствуют значительному сокращению вычислительной сложности матрицы  . Сначала отметим, что
. Сначала отметим, что 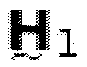 представляет собой разреженную матрицу. Она будет всегда иметь одну и ту же форму для различных длин преобразования N и включает в себя исключительно элементы 0,5 и -0,5. Используется следующая формула:
представляет собой разреженную матрицу. Она будет всегда иметь одну и ту же форму для различных длин преобразования N и включает в себя исключительно элементы 0,5 и -0,5. Используется следующая формула:
 .
.
Существует прямая связь между матрицами  и
и 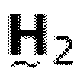 , приводящая к тому, что:
, приводящая к тому, что:
 ,
,
где:
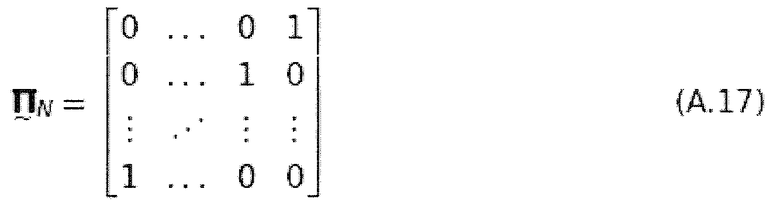 .
.
Таким образом,  представляет собой матрицу размером
представляет собой матрицу размером 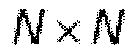 , которая при умножении слева инвертирует порядок строк, а при умножении справа инвертирует порядок столбцов. Таким образом, уравнение А.16 может быть интерпретировано как зеркальное отображение значений матрицы
, которая при умножении слева инвертирует порядок строк, а при умножении справа инвертирует порядок столбцов. Таким образом, уравнение А.16 может быть интерпретировано как зеркальное отображение значений матрицы 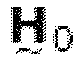 относительно ее побочной диагонали. Используя эти свойства, сложность, требуемая для вычисления
относительно ее побочной диагонали. Используя эти свойства, сложность, требуемая для вычисления  , может быть уменьшена от первоначальных 4N3 необходимых операций (см. уравнение А.11d) до одной четверти от этого.
, может быть уменьшена от первоначальных 4N3 необходимых операций (см. уравнение А.11d) до одной четверти от этого.
Далее будет обсуждаться быстрое преобразование DCT-IV. Реализация DCT-IV зависит от алгоритма быстрого преобразования DCT-IV. Преимуществом этой реализации является эффективное вычисление преобразования и связанная с этим короткая алгоритмическая задержка. Ядром преобразования DCT-IV являются два преобразования DCT-III в соответствии с уравнением 2.14c, соединенные параллельно. Аналогично FFT, оно составлено из так называемой перекрестной структуры и конвейерной структуры (Rao and Yip, 2001). Сложность этого алгоритма составляет 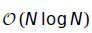 и сопоставима с необходимой вычислительной сложностью FFT. Конкретная схема DCT-III проиллюстрирована на Фиг. 19. В частности, Фиг. 19 иллюстрирует быструю универсальную структуру DCT-III/DST-III (Rao and Yip, 2001).
и сопоставима с необходимой вычислительной сложностью FFT. Конкретная схема DCT-III проиллюстрирована на Фиг. 19. В частности, Фиг. 19 иллюстрирует быструю универсальную структуру DCT-III/DST-III (Rao and Yip, 2001).
Входная последовательность xn преобразуется в спектральные значения DCT-II 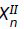 . Так как DCT-III представляет собой обратное преобразование к DCT-II, эти два преобразования могут быть вычислены с использованием этой структуры. Эта универсальная структура для вычисления DCT-III/DST-III и соответствующих обратных преобразований DCT-II и DST-II формирует основу для DCT-IV в соответствии с уравнением 2.14d. Фиг. 20 показывает реализованную схему DCT-IV. Таким образом, Фиг. 20 показывает структуру быстрого преобразования DCT-IV (Rao and Yip, 2001).
. Так как DCT-III представляет собой обратное преобразование к DCT-II, эти два преобразования могут быть вычислены с использованием этой структуры. Эта универсальная структура для вычисления DCT-III/DST-III и соответствующих обратных преобразований DCT-II и DST-II формирует основу для DCT-IV в соответствии с уравнением 2.14d. Фиг. 20 показывает реализованную схему DCT-IV. Таким образом, Фиг. 20 показывает структуру быстрого преобразования DCT-IV (Rao and Yip, 2001).
Показанные структуры могут быть реализованными, например, на языке программирования C. Соответствующими функциями являются dct_processor() для универсального преобразования DCT-III/DST-III (DST-II/DST-II), и fdcstiv1d() для быстрого преобразования DCT-IV/DST-IV. Никакой быстрой разновидности этого преобразования в системе Matlab не реализовывалось, поскольку производительность алгоритма здесь неважна.
Следующий раздел служит для описания функций системы Matlab и функций языка программирования C.
Функции Matlab:
decoder_hsbe()
Описание:
decoder_hsbe() представляет собой декодер для гармонического расширения спектрального диапазона (HSBE). Низкочастотный сигнал в области MDCT при этом расширяется спектрально так, что гармоническая структура сигнала сохраняется. Обратное фильтрование LPC выполняется для восстановления огибающей. Сигнал преобразуется во временную область посредством обратного преобразования MDCT.
Прототип:
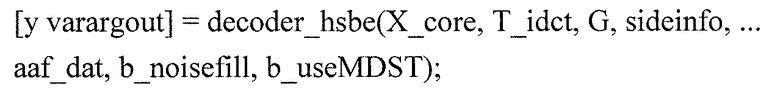
Выход:
y - восстановленный временной сигнал,
varargout(1) - расширенный спектр MDCT перед адаптацией огибающей,
varargout(2) - расширенный спектр MDST перед адаптацией огибающей,
varargout(3) - комплексный спектр перед адаптацией огибающей.
Вход:
X_core - основная полоса частот сигнала в области MDCT,
T_idct - обратная матрица преобразования DCT-IV,
G - обратная матрица свертки для iMDCT в ромбовидной форме,
sideinfo - информация о стороне,
aaf_dat - база данных с коэффициентами устранения искажений фильтра устранения искажений.
Опциональный вход:
b_noisefill - булевская величина, указывает, должен ли быть добавлен шум, стандартное значение: ложь,
b_useMDST - булевская величина, указывает, должно ли использоваться предварительно рассчитанное MDST. Если да, то аргумент X_core должен быть комплексным. Стандартное значение: ложь.
AAFCreator.m
Описание:
Инструмент создания (AAF) фильтра устранения искажений FIR «AAFCreator»: инструмент создания фильтра FIR AAF вычисляет фильтры устранения искажений, требуемые для устранения искажений в поддиапазонах, сдвинутых алгоритмом HSBE. Фильтры представляют собой фильтры FIR в базе данных. База данных хранится как файл с расширением .mat и содержит одномерный массив struct. Каждая запись в базе данных включает в себя индикацию относительно угла, для которого фильтр FIR должен использоваться, и коэффициенты фильтрации в качестве вектора.
Прототип:
Скрипт Matlab, без функционального имени.
Выход:
.bmp - графические файлы с импульсной характеристикой AAF и результатом устранения искажений,
.mat - база данных с фильтрами AAF в формате файла MAT,
.wav - импульсная характеристика AAF в виде аудиофайла формата RIFF.
Вход:
fs - частота оцифровки тестового сигнала,
NMDCT - длина преобразования N,
sig_typ - тип тестового сигнала,
f - частота тестового сигнала,
t - продолжительность тестового сигнала,
phi - фазовый угол φ, возможно несколько углов,
num_opt - количество проходов оптимизации,
num_alias - самый высокий порядок подавляемых компонентов искажений,
b_save_wav - булевская величина, указывает, должны ли храниться .wav файлы,
b_save_bmp - булевская величина, указывает, должны ли храниться .bmp файлы,
b_break - булевская величина, указывает, должны ли выводиться промежуточные результаты,
path_bmp - путь для сохранения файлов .bmp,
path_wav - путь для сохранения файлов .wav.
AAFoptimizer()
Описание:
AAFoptimizer() генерирует фильтр (AAF) устранения искажений как фильтр FIR. Алгоритм численно оптимизирует компоненты искажения, обнаруженные распознаванием пиков, посредством последовательных приближений.
Прототип:
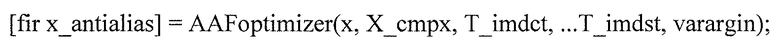
Выход:
fir - импульсная характеристика фильтра устранения искажений во временной области,
x_antialias - входной сигнал x, очищенный от искажения фильтром fir.
Вход:
X - временной сигнал с компонентами искажений,
X_cmpx - комплексное представление x в области MDCT/MDST,
T_imdct - матрица обратного преобразования MDCT,
T_imdst - матрица обратного преобразования MDST.
Опции:
varargin(1) - наивысший порядок подавляемых компонентов искажений; стандартное значение: 4,
varargin(2) - количество проходов оптимизации; стандартное значение: 3,
varargin(3) - фазовый угол φ, с использованием которого модулировался сигнал x; стандартное значение: 0,
varargin(4) - булевская величина, указывает, должен ли вычерчиваться график; стандартное значение: ложь,
varargin(5) - булевская величина, указывает, должны ли быть сохранены вычерченные графики; стандартное значение: ложь,
varargin(6) - путь для сохранения файлов .bmp; стандартное значение: ноль.
Функции языка C
HSBE processing()
Описание:
HSBE processing() является основным интерфейсом для статической библиотеки hsbe.lib, предназначенной для расширения полосы частот посредством HSBE. В текущей версии 1.0 часть сигнала во временной области преобразуется с использованием MDCT/MDST и расширяется спектрально так, чтобы сохранялась гармоническая структура. Комплексный сигнал с расширенной полосой частот преобразуется обратно во временную область и выводится. Восстановления огибающей, как это сделано в функции Matlab decoder_hsbe(), не выполняется.
Прототип:

Выход:
HSBE_RESULT - код ошибки,
pSamplesOut - указатель на вектор временного сигнала с расширенной полосой частот.
Вход:
HSBEhandle - структура дескриптора HSBE,
pSamplesIn - указатель на вектор входного сигнала,
nSamplesIn - длина преобразования N,
frequencyOffset - частота задержки flag как нормализованная частота.
HSBEinit()
Описание:
HSBEinit() представляет собой функцию для инициализации HSBE. Здесь резервируется требуемая оперативная память, вычисляется функция окна, а также вычисляется матрица преобразования MDCT/MDST  . В дополнение к этому в дескриптор вводятся все параметры, требуемые для функции HSBE processing().
. В дополнение к этому в дескриптор вводятся все параметры, требуемые для функции HSBE processing().
Прототип:

Выход:
HSBE_RESULT - код ошибки,
HSBEhandle - указатель на структуру дескриптора HSBE.
Вход:
HSBEhandle - указатель на структуру дескриптора HSBE,
nSamplesIn - длина преобразования N,
f_core - частота среза fg основной полосы как нормализованная частота,
f_hsbe - максимальная восстанавливаемая частота как нормализованная частота,
windowtype - тип функции окна, которая должна использоваться,
flags - флаги проверки.
HSBEfree()
Описание:
HSBE free() высвобождает ресурсы, затребованные функцией HSBEinit().
Прототип:
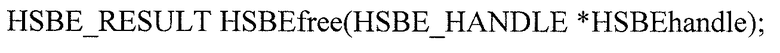
Выход:
HSBE_RESULT - код ошибки,
HSBEhandle - указатель на структуру дескриптора HSBE.
Вход:
HSBEhandle - указатель на структуру дескриптора HSBE.
Хотя некоторые аспекты были описаны в соединении с устройством, следует понимать, что эти аспекты также представляют описание соответствующего способа, так что блок или конструктивный элемент устройства также должны пониматься как соответствующая этап способа или характеристика этапа способа. По аналогии, аспекты, описанные в соединении с этапом способа или как этап способа, также представляют собой описание соответствующего блока или детали или характеристики соответствующего устройства. Некоторые или все этапы способа могут быть выполнены аппаратным устройством (или используя аппаратное устройство), такое как, например, микропроцессор, программируемый компьютер или электронная схема. В некоторых вариантах осуществления некоторые или несколько из самых важных этапов способа могут выполняться таким устройством.
В зависимости от конкретных требований реализации варианты осуществления настоящего изобретения могут быть реализованы либо в виде аппаратных средств, либо в виде программного обеспечения. Реализация может быть выполнена с использованием цифрового носителя, такого как, например, гибкий диск, DVD, диск Blu-ray, CD, ROM, PROM, EPROM, EEPROM или флэш-память, жесткий диск или другая магнитная или оптическая память, на которую сохранены электронночитаемые управляющие сигналы, которые в состоянии взаимодействовать или взаимодействуют с программируемой компьютерной системой так, что будет выполняться соответствующий способ. Таким образом, цифровой носитель может быть машиночитаемым.
Некоторые варианты осуществления в соответствии с настоящим изобретением включают в себя носитель данных, который включает в себя электронночитаемые управляющие сигналы, которые в состоянии взаимодействовать с программируемой компьютерной системой так, что будет выполняться один из описанных в настоящем документе способов.
В большинстве случаев варианты осуществления настоящего изобретения могут быть реализованы как компьютерный программный продукт, включающий в себя код программы, являющийся эффективным для выполнения одного из способов при выполнении компьютерного программного продукта на компьютере.
Код программы может, например, быть сохранен на машиночитаемом носителе.
Другие варианты осуществления включают в себя компьютерную программу для выполнения одного из описанных в настоящем документе способов, сохраненную на машиночитаемом носителе. Другими словами, одним вариантом осуществления способа в соответствии с настоящим изобретением является компьютерная программа, включающая в себя код программы для выполнения одного из способов, описанных в настоящем документе, при выполнении компьютерной программы на компьютере.
Таким образом, другой вариант осуществления способа в соответствии с настоящим изобретением представляет собой носитель информации (или цифровой носитель или машиночитаемый носитель), на который была записана компьютерная программа для выполнения одного из описанных в настоящем документе способов.
Таким образом, другой вариант осуществления способа в соответствии с настоящим изобретением представляет собой поток данных или последовательность сигналов, представляющих компьютерную программу для выполнения одного из описанных в настоящем документе способов. Поток данных или последовательность сигналов могут, например, быть выполнены с возможностью их передачи через соединение для передачи данных, например, через Интернет.
Другой вариант осуществления включает в себя средства обработки, такие как, например, компьютер или программируемое логическое устройство, выполненное с возможностью выполнения одного из описанных в настоящем документе способов.
Другой вариант осуществления включает в себя компьютер, на который была установлена компьютерная программа для выполнения одного из описанных в настоящем документе способов.
Другой вариант осуществления в соответствии с изобретением включает в себя устройство или систему, выполненные с возможностью передачи получателю компьютерной программы для выполнения по меньшей мере одного из способов, описанных в настоящем документе. Передача может осуществляться, например, электронно или оптически. Получатель может быть, например, компьютером, мобильным устройством, запоминающим устройством и т.п. Устройство или система могут включать в себя, например, файловый сервер для передачи компьютерной программы получателю.
В некоторых вариантах осуществления программируемое логическое устройство (например, программируемая пользователем логическая микросхема (FPGA)) может использоваться для того, чтобы выполнить некоторую или всю функциональность описанных в настоящем документе способов. В некоторых вариантах осуществления программируемая пользователем логическая микросхема может сотрудничать с микропроцессором для того, чтобы выполнить один из описанных в настоящем документе способов. Вообще говоря, в некоторых вариантах осуществления эти способы выполняются на стороне любого устройства. Это могут быть универсально используемые аппаратные средства, такие как компьютерный процессор (CPU), или аппаратные средства, конкретные для данного способа, как, например, специализированная интегральная схема (ASIC).
Описанные выше варианты осуществления представляют собой лишь иллюстрацию принципов настоящего изобретения. Следует понимать, что модификации и вариации описанных в настоящем документе компоновок и деталей очевидны для других специалистов в данной области техники. Следовательно, настоящее изобретение ограничено исключительно контекстом следующей формулы изобретения, но не конкретными деталями, представленными в настоящем документе при описании и обсуждении вариантов осуществления.
Значение сокращений:
AAC - усовершенствованное кодирование звука.
AAF - фильтр устранения искажений.
ac-3 - кодер адаптивного преобразования системы Dolby digital 3.
BWE - расширение полосы частот.
CD - компакт-диск.
CM-BWE - непрерывно модулируемое расширение полосы частот.
DCT - дискретное косинусоидальное преобразование.
DFT - дискретное преобразование Фурье.
DST - дискретное синусоидальное преобразование.
DVD - цифровой многоцелевой диск.
FFT - быстрое преобразование Фурье.
FIR - конечная импульсная характеристика.
HBE - гармоническое расширение полосы частот.
HE-AAC -высокоэффективное усовершенствованное кодирование звука MPEG-4.
HF - высокая частота.
HSBE - гармоническое спектральное расширение полосы часто.т
JPEG - совместная экспертная группа по фотографии.
KiB - кибибайт=210 байтов=1024 байта.
LOT - ортогональное преобразование с перекрытием.
LPC - кодирование с линейным предсказанием.
LTI - линейный независимый от времени.
MDCT - модифицированное дискретное косинусоидальное преобразование.
MDST - модифицированное дискретное синусоидальное преобразование.
MiB - мебибайт=220 байтов=1048576 байтов.
mp3 - MPEG-1 аудиокодирование, уровень III.
PC - персональный компьютер.
PCM - импульсно-кодированная модуляция.
PR - точное восстановление.
QMF - квадратурный зеркальный фильтр.
SBR - репликация спектрального диапазона.
SNR - отношение сигнал-шум.
TDA - искажение во временной области.
TDAC - устранение искажения во временной области.
USAC - объединенное кодирование речи и аудио.
VoIP -передача речи по интернет-протоколу.
Значение использованных символов:
e - число Эйлера.
j - мнимая единица.
Im - мнимая часть функции.
ld - логарифм по основанию два.
log - логарифм по основанию десять.
* - комлексно сопряженный.
Re - вещественная часть функции.
 - символ Ландо для оценки сложности.
- символ Ландо для оценки сложности.
T - транспонированный.
 - оператор округления.
- оператор округления.
 - оператор округления в меньшую сторону.
- оператор округления в меньшую сторону.
 - множество вещественных чисел.
- множество вещественных чисел.
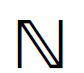 - множество неотрицательных целых чисел.
- множество неотрицательных целых чисел.
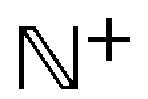 - множество положительных целых чисел.
- множество положительных целых чисел.
 - множество целых чисел.
- множество целых чисел.
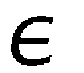 - коэффициент нормализации,
- коэффициент нормализации, 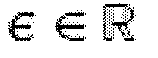 .
.
σ - коэффициент расширения, индекс окна,  .
.
τ - коэффициент модуляции, 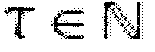 .
.
φ - фазовый угол, 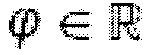 .
.
 - нормализованная частота,
- нормализованная частота, 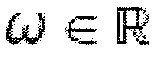 .
.
b - индекс блока, 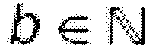 .
.
B - ширина полосы, 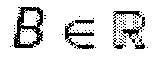 .
.
ƒ - частота, 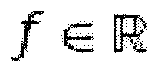 .
.
k - индекс дискретной частоты,  .
.
m - индекс дискретной фазы, 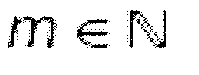 .
.
M - фазовое число, 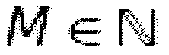 .
.
n - индекс дискретного времени, 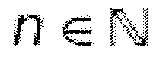 .
.
N - длина преобразования, 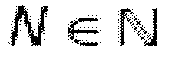 .
.
t - время,  .
.
W - комплексный вращающийся фазор.
h[n] - импульсная характеристика фильтра FIR.
H[z] - передаточная функция h[n] в области z.
pm[n] - m-я фаза дискретного сигнала.
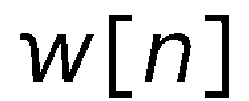 - функция окна в области дискретного времени.
- функция окна в области дискретного времени.
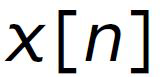 - реальный сигнал в области дискретного времени.
- реальный сигнал в области дискретного времени.
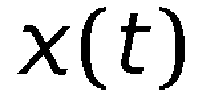 - реальный сигнал в области непрерывного времени.
- реальный сигнал в области непрерывного времени.
X(ƒ) - сигнал в области непрерывной частоты.
X[k] - сигнал в области дискретной частоты.
 - импульсная характеристика h [n] в векторной записи.
- импульсная характеристика h [n] в векторной записи.
 - H[z] в векторной записи.
- H[z] в векторной записи.
 - сигнал
- сигнал 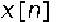 в векторной записи.
в векторной записи.
 - матрица задержки.
- матрица задержки.
 - матрица окна в ромбовидной форме.
- матрица окна в ромбовидной форме.
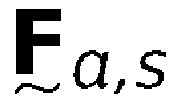 - матрица свертки.
- матрица свертки.
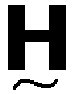 - многофазная матрица преобразования.
- многофазная матрица преобразования.
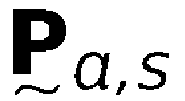 - многофазная матрица.
- многофазная матрица.
 - матрица преобразования.
- матрица преобразования.
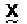 - блочная матрица вектора сигнала x.
- блочная матрица вектора сигнала x.
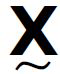 - преобразованный сигнал.
- преобразованный сигнал.
Литература
[Ahmed u. a. 1974] Ahmed, N.; Natarajan, T.; Rao, K.R.: Discrete Cosine Transform. In: Computers, IEEE Transactions on C-23 (1974), Januar, Nr. 1.
[Bosi und Goldberg 2003] Bosi, M.; Goldberg, R.E.: Introduction to Digital Audio Coding and Standards. 2nd edition. Boston; Dordrecht; London: Kluwer Academic Publishers, 2003.
[Britanak u. a. 2007] Britanak, V.; Yip, P.C.; Rao, K.R.: Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations. Amsterdam; u.a.: Elsevier, 2007.
[Burrus und Parks 1985] Burrus, C.S.; Parks, T.: DFT/FFT and Convolution Algorithms: Theory and Implementation. New York : John Wiley & Sons Ltd., 1985.
[Cheng 2004] Cheng, C.: Method for Estimating Magnitude and Phase in the MDCT Domain. In: Audio Engineering Society Convention 116, Mai 2004.
[Dolson 1986] Dolson, M: The Phase Vocoder: A Tutorial. In: Computer Music Journal 10 (1986), Nr. 4.
[Ekstrand 2002] Ekstrand, P.: Bandwidth Extension of Audio Signals by Spectral Band Replication. In: Proceedings of 1st IEEE Benelux Workshop on MPCA, Leuven, Belgium. Bd. 1, November 2002.
[Fastl und Zwicker 2007] Fastl, H.; Zwicker, E.: Psychoacoustics: Facts and Models. 3. Auflage. Berlin; Heidelberg; New York: Springer, 2007.
[Jordan-Engeln und Reutter 1978] Jordan-Engeln, G.; Reutter, F.: Numerische Mathematik für Ingenieure. 2nd revised edition. Mannheim: Bibliographisches Institut, 1978.
[Kiencke und Jäkel 2005] Kiencke, U.; Jäkel, H.: Signale und Systeme. 3rd revised edition. München; Wien: Oldenburg Verlag, 2005.
[Larsen und Aarts 2004] Larsen, E.; Aarts, R.M.: Audio Bandwidth Extension: Application of Psychoacoustics, Signal Processing and Loudspeaker Design. Chichester: John Wiley & Sons Ltd., 2004.
[Lochmann 1990] Lochmann, D.: Digitale Nachrichtentechnik: Digitale Modulation und Signalverarbeitung. Bd. 1. Berlin: VBE Verlag Technik, 1990.
[Malvar 1992] Malvar, H.S.: Signal Processing with Lapped Transforms. Boston; London: Artech House, 1992.
[Malvar und Staelin 1989] Malvar, H.S.; Staelin, D.H.: The LOT: transform coding without blocking effects. In: Acoustics, Speech and Signal Processing, IEEE Transactions on 37 (1989), April, Nr. 4.
[Nagel und Disch 2009] Nagel, F.; Disch, S.: A harmonic bandwidth extension method for audio codecs. In: Acoustics, Speech and Signal Processing, 2009. ICASSP 2009. IEEE International Conference on, April 2009.
[Nagel u. a. 2010] Nagel, F.; Disch, S.; Wilde, S.: A continuous modulated single sideband bandwidth extension. In: Acoustics Speech and Signal Processing (ICASSP), 2010 IEEE International Conference on, März 2010.
[Princen und Bradley 1986] Princen, J.; Bradley, A.: Analysis/Synthesis filter bank design based on time domain aliasing cancellation. In: Acoustics, Speech and Signal Processing, IEEE Transactions on 34 (1986), oct, Nr. 5.
[Princen u. a. 1987] Princen, J.; Johnson, A.; Bradley, A.: Subband/Transform coding using filter bank designs based on time domain aliasing cancellation. In: Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP '87. Bd. 12, April 1987.
[Rao und Yip 2001] Rao, K.R.; Yip, P.C.: The Transform and Data Compression Handbook. London; New York; Washington, D.C.: CRC Press, 2001.
[Schuller und Smith 1996] Schuller, G.D.T.; Smith, M.J.T.: New framework for modulated perfect reconstruction filter banks. In: Signal Processing, IEEE Transactions on 44 (1996), August, Nr. 8.
[Weinzierl 2008] Weinzierl, S.: Handbuch der Audiotechnik. Berlin; Heidelberg: Springer, 2008.
[Wilde 2009] Wilde, Stephan: Entwicklung von Zeitbereichsverfahren zur Bandbreitenerweiterung von Audiosignalen, Friedrich-Alexander-Universität Erlangen-Nürnberg, dissertation, 2009.
[Yost 1994] Yost, W.A.: Fundamentals of Hearing: An Introduction. 3rd edition. San Diego; New York; Boston; London; Sydney; Tokyo: Academic Press, 1994.
[Zölzer 2005] Zölzer, U.: Digitale Audiosignalverarbeitung. 3rd revised and extended edition. Stuttgart; Leipzig; Wiesbaden: Teubner, 2005.
| название | год | авторы | номер документа |
|---|---|---|---|
| ДЕКОДЕР ДЛЯ ДЕКОДИРОВАНИЯ КОДИРОВАННОГО АУДИОСИГНАЛА И КОДЕР ДЛЯ КОДИРОВАНИЯ АУДИОСИГНАЛА | 2016 |
|
RU2691231C2 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ ДЕКОДИРОВАНИЯ ИЛИ КОДИРОВАНИЯ ЗВУКОВОГО СИГНАЛА С ИСПОЛЬЗОВАНИЕМ ЗНАЧЕНИЙ ИНФОРМАЦИИ ЭНЕРГИИ ДЛЯ ПОЛОСЫ ЧАСТОТ ВОССТАНОВЛЕНИЯ | 2014 |
|
RU2649940C2 |
| УСТРОЙСТВО И СПОСОБ ДЕКОДИРОВАНИЯ КОДИРОВАННОГО ЗВУКОВОГО СИГНАЛА | 2009 |
|
RU2483366C2 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ ДЕКОДИРОВАНИЯ И КОДИРОВАНИЯ АУДИОСИГНАЛА С ИСПОЛЬЗОВАНИЕМ АДАПТИВНОГО ВЫБОРА СПЕКТРАЛЬНЫХ ФРАГМЕНТОВ | 2014 |
|
RU2643641C2 |
| СОКРАЩЕННОЕ ДЕКОДИРОВАНИЕ | 2016 |
|
RU2683487C1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ КОДИРОВАННОГО АУДИОСИГНАЛА С ИСПОЛЬЗОВАНИЕМ ВРЕМЕННОГО ФОРМИРОВАНИЯ ШУМА/НАЛОЖЕНИЙ | 2014 |
|
RU2607263C2 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ КОДИРОВАНИЯ ИЛИ ДЕКОДИРОВАНИЯ ЗВУКОВОГО СИГНАЛА С ИНТЕЛЛЕКТУАЛЬНЫМ ЗАПОЛНЕНИЕМ ИНТЕРВАЛОВ В СПЕКТРАЛЬНОЙ ОБЛАСТИ | 2014 |
|
RU2635890C2 |
| АУДИОКОДЕР, АУДИОДЕКОДЕР И СВЯЗАННЫЕ СПОСОБЫ С ИСПОЛЬЗОВАНИЕМ ДВУХКАНАЛЬНОЙ ОБРАБОТКИ В ИНФРАСТРУКТУРЕ ИНТЕЛЛЕКТУАЛЬНОГО ЗАПОЛНЕНИЯ ИНТЕРВАЛОВ ОТСУТСТВИЯ СИГНАЛА | 2014 |
|
RU2646316C2 |
| АУДИОКОДЕР, АУДИОДЕКОДЕР И СВЯЗАННЫЕ СПОСОБЫ ОБРАБОТКИ МНОГОКАНАЛЬНЫХ АУДИОСИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ КОМПЛЕКСНОГО ПРЕДСКАЗАНИЯ | 2011 |
|
RU2577195C2 |
| КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ АУДИОСИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ ГРЕБЕНОК ФИЛЬТРОВ С КОМПЛЕКСНЫМ ЗНАЧЕНИЕМ | 2005 |
|
RU2407069C2 |
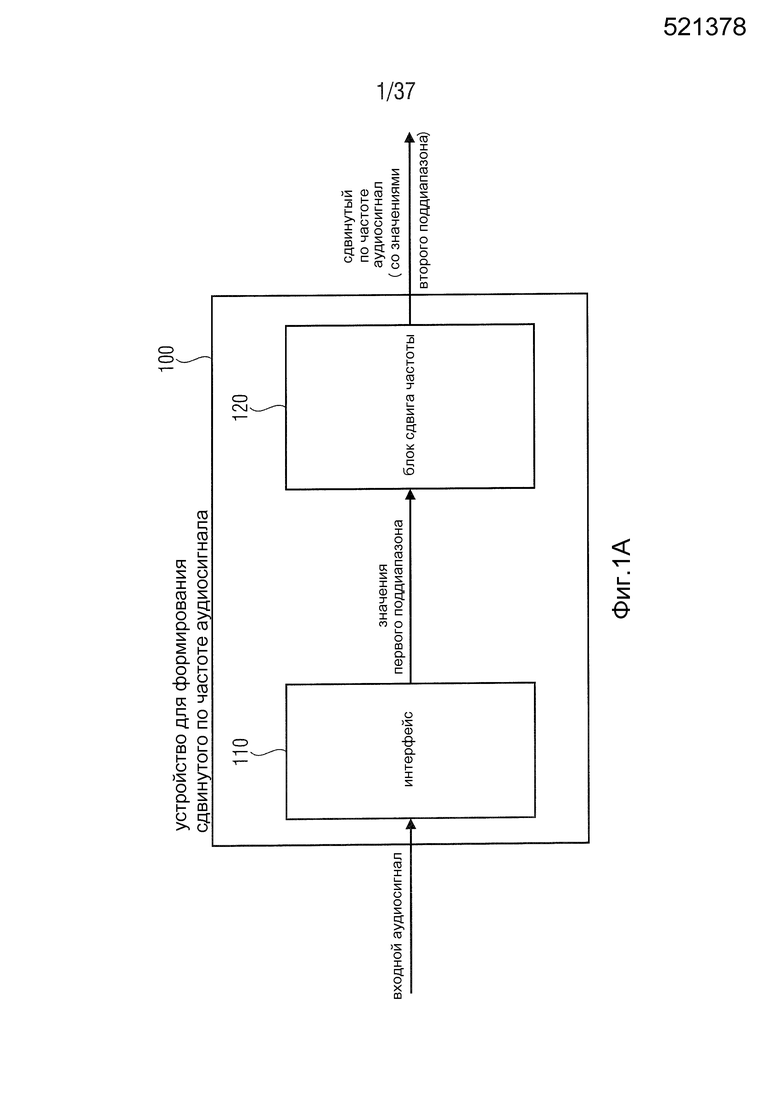
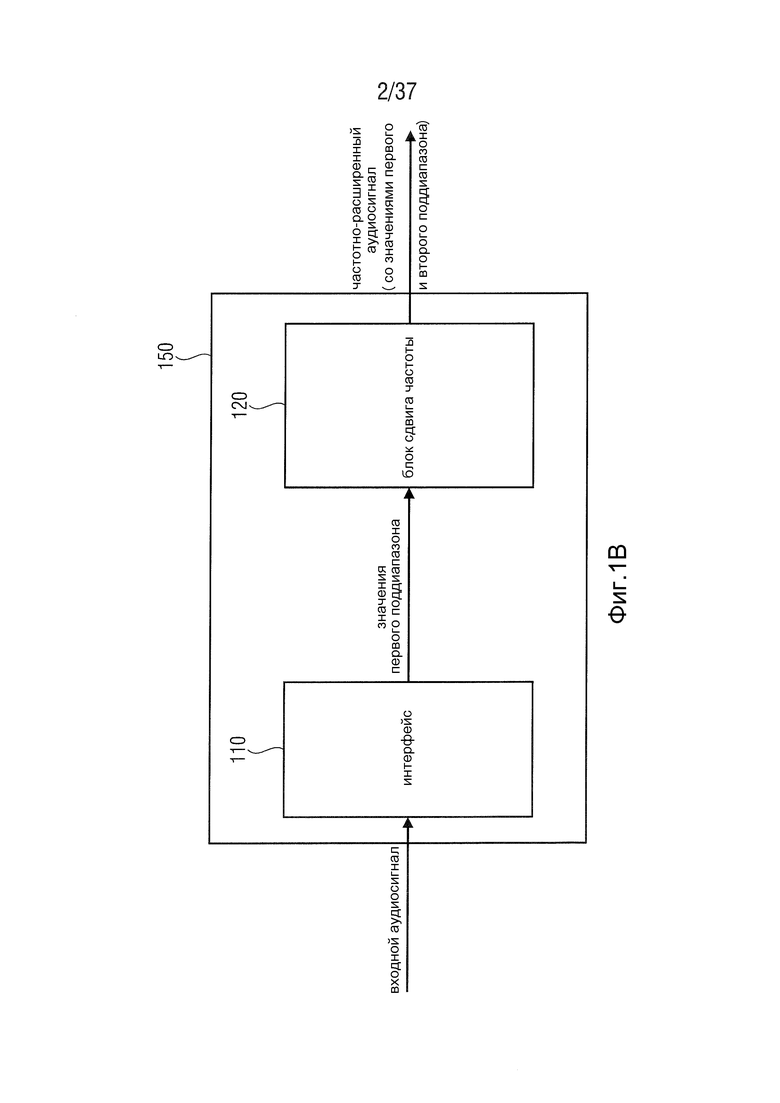
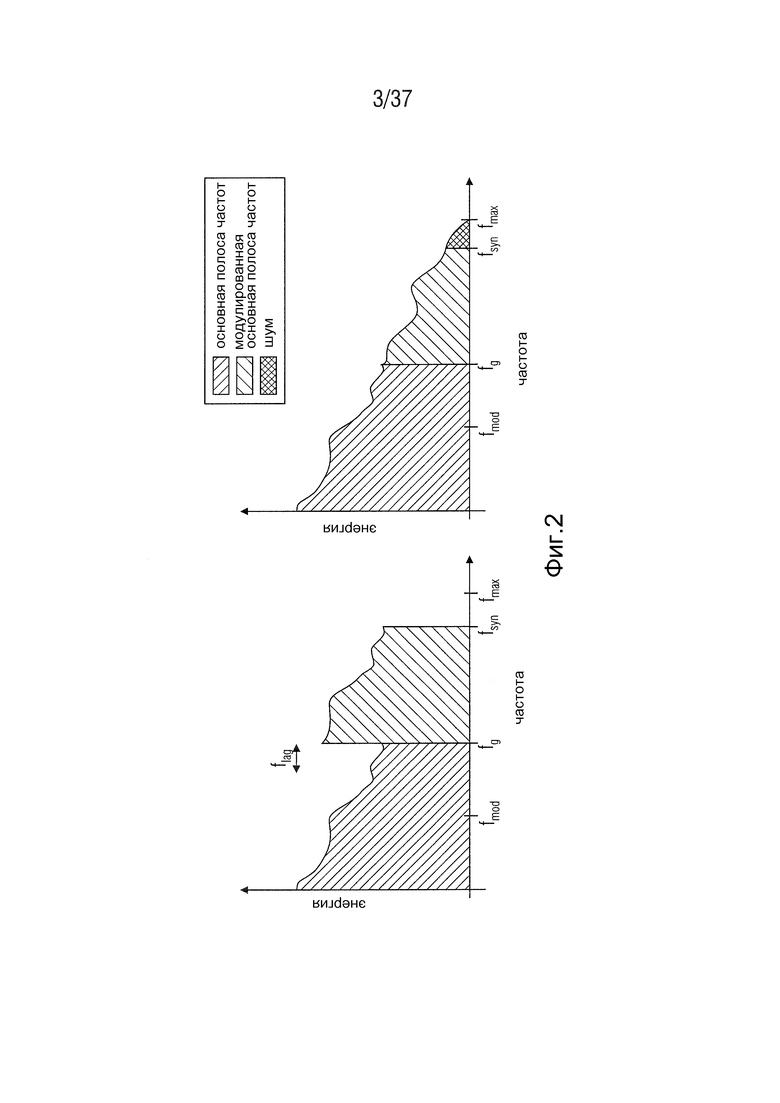
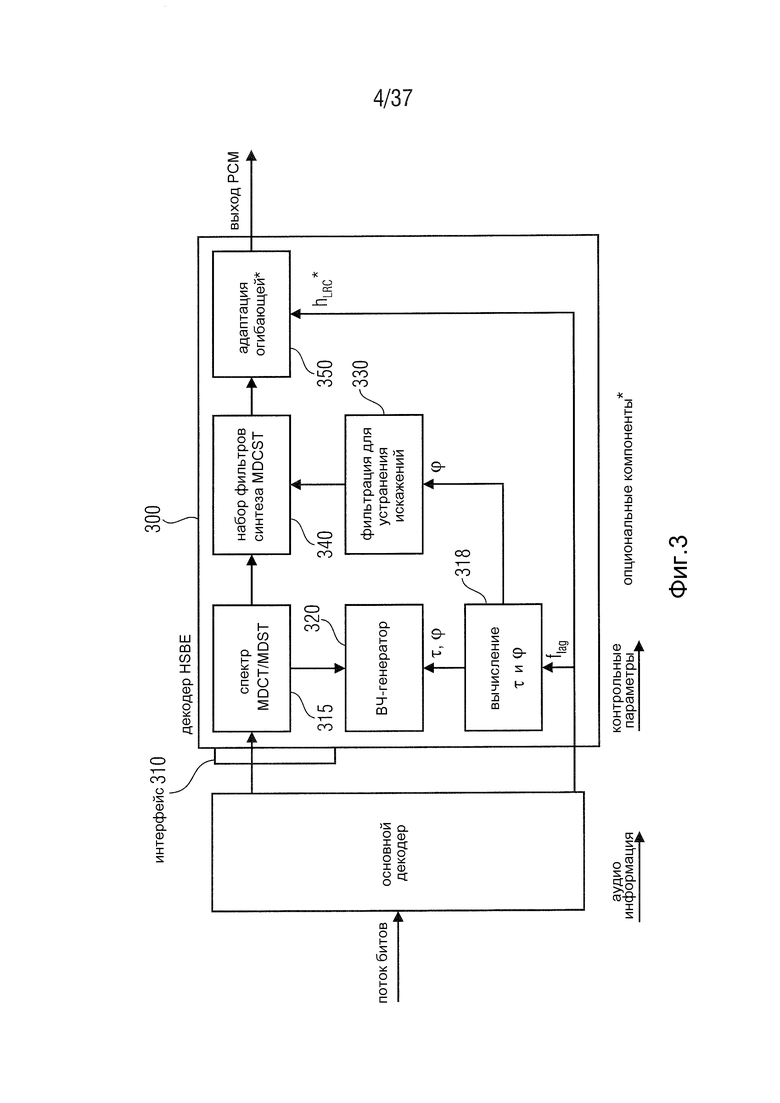
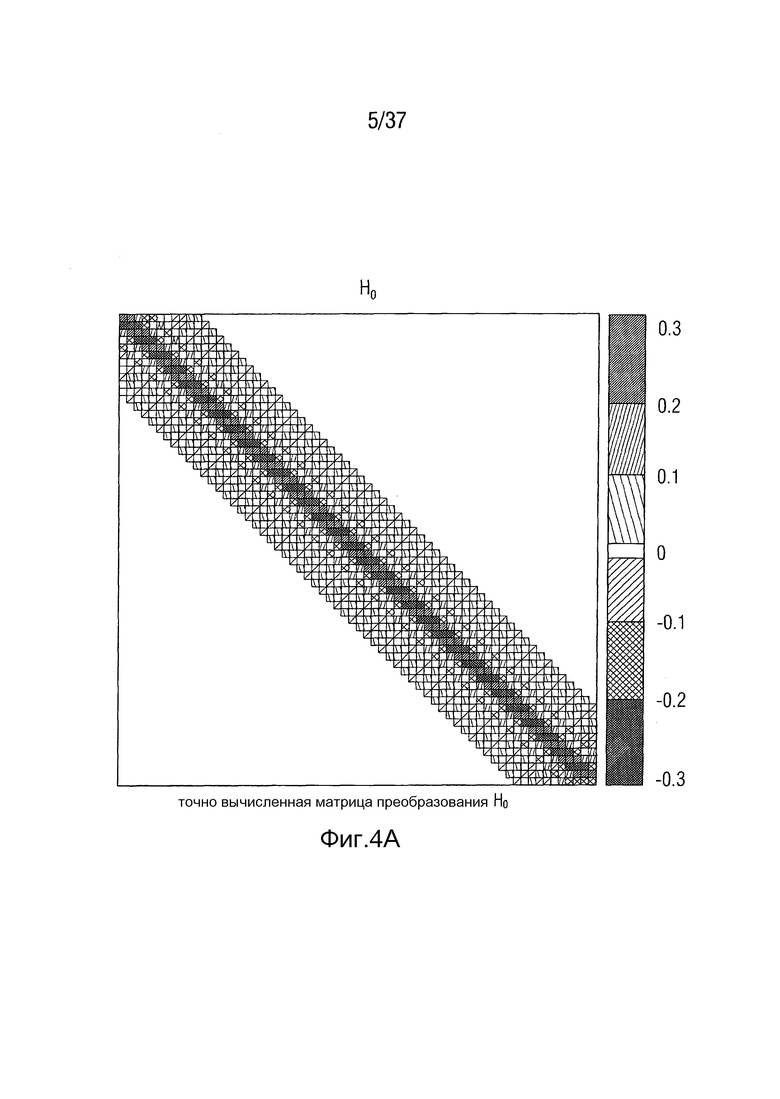
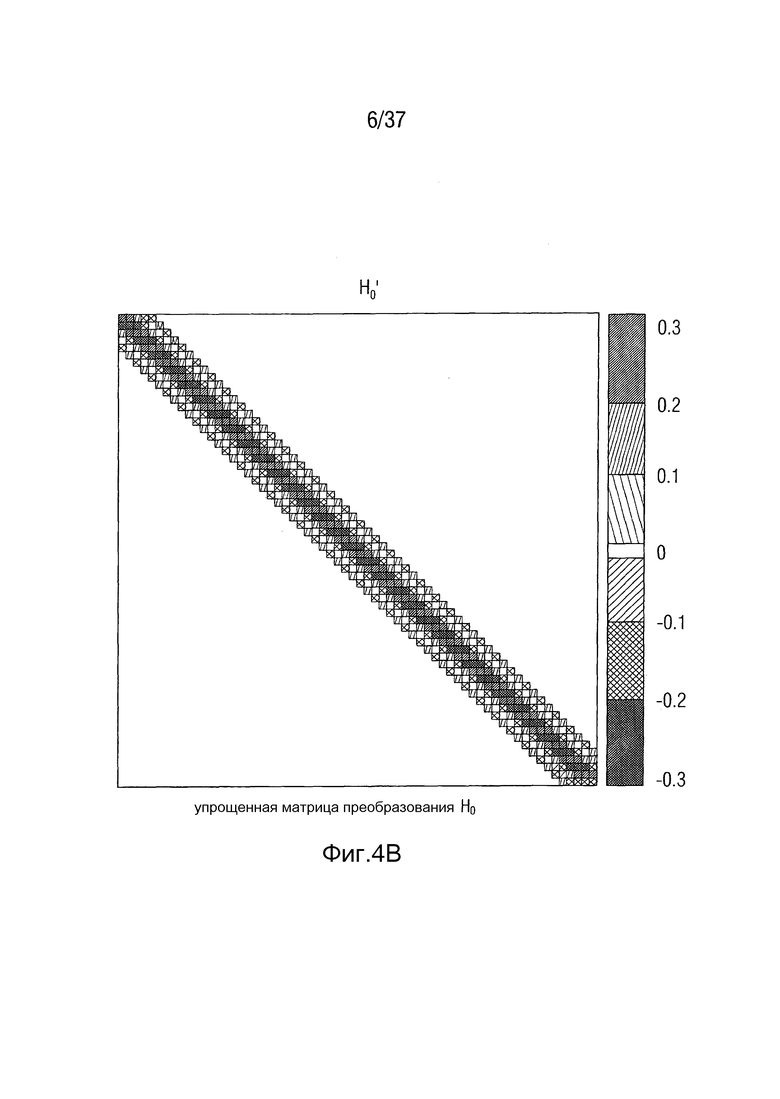
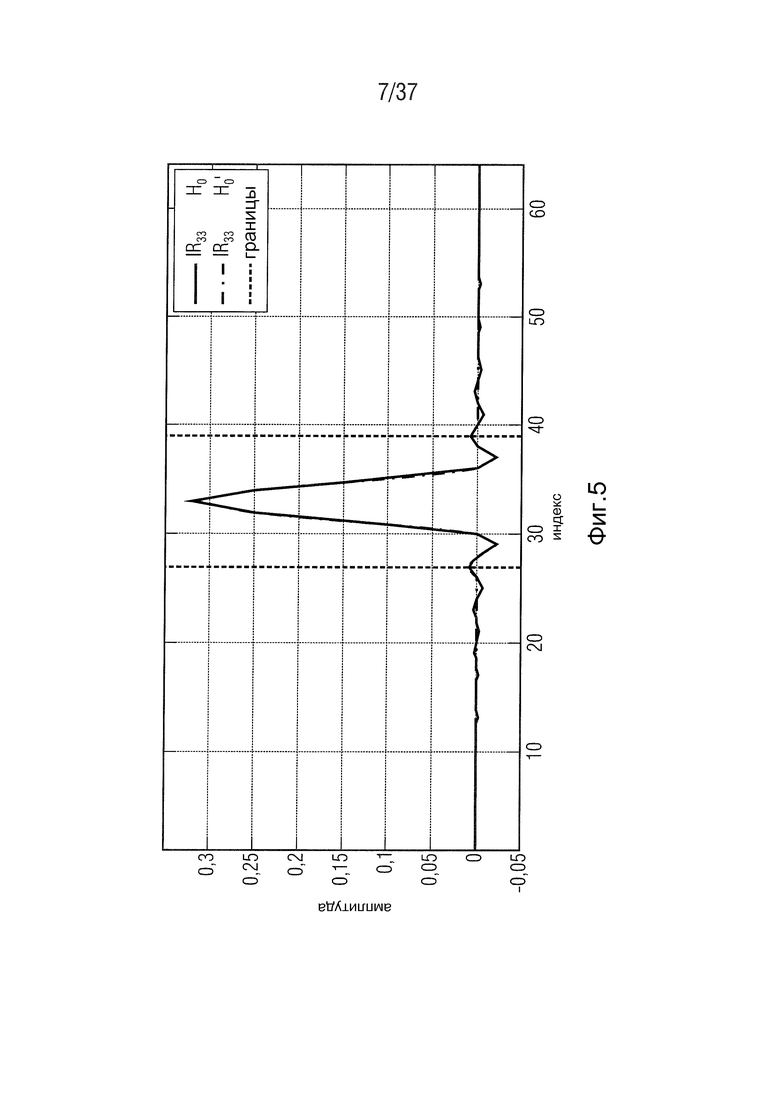
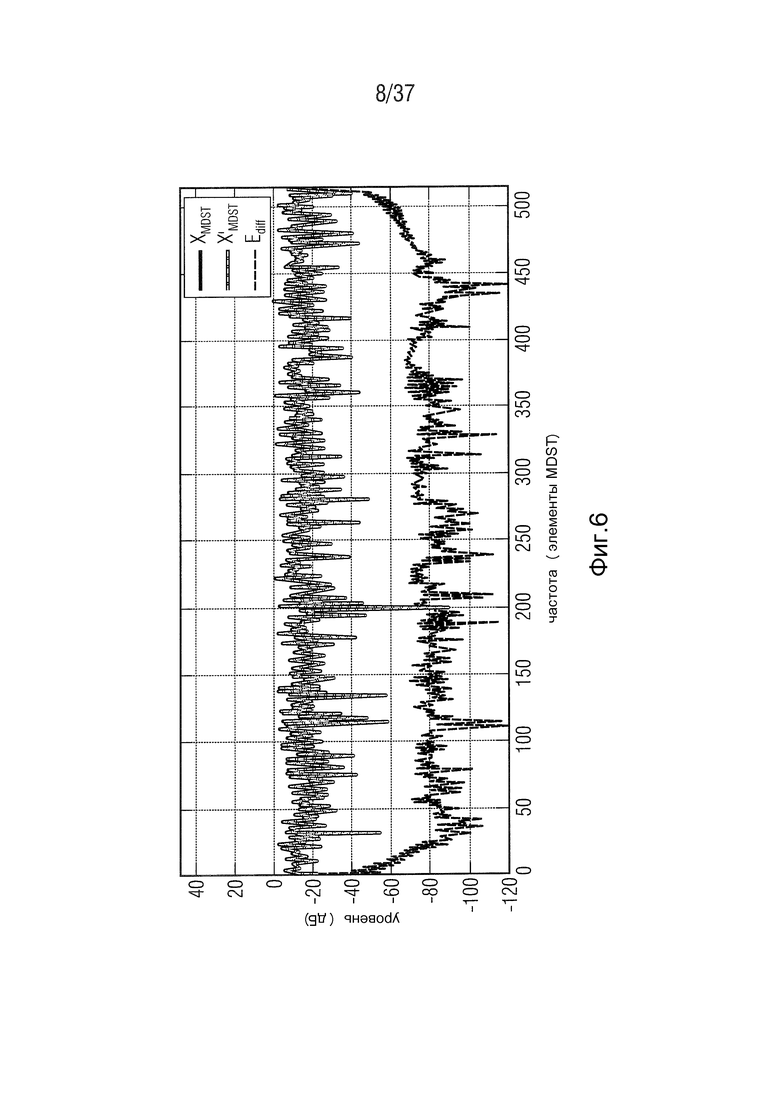
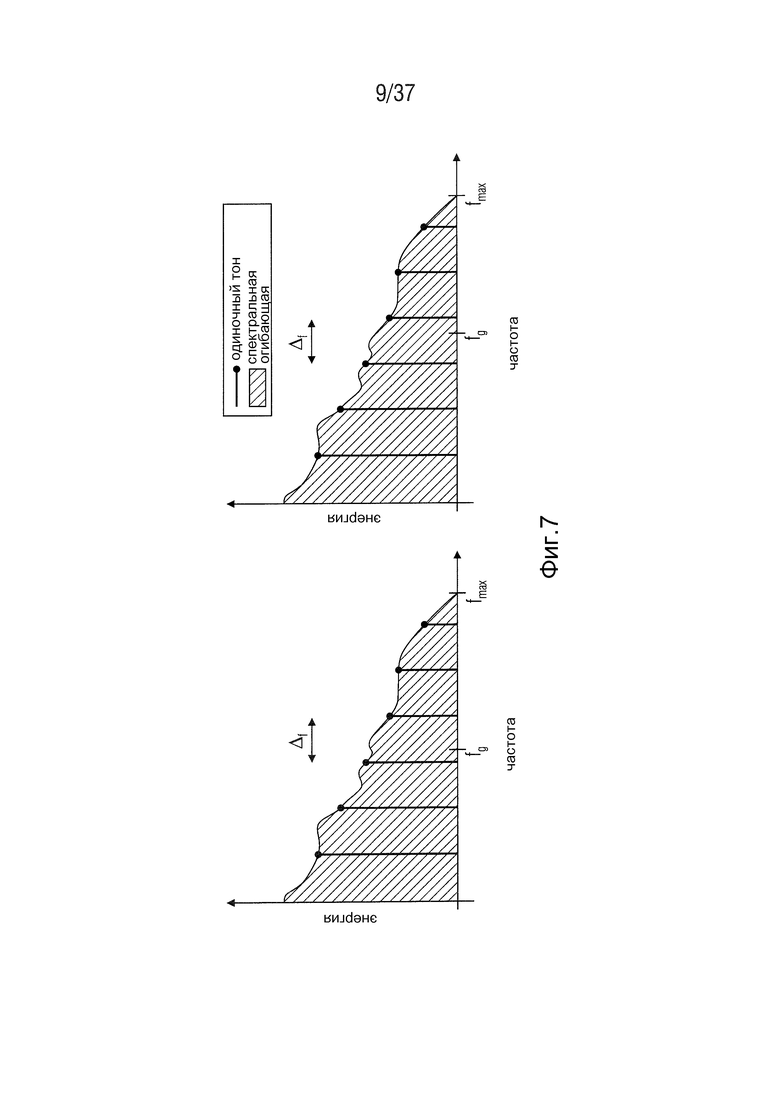
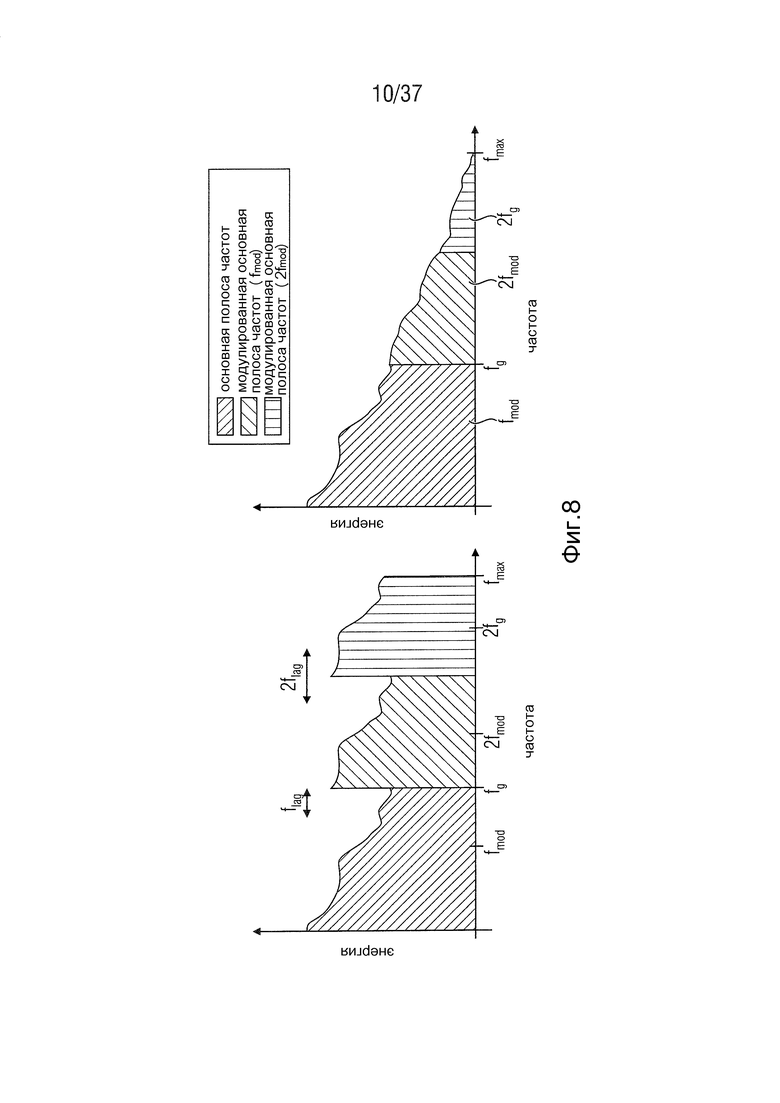
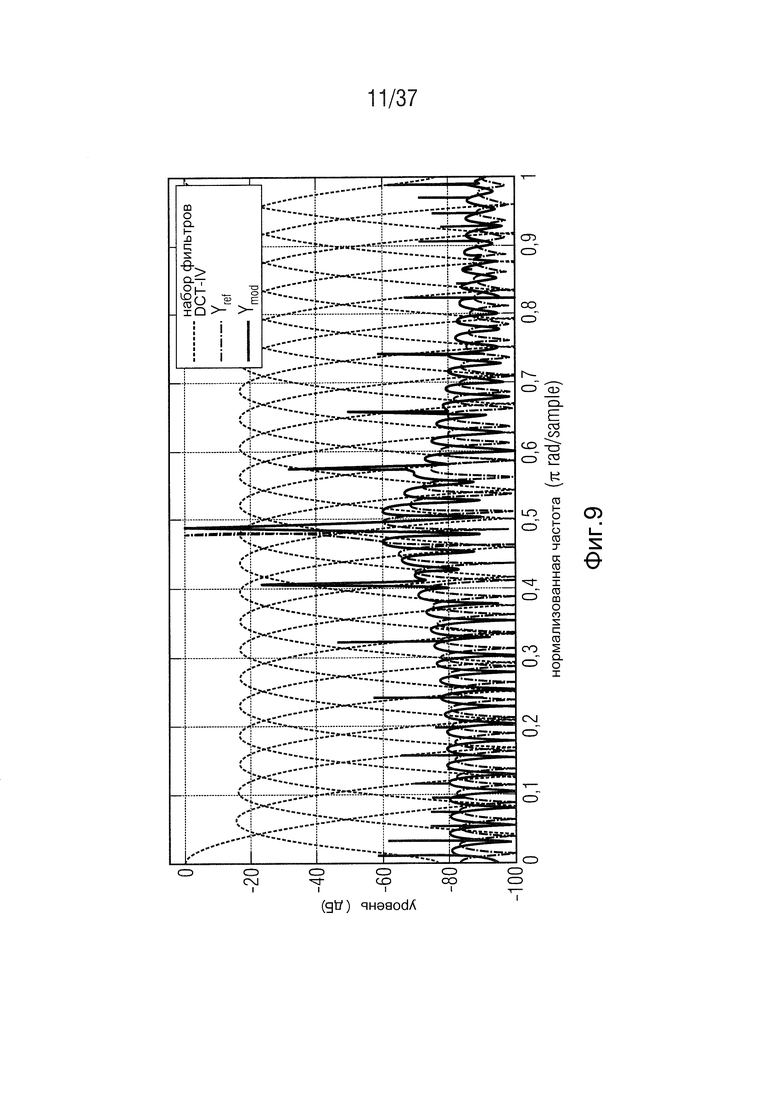
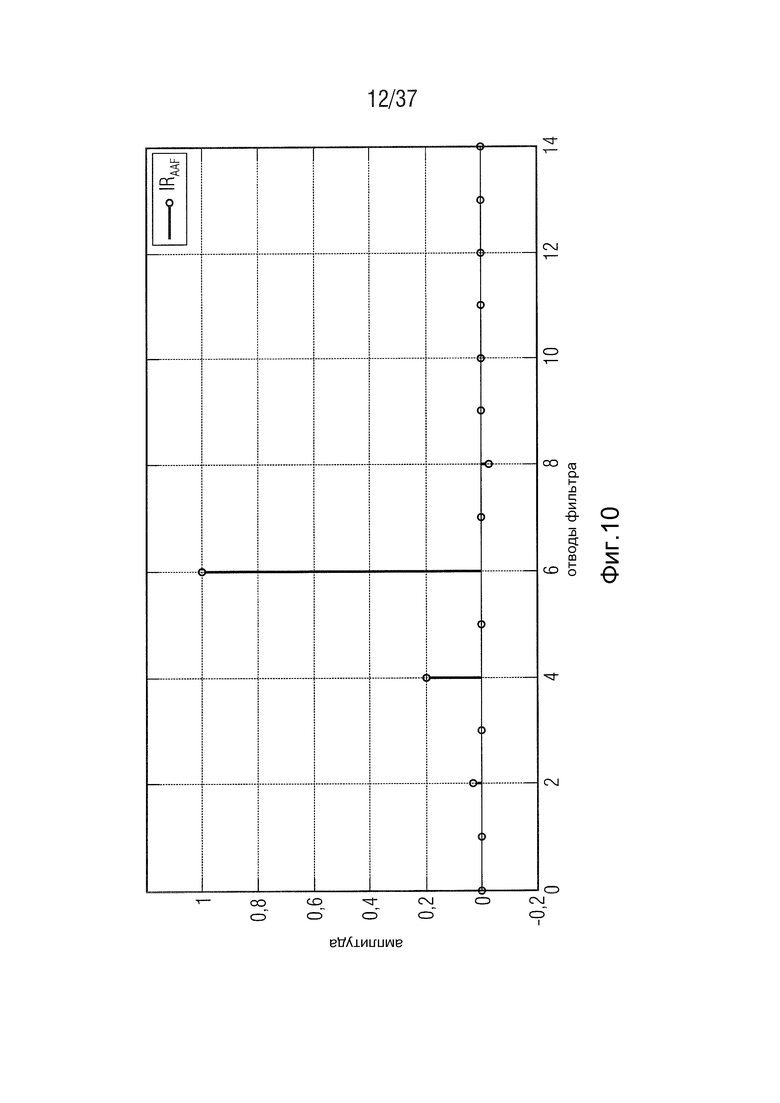
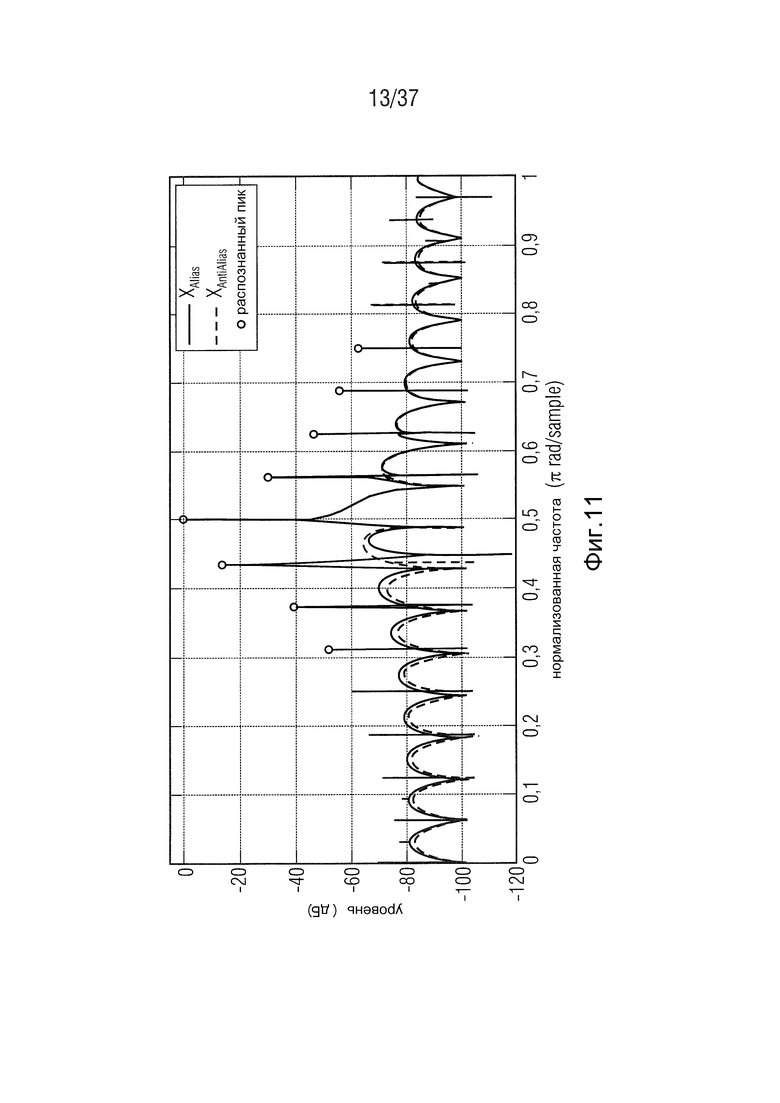
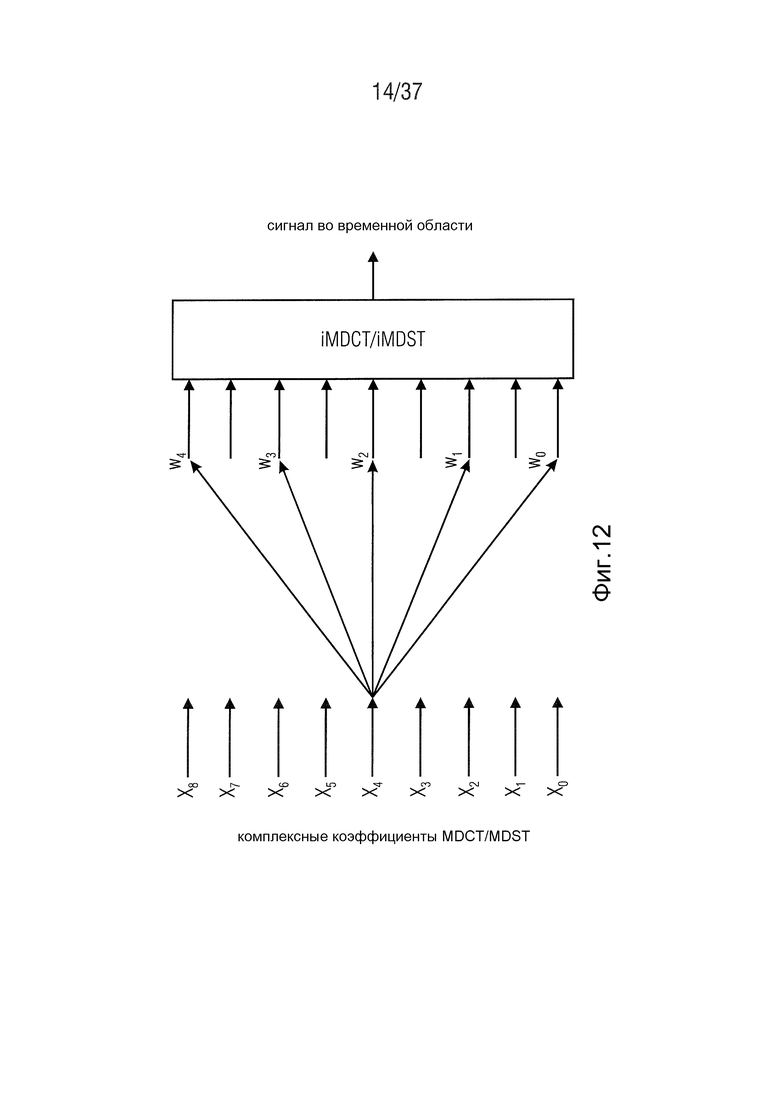
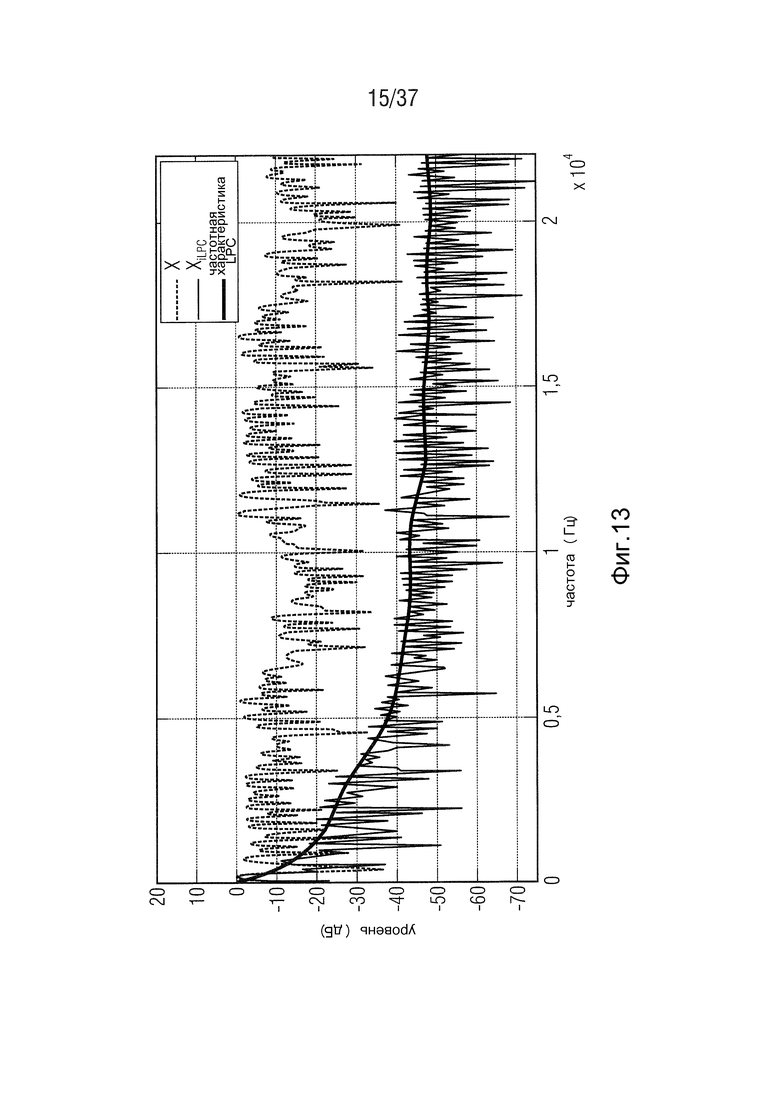
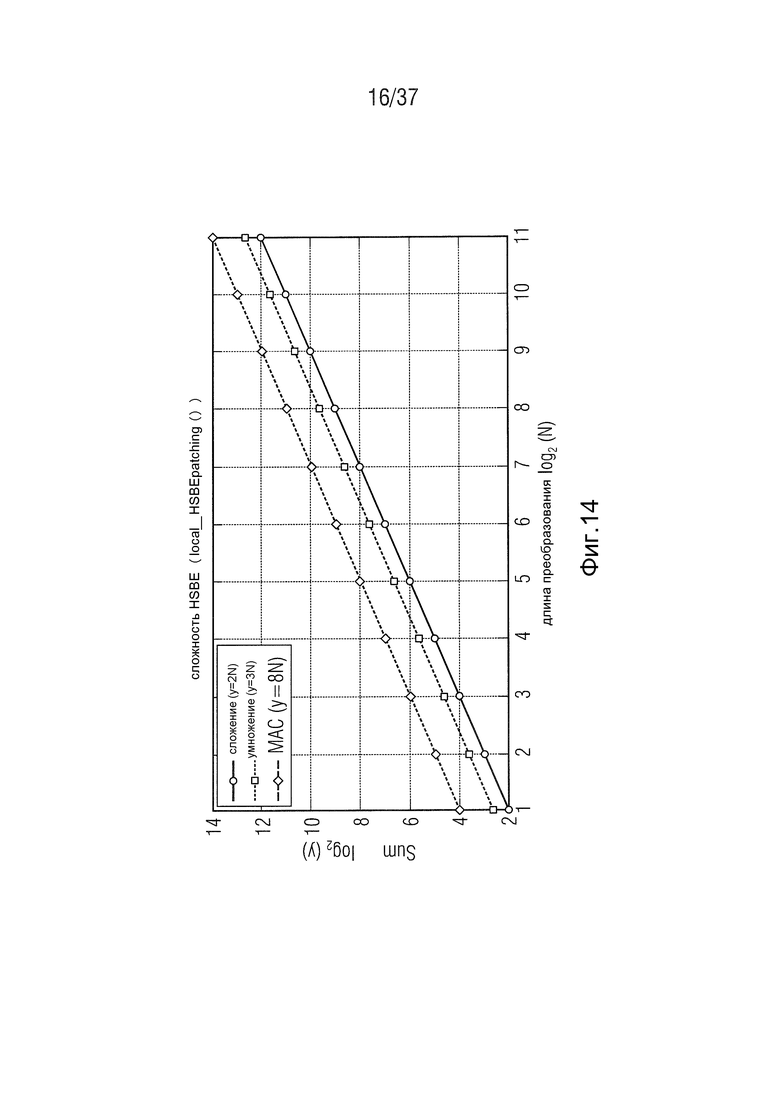
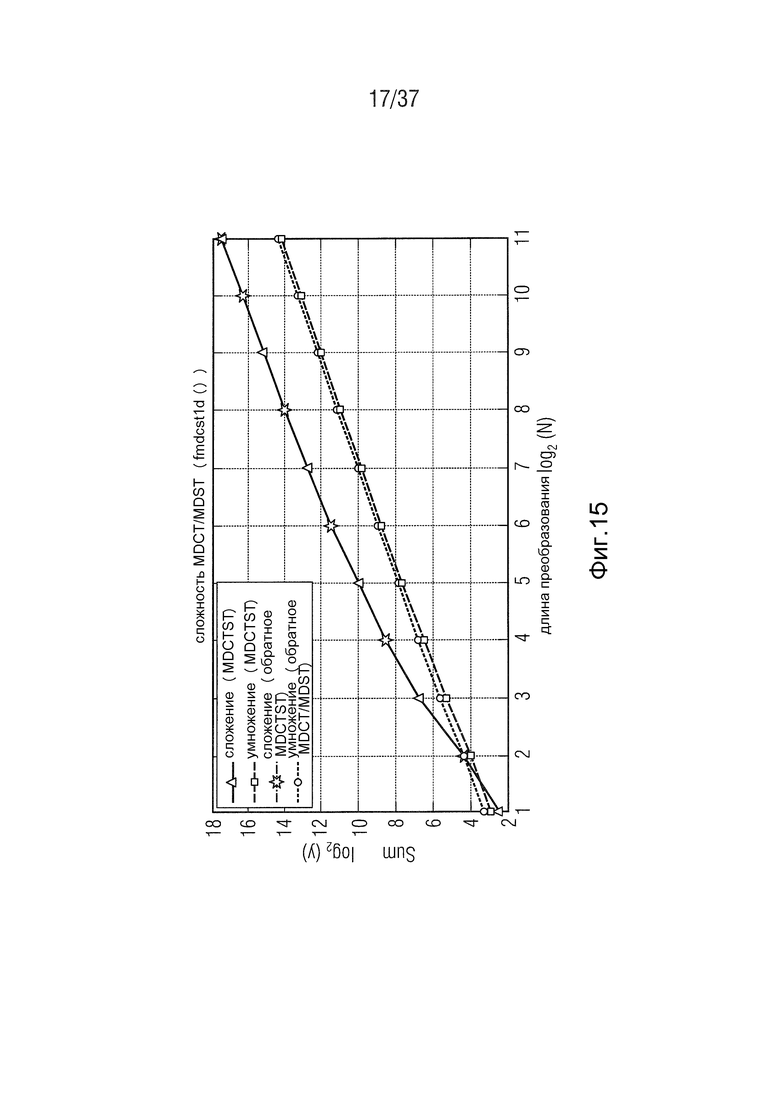
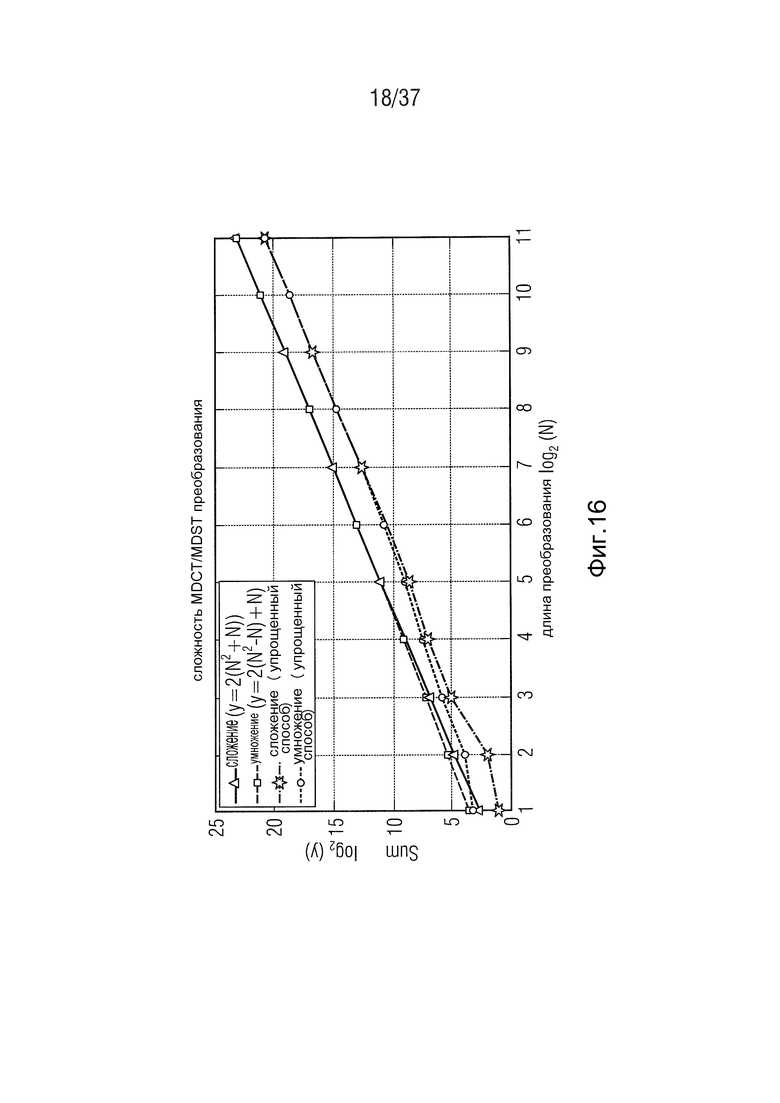
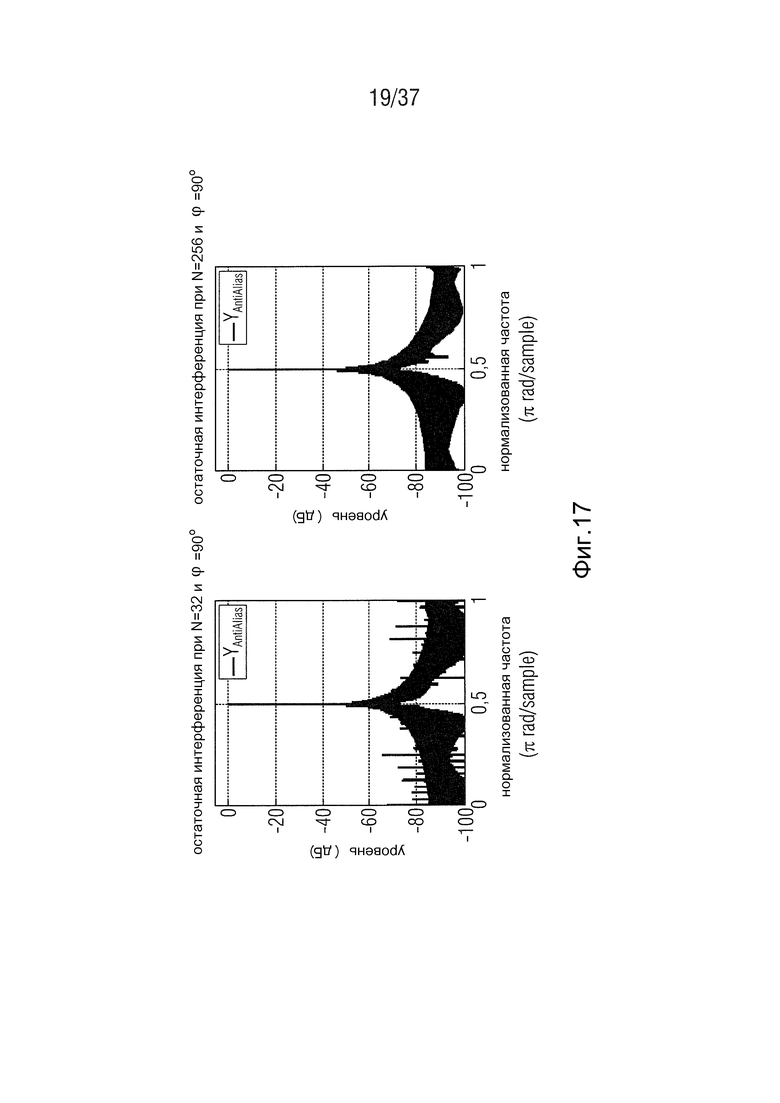

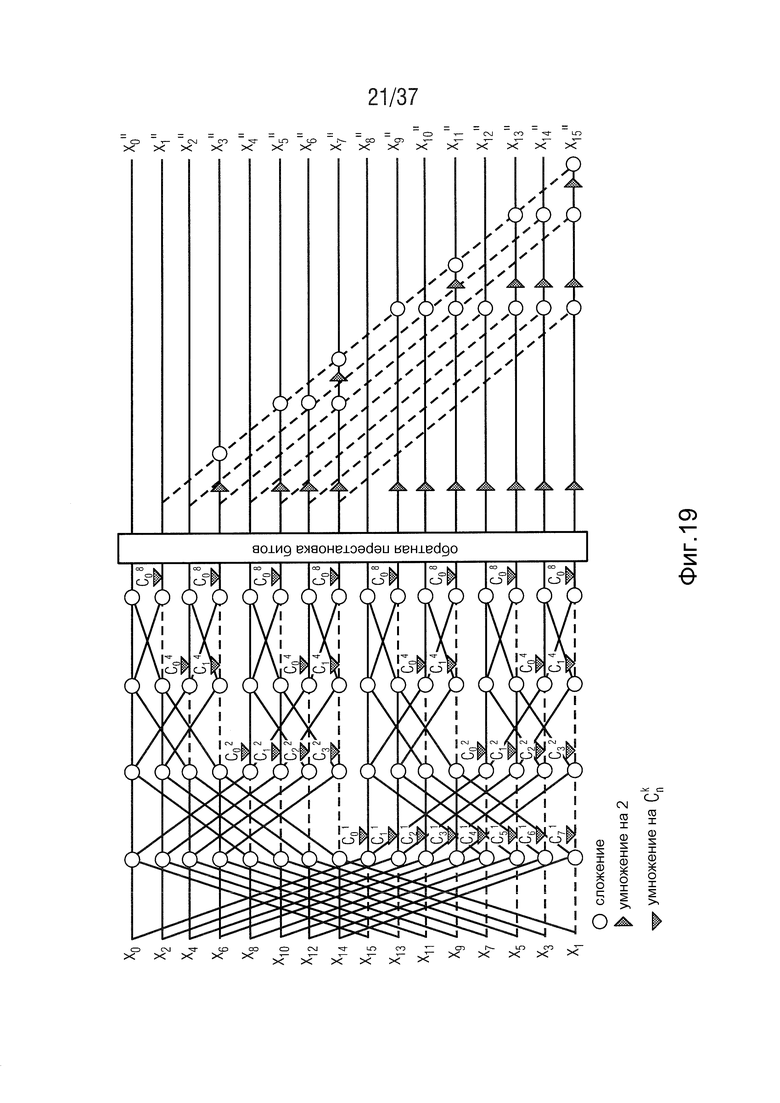
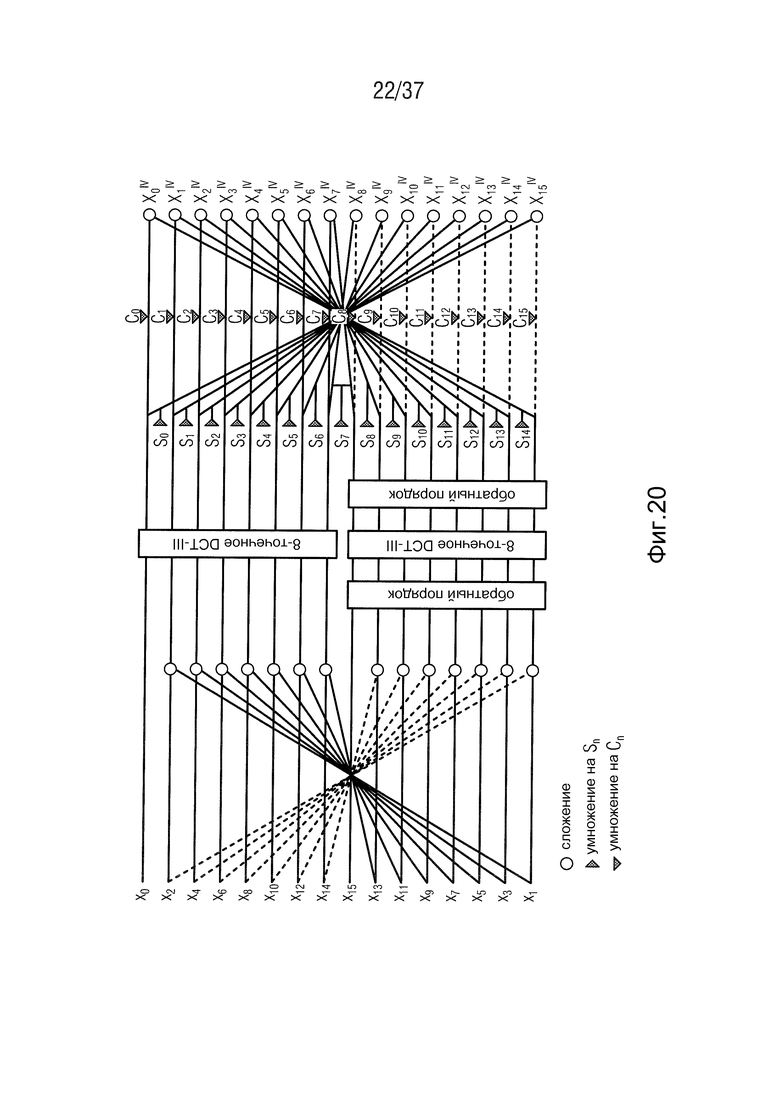
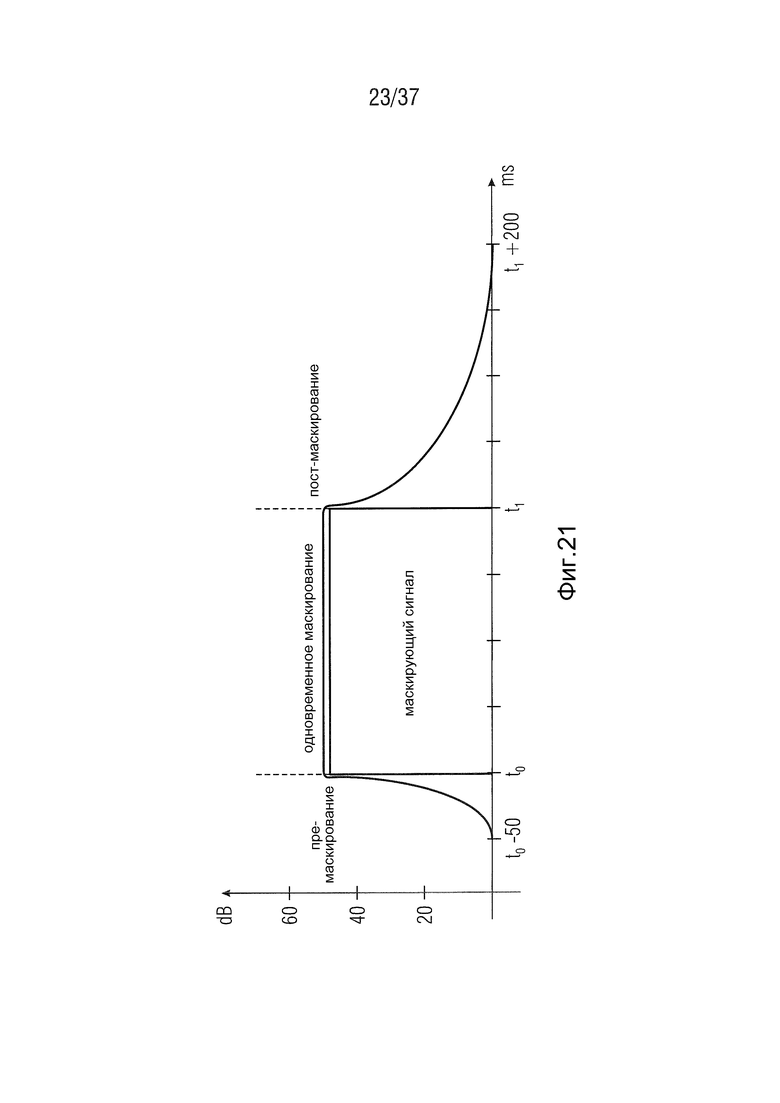
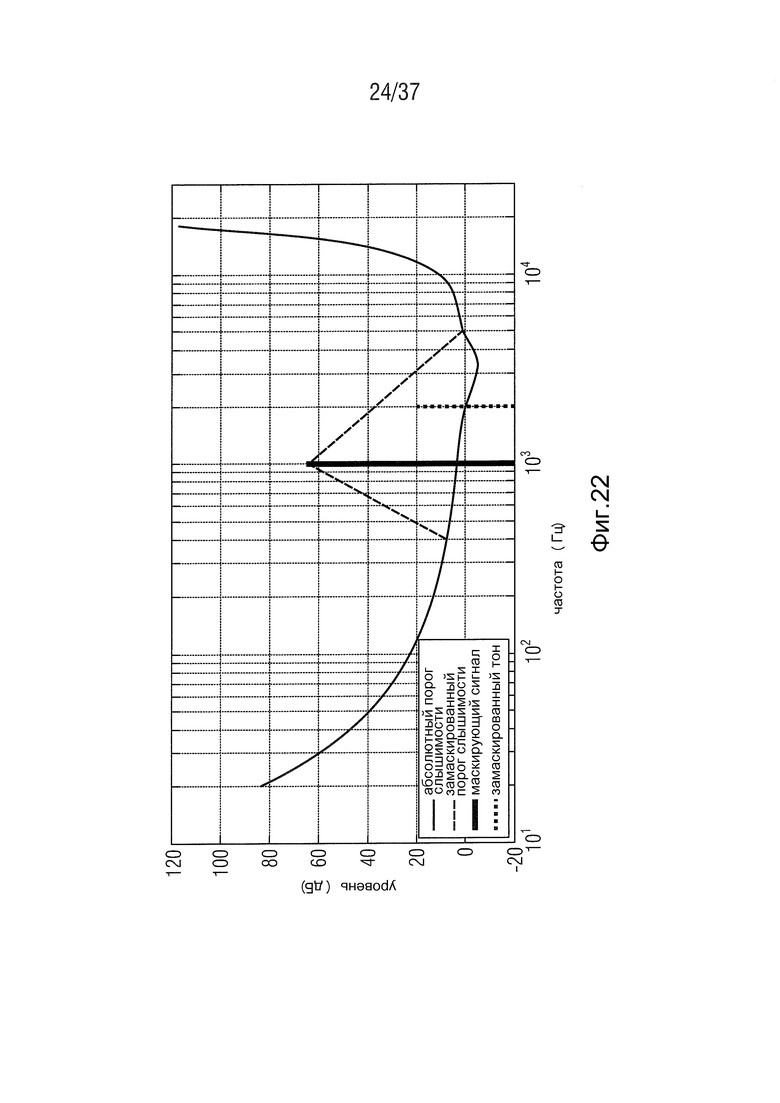
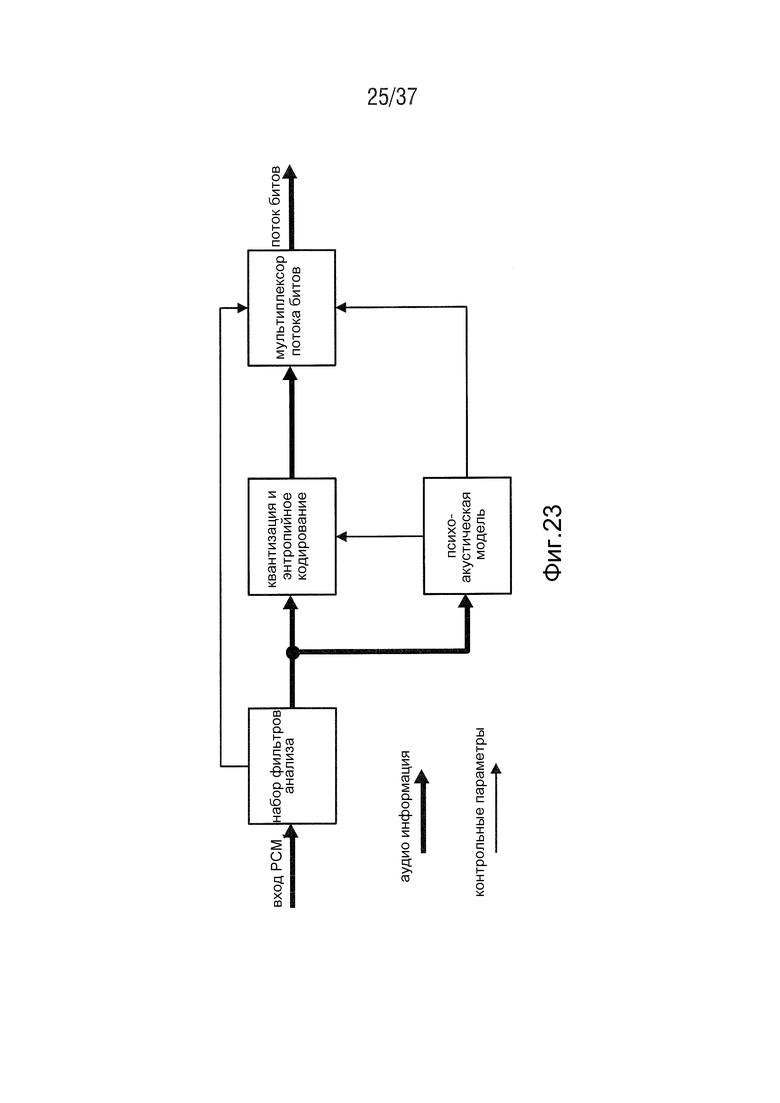
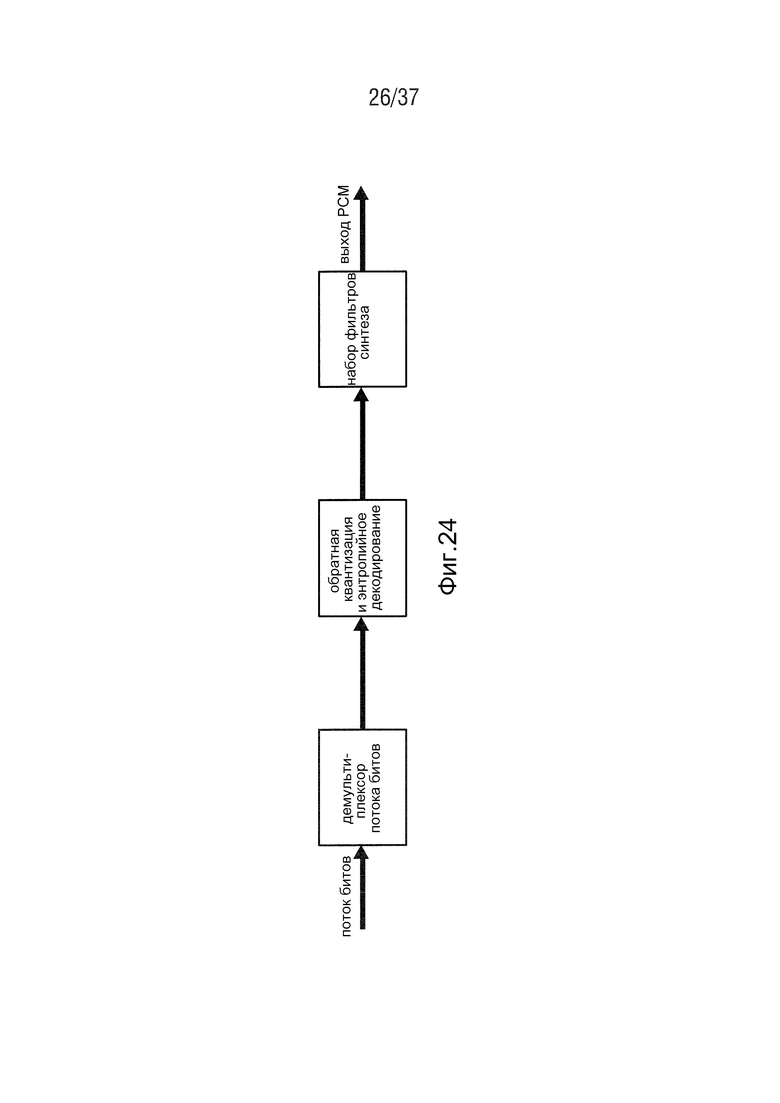
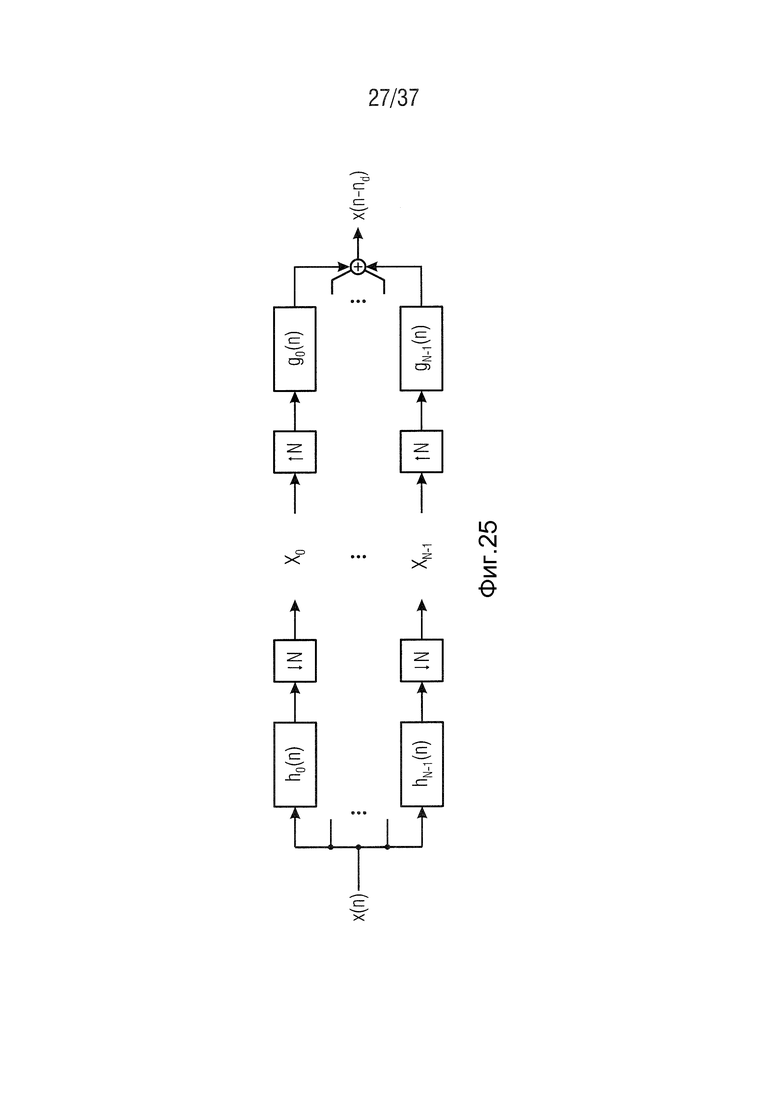
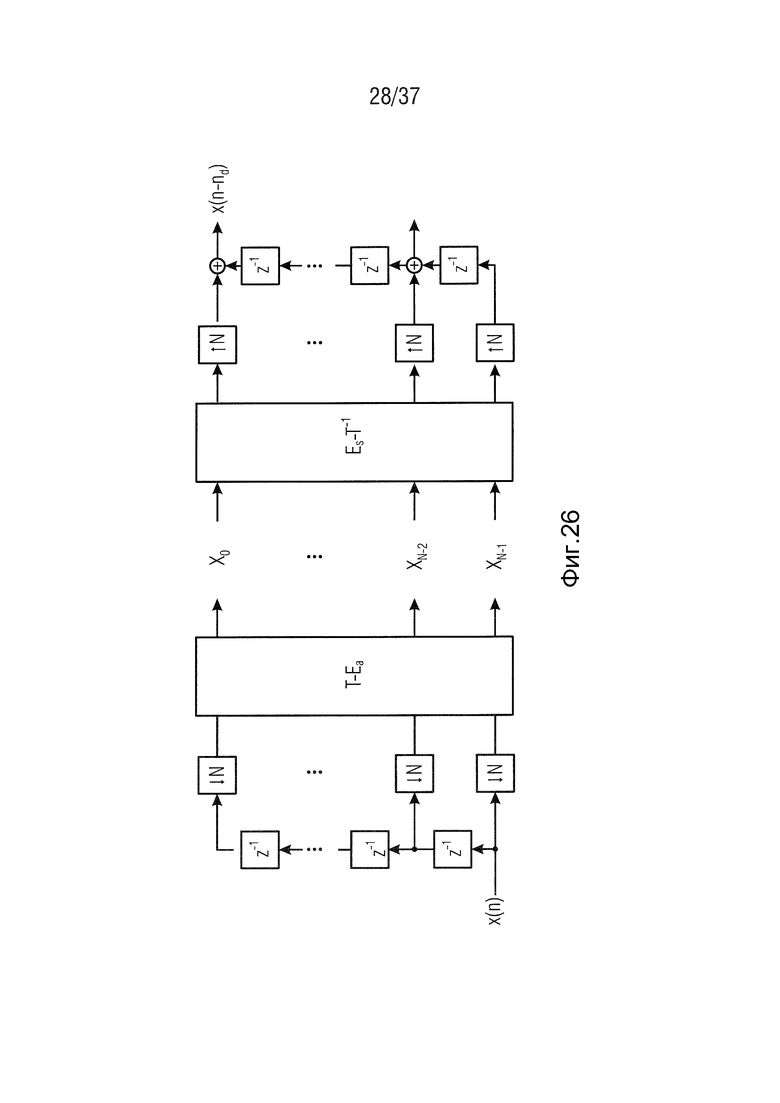
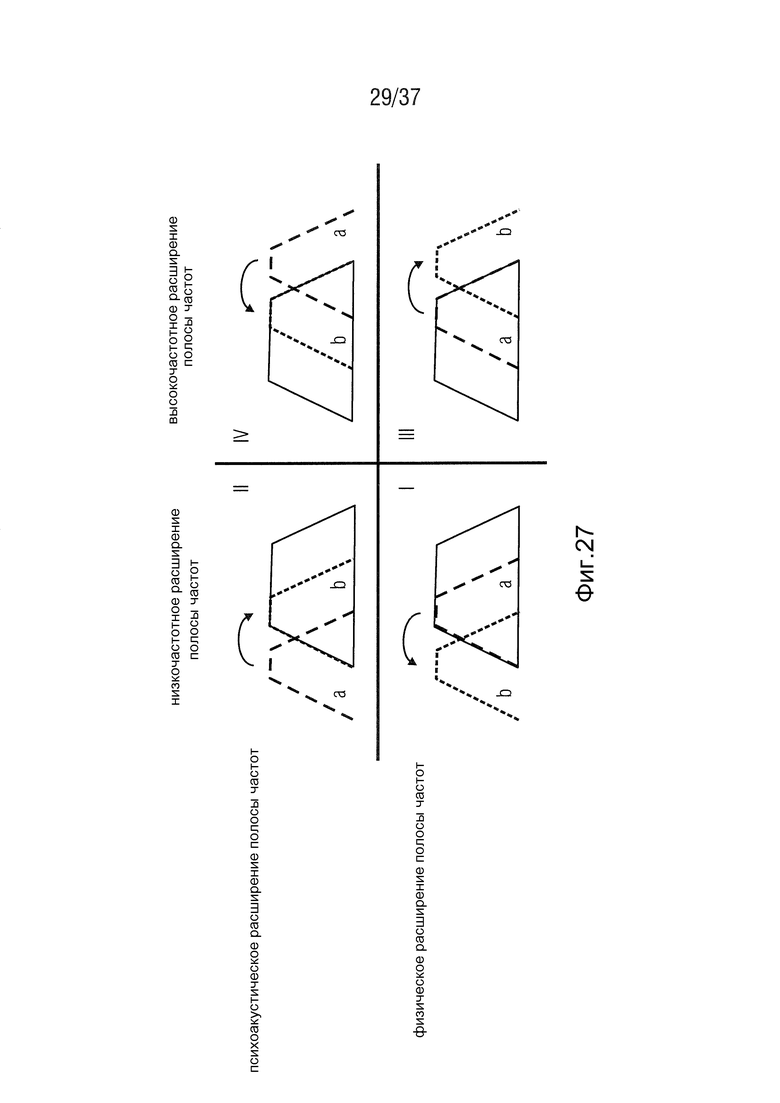
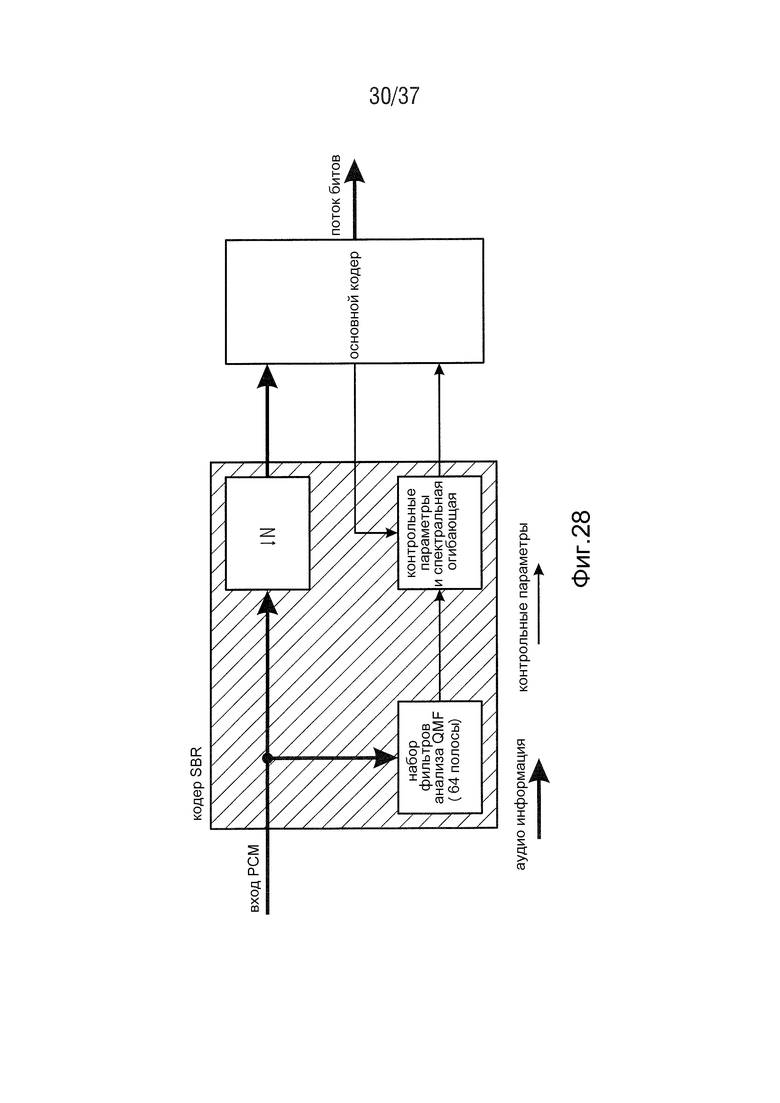
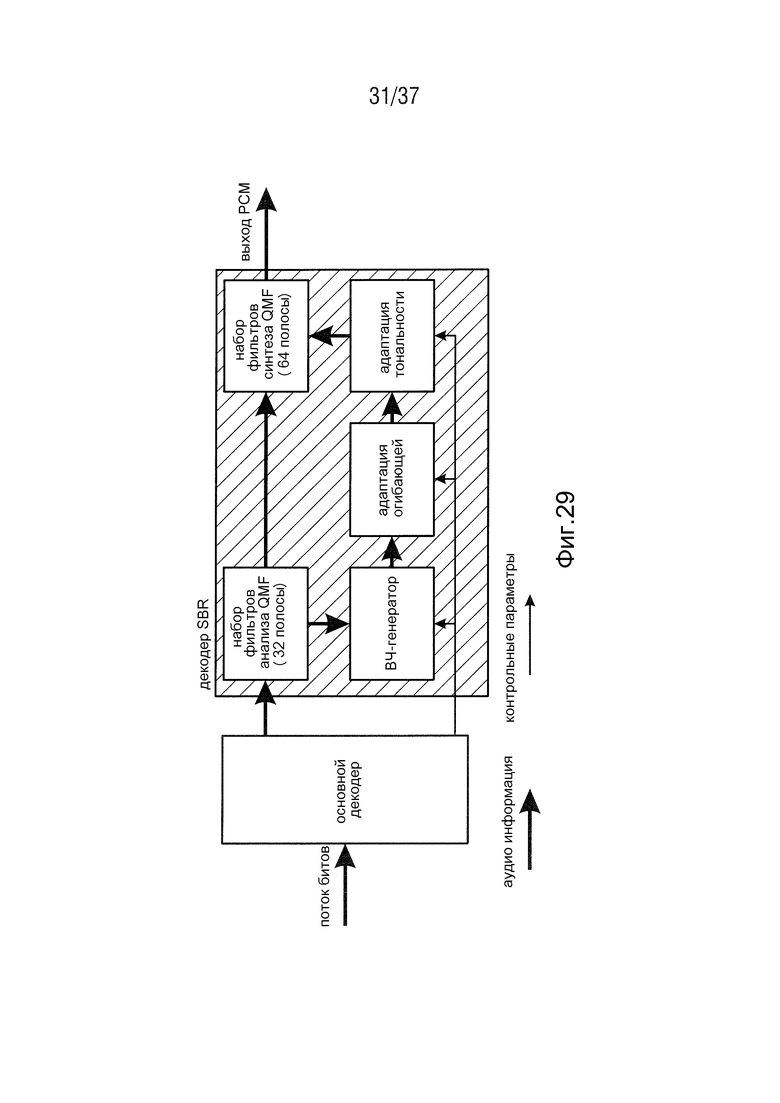
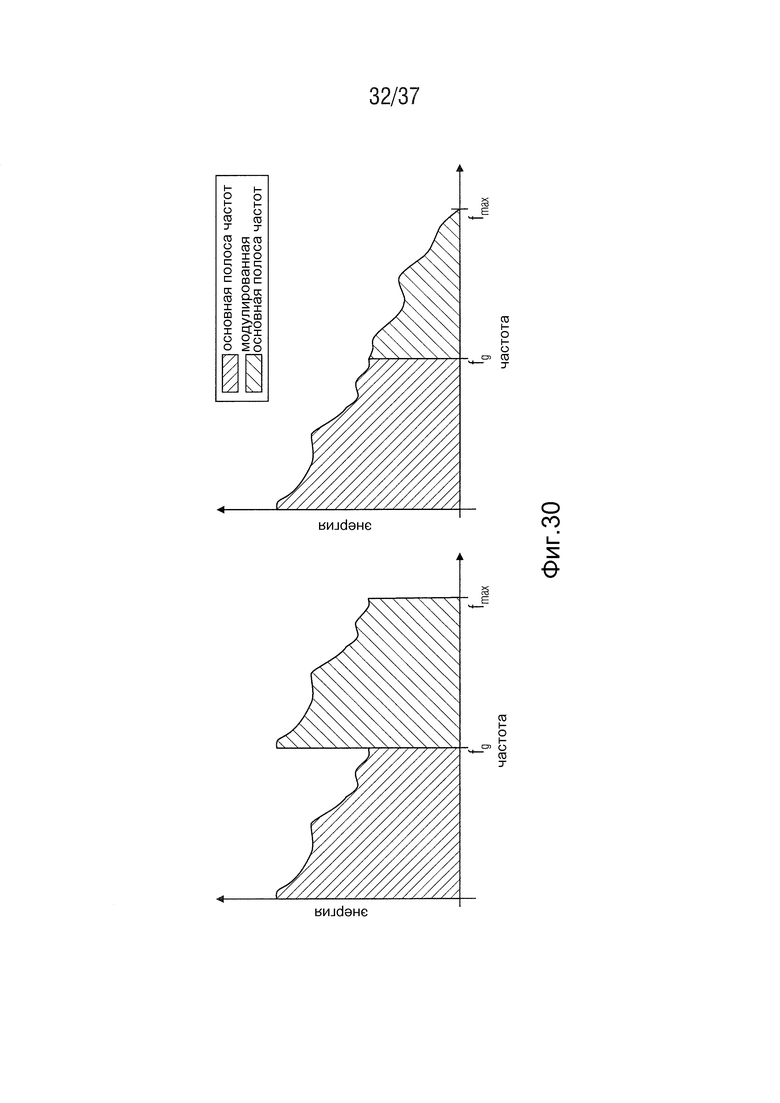
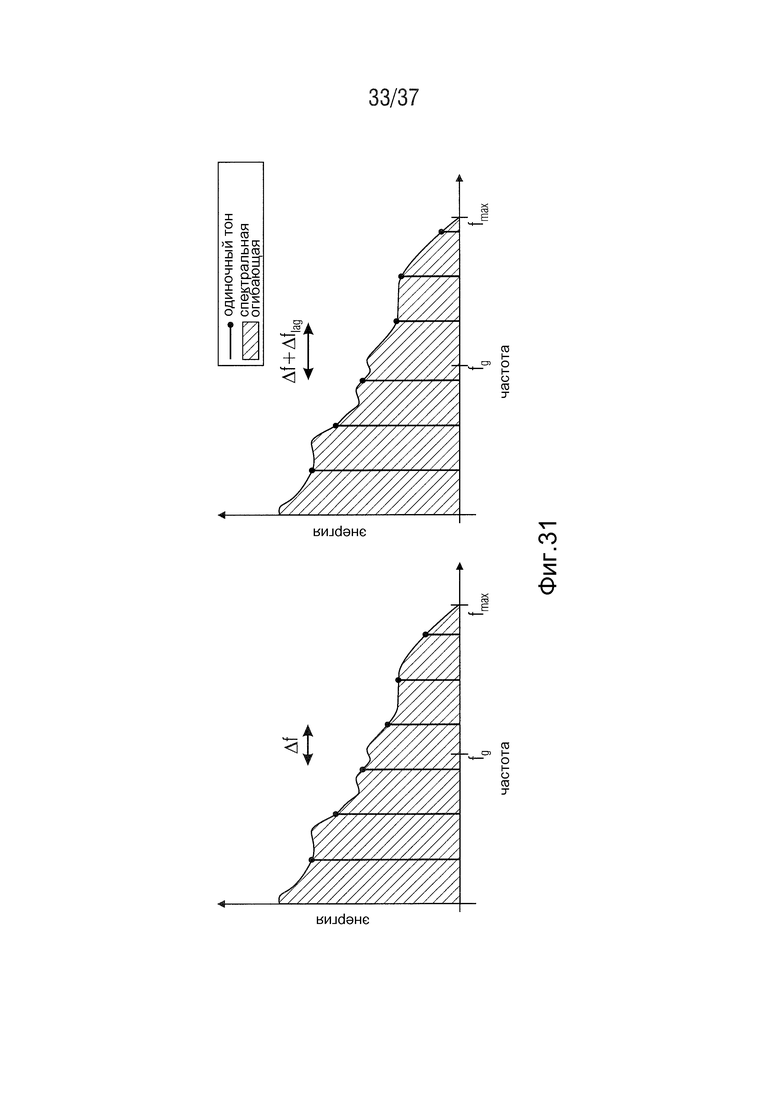
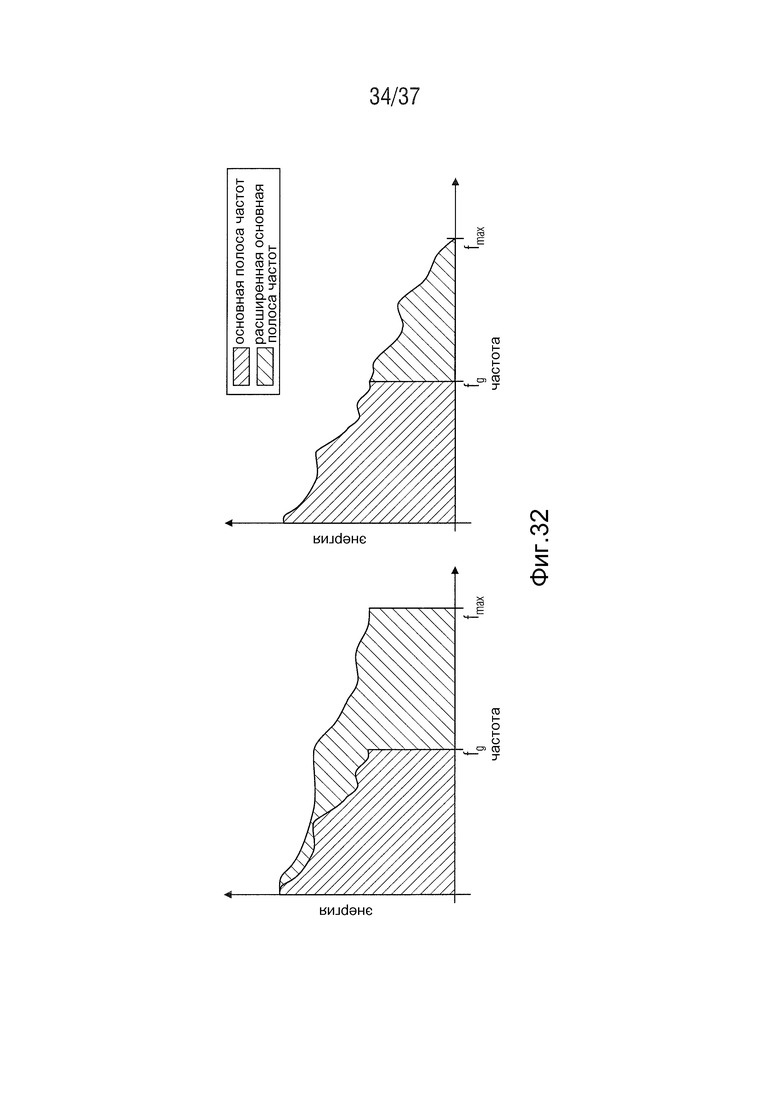
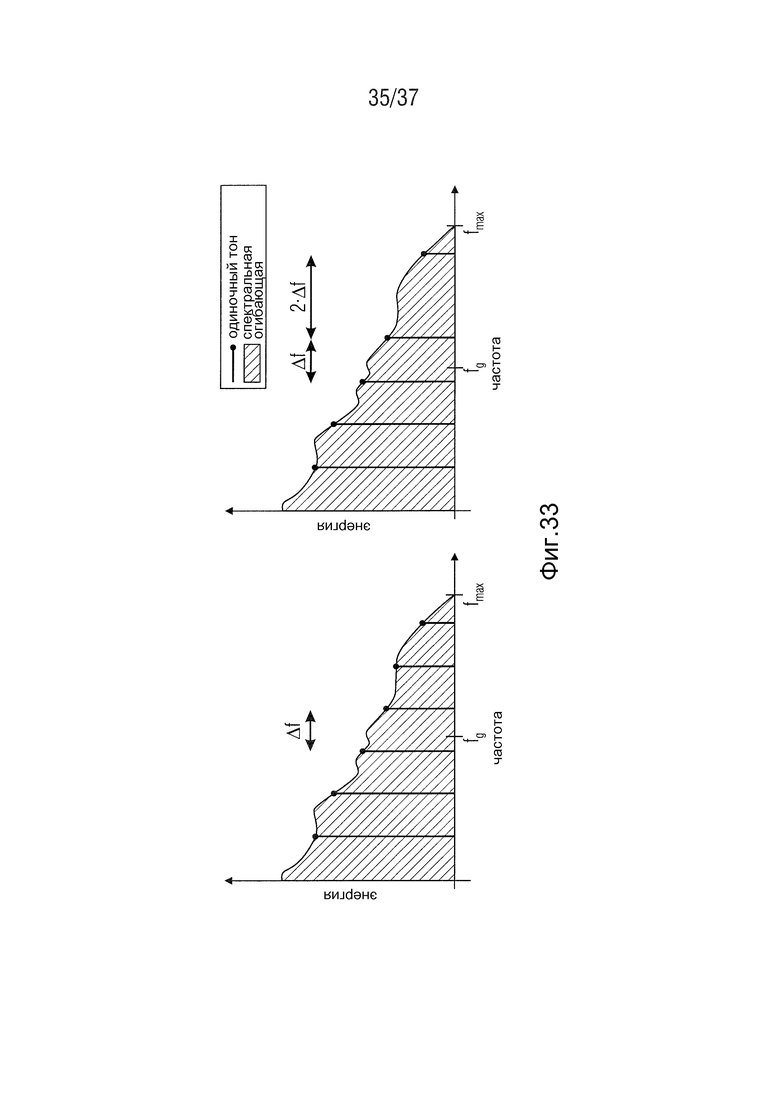
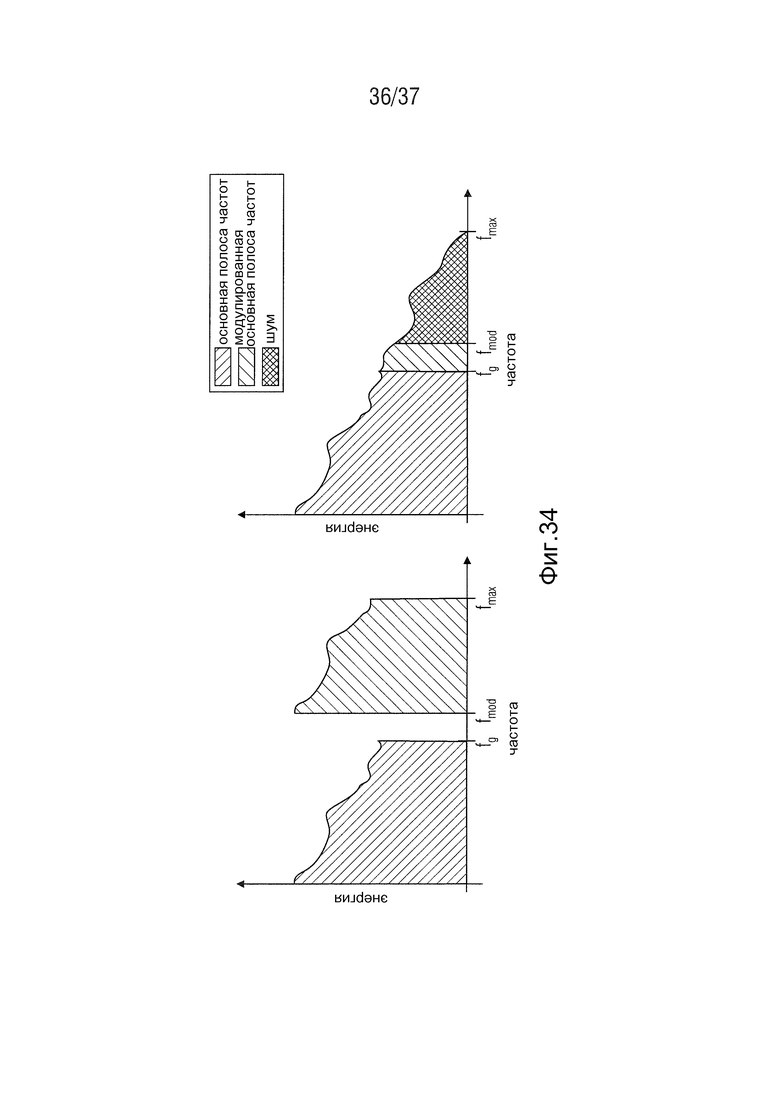
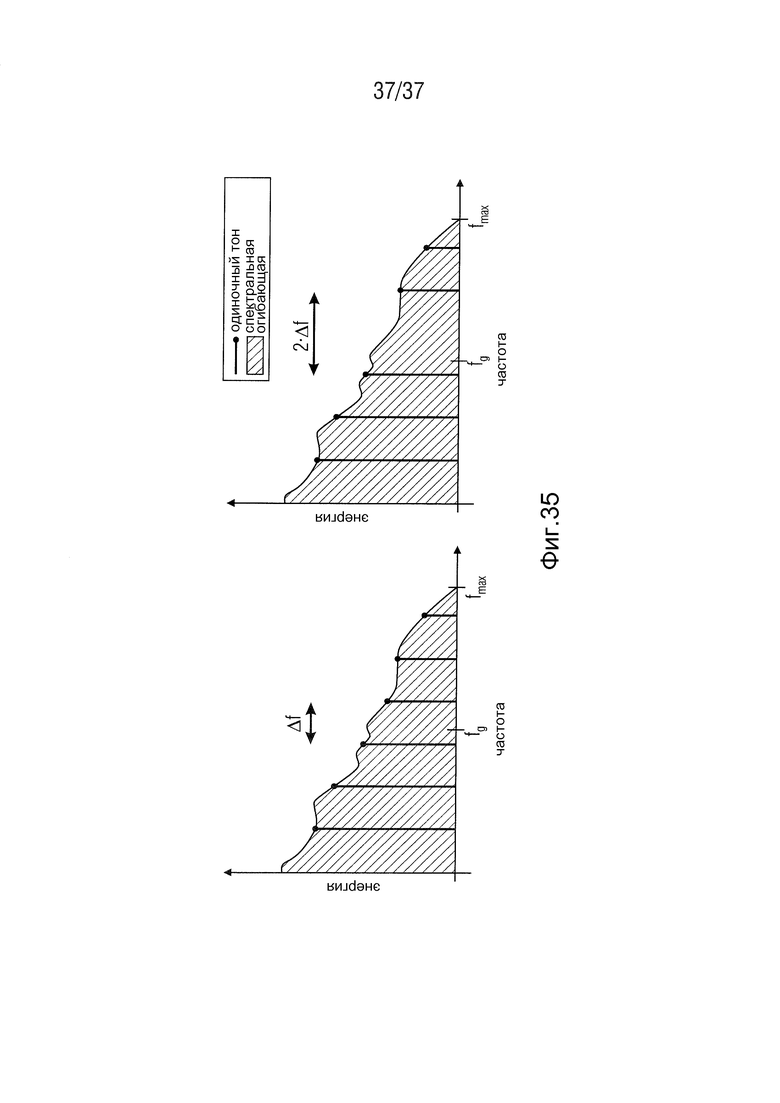
Изобретение относится к обработке аудиосигналов и предназначено для для произвольных сдвигов частоты в области поддиапазонов. Технический результат - повышение качества воспроизведения аудиосигнала. Устройство для формирования сдвинутого по частоте аудиосигнала, основанного на входном аудиосигнале, содержит интерфейс и блок сдвига частоты. Интерфейс выполнен с возможностью получения входного аудиосигнала. Блок сдвига частоты выполнен с возможностью формирования сдвинутого по частоте аудиосигнала. Блок сдвига частоты дополнительно выполнен с возможностью формирования одного из значений второго поддиапазона на основе одного из значений первого поддиапазона так, что второй фазовый угол этого значения второго поддиапазона отличается от первого фазового угла этого значения первого поддиапазона на разность фазового угла, причем разность фазового угла зависит от частотной информации, указывающей, на какую разность частот должен быть сдвинут входной аудиосигнал для того, чтобы получить сдвинутый по частоте аудиосигнал, а также зависит от ширины полосы частот одного из первых поддиапазонов. 3 н. и 21 з.п. ф-лы, 37 ил., 5 табл.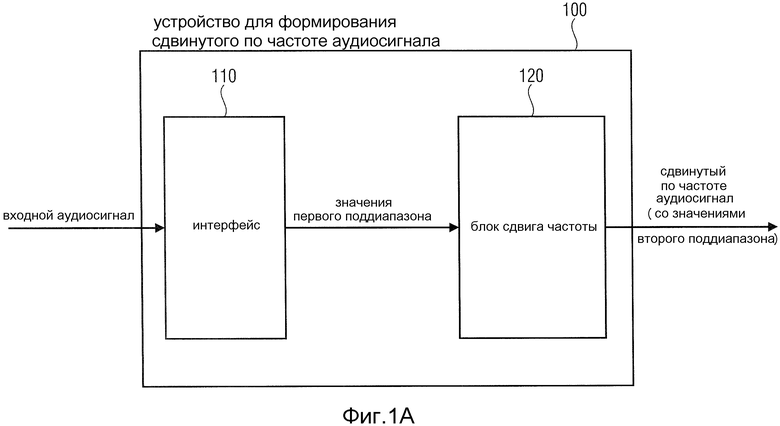
1. Устройство (100; 150; 300) для формирования сдвинутого по частоте аудиосигнала на основе входного аудиосигнала, в котором входной аудиосигнал для множества первых поддиапазонов может быть представлен одним или несколькими значениями первых поддиапазонов, причем устройство (100; 150; 300) включает в себя:
интерфейс (110; 310) для получения входного аудиосигнала, и
блок (120; 320) сдвига частоты для формирования сдвинутого по частоте аудиосигнала, который для множества вторых поддиапазонов включает в себя одно или несколько значений каждого из вторых поддиапазонов,
в котором каждое из значений первого и второго поддиапазона включает в себя информацию об одном соответствующем фазовом угле, и
в котором блок (120; 320) сдвига частоты выполнен с возможностью формирования одного из значений второго поддиапазона на основе одного из значений первого поддиапазона так, что второй фазовый угол упомянутого значения второго поддиапазона может отличаться от первого фазового угла упомянутого значения первого поддиапазона на разность фазового угла, причем разность фазового угла зависит от частотной информации, указывающей, на какую разницу частот должен быть сдвинут входной аудиосигнал для получения сдвинутого по частоте аудиосигнала, и причем разность фазового угла зависит от ширины полосы частот одного из первых поддиапазонов.
2. Устройство (100; 150; 300) по п. 1, в котором блок (120; 320) сдвига частоты выполнен с возможностью определения одного из первых поддиапазонов на основе частотной информации для каждого из вторых поддиапазонов, причем блок (120; 320) сдвига частоты дополнительно выполнен с возможностью формирования одного или нескольких из значений соответствующего второго поддиапазона на основе одного или нескольких из значений соответствующего первого определенного поддиапазона, причем блок (120; 320) сдвига частоты дополнительно выполнен с возможностью
формирования каждого одного из значений второго поддиапазона на основе каждого одного из значений соответствующего первого поддиапазона, определенного так, что информация о фазовом угле соответствующего значения второго поддиапазона зависит от информации о фазовом угле соответствующего значения первого поддиапазона и от отношения разности частот, на которую должен быть сдвинут входной аудиосигнал, и ширины полосы частот этого поддиапазона.
3. Устройство (100; 150; 300) по п. 1,
в котором каждое из значений первого поддиапазона и каждое из значений второго поддиапазона могут быть представлены как комплексные числа,
в котором блок (120, 320) сдвига частоты выполнен с возможностью определения значения результата комплексной экспоненциальной функции, и
в котором блок (120; 320) сдвига частоты выполнен с возможностью формирования по меньшей мере одного из значений второго поддиапазона на основе одного из значений первого поддиапазона путем умножения первого комплексного числа, представляющего это одно из значений первого поддиапазона на значение результата для того, чтобы получить второе комплексное число, представляющее это одно из значений второго поддиапазона.
4. Устройство (100; 150; 300) по п. 3,
в котором блок (120; 320) сдвига частоты выполнен с возможностью определения значения результата комплексной экспоненциальной функции следующего вида:
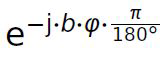 ,
,
где j является мнимой единицей, b является целым числом, а 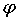
5. Устройство (100; 150; 300) по п. 1,
в котором блок (120; 320) сдвига частоты выполнен с возможностью формирования этого одного из значений второго поддиапазона на основе этого одного из значений первого
поддиапазона, и
в котором значения первого поддиапазона представляют собой первые коэффициенты MDCT входного аудиосигнала, которые являются коэффициентами модифицированного дискретного косинусоидального преобразования входного аудиосигнала, или в котором значения первого поддиапазона представляют собой первые коэффициенты QMF входного аудиосигнала, которые являются коэффициентами преобразования QMF входного аудиосигнала.
6. Устройство (100; 150; 300) по п. 1,
которое дополнительно включает в себя блок (315) преобразования MDCT/MDST,
в котором блок (315) преобразования MDCT/MDST выполнен с возможностью получения одного или нескольких первых коэффициентов MDCT входного аудиосигнала, которые являются коэффициентами модифицированного дискретного косинусоидального преобразования входного аудиосигнала,
в котором блок (315) преобразования MDCT/MDST выполнен с возможностью определения на основе одного или нескольких из первых коэффициентов MDCT входного аудиосигнала одного или нескольких первых коэффициентов MDST входного аудиосигнала, которые являются коэффициентами модифицированного дискретного синусоидального преобразования, и
в котором блок (120; 320) сдвига частоты выполнен с возможностью формирования каждого из значений второго поддиапазона на основе каждого одного из значений первого поддиапазона, причем каждое из значений первого поддиапазона основано на одном из первых коэффициентов MDCT и одном из первых коэффициентов MDST, определенного на основе этого первого коэффициента MDCT.
7. Устройство (100; 150; 300) по п. 6,
в котором блок (120; 320) сдвига частоты выполнен с возможностью формирования каждого из значений второго поддиапазона на основе каждого одного из значений первого поддиапазона, причем каждый из первых коэффициентов MDCT и каждый из первых коэффициентов MDST имеют вещественное значение, и причем каждое из значений первого поддиапазона представляет
сумму одного из первых коэффициентов MDCT и одного из первых коэффициентов MDST, умноженного на мнимую единицу j, который определен на основе этого первого коэффициента MDCT.
8. Устройство (100; 150; 300) по п. 6,
в котором блок (315) преобразования MDCT/MDST выполнен с возможностью определения одного или нескольких первых коэффициентов MDST входного аудиосигнала на основе одного или нескольких первых коэффициентов MDCT входного аудиосигнала,
в котором первые коэффициенты MDCT входного аудиосигнала могут быть представлены как матричные коэффициенты матрицы коэффициентов MDCT 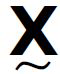 , которая включает в себя один или несколько столбцов,
, которая включает в себя один или несколько столбцов,
в котором входной аудиосигнал подразделен на блоки,
в котором каждый из столбцов матрицы коэффициентов MDCT 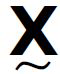 представляет один из блоков входного аудиосигнала,
представляет один из блоков входного аудиосигнала,
в котором каждый из столбцов матрицы коэффициентов MDCT 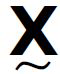 формирует спектр MDCT соответствующего блока входного аудиосигнала, и
формирует спектр MDCT соответствующего блока входного аудиосигнала, и
в котором блок (315) преобразования MDCT/MDST определяет матричные коэффициенты матрицы преобразования  так, что при матричном умножении матрицы преобразования
так, что при матричном умножении матрицы преобразования  на матрицу коэффициентов MDCT
на матрицу коэффициентов MDCT 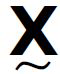 получается матрица коэффициентов MDST
получается матрица коэффициентов MDST  , матричные коэффициенты которой представляют собой первые коэффициенты MDST.
, матричные коэффициенты которой представляют собой первые коэффициенты MDST.
9. Устройство (100; 150; 300) по п. 6,
в котором блок (315) преобразования MDCT/MDST выполнен с возможностью определения одного или нескольких первых коэффициентов MDST входного аудиосигнала на основе одного или нескольких первых коэффициентов MDCT входного аудиосигнала,
в котором первые коэффициенты MDCT входного аудиосигнала могут быть представлены как матричные коэффициенты матрицы коэффициентов MDCT 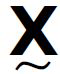 , которая включает в себя один или несколько столбцов,
, которая включает в себя один или несколько столбцов,
в котором входной аудиосигнал подразделен на блоки, причем
каждый из столбцов матрицы коэффициентов MDCT 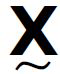 представляет один из блоков входного аудиосигнала,
представляет один из блоков входного аудиосигнала,
и в котором блок (315) преобразования MDCT/MDST выполнен с возможностью применения следующей формулы:
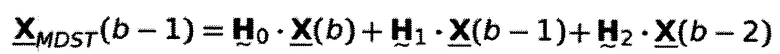
для того, чтобы определить первые коэффициенты MDST,
где 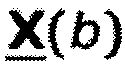 представляет собой b-й столбец матрицы
представляет собой b-й столбец матрицы 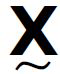 ,
,
где 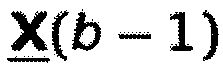 представляет собой b-1-й столбец матрицы
представляет собой b-1-й столбец матрицы 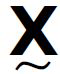 ,
,
где 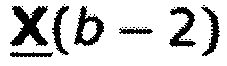 представляет собой b-2-й столбец матрицы
представляет собой b-2-й столбец матрицы 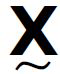 ,
,
где  представляет собой первую подматрицу,
представляет собой первую подматрицу,
где 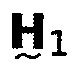 представляет собой вторую подматрицу,
представляет собой вторую подматрицу,
где 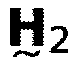 представляет собой третью подматрицу, и
представляет собой третью подматрицу, и
где  представляет собой спектр MDST блока b-1, который включает в себя первые коэффициенты MDST.
представляет собой спектр MDST блока b-1, который включает в себя первые коэффициенты MDST.
10. Устройство (100; 150; 300) по п. 9,
в котором блок (315) преобразования MDCT/MDST выполнен с возможностью применения следующей формулы:
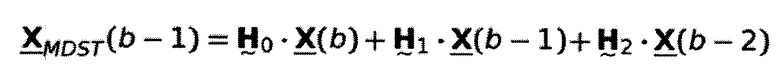
для того, чтобы определить первые коэффициенты MDST,
в котором два или несколько матричных коэффициентов первой подматрицы  имеют значение 0, в котором два или несколько матричных коэффициентов второй подматрицы
имеют значение 0, в котором два или несколько матричных коэффициентов второй подматрицы 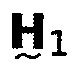 имеют значение 0, и в котором два или больше матричных коэффициентов третьей подматрицы
имеют значение 0, и в котором два или больше матричных коэффициентов третьей подматрицы 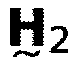 имеют значение 0.
имеют значение 0.
11. Устройство (100; 150; 300) по п. 9,
в котором блок (315) преобразования MDCT/MDST выполнен с возможностью применения следующей формулы:
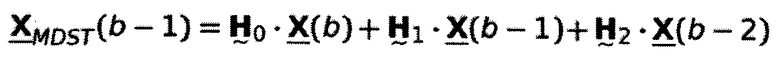
для того, чтобы определить первые коэффициенты MDST,
в котором вторая субматрица 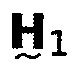 имеет следующий вид:
имеет следующий вид:

где «...» означает, что те же самые значения предыдущих матричных коэффициентов второй подматрицы 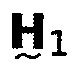 продолжаются в последующих матричных коэффициентах второй подматрицы
продолжаются в последующих матричных коэффициентах второй подматрицы 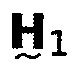 .
.
12. Устройство (100; 150; 300) по п. 1, причем устройство (100; 150; 300) дополнительно включает в себя блок (330) фильтрации, причем блок (330) фильтрации выполнен с возможностью фильтрации значений второго поддиапазона путем применения фильтра, который включает в себя множество коэффициентов фильтрации, так что паразитные компоненты значений второго поддиапазона, образовавшиеся при формировании значений второго поддиапазона на основе значений первого поддиапазона, уменьшаются.
13. Устройство (100; 150; 300) по п. 12,
в котором блок (120; 320) сдвига частоты выполнен с возможностью формирования этого одного из значений второго поддиапазона на основе одного из значений первого поддиапазона так, что второй фазовый угол этого значения второго поддиапазона отличается от первого фазового угла этого значения первого поддиапазона на разность фазового угла,
в котором блок (330) фильтрации выполнен с возможностью фильтрации значений второго поддиапазона путем применения фильтра, и в котором один или несколько из коэффициентов фильтрации зависят от разности фазового угла.
14. Устройство (100; 150; 300) по п. 13,
причем устройство (100; 150; 300) дополнительно включает в себя память или базу данных,
в котором один или несколько из коэффициентов фильтрации зависят от разности фазового угла,
в котором блок (330) фильтрации выполнен с возможностью считывать коэффициенты фильтрации из памяти или базы данных в зависимости от разности фазового угла, и
в котором блок (330) фильтрации выполнен с возможностью фильтрации значений второго поддиапазона путем применения фильтра, который включает в себя считывание фильтра из памяти или базы данных.
15. Устройство (100; 150; 300) по п. 12,
в котором блок (330) фильтрации выполнен с возможностью фильтрации каждого из одного или нескольких значений второго поддиапазона каждого из вторых поддиапазонов для того, чтобы получить одно или несколько отфильтрованных значений поддиапазона для каждого из вторых поддиапазонов,
в котором блок (330) фильтрации выполнен с возможностью определения каждого из отфильтрованных значений поддиапазона путем вычисления суммы первого слагаемого, или одного, или нескольких дополнительных слагаемых,
в котором первое слагаемое представляет собой одно из значений второго поддиапазона одного из вторых поддиапазонов,
в котором одно или несколько дополнительных слагаемых представляют собой одно или несколько значений взвешенного поддиапазона, и
в котором блок (330) фильтрации выполнен с возможностью определения каждого из этих одного или нескольких значений взвешенного поддиапазона путем умножения одного из коэффициентов фильтрации на каждое одно дополнительное значение поддиапазона других дополнительных поддиапазонов.
16. Устройство (100; 150; 300) по п. 12,
в котором блок (330) фильтрации выполнен с возможностью фильтрации значений второго поддиапазона путем применения фильтра, который включает в себя множество коэффициентов фильтрации, таким образом, что паразитные компоненты значений второго поддиапазона уменьшаются,
в котором коэффициенты фильтрации имеют упорядоченную последовательность, причем в этой последовательности за каждым коэффициентом фильтра, не равным нулю, следует коэффициент фильтра, равный нулю.
17. Устройство (100; 150; 300) по п. 1, в котором интерфейс (110; 310) выполнен с возможностью получать частотную информацию, указывающую, на какую разницу частот должны быть сдвинуты значения первого поддиапазона входного аудиосигнала.
18. Устройство (100; 150; 300) по п. 1,
причем устройство (100; 150; 300) дополнительно включает в себя блок (340) преобразования синтеза, и
в котором блок преобразования синтеза выполнен с возможностью получения сдвинутого по частоте аудиосигнала путем преобразования значений второго поддиапазона во множество отсчетов во временной области.
19. Устройство (150) по п. 1,
причем устройство (150) выполнено с возможностью формирования частотно-расширенного аудиосигнала,
которое выполнено с возможностью формирования частотно-расширенного аудиосигнала путем формирования устройством (150) значений второго поддиапазона сдвинутого по частоте аудиосигнала, причем частотно-расширенный аудиосигнал включает в себя значения первого поддиапазона входного аудиосигнала и значения второго поддиапазона сдвинутого по частоте аудиосигнала.
20. Устройство (150) по п. 19,
причем устройство (150) дополнительно включает в себя блок (340) преобразования синтеза, и
в котором блок преобразования синтеза выполнен с возможностью получения частотно-расширенного аудиосигнала путем преобразования значений первого поддиапазона и значений второго поддиапазона во множество отсчетов во временной области.
21. Устройство (150) по п. 19, причем устройство (150 дополнительно включает в себя блок (350) адаптации огибающей, выполненный с возможностью фильтрации частотно-расширенного аудиосигнала так, что спектральная огибающая накладывается на частотно-расширенный сигнал.
22. Устройство (150) по п. 21, причем устройство (150) блок (350) адаптации огибающей выполнен с возможностью фильтрации
частотно-расширенного аудиосигнала посредством обратного фильтрования с использованием коэффициентов LPC для наложения спектральной огибающей на частотно-расширенный сигнал.
23. Способ формирования сдвинутого по частоте аудиосигнала, основанного на входном аудиосигнале, в котором входной аудиосигнал для множества первых поддиапазонов может быть представлен одним или несколькими значениями первого поддиапазона, включающий в себя:
получение входного аудиосигнала, и
формирование сдвинутого по частоте аудиосигнала, который для множества вторых поддиапазонов включает в себя одно или несколько значений каждого из вторых поддиапазонов,
в котором каждое из значений первого и второго поддиапазона включает в себя информацию о соответствующем фазовом угле, и
в котором одно из значений второго поддиапазона формируется на основе одного из значений первого поддиапазона так, что второй фазовый угол этого значения второго поддиапазона может отличаться от первого фазового угла этого значения первого поддиапазона на разность фазового угла, которая зависит от частотной информации, указывающей, на какую разность частот должен быть сдвинут входной аудиосигнал для получения сдвинутого по частоте аудиосигнала, а также зависит от ширины полосы частот одного из первых поддиапазонов.
24. Машиночитаемый носитель, на котором сохранена компьютерная программа для выполнения способа по п. 23, когда эта компьютерная программа выполняется на компьютере или сигнальном процессоре.
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| УСТРОЙСТВО, СПОСОБ И НОСИТЕЛЬ С ПРОГРАММНЫМ КОДОМ ДЛЯ ГЕНЕРИРОВАНИЯ ПРЕДСТАВЛЕНИЯ СИГНАЛА С РАСШИРЕННЫМ ДИАПАЗОНОМ ЧАСТОТ НА ОСНОВЕ ПРЕДСТАВЛЕНИЯ ВХОДНОГО СИГНАЛА С ИСПОЛЬЗОВАНИЕМ СОЧЕТАНИЯ ГАРМОНИЧЕСКОГО РАСШИРЕНИЯ ДИАПАЗОНА ЧАСТОТ И НЕГАРМОНИЧЕСКОГО РАСШИРЕНИЯ ДИАПАЗОНА ЧАСТОТ | 2010 |
|
RU2452044C1 |
| МНОГОРЕЖИМНОЕ УСТРОЙСТВО КОДИРОВАНИЯ | 2000 |
|
RU2262748C2 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| WO 2010136459 A1, 02.12.2010 | |||
| ПЛОСКОСТНАЯ ДЕТАЛЬ С ВЕНТИЛЯЦИОННЫМ ОТВЕРСТИЕМ | 2002 |
|
RU2269189C2 |
Авторы
Даты
2016-08-27—Публикация
2013-07-01—Подача