Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления и др.
Известны логические процессоры (например, патент РФ 2251142, кл. G06F 7/38, 2005 г.), которые содержат мажоритарные элементы и реализуют любую из n простых симметричных булевых функций, зависящих от n аргументов - входных двоичных сигналов [1].
К причинам, препятствующим достижению указанного ниже технического результата при использовании известных логических процессоров, относятся ограниченные функциональные возможности, обусловленные тем, что реализуются только простые симметричные булевые функции, зависящие от n аргументов - входных двоичных сигналов, низкое быстродействие, обусловленное большой задержкой сигнала в схеме, и высокая сложность, обусловленная большим количеством мажоритарных элементов.
Наиболее близким устройством того же назначения к заявленному изобретению по совокупности признаков является принятый за прототип логический процессор (патент РФ 2294008, кл. G06F 7/57, 2007 г.), который содержит мажоритарные элементы и реализует любую из n простых симметричных булевых функций, зависящих от n аргументов - входных двоичных сигналов.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известных логических процессоров, относятся ограниченные функциональные возможности, обусловленные тем, что реализуются только простые симметричные булевые функции, зависящие от n аргументов - входных двоичных сигналов, низкое быстродействие, обусловленное большой задержкой сигнала в схеме, т.к. выход предыдущего мажоритарного элемента соединен со вторым входом последующего мажоритарного элемента, и высокая сложность, обусловленная большим количеством мажоритарных элементов. Это объясняется тем, что в прототипе «мажоритарные элементы, которые имеют по три входа и сгруппированы в V+1 групп так, что (V+1)-я группа содержит V-1 мажоритарных элементов, в каждой группе выход предыдущего мажоритарного элемента соединен со вторым входом последующего мажоритарного элемента, а выход (V-1)-го мажоритарного элемента (V+1)-й группы является выходом логического процессора, при этом
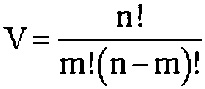 ,
,
(n≠1 - любое натуральное число, m=0,5(n+1) либо m=0,5n при нечетном либо четном n соответственно), i-я (i=1, …, V) группа содержит m-1 мажоритарных элементов» [2].
Техническим результатом заявляемого изобретения является расширение функциональных возможностей за счет возможности реализации симметричных булевых функций как с прямым, так и с инверсным вхождением, повышение быстродействия и уменьшение сложности логического процессора.
Указанный технический результат изобретения достигается тем, что логический процессор, содержащий n информационных входов, n настроечных входов, выход логического процессора, имеет также вход задания вида аргументов, n элементов НЕРАВНОЗНАЧНОСТЬ, сумматор, дешифратор, n элементов ИЛИ, n элементов И, причем i-ый информационный вход соединен с первым входом i-го элемента НЕРАВНОЗНАЧНОСТЬ, вход задания вида аргумента соединен со вторыми входами элементов НЕРАВНОЗНАЧНОСТЬ, выход i-го элемента НЕРАВНОЗНАЧНОСТЬ соединен с i-м входом сумматора, (i=1, …, n), j-ый выход сумматора соединен с j-ым входом дешифратора, (j=1, …, k), s-ый выход дешифратора соединен с соответствующим входом элементов ИЛИ с первого по s-ый, (s=1, …, n-1), n-ый выход дешифратора соединен с соответствующим входом элементов ИЛИ с первого по (n-1)-ый и с первым входом n-го элемента И, выход i-го элемента ИЛИ соединен с первым входом i-го элемента И, (i=1, …, n-1), j-ый настроечный вход соединен со вторым входом j-го элемента И, (j=1, …, n), выходы элементов И соединены с соответствующими входами n-го элемента ИЛИ, выход которого соединен с выходом логического процессора.
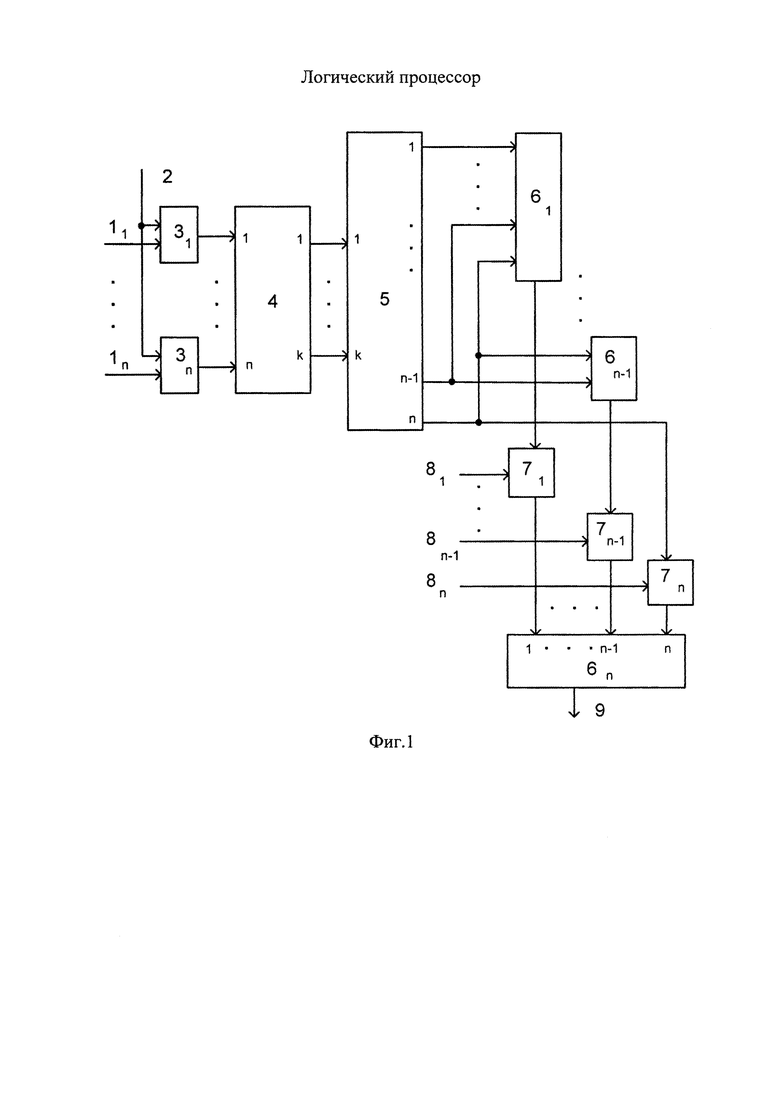
На чертеже представлена схема заявляемого логического процессора.
Логический процессор содержит n информационных входов 11, …, 1n, вход задания вида аргументов 2, n элементов НЕРАВНОЗНАЧНОСТЬ 31…3n, сумматор 4, дешифратор 5, n элементов ИЛИ 61, …, 6n, n элементов И 71, …, 7n, n настроечных входов 81, …, 8n, выход логического процессора 9, причем i-ый информационный вход 1i соединен с первым входом i-го элемента НЕРАВНОЗНАЧНОСТЬ 3i, вход задания вида аргумента 2 соединен со вторыми входами элементов НЕРАВНОЗНАЧНОСТЬ 31, …, 3n, выход i-го элемента НЕРАВНОЗНАЧНОСТЬ 2i соединен с i-м входом сумматора 4, i=1, …, n, j-ый выход сумматора 4 соединен с j-ым входом дешифратора 5, j=1, …, k, s-ый выход дешифратора 5 соединен с соответствующим входом элементов ИЛИ с первого 61 по s-ый 6s, s=1, …, n-1, n-ый выход дешифратора соединен с соответствующим входом элементов ИЛИ 6 с первого 61 по (n-1)-ый 6n-1 и с первым входом n-го элемента И 7n, выход i-го элемента ИЛИ 6i соединен с первым входом i-го элемента И 7i, i=1, …, n-1, j-ый настроечный вход 8j соединен со вторым входом j-го элемента И 7j, j=1, …, n, выходы элементов И соединены с соответствующими входами n-го элемента ИЛИ 6n, выход которого соединен с выходом логического процессора 9.
Работа предлагаемого логического процессора осуществляется следующим образом. Пусть необходимо реализовать простую симметрическую булевую функцию с рангом T (количеством аргументов, входящих в конъюнкции в дизъюнктивной нормальной форме). На вход 8T подается сигнал «1», а на остальные настроечные входы - сигнал «0». Например, для реализации симметричной булевой функции для n=5
Z=X1X2X3 v X1X2X4 v X1X2X5 v X1X3X4 v X1X3X5 v X1X4X5 v X2X3X4 v X2X3X5 v X2X4X5 v X3X4X5
значение T=3.
Для реализации простой симметрической булевой функции на вход задания вида аргументов 2 подается сигнал «0», при этом на выходы элементов НЕРАВНОЗНАЧНОСТЬ 3 поступают значения входных аргументов в прямом виде. Для реализации симметрической булевой функции с инверсными аргументами на вход задания вида аргументов 2 подается сигнал «1», при этом на выходы элементов НЕРАВНОЗНАЧНОСТЬ 3 поступают значения входных аргументов в инверсном виде.
Сумматор 4 имеет n двоичных входов и k двоичных выходов, где k=]log2n[, ]…[ означает ближайшее целое, не меньшее, чем выражение в скобках. Например, для n=4 значение k=2, а для n=5 значение k=3. На выходе сумматора 4 формируется двоичный код, десятичный эквивалент которого равен количеству единиц. Вес i-го двоичного разряда на выходах сумматора 4 (и соответственно на входах дешифратора 5) 2i-1, где i - номер выхода. Дешифратор 5 является неполным. Вывод дешифратора 5, соответствующий входному набору «00…0», не используется. Не используются выходы дешифратора с номером, большим n. На выходах дешифратора 5 формируется унитарный код, в котором только одно значение «1» на выходе с номером, соответствующим количеству единиц в значениях аргументов. На выходе элемента ИЛИ 6i формируется сигнал «1», если количество значений «1» среди значений аргументов не менее значения i, i=1, …, n. Как указывалось выше, для реализации симметрической булевой функции ранга T на настроечный вход 8T подается сигнал «1» и в результате на выходе элемента ИЛИ 6n и, соответственно, на выходе логического процессора 9 формируется сигнал «1» для тех значений входных аргументов, в которых не менее T значений аргументов равны «1». Аналогично для реализации симметрических булевых функций с инверсными значениями аргументов.
Сравним характеристики прототипа и заявляемого устройства.
1. Заявленное устройство имеет более широкие функциональные возможности за счет возможности реализации симметрических булевых функций как с прямым, так и с инверсным вхождением.
2. Задержка сигнала в заявленном устройстве постоянная, а в прототипе за счет использования мажоритарных элементов, которые «имеют по три входа и сгруппированы в V+1 групп так, что (V+1)-я группа содержит V-1 мажоритарных элементов, в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента» [2], с ростом значения количества аргументов n будет увеличиваться время задержки сигнала. Таким образом, быстродействие схемы будет падать.
3. С ростом количества аргументов n в заявленном устройстве сложность растет пропорционально этому значению, а в прототипе определяется функцией 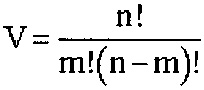
и, например, при n=5, m=3 V=10, при n=7, m=4 V=35, при n=10, m=5 V=252 и т.д.
Следовательно, заявленное устройство имеет меньшую аппаратную сложность и большее быстродействие при расширении функциональных возможностей прототипа.
Использованные источники
1. Логический процессор (RU №2251142 C1, МПК G06F 7/38, заявлено 16.06.2003, опубликовано 27.04.2005).
2. Логический процессор (RU №2294008 C1, МПК G06F 7/57, заявлено 03.11.2005, опубликовано 20.02.2007).
| название | год | авторы | номер документа |
|---|---|---|---|
| ЛОГИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ | 2016 |
|
RU2626345C1 |
| МНОГОФУНКЦИОНАЛЬНОЕ ЛОГИЧЕСКОЕ УСТРОЙСТВО | 2015 |
|
RU2610247C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2015 |
|
RU2618899C1 |
| ЛОГИЧЕСКИЙ МОДУЛЬ | 2015 |
|
RU2609743C1 |
| ЛОГИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ | 2015 |
|
RU2602331C1 |
| УНИВЕРСАЛЬНЫЙ МАЖОРИТАРНЫЙ МОДУЛЬ | 2015 |
|
RU2610246C1 |
| НАСТРАИВАЕМЫЙ ЛОГИЧЕСКИЙ МОДУЛЬ | 2016 |
|
RU2626343C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ ДЛЯ ОТКАЗОУСТОЙЧИВЫХ СИСТЕМ | 2016 |
|
RU2626347C1 |
| УСТРОЙСТВО ДЛЯ МАЖОРИТАРНОГО ВЫБОРА СИГНАЛОВ | 2016 |
|
RU2628890C1 |
| МНОГОФУНКЦИОНАЛЬНЫЙ МАЖОРИТАРНЫЙ МОДУЛЬ | 2016 |
|
RU2626346C1 |
Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики и функциональных узлов систем управления. Технический результат заключается в уменьшении аппаратных затрат и повышении быстродействия логического процессора. Технический результат достигается за счет логического процессора, который содержит n информационных входов 11, …, 1n, вход задания вида аргументов, n элементов НЕРАВНОЗНАЧНОСТЬ 31…3n, сумматор, дешифратор, n элементов ИЛИ 61, …, 6n, n элементов И 71, …, 7n, n настроечных входов 81, …, 8n и выход логического процессора. 1 ил.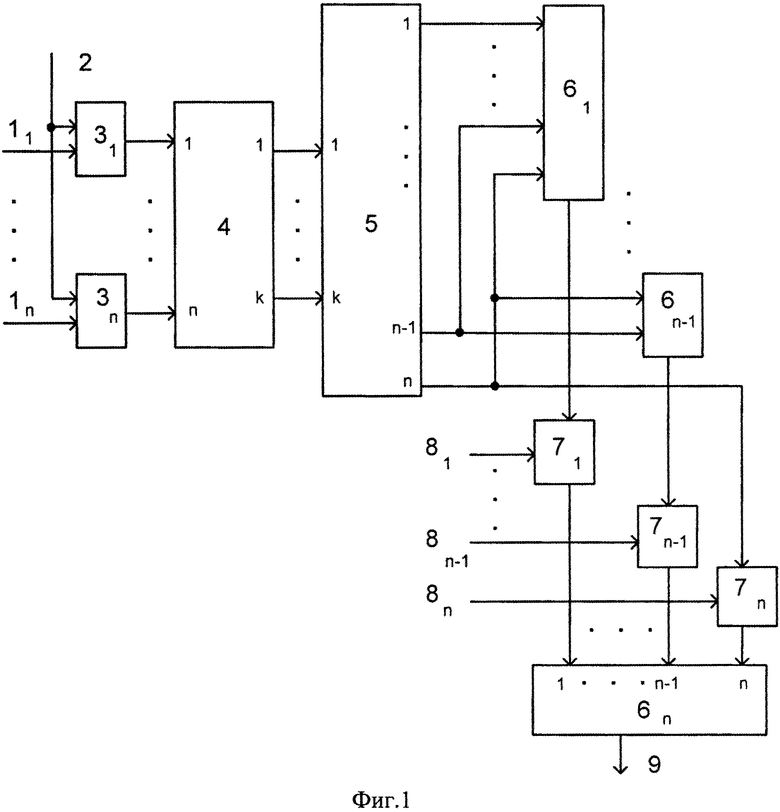
Логический процессор для реализации симметричных булевых функций, зависящих от n аргументов, содержащий n информационных входов, n настроечных входов, выход логического процессора, отличающийся тем, что содержит вход задания вида аргументов, n элементов НЕРАВНОЗНАЧНОСТЬ, сумматор, дешифратор, n элементов ИЛИ, n элементов И, причем i-ый информационный вход соединен с первым входом i-го элемента НЕРАВНОЗНАЧНОСТЬ, вход задания вида аргумента соединен со вторыми входами элементов НЕРАВНОЗНАЧНОСТЬ, выход i-го элемента НЕРАВНОЗНАЧНОСТЬ соединен с i-м входом сумматора, (i=1, …, n), j-ый выход сумматора соединен с j-ым входом дешифратора, (j=1, …, k), s-ый выход дешифратора соединен с соответствующим входом элементов ИЛИ с первого по s-ый, (s=1, …, n-1), n-ый выход дешифратора соединен с соответствующим входом элементов ИЛИ с первого по (n-1)-ый и с первым входом n-го элемента И, выход i-го элемента ИЛИ соединен с первым входом i-го элемента И, (i=1, …, n-1), j-ый настроечный вход соединен с вторым входом j-го элемента И (j=1, …, n), выходы элементов И соединены с соответствующими входами n-го элемента ИЛИ, выход которого соединен с выходом логического процессора.
| ЛОГИЧЕСКИЙ ПРОЦЕССОР | 2005 |
|
RU2294008C1 |
| ЛОГИЧЕСКИЙ ПРОЦЕССОР | 2012 |
|
RU2491613C1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| US 7694304 B2, 06.04.2010 | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
Авторы
Даты
2017-02-02—Публикация
2015-10-05—Подача