Область техники, к которой относится изобретение
Настоящее изобретение относится к области расчетов упругой анизотропии и, в частности, к способу расчета параметра упругой анизотропии для геологического подземного пласта.
Уровень техники
При моделировании свойств геологических подземных пластов необходимо учитывать анизотропию подземных пластов. Некоторые подземные пласты являются относительно изотропными, однако другие подземные пласты, например сланцевые, демонстрируют анизотропные свойства. Неучет анизотропии подземного пласта может привести к погрешностям и ошибочной интерпретации моделируемых свойств геологического подземного пласта.
Существуют различные способы, позволяющие охарактеризовать анизотропию. В области геофизики анизотропию типа трансверсальной изотропии с вертикальной осью (VTI, vertical transverse isotropy), являющейся осью симметрии, обычно характеризуют с использованием параметров Томсена, раскрытых в работе «Thomsen, L., 1986, «Weak elastic anisotropy»: Geophysics, 51, 1954-1966». Параметры Томсена представляют собой безразмерные соотношения компонент тензора модуля упругости. Параметрами Томсена являются:


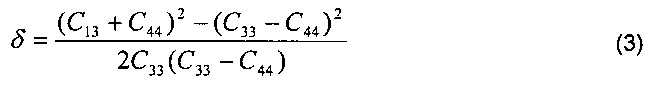
Cij представляет собой тензор модуля упругости (в обозначениях Фойгта), характеризующий упругость среды. Для подземных пластов слоистых пород параметры Томсена, как правило, имеют значение, меньшее 1.
Для некоторых типов подземного пласта, например сланцевого, на степень анизотропии непосредственно влияет пористость. Это связано с тем, что по мере уплотнения пласта глинистых сланцев пористость уменьшается и пластинки выравниваются в предпочтительном направлении, что приводит к более выраженной анизотропии. Поэтому более старые пласты глинистых сланцев стремятся к проявлению более высокой степени анизотропии, чем более молодые пласты глинистых сланцев.
Следующие уравнения (Wang, Z., 2002, «Seismic anisotropy in sedimentary rocks, part 2: Laboratory data», Geophysics 67, 1423-1440) показывают, каким образом могут быть получены параметры Томсена с использованием только пористости:


где Ф обозначает пористость. Пористость Ф в данном примере вычисляли по весу образцов до и после высушивания при комнатной температуре. Константы выводят эмпирически, используя линейную регрессию данных измерений образца керна, при этом они относятся к конкретному типу литологического состава (в данном случае чистый сланец). Используя эту модель, можно прогнозировать ε и γ, используя только пористость. Принимая во внимание, что для нахождения ε и γ этой модели в качестве входных данных требуется только пористость, она предназначена для использования только в случае чисто сланцевых подземных пластов, при этом моделируемая анизотропия имеет высокую степень неопределенности. Кроме того, эта модель напрямую не связана с объемной долей глинистых минералов, которая считается важным параметром при прогнозировании анизотропии в сланцевых подземного пластах. Другое ограничение этой модели состоит в том, что, как показали исследования по расчету анизотропии на основе каротажных данных, упругая анизотропия необязательно связана с пористостью. Поэтому возможно, что вычисления параметров Томсена с использованием пористости не всегда будут давать значимые результаты.
В работе «Hornby В., Howie J.M. and Ince D.W., 2003, «Anisotropy correction for deviated-well sonic logs: Application to seismic well tie», Geophysics 68, том 68, 464-471» раскрыт следующий метод вычисления ε и δ, когда рассматриваемый подземный пласт не является чисто сланцевым:


εsh и δsh представляют собой параметры Томсена для чистого сланца, a VSH - объемную долю сланца. Если VSH опускается ниже входного эталонного значения, то предполагают, что порода является изотропной. Это метод считают действительным только для ε и δ, но не для γ. Кроме того, данная модель требует калибровки по ряду скважин с различными отклонениями. В данном методе анизотропия подземного пласта пропорциональна VSH, обычно имеющей значение 1 в неколлекторской части скважины, включая покрывающую породу в соответствии с определением сланца. Поскольку различные количества глины, содержащейся в сланцевом подземном пласте, приводят к образованию анизотропии, даже если VSH равна единице, доля глинистых минералов может быть низкой.
Раскрытие изобретения
Целью настоящего изобретения является предложение способа расчета параметров анизотропии для геологических подземных пластов. Эти параметры могут применяться в петрофизических моделях, где, например, расчетные значения параметров анизотропии не могут быть получены с помощью других источников. Согласно первому аспекту предлагается способ расчета параметра анизотропии петрофизической модели для геологического подземного пласта. Определяют объемную долю сухих глинистых минералов в геологическом подземном пласте. Также определяют общую пористость геологического подземного пласта. Значение анизотропного параметра определяют, используя объемную долю сухих глинистых минералов, общую пористость и константы, полученные эмпирическим путем.
Анизотропный параметр в некоторых случаях представляет собой параметр γ Томсена, хотя аналогичный метод можно также применять для расчета других типов параметра анизотропии. В этом случае в дополнительном способе расчета анизотропного параметра используется уравнение 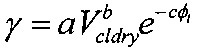 , где a, b и с представляют собой указанные константы, получаемые эмпирическим путем, Vcldry представляет объемную долю сухих глинистых минералов, a Фt - общую пористость. В некоторых случаях способ содержит также расчет любого из параметров ε и δ Томсена с использованием расчетного значения γ и по меньшей мере одной дополнительной эмпирически выведенной константы.
, где a, b и с представляют собой указанные константы, получаемые эмпирическим путем, Vcldry представляет объемную долю сухих глинистых минералов, a Фt - общую пористость. В некоторых случаях способ содержит также расчет любого из параметров ε и δ Томсена с использованием расчетного значения γ и по меньшей мере одной дополнительной эмпирически выведенной константы.
В качестве варианта способ содержит определение эмпирически выведенных констант с использованием каротажных данных, выбираемых из любых следующих данных: данных преломленных сдвиговых волн, данных сдвиговых волн с использованием скрещенных диполей, данных низкочастотных волн Стоунли и данных продольных волн.
В качестве варианта способ содержит определение значения компоненты С44 тензора модуля упругости для подземного пласта с использованием любых следующих данных: данных дипольных сдвиговых волн и преломленных сдвиговых волн, полученных в вертикальной или почти вертикальной скважине. Значение компоненты С66 тензора модуля упругости определяют для подземного пласта, используя данные низкочастотных сдвиговых волн Стоунли, полученные в вертикальной или почти вертикальной скважине. Калибровочное значение для анизотропного параметра определяют, используя компоненты С44 и С66 тензора модуля упругости. Любые из эмпирически выведенных констант определяют с помощью определенного калибровочного значения анизотропного параметра. В некоторых случаях константы, получаемые эмпирическим путем, калибруют с помощью определенного калибровочного значения анизотропного параметра, выполняя регрессию.
Если константы, получаемые эмпирическим путем, нельзя получить, используя каротажные данные, то в некоторых случаях в качестве эмпирически выведенных констант можно использовать значения по умолчанию.
В качестве еще одного варианта способ содержит определение объемной доли сухих глинистых минералов с помощью индекса содержания глинистых минералов и дополнительной эмпирически выведенной константы.
Согласно второму аспекту предлагается компьютерное устройство, выполненное с возможностью расчета анизотропного параметра петрофизической модели для геологического подземного пласта. Устройство снабжено процессором для определения значения анизотропного параметра с помощью объемной доли сухих глинистых минералов в геологическом подземном пласте, значения общей пористости геологического подземного пласта и по меньшей мере одной эмпирически выведенной константы.
В дополнительном варианте осуществления анизотропный параметр представляет собой параметр γ Томсена, а процессор выполнен с возможностью расчета γ по уравнению 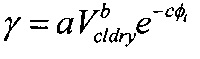 , где a, b и с представляют собой константы, получаемые эмпирическим путем, Vcldry - объемная доля сухих глинистых минералов, а Фt - общая пористость. В некоторых случаях процессор также выполнен с возможностью расчета любого из параметров ε и δ Томсена с использованием расчетного значения γ и по меньшей мере одной дополнительной эмпирически выведенной константы.
, где a, b и с представляют собой константы, получаемые эмпирическим путем, Vcldry - объемная доля сухих глинистых минералов, а Фt - общая пористость. В некоторых случаях процессор также выполнен с возможностью расчета любого из параметров ε и δ Томсена с использованием расчетного значения γ и по меньшей мере одной дополнительной эмпирически выведенной константы.
В качестве варианта процессор также выполнен с возможностью определения эмпирически выведенных констант с использованием каротажных данных, выбираемых из любых следующих данных: данных преломленных сдвиговых волн, данных сдвиговых волн с использованием скрещенных диполей, данных низкочастотных волн Стоунли и данных продольных волн.
В некоторых случаях процессор выполнен с возможностью определения значения компоненты С44 тензора модуля упругости для подземного пласта с использованием любых следующих данных: данных дипольных сдвиговых волн и данных преломленных сдвиговых волн, определения значения компоненты С66 тензора модуля упругости для подземного пласта с использованием данных низкочастотных волн Стоунли, определения калибровочного значения для анизотропного параметра с использованием компонент С44 и С66 тензора модуля упругости и калибрования любых из эмпирически выведенных констант с использованием определенного калибровочного значения анизотропного параметра.
Компьютерное устройство в некоторых случаях снабжено базой данных, выполненной с возможностью хранения значений любых эмпирически выведенных констант.
Согласно третьему аспекту предлагается компьютерная программа, содержащая машиночитаемый код, которая, при запуске на компьютерном устройстве, вызывает выполнение компьютерным устройством способа, описанного выше в первом аспекте изобретения.
Согласно четвертому аспекту предлагается компьютерный программный продукт, содержащий машиночитаемый носитель и компьютерную программу, как описано выше в третьем аспекте. Компьютерная программа храниться на машиночитаемом носителе.
Краткое описание чертежей
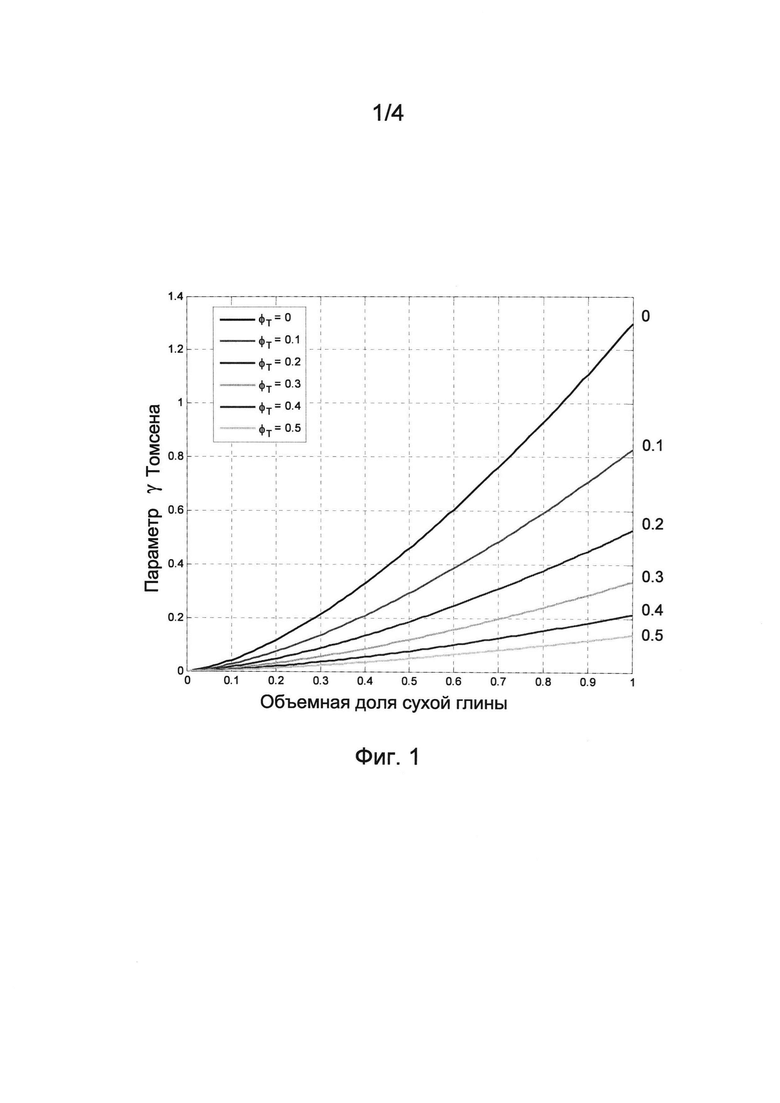
На ФИГ. 1 представлен график, изображающий гамма-параметры Томсена в зависимости от объемной доли сухих глинистых минералов для различных значений общей пористости.
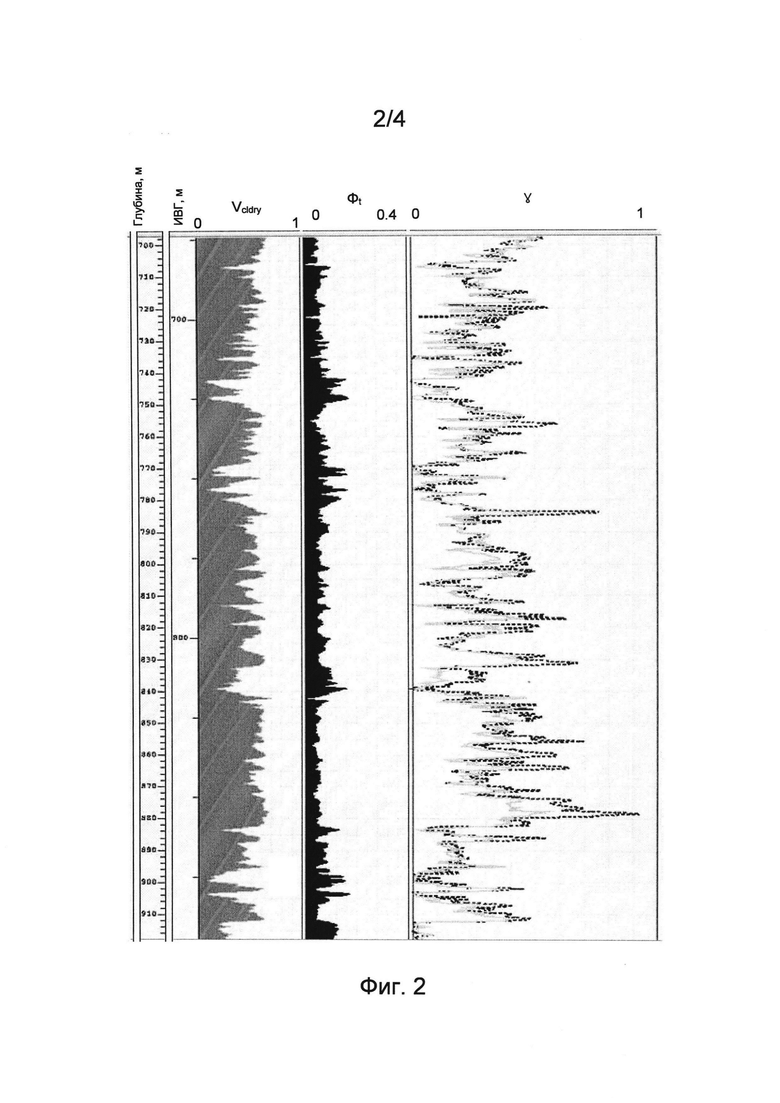
На ФИГ. 2 представлен пример данных для прогнозирования локально калиброванного параметра γ на основе доли сухих глинистых минералов и общей пористости.
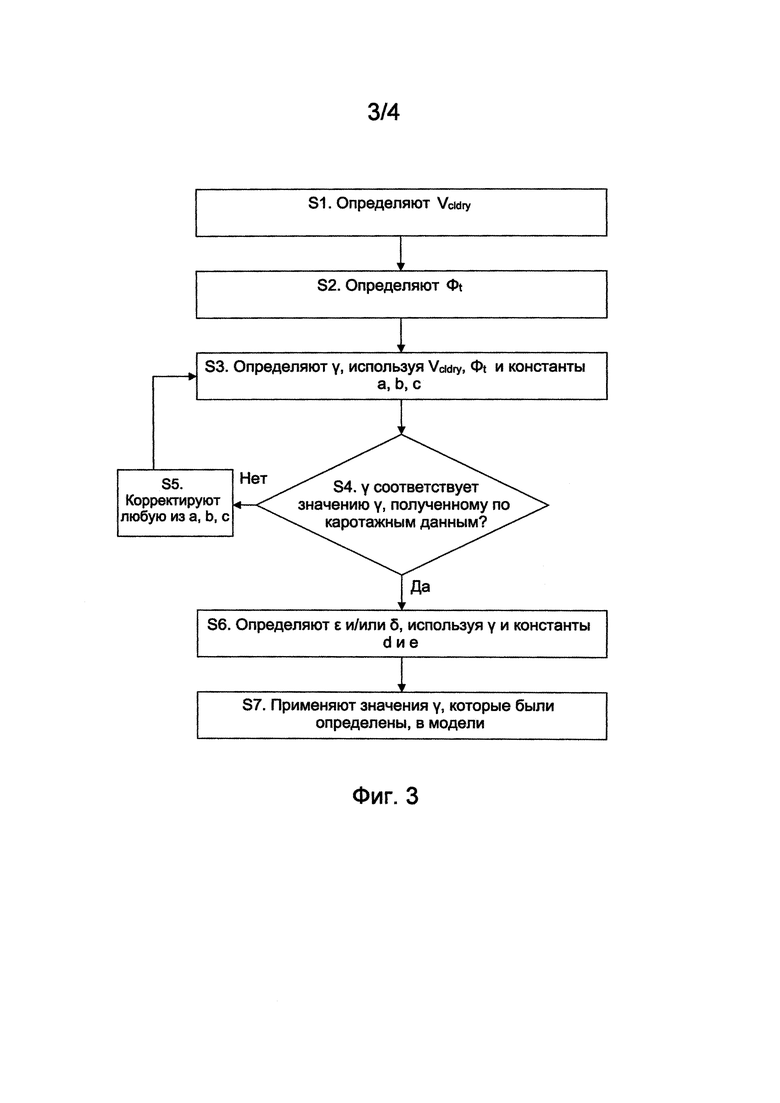
На ФИГ. 3 показана блок-схема, иллюстрирующая шаги согласно одному из вариантов осуществления изобретения.
На ФИГ. 4 схематически показана структурная схема устройства согласно одному из вариантов осуществления изобретения.
Осуществление изобретения
Раскрыта модель, применимая для прогнозирования параметров анизотропии. В приведенных ниже примерах термин «анизотропия» используется для обозначения упругой динамической анизотропии типа трансверсальной изотропии с вертикальной осью симметрии (ТИВОС). Сланцевые подземные пласты представлены в качестве геологических подземных пластов, к которым применяется модель, однако следует понимать, что эту модель можно применять к любому типу геологического подземного пласта, демонстрирующего анизотропные свойства. Описанные выше параметры Томсена используются в качестве примеров анизотропных параметров, которые можно прогнозировать.
Было установлено, что параметр γ Томсена можно рассчитать, используя общую пористость сланцевого подземного пласта, объемную долю сухих глинистых минералов и константы, получаемые эмпирическим путем. Кроме того, используя расчетное значение γ и дополнительные константы, получаемые эмпирическим путем, можно рассчитать другие параметры Томсена, δ и ε, для этих подземных пластов.
Сланцевый подземный пласт можно охарактеризовать как подземный пласт, в котором присутствуют три следующие основные составляющие:
- плоские частицы, состоящие, главным образом, из пластинок глинистого минерала (но не ограничиваясь ими);
- круглые частицы, состоящие, главным образом, из илового кварца и (или) зерен песка; и
- пористость.
Для фиксированной объемной доли глинистых минералов относительное количество круглых частиц и значение пористости могут отличаться.
Объемную долю глинистых минералов и общую пористость измеряют или рассчитывают, используя данные каротажа скважин.
Расчет γ выполняют по уравнению 8:

где Vcldry - объемная доля сухих глинистых минералов, φt - общая пористость, а а, b и с - константы. Член пористости в уравнении 8 учитывает воздействие изменения пористости на анизотропию. Vcldry и φt рассчитывают по данным каротажа.
На ФИГ. 1 показано, как значения γ возрастают с увеличением значений объемной доли сухой глины. Из графика видно также, что значения γ убывают с возрастанием общей пористости.
Константы a, b и с изменяются в соответствии с такими факторами, как тип глинистых минералов, глубина отложений, возраст, пластовое давление и температура и так далее. Поэтому желательно откалибровать модель, чтобы обеспечить точный расчет γ с помощью констант a, b и с. Калибровка выполняется локально для исследуемого месторождения и/или подземного пласта и подробнее рассматривается ниже.
Было также установлено, что ε и δ можно рассчитать непосредственно, используя расчетное значение γ и дополнительные константы, эмпирически выведенные по уравнениям 8 и 9:


где d и е - дополнительные константы, получаемые эмпирическим путем.
Петрофизический метод, как правило, предусматривает вычисление такого параметра, как индекс содержания глинистых минералов (Vcli) вместо Vcldry. Vcli имеет значение 0 для самых чистых песков (поскольку они не содержат глины) и 1 для песков, наиболее богатых глиной. Vcli часто обозначают как Vsh (объемная доля сланца). Однако параметр Vcli необязательно напрямую связан с объемной долей сланца, так как в дополнение к глинистым минералам сланец может содержать ил. В этом случае Vcldry может быть связан с Vclj с помощью следующего уравнения 11:

где f - константа, имеющая, как правило, значение от 0,3 до 0,7. Константу f, как правило, рассчитывают, используя, например, рентгеновский структурный анализ, когда находят долю глинистых минералов.
Однако в некоторых случаях можно выполнить прямой расчет объемной доли сухих глинистых минералов. Это можно сделать, применяя, например, усовершенствованные каротажные инструменты и (или) калибровку с использованием рентгеновского структурного анализа (РСА) или аналогичного исследования, или используя знания о типе глин, полученные другим способом.
Чтобы получить как можно более точное расчетное значение γ, константы могут быть найдены путем калибровки модели с использованием каротажных или других доступных данных. Существуют несколько различных типов данных, которые можно использовать для расчета значений γ, δ и ε. Сравнивая значения γ, δ и ε, найденные с использованием каротажных (или других) данных со значениями, полученными с использованием уравнений 8-11, можно выполнить расчет констант а, b, с, d, е и f с большей точностью, используя, как правило, регрессионный метод, например линейную регрессию.
Следует понимать, что в каждом случае могут быть доступны различные каротажные данные (такие как данные акустического каротажа), поэтому различные каротажные данные можно использовать для расчета любого из параметров γ, δ и ε различными способами. В следующих примерах представлены различные типы каротажных данных, используемых для расчета значений любого из параметров γ, δ и ε.
1. Данные сдвиговых волн.
Данные сдвиговых волн могут быть получены в вертикальных скважинах с использованием измерений диполей и (или) преломленных сдвиговых волн. Эти данные, в сочетании с данными плотностного каротажа подземного пласта, можно использовать для нахождения компоненты С44 тензора модуля упругости с использованием следующего уравнения 12:

где ρb - объемная плотность, a Vsν - скорость распространяющейся в вертикальном направлении сдвиговой волны, полученной с помощью измерений диполей и (или) преломленных сдвиговых волн.
Данные низкочастотных волн Стоунли можно использовать для нахождения упругой жесткости С66 при сдвиге (см., например, «Tang, X., 2001, «Determining formation shear-wave transverse isotropy from borehole Stoneley-wave measurements)). Geophysics, 68, 118-126)». После нахождения C44 и C66 с использованием каротажных данных вычисление γ можно выполнить с помощью уравнения 2.
На ФИГ. 2 представлен пример параметра γ при различных глубинах. На графике показана глубина в метрах и истинная вертикальная глубина (ИВГ) относительно среднего уровня моря в метрах. В этом случае значения a, b и с откалиброваны с использованием каротажных данных, как описано выше. Показаны Vcldry и Фt. Приведены два графика γ; пунктирной линией показаны значения γ, рассчитанные с использованием инверсии волны Стоунли и дипольных данных. Сплошной линией показаны значения γ, рассчитанные с использованием Vcldry и Фt по уравнению 8. В этом случае константа b была скорректирована до значения 3, при этом использовались значения по умолчанию или константы а и с (1,3 и 4,5 соответственно).
Значения γ, рассчитанные с помощью уравнения 8, имеют хорошую корреляцию со значениями, полученными с использованием каротажных данных. Модель уравнения 8 можно использовать в дальнейшем для прогнозирования значений γ на других участках, где каротажные данные отсутствуют.
2. Искривленные скважины.
Для искривленных скважин, имеющих искривление большее, чем типичные 30-40°, данные скрещенных диполей можно использовать для нахождения сочетаний ε, δ и γ, а также вертикальной медленности (Vp0) продольной волны и вертикальной медленности (Vs0) сдвиговой волны для конкретного искривления скважины по уравнениям Томсена, показанным ниже как уравнения 13.
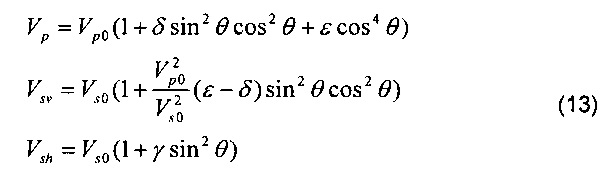
Например, если Vp, Vsh и Vsv измеряют в одном и том же подземном пласте в двух разных скважинах с различными искривлениями θ, это позволит получить все 5 используемых параметров. На практике для наблюдения эффектов анизотропии искривление одной из скважины должно быть достаточно большим.
3. Медленность продольной волны.
Каротажные данные, обеспечивающие значения медленности продольной волны, можно использовать для получения комбинаций ε, δ и Vp0, используемых, в свою очередь, для калибровки значений а, b, с, d, е или f. Например, если Vp измеряют через один и тот же подземный пласт в трех разных скважинах с различным искривлением θ, уравнение Томсена можно использовать для нахождения значений трех неизвестных Vp0, δ и ε. На практике искривления двух скважин должны быть достаточно велики, чтобы наблюдать эффекты анизотропии. Искривления этих двух скважин также должны отличаться на достаточную величину (20-30 градусов).
Следует понимать, что другие типы данных также могут использоваться для калибровки модели уравнений 8-11 и нахождения точных значений любой из констант а, b, с, d, е, f. Любое сочетание таких данных можно использовать, чтобы способствовать локальной калибровке модели.
В случае, если имеющихся каротажных (или других) данных недостаточно для нахождения значений различных констант, описанных выше, для получения всех или любых констант а, b, с, d, е и f можно использовать значения по умолчанию. Значения по умолчанию для каждой константы приведены в таблице 1. Следующие способы могут служить в качестве примера для расчета этих значений.
Константы a, b и с можно рассчитывать, сравнивая расчет γ, выполненный на основе расширенных данных акустического каротажа в различных вертикальных скважинах, с прогнозами модели, выполненными с использованием уравнения 8, при этом константы представляют наилучшее общее соответствие двух методов.
Константы d и е могут быть получены на основе ультразвуковых измерений на различных образцах керна.
Константа f может быть принята в качестве средней доли сухих глинистых минералов в сланцах.
Представленные выше способы расчета значений для констант а, b, с, d, е и f приведены только в качестве примера. Следует понимать, что для расчета подходящих значений можно использовать и другие методы.
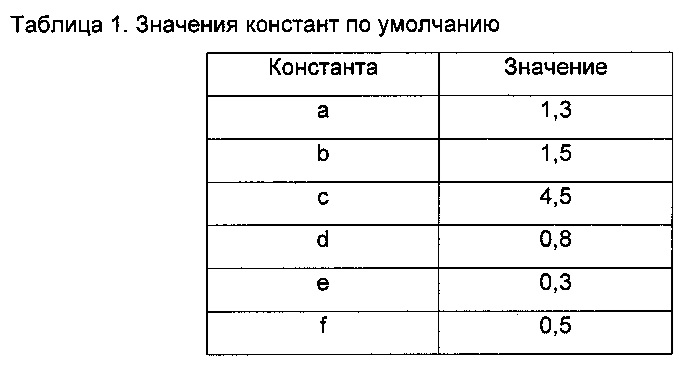
Приведенные выше значения для a, b и с использовали для получения значений у, показанных на ФИГ. 1.
На ФИГ. 3 показана блок-схема, иллюстрирующая шаги по нахождению констант согласно одному из вариантов осуществления изобретения. Следующая нумерация соответствует нумерации, приведенной на ФИГ. 3.
S1. Определяют значение Vcldry для подземного пласта. Как описано выше, оно может быть найдено непосредственно или с помощью Vcli.
S2. Определяют значение Фt для подземного пласта.
S3. Используют уравнение 8 для определения γ с использованием Vcldry, Фt и констант a, b и с.
S4. При наличии каротажных данных с их помощью находят альтернативные значения γ. Если альтернативные значения γ хорошо соответствуют значениям γ, определенным на шаге S2, процесс продолжают на шаге S6, в противном случае процесс продолжают на шаге S5.
S5. Вносят поправку в любые значения a, b и с, и процесс возвращается к шагу S3. Как правило, процесс является итеративным, при этом шаги S3-S5 повторяются, пока не будет достигнута хорошая корреляция между значениями γ, определенными с помощью уравнения 8, и альтернативными значениями γ, определенными с помощью каротажных данных.
S6. При необходимости находят значения ε и δ с использованием определенных значений параметра γ и констант d и е.
S7. Определенные значения для параметров γ, δ и/или ε Томсена можно затем применить в петрофизической модели для моделирования анизотропного подземного пласта в области, находящейся на расстоянии от скважины.
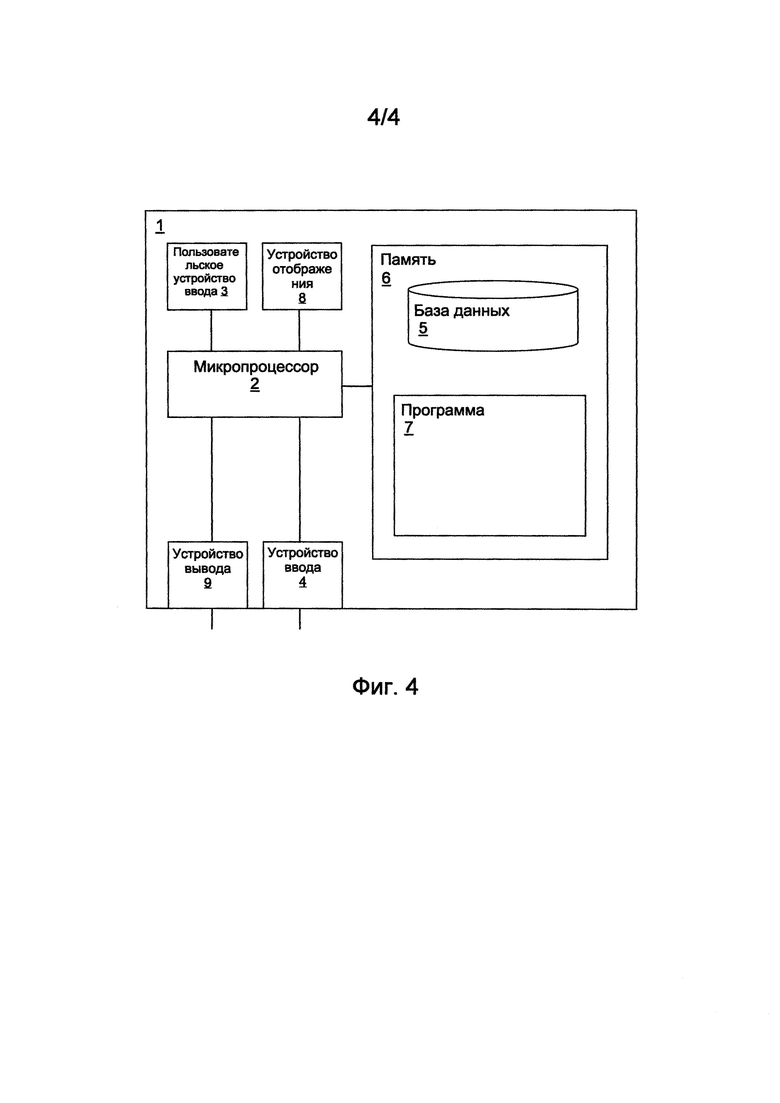
Обратимся теперь к ФИГ. 4, иллюстрирующей компьютерное устройство 1, которое может использоваться для реализации описанных выше процедур. Компьютерное устройство 1 оснащено процессором 2 для выполнения вычислений и определения любых из описанных выше констант. Процессор 2 может содержать единственный процессор или может содержать более чем один физический процессор.
Для определения значений γ процессору 2 необходимы данные. Процессор может получить данные несколькими способами. Компьютерное устройство 1 может быть оснащено пользовательским устройством 3 ввода, таким как сенсорный экран, мышь или клавиатура, позволяющим пользователю вводить данные. Компьютерное устройство 1 может быть оснащено устройством 4 ввода для приема данных. Примером устройства 4 ввода может служить приемник для приема данных от удаленного источника и устройство ввода-вывода, такое как дисковый накопитель. Данные могут также храниться в базе данных 5, которая в варианте осуществления, представленном на ФИГ. 4, показана размещенной на машиночитаемом носителе в виде памяти 6. База данных 5 может использоваться для хранения значений констант и любых других упомянутых выше значений, таких как γ, Ф, ε, δ и т.д., в дополнение к соответствующим каротажным данным, которые можно использовать для вычисления значений γ и калибровки значений констант.
Память 6 можно также использовать для хранения компьютерной программы 7, которая, при исполнении процессором 2, вызывает выполнение процессором 2 любых вычислений и калибровок, описанных выше.
Для представления данных и результатов пользователю может также предусматриваться устройство 8 отображения. Альтернативно или дополнительно может предусматриваться устройство 9 вывода, позволяющее компьютерному устройству 1 выводить результаты обработки на другое устройство. Это может быть, например, принтер. Альтернативно устройство 9 вывода может представлять собой передатчик для передачи данных удаленному сетевому устройству.
Было показано, что получаемые на основе каротажа расчеты γ можно выполнить с использованием полученных с помощью каротажа значений общей пористости и объемной доли сухих глинистых минералов. Константы, получаемые эмпирическим путем, используют для получения значения γ, причем эти константы можно уточнять для предоставления более точных значений γ с помощью каротажных параметров, таких как данные каротажа с использованием сдвиговых волн и продольных волн, данные низкочастотных волн Стоунли и т.д. Это обеспечивает возможность локальной калибровки расчетов γ для конкретного подземного пласта.
Кроме того, расчетные значения γ непосредственно связаны с другими параметрами анизотропии Томсена, ε и δ в случае сланцевых подземных пластов. Поэтому расчетные значения γ можно использовать с целью получения расчетных значений для ε и δ. Эти параметры Томсена могут применяться в петрофизической модели для моделирования свойств геологического подземного пласта или рассматриваемого подземного пласта.
При точном определении всех входных данных, явном использовании объема глинистых минералов, прямой связи между всеми тремя анизотропными параметрами γ, ε и δ описанные выше методы могут применяться в большом количестве различных ситуаций. Например, на зрелом месторождении благодаря проведению каротажа скважин может быть доступно большое количество данных, которые можно использовать, чтобы получить значения констант, обеспечивающие очень точные расчеты параметров Томсена. Это позволяет точно моделировать новые площади зрелого месторождения. С другой стороны, на разведываемых площадях, где доступных каротажных данных меньше, может не оказаться другого способа для расчета параметров анизотропии. В этом случае удовлетворительный расчет параметров анизотропии можно выполнить с использованием комбинации любых доступных данных и значений по умолчанию для сланца, приведенных в таблице 1. Следует понимать, что значения по умолчанию могут отличаться для различных областей или различных типов анизотропного геологического подземного пласта.
Специалисту в данной области техники понятно, что описанные выше варианты осуществления могут подвергаться различным модификациям без выхода за рамки настоящего изобретения, определяемые приложенной формулой изобретения. Так, параметры Томсена используются в качестве иллюстративных параметров, описывающих анизотропные параметры подземного пласта геологической среды. Однако следует понимать, что данное изобретение может применяться для отыскания других типов параметров, используемых в качестве характеристик анизотропии подземного пласта геологической среды. Кроме того, раскрытые в описании методы относятся к сланцевым подземного пластам, однако следует понимать, что аналогичные методы могут применяться и к другим типам анизотропного геологического подземного пласта. Приведены некоторые примеры каротажных данных, которые могут использоваться для калибровки констант и повышения их точности. Необходимо понимать, что при калибровке значений констант могут также использоваться другие типы каротажных данных, когда известно, что они связаны с каким-либо из анизотропных параметров.
Изобретение относится к области геофизики и может быть использовано для определения параметров упругой анизотропии для геологического подземного пласта. Предложены способ и устройство для расчета анизотропного параметра петрофизической модели для геологического подземного пласта. Согласно заявленному предложению определяют объемную долю сухих глинистых минералов в геологическом подземном пласте. Кроме того, определяют общую пористость геологического подземного пласта. Значение анизотропного параметра определяют, используя объемную долю сухих глинистых минералов, общую пористость и константы, получаемые эмпирическим путем. Полученные в результате параметры анизотропии можно применять в петрофизических моделях, где, например, расчетные значения параметров анизотропии не могут быть получены с помощью других источников. Технический результат – повышение точности и достоверности получаемых данных. 3 н. и 13 з.п. ф-лы, 4 ил.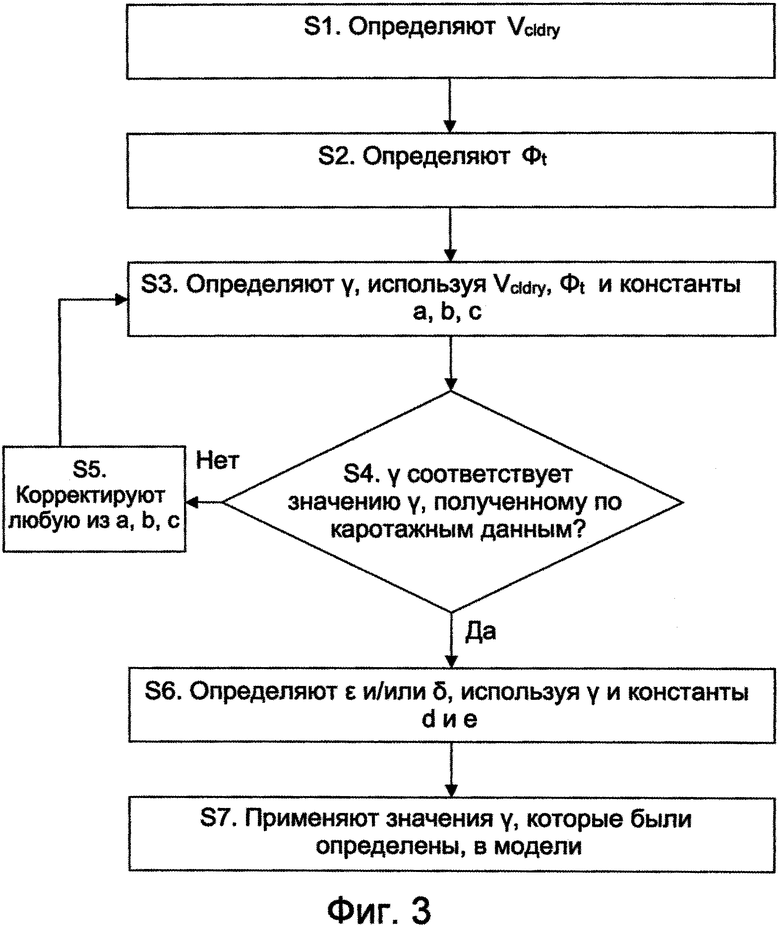
1. Способ расчета параметра анизотропии петрофизической модели для геологического подземного пласта, содержащий следующие шаги:
определяют объемную долю сухих глинистых минералов в геологическом подземном пласте;
определяют общую пористость геологического подземного пласта;
определяют значение анизотропного параметра, используя объемную долю сухих глинистых минералов, общую пористость и константы, получаемые эмпирическим путем.
2. Способ по п. 1, отличающийся тем, что анизотропный параметр представляет собой параметр γ Томсена.
3. Способ по п. 2, отличающийся тем, что анизотропный параметр рассчитывают по уравнению
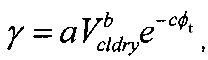
где a, b и c - это указанные константы, получаемые эмпирическим путем, Vcldry - объемная доля сухих глинистых минералов, a Фt - общая пористость.
4. Способ по п. 2 или 3, отличающийся тем, что дополнительно содержит расчет любого из параметров ε и δ Томсена с использованием рассчитанного значения γ и по меньшей мере одной дополнительной константы, получаемой эмпирическим путем.
5. Способ по п. 1, отличающийся тем, что дополнительно содержит определение констант, получаемых эмпирическим путем, с использованием каротажных данных, выбираемых из любых следующих данных: данных преломленных сдвиговых волн, данных сдвиговых волн с использованием скрещенных диполей, данных низкочастотных волн Стоунли и данных продольных волн.
6. Способ по п. 5, отличающийся тем, что дополнительно содержит следующие шаги:
определяют значение компоненты C44 тензора модуля упругости для подземного пласта, используя любые следующие данные: данные дипольных сдвиговых волн и данные преломленных сдвиговых волн, полученные в вертикальной или почти вертикальной скважине;
определяют значение компоненты C66 тензора модуля упругости для подземного пласта, используя данные низкочастотных сдвиговых волн Стоунли, полученные в вертикальной или почти вертикальной скважине;
определяют калибровочное значение для анизотропного параметра, используя компоненты C44 и C66 тензора модуля упругости;
калибруют любые из констант, полученных эмпирическим путем, с помощью калибровочного значения анизотропного параметра, которое было определено.
7. Способ по п. 6, отличающийся тем, что константы, получаемые эмпирическим путем, калибруют с помощью калибровочного значения анизотропного параметра, которое было определено, путем выполнения регрессии.
8. Способ по п. 5, отличающийся тем, что дополнительно содержит, в случае если константы, получаемые эмпирическим путем, не могут быть получены, используя каротажные данные, использование значений по умолчанию для указанных констант.
9. Способ по п. 1, отличающийся тем, что дополнительно содержит определение объемной доли сухих глинистых минералов, используя индекс глины и дополнительные константы, получаемые эмпирическим путем.
10. Компьютерное устройство, выполненное с возможностью расчета параметра анизотропии петрофизической модели для геологического подземного пласта, содержащее:
процессор для определения значения анизотропного параметра с использованием объемной доли сухих глинистых минералов в геологическом подземном пласте, величины общей пористости геологического подземного пласта и констант, получаемых эмпирическим путем.
11. Компьютерное устройство по п. 10, отличающееся тем, что анизотропный параметр представляет собой параметр γ Томсена, а процессор выполнен с возможностью расчета γ по уравнению
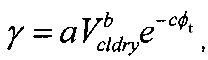
где a, b и c - это указанные константы, получаемые эмпирическим путем, Vcldry - объемная доля сухих глинистых минералов, а Фt - общая пористость.
12. Компьютерное устройство по п. 11, отличающееся тем, что процессор выполнен с возможностью расчета любого из параметров ε и δ Томсена с использованием рассчитанного значения γ и по меньшей мере одной дополнительной константы, получаемой эмпирическим путем.
13. Компьютерное устройство по п. 10, отличающееся тем, что процессор выполнен с возможностью определения констант, получаемых эмпирическим путем, с использованием каротажных данных, выбираемых из любых следующих данных: данных преломленных сдвиговых волн, данных сдвиговых волн с использованием скрещенных диполей, данных низкочастотных волн Стоунли и данных продольных волн.
14. Компьютерное устройство по п. 13, отличающееся тем, что процессор выполнен с возможностью определения значения компоненты C44 тензора модуля упругости для подземного пласта с использованием любых следующих данных: данные дипольных сдвиговых волн и данные преломленных сдвиговых волн, определения значения компоненты C66 тензора модуля упругости для подземного пласта с использованием данных низкочастотных волн Стоунли, определения калибровочного значения для анизотропного параметра с использованием компонент C44 и C66 тензора модуля упругости и калибрования любых из констант, получаемых эмпирическим путем, с использованием калибровочного значения анизотропного параметра, которое было определено.
15. Компьютерное устройство по п. 10, отличающееся тем, что дополнительно содержит базу данных, выполненную с возможностью хранения значений любых констант, получаемых эмпирическим путем.
16. Машиночтаемый носитель, содержащий машиночитаемый код, который, при запуске на компьютерном устройстве, вызывает выполнение компьютерным устройством способа по п. 1.
| Машина для многокрасочного печатания | 1928 |
|
SU10794A1 |
| US 20100312534 A1, 09.12.2010 | |||
| US 20050090986 A1, 28.04.2005 | |||
| US 20100326669 A1, 30.12.2010 | |||
| US 6493632 B1, 10.12.2002. | |||
Авторы
Даты
2017-02-21—Публикация
2012-07-10—Подача