ИНВЕРСИЯ АНИЗОТРОПИИ МНОГОСКВАЖИННОЙ СИСТЕМЫ Российский патент 2016 года по МПК G01V1/40 G01V1/28 G06F17/10 

РОДСТВЕННАЯ ЗАЯВКА

Данная заявка испрашивает приоритет, заявленный в предварительной заявке на патент США № 61/512,280, зарегистрированный 27 июля 2011 г. под названием «Способ инверсии анизотропии многоскважинной системой» (номер в реестре 26.0657 US PSP), который включен в полном объеме в описание настоящей заявки в качестве ссылки.

УРОВЕНЬ ТЕХНИКИ ИЗОБРЕТЕНИЯ

Земной пласт, которые включают слои, в которых упругость среды может быть изотропна, анизотропна или изотропна по одним параметрам и анизотропна по другим. Такой слой может быть охарактеризован при помощи сейсмических исследований, в которых, например, упругие волны, сгенерированные источником, проходят через такой слой, где принимаются одним или несколькими датчиками. Решения, основанные на таком определении характеристик, могут включать в себя значительные денежные затраты, например, добыча нефти, газа и т.д. Различные технологии, техники и т.д., описанные в данной заявке, имеют отношение к определению параметров слоя.

КРАТКОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Способ, который включает предоставление данных медленности продольной и поперечной волны в однородном, анизотропном пласте в наклонной скважине; предоставление зависимости между нормальной и тангенциальной податливостью; и, исходя из этих данных и зависимости, выдачу модели для подсчета значения параметров анизотропии, которые характеризуют однородный, анизотропный пласт (например, вдоль буровой скважины под углом, перпендикулярным трансверсальной изотропии с вертикальной осью симметрии). Система может включать процессор; память; команды, выполняемые процессором, которые хранятся в памяти и выполняются процессором для подсчета значений параметров анизотропии, которые характеризуют однородный, анизотропный пласт (например, вдоль буровой скважины под углом перпендикулярным трансверсальной изотропии с вертикальной осью симметрии), основанные, по меньшей мере, частично на данных медленности продольной и поперечной волн по разным углам наклонной буровой скважины в однородном, анизотропном пласте. Компьютерный носитель данных может включать команды, выполняемые компьютером, для выдачи их компьютерному устройству с целью: доступности модели и измеренных данных по меньшей мере для наклонной скважины в пласте; регулировать коэффициенты упругости модели с целью минимизации целевой функции, которая зависит от синтетических данных, подсчитанных при помощи модели, и измеренных данных, чтобы предоставить модели оптимизированные коэффициенты упругости; провести регрессивный анализ эмпирического соотношения, которое включает в себя параметр, заменимый по меньшей мере одним из оптимизированных коэффициентов упругости; и подсчета параметра Томсена для горизонтальной части скважины в пласте, основанного по меньшей мере частично на модели, оптимизированном коэффициенте упругости для модели и регрессивном анализе эмпирического соотношения. Различные устройства, системы, способы и т.д. также раскрыты в данной заявке.

Данное резюме приведено, чтобы представить процесс выбора концепций, которые дополнительно описаны ниже детально. Целью данного резюме не является определить ключевые или существенные особенности тематики, заявленной в данной заявке, как и не является целью ограничить масштаб тематики, заявленной в данной заявке.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Особенности и преимущества описанных примеров реализации могут быть более ясны из нижеследующего описания наряду с чертежами.

Фигура 1 иллюстрирует пример системы каротажных данных;

Фигуры 2А-D иллюстрируют примеры сочетаний источников и приемников;

Фигура 3 иллюстрирует пример способа;

Фигуры 4A-B иллюстрируют пример поведения медленности для наклонной скважины в анизотропном пласте;

Фигуры 5А-В иллюстрируют пример поведения медленности для нескольких наклонных скважин в анизотропном пласте;

Фигуры 6А-В иллюстрируют пример поведения медленности для вертикальной и наклонной скважин в анизотропном пласте;

Фигуры 7А-В иллюстрируют примеры модели подсчета синтетических данных для нагнетательной и наклонной эксплуатационной скважин;

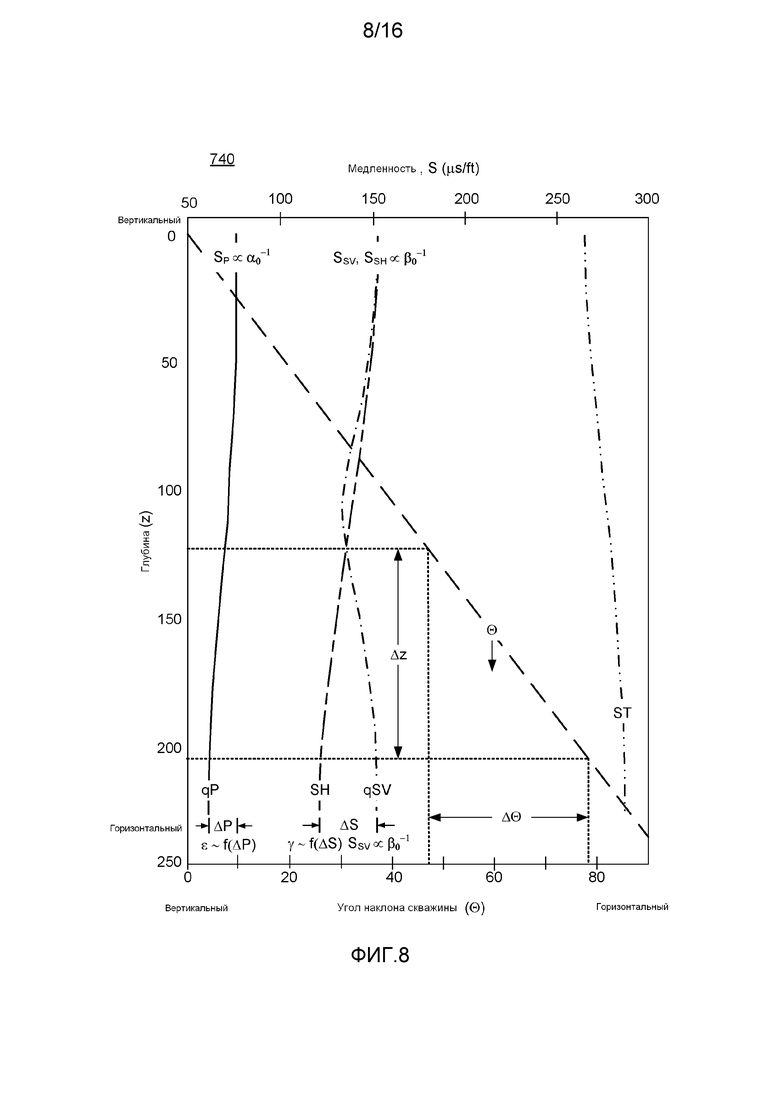
Фигура 8 иллюстрирует модель подсчета синтетических данных наклонной эксплуатационной скважины, показанной на фигуре 7А-В.

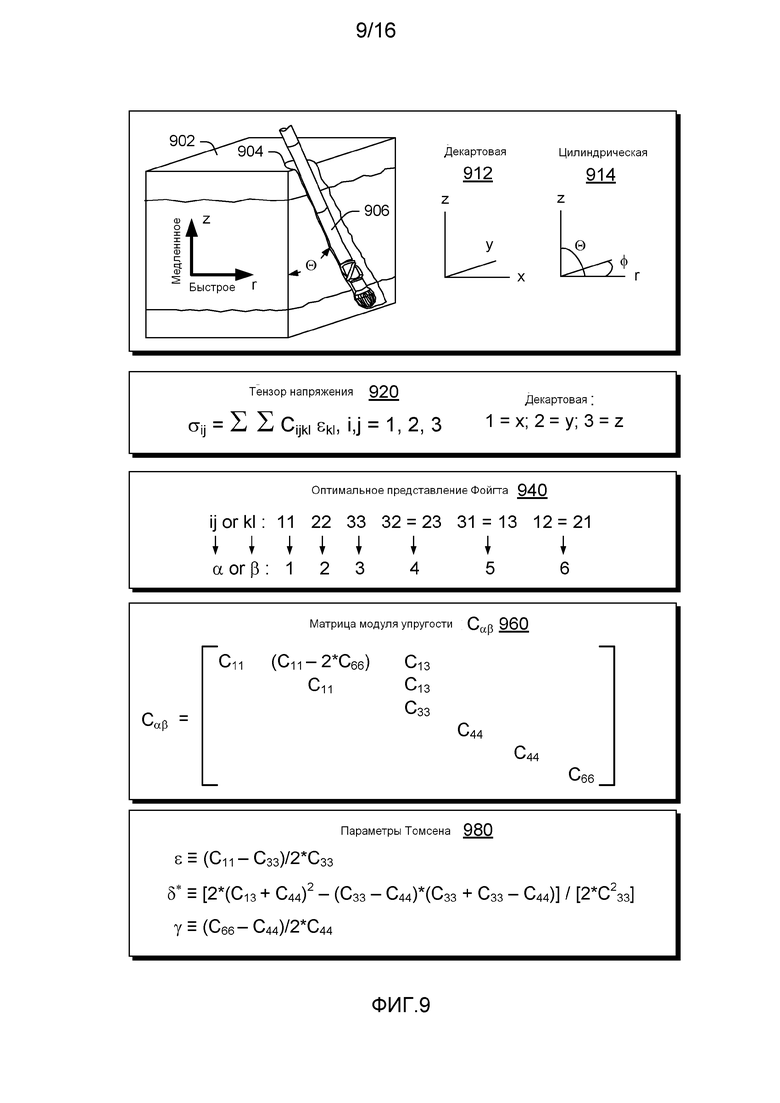
Фигура 9 иллюстрирует примеры уравнений пласта;

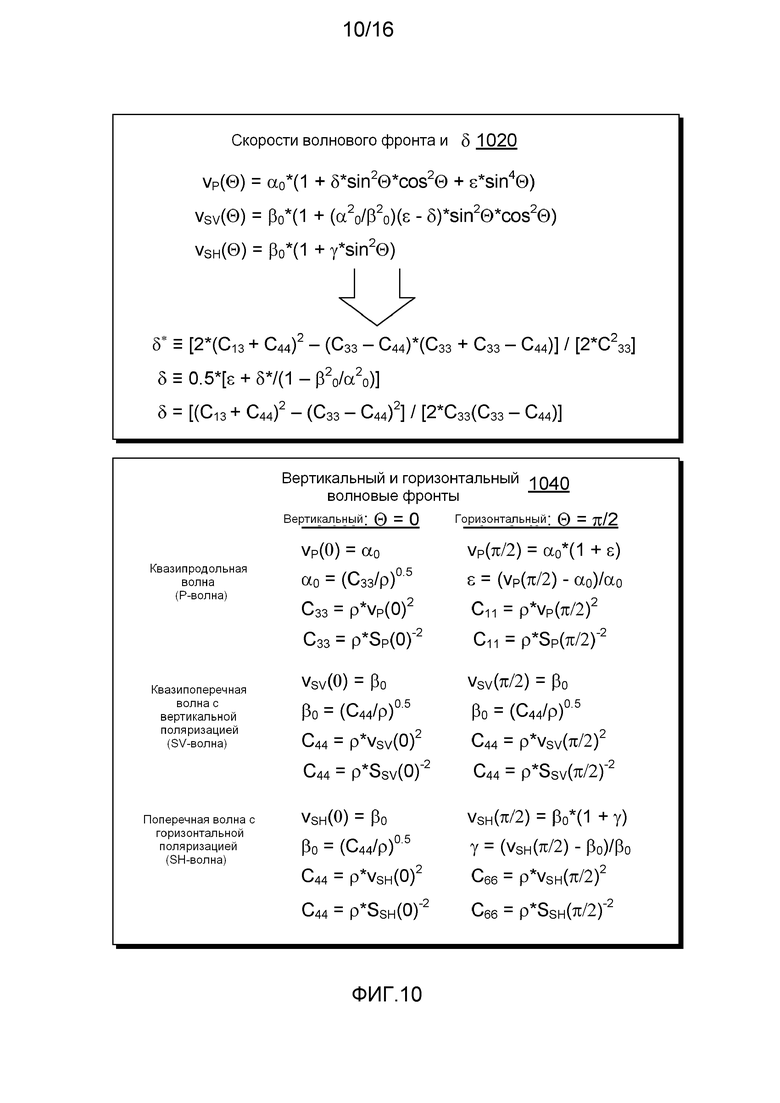
Фигура 10 иллюстрирует примеры уравнений скоростей волнового фронта и волнового фронта пласта;

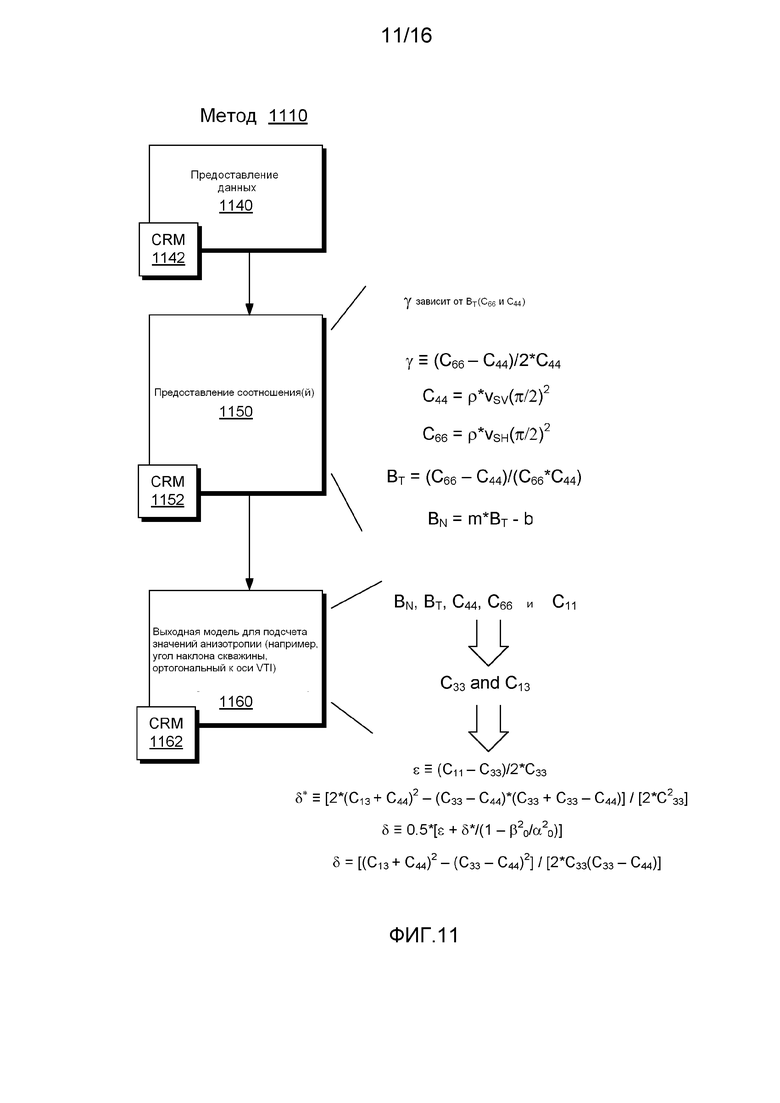
Фигура 11 иллюстрирует пример способа выдачи модели для расчета неизвестных параметров анизотропии;

Фигура 12 иллюстрирует серию графиков данных пласта;

Фигура 13 иллюстрирует серию графиков данных и параметров пласта, показанного на Фигуре 12;

Фигура 14 иллюстрирует пример соотношения параметров податливости;

Фигура 15 иллюстрирует серию графиков параметров Томсена, некоторые из которых зависят от соотношения, показанного на Фигуре 13; и

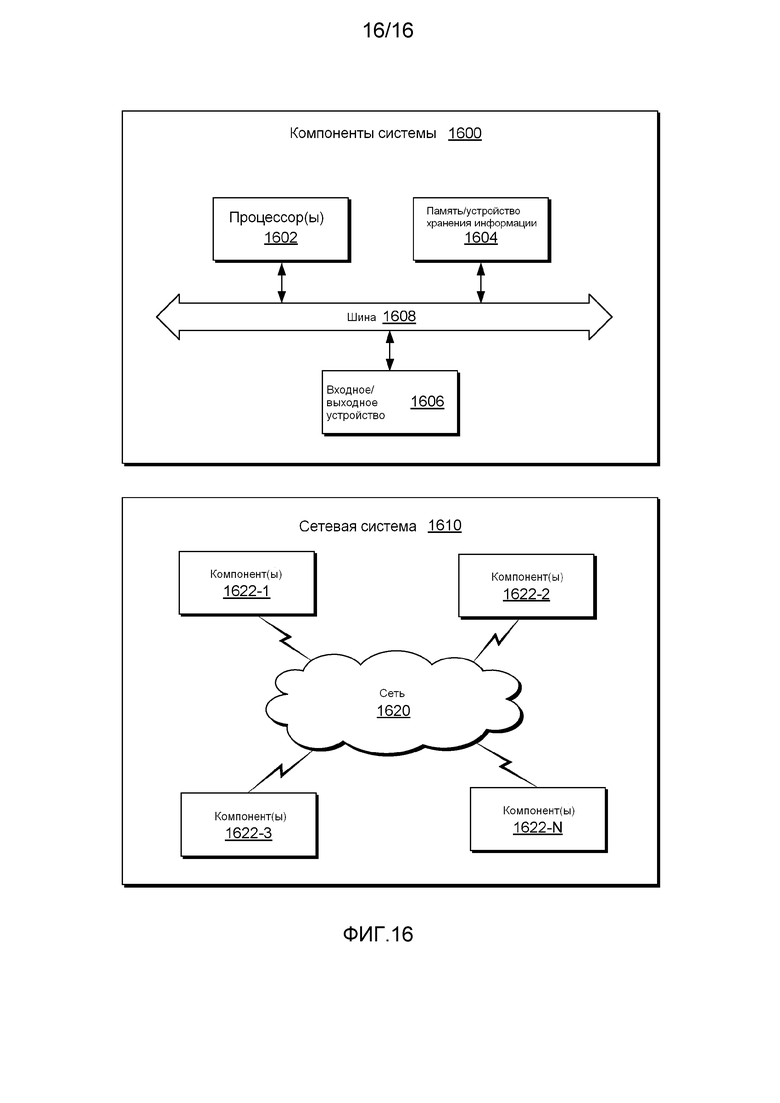
Фигура 16 иллюстрирует компоненты системы и сетевую систему.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Нижеприведенное описание включает наилучший способ из представленных на сегодняшний момент для применения на практике описанных реализаций. Данное описание не является ограничением, а скорее заявлено только с целью описания главных принципов реализаций. Объем описанных реализаций должен быть определен со ссылкой на представленную формулу изобретения.

Земной пласт может включать слои, в которых упругость среды может быть изотропна, анизотропна или изотропна по одним параметрам и анизотропна по другим. Как пример, порода может быть анизотропна и быть трансверсально изотропной «TI» (например, анизотропна с локальной полярностью). Знание изотропии, анизотропии и т.д. могут помочь с, например, планированием, исследованием и развитием одного или нескольких пластовых резервуаров.

В качестве примера параметров, которые могут характеризировать анизотропию слоя (например, сейсмическая анизотропия), рассматриваются параметры Томсена ε, δ и γ (см., например, Томсен, «Weak elastic anisotropy», Geophysics, Vol. 51, No. 10, pp. 1954-1966, October 1986). Параметр Томсена δ описывает разницу в значениях глубины между каротажами (например, фактической глубиной) и сейсмической глубиной. Что касается параметра Томсена ε, он описывает разницу между вертикальными и горизонтальными продольными волнами (например, P или P-волна, или квазипродольная волна qP, или qP-волна). Параметр Томсена γ описывает разницу между поперечными волнами с горизонтальной и вертикальной поляризацией (например, горизонтальная поперечная волна SH или SH-волна, вертикальная поперечная волна SV или SV-волна, или квазивертикальная поперечная волна qSV или qSV-волна). Таким образом, параметры Томсена ε и γ могут быть рассчитаны по волновым данным, а расчет параметра Томсена δ, в свою очередь, требует больше данных. Как указано Томсеном (1986г.), параметр δ отвечает за большинство анизотропных явлений слоев, являющихся предметом исследования геофизики, и некоторых явлений, которыми нельзя пренебрегать, даже если анизотропия слабая.

Как пример, способ может включать подсчет параметра δ для горизонтальной части скважины в пласте, если есть по меньшей мере некоторые данные в диапазоне углов наклона (от приблизительно 40 градусов до приблизительно 90 градусов) в пласте. В таком примере соотношение между нормальной и тангенциальной (или поперечной) податливостью (например, B_N и B_T) может быть подсчитано в случае, если тангенциальная податливость (например, B_T) может быть представлена в единицах коэффициентов упругости, которые могут быть теми же самыми коэффициентами, которые определяют параметр Томсена γ.

Параметры Томсена, как и другие параметры, могут использоваться в различных областях разработки нефтяных месторождений, таких как: заканчивание скважины, построение модели сейсмической скорости миграции, устойчивость ствола скважины, создание гидравлического разрыва пласта и его мониторинг. Как пример, в рамках разработки коллектора сланцевого газа, знание параметров анизотропии могут помочь в планировании, проведении работ и т.д., особенно, когда одна или несколько конфигураций скважин могут отличаться в диапазоне от вертикально до горизонтально направленных.

Как пример, для прогнозирования и применения одного или нескольких значений параметров, способ может включать получение акустических данных в двух или нескольких скважинах с наклоном ствола, которые находятся в одном пласте (например, слое пласта); установление соответствия между глубинами двух или нескольких скважин при помощи корреляции свойств изотропного пласта (например, исходя из диаграмм нейронного каротажа, гамма-каротажа и т.д.); использование данных акустической медленности двух или нескольких скважин для вычислений сейсмической анизотропии (например, вычислений одного или нескольких параметров); определение корреляций между инвертированными параметрами и параметрами, которые могут быть измерены в горизонтальной скважине; и применение подсчитанных корреляций для прогнозирования неизвестных параметров вдоль горизонтальной скважины, исходя из измеренных свойств. В этом примере мы рассматривали две или несколько скважин, рассмотрим другой пример, когда акустические данные могут быть предоставлены для диапазона углов (например, относительно оси симметрии слоя TI), в данном случае акустические данные определяются по результатам измерений в одной или нескольких скважинах, на основе по меньшей мере части которых можно предсказать один или нескольких параметров. Различные примеры работают с величиной медленности, так как скорость можно заменить, исходя из зависимости медленности и скорости.

Фигуры 1 и 2, описанные ниже, показывают некоторые примеры технологий и техник, которые можно применять для сбора акустических данных. Приведены различные примеры способов, систем и т.д., которые могут включать использование акустических данных.

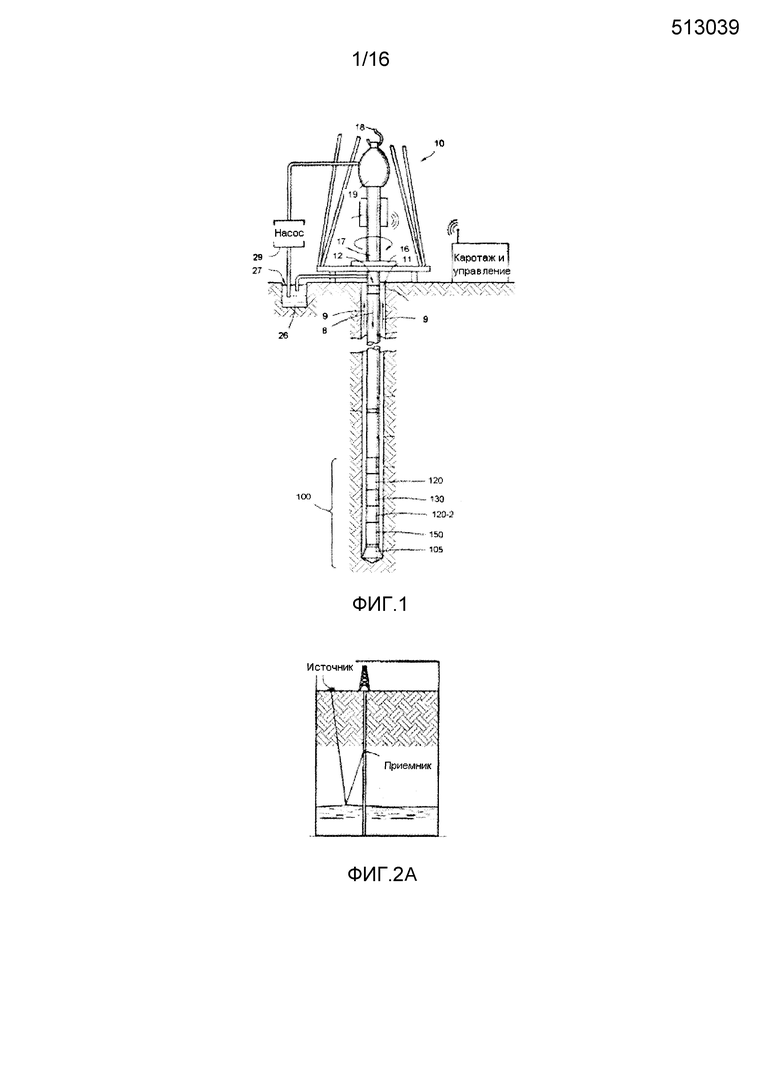
Фигура 1 иллюстрирует систему буровой площадки, в которой можно воплотить различные примеры реализаций заявленного способа. Буровая площадка может быть установлена как в прибрежной зоне, так и в открытом море. В примере системы, показанной на Фигуре 1, буровая скважина 11 сформирована в подземном пласте при помощи всем хорошо известного на практике бурения. Различные примеры реализаций также могут использовать направленное бурение, как будет описано в данной заявке.

Бурильная колонна 12 располагается внутри буровой скважины 11 с компоновкой низа 100, которая включает буровое долото 105 на самом конце. Наземная система включает платформу и монтаж буровой вышки 10, расположенную над скважиной 11, вышка 10 включает буровой ротор 16, ведущую бурильную трубу 17, крюк 18 и вертлюг 19. Бурильная колонна 12 вращается при помощи бурового ротора 16, под током источника, не показанного на фигуре, что приводит в движение бурильную трубу 17 в самом вверху бурильной колонны. Бурильная колонна 12 подвешивается на крюк 18, прикрепленный к талевому блоку (не показан), через ведущую бурильную трубу 17 и вертлюг 19, что позволяет вращать бурильную колонну относительно крюка. В качестве примера может быть использована самая лучшая система привода.

В данном примере такой реализации наземная система дополнительно включает буровой раствор 26, хранимый в амбаре 27 на буровой площадке. Насос 29 поставляет буровой раствор 26 внутрь бурильной колонны 12 через отверстие в вертлюге 19, вследствие чего буровой раствор поступает вниз через всю бурильную колонну 12, как обозначено стрелкой 8. Буровой раствор выходит через отверстие в буровом долоте 105, а затем поднимается вверх по затрубному пространству между бурильной колонной и стеной скважины, как обозначено стрелками 9. Таким хорошо известным способом буровой раствор смазывает буровое долото 105 и переносит буровой шлам на поверхность, так как раствор возвращается в амбар 27 для рециркуляции.

Компоновка 100 низа проиллюстрированного примера включает модуль 120 каротажа в процессе бурения (LWD), модуль 130 измерения в процессе бурения (MWD), роторно-управляемую систему и двигатель, а также буровое долото 105.

LWD модуль 120 находится в корпусе воротника бура специального типа, согласно практике, принятой в промышленности, и может содержать один или несколько типов каротажных приборов. Также будет понятно, что более чем один модуль LWD и/или модуль MWD могут использоваться, например, как показано позицией 120-2. Позиция 120 обозначена для примера, модуль может находиться на позиции 120-2 и т.д. Модуль LWD может измерять, обрабатывать, хранить информацию также, как и взаимодействовать с наземным оборудованием. В настоящем примере реализации модуль LWD включает в себя сейсмическое измерительное устройство.

MWD модуль 130 также помещен в воротник бура специального типа, согласно практике, принятой в промышленности, и может содержать один или более устройств для измерения характеристик буровой колонны и долота. MWD прибор дополнительно включает устройство (не показано) для генерирования электричества в скважинную систему. Это может быть турбогенератор, приводимый в действие потоком бурового раствора, отсюда должно быть ясно, что могут применяться другие источники и/или системы питания. В примере реализации, показанном на фигуре 1, модуль MWD включает один или несколько следующих типов измерительных устройств: измерительное устройство нагрузки на буровое долото, крутящего момента, вибрации, импульса, скачкообразного движения, направления и наклона.

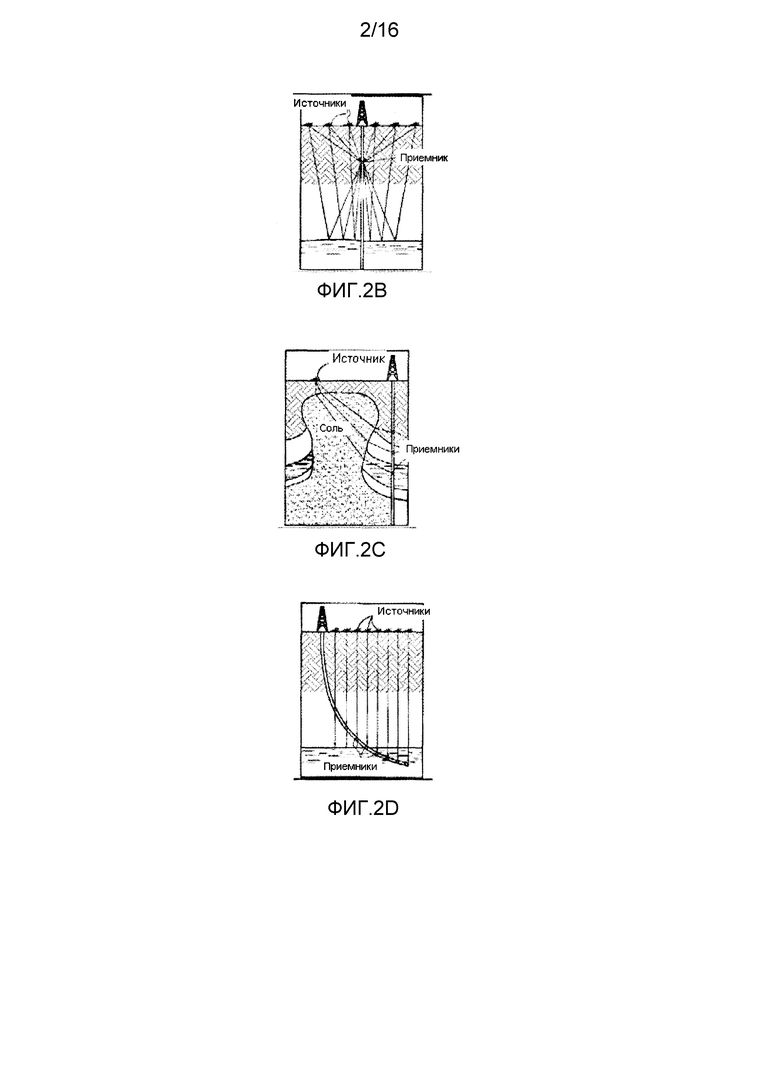
Фигуры 2А, 2В, 2С и 2D иллюстрируют устройство для сейсморазведки в процессе бурения, которым может быть устройство LWD 120 или часть комплекса LWD 120А типа, раскрытого в книге П. Бретона и других «Well Positioned Seismic Measurements», Oilfield Review, pp. 32-45, Spring, 2002, которая включена в описание настоящей заявки в качестве ссылки. Скважинное устройство LWD может иметь один единственный приемник (как показано на Фигурах 2А и 2В) или несколько приемников (как показано на Фигурах 2С и 2D), и может применяться в соединении с одним сейсмическим источником на поверхности (как показано на Фигурах 2А и 2С) или несколькими сейсмическими источниками на поверхности (как показано на Фигурах 2В и 2D). Соответственно, Фигура 2А, где происходит отражение одной волны от границы пласта, - продольное вертикальное сейсмическое профилирование (ВСП), в данном случае используется один источник и один приемник, а Фигура 2В, где происходит отражение нескольких волн от границы пласта, - уровенное ВСП с использованием нескольких источников и одного приемника. Фигура 2С, где происходит преломление волны от границы соляного купола, - ВСП в «случае солевых отложений» с использованием одного источника и нескольких приемников, Фигура 2D, где происходит отражение нескольких волн от границы пласта, называется ВСП в наклонной скважине способом вертикально падающих волн с использованием нескольких источников и нескольких приемников.

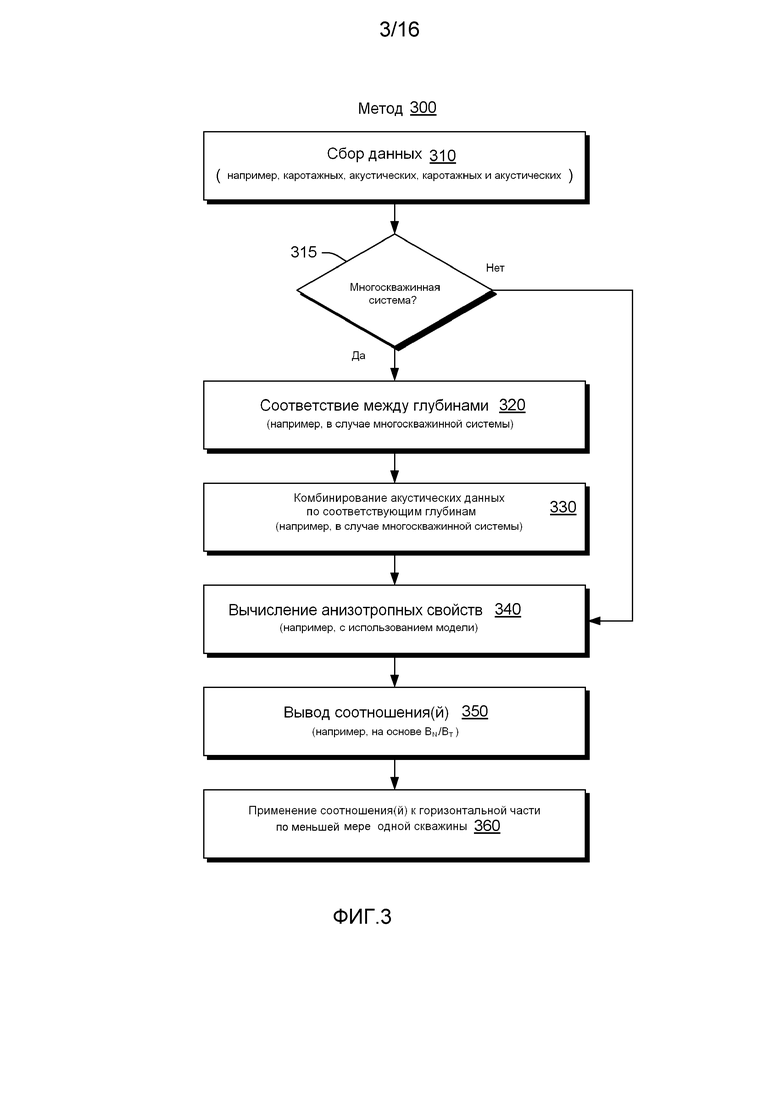
Фигура 3 показывает пример способа 300 для прогнозирования одного или нескольких параметров и для применения этих параметров в подсчетах. Способ 300 включает блок 310 сбора данных, логический блок 315 для определения, относятся ли собранные данные к нескольким скважинам, блок 320 соответствия для определения соответствия глубин многоскважинной системы (на основании данных каротажа, нейтронного, гамма и т.д.), блок 330 комбинирования для комбинирования акустических данных на соответствующих глубинах, где акустические данные взяты в многоскважинной системе, вычислительный блок 340 для определения одного или нескольких анизотропных свойств, на основании по меньшей мере части акустических данных (например, один или несколько анизотропных параметров, которые характеризуют слой или среду), блок 350 вывода для вывода одного или нескольких соотношений (например, эмпирического или другого), на основании по меньшей мере части расчетов вычислительного блока 340 (например, которые могут применяться в процессе инверсии), прикладной блок 360 для применения одного или нескольких соотношений к слою или среде, например, где слой или среда пролегают в горизонтальном направлении (например, ортогонально к оси симметрии слоя TI).

В качестве примера, способ 300 может включать сбор акустических данных в двух или более скважинах с наклоном ствола, расположенный в одном и том же пласте (например, слое пласта) в блоке 310 сбора данных; определение принадлежности акустических данных к нескольким скважинам происходит в логическом блоке 315; определение соответствия глубин между двумя или несколькими скважинами при помощи корреляции свойств изотропного пласта (например, на основе каротажных данных, таких как нейтронного каротажа, гамма-каротажа и т.д.) в блоке 320 соответствия и блоке 330 комбинирования; применение акустических данных медленности из двух или нескольких скважин для подсчета сейсмической анизотропии в вычислительном блоке 340; определение корреляций между инвертированными параметрами (например, в вычислительном блоке 340) и параметрами, которые можно измерить в горизонтальной скважине, в блоке 350 вывода; и применение корреляций для прогнозирования неизвестных параметров горизонтальной скважины, исходя из измеренных свойств, в прикладном блоке 360. Этот пример рассматривает две или несколько скважин, в качестве другого примера, акустические данные могут быть предоставлены для диапазона углов (например, относительно оси симметрии слоя TI) в том случае, когда акустические данные определяются по результатам измерений в одной скважине или многоскважинной системы, и один или несколько параметров могут быть спрогнозированы на основе по меньшей мере части акустических данных.

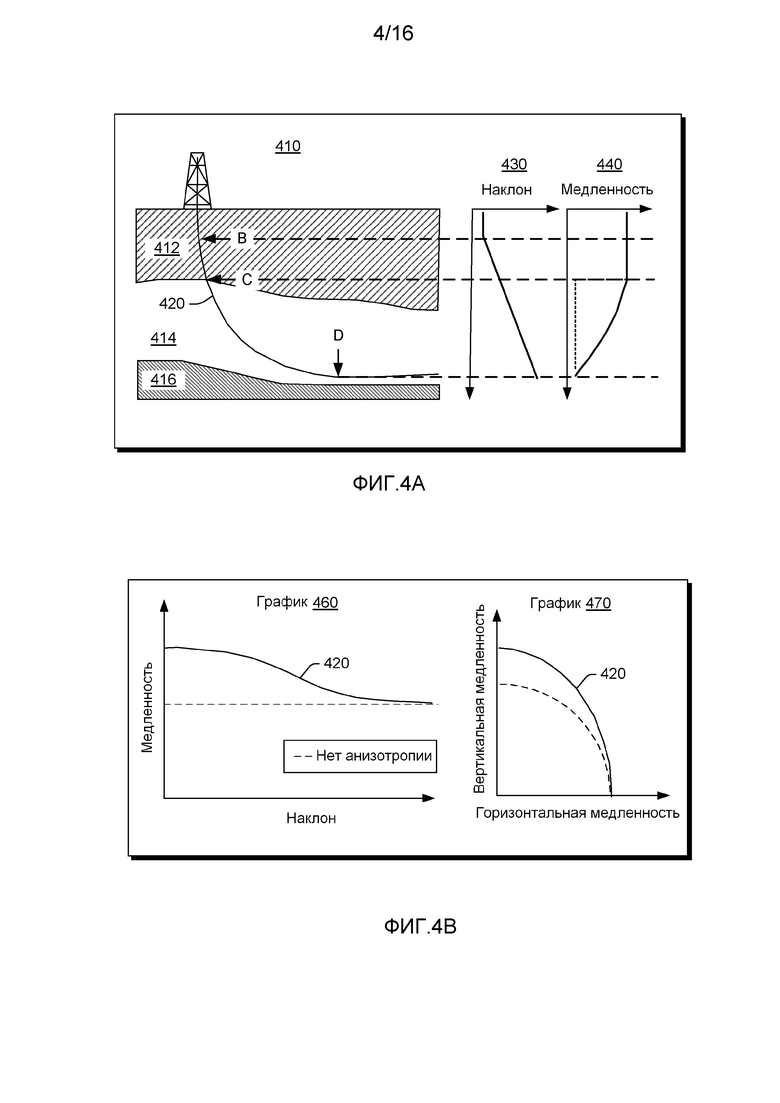
Фигура 4А показывает схематическое поперечное сечение земной коры 410, которое включает целевой пласт 414 между верхним пластом 412 и нижним пластом 416. Как показано, одна наклонная скважина 420 входит в целевой пласт 414 почти под вертикальным углом (обозначено С), который потом переходит в горизонтальное направление (обозначено D). График 430 показывает изменение наклона скважины 420 как функцию от глубины, на которой происходят изменения наклона между В и С, С и D (то есть внутри целевого пласта 414). Такие скважины могут быть пробурены в нетрадиционном газовом коллекторе с низкой проницаемостью (например, Haynesville Shale, Barnett Shale и т.д.). В случае, если каротажные измерения сняты с наклонных частей скважины 420 (например, от точки В до С и от точки С до D), значения сигналов могут отличаться, даже если пласт однороден по своей структуре, так как существует такое явление как анизотропия.

В примере, показанном на Фигуре 4А, верхний пласт 412 может рассматриваться как перекрывающие породы, которые могут быть настолько изотропны, что медленность не меняется в наклонной части скважины 420 (от точки В до С), потому что верхний пласт 412 однородный и изотропный. Тем не менее в целевом пласте 414, наклон ствола скважины 420 изменяется (от точки С до D) и, даже с учетом того, что целевой слой 414 однородный, медленность (см. график 440) меняется, потому что целевой пласт 414 в какой-то степени анизотропный. В случае, когда целевой пласт 414 стал полностью изотропным, измеренная медленность будет оставаться постоянной во всем целевом пласте 414 (см., например, пунктирную линию на графике 440) для всей скважины 420 внутри целевого пласта 414.

На Фигуре 4В показаны графики зависимости медленности от наклона скважины 460 и зависимости вертикальной медленности от горизонтальной 470. На графиках 460 и 470 измеренная медленность в наклонной части скважины, в случае, если пласт анизотропный, показано сплошной линией, а для изотропного пласта (например, без анизотропии) показано пунктирной линией. На графике 460 медленность расположена по вертикальной оси, а наклон ствола скважины - по горизонтальной. Такие же данные показаны на графике 470 с использованием полярного представления, где изотропное поведение изображается круговым сегментом (например, в отличие от эллиптического сегмента для анизотропного случая).

Таким образом, разница между изотропным и анизотропным поведением может быть показана графическим изображением зависимости медленности от наклона ствола скважины. Анализируя эти данные, становится возможным вычислить некоторые параметры упругости пласта; следует отметить, что такие параметры могут применяться в различных областях разработки нефтяных месторождений, таких как: заканчивание скважины, устойчивость ствола скважины, создание гидравлического разрыва пласта и его мониторинг, определение миграции глубин по исходным сейсмограммам.

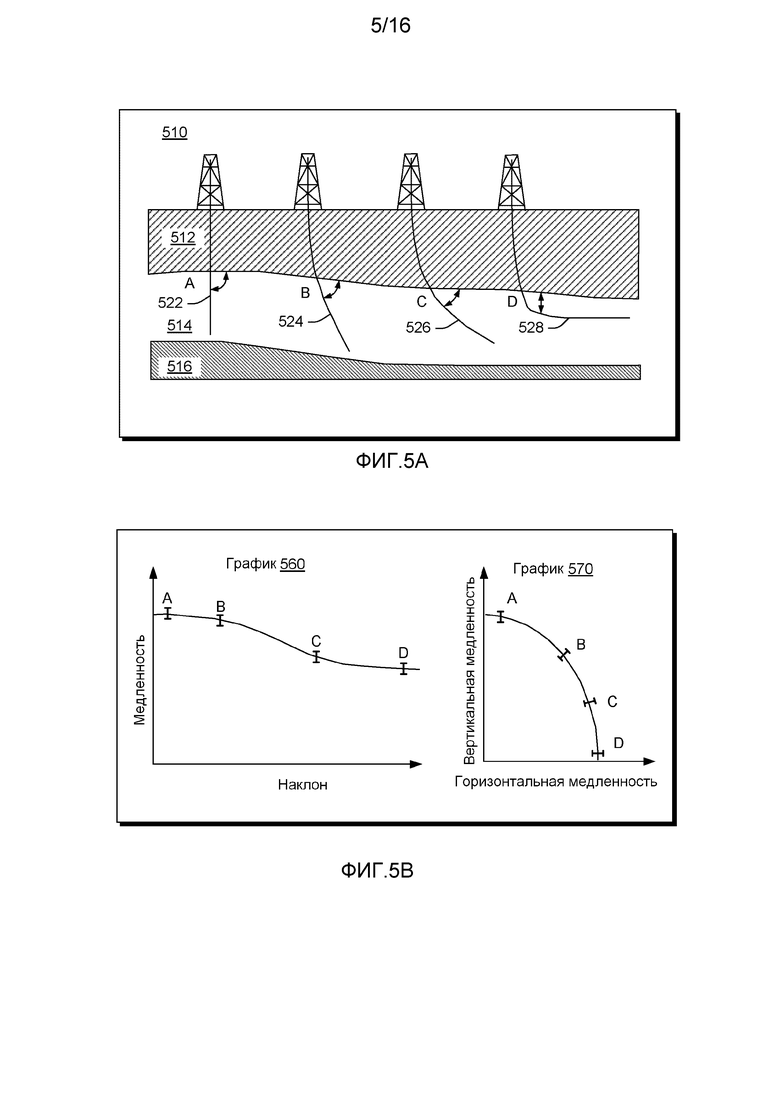
Акустические данные, снятые в наклонных скважинах, зависят от упругости анизотропии, что в результате приводит к зависимости скорости от угла. В качестве примера, продольные акустические измерения нескольких наклонных скважин внутри одного и того же пласта могут использоваться при подсчете упругости анизотропии. Фигура 5А показывает схематическое поперечное сечение земной коры 510, которое включает целевой пласт 514 между верхним пластом 512 и нижним пластом 516. Внутри целевого пласта 514 размещены разные скважины 522, 524, 526 и 528, каждая из которых имеет общий угол наклона, варьирующийся примерно от 0 до 90 градусов, например, относительно вертикального направления (0 градусов), что может соответствовать оси симметрии доминирующего слоя целевого пласта 514.

На примере Фигуры 5А, способ может включать многоскважинный подход для подсчета анизотропии пласта от данных нескольких скважин по разным углам наклона в одном и том же пласте (например, разные углы для каждой из скважин системы). В качестве такого примера, данные медленности с таких скважин могут быть выведены как функция от угла наклона скважины, как показано на графиках 560 и 570 Фигуры 5В, из чего можно подсчитать параметры анизотропии пласта 514. В примере, показанном на Фигурах 5А и 5В, четыре скважины 522, 524, 526 и 528, каждая из которых имеет разный угол наклона ствола (см. точки от А до D), проникают в анизотропный пласт 514. Графики 560 и 570 показывают усредненные данные медленности в пласте, изображенные как функция от угла наклона скважины для четырех разных углов (например, один из которых составляет примерно 0 градусов, а другой - примерно 90 градусов). Так как пласт 514 анизотропный, то медленность в нем варьирует в зависимости от угла наклона скважины.

В качестве примера, что показывает случай на Фигурах 5А и 5В, алгоритм может использовать способ наименьших квадратов между измеренными скоростями Р-волн как функцию от угла наклона ствола скважины относительно плоскости пласта (например, горизонтально залегающий пласт) и строить модель скоростей группы Р-волн для анизотропной модели. Такая анизотропная модель может быть модифицирована до тех пор, пока разница между измеренными и смоделированными акустическими данными продольных волн не станет минимальной.

Другой подход для такого же случая может рассчитывать на данные по трем заданным угловым диапазонам (приблизительно вертикальный, приблизительно горизонтальный и равный приблизительно 45 градусов). Для приблизительно вертикального и горизонтального углов/направлений существуют аналитические выражения для группы скоростей, из которого можно подсчитать определенную постоянную упругости. Тем не менее относительно данных на 45 градусах, может быть сделано допущение, что фазовые углы не сильно отличаются от группы углов. Такое допущение может дать следующие результаты: во-первых, данные будут доступны для вертикального и горизонтального направлений (например, вертикальный и горизонтальный угол скважины относительно оси симметрии VTI); и, во-вторых, группа углов близкая по значению к фазовым углам может оказаться недействительна, из-за сложности поведения qSV-волн при некоторых комбинациях постоянных упругости.

Что касается другого подхода, включающего акустические данные о P-, S- и трубной волне (например, «волне Стоунли»), то, в данном случае, возможно подсчитать параметры упругости анизотропии. Такая техника основана на включении данных от скважин, которые, главным образом, вертикальны (см., например, скважина 522 на Фигуре 5А). Такой подход использует уравнение плосковолновой скорости (фазовой) со слабой анизотропией, которое не всегда может подойти, особенно, если присутствует qSV-волна, когда могут возникнуть тройственности. В вышеуказанном подходе, P, SV и SH акустические данные от вертикальной нагнетательной скважины и данные от наклонной скважины могут использоваться для подсчета средней анизотропии по пласту.

В еще одном подходе сигнал от поперечной волны от одной скважины может быть проанализирован в терминах «мнимой анизотропии», подсчитанной из разницы в скоростях SV и SH волн. При таком подходе мнимая анизотропия выражается в виде функции зависимости от угла наклона скважины, что позволяет определить три разных режима в зависимости от разницы двух параметров Томсена ε и δ.

Как пример, способ 300 может включать данные о поперечной волне в вычислительный процесс, дополнительно включать данные о трубной волне (например, волне Стоунли) и прогнозировать один или несколько параметров для определения характеристик пласта (например, слоя) без допущения, что анизотропия «слабая» (см., например, Томсен 1986г.). Дополнительно, способ 300 может вычислять одно или несколько подмножеств постоянных упругости (например, или эквивалентных параметров), используя одно или несколько множеств: волны P, SV, SH, трубная/Стоунли (например, включая qP, qSV составляющие и т.д.). В качестве примера, способ 300 может применяться в случаях, когда присутствует латеральная однородность (например, без применения условия, что вертикальная однородность существует).

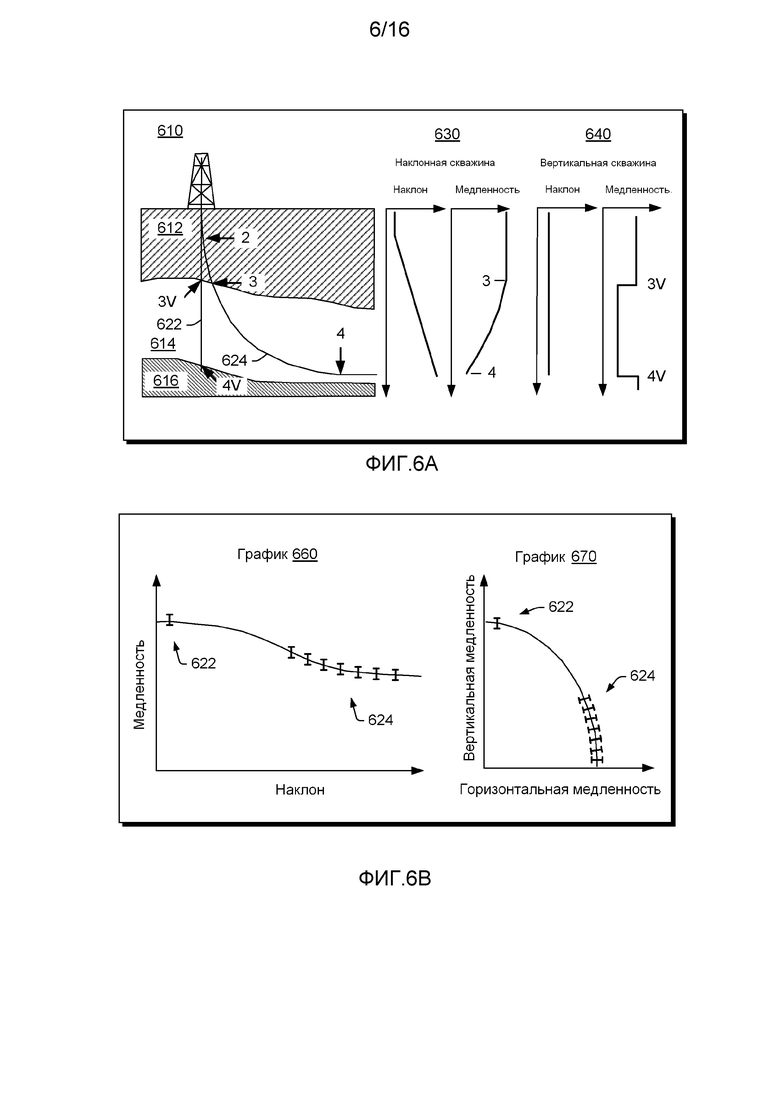
В качестве примера, способ может включать использование акустических данных от нагнетательной скважины (например, необязательно вертикальной) и части наклонной скважины (например, изгиба). Фигура 6А показывает схематический поперечный разрез земной коры 610, который включает целевой пласт 614 между верхним пластом 612 и нижним пластом 614. В целевом пласте 614 размещены две скважины 622 и 624, из которых скважина 622, главным образом, вертикальная (например, 0 градусов), а скважина 624 наклонная с изгибом в диапазоне углов от приблизительно 45 градусов до приблизительно 90 градусов (например, от 40 градусов до 90 градусов), например, относительно вертикального направления (0 градусов), что может соответствовать оси симметрии доминирующего слоя целевого пласта 614 (например, слоя TI). Фигура 6А также показывает графики 630 наклона и медленности по отношению к глубине наклонной скважины 624 и графики 640 наклона и медленности по отношению к глубине скважины 622. В примере Фигуры 6А скважина 622 может быть нагнетательная, а наклонная скважина 624 может быть эксплуатационная.

Фигура 6А показывает различные точки скважин 622 и 624, где, например, наклонная часть скважины 624 (от точки 2 до точки 4) не лежит вся в целевом пласте 614; таким образом, целевой пласт 614 ограничен диапазоном углов. Также, в наклонной части скважины 624, которая находится в целевом пласте 614 (от точки 3 до точки 4), углы больше чем в перекрывающих породах (в верхнем пласте 612). Как пример, данные скважины 622 (например, вертикальной нагнетательной) (например, от точки 3V до точки 4V) могут быть использованы для вычислений в рамках целевого пласта 614 по приблизительно вертикальному направлению (например, углы, равные или приблизительно равные 0 градусов). Если существует множество данных скважины 622 (например, внутри целевого пласта 614) и другое множество данных скважины 624 (например, внутри целевого пласта 614), то способ может включать комбинацию этих двух множеств данных для улучшения результатов подсчета одного или нескольких свойств анизотропии целевого пласта 614.

Фигура 6В показывает графики 660 и 670 комбинированных данных, которые можно сравнить с графиками 560 и 570 Фигуры 5В. На графиках 660 и 670 представлены данные вертикальной медленности по углу, равному или приблизительно равному 0 градусов наклона, и данные наклонной части с наклоном больше чем приблизительно 45 градусов до приблизительно 90 градусов (например, в диапазоне от 40 градусов до 90 градусов). Опять же, графики 560 и 570 Фигуры 5В показывают данные для четырех дискретных углов (например, скважины 522, 524, 526 и 528), которые включают вертикальное и горизонтальное направления (например, по двум точкам для двух углов между вертикальным и горизонтальным направлением). На графиках 660 и 670 Фигуры 6В, в качестве примера, показаны семь точек по углам больше чем приблизительно 45 градусов.

В качестве примера, для описанных вертикальной скважины и наклонной скважины с наклонной частью больше чем приблизительно 40 градусов до приблизительно 90 градусов (например, включая данные по наклону приблизительно 45 градусов и данные по дополнительным, большим углам), находящиеся внутри целевого пласта, глубины могут быть определены при помощи корреляции каротажа. В таком примере акустические данные вертикальной скважины на одной глубине могут быть объединены с акустическими данными наклонной скважины на такой же глубине в пласте. Такие объединенные акустические данные (например, акустические измерения волн) могут использоваться для подсчета свойств упругости пласта на этой глубине. Имея в наличии подсчитанную анизотропию, корреляции могут быть выполнены между (а) параметрами, которые могут быть измерены в горизонтальной части пласта (например, в наклонной скважине), и (b) неизвестными особенностями. Одно или несколько соотношений, основанные на корреляции (например, между измеряемыми параметрами и неизвестными особенностями), могут потом использоваться для прогнозирования одного или нескольких неизвестных особенностей пласта вдоль горизонтальной части пласта, исходя из измеренных значений параметров пласта.

В качестве примера, акустические данные могут быть вычислены при помощи измерений талевого каната, с использованием LWD измерений или других техник. В наклонной части скважины внутри пласта акустические данные зависят от анизотропии таким образом, что медленность пласта является функцией от угла наклона ствола скважины (например, на различных глубинах для одной наклонной скважины). Такие вариации значения медленности могут использоваться при подсчете упругих свойств пласта и связанных с ними характеристик. Такая информация будет полезна для широкого диапазона операций, таких как: процесс заканчивания скважины, избегание неустойчивости ствола скважины, определение точки для отводящей скважины в нетрадиционных природных породах, таких как сланец, создание гидравлических разрывов, мониторинг с помощью микросейсмических исследований.

Упругие свойства многих типов горных пород можно аппроксимировать с помощью Трансверсальной Изотропии с Вертикальной осью симметрии (VTI или Tl). Физические свойства вещества VTI теоретически идентичны по направлению оси симметрии. В случае горизонтальной множественной слоистости осадочной горной породы ось симметрии вертикальна. Для такой системы тензор упругой деформации может быть описан с использованием пяти коэффициентов упругости: С₁₁, С₃₃, С₄₄, С₆₆ и С₁₃. Данные пять коэффициентов упругости соответствуют коэффициентам тензора напряжений, представленного как «оптимальное представление» (см, например, оптимальное представление Фойгта 940 Фигуры 9).

Пять коэффициентов упругости описывают изменение скорости для трех разных типов волн, квазипродольной волны (qP), квазипоперечной волны с вертикальной поляризацией (qSV) и поперечной волны с горизонтальной поляризацией (SH). Поведение qP и qSV волн зависит от коэффициентов упругости С₁₁, С₃₃, С₄₄ и С₁₃, которые можно интерпретировать как параметры пласта. Что касается поведения SH волны, то оно зависит от значений коэффициентов С₄₄ и С₆₆.

В качестве примера, модель может быть определена на основе коэффициентов упругости (например, или подмножества). Собираемые акустические данные (например, в вертикальной нагнетательной скважины и наклонной эксплуатационной скважины, или по другому сценарию) могут интерпретироваться как данные для модели. В качестве примера, на основе использования такой модели и данных, способ может включать подсчет значений коэффициентов упругости или соответствующих эквивалентов, исходя из акустических данных, измеренных в вертикальной части скважины (например, нагнетательной скважины) и наклонной части скважины (например, наклонной эксплуатационной скважины).

На основании модели, которая описывает анизотропию пласта, могут быть вычислены синтетические данные. На основании измеренных данных вертикальной части скважины в пласте и наклонной части скважины в пласте (например, или данных с других точек) может быть произведен процесс согласования данных, который сопоставляет синтетические данные и измеренные данные. Такой процесс согласования может включать корректировку модели (например, один или несколько параметров модели, которые могут включать один или несколько из вышеуказанных пяти коэффициентов упругости, или эквивалентных им), чтобы минимизировать разницу (или разницы) между по меньшей мере некоторыми из измеренных и синтетических данных.

Что касается модели для подсчета (например, генерирования) синтетических данных, в качестве примера, может быть применена трехмерная конечно-разностная методика. Маллан и др., 2011 г., «Simulation of borehole sonic waveforms in dipping, anisotropic, and invaded formations», (Geophysics, Vol. 76, No. 4, pp. Е127-Е139), который включен в описание настоящей заявки в качестве ссылки, описывает примеры трехмерной конечно-разностной методики (3D FDTD), примененной в пластах с TI симметрией, где скорости продольной и поперечной волны были приравнены к своим коэффициентам упругости С₁₁, С₃₃, С₄₄ и С₆₆. Коэффициенты упругости С₁₂, С₁₃ были получены из комбинаций коэффициентов упругости С₁₁ и С₆₆, С₃₃ и С₄₄ соответственно. 3D FDTD методика обеспечивает численное моделирование акустических измерений скважины, используя Декартовую (прямоугольную) систему координат. 3D FDTD решения и дифференциальные уравнения скорость-напряжение, которые включают 3D вектор скорости, напряжения и тензоры напряжения, связаны между собой через тензор жесткости четвертого ранга, который описывает TI слой (то есть с коэффициентами упругости С₁₁, С₃₃, С₄₄, С₆₆ и С₁₃). 3D FDTD методика включает дискретизацию уравнений с использованием сдвинутой сетки, центральной конечной разности второго порядка в пространстве и во времени. В качестве примера, сетка FD с 1260х181х92 ячейками была использована для осей z, x и y, соответственно. Статья Маллана и других представляет результаты симуляции для вертикальной скважины с акустической энергией, характеризующейся кольцевым плавающим проникающим фронтом. Статья также представляет результаты симуляции для наклонной скважины с целью выявления глубины залегания TI. В качестве примера, 3D FDTD методика может быть реализована для вычисления полной формы волны (например, синтетических данных), которые потом могут быть согласованы с измеренными формами волны (например, измеренными данными формы волны).

В качестве примера, вышеуказанная методика 3D FDTD может применяться в подсчете синтетических данных. В таком примере команды записываются в компьютерный носитель информации и могут выполняться одним или двумя процессорами компьютера для подсчета синтетических данных. Как показано, методика 3D FDTD включает различные коэффициенты, переменные и т.д. Если способ включает минимизацию разницы (разниц) между синтетическими и измеренными данными, то один или несколько коэффициентов, переменных и т.д. модели могут быть отрегулированы для минимизации такой разницы (разниц). Дополнительно, как может быть ясно, один или несколько коэффициентов, переменные и т.д. могут зависеть от глубины. Например, так как измеренные данные могут зависеть от глубины, модель может включать коэффициенты, переменные и т.д., которые зависят от глубины для возможности согласования параметров (например, минимизировать одну или несколько разниц).

Как указано, способ может включать согласование подсчитанных, синтетических данных о форме волны с измеренными данными формы волны. В качестве другого примера, скорости могут быть подсчитаны с использованием модели, которая моделирует скорости как от точечного источника (например, группы скоростей), расположенного в однородном слое. В качестве примера, в случае слабой анизотропии, модель, которая моделирует плосковолновые скорости (например, «фазовые скорости»), вступающие в однородном слое, может подходить для предоставления синтетических данных (например, и для согласования, минимизации и т.д.).

Для материалов с TI анизотропией существуют аналитические выражения для изменений плосковолновой скорости («фазовой») (см, например, Thomsen, 1986г.). Такие выражения плосковолновой скорости могут подходить, в случае, если энергия источника возбуждает плоские волны, или слабая анизотропия. В случае, если источник представлен как точечный источник, то скорости, которые измеряются, являются группами скоростей, для которых существуют несогласованные аналитические выражения для подсчета групп скоростей волн qP и qSV для заданного направления групп. Эти скорости от «точечного источника» (группы) могут тем не менее быть подсчитаны для заданного плосковолнового направления с помощью решения уравнения Кельвина-Кристоффела, после чего возможно подсчитать вектор группы скоростей, направление которого задает направление группе (см., например, Musgrave, 1970, Crystal Acoustics, Holden-Day, San Francisco; Auld, 1990, Acoustic Fields and Waves in Solids, Krieger Publishing Company, NY).

В случае дипольного акустического каротажа, измеренные скорости являются группой скоростей (Hornby et al., 2003, Do we measure phase or group velocity with dipole sonic tools?, 65th EAGE Conference, Extended Abstracts, F-29). В качестве примера, способ может включать таблицу соответствия векторов скоростей точечного источника (то есть «группы») по разным направлениям модели. В таком примере таблица соответствия потом может быть исследована для нахождения направлений точечного источника (т.е. «группы»), которые близки к направлению вертикальной части (например, нагнетательной или другой скважины) и наклонным направлениям (например, наклонной скважины, которая может быть эксплуатационной скважиной) измеренных данных. Подсчитанные направления точечного источника (то есть «группы») (например, на основании по меньшей мере части таблицы соответствия) потом могут быть сравнимы с измеренными акустическими данными, используя, например, целевую функцию. В качестве примера целевой функции, рассмотрим следующее уравнение:

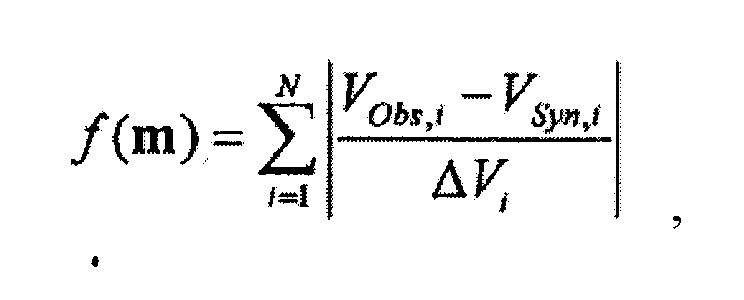
где m - это модель, описывающая свойства упругости пласта, N - это число точек, которые использовались для снятия данных каротажа, V_Obs,i - измеряемые скорости, V_Syn,i - соответствующие синтетические скорости, подсчитанные для данной модели и данного наклона скважины. Так как это уравнение включает скорости, то медленность можно заменить (например, или другие соответствующие переменные, которые согласуются с данными).

В качестве примера, после того как способом найдено оптимальное соответствие между измеренными и синтетическими данными, подсчитанными моделью, модель может быть использована для различных целей. Например, параметры анизотропии можно использовать в конструировании модели скорости для использования в определении местоположения микросейсмических явлений, вызванных операциями гидроразрыва. В качестве примера, подход, описанный Erwemi et al., 2010 г., «Anisotropic velocity modeling for microseismic processing: Part 3 - borehole sonic calibration case study» (2010 SEG Annual Meeting, Denver, Colorado, Expanded Abstracts 29, pp. 508-512), может применяться в соединении с согласованной моделью (например, согласованной моделью на основе измеренных и синтетических данных).

В качестве другого примера, согласованная модель может быть построена способом, который использует подсчет параметров анизотропии, с целью компенсации или регулировки данных акустического каротажа наклонной части скважины (см., например, Hornby et al., 2003, "Anisotropy correction for deviated-well sonic logs: Application to seismic well tie," Annual International Meeting, SEG No. 69, Vol. 68, No. 2, pp. 464-471).

В качестве еще одного примера, согласованная модель может быть построена способом с целью вычисления особенностей анизотропии. В таком примере особенностью может быть соотношение B_N/B_T (Sayers, 2008 г., «The effect of low aspect ratio pores on the seismic anisotropy of shales,» 2008 SEG Annual Meeting, Las Vegas, Nevada, Expanded Abstracts 27, pp. 2750-2754»), которое показано в отношении газонасыщенности в залежах сланца. Соотношение B_N/B_T может описать или охарактеризовать деформацию межчастичных областей слоя под приложенным напряжением. В соответствии с Sayers (2008г.), у которого были сделаны допущения, что слой состоит из направленных глинистых частиц, параметр Томсена γ может быть смоделирован в зависимости от свойств межчастичной области через тангенциальную (поперечную) податливость B_T.

Снова ссылаясь на способ 300 на Фигуре 3, в качестве примера, соотношение B_N/B_T может быть использовано в процедуре вывода, которая получает соотношение (см., например, блок 350 вывода). В таком примере подсчет соотношения B_N/B_T может быть применен в прогнозировании одного или нескольких анизотропных параметров в горизонтальной скважине, пробуренной внутри VTI пласта. Например, способ 300 Фигуры 3, прикладной блок 360 может использовать коэффициент B_N/B_T как выведенное соотношение для горизонтальной части по меньшей мере одной скважины для прогнозирования одного или нескольких анизотропных параметров в случае, когда один или несколько анизотропных параметров включают параметр Томсена δ или эквивалентный.

Что касается параметров нормальной и тангенциальной (поперечной) податливости B_N и B_T, то параметр B_T может быть определен по коэффициентам упругости С₄₄ и С₆₆, которые могут быть теми же самими коэффициентами упругости, которые могут быть использованы для определения параметра Томсена γ; тем не менее надо иметь в виду, что параметры податливости B_N и B_T имеют размерность обратную напряжению, а параметр Томсена γ - безразмерный. Таким образом, если параметр Томсена γ известен (то есть связан с горизонтальной частью скважины) или, более определенно, если С₄₄ и С₆₆ известны, то становится возможным определить B_T (например, исходя из данных С₄₄ и С₆₆), и из соотношения между B_T и B_N становится возможным определить B_N. Относительно коэффициентов С₄₄ и С₆₆ эти значения коэффициентов упругости могут быть определены из данных медленности поперечной волны (например, волн S_SH и S_SV, или S_qSV) и плотности (см., Фигура 10). По известным B_N и С₁₁ становится возможным определить коэффициенты упругости С₁₃ и С₃₃. Относительно С₁₁, его можно определить, например, исходя из продольной медленности (например, Sp или S_qP) и плотности вдоль горизонтальной части скважины (см., например, Фигуру 10). Таким образом, через соотношение B_T и B_N можно определить значения пяти коэффициентов упругости С₁₁, С₁₃, С₃₃, С₄₄ и С₆₆. Как показано на Фигурах 9 и 10, значения этих пяти коэффициентов упругости позволяют определить параметры Томсена ε, δ (δ^*) и γ. Как было отмечено Томсеном (1986г.), касательно этих трех параметров, существует особый интерес к параметру Томсена δ (например, δ^*), который может характеризовать изменения скорости вертикальной Р-волны, угловую зависимость скорости SV-волны и т.д. Знание параметра Томсена δ (например, δ^*) может быть полезно по разным причинам (например, изображения/влияния глубины, характеристика слоя, состав слоя и т.д.).

В качестве примера, при наличии данных одного или нескольких подсчитанных значений для одного или нескольких анизотропных параметров горизонтальной части скважины (например, включая параметр Томсена δ или эквивалентный) для пласта, способ может включать прогнозирование будущей эксплуатации пласта. В качестве другого примера, можно определить общее органическое содержание (TOC) в залежах сланца (то есть, если пласт сланцевый). Такой пример может применять корреляцию между TOC и анизотропными параметрами сланца (например, указанное Sondergeld et al., 2000, "Ultrasonic measurement of anisotropy on the Kimmeridge Shale," 2000 SEG Annual Meeting, Calgary, Alberta, Expanded Abstracts 19, pp. 1858-1861). Возвращаясь обратно к способу 300 на Фигуре 3, такой способ может вывести один или несколько значений, которые могут использоваться для вычисления признаков (или даже измерений) TOC.

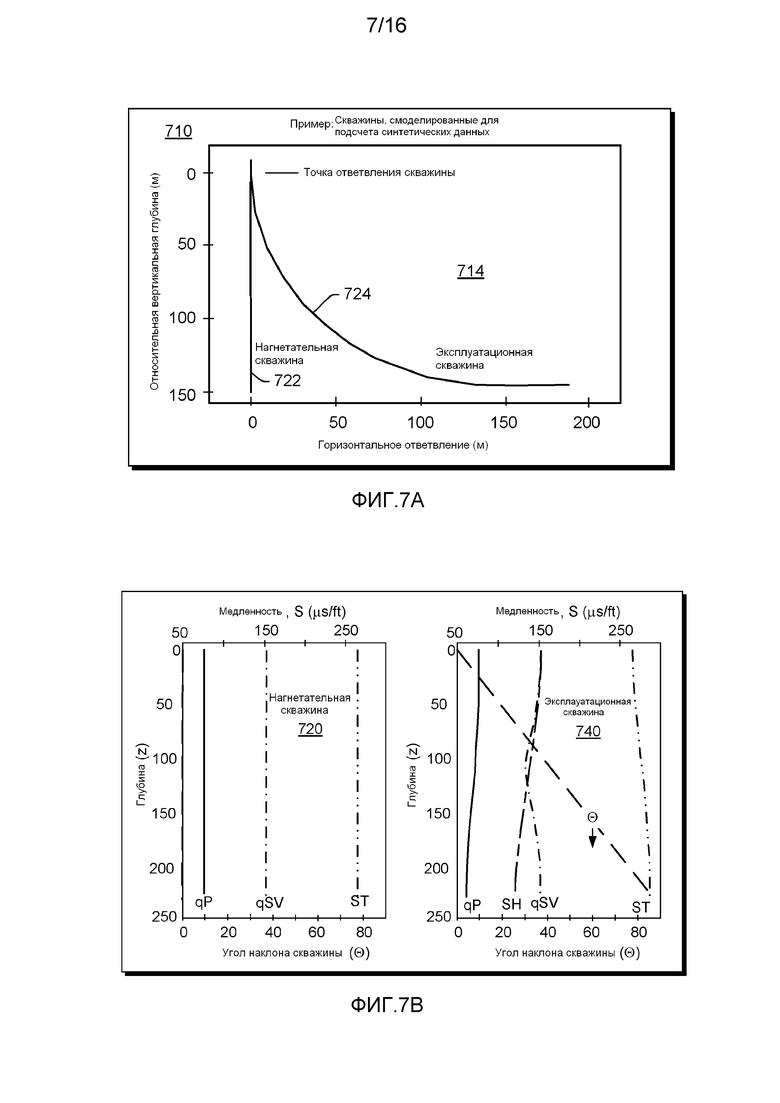
В примере, описанном ниже, модель используется для вычисления синтетических данных. Синтетические данные генерируются для двух скважин с использованием модели, которая моделирует скважины как вертикальную нагнетательную и наклонную эксплуатационную скважину с постоянной степенью набора угла 12 градусов с шагом 30 м, в результате чего эксплуатационная скважина из вертикальной переходит в горизонтальную меньше чем через 150 м в диапазоне вертикальной глубины. В наклонной части скважины пласт представляется как однородный со следующими свойствами упругости: скорость вертикальной Р-волны - 4000 м/с, скорость вертикальной S-волны - 2000 м/с, параметр Томсена ε - 0,3, дельта Томсена - 0,1, параметр Томсена γ - 0,3 и плотность - 2,09 г/см³. Свойства флюида в скважине: скорость флюида - 1500 м/с и плотность флюида - 1,5 г/см³.

Фигура 7А показывает график 710 зависимости относительной вертикальной глубины в метрах от горизонтального ответвления в метрах для вышеуказанной нагнетательной скважины 722 и эксплуатационной скважины 724 в принятом однородном пласте 714. Фигура 7В показывает графики 720 и 740 синтетических данных (например, акустических данных) для вертикальной нагнетательной скважины 722 и наклонной эксплуатационной скважины 724, соответственно. Графики 720 и 740 показывают зависимость медленности (в большем масштабе) от глубины и угол наклона скважины (в меньшем масштабе) от глубины. Для эксплуатационной скважины 724, как показано на графике 740, квазипродольная волна (qP) и поперечная волна с горизонтальной поляризацией (SH) показывают уменьшение медленности, так как эксплуатационная скважина 724 меняет угол от вертикального до горизонтального. Изменение этих скоростей в однородном пласте (то есть пласте 714) происходят из-за анизотропных явлений. Из этих синтетических данных, или подмножеств, qP, qSV, SH и низкой частоты волны Стоунли (также известной как трубной волны) акустические данные могут быть извлечены по данным наклонной части эксплуатационной скважины 724 и одного или нескольких параметров анизотропии. Относительно графика 720, так как пласт 714 однородный и нагнетательная скважина 722 вертикальна, значения qP, qSV и ST относительно глубины не меняются.

Фигура 8 показывает график 740 Фигуры 7 синтетических данных, увеличенный и с дополнительными данными. В особенности, данные представляют α₀, β₀, ε, γ, Δz и Δθ. Как показано, диапазон глубины Δz отвечает диапазону угла Δθ от приблизительно 45 градусов до приблизительно 80 градусов (например, в диапазоне от 40 градусов до 90 градусов). В этих диапазонах меняются значения синтетических данных SH и qSV, разница между этими значениями (ΔS) в горизонтальной части (то есть приблизительно 90 градусов или π/2) соотносится с параметром Томсена γ, например, рассмотрим уравнение γ=(v_SH(π/2)-β₀)/β₀, где v_SH(π/2) - это горизонтальная скорость поперечной волны SH, а β₀ - это вертикальная скорость звука для поперечной волны (например, V_SV(0), V_SH(0)). Дополнительно, для qP-волны изменение в значении возникает от вертикальной части (например, приблизительно 0 градусов) до горизонтальной части (например, почти 90 градусов), где изменение (ΔР) соотносится с параметром Томсена ε, например, рассмотрим уравнение ε=(V_P(π/2)-α₀)/α₀, где V_P(π/2) - это горизонтальная скорость продольной волны Р (например, qP), α₀ - вертикальная скорость звука для продольных волн (например, V_P(0)). На графике 740 параметры анизотропии α₀ и β₀ показаны в отношении медленности с учетом того, что медленность и скорость величины обратные. В особенности, параметр α₀ аппроксимирован значением медленности или значениями SH в вертикальной части и qSV в вертикальной и горизонтальной. На графике 740 синтетических данных, диапазон Δθ можно интерпретировать как зону наилучшего восприятия: диапазон углов, где акустические данные показывают разницу изменений между SH и qSV вследствие анизотропии пласта (например, в отношении медленности или скорости).

Что касается примера, где могут быть сделаны измерения, Фигура 9 показывает пример слоистой геологической среды 902 с наклонной скважиной 904 и скважинное устройство 906 в Декартовой (прямоугольной) системе 912 координат и цилиндрической системе 914 координат. В таком примере, скважинное устройство 906 может включать приборы для снятия измерений (например, приемник, трансмиттер, приемник и трансмиттер и т.д.); на Фигурах 1 и 2 показаны разные примеры. В Декартовой (прямоугольной) системе 912 координат тензор 920 напряжения может быть представлен частью коэффициентов упругости. Как было указано, оптимальное представление 940 Фойгта может изменить коэффициенты упругости с целью уменьшения общего количества коэффициентов. Такое представление может также изменить индексы i, j, k и l на α и β, например, для матрицы 960 модуля упругости С_αβ. Как показано на Фигуре 9, параметры 980 Томсена могут быть описаны различными коэффициентами упругости матрицы модуля 960 упругости.

Фигура 10 показывает пример уравнения для скоростей волнового фронта и параметра 1020 Томсена δ, и разные примеры уравнений 1040 для вертикального и горизонтального волнового фронта. В уравнении 1040, «v» относится к скорости, а «S» к медленности. Уравнения 1040 можно сравнить с графиком 740 Фигур 7 и 8 для понимания того, как различные коэффициенты, переменные и т.д. соотносятся с данными медленности (например, или данными скорости).

Фигура 11 показывает пример способа 1110, который включает блок 1140 предоставления данных, блок 1150 предоставления соотношения и блок 1160 выхода. Фигура 11 также показывает различные блоки 1142, 1152 и 1162 компьютерных носителей информации (CRM), которые могут включать команды, выполняемые компьютером для управления компьютерным устройством с целью выполнения одного или нескольких действий способа 1110. На Фигуре показаны несколько отдельных блоков CRM, но каждый CRM может включать команды для выполнения одного или нескольких действий, связанных с блоком 1140 предоставления данных, блоком 1150 предоставления соотношения и блоком 1160 выхода.

Что касается блока 1140 предоставления данных, то он может предоставлять данные медленности продольных и поперечных волн для однородного, анизотропного пласта при углах наклона скважины больше чем приблизительно 40 градусов и меньше чем приблизительно 90 градусов, как определено (VTI) с вертикальной осью. Дополнительно, могут быть предоставлены другие данные, например, акустические данные для угла, равного приблизительно 90 градусов, акустические данные для угла, равного приблизительно 0 градусов, или комбинация таковых. Такие данные могут постоянно храниться в устройстве хранения информации, например, быть доступны через сетевой интерфейс. Таким образом, блок 1140 предоставления данных может иметь доступ к данным из устройств хранения информации.

Что касается блока 1150 предоставления соотношения, в примере Фигуры 11, для конкретного типа слоя, может быть сделано допущение, что параметр B_T зависит от параметра Томсена γ, который может быть измерен в горизонтальной части скважины (например, или, наоборот, подсчитанный на основе измеренных данных), и эмпирическое соотношение может быть предоставлено с целью подсчета параметров упругости вдоль горизонтальной части скважины (например, блок 1160 выхода). В качестве примера, блок 1150 предоставления соотношения может предоставить соотношение для B_N и B_T. Такое соотношение может быть заранее известным соотношением, например, хранимое в устройстве хранения информации; таким образом, блок 1150 предоставления соотношения может иметь доступ к соотношению, зависимым величинам и т.д. Что касается величин B_N и B_T, то они могут быть предоставлены через вычисления, основанные на проанализированных данных пласта, данных из одного или нескольких аналогичных пластов или комбинации таковых. Например, для сланцевого пласта, податливости могут быть подсчитаны на основе данных из другого сланцевого пласта. В случае, если значения B_N и B_T подсчитываются, то потом можно провести регрессивный анализ для подбора соотношения (например, уравнения). Как показано на Фигуре 11, такое соотношение может быть представлено в виде функции зависимости B_N от B_T: B_N=m*B_T-b (например, где подобранный параметр m - это наклон, а подобранный параметр b - это отрезок пласта).

Как было отмечено, параметр Томсена γ может быть определен из комбинации значений скорости, комбинации значений медленности или комбинации одного или нескольких значений скорости и одного или нескольких значений медленности, где значения включают значения медленности и скорости SH волны в горизонтальной части скважины в пласте (например, V_SH или S_SH для угла равного приблизительно 90 градусов). В качестве примера, параметр Томсена γ может быть определен из медленной и быстрой поперечной волны в горизонтальной части скважины в пласте. В качестве примера, скорость, медленность или скорость и медленность могут определить С₄₄ и С₆₆ (см. также вертикальный и горизонтальный волновой фронт 1040 Фигуры 10).

В случае, когда B_T может быть представлен из известных коэффициентов упругости (например, C₄₄ и С₆₆), соотношение B_N/B_T, как предоставленное соотношение, может применяться для подсчета B_N (например, для вышеуказанного уравнения, которое устанавливает зависимость B_N и B_T в соответствии с постоянными линейного регрессивного анализа). Зная такое соотношение между B_N и B_T, как пример, потом способ может вывести модель (например, блок 1160 вывода) для подсчета одного или нескольких параметров Томсена ε и δ вдоль горизонтальной части скважины. В таком примере, используя предоставленное соотношение (например, с помощью линейного регрессивного анализа), может быть спрогнозирован B_N (например, как функция зависимости от B_T, которая работает с теми же самыми коэффициентами, которые определяют параметр γ). Если известны значения B_N, B_T, C₄₄, C₆₆ и С₁₁ вдоль горизонтальной части скважины (например, эксплуатационной скважины), при помощи использования модели, которая может соответствовать предоставленным данным блока 1140 предоставления данных, становится возможным подсчитать оставшиеся два коэффициента упругости С₃₃ и С₁₃. В примере Фигуры 11, параметры Томсена ε и δ для горизонтальной части могут быть подсчитаны одним или несколькими уравнениями (например, включая δ*). Дополнительно, надо учитывать, что параметр Томсена δ (и δ*) зависит от С₃₃ и С₁₃. В качестве примера, способ 1110 Фигуры 11 может предоставить подсчет величин коэффициентов упругости С₃₃ и С₁₃ для любой цели.

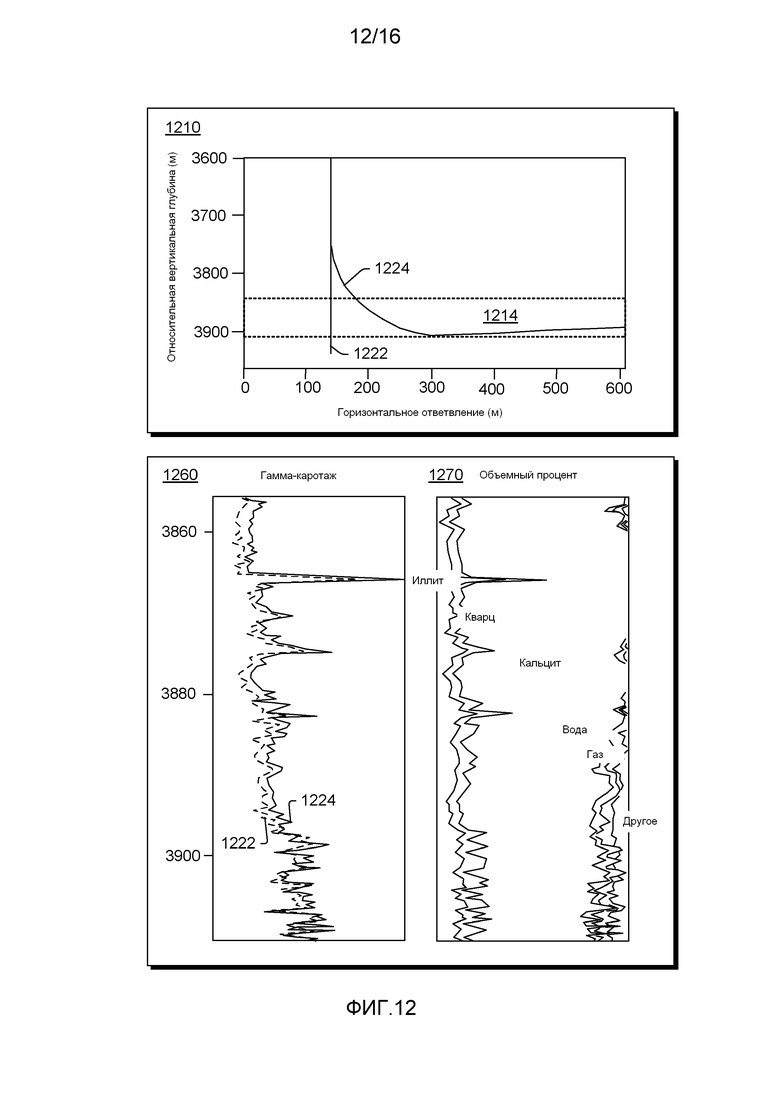
В качестве примера, способ был реализован с использованием данных, собранных в вертикальной нагнетательной скважине и боковой эксплуатационной скважине, пробуренных в месте пролегания сланцевого газа. В вертикальной нагнетательной скважине сланцевый газ был встречен на вертикальной глубине примерно 3860 м. Эксплуатационная скважина была пробурена со степенью набора угла 11 градусов с шагом 30 м (радиус 150 м). Эксплуатационная скважина была пробурена со слабо выраженной горизонтальностью общей горизонтальной протяженностью примерно 1,4 км. Скважинный каротаж был проведен в вертикальной нагнетательной скважине и горизонтальной части эксплуатационной скважины. Из сопоставления гамма-каротажа в вертикальной нагнетательной скважине и ответвленной части эксплуатационной скважины хорошо видно соответствие, показывающее, что пласты были, главным образом, латерально однородными в межскважинном пространстве протяженностью 150 м (например, с целью обеспечения гарантии, что по меньшей мере наклонная часть расположена внутри сланца, данные такой части могут использоваться в способе для определения одного или нескольких параметров, коэффициентов упругости и т.д.).

Фигура 12 показывает график 1210 вышеупомянутой вертикальной скважины 1222 и вышеупомянутой эксплуатационной скважины 1224 в пласте 1214 вертикальной глубины в метрах и горизонтального ответвления в метрах. Фигура 12 также показывает графики 1260 и 1270 гамма-каротажа и литологического каротажа соответственно, после проведения корреляции глубины (см., например, блок 320 соответствия способа 300 Фигуры 3). Как показано на графике 1270 зависимости объемного процента от глубины, литологический каротаж позволяет определить расположение слоев иллита (например, нерасширяющийся, глинистый, слюдяной минерал), кварца, кальцита, воды, газа и другие. На глубине, большей, чем приблизительно 3880 метров, объемный процент воды и газа возрастает.

С заданными данными с помощью способа была вычислена анизотропия в диапазоне глубин 75 м (см., например, Δz Фигуры 7) от 3835 м до 3910 м, в соответствии с наклоном скважины от угла, равного приблизительно 35 градусов, до угла, равного приблизительно 80 градусов (см. Δθ, например, Фигуры 7), измеренная в диапазоне приблизительно 150 м, от вертикальной части до наклонной. Такой процесс может включать подгонку коэффициентов упругости модели к измеренным данным, чтобы модель выдавала синтетические данные, которые совпадают с измеренными данными. Как было отмечено, могут применяться одна или несколько моделей, выбранных из множества типов моделей (например, 3D FDTD, точечный источник и т.д.).

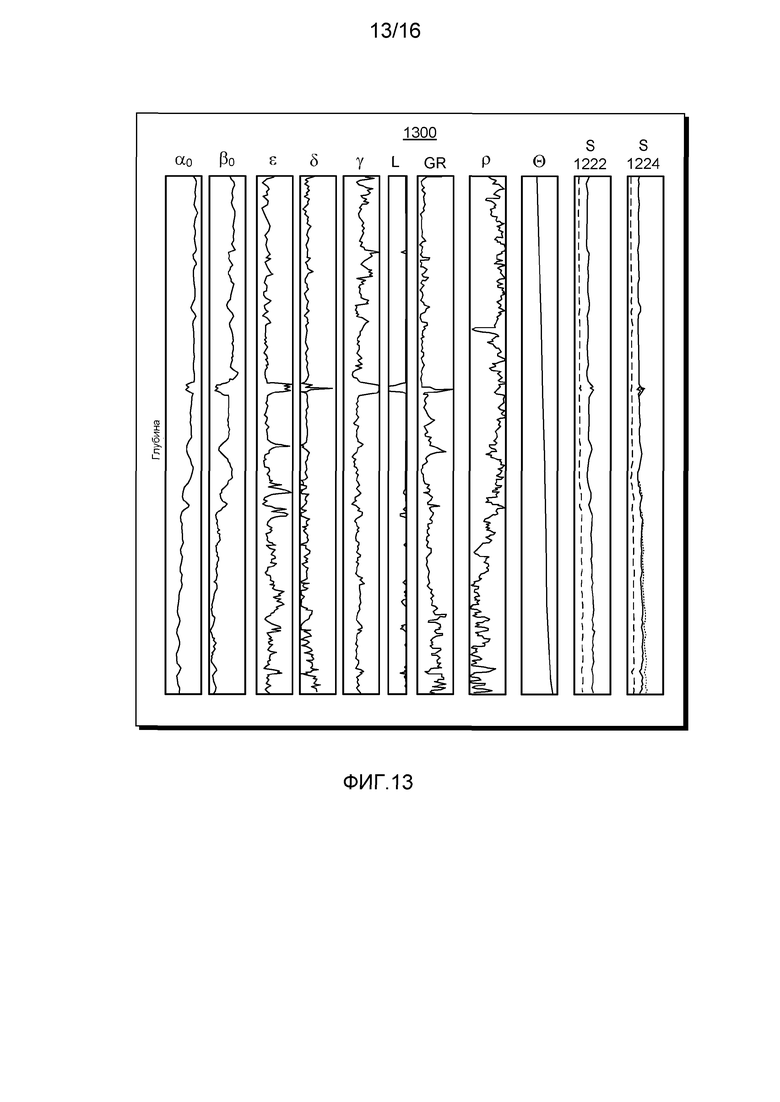
Фигура 13 показывает серию графиков 1300 с результатами инверсии многоскважинной системы, которые включают параметры Томсена (α₀, β₀, ε, δ и γ), функцию правдоподобия для наиболее вероятной модели (обозначенной L), гамма-каротаж (обозначенный GR), плотность (ρ), наклон скважины (θ), смоделированные (жирные серые линии) и измеренные медленности для нагнетательной скважины 1222 и эксплуатационной скважины 1224.

Параметры Томсена в серии графиков 1300 отвечают значениям, зависящим от глубины для наиболее вероятной модели, например, которые подобраны после процесса согласования, которые минимизируют разницы между измеренными и синтетическими данными. На графике 1300 не показано, для параметров Томсена, но некоторые отклонения присутствуют по графическим значениям, например, в соответствии с условной плотностью распределения вероятности (PDF). В качестве примера, условная PDF может быть использована для изображения разложения параметров (например, широкое или узкое распределение). Условные PDF могут быть рассмотрены как срезы многомерного пространства модели, и могут быть подсчитаны, например, удержанием параметров модели постоянными, кроме одного параметра модели. В случае, если параметр модели легко раскладывается, условная PDF будет с острым максимумом вокруг оптимального решения. И наоборот, если условная PDF представлена в плоском виде, то параметр не так легко раскладывается. В качестве примера, способ может включать визуализацию распределения, например, связанную с условной PDF наиболее вероятной модели (например, в любой точке во время процесса согласования). В таком примере, пользователь может спокойно визуализировать согласование и определиться, надо ли выполнять дальнейшие операции в попытке уменьшить распределение (например, для одного или нескольких параметров Томсена).

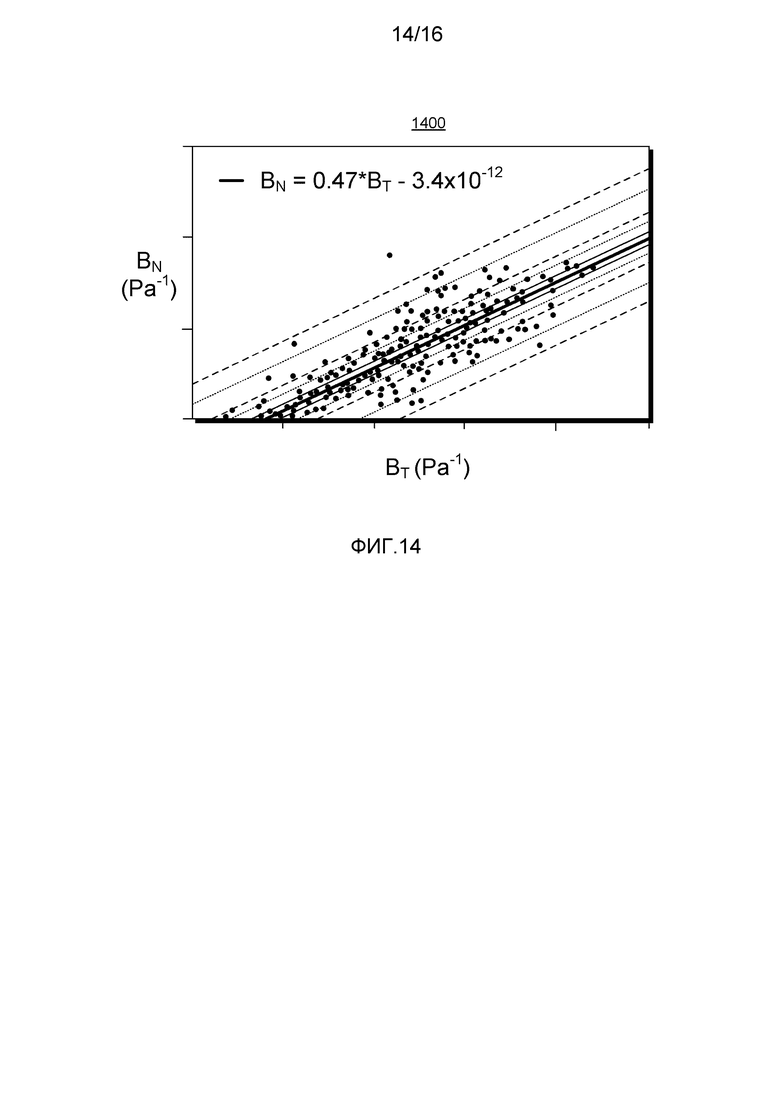
В качестве примера, анизотропный сланцевый слой может быть смоделирован, используя низкий поровый коэффициент, характеризующийся их нормальной и тангенциальной (поперечной) податливостью B_N и B_T соответственно (см., например, Sayers, 2008г.). Фигура 14 показывает график 1400 этих податливостей, высчитанных для пласта сланцевого газа. В особенности, график 1400 показывает B_N и B_T в виде кроссплота для предоставления линейной зависимости, которая может быть определена процессом линейной регрессии; необходимо учитывать, что другие соотношения и процессы регрессии тоже могут применяться (например, нелинейные или другие). Как указано, два параметра B_N и B_T сильно скорректированы коэффициентом корреляции 0,85, при помощи линейной регрессии получилось следующее соотношение B_N=0,47*B_T-3,4×10^-12 (например, подобранный параметр m=0,47 и подобранный параметр b=3,4x10^-12). Фигура 14 также показывает пунктирные и точечные линии областей неопределенности (например, стандартные отклонения и т.д.).

В примере на Фигурах 12 и 13 два параметра B_N и B_T представлены с наибольшей степенью корреляции по сравнению со всеми другими комбинациями параметров анизотропии. Как указано, если параметр BT может быть тесно связан с параметром Томсена γ по коэффициентам упругости, что может быть измерено в горизонтальной части скважины, то эмпирическое соотношение можно использовать для прогнозирования оставшихся параметров упругости вдоль горизонтальной части скважины.

В качестве примера рассмотрим результаты анализа линейной регрессии графика 1400 Фигуры 14, где BN=0,47*BT-3,4x10^-12. В этом примере, параметр BT подсчитан в горизонтальной части эксплуатационной скважины 1224, исходя из измеренных быстрой и медленной податливости поперечной волны и плотности (обозначенные S_SH, S_SV и ρ соответственно):

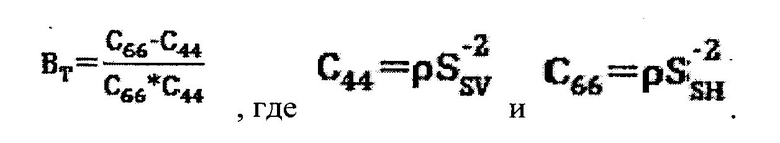
Таким же образом, постоянная упругости С₁₁ может быть подсчитана из продольной податливости (S_P) и плотности (ρ) вдоль горизонтальной части эксплуатационной скважины: С₁₁=ρS_p ^-2.

Используя полученное соотношение линейной регрессии, можно спрогнозировать B_N. Зная B_N, B_T, С₄₄, С₆₆ и С₁₁ вдоль горизонтальной части эксплуатационной скважины 1224, оставшиеся два параметра упругости С₃₃ и С₁₃ можно подсчитать следующим образом:

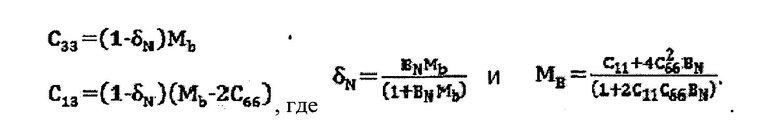
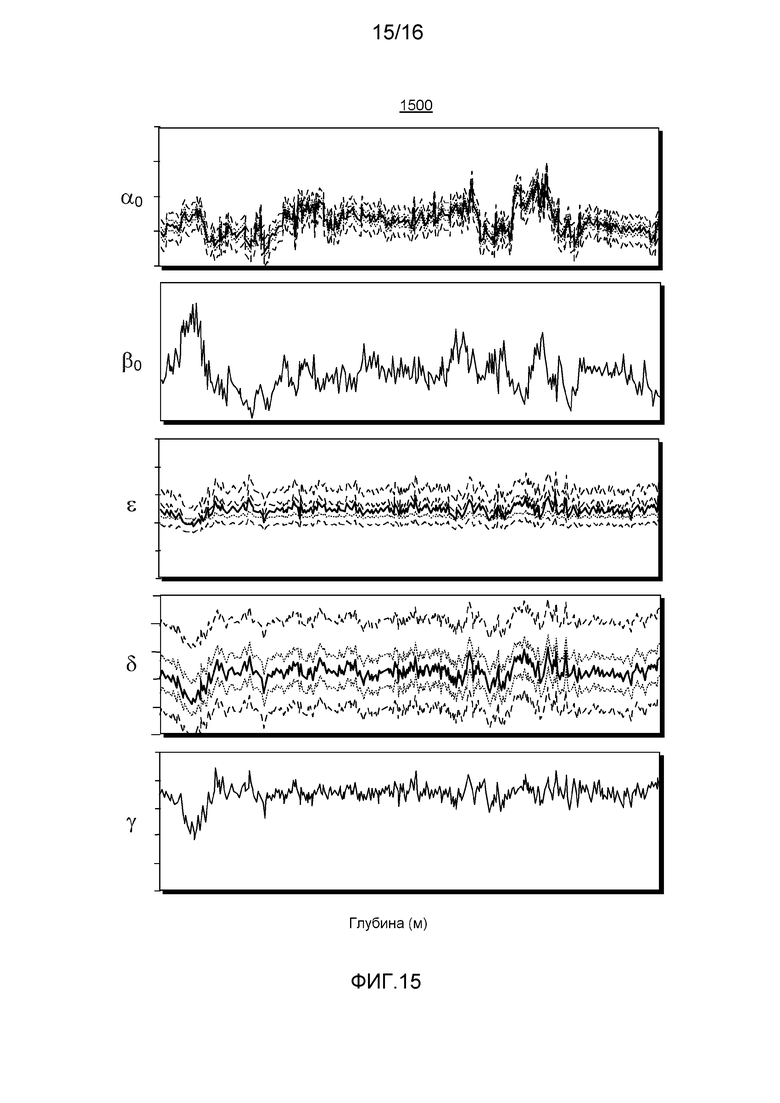
Фигура 15 показывает серию графиков 1500 для подсчитанных параметров Томсена вдоль горизонтальной эксплуатационной части вместе с подсчитанными ошибками и неопределенностями (см. пунктирные линии вокруг жирных линий спрогнозированных параметров Томсена). Эти ошибки основаны на стандартном отклонении ошибок после регрессивного анализа (см., например, график 1400 Фигуры 14, где неопределенность представлена пунктирными и точечными линиями). Необходимо учитывать, что параметр Томсена γ и вертикальная поперечная скорость (β₀) могут быть напрямую измерены по горизонтальному направлению (например, данные вертикальной части могут быть опциональными).

В качестве примера, в соответствии со способом, таким как способ 300 на Фигуре 3 или способом 1110 на Фигуре 11, спрогнозированные свойства упругости вдоль горизонтальной части эксплуатационной скважины могут быть определены, опционально вместе с неопределенностью, например, исходя из соотношения B_N и B_T. Такой способ может включать данные из только наклонной части или в комбинации с горизонтальной частью, наклонной в комбинации с вертикальной частью или наклонной в комбинации с горизонтальной частью и вертикальной частью. Если достаточная информация о наклоне известна, то модель может подсчитать один или несколько параметров для определения значений С₃₃ и С₁₃, и, например, параметр Томсена δ (например, или δ*).

Если способ в соответствии с Фигурами 12, 13, 14 и 15 может выполняться несколько раз, как описано способом 1110 на Фигуре 11, то модель может стать выходной для подсчета значений (например, блок 1160), исходя из входных данных (например, блок 1140) и соотношения (например, блок 1150).

В качестве примера, способ может включать предоставление данных о медленности продольной и поперечной волны для однородного, анизотропного пласта в наклонной скважине с углом больше чем 40 градусов и меньше чем 90 градусов, как определено осью симметрии VTI; предоставление соотношения нормальной и тангенциальной податливости (B_N и B_T); и, исходя из данных и соотношения, вывод модели для подсчета значений параметров анизотропии (например, α₀, ε, δ), которые характеризуют однородный, анизотропный пласт вдоль наклона под углом 90 градусов, как определено осью симметрии VTI. В таком примере, соотношение нормальной и тангенциальной податливости может быть линейное.

В качестве примера, модель для подсчета значений параметров анизотропии может включать входной параметр, который зависит от медленности поперечной волны с горизонтальной поляризацией для однородного, анизотропного пласта под углом 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии (например, для γ), и входной параметр, который зависит от медленности другой поперечной волны для однородного, анизотропного пласта под углом 0 градусов или 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии (например, для β₀).

В качестве примера, способ может включать подбор соотношения нормальной и тангенциальной податливости (B_N и B_T), чтобы предоставить подобранное соотношение. Как пример, модель для подсчета значений параметров анизотропии может предоставить значения неопределенности для подсчета параметров анизотропии, например, неопределенность в подборе соотношения нормальной и тангенциальной податливости (B_N и B_T) может дать значения неопределенности для подсчета параметра анизотропии (например, вдоль скважины с углом 90 градусов относительно оси симметрии VTI).

В качестве примера, способ может предоставлять данные плотности для однородного, анизотропного слоя. Как пример, такие данные, также как данные медленности продольной и поперечной волн, могут включать данные от одной наклонной скважины или данные от нескольких наклонных скважин. Как пример, данные медленности продольной и поперечной волн могут включать данные множества глубин в однородном, анизотропном пласте.

В качестве примера, система может включать: один или несколько процессоров; память; команды, хранимые в памяти и выполняемые по меньшей мере одним или несколькими процессорами, подсчета значений параметров анизотропии (например, α₀, ε, δ), которые характеризуют однородный, анизотропный пласт вдоль скважины под углом 90 градусов, как определено осью симметрии VTI, исходя из данных медленности продольной и поперечной волн множества разных наклонных углов скважины в однородном, анизотропном пласте, данных плотности для однородного, анизотропного пласта, медленности поперечной волны с горизонтальной поляризацией для однородного, анизотропного пласта под углом 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии (например, для γ), и медленности поперечной волны для однородного, анизотропного пласта для угла 0 градусов или 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии (например, β₀). В таком примере, команды могут быть включены для получения доступа к эмпирическому соотношению между параметром тангенциальной податливости (B_T) и параметром нормальной податливости (B_N). Такое соотношение может быть основано на данных сланцевого пласта для подсчета B_T и B_N. Как пример, может быть использовано уравнение B_T=(C₆₆-C₄₄)/(C₆₆*C₄₄), где С₆₆ и С₄₄ - коэффициенты матрицы модуля упругости.

В качестве примера, система может включать команды, хранимые в памяти и выполняемые одним или несколькими процессорами, обеспечения доступа к подобранному соотношению между параметром податливости (B_T) и другим параметром податливости (B_N), например, которое находится в запоминающем устройстве (например, посредством сетевого интерфейса или другого интерфейса).

В качестве примера, система может включать команды подсчета значений параметров анизотропии при помощи вычисления B_T, определения B_N на базе B_T, подбора соотношения и подсчета значений коэффициентов С₃₃ и С₁₃ матрицы модуля упругости в соответствии с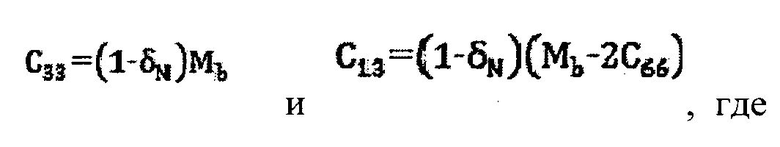

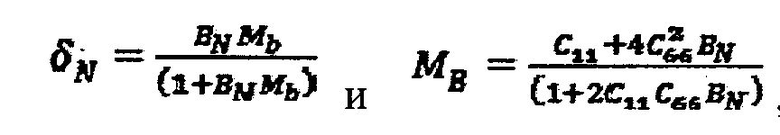
и С₁₁ и С₆₆ - коэффициенты матрицы модуля упругости.

В качестве примера, один или несколько компьютерных носителей информации могут включать компьютерные команды для управления вычислительным устройством с целью: доступа модели и измеренных данных для по меньшей мере наклонной скважины в пласте; регулировать коэффициенты упругости модели для минимизации целевой функции, которая зависит от синтетических данных, подсчитанных с использованием модели и измеренных данных, для предоставления модели оптимизированных коэффициентов упругости; выполнения регрессивного анализа по эмпирическому соотношению, которое включает параметр, заменимый по меньшей мере одним из оптимизированных коэффициентов упругости; и подсчета одного или нескольких параметров Томсена для горизонтальной части скважины в пласте, исходя из по меньшей мере части модели, оптимизированных коэффициентов упругости для модели и регрессивного анализа эмпирического соотношения. В таком примере, параметр, заменимый по меньшей мере одним из оптимизированных коэффициентов упругости, может быть тангенциальной податливостью (B_T). В таком примере по меньшей мере один из оптимизированных коэффициентов упругости может включать коэффициент упругости, который определяет параметр Томсена γ.

Фигура 16 показывает компоненты примера вычислительной системы 1600 и примера сетевой системы 1610. Система 1600 включает один или несколько процессоров 1602, память и/или компоненты запоминающего устройства 1604, один или несколько входных и/или выходных устройств 1606 и шину 1608. В примере данного исполнения, команды могут храниться в одном или нескольких компьютерных устройствах (например, память/компоненты запоминающего устройства 1604). Такие команды могут быть прочитаны одним или нескольким процессором (например, процессор(ы) 1602) с помощью коммуникационной шины (например, шина 1608), которая может быть как проводной, так и беспроводной. Один или несколько процессоров могут выполнять такие команды для воплощения (полного или частичного) одной или нескольких операций (например, как часть способа). Пользователь может видеть выходные данные и взаимодействовать с процессом с помощью входного/выходного устройства (например, устройство 1606). В примере данного исполнения, компьютерный носитель данных может быть компонентом запоминающего устройства, таким как устройство физической памяти, например микросхема, комплект микросхем, карта памяти и т.д. (например, компьютерный носитель данных).

В примере данного исполнения, компоненты могут быть распределены так, как в сетевой системе 1610. Сетевая система 1610 включает компоненты 1622-1, 1622-2, 1622-3, …1622-N. Например, компоненты 1622-1 могут включать процессор(ы) 1602, а компонент(ы) 1622-3 могут включать память, доступную процессору(ам) 1602. Дополнительно, компонент(ы) 1622-2 могут включать входное/выходное устройство для отображения и дополнительного взаимодействия с способом. Сеть может быть подключена к интернету, интрасети, сотовой связи и спутниковой связи и т.д.

Хотя только некоторые исполнения примера были детально описаны выше, те, кто имеет опыт на практике, быстро поймут, что может быть множество модификаций исполнения. Соответственно, все такие модификации охватывают объем раскрытия данной заявки, как определено в следующей формуле. В формуле, пункты «средство плюс функция» намерены покрыть все конструкции, описанные в данной заявке, с целью повторения, то есть не только конструкционные эквиваленты, но и эквивалентные конструкции. Таким образом, хотя гвоздь и винт могут быть не конструкционными эквивалентами, гвоздь имеет цилиндрическую поверхность для закрепления деревянных частей вместе, когда винт имеет винтовую поверхность для скрепления деревянных частей, поэтому гвоздь и винт могут быть эквивалентными конструкциями. Это выражает намерения заявителя не ссылаться на 35 U.S.C. § 112, параграф 6 по любым ограничениям любого пункта формулы в данной заявке, кроме тех, в которых употребляется выражение «средства для» вместе с соответствующей функцией.

Изобретение относится к области геофизики и может быть использовано при обработке сейсмических данных. Предложен способ определения параметров анизотропии, который включает предоставление информации о медленности продольной и поперечной волны в однородном, анизотропном пласте в наклонной скважине с углом наклона больше чем 40 градусов и меньше чем 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии (VTI), предоставление зависимости между нормальной и тангенциальной податливостью, и, исходя из этих данных и зависимости, выдачу модели для подсчета значения параметров анизотропии (например, α₀, ε, δ), которые характеризуют однородный, анизотропный пласт (например, вдоль скважины под углом 90 градусов). Различные другие устройства, системы, способы, т.д. также раскрыты в данной заявке. Технический результат - повышение точности получаемых данных. 2 н. и 15 з.п. ф-лы, 23 ил.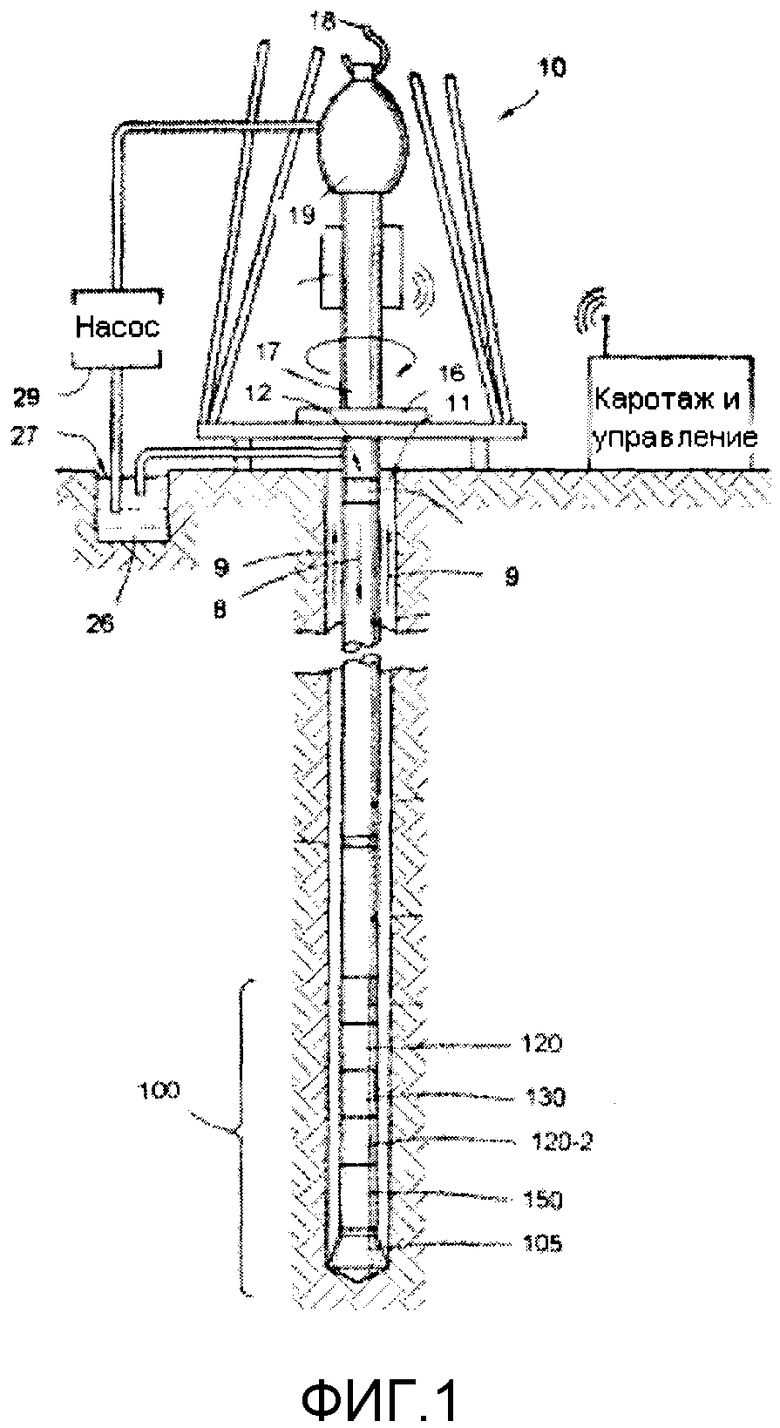

1. Способ определения значений параметров анизотропии, содержащий:
предоставление данных медленности продольной и поперечной волны для однородного, анизотропного пласта в наклонной скважине с углами больше чем 40 градусов и меньше чем 90 градусов, как определено трансверсальной изотропией с вертикальной осью;
предоставление соотношения нормальной и тангенциальной податливости; и на основе данных и отношения выходной модели для подсчета значений параметров анизотропии, которые характеризуют однородный, анизотропный пласт вдоль скважины с углом наклона 90 градусов, как определено трансверсальной изотропией с вертикальной осью.

2. Способ по п. 1, в котором соотношение нормальной и тангенциальной податливости представляется как линейное соотношение.

3. Способ по п. 1, в котором модель для подсчета значений параметров анизотропии включает входной параметр, который зависит от медленности поперечной волны с горизонтальной поляризацией для однородного, анизотропного пласта с углом 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии, и входной параметр, который зависит от медленности другой поперечной волны для однородного, анизотропного пласта с углом 0 градусов или 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии.

4. Способ по п. 1 дополнительно включает подбор соотношения нормальной и тангенциальной податливости для предоставления подобранного соотношения.

5. Способ по п. 1, в котором модель для подсчета значений параметров анизотропии, дополнительно, предоставляет значения неопределенностей для подсчета параметров анизотропии.

6. Способ по п. 5, в котором неопределенность в подобранном соотношении нормальной и тангенциальной податливости предоставляет значения неопределенностей для подсчета параметра анизотропии.

7. Способ по п. 1 дополнительно включает предоставление данных плотности для однородного, анизотропного пласта.

8. Способ по п. 1, в котором предоставление данных податливости продольной и поперечной волн включает доступ к данным медленности продольной и поперечной волны на устройстве хранения информации.

9. Способ по п. 1, в котором данные медленности продольной и поперечной волны включают данные от одиночной наклонной скважины.

10. Способ по п. 1, в котором данные медленности продольной и поперечной волны включают данные от множества наклонных скважин.

11. Способ по п. 1, в котором данные медленности продольной и поперечной волны включают данные множества глубин в однородном, анизотропном пласте.

12. Система для определения значений параметров анизотропии, содержащая:
один или несколько процессоров;
память; и
команды, выполняемые процессором, хранящиеся в памяти и выполняющиеся по меньшей мере одним или несколькими процессорами для подсчета значений параметров анизотропии, которые характеризуют однородный, анизотропный пласт вдоль скважины с углом 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии, основанные на:
данных медленности продольной и поперечной волны для множества разных углов наклона скважины в однородном, анизотропном пласте,
данных плотности для однородного, анизотропного пласта,
медленности поперечной волны с горизонтальной поляризацией для однородного, анизотропного пласта под углом 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии, и
медленности поперечной волны для однородного, анизотропного пласта под углом 0 или 90 градусов, как определено трансверсальной изотропией с вертикальной осью симметрии.

13. Система по п. 12 дополнительно включает команды, хранимые в памяти и выполняемые по меньшей мере одним или несколькими процессорами, для доступности эмпирического соотношения между параметром тангенциальной податливости и параметром нормальной податливости.

14. Система по п. 13, в которой эмпирическое соотношение включает соотношение, основанное на данных сланцевого пласта, для вычисления тангенциальной податливости B_T и нормальной податливости B_N.

15. Система по п. 13, в которой тангенциальная податливость B_T=(C₆₆-C₄₄)/(C₆₆*C₄₄), где C₆₆ и C₄₄ - коэффициенты матрицы модуля упругости.

16. Система по п. 13 дополнительно включает команды, хранимые в памяти и выполняемые по меньшей мере одним или несколькими процессорами, для доступности соответствующего соотношения между параметром тангенциальной податливости B_T и параметром нормальной податливости B_N.

17. Система по п. 16, в которой команды для подсчета значения параметров анизотропии содержат команды для подсчета тангенциальной податливости B_T, определения нормальной податливости B_N, исходя из тангенциальной податливости B_T и подобранного соотношения, и для подсчета значений коэффициентов С₃₃ и C₁₃ матрицы модуля упругости в соответствии с:

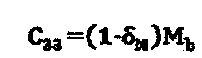
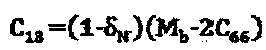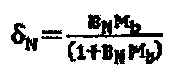, где и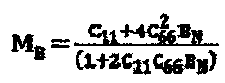
C₁₁ и C₆₆ - коэффициенты матрицы модуля упругости.