Заявленное техническое решение относится к области электросвязи и информационных технологий, а именно к технике сжатия и восстановления избыточной двоичной информации и ее помехоустойчивого кодирования и декодирования при передаче информации по каналам с ошибками.
Заявленное изобретение может быть использовано для обеспечения достоверности избыточной двоичной информации, передаваемой по каналам с ошибками.
Известен способ адаптивного помехоустойчивого кодирования и декодирования по патенту РФ 2375824 МПК Н04L 1/20 (2006.01) от 10.12.2009, заключающийся в том, что на передающей стороне исходную информацию кодируют помехоустойчивым кодом с переменными параметрами, далее помехоустойчивый код передают в канал связи, на приемной стороне помехоустойчивый код декодируют с обнаружением и исправлением ошибок в зависимости от корректирующей способности выбранного кода, по результатам декодирования помехоустойчивого кода оценивают качество канала связи и выбирают переменные параметры помехоустойчивого кода, обеспечивающие заданную вероятность правильного приема помехоустойчивого кода, и далее эти параметры помехоустойчивого кода сообщают на передающую сторону, отличающийся тем, что на приемной стороне по результатам декодирования помехоустойчивого кода рассчитывают начальную величину избыточности помехоустойчивого кода, обеспечивающую заданную вероятность правильного приема помехоустойчивого кода, оценивают вероятность правильного приема помехоустойчивого кода с выбранными параметрами, вычисляют величину отклонения полученной вероятности правильного приема помехоустойчивого кода от заданной вероятности правильного приема кода и в зависимости от величины этого отклонения корректируют величину избыточности помехоустойчивого кода, которую передают на передающую сторону, где формируют помехоустойчивый код с полученной избыточностью.
Недостатком указанного аналога является неэффективное использование пропускной способности канала передачи, вызванное отсутствием сжатия избыточной двоичной информации при обмене данными по каналам передачи с ошибками.
Известен также способ совместного сжатия и помехоустойчивого кодирования и декодирования речевых сообщений, описанный, например, в книге С.Н. Кириллов, В.Т. Дмитриев, Д.Е. Крысяев, С.С. Попов "Исследование качества передаваемой речевой информации при различном сочетании алгоритмов кодирования источника и канала связи в условиях воздействия помех". - Рязань, Вестник РГРТУ, Выпуск 23, 2008. Данный способ заключается в том, что предварительно формируют множество способов сжатия речевого сигнала, таких как импульсно-кодовая модуляция, адаптивная дельта-модуляция, адаптивная дифференциальная импульсно-кодовая модуляция, и множество способов помехоустойчивого кодирования, таких как кодирование Хэмминга, кодирование Боуз-Чоудхури-Хоквингема, на передающей стороне от отправителя получают очередную часть речевого сигнала длиною речевая фраза, который преобразуют в сжатую двоичную последовательность с помощью одного из способов сжатия речевого сигнала, выполняют помехоустойчивое кодирование сжатой двоичной последовательности с помощью одного из способов помехоустойчивого кодирования, передают на приемную сторону по каналу прямой связи очередную часть кодированной последовательности вместе с информацией об использованном способе сжатия речевого сигнала и способе помехоустойчивого кодирования, на приемной стороне получают очередную часть принятой последовательности, очередную часть принятой последовательности последовательно декодируют с использованием соответствующих способа помехоустойчивого декодирования и способа восстановления речевого сигнала, вычисляют оценку качества восстановленного речевого сигнала и полученную оценку сравнивают с пороговым значением качества, если вычисленная оценка качества восстановленного речевого сигнала не хуже предварительно установленного порогового значения качества, то передают получателю очередную часть восстановленной информационной последовательности и передающей стороне от отправителя получают очередную часть речевого сигнала и выполняют последующие действия, иначе передают по каналу обратной связи требование изменить способ сжатия речевого сигнала и способ помехоустойчивого кодирования, и выполняют последующие действия.
Недостатком указанного аналога является большая задержка передачи сообщений по каналу связи, вызванная необходимостью подбора подходящих способа сжатия речевого сигнала и способа помехоустойчивого кодирования.
Наиболее близким по своей технической сущности к заявленному способу совместного арифметического и помехоустойчивого кодирования и декодирования является способ совместного арифметического и помехоустойчивого кодирования и декодирования по патенту США 6892343 МПК Н04M 13/00 (2006.01) от 10.05.2005. Способ - прототип совместного арифметического и помехоустойчивого кодирования и декодирования заключается в том, что предварительно на передающей стороне устанавливают начальный интервал арифметического кодирования и на приемной стороне соответствующий ему начальный интервал арифметического декодирования, на передающей стороне от источника информации принимают очередную часть информационной последовательности длиной k≥1 бит, разделяют текущий интервал арифметического кодирования на текущий подынтервал кодирования нулевого символа и на текущий подынтервал кодирования единичного символа, из предварительно сформированного множества выбирают проверочные символы длиной r≥1 бит и формируют очередную часть помехоустойчивой последовательности из очередной части информационной последовательности и выбранных проверочных символов, выполняют арифметическое кодирование очередной части помехоустойчивой последовательности в очередную часть кодированной последовательности, преобразуют очередную часть кодированной последовательности в очередную часть модулированной последовательности, передают очередную часть модулированной последовательности на приемную сторону, выполняют на передающей стороне перечисленные действия до тех пор, пока поступают очередные части информационной последовательности, на приемной стороне получают очередную часть принятой последовательности, преобразуют ее в двоичную последовательность, которую запоминают, разделяют текущий интервал арифметического декодирования на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа, запомненные очередные части принятой последовательности арифметически декодируют в очередные части декодированной последовательности, из которых выделяют очередные части восстановленной информационной последовательности и декодированные проверочные символы, если декодированные проверочные символы принадлежат предварительно сформированному множеству проверочных символов, то делают вывод об отсутствии ошибок передачи и передают получателю очередную часть восстановленной информационной последовательности, иначе поочередно инвертируют один или несколько битов в запомненных очередных частях принятой последовательности и выполняют их арифметическое декодирование до достижения вывода об отсутствии ошибок передачи, выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные части принятой последовательности.
Особенностью способа-прототипа является то, что на передающей стороне выполняют выбор проверочных символов, а затем сжатие очередных частей информационной последовательности и проверочных символов путем арифметического кодирования, а на приемной стороне обнаруживают ошибки передачи при их наличии, а при их обнаружении методом проб и ошибок выполняют их исправление. Способ-прототип совместного арифметического и помехоустойчивого кодирования и декодирования обеспечивает возможность обнаружения и исправления ошибок передачи.
Однако в данном способе-прототипе совместного арифметического и помехоустойчивого кодирования и декодирования исправление ошибок передачи выполняют методом перебора, поочередно инвертируя один или несколько битов в запомненных очередных частях принятой последовательности и выполняя их арифметическое декодирование до достижения вывода об исправлении этих ошибок. При длине N бит запомненных очередных частей принятой последовательности и числе W исправляемых ошибок это требует параллельной или последовательной работы в среднем порядка NW/2 арифметических декодеров с соответствующим числом устройств обнаружения ошибок. При арифметическом декодировании сжатых избыточных двоичных последовательностей наличие ошибки передачи выявляется при длине запомненных очередных частях принятой последовательности вплоть до десятков бит. Поэтому в данном способе-прототипе совместного арифметического и помехоустойчивого кодирования и декодирования очень велика сложность реализации исправления многократных ошибок передачи.
Таким образом, недостатком ближайшего аналога (прототипа) совместного арифметического и помехоустойчивого кодирования и декодирования избыточной двоичной информации является практически нереализуемая сложность исправления ошибок передачи при кратности ошибок более одной.
Техническим результатом заявляемого решения является разработка способа совместного арифметического и помехоустойчивого кодирования и декодирования избыточной двоичной информационной последовательности, обеспечивающего возможность практической реализации исправления многократных ошибок передачи.
Указанный технический результат в заявляемом способе совместного арифметического и помехоустойчивого кодирования и декодирования достигается тем, что в известном способе совместного арифметического и помехоустойчивого кодирования и декодирования, заключающимся в том, что предварительно на передающей стороне устанавливают начальный интервал арифметического кодирования и на приемной стороне соответствующий ему начальный интервал арифметического декодирования, на передающей стороне от источника информационной последовательности принимают очередную часть информационной последовательности длиной k≥1 бит, разделяют текущий интервал арифметического кодирования на текущий подынтервал кодирования нулевого символа и на текущий подынтервал кодирования единичного символа, выбирают проверочные символы длиной r≥1 бит, формируют очередную часть помехоустойчивой последовательности из очередной части информационной последовательности и выбранных проверочных символов, выполняют арифметическое кодирование очередной части помехоустойчивой последовательности в очередную часть кодированной последовательности, передают очередную часть последовательности на приемную сторону, выполняют на передающей стороне перечисленные действия до тех пор, пока поступают очередные части информационной последовательности, на приемной стороне получают очередную часть принятой последовательности, разделяют текущий интервал арифметического декодирования принятой последовательности на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа, арифметически декодируют принятую последовательность в очередные части декодированной последовательности, из которых выделяют очередные части восстановленной информационной последовательности и декодированные проверочные символы, передают получателю очередную часть восстановленной информационной последовательности, выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные части принятой последовательности, дополнительно предварительно устанавливают предельное число альтернативных принятых последовательностей Z≥2 и величину задержки декодирования Т≥2, а также значения метрики альтернативных принятых последовательностей в нулевое значение.
На передающей стороне проверочные символы выбирают как нулевые символы, если определенная арифметическим кодированием текущая вероятность нулевых символов информационной последовательности больше или равна текущей вероятности единичных символов информационной последовательности, иначе выбирают проверочные символы как единичные символы. На передающей стороне передают очередную часть кодированной последовательности на приемную сторону, а на приемной стороне получают очередную часть принятой последовательности и считывают из нее очередной бит, разделяют текущий интервал арифметического декодирования каждой альтернативной принятой последовательности на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа этой последовательности. Для каждой альтернативной принятой последовательности формируют продолжение в виде нулевого символа и продолжение в виде единичного символа, вычисляют значение метрики продолжения в виде нулевого символа и значение метрики продолжения в виде единичного символа относительно очередного бита очередной части принятой последовательности, причем значение метрики продолжения в виде нулевого символа относительно очередного бита очередной части принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является нулевым битом, иначе вычисляют как единичное значение, а значение метрики продолжения в виде единичного символа относительно очередного бита очередной части принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является единичным битом, иначе вычисляют как единичное значение.
Для каждой альтернативной принятой последовательности с ее продолжением вычисляют значение ее метрики суммированием метрики самой последовательности и ее продолжения, арифметически декодируют каждую альтернативную принятую последовательность с ее продолжением в очередные части соответствующей ей альтернативной декодированной последовательности, из которых выделяют очередные части альтернативной восстановленной информационной последовательности и альтернативные декодированные проверочные символы.
Если альтернативные декодированные проверочные символы являются нулевыми символами при условии, что определенная арифметическим декодированием текущая вероятность нулевых символов альтернативной восстановленной информационной последовательности больше или равна текущей вероятности единичных символов этой последовательности, или если альтернативные декодированные проверочные символы являются единичными символами при условии, что определенная арифметическим декодированием текущая вероятность единичных символов альтернативной восстановленной информационной последовательности больше текущей вероятности нулевых символов этой последовательности, то альтернативные декодированные проверочные символы являются допустимыми.
Если альтернативные декодированные проверочные символы являются допустимыми, то запоминают очередные части альтернативной восстановленной информационной последовательности соответствующей альтернативной принятой последовательности с ее продолжением, иначе устанавливают значение метрики этой альтернативной принятой последовательности с ее продолжением в максимальное значение.
Сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями и выбирают из них не более Z альтернативных принятых последовательностей с их продолжениями, имеющих наименьшие значения метрики, в которые дописывают соответствующие им продолжения, для этих альтернативных принятых последовательностей запоминают очередные части соответствующей им альтернативной восстановленной информационной последовательности и значения метрики.
Считывают очередной бит очередной части принятой последовательности и если его номер меньше числа Т, то выполняют перечисленные действия на приемной стороне, иначе сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них альтернативную принятую последовательность с наименьшим значением метрики.
Передают получателю в качестве очередной части восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности очередную часть альтернативной восстановленной информационной последовательности. Выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные части принятой последовательности.
В предлагаемой совокупности действий на приемной стороне при декодировании каждого очередного бита очередной части принятой последовательности сохраняют и продолжают ограниченное число Z альтернативных принятых последовательностей с их продолжениями, имеющих наименьшие значения метрики, то есть обеспечивающих максимизацию вероятности исправления ошибок передачи, а все остальные последовательности стирают. Сложность декодирования ограниченного число Z альтернативных принятых последовательностей с их продолжениями существенно меньше сложности декодирования NW/2 принятых последовательностей, как предлагается в способе-прототипе.
Поэтому указанная новая совокупность действий позволяет при выполнении совместного арифметического и помехоустойчивого кодирования и декодирования избыточной двоичной информационной последовательности обеспечить возможность практической реализации исправления многократных ошибок передачи.
Заявленный способ поясняется чертежами, на которых показаны:
- на фиг. 1 - общая схема совместного арифметического и помехоустойчивого кодирования и декодирования;
- на фиг. 2 - схема блока декодирования 7;
- на фиг. 3 - алгоритм совместного арифметического и помехоустойчивого кодирования на передающей стороне;
- на фиг. 4 - таблица состояний арифметического кодирования первых шести очередных частей помехоустойчивой последовательности;
- на фиг. 5 - временные диаграммы арифметического кодирования первых двух очередных частей помехоустойчивой последовательности;
- на фиг. 6 - временные диаграммы совместного арифметического и помехоустойчивого кодирования первых шести очередных частей помехоустойчивой последовательности;
- на фиг. 7 - временные диаграммы совместного арифметического и помехоустойчивого декодирования первых шести очередных частей принятой последовательности на приемной стороне;
- на фиг. 8 - алгоритм совместного арифметического и помехоустойчивого декодирования на приемной стороне;
- на фиг. 9 - вид альтернативных принятых последовательностей в виде древовидной структуры;
- на фиг. 10 - примерный вид выбираемых не более L=8 альтернативных принятых последовательностей;
- на фиг. 11 - таблица состояний декодирования альтернативной принятой последовательности вида "00101110 0";
- на фиг. 12 - таблица состояний декодирования альтернативной принятой последовательности вида "00101110 1";
- на фиг. 13 - таблица состояний декодирования альтернативной принятой последовательности вида "00101110 00";
- на фиг. 14 - таблица состояний декодирования альтернативной принятой последовательности вида "00101110 10";
- на фиг. 15 - таблица состояний декодирования альтернативной принятой последовательности "00101110 11";
- на фиг. 16 - таблица состояний декодирования альтернативной принятой последовательности вида "00101110 010110";
- на фиг. 17 - таблица состояний декодирования альтернативной принятой последовательности с ее последовательными продолжениями вида "00101110 000110";
- на фиг. 18 - сравнение сложности практической реализации исправления многократных ошибок передачи для способа-прототипа и предлагаемого способа.
Реализация заявленного способа представлена на примере системы совместного арифметического и помехоустойчивого кодирования и декодирования, показанной на фиг. 1. На передающей стороне выполняют совместное арифметическое и помехоустойчивое кодирование очередных частей информационной последовательности, а на приемной стороне - совместное арифметическое и помехоустойчивое декодирование принятой последовательности с обнаружением и исправлением ошибок канала передачи. На передающей стороне при получении от отправителя двоичного символа очередной части информационной последовательности при получении нулевого символа счетчик числа нулевых символов 1 увеличивает число нулевых символов кодирования на единичное значение, а при получении единичного символа счетчик числа единичных символов 2 увеличивает число единичных символов кодирования на единичное значение. Пропорционально подсчитанным числам нулевых и единичных символов кодирования в формирователе границ подынтервалов 3 текущий интервал арифметического кодирования разделяют в арифметическом кодере 5 на текущий подынтервал кодирования нулевого символа и на текущий подынтервал кодирования единичного символа. В блоке выбора проверочных символов 4 выбирают проверочные символы, которые вместе с символами очередной части информационной последовательности кодируют в арифметическом кодере 5 в очередную часть кодированной последовательности и передают по каналу передачи на приемную сторону.
На приемной стороне в Z блоках декодирования 7 принимают очередные части принятой последовательности. Схема блока декодирования 7 показана на фиг. 2. В блоке декодирования 7 формирователь альтернативной принятой последовательности (АПП) с нулевым продолжением 7.1 и формирователь АПП с единичным продолжением 7.8 формируют альтернативные принятые последовательности с соответствующими продолжениями, которые в арифметическом декодере 7.2 и арифметическом декодере 7.9, соответственно, арифметически декодируют в очередные части соответствующих им альтернативных декодированных последовательностей. При декодировании нулевого символа из АПП с нулевым продолжением счетчик числа нулевых символов 7.3 увеличивает число нулевых символов декодирования этой последовательности на единичное значение, а при декодировании единичного символа счетчик числа единичных символов 7.4 увеличивает число единичных символов декодирования на единичное значение. Пропорционально подсчитанным числам нулевых и единичных символов декодирования в формирователе границ подынтервалов 7.6 текущий интервал арифметического декодирования АПП с нулевым продолжением разделяют на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа для данной последовательности.
Соответственно, при декодировании нулевого символа из АПП с единичным продолжением счетчик числа нулевых символов 7.10 увеличивает число нулевых символов декодирования этой последовательности на единичное значение, а при декодировании единичного символа счетчик числа единичных символов 7.11 увеличивает число единичных символов декодирования на единичное значение. Пропорционально подсчитанным числам нулевых и единичных символов декодирования в формирователе границ подынтервалов 7.13 текущий интервал арифметического декодирования АПП с единичным продолжением разделяют на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа для данной последовательности.
В блоке вычисления метрики АПП 7.7 для каждой альтернативной принятой последовательности с ее продолжением вычисляют значение ее метрики суммированием метрики самой последовательности и ее продолжения, где метрику продолжения вычисляют как степень подобия соответствующего продолжения очередному биту очередной части принятой последовательности. В арифметических декодерах 7.2 и 7.9 из очередных частей соответствующих альтернативных декодированных последовательностей выделяют очередные части альтернативной восстановленной информационной последовательности и альтернативные декодированные проверочные символы (АВПС). Если при проверке в блоке проверки проверочных символов 7.5 АВПС, соответствующие альтернативной принятой последовательности с нулевым продолжением, являются допустимыми, то в блоке выбора АПП 8 запоминают очередные части альтернативной восстановленной информационной последовательности соответствующие альтернативной принятой последовательности с нулевым продолжением, иначе в блоке вычисления метрики АПП 7.7 устанавливают значение метрики этой альтернативной принятой последовательности с нулевым продолжением в максимальное значение.
Соответственно, если при проверке в блоке проверки проверочных символов 7.12 АВПС, соответствующих альтернативной принятой последовательности с единичным продолжением, являются допустимыми, то в блоке выбора АПП 8 запоминают очередные части альтернативной восстановленной информационной последовательности соответствующие альтернативной принятой последовательности с единичным продолжением, иначе в блоке вычисления метрики АПП 7.7 устанавливают значение метрики этой альтернативной принятой последовательности с единичным продолжением в максимальное значение.
В блоке выбора АПП 8 сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями и выбирают из них не более Z альтернативных принятых последовательностей с их продолжениями, имеющих наименьшие значения метрики, в которые дописывают соответствующие им продолжения, для этих альтернативных принятых последовательностей запоминают очередные части соответствующей им альтернативной восстановленной информационной последовательности и значения метрики.
Начиная с T-го бита принятой последовательности в блоке выбора АПП 8 сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них альтернативную принятую последовательность с наименьшим значением метрики и передают получателю в качестве очередной части восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности очередную часть альтернативной восстановленной информационной последовательности.
В способе реализуется следующая последовательность действий.
Алгоритм совместного арифметического и помехоустойчивого кодирования на передающей стороне представлен на фигуре 3.
Способы предварительной установки на передающей стороне начального интервала арифметического кодирования и на приемной стороне соответствующего ему начального интервала арифметического декодирования известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Начальный интервал арифметического кодирования начинается от его начального нижнего значения и заканчивается его начальным верхним значением. Начальное нижнее значение интервала кодирования устанавливают в минимальное значение интервала кодирования, а начальное верхнее значения интервала кодирования - в максимальное значение. Например, при представлении значений интервала кодирования восемью двоичными символами, начальное нижнее значение интервала кодирования арифметического кодирования L[0] в момент времени t=0 устанавливают в минимальное значение, равное нулевому значению в десятичном представлении или 00000000 в двоичном представлении, где старшие двоичные символы записывают слева, а начальное верхнее значение интервала кодирования арифметического кодирования H[0] устанавливают в максимальное значение, равное 255 в десятичном представлении или 11111111 в двоичном представлении. Пример начального интервала арифметического кодирования представлен на фиг. 4 при t=0 (первая строка) и на фиг. 5 при t=0.
Также предварительно устанавливают предельное число альтернативных принятых последовательностей Z≥2 и величину задержки декодирования Т≥2, а также устанавливают значения метрики альтернативных принятых последовательностей в нулевое значение. Способы предварительной установки предельного числа альтернативных принятых последовательностей Z и величины задержки декодирования Т, известны и описаны, например, в книге Б. Скляр "Цифровая связь. Теоретические основы и практическое применение". - М, Издательский дом "Вильяме", 2003, стр. 430-439. Например, рекомендуется выбирать предельное число альтернативных принятых последовательностей Z из ряда значений вида 2, 4, 8, 16 с учетом того, что при увеличении выбранного числа Z можно исправить большее число ошибок передачи, но при этом линейно растет сложность реализации исправления ошибок.
Величина задержки декодирования Т численно равна количеству битов очередных частей принятой последовательности, после декодирования которых принимают решение об очередной части восстановленной информационной последовательности. Например, рекомендуется выбирать величину задержки декодирования численно равную (2…4)×Z, что позволяет исправлять наиболее часто встречающиеся комбинации ошибок передачи без существенного роста сложности реализации исправления ошибок. Способы предварительной установки значения метрики альтернативных принятых последовательностей в нулевое значение известны и описаны, например, в книге Б. Скляр "Цифровая связь. Теоретические основы и практическое применение". - М., Издательский дом "Вильямс", 2003, стр. 432-434.
На передающей стороне от источника информации принимают очередную часть информационной последовательности длиной k≥1 бит. Примерный вид первых шести очередных частей двоичной ИП длиной k=2 бита показан на фиг. 6(a). Например, первая часть ИП имеет вид "00", вторая часть - "01", третья часть - "01" и т.д. Единичные значения битов на фигурах показаны в виде заштрихованных импульсов, нулевые значения битов - в виде незаштрихованных импульсов.
Способы разделения текущего интервала арифметического кодирования на текущий подынтервал кодирования нулевого символа и на текущий подынтервал кодирования единичного символа известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Для арифметического кодирования очередного по счету, t-го символа, где t=1, 2,…, длину текущего интервала арифметического кодирования I[t-1], равную I[t-1]=H[t-1]-L[t-1], разделяют на значение текущего подынтервала нулевого символа D0[t-1] и значение текущего подынтервала единичного символа D1[t-1]. Для этого подсчитывают текущее число нулевых символов информационной последовательности и проверочных символов N∑0[t-1], суммируя текущее число нулевых символов информационной последовательности Ninf0[7-1] и текущее число нулевых проверочных символов Nproν0[t-1] в виде: N∑0[t-1]=Ninf0[t+1]+Nproν0[t-1]. Аналогичным образом подсчитывают текущее число единичных символов информационной последовательности и проверочных символов N∑1[t-1], суммируя текущее число единичных символов информационной последовательности и текущее число единичных проверочных символов: N∑1[t-1]=Ninf1[t-1]+Nproν1[t-1]. Например, в начальный момент при t=0 текущее число нулевых символов информационной последовательности и проверочных символов N∑0[0] установлено в значение 1, где Ninf0[0]=1 и Nproν0[0]=0, и текущее число единичных символов информационной последовательности и проверочных символов N∑1[0] установлено в значение 1, где Ninf1[0]=1 и Nproν1[0]=0. Способы установки в начальный момент арифметического кодирования числа нулевых и единичных символов информационной последовательности в единичное значение известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 124-130. Например, как показано на фиг. 4 в первой строке при t=0, в верхней строчке указано единичное число нулевых символов информационной последовательности (графа N0) и единичное число единичных символов информационной последовательности (графа N1). Соответственно, там же в нижней строчке при t=0 указано единичное число нулевых символов информационной последовательности и проверочных символов (графа N0) и единичное число единичных символов информационной последовательности и проверочных символов (графа N1). В графе N указывается общее число нулевых и единичных символов, в верхней строчке только для символов информационной последовательности, а в нижней строчке для символов информационной последовательности и проверочных символов. При кодировании первого по счету информационного символа, являющегося, например, нулевым символом, текущее число нулевых символов информационной последовательности увеличивается на единичное значение: Ninf0[1]=2, соответственно, текущее число нулевых символов информационной последовательности и проверочных символов становится равным N∑0[1]=2, как показано на фиг. 4 во второй строке при t=1.
Начиная с момента кодирования первого и последующих проверочных символов при t=3, t=6, t=9 и так далее, текущее число нулевых или единичных символов информационной последовательности начинает отличаться от текущего числа нулевых или единичных, соответственно, символов информационной последовательности и проверочных символов, как показано, например, на фиг. 4 в пятой строке при t=3.
Затем вычисляют текущую вероятность нулевых символов информационной последовательности и проверочных символов P∑0[t] по правилу: p∑0[t]=N∑0[t]/(N∑0[t]+N∑1[t]) и текущую вероятность единичных символов информационной последовательности и проверочных символов p∑1[t] по правилу: p∑1[t]=N∑1[t]/(N∑0[t]+N∑1[t). Например, как показано на фиг. 4 в первой строке при t=0, в нижней строчке указано значение текущей вероятности нулевых символов информационной последовательности и проверочных символов (графа р0) и значение текущей вероятности единичных нулевых символов информационной последовательности и проверочных символов (графа p1), где начальные значения равны 0,5.
Длину текущего подынтервала единичного символа D1[t] определяют по формуле вида D1[t]=I[t]×p1[t], а длину текущего подынтервала нулевого символа D0[t] определяют по формуле вида D0[t]=I[f]-D1[t]. Например, длина начального подынтервала единичных символов D1[0] имеет десятичное значение 128 или 10000000 в двоичном представлении, а длина начального подынтервала нулевых символов D0[0] имеет десятичное значение 127 или 01111111 в двоичном представлении. Подынтервал единичных символов расположен сверху подынтервала нулевых символов, как показано, например, на фиг. 5. Верхнюю границу подынтервала нулевого символа обозначают как значение Q, и данный подынтервал начинается снизу от нижней границы интервала кодирования арифметического кодирования включительно до значения Q исключительно, а подынтервал единичного символа простирается от значения Q включительно до верхней границы интервала кодирования арифметического кодирования исключительно. Начальное значение Q имеет десятичное значение 127, как показано на фиг. 4 в первой строке при t=0.
Проверочные символы длиной r≥1 бит выбирают как нулевые символы, если определенная арифметическим кодированием текущая вероятность нулевых символов информационной последовательности больше или равна текущей вероятности единичных символов информационной последовательности, иначе выбирают проверочные символы как единичные символы. Такой способ выбора проверочных символов обеспечивает выбор проверочных символов с преобладанием нулевых или единичных символов в соответствии с преобладанием нулевых или единичных символов в информационной последовательности, что повышает коэффициент сжатия арифметического кодирования помехоустойчивой последовательности, состоящей из избыточной информационной последовательности и выбранных проверочных символов.
Выбор очередных проверочных символов выполняют следующим образом. Для выбора очередного проверочного символа, являющегося t-ым по счету среди символов информационной последовательности и проверочных символов, подсчитывают текущую вероятность кодируемых нулевых символов информационной последовательности pinf0[t-1] по правилу pinf0[t-1]=Ninf0[t-1]/(Ninf0[t-1]+Ninf1[t-1]) и текущую вероятность кодируемых единичных символов информационной последовательности pinf1[t-1] по правилу pinf1[t-1]=Ninf1[t-1]/(Ninf0[t-1]+Ninf1[t-1]), где Ninf0[t-1] и Ninf1[t-1] - число кодируемых нулевых символов информационной последовательности и число кодируемых единичных символов информационной последовательности, соответственно, на момент [t -1].
Если выполняется соотношение вида pinf0[t-1]≥pinf1[t-1], то преобладают нулевые символы информационной последовательности и очередной проверочный символ выбирают как имеющий нулевое значение, иначе преобладают единичные символы информационной последовательности и очередной проверочный символ выбирают как имеющий единичное значение. Например, как показано на фиг. 4, в момент времени t=3 после кодирования первых двух информационных символов выбирают проверочный символ, который является единственным проверочным символом (r=1) для двух информационных символов (k=2). При числе очередных проверочных символов больше одного правило выбора этих символов не меняется.
На момент выбора указанного в примере проверочного символа вероятность кодируемых нулевых символов информационной последовательности составляет pinf0[2]=3/4 и вероятность кодируемых единичных символов информационной последовательности - pinf1[2]=1/4. В силу преобладания нулевых символов информационной последовательности очередной проверочный символ при t=3 выбирают как имеющий нулевое значение. Так как и далее число нулевых символов информационной последовательности превышает число единичных символов на моменты выбора проверочных символов при t=6, t=9, t=12, t=15 и t=18, как показано на фиг. 4, то и последующие проверочные символы выбирают как имеющие нулевое значение для показанного примера. Примерный вид выбранных проверочных символов для первых шести очередных частей информационной последовательности показан на фиг. 6(б).
Формирование очередной части помехоустойчивой последовательности из очередной части информационной последовательности и выбранных проверочных символов может быть построено, например, как считывание в очередную часть помехоустойчивой последовательности сначала очередной части информационной последовательности, а вслед за ней считывание выбранных проверочных символов. Способы считывания проверочных символов вместе с очередной частью информационной последовательности в очередную часть помехоустойчивой последовательности известны и описаны, например, в книге В. Шило "Популярные цифровые микросхемы". - М., Радио и связь, 1987, 104-123, с использованием регистров сдвига с параллельной и последовательной записью/считыванием двоичных последовательностей. Для этого очередная часть двоичной информационной последовательности с первого по k-ый бит параллельно записывают в первые по счету ячейки памяти регистр сдвига длиной k+r бит. Проверочные символы в виде двоичной последовательности длиной r бит параллельно записывают в последующие, начиная с k+1-ой, ячейки памяти этого же регистра сдвига. В результате в регистре сдвига записана очередная часть помехоустойчивой последовательности длиной k+r бит. Например, первая часть помехоустойчивой последовательности (ПП) имеет вид "000", вторая часть - "010", третья часть - "010", как показано на фиг. 6(в). Также возможно изменение порядка следования информационных и проверочных символов в помехоустойчивой последовательности.
Способы арифметического кодирования очередной части помехоустойчивой последовательности в очередную часть кодированной последовательности известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Они заключаются в последовательном сжатии двоичных символов очередной части помехоустойчивой последовательности в очередную часть кодированной последовательности в соответствии с текущими значениями интервала кодирования арифметического кодирования и текущими значениями вероятностей нулевых символов и единичных символов информационной последовательности и проверочных символов. По мере поступления на вход двоичных символов подсчитывают текущее число нулевых символов информационной последовательности и проверочных символов и текущее число единичных символов информационной последовательности и проверочных символов, пропорционально которым текущий интервал кодирования арифметического кодирования делят на текущий подынтервал кодирования нулевого символа и текущий подынтервал кодирования единичного символа, в соответствии с которыми арифметический кодер последовательно формирует кодированную последовательность (КП).
При поступлении на вход арифметического кодирования очередного двоичного символа очередной части помехоустойчивой последовательности, являющегося единичным двоичным символом, текущий интервал кодирования этого символа устанавливают равным предыдущему подынтервалу кодирования единичного символа, а при поступлении на вход арифметического кодирования нулевого двоичного символа, текущий интервал кодирования этого символа устанавливают равным предыдущему подынтервалу кодирования нулевого символа. Например, при поступлении на вход арифметического кодирования первого двоичного символа первой части помехоустойчивой последовательности, являющегося нулевым двоичным символом, нижнее значение интервала кодирования первого символа L[1] устанавливают равным начальному нижнему значению интервала кодирования арифметического кодирования L[0], равному, например, десятичному значению 0, а верхнее значение интервала кодирования первого символа арифметического кодирования H[1] устанавливают равным значению Q, равному, например, 127, как показано на фиг. 4 и на фиг. 5 при t=1.
Самый левый бит двоичного представления значения L[1] сравнивают с самым левым битом двоичного представления значения H[1], например, вида 00000000 и 01111111, соответственно, как показано на фиг. 3 при t=1. При их совпадении значение самого левого бита двоичных представлений значений L[1] и H[1] считывают в качестве очередного бита очередной части кодированной последовательности (Закод. символ на фиг. 4). Например, при кодировании первой части помехоустойчивой последовательности первым битом первой части КП является совпавший при сравнении нулевой двоичный символ, как показано на фиг. 4, третья строка сверху. Считанный бит удаляют из двоичных представлений значений L[1] и H[1], которые уменьшаются до длины 7 бит вида 0000000 и 1111111, соответственно. Двоичные символы двоичных представлений значений L[1] и H[1] сдвигают справа налево на один разряд и справа к ним дописывают по нулевому двоичному символу. Например, двоичные представления значений L[1] и H[1] приобретают вид 00000000 и 11111110, соответственно. Способы считывания двоичных символов с удалением считанных символов известны и описаны, например, в книге: В. Шило "Популярные цифровые микросхемы". - М., Радио и связь, 1987, 104-123, с использованием регистров сдвига с параллельной и последовательной записью/считыванием двоичных последовательностей. Операции сдвига справа налево на один разряд и дописывания справа нулевого двоичного символа увеличивают значения L[t] и H[t] в 2 раза и называются нормализацией параметров арифметического кодирования. Способы сдвига на один разряд в сторону старших разрядов двоичных последовательностей и записи в освободившийся младший разряд нулевого двоичного символа известны и описаны, например, в книге: В. Шило "Популярные цифровые микросхемы". - М., Радио и связь, 1987, 104-123, с использованием регистров сдвига с параллельной и последовательной записью/считыванием двоичных последовательностей, и по своей сути являются умножением на два десятичных значений нижнего и верхнего значений интервала кодирования.
После каждого выполнения нормализации повторно самый левый бит двоичного представления нижнего значения интервала кодирования сравнивают с самым левым битом двоичного представления верхнего значения интервала кодирования. При их совпадении значение самого левого бита этих двоичных представлений считывают в качестве следующего бита очередной части КП, иначе переходят к кодированию следующего символа и так далее, как показано на фиг. 4.
После выполнения арифметического кодирования каждого очередного символа уточняют число закодированных нулевых символов информационной последовательности и проверочных символов и число закодированных единичных символов информационной последовательности и проверочных символов. Так как первый закодированный символ в указанном примере является нулевым, то число закодированных нулевых символов информационной последовательности и проверочных символов увеличивают на единичное значение и оно составляет N∑0[1]=2, число закодированных единичных символов информационной последовательности и проверочных символов осталось равным N∑1[1]=1, соответственно, суммарное число закодированных нулевых и единичных символов информационных и проверочных стало равным 3. Пересчитывают текущее значение вероятности нулевых символов информационной последовательности и проверочных символов p∑0[1]=2/3 и текущее значение вероятности единичных символов информационной последовательности и проверочных символов p∑1[1]=1/3. В соответствии с этим длина подынтервала нулевого символа D0[1] становится в 2 раза больше длины подынтервала единичного символа D1[1], как показано на фиг. 4, третья строка сверху и на фиг. 5 при t=1 после нормализации.
Выполняют арифметическое кодирование следующего двоичного символа, как показано на фиг. 4 и на фиг. 5. Арифметическое кодирование проверочных символов не отличается от порядка кодирования символов информационной последовательности.
При поступлении на вход арифметического кодирования символа, являющегося единичным символом, нижнее значение интервала кодирования устанавливают равным предыдущему значению Q, а верхнее значение интервала кодирования устанавливают равным предыдущему верхнему значению интервала кодирования. Например, при арифметическом кодировании пятого по счету символа (t=5), являющегося единичным символом, нижнее значение интервала кодирования L[5] устанавливают равным значению Q[4], равному, например, 169, а верхнее значение интервала кодирования Н[5] устанавливают равным верхнему значению интервала кодирования Н[4], равному, например, 203, как показано на фиг. 4 при t=5.
Примерный вид арифметического кодирования первых шести очередных частей помехоустойчивой последовательности вида "000", "010", "010", "000", "100" и "010" в соответствующие очередные части кодированной последовательности вида "00", "1", "011", "_", "100001" и "10" показан на фиг. 6(г). Например, четвертая часть помехоустойчивой последовательности является пустой (не содержит двоичных символов).
Способы передачи на приемную сторону очередной части кодированной последовательности известны и описаны, например, в книге А.Г. Зюко, Д.Д. Кловский, М.В. Назаров, Л.М. Финк "Теория передачи сигналов". - М.: Радио и связь, 1986, стр. 11. Примерный вид первых шести частей принятой последовательности (Пр. П) показан на фиг. 7(a). Принятая последовательность при передаче искажена в третьем и четвертом битах пятой части принятой последовательности и имеет вид "00", "1", "011", "_", "101101" и "10".
Алгоритм совместного арифметического и помехоустойчивого декодирования на приемной стороне представлен на фиг. 8.
Для инициализации арифметического декодирования необходимо принять первые по счету NR двоичных символов очередных частей принятой последовательности, где NR есть число двоичных символов представления значений интервала кодирования и, соответственно, интервала декодирования. Например, при представлении значений интервала кодирования и интервала декодирования восемью двоичными символами, принимают первые восемь бит принятой последовательности вида "00101110", являющихся битами с первой по четвертую и первыми битами пятой части принятой последовательности, причем на приемной стороне получают очередные части принятой последовательности без выделения границ этих очередных частей.
Действия арифметического и помехоустойчивого декодирования принятой последовательности на приемной стороне выполняют путем декодирования нескольких альтернативных принятых последовательностей. В момент времени считывания первого после начальных NR бит бита очередной части принятой последовательности, обозначенного моментом времени t=1, для начальной принятой последовательности, состоящей из первых по счету NR двоичных символов очередных частей принятой последовательности, формируют продолжение в виде нулевого символа и продолжение в виде единичного символа. Например, для начальной принятой последовательности вида "00101110" формируют 2 продолжения: альтернативную принятую последовательности (АПП) с продолжением в виде нулевого символа "00101110 0", и альтернативную принятую последовательность с продолжением в виде единичного символа "00101110 1". При считывании следующего бита очередной части принятой последовательности (момент времени t=2) для каждого из имеющиеся двух альтернативных принятых последовательностей формируют продолжения в виде нулевого символа и продолжение в виде единичного символа, в результате на момент времени t=2 число альтернативных принятых последовательностей становится 4, на момент времени t=3 число альтернативных принятых последовательностей может достичь 8 и т.д.
Вид альтернативных принятых последовательностей в виде описанной древовидной структуры показан на фиг. 9. Такая структура альтернативных принятых последовательностей потенциально позволяет исправлять многократные ошибки передачи в принятой последовательности. Для каждой альтернативной принятой последовательности выполняют описанные далее действия арифметического и помехоустойчивого декодирования. Так как число альтернативных принятых последовательностей в такой древовидной структуре удваивается в каждый последующий момент времени t, что экспоненциально увеличивает сложность реализации исправления ошибок передачи, то для уменьшения этой сложности в каждый момент t среди альтернативных принятых последовательностей с их продолжениями выбирают и далее продолжают не более L альтернативных принятых последовательностей, наиболее близкие по метрике Хэмминга к принятой последовательности, а остальные альтернативные принятые последовательности стирают. Например, при предварительно установленном предельном числе альтернативных принятых последовательностей Z=8 примерный вид выбираемых не более Z альтернативных принятых последовательностей показан на фиг. 10. Видно, что в этой структуре, называемой усеченным деревом альтернативных принятых последовательностей, число продолжаемых альтернативных принятых последовательностей в каждый момент t не превышает заданного значения Z=8. Например, число продолжаемых принятых последовательностей при декодировании девятого по счету символа принятой последовательности равно 2, при декодировании десятого символа - 4, при декодировании последующих четырех символов - по 8. Не получают своего продолжения альтернативные принятые последовательности из которых при декодировании выделяют альтернативные декодированные проверочные символы, не являющиеся допустимыми, что означает, что в них не исправлены ошибки передачи. На фиг. 10 показано, что при выявлении недопустимых декодированных проверочных символов значение метрики соответствующей им альтернативной принятой последовательности с ее продолжением устанавливают в максимальное значение (М=Мах), и такая последовательность не получит продолжения. Выявление недопустимых декодированных проверочных символов на фиг. 10 и последующий за этим не выбор такого пути показано символом 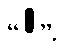 На фиг. 10 также показано, что среди текущих альтернативных принятых последовательностей с их продолжениями выбирают не более Z последовательностей, имеющих наименьшие значения метрики, остальные последовательности не получают продолжения, что показано символом "X".
На фиг. 10 также показано, что среди текущих альтернативных принятых последовательностей с их продолжениями выбирают не более Z последовательностей, имеющих наименьшие значения метрики, остальные последовательности не получают продолжения, что показано символом "X".
При этом решение о выборе среди продолжаемых альтернативных принятых последовательностей требуемой принятой последовательности с исправленными ошибками передачи принимают с предварительно установленной задержкой декодирования Т. Например, на фиг. 10 показан пример принятия решения о выборе альтернативной принятой последовательности с исправленными ошибками передачи с задержкой декодирования T=16. При декодировании шестнадцатого по счету символа принятой последовательности с минимальной среди альтернативных принятых последовательностей метрикой М=2 остается и будет выбрана единственная последовательность, продолжение которой обозначено многоточием, для которой исправлены две описанные выше ошибки передачи. Соответствующую выбранной альтернативной принятой последовательности очередную часть альтернативной восстановленной информационной последовательности передают получателю в качестве очередной части восстановленной информационной последовательности. Далее принимают следующий бит очередной части принятой последовательности, для выбранной альтернативной принятой последовательности формируют продолжения и выполняют перечисленные действия до тех пор, пока поступают очередные части принятой последовательности.
Детально опишем действия арифметического и помехоустойчивого декодирования на приемной стороне.
Способы разделения текущего интервала арифметического декодирования каждой альтернативной принятой последовательности на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа этой последовательности идентичны способам разделения текущего интервала арифметического кодирования на текущий подынтервал кодирования нулевого символа и на текущий подынтервал кодирования единичного символа. Верхнюю границу текущего подынтервала декодирования нулевого символа обозначают как значение QQ, и данный подынтервал начинается снизу от нижней границы текущего интервала декодирования LL до значения QQ исключительно, а текущий подынтервал декодирования единичного символа простирается от значения QQ включительно до верхней границы текущего интервала декодирования НН исключительно. Например, для начальной принятой последовательности вида "00101110" значение нижней границы текущего интервала декодирования равно LL[Q]=0, а значение верхней границы текущий интервала декодирования - НН[0]=255, как показано на фиг. 11 в первой строке при t=0.
Длину текущего интервала арифметического декодирования каждой альтернативной принятой последовательности II[7-1], равную II[t-1]=HH[t-1]-LL[t-1], разделяют на значение текущего подынтервала нулевого символа DD0[t-1] и значение текущего подынтервала единичного символа DD1[t-1]. Для этого подсчитывают текущее число нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов альтернативной принятой последовательности NN∑0[t-1], суммируя текущее число нулевых символов альтернативной восстановленной информационной последовательности NNinf0[t-1] и текущее число нулевых альтернативных декодированных проверочных символов NNproν0[t-1] в виде: NN∑0[t-1]=NNinf0[t-1]+NNproν0[t-1]. Аналогичным образом подсчитывают текущее число единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов каждой альтернативной принятой последовательности NN∑1[t-1], суммируя текущее число единичных символов альтернативной восстановленной информационной последовательности и текущее число единичных альтернативных декодированных проверочных символов: NN∑1[t-1]=NNinf1[t-1]+NNproν1[t-1]. Например, в начальный момент при t=0 текущее число нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов каждой альтернативной принятой последовательности NN∑0[0] установлено в значение 1, где NNinf0[0]=1 и NNproν0[0]=0, и текущее число единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов NN∑1[0] установлено в значение 1, где NNinf1[0]=1 и NNproν1[0]=0.
Например, как показано на фиг. 11 в первой строке при t=0 для начальной принятой последовательности вида "00101110", в верхней строчке указано единичное число нулевых символов альтернативной восстановленной информационной последовательности (графа NN0) и единичное число единичных символов этой же восстановленной информационной последовательности (графа NN1). Соответственно, там же в нижней строчке при t=0 указано единичное число нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов (графа NN0), также единичное число единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов (графа NN1). В графе NN указывается общее число нулевых и единичных символов, в верхней строчке только для символов альтернативной восстановленной информационной последовательности, а в нижней строчке для символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов.
Затем вычисляют текущую вероятность нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов pp∑0[t] по правилу: pp∑0[t]=NN∑0[t]/(NN∑0[t]+NN∑1[t]) и текущую вероятность единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов pp∑1[t] по правилу: pp∑1[t]=NN∑1[t]/(NN∑0[t]+NN∑1[t]). Например, как показано на фиг. 11 в первой строке при t=0, в нижней строчке указано значение начальной вероятности нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов (графа рр0) и значение начальной вероятности единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов (графа pp1), где начальные значения равны 0,5.
Длину текущего подынтервала единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов DD1[t] определяют по формуле вида DD1[t]=II[t]×pp∑1[t], а длину текущего подынтервала нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов DD0[t] определяют по формуле вида DD0[t]=II[t]-DD1[t]. Например, длина начального подынтервала единичных символов DD1[0] имеет десятичное значение 128 или 10000000 в двоичном представлении, а длина начального подынтервала нулевых символов DD0[0] имеет десятичное значение 127 или 01111111 в двоичном представлении. Подынтервал единичных символов расположен сверху подынтервала нулевых символов, как показано, например, на фиг. 11. Верхнюю границу подынтервала нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов обозначают как значение QQ, и данный подынтервал начинается снизу от нижней границы интервала декодирования арифметического декодирования включительно до значения QQ исключительно, а подынтервал единичных символов простирается от значения QQ включительно до верхней границы интервала декодирования арифметического декодирования исключительно. Начальное значение QQ имеет десятичное значение 127, как показано на фиг. 11 в первой строке при t=0.
В начальный момент альтернативные принятые последовательности состоят из начальной принятой последовательности, имеющей предварительно установленное нулевое значение метрики (М=0).
После считывания очередного бита очередной части принятой последовательности для каждой альтернативной принятой последовательности формируют продолжение в виде нулевого символа и продолжение в виде единичного символа. Например, альтернативная принятая последовательность с продолжением в виде нулевого символа получает вид "00101110 0", как показано на фиг. 11, а альтернативная принятая последовательность с продолжением в виде единичного символа получает вид "00101110 1", как показано на фиг. 12.
После формирования продолжения вычисляют значение метрики продолжения в виде нулевого символа и значение метрики продолжения в виде единичного символа относительно очередного бита очередной части принятой последовательности, при этом значение метрики продолжения в виде нулевого символа относительно очередного бита очередной части принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является нулевым битом, иначе вычисляют как единичное значение, а также значение метрики продолжения в виде единичного символа относительно очередного бита очередной части принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является единичным битом, иначе вычисляют как единичное значение. Например, как показано на фиг. 11, очередной бит очередной части Пр.П, следующий после считывания восьми битов начального пути декодирования, имеет единичное значение. Поэтому относительно этого бита метрика продолжения в виде нулевого символа имеет единичное значение, а метрика продолжения в виде единичного символа имеет нулевое значение.
Затем для каждой альтернативной принятой последовательности с продолжением вычисляют значение его метрики суммированием метрики самого пути и метрики его продолжения. Например, метрика альтернативной принятой последовательности "00101110 0" с продолжением в виде нулевого символа получает единичное значение (М=1), а метрика альтернативной принятой последовательности "00101110 1" с продолжением в виде единичного символа получает нулевое значение (М=0).
Способы арифметического декодирования альтернативной принятой последовательности с ее продолжением в очередные части соответствующей ей альтернативной декодированной последовательности известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Они заключаются в последовательном декодировании альтернативной принятой последовательности с ее продолжением в соответствии с текущими значениями интервала декодирования арифметического декодирования этой последовательности и текущими значениями вероятности декодируемых нулевых символов и единичных символов этой последовательности.
Примерный вид арифметического декодирования альтернативной принятой последовательности с ее продолжением "00101110 0" в символы первой части соответствующей ей альтернативной декодированной последовательности показан на фиг. 11. Первоначально на вход арифметического декодирования считаны первые по очереди 8 бит вида "00101110", что соответствует десятичному числу 46. Текущие считываемые биты (сч.) показаны во втором столбце, в третьем столбце этой же таблицы (Вх. данные) показано текущее значение считанных данных. Текущее значение считанных данных сравнивают с границами начального значения подынтервала декодирования нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов DD0[0], находящимися, например, в пределах от 0 до 127, и с границами начального значения подынтервала декодирования единичных символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов DD1[0], находящимися, например, в пределах от 127 до 255. В зависимости от того, в пределах какого подынтервала декодирования символов оказалось текущее значение считанных данных, принимают решение о значении текущего символа альтернативной декодированной последовательности (Дек. сим.).
Например, так как текущее значение считанных данных оказалось меньше значения QQ(46<127), то первый декодированный символ является нулевым и следующие границы интервала декодирования устанавливают соответствующими границам значения подынтервала декодирования нулевых символов DD0[0]. В результате декодирования
первого символа устанавливают нижнее значение интервала декодирования арифметического декодирования LL[1] равным предыдущему значению LL[0], например, LL[1]=0, а верхнее значение интервала декодирования арифметического декодирования HH[1] - равным значению QQ, например, HH[1]=127, как показано на фиг. 11 во второй строке при t=1.
После декодирования каждого символа пересчитывают текущее значение вероятности декодированных нулевых символов альтернативной восстановленной информационной последовательности и альтернативных декодированных проверочных символов и текущее значение вероятности декодированных единичных символов этой же последовательности, например, после декодирования первого символа, являющегося нулевым, по формуле вида pp∑0[1]=NN∑0[1]/(NN∑0[1]+NN∑1[1])=2/3 и по формуле вида pp∑1[1]=NN∑1[1]/(NN∑0[1]+NN∑1[1])=1/3, соответственно.
После каждого изменения состояния арифметического декодирования (Сост. дек.) самый левый бит двоичного представления значения LL сравнивают с самым левым битом двоичного представления значения HH, например, при t=1 вида "0000 0000" и "0111 1111", соответственно. При их совпадении выполняют нормализацию арифметического декодирования: значение самого левого бита двоичных представлений значений LL и HH удаляют и двоичные символы двоичных представлений значений LL и НН сдвигают справа налево на один разряд и справа к ним в младший разряд дописывают по нулевому двоичному символу. Одновременно с этим, значение самого левого бита входных данных удаляют и двоичные символы входных данных сдвигают справа налево на один разряд и справа к ним дописывают следующий считанный двоичный символ данной альтернативной принятой последовательности с ее продолжением. Как было описано выше, следующим считанным двоичным символом является девятый по счету символ данной альтернативной принятой последовательности с ее продолжением, имеющий нулевое значение. Со считыванием этого бита метрика данной альтернативной принятой последовательности с, ее продолжением "00101110 0" приняла единичное значение (М=1), как показано на фиг. 11 в четвертой графе. С учетом считанного двоичного символа, входные данные получили двоичное представление "01011100" и десятичное значение 92. Переменная LL сохранила десятичное значение 0, а НН - получила десятичное значение 254 и двоичное представление "11111110". Повторно самый левый бит двоичного представления значения LL сравнивают с самым левым битом двоичного представления значения НН, и если они снова совпадают, то выполняют повторную нормализацию идентичным образом и т.д.
В результате арифметического декодирования альтернативной принятой последовательности с продолжением в виде нулевого символа вида "00101110 0", показанной на фиг. 7(б), декодируют, например, три символа первой части соответствующей ей альтернативной декодированной последовательности (АДП), имеющие вид "000", как показано на фиг. 7(в) и на фиг. 11.
Способы выделения из очередной части АДП очередной части альтернативной восстановленной информационной последовательности (АВИП) и альтернативных декодированных проверочных символов (АДПС) известны и описаны, например, в книге В. Шило "Популярные цифровые микросхемы". - М, Радио и связь, 1987, 104-123, с использованием регистров сдвига с параллельной и последовательной записью/считыванием двоичных последовательностей. Очередную часть альтернативной декодированной последовательности последовательно записывают в ячейки памяти регистра сдвига длиной k+r бит. Из первых по счету ячеек памяти этого регистра сдвига параллельно считывают очередную часть альтернативной восстановленной информационной последовательности длиной k бит. Из последующих, начиная с k+1-ой, ячейки памяти этого же регистра сдвига параллельно считывают альтернативные декодированные проверочные символы длиной r бит. Например, из первой части АДП вида "000" выделяют первую часть АВИП вида "00", как показано на фиг. 7(г), и АДПС вида "0", как показано на фиг. 7(д).
Если альтернативные декодированные проверочные символы являются нулевыми символами при условии, что определенная арифметическим декодированием текущая вероятность нулевых символов альтернативной восстановленной информационной последовательности больше или равна текущей вероятности единичных символов этой последовательности, или если альтернативные декодированные проверочные символы являются единичными символами при условии, что определенная арифметическим декодированием текущая вероятность единичных символов альтернативной восстановленной информационной последовательности больше текущей вероятности нулевых символов этой последовательности, то альтернативные декодированные проверочные символы являются допустимыми. Поэтому для установления допустимости АДПС вычисляют текущую вероятность нулевых символов альтернативной восстановленной информационной последовательности и, соответственно, текущую вероятность единичных символов этой последовательности. Текущую вероятность нулевых символов альтернативной восстановленной информационной последовательности pinf0[t] подсчитывают по правилу pinf0[t]=Ninf0[t]/(Ninf0[t]+Ninf1[t]) и текущую вероятность единичных символов альтернативной восстановленной информационной последовательности pinf1[t] - по правилу pinf1[f]=Ninf1[t]/(Ninf0[t]+Ninf1[t]), где Ninf0[t] и Ninf1[t]- число нулевых символов альтернативной восстановленной информационной последовательности и число единичных символов альтернативной восстановленной информационной последовательности, соответственно, на момент декодирования t-го символа альтернативной декодированной последовательности.
Например, после декодирования альтернативного декодированного проверочного символа из первой части АДП, соответствующей альтернативной принятой последовательности с ее продолжением вида "00101110 0" текущая вероятность нулевых символов альтернативной восстановленной информационной последовательности равна pinf0[3]=3/4, а текущая вероятность единичных символов альтернативной восстановленной информационной последовательности - pinf1[3]=1/4, как показано, например, на фиг. 11 в пятой строке при t=3 в верхней строчке. Следовательно, для данного альтернативного декодированного проверочного символа, являющегося нулевым символов, выполняется соотношение pinf0[3]≥pinf1[3] и этот альтернативный декодированный проверочный символ является допустимым. Таким образом, на текущий момент в альтернативной принятой последовательности с ее продолжением вида "00101110 0" недопустимых альтернативных декодированных проверочных символов не выявлено и запоминают соответствующие ей очередные части альтернативной восстановленной информационной последовательности и значение метрики, равное М=1.
Аналогичным образом выполняют арифметическое декодирование альтернативной принятой последовательности с ее единичным продолжением вида "00101110 1", показанной на фиг. 7(e), в три символа первой части соответствующей ей АДП, примерный вид которой показан на фиг. 7(ж) и фиг. 12. Видно, что эта последовательность также привела к декодированию допустимого АДПС, и запоминают соответствующие ей очередные части альтернативной восстановленной информационной последовательности и значение ее метрики. Метрика этой альтернативной принятой последовательности с ее продолжением сохранила нулевое значение (М=0), то есть на момент считывания и декодирования данного бита принятой последовательности ее шансы на выбор в качестве альтернативной принятой последовательности с наименьшим значением метрики являются предпочтительными по сравнению с ранее рассмотренной альтернативной принятой последовательностью с ее продолжением вида "00101110 0".
Затем сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями и выбирают из них не более Z альтернативных принятых последовательностей, имеющих наименьшие значения метрики. Данные способы известны и описаны, например, в книге М. Сибуя, Т. Ямамото "Алгоритмы обработки данных". - М., Мир, 1986, стр. 122-134, и заключаются в поочередном сравнении между собой значений метрики АПП с их продолжениями, сортировке последовательностей по мере возрастания значений метрики и выборе среди отсортированных последовательностей первых Z последовательностей с наименьшими значениями метрики. Например, после считывания и декодирования текущего, девятого по счету, бита принятой последовательности, альтернативных принятых последовательностей с их продолжениями насчитывается две, поэтому при установленном значении Z=8 выбирают обе рассмотренные выше альтернативные принятые последовательности с их продолжениями.
В выбранные принятые последовательности с их продолжениями дописывают соответствующие им продолжения, для этих АПП запоминают очередные части соответствующих им альтернативных восстановленных информационных последовательностей и значения метрики. Например, в результате сохранены АПП вида "00101110 0" с соответствующей ей альтернативной восстановленной информационной последовательностью вида "000" и метрикой М=1, а также АПП вида "00101110 1" с соответствующей ей альтернативной восстановленной информационной последовательностью вида "000" и метрикой М=0.
Затем считывают очередной бит принятой последовательности, десятый по счету, и если его номер меньше числа Т, то выполняют перечисленные действия на приемной стороне. Например, десятый номер очередного бита принятой последовательности меньше установленной величины задержки декодирования T=16. Для АПП вида "00101110 0" формируют продолжение в виде нулевого символа и продолжение в виде единичного символа. Для полученной АПП с продолжением в виде нулевого символа вида "00101110 00" вычисляют ее метрику, равную М=2, и для полученной АПП с продолжением в виде единичного символа вида "00101110 01" вычисляют ее метрику, равную М=1.
Арифметическое декодирование АПП с продолжением в виде нулевого символа вида "00101110 00" представлено, например, на фиг. 13. Декодирование данной последовательности является продолжением декодирования предшествующей ей АПП с продолжением в виде единичного символа вида "00101110 1", ранее представленного на фиг. 11. После третьего декодированного символа на момент времени t=3 по ранее описанному правилу выполняют нормализацию: из текущего продолжения считывают нулевой символ, с учетом которого входные данные получают значение 184, при нормализации устанавливают текущее нижнее значение интервала декодирования арифметического кодирования LL[3]=0, текущее верхнее значение интервала декодирования арифметического кодирования НH[3]=254 и значение QQ[3]=169. Затем на момент времени t=4 декодируют четвертый по счету символ альтернативной декодированной последовательности, являющийся нулевым символом, и на момент времени t=5 декодируют пятый символ альтернативной декодированной последовательности, являющийся единичным символом. Заметим, что при считывании очередных битов АПП может декодироваться разное число символов АДП. Видно, что на момент времени t=5 для данной АПП с продолжением в виде нулевого символа вида "00101110 00" не декодирована полностью вторая часть соответствующей альтернативной декодированной последовательности.
Аналогичным образом выполняют арифметическое декодирование АПП с продолжением в виде единичного символа вида "00101110 01".
Также при считывании десятого по счету очередного бита принятой последовательности для АПП вида "00101110 1" формируют продолжение в виде нулевого символа и продолжение в виде единичного символа. Для полученной АПП с продолжением в виде нулевого символа вида "00101110 10" вычисляют ее метрику, равную М=1, и для полученной АПП с продолжением в виде единичного символа вида "00101110 11" вычисляют ее метрику, равную М=0.
Арифметическое декодирование АПП с продолжением в виде нулевого символа вида "00101110 10" представлено, например, на фиг. 14, а альтернативной принятой последовательности с продолжением в виде единичного символа вида "00101110 11" представлено, например, на фиг. 15. Декодирование данных последовательностей является продолжением декодирования предшествующей ей АПП с продолжением в виде нулевого символа вида "00101110 0", ранее представленного на фиг. 12. Результаты декодирования этих последовательностей сходны с результатами декодирования АПП с продолжением в виде нулевого символа вида "00101110 00", за исключением различий в значениях входных данных и метриках. Как показано, например, на фиг. 10, на этом этапе АПП с их продолжениями выбирают 4 из текущего их числа 4, далее при считывании одиннадцатого по счету символа принятой последовательности - 8 из текущего их числа 8.
При считывании двенадцатого по счету символа принятой последовательности арифметически декодируют 16 АПП с их продолжениями. При этом в АПП с продолжениями вида "00101110 1101", "00101110 1110" и "00101110 1111" выявляют недопустимые альтернативные декодированные проверочные символы и эти последовательности не выбирают в число Z альтернативных принятых последовательностей с их продолжениями, имеющих наименьшие значения метрики. В частности, отвергнутой оказалась АПП с продолжением вида "00101110 1101", имеющая до того наименьшее значение метрики (М=0).
Среди оставшихся АПП с их продолжениями выбирают три АПП с их продолжениями со значением метрики М=1 вида "00101110 0101", "00101110 1001" и "00101110 1100" и пять АПП с их продолжениями со значением метрики М=2. На этом этапе отвергнутыми оказались все АПП с продолжениями, имеющими значения метрики М=3 и М=4.
При считывании тринадцатого по счету символа принятой последовательности из трех АПП с соответствующими продолжениями со значением метрики М=1 осталась только одна последовательность со значением метрики М=1 вида "00101110 01011". При считывании четырнадцатого по счету символа принятой последовательности из этой АПП с ее продолжением вида "00101110 010110", показанной на фиг. 7(з), на момент времени t=12 выполнено декодирование четырех частей альтернативной декодированной последовательности вида "000 010 010 001", показанной на фиг. 7(и), из четвертой части которой выделен альтернативный декодированный проверочный символ, являющийся единичным символом. В результате его проверки выявлена его недопустимость, так как текущая вероятность нулевых символов альтернативной восстановленной информационной последовательности pinf0[12]=6/10 превышает текущую вероятность единичных символов альтернативной восстановленной информационной последовательности pinf1[12]=4/10, что является условием признания допустимым только нулевого альтернативного декодированного проверочного символа.
При выявлении недопустимого альтернативного декодированного проверочного символа, устанавливают значение метрики соответствующей ему альтернативной принятой последовательности с ее продолжением в максимальное значение. Например, устанавливают значение метрики АПП с ее продолжением вида "00101110 010110" равным М=1000, что неизбежно приведет к тому, что эта АПП с ее продолжением не будет выбрана в L АПП, имеющие наименьшие значения метрики.
В результате среди оставшихся АПП с их продолжениями нет ни одной последовательности со значением метрики М=1 и имеются 3 последовательности со значением метрики М=2, как показано, например, на фиг. 10. При считывании последующих символов принятой последовательности в двух из указанных трех последовательностей с соответствующими продолжениями, имеющих значение метрики М=2, будут выявлены недопустимые альтернативные декодированные проверочные символы. Со значением метрики М=2 оставшаяся последовательность с соответствующим продолжением вида "00101110 000110" будет последовательностью с наименьшим значением метрики, удовлетворяющей требованию допустимости альтернативных декодированных проверочных символов, как показано, например, на фиг. 17.
Если номер очередного бита очередной части принятой последовательности не меньше числа Т, то сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них альтернативную принятую последовательность с наименьшим значением метрики, передают получателю в качестве очередной части восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности очередную часть альтернативной восстановленной информационной последовательности. Например, при T=16 альтернативная принятая последовательность с ее последовательными продолжениями вида "00101110 000110" имеет наименьшее значение метрики М=2. Как показано на фиг. 17, в результате ее арифметического декодирования сформирована АДП вида "000 010 010 000 1", показанная, например на фиг. 7(л), содержащая первые 4 части альтернативной восстановленной информационной последовательности вида "00 01 01 00", показанные, например на фиг. 7(м). Из них передают получателю в качестве первой части восстановленной информационной последовательности первую часть данной альтернативной восстановленной информационной последовательности вида "00", показанную, например на фиг. 7(н). Затем по мере считывания и декодирования очередных битов очередных частей принятой последовательности передают получателю следующие части восстановленной информационной последовательности.
Проверка теоретических предпосылок заявленного способа совместного арифметического и помехоустойчивого кодирования и декодирования проверялась путем его аналитических исследований.
Было выполнено совместное арифметическое и помехоустойчивое кодирование и декодирование нескольких очередных частей информационной последовательности с использованием способа-прототипа и предлагаемого способа, результаты показаны на фиг. 18. В соответствии со способом - прототипом и предлагаемым способом выполнялось совместное арифметическое и помехоустойчивое кодирование и декодирование очередных частей информационной последовательности длиной k=4 бит общей длиной 1024 бит, при использовании проверочных символов длиной r=1 бит.
На длине N бит запомненных очередных частей принятой последовательности для способа-прототипа и длине и величине задержки декодирования T для предлагаемого способа, при условии N=Т, на кодированную последовательность накладывались ошибки передачи в следующих вариантах: только одна ошибка (W=1), две ошибки (W=2), три ошибки (W=3). Для каждого значения W конфигурации ошибок случайным образом генерировались 1000 раз. На приемной стороне подсчитывалось среднее число вариантов инвертирования битов принятой последовательности для исправления ошибок для способа-прототипа, а для предлагаемого способа - требуемое число альтернативных принятых последовательностей для исправления ошибок. Выявлено, что для исправления ошибок кратности от W=1 до W=3 согласно способа-прототипа необходимо выполнить в среднем от 6 до 869 попыток декодирования принятой последовательности с инвертированными битами, а для исправления этих же ошибок согласно предлагаемого способа требуемое число альтернативных принятых последовательностей лежит в диапазоне значений от 4 до 11. Сложность практической реализации исправления ошибок передачи прямо пропорциональна числу попыток декодирования принятой последовательности с инвертированными битами и требуемому числу альтернативных принятых последовательностей, соответственно.
Проведенные исследования подтверждают, что при использовании предлагаемого способа совместного арифметического и помехоустойчивого кодирования и декодирования избыточной двоичной информационной последовательности обеспечивается возможность практической реализации исправления многократных ошибок передачи.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2018 |
|
RU2702724C2 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2019 |
|
RU2712096C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2019 |
|
RU2718213C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ (ВАРИАНТЫ) | 2016 |
|
RU2611022C1 |
| СПОСОБ СОВМЕСТНОГО СЖАТИЯ И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2015 |
|
RU2595955C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2015 |
|
RU2629455C2 |
| СПОСОБ АРИФМЕТИЧЕСКОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2020 |
|
RU2752868C1 |
| СПОСОБ АРИФМЕТИЧЕСКОГО КОДИРОВАНИЯ С ШИФРОВАНИЕМ | 2017 |
|
RU2656713C1 |
| СПОСОБ АРИФМЕТИЧЕСКОГО КОДИРОВАНИЯ С ШИФРОВАНИЕМ | 2015 |
|
RU2595953C1 |
| СПОСОБ АУТЕНТИФИКАЦИИ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2014 |
|
RU2568268C1 |

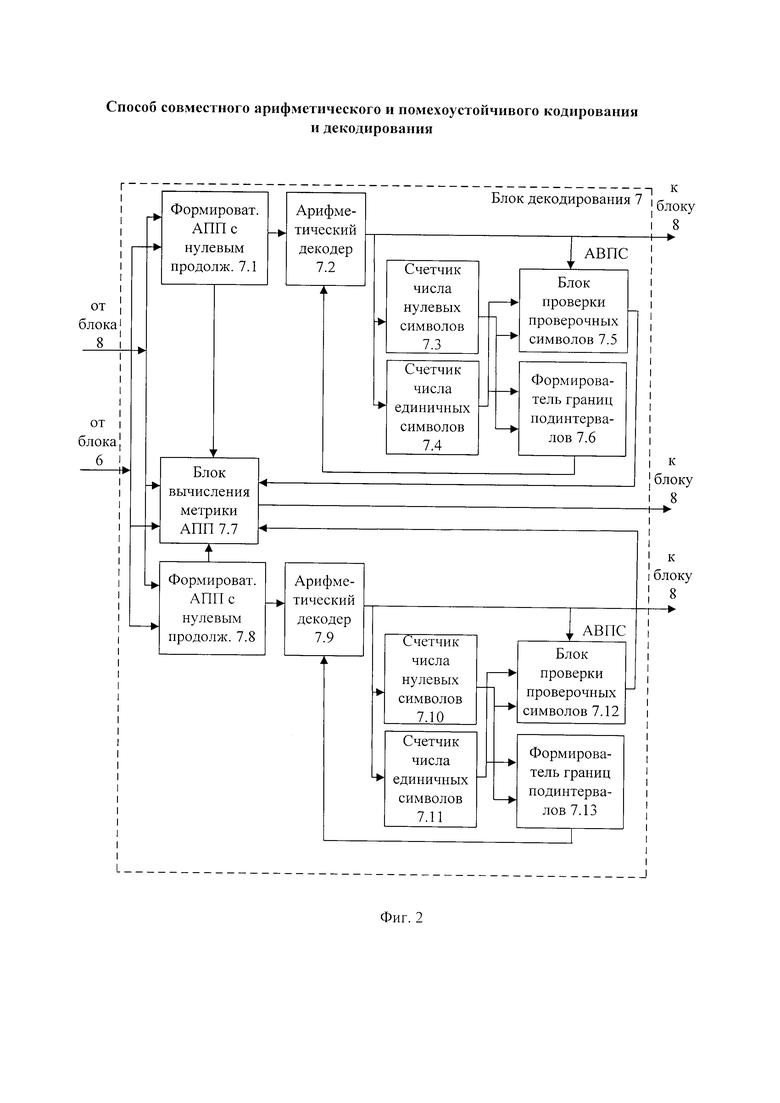
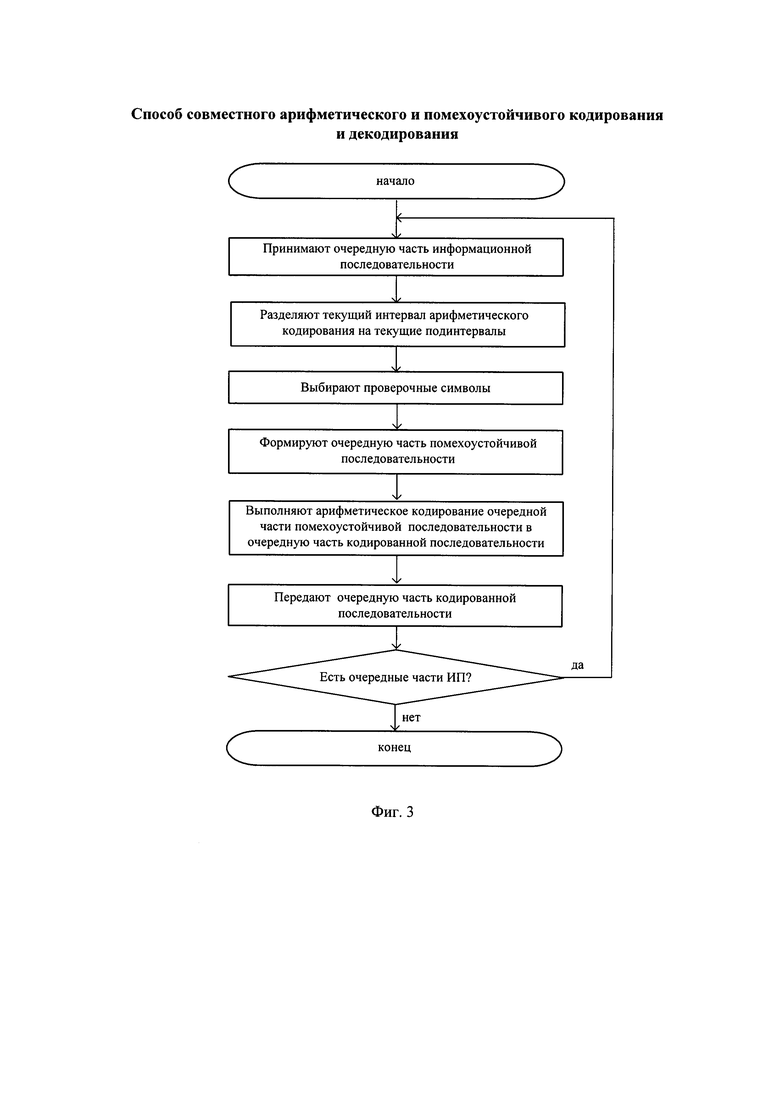








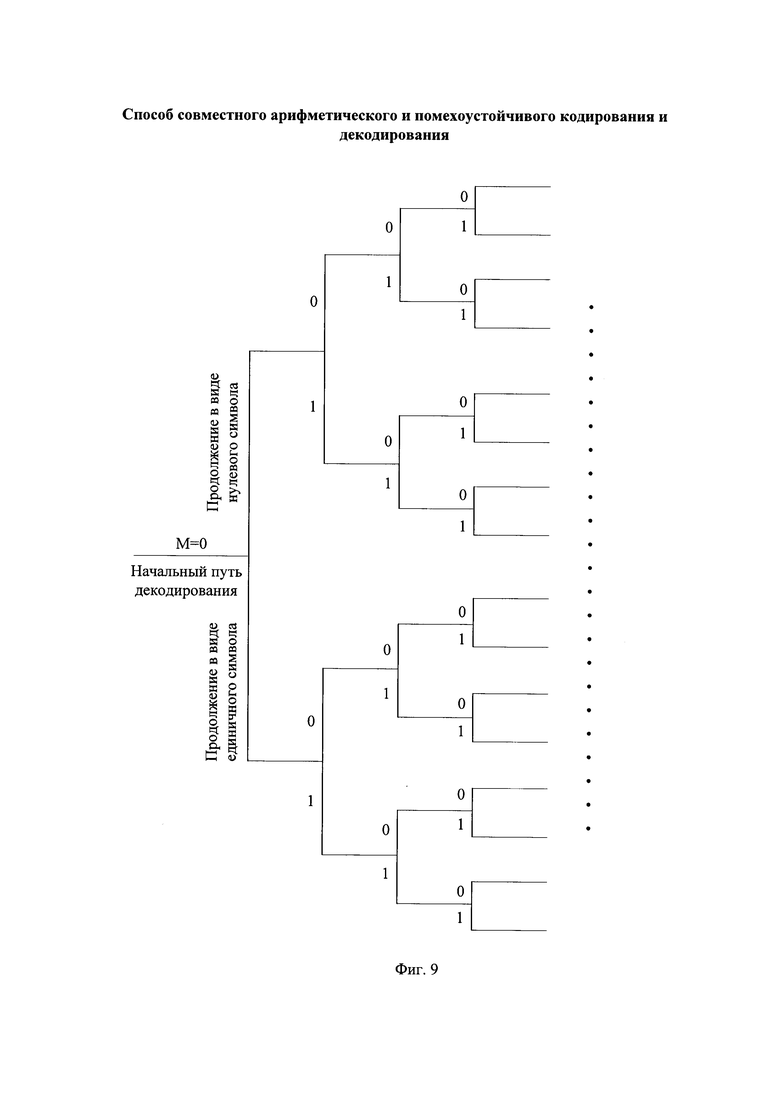
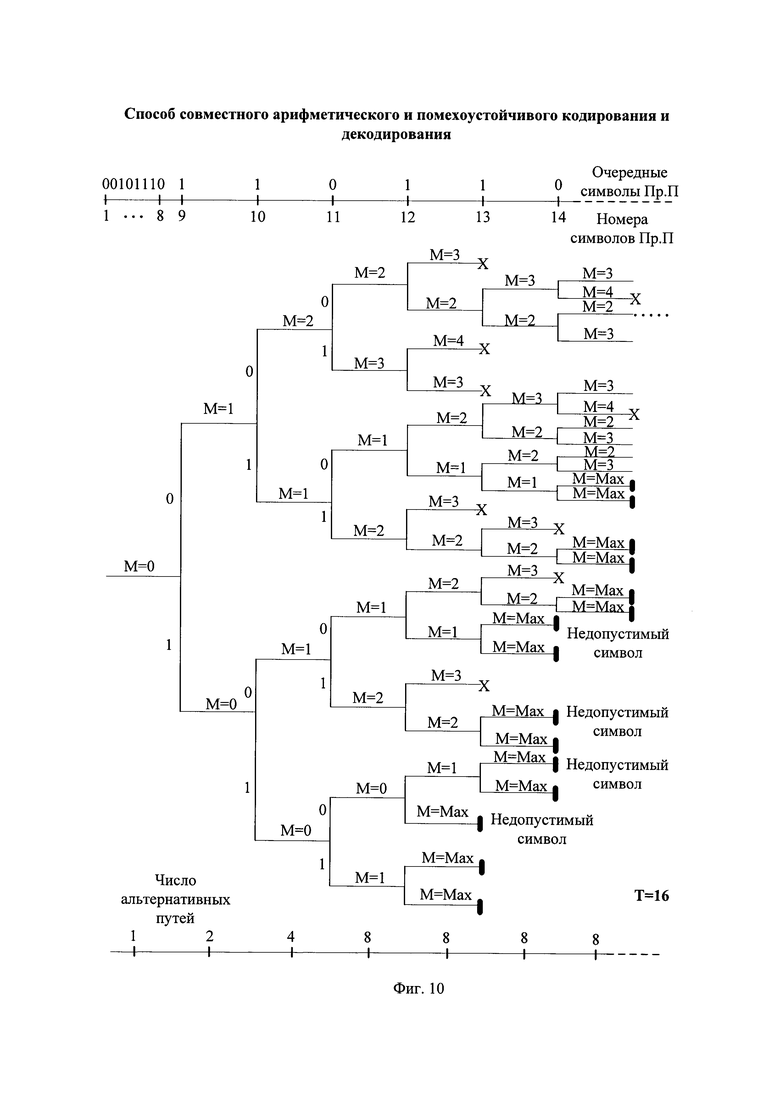

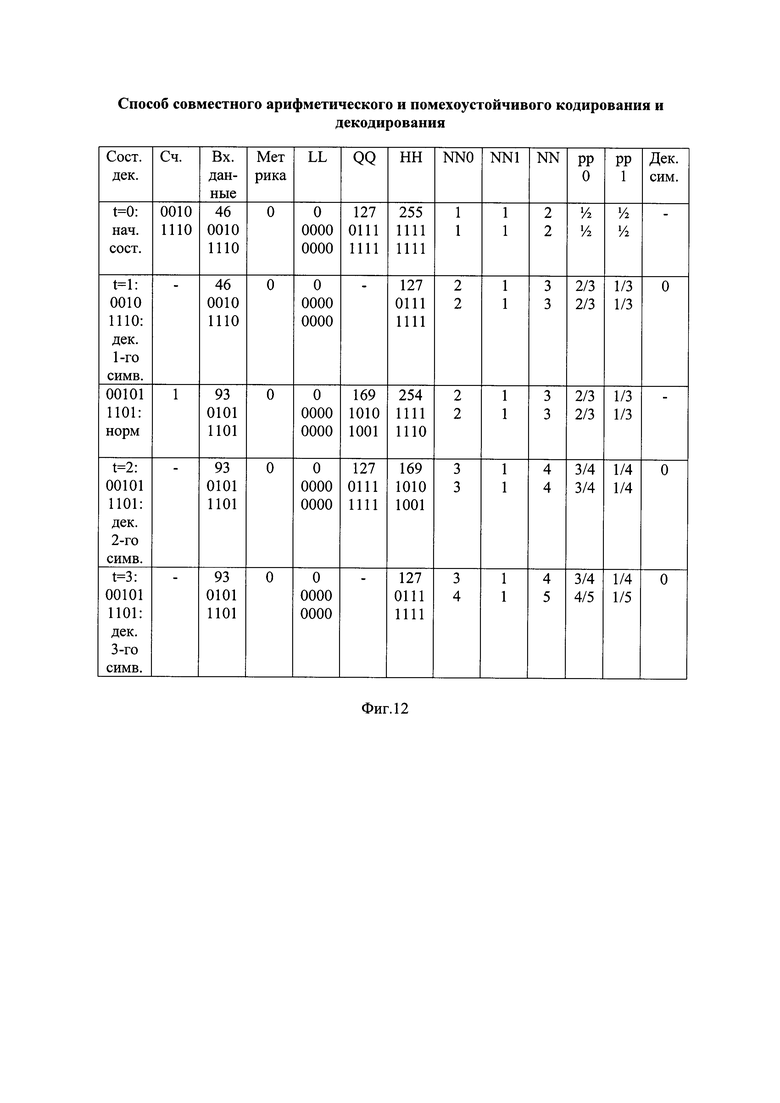

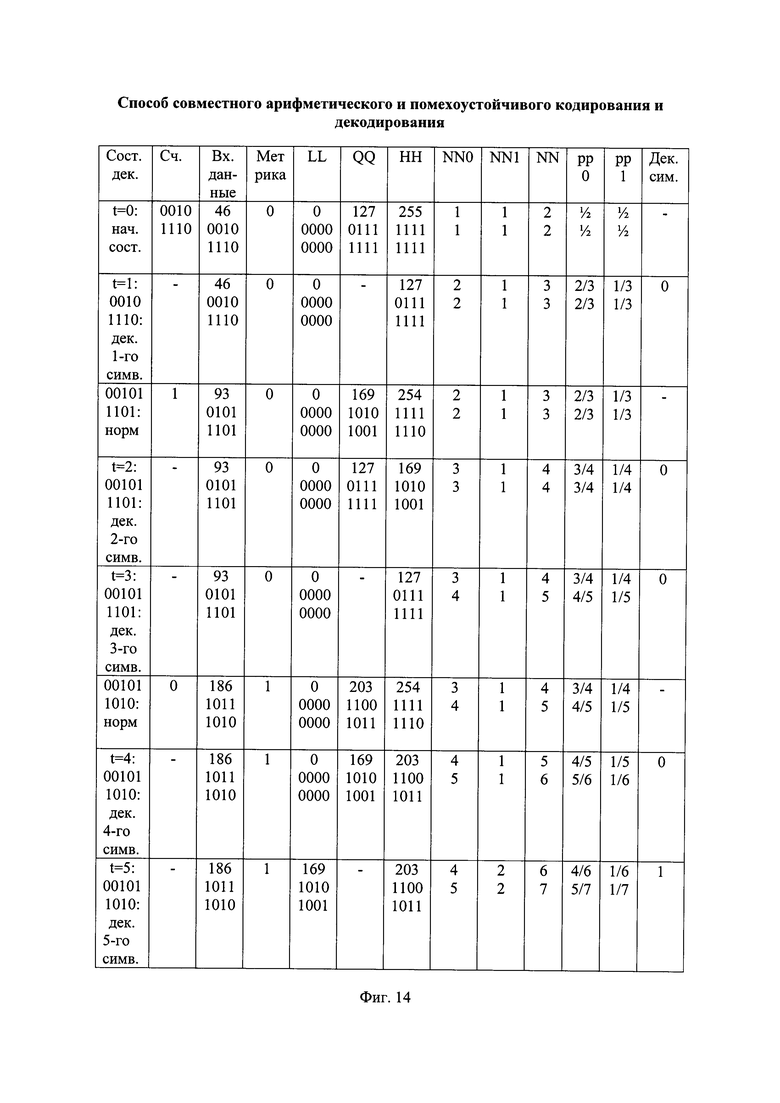


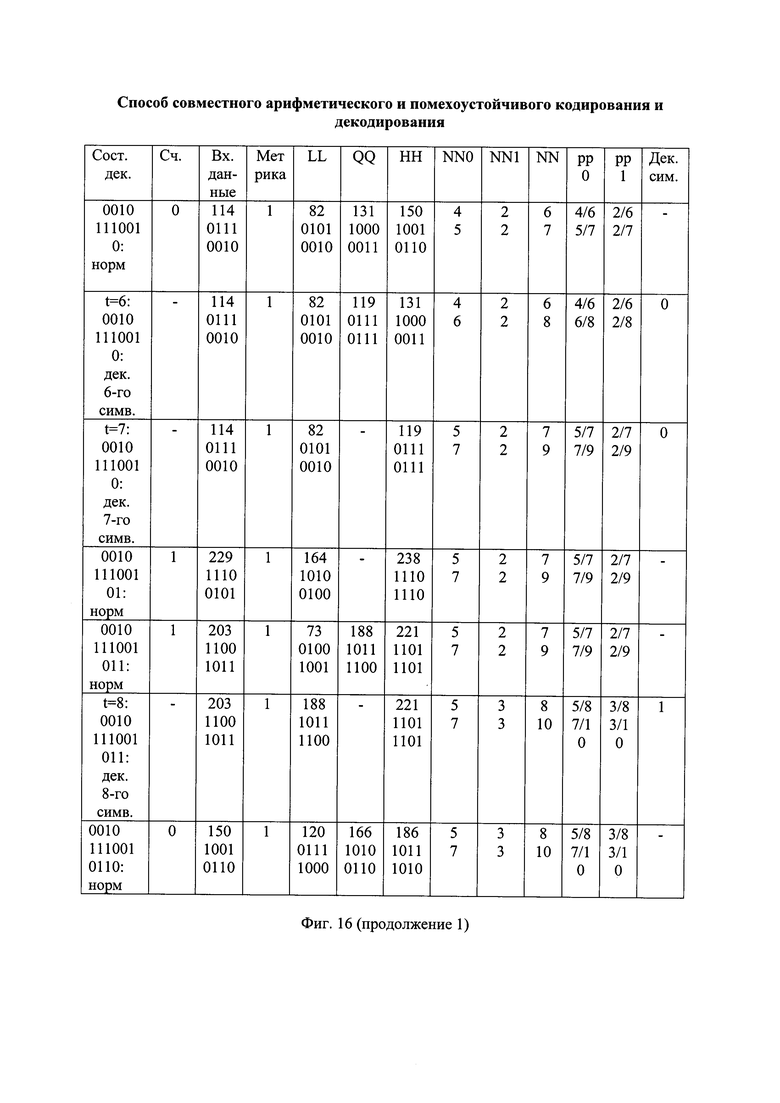


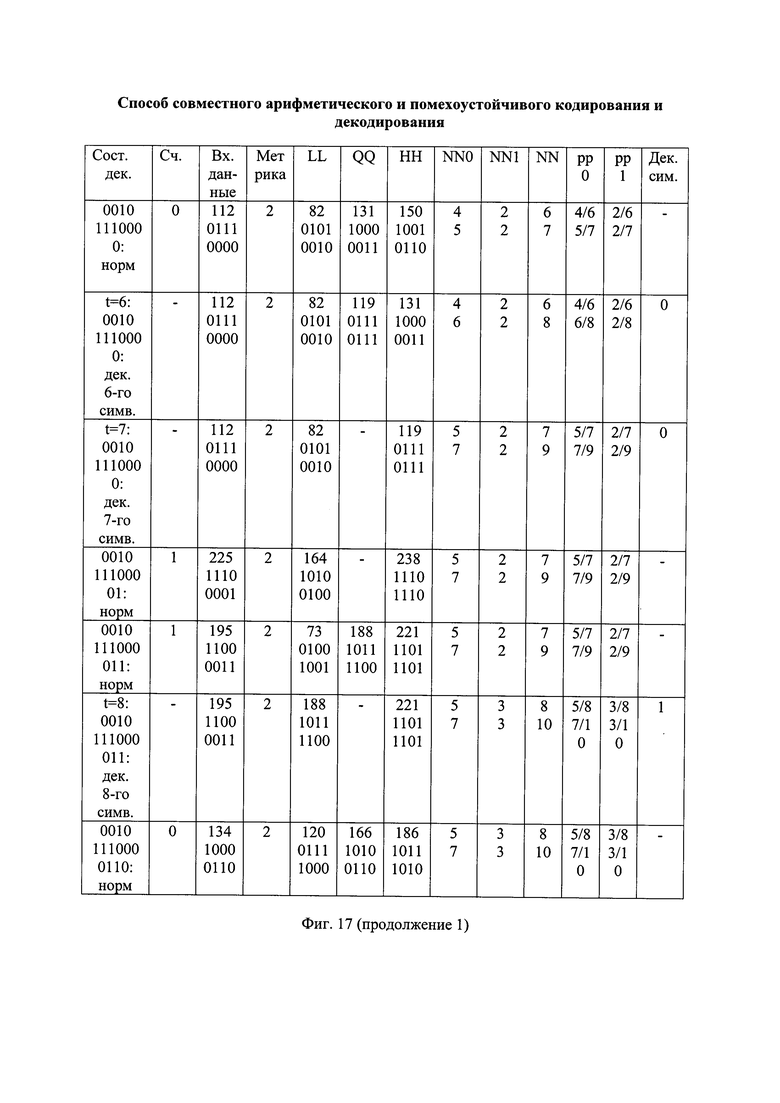
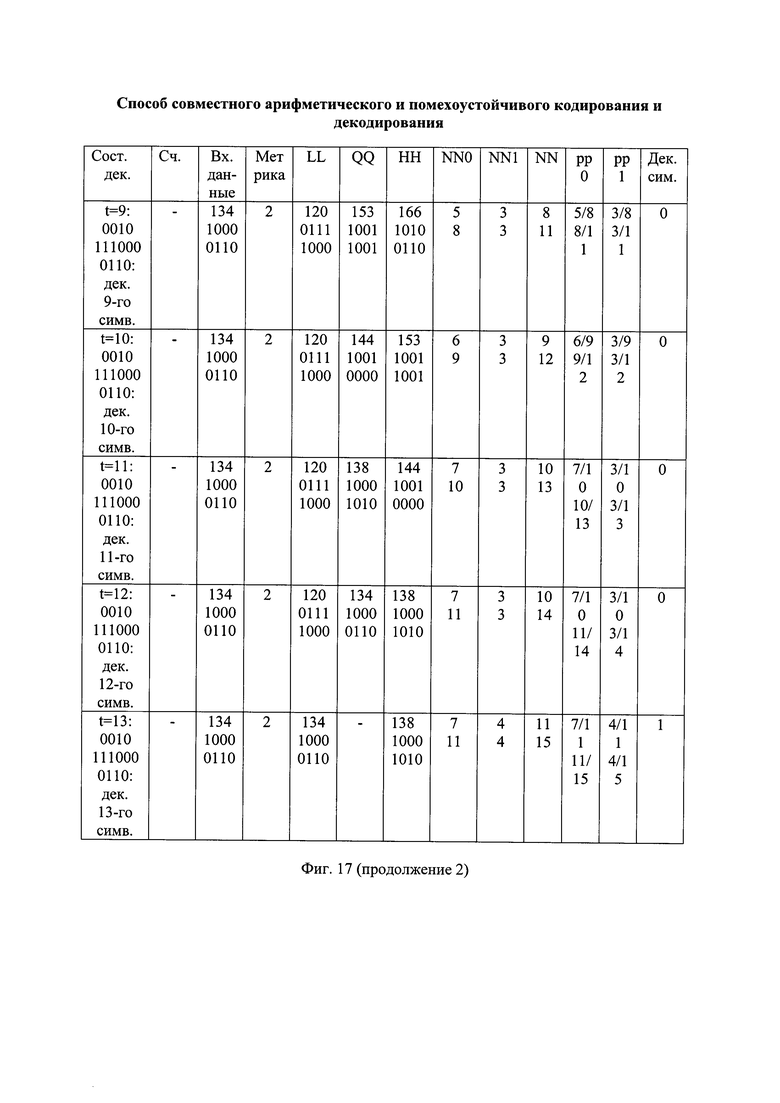

Изобретение относится к технике помехоустойчивого кодирования и декодирования при передаче информации по каналам с ошибками. Технический результат - совместное арифметическое и помехоустойчивое кодирование и декодирование избыточной двоичной информационной последовательности, обеспечивающее возможность практической реализации исправления многократных ошибок передачи. В соответствии с изобретением для очередных частей передаваемой информационной последовательности выбирают проверочные символы, арифметически совместно кодируют, передают, формируют не более предельного числа Z≥2 альтернативных принятых последовательностей и вычисляют степень их подобия с принятой последовательностью в виде метрики, арифметически декодируют альтернативные принятые последовательности, выделяют очередные части альтернативной восстановленной информационной последовательности и альтернативные декодированные проверочные символы и, если последние являются допустимыми, продолжают эти альтернативные принятые последовательности, из которых выбирают последовательность с наименьшей метрикой, из которой с заданной задержкой декодирования выделяют очередную часть восстановленной информационной последовательности, которую передают получателю. 3 з.п. ф-лы, 18 ил.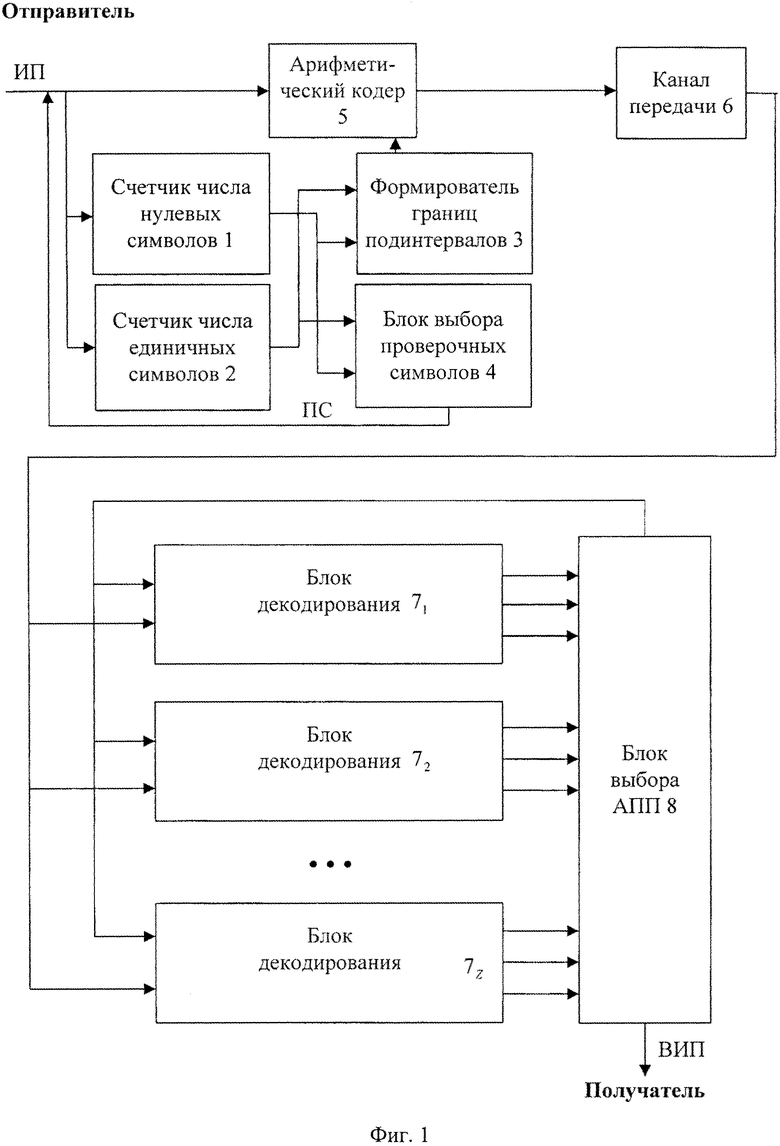
1. Способ совместного арифметического помехоустойчивого кодирования и декодирования, заключающийся в том, что предварительно на передающей стороне устанавливают начальный интервал арифметического кодирования и на приемной стороне соответствующий ему начальный интервал арифметического декодирования, на передающей стороне от источника информационной последовательности принимают очередную часть информационной последовательности длиной k≥1 бит, разделяют текущий интервал арифметического кодирования на текущий подынтервал кодирования нулевого символа и на текущий подынтервал кодирования единичного символа, выбирают проверочные символы длиной r≥1 бит, формируют очередную часть помехоустойчивой последовательности из очередной части информационной последовательности и выбранных проверочных символов, выполняют арифметическое кодирование очередной части помехоустойчивой последовательности в очередную часть кодированной последовательности, передают очередную часть последовательности на приемную сторону, выполняют на передающей стороне перечисленные действия до тех пор, пока поступают очередные части информационной последовательности, на приемной стороне получают очередную часть принятой последовательности, разделяют текущий интервал арифметического декодирования принятой последовательности на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа, арифметически декодируют принятую последовательность в очередные части декодированной последовательности, из которых выделяют очередные части восстановленной информационной последовательности и декодированные проверочные символы, передают получателю очередную часть восстановленной информационной последовательности, выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные части принятой последовательности, отличающееся тем, что предварительно устанавливают предельное число альтернативных принятых последовательностей Z≥2 и величину задержки декодирования Т≥2, а также значения метрики альтернативных принятых последовательностей в нулевое значение, на передающей стороне передают очередную часть кодированной последовательности на приемную сторону, а на приемной стороне получают очередную часть принятой последовательности и считывают из нее очередной бит, разделяют текущий интервал арифметического декодирования каждой альтернативной принятой последовательности на текущий подынтервал декодирования нулевого символа и на текущий подынтервал декодирования единичного символа этой последовательности, для каждой альтернативной принятой последовательности формируют продолжение в виде нулевого символа и продолжение в виде единичного символа, вычисляют значение метрики продолжения в виде нулевого символа и значение метрики продолжения в виде единичного символа относительно очередного бита очередной части принятой последовательности, для каждой альтернативной принятой последовательности с ее продолжением вычисляют значение ее метрики суммированием метрики самой последовательности и ее продолжения, арифметически декодируют каждую альтернативную принятую последовательность с ее продолжением в очередные части соответствующей ей альтернативной декодированной последовательности, из которых выделяют очередные части альтернативной восстановленной информационной последовательности и альтернативные декодированные проверочные символы, если альтернативные декодированные проверочные символы являются допустимыми, то запоминают очередные части альтернативной восстановленной информационной последовательности соответствующей альтернативной принятой последовательности с ее продолжением, иначе устанавливают значение метрики этой альтернативной принятой последовательности с ее продолжением в максимальное значение, сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями и выбирают из них не более Z альтернативных принятых последовательностей с их продолжениями, имеющих наименьшие значения метрики, в которые дописывают соответствующие им продолжения, для этих альтернативных принятых последовательностей запоминают очередные части соответствующей им альтернативной восстановленной информационной последовательности и значения метрики, считывают очередной бит очередной части принятой последовательности и, если его номер меньше числа Т, выполняют перечисленные действия на приемной стороне, иначе сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них альтернативную принятую последовательность с наименьшим значением метрики, передают получателю в качестве очередной части восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности очередную часть альтернативной восстановленной информационной последовательности, выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные части принятой последовательности.
2. Способ по п. 1, отличающийся тем, что на передающей стороне проверочные символы выбирают как нулевые символы, если определенная арифметическим кодированием текущая вероятность нулевых символов информационной последовательности больше или равна текущей вероятности единичных символов информационной последовательности, иначе выбирают проверочные символы как единичные символы, а на приемной стороне, если альтернативные декодированные проверочные символы являются нулевыми символами при условии, что определенная арифметическим декодированием текущая вероятность нулевых символов альтернативной восстановленной информационной последовательности больше или равна текущей вероятности единичных символов этой последовательности, или если альтернативные декодированные проверочные символы являются единичными символами при условии, что определенная арифметическим декодированием текущая вероятность единичных символов альтернативной восстановленной информационной последовательности больше текущей вероятности нулевых символов этой последовательности, то альтернативные декодированные проверочные символы являются допустимыми.
3. Способ по п. 1, отличающийся тем, что значение метрики продолжения в виде нулевого символа относительно очередного бита очередной части принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является нулевым битом, иначе вычисляют как единичное значение.
4. Способ по п. 1, отличающийся тем, что значение метрики продолжения в виде единичного символа относительно очередного бита очередной части принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является единичным битом, иначе вычисляют как единичное значение.
| СПОСОБ АДАПТИВНОГО ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2007 |
|
RU2375824C2 |
| RU 2011135321 A, 10.03.2013 | |||
| ЦИФРОВОЙ КОМПЬЮТЕР С ВОЗМОЖНОСТЬЮ ПАРАЛЛЕЛЬНОГО ВЫПОЛНЕНИЯ ДВУХ И БОЛЕЕ КОМАНД | 1991 |
|
RU2109333C1 |
| US 6892343 B2, 10.05.2005 | |||
| US 6044485 A1, 28.03.2000 | |||
| US 6504496 B1, 07.01.2003 | |||
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| US 5717394 A1, 10.02.1998 | |||
| US 9009560 B1, 14.04.2015. | |||
Авторы
Даты
2017-05-29—Публикация
2016-07-20—Подача