Заявленное техническое решение относится к области электросвязи и информационных технологий, а именно к технике сжатия и восстановления избыточной двоичной информации и ее помехоустойчивого кодирования и декодирования при передаче информации по каналам с ошибками.
Заявленное изобретение может быть использовано для обеспечения достоверности избыточной двоичной информации, передаваемой по каналам с ошибками.
Известен способ адаптивного помехоустойчивого кодирования и декодирования по патенту РФ 2375824 МПК H04L 1/20 (2006.01) от 10.12.2009, заключающийся в том, что на передающей стороне исходную информацию кодируют помехоустойчивым кодом с переменными параметрами, далее помехоустойчивый код передают в канал связи, на приемной стороне помехоустойчивый код декодируют с обнаружением и исправлением ошибок в зависимости от корректирующей способности выбранного кода, по результатам декодирования помехоустойчивого кода оценивают качество канала связи и выбирают переменные параметры помехоустойчивого кода, обеспечивающие заданную вероятность правильного приема помехоустойчивого кода, и далее эти параметры помехоустойчивого кода сообщают на передающую сторону, отличающийся тем, что на приемной стороне по результатам декодирования помехоустойчивого кода рассчитывают начальную величину избыточности помехоустойчивого кода, обеспечивающую заданную вероятность правильного приема помехоустойчивого кода, оценивают вероятность правильного приема помехоустойчивого кода с выбранными параметрами, вычисляют величину отклонения полученной вероятности правильного приема помехоустойчивого кода от заданной вероятности правильного приема кода и в зависимости от величины этого отклонения корректируют величину избыточности помехоустойчивого кода, которую передают на передающую сторону, где формируют помехоустойчивый код с полученной избыточностью.
Недостатком указанного аналога является неэффективное использование пропускной способности канала передачи, вызванное отсутствием сжатия избыточной двоичной информации при обмене данными по каналам передачи с ошибками.
Известен также способ совместного сжатия и помехоустойчивого кодирования и декодирования речевых сообщений, описанный, например, в книге С.Н. Кириллов, В.Т. Дмитриев, Д.Е. Крысяев, С.С. Попов "Исследование качества передаваемой речевой информации при различном сочетании алгоритмов кодирования источника и канала связи в условиях воздействия помех". - Рязань, Вестник РГРТУ, Выпуск 23, 2008. Данный способ заключается в том, что предварительно формируют множество способов сжатия речевого сигнала, таких как импульсно-кодовая модуляция, адаптивная дельта-модуляция, адаптивная дифференциальная импульсно-кодовая модуляция, и множество способов помехоустойчивого кодирования, таких как кодирование Хэмминга, кодирование Боуз-Чоудхури-Хоквингема, на передающей стороне от отправителя получают очередную часть речевого сигнала длиною речевая фраза, который преобразуют в сжатую двоичную последовательность с помощью одного из способов сжатия речевого сигнала, выполняют помехоустойчивое кодирование сжатой двоичной последовательности с помощью одного из способов помехоустойчивого кодирования, передают на приемную сторону по каналу прямой связи очередную часть кодированной последовательности вместе с информацией об использованном способе сжатия речевого сигнала и способе помехоустойчивого кодирования, на приемной стороне получают очередную часть принятой последовательности, очередную часть принятой последовательности последовательно декодируют с использованием соответствующих способа помехоустойчивого декодирования и способа восстановления речевого сигнала, вычисляют оценку качества восстановленного речевого сигнала и полученную оценку сравнивают с пороговым значением качества, если вычисленная оценка качества восстановленного речевого сигнала не хуже предварительно установленного порогового значения качества, то передают получателю очередную часть восстановленной информационной последовательности и передающей стороне от отправителя получают очередную часть речевого сигнала и выполняют последующие действия, иначе передают по каналу обратной связи требование изменить способ сжатия речевого сигнала и способ помехоустойчивого кодирования, и выполняют последующие действия.
Недостатком указанного аналога является большая задержка передачи сообщений по каналу связи, вызванная необходимостью подбора подходящих способа сжатия речевого сигнала и способа помехоустойчивого кодирования.
Наиболее близким по своей технической сущности к заявленному способу совместного арифметического и помехоустойчивого кодирования и декодирования является способ совместного арифметического и помехоустойчивого кодирования и декодирования по патенту США 6892343 МПК Н04М 13/00 (2006.01) от 10.05.2005. Способ-прототип совместного арифметического и помехоустойчивого кодирования и декодирования заключается в том, что предварительно на передающей стороне устанавливают начальный интервал арифметического кодирования и на приемной стороне соответствующий ему начальный интервал арифметического декодирования, на передающей стороне от источника информации принимают очередную часть информационной последовательности длиной k≥1 бит, разделяют текущий интервал арифметического кодирования длиною D>2 на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа, из предварительно сформированного множества выбирают проверочные символы длиной r≥1 бит и формируют очередную часть помехоустойчивой последовательности из очередной части информационной последовательности и выбранных проверочных символов, выполняют арифметическое кодирование очередной части помехоустойчивой последовательности в очередную часть кодированной последовательности, преобразуют очередную часть кодированной последовательности в очередную часть модулированной последовательности, передают очередную часть модулированной последовательности на приемную сторону, выполняют на передающей стороне перечисленные действия до тех пор, пока поступают очередные части информационной последовательности, на приемной стороне принимают очередную часть последовательности, преобразуют ее в двоичную последовательность, которую запоминают, разделяют текущий интервал арифметического декодирования длиною DD>2 на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа, запомненные очередные части принятой последовательности арифметически декодируют в очередные части декодированной последовательности, из которых выделяют очередные части восстановленной информационной последовательности и декодированные проверочные символы, если декодированные проверочные символы принадлежат предварительно сформированному множеству проверочных символов, то делают вывод об отсутствии ошибок передачи и передают очередную часть восстановленной информационной последовательности, иначе поочередно инвертируют один или несколько битов в запомненных очередных частях принятой последовательности и выполняют их арифметическое декодирование до достижения вывода об отсутствии ошибок передачи, выполняют перечисленные действия на приемной стороне до тех пор, пока на приемной стороне поступают очередные части принятой последовательности.
Особенностью способа-прототипа является то, что на передающей стороне выполняют выбор проверочных символов, а затем сжатие очередных частей информационной последовательности и проверочных символов путем арифметического кодирования, а на приемной стороне после арифметического декодирования обнаруживают ошибки передачи при их наличии, а при их обнаружении методом проб и ошибок выполняют их исправление. Способ-прототип совместного арифметического и помехоустойчивого кодирования и декодирования обеспечивает возможность обнаружения и исправления ошибок передачи.
Однако в данном способе-прототипе совместного арифметического и помехоустойчивого кодирования и декодирования информационной последовательности исправление ошибок передачи выполняют методом перебора, поочередно инвертируя один или несколько битов в запомненных очередных частях принятой последовательности и выполняя их арифметическое декодирование до достижения вывода об исправлении этих ошибок с использованием проверочных символов. При длине N бит запомненных очередных частей принятой последовательности и числе W исправляемых ошибок это требует параллельной работы порядка Nw/2 арифметических декодеров с соответствующим числом устройств обнаружения ошибок. При арифметическом декодировании сжатых избыточных двоичных последовательностей наличие ошибок передачи выявляется при длине запомненных очередных частях принятой последовательности вплоть до десятков бит и более. Поэтому в данном способе-прототипе совместного арифметического и помехоустойчивого кодирования и декодирования исправление ошибок передачи при кратности ошибок более одной требует использования многих тысяч арифметических декодеров с соответствующим числом устройств обнаружения ошибок, что является практически нереализуемым.
Таким образом, недостатком ближайшего аналога (прототипа) совместного арифметического и помехоустойчивого кодирования и декодирования информационной последовательности является низкая помехоустойчивость передачи очередных частей кодированной последовательности, обусловленная практической невозможностью исправления ошибок передачи при кратности ошибок более одной.
Техническим результатом заявляемого решения является разработка способа совместного арифметического и помехоустойчивого кодирования и декодирования, обеспечивающего повышение помехоустойчивости передачи очередных частей кодированной последовательности при воздействии многократных ошибок передачи.
Указанный технический результат в заявляемом способе совместного арифметического и помехоустойчивого кодирования и декодирования достигается тем, что в известном способе совместного арифметического и помехоустойчивого кодирования и декодирования, заключающимся в том, что предварительно на передающей стороне устанавливают начальный интервал арифметического кодирования и на приемной стороне соответствующий ему начальный интервал арифметического декодирования, на передающей стороне от источника информационной последовательности принимают очередную часть информационной последовательности длиной k≥1 бит, разделяют текущий интервал арифметического кодирования длиною D>2 на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа, выполняют арифметическое кодирование очередной части последовательности в очередную часть кодированной последовательности, передают очередную часть последовательности на приемную сторону, выполняют на передающей стороне перечисленные действия до тех пор, пока поступают очередные части информационной последовательности, на приемной стороне принимают последовательность, разделяют текущий интервал арифметического декодирования на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа, арифметически декодируют очередные части принятой последовательности в очередные части последовательности, выполняют перечисленные действия на приемной стороне до тех пор, пока на приемной стороне поступает последовательность, передают восстановленную информационную последовательность, дополнительно предварительно устанавливают предельное число Z≥2 альтернативных принятых последовательностей и значение метрики альтернативных принятых последовательностей в нулевое значение.
На передающей стороне после приема очередной части информационной последовательности из текущего интервала арифметического кодирования длиною D>2 выделяют текущий разрешенный подинтервал кодирования длиною Dβ>2, который разделяют на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа. Причем длину Dβ текущего разрешенного интервала кодирования выбирают как Dβ=β⋅D, где значение коэффициента помехоустойчивости β устанавливают в пределах 0<β<1. Выполняют арифметическое кодирование очередной части информационной последовательности в очередную часть кодированной последовательности.
Передают очередную часть кодированной последовательности на приемную сторону, а на приемной стороне принимают очередной бит последовательности. Из текущего интервала арифметического декодирования длиною DD>2 каждой альтернативной принятой последовательности выделяют текущий разрешенный интервал декодирования длиною DDβ>2, который разделяют на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа этой последовательности. Причем длину DDβ текущего разрешенного интервала декодирования устанавливают из условия DDβ=β⋅DD.
Для каждой альтернативной принятой последовательности формируют продолжение последовательности в виде нулевого символа и продолжение последовательности в виде единичного символа, устанавливают значение метрики продолжения последовательности в виде нулевого символа и значение метрики продолжения последовательности в виде единичного символа относительно очередного бита принятой последовательности. Значение метрики продолжения последовательности в виде нулевого символа относительно очередного бита принятой последовательности устанавливают как нулевое значение, если очередной бит принятой последовательности является нулевым битом, иначе устанавливают как единичное значение. Значение метрики продолжения последовательности в виде единичного символа относительно очередного бита принятой последовательности устанавливают как нулевое значение, если очередной бит принятой последовательности является единичным битом, иначе устанавливают как единичное значение.
Для каждой альтернативной принятой последовательности с ее продолжением последовательности вычисляют значение ее метрики, для чего суммируют значения метрики данной последовательности и метрики ее продолжения последовательности. Арифметически декодируют каждую альтернативную принятую последовательность с ее продолжением последовательности в очередные части соответствующей ей альтернативной восстановленной последовательности, если текущее значение принятой последовательности находится в пределах текущего разрешенного интервала декодирования альтернативной принятой последовательности, то запоминают очередные части альтернативной восстановленной информационной последовательности, соответствующие этой последовательности, иначе стирают данную альтернативную принятую последовательность с ее продолжением последовательности.
Сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями последовательности и выбирают из них не более предельного числа Z альтернативных принятых последовательностей, имеющих наименьшие значения метрики, которые дополняют соответствующими им продолжениями последовательности. Для этих альтернативных принятых последовательностей запоминают очередные части соответствующих им альтернативных восстановленных информационных последовательностей и значения метрики, выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные биты принятой последовательности. Далее сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них последовательность с наименьшим значением метрики, после чего передают в качестве восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности альтернативную восстановленную информационную последовательность.
В предлагаемой совокупности действий на передающей стороне при арифметическом кодировании очередной части информационной последовательности в очередную часть кодированной последовательности последнюю формируют в соответствии с текущим разрешенным интервалом кодирования, а на приемной стороне при декодировании очередных частей принятой последовательности стирают те альтернативные принятые последовательности, которые не могут быть сформированы на передающей стороне в соответствии с текущим разрешенным интервалом, среди оставшихся сохраняют и продолжают ограниченное число Z альтернативных принятых последовательностей с их продолжениями последовательности, имеющих наименьшие значения метрики, и после приема всей последовательности среди лучших по критерию метрики продолжаемых альтернативных принятых последовательностей выбирают последовательность с наименьшим значением метрики, которая с наибольшей вероятностью совпадает со сформированной на передающей стороне кодированной последовательностью. Тем самым выполняют исправление ошибок канала передачи, причем кратность исправленных ошибок в принятой последовательности обеспечивается не меньшей значения метрики выбранной альтернативной принятой последовательности. Данный способ декодирования относится к классу методов декодирования сообщения в целом, которые теоретически способны достичь предельно высокой помехоустойчивости передачи сообщений. Благодаря тому, что при декодировании очередных битов принятой последовательности стирают альтернативные принятые последовательности, которые не обеспечивают исправление ошибок, и продолжают ограниченное число Z нестертых альтернативных принятых последовательностей с их продолжениями последовательности, которые обеспечивают максимизацию вероятности исправления ошибок передачи, обеспечивается возможность исправления многократных ошибок передачи путем декодирования ограниченного числа альтернативных принятых последовательностей. Способность исправлять многократные ошибки канала передачи увеличивается при уменьшении значения коэффициента помехоустойчивости β и увеличении предельного числа Z альтернативных принятых последовательностей. В заявленном способе совместного арифметического и помехоустойчивого кодирования и декодирования коэффициент помехоустойчивости β, выбираемый в пределах 0<β<1, является эквивалентом скорости помехоустойчивого кода 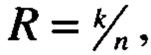 где k≥1 есть длина очередной части информационной последовательности, а n=k+r есть длина очередной части помехоустойчивой последовательности, состоящей из k информационных символов и из r≥1 проверочных символов.
где k≥1 есть длина очередной части информационной последовательности, а n=k+r есть длина очередной части помехоустойчивой последовательности, состоящей из k информационных символов и из r≥1 проверочных символов.
Поэтому указанная новая совокупность действий при выполнении совместного арифметического и помехоустойчивого кодирования и декодирования информационной последовательности позволяет обеспечить повышение помехоустойчивости передачи очередных частей кодированной последовательности при воздействии многократных ошибок передачи.
Заявленный способ поясняется чертежами, на которых показаны:
- на фиг. 1 - общая схема совместного арифметического и помехоустойчивого кодирования и декодирования;
- на фиг. 2 - схема блока декодирования 7;
- на фиг. 3 - алгоритм совместного арифметического и помехоустойчивого кодирования на передающей стороне;
- на фиг. 4 - таблица состояний совместного арифметического и помехоустойчивого кодирования первых двенадцати очередных частей информационной последовательности;
- на фиг. 5 - временные диаграммы совместного арифметического и помехоустойчивого кодирования первых двух очередных частей информационной последовательности;
- на фиг. 6 - временные диаграммы совместного арифметического и помехоустойчивого кодирования первых 12 очередных частей информационной последовательности;
- на фиг. 7 - временные диаграммы совместного арифметического и помехоустойчивого декодирования первых 19 битов принятой последовательности на приемной стороне;
- на фиг. 8 - алгоритм совместного арифметического и помехоустойчивого декодирования на приемной стороне;
- на фиг. 9 - представление альтернативных принятых последовательностей в виде древовидной структуры;
- на фиг. 10 - примерный вид выбираемых не более Z=12 альтернативных принятых последовательностей;
- на фиг. 11 - таблица состояний декодирования альтернативной принятой последовательности вида "0000 1100 0";
- на фиг. 12 - таблица состояний декодирования альтернативной принятой последовательности вида "0000 1100 1";
- на фиг. 13 - таблица состояний декодирования альтернативной принятой последовательности вида "0000 1100 1001 0001";
- на фиг. 14 - таблица состояний декодирования альтернативной принятой последовательности вида "0000 1100 0101 0001 001".
Реализация заявленного способа представлена на примере системы совместного арифметического и помехоустойчивого кодирования и декодирования, показанной на фиг. 1. На передающей стороне выполняют совместное арифметическое и помехоустойчивое кодирование очередных частей информационной последовательности (ИП), а на приемной стороне - совместное арифметическое и помехоустойчивое декодирование принятой последовательности с исправлением ошибок канала передачи.
На передающей стороне формирователь текущего интервала кодирования 1 формирует текущий интервал арифметического кодирования в зависимости от принимаемой информационной последовательности. Из текущего интервала арифметического кодирования формирователь текущего разрешенного интервала кодирования 2 выделяет меньший по длине текущий разрешенный интервал кодирования. Формирователь текущего нулевого подинтервала 3 и формирователь текущего единичного подинтервала 4 разделяют текущий разрешенный интервал кодирования на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа, соответственно. При получении от отправителя нулевого символа очередной части информационной последовательности увеличивается текущий подинтервал кодирования нулевого символа и пропорционально уменьшается текущий подинтервал кодирования единичного символа, а при получении от отправителя единичного символа очередной части информационной последовательности увеличивается текущий подинтервал кодирования единичного символа и пропорционально уменьшается текущий подинтервал кодирования нулевого символа. На основе данных текущих подинтервалов очередные двоичные символы очередной части информационной последовательности арифметически кодируют в арифметическом кодере 5 в очередную часть кодированной последовательности, которую передают по каналу передачи 6 на приемную сторону.
На приемной стороне в Z блоках декодирования 7 принимают очередные биты принятой последовательности. Схема блока декодирования 7 показана на фиг. 2. В каждом блоке декодирования 7 формирователь альтернативной принятой последовательности (АПП) с нулевым продолжением 7.1 и формирователь АПП с единичным продолжением 7.9 формируют альтернативные принятые последовательности с соответствующими продолжениями последовательности, которые в арифметическом декодере 7.2 и арифметическом декодере 7.10, соответственно, арифметически декодируют в очередные части соответствующих им альтернативных восстановленных информационных последовательностей.
При декодировании двоичных символов из АПП с нулевым продолжением по результату декодирования очередного восстановленного информационного символа в формирователе текущего интервала декодирования 7.3 формируют текущий интервал арифметического декодирования, из которого формирователь текущего разрешенного интервала декодирования 7.4 выделяет меньший по длине текущий разрешенный интервал декодирования. Из текущего разрешенного интервала декодирования в формирователе текущего нулевого подинтервала декодирования 7.6 и в формирователе текущего единичного подинтервала декодирования 7.7 формируют, соответственно, текущий нулевой подинтервал декодирования и текущий единичный подинтервал декодирования. При арифметическом декодировании в арифметическом декодере 7.2 нулевого символа очередной части восстановленной информационной последовательности из АПП с нулевым продолжением в формирователе текущего нулевого подинтервала декодирования 7.6 и формирователе текущего единичного подинтервала декодирования 7.7 увеличивают текущий подинтервал декодирования нулевого символа и пропорционально уменьшают текущий подинтервал декодирования единичного символа для данной АПП, а при декодировании единичного символа - увеличивают текущий подинтервал декодирования единичного символа и пропорционально уменьшают текущий подинтервал декодирования нулевого символа для данной АПП.
Аналогичные действия выполняют при декодировании двоичных символов из АПП с единичным продолжением с использованием формирователя АПП с единичным продолжением 7.9, арифметического декодера 7.10, формирователя текущего интервала декодирования 7.11, формирователя текущего разрешенного подинтервала декодирования 6.12, формирователя текущего нулевого подинтервала декодирования 6.14 и формирователя текущего единичного подинтервала декодирования 7.15.
В блоке вычисления метрики АПП 7.8 для каждой альтернативной принятой последовательности с ее продолжением вычисляют значение ее метрики суммированием метрики самой последовательности и метрики ее продолжения, где значения метрики продолжения последовательности устанавливают в соответствующее значение в зависимости от соотношения между двоичным значением продолжения последовательности и значением очередного бита принятой последовательности. Из блока вычисления метрики АПП 7.8 вычисленные значение метрики каждой альтернативной принятой последовательности с ее продолжением передают в блок выбора альтернативной принятой последовательности АПП 8.
Если при проверке в блоке проверки интервала 7.5, соответственно, в блоке проверки интервала 7.13, текущее значение альтернативной принятой последовательности находится в пределах текущего разрешенного интервала арифметического декодирования соответствующей альтернативной принятой последовательности с ее продолжением последовательности, то в блоке выбора АПП 8 запоминают очередные части альтернативной восстановленной информационной последовательности, соответствующие альтернативной принятой последовательности с ее продолжением, иначе стирают данную альтернативную принятую последовательность с ее продолжением.
В блоке выбора АПП 8 сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями последовательности и выбирают из них не более предельного числа Z альтернативных принятых последовательностей, имеющих наименьшие значения метрики, которые дополняют соответствующими им продолжениями последовательности, для этих альтернативных принятых последовательностей запоминают очередные части соответствующей им альтернативной восстановленной информационной последовательности и значения метрики.
После поступления всех бит принятой последовательности на приемную сторону в блоке выбора АПП 8 сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них единственную альтернативную принятую последовательность с наименьшим значением метрики и передают получателю в качестве восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности альтернативную восстановленную информационную последовательность.
В способе реализуют следующую последовательность действий.
Алгоритм совместного арифметического и помехоустойчивого кодирования на передающей стороне представлен на фигуре 3.
Способы предварительной установки на передающей стороне начального интервала арифметического кодирования длиною D>2 и на приемной стороне соответствующего ему начального интервала арифметического декодирования длиною DD>2 известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Начальный интервал арифметического кодирования начинается от его начального нижнего значения и заканчивается его начальным верхним значением. Начальное нижнее значение интервала кодирования устанавливают в минимальное значение интервала кодирования, а начальное верхнее значения интервала кодирования - в максимальное значение этого интервала. Например, при представлении значений интервала кодирования восемью двоичными символами (разрядность представления интервалов NR=8 бит), начальное нижнее значение интервала кодирования арифметического кодирования L[0] в момент времени t=0 устанавливают в минимальное значение, равное нулевому значению в десятичном представлении или 0000 0000 в двоичном представлении, где старшие двоичные символы записывают слева, а начальное верхнее значение интервала кодирования арифметического кодирования H[0] устанавливают в максимальное значение, равное 255 в десятичном представлении или 1111 1111 в двоичном представлении. Пример начального интервала арифметического кодирования длиною D[0]=256 представлен на фиг. 4 при t=0 (первая строка) и на фиг. 5 при t=0.
Также предварительно устанавливают предельное число Z≥2 альтернативных принятых последовательностей и значение метрики альтернативных принятых последовательностей в нулевое значение. Способы предварительной установки предельного числа Z альтернативных принятых последовательностей известны и описаны, например, в книге Д. Прокис "Цифровая связь". - М., Радио и связь, 2000, стр. 328-349. Например, для исправления двукратных ошибок рекомендуется выбирать предельное число Z альтернативных принятых последовательностей из диапазона значений 8…16, для исправления трехкратных ошибок рекомендуется выбирать предельное число Z альтернативных принятых последовательностей из диапазона значений 17…32, с учетом того, что при увеличении выбранного числа Z можно исправить большее число ошибок передачи, но при этом линейно растет сложность устройств реализации исправления ошибок. Например, для рассматриваемого далее примера установим предельное число Z альтернативных принятых последовательностей равным Z=12.
Способы предварительной установки значения метрики альтернативных принятых последовательностей в нулевое значение известны и описаны, например, в книге Б. Скляр "Цифровая связь. Теоретические основы и практическое применение". - М., Издательский дом "Вильямс", 2003, стр. 432-434. Изначально, до начала приема последовательности на приемной стороне альтернативные принятые последовательности имеют нулевую длину.
На передающей стороне от источника информационной последовательности принимают очередную часть информационной последовательности длиной k≥1 бит. Примерный вид первых 13 очередных частей двоичной ИП длиной k=1 бит показан на фиг. 6(a). Например, первая часть ИП имеет вид "0", вторая часть - "0", четвертая часть - "1" и т.д. Единичные значения битов на фигурах показаны в виде заштрихованных импульсов, нулевые значения битов - в виде незаштрихованных импульсов.
Из текущего интервала арифметического кодирования длиною D>2 выделяют текущий разрешенный интервал кодирования длиною Dβ>2, причем длину Dβ текущего разрешенного интервала кодирования выбирают как Dβ=β⋅D, где коэффициент помехоустойчивости β выбирают в пределах 0<β<1, текущий разрешенный интервал кодирования разделяют на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа. В заявленном способе совместного арифметического и помехоустойчивого кодирования и декодирования коэффициент помехоустойчивости β является эквивалентом скорости помехоустойчивого кода R, определяемой как отношение длины информационных символов к длине кодированных символов R=k/n, где скорость помехоустойчивого кода выбирается в пределах 0<R<1. Чем меньше значение коэффициента помехоустойчивости β, тем большее число ошибок канала передачи возможно исправить в заявляемом способе совместного арифметического и помехоустойчивого кодирования и декодирования. Для приведенного далее примера выберем значение β=0,6. Например, для начального интервала арифметического кодирования длиною D=256 выделяют начальный разрешенный интервал кодирования длиною Dβ=256×0,6=154 (вычисления выполняют с округлением до ближайшего целого числа). В результате интервал арифметического кодирования разделяют на разрешенный интервал кодирования и на неразрешенный интервал кодирования. Аналогично, в помехоустойчивом кодировании с обнаружением ошибок множество всех кодовых комбинаций разделяют на множество разрешенных кодовых комбинаций, состоящее из неискаженных ошибками передачи кодовых последовательностей, и на множество неразрешенных кодовых комбинаций, состоящее из искаженных ошибками передачи кодовых последовательностей. Если при приеме принятая последовательность принадлежит множеству неразрешенных кодовых комбинаций, то при использовании помехоустойчивого кодирования обнаружена ошибка в принятых данных. В отличие от этого в предлагаемом способе совместного арифметического и помехоустойчивого кодирования и декодирования ошибка в принятой последовательности выявляется, если текущее состояние арифметического декодирования не соответствует разрешенному интервалу декодирования.
Выделение текущего разрешенного интервала кодирования из текущего интервала арифметического кодирования может быть выполнено различными способами: начиная от нижнего или верхнего значения интервала кодирования, или в центральной части текущего интервала арифметического кодирования, в виде сплошного интервала или в виде совокупности подинтервалов, перемежающихся подинтервалами из неразрешенного интервала арифметического кодирования. Возможности по обнаружению и исправлению ошибок передачи при этом в заявляемом способе не меняются. Например, для удобства реализации предлагается выделение текущего разрешенного интервала кодирования длиной D из текущего интервала арифметического кодирования в виде двух подинтервалов, первый подинтервал, называемый текущий подинтервал кодирования нулевого символа, начинается от нижнего значения L интервала кодирования, второй подинтервал, называемый текущий подинтервал кодирования единичного символа, начинается от верхнего значения Н интервала кодирования. Соответственно, между текущим подинтервалом кодирования нулевого символа и текущим подинтервалом кодирования нулевого символа находится оставшаяся часть текущего интервала арифметического кодирования, отнесенная к текущему неразрешенному интервалу кодирования. Нижнее значение L0 текущего подинтервала кодирования нулевого символа совпадает с нижним значением интервала арифметического кодирования L0=L, и верхнее значение H1 текущего подинтервала кодирования единичного символа совпадает с верхним значением интервала арифметического кодирования Н1=Н.
Способы разделения текущего разрешенного интервала арифметического кодирования на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Для арифметического кодирования очередного по счету, t-го символа, где t=1, 2, …, длину Dβ текущего разрешенного интервала арифметического кодирования, равную Dβ=β⋅D, где D=H1-L0, разделяют на длину D0 текущего подинтервала кодирования нулевого символа и длину D1 текущего подинтервала кодирования единичного символа D1. Для этого подсчитывают текущее число нулевых символов ИП N0 и текущее число единичных символов ИП N1, закодированных в арифметическом кодере. Например, в начальный момент при t=0 текущее число нулевых символов ИП N0[0] установлено в значение 1 и текущее число единичных символов ИП N1[0] установлено в значение 1. Способы установки в начальный момент арифметического кодирования числа нулевых и единичных символов ИП в единичное значение известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 124-130. Например, как показано на фиг. 4 в первой строке при t=0 указано единичное число нулевых символов ИП (графа N0) и единичное число единичных символов ИП (графа N1). В графе N указывается общее число принятых символов с учетом установленных в начальный момент нулевых и единичных символов ИП.
Вычисляют текущую вероятность кодирования нулевых символов ИП p0[t] по правилу: p0[t]=N0[t]/(N0[t]+N1[t]) и текущую вероятность кодирования единичных символов ИП p1[t] по правилу: pl[t]=N1[t]/(N0[t]+N1[t]). Например, как показано на фиг. 4 в первой строке при t=0, указано значение текущей вероятности кодирования нулевых символов ИП (графа p0) и значение текущей вероятности кодирования единичных символов ИП (графа p1), где начальные значения равны 0,5.
Длину текущего подинтервала кодирования нулевого символа D0[t] определяют по формуле вида D0[t]=Dβ[t]×p0[t], а длину текущего подинтервала кодирования единичного символа D1[t] определяют по формуле вида D1[t]=Dβ[t]-D0[t]. Например, длина начального интервала кодирования D[0] имеет десятичное значение 256, длина начального разрешенного интервала кодирования Dβ=256×0,6=154, длина начального подинтервала кодирования нулевых символов D0[0] имеет десятичное значение 77, и длина начального подинтервала кодирования единичных символов D1[0] имеет десятичное значение 77. Подинтервал кодирования единичных символов расположен сверху подинтервала кодирования нулевых символов, как показано, например, на фиг. 5. Нижнюю границу текущего подинтервала кодирования нулевого символа обозначают как значение L0, а его верхнюю границу обозначают как Lk, и данный подинтервал начинается снизу от нижней границы текущего интервала арифметического кодирования включительно до значения Lk исключительно. Нижнюю границу текущего подинтервала кодирования единичного символа обозначают как значение Hk, а его верхнюю границу обозначают как H1, и данный подинтервал начинается сверху от верхней границы текущего интервала арифметического кодирования исключительно до значения Hk включительно. Например, в момент времени t=0 текущий подинтервал кодирования нулевого символа начинается от нижнего значения текущего интервала кодирования и имеет нижнее значение в десятичном представлении 0 или 0000 0000 в двоичном представлении, и имеет верхнее значение в десятичном представлении 76 или 0100 1100 в двоичном представлении. Соответственно, текущий подинтервал кодирования единичного символа имеет верхнее значение, совпадающее с верхним значением интервала кодирования, и имеет верхнее значение в десятичном представлении 255 или 1111 1111 в двоичном представлении и нижнее значение в десятичном представлении 178 или 1011 0010 в двоичном представлении, как показано на фиг. 4 во второй строке и на фиг. 5 при t=0 в строке выделение разрешенного интервала кодирования "Выделен. разреш. инт".
Способы арифметического кодирования очередной части ИП в очередную часть кодированной последовательности (КП) известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Они заключаются в последовательном сжатии двоичных символов очередной части ИП в очередную часть КП в соответствии с текущими значениями подинтервала кодирования нулевого символа и подинтервала кодирования единичного символа. При поступлении на вход арифметического кодирования очередного двоичного символа очередной части ИП, являющегося единичным двоичным символом, текущий интервал арифметического кодирования этого символа устанавливают равным подинтервалу кодирования единичного символа, а при поступлении на вход арифметического кодирования нулевого двоичного символа, текущий интервал арифметического кодирования этого символа устанавливают равным подинтервалу кодирования нулевого символа.
Например, при поступлении на вход кодирования двоичного символа первой части ИП, являющегося нулевым двоичным символом, текущий интервал кодирования устанавливают равным подинтервалу кодирования нулевого символа, и нижнее значение L0[1] текущего интервала арифметического кодирования устанавливают в значение 0, а верхнее значение H1[1] - в десятичное значение 76, как показано на фиг. 4 и на фиг. 5 при t=1.
При арифметическом кодировании самый левый бит двоичного представления значения L0[1] сравнивают с самым левым битом двоичного представления значения H1[1], например, вида 0000 0000 и 0100 1100, соответственно, как показано на фиг. 4 при t=1. При их совпадении значение самого левого бита двоичных представлений значений L0[1] и H1[1] считывают в качестве очередного бита очередной части кодированной последовательности (Закод. символ, как показано на фиг. 4). Например, при кодировании первой части ИП первым битом первой части КП является совпавший при сравнении нулевой двоичный символ, как показано на фиг. 4, четвертая строка сверху. Считанный бит удаляют из двоичных представлений значений L0[1] и H1[1], которые уменьшают до длины 7 бит вида 0000 000 и 100 1100, соответственно. Двоичные символы двоичных представлений значений L0[1] и H1[1] сдвигают справа налево на один разряд и справа к ним дописывают по нулевому двоичному символу. Например, двоичные представления значений L0[1] и H1[1] приобретают вид 0000 0000 и 1001 1000, соответственно. Способы считывания двоичных символов с удалением считанных символов известны и описаны, например, в книге: В. Шило "Популярные цифровые микросхемы". - М., Радио и связь, 1987, 104-123, с использованием регистров сдвига с параллельной и последовательной записью/считыванием двоичных последовательностей. Операции сдвига справа налево на один разряд и дописывания справа нулевого двоичного символа увеличивают значения L0[t] и H1[t] в 2 раза и называются нормализацией параметров арифметического кодирования. Способы сдвига на один разряд в сторону старших разрядов двоичных последовательностей и записи в освободившийся младший разряд нулевого двоичного символа известны и описаны, например, в книге: В. Шило "Популярные цифровые микросхемы". - М., Радио и связь, 1987, 104-123, с использованием регистров сдвига с параллельной и последовательной записью/считыванием двоичных последовательностей, и по своей сути являются умножением на два десятичных значений нижнего и верхнего значений интервала арифметического кодирования.
После каждого выполнения нормализации повторно самый левый бит двоичного представления нижнего значения интервала кодирования сравнивают с самым левым битом двоичного представления верхнего значения интервала кодирования. При их совпадении значение самого левого бита этих двоичных представлений считывают в качестве следующего бита очередной части КП, иначе переходят к кодированию следующего символа и так далее, как показано на фиг. 4.
В результате кодирования первой части информационной последовательности вида "0", показанной на фиг. 6(a), сформирована первая часть кодированной последовательности вида "0", показанная на фиг. 6(б), которую передают на приемную сторону.
При поступлении следующей части ИП ее кодирование в очередную часть КП выполняют идентично. После выполнения арифметического кодирования каждого очередного символа уточняют число закодированных нулевых символов ИП и число закодированных единичных символов ИП. Так как закодированный символ в указанном примере является нулевым, то число закодированных нулевых символов ИП увеличивают на единичное значение и оно составляет N0[1]=2, число закодированных единичных символов информационной последовательности осталось равным N1[1]=1, соответственно, суммарное число закодированных нулевых и единичных информационных символов стало равным 3. Пересчитывают текущее значение вероятности кодирования нулевых символов ИП р0[1]=2/3 и текущее значение вероятности кодирования единичных символов ИП p1[1]=1/3.
Перед выполнением арифметического кодирования следующего символа заново из текущего интервала арифметического кодирования выделяют текущий разрешенный интервал кодирования, который разделяют на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа. Например, перед кодированием второго по счету символа ИП
длина текущего интервала арифметического кодирования составляет D=152, длина текущего разрешенного интервала кодирования Dβ=152×0,6=92. Длина текущего подинтервала нулевого символа составляет 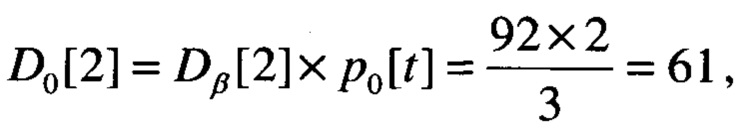 а длина текущего подинтервала единичного символа D1[2]=Dβ[2]-D0[2]=92-61=31. Поэтому текущий подинтервал нулевого символа находится в промежутке десятичных значений от 0 до 61 или в промежутке двоичных значений от 0000 0000 до 0011 1101, а текущий подинтервал единичного символа находится в промежутке от 121 до 152, как показано на фиг. 4 в пятой строке "Выделен. разреш. инт".
а длина текущего подинтервала единичного символа D1[2]=Dβ[2]-D0[2]=92-61=31. Поэтому текущий подинтервал нулевого символа находится в промежутке десятичных значений от 0 до 61 или в промежутке двоичных значений от 0000 0000 до 0011 1101, а текущий подинтервал единичного символа находится в промежутке от 121 до 152, как показано на фиг. 4 в пятой строке "Выделен. разреш. инт".
Выполняют арифметическое кодирование второго и последующих двоичных символов ИП, как показано на фиг. 4 и на фиг. 5. При выполнении нормализации считывают двоичные символы в очередную часть кодированной последовательности. Примерный вид арифметического кодирования первых 12 очередных частей ИП вида "0001 0010 1001" в соответствующие очередные части КП вида "0", "00", "0", "110", "0" и так далее показан на фиг. 6(б). Заметим, что при фиксированной длине очередных частей ИП в результате их арифметического кодирования сформированы очередные части КП переменной длины, что, в частности, определяется переменной избыточностью сжимаемых частей ИП. Например, восьмая часть КП имеет нулевую длину (не содержат передаваемых символов). В целом КП длиною 19 бит имеет вид "0000 1100 0101 0001 001".
Способы передачи на приемную сторону очередной части КП известны и описаны, например, в книге А.Г. Зюко, Д.Д. Кловский, М.В. Назаров, Л.М. Финк "Теория передачи сигналов". - М.: Радио и связь, 1986, стр. 11. Примерный вид первых 12 частей принятой последовательности (Пр. П) показан на фиг. 7(a). Пусть принятая последовательность общей длиной 19 битов при передаче искажена в девятом и десятом битах принятой последовательности и имеет вид "0000 1100 1001 0001 001".
Алгоритм совместного арифметического и помехоустойчивого декодирования на приемной стороне представлен на фиг. 8.
Для инициализации арифметического декодирования необходимо принять первые по счету NR двоичных символов Пр.П, где NR есть число двоичных символов представления значений интервалов кодирования и, соответственно, интервалов декодирования. Например, при представлении значений интервала кодирования и интервала декодирования восемью двоичными символами (NR=8 бит), принимают первые восемь бит Пр.П вида "0000 1100", как показано на фиг. 11 в столбце считывание двоичных символов "Сч." в начальный момент времени t=0. Принятая последовательность "0000 1100" имеет текущее значение 12, вычисляемое как десятичное значение данной двоичной последовательности, в которой наиболее значимый бит находится слева (в начале последовательности), а наименее значимый бит находится справа (в конце последовательности).
Опишем в общем виде совместное арифметическое и помехоустойчивое декодирования Пр.П на приемной стороне. Действия совместного арифметического и помехоустойчивого декодирования Пр.П на приемной стороне выполняют путем декодирования нескольких альтернативных принятых последовательностей (АПП). Например, в начальный момент времени имеется единственная альтернативная принятая последовательность, совпадающая с первыми восемью битами Пр.П вида "0000 1100". В момент времени считывания первого после начальных NR бит очередной бита принятой последовательности, обозначенного моментом времени t=1, для начальной принятой последовательности, состоящей из первых по счету NR двоичных символов принятой последовательности, формируют продолжение АПП в виде нулевого символа и продолжение последовательности в виде единичного символа, как показано на фиг. 9. При считывании следующего бита принятой последовательности (момент времени t=2) для каждой из имеющихся двух АПП формируют продолжения в виде нулевого символа и продолжение в виде единичного символа, в результате на момент времени t=2 число АПП становится 4, на момент времени t=3 число АПП достигает 8 и т.д. Представление альтернативных принятых последовательностей в виде описанной древовидной структуры показано на фиг. 9. Такая структура АПП потенциально позволяет исправлять многократные ошибки передачи в принятой последовательности, причем место ошибок в Пр.П может быть произвольным. Для каждой АПП выполняют описанные далее действия совместного арифметического и помехоустойчивого декодирования.
Например, при предварительно установленном предельном числе Z=12 АПП примерный вид выбираемых не более Z альтернативных принятых последовательностей показан на фиг. 10. Видно, что в этой структуре, называемой усеченным деревом альтернативных принятых последовательностей, число продолжаемых АПП в каждый момент t не превышает заданного значения Z. Например, для начальной альтернативной принятой последовательности вида "0000 1100" формируют 2 продолжения: АПП с продолжением последовательности в виде нулевого символа "0000 1100 0", и АПП с продолжением последовательности в виде единичного символа "0000 1100 1". Для АПП с продолжением последовательности в виде нулевого символа "0000 1100 0" значение метрики продолжения последовательности в виде нулевого символа относительно очередного единичного, девятого по счету на фиг. 10 бита, принятой последовательности устанавливают в единичное значение. Так как метрика начальной альтернативной принятой последовательности предварительно установлена в нулевое значение, то АПП с продолжением последовательности в виде нулевого символа "0000 1100 0" имеет значение метрики М=1, как показано на фиг. 10. Для АПП с продолжением последовательности в виде единичного символа "0000 1100 1" значение метрики продолжения последовательности в виде единичного символа относительно единичного очередного, девятого по счету на фиг. 10. бита, принятой последовательности, устанавливают в нулевое значение. Соответственно, АПП с продолжением последовательности в виде единичного символа "0000 1100 1" имеет значение метрики М=0, как показано на фиг. 10.
В результате, число продолжаемых АПП при декодировании девятого по счету символа принятой последовательности равно 2, это число не превышает предельного числа Z=12 АПП и обе альтернативные принятые последовательности продолжают, образуя при декодировании очередного, десятого по счету на фиг. 10 бита, принятой последовательности четыре последовательности со значениями метрики от М=0 до М=2, которые при декодировании очередного, одиннадцатого по счету на фиг. 10 бита, принятой последовательности образуют 8 последовательностей со значениями метрики от М=0 до М=3, которые при декодировании очередного, двенадцатого по счету на фиг. 10 бита, принятой последовательности образуют 16 последовательностей со значениями метрики от М=0 до М=4. Так как число АПП с их продолжениями уже превышает предельное число Z АПП, то из этих последовательностей выбирают Z=12 альтернативных принятых последовательностей с их продолжениями с наименьшими значениями метрики. Например, АПП с ее продолжением с метрикой М=4 и три АПП с их продолжениями с метрикой М=3 стирают, что показано символом "X" на фиг. 10. По принципу максимального правдоподобия в теории помехоустойчивого кодирования, как описано в книге Б. Скляр "Цифровая связь. Теоретические основы и практическое применение". - М., Издательский дом "Вильямс", 2003, стр. 422-431, чем больше альтернативная принятая последовательность с ее продолжением отличается от принятой последовательности по значению метрики М, тем меньше вероятность того, что именно она позволит исправить ошибки передачи, что дает основание такую последовательность стирать.
Далее, число продолжаемых АПП при декодировании тринадцатого, четырнадцатого и пятнадцатого символов АПП по порядку символов принятой последовательности остается равным предельному числу Z=12 АПП, а при декодировании шестнадцатого символа по счету символов принятой последовательности число продолжаемых АПП с их продолжениями уменьшается до девяти. Это произошло потому, что во многих ранее продолжаемых АПП текущее значение альтернативной принятой последовательности оказалось вне пределов текущего разрешенного интервала арифметического декодирования этих АПП, то есть такие последовательности не могли быть сформированы на передающей стороне и, соответственно, они подлежат стиранию и их далее не продолжают, как показано символом  на фиг. 10. При этом оказалась стертой альтернативная принятая последовательность с ее продолжением вида "0000 1100 1001 000" со значением метрики М=0, которая по этой причине ранее считалась наиболее предпочтительной при выборе среди альтернативных принятых последовательностей.
на фиг. 10. При этом оказалась стертой альтернативная принятая последовательность с ее продолжением вида "0000 1100 1001 000" со значением метрики М=0, которая по этой причине ранее считалась наиболее предпочтительной при выборе среди альтернативных принятых последовательностей.
Далее, число продолжаемых АПП при декодировании семнадцатого символа АПП по счету символов принятой последовательности снизилось до пяти, а при декодировании восемнадцатого и девятнадцатого символов АПП до четырех, а среди которых одна АПП имеет метрику М=2, две АПП - М=3 и одна АПП - М=4. В ходе дальнейшего декодирования лучшей по значению метрики будет альтернативная принятая последовательность, продолжающая выявленную АПП с метрикой М[19]=2, поэтому по окончании приема символов на приемной стороне среди альтернативных принятых последовательностей выбирают АПП с наименьшим значением метрики. В нашем случае выбирают АПП вида "0000 1100 0101 0001 001" со значением метрики М=2, для которой выполняется исправление двух ошибок передачи в принятой последовательности. Передают получателю в качестве восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности альтернативную восстановленную информационную последовательность.
Детально опишем действия совместного арифметического и помехоустойчивого декодирования на приемной стороне.
Способы выделения текущего разрешенного интервала декодирования длиною DDβ>2 из текущего интервала арифметического декодирования длиною DD>2 каждой альтернативной принятой последовательности на приемной стороне и его разделения на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа идентичны способам выделения текущего разрешенного интервала кодирования длиною Dβ>2 из текущего интервала арифметического кодирования длиною D>2 и его разделения на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа на передающей стороне. Длину DDβ текущего разрешенного интервала декодирования каждой альтернативной принятой последовательности выбирают как DDβ=β⋅DD. Например, для выбранного значения β=0,6 для начального интервала арифметического декодирования длиною DD=256 выделяют начальный разрешенный интервал декодирования длиною DDβ=256×0,6=154, как показано на фиг. 11 в первой строке в начальный момент времени t=0. В начальный момент времени имеется только одна альтернативная принятая последовательность вида "0000 1100" со значением 12, как показано в столбце Пр. П.
Для каждой альтернативной принятой последовательности выделение текущего разрешенного интервала декодирования из текущего интервала арифметического декодирования выполняют в виде двух подинтервалов. Первый подинтервал, называемый текущий подинтервал декодирования нулевого символа, начинается от нижнего значения интервала декодирования LL, второй подинтервал, называемый текущий подинтервал декодирования единичного символа, начинается от верхнего значения интервала декодирования НН. Соответственно, между текущим подинтервалом декодирования нулевого символа и текущим подинтервалом декодирования единичного символа находится оставшаяся часть текущего интервала арифметического декодирования, отнесенная к текущему неразрешенному интервалу декодирования. Нижнее значение текущего подинтервала декодирования нулевого символа LL0 совпадает с нижним значением интервала кодирования LL0=LL, и верхнее значение текущего подинтервала кодирования единичного символа НН1 совпадает с верхним значением интервала кодирования HH1=НН.
Длину текущего разрешенного интервала арифметического декодирования DDβ каждой АПП разделяют на длину текущего подинтервала нулевого символа DD0 и длину текущего подинтервала единичного символа DD1. Для этого подсчитывают текущее число нулевых декодированных символов NN0 и текущее число единичных декодированных символов NN1 этой АПП, восстановленных в арифметическом декодере. Например, для каждой АПП в начальный момент при t=0 текущее число нулевых декодированных символов NN0[0] установлено в значение 1 и текущее число единичных декодированных символов NN1[0] установлено в значение 1. Например, как показано на фиг. 11 в первой строке при t=0 указано единичное число нулевых декодированных символов (графа NN0) и единичное число единичных декодированных символов (графа NN1). В графе NN указывается общее число принятых символов с учетом установленных в начальный момент нулевых и единичных декодированных символов.
Для каждой АПП вычисляют текущую вероятность нулевых декодированных символов pp0[t] по правилу: pp0[t]=NN0[t]/(NN0[t]+NN1[t]) и текущую вероятность единичных декодированных символов pp1[t] по правилу: pp1[t]=NN1[t]/(NN0[t]+NN1[t]). Например, как показано на фиг. 11 в первой строке при t=0, начальные значения вероятности нулевых декодированных символов (графа pp0) и вероятности единичных декодированных символов (графа pp1) равны 0,5.
Для каждой АПП длину текущего подинтервала нулевого декодированного символа DD0[t] определяют по формуле вида DD0[t]=DDβ[t]×pp1[t], а длину текущего подинтервала единичного декодированного символа DD1[t] определяют по формуле вида DD1[t]=DDβ[t]-DD0[t]. Например, длина начального интервала декодирования DD[0] имеет десятичное значение 256, длина начального разрешенного интервала декодирования DDβ[0]=256×0,6=154, длина начального подинтервала декодирования нулевого символа DD0[0] имеет десятичное значение 77, и длина начального подинтервала декодирования единичного символа D1[0] имеет десятичное значение 77. Подинтервал декодирования единичного символа расположен сверху подинтервала декодирования нулевого символа. Нижнюю границу текущего подинтервала декодирования нулевого символа обозначают как значение LL0, а его верхнюю границу обозначают как LLk, и данный подинтервал начинается снизу от нижней границы текущего интервала декодирования арифметического декодирования включительно до значения LLk исключительно. Верхнюю границу текущего подинтервала декодирования единичного символа обозначают как значение НН1, а его нижнюю границу обозначают как HHk, и данный подинтервал начинается сверху от верхней границы текущего интервала декодирования арифметического декодирования исключительно до значения HHk включительно. Например, в момент времени t=0 подинтервал декодирования нулевого символа имеет нижнее значение в десятичном представлении 0 или 0000 0000 в двоичном представлении, и имеет верхнее значение в десятичном представлении 76 или 0100 1100 в двоичном представлении, как показано на фиг. 11 в строке выделение разрешенного интервала "Выделен. разреш. инт". Соответственно, текущий подинтервал кодирования единичного символа имеет верхнее значение в десятичном представлении 255 или 1111 1111 в двоичном представлении и нижнее значение в десятичном представлении 178 или 1011 0010 в двоичном представлении.
Для каждой АПП формируют продолжение последовательности в виде нулевого символа и продолжение в виде единичного символа. Например, из начальной АПП вида "0000 0110" формируют АПП с продолжением в виде нулевого символа вида "0000 0110 0", и АПП с продолжением в виде единичного символа вида "0000 0110 1", как показано на фиг. 10. Верхнее по рисунку ребро графического представления каждой АПП обозначено как продолжение последовательности в виде нулевого символа "0", а нижнее ребро - как продолжение последовательности в виде единичного символа "1".
После формирования продолжения последовательности вычисляют значение метрики продолжения в виде нулевого символа и значение метрики продолжения в виде единичного символа относительно очередного бита принятой последовательности, при этом значение метрики продолжения в виде нулевого символа относительно очередного бита принятой последовательности вычисляют как нулевое значение, если очередной бит очередной части принятой последовательности является нулевым битом, иначе вычисляют как единичное значение, а также значение метрики продолжения в виде единичного символа относительно очередного бита принятой последовательности вычисляют как нулевое значение, если очередной бит принятой последовательности является единичным битом, иначе вычисляют как единичное значение. Например, как показано на фиг. 10, очередной бит Пр.П, следующий после считывания восьми битов начального пути декодирования, имеет единичное значение. Поэтому относительно этого бита метрика продолжения последовательности в виде нулевого символа имеет единичное значение, а метрика продолжения последовательности в виде единичного символа имеет нулевое значение.
Затем для каждой АПП с ее продолжением последовательности вычисляют значение его метрики, для чего суммируют значения метрики данной последовательности и метрики ее продолжения последовательности. Например, с учетом того, что метрика начальной АПП вида "0000 0110" имеет нулевое значение, метрика АПП вида "0000 0110 0" с продолжением в виде нулевого символа получает единичное значение (М=1), а метрика АПП "0000 0110 1" с продолжением в виде единичного символа получает нулевое значение (М=0), как показано на фиг. 10.
Способы арифметического декодирования каждой АПП с ее продолжением последовательности в очередные части соответствующей ей альтернативной восстановленной информационной последовательности (АВП) известны и описаны, например, в книге Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин "Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео". - М., ДИАЛОГ-МИФИ, 2002, стр. 35-43. Они заключаются в последовательном декодировании каждой АПП с ее продолжением в соответствии с текущими значениями подинтервала декодирования нулевого символа и подинтервала декодирования единичного символа этой АПП.
Примерный вид арифметического декодирования начальной АПП вида "0000 0110" с ее последующим нулевым продолжением в символы очередной части соответствующей ей АВП показан на фиг. 11. Для декодирования первого символа очередной части АВП текущее значение альтернативной принятой последовательности, равное 12, сравнивают с границами текущего значения подинтервала декодирования нулевого символа АПП DD0[0], находящимися, например, в пределах от 0 до 76, и с границами текущего значения подинтервала декодирования единичного символа АПП DD1[0], находящимися, например, в пределах от 178 до 255, как показано на фиг. 11 во второй строке при t=0. Текущее значение альтернативной принятой последовательности определяется как десятичное значение этой последовательности и указывается в графе "Пр. П". В зависимости от того, в пределах какого подинтервала декодирования символов оказалось текущее значение альтернативной принятой последовательности, принимают решение о значении текущего символа (Дек. сим.) альтернативной восстановленной информационной последовательности, указываемого в правой графе фиг. 11. Так как в данном примере текущее значение альтернативной принятой последовательности оказалось в пределах подинтервала декодирования нулевого символа, то первый декодированный символ является нулевым и следующие границы текущего интервала декодирования устанавливают соответствующими границам значения подинтервала декодирования нулевого символа данной АПП DD0[0]. В результате декодирования первого символа устанавливают нижнее значение интервала декодирования арифметического декодирования LL равным значению LL0[0], например, LL0[1]=0, а верхнее значение интервала декодирования арифметического декодирования НН - равным значению LLk[01]=76, как показано на фиг. 11 в третьей строке при t=1.
После декодирования каждого символа пересчитывают текущее значение вероятности нулевого символа АВП и текущее значение вероятности единичного символа этой же последовательности, например, после декодирования первого символа, являющегося нулевым, по формуле вида рр0[1]=NN0[1]/(NN0[1]+NN1[1])=2/3 и по формуле вида pp1[1]=NN1[1]/(NN0[1]+NN1[1])=1/3, соответственно, как показано на фиг. 11 в третьей строке при t=1.
После каждого изменения состояния арифметического декодирования самый левый бит двоичного представления значения LL интервала декодирования сравнивают с самым левым битом двоичного представления значения НН, например, при t=1 значение LL вида "0000 0000" и значение НН вида "0100 1100", соответственно. При их совпадении выполняют нормализацию арифметического декодирования: значение самого левого бита двоичных представлений значений LL и НН удаляют и символы двоичных представлений значений LL и НН сдвигают справа налево на один разряд и справа к ним в младший разряд дописывают по нулевому двоичному символу. Например, при этом переменная LL сохранила десятичное значение 0, а НН - получила десятичное значение 152 и двоичное представление "1001 1000", как показано на фиг. 11 в строке "нормализация". Одновременно с этим, самый левый бит текущего значения альтернативной принятой последовательности удаляют и двоичные символы этой последовательности сдвигают справа налево на один разряд и справа к ним дописывают следующий считанный двоичный символ альтернативной принятой последовательности. Например, следующим считанным двоичным символом является девятый по счету символ альтернативной принятой последовательности, имеющий нулевое значение. С учетом считанного двоичного символа, текущее значение АПП получило десятичное значение 24 и двоичное представление "0001 1000", как показано на фиг. 11 в строке "нормализация".
Повторно самый левый бит двоичного представления значения LL сравнивают с самым левым битом двоичного представления значения НН, и если они снова совпадают, то повторно выполняют нормализацию идентичным образом и т.д.
Далее из текущего интервала арифметического декодирования выделяют текущий разрешенный интервал декодирования каждой альтернативной принятой последовательности, который в свою очередь разделяют на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа. Например, из текущего интервала арифметического декодирования в пределах от 0 до 152 данной АПП выделяют текущий разрешенный интервал декодирования длиной DDβ=92, который разделяют на текущий подинтервал декодирования нулевого символа в пределах от 0 до 61 и на текущий подинтервал декодирования единичного символа в пределах от 121 до 152. Так как текущее значение вероятности нулевого символа данной АПП в 2 раза больше текущего значения вероятности единичного символа этой АПП, то, соответственно, длина текущего подинтервала декодирования нулевого символа в 2 раза больше текущего подинтервала декодирования единичного символа этой АПП, как показано на фиг. 11 в предпоследней строке "выделен. разреш. инт.".
Выполняют арифметическое декодирование данной АПП с ее продолжением последовательности вида "0000 0110 0" в символ очередной части соответствующей ей АВП. Так как текущее значение АПП, равное 24, находится в пределах текущего подинтервала декодирования нулевого символа, то декодируют нулевой символ. В результате арифметического декодирования АПП с продолжением последовательности в виде нулевого символа вида "0000 0110 0", показанной на фиг. 7(б), декодируют, например, символы двух первых частей соответствующей ей АВП, имеющей вид "0 0", как показано на фиг. 7(в) и на фиг. 11.
Действия для альтернативной принятой последовательности вида "0000 1100 1", сформированной из начальной АПП вида "0000 1100" с продолжением последовательности в виде единичного символа, показаны на фиг. 12. Отличием от ранее рассмотренных действия для АПП вида "0000 1100 0" является только текущее значение данной АПП, равное 25, полученное после считывания единичного символа. В результате арифметического декодирования АПП с продолжением последовательности в виде единичного символа вида "0000 0110 1", показанной на фиг. 7(г), декодируют, например, символы двух первых частей соответствующей ей АВП, имеющей вид "0 0", как показано на фиг. 7(д) и на фиг. 12.
Если текущее значение альтернативной принятой последовательности находится в пределах ее текущего разрешенного интервала декодирования, то запоминают очередные части альтернативной восстановленной информационной последовательности, соответствующие этой последовательности, иначе стирают данную альтернативную принятую последовательность с ее продолжением последовательности. Например, на момент приема девятого по счету символа принятой последовательности для АПП вида "0000 1100 0" и АПП вида "0000 1100 1" запоминают первые две очередные части соответствующих им альтернативных восстановленных информационных последовательностей.
Сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями последовательности и выбирают из них не более предельного числа Z альтернативных принятых последовательностей, имеющих Наименьшие значения метрики, которые дополняют соответствующими им продолжениями последовательности, Данные способы известны и описаны, например, в книге М. Сибуя, Т. Ямамото "Алгоритмы обработки данных". - М., Мир, 1986, стр. 122-134, и заключаются в поочередном сравнении между собой значений метрики АПП с их продолжениями, сортировке последовательностей по мере возрастания значений метрики и выборе среди отсортированных последовательностей первых Z последовательностей с наименьшими значениями метрики.
Например, на момент приема девятого по счету символа принятой последовательности имеются только две АПП: АПП с продолжением последовательности в виде нулевого символа вида "0000 1100 0" и АПП с продолжением последовательности в виде единичного символа вида "0000 1100 1" со значениями метрики М=0 и М=1, соответственно. Так как число этих АПП не превышает предельного числа Z=12 альтернативных принятых последовательностей, имеющих наименьшие значения метрики, то обе последовательности выбирают и сохраняют. В результате их дополнения соответствующими им продолжениями последовательности первая АПП приобретает вид "0000 1100 0", а вторая АПП - "0000 1100 1". Для АПП вида "0000 1100 0" запоминают очередные части соответствующей ей АВП вида "0 0" и значение метрики М=1. Для АПП вида "0000 1100 1" запоминают очередные части соответствующей ей АВП вида "0 0" и значение метрики М=0.
При получении следующего бита принятой последовательности каждая из двух сохраненных АПП получает по два продолжения последовательности и т.д.
При декодировании очередного, десятого по счету на фиг. 10 бита принятой последовательности четыре АПП со значениями метрики от М=0 до М=2, которые при декодировании очередного, одиннадцатого по счету на фиг. 10 бита, принятой последовательности образуют 8 последовательностей со значениями метрики от М=0 до М=3, которые при декодировании очередного, двенадцатого по счету на фиг. 10 бита, принятой последовательности образуют 16 последовательностей со значениями метрики от М=0 до М=4. Так как число АПП с их продолжениями уже превышает предельное число Z АПП, то из этих последовательностей выбирают Z=12 альтернативных принятых последовательностей с их продолжениями с наименьшими значениями метрики.
Например, одну АПП с ее продолжением с метрикой М=4 и три АПП с их продолжениями с метрикой М=3 стирают, что показано символом "X" на фиг. 10. По принципу максимального правдоподобия в теории помехоустойчивого кодирования, как описано в книге Б. Скляр "Цифровая связь. Теоретические основы и практическое применение". - М., Издательский дом "Вильямс", 2003, стр. 422-431, чем больше альтернативная принятая последовательность с ее продолжением отличается от принятой последовательности по значению метрики Хэмминга, тем меньше вероятность того что именно она позволит исправить ошибки передачи, что дает основание такую последовательность отбрасывать.
Далее, число продолжаемых АПП при декодировании тринадцатого, четырнадцатого и пятнадцатого символов по счету символов принятой последовательности остается равным предельному числу Z=12 благодаря стиранию части АПП, а при декодировании шестнадцатого символа по счету принятой последовательности число продолжаемых АПП с их продолжениями уменьшается до девяти. Это произошло потому, что во многих ранее продолжаемых АПП их текущее значение оказалось вне пределов текущего разрешенного интервала арифметического декодирования этих АПП, то есть такие последовательности не могли быть сформированы на передающей стороне и, соответственно, они подлежат стиранию и их далее не продолжают, как показано символом  на фиг. 10.
на фиг. 10.
Например, оказалась стертой альтернативная принятая последовательность с ее продолжением вида "0000 1100 0110 0110" со значением метрики М=0, которая по этой причине ранее считалась наиболее предпочтительной при выборе среди альтернативных принятых последовательностей. Действия для альтернативной принятой последовательности вида "0000 1100 1001 0001", идентичной принятой последовательности, показаны на фиг. 13. В результате декодирования первых шестнадцати символов данной последовательности, показанной на фиг. 7(e), получена АВП вида "000 1 0", показанная на фиг. 7(ж). Например, при декодировании четвертого по счету символа очередной части АВП текущее значение альтернативной принятой последовательности, равное 201, сравнивают с границами текущего значения подинтервала декодирования нулевого символа АПП DD0, находящимися в пределах от 0 до 106, и с границами текущего значения подинтервала декодирования единичного символа АПП DD1, находящимися в пределах от 193 до 220, как показано на фиг. 13 в девятой строке. Так как текущее значение альтернативной принятой последовательности оказалось в пределах подинтервала декодирования единичного символа, то четвертый декодированный символ является единичным и следующие границы текущего интервала декодирования устанавливают соответствующими границам значения подинтервала декодирования единичного символа данной АПП DD1. В результате декодирования устанавливают нижнее значение интервала декодирования арифметического декодирования LL равным значению нижней границы текущего подинтервала декодирования единичного символа, а верхнее значение интервала декодирования арифметического декодирования НН - равным верхней границы текущего подинтервала декодирования единичного символа, как показано на фиг. 13 в строке при t=4.
При получении шестнадцатого символа принятой последовательности текущее значение альтернативной принятой последовательности, равное 145, сравнивают с пределами текущего разрешенного интервала декодирования АПП, который состоит из текущего подинтервала декодирования нулевого символа АПП DD0 в пределах от 16 до 91, и из текущего значения подинтервала декодирования единичного символа АПП DD1 в пределах от 160 до 190, как показано на фиг. 13 в предпоследней строке. Так как текущее значение АПП не находится в пределах текущего разрешенного интервала декодирования данной АПП, то стирают данную альтернативную принятую последовательность с ее продолжением последовательности. Факт стирания данной альтернативной принятой последовательности с ее продолжением отмечают символом  на фиг. 10.
на фиг. 10.
При получении шестнадцатого и последующих символов принятой последовательности множество альтернативных принятых последовательностей имеет текущее значение за пределами текущего разрешенного интервала декодирования этой АПП и, соответственно, подлежит стиранию как альтернативные принятые последовательности, которые с учетом возможного воздействия различных комбинаций ошибок канала передачи не могут быть сформированы на передающей стороне совместным арифметическим и помехоустойчивым кодированием. В результате этого в данном примере число продолжаемых АПП при декодировании восемнадцатого символа по счету символов принятой последовательности снизилось до четырех, среди которых одна АПП имеет метрику М=2, две АПП - М=3 и одна АПП - М=4.
Декодирование АПП вида "0100 0000 0101 0001 001" со значением метрики М=2 показано на фиг. 14. При арифметическом декодировании девятнадцати символов данной АПП, показанных на фиг. 7(з), декодированы первые девять частей альтернативной восстановленной информационной последовательности вида "000100101", показанной на фиг. 7(и). Как показано на фиг. 10, данная АПП имеет метрику М=2 и является одной из четырех АПП, сохранившихся из всех АПП при приеме первых девятнадцати бит принятой последовательности. Однако остальные три АПП имеют значения метрики М=3 и М=4. В ходе дальнейшего декодирования наименьшей по значению метрики будет обладать альтернативная принятая последовательность, продолжающая выявленную АПП с метрикой М[19]=2, так как остальные три АПП при любых их возможных продолжениях не могут обеспечить значение метрики меньше М=3.
После прекращения поступления очередных битов принятой последовательности сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них последовательность с наименьшим значением метрики. В приведенном примере будет выбрано продолжение АПП вида "0100 0000 0101 0001 001" со значением метрики на девятнадцатом принятом бите М[19]=2, для которой выполняется исправление двух ошибок передачи на первых девятнадцати битах принятой последовательности.
Далее передают получателю в качестве восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности альтернативную восстановленную информационную последовательность. Выбранному в примере продолжению АПП вида "0100 0000 0101 0001 001" соответствуют первые девять частей альтернативной восстановленной информационной последовательности вида "000100101", показанные на фиг. 7(и).
В данном примере совместное арифметическое и помехоустойчивое кодирование и декодирование обеспечивает исправление двух ошибок передачи в принятой последовательности.
Проверка теоретических предпосылок заявленного способа совместного арифметического и помехоустойчивого кодирования и декодирования выполнялась путем его аналитических исследований.
Было выполнено совместное арифметическое и помехоустойчивое кодирование и декодирование очередных частей длиной k=1 бит избыточной информационной последовательности общей длиной 1024 бит с использованием способа-прототипа, для которого выбирались значения скорости помехоустойчивого кода R=1/2 и R=2/3. Также было выполнено совместное арифметическое и помехоустойчивое кодирование и декодирование очередных частей длиной k=1 бит этой же избыточной информационной последовательности общей длиной 1024 бит с использованием предлагаемого способа при выборе значения коэффициента помехоустойчивости β равным скорости помехоустойчивого кода R=1/2 и R=2/3. Выявлено, что при передаче кодированных последовательностей по каналу связи с ошибками во всех случаях обеспечивается исправление большего числа ошибок передачи с использованием предлагаемого способа по сравнению со способом-прототипом. При этом, при увеличении предельного числа Z альтернативных принятых последовательностей до 17…32, кроме однократных и двухкратных ошибок, обеспечивают исправление трехкратных ошибок передачи.
Проведенные исследования подтверждают, что при использовании предлагаемого способа совместного арифметического и помехоустойчивого кодирования и декодирования обеспечивается повышение помехоустойчивости передачи очередных частей кодированной последовательности при воздействии многократных ошибок передачи.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2018 |
|
RU2702724C2 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2019 |
|
RU2718213C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2016 |
|
RU2620731C1 |
| СПОСОБ АРИФМЕТИЧЕСКОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2020 |
|
RU2752868C1 |
| СПОСОБ АРИФМЕТИЧЕСКОГО КОДИРОВАНИЯ С ШИФРОВАНИЕМ | 2017 |
|
RU2656713C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2015 |
|
RU2629455C2 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ (ВАРИАНТЫ) | 2016 |
|
RU2611022C1 |
| СПОСОБ СОВМЕСТНОГО СЖАТИЯ И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2015 |
|
RU2595955C1 |
| СПОСОБ АУТЕНТИФИКАЦИИ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ (ВАРИАНТЫ) | 2014 |
|
RU2589345C1 |
| СПОСОБ АРИФМЕТИЧЕСКОГО КОДИРОВАНИЯ С ШИФРОВАНИЕМ | 2015 |
|
RU2595953C1 |
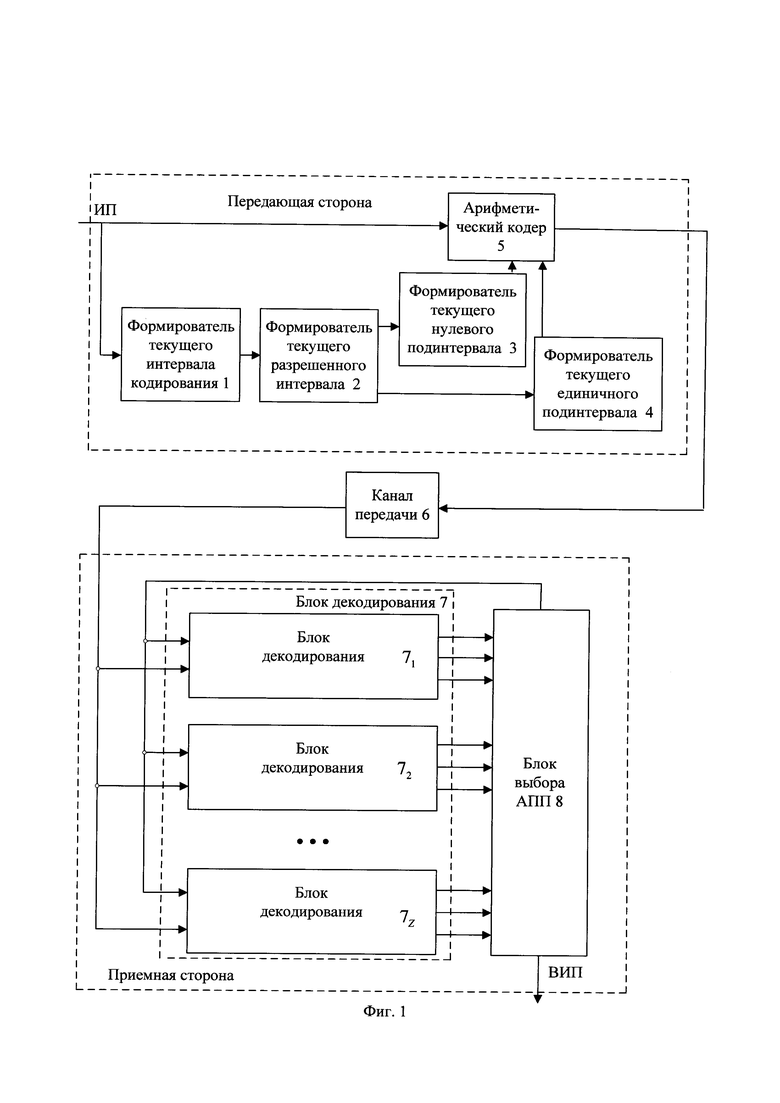
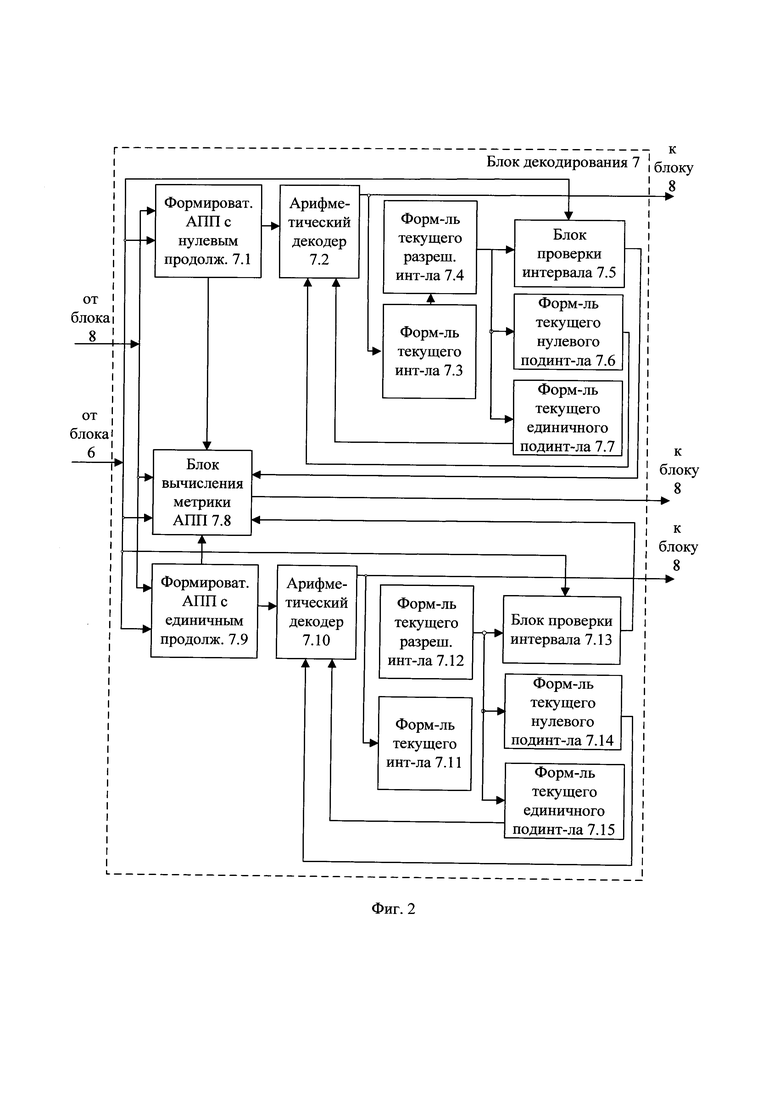
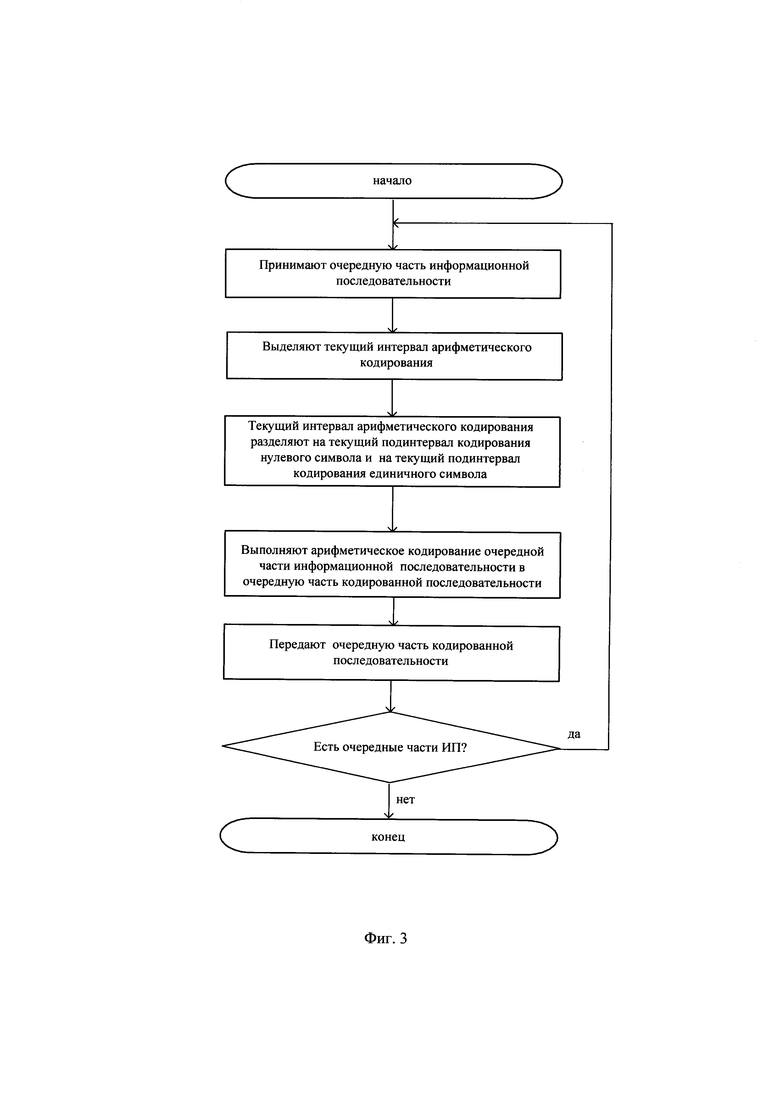
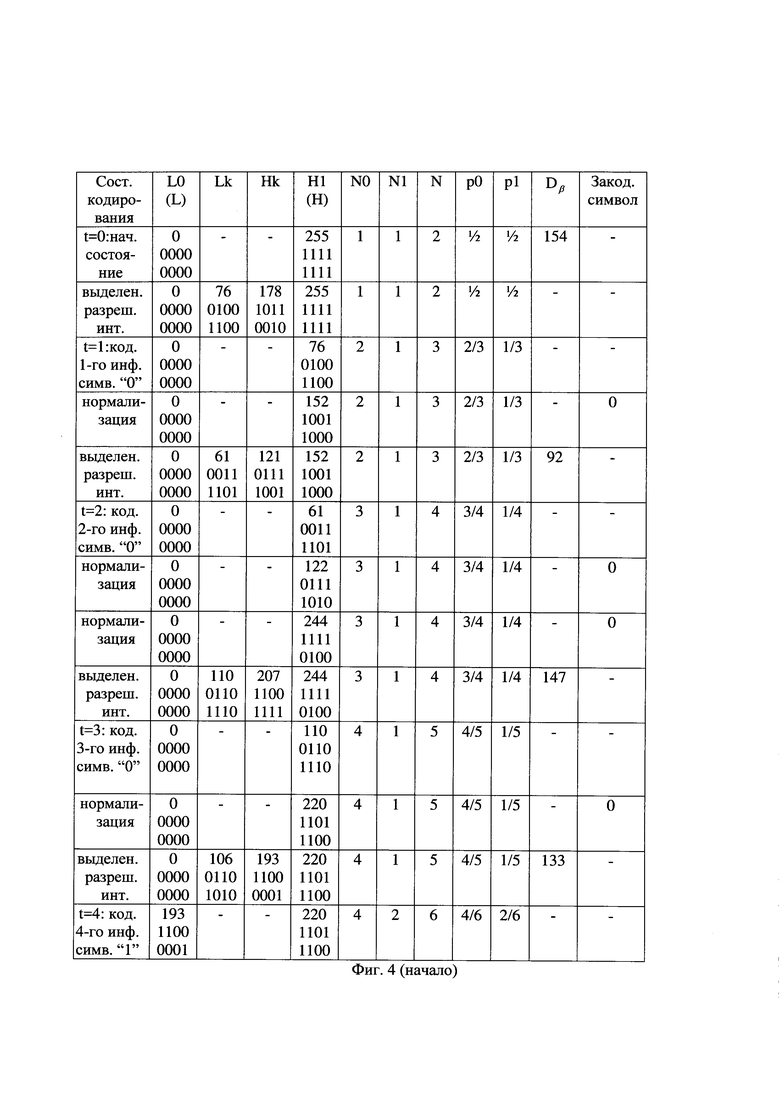
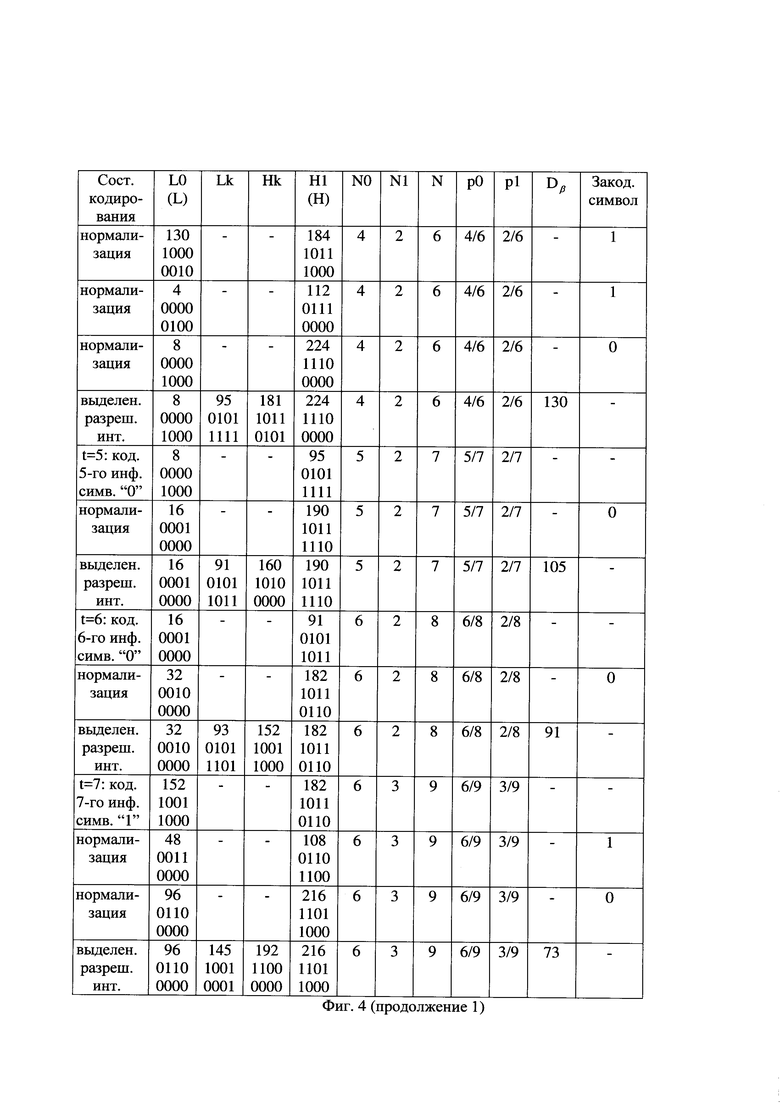
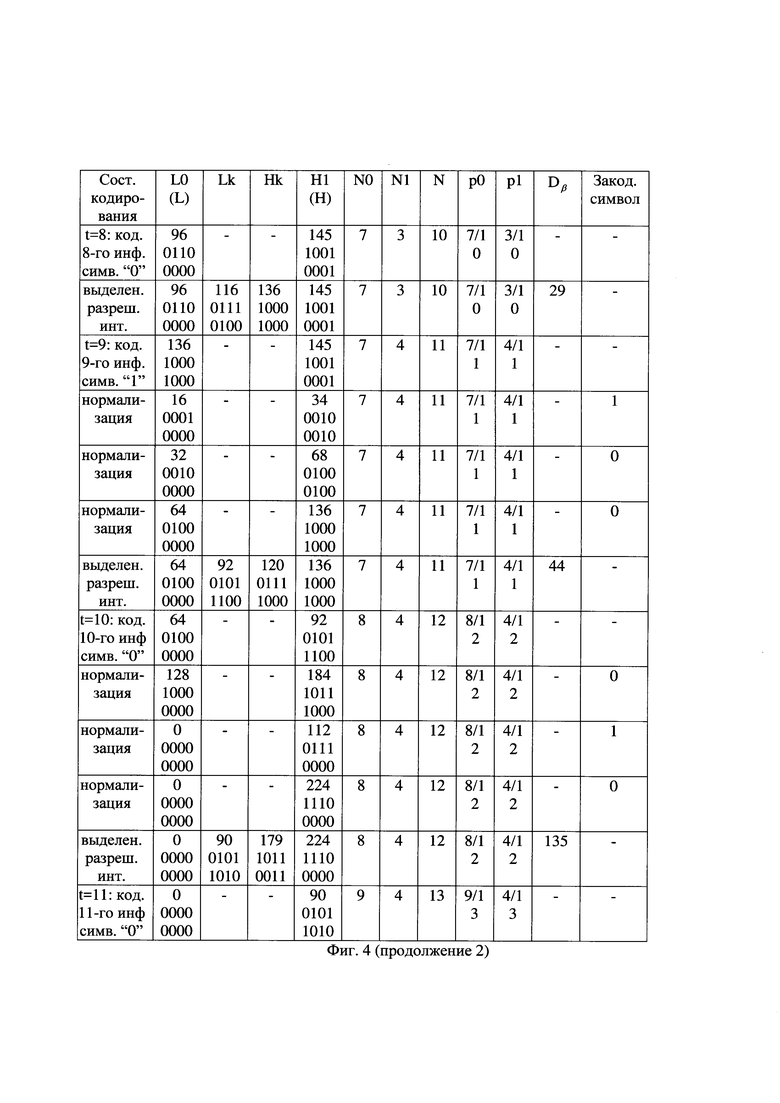
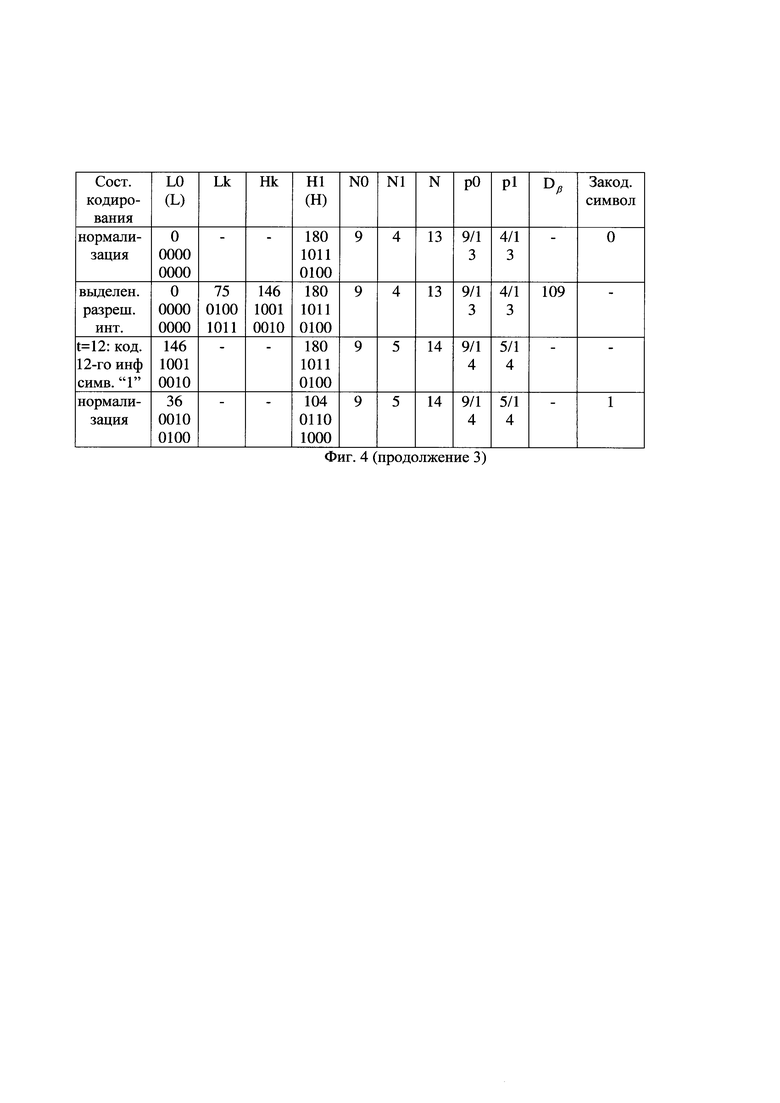


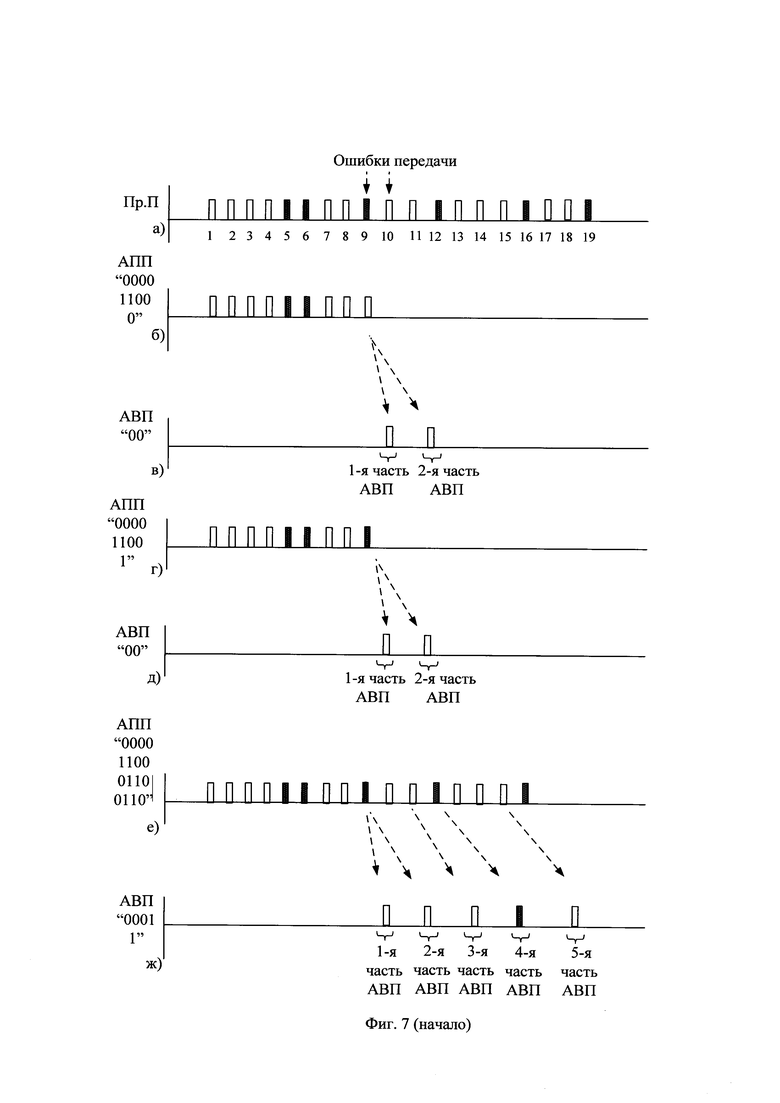

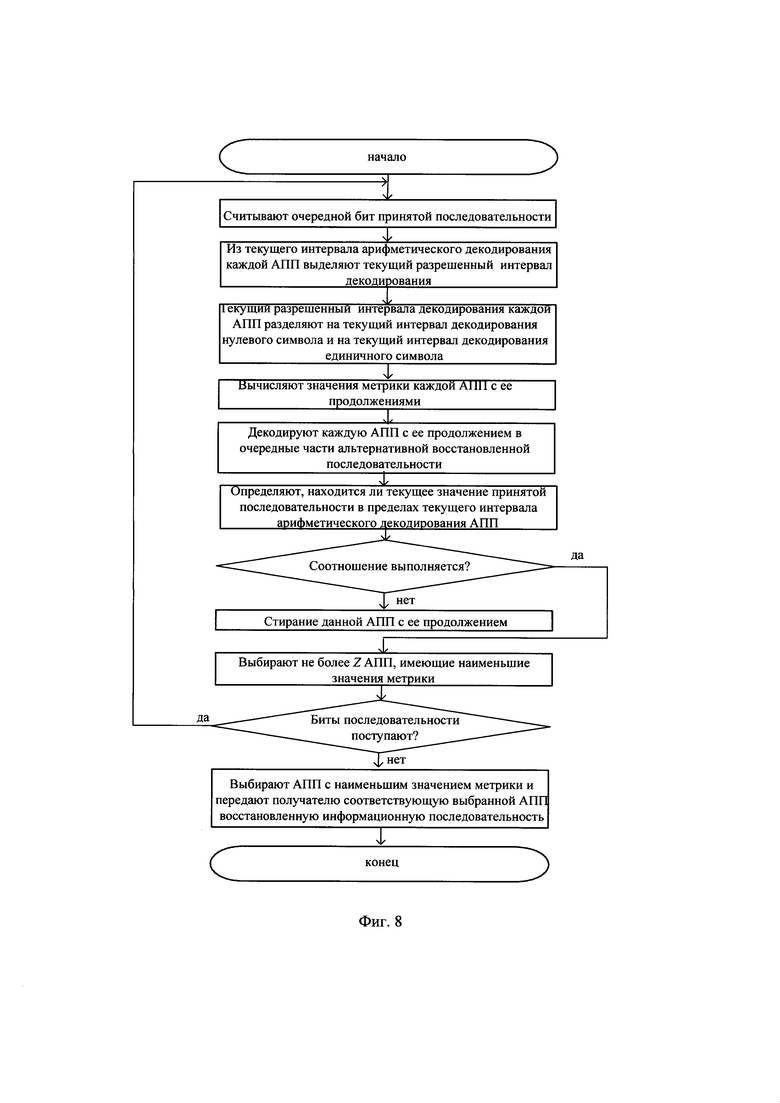
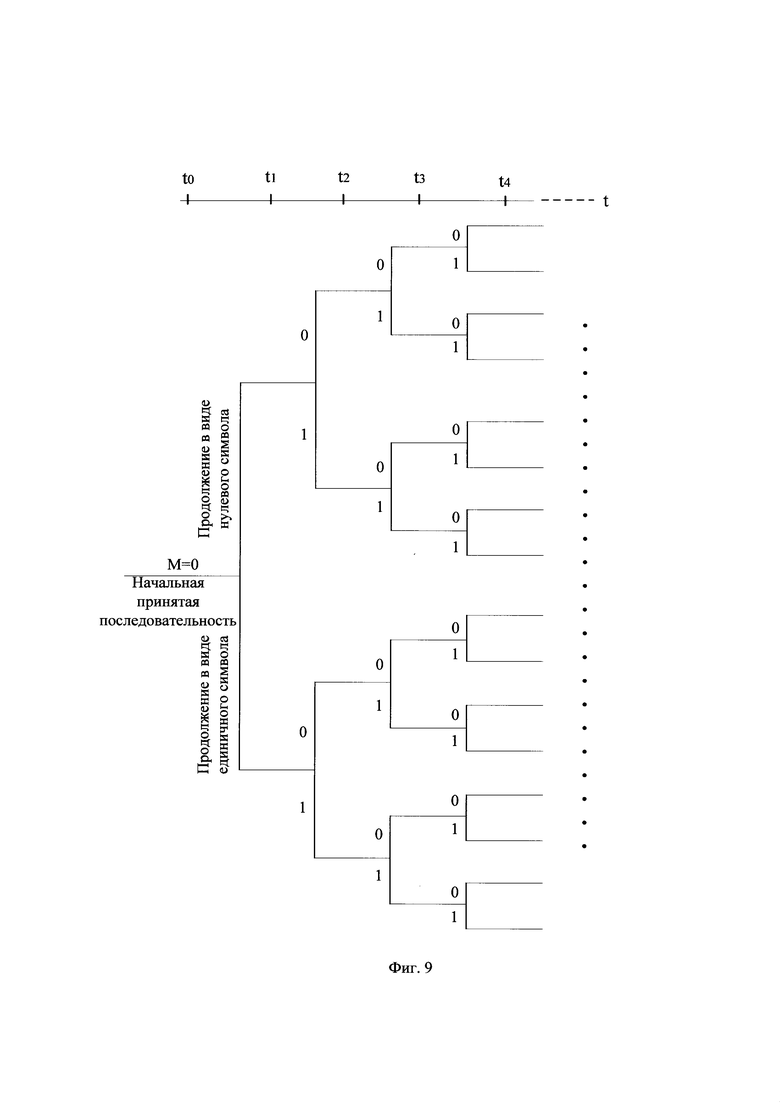
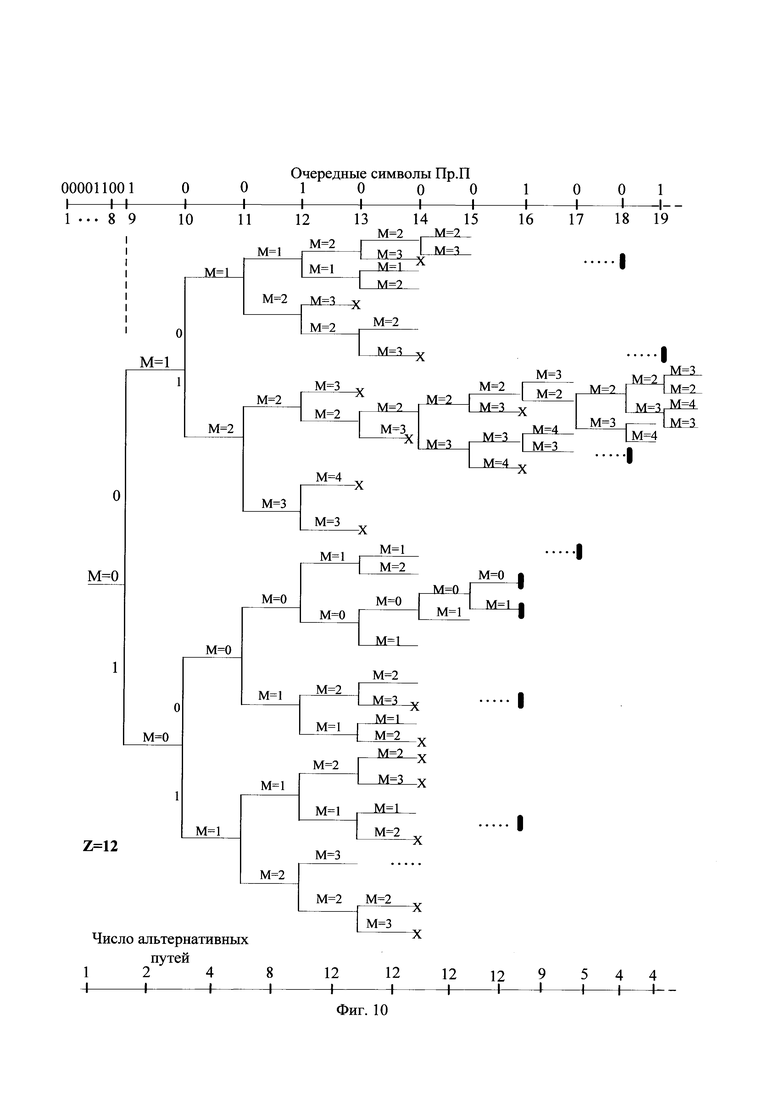
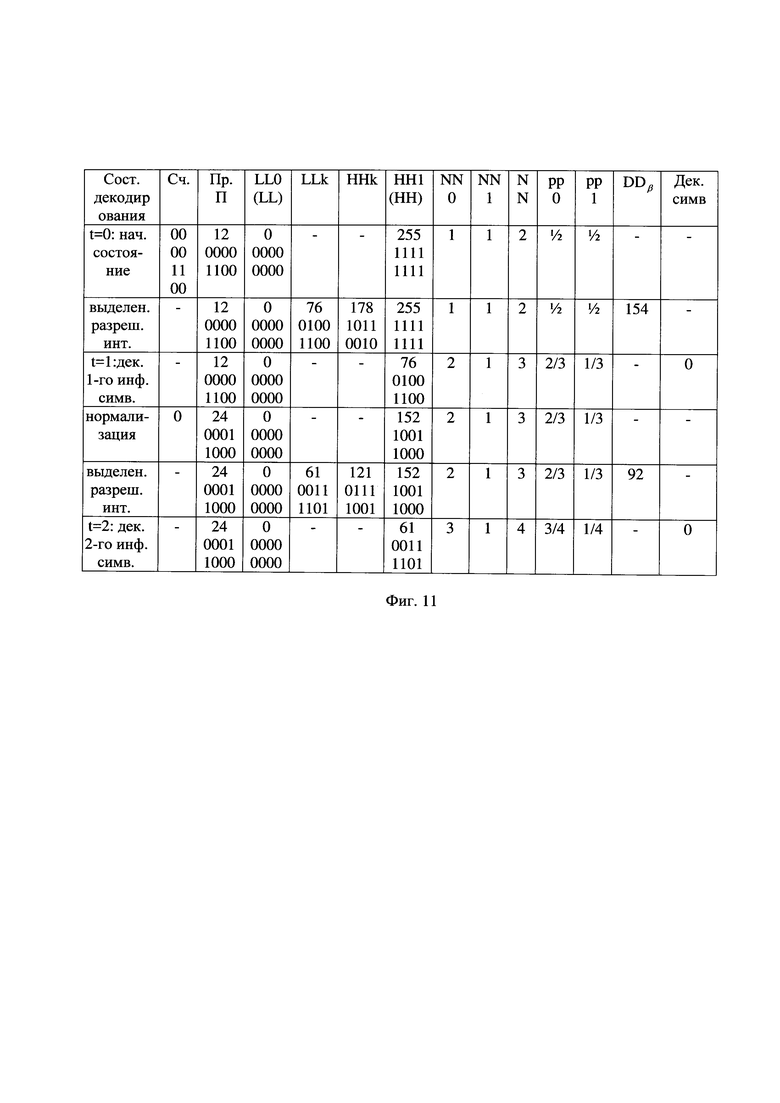
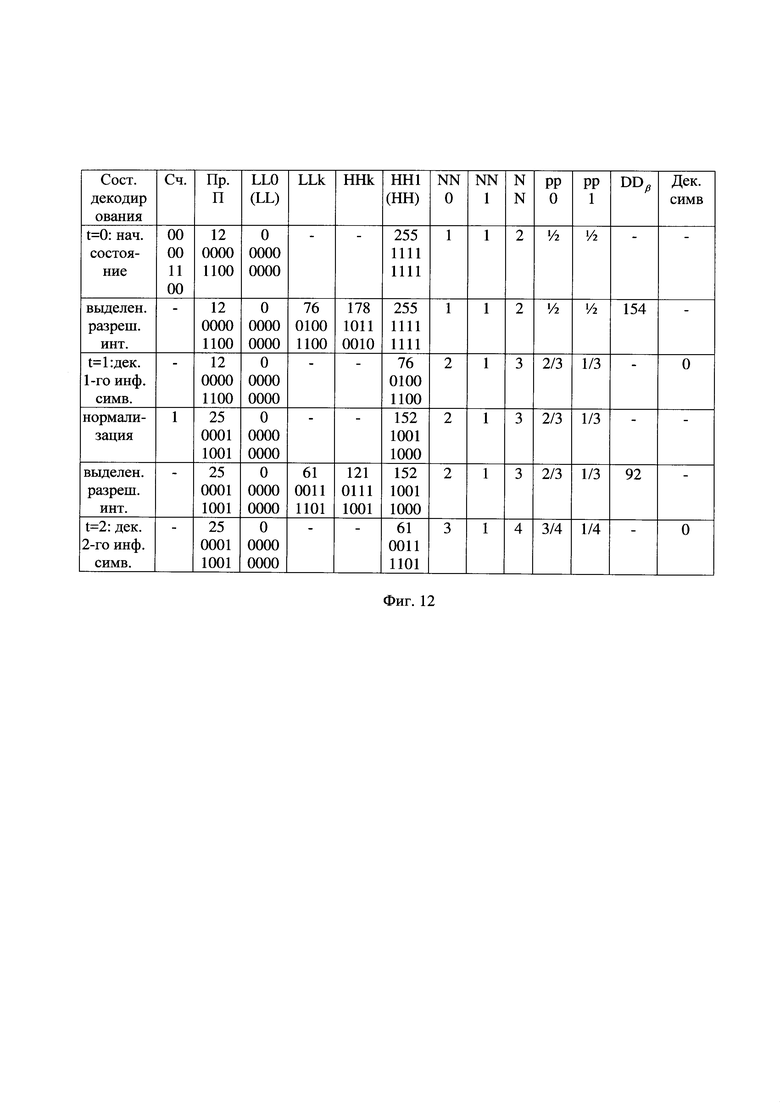
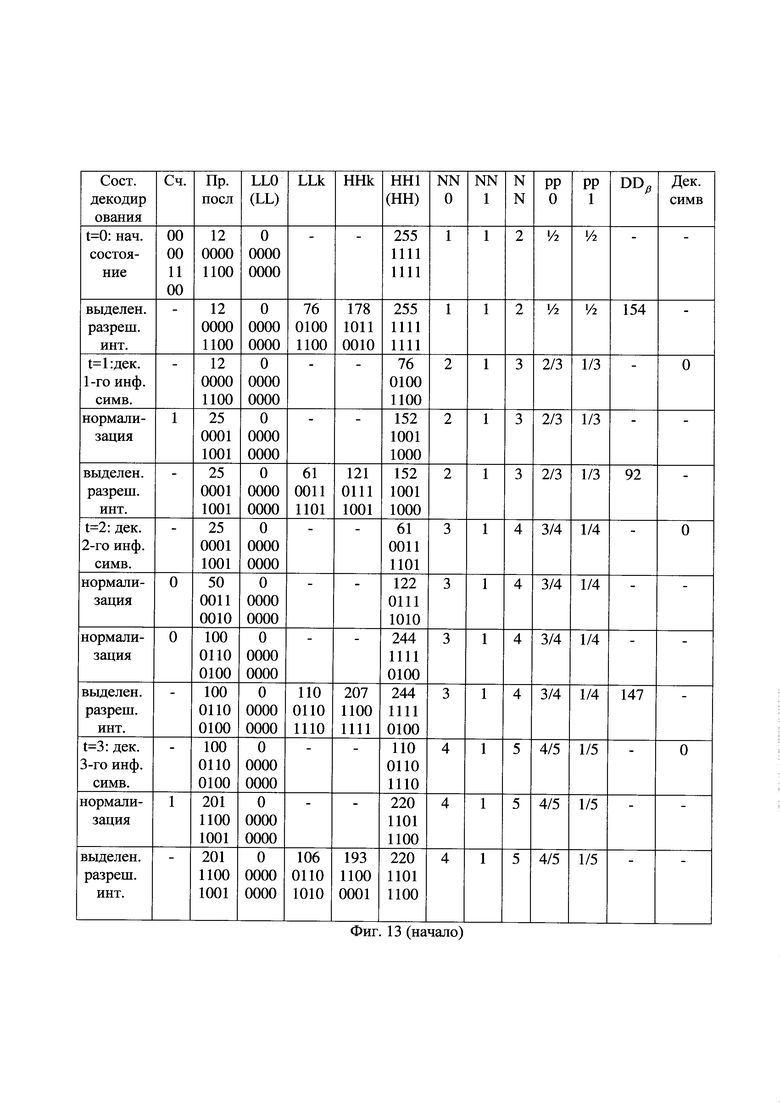
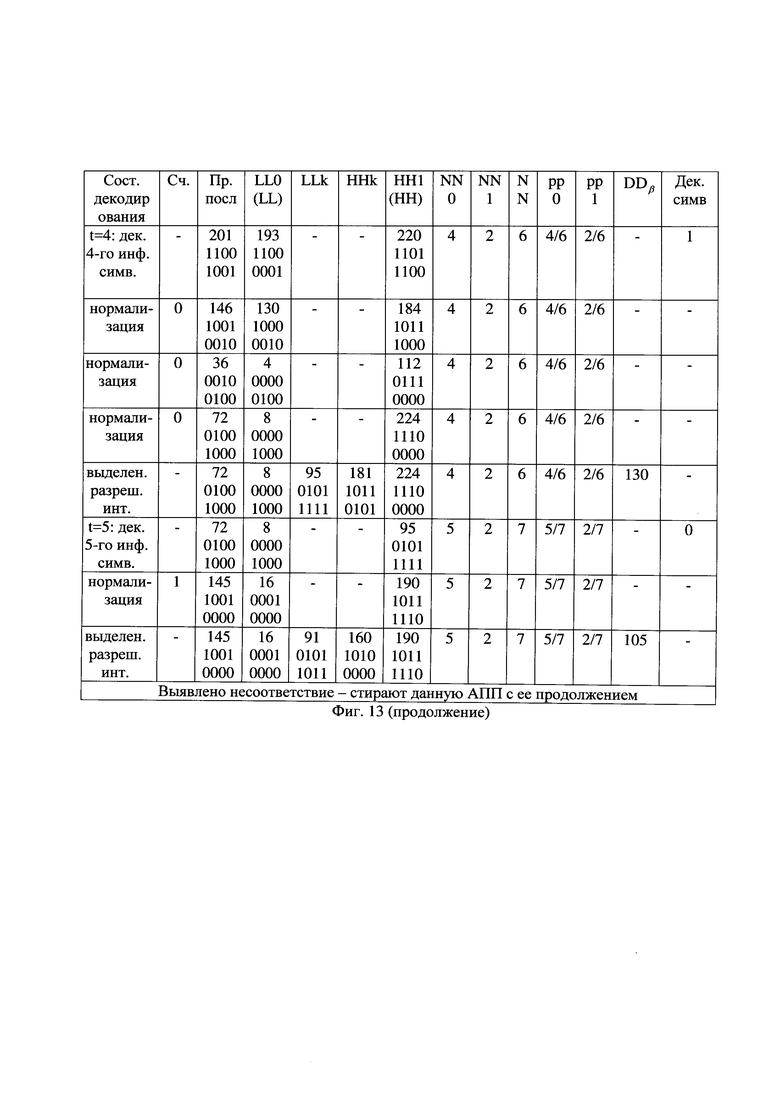
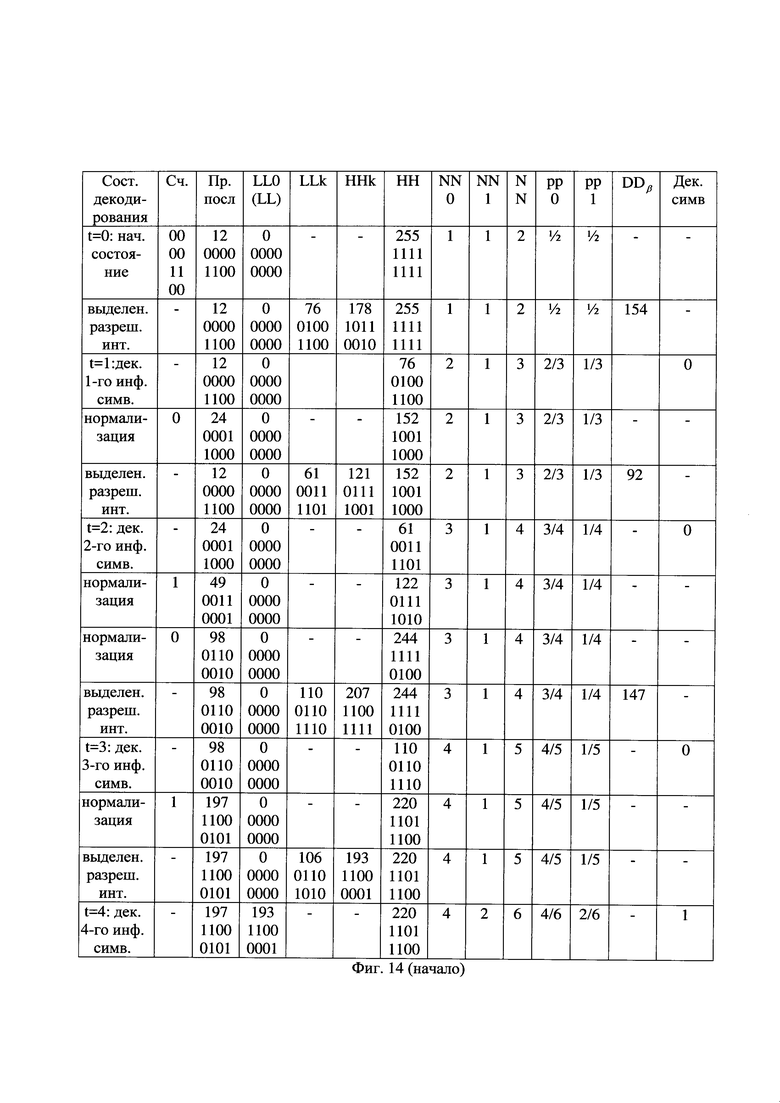
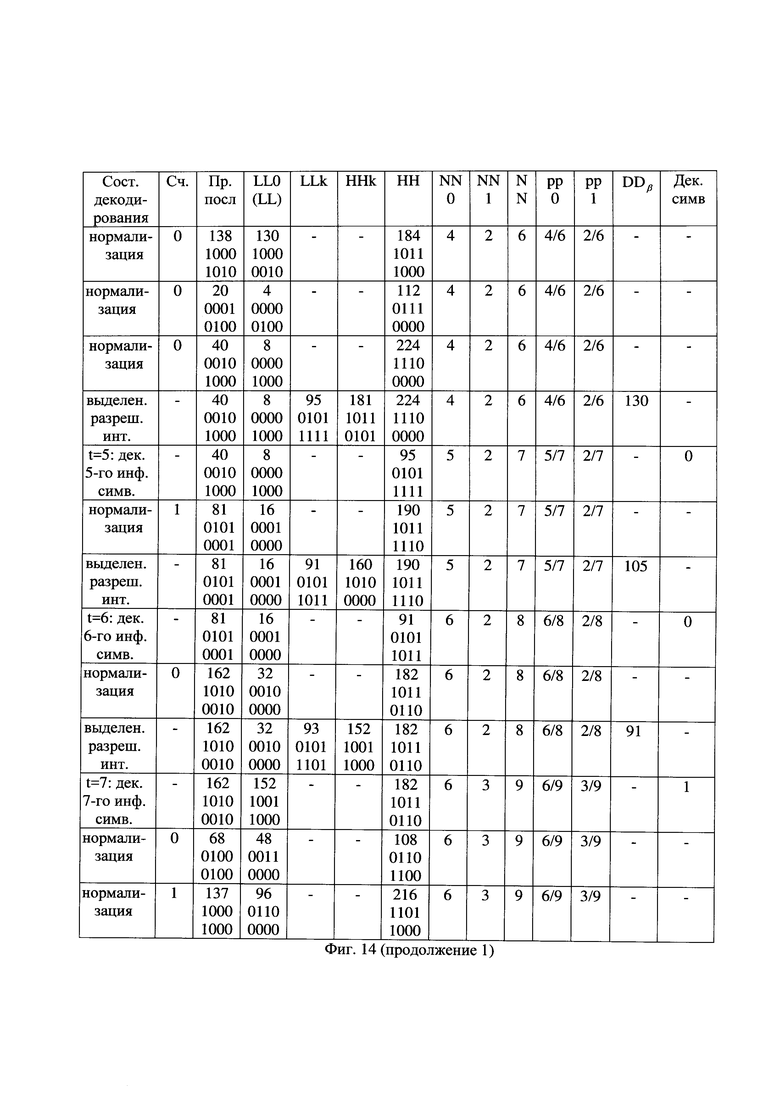
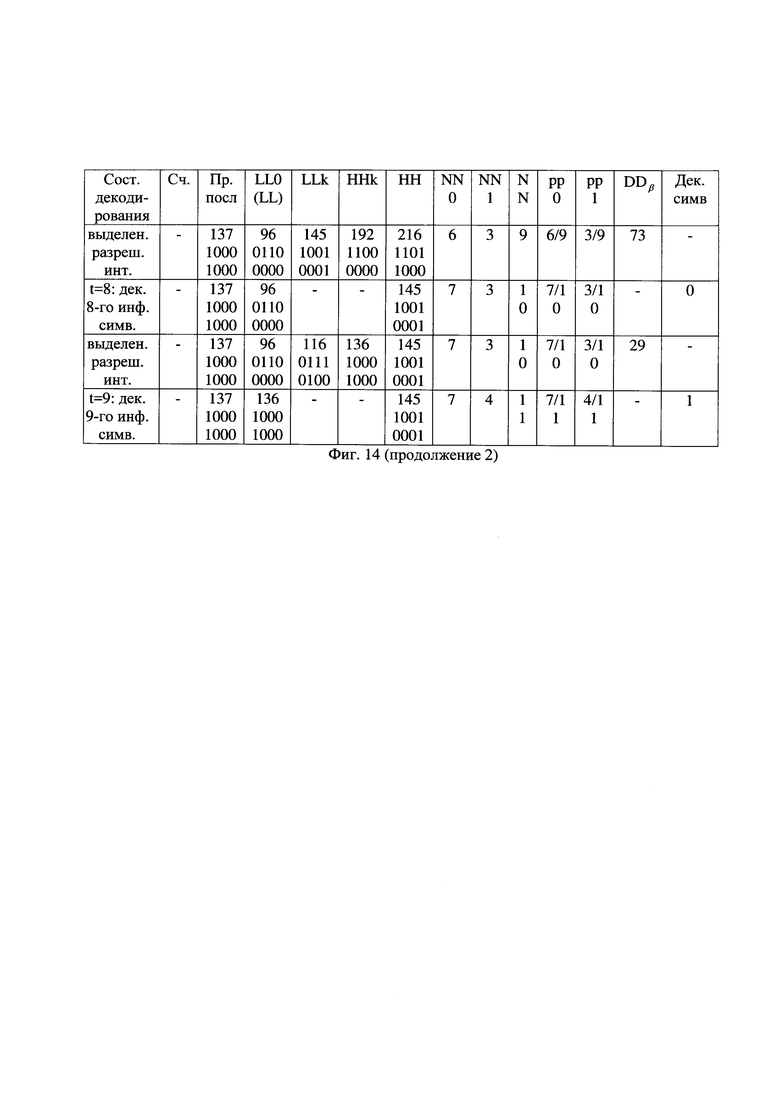
Изобретение относится к области электросвязи и информационных технологий. Технический результат заключается в повышении помехоустойчивости передачи очередных частей кодированной последовательности при воздействии многократных ошибок передачи. Такой результат достигается тем, что на передающей стороне выполняют арифметическое кодирование очередной части информационной последовательности (ИП) длиной k≥1 бит, из текущего интервала арифметического кодирования длиной D>2 выделяют текущий разрешенный интервал кодирования длиной Dβ>2 по правилу Dβ=β⋅D, где коэффициент помехоустойчивости β выбирают в пределах 0<β<1, текущий разрешенный интервал кодирования разделяют на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа, выполняют арифметическое кодирование очередной части ИП в очередную часть кодированной последовательности, на приемной стороне сохраняют и продолжают не более Z≥2 альтернативных принятых последовательностей (АПП), наиболее близких по метрике Хэмминга к принятой последовательности, АПП арифметически декодируют с контролем соответствия текущего значения АПП текущему разрешенному подинтервалу декодирования, выбирают альтернативную принятую последовательность с наименьшим значением метрики и декодированные из нее очередные части восстановленной информационной последовательности передают получателю. 3 з.п. ф-лы, 14 ил.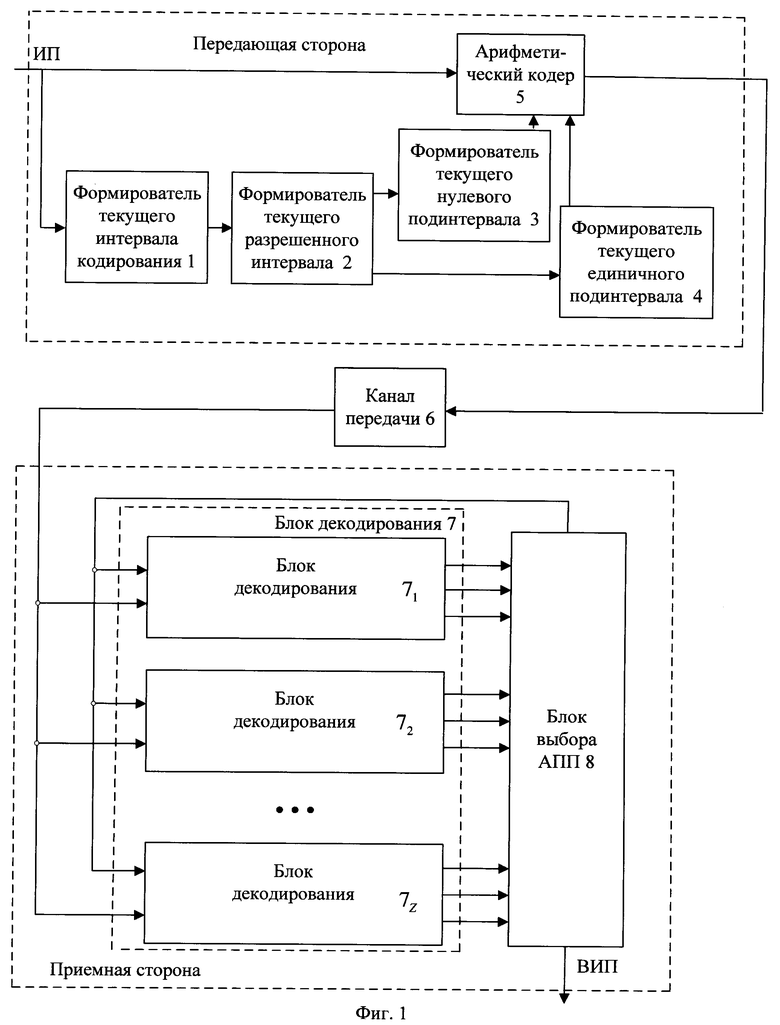
1. Способ совместного арифметического и помехоустойчивого кодирования и декодирования, заключающийся в том, что предварительно на передающей стороне устанавливают начальный интервал арифметического кодирования и на приемной стороне соответствующий ему начальный интервал арифметического декодирования, на передающей стороне от источника информационной последовательности принимают очередную часть информационной последовательности длиной k≥1 бит, разделяют текущий интервал арифметического кодирования на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа, выполняют арифметическое кодирование очередной части последовательности в очередную часть кодированной последовательности, передают очередную часть последовательности на приемную сторону, выполняют на передающей стороне перечисленные действия до тех пор, пока поступают очередные части информационной последовательности, на приемной стороне принимают последовательность, разделяют текущий интервал арифметического декодирования на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа, арифметически декодируют очередные части принятой последовательности в очередные части последовательности, выполняют перечисленные действия на приемной стороне до тех пор, пока поступает принятая последовательность, передают восстановленную информационную последовательность, отличающийся тем, что предварительно устанавливают предельное число Z≥2 альтернативных принятых последовательностей и значение метрики альтернативных принятых последовательностей в нулевое значение, на передающей стороне после приема очередной части информационной последовательности из текущего интервала арифметического кодирования длиной D>2 выделяют текущий разрешенный интервал кодирования длиной Dβ>2, который разделяют на текущий подинтервал кодирования нулевого символа и на текущий подинтервал кодирования единичного символа, и выполняют арифметическое кодирование очередной части информационной последовательности в очередную часть кодированной последовательности, которую передают на приемную сторону, на приемной стороне принимают очередной бит последовательности, из текущего интервала арифметического декодирования длиной DD>2 каждой альтернативной принятой последовательности выделяют текущий разрешенный интервал декодирования длиной DDβ>2, который разделяют на текущий подинтервал декодирования нулевого символа и на текущий подинтервал декодирования единичного символа этой последовательности, для каждой альтернативной принятой последовательности формируют продолжение последовательности в виде нулевого символа и продолжение последовательности в виде единичного символа, устанавливают значение метрики продолжения последовательности в виде нулевого символа и значение метрики продолжения последовательности в виде единичного символа относительно очередного бита принятой последовательности, для каждой альтернативной принятой последовательности с ее продолжением последовательности вычисляют значение ее метрики, для чего суммируют значения метрики данной последовательности и метрики ее продолжения последовательности, арифметически декодируют каждую альтернативную принятую последовательность с ее продолжением последовательности в очередные части соответствующей ей альтернативной восстановленной последовательности, если текущее значение принятой последовательности находится в пределах текущего разрешенного интервала декодирования альтернативной принятой последовательности, то запоминают очередные части альтернативной восстановленной информационной последовательности, соответствующие этой последовательности, иначе стирают данную альтернативную принятую последовательность с ее продолжением последовательности, сравнивают между собой значения метрики альтернативных принятых последовательностей с их продолжениями последовательности и выбирают из них не более предельного числа Z альтернативных принятых последовательностей, имеющих наименьшие значения метрики, которые дополняют соответствующими им продолжениями последовательности, для этих альтернативных принятых последовательностей запоминают очередные части соответствующих им альтернативных восстановленных информационных последовательностей и значения метрики, выполняют перечисленные действия на приемной стороне до тех пор, пока поступают очередные биты принятой последовательности, сравнивают между собой значения метрики альтернативных принятых последовательностей и выбирают из них последовательность с наименьшим значением метрики, после чего передают в качестве восстановленной информационной последовательности соответствующую выбранной альтернативной принятой последовательности альтернативную восстановленную информационную последовательность.
2. Способ по п. 1, отличающийся тем, что на передающей стороне длину Dβ текущего разрешенного интервала кодирования выбирают как Dβ=β⋅D, где значение коэффициента помехоустойчивости β устанавливают в пределах 0<β<1, а на приемной стороне длину DDβ текущего разрешенного интервала декодирования выбирают из условия DDβ=β⋅DD.
3. Способ по п. 1, отличающийся тем, что значение метрики продолжения последовательности в виде нулевого символа относительно очередного бита принятой последовательности устанавливают как нулевое значение, если очередной бит принятой последовательности является нулевым битом, иначе устанавливают как единичное значение.
4. Способ по п. 1, отличающийся тем, что значение метрики продолжения последовательности в виде единичного символа относительно очередного бита принятой последовательности устанавливают как нулевое значение, если очередной бит принятой последовательности является единичным битом, иначе устанавливают как единичное значение.
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2016 |
|
RU2620731C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ (ВАРИАНТЫ) | 2016 |
|
RU2611022C1 |
| СПОСОБ СОВМЕСТНОГО АРИФМЕТИЧЕСКОГО И ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2015 |
|
RU2629455C2 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2609747C1 |
| US 6892343 B2, 10.05.2005 | |||
| US 7139960 B2, 21.11.2006 | |||
| US 9391646 B2, 12.07.2016. | |||
Авторы
Даты
2020-01-24—Публикация
2019-04-24—Подача