Изобретение относится к учебным моделям на основе системы оптических и механических элементов для моделирования бинарных и других пространственных и энергетических взаимоотношений элементов различной природы: макро- и микросистем или систем различных информационных уровней. Модель дает возможность реализовать динамическое изменение формы системы. Изобретение может быть использовано в исследованиях геофизических сред, в учебных и других целях в таких областях как геология, кристаллография, астрофизика и астробиология, а также в качестве составной части различных технических устройств.
Известно изобретение [1], в основе которого лежит создание модели искусственного кристалла, предусматривающего кристаллическую решетку, состоящую из шести тетраэдров, и подразумевающего наличие в структуре кристалла «всех химических элементов таблицы Менделеева». Размером и соотношением сторон элементарных ячеек-пирамидок, симметричностью их расположения в кристаллической решетке моделируются различные взаимоотношения между химическими элементами и распределение энергий [1].
Известно изобретение «ДЕМОНСТРАЦИОННАЯ МОДЕЛЬ КРИСТАЛЛА» [2]. Изобретение предназначено для моделирования блочного строения и процессов пластической и упругой деформации квазисимметричных кристаллов различной формы. Получение различных фигур обеспечивается деформацией исходной модели куба. «При построении моделей, из эстетических соображений, а также для того, чтобы ввести число (меру), длину ребер (линий связи) субграней фигур принимают равной одному из чисел Фибоначчи, представленных рядом: 0, 1, 1, 2, 3, 5, 8, 13, 21 и т.д.» [2].
Отличительной особенностью предлагаемой модели от известных изобретений является возможность демонстрации «слабых» энергетических взаимосвязей элементов и пространственное их взаимное распределение, основанное на балансе масс, являющемся следствием закона сохранения информации и энергии.
Техническая реализация заявляемой модели представляет собой систему, состоящую из физически непрерывного контура, объединяющего элементы с массами m1, m2, m3, m4. Контур моделирует относительно гибкую связь между элементами и выполнен в виде спиральных структур.
В основу структуризации взаимного распределения масс положен матричный метод попарных отношений между следующими критериальными факторами: возможные бинарные взаимоотношения энергетических компонентов излучений видимого диапазона (представлены в таблице 1), возможных взаимоотношений (весовых коэффициентов) основных нуклеотидов, как элементов системы, несущих информационную составляющую биополимеров ДНК (представлены в таблице 2), а также весовые коэффициенты бинарных отношений химических элементов периодической системы Д.И. Менделеева.
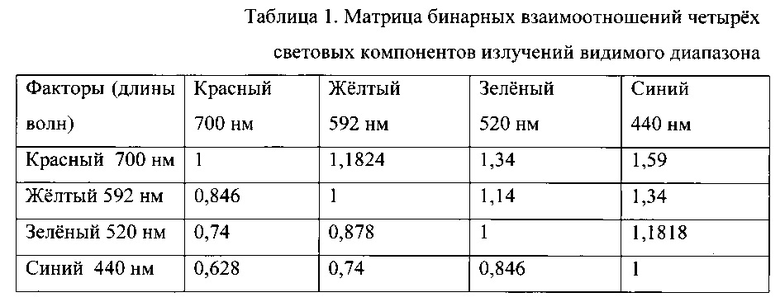
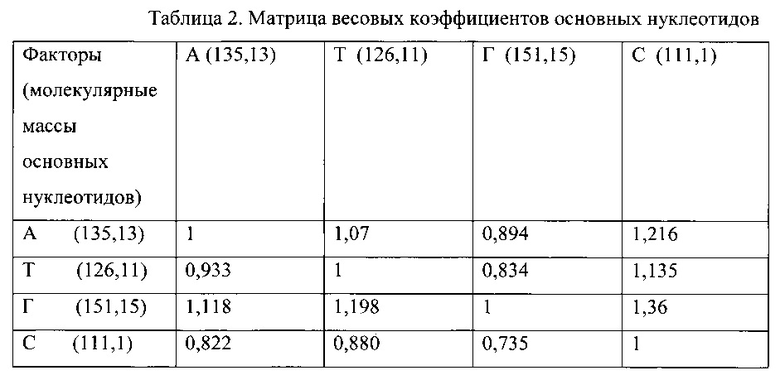
Где А - аденин (135,13) - C5N5H5
Т - тимин (126,11) - C5N2O2H6
С - цитозин (111,1) - C4N3OH5
Г - гуанин (151,15) - C5N5OH5
Сопоставлением данных возможных бинарных пространственных и энергетических взаимоотношений элементов таких систем, как химические элементы, молекулярно-биологические и квантовые, выявлен простейший «контур», объединяющий элементы системы в закономерном распределении информационно-энергетического баланса таким образом: отношения масс элементов m1/m2~m3/m4, при этом комплементарными элементами будут: m1 и m4; m2 и m3.
Контур, выполненный в виде спиралей с помощью светопроводящих, электропроводящих или комбинированных материалов, моделирует относительно гибкую связь между элементами. Элементы системы могут иметь для лучшей наглядности разный объем, различный цвет, различную прозрачность или сами являться источниками излучений (например, выполненные из светодиодов), иметь в своем составе энергоносители или другие маркеры и потоки.
Распределение элементов и объединяющих спиралей показано на Фиг. 1.
Модель «Квантовый контур» определяется следующими характеристиками системы: элементы модели взаимосвязаны между собой четырьмя гибкими связями в виде спиралей таким образом, что комплементарные элементы попарно связаны скрещивающимися спиралями, витки которых не входят в зацепление друг с другом и размещены друг относительно друга на величину близкую к 90°. Две другие связи между элементами соединяют между собой элементы из разных взаимодополняющих бинарных систем.
Динамические изменения формы модели происходят при следующем взаимном расположении элементов без разрыва связей (без нарушения информационно-энергетического баланса).
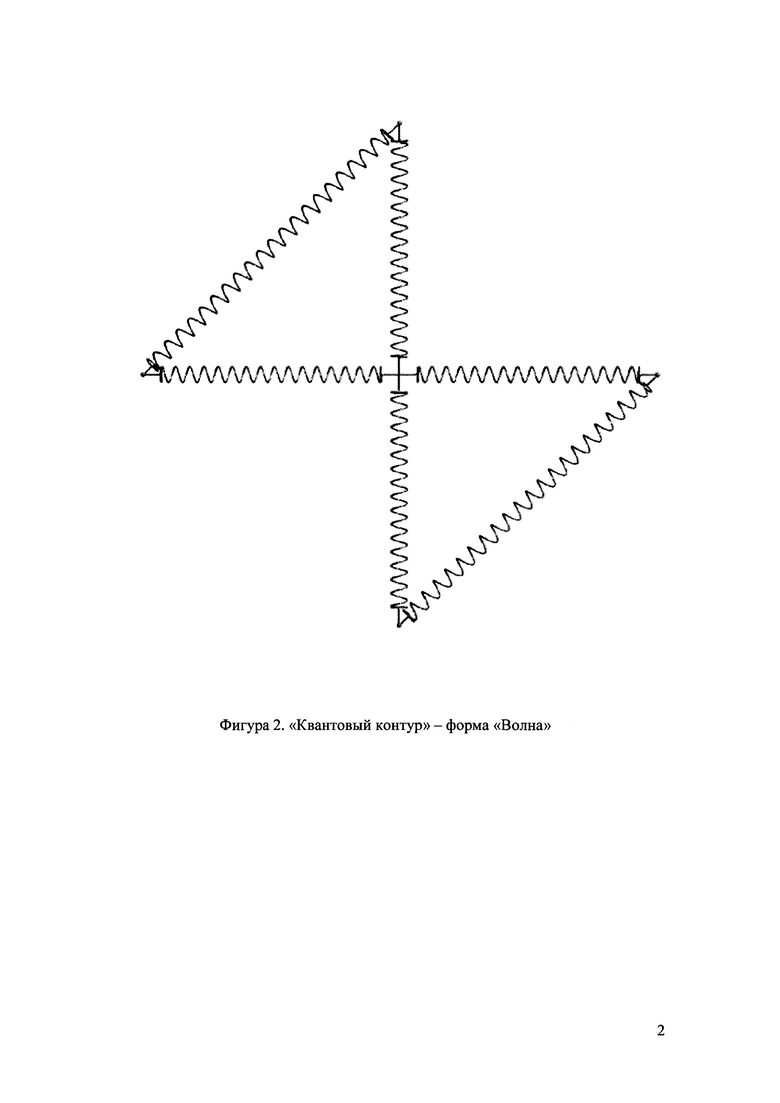
Форма 1. «Волна». Моделируется вращательным и поступательным движением системы относительно оси, определяемой как центр масс в средах, обладающих малым сопротивлением. Форма системы ограничивается упругим растяжением спиралей благодаря центробежной силе и силе упругости спиральных связей. Показана на Фиг. 2.
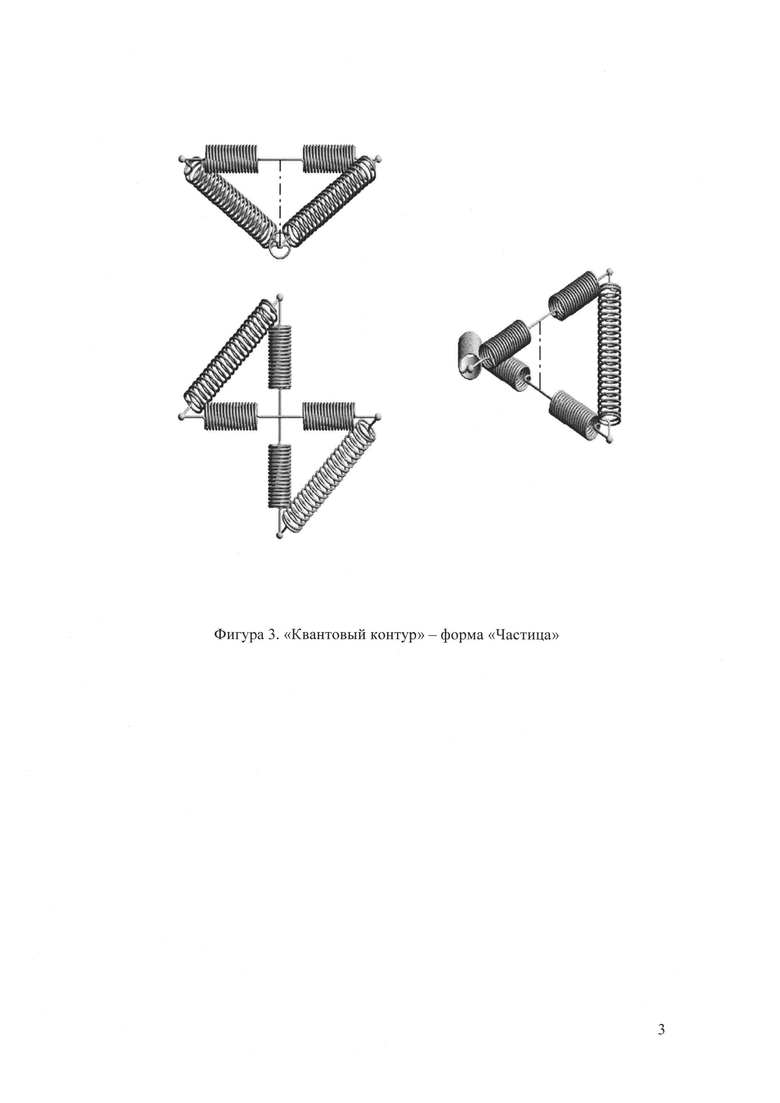
Форма 2. «Частица». Моделируется сжатием всех четырех пружин, что приводит к сближению всех элементов, т.е. сосредоточению масс в небольшом объеме, тем самым увеличивается проходимость в среде, обладающей определенной вязкостью или наличием пор. Такая форма моделирует упругое столкновение системы с элементами среды. Показана на Фиг. 3.
Форма 3. «Винт». Моделирует и демонстрирует повышенную проникающую способность системы, благодаря перегибу и сложению спиралей одна в другую и сжатию двух других спиралей. Образуя своеобразный цуг элементов. Гибкость винта обеспечивает прохождение через среды, имеющие узкие извилистые поры или повышенную вязкость. Показана на Фиг. 4.
Форма 4. Разрыв одной из связей возможен для моделирования и демонстрации различных трип летных взаимоотношений элементов. На рисунке не показана.
Литература
1. Курбанов М.А. Универсальная модель искусственного кристалла. Патент на Изобретение RU 2182729, 13.11.2000.
2. Чепижный К.И. Демонстрационная модель кристалла. Патент на Изобретение RU 2004935, 06.04.1989.


Изобретение относится к учебным моделям, в частности, к учебным моделям для демонстрации пространственных и энергетических связей элементов макро- и микросистем, систем различных информационных уровней. Учебная модель представляет собой физически непрерывный контур, образованный спиральными структурами с четырьмя прикрепленными к ним массами. При этом спиральные структуры выполнены с возможностью упругой деформации, сгиба в центре масс модели и совмещения витков без взаимного зацепления. Техническим результатом изобретения является возможность демонстрации слабых энергетических связей элементов и пространственного распределение указанных связей. 4 ил. 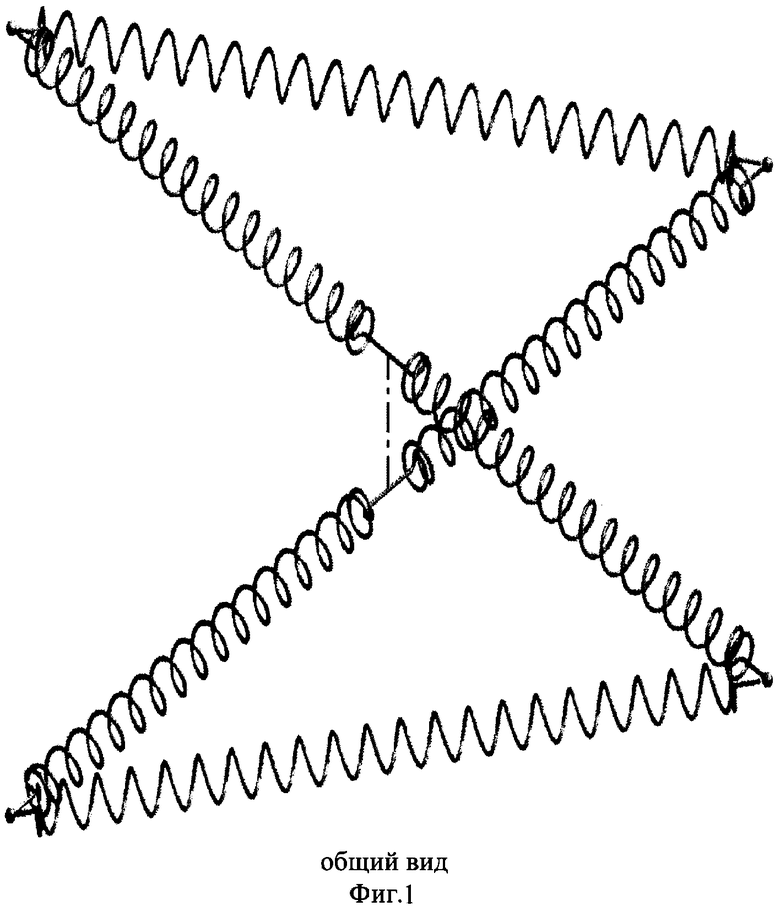
Учебная модель «Квантовый контур», отображающая пространственные и энергетические отношения, взаимосвязи элементов макро- и микросистем на основе информационно-энергетического баланса, отличающаяся тем, что связи между элементами представляют собой физически непрерывный контур, образованный спиралевидными структурами, выполненными с возможностью: упругой деформации, сгиба в зоне центра масс элементов и совмещения витков спиралевидной структуры без взаимного зацепления витков.
| RU 2003183 C1, 15.11.1993 | |||
| Полуавтомат для набивки шариков в сепараторы подшипников качения | 1949 |
|
SU85728A1 |
| КОНСТРУКТОР МОДЕЛЕЙ ЭЛЕКТРОННЫХ ОБОЛОЧЕК И ЯДЕР АТОМОВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ | 2013 |
|
RU2558477C2 |
| Электрическая печь сопротивления | 1934 |
|
SU43096A1 |
| US 20060099877 A1, 11.05.2006. | |||
Авторы
Даты
2017-07-04—Публикация
2015-12-15—Подача