Изобретение относится к контрольно-измерительной технике и может быть использовано для определения температурного коэффициента скорости ультразвука в твердых телах.
Известен способ определения температурного коэффициента скорости ультразвука, заключающийся в измерении изменений с температурой временных интервалов между эхо-импульсами из двух слоев иммерсионной жидкости с образца с фиксированными расстояниями между двумя преобразователями и между одним из преобразователей и ближайшей поверхностью образца (Недбай Александр Иванович. Способ определения температурного коэффициента скорости ультразвука (RU 1742632).
В качестве прототипа выбран способ определения температурного коэффициента скорости ультразвука, заключающийся в том, что в образце возбуждают бегущую ультразвуковую волну, измеряют ее скорость, нагревают образец до заданной температуры; повторно определяют скорость и по результатам измерений рассчитывают температурный коэффициент скорости ультразвука. (Авторское свидетельство СССР №325511, кл. G01Н 5/00, 1972 (прототип)).
Недостатком указанных выше способов является то, что в общем случае температурный коэффициент не является константой и зависит от структурного состояния материала, изменяющегося, например, в результате пластического деформирования, поэтому при указанных выше способах определение численного значения температурного коэффициента необходимо было бы производить после каждого акта пластического деформирования, что трудоемко и не всегда осуществимо.
Задачей, на достижение которого направлено данное изобретение, является повышение точности определения скорости распространения упругих волн в твердых телах при различных температурах и величинах пластической деформации.
Технический результат достигается тем, что, как и в прототипе, в образце возбуждают бегущую ультразвуковую волну, измеряют ее скорость, нагревают образец до заданной температуры, повторно определяют скорость и по результатам измерений рассчитывают температурный коэффициент скорости ультразвука.
Новым является то, что температурный коэффициент определяют как минимум для двух значений величины пластической деформации и устанавливают зависимость температурного коэффициента от величины пластической деформации, которую используют в дальнейшем для определения температурного коэффициента при промежуточных значениях величины пластической деформации.
Сущность предлагаемого способа заключается в следующем.
В материале возбуждают бегущую ультразвуковую волну, измеряют ее скорость, нагревают образец до заданной температуры, повторно определяют скорость и по результатам измерений рассчитывают температурный коэффициент скорости ультразвука. Затем материал деформируют на определенную величину пластической деформации. Затем в деформированном материале возбуждают бегущую ультразвуковую волну, измеряют ее скорость, нагревают образец до заданной температуры, повторно определяют скорость и по результатам измерений рассчитывают температурный коэффициент скорости ультразвука в деформированном материале. Получают зависимость температурного коэффициента скорости ультразвука от деформации.
Для определения величины пластической деформации измеряют время распространения поперечных упругих волн, поляризованных вдоль и поперек оси деформирования. Рассчитывают параметр акустической анизотропии, зависящий от величины пластической деформации и не зависящий от температуры по формуле

где τzx, τzy - время распространения поперечных упругих волн, поляризованных вдоль и поперек оси деформирования.
Расчет пластической деформации производят с помощью выражения:

где ΔА=А-А0, А0 - значение параметра акустической анизотропии в недеформированном образце, А - значение параметра акустической анизотропии, соответствующее текущей величине пластической деформации, kε - коэффициент, определяемый из эксперимента.
Таким образом, предлагаемый способ позволяет учесть влияние температуры и пластического деформирования на температурный коэффициент скорости распространения акустических колебаний в твердых телах, а значит, повысить точность определения скорости распространения упругих волн в твердых телах при различных температурах и величинах пластической деформации.
Пример применения
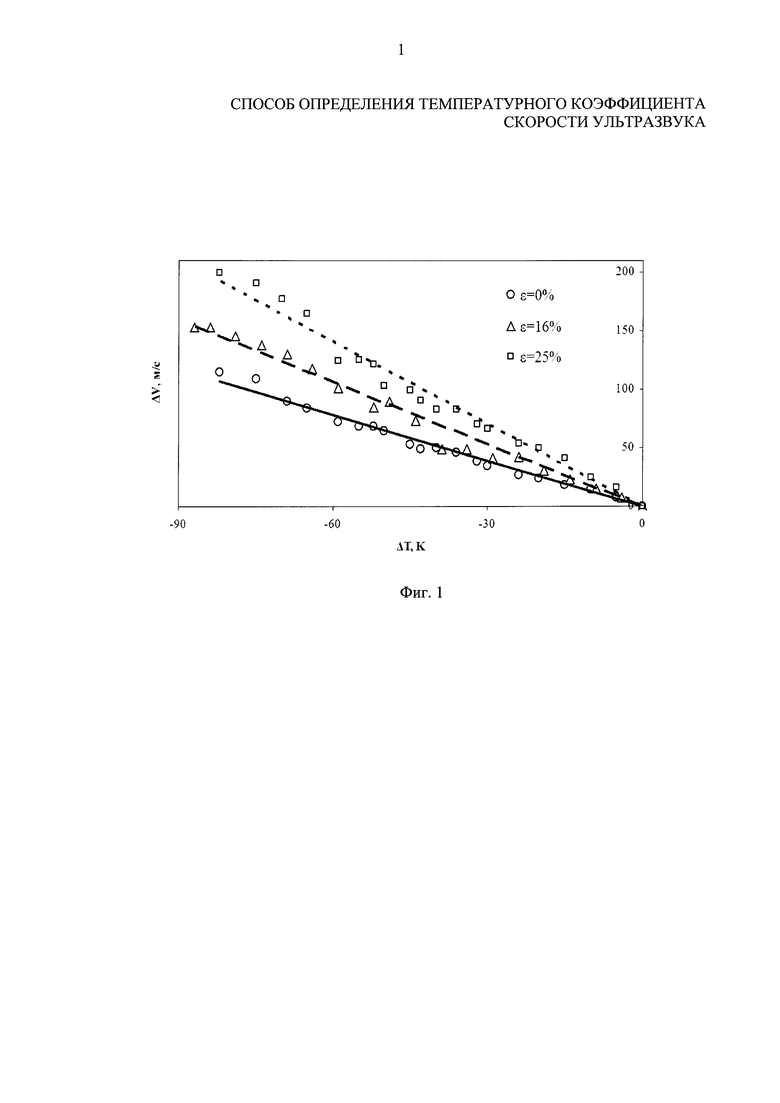
В образце из алюминиевого сплава возбуждали ультразвуковые продольные и поперечные волны, измеряли скорости их распространения. Затем образец медленно охлаждали и в процессе охлаждения повторно определяли скорости распространения волн. Затем образец подвергали пластическому деформированию при одноосном растяжении на величину 16% и снова при медленном охлаждении определяли скорости распространения ультразвуковых волн. При последующей операции образец подвергали пластическому деформированию при одноосном растяжении на величину 25% и снова при медленном охлаждении определяли скорости распространения ультразвуковых волн. Строили график зависимости изменения скорости распространения продольных волн от изменения температуры (фиг. 1).
Рассчитывали температурный коэффициент скорости ультразвука при различных значениях величины пластической деформации. Зависимость температурного коэффициента скорости ультразвука в алюминиевом сплаве от величины пластической деформации ε можно представить в виде:
Kv=-4.1⋅ε-1.24.
Для каждого значения величины пластической деформации рассчитывали параметр акустической анизотропии по формуле (1). Зная величину пластической деформации и соответствующее значение параметра акустической анизотропии, определили коэффициент kε=-2014. Как показали экспериментальные исследования, параметр акустической анизотропии не зависит от температуры, коэффициент kε не изменяется в процессе нагрева в исследуемом диапазоне температур.
Окончательное выражение для расчета температурного коэффициента скорости ультразвука в алюминиевом сплаве принимает следующий вид:
Kv=8057.4⋅ΔА-1.24.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ ультразвукового контроля поврежденности материалов при различных видах механического разрушения | 2023 |
|
RU2803019C1 |
| СПОСОБ ОЦЕНКИ МЕХАНИЧЕСКИХ СВОЙСТВ МЕТАЛЛОВ ПРИ ПЛАСТИЧЕСКОМ ДЕФОРМИРОВАНИИ | 2002 |
|
RU2251101C2 |
| Способ пластической деформации алюминия и его сплавов | 2016 |
|
RU2661980C1 |
| Способ пластической деформации алюминия и его сплавов | 2019 |
|
RU2724209C1 |
| Способ определения температурного коэффициента скорости ультразвука | 1981 |
|
SU968622A1 |
| Способ оценки модуля объемного сжатия материала | 1989 |
|
SU1739279A1 |
| Способ испытания листового металла | 2018 |
|
RU2682127C1 |
| Способ пластической деформации сплавов из алюминия | 2016 |
|
RU2653741C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПОВРЕЖДЕННОСТИ МЕТАЛЛОВ | 2017 |
|
RU2671421C1 |
| СПОСОБ ИЗМЕРЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В ОБОДЬЯХ ЦЕЛЬНОКАТАНЫХ ЖЕЛЕЗНОДОРОЖНЫХ КОЛЕС | 2012 |
|
RU2497108C1 |
Способ может быть использован в машиностроении, гидроэнергетике и других отраслях промышленности, требующих применения в производстве ультразвукового контроля. Для определения температурного коэффициента скорости ультразвука используются данные об изменении акустических характеристик материала. Сущность способа заключается в том, что в недеформированном и деформированном материале при разных температурах возбуждают упругие волны, определяют скорость их распространения и по результатам измерений рассчитывают температурный коэффициент скорости ультразвука. Используя полученную аналитическую зависимость, можно определять температурный коэффициент для промежуточных значений температуры и величины пластической деформации, причем деформацию можно определять акустическим способом, измеряя параметр акустической анизотропии, не зависящий от температуры. Технический результат – повышение точности получаемых данных. 1 з.п. ф-лы, 1 ил.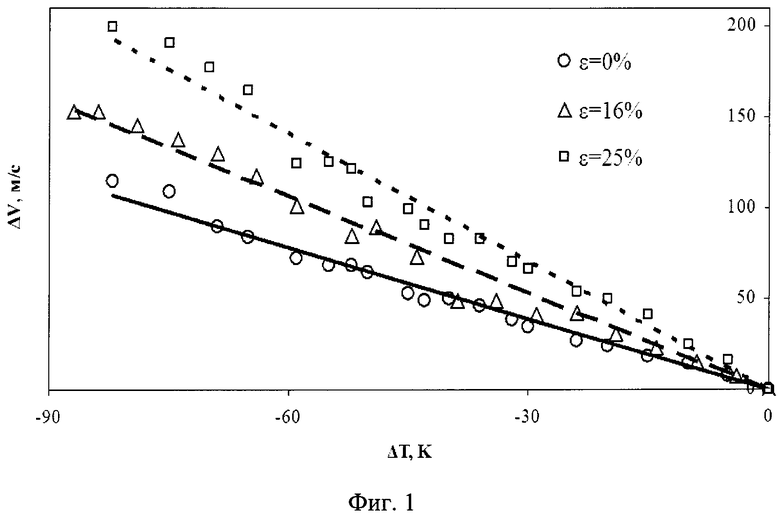
1. Способ определения температурного коэффициента скорости ультразвука, заключающийся в том, что в образце возбуждают бегущую ультразвуковую волну, измеряют ее скорость, нагревают образец до заданной температуры, повторно определяют скорость и по результатам измерений рассчитывают температурный коэффициент скорости ультразвука, отличающийся тем, что температурный коэффициент определяют как минимум для двух значений величины пластической деформации и устанавливают зависимость температурного коэффициента от величины пластической деформации, которую используют в дальнейшем для определения температурного коэффициента при промежуточных значениях величины пластической деформации.
2. Способ определения температурного коэффициента скорости ультразвука в твердых телах по п. 1, отличающийся тем, что величину пластической деформации определяют по времени прохождения поперечных упругих волн различной поляризации.
| СПОСОБ ИЗМЕРЕНИЯ ТЕМПЕРАТУРНОГО КОЭФФИЦИЕНТА СКОРОСТИ РАСПРОСТРАНЕНИЯ АКУСТИЧЕСКИХ КОЛЕБАНИЙВ СРЕДАХ | 0 |
|
SU325511A1 |
| Способ определения температурного коэффициента скорости ультразвука | 1981 |
|
SU968622A1 |
| А.В | |||
| Гончар, В.В | |||
| Мишакин, "ОЦЕНКА ВЕЛИЧИНЫ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ В СТРУКТУРНО-НЕОДНОРОДНЫХ МАТЕРИАЛАХ С ПОМОЩЬЮ УЛЬТРАЗВУКОВЫХ И МЕТАЛЛОГРАФИЧЕСКИХ ИССЛЕДОВАНИЙ", Труды Нижегородского государственного технического университета им | |||
| Р.Е | |||
| Алексеева, номер 3(96), 2012 г., с.221-226 | |||
| Способ определения температурного коэффициента скорости ультразвука | 1989 |
|
SU1742632A1 |
| Способ определения температурного коэффициента скорости ультразвука | 1989 |
|
SU1732177A1 |
| Способ оценки внутренних напряжений в образце | 1988 |
|
SU1682906A1 |
Авторы
Даты
2017-07-28—Публикация
2016-10-31—Подача