ПЕРЕКРЕСТНАЯ ССЫЛКА НА РОДСТВЕННЫЕ ЗАЯВКИ
Данная заявка испрашивает приоритет заявки на патент США № 61/972990, поданной 31 марта 2014 года изобретателями Radompon Sungkorn, Jonas Toelke, Yaoming Mu, Carl Sisk, Avrami Grader и Naum Derzhi и озаглавленной «Определение стандартного элемента объема по статистическим данным кластерного анализа», которая полностью включена в данную заявку посредством ссылки.
ПРЕДПОСЫЛКИ ИЗОБРЕТЕНИЯ
Современные технологии формирования изображений, такие как микроскопия и спектроскопия, часто применяются учеными и инженерами для изучения интересующих их материалов. Такие технологии позволяют получать двухмерное (или более) увеличенное изображение материала (или по меньшей мере его части). Далее к полученному изображению могут быть применены методы анализа для наглядного представления внутренней структуры материала и/или характеристики материала. В зависимости от метода анализа измеряют и количественно оценивают ряд характерных свойств, таких как структура, тип и количество отдельных фаз, морфология фазы и химические свойства фазы.
Вне зависимости от измеряемых характерных свойств признано, что большинство натуральных и искусственных материалов обладают высокой степенью неоднородности, зачастую обусловленной непостоянным размером пустот и зерен. Из-за такой неоднородности часто бывает сложно найти подходящий объем образца, который для осуществления инженерного анализа можно было бы считать стандартным для материала в целом. Как правило, наименьший такой объем (или, в случае двухмерного изображения, наименьшую такую площадь) называют стандартным элементом объема («REV»).
Существует ряд методов определения REV, по меньшей мере один из которых предоставляет приемлемые результаты для относительно однородных материалов. См., например, Costanza-Robinson и др. «Оценка REV в отношении пористости, насыщенности влагой и площади водно-воздушных поверхностей раздела в ненасыщенных пористых средах: Выводы о качестве данных», журнал «Water Resources Research», том 47, W07513, 2011. Однако в случае применения к относительно неоднородным материалам существующие способы могут иметь ряд недостатков, в том числе завышенная оценка, предъявление излишних требований к области исследования, предъявление излишне строгих требований к расположению части образца и общая несостоятельность.
КРАТКОЕ ИЗЛОЖЕНИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Соответственно, в данной заявке раскрываются системы и способы для выполнения определения стандартного элемента объема («REV») по статистическим данным кластерного анализа. В контексте раскрываемых систем и способов понятие REV рассматривается в широком смысле, чтобы количество и тип свойств REV можно было выбирать в зависимости от материала, благодаря чему достигается лучшее представление материала, включающее размер REV, а также количество и местоположение отдельных областей в материале.
Для раскрываемых систем и способов может быть полезным новый способ кластеризации, который также раскрывается в данной заявке с этой и другими целями. Новый способ кластеризации работает на сложных и/или больших наборах данных, позволяя определять количество кластеров и их соответствующие параметры. Итерационный процесс разделения - слияния применяется для разделения кластеров с низкой вероятностью представления набора данных перед слиянием тех кластеров, на необходимость слияния которых указывает критерий, основанный на наборе данных.
КРАТКОЕ ОПИСАНИЕ ГРАФИЧЕСКИХ МАТЕРИАЛОВ
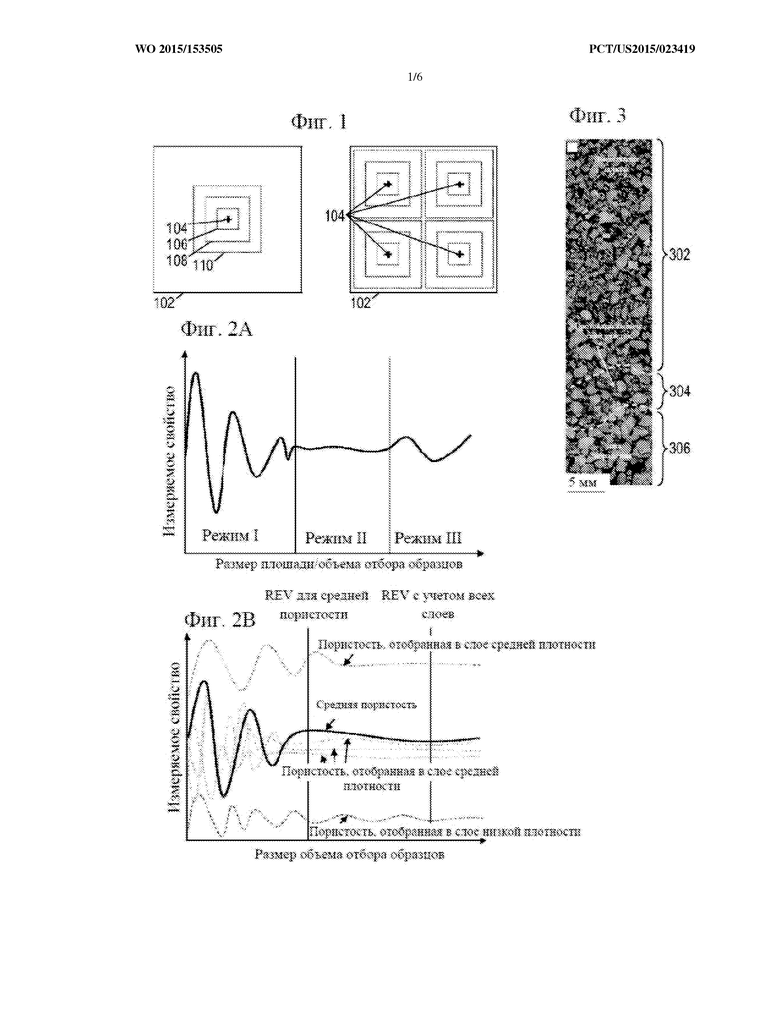
На фиг. 1 показано иллюстративное отношение образца к нескольким частям образца.
На фиг. 2A-2B показана иллюстративная зависимость свойства от размера части образца.
На фиг. 3 представлено изображение иллюстративного неоднородного образца.
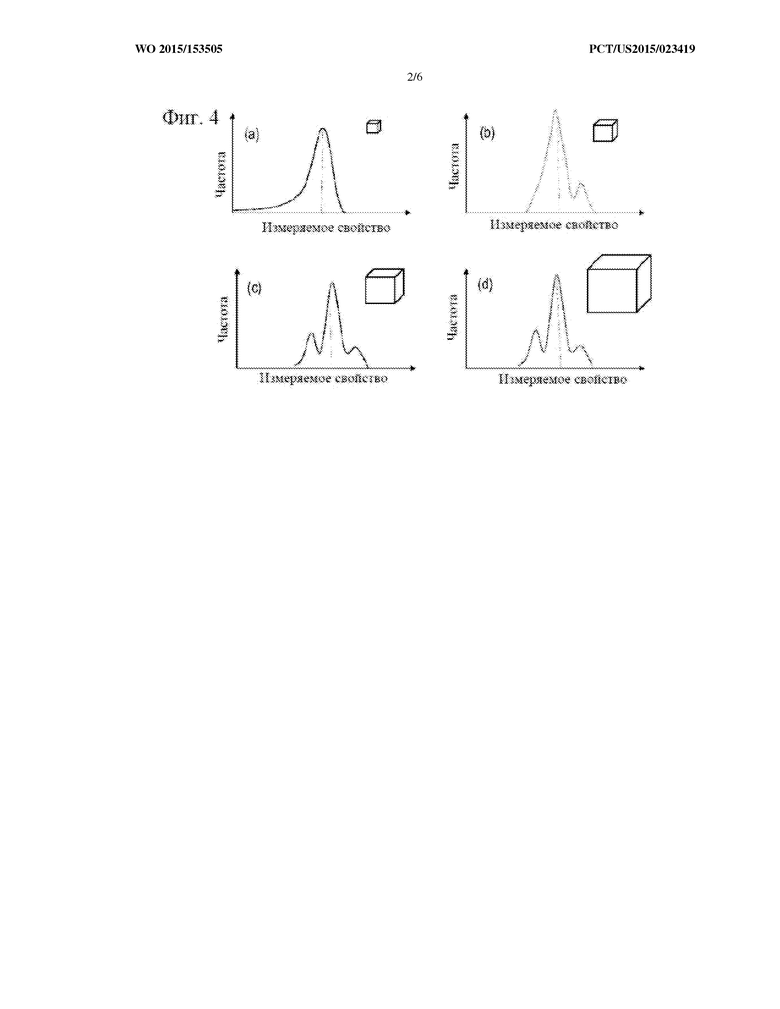
На фиг. 4(a-d) показана иллюстративная зависимость размера части образца от распределения свойств.
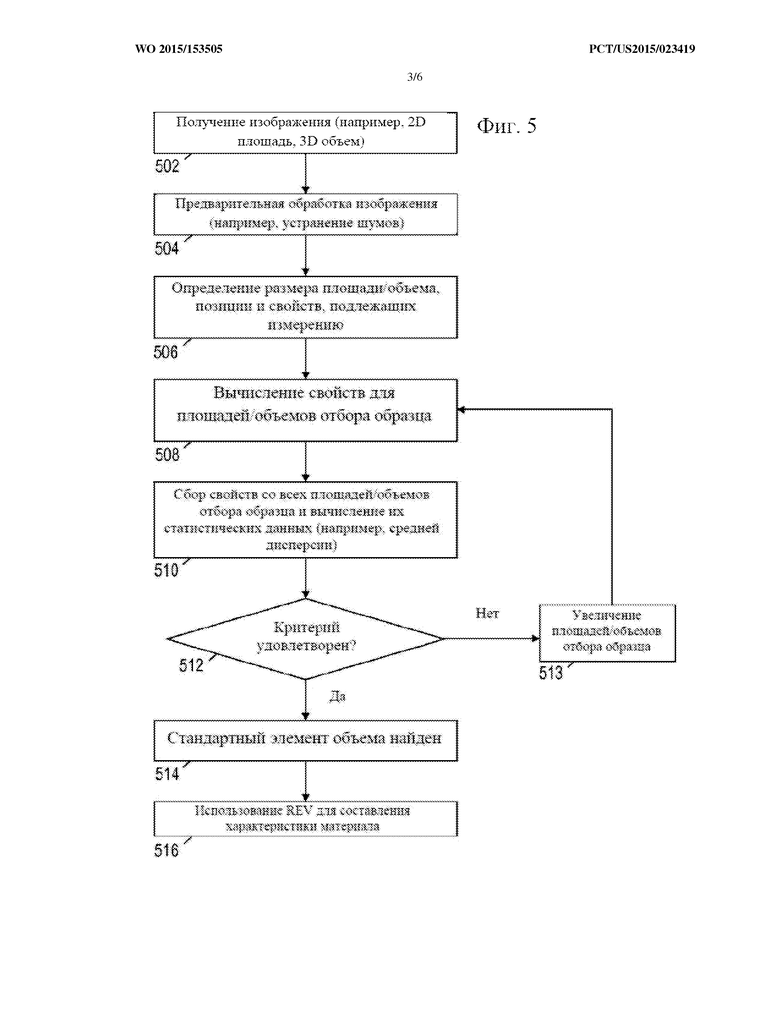
На фиг. 5 представлена блок-схема иллюстративного способа определения REV.
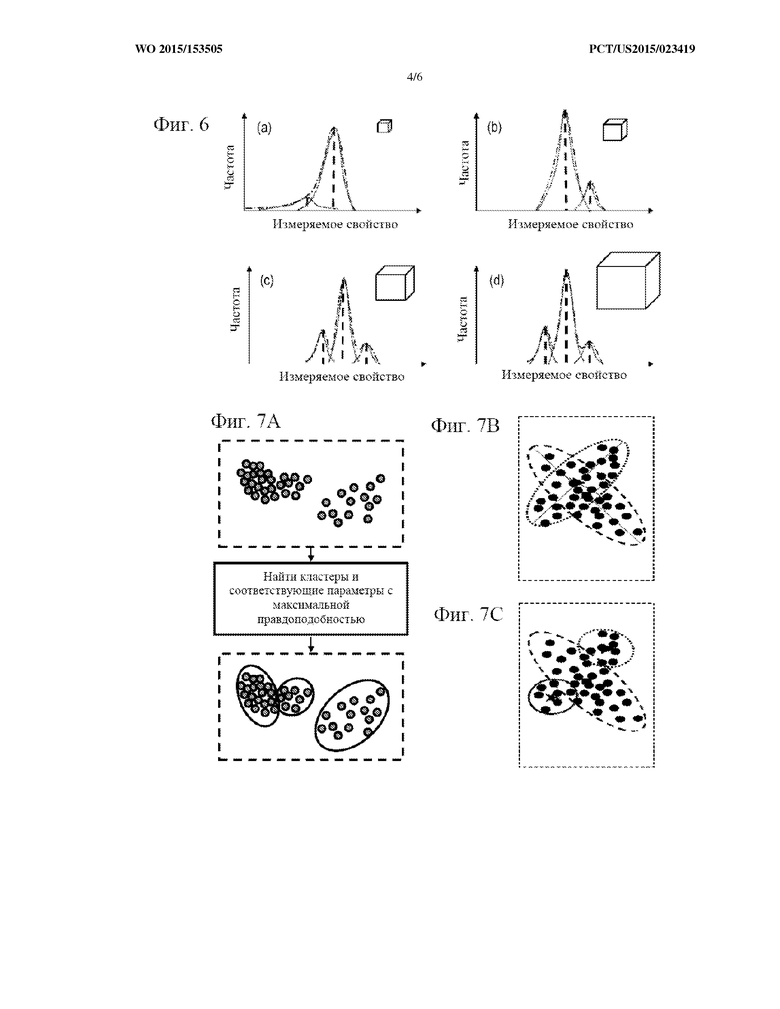
На фиг. 6(a-d) показана смешанная модель распределения для распределений свойств, показанных на фиг. 4.
На фиг. 7A-7C изображен иллюстративный процесс кластеризации.
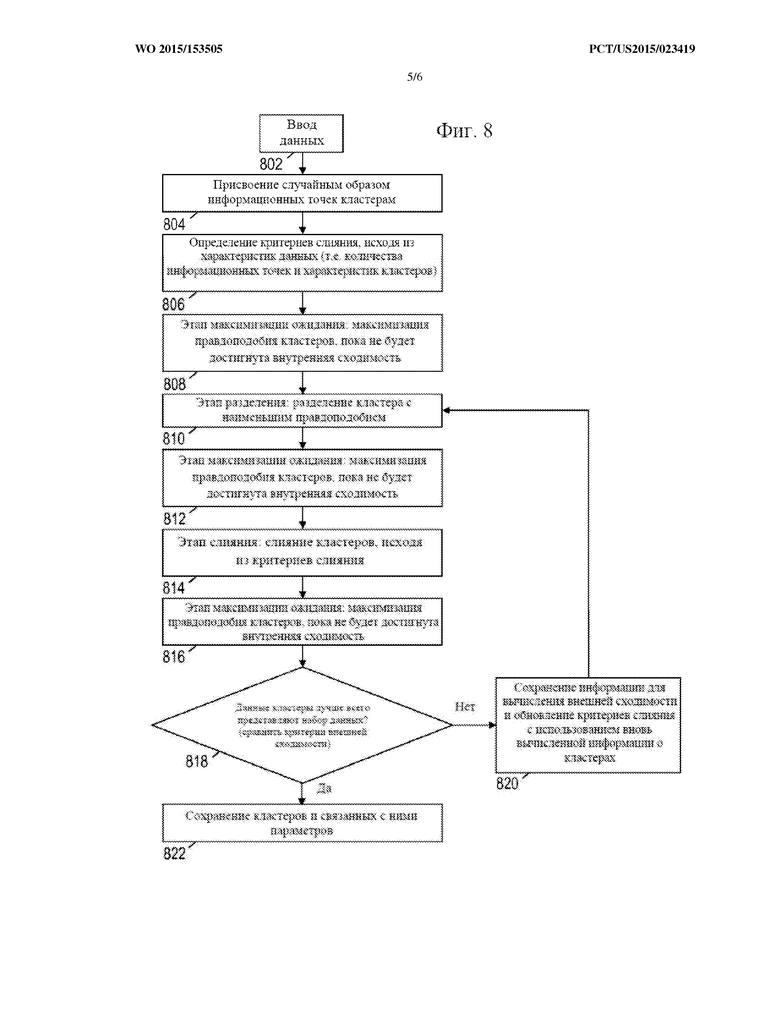
На фиг. 8 представлена блок-схема иллюстративного способа кластеризации.
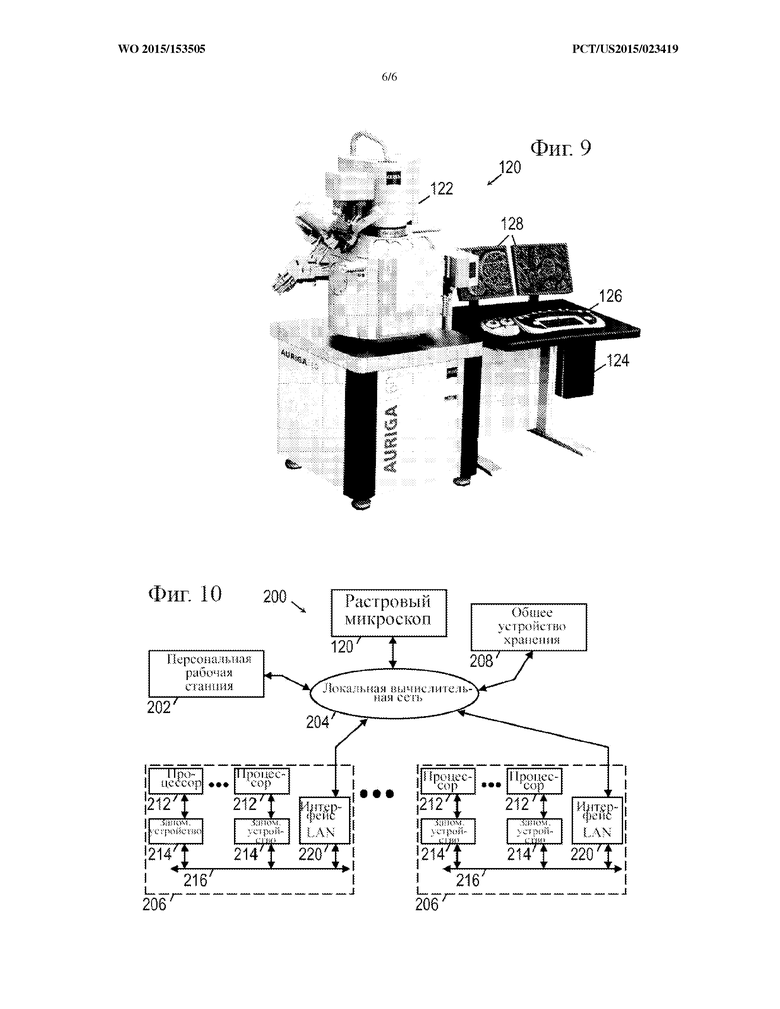
На фиг. 9 представлена иллюстративная система формирования изображений.
На фиг. 10 представлена иллюстративная компьютерная система, которая может быть использована для осуществления раскрываемых способов.
ПОДРОБНОЕ ОПИСАНИЕ
Сначала будет пересмотрен традиционный подход к определению стандартного элемента объема («REV»). Для удобства в графических материалах представлены двухмерные изображения, но описываемые принципы также применимы к трехмерным объемам. На фиг. 1 показано изображение 102 образца (продублированное для лучшей иллюстрации использования потенциально перекрывающихся частей образца), где количество позиций 104 частей образца выбрано случайным или систематическим образом. При поиске REV образца применяется пошаговое увеличение размеров части образца, показанное на фиг. 1 как увеличивающиеся периметры 104, 106, 108 и 110. Для каждой из частей образца измеряют выбранное свойство, измерения объединяют и строят график зависимости от размера части образца (обычно, хотя и необязательно, выраженной в виде длины одного края).
На фиг. 2A показан пример такого графика для относительно однородного материала, где средняя пористость части образца (отношение площади пустот к общей площади) показана на графике в виде зависимости от боковой длины части образца. График можно разделить на три режима I, II, III, исходя из изменчивости зависимости кривой от размера части образца. По мере того как размер части образца постепенно увеличивается, начиная почти с нуля (режим I), кривая демонстрирует сильную, но постепенно затихающую изменчивость, пока не стабилизируется и не войдет в диапазон малой зависимости от размера образца (режим II). Во многих случаях, если размер образца продолжает увеличиваться, из-за неоднородности более крупного масштаба кривая снова начинает демонстрировать изменчивость (режим III). Традиционно, границу между режимами I и II выбирают в качестве размера REV. Различные решения, принимаемые в ходе данного анализа (форма и количество частей образца, выбор позиции части образца, измеряемое свойство части образца, статистические методы, применяемые для объединения измерений частей образца, порог определения стабильности), могут влиять на получаемое в результате значение REV, но данный подход в целом является репрезентативным.
Однако, как показывает пример, изображенный на фиг. 3, многие исследуемые материалы относительно неоднородны. На этом изображении темные участки представляют пористое пространство, а светлые участки представляют зерна. Характеристика пористости показывает, что данный материал содержит три отдельных слоя: слой 302 вмещающей породы, протокатакластический слой 304 и слой 306 зоны поражения, у каждого из которых своя пористость. (У слоя 306 зоны поражения наибольшая пористость, в слое 302 вмещающей породы более мелкая зернистость и сниженная пористость, а промежуточный слой 304 содержит смесь мелких и крупных зерен, что дает наименьшую пористость.) Процедура определения REV, описанная в связи с фиг. 1 и 2, предоставляет плохие результаты, когда ее применяют к неоднородным материалам. Если позиции всех частей образца ограничены одним слоем, оставшаяся часть образца не получает адекватной характеристики, а включение нескольких слоев не передает истинной неоднородности образца.
Для простоты изложения предположим, например, что имеется пять позиций частей образца, причем одна из них в слое 302 вмещающей породы, три в протокатакластическом слое 304 и одна в зоне 306 поражения. Зависимость пористости пяти частей образца от размера части образца показана пунктирными линиями на фиг. 2B. Если рассматривать кривые по отдельности, кривая слоя с малой пористостью дает размер REV, представленный крайней справа вертикальной прямой. Однако средняя кривая (показана сплошной линией) дает размер REV, представленный первой вертикальной прямой. Обратите внимание на большое расхождение между этими двумя результатами.
Соответственно, предлагается заменить критерий стабильности соотношения свойство/размер на критерий распределение свойств/размер. На каждой из фиг. 4(a-d) для частей образца разного размера показана иллюстративная гистограмма или функция распределения вероятности для измерений свойств, полученных для частей образца разного размера. Можно видеть, что при малых размерах части образца распределения свойств изменяются в зависимости от размера, переходя в данном примере от одновершинного распределения к двухвершинному распределению и далее к трехвершинному распределению. Однако при достаточно больших размерах части образца распределение остается стабильным и нечувствительным к размеру части образца. Минимальный размер, при котором происходит эта стабилизация, можно рассматривать как REV.
Критерий стабильности распределения может быть выражен в различных формах. В одном предельном случае распределение можно характеризовать исключительно по его среднему значению, что соответствует средним показателям для частей образца, представленным на графиках фиг. 2A-2B, но этому предельному случаю свойственны описанные ранее недостатки. Даже совместное использование среднего значения и дисперсии распределения вероятно предоставит определение REV на уровне фиг. 4(b), а не на более приемлемом уровне фиг. 4(c). В противоположном предельном случае можно стремиться к совершенному паросочетанию кривых распределения при смежных размерах части образца с использованием определенного порога среднеквадратичной ошибки. Это «совершенное паросочетание» оказывается излишне строгим и дает чрезмерно крупные размеры REV.
Вместо этого, как показано на фиг. 6(a-d), распределение свойств можно рассматривать как сочетание одновершинных распределений (например, гауссовых пиков), где каждое распределение представляет отличный компонент всего образца, и для определения количества, позиции и дисперсии одновершинных распределений применяется метод статистического анализа. Минимальный размер, при котором эти параметры стабилизируются (в пределах заданного порога), является размером предпочтительного REV. В некоторых вариантах осуществления порог, используемый для определения стабилизации параметров, можно повышать или понижать для ускорения или отладки процесса определения REV.
Кроме того, следует обратить внимание, что искомые одновершинные распределения необязательно должны быть ограничены распределениями одной переменной, как показано на фиг. 6. Скорее всего для определения количества, местоположения и дисперсии составляющих пиков могут анализироваться многомерные распределения свойств. Ожидается, что увеличенный объем информации, получаемой благодаря использованию нескольких свойств (например, пористость; структура пор, включая метрику Минковского для геометрии пор; матричный состав пор, включая фазовую долю, морфологию фазы, долю неорганических веществ, проницаемость, фактор формации, капиллярное давление, относительную проницаемость), усовершенствует определение размера REV.
На фиг. 5. показана блок-схема способа. В блоке 502 захватывается изображение образца, а в блоке 504 оно может подвергаться предварительной обработке для получения изображения, которое лучше подходит для последующих этапов анализа, например, за счет устранения шумов и определения каждого пикселя как матрицы, или пустоты, или пористого материала. В блоке 506 система задает позиции и исходные размеры частей образца. Количество частей образца предпочтительно зависит от объема совокупности (т.е. количества пикселей/вокселей), выбранного доверительного уровня, выбранного доверительного интервала и стандартного отклонения. Точки отбора образца могут выбираться случайным или систематическим образом в пределах материала. Альтернативно, если это целесообразно, свойства материала можно перекрывающимся или не перекрывающимся образом вычислять при выбранном размере части образца, избегая проблемы выбора подходящего количества и местоположения точек отбора образцов.
Блоки 508-513 представляют поисковый цикл, который повторяется для ряда частей образца с последовательно возрастающим размером. В блоке 508 измеряются выбранные свойства для текущих частей образца. Выбранные свойства задаются заранее, и их количество может варьироваться. Каждое из этих свойств будет измеряться и анализироваться в совокупности.
В блоке 510 измерения свойств части образца собирают и используют для анализа совокупного распределения свойств для данного размера части образца. Для определения количества, позиции и дисперсии составляющих мод/групп/кластеров может применяться любой из множества доступных методов статистического анализа, в том числе метод максимизации ожидания и его вариации, логистическая регрессия и вариации метода байесовской регрессии. (Наиболее подходящий способ кластеризации подробнее обсуждается далее.) При анализе распределения одного свойства анализ дает среднее значение, дисперсию и долю (относительный вес) каждого кластера. Когда анализируют несколько свойств, анализ предоставляет вектор средних значений, матрицу ковариаций и скалярную долю для каждого кластера.
В блоке 512 результаты анализа сравнивают с результатами, определенными для предыдущего размера части образца, и, если результаты не совпадают в пределах определенного порога, размер части образца увеличивают в блоке 513, и цикл повторяется. Когда достигается совпадение, в блоке 514 размер REV устанавливается по предыдущему размеру части образца, и в блоке 516 этот размер REV используется для дальнейшей характеристики образца.
Как показано на фиг. 7A, при новом способе кластеризации, предусмотренном в данном документе, берется набор точек (например, векторов, представляющих измерения свойств части образца), которые затем группируются в кластеры. Кластеры могут соответствовать сумме параметризованных гауссовых распределений, где параметрам задаются такие значения, которые обеспечивают максимальное правдоподобие представления набора точек. Новому способу присущи определенные признаки известных способов максимизации ожидания (EM), которые описаны, например, в следующих источниках, содержание которых полностью включено в данный документ посредством ссылки:
Chickering D.; Fast clustering with sparse data; патент EP1173816 B1.
Thiesson B. и Wang C.; Variational EM method for mixture modeling with component-dependent partitions; патент US8504491.
Wang и др.; Estimation for the number of components in a mixture model using stepwise split-and-merge EM method; Pattern Recognition Letters, 2004, том. 25, с. 1799 – 1809.
Zhang и др.; EM methods for Gaussian mixtures with split-and-merge operation; Pattern Recognition, 2003; том 36, с. 1973 – 1983.
Ma J. и He Q.; A dynamic merge-or-split learning method on Gaussian mixture for automated model selection; в сборнике под редакцией Gallagher и др. ; IDEAL 2005, LNCS 3578, 2005, с. 203-210.
Blekas K. и Lagaris I.E.; Split-merge incremental learning (SMILE) of mixture models; Artificial Neural Networks – ICANN 2007, Lecture Notes in Computer Science, том 4669, 2007, с. 291 – 300.
Ueda и др.; SMEM method for mixture models; Neural Computation, том 12, 2000, с. 2109 – 2128.
Do C.B. и Batzoglou S.; What is the expectation maximization method?; Nature Biotechnology, 2008, том 26, с. 897 – 899.
Bishop C.M.; Pattern recognition and machine learning: Ch.9 Mixture Models and EM; Springer, 2006.
В отличие от существующих способов, новый способ выгоден тем, что позволяет избежать решений такого вида, как показано на фиг. 7B, когда распределение выражается через перекрывающиеся или пересекающиеся подмножества точек. Вместо этого, как показано на фиг. 7C, приемлемые решения существуют только в виде кластеров с минимальным перекрытием и по меньшей мере минимальным разделением между средними значениями (на основании дисперсии отдельных кластеров). Кроме того, данное требование удовлетворяется без привлечения неоправданно больших вычислительных ресурсов, которые нужны по меньшей мере для некоторых из существующих методов EM.
Кроме набора входных точек, новый способ требует только порогового значения для определения сходимости. Исходя из этих входных данных, способ итерационным образом регулирует количество кластеров и связанных с ними параметров, чтобы добиться максимального правдоподобия, т.е. правдоподобия того, что данные кластеры являются лучшим представлением набора данных. В конце способа достигается смешанная модель, основанная на вычисленных кластерах и связанных с ними параметрах, включающая оптимальное количество четко разделенных кластеров, представляющих набор данных и вычислительные ресурсы.
Как показано на фиг. 8, способ кластеризации начинается с блока 802, в котором получают набор входных точек. В блоке 804 способ генерирует набор случайных параметров кластера (в том числе среднее значение, дисперсию и вес для каждого из множества кластеров, определенных исходя из количества входных точек) и присваивает каждую из точек ее наиболее репрезентативному кластеру.
В блоке 806 способ определяет два критерия слияния исходя из набора данных. Первым критерием слияния является критическая степень слияния. В работе Ma (2005), ссылка на которую включена в данный документ, этот критерий определяется следующим образом:
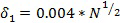 ,
,
где N представляет собой количество информационных точек. Чтобы задать максимальный порог для слияния двух разных кластеров, также могут использоваться другие критические критерии слияния.
Способ по настоящему изобретению дополнительно определяет второй критерий слияния, чтобы добиться минимального расстояния между кластерами. Если центры кластеров меньше порогового расстояния, производится их слияние. С этой целью могут использоваться различные критерии расстояния, в том числе евклидово расстояние, расстояние Махаланобиса и расстояние, основанное на размере бина. Одно особенно подходящее измерение расстояния, основанное на размере бина, основано на модифицированной формуле Стерджесса. Второй критерий слияния является следующим:
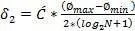 ,
,
где 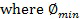 и
и 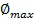 представляют максимальное и минимальное значение наблюдаемой величины соответственно, а
представляют максимальное и минимальное значение наблюдаемой величины соответственно, а 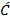 является характеристическим числом кластеров. Характеристическое число кластеров
является характеристическим числом кластеров. Характеристическое число кластеров 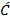 можно оценить, исходя из количества и расстояния между текущими кластерами. Например, если набор данных описан с использованием комбинации гауссовых распределений, и расстояние между средними значениями µ двух кластеров меньше любого из их стандартных отклонений
можно оценить, исходя из количества и расстояния между текущими кластерами. Например, если набор данных описан с использованием комбинации гауссовых распределений, и расстояние между средними значениями µ двух кластеров меньше любого из их стандартных отклонений 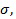 , то один из них не берется в расчет. Напротив, если два кластера четко разделены, т.е. расстояние между их средними значениями больше каждого из их стандартных отклонений, они оба берутся в расчет. Следовательно, второй случай дает больший второй критерий слияния. Критерий слияния можно рассматривать как способ минимизации количества кластеров при сохранении репрезентативности вычисляемых кластеров.
, то один из них не берется в расчет. Напротив, если два кластера четко разделены, т.е. расстояние между их средними значениями больше каждого из их стандартных отклонений, они оба берутся в расчет. Следовательно, второй случай дает больший второй критерий слияния. Критерий слияния можно рассматривать как способ минимизации количества кластеров при сохранении репрезентативности вычисляемых кластеров.
В блоке 808 способ выполняет этап максимизации ожидания (оптимизации), корректируя параметры текущего кластера, чтобы максимально увеличить их правдоподобие. Операцию максимизации ожидания активно обсуждают в литературе, в том числе в упомянутых выше публикациях. Для полноты описания кратко повторно рассмотрим этап максимизации ожидания. Пусть набором данных 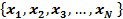 будут случайные информационные точки размера N, взятые из d-мерного набора данных. d-мерная смешанная модель для данного набора данных может быть записана следующим образом:
будут случайные информационные точки размера N, взятые из d-мерного набора данных. d-мерная смешанная модель для данного набора данных может быть записана следующим образом:
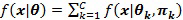 ,
,
где 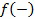 представляет функцию выбранной плотности распределения с C компонентами (т.е. с составляющими кластерами),
представляет функцию выбранной плотности распределения с C компонентами (т.е. с составляющими кластерами), 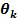 представляет собой вектор соответствующих параметров функции плотности распределения для kго компонента, и
представляет собой вектор соответствующих параметров функции плотности распределения для kго компонента, и 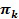 представляет собой комбинированный вес kго компонента. На этапе максимизации ожидания ожидаемая логарифмическая функция правдоподобия смешанной модели вычисляется по:
представляет собой комбинированный вес kго компонента. На этапе максимизации ожидания ожидаемая логарифмическая функция правдоподобия смешанной модели вычисляется по:
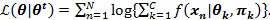 .
.
Затем параметры, которые максимизируют 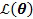 , вычисляются по:
, вычисляются по: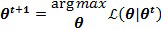 ,
,
где arg max означает аргумент максимума. Процедура повторяется для t = 1, 2, 3,… раз, пока не будет достигнута сходимость, основанная на логарифмическом правдоподобии. Затем способ переходит к следующему этапу.
В блоке 810 способ выполняет операцию разделения (S) на кластере, имеющем наименьшее локальное логарифмическое правдоподобие, чтобы повысить общее правдоподобие смешанной модели. Локальное логарифмическое правдоподобие можно вычислить по:
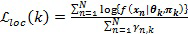 ,
,
где ответственность 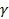 информационной точки n в kом кластере равна:
информационной точки n в kом кластере равна:
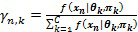 .
.
При разделении кластер с минимальным логарифмическим правдоподобием делится на два кластера, которые смещены относительно локального максимума. Например, в случае, когда данные описаны с использованием смешанной модели на основе гауссовой функции распределения со средним значением 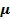 , дисперсией
, дисперсией 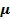 и комбинированным весом
и комбинированным весом 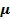 , кластер с индексом
, кластер с индексом 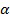 может быть разделен на кластеры
может быть разделен на кластеры 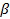 и
и 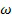 следующим образом:
следующим образом:
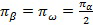 ,
,
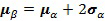 ,
,
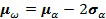 ,
,
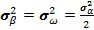 .
.
После этапа разделения в блоке 812 выполняется еще один этап максимизации ожидания, чтобы максимально увеличить общее логарифмическое правдоподобие с включением нового кластера. Затем, с использованием новых параметров, в блоке 814 выполняется операция слияния. В ходе новой операции слияния (M), осуществляемой с помощью способа по настоящему изобретению, степень слияния между каждой парой кластеров i, j вычисляется так:
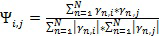 .
.
Степень слияния с минимальным значением сравнивают с критической степенью слияния 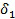 , т.е. с первым критерием слияния. Если минимальная степень слияния меньше
, т.е. с первым критерием слияния. Если минимальная степень слияния меньше 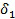 , данная пара кластеров подвергнется слиянию в конце этапа слияния. По меньшей мере в некоторых вариантах осуществления каждая из пар кластеров, у которых степень слияния меньше первого критерия слияния, одновременно подвергается слиянию.
, данная пара кластеров подвергнется слиянию в конце этапа слияния. По меньшей мере в некоторых вариантах осуществления каждая из пар кластеров, у которых степень слияния меньше первого критерия слияния, одновременно подвергается слиянию.
Однако перед выполнением такого слияния оценивается расстояние между каждым данным кластером и остальными кластерами. Например, для одномерных данных с гауссовым распределением расстояние 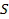 между iм и jм кластерами можно вычислить из абсолютной разности средних значений
между iм и jм кластерами можно вычислить из абсолютной разности средних значений 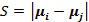 . Пары кластеров подлежат слиянию всякий раз, когда расстояние
. Пары кластеров подлежат слиянию всякий раз, когда расстояние 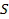 меньше минимального расстояния
меньше минимального расстояния 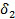 , т.е. второго критерия слияния.
, т.е. второго критерия слияния.
После того как все пары проходят оценивание и одной или более предписывается слияние, соответствующие параметры подвергающихся слиянию кластеров объединяются. В случае, когда данные описаны с использованием смешанной модели на основе гауссовой функции распределения с рассмотренными выше параметрами, параметры нового кластера 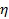 (полученного в результате операции слияния) могут быть вычислены следующим образом:
(полученного в результате операции слияния) могут быть вычислены следующим образом:
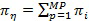 ,
,
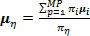 ,
,
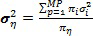 ,
,
где суммирование от 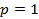 до MP представляет собой суммирование всех пар слияния, которые удовлетворили критериям слияния. В блоке 816 после этапа слияния снова повторяется этап максимизации ожидания, чтобы максимально увеличить общее логарифмическое правдоподобие.
до MP представляет собой суммирование всех пар слияния, которые удовлетворили критериям слияния. В блоке 816 после этапа слияния снова повторяется этап максимизации ожидания, чтобы максимально увеличить общее логарифмическое правдоподобие.
В блоке 818 способ определяет, достигнута ли сходимость, путем сравнения логарифмического правдоподобия до этапа 810 разделения и после этапа слияния (после блока 816). Сходимость выявляется, когда разность логарифмических правдоподобий меньше заранее определенного критерия сходимости, и параметры полученного в результате кластера отображаются и/или сохраняются для дальнейшего использования в блоке 822. Например, когда сходимость достигнута, индексное значение кластера или распределения свойств может быть присвоено каждой из нескольких информационных точек, используемых для представления измерений свойств посредством цифровых 2D- или 3D-изображений. Далее, когда информационные точки соответствуют известным координатам на цифровых 2D- или 3D-изображениях, индексное значение кластера или распределения свойств может быть пространственным образом присвоено частям образца в пределах цифровых 2D- или 3D-изображений. Индексные значения распределения свойств могут использоваться для последующего анализа и характеристики соответствующего образца. Больше информации о возможностях последующего анализа, для которых могут быть полезными индексные значения распределения свойств, можно узнать из документа Radompon Sungkorn и др. «Digital Rock Physics-Based Trend Determination and Usage for Upscaling», номер патентного реестра INGRA-012B, заявка согласно PCT под серийным номером _______, поданная ________, причем указанная заявка полностью включена в данную заявку посредством ссылки. Если определено, что сходимость не достигнута (блок 818 определения), информация о логарифмическом правдоподобии сохраняется для дальнейшего использования и критерии слияния обновляются (блок 820), после чего в способе происходит возврат к блоку 810.
Способы, представленные на фиг. 5 и фиг. 8, можно компьютеризовать, используя данные, полученные из изображений, представляющих образец. Согласно контексту, на фиг. 9-10 показан иллюстративный контекст использования этих способов. На фиг. 1 показан иллюстративный растровый электронный микроскоп 120 с фокусированным ионным пучком высокого разрешения, содержащий камеру 122 наблюдения, в которую помещают образец материала. Компьютер 124 сообщается с инструментальными средствами камеры наблюдения, чтобы управлять процессом измерения. Программное обеспечение на компьютере 124 взаимодействует с пользователем посредством пользовательского интерфейса, включающего одно или более устройства 126 ввода (таких как клавиатура, мышь, джойстик, световое перо, сенсорная панель или сенсорный экран) и одно или более устройства 128 вывода (таких как экран или принтер).
Для формирования изображений с высоким разрешением из камеры 122 наблюдения, как правило, выводят воздух и другие газы. Пучок электронов или ионов может быть проведен по поверхности образца для получения изображения с высоким разрешением. Более того, энергию ионного пучка можно увеличивать, чтобы снимать тонкие слои образца, получая изображения образца на разной глубине. При совмещении эти изображения дают трехмерное изображение образца. В качестве иллюстративного примера этих возможностей некоторые системы позволяют получать такие изображения величиной 40x40x40 кубических микрометров при разрешении 10 нанометров.
Однако описанная выше система является всего лишь одним примером технологий, доступных для формирования изображений образца. Просвечивающие электронные микроскопы (TEM) и трехмерные томографические рентгеновские просвечивающие микроскопы представляют собой две другие технологии, которые могут применяться для получения цифровой модели образца. Независимо от способа получения изображений, описанное выше раскрытие применимо при условии, что разрешение является достаточным для выявления пористой структуры образца.
На источник образца, в случае образца породной формации, не налагается никаких особенных ограничений. Например, в случае образцов породной формации, образцом могут быть керны, отобранные боковым грунтоносом, полноразмерные керны, обломки выбуренной породы, пробы пород из обнажений или другие источники образцов, способные предоставить подходящие образцы для анализа с использованием способов согласно данному раскрытию.
На фиг. 2 представлен пример более крупной системы 200, в которой может применяться растровый микроскоп 120. В более крупной системе 200 персональная рабочая станция 202 сообщается с растровым микроскопом 120 посредством локальной вычислительной сети (LAN) 204. Кроме того, LAN 204 обеспечивает взаимодействие между растровым микроскопом 120, персональной рабочей станцией 202, одной или более платформами 206 высокопроизводительных вычислений и одним или более общими устройствами 208 хранения (такими как RAID, NAS, SAN или тому подобное). Платформа 206 высокопроизводительных вычислений в целом использует несколько процессоров 212, каждый из которых сообщается с локальным запоминающим устройством 214. Внутренняя шина 216 обеспечивает связь высокой пропускной способности между несколькими процессорами (посредством локальных запоминающих устройств) и сетевым интерфейсом 220. Резидентное программное обеспечение параллельной обработки данных в запоминающих устройствах 214 позволяет нескольким процессорам совместно разбивать и выполнять подлежащие выполнению задачи ускоренным образом, обращаясь к общему устройству 208 хранения, когда нужно вывести результаты и/или получить входные данные и промежуточные результаты.
Как правило, пользователь использует персональную рабочую станцию 202 (такую как стационарный компьютер или ноутбук), чтобы взаимодействовать с более крупной системой 200. Программное обеспечение в запоминающем устройстве персональной рабочей станции 202 предписывает одному или более процессорам взаимодействовать с пользователем посредством пользовательского интерфейса, позволяя пользователю, например, создавать и запускать на исполнение программное обеспечение для обработки изображений, полученных растровым микроскопом. Для задач с малой вычислительной нагрузкой программное обеспечение может выполняться на персональной рабочей станции 202, тогда как задачи с большой вычислительной нагрузкой могут предпочтительно решаться на платформе 206 высокопроизводительных вычислений.
При адаптации к использованию в иллюстративных системах способы можно модифицировать, чтобы одна или более операции могли выполняться параллельно, чтобы воспользоваться доступностью ресурсов параллельной обработки. Более того, последовательность этапов может варьироваться, так чтобы некоторые этапы выполнялись потенциально теоретическим образом. Такие вариации находятся в пределах объема формулы изобретения. Раскрываемые способы выгодным образом снижают сложность вычислений до уровня, на котором наборы данных порядка O(108) пикселей могут быть проанализированы своевременно. Описанные выше системы и способы могут применяться во многих отраслях, в том числе в анализе подземных вод и углеводородных пластов, в горной промышленности, в тканевом анализе и структурном анализе материалов. Раскрытые выше способы кластеризации имеют еще более широкое применение, включая статистический анализ данных и анализ информации в малых и больших наборах данных из всех областей деятельности, включая, в частности, генетику и другие медицинские науки.
Изобретение относится к области геологии и может быть использовано для определения стандартного элемента по статистическим данным кластерного анализа. Иллюстративный способ включает получение двухмерных (2D) или трехмерных (3D) цифровых изображений образца породы. Способ также включает итерационный анализ измерений свойств, собранных для всех цифровых изображений, с использованием частей образца разного размера, чтобы определить сходимость распределения свойств в зависимости от размера части образца. Способ также включает выбор наименьшего размера части образца, соответствующего сходимости распределения свойств, в качестве стандартного элемента площади или объема для образца породы. Технический результат – повышение репрезентативности получаемых данных. 2 н. и 20 з.п. ф-лы, 10 ил.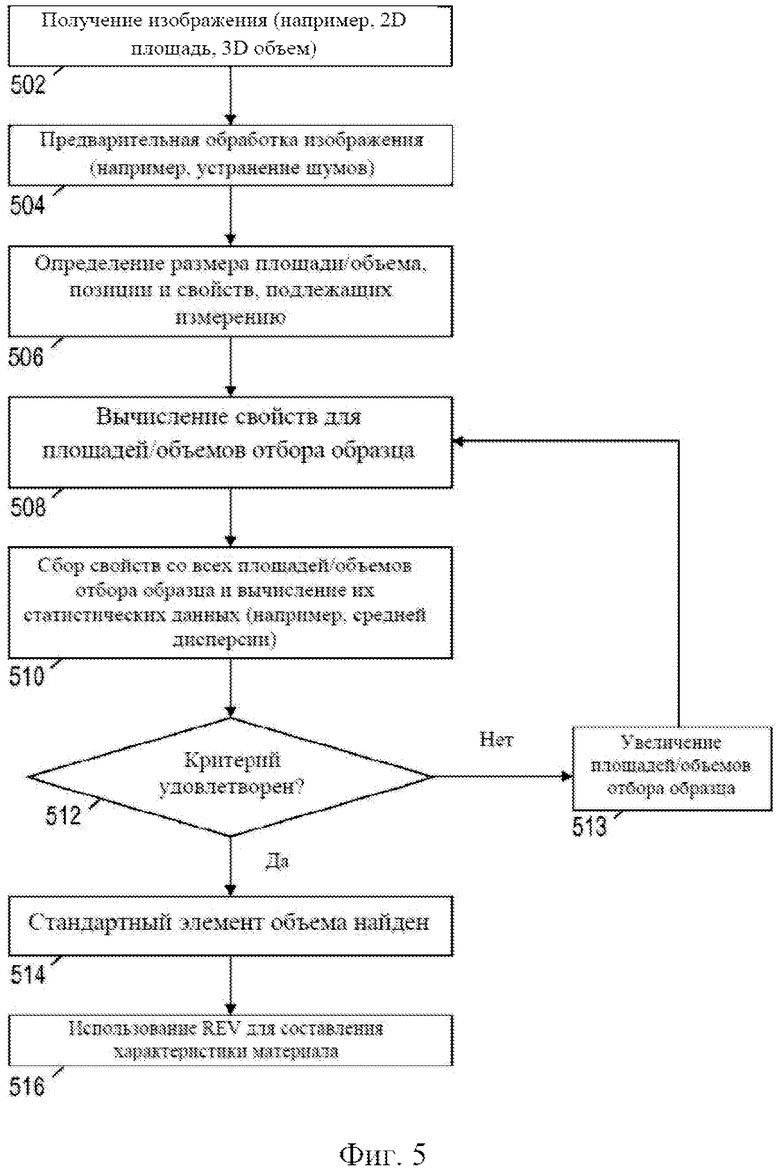
1. Способ определения стандартного элемента площади или объема для образца породы, который включает:
получение двухмерных (2D) или трехмерных (3D) цифровых изображений образца породы;
итерационный анализ измерений свойств, собранных для всех цифровых изображений, с использованием разных размеров частей образца для определения сходимости распределения свойств в зависимости от размера части образца; и
выбор наименьшего размера части образца, соответствующего сходимости распределения свойств, в качестве стандартного элемента площади или объема для образца породы.
2. Способ по п. 1, отличающийся тем, что итерационный анализ измерений свойств включает представление измерений свойств в виде набора информационных точек и группировку набора информационных точек в кластеры путем вычисления параметризованной функции, представляющей логарифмическое правдоподобие того, что данные кластеры являются наилучшим представлением набора информационных точек.
3. Способ по п. 2, отличающийся тем, что вычисление параметризованной функции включает представление измерений свойств с использованием по меньшей мере одной гауссовой составляющей.
4. Способ по п. 3, отличающийся тем, что вычисление параметризованной функции включает представление одного измерения свойств с использованием по меньшей мере двух гауссовых составляющих.
5. Способ по п. 3, отличающийся тем, что вычисление параметризованной функции включает представление нескольких измерений свойств с использованием по меньшей мере одной гауссовой составляющей для каждого из нескольких измерений свойств.
6. Способ по п. 2, отличающийся тем, что дополнительно включает присвоение индексного значения распределения свойств каждой из информационных точек в ответ на выявленную сходимость распределения свойств.
7. Способ по п. 6, отличающийся тем, что дополнительно включает пространственное присвоение индексного значения распределения свойств частям образца на цифровых 2D- или 3D-изображениях и использование индексных значений распределения для последующего анализа образца породы.
8. Способ по п. 3, отличающийся тем, что дополнительно включает максимизацию параметризованной функции путем разделения или слияния по меньшей мере одной гауссовой составляющей.
9. Способ по п. 3, отличающийся тем, что дополнительно включает сравнение гауссовых составляющих, соответствующих разным размерам частей образца, для определения сходимости распределения свойств в зависимости от размера части образца.
10. Способ по п. 8, отличающийся тем, что дополнительно включает обновление критериев слияния в ответ на определение того, что сходимость распределения свойств в пределах допускаемого порога не достигнута.
11. Способ по п. 8, отличающийся тем, что дополнительно включает применение критериев слияния на основе формулы Стерджесса.
12. Система определения стандартного элемента площади или объема для образца породы, которая содержит:
запоминающее устройство с программным обеспечением; и
один или более процессоров, сопряженных с запоминающим устройством, для выполнения программного обеспечения, при этом программное обеспечение предписывает одному или более процессорам:
получать двухмерные (2D) или трехмерные (3D) цифровые изображения образца породы;
осуществлять итерационный анализ измерений свойств, собранных для всех цифровых изображений, с использованием разных размеров частей образца для определения сходимости распределения свойств в зависимости от размера части образца; и
выбирать наименьший размер части образца, соответствующий сходимости распределения свойств, в качестве стандартного элемента площади или объема для образца породы.
13. Система по п. 12, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам осуществлять итерационный анализ измерений свойств путем представления измерений свойств в виде набора информационных точек и путем группировки набора информационных точек в кластеры, исходя из параметризованной функции, представляющей логарифмическое правдоподобие того, что данные кластеры являются лучшим представлением набора информационных точек.
14. Система по п. 13, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам представлять измерения свойств с использованием по меньшей мере одной гауссовой составляющей.
15. Система по п. 14, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам представлять одно измерение свойств с использованием по меньшей мере двух гауссовых составляющих.
16. Система по п. 14, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам представлять несколько измерений свойств с использованием по меньшей мере одной гауссовой составляющей для каждого из нескольких измерений свойств.
17. Система по п. 13, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам присваивать индексное значение распределения свойств каждой из информационных точек в ответ на выявленную сходимость распределения свойств.
18. Система по п. 13, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам пространственное присвоение индексного значения распределения свойств частям образца на цифровых 2D- или 3D-изображениях и использование индексных значений распределения для последующего анализа образца породы.
19. Система по п. 14, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам сравнивать гауссовы составляющие, соответствующие разным размерам частей образца, для определения сходимости распределения свойств в зависимости от размера части образца.
20. Система по п. 12, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам максимизировать параметризованную функцию путем разделения или слияния по меньшей мере одной гауссовой составляющей.
21. Система по п. 20, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам обновлять критерии слияния в ответ на определение того, что сходимость распределения свойств не достигнута.
22. Система по п. 20, отличающаяся тем, что программное обеспечение дополнительно предписывает одному или более процессорам применять критерии слияния на основе формулы Стерджесса.
| US 20130262028 A1, 03.10.2013 | |||
| WO 2012118867 A2, 07.09.3012 | |||
| US 20090259446 A1, 15.10.2009 | |||
| US 20140044315 A1, 13.02.2014. |
Авторы
Даты
2018-01-25—Публикация
2015-03-30—Подача