ПЕРЕКРЕСТНАЯ ССЫЛКА НА РОДСТВЕННУЮ ЗАЯВКУ
[01] По этой заявке испрашивается преимущество приоритета предварительной заявки №61/990860 на патент США, поданной 9 мая 2014 года, под названием ʺEfficient line search methods for multi-parameter full wavefield inversionʺ, которая полностью включена в эту заявку путем ссылки.
ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
[02] В общем, это раскрытие относится к области геофизической разведки углеводородов, а более конкретно, к обработке сейсмических данных. В частности, раскрытие относится к способу выполнения эффективных линейных поисков при многопараметрической инверсии полного волнового поля (ИПВП) сейсмических данных для получения модели физических свойств геологической среды. Такая модель может быть полезной при разведке или добыче углеводородов.
ПРЕДПОСЫЛКИ СОЗДАНИЯ ИЗОБРЕТЕНИЯ
[03] Инверсия полного волнового поля является нелинейным способом инверсии, которым восстанавливают модель геологической среды путем минимизации несоответствия между моделируемыми и наблюдаемыми сейсмическими волновыми полями. Вследствие высоких вычислительных затрат, связанных с инверсией полного волнового поля, при обычных реализациях используют способы локальной оптимизации для оценивания оптимальных параметров модели. Широко используемым способом локальной оптимизации является градиентный способ первого порядка (например, способ скорейшего спуска или нелинейных сопряженных градиентов), в котором только информацию о градиенте целевой функции используют для определения направления поиска. Хотя градиентный способ первого порядка является относительно эффективным, поскольку для него требуется вычисление только градиента целевой функции, его сходимость обычно является медленной. Сходимость инверсии полного волнового поля можно значительно улучшить при использовании способа второго порядка. Эта улучшенная сходимость достигается, поскольку в способах второго порядка используют информацию как о градиенте, так и кривизне целевой функции для определения оптимального направления поиска в пространстве параметров модели. (Единичный вектор s направления поиска связан с процессом обновления модели в соответствии с mобновленная=m+αs, где α (скалярная величина) является длиной шага).
[04] Основное различие между способами первого и второго порядков заключается в том, что в способах второго порядка градиент предобуславливают при использовании обратного гессиана (например, способа Гаусса-Ньютона/Ньютона) или при использовании обратного или проектируемого гессиана (например, способа подпространства). Гессиан представляет собой матрицу частных производных второго порядка целевой функции по параметрам модели. В общем случае способы второго порядка являются привлекательными не только вследствие их относительно высокой скорости сходимости, но также и вследствие возможности уравновешивания градиентов для различных классов параметров и выполнения значащих обновлений классов параметров с различной чувствительностью данных (например, скорости, анизотропии, затухания и т.д.) в контексте многопараметрической инверсии. В способах второго порядка оптимальное масштабирование классов параметров с использованием гессиана является критическим при многопараметрической инверсии, если такие классы параметров должны быть обращены одновременно. Однако поскольку для этого требуются значительные затраты на вычисление инверсии гессиана, это является главным препятствием широкого использования на практике способов второго порядка. Другой недостаток способов второго порядка заключается в том, что в случае, если целевая функция не является квадратичной или выпуклой (например, когда исходная модель далека от истинной модели), гессиан или его приближение может неточно прогнозировать форму целевой функции. Следовательно, градиенты для различных классов параметров могут не масштабироваться надлежащим образом, что может приводить к субоптимальным направлениям поиска.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[05] В одном варианте осуществления изобретением является способ итеративного обращения сейсмических данных для одновременного получения модели по меньшей мере двух физических свойств геологической среды, при этом способ содержит:
(а) для каждого физического свойства вычисление градиента целевой функции применительно к параметрам физического свойства, при этом целевая функция определяет несоответствие между всеми сейсмическими данными или частью сейсмических данных и соответствующими моделируемыми на основе модели сейсмическими данными;
(b) для каждого физического свойства вычисление направления поиска в пространстве модели на основании градиента;
(с) чередование линейных поисков между направлениями поиска или среди них для по меньшей мере двух физических свойств, чтобы определить оптимальные длины шагов по каждому из направлений поиска; и
(d) использование оптимальных длин шагов для обновления модели.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
[06] Настоящее изобретение и преимущества его станут более понятными при обращении к нижеследующему подробному описанию и сопровождающим чертежам, на которых:
фиг. 1 - иллюстрация оптимального направления поиска в альтернирующем однопроходном линейном поиске согласно варианту осуществления настоящего изобретения;
фиг. 2 - иллюстрация субоптимального направления поиска, которое может проистекать из альтернирующего однопроходного линейного поиска согласно варианту осуществления настоящего изобретения;
фиг. 3 - иллюстрация оптимального направления поиска при использовании альтернирующего двухпроходного линейного поиска согласно варианту осуществления настоящего изобретения;
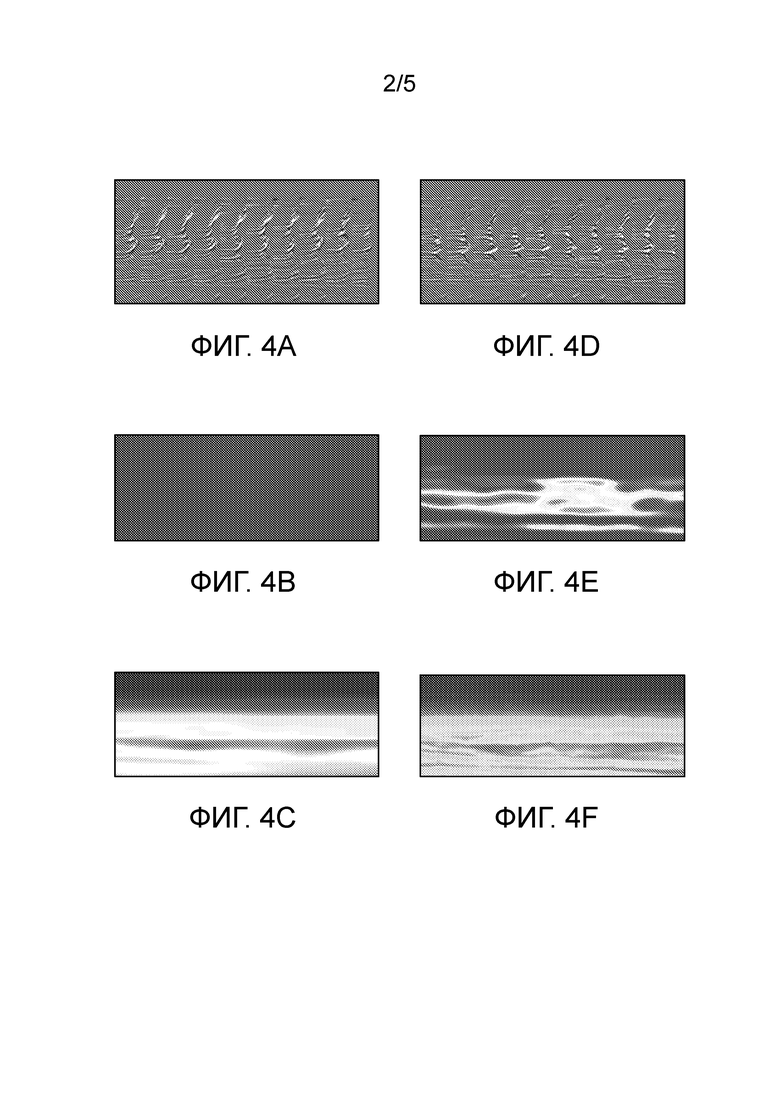
фиг. 4А-4F - иллюстрации тестового примера способа настоящего изобретения, исходной модели и конечной обращенной модели двух параметров (скорости и анизотропии), и приведенных для сравнения данных после миграции при использовании исходной и конечной моделей;
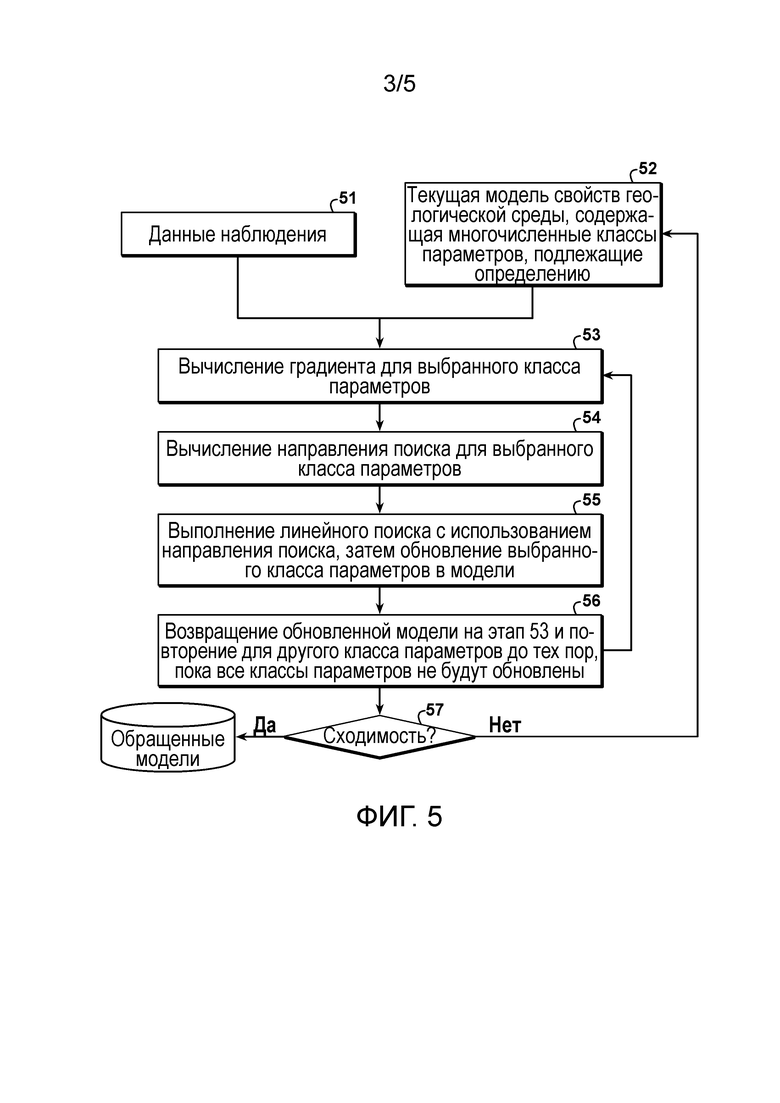
фиг. 5 - блок-схема последовательности действий, показывающая основные этапы альтернирующего однопроходного линейного поиска согласно способу настоящего изобретения;
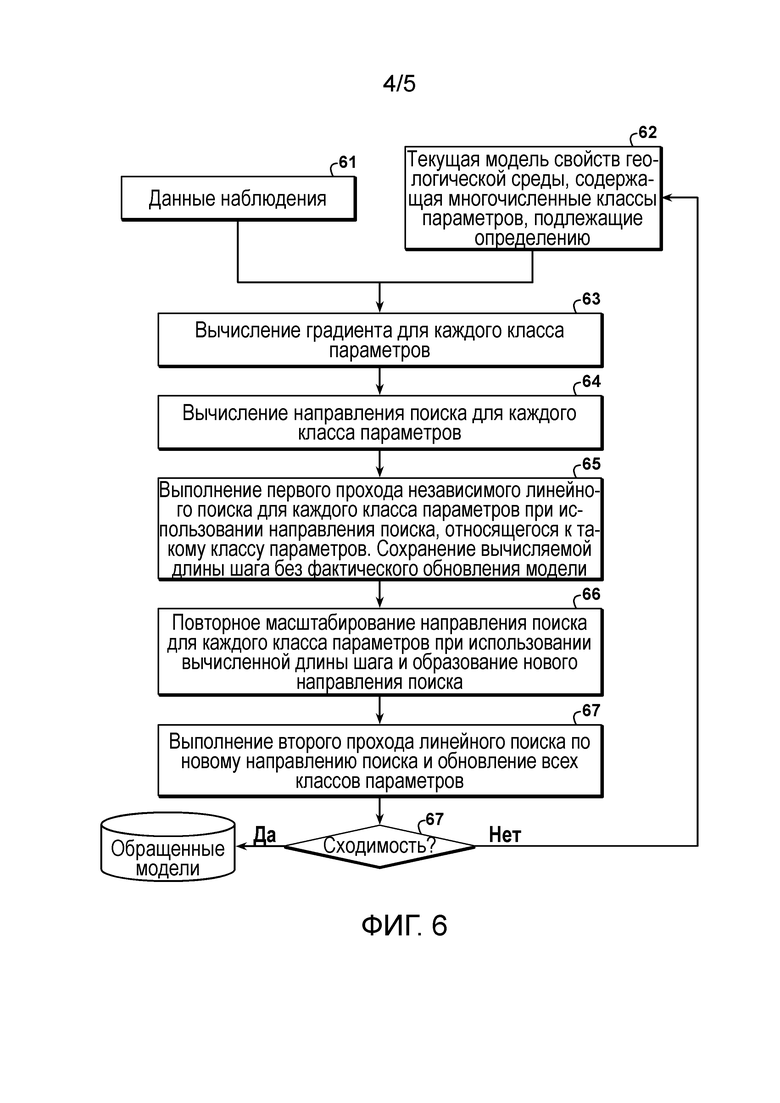
фиг. 6 - блок-схема последовательности действий, показывающая основные этапы альтернирующего двухпроходного линейного поиска согласно способу настоящего изобретения; и
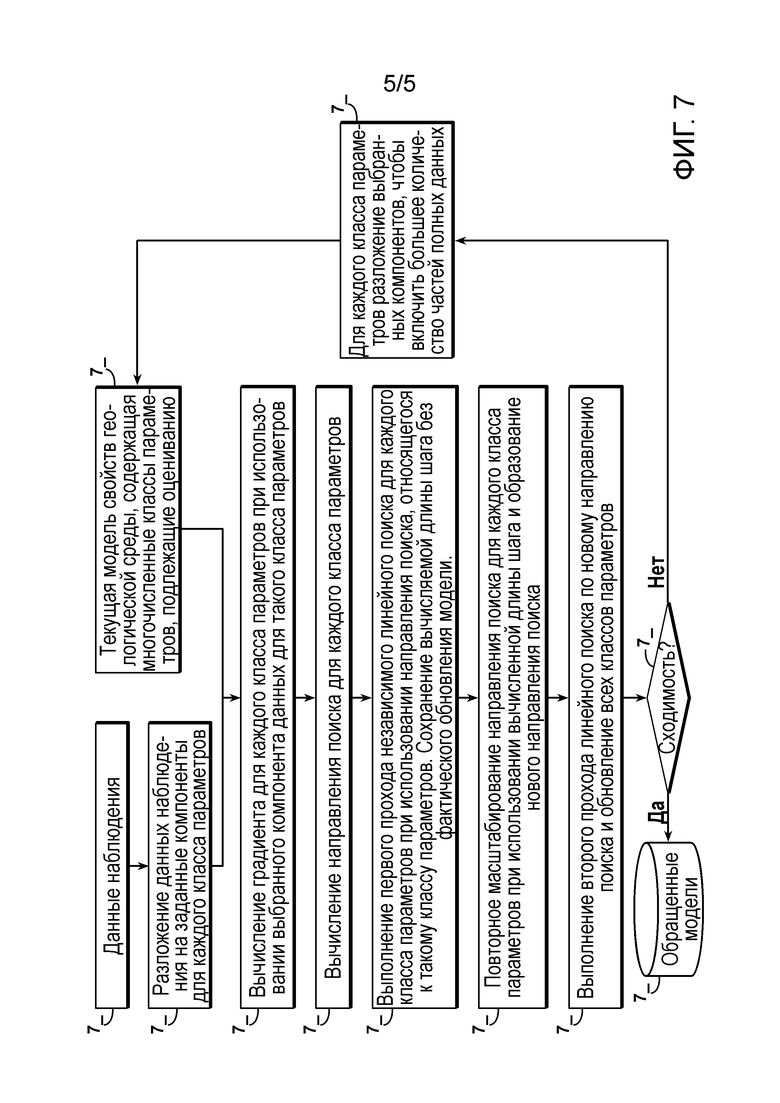
фиг. 7 - блок-схема последовательности действий, показывающая основные этапы расширенного альтернирующего двухпроходного линейного поиска, раскрытого в этой заявке, в котором способ каскадной инверсии объединен с альтернирующим двухпроходным линейным поиском.
[07] Вследствие ограничений, накладываемых правилами выдачи патентов на использование цвета на чертежах, некоторые из фиг. 4А-4F представляют собой черно-белые репродукции чертежей, исходно выполненных в цвете.
[08] Изобретение будет описано применительно к примерам вариантов осуществления. Однако в той части, в которой нижеследующее подробное описание является характерным для конкретного варианта осуществления или конкретного использования изобретения, оно предполагается только иллюстративным и не должно толковаться как ограничивающее объем изобретения. С другой стороны, оно предполагается охватывающим все варианты, модификации и эквиваленты, которые могут быть включены в объем изобретения, определяемый прилагаемой формулой изобретения.
ПОДРОБНОЕ ОПИСАНИЕ ПРИМЕРОВ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ
[09] Настоящим изобретением ликвидируется разрыв между способами оптимизации первого порядка и второго порядка путем использования того, что можно назвать альтернирующим одно/двухпроходным способом линейного поиска, для которого не требуется подробная информация из матрицы Гесса, но которым аппроксимируют информацию второго порядка в продолжение последовательных линейных поисков. Будет показано, что способом настоящего изобретения можно надлежащим образом масштабировать градиенты для классов параметров с различной чувствительностью данных и можно одновременно выполнять важные обновления многочисленных классов параметров. На практике, способ настоящего изобретения может быть более робастным, чем основанный на гессиане способ второго порядка, поскольку не предполагается, что целевая функция является квадратичной, и он также может быть значительно менее затратным, если каждый линейный поиск может быть эффективно реализован.
[10] Хотя для простоты теория описывается с использованием двух классов параметров, изобретение применимо для одновременной инверсии любого количества классов параметров и распространение способов на количество классов параметров больше двух является простым. В случае, когда два класса параметров должны быть обращены, модель можно выразить в виде вектора, содержащего две различные подмодели, то есть 
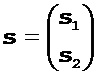
где s1 и s2 представляют собой направления поиска первого и второго класса параметров, соответственно. Способом первого порядка обычно обновляют модель m совместно с направлением s. Одна основная проблема этого способа заключается в том, что, если классы параметров модели являются физическими величинами с очень различными единицами измерений и чувствительностями к целевой функции инверсии полного волнового поля (например, скорости, анизотропии, затухания и т.д.), то результирующее направление поиска, получаемое на основании градиента инверсии полного волнового поля, обычно будет иметь совершенно разные величины, то есть величина s1 может значительно отличаться от величины s2. В инверсии полного волнового поля это часто приводит к выбору траектории сходимости, по которой преимущественно обновляются классы параметров, являющиеся более чувствительными к целевой функции, тогда как сохраняются классы параметров, которые являются менее чувствительными к целевой функции, обновляемыми с трудом. Следовательно, инверсия полного волнового поля может сходиться к субоптимальному решению. Ниже описываются два различных варианта осуществления альтернирующего способа на основе линейного поиска, в котором эта проблема решена совместно с задачей обеспечения оптимальных обновлений одновременно для всех классов параметров без систематической ошибки для определенных классов параметров вследствие различных единиц измерения или чувствительности данных.
Способ I. Альтернирующий однопроходный линейный поиск
[11] Для начала определяют два базисных вектора, каждый из которых содержит направление поиска для конкретного класса параметров модели:
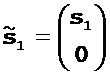

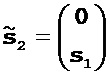
где 0 обозначает вектор, содержащий нули. После этого исходное направление поиска можно записать как сумму приведенных выше двух базисных векторов, которые ортогональны друг к другу (то есть, 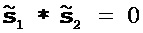
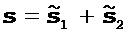
[12] В этом первом способе два класса параметров модели обновляют с чередованием при использовании основных этапов, показанных на фиг. 5. Текущую модель 52 используют для моделирования прогнозируемых данных, которые объединяют с измеряемыми данными 51 для вычисления целевой функции, а затем на этапе 53 вычисляют градиент целевой функции применительно к первому параметру модели, чтобы получить направление 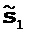
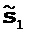
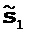
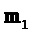
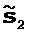
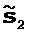
[013] Более подробно, линейный поиск включает в себя модельные сейсмические данные для различных длин шагов по направлению поиска в пространстве параметров весьма многомерной модели. Выбирают длину шага, при которой минимизируется несоответствие между модельными данными и измеряемыми данными. В способе I, описанном выше, после обновления первого физического свойства в модели на следующем этапе эту обновленную модель используют, чтобы выполнить моделирование данных для линейного поиска, чтобы обновить второе физическое свойство. Хотя при этом втором линейном поиске обновляют только второе физическое свойство, обновление первого физического свойства на основании первого линейного поиска будет влиять на модельные данные при втором линейном поиске и поэтому будет влиять на результирующее обновление второго физического свойства.
[14] Для дальнейшего пояснения фиг. 1 решение показано звездой в центре контуров целевых функций, которые представляют собой эллипсы, а не окружности, поскольку параметр m1 модели является более чувствительным, чем m2, к целевой функции. На фиг. 1 показано, что в этой ситуации решение может быть достигнуто за один цикл итерационного процесса при выполнении двух независимых этапов с использованием альтернирующего однопроходного линейного поиска согласно варианту осуществления способа настоящего изобретения. На фиг. 1 также показано, что традиционный линейный поиск s отклоняется от правильного направления, и потребуется дополнительное количество итераций для достижения решения. На фиг. 2 показан случай, когда альтернирующий однопроходный линейный поиск может быть проблематичным, то есть, когда m1 и m2 связаны, как показано контуром целевой функции, который наклонен, и это означает сильную корреляцию между этими двумя классами параметров. В таких случаях при альтернирующем однопроходном линейном поиске могут потребоваться дополнительные итерации для нахождения оптимального направления поиска. На фиг. 3 показано, каким образом эта проблема может быть решена альтернирующим двухпроходным линейным поиском согласно варианту осуществления настоящего изобретения, поясняемым ниже.
Способ II. Альтернирующий двухпроходный линейный поиск
[015] Некоторые из идентифицированных выше недостатков способа I можно ослабить путем модификации способа I. Как показано на фиг. 6, данные 61 наблюдений и текущую модель 62 геологической среды используют при вычислении (этап 63) градиента целевой функции для каждого класса параметров, вычислении (этап 64) направления поиска для каждого класса параметров. На этапе 65 выполняют первый проход независимого линейного поиска для каждого класса параметров, используя направление поиска, вычисленное на этапе 64 для каждого класса параметров. Вычисленные длины шагов сохраняют, но обновление модели еще не выполняют. На этапе 66 один из аспектов этого модифицированного способа аналогичен так называемому способу подпространства (Kennett et al., 1988), в котором вместо обновления всех классов моделей чередованием сначала рекомбинируют два базисных вектора 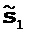
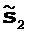
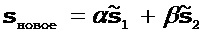
После этого получают новое объединенное направление поиска, выполняют второй проход линейного поиска (используя новое направление поиска), чтобы одновременно обновить оба класса параметров (этап 67). Основное различие между этим способом и хорошо известным способом подпространства (Kennett et al., 1988) заключается в оценивании масштабирующих множителей α и β. В способе подпространства масштабирующий множители определяют, обращая следующую проекционную матрицу Гесса:
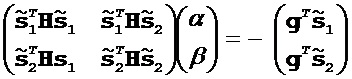
где Н - матрица Гесса. В предпочтительных вариантах осуществления способа II вместо использования гессиана оценивают оптимальные масштабирующие множители в продолжение линейных поисков (этап 65). В этом двухпараметрическом примере способа II из настоящего раскрытия прежде всего выполняют два независимых линейных поиска согласно нижеследующему:
(i) сначала оптимальную длину α шага задают так, чтобы минимизировать целевую функцию по направлению поиска, определяемому 
(ii) затем оптимальную длину β шага задают так, чтобы минимизировать целевую функцию по направлению поиска, определяемому 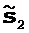
[16] Заметим, что в способе не обновляют параметры модели, используя оцениваемые длины шагов, и это представляет собой одно из основных различий между этим способом двухпроходного линейного поиска и ранее описанным способом однопроходного линейного поиска. После определения масштабирующих множителей новое направление поиска образуют, используя уравнение (4). Затем выполняют второй проход линейного поиска, используя новое направление sновое поиска, чтобы обновить оба класса параметров, то есть делают попытку найти такую длину λ шага, при которой целевая функция минимизируется по направлению sновое. Этот способ можно назвать способом альтернирующего двухпроходного линейного поиска: при первом проходе линейного поиска определяют относительное масштабирование между различными компонентами поиска и оцениваемое масштабирование используют для эффективного поворота исходного направления поиска, чтобы получить новое направление поиска; затем на втором проходе линейного поиска обновляют параметры модели, используя новое направление поиска. Поскольку масштабирующие множители определяют при независимых линейных поисках, то масштабирование исходного направления поиска (или градиента) после этого можно корректировать, используя оцениваемые масштабирующие множители. Относительные величины каждого компонента объединенного направления поиска определяются главным образом чувствительностью каждого класса параметров по направлению базисного вектора, то есть чувствительностью m1 по направлению s1 и чувствительностью m2 по направлению s2.
Практические соображения и расширения
Определение масштабирования при исчерпывающем поиске
[17] В способе альтернирующего двухпроходного линейного поиска, раскрытом в этой заявке, одна задача заключается в том, что при первом проходе линейного поиска находят надлежащие масштабирующие множители (длины шагов) для каждого класса параметров. Для этого можно выполнить исчерпывающий линейный поиск, чтобы найти точки перегиба при выполнении первого прохода линейного поиска. Например, применительно к инверсии двух классов параметров это означает итерационное сканирование значений целевой функции при возмущении соединенной в цепь модели m по направлению 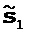
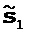
do while
αi←αi+Δα
compute 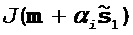
if 
i←i+1
end
где Δα - вводимое пользователем значение приращения, а J - значение целевой функции. Подобным же образом оптимальный масштабирующий множитель β для второго класса параметров может быть найден при возмущении m по направлению 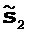
Расширенное, включающее методологию каскадное разложение наборов данных
[18] Кроме того, способ настоящего изобретения может быть расширен путем включения способа каскадной инверсии, описанного в родственной заявке на изобретение ʺA method for estimating multiple subsurface parameters by cascaded inversion of wavefield componentʺ, изобретатели Ayeni и соавторы, которая путем ссылки включена в эту заявку во все разделы, которые допускают это. Это расширение позволяет без труда накладывать условия на оцениваемые градиенты (и следовательно, на направления поиска) при использовании частей данных, наиболее чувствительных к индивидуальным классам параметров. Вариант осуществления расширенного способа настоящего изобретения кратко изложен на блок-схеме последовательности действий из фиг. 7. Расширенный способ, раскрытый в этой заявке, отличается от способа, описанного Ayeni и соавторами, по меньшей мере тем, что в настоящем изобретении все классы параметров обновляются одновременно при каждой итерации, тогда как в инверсии, представленной Ayeni и соавторами, при каждой итерации обновляется только один класс параметров.
Рассмотрение затрат при многочисленных линейных поисках
[19] По сравнению с обычными градиентными способами первого порядка в альтернирующем одно/двухпроходном способе необходимо выполнять намного больше линейных поисков, которые могут быть затратными. Чтобы ослабить эти недостатки, можно использовать только небольшой поднабор (поднаборы) излучений источника, которые предпочтительно случайным образом выбирать из всей съемки для выполнения линейных поисков. Эти случайным образом выбираемые излучения можно использовать при первом проходе и/или втором проходе линейных поисков.
ПРИМЕРЫ
[20] В качестве тестового примера способ альтернирующего двухпроходного линейного поиска, описанный в этой заявке, был применен к анизотропной (вертикально-поперечной изотропной) инверсии образца трехмерных полевых данных. В этом примере одновременно обращали два класса параметров: параметр η анизотропии Томсона и скорость VНПВ с учетом нормального приращения времени. В течение инверсии другой параметр δ анизотропии Томсона полагали равным нулю и он был фиксированным в продолжение инверсии. На фиг. 4A-4F представлены для сравнения модели и мигрированные сейсмограммы, полученные на основании исходных и обращенных моделей. На фиг. 4А и 4D показаны сейсмограммы глубинной миграции Кирхгофа, полученные на основании исходной (4А) и конечной (4D) моделей. На фигурах 4В и 4Е показаны исходная и конечная модели η, соответственно, тогда как на фиг. 4С и 4F показаны исходная и обращенная модели VНПВ. Заметим, что мигрированные сейсмограммы после применения миграции с использованием обращенных моделей VНПВ и η при инверсии полного волнового поля, полученные по способу альтернирующего двухпроходного линейного поиска (мигрированные сейсмограммы, показанные на 4D), являются плоскими относительно сейсмограмм, показанных на фиг. 4А, миграция которых была выполнена с использованием начальных моделей, что показывает точность полученных моделей.
[21] Приведенное выше описание касается конкретных вариантов осуществления настоящего изобретения, предназначенных для иллюстрации его. Однако для специалиста в данной области техники очевидно, что возможны многочисленные модификации и изменения вариантов осуществления, описанных в этой заявке. Все такие модификации и изменения предполагаются находящимися в объеме настоящего изобретения, определяемом прилагаемой формулой изобретения. Как должно быть очевидно для специалистов в данной области техники, все практические применения способа настоящего изобретения осуществляются при использовании компьютера, программируемого в соответствии с раскрытием предмета изобретения, изложенным в этой заявке.
Список литературы
1) Kennett B. L. N., M. S. Sambridge and P.R. Williamson, ʺSubspace methods for large inverse problems with multiple parameter classesʺ, Geophysical Journal, 94, 237-247 (1988).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБЫ ДЛЯ АППРОКСИМАЦИИ ОПЕРАЦИИ УМНОЖЕНИЯ ГЕССИАНА НА ВЕКТОР В ПОЛНОЙ ИНВЕРСИИ ВОЛНОВОГО ПОЛЯ | 2012 |
|
RU2613216C2 |
| СПОСОБЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ГЕОЛОГИЧЕСКОЙ СРЕДЫ ПРИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ И ОБРАТНОЙ МИГРАЦИИ ВО ВРЕМЕННОЙ ОБЛАСТИ | 2011 |
|
RU2545487C2 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ С КОМПЕНСАЦИЕЙ ПОКАЗАТЕЛЯ КАЧЕСТВА | 2016 |
|
RU2693495C1 |
| ИНВЕРСИЯ ОДНОВРЕМЕННЫХ ИСТОЧНИКОВ ДЛЯ ДАННЫХ СЕЙСМОПРИЕМНОЙ КОСЫ С ВЗАИМНОКОРРЕЛЯЦИОННОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ | 2011 |
|
RU2587498C2 |
| ГИБРИДНЫЙ СПОСОБ ДЛЯ ПОЛНОВОЛНОВОЙ ИНВЕРСИИ С ИСПОЛЬЗОВАНИЕМ СПОСОБА ОДНОВРЕМЕННЫХ И ПОСЛЕДОВАТЕЛЬНЫХ ИСТОЧНИКОВ | 2011 |
|
RU2570827C2 |
| ИТЕРАТИВНАЯ ИНВЕРСИЯ ДАННЫХ ОТ ОДНОВРЕМЕННЫХ ГЕОФИЗИЧЕСКИХ ИСТОЧНИКОВ | 2007 |
|
RU2435215C2 |
| КОДИРОВАНИЕ ОДНОВРЕМЕННЫХ ИСТОЧНИКОВ И РАЗДЕЛЕНИЕ ИСТОЧНИКОВ В КАЧЕСТВЕ ПРАКТИЧЕСКОГО РЕШЕНИЯ ПО ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ | 2011 |
|
RU2582480C2 |
| СКОРОСТЬ СХОДИМОСТИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ ПРИ ИСПОЛЬЗОВАНИИ ФОРМИРОВАНИЯ СПЕКТРА | 2012 |
|
RU2577387C2 |
| ОРТОГОНАЛЬНОЕ КОДИРОВАНИЕ ИСТОЧНИКА И ПРИЕМНИКА | 2013 |
|
RU2612896C2 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ ПРИ НАЛИЧИИ ПЛОЩАДНОГО И ТОЧЕЧНОГО ИСТОЧНИКОВ | 2017 |
|
RU2706831C1 |

Изобретение относится к области геофизики и может быть использовано при обработке сейсмических данных. Предложен способ одновременного обращения сейсмических данных полного волнового поля для многочисленных классов параметров физических свойств (например, скорости и анизотропии), включающий в себя вычисление градиента, то есть направления поиска, целевой функции для каждого класса параметров. Далее осуществляют применение первого прохода независимого линейного поиска (предпочтительно, исчерпывающего) к каждому классу параметров, чтобы получить соответствующую длину шага по направлению поиска для каждого класса параметров. Способ также включает использование длин шагов, чтобы задать относительное масштабирование между градиентами всех классов параметров. Далее каждое масштабированное направление поиска рекомбинируют, чтобы образовать новое направление поиска, и второй проход нового линейного поиска выполняют по новому направлению поиска, а все параметры одновременно обновляют в соответствии с полученной длиной шага. В отличие от варианта осуществления предшествующего альтернирующего двухпроходного поиска модель можно обновлять после каждого первого прохода линейного поиска и не выполнять для этого второй проход линейного поиска. Технический результат – повышение точности получаемых данных. 10 з.п. ф-лы, 13 ил.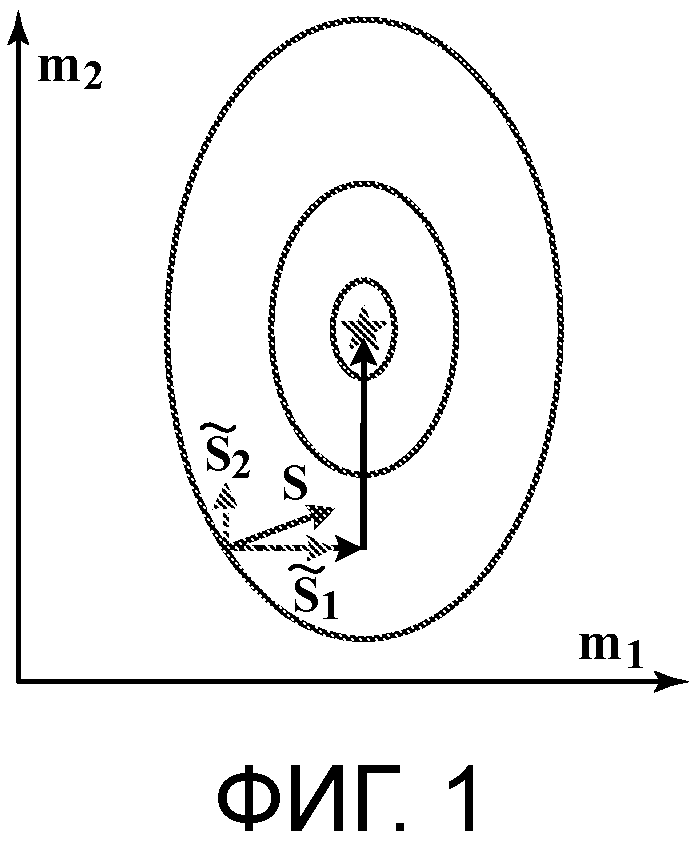
1. Способ итеративного обращения сейсмических данных для одновременного получения модели по меньшей мере двух физических свойств геологической среды, при этом способ содержит этапы, на которых:
(а) для каждого физического свойства вычисляют градиент целевой функции применительно к параметрам физического свойства, при этом целевая функция определяет несоответствие между всеми сейсмическими данными или частью их и соответствующими моделируемыми на основе модели сейсмическими данными;
(b) для каждого физического свойства вычисляют направление поиска в пространстве модели на основании градиента;
(с) выполняют чередование линейных поисков между направлениями поиска или среди них для по меньшей мере двух физических свойств, чтобы определить оптимальные длины шагов по каждому из направлений поиска; и
(d) используют оптимальные длины шагов для обновления модели.
2. Способ по п. 1, в котором этапы (с)-(d) содержат:
(i) выполнение первого линейного поиска для первого физического свойства и использование оптимальной длины шага из первого линейного поиска для обновления модели, образование первой обновленной модели;
(ii) после этого выполнение второго линейного поиска для второго физического свойства, использование первой обновленной модели и затем использование оптимальной длины шага из второго линейного поиска для повторного обновления модели, образование второй обновленной модели; и
(iii) дальнейшее обновление модели, как на (ii), любых дополнительных моделируемых физических свойств, образование конечной обновленной модели при текущей итерации инверсии.
3. Способ по п. 2, в котором первый и второй или любые дополнительные линейные поиски представляют собой исчерпывающие линейные поиски, выполняемые для нахождения точек перегиба целевой функции в зависимости от длины шага.
4. Способ по п. 1, в котором этапы (c)-(d) содержат:
(i) выполнение первого линейного поиска для первого физического свойства, использование исходной модели и сохранение оптимальной длины шага из первого линейного поиска, но еще не обновление модели;
(ii) выполнение второго линейного поиска для второго физического свойства, использование исходной модели и сохранение оптимальной длины шага из второго линейного поиска, но еще не обновление модели;
(iii) выполнение линейного поиска с использованием исходной модели и сохранение оптимальной длины шага, как на (ii), для любых дополнительных моделируемых физических свойств; и
(iv) использование сохраняемых длин шагов из (i)-(iii) для вычисления нового направления поиска, затем выполнение второго прохода линейного поиска по новому направлению поиска, определение оптимальной длины шага при втором проходе и использование его для образования обновленной модели при текущей итерации инверсии.
5. Способ по п. 4, в котором на этапе (а) одну или несколько частей сейсмических данных выбирают и используют, чтобы вычислить градиент для каждого физического свойства, при этом одну или несколько частей определяют в соответствии с выбираемым критерием, основанным на чувствительности физического свойства к данным.
6. Способ по п. 5, также содержащий, при следующей итерации итеративной инверсии, распространение выбранной части или частей сейсмических данных на по меньшей мере одно из по меньшей мере двух физических свойств, чтобы включить большее количество частей сейсмических данных.
7. Способ по п. 4, в котором первый и второй и любые дополнительные линейные поиски в продолжение до (iii) представляют собой исчерпывающие линейные поиски, выполняемые для нахождения точек перегиба целевой функции в зависимости от длины шага.
8. Способ по п. 1, в котором некоторые излучения источника в сейсмических данных отбрасывают и не используют в способе, чтобы уменьшить вычислительные затраты и время.
9. Способ по п. 1, в котором инверсия данных представляет собой инверсию полного волнового поля.
10. Способ по п. 1, в котором по меньшей мере два физических свойства содержат по меньшей мере две из скорости продольной волны, скорости поперечной волны, скорости с учетом нормального приращения времени, одного или нескольких параметров анизотропии и затухания.
11. Способ по п. 1, в котором направление поиска вычисляют без предобусловливания градиента гессианом целевой функции.
| WO 2012134621 A1, 04.10.2012 | |||
| US 20110194379 A1, 11.08.2011 | |||
| CN 103091711 A, 08.05.2013 | |||
| US 20110267923 A1, 03.11.2011 | |||
| US 20110238390 A1, 29.09.2011. |
Авторы
Даты
2018-03-30—Публикация
2015-03-26—Подача