Область техники, к которой относится изобретение
Изобретение относится к вычислительному устройству, сконфигурированному для вычисления функции от одних или нескольких входных данных, причем входные данные имеют входной битовый размер, причем устройство содержит устройство хранения, хранящее одну или несколько таблиц соответствия, используемых при вычислении упомянутой функции, причем таблицы соответствия преобразуют входные значения в выходные значения.
Уровень техники
Безопасность компьютерно-реализованной системы зависит от множества факторов. С одной стороны, есть безопасность базового абстрактного протокола и шифрования. Когда задействованное шифрование нарушено, система также, как правило, будет нарушена. С другой стороны, есть безопасность, относящаяся к самому осуществлению.
Например, давно известно, что компьютерные системы допускают утечку некоторой информации через так называемые сторонние каналы. Наблюдение за поведением ввода-вывода компьютерной системы может не обеспечивать какой-либо полезной информации о критичной информации, такой как секретные ключи, используемые компьютерной системой. Но компьютерная система имеет другие каналы, за которыми можно наблюдать, например, ее расход мощности или электромагнитное излучение; эти каналы называются сторонними каналами. Например, малые вариации в мощности, потребляемой различными инструкциями, и вариации в мощности, потребляемой во время исполнения инструкций, могут быть измерены. Измеренная вариация может соотноситься с критичной информацией, такой как криптографические ключи. Эта дополнительная информация о секретной информации, помимо наблюдаемого и намеренного поведения ввода-вывода, называется сторонними каналами. Через сторонний канал компьютерная система может допускать "утечку" секретной информации в течение его использования. Наблюдение и анализ стороннего канала может давать злоумышленнику доступ к более хорошей информации, чем может быть получена из одного криптоанализа поведения ввода-вывода. Одним известным типом атаки по сторонним каналам является так называемый дифференциальный анализ мощности (DPA).
Существуют другие способы атаки системы. Относящимися к классической атаке по сторонним каналам являются атаки с внесением неисправностей. Здесь в базовых аппаратных средствах намеренно вызывается неисправность. Ввиду неисправности устройство будет производить неправильные ответы. Если конкретный тип ошибок относится к секретной информации, то анализ ошибок может раскрыть секретную информацию. В частности, атаки светом, также известные как атаки вспышками, являются особенно действенным способом внести неисправности. При атаке светом производятся вспышки лазерного света на цепь в течение вычисления для искажения промежуточных значений.
Например, известная атака на алгоритм подписи RSA вносит неустойчивые неисправности в целевую машину путем регулирования источника напряжения системы. Злоумышленники не нуждаются в доступе к внутренним компонентам кристалла-жертвы, они попросту собирают поврежденные выходные данные подписи из системы во время подвергания ее неустойчивым неисправностям. Когда собрано достаточное количество поврежденных сообщений, частный ключ может быть извлечен через офлайн-анализ.
Один способ противостоять атакам с неисправностями состоит в проверке вычислений. Например, путем выполнения критических вычислений дважды. В конкретном случае RSA-подписей, подпись может быть проверена посредством алгоритма проверки RSA. Таким образом, атака с неисправностями обнаруживается, и избегается то, что ошибочные значения покидают вычислительное устройство.
Еще более сильной атакой на компьютер является так называемое обратное проектирование. Во многих сценариях безопасности злоумышленники могут иметь полный доступ к компьютеру. Это дает им возможность разобрать программу и получить любую информацию о компьютере и программе. При достаточном усилии любой ключ, скрытый, например, в программе, может быть найден злоумышленником.
Защита против этого сценария атаки показала себя очень трудной. Одним типом контрмеры является так называемая криптография "белый ящик". При криптографии "белый ящик" ключ и алгоритм комбинируются. Получившийся алгоритм работает только для одного конкретного ключа. Далее алгоритм может осуществляться в виде так называемой сети таблиц соответствия. Вычисления преобразуются в последовательность соответствий в зависимых от ключа таблицах. См., например, работу "White-Box Cryptography and an AES Implementation" ("Криптография "белый ящик" и осуществление AES") авторства S. Chow, P. Eisen, H. Johnson, P.C. van Oorschot для примера этого подхода.
Как осуществления функциональных возможностей в компьютерных аппаратных средствах, так и компьютерные программные средства уязвимы для вышеупомянутых атак по сторонним каналам. Проблема однако является наиболее сильной в программных средствах. По сравнению с осуществлениями в аппаратных средствах, программные средства относительно медленны и потребляют относительно большое количество мощности. Оба фактора способствуют атакам по сторонним каналам.
Были предприняты попытки увеличить сопротивление компьютерных программ против атак по сторонним каналам путем изменения их компиляции.
Патент США 7996671 предлагает увеличение сопротивления компьютерных программ против атак по сторонним каналам путем улучшенной компиляции. Поскольку атаки с анализом мощности полагаются на измеренный расход мощности, сопротивление увеличивается путем компилирования с целью уменьшения расхода мощности. Компилятор прогнозирует компиляцию, которая является наиболее энергосберегающей, и выбирает ее. Наблюдается, что уменьшение потребления энергии увеличивает шум/вариацию мощности и улучшает сопротивление сторонних каналов.
Если одного подхода с уменьшением энергии недостаточно для представления достаточного шума/вариации мощности, то подход компилятора, который используется для оптимизации энергии, может быть использован для внесения элемента случайности в расход мощности в критических частях кодов, таких как криптографические алгоритмы. Это осуществляется во время компиляции путем намеренного генерирования кода с различными требованиями к мощности.
Текущие подходы к проблеме сторонних каналов, которые вносят случайность в вычисление, показали себя менее чем удовлетворительными.
Сущность изобретения
Будут обеспечены преимущества, если решить эти и другие проблемы безопасности. Злоумышленники заметили, что упомянутая контрмера на основе компиляции против атак по сторонним каналам может быть в некоторой степени успешной для противостояния пассивным сторонним каналам, таким как DPA, но не активным атакам, таким как атаки с неисправностями и обратное проектирование.
Обеспечено вычислительное устройство, сконфигурированное для вычисления функции от одних или нескольких входных данных. Устройство сконфигурировано для получения одних или нескольких входных данных в виде одних или нескольких закодированных входных данных. Устройство содержит устройство хранения, хранящее одну или несколько таблиц соответствия, используемых при вычислении упомянутой функции, причем таблицы соответствия преобразуют входные значения в выходные значения, причем входные значения таблицы соответствия имеют битовый размер, равный первому битовому размеру (n1) кодового слова первого кода исправления ошибок, причем таблица соответствия строится в отношении первого кода исправления ошибок, второго кода исправления ошибок, первого порога ошибок и второго порога ошибок так, чтобы любые два входных значения, каждое из которых отличается не более чем на некоторое число бит первого порога ошибок от одного и того же кодового слова первого кода исправления ошибок, преобразовывались в соответствующие выходные значения, каждое из которых отличается не более чем на некоторое число бит второго порога ошибок от одного и того же кодового слова второго кода исправления ошибок. Первый порог ошибок не меньше 1 и не больше способности (t1) к исправлению ошибок у первого кода исправления ошибок, и второй порог ошибок не больше способности (t2) к исправлению ошибок у второго кода исправления ошибок.
Закодированные входные данные могут быть получены путем применения функции кодирования к одним из упомянутых входных данных, причем функция кодирования преобразует входные данные в соответствующее кодовое слово кода исправления ошибок. Необязательно, закодированные входные данные могут быть повреждены до некоторой степени; число вплоть до первого порога битовых ошибок, соответствующих первой таблице соответствия, которая будет применяться к входным значениям, может добавляться к закодированным входным значениям. В общем случае, добавление битовых ошибок может быть выполнено посредством изменения, т.е. инвертирования бит, в этом случае вплоть до числа бит первого порога ошибок. В некоторых приложениях программа будет фактически принимать закодированные входные данные непосредственно. Компилятор может быть сконфигурирован для произведения вспомогательной программы для преобразования незакодированных значений в закодированные значения. Вспомогательная программа может быть использована другими приложениями, которым необходимо обеспечить закодированные входные значения.
Использование закодированных входных значений вместо самих входных значений способствует обфускации программы, т.е. увеличивается сложность обратного проектирования программы. Сохраненные таблицы соответствия имеют свойства исправления ошибок. Эти свойства могут быть задействованы двумя способами. Все закодированные входные значения, которые различаются не более чем на число бит, равное способности к исправлению ошибок (также называемой "t"), от одного и того же кодового слова, обрабатываются одним и тем же образом таблицей соответствия. Таким образом, атака с неисправностями, вызывающая не более "t" битовых ошибок, не вызовет ошибку, относящуюся к безопасности, например ошибку корреляции с ключом. Атаки с неисправностями становятся все более сложными с каждой дополнительной ошибкой, которая должна быть внесена. Путем выполнения вычислений с использованием таблиц исправления ошибок атаки с неисправностями становится труднее выполнить. С другой стороны, таблица соответствия не обязана выдавать один и тот же результат для двух входных данных, которые принадлежат к одному и тому же входному значению, т.е. близки к одному и тому же кодовому слову. Поскольку таблица соответствия устойчива против ошибок, эти ошибки могут также быть добавлены специально. Обратное проектирование сильнее усложняется, когда распределяется фиксированное взаимоотношение между значениями и кодированием. Когда используются таблицы исправления ошибок, одно входное значение может быть представлено множеством закодированных значений. В частности, автоматизированное обратное проектирование, которое зависит от нахождения корреляций между входными значениями, выходными значениями и внутренними переменными, будет требовать данные от существенно большего количества запусков для преодоления этого статистического препятствия. Два способа, которыми таблицы исправления ошибок противостоят атакам с неисправностями и с обратным проектированием, должны исключать друг друга, оба могут быть использованы одновременно.
Интересно то, что код исправления ошибок не обязан быть одним и тем же для каждой таблицы соответствия. Коды исправления ошибок не обязаны даже иметь одни и те же параметры для каждой таблицы соответствия. Использование различных кодов исправления ошибок обеспечивает преимущества для обфускации, но также сильно увеличивает гибкость системы. Обычно функция, осуществляемая таблицами соответствия, использует так называемую сеть таблиц. Благодаря обеспечению возможности множества различных таблиц исправления ошибок эти таблицы не обязаны быть одного размера; это сильно способствует экономии в плане необходимых требований размера, поскольку таблицы, которые могут быть малыми, могут в действительности быть сделаны малыми. В одном варианте осуществления устройства функция осуществляется в качестве сети таблиц, построенных в отношении множества различных первых кодов исправления ошибок и множества различных вторых кодов исправления ошибок. В сети таблиц соответствия используемые коды исправления ошибок должны подойти: если выходные данные из первой таблицы подаются во вторую таблицу, второй код исправления ошибок первой таблицы должен быть первым кодом исправления ошибок для второй таблицы.
Действительно, в одном варианте осуществления одна или несколько таблиц соответствия, используемых при вычислении упомянутой функции, содержат первую и вторую таблицу соответствия, используемые при вычислении упомянутой функции, причем первая таблица соответствия построена в отношении первого первого кода исправления ошибок и первого второго кода исправления ошибок, вторая таблица соответствия построена в отношении второго первого кода исправления ошибок и второго второго кода исправления ошибок, причем первый второй код исправления ошибок равен второму первому коду исправления ошибок.
Однако, это не необходимо: в одном варианте осуществления первый код исправления ошибок таблицы соответствия тот же самый, что и второй код исправления ошибок этой таблицы соответствия. В одном варианте осуществления все первые коды исправления ошибок таблиц соответствия одни и те же и те же самые, что и все вторые коды исправления ошибок таблиц соответствия.
Первый и второй пороги ошибок обеспечивают возможность достижения компромисса между сопротивлением неисправностям и увеличенной обфускацией.
Например, в одном варианте осуществления второй порог ошибок равен нулю. В этом варианте осуществления любые два входных значения, каждое из которых отличается не более чем на некоторое число бит первого порога ошибок от одного и того же кодового слова, преобразуются в одно и то же второе кодовое слово. Этот вариант осуществления оптимально защищает против внесений неисправностей. Неисправности, которые вносятся в промежуточные значения, автоматически исправляются, как только любое вычисление выполняется над ними. Это тип таблицы соответствия также является лучшим, если намеренные неисправности вносятся динамически в программу вместо фиксирования в таблицах. Подобным образом, путем выбора первого порога ошибок, равного способности (t1) к исправлению ошибок у первого кода исправления ошибок, способности к исправлению ошибок увеличиваются. В предпочтительном варианте осуществления, эти два выбора комбинируются.
В одном варианте осуществления вычислительное устройство сконфигурировано для вычисления функции в так называемой сети таблиц соответствия. Путем применения последовательности доступов табличного поиска в таблицах соответствия, сохраненных в устройстве хранения, получается последовательность промежуточных результатов. Промежуточные результаты включают в себя закодированные входные значения и выходные значения доступов табличного поиска в последовательности, причем один из промежуточных результатов является закодированным результатом функции. Обеспечивающие преимущества эффекты таблиц исправления ошибок сильнее, если они применяются к большей части программы. При осуществлении функции в виде сети таблиц эффекты обфускации значительно увеличиваются.
Построение сети таблиц проще, если первая и вторая функции исправления ошибок одни и те же для каждой из таблиц соответствия в сети. В таком случае, выходное значение одной таблицы может быть непосредственно использовано в качестве входного значения другой таблицы. Однако при некоторой осторожности таблицы могут иметь различные коды исправления ошибок. Например, можно обеспечить, чтобы второй код исправления ошибок одной таблицы был равен первому коду исправления ошибок другой таблицы. Кроме того, путем преобразования оператора тождественности получится преобразование таблиц, которое преобразует из одного кодирования в другое.
Для простоты многие из примеров будут использовать один код исправления ошибок и для приема входных данных, и для обеспечения выходных данных, и для всех промежуточных значений. Однако следует заметить, что это не необходимо, и в действительности это может обеспечивать преимущества для обеспечения возможности увеличенной сложности различных первых и вторых кодов исправления ошибок, т.е. для получения дополнительной обфускации и/или получения уменьшения занимаемого места сохраненных таблиц соответствия. Не необходимо даже то, чтобы первый код исправления ошибок и второй код исправления ошибок имели одно и то же минимальное расстояние, как это не необходимо и для различных таблиц. Однако удобно, если все используемые коды исправления ошибок имеют одно и то же минимальное расстояние, поскольку это обеспечивает минимальную защиту против ошибок, в то время как это помогает избежать необходимости делать таблицы больше чем необходимо для удовлетворения этой минимальной защиты.
Вариант осуществления вычислительного устройства сконфигурирован для вычисления функции от одних или нескольких входных данных. Устройство содержит устройство хранения, хранящее одну или несколько таблиц соответствия, используемых при вычислении упомянутой функции, причем таблицы соответствия преобразуют входные значения в выходные значения, причем входные значения и выходные значения имеют битовый размер, равный битовому размеру кодового слова, причем таблицы соответствия строятся в отношении кода исправления ошибок так, чтобы любые два входных значения, каждое из которых отличается не более, чем в "t" битах от одного и того же кодового слова, преобразовывались в соответствующие выходные значения, каждое из которых отличается не более, чем в "t" битах от дополнительного одного и того же кодового слова. Значение "t" также называется "способностью к исправлению ошибок" кода.
Например, вычислительное устройство сконфигурировано для получения одних или нескольких входных данных в виде одних или нескольких закодированных входных данных, причем закодированные входные данные получаются путем применения функции кодирования к одним из упомянутых входных данных, причем функция кодирования преобразует входные данные в соответствующее кодовое слово кода исправления ошибок t, причем кодовые слова имеют битовый размер кодового слова, больший чем битовый размер входных данных. Входные данные до кодирования имеют входной битовый размер, а после кодирования битовый размер кодового слова.
Функция от одних или нескольких входных данных может являться осуществлением приложения безопасности, например функцией подписи или дешифрования. В частности, функциональные возможности, которые обрабатывают критичные для безопасности значения, такие как ключ, авторизация, доступ и т.п., получают преимущества от таблиц исправления ошибок.
Получение закодированных входных данных может быть выполнено посредством самого вычислительного устройства путем применения функции кодирования к одним из упомянутых входных данных, например, посредством модуля кодирования. Это может также быть выполнено вне вычислительного устройства, в этом случае вычислительное устройство непосредственно приняло закодированные входные данные. Следует заметить, что кодирование с кодированием исправления ошибок может хорошо комбинироваться с кодированием обфускации, например так, как в известной криптографии "белый ящик".
Например, если Y обозначает незакодированную область, т.е. простые (входные) значения. И X обозначает пространство кодовых слов. Пусть M - вложение области Y в большую область X, и пусть M-1 - преобразование из области X в Y, где малая ошибка e в значении M(v) из X все так же преобразуется обратно в v. Кодирование входного значения y может быть выполнено посредством вычисления M(y). Последнее может быть выполнено путем применения функции кодирования, например линейного матричного умножения, и т.п., но также посредством таблицы соответствия. Пусть g - функция из Y в Y, которая осуществляет обфускацию. Применение g скрывает значение переменных. Это может комбинироваться с кодированием, данным выше, следующим образом: y преобразуется в M(g(y)). Например, g может быть выбрано случайным образом, по меньшей мере g не является тождеством.
Использование осуществления функции на основе таблиц, например, полученной специальным компилятором или выполненной вручную, приведет к большему занимаемому месту. Кроме того, поскольку кодирование увеличивает размер значений, таблицы больше, чем без кодирования исправления ошибок. Для многих приложений преимущества перевешивают это увеличение в объеме. Некоторые интересные коды, которые можно использовать, для первого и/или второго кода исправления ошибок, следующие: [7, 4, 3], [11, 4, 5], [12, 8, 3], [16, 8, 5], [21, 16, 3]. Эти коды комбинируют относительно низкое значение "t", т.е. 1 или 2, с размером незакодированных блоков, который хорошо соотносится с двоичными архитектурами. Однако нет причин ограничивать незакодированный входной битовый размер (k) степенями 2, хотя это удобно. В последнем случае можно использовать такие коды, как [9, 5, 3], [13, 5, 5], [10, 6, 3], [14, 6, 5] и т.д.
Использования кодов, имеющих равное минимальное расстояние, возможно, хотя нечетное минимальное расстояние предпочтительно. Это означает, что такие коды, как [8, 4, 4], [10, 4, 4], также могут быть использованы.
Использование равного минимального расстояния (d) может быть важно для обнаружения неисправностей. При d=2t можно исправить (t-1) ошибок и обнаружить вплоть до t битовых ошибок. Например, может быть добавлена логика ошибок, которая проверяет, присутствует ли t ошибок. Также, при использовании несовершенного кода логика ошибок может обнаруживать неисправимые битовые комбинации. Когда такая проблема обнаруживается, могут быть предприняты надлежащие действия, например отмена процесса, выдача ошибки и т.д.
Хотя линейные коды должны быть предпочтительны, поскольку они существенно упростят проектирование компилятора, линейная структура не приводит к улучшенной таблице соответствия. Это означает, что нелинейные коды также могут быть использованы, такие как [14, 7, 5], [15, 7, 6], [15, 8, 5] и [16, 8, 6].
Однако для сохранения малого размера таблиц предпочтительно сохранять n малым, например 12 или ниже, или даже ниже 11; и сохранять размерность малой, например 8 или меньше, возможно 4.
Один аспект изобретения касается построения таблицы соответствия, из оператора, преобразующего битовые строки входного битового размера в битовые строки входного битового размера. Эти способы предпочтительно являются компьютерно-реализованными способами. Получающаяся в результате таблица соответствия предпочтительно сохраняется на считываемом компьютером носителе.
В одном варианте осуществления способа генерируется поднабор всех исправимых битовых строк битового размера (n1) кодового слова. Оператор применяется к декодированию генерируемой исправимой битовой строки; причем декодирование выполняется согласно первому коду исправления ошибок. Результат закодирован в кодовое слово второго кода исправления ошибок, возможно добавляющего одну или несколько ошибок. Строится таблица соответствия, в которой генерируемая исправимая битовая строка преобразуется в закодированную в кодовое слово, включающее в себя необязательные одну или несколько ошибок. Число бит в незакодированном входном значении оператора не больше размерности первого кода исправления ошибок. Число бит в незакодированном выходном значении оператора равно не больше размерности второго кода исправления ошибок.
Для построения таблиц соответствия исправления ошибок существует по меньшей мере два базовых подхода. В обоих подходах строятся исправимые битовые строки того же самого размера, что и размер кодового слова первого кода исправления ошибок; вычисляется результат оператора, соответствующий исправимым битовым строкам; и кодовое слово из второго кода исправления ошибок находится путем кодирования результата оператора. Последний этап, возможно, включает в себя добавление битовых ошибок, т.е. добавляет исправимую битовую ошибку. Затем строится таблица соответствия, преобразующая исправимые битовые строки в результаты оператора.
Исправимые битовые строки того же самого размера, что и размер кодового слова первого кода исправления ошибок, которые строятся, могут быть найдены по меньшей мере двумя способами:
В первом подходе исправимые битовые строки генерируются непосредственно. Для совершенного кода это может попросту быть генерированием всех возможных битовых строк некоторой заданной длины. В более улучшенном осуществлении это может быть генерированием всех возможных битовых строк некоторой заданной длины, но с отфильтровыванием декодируемых битовых строк. Некоторые специальные коды имеют специальные алгоритмы для генерирования декодируемых битовых строк.
Во втором подходе генерируются незакодированная битовая строка битового размера, равного размерности первого кода исправления ошибок. Это может быть осуществлено путем непосредственного генерирования всех строк некоторой заданной длины. Генерируемые битовые строки затем кодируются для получения кодовых слов первого кода исправления ошибок. Из полученных кодовых слов исправимые битовые строки могут быть получены путем добавления исправимых битовых комбинаций. Добавлением исправимых битовых комбинаций может быть добавление битовых ошибок в числе, не превышающем первый порог ошибок, к кодовому слову, т.е. изменение битов кодового слова в числе, не превышающем первый порог ошибок.
Например, в одном варианте осуществления исправимые битовые строки кодовых слов получаются путем генерирования битовых строк, имеющих тот же самый размер, что и первый битовый размер (n1) кодового слова первого кода исправления ошибок. В одном варианте осуществления генерируются все битовые строки этого размера. Например, в одном варианте осуществления исправимые битовые строки кодового слова получаются путем генерирования битовых строк, имеющих тот же самый размер, что и первый входной битовый размер (k1), кодирования генерируемой битовой строки в кодовое слово первого кода исправления ошибок, генерирования всех исправимых ошибочных комбинаций и применения исправимой ошибочной комбинации к закодированной генерируемой битовой строке. В одном варианте осуществления генерируются все битовые строки и/или исправимая ошибочная комбинация.
Оператором может быть элементарный оператор, такой как арифметический оператор или логический оператор. Однако оператором может быть комплексный оператор, такой как выражение, содержащее множество базовых операторов, или даже алгоритм, принимающий входные значения и производящий выходные значения. В частности, оператор может быть функцией; но обычно функция требует применения множества операторов.
Таблицы соответствия, получаемые способами для построения таблицы соответствия, могут быть использованы в вычислительном устройстве.
Один аспект изобретения касается компилятора для компилирования первой компьютерной программы, написанной на первом компьютерном языке программирования, во вторую компьютерную программу. Компилятор содержит генератор кода для генерирования второй компьютерной программы путем генерирования таблиц и кода на машинном языке, причем генерируемые таблицы и генерируемый код на машинном языке вместе формируют вторую компьютерную программу, причем генерируемый код на машинном языке обращается к таблицам. Компилятор сконфигурирован для определения арифметического или логического выражения в первой компьютерной программе, причем выражение зависит от по меньшей мере одной переменной, и генератор кода сконфигурирован для генерирования одной или нескольких таблиц, представляющих предварительно вычисленные результаты идентифицированного выражения для множества значений переменной и для генерирования кода на машинном языке для осуществления идентифицированного выражения во второй компьютерной программе путем осуществления доступа к генерируемой одной или нескольким таблицам, представляющим предварительно вычисленные результаты. Одна или несколько таблиц могут генерироваться согласно любому из способов построения, описанных здесь.
Компилятор имеет преимущества, поскольку он защищает программиста от сложностей, ассоциированных с использованием таблиц исправления ошибок. В особенности, когда используется множество кодов исправления ошибок, сложности становятся невозможными для работы в ручную.
Один аспект изобретения касается способа для вычисления функции от одних или нескольких входных данных, причем способ содержит сохранение одной или нескольких таблиц соответствия, причем таблицы соответствия преобразуют входные значения в выходные значения, причем входные значения таблицы соответствия имеют битовый размер, равный первому битовому размеру (n1) кодового слова первого кода исправления ошибок, причем таблица соответствия строится в отношении первого кода исправления ошибок, второго кода исправления ошибок, первого порога ошибок и второго порога ошибок так, чтобы любые два входных значения, каждое из которых отличается не более чем на некоторое число бит первого порога ошибок от одного и того же кодового слова первого кода исправления ошибок, преобразовывались в соответствующие выходные значения, каждое из которых отличается не более чем на некоторое число бит второго порога ошибок от одного и того же кодового слова второго кода исправления ошибок, причем первый порог ошибок не меньше 1 и не больше способности (t1) к исправлению ошибок у первого кода исправления ошибок, и второй порог ошибок не больше способности (t2) к исправлению ошибок второго кода исправления ошибок, с использованием одной или нескольких таблиц соответствия при вычислении функции, содержащей применение одной или нескольких таблиц соответствия к закодированным значениям.
Вычислительное устройство является электронным устройством; оно может быть мобильным электронным устройством, таким как мобильный телефон, ресивер цифрового телевидения, компьютер и т.п.
Способ согласно изобретению может осуществляться на компьютере в качестве компьютерно-реализованного способа, или в специализированных аппаратных средствах или в комбинации того и другого.
Исполняемый код для способа согласно изобретению может сохраняться на компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя устройства памяти, оптические устройства хранения, интегрированные цепи, серверы, сетевые программные средства и т.д. Предпочтительно компьютерный программный продукт содержит некратковременные средства программного кода, сохраненные на считываемом компьютером носителе для выполнения способа согласно изобретению, когда упомянутый программный продукт исполняется на компьютере.
В предпочтительном варианте осуществления компьютерная программа содержит средства компьютерного программного кода, выполненные с возможностью выполнения всех этапов способа согласно изобретению, когда компьютерная программа запущена на компьютере. Предпочтительно компьютерная программа осуществляется на считываемом компьютером носителе.
Краткое описание чертежей
Эти и другие аспекты изобретения ясны из и будут освещены со ссылками на варианты осуществления, описанные далее. На чертежах
фиг.1 изображает схему, иллюстрирующую таблицу соответствия исправления ошибок,
фиг.2 изображает структурную схему, иллюстрирующую вычислительное устройство,
фиг.3 изображает структурную схему, иллюстрирующую сеть таблиц соответствия,
фиг.4 изображает блок-схему, иллюстрирующую способ для генерирования таблицы соответствия для оператора,
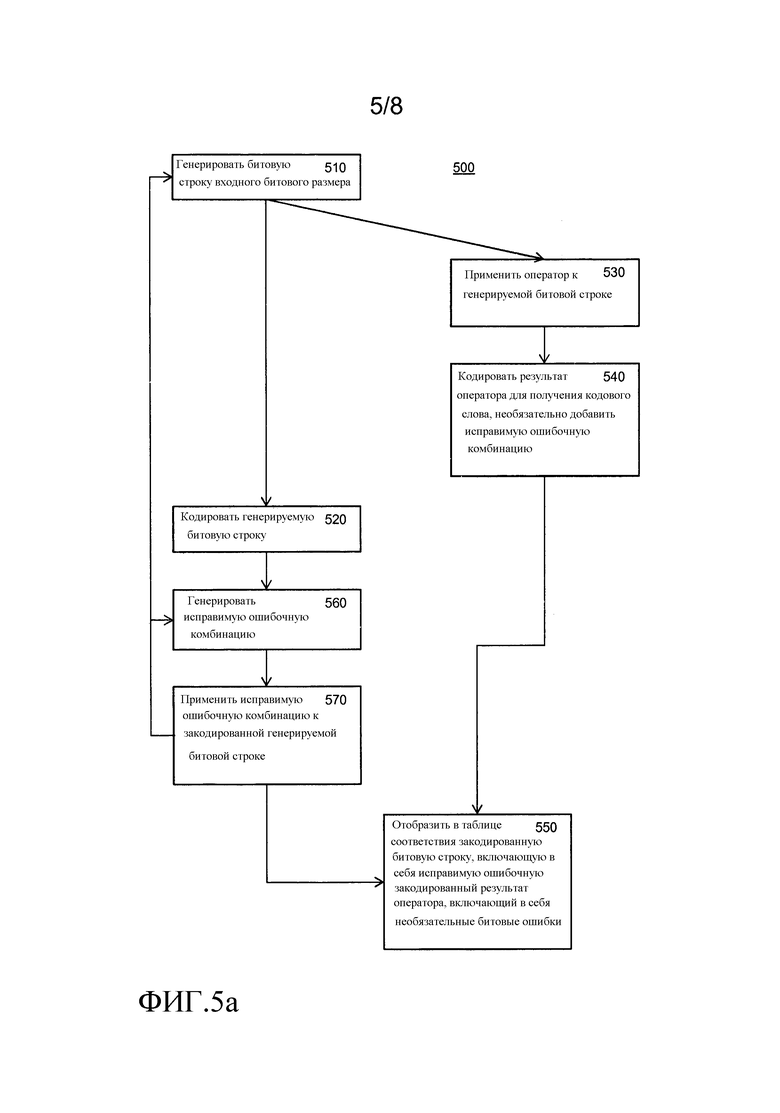
фиг.5 изображает блок-схему, иллюстрирующую способ для генерирования таблицы соответствия для оператора,
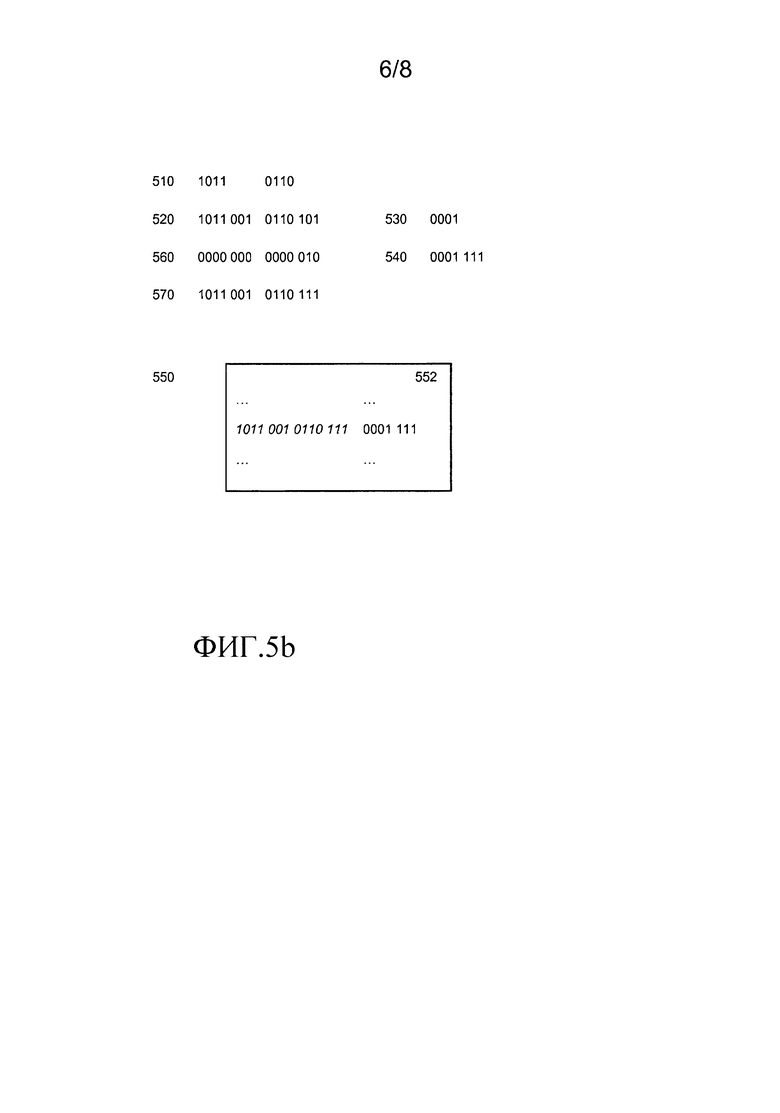
фиг.5b изображает примерные значения, соответствующие фиг.5a,
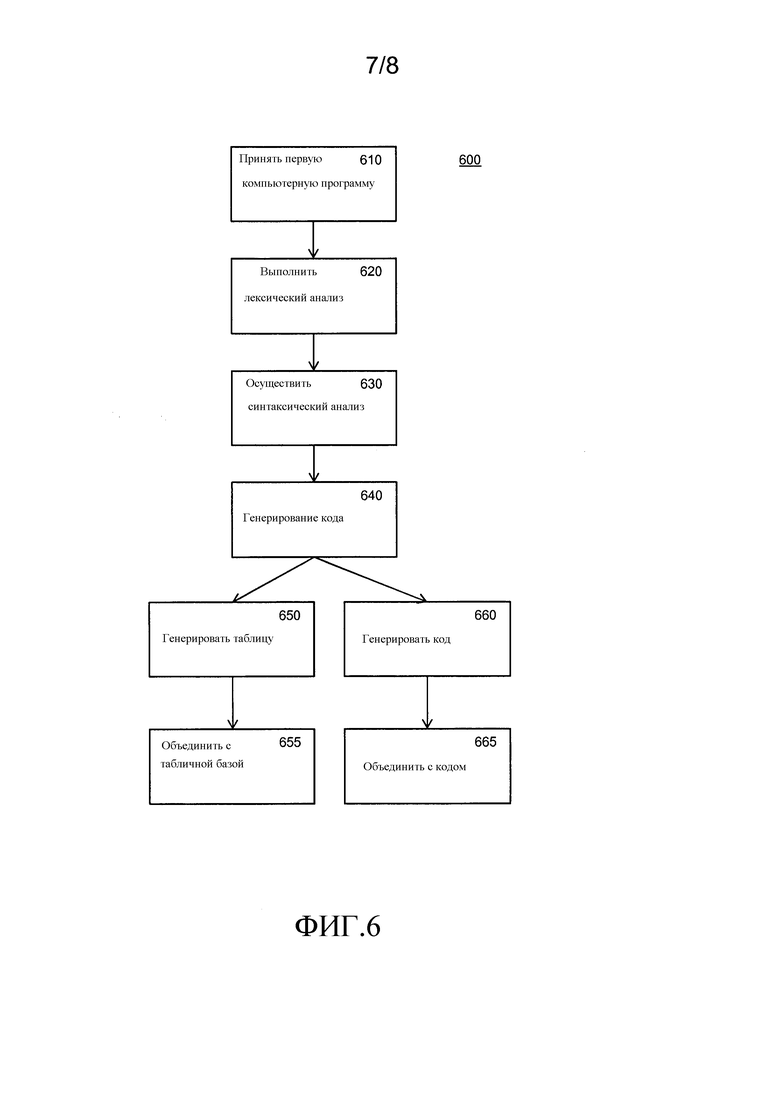
фиг.6 изображает блок-схему, иллюстрирующую компиляцию,
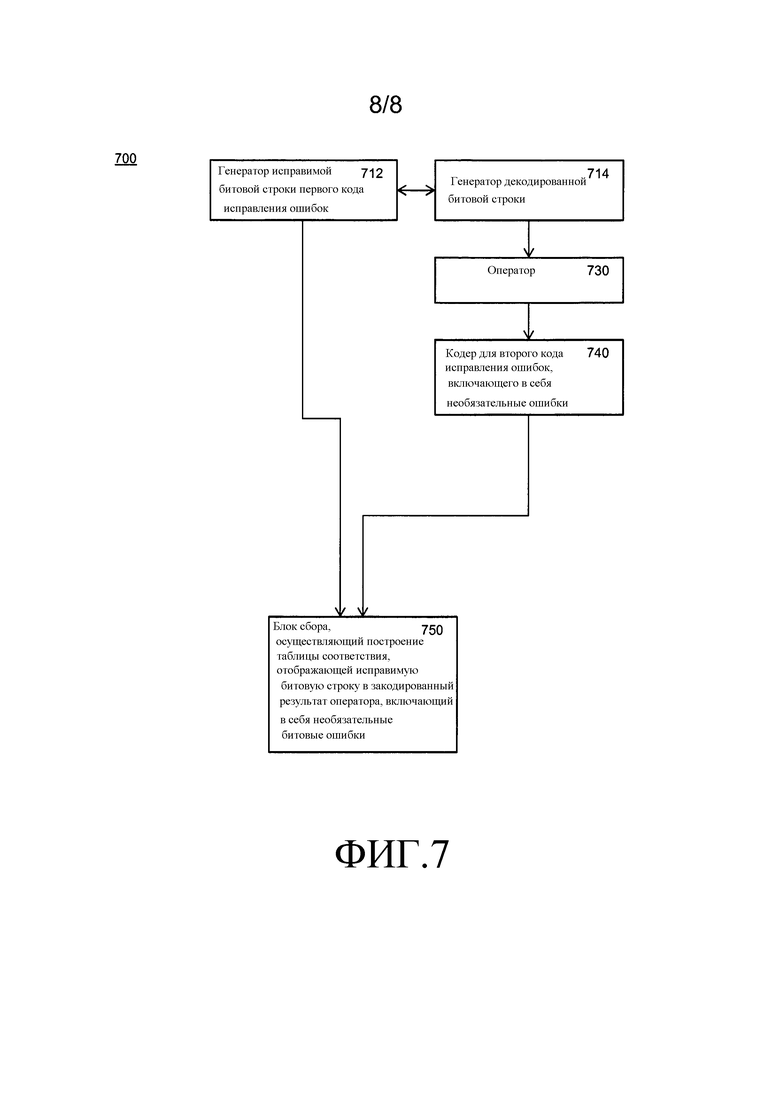
фиг.7 изображает структурную схему, иллюстрирующую устройство для построения таблицы соответствия.
Следует заметить, что элементы, которые имеют одни и те же ссылочные позиции на различных чертежах, имеют одни и те же структурные признаки и одни и те же функции или являются одними и теми же сигналами. Если функция и/или структура такого элемента уже была объяснена, нет необходимости для повторного ее объяснения в подробном описании.
Подробное описание вариантов осуществления
В то время как настоящее изобретение зависимо от варианта осуществления во многих различных формах, показаны на чертежах и будут подробно описаны здесь один или несколько конкретных вариантов осуществления с пониманием, что настоящее раскрытие должно расцениваться в качестве примера принципов изобретения и не предназначено для ограничения изобретения конкретными вариантами осуществления, показанными и описанными.
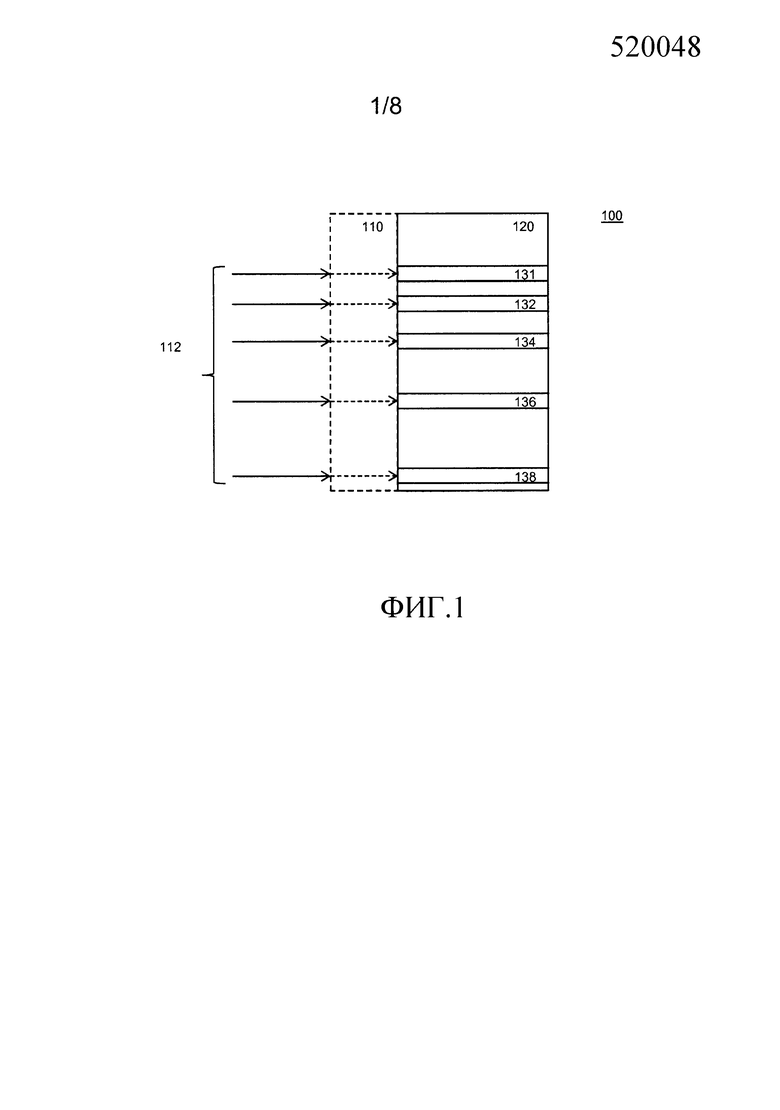
Фиг.1 поясняет таблицы исправления ошибок соответствия. Таблица соответствия преобразует входное значение в выходное значение путем извлечения выходного значения из устройства хранения в местоположении памяти под управлением входного значения.
Таблица 100 соответствия содержит выходные значения 120. Каждое выходное значение соответствует входному значению. Входные значения схематически указаны как 110. Следует заметить, что входные значения не обязательно должны сохраняться. Часто входные значения подразумеваются из контекста. Например, входные значения обычно имеют фиксированное отношение в адресе памяти, в котором выходное значение сохраняется. В общей ситуации в таблице соответствия перечисляются все значения в конкретном диапазоне и перечисляются в сортированном порядке. Это является ситуацией, в которой входные значения не обязательно сохранять в памяти. Если не хранить входные значения, сокращается расход места в хранилище, обычно в два раза. С другой стороны, явное хранение входных значений тоже имеет преимущества. Например, когда входные значения сохраняются, выходные значения могут быть в любом, даже случайном, порядке. Выходное значение можно найти путем поиска соответствия входного значения, что несколько упрощает код. Важно, однако, что путем явного хранения входных значений таблица соответствия может легко опускать значения. Например, если таблица соответствия представляет некоторые функция или оператор, то любое неиспользуемое входное значение может опускаться. Кроме того, как объяснено ниже, это также обеспечивает возможность использования кодирований, которые не используют все возможные битовые комбинации. В этом случае хранение входных значений может даже уменьшать потребности в хранилище.
Таблица 100 соответствия имеет особое свойство в отношении кода исправления ошибок C. Код C содержит 2k кодовых слов из n бит. Любые два кодовых слова в C отличаются не менее, чем на d бит. Параметры кода называются кодом [n,k,d]. Число t=floor((d-1)/2) обозначает число битовых ошибок, которые могут быть исправлены. То есть, если инвертируется не больше, чем t бит в кодовом слове, то существует уникальное кодовое слово, которое является наиближайшим к получающейся в результате битовой строке. Число k называется размерностью кода, число d называется минимальным расстоянием. Использование размерности слова не подразумевает, что линейный код необходим, хотя это предпочтительно. Мы будем использовать размерность слова для указания, что код содержит по меньшей мере 2 в степени размерности кодовых слов.
Число t называется способностью к исправлению ошибок кода. Если необходимо указать, что первый код исправления ошибок может отличаться от второго кода исправления ошибок, добавляется индекс, чтобы, таким образом, делалась ссылка на n1, k1, t1 и на n2, k2, t2. Однако в большинстве случаев мы будем предоставлять примеры, в которых используется один и тот же код, и в таком случае номер может опускаться. Обобщение примеров для двух различных кодов, когда пример для двух равных кодов обеспечен, прямолинейно.
Таблица 100 соответствия имеет свойство, что любые два входных значения, которые отличаются не более чем на t бит от одного и того же кодового слова, имеют соответствующие выходные значения, которые также отличаются не более чем на t бит от (возможно другого) кодового слова. В особом случае все выходные значения являются кодовыми словами. В последнем случае любые два входных значения, которые отличаются не более чем на t бит от одного и того же кодового слова, имеют одни и те же выходные значения, которые являются кодовыми словами.
На фиг.1, входные данные 112 отличаются не более чем на t бит от одного и того же кодового слова. Например, если t=1 и n>=5, пять входных данных 112 могли быть получены из одного кодового слова и инвертирования 5 различных бит; например, если t>1 и n>3, пять входных данных 112 могли быть получены из одного кодового слова и инвертирования 3 бит, и т.д. Число 5 входных данных является примером и может быть больше или меньше. Скажем, 4, или 6, или 8 и т.д. Каждые входные данные множества входных данных 112 соответствует ровно одной выходной величине 131-138.
Изобретатели обнаружили, что концепция таблиц исправления ошибок очень многофункциональная и имеет множество применений. Прежде всего, если вычислительная среда чувствительна к инверсии бит, как может случиться при атаке, такой как атаки светом, таблица исправления ошибок автоматически исправит инверсию бита во входных данных. То же самое относится к менее надежным аппаратным средствам или аппаратным средствам, используемым в неблагоприятных условиях, например при высоких уровнях радиации.
Другое применение состоит в коде обфускации. Поскольку вычисления с использованием таблиц исправления ошибок устойчивы против некоторых ошибок, можно внести ошибки специально, чтобы сделать сложнее обратное проектирование кода. Можно внести ошибки специально посредством средства добавления ошибок, например генератора случайных чисел, управляющего XOR. Однако ошибки могут также быть внесены в самой таблице. В этом применении выходными значениями являются не кодовые слова, а кодовые слова, в которых некоторое число бит инвертировано. Число инвертированных бит должно быть меньше или равно t, грани исправления ошибок.
Для построения таблицы исправления ошибок, принимающей множество входных данных, можно использовать каррирование. можно также выполнять конкатенацию входных данных. Если дан код C, конкатенация C||C также является кодом.
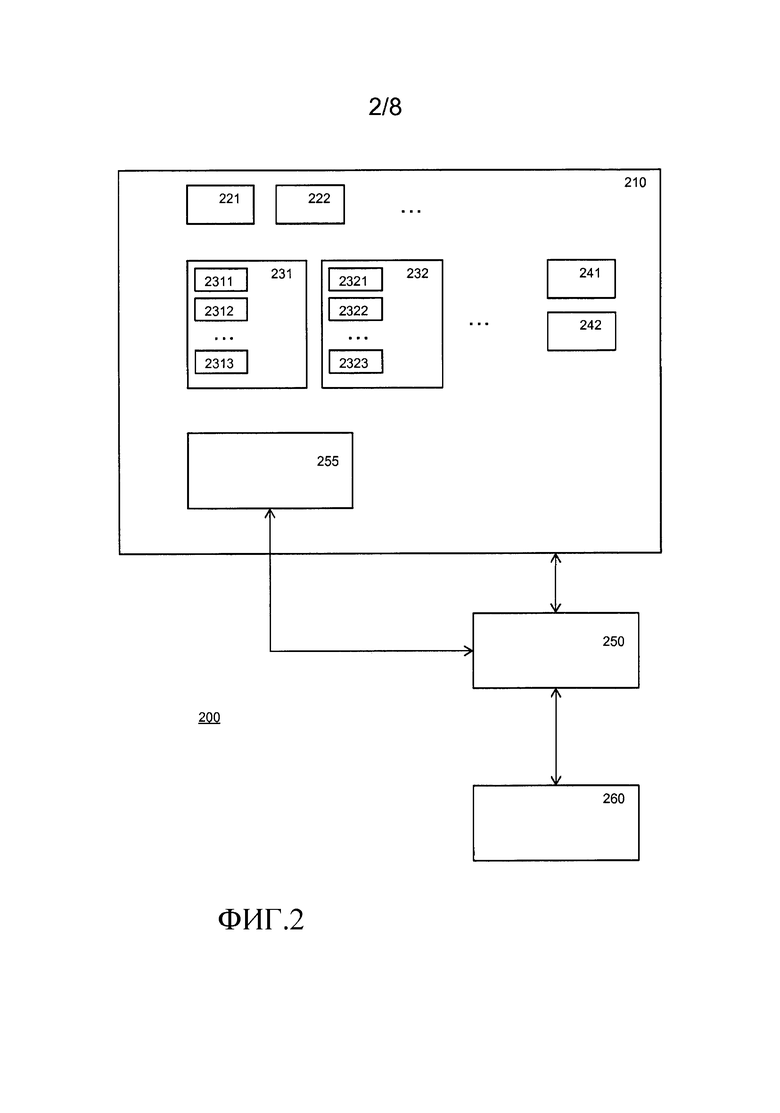
Фиг.2 изображает вычислительное устройство, имеющее устройство 210 хранения. Устройство 210 хранения обычно является одним или нескольким энергонезависимыми средствами памяти, но также может быть жестким диском, оптическим диском и т.д. Устройство 210 хранения может также быть энергозависимым средством памяти, содержащим загруженные или другим образом принятые данные. Вычислительное устройство 200 содержит процессор 250. Процессор обычно исполняет код 255, сохраненный в памяти. Для удобности код может сохраняться в памяти 210. Код побуждает процессор исполнять вычисление. Устройство 200 может содержать необязательное I/O-устройство 260 для приема входных значений и/или передачи результатов. I/O-устройством 260 может быть сетевое соединение, сменное устройство хранения и т.д.
Устройство 210 хранения может содержать таблицу 241 соответствия кодирования, которая принимает слова данных в качестве входного значения и имеет кодовые слова, возможно включающие в себя ошибки, в качестве выходных значений. Например, входные значения имеют "k" биты, в то время как выходные значения имеют "n" бит, что соответствует коду [n,k,d].
Устройство 210 хранения может содержать таблицу 242 декодирования для декодирования кодового слова в его биты данных. Таблица может быть использована для вывода через устройство 260.
Устройство 210 хранения содержит сводные входные таблицы соответствия, как описано выше. Показаны таблицы 221 и 222. Например, эти таблицы могли быть построены для представления одноместных функций, таких как отрицание.
Интересно то, что также возможно иметь таблицы исправления ошибок, имеющие более одних входных данных; причем таблицы соответствия преобразуют множество входных значений в выходные значения, причем входные значения и выходные значения имеют битовый размер, равный битовому размеру (n) кодового слова, причем таблицы соответствия строятся в отношении кода исправления ошибок; два набора из множества входных значений, которые различаются так, чтобы соответствующие входные значения различались не более чем на "t" бит от одного и того же кодового слова, преобразуются в соответствующие выходные значения, каждое из которых отличается не более чем на "t" бит от дополнительного одного и того же кодового слова. Фиг.2 изображает таблицы 231, 232 соответствия для множества входных данных.
Таблица соответствия, имеющая множество входных значений, может быть представлена различными способами. Один имеющий преимущества способ предназначен для использования каррирования: путем фиксирования одного входного значения таблица соответствия для "r" входных значений уменьшается до оператора, имеющего только r-1 входных значений. Такие меньшие таблицы соответствия сохраняются для всех значений фиксированного компонента операции. В качестве альтернативы, входные значения могут подвергаться конкатенации. Последнее удобно, если не все битовые строки допускаются в качестве входных значений. Фиг.2 использует подход каррирования: 2311-2323 являются таблицами соответствия для одних входных данных.
В одном варианте осуществления вычислительное устройство может работать следующим образом в течение операции: вычислительное устройство 200 принимает входные значения. Входные значения кодируются, например посредством таблицы 241 кодирования. Таким образом, входные значения получаются в виде закодированных входных значений. Следует заметить, что входные значения могут быть получены в виде закодированных входных значений непосредственно. Процессор 250 исполняет программу 255 в памяти 210. Программа побуждает процессор применить таблицы соответствия к закодированным входным значениям или к получающимся в результате выходным значениям. Таблицы соответствия могут создаваться для любой логической или арифметической функции, таким образом, любое вычисление может выполняться посредством последовательности таблиц соответствия. При криптографии "белый ящик" это используется для обфускации программы. В этом случае промежуточные значения кодируются для обфускации, как и таблицы соответствия. Следует заметить, что это может комбинироваться, обеспечивая преимущества, со свойством исправления ошибок.
В какой-то момент получающееся в результате значение находится. Если необходимо, результат может быть декодирован, например, с использованием таблицы 242 декодирования. Но результат может также быть экспортирован в закодированной форме. Входные значения могут также быть получены от устройств ввода, и выходные значения могут быть использованы для преобразования на экране.
Вычисление выполняется над закодированными словами данных, т.е. кодовыми словами, возможно включающими в себя вплоть до t ошибок. Вычисление выполняется путем применения последовательности доступов табличного поиска. Используемые входные значения могут быть входными значениями, принятыми извне вычислительного устройства, но могут также быть получены от предыдущего доступа к таблице соответствия. Таким образом, получаются промежуточные результаты, которые могут затем быть использованы для новых доступов к таблице соответствия. В какой-то момент один из промежуточных результатов является закодированным результатом функции.
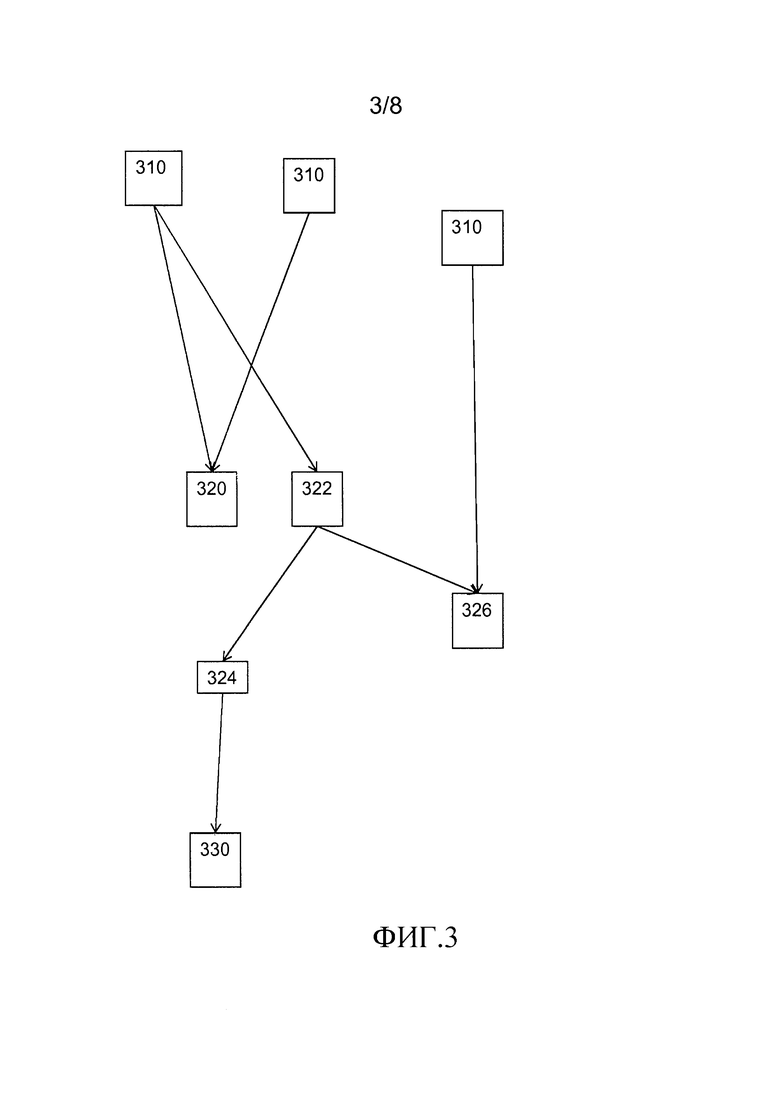
Фиг.3 изображает сеть таблиц. Большинство функций может быть выражено в виде сети таблиц. В частности, любая композиция арифметических и логических операций может быть так выражена. Например, сеть таблиц может быть осуществлением, например, шифрования. Показано 8 таблиц из множества таблиц. Таблица преобразует входное значение в выходное значение посредством поиска соответствия входного значения в таблице. Показано три входных таблицы 310, для приема входных данных извне осуществления функции. Показана одна из выходных таблиц 330. Выходные таблицы 330 вместе формируют выходные данные осуществления функции, например путем конкатенации. Показано четыре таблицы из промежуточных таблиц 320, которые принимают по меньшей мере одни входные данные от другой одной из таблиц, и которые производят выходную величину для использования в качестве входных данных для по меньшей мере одной другой таблицы. Таблицы 310, 320 и 330 вместе формируют сеть. Шифрование может быть блочным шифрованием; блочное шифрование может быть сконфигурировано для шифрования или для дешифрования. Блочное шифрование шифрует блочное шифрование, например AES. Осуществление может быть для конкретного ключа, в случае чего таблицы могут зависеть от конкретного ключа.
В качестве примера, предположим, что таблица 322 представляет оператор, преобразующий k1 бит в k2 бит, тогда таблица 322 соответствия была построена в отношении первого кода исправления ошибок [n1, k1, d1] и второго кода исправления ошибок [n2, k2, d2]. Таблица будет преобразовать n1 бит в n2 бит. Разработчик имеет выбор отобразить все возможные строки из n1 бит, независимо от того, декодируется битовая строка или нет, или отобразить только битовые строки, которые декодируются. С использованием первой опции, таблица имеет размер n2*2∧n1 бит. Таблица 324 соответствия, которая принимает входные значения от таблицы 322, представляет оператор, преобразующий k2 бит в k3 бит. Таблица 322 соответствия строится в отношении первого кода исправления ошибок [n2, k2, d2].
Таблица 326 соответствия представляет оператор, имеющий два ввода (входные данные) и одну выходную величину. Построение таблиц соответствия для одноместных операторов может быть расширено до двуместных операторов. Например, вторые входные данные могут быть отвергнуты каррированием; со ссылкой на методику преобразования функции, каррирование является методикой преобразования функции, которая принимает множество из n аргументов (или набор из n аргументов) таким образом, что он может называться цепью функций, у каждой из которых единственный аргумент. Когда используется этот подход, таблица 326 соответствия осуществляется как множество одноместных таблиц соответствия. С другой стороны можно также генерировать исправимые битовые строки для каждых входных данных и выполнять конкатенацию результатов. Таким образом, таблица соответствия генерируется непосредственно, и получается одна единственная, а не больше, таблица соответствия. Хотя структура таблиц соответствия может отличаться на основе построения, они имеют равный размер и одни и те же свойства. Следует заметить, что не обязательно множество входных значений кодируется согласно одному и тому же коду исправления ошибок.
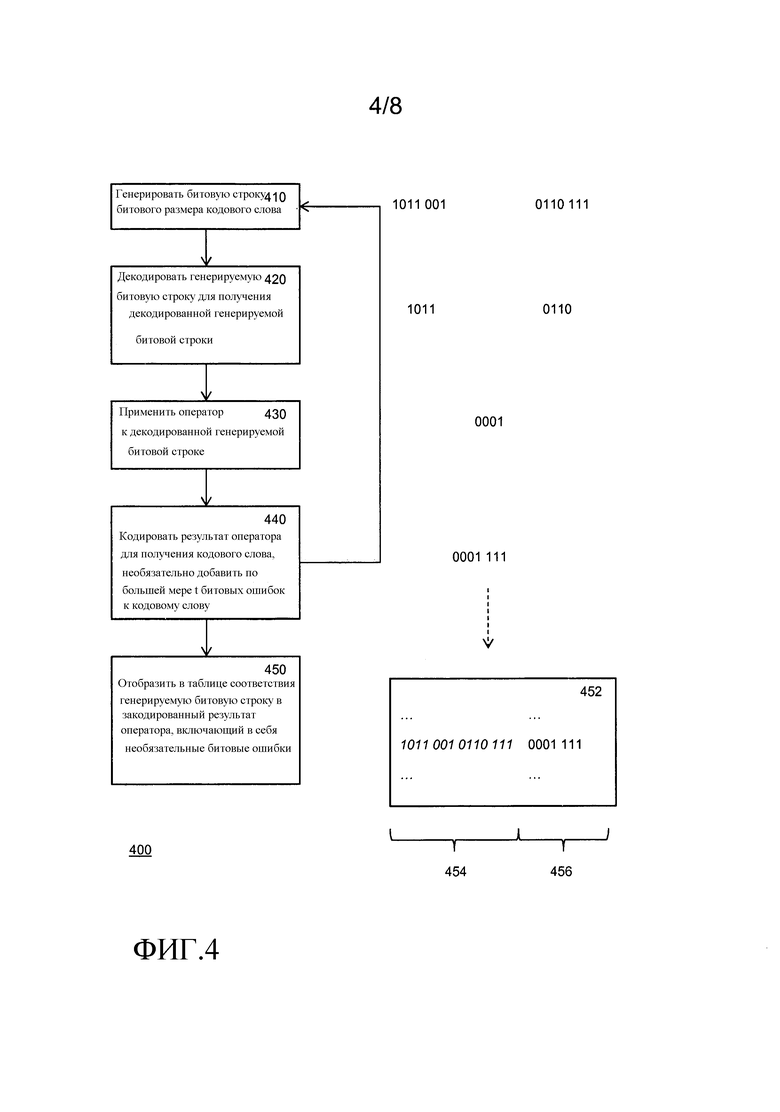
Фиг.4 изображает способ 400 для создания функций исправления ошибок. В примерах для фиг.4 и 5 ниже мы будем использовать код Хэмминга [7,4,3]. Кодовые слова имеют длину 7 бит, кодируют 4 бита данных. Код может исправлять единственную ошибку, т.е. t= 1. Мы будем использовать построение, в котором кодовые слова имеют форму d1 d2 d3 d4 p1 p2 p3, здесь d1-d4- биты данных, p1=d1+d2+d4, p2=d2+d3+d4, p3=d1+d3+d4 - биты проверки на четность, и + обозначает сложение по модулю два.
Предполагается, что обеспечивается оператор, для которого желательна таблица соответствия исправления ошибок. Мы будем предполагать функцию от двух входных данных, но 1 или более 2 возможны. Оператором могут быть общие операторы, такие как сложение (plus), деление по модулю (mod), умножение (mul) и т.п. но оператор может также быть характерным для приложения, например s-блок AES.
В рассмотрении ниже мы будем предполагать, что оператором является двоичный оператор, принимающий два входных значения. В качестве примера используется арифметическое сложение. Чтобы пример оставался удобным, входные значения имеют 4 бита в ширину, а закодированные входные значения имеют 7 бит в ширину. На практике намного большие входные значения и/или кодирования могут быть использованы, что будет соответственно приводить к гораздо большим таблицам.
На этапе 410 генерируются битовые строки битового размера (n) кодового слова. Генерируемые битовые строки являются возможными входными значениями в окончательные таблицы соответствия. В примере генерируются строки 1011001 и 0110111. Следует заметить, что первая является кодовым словом, а последняя не является. Генерируемые битовые строки декодируются, например, с использованием алгоритма исправления ошибок, с целью получения декодированной генерируемой битовой строки. Декодированные строки имеют битовый размер (k) входного значения, здесь 4 бита. Следует заметить, что ошибка во второй генерируемой битовой строке была исправлена. В этом случае, т.е. при коде Хэмминга [7,4,3], используется так называемый совершенный код. Совершенные коды имеют то преимущество, что любая генерируемая битовая строка может быть декодирована в уникальную декодированную битовую строку. Несовершенные коды могут быть использованы; в этом случае, средство разрешения конфликтов используется для выбора декодированной битовой строки из декодированных битовых строк, которые получаются наиближайшими. Средство разрешения конфликтов является детерминистическим, например оно может накладывать упорядочение, например лексикографическое упорядочение. В качестве альтернативы, некоторые входные строки могут не декодироваться, а вместо этого сообщается об "ошибке декодирования" и предпринимается надлежащее действие. Это может также быть примечаниями в таблице, например, недекодируемая битовая строка может быть обеспечена как выходная для недекодируемой входной строки. Предпочтительно недекодируемая битовая строка случайна во избежание случайного внесения корреляций ключей, и т.д.
Оператор применяется к результату декодирования генерируемой битовой строки. В этом случае были сгенерированы две битовых строки, и оператор применяется к обеим из них. В этом случае выполняется прибавление 4 бит. Результат закодирован для получения кодового слова. Необязательно, к кодовому слову может быть добавлено не более, чем t битовых ошибок. В этом случае один бит кодового слова может быть инвертирован. Наконец, таблица соответствия строится так, чтобы генерируемая битовая строка преобразовывалась в закодированный результат оператора, включающий в себя вспомогательные битовые ошибки.
Процесс повторяется, пока не сгенерирована вся желаемая битовая строка. Обычно все битовые строки кода битового размера (n) генерируются по порядку. В случае, когда оператор имеет множество входных данных, генерируется множество битовых строк.
В этом примере способ может генерировать все комбинации двух строк из 7 бит. То есть генерируются все 2∧14 битовых строк. Результаты перечисляются в таблице 452 соответствия. С левой стороны, указанные как 454, находятся входные значения, и с правой стороны на 456 находятся соответствующие выходные значения. Следует заметить, что входные значения не обязательно должны быть перечислены явным образом. В особенности, если генерируются все битовые строки, то входная сторона может опускаться.
Фиг.5a изображает альтернативный способ построения таблиц исправления ошибок. Фиг.5b изображает, как может строиться одна и та же таблица, показывая, как одна и та же запись таблицы может входить в окончательную таблицу соответствия, как на фиг.4.
На этапе 510 генерируются битовые строки входного битового размера (k). Генерируемые битовые строки используются на этапе 530 путем применения оператора к генерируемой битовой строке и кодирования результата на этапе 540. Как на фиг.4, необязательно намеренные ошибки (вплоть до t) могут добавляться к кодовому слову. Генерируемые битовые строки также используются на этапе 520 для генерирования кодирования, т.е. кодирования в качестве кодового слова. На этапе 560 генерируются исправимые ошибочные комбинации. Не является необходимым, чтобы все возможные входные значения были представлены таблицей соответствия. Вместо этого можно ограничить входные значения кодовыми словами плюс ограниченный набор исправимых входных значений. Если код является совершенным и набор исправимых входных значений равен всем комбинациям с вплоть до t единичных бит, и остальные нули. Результат является тем же самым. Однако, можно предпочесть добавить менее чем t ошибок. Если код несовершенен и набор исправимых входных значений равен всем комбинациям с вплоть до t единичных бит, и остальные нули, набор входных значений будет строго меньше всех возможных битовых строк. Должно быть соответствие между исправимыми битовыми комбинациями, добавляемыми на этапе 560, и ошибкой, добавляемой на этапе 540.
Как на фиг.4, так и на фиг.5 поднабор из всех исправимых битовых строк битового размера (n) кодового слова генерируются, оператор применяется к результату декодирования генерируемой исправимой битовой строки, причем результат закодирован в кодовое слово, возможно с добавлением одной или более ошибок. Строится таблица соответствия, в которой генерируемая исправимая битовая строка преобразуется в закодированную в кодовое слово, включающее в себя вспомогательные одну или несколько ошибок.
Фиг.6 изображает в виде блок-схемы способ 600 компилирования. На этапе 610 первая компьютерная программа принимается приемником. На этапе 620 лексический анализ выполняется, например, для определения лексем, лексическим анализатором. Возможно, обработка, такая как макрорасширение, также выполняется. На этапе 630 осуществляется синтаксический анализ программы посредством синтаксического анализатора. Например, синтаксический анализатор генерирует синтаксическое дерево согласно формальной грамматике языка программирования первой программы. Синтаксический анализатор определяет различные языковый конструкции в программе и вызывает надлежащие подпрограммы генерирования кода. В частности, идентифицируется оператор или множество операторов. В таком случае, на этапе 640 генерирование кода выполняется генератором кода. Во время генерирования кода генерируется некий код и, если необходимо, сопроводительные таблицы. Сопроводительными таблицами являются таблицы исправления ошибок. Генерируемый код не обязательно должен, и в общем случае не будет, содержать оператор, поскольку он замещается одной или несколькими таблицами соответствия. Например, синтаксический анализатор определит операцию сложения и переведет это в таблицу соответствия для инструкции сложения и в генерируемый код для применения таблицы соответствия к верным значениям.
На этапе 655 генерируемые таблицы объединяются в табличную базу, поскольку вполне может случиться, что некоторые таблицы генерируются множество раз, в таком случае не необходимо сохранять их множество раз. Например, таблица сложения может требоваться и генерироваться только один раз. Когда весь код объединен и все таблицы объединены, компиляция завершается. Необязательно, может существовать этап оптимизации.
Обычно, компилятор использует закодированные области, т.е. секции программы, в которых все значения или по меньшей мере все значения, соответствующие некоторым критериям, кодируются, т.е. имеют битовый размер (n) кодового слова. В закодированной области операции могут исполняться путем исполнения таблицы соответствия. Когда происходит вход в закодированную область, все значения кодируются, когда закодированная область покидается, значения декодируются. Критерий может быть тем, что значения коррелируют, или зависит от критичной информации безопасности, например криптографического ключа.
Интересный способ для создания компилятора состоит в следующем. На этапе 630 выполняется промежуточная компиляция. Она может быть на промежуточный язык, например язык межрегистровых пересылок или подобное, но может также быть компиляция кода на машинном языке. Это означает, что для этапов 610-630 с фиг.6 может быть использован стандартный компилятор, который не производит таблиц исправления ошибок. Однако на этапе 640 генерирование кода выполняется на основе промежуточной компиляции. Например, если был использован код на машинном языке, каждая инструкция замещается соответствующим безоператорным осуществлением этой инструкции, т.е. осуществлением этой инструкция на основе таблицы. Это представляет конкретный непосредственный способ для создания компилятора. Чертежи 6 также могут быть использованы для генерирования компилятора, который производит не машинный язык, а второй язык программирования.
В одном варианте осуществления, компилятор является компилятором для компилирования первой компьютерной программы, написанной на первом компьютерном языке программирования во вторую компьютерную программу, компилятор содержит генератор кода для генерирования второй компьютерной программы путем генерирования таблиц и кода на машинном языке, причем генерируемые таблицы и генерируемый код на машинном языке вместе формируют вторую компьютерную программу, причем генерируемый код на машинном языке обращается к таблицам, причем компилятор сконфигурирован для определения арифметического или логического выражения в первой компьютерной программе, причем выражение зависит от по меньшей мере одной переменной, и генератор кода сконфигурирован для генерирования одной или нескольких таблиц исправления ошибок, представляющих предварительно вычисленные результаты идентифицированного выражения для множества значений переменной и для генерирования кода на машинном языке для осуществления идентифицированного выражения во второй компьютерной программе путем осуществления доступа к генерируемой одной или нескольким таблицам, представляющим предварительно вычисленные результаты. Предпочтительно, если код на машинном языке, генерируемый для осуществления идентифицированного выражения, не содержит самих арифметических или логических машинных инструкций, по меньшей мере никаких арифметических или логических машинных инструкций, относящихся к критичной информации.
Это снижает утечки сторонних каналов второй компьютерной программы ниже, поскольку она содержит меньше арифметических или логических операций. Предпочтительно, если все арифметические и логические выражения и подвыражения замещаются осуществлениями доступа к таблицам. Поскольку те инструкции, которые составляют арифметическое или логическое выражение или подвыражения, отсутствуют, они не могут привести к утечке какой-либо информации. Таблица предварительно вычисляется; мощность, потребляемая для выполнения арифметического или логического поведения, заключенного в таблице, не видна в течение исполнения программы. Поскольку таблица является исправляющей ошибки, программа также более устойчива против атак с внесением неисправностей. Если намеренные ошибки добавляются в программе либо динамически в течение исполнения, либо в таблице соответствия, взаимоотношения между внутренней переменной и внешним результатом дополнительно усложнятся, таким образом, делая обратное проектирование более сложным.
Фиг.7 изображает устройство, выстраивающие таблицы 700 соответствия. Устройство содержит генератор 712 исправимых битовых строк и генератор 714 декодированных битовых строк. Генераторы 712 и 714 работают совместно для произведения всех строк, которые таблица соответствия должна принять в качестве входных данных, т.е. исправимых битовых строк и соответствующих незакодированных строк. Генератор 712 производит строки битового размера (n1) кодового слова. Генератор 714 производит строки входного битового размера (k1) оператора. Оба генератора соответствуют первому коду исправления ошибок. Пара может использовать любой из подходов для построения таблицы соответствия, как описано здесь.
Выходные данные генератора 714 используются оператором 730. Оператор 730 сконфигурирован для выполнения оператора на незакодированной, т.е. декодированной, битовой строке. Выходные данные оператора 730 имеют k2 бит. Размер k1 может быть равен k2. Результат оператора закодирован для второго кода исправления ошибок посредством кодера 740. Наконец, средство 750 сбора собирает исправимые битовые строки, принятые от генератора 712, и соответствующие закодированные результаты кодера 740, для произведения таблицы соответствия. Если отношение между входными данными в получающуюся таблицу соответствия и местоположением выходной величины может легко быть получено, например, поскольку средство сбора в действительности включает в себя все битовые строки размера, равного размеру кодового слова первого кода исправления ошибок, то исправимые битовые строки не должны включаться в таблицу соответствия.
Средство сбора может добавлять некоторые или все из битовых ошибок. Местоположения, в которых битовые ошибки добавляются, могут зависеть от исправимой строки, например, если входная строка имеет битовую ошибку в позиции, т.е. битовая ошибка добавляется в позиции i+1 во втором коде исправления ошибок.
Ниже дается дополнительное улучшение варианта осуществления. Наиболее общей инструкцией в программе являются операции и сохранение ее результата. Эти операции включают в себя такие хорошо известные операции, как сложение (+), вычитание (-), умножение (*) и т.д. Компилятор выявляет эти инструкции, то есть он раскладывает выражение, написанное на некотором языке высокого уровня в эти известные операции. Таблицы могут быть использованы для всех использованных операций, как операций в программах, так и, если используется VM, для операций VM, на которой исполняется программа. Безопасность может дополнительно быть улучшена путем наделения этих таблиц особыми признаками или свойствами.
Для каждой операции могут быть использованы таблицы. Таблица определяется согласно операции. Без кодирования, например, для одноместного оператора Opm таблицаOpm[x]==Opm(x) или для двуместного оператора Opd таблицаOpd[x][y]==Opd(x,y). Следует заметить, что для неодноместной операции компилятор может осуществлять доступ к таблице в качестве множества доступов, этот процесс известен как каррирование. То есть X=таблицаOpd[x], за чем следует X[y]. Следует заметить: в отношении памяти для восьмибитного пути данных 14 двуместных операторов потребуют использования памяти, равной 1 мегабайту, что считается приемлемым. Следует заметить, что некоторые или все таблицы могут сохраняться в ROM и некоторые или все таблицы могут сохраняться в другой памяти, либо энергозависимой, либо энергонезависимой. Добавление кодирования исправления ошибок может быть выполнено путем замещения кодирования в вышеприведенной формуле.
Единство компилятора/компоновщика и VM поддерживается посредством замещения использования операции доступом к таблице операции. Базовая платформа должна быть использована только для инструкций перехода управления и записывает/считывает в/из реестров и памяти.
В более улучшенном варианте осуществления компилятор может осуществлять полные выражения в виде таблиц. Например, выражение: X2+Y2 может быть осуществлено посредством двух умножений и одного сложения, в результате чего получается по меньшей мере три операции (или больше при каррировании). Однако оно также может быть осуществлено в виде таблицы X2+Y2 и быть скомпилировано в осуществление доступа к таблице. Это даст в результате один (два при каррировании) доступ к таблице.
Если VM используется для исполнения компилированной программы, то единство между компилятором/компоновщиком и VM может поддерживаться путем передачи таблиц к VM. Помеченные таблицы становятся выходными данными из компилятора и входными данными для VM. В коде, обеспеченном компилятором, к этим меткам затем выполняется обращение. Это может быть улучшением в отношении памяти, поскольку таблицы неиспользуемых операций могут опускаться. В одном варианте осуществления компилятор содержит блок выражения для определения первой программы, причем выражение назначает значение одному, двум или множеству числовых входных данных, причем генератор кода сконфигурирован для генерирования таблицы, представляющей результат выражения для всех значений числовых входных данных. Интересно то, что выражение не обязательно должно быть равно существующей инструкции машинного кода.
Интересно то, что виртуальная машина, выполненная с возможностью исполнения программы на конкретном языке программирования VM, может быть скомпилирована для использования таблиц исправления ошибок. Это само по себе будет порождать некоторые из свойств исправления ошибок в любой программе, которая исполняется на VM. Однако также программа может быть получена путем компилирования программы на некотором дополнительном языке в язык программирования VM. Последняя компиляция может также быть компилирована для использования таблиц исправления ошибок.
Например, можно использовать переведенные в табличный вид инструкции виртуальной машины, дополненные исправлением ошибок, для осуществления самой VM. Мы поясняем это для дополнения инструкции сложения механизмом исправления ошибок. Другие инструкции могут обрабатываться подобным образом.
Первым этапом может быть добавление свойства исправления ошибок к инструкции, в настоящем случае к инструкции сложения. Пусть M - вложение области Y в большую область X, и пусть M-1- преобразование из области X в Y, где малая ошибка e в значении M(v) из X все так же преобразуется обратно в v. Кратко M-1(M(v)⊕e)=v. Здесь ⊕ обозначает сложение в X. Обычно X состоит из двоичных строк равной длины, ⊕ обозначает побитное сложение строк по модулю два, и ошибка e является "малой", если имеет мало ненулевых компонентов (или, в терминах кодирования, если она имеет малый вес Хэмминга). Мы обозначили через E набор ошибок, которые мы хотим исправить, и множество {M(v)⊕e|v∈Y, e∈E} через S. Кодирование исправления ошибок осуществляется таким образом, что каждый элемент s в S может быть записан уникальным образом как s=M(v)⊕e с v в Y и e в E; тогда мы имеем, что M-1(s)=M-1(M(v)⊕e)=v. Для элементов x в X, которые не в S, M-1(x) не определено.
В качестве игрового примера мы взяли Y={0,1,2,3}, X={0,1}5, и E={00000,10000,01000,00100,00010,00001} (то есть мы хотим исправить одну битовую ошибку). Мы определяем M как M(0)=00000, M(1)=01110, M(2)=10101 и M(3)= 11011.
Ясно, что мы имеем
M(0)⊕E=E={00000,10000,01000,00100,00010,00001}
Μ(1)⊕Ε={01110,11110,00110,01010,01100,01111}
M(2)⊕E={10101,00101,11101,10001,10111,10100}
M(3)⊕E={11011,01011,10011,11111,11001,11011}.
Путем проверки мы видим, что каждый элемент S={M(u)⊕e|u∈Y, e∈E}{} может быть записан уникальным образом как M(u)⊕e с u в Y и e в E. Набор S, таким образом, является набором декодируемых битовых строк.
Существует восемь элементов X, которых нет в S (а именно 11000, 10110, 01101, 00011, 10010, 11100, 00111, 01001); M-1 не определяется для этих восьми элементов.
Подобно подходу обфускации мы теперь вводим:
add(x,y)==M(M-1(x)+M-1(y))
для всех x и y в S.
Функция add(x,y) не определяется, если по меньшей мере один из x и y не присутствует в S. Предполагается, что всегда, когда add(x,y) вызывается с такими недействительными входными данными, эта инструкция не исполняется и обозначается ошибка.
Таким образом, мы дополняем исходное сложение свойствами исправления ошибок, и следует заметить, что выражение за исключением O или M эквивалентное.
В игровом примере числа, которые могут быть представлены двумя битами, были преобразованы в строки из пяти бит, чтобы обеспечить возможность исправления одного бита. В общем случае числа, которые могут быть представлены k битами, могут быть закодированы в битовые строки длины k+r так, чтобы могла быть исправлена одна ошибка ошибочного бита, где r такое, чтобы k+r≤2r-1. Так что, например, для k=8-битных чисел мы можем обойтись r=4 избыточными битами; для k=32-битного числа мы можем обойтись r=6 избыточными битами. В последнем случае, поскольку закодированные строки имеют длину 38, набор E имеет 39 элементов и размер памяти будет умножен на коэффициент 39.
Следует заметить, что множество различных способов исполнения способа, описанного здесь, возможны, в частности, описанные в формуле изобретения и/или со ссылками на чертежи 4, 5 и 6. Это будет очевидно специалисту в данной области техники. Например, порядок этих этапов может варьироваться или некоторые этапы могут исполняться параллельно. Кроме того, между этапами могут быть добавлены другие этапы способа. Добавленные этапы могут представлять улучшение способов, описанных здесь, или могут не относиться к способу. Например, этапы 520 и 530, или 620 и 630 и т.д. могут исполняться, по меньшей мере частично, параллельно. Кроме того, некоторый заданный этап может быть не полностью завершен, прежде чем начинается следующий этап.
Способ согласно изобретению может исполняться с использованием программных средств, которые содержат инструкции для побуждения процессорной системы выполнять способ 400, 500 или 600. Программные средства могут включать в себя только этапы, выполняемые конкретной подсущностью системы. Программные средства могут сохраняться на подходящем носителе данных, таком как жесткий диск, гибкий диск, память и т.д. Программные средства могут посылаться в качестве сигнала по проводу, или беспроводным образом, или с использованием сети данных, например Интернета. Программные средства могут быть сделаны доступными для скачивания и/или для удаленного использования на сервере.
Следует понимать, что изобретение также распространяется на компьютерные программы, в частности компьютерные программы на или в носителе, выполненном с возможностью вводить изобретение в осуществление на практике. Программа может иметь форму исходного кода, объектного кода, промежуточного источника кода и объектного кода, такого как частично скомпилированная форма, или любую другую форму, подходящую для использования в осуществлении способа согласно изобретению. Вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером инструкции, соответствующие каждому из этапов обработки по меньшей мере одного из изложенных способов. Эти инструкции могут подразделяться на подпрограммы и/или сохраняться в одном или нескольких файлах, которые могут быть связаны статически или динамически. Другой вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером инструкции, соответствующие каждому из средств по меньшей мере одной из изложенных систем и/или продуктов.
Следует заметить, что вышеупомянутые варианты осуществления иллюстрируют, а не ограничивают изобретение, и что специалисты в данной области техники будут иметь возможность осуществить множество альтернативных вариантов осуществления.
В формуле изобретения любые позиционные обозначения, помещенные в скобках, не должны толковаться как ограничивающие пункт формулы. Использование глагола "содержать" и его спряжений не исключает наличия элементов или этапов помимо указанных в пункте формулы. Упоминание элемента в единственном числе не исключает наличия множества таких элементов. Изобретение может осуществляться посредством аппаратных средств, содержащих несколько отдельных элементов, и посредством подходящим образом программируемого компьютера. В пункте об устройстве, где перечисляется несколько средств, несколько из этих средств могут осуществляться одним и тем же элементом аппаратных средств. Сам факт того, что конкретные меры перечислены во взаимно различных зависимых пунктах формулы изобретения, не указывает, что комбинация этих мер не может быть использована для обеспечения преимуществ.
Список ссылочных позиций:
100 таблица соответствия
110 Входные данные в таблицу (в действительности не сохраняемые в памяти)
112 множество входных данных, которые отличаются не более чем на "t=floor((d-1)/2)" бит от кодового слова
120 содержимое таблицы
131-138 результаты таблицы для входных данных 112
200 вычислительное устройство
210 устройство хранения
221, 222 таблицы соответствия для одних входных данных
231, 232 таблицы соответствия для множества входных данных
2311-2323 таблицы соответствия для одних входных данных
241 таблица соответствия кодирования
242 таблица соответствия декодирования
255 код на машинном языке
250 компьютерный процессор
260 I/O-устройство
310 входная таблица
320 промежуточная таблица
330 выходная таблица
452 таблица соответствия
454 входная часть
456 выходная часть
552 таблица соответствия
700 устройство для построения таблицы соответствия
712 генератор исправимой битовой строки
714 генератор декодированной битовой строки
730 оператор
740 кодер для второго кода исправления ошибок
750 средство сбора
| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, КОНФИГУРИРУЕМОЕ С ПОМОЩЬЮ ТАБЛИЧНОЙ СЕТИ | 2013 |
|
RU2661308C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, СОДЕРЖАЩЕЕ СЕТЬ ТАБЛИЦ | 2013 |
|
RU2676454C2 |
| СПОСОБ ВСТРАИВАНИЯ ЦИФРОВОГО ВОДЯНОГО ЗНАКА В ПОЛЕЗНЫЙ СИГНАЛ | 2006 |
|
RU2405218C2 |
| СПОСОБ И УСТРОЙСТВО ЗАПИСИ ДАННЫХ, НОСИТЕЛЬ ДАННЫХ И СПОСОБ И УСТРОЙСТВО ВОСПРОИЗВЕДЕНИЯ ДАННЫХ | 1996 |
|
RU2191423C2 |
| ДЕКОДИРОВАНИЕ ВЫСОКОИЗБЫТОЧНЫХ КОДОВ С КОНТРОЛЕМ ЧЕТНОСТИ С ИСПОЛЬЗОВАНИЕМ МНОГОПОРОГОВОГО ПРОХОЖДЕНИЯ СООБЩЕНИЯ | 2004 |
|
RU2337478C2 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ КОМПЬЮТЕРНЫХ КОДОВ | 2023 |
|
RU2820092C1 |
| СПОСОБЫ И УСТРОЙСТВО ДЛЯ ОБЕСПЕЧЕНИЯ КОРРЕКТНОГО ПРЕДВАРИТЕЛЬНОГО ДЕКОДИРОВАНИЯ | 2006 |
|
RU2405188C2 |
| СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ НА ОСНОВЕ ЗАПРЕТА ОПРЕДЕЛЕННЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ДАННЫХ | 2012 |
|
RU2491716C1 |
| КОДИРОВАНИЕ И ПЕРЕОТОБРАЖЕНИЕ СООБЩЕНИЯ | 2007 |
|
RU2407146C2 |
| СТРУКТУРА ДЕКОДЕРА ДЛЯ ОПТИМИЗИРОВАННОГО УПРАВЛЕНИЯ ОБРАБОТКОЙ ОШИБОК В ПОТОКОВОЙ ПЕРЕДАЧЕ МУЛЬТИМЕДИЙНЫХ ДАННЫХ | 2006 |
|
RU2374787C2 |
Изобретение относится к вычислению функции от одних или нескольких входных данных. Технический результат – расширение арсенала технических средств вычисления функции от одних или нескольких входных данных. Вычислительное устройство, сконфигурированное для вычисления функции от одних или нескольких входных данных, причем устройство содержит устройство хранения, хранящее одну или несколько таблиц соответствия, используемых при вычислении упомянутой функции, причем таблицы соответствия преобразуют входные значения в выходные значения, причем таблица соответствия построена в отношении первого кода исправления ошибок, второго кода исправления ошибок, первого порога ошибок и второго порога ошибок так, чтобы любые два входных значения преобразовывались в соответствующие выходные значения, причем первый порог ошибок является некоторым числом, которое не меньше 1 и не больше значения (t1) способности к исправлению ошибок у первого кода исправления ошибок, и второй порог ошибок является некоторым числом, которое не больше значения (t2) способности к исправлению ошибок у второго кода исправления ошибок. 5 н. и 9 з.п. ф-лы, 8 ил.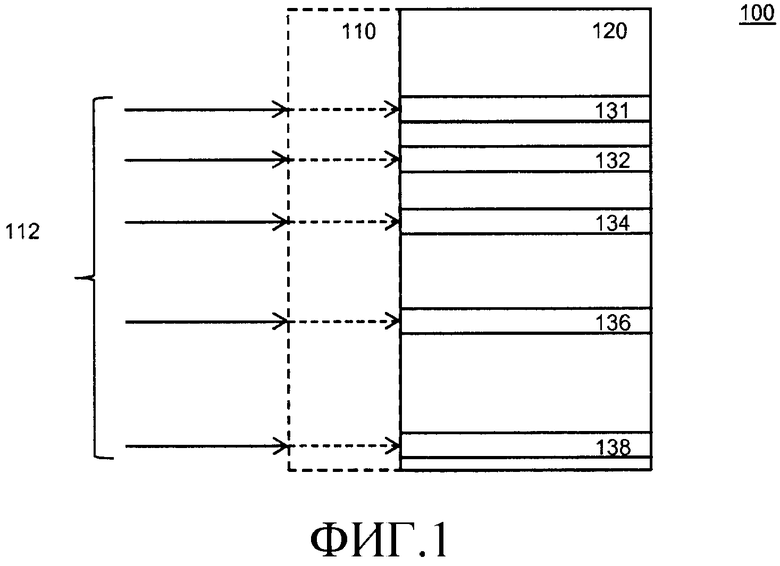
1. Вычислительное устройство, сконфигурированное для вычисления функции от одних или нескольких входных данных, причем
- устройство содержит устройство хранения, хранящее одну или несколько таблиц соответствия, используемых при вычислении упомянутой функции, причем таблицы соответствия преобразуют входные значения в выходные значения, причем таблица соответствия построена в отношении первого кода исправления ошибок, второго кода исправления ошибок, первого порога ошибок и второго порога ошибок так, чтобы любые два входных значения, каждое из которых отличается не более чем на некоторое число бит первого порога ошибок от одного и того же кодового слова первого кода исправления ошибок, преобразовывались в соответствующие выходные значения, каждое из которых отличается не более чем на некоторое число бит второго порога ошибок от одного и того же кодового слова второго кода исправления ошибок, причем
- первый порог ошибок является некоторым числом, которое не меньше 1 и не больше значения (t1) способности к исправлению ошибок у первого кода исправления ошибок, и второй порог ошибок является некоторым числом, которое не больше значения (t2) способности к исправлению ошибок у второго кода исправления ошибок.
2. Вычислительное устройство по п. 1, в котором первый код исправления ошибок является тем же самым, что и второй код исправления ошибок.
3. Вычислительное устройство по любому из предшествующих пунктов, в котором первый порог ошибок равен значению (t1) способности к исправлению ошибок у первого кода исправления ошибок.
4. Вычислительное устройство по любому из предшествующих пунктов, в котором второй порог ошибок равен нулю.
5. Вычислительное устройство по любому из предшествующих пунктов, при этом устройство сконфигурировано для получения одних или нескольких входных данных в виде одних или нескольких закодированных входных данных, причем закодированные входные данные получаются путем применения функции кодирования к одним из упомянутых входных данных, причем функция кодирования преобразует входные данные в соответствующее кодовое слово кода исправления ошибок с возможностью добавления некоторого числа битовых ошибок первого порога ошибок.
6. Вычислительное устройство по любому из предшествующих пунктов, в котором вычислительное устройство сконфигурировано для вычисления функции путем применения последовательности обращений к таблице соответствия к последовательности промежуточных результатов, причем промежуточные результаты включают в себя закодированные входные значения и выходные значения обращений к таблице соответствия в последовательности, причем один из промежуточных результатов является закодированным результатом функции.
7. Вычислительное устройство по любому из предшествующих пунктов, в котором любой из первого или второго кода исправления ошибок является любым из следующих: [7, 4, 3], [11, 4, 5], [12, 8, 3], [16, 8, 5], [21, 16, 3] и [9, 5, 3], [13, 5, 5], [10, 6, 3], [14, 6, 5] и [8, 4, 4], [10, 4, 4].
8. Вычислительное устройство по любому из пп. 1-7, в котором таблица соответствия из одной или нескольких таблиц соответствия, используемых при вычислении упомянутой функции, была построена из оператора, преобразующего битовые строки входного битового размера (k) в битовые строки выходного битового размера (k), способом по п. 11 или 12.
9. Вычислительное устройство по п. 8, в котором оператор является взаимно однозначным соответствием.
10. Вычислительное устройство по п. 8, в котором оператор является тождеством.
11. Способ построения таблицы соответствия для оператора, преобразующего битовые строки входного битового размера (k1) в битовые строки выходного битового размера (k2), причем способ содержит этапы, на которых
- генерируют битовые строки, причем генерируемые битовые строки имеют тот же самый размер, что и битовый размер (n1) кодового слова первого кода исправления ошибок, причем первый код исправления ошибок имеет размерность по меньшей мере входного битового размера (k1), и
- для каждой декодируемой сгенерированной битовой строки декодируют сгенерированную битовую строку так, чтобы получить декодированную сгенерированную битовую строку, причем декодирование соответствует первому коду исправления ошибок,
- применяют оператор к декодированной сгенерированной битовой строке, и
- кодируют результат оператора для получения кодового слова второго кода исправления ошибок с возможностью добавления битовых ошибок в числе, не превышающем число второго порога ошибок, к кодовому слову, причем число второго порога ошибок не больше значения (t2) способности к исправлению ошибок у второго кода исправления ошибок, причем второй код исправления ошибок имеет размерность не менее выходного битового размера (k2), и
- преобразуют в таблице соответствия декодируемую сгенерированную битовую строку в закодированный результат оператора, включающий в себя вспомогательные битовые ошибки.
12. Способ построения таблицы соответствия для оператора, преобразующего битовые строки входного битового размера (k1) в битовые строки выходного битового размера (k2), причем способ содержит этапы, на которых
- генерируют битовые строки, имеющие тот же самый размер, что и входной битовый размер (k1),
- для каждой сгенерированной битовой строки применяют оператор к сгенерированной битовой строке и
- кодируют результат оператора для получения кодового слова из второго кода исправления ошибок с возможностью добавления исправимой ошибочной комбинации к кодовому слову, причем второй код исправления ошибок имеет размерность не менее выходного битового размера (k2),
- кодируют сгенерированную битовую строку для получения кодового слова из первого кода исправления ошибок, причем первый код исправления ошибок имеет размерность не менее входного битового размера (k1), и
- для каждой исправимой ошибочной комбинации применяют исправимую ошибочную комбинацию к закодированной сгенерированной битовой строке для получения закодированных входных значений,
- преобразуют в таблице соответствия закодированные входные значения в закодированный результат оператора, включающий в себя вспомогательные битовые ошибки.
13. Компилятор для компилирования первой компьютерной программы, написанной на первом компьютерном языке программирования, во вторую компьютерную программу,
- компилятор содержит генератор кода для генерирования второй компьютерной программы путем генерирования таблиц и кода на машинном языке, причем генерируемые таблицы и генерируемый код на машинном языке вместе формируют вторую компьютерную программу, причем генерируемый код на машинном языке привязан к таблицам, при этом
- компилятор сконфигурирован для идентификации арифметического или логического выражения в первой компьютерной программе, причем выражение зависит от по меньшей мере одной переменной, и генератор кода сконфигурирован для генерирования одной или нескольких таблиц, представляющих предварительно вычисленные результаты идентифицированного выражения для множества значений переменной, и для генерирования кода на машинном языке для осуществления идентифицированного выражения во второй компьютерной программе путем обращения к сгенерированной одной или нескольким таблицам, представляющим предварительно вычисленные результаты, при этом одна или несколько таблиц генерируются по любому из пп. 11 и 12.
14. Способ для вычисления функции от одних или нескольких входных данных, причем входные данные имеют входной битовый размер (k), причем способ содержит этапы, на которых
- сохраняют одну или несколько таблиц соответствия, причем таблицы соответствия преобразуют входные значения в выходные значения, причем входные значения таблицы соответствия имеют битовый размер, равный первому битовому размеру (n1) кодового слова первого кода исправления ошибок, причем таблица соответствия строится в отношении первого кода исправления ошибок, второго кода исправления ошибок, первого порога ошибок и второго порога ошибок так, чтобы любые два входных значения, каждое из которых отличается не более чем на некоторое число бит первого порога ошибок от одного и того же кодового слова первого кода исправления ошибок, преобразовывались в соответствующие выходные значения, каждое из которых отличается не более чем на некоторое число бит второго порога ошибок от одного и того же кодового слова второго кода исправления ошибок, причем первый порог ошибок не меньше 1 и не больше значения (t1) способности к исправлению ошибок у первого кода исправления ошибок и второй порог ошибок не больше значения (t2) способности к исправлению ошибок у второго кода исправления ошибок,
- используют одну или несколько таблиц соответствия при вычислении функции, что содержит применение одной или нескольких таблиц соответствия к закодированным значениям.
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| СПОСОБ ЗАЩИТЫ ТЕКСТОВОЙ ИНФОРМАЦИИ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА | 2010 |
|
RU2439693C1 |
Авторы
Даты
2018-06-08—Публикация
2013-10-21—Подача