ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Изобретение относится к вычислительному устройству, выполненному с возможностью вычисления функции данных по входному значению функции, причем устройство содержит электронное хранилище, хранящее первую табличную сеть, сконфигурированную для функции данных, причем вычислительное устройство содержит электронный процессор, подключенный к хранилищу и выполненный с возможностью получения множественных входов первой таблицы для первой табличной сети, причем множественные входы первой таблицы включают в себя входное значение функции, и вычисления функции данных путем применения первой табличной сети к множественным входам первой таблицы для создания множественных выходов первой таблицы, причем множественные выходы первой таблицы включают в себя выходное значение функции, причем выходное значение функции соответствует результату применения функции данных к входному значению функции.
УРОВЕНЬ ТЕХНИКИ ИЗОБРЕТЕНИЯ
В традиционной криптографии обычно предполагалось, что нарушитель получает доступ только к входным и выходным значениям защищенной системы. Например, нарушитель мог бы наблюдать открытый текст, входящий в систему, и наблюдать зашифрованный текст, выходящий из системы. Хотя нарушитель мог бы попытаться получить преимущество путем анализа таких входных/выходных пар, возможно даже с использованием мощных в вычислительном отношении способов, у него не предполагалось прямого доступа к системе, которая реализовывала поведение по входу/выходу.
В последнее время стало необходимым принимать во внимание модели угроз, в которых предполагается, что нарушитель обладает некоторыми сведениями о реализации. Например, можно рассмотреть угрозу от анализа через сторонний канал и реверсивного проектирования. Кроме того, вопросы, которые ранее ассоциировались главным образом с проблемами безопасности, распространились в другие области, например конфиденциальность. Хотя остаются вопросом первостепенной важности криптографические системы, обрабатывающие секретную информацию, например криптографические ключи, также стала важна защита других программ, например, обрабатывающих относящуюся к конфиденциальности информацию.
Уже давно известно, что компьютерные системы допускают утечку некоторой информации через так называемые сторонние каналы. Наблюдение поведения компьютерной системы по входу-выходу не может предоставить никакой полезной информации о конфиденциальной информации, например, используемых компьютерной системой секретных ключах. Но компьютерная система имеет другие каналы, которые можно наблюдать, например, ее энергопотребление или электромагнитное излучение; эти каналы именуются сторонними каналами. Например, можно измерить небольшие изменения в энергии, потребляемой разными инструкциями, и изменения в энергии, потребляемой при исполнении инструкций. Измеренное изменение можно соотнести с конфиденциальной информацией, например криптографическими ключами. Эта дополнительная информация о секретной информации, помимо наблюдаемого и запланированного поведения по входу-выходу, называется сторонним каналом. Через сторонний канал компьютерная система в ходе использования может "допустить утечку" секретной информации. Наблюдение и анализ стороннего канала могут предоставить нарушителю доступ к лучшей информации, чем можно получить только из криптоанализа поведения по входу-выходу. Одним известным типом атаки по сторонним каналам является так называемый разностный анализ мощности (DPA).
Современные подходы к проблеме сторонних каналов вносят в вычисление случайность. Например, между реальными операциями, которые исполняют программу, можно вставить фиктивные инструкции, чтобы сделать неясной связь между энергопотреблением и данными, над которыми работает программа.
Еще более сильной атакой на компьютер является так называемое реверсивное проектирование. Во многих сценариях безопасности нарушители могут иметь полный доступ к компьютеру. Это дает им возможность деассемблировать программу и получить любую информацию о компьютере и программе. При достаточном усилии нарушитель может обнаружить любой ключ, скрытый, например, в программе.
Доказано, что защита от этого сценария атаки очень сложна. Одним типом контрмеры является так называемая криптография на основе белого ящика. В криптографии на основе белого ящика объединяются ключ и алгоритм. Результирующий алгоритм работает только для одного конкретного ключа. Затем алгоритм можно реализовать в виде так называемой табличной сети поиска. Вычисления преобразуются в последовательность поисков в зависящих от ключа таблицах. Пример этого подхода см., например, в "White-Box Cryptography and an AES Implementation" за авторством S. Chow, P. Eisen, H. Johnson, P.C. van Oorschot.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Известные контрмеры против атак компьютерных систем по сторонним каналам не являются полностью удовлетворительными. Например, внесению случайности можно противодействовать посредством статистического анализа. Обфускации программного обеспечения можно противодействовать посредством усовершенствованного анализа работы программы. Таким образом, существуют необходимость в лучших контрмерах и увеличению их количества.
Например, один подход к обфускации компьютерной программы состоит в кодировании входных значений и в работе, по мере возможности, над закодированными значениями. Для осуществления вычислений можно даже использовать так называемые табличные сети. Такую табличную сеть можно изготавливать вручную или посредством специализированных программ, например, в случае криптографии на основе белого ящика, или посредством компиляторов общего назначения. Предполагалось, что, вообще говоря, таблица затемняет тип осуществляемой операции. Однако авторы изобретения установили, что это, в целом, не соответствует действительности.
Даже если вход(ы) и выход(ы) функции кодируются, статистические свойства отношений входа/выхода могут указывать, какая функция кодируется. Ниже приведен пример этого явления.
Рассмотрим W={0, 1, …, N-1}, кодирование E, и его соответствующее декодирование D=E-1. Пусть F и G обозначают закодированное сложение по модулю N и закодированное умножение по модулю N, соответственно. Таким образом, по определению F: W×W→W как F(x,y)=E(D(x)⊕ND(y)), где ⊕N обозначает сложение по модулю N, и G: W×W→W как G(x,y)=E(D(x)*N D(y)), где *N обозначает умножение по модулю N.
Для каждого фиксированного x имеем {F(x,y)|y∈W}=W. Также, для каждого ненулевого x∈W и простого числа N, имеем {G(x,y)|y∈W}=W, и {G(0,y)|y∈W}=E(0). Для N, не являющегося простым числом, возникают аналогичные картины.
В результате, независимо от кодирования E, можно определить, что F не может быть закодированным умножением по модулю N, и что G не может быть закодированным сложением по модулю N. Нарушитель может делать это по меньшей мере двумя способами. Он может фиксировать два разных элемента x1 и x2 в W и для H∈{F,G}, сравнивать H(x1,y) и H(x2,y) для всех y. Если эти величины отличаются для всех y, то H не может представлять умножение по модулю N; если эти величины согласуются для некоторого y, то H не может представлять сложение по модулю N. Нарушитель, который не может выбрать, какие записи таблицы считывать, но может наблюдать результаты обращений выполняющейся программы, реализованной программными средствами, к таблице, может использовать тот факт, что каждый элемент W возникает также часто в качестве выхода, как с G, элемент E(0) возникает в качестве выхода гораздо чаще. Поэтому, если элемент W возникает гораздо чаще, чем другие элементы W в качестве выхода H, то H с гораздо большей вероятностью будет подверженным обфускации умножением по модулю N, чем подверженным обфускации сложением по модулю N.
Другими словами, даже в случае использования одного из наилучших доступных способов обфускации программного обеспечения, т.е. если использовать для вычислений полное кодирование входных и выходных значений и табличных сетей, то все же некоторую информацию можно получать путем обследования программы. Эта ситуация крайне нежелательна.
Было установлено, что эта проблема решается путем введения табличных сетей, которые действуют одновременно на множественных входных значениях. Табличная сеть может применять разные функции к разным входам или группам входов. Использование кодирования, которое шифрует в единое значение два или более из множественных входов совместно в единое значение, не позволяет нарушителю определять, для какой функции предназначена табличная сеть, поскольку, в действительности, она осуществляет две функции. См. предварительную заявку США № US 61/740,691, озаглавленную "Computing device comprising a table network", поданную 21 декабря 2012 г., и/или европейскую патентную заявку под тем же названием "Computing device comprising a table network", с датой подачи 27 декабря 2012 г. и номером дела EP12199387.
Хотя эта система значительно добавляет в безопасности, остается вектор атаки, в особенности, при дополнительном расширении модели атаки. Предполагается не только, что нарушитель имеет полный доступ, что позволяет ему наблюдать все, что происходит в системе, но также, что нарушитель способен модифицировать программу. Рассмотрим две таких модификации, модификация записей таблицы и модификация переменных. Первый тип модификации предполагает меньшие усилия со стороны нарушителя, поскольку изменение может происходить до начала выполнения программы; последний тип модификации осуществляется в ходе выполнения программы и поэтому считается более трудным. Например, нарушитель может попытаться предпринять следующую атаку (скорее всего, в автоматическом режиме). Он модифицирует запись в таблице и запускает модифицированную программу для различных входов. Если ни один из прогонов не показывает никакого различия в выходе исходной программы и модифицированной программы, то он заключает, что модифицированная запись таблицы и немодифицированная запись таблицы равны, если данные считаются соответствующими и отличаются только в вычислениях обфускации, т.е. так называемые переменные состояния и функции состояния. При наличии достаточного времени может быть построена карта из классов равных значений, если вычисление считается правильным. По сути, переменная состояния, таким образом, исключается. В частности, благодаря кодированию, нарушитель не будет способен наблюдать непосредственно, одинаковы ли значения данных, хотя значения состояния отличаются, но способен вывести это, анализируя результат модификаций таблицы.
Преимущественно было бы иметь вычислительное устройство, выполненное с возможностью вычисления функции данных на входном значении функции с повышенной устойчивостью к модификациям программы.
Предусмотрено вычислительное устройство, выполненное с возможностью вычисления функции данных на входном значении функции, которое решает, по меньшей мере, этот вопрос.
Вычислительное устройство содержит электронное хранилище и электронный процессор, подключенный к хранилищу. Электронное хранилище выполнено с возможностью хранения первой табличной сети, сконфигурированный для функции f данных, и второй табличной сети, выполненной с возможностью взаимодействия с первой табличной сетью для противодействия изменениям, вносимым в первую табличную сеть.
Процессор выполнен с возможностью, например, посредством надлежащего кода компьютерного процессора, получения множественных входов первой таблицы для первой табличной сети, причем множественные входы первой таблицы включают в себя входное значение функции, и вычисления функции данных путем применения первой табличной сети к множественным входам первой таблицы для создания множественных выходов первой таблицы, причем множественные выходы первой таблицы включают в себя выходное значение функции, причем выходное значение функции соответствует результату применения функции данных к входному значению функции.
Процессор также выполнен с возможностью получения множественных входов второй таблицы для второй табличной сети, причем входы второй таблицы включают в себя множественные выходы первой таблицы, и входы второй таблицы совместно используют по меньшей мере один вход с множественными входами первой таблицы, и применения второй табличной сети к множественным входам второй таблицы, причем вторая табличная сеть выполнена с возможностью проверки для, по меньшей мере, конкретного одного из множественных выходов первой таблицы, могла ли немодифицированная первая табличная сеть получить упомянутый конкретный один из множественных выходов первой таблицы из данного по меньшей мере одного из множественных входов первой таблицы.
Вторая табличная сеть создает выходы второй таблицы, включающие в себя защищенный выход функции, причем защищенный выход функции равен выходу функции в случае успешной проверки, и защищенный выход функции не равен выходу функции в случае неуспешной проверки. Например, вторую табличную сеть можно сконфигурировать так, чтобы защищенный выход функции всегда был неравным в случае неуспешной проверки. Однако, в преимущественной реализации выход рандомизируется, например, выход в случае неуспешной проверки выбирается случайным образом при построении таблиц. В последнем случае время от времени можно иметь равный выход. Используя переменные состояния и случайный выход в качестве эталона, можно требовать, чтобы выход был неравным в случае неуспешной проверки, по меньшей мере, в 90% случаев, т.е. всех записей таблицы, т.е. всевозможных входов первой таблицы.
Таким образом, это вычислительное устройство подвергается глубокой обфускации и защищается от изложенной выше атаки с модификацией. В действительности, первая табличная сеть действует над множественными входами и создает множественные выходы. Из множественных входов по меньшей мере один является входом в функцию данных, и из множественных выходов по меньшей мере один является выходом функции. В вышеупомянутой патентной заявке описано, что такие табличные сети можно строить по-разному. При таком построении функцию данных можно оценивать для всевозможных входных значений.
Вторая табличная сеть проверяет часть вычисления первой табличной сети. Для этого вторая табличная сеть принимает выход первой табличной сети, и совместно использует, по меньшей мере, часть множественных входов с первой табличной сетью. Поскольку вторая табличная сеть не обязана иметь все множественные входные значения, вторая табличная сеть не может осуществлять полное вычисление. Тем не менее, вторая табличная сеть выбирается таким образом, чтобы она могла осуществлять проверку для по меньшей мере одного из множественных выходов первой таблицы, могла ли немодифицированная первая табличная сеть обеспечить другое значение. Другими словами, вторая табличная сеть проверяет существование множественного входа первой таблицы, включающего в себя вводимый по меньшей мере один из множественных входов первой таблицы, из которых немодифицированная первая табличная сеть получает конкретный один из множественных выходов первой таблицы. Один практический путь для достижения этого состоит в осуществлении, частично или полностью, того же вычисления, которое осуществляла первая табличная сеть, но это не является строго необходимым, например, с учетом части входа функции можно заключить, что некоторые выходы функции стали невозможными. Также в последнем примере эта совместимость будет устанавливаться путем перечисления в ходе компиляции, и поиск ее будет осуществляться в ходе выполнения.
Вторая табличная сеть может совместно использовать вход с множественными входами первой таблицы по меньшей мере двумя способами. Первый вариант состоит в том, что один из входов первой табличной сети копируется во вторую табличную сеть. Следствие этого подхода состоит в том, что в случае, когда вход кодируется совместно с другими входами, они также будут входами во вторую табличную сеть. Это может приводить к созданию слишком крупных таблиц; до известной степени, это можно исправить с использованием таблиц извлечения, например таблиц извлечения состояния, для получения одного или более входов, например, состояния, из совместно кодируемых входов. Второй вариант предусматривает использование теневых переменных, то есть поддерживается один или более из множественных входов первой сети по меньшей мере дважды, возможных при разном кодировании. Например, первая табличная сеть может иметь входы функции и состояния, тогда как вторая табличная сеть совместно использует только входы состояния. В этом случае входы второй табличной сети не нужно непосредственно копировать из входов первой табличной сети; две сети имеют один или более общих входов, но общие входы не обязательно поступают непосредственно из одного и того же источника. Это может приводить к меньшим таблицам во второй табличной сети. С другой стороны, это требует, по меньшей мере, в частях программы, чтобы некоторые из переменных поддерживались дважды, т.е. в качестве так называемых теневых переменных.
В случае, когда вторая табличная сеть обнаруживает модификацию первой табличной сети, она модифицирует выход функции, т.е. выводит защищенный выход функции, не равный выходу функции. Это приводит к тому, что нарушитель будет видеть изменения вследствие своей модификации гораздо чаще, чем указывает вероятность. Например, даже если нарушитель модифицирует несвязанные данные (например, состояния), вторая табличная сеть может обнаруживать это, что, в свою очередь, приводит к распространению изменения на переменные данных. Вышеописанная атака становится гораздо труднее, а то и вовсе невозможной.
Согласно варианту осуществления, множественные входы первой таблицы дополнительно включают в себя входное значение состояния, и множественные выходы первой таблицы дополнительно включают в себя выходное значение состояния, причем выходное значение состояния равно результату применения функции состояния к входному значению состояния, и вторая табличная сеть выполнена с возможностью использовать в качестве входа входное значение состояния, вторая табличная сеть выполнена таким образом, что защищенный выход функции равен выходу функции в случае, когда результат применения функции состояния к входному значению состояния равен значению состояния, включенному во множественные выходы первой таблицы, вводимые во вторую табличную сеть.
Вычисление независимо друг от друга двух функций, функции данных и функции состояния, в одной и той же табличной сети дает возможность проверять одну из них. Таким образом, объем работы, которая должна быть выполнена во второй табличной сети, уменьшается. В результате, можно построить вторую табличную сеть с меньшим количеством входов, что приводит к значительно меньшей таблице.
Согласно варианту осуществления, первая табличная сеть выполнена с возможностью использовать в качестве входа закодированное входное значение, причем закодированное входное значение объединяет входное значение функции с входным значением состояния, совместно кодируемые в единое значение, и первая табличная сеть выполнена с возможностью создания, в качестве выхода, первого закодированного выходного значения, причем первое закодированное выходное значение объединяет выходное значение функции с выходным значением состояния, совместно кодируемые в единое значение, причем выходное значение состояния равно результату применения функции состояния к входному значению состояния, вторая табличная сеть выполнена с возможностью использовать в качестве входа первое закодированное выходное значение первой табличной сети и по меньшей мере одно из входного значения состояния и входного значения функции, причем вторая табличная сеть выполнена с возможностью создания, в качестве выхода, второго закодированного выходного значения, причем закодированное выходное значение содержит защищенный выход функции.
Совместное кодирование некоторых или всех из множественных входов и/или некоторых или всех из множественных выходов значительно затрудняет реверсивное проектирование устройства. Нарушитель не знает непосредственно, что представляет значение, или чем в действительности является значение.
Кодирование (часто обозначаемое ‘E’) является, по меньшей мере, частично обратимым, то есть, для некоторых кодированных пар входного значения функции и входного значения состояния, входное значение функции и/или входное значение состояния можно восстановить; аналогично, для закодированной пары выходного значения функции и выходного значения состояния. В практической реализации операции кодирования обычно выбираются как полностью обратимые, хотя, как упомянуто выше, это не является строго необходимым. Таким образом, для полностью обратимого кодирования можно восстановить как входное значение функции, так и входное значение состояния для любой закодированной пары входного значения функции и входного значения состояния. Аналогично, из закодированной пары выходного значения функции и выходного значения состояния можно восстановить выходное значение функции и выходное значение состояния.
Кодирование является частным, то есть в разных реализациях системы могут по-разному совместно кодировать входные или выходные значения.
Кроме того, кодирование наследует, по меньшей мере частично, принцип диффузии. Значения в закодированном значении зависят от большой части закодированного значения. Например, при восстановлении входного/выходного значения из закодированного входного/выходного значения входное/выходное значение зависит, предпочтительно, от всех закодированных входных/выходных значений; по меньшей мере, оно зависит от большего количества битов, чем битовый размер самого входного/выходного значения. Это приводит к тому, что информация о входном/выходном значении распределяется по многим битам. Предпочтительно, чтобы при наличии доступа только к части закодированного значения было невозможно восстановить значения, которые оно кодирует, даже если в точности знать функцию кодирования/декодирования. Заметим, что традиционно при шифровании часто используется ключ. Использование кодирования на основе ключа является привлекательной возможностью, но в силу сравнительно малого размера входных/выходных значений кодирование также можно представить в виде таблицы. По этой причине кодирование и шифрование в контексте значений переменных, например, входных/выходных значений или промежуточных значений, используются взаимозаменяемо.
Поскольку табличная сеть может представлять две функции, и, в действительности, закодированные входные значения содержат два входа (функции и состояния), из табличной сети невозможно определить, относится ли закодированная версия к функции данных или функции состояния. В действительности, табличная сеть обеспечена полностью для вычисления любой функции и, в действительности, не вычисляет обе функции от независимой переменной или множества переменных (в вариантах осуществления функций данных и/или функций состояния имеющих множественные входы).
Например, применительно к вышеприведенному примеру будет получена табличная сеть, которую можно использовать для осуществления сложения и умножения. Обследуя табличную сеть, не удается определить, какое из них используется, поскольку фактически табличная сеть может осуществлять любое из них.
Функция данных может принимать одно или несколько входных значений. Функция состояния может принимать одно или несколько входных значений. Согласно варианту осуществления, количество входных значений функции данных и состояния одинаково. Например, устройство может быть выполнено с возможностью получения множественных входных значений функции в качестве множественных закодированных входных значений. Каждое из множественных закодированных входных значений объединяет входное значение функции множественных входных значений с входным значением состояния множественных входных значений состояния, совместно зашифрованные в единое значение. Табличная сеть выполнена с возможностью использовать в качестве входа множественные кодированные входные значения и создавать в качестве выхода закодированное выходное значение. Закодированное выходное значение объединяет выходное значение функции с выходным значением состояния, совместно зашифрованные в единое значение. Выходное значение функции равно результату применения функции данных к множественным входным значениям функции, и выходное значение состояния равно результату применения функции состояния к множественным входным значениям состояния.
Согласно варианту осуществления, вторая табличная сеть выполнена с возможностью создания, в качестве выхода, второго закодированного выходного значения, причем закодированное выходное значение объединяет защищенное выходное значение функции с защищенным выходным значением состояния, совместно зашифрованные в единое значение, причем защищенное выходное значение состояния равно результату применения перестановки состояний к выходному значению состояния.
Добавление второй табличной сети, которая противодействует модификациям первой сети, дополнительно затрудняет атаку на систему. Однако если нарушитель может найти вторую табличная сеть, он может определить из ее выхода, совершила ли она изменение. Всегда модифицируя значение состояния в выходе второй табличной сети, нарушитель не может понять, нужна ли вторая табличная сеть для применения изменения к выходу функции, поскольку закодированное значение будет меняться целиком, даже если только одно значение в ней изменяется.
Согласно варианту осуществления, вторая табличная сеть содержит таблицу состояний и сеть таблиц совмещения, причем таблица состояний сконфигурирована для функции состояния, процессор выполнен с возможностью применения таблицы состояний к входному значению состояния для получения параллельного выходного значения состояния, сеть таблиц совмещения выполнена с возможностью принимать в качестве входа, по меньшей мере, параллельное выходное значение состояния и выходное значение состояния, принятое от первой табличной сети. Таким образом, таблицы состояния могут быть параллельными таблицами функций. Множественные таблицы состояния и функций могут использоваться до осуществления сети таблиц совмещения. Это сокращает количество проверок, проводимых в отношении модификации, в процессе их обнаружения. Таким образом, размер кода уменьшается.
Согласно варианту осуществления, вторая табличная сеть содержит модифицированную таблицу состояний и сеть таблиц совмещения, причем таблица состояний выполнена с возможностью принимать в качестве входа входное значение состояния и вычислять модифицированное значение состояния, причем модифицированное значение состояния равно результату применения функции состояния к входному значению состояния, а затем дополнительной функции состояния, сеть таблиц совмещения выполнена с возможностью использовать в качестве входа выходное значение состояния и модифицированное выходное значение состояния и проверять, что дополнительная функция состояния, применяемая к выходному значению состояния, дает модифицированное выходное значение состояния.
В таблице состояний осуществляется композиция функций для функции состояния и дополнительной функции состояния, тогда как в первой табличной сети используется только функция состояния. Таблица совмещения проверяет, имеет ли переменная состояния предполагаемое значение. Заметим, что выход проверяется не обязательно в отношении того, как он получен. Это защищает от атак, которые пытаются удалить сеть таблиц совмещения и заменить ее выход, например, выходом первой табличной сети. Такая попытка не увенчается успехом, поскольку переменная состояния и переменная данных больше не выполняются параллельно.
Второй табличной сети не требуется работать над значениями состояния; могут использоваться другие части множественных входов. Согласно варианту осуществления, вторая табличная сеть выполнена с возможностью использовать в качестве входа входное значение функции, вторая табличная сеть выполнена таким образом, что защищенный выход функции равен выходу функции в случае, когда результат применения функции данных к входному значению функции равен выходному значению функции, закодированному в первом закодированном выходном значении.
Вход и выход функции могут иметь 4, 5, 6, 7 или 8 битов, возможно, еще больше, например 16 битов, входные и выходные значения состояния одного размера, или, возможно, меньше, например 2 или 3 бита. Практически, значения функции и состояния, выбираются каждые 4 бита, и закодированные значения, содержащие значение функции и состояния, как 8 битов.
Аспект изобретения относится к компилятору, выполненному с возможностью приема функции данных и создания первой и второй табличной сети, в котором первая табличная сеть выполнена с возможностью принимать множественные входы первой таблицы для первой табличной сети, причем множественные входы первой таблицы включают в себя входное значение функции, и создавать множественные выходы первой таблицы, причем множественные выходы первой таблицы включают в себя выходное значение функции, причем выходное значение функции соответствует результату применения функции данных к входному значению функции, вторая табличная сеть выполнена с возможностью взаимодействия с первой табличной сетью для противодействия модификациям, вносимым в первую табличную сеть, вторая табличная сеть выполнена с возможностью принимать множественные входы второй таблицы, причем входы второй таблицы включают в себя множественные выходы первой таблицы и по меньшей мере, один из множественных входов первой таблицы, причем вторая табличная сеть выполнена с возможностью проверки для, по меньшей мере, конкретного одного из множественных выходов первой таблицы, могла ли немодифицированная первая табличная сеть получить упомянутый конкретный один из множественных выходов первой таблицы из данного по меньшей мере одного из множественных входов первой таблицы, вторая табличная сеть создает выходы второй таблицы, включающие в себя защищенный выход функции, причем защищенный выход функции равен выходу функции в случае успешной проверки, и защищенный выход функции не равен выходу функции в случае неуспешной проверки.
Вычислительное устройство представляет собой электронное устройство, например, мобильное электронное устройство, мобильный телефон, телевизионную приставку, компьютер и т.п.
Способ согласно изобретению можно реализовать на компьютере в виде реализуемого компьютером способа или в специализированном оборудовании, или их комбинации. Исполнимый код для способа согласно изобретению может храниться в виде компьютерного программного продукта. Примеры компьютерных программных продуктов включают в себя запоминающие устройства, оптические запоминающие устройства, интегральные схемы, серверы, онлайновое программное обеспечение и т.д. Предпочтительно, компьютерный программный продукт содержит нетранзиторное средство программного кода, хранящееся на считываемом-компьютером носителе для осуществления способа согласно изобретению, когда упомянутый программный продукт выполняется на компьютере.
В предпочтительном варианте осуществления, компьютерная программа содержит средство кода компьютерной программы, выполненное с возможностью осуществления всех этапов способа согласно изобретению, когда компьютерная программа выполняется на компьютере. Предпочтительно, компьютерная программа реализована на считываемом-компьютером носителе.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Эти и другие особенности изобретения очевидны из описанных ниже вариантов осуществления и будут объясняться со ссылкой на них. На чертежах:
Фиг. 1 - схематическая диаграмма, иллюстрирующая табличную сеть, реализующую функцию данных и функцию состояния,
Фиг. 2 - блок-схема, иллюстрирующая вычислительные устройства 202 и 204, конфигурируемые с помощью табличной сети,
Фиг. 3 - блок-схема, иллюстрирующая табличную сеть,
Фиг. 4 - блок-схема, иллюстрирующая табличные сети в целом,
Фиг. 5 - блок-схема, иллюстрирующая вычислительное устройство,
Фиг. 6 - блок-схема алгоритма, иллюстрирующая компилятор,
Фиг. 7 - блок-схема алгоритма, иллюстрирующая способ для вычисления функции,
Фиг. 8a и 8b - блок-схемы, иллюстрирующие табличную сеть,
Фиг. 9 - схема, иллюстрирующая процесс выполнения программы.
Следует отметить, что элементы, которые имеют одинаковые ссылочные позиции на разных фигурах, обладают одинаковыми структурными признаками и одинаковыми функциями либо одинаковыми сигналами. Там, где объяснена функция и/или структура такого элемента, отсутствует необходимость его повторяющегося объяснения в подробном описании.
ПОДРОБНЫЕ ВАРИАНТЫ ОСУЩЕСТВЛЕНИЯ
Хотя это изобретение допускает вариант осуществления во многих разных формах, один или более конкретных вариантов осуществления показаны на чертежах и будут подробно описаны в этом документе исходя из предположения, что настоящее раскрытие изобретения нужно рассматривать как пример принципов изобретения, и оно не имеет целью ограничить изобретение конкретными показанными и описанными вариантами осуществления.
Фиг. 4 иллюстрирует обобщенное понятие табличной сети, показанной в виде табличной сети 400. Большинство функций может быть выражено в виде сети таблиц. В частности, так можно выразить любую композицию арифметических и логических операций. Например, сеть таблиц может быть некоторой реализацией, например, шифра. Показано 8 таблиц из множественных таблиц. Таблица преобразует входное значение в выходное значение путем поиска входного значения по таблице. Показаны три входные таблицы 410 для приема входных данных извне по отношению к реализации функции. Показана одна из выходных таблиц 430. Выходные таблицы 430 совместно образуют выход реализации функции, например путем конкатенации. Показаны четыре таблицы из промежуточных таблиц 420, 422, 424, 426, которые принимают по меньшей мере один вход от другой из таблиц, и которые создают результат для использования в качестве входа по меньшей мере для одной другой таблицы; например, на схеме промежуточные таблицы 422 и 410 предоставляют вход для таблицы 426. Таблицы совместно образуют сеть. Шифр может быть блочным шифром; блочный шифр может конфигурироваться для шифрования или для дешифрования. Блочный шифр шифрует некий блок, например AES. Реализация может быть предназначена для конкретного ключа, и в этом случае таблицы могут зависеть от конкретного ключа.
Поисковая таблица 426 представляет собой оператор, имеющий два входа и один выход. Построение поисковых таблиц для одноместных операторов можно распространить на двухместные операторы. Например, второй вход может быть "каррированным"; согласно методу преобразования функций, каррирование является методом преобразования функции, который принимает n множественных аргументов (или кортеж из n аргументов) таким образом, что это можно назвать цепочкой функций, причем каждая - с единичным аргументом. Когда используется этот подход, поисковая таблица 426 реализуется в виде множественных одноместных поисковых таблиц. С другой стороны, также можно сформировать битовые строки для каждого входа и объединить результаты. Таким образом, непосредственно генерируется поисковая таблица, и получается одна единственная, но более крупная поисковая таблица. Хотя компоновка поисковых таблиц может отличаться на основе этого построения, они имеют равный размер и одинаковые свойства. Заметим, что не требуется, чтобы множественные входные значения кодировались в соответствии с одинаковым кодированием.
Табличная сеть может использовать множественные таблицы, кодирующие две функции, или иметь в качестве подсети табличные сети, которые кодируют для двух функций. Кроме того, табличная сеть может заключать в себе одну или первую и вторую табличную сеть, чтобы нарушитель не мог использовать модификацию таблицы и/или переменной для получения полезной информации о системе.
Система может конфигурироваться для использования той функции состояния или данных в табличной сети в зависимости от текущего кодирования. Методы обфускации табличных сетей могут применяться также в табличных сетях, как описано в этом документе.
Например, предположим, что вторая таблица принимает выход первой таблицы в качестве входа, тогда выход первой таблицы можно кодировать с помощью секретного кодирования, например, выбранного случайным образом, и вход второй таблицы можно кодировать с помощью обратного кодирования.
На Фиг. 1 показана табличная сеть 180, вложенная в более крупную табличную сеть 100. Можно видеть, что табличная сеть 180 содержит только одну таблицу 130. Как отмечается, можно реализовать таблицу 130 в виде табличной сети с компромиссом, например, между размером таблицы и безопасностью. На фиг. 1 таблицы представлены с помощью прямоугольников, а значения представлены с помощью прямоугольника с отрезанным правым верхним углом.
Табличная сеть 180 выполнена с возможностью использовать множественные закодированные входные значения в качестве входа, и показаны закодированные входные значения 122 и 124. Табличная сеть 180 выполнена с возможностью создания в качестве выхода закодированного выходного значения 160. В описании ниже будем предполагать функции данных и функции состояния, имеющие два входных значения и единое выходное значение. Однако варианты осуществления можно распространить на любое количество входных значений и/или выходных значений. В частности, возможны функции данных/состояния с одним входом и одним выходом, и возможны функции данных/состояния с двумя входами и одним выходом.
Табличная сеть 180 сконфигурирована для функции данных и хранится в электронном хранилище, подключенном к электронному процессору, выполненному с возможностью вычисления функции данных путем применения табличной сети.
Закодированное значение 122 получается из входного значения 102 функции и входного значения 112 состояния. Например, эту операцию может выполнять кодер 110. Кодер 110 может входить в состав того же устройства, где хранится табличная сеть 180, но не обязательно. Входные значения могут приниматься уже в закодированной форме и/или передаваться в закодированной форме. Либо они могут приниматься/передаваться в незакодированной форме. В последнем случае их можно кодировать и использовать внутри в закодированной форме. Также может иметь место перекодирование, например, если вне устройства используется другое кодирование. Например, выходное значение 162 функции и выходное значение 164 состояния можно получить из декодера 170.
Закодированный вход функции данных может быть выходом другой таблицы либо табличной сети. Последняя может быть или не быть табличной сетью, сконфигурированной для двух функций. Путем объединения табличных сетей, сконфигурированных для разных функций данных, можно построить все программы.
Кодер/декодер 110 и 170 можно реализовать как устройства, выполняющие взаимно обратные операции. Кодер 110 можно реализовать следующим образом. Формируется список всех возможных комбинаций входного значения функции и входного значения состояния. Например, если оба они являются 4-битовыми, то существует 16*16=256 возможных комбинаций. Можно задать произвольную биекцию множества из 256 комбинаций самого в себя. То же самое применяется к другим размерам. Также можно использовать функцию шифрования, например, можно применять 8-битовый блочный шифр с использованием некоторого секретного ключа кодирования.
Закодированное входное значение содержит взаимозависимые входное значение 102 функции и входное значение 112 состояния, например вход функции может зависеть от всех битов закодированного входа. Таким образом, зная лишь часть закодированного входного значения 122, в общем случае, невозможно найти ни входное значение 102 функции, ни входное значение 112 состояния.
Ряд вариантов осуществления представлен ниже с использованием языка математики. Одно преимущество объединения входных значений функции со значениями состояния состоит в том, что входы функции имеют множественные представления. Функция f относится к функции данных, а g - к функции состояния. Функция f кодируется в F таким образом, что значение в области F имеет множественные экземпляры. Чтобы скрыть, какая функция f кодируется, вход(ы) и выход(ы) f имеют множественные представления в области и диапазоне закодированной версии F для f. Функция F строится таким образом, что всякий раз, когда X является экземпляром x, F(X) является экземпляром f(x). В дальнейшем иногда употребляется термин "длинная" переменная (вход/выход F) и "короткая" переменная (вход/выход f), чтобы подчеркнуть, что каждый вход/выход f соответствует множественному входу/выходу F, в результате чего для представления входов/выходов из F обычно требуется больше битов, чем для представления входов/выходов из f. Ниже описан один подход к получению множественных представлений для операндов. Снова заметим, что для простоты рассматриваются функции с равными входными и выходными символами; это допускает обобщение.
Пусть W обозначает множество операндов, которые нужно закодировать. Введем конечное множество ∑ "состояний" и конечное множество V с кардинальным числом, равным произведению кардинальных чисел W и ∑. Секретная функция E кодирования обеспечивает взаимно-однозначное отображение элементов W×∑ в V. Экземпляры элемента w в W являются элементами множества
Ω(w)={E(w,σ)|σ∈∑}.
Количество экземпляров каждого элемента в W, таким образом, равно кардинальному числу для ∑. В результате тракты данных, переносящие символы от V, шире трактов данных для переноса символов от W. Например, если W является множеством 16-битовых целых чисел, и пространство ∑ состояний имеет 16=24 элементов, то тракты данных для V используют 16+4=20 битов, тогда как тракты данных для W используют 16 битов.
Нижеследующий вариант осуществления кодирует функцию двух переменных. Рассмотрим функцию f: W×W→W, которую нужно кодировать. Строим функцию F: V×V→V таким образом, что для всех w1,w2∈W и σ1,σ2∈∑ имеем
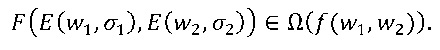
Иными словами: F отображает любую пару экземпляров w1 и w2 в экземпляр f(w1,w2).
Состояние экземпляра f(w1,w2) может зависеть от обоих операндов w1 и w2, и даже могло бы зависеть от обоих состояний σ1 и σ2, детерминистически или случайно. Точнее говоря, состояние может зависеть только от состояний σ1 и σ2, что можно реализовать путем принятия функции g: ∑×∑→∑ и путем задания
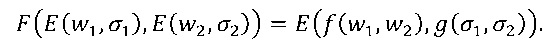
Возникает любопытный частный случай вышеприведенного варианта осуществления, если допустить ∑=W. Тогда функция F, которая кодирует f с использованием функции E, также кодирует функцию g, хотя и с другой функцией Ẽ кодирования. Таким образом, нельзя логически вывести, какая из двух функций, f или g, реализуется с помощью F. Зададим Ẽ (x,y)=E (y,x). Путем вычисления находим, что
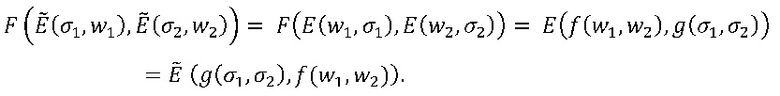
Таблица для F, таким образом, реализует функцию f, если используется кодирование E, и функцию g, если в качестве функции кодирования используется Ẽ. Таким образом, доказано, что из одной только таблицы 130 невозможно определить, какая функция используется, поскольку она могла бы кодировать по меньшей мере две функции.
Таблица для F может служить для вычисления как f, так и g. В действительности, если используется E, то таблица для F реализует f, как упоминалось раньше. Та же таблица может также использоваться для реализации g путем предварительной и последующей обработки входов и выходов с помощью функции ẼE-1. Точнее говоря, пусть w1,w2∈W, σ1,σ2∈∑, и зададим vi=E(wi,σi), i=1, 2. Тогда имеем
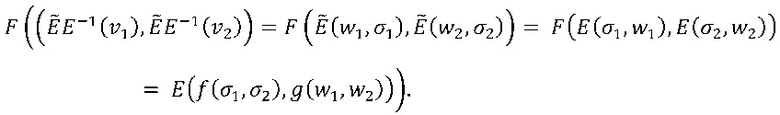
Следовательно, имеем
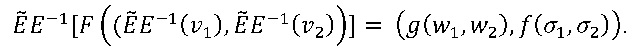
Закодированные входные значения могут быть входными значениями в компьютерную программу, возможно, содержащими функцию данных или представленными ей. Компьютерная программа может выполняться на компьютере. Инструкции компьютерной программы можно представить с помощью функции данных. Операции кодирования и операции декодирования могут управляться секретным ключом. Сами таблицы кодирования и декодирования могут рассматриваться как такой ключ. Если применяется инструкция f, действующая над данными, закодированными с помощью кодирования Ek, то она сначала декодирует данные, затем f применяется к декодированным данным, и результат впоследствии опять кодируется. Таким образом, данные x обеспечивают выход F(x)=Ek(f(Dk(x))). Путем непосредственного сохранения функции F, например, в виде поисковой таблицы, скрывается функция f и ее семантика. В конкретном варианте осуществления декодирование является левой обратной функцией кодирования, то есть DkEk(x))=x для всех x. Преимущество обеспечивается за счет того, что, если две функции f и g кодируются и декодируются с помощью одинаковых функций Ek и Dk, то закодированную версию функции f(g(x)) можно получить с помощью последовательного использования таблиц для G(x)=Ek(g(Dk(x))) и F(x)=Ek(f(Dk(x))). В действительности видно, что для каждого x имеем Ek(f(g(Dk(x))))=F(G(x)), так что закодированную версию для f(g(x)) можно получить из последующих обращений к таблицам для G и для F. Таким образом, можно применять последовательности операций без кодирования и декодирования между последовательными операциями, таким образом, значительно повышая безопасность. Согласно варианту осуществления, кодирование и декодирование осуществляются только на защищенной стороне, тогда как все закодированные операции осуществляются на открытой, незащищенной стороне. Выход(ы) одной или более закодированных функций может служить в качестве входа(ов) в другую закодированную функцию. Как было показано выше, это можно без труда организовать, если операции кодирования и операции декодирования являются взаимно обратными. Предпочтительный вариант осуществления для выполнения последовательности операций согласно настоящему изобретению выглядит следующим образом. Сначала в защищенной области "короткие" переменные преобразуются в "длинные" переменные. Привлекается рандомизация, чтобы убедиться, что "длинные" переменные возникают приблизительно так же часто. Этого можно добиться, например, с помощью устройства, которое формирует случайное состояние σ∈∑, и отображения переменной x в Ek(x,σ), где Ek является кодированием "длинных" переменных. После всех вычислений на открытой стороне, проходящих с использованием "длинных" переменных, на защищенной стороне применяется декодирование Dk, и затем определяется "короткая" переменная, соответствующая декодированной длинной переменной. В качестве альтернативы декодирование и определение короткой переменной осуществляется на одном, объединенном этапе. Буква k обозначает секретный, например, секретный ключ.
Наличие множественных экземпляров для переменных подразумевает, что тракты данных становятся длиннее. Также это подразумевает, что становится больше таблица для реализации закодированной версии F от f. Например, рассмотрим функцию f(x,y), которая в качестве входа имеет две 16-битовые переменные x и y, а в качестве выхода - 16-битовую переменную. Таблица для реализации закодированной версии f в отсутствие множественных экземпляров использует таблицу с 216×216 записями, причем каждая запись таблицы является 16-битовой, что равносильно размеру таблицы 236 битов. Теперь предположим, что каждая 16-битовая переменная имеет 16 экземпляров; множество экземпляров, таким образом, можно представить 20 битами. Теперь будем использовать таблицу с 220×220 записями, причем каждая запись таблицы является 20-битовой, что равносильно таблице с размером 5×242 битов. Таким образом, таблица в 5×26=320 раз больше, чем без множественных экземпляров.
Ниже приводится пример построения кодера 110, декодера 170 и таблиц 212 и 214 средства извлечения состояния. Предположим единый вход функции и единый вход состояния (и того, и другого может быть больше), каждый по 4 бита.
Два первых столбца перечисляют все возможные комбинации входных значений функции и входных значений состояния. Последний столбец перечисляет случайную перестановку числа от 0 до 255 в двоичном виде. Заметим, что шифрование является безупречным в том смысле, что даже при точном знании 256 – 2=254 пар входа-выхода две оставшиеся пары по-прежнему имеют один бит неопределенности. Безупречное кодирование в теоретико-информационном смысле желательно, но не является необходимым для хороших результатов; например, менее безупречное, но все же очень практичное кодирование можно получить с использованием, например, 8-битного блочного шифра, т.е. блочного шифра, имеющего размер блока, равный сумме входа функции и входа состояния.
Таблица кодирования получается путем сортировки по первым двум столбцам, результирующая таблица показывает, как получить последний столбец (кодирование) из первых двух. Сортировка по последнему столбцу дает таблицу, которая декодирует вместо кодирования. Удаление первого столбца и сортировка по последнему столбцу дает функцию средства извлечения состояния. Заметим, что в целом не нужно хранить входной и выходной столбец. Например, если входной столбец сортируется и содержит все возможные комбинации, то его можно исключить.
Фиг. 2 иллюстрирует табличные сети 204 и 202 для использования в вычислительном устройстве, имеющем электронное хранилище и электронный процессор, например устройстве, показанном на фиг. 5 (см. ниже).
Для табличной сети 202 показаны две первые табличные сети 212 и 214. Первая таблица 214 в качестве входа использует выход 216 первой таблицы 212. Табличные сети 212 и 214 могут относиться к типу табличной сети 180. Первая таблица 212 принимает множественные входы 210 и создает множественные выходы, среди входов присутствует входное значение функции, а среди выходов присутствует выходное значение функции. Для наглядности схем, множественные входы и множественные выходы не показаны по отдельности, если это не считается полезным при описании. Выходное значение функции для таблицы 212 используется в качестве дополнительного входа для таблицы 214, которая, в свою очередь, создает множественные выходы. Множественные входы и выходы таблиц 212 и 214 кодируются, чтобы нарушитель не смог определить, по меньшей мере, не из единого значения, какая часть соответствует фактическим данным, а какая - нет. Например, таблицы 212 и 214 могут принимать в качестве входа один или более закодированных входов, каждый из которых объединяет вход функции с входом состояния, и каждый может создавать один или более закодированных выходов. Часто используемой комбинацией является прием двух или более закодированных входов и создание одного закодированного выхода.
Использование сети 202 является преимущественным, поскольку таблицы 212 и 214 выполняют вычисления над данными, которые не являются непосредственно релевантными для конечных результатов программы, частью которой является табличная сеть 202. Однако нарушитель способен атаковать систему путем модификации записей таблицы и наблюдения результата. Он ищет изменения, которые, по его мнению, не влияют на работу программы, поскольку из этого он может заключить, что исходные и модифицированные значения равны, так как рассматриваются данные функции.
Для предотвращения этой атаки табличная сеть 204 строится как альтернатива табличной сети 202. Табличная сеть 204 содержит первые табличные сети 222 и 224, и, дополнительно, табличные сети 232 и 234. Первые табличные сети 222 и 224 можно выбрать в равными таблицам 212 и 214 соответственно.
Табличная сеть 232 в качестве входа принимает выход 226 табличной сети 222 и совместно использует по меньшей мере часть своего входа с входами 220 табличной сети 222. Вторая табличная сеть способна проверять, совместимы ли выходы 226, принятые из таблицы 222, с тем, что таблица 232 получает из входов 220. В частности, таблица 232 проверяет, по меньшей мере, для конкретного, а, предпочтительнее, для всех множественных выходов 226 первой таблицы, могла ли немодифицированная первая табличная сеть 222 получить конкретный из множественных выходов первой таблицы из заданного по меньшей мере одного из множественных входов первой таблицы. Таблица (или табличная сеть) 232 может выполнять это с помощью операции поиска в таблице. В ходе построения таблицы 232 определяется, чем являются всевозможные входы 220, и чем являются все соответствующие выходы 226, фактически, это может быть частью построения самой таблицы 222. Далее создается таблица, которая для каждой комбинации входа и выхода таблицы 232 отмечает, соответствует ли она паре входа/выхода таблицы 222. На основе этого определения таблица 232 имеет разный выход (см. ниже). Другими словами, таблица 222 определяет существование множественного входа первой таблицы, включающего в себя вводимый по меньшей мере один из множественных входов первой таблицы, из которых немодифицированная первая табличная сеть получает конкретный один из множественных выходов первой таблицы.
Практическим способом достижения этого является наличие одного выхода из 226, который вычисляется только из части входов 220. Например, входы 220 могут содержать вход состояния и функции. Выход 226 может содержать выход функции, который является функцией, применяемой к входу функции, и выход состояния. Выход состояния зависит, предпочтительно, только от входа состояния, но также может зависеть от входа функции. Принимая во внимание вход функции и все выходы таблицы 222, таблица 232 может проверить, что вход функции и выход функции соответствуют, т.е., дает ли выход функции функция данных, применяемая к входу функции. Альтернативно или дополнительно, принимая во внимание вход состояния и все выходы таблицы 222, таблица 232 может проверить, что вход состояния и выход состояния соответствуют, т.е., дает ли выход состояния функция состояния, применяемая к входу состояния. В предпочтительных вариантах осуществления вторая табличная сеть, по меньшей мере, проверяет переменные состояния. Выявление такого рода ошибок (т.е. модифицированного состояния) считается важным, поскольку они могут приводить к немодифицированному выходу программы (т.е. если значение функции оказывается не измененным). Последний вид изменений несет особенно много информации для нарушителя.
Обычно таблица 232 будет перенаправлять выход из 226 для использования в следующей таблице/табличной сети, выполняя, возможно, некоторый этап обработки над ним. Однако если таблица 232 обнаруживает ошибку, т.е. входы и выходы таблицы 222 можно получить только путем вмешательства в таблицу 222 или, возможно, в сами переменные, то таблица 232 рандомизирует, по меньшей мере, часть выхода 226 перед его передачей. Под выходным значением, которое проходит через вторую табличную сеть, подразумевается защищенное выходное значение. Защищенное значение полезно для дальнейшего вычисления, если никакой ошибки не обнаружено, но подвергнуто рандомизации, если было обнаружено вмешательство.
Эффект защищенных переменных состоит в том, что информация, которую можно узнать путем вмешательства, значительно уменьшается. Нарушитель обнаружит, что если он вмешивается, то выход изменяется, и программа не будет функционировать нормально, но это нужно предполагать при вмешательстве; нарушитель не узнает ничего из этого факта как такового. Однако вследствие рандомизации исчезает полезная информация, например какие изменения соответствуют состоянию, а какие - данным функции. Рандомизация предпочтительна, но также возможны более тонкие изменения при условии, что защищенный выход функции не равен выходу функции в случае неуспешной проверки. Заметим, что рандомизация фиксируется в таблице(ах) в ходе их построения. Для применения табличной сети не нужен никакой генератор случайных чисел.
Выход таблицы 232 перенаправляется в следующую табличную сеть, здесь это таблицы 224 и 234. Это соответствует таблице 214, которая принимала бы выход в незащищенной сети. Здесь 224 является первой табличной сетью, а 234 является второй табличной сетью.
Табличная сеть 204 хранится в электронном хранилище, например, флэш-памяти или RAM, и используется электронным процессором, т.е. путем применения табличной сети к данным, принятым извне устройства или сгенерированным в устройстве. Заметим, что в типичных вариантах осуществления входы в табличную сеть кодируются в соответствии с кодированием, секретным для нарушителя. Для табличных сетей кодирование является прозрачным, оно не привлекает никакой дополнительной обработки после того, как создается таблица. Таким образом, применение таблицы к простому значению или к закодированному значению одинаково в требовании к обработке. Заметим, что операции кодирования можно легко изменять между таблицами. Кодирование является отображением между простым значением и значением, используемым внутри.
Предпочтительно, чтобы табличная сеть 204 действовала над переменными, которые объединяют значение функции со значением состояния. Поскольку система также вычисляет значения состояния, нарушитель не может отличить из таблицы, для какой функции она осуществляет кодирование, поскольку таблица одновременно осуществляет две функции. Роль переменной состояния и переменной функции может чередоваться по ходу программы. В этих вариантах осуществления таблицы выполняют две функции одновременно. Однако количество функций, выполняемых одновременно, также можно выбрать больше, дополнительно усложняя анализ нарушителем. Например, таблица может представлять три функции, например функцию данных и первую и вторую функцию состояния; возможны еще большие количества функций, например 4 или 5.
Ниже на языке математики приводится список возможных вариантов осуществления второй табличной сети. В этих примерах u, v, x, y являются переменными, которые кодируют значение функции и значение состояния; p, q, a являются значениями состояния; w является значением функции. Переменная v является окончательным результатом первой и второй табличной сети, который может использоваться в дальнейшей обработке, например, таблиц. Функция f является функцией данных; g, g1 и g2 являются функциями состояния. Функция σ является средством извлечения состояния, ρ - средством извлечения значения функции, а E - функцией кодера, т.е. σ(E(w,p))=p и ρ(E(w,p))=w; все эти функции можно реализовать в виде таблиц.
Функция P является функцией над переменными состояния, предпочтительно, перестановкой. Функция F соответствует f, но переносится в закодированную область, т.е.
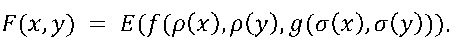
Буква z обозначает функцию совмещения, если первый вход соответствует второму и дополнительным входам, выход является первым входом, возможно, с некоторой дополнительной обработкой, если нет, то выход изменяется, например, рандомизируется.
В этих вариантах осуществления таблицы действуют на двух входах функции. Однако число входов может выбираться по желанию. Система может применяться к функциям с одиночным входом, но, что интересно, также к функциям с множественными входами. В качестве примера будем использовать состояние и функции, которые составляют 4 бита, и объединенные операции их кодирования, которые составляют 8 бит. Конечно, возможны другие размеры; например, 2 бита для состояния, 6 бит для функции и т. д.
Во всех примерах ниже первая табличная сеть реализует функцию u=F(x,y). Это может выполняться одной таблицей с двумя закодированными входами и одним закодированным выходом.
Вторая табличная сеть может быть любым из следующего:
1. Вторая табличная сеть в качестве входа принимает x, y и u, т.е. все входы и выход первой табличной сети. Вторая табличная сеть содержит три таблицы. Первые две являются средствами извлечения состояния, а третья является таблицей совмещения: Вход x, y. P=σ(x); q=σ(y); v=E(z(u,p,q), P(σ(u))). Здесь z(u,p,q)=ρ(u), если g(p,q)=σ(u), и случайная в противном случае. Другими словами, вторая табличная сеть проверяет, что первая табличная сеть правильно вычислила функцию состояния. Если проверка успешна, то u и v имеют равные значения, но разные состояния. Если проверка обнаруживает ошибку, то значение v отличается от значения u. Заметим, что состояние принимает искажение в виде перестановки P. Этот вариант осуществления использует три таблицы с размерами входа 8, 8 и 16 бит.
2. Вторая табличная сеть в качестве входа принимает x, y и u. Вторая табличная сеть содержит одну таблицу. Вход x, y. V=E(z(u,x,y), P(σ(u))). Здесь z(u,x,y)=ρ(u), если F(x,y)=u, и случайная в противном случае. Здесь проверяется полное вычисление первой табличной сети. Таблица имеет размер входа 8+8+8=24 бита.
3. Вторая табличная сеть в качестве входа принимает x, y и u. Вторая табличная сеть содержит две таблицы. Вход x, y. a=g(σ(x), σ(y)); v=E(z(u,a),P(σ(u))). Здесь z(u,a)=ρ(u), если σ(u)=a, и случайная в противном случае. Здесь проверяется только часть с состоянием первой табличной сети. Таблицы имеют размер входа 16 и 12 бит. В качестве варианта можно использовать: v=E(z(u,a),P(a)) для таблицы совмещения. Это изменение, в частности, уместно, если проверка терпит неудачу.
В качестве дополнительного варианта вторая табличная сеть использует: :=σ(x); q=σ(y); a=g(p,q); v=E(z(u,a),P(σ(u)). Здесь вторая таблица использует 3 таблицы, но имеет входы только в 8, 8 и 12 бит.
4. Устройство действует над двумя видами переменных: закодированными переменными, которые имеют и значение состояния и функции ("длинные" переменные), и соответствующей переменной только состояния (переменные состояния). Последняя также может кодироваться, но имеет меньший размер. При примерном размере "длинные переменные" содержат значение функции и значение состояния и составляют 8 бит, а соответствующая переменная состояния составляет 4 бита. Длинная переменная и переменная состояния соответствуют в том смысле, что их переменные состояния находятся в проверяемом отношении, например, равны.
Первая табличная сеть действует над длинными переменными x и y, как указано выше. Вторая табличная сеть в качестве входа принимает соответствующие переменные состояния и u. Наличие переменной состояния, соответствующей длинной переменной, позволяет сделать разные подмножества из множественного входа первой таблицы доступными второй таблице. Под τx и τy подразумеваются переменные состояния, соответствующие x и y. Заметим, что переменные состояния являются частью входа первой табличной сети, поскольку закодированные длинные переменные содержат переменные состояния, т.е. τx=σ(x), τy=σ(y). Вторая табличная сеть совместно использует эти входы, поскольку она использует в качестве входа τx, τy, и u содержит две таблицы для вычисления τu=g(τx,τy); v=E(z(u,τu),P(τu)). Здесь z(u,τu)=ρ(u), если σ(u)=τu, и случайна в противном случае. Входы в таблицы во второй сети составляют только 8 и 12 бит. Заметим, что τx, τy могут быть обособленными переменными, которые отслеживаются независимо от фактического значения σ(x) и σ(y). Программа сконфигурирована так, что эти значения можно сверять друг с другом, например, на предмет равенства.
5. Вторая табличная сеть в качестве входа принимает τx, y, и вторая табличная сеть содержит две таблицы для вычисления τu=g2(g1(τx,τy)).; v=E(z(u,τu),P(τu)). Здесь z(u,τu)=ρ(u), если g2(σ(u))=τu, и случайная в противном случае. Здесь g1 является функцией g состояния, используемой в первой табличной сети. Таблица вычисления состояния во второй табличной сети осуществляет дополнительную функцию над значениями состояния, которая не выполняется в первой табличной сети. Таблица совмещения затем проверяет этот факт и вводит соответствующую поправку. Таким образом, нарушителю невозможно пропустить таблицу совмещения, поскольку это привело бы к несовмещенным значениям состояния и функции. В следующей таблице совмещения несовпадение было бы обнаружено и исправлено.
Заметим, что эти примеры отличаются в ряде аспектов. Прежде всего, они имеют разные размеры входа и выхода, что приводит к разным размерам таблиц. Размер таблицы является важным критерием, если размер программы должен оставаться в неких границах. Также примеры отличаются в том, какие значения доступны нарушителю. Для нарушителя считается преимуществом, если значения состояния доступны без кодирования с помощью значения функции. В зависимости от точных требований к размеру и безопасности можно сделать выбор между этими альтернативами. Заметим, что не требуется, чтобы программа использовала только один вариант выбора. Разные вторые таблицы могут использовать разные варианты.
Фиг. 3, 8a и 8b иллюстрируют некоторое количество этих возможностей для функции данных и функции состояния, принимающих единственный вход. Например, фиг. 3 иллюстрирует вычислительное устройство 300. В устройстве хранятся первая табличная сеть 310 и вторая табличная сеть 340.
Первая табличная сеть 310 в качестве входа 305 принимает длинную переменную x=E(w,p). Таблица 310 построена для применения функции f 312 к части с функцией и функции g 314 к части с состоянием. Заметим, что при фактической реализации эти части не являются непосредственно видимыми; таблица 310 действует непосредственно на закодированное значение путем поиска значения в заранее вычисленной таблице. Таблица 310 создает выход 307: u=E (f(w),g(p)). Вторая табличная сеть содержит две таблицы: таблицу 320 и 330. Вторая табличная сеть принимает x в качестве входа и применяет к нему таблицу 320 средства извлечения состояния для получения извлеченного состояния 322: p=σ(x). Извлеченное состояние 322 и выход 307 являются входами в таблицу 330 совмещения. Таблица совмещения построена из функции z 332 и перестановки 334. Здесь z(u,p)=ρ(u), если σ(u)=p, и случайная в противном случае. Перестановка 334 применяет перестановку к состоянию, здесь был выбор для состояния, полученного из таблицы 310, но также было возможно состояние из таблицы 320. Наличие перестановки в таблице совмещения гарантирует, что выход таблицы всегда меняется независимо от того, обнаружено ли изменение. Это предотвращает атаку, в которой изменение в таблице 330 используется для определения изменений, внесенных путем вмешательства. Также таблица 330 является единой таблицей, в которой функции 332 и 334 не являются отдельно видимыми.
Фиг. 8a иллюстрирует вычислительное устройство 800, содержащее рабочее запоминающее устройство, хранящее совокупность длинных переменных, кодирующих значение функции и значение состояния, и соответствующую совокупность переменных состояния. Каждой переменной из совокупности длинных переменных соответствует конкретная переменная из совокупности переменных состояния. Длинная переменная и переменная состояния имеют поддающееся проверке отношение. Например, длинная переменная кодирует значение состояния, которое также кодируется в переменной состояния. Например, длинная переменная кодирует значение состояния, тогда как переменная состояния кодирует функцию того значения состояния.
Табличная сеть хранится на устройстве 800. Первая табличная сеть 310 используется как описано выше, принимая в качестве входа длинную переменную (показана ситуация, в которой принимается одна длинная переменная, но возможно и больше, формулы выше иллюстрируют ситуацию, в которой принимаются две длинные переменные, также возможно и больше).
Таблица 310 принимает множественные входы, т.е. значение функции и значение состояния. Заметим, что эти два входа кодируются совместно; тем не менее, таблица 310 действует над входами разными способами. В частности, таблица 310 может очень хорошо действовать над входом функции и состояния независимо друг от друга.
Вторая табличная сеть содержит таблицу 810 функции состояния и таблицу 330 совмещения. Для таблицы 330 может использоваться такая же таблица, как на фиг. 3. Таблица 810 функции состояния в качестве входа принимает подмножество множественных входов таблицы 310; в частности, принимаются значения состояния. Это можно реализовать путем применения таблицы 810 к переменным состояния, соответствующим длинным переменным, к которым применяется таблица 310; в качестве альтернативы 805 может быть частью тракта, который развивается независимо от развития тракта 305. Таблица 810 реализует такую же функцию состояния, как и таблица 310.
В предпочтительных реализациях функция состояния, используемая таблицей 810 функции состояния и таблицей 310, действует независимо от функции. Это значительно упрощает реализацию. Тем не менее возможно внести зависимости значения функции в таблицу функции состояния. В этом случае таблица 810 функции состояния использует в своем вычислении часть промежуточных результатов из таблицы 310. Следует позаботиться о том, чтобы не показывать значения функции в открытом виде, когда это осуществляется; с другой стороны, если следующее состояние зависит только от настоящих состояний, а не от значений функции, показ значений состояния не так важен.
Таблица 810 создает в качестве выхода 807 результат применения функции состояния к значению состояния: g(τx). Заметим, что это значение является значением состояния (не объединенным со значением функции), но в типичной реализации будет кодироваться. В табличных сетях кодирование данных - не редкость, поскольку это никоим образом не мешает обработке. Что интересно, множественные входы, например значения функции и состояния, можно кодировать совместно, т.е. зашифрованными в единое значение. Кодирование переменной состояния может выполняться с помощью случайной перестановки пространства состояний. Выход таблицы 340 может использоваться при последующей обработке, например, в дополнительных табличных сетях.
Фиг. 8b описывает любопытное изменение. Показана первая табличная сеть, содержащая таблицу 310, принимающую длинные входы 305 и 815, и таблицу 830, использующую выход 305 таблицы 310 и дополнительно длинный вход 836. Таблицы 310 и 830 допускают вычисление более сложной функции множественных закодированных входов. Таблицам 310 и 830 соответствуют таблицы 810 и 820 функции состояния. Они принимают в качестве входа переменные состояния, соответствующие длинным переменным, используемым таблицами 310 и 830, т.е.: переменные 805, 806, 807, 816, 817 состояния соответствуют длинным переменным 305, 815, 307, 836 и 837 соответственно.
Что интересно, это дает возможность выполнить сегмент компьютерной программы два раза, один раз с использованием табличной сети, действующей над длинными переменными, и один раз действуя над соответствующими переменными состояния. В конце сегмента таблица совмещения проверяет, по-прежнему ли синхронны две программы.
Это дополнительно показано на фиг. 9. Как на всех фигурах, выполнение программы идет на фигуре сверху вниз. На этапе 910 программа выполняется в единой последовательности выполнения. Никаких дополнительных проверок не проводится. В некоторый момент времени входят в более чувствительную к безопасности часть. В той точке программа разделяется на две части, например слева оцениваются переменные состояния, тогда как справа оцениваются длинные переменные. Это происходит на этапе 920. В некоторый момент времени вводится еще более важная часть. В этот момент времени, например, длинные переменные дважды оцениваются полностью. В конце той части таблица совмещения гарантирует, что не сделаны никакие изменения; это осуществляется на этапе 930. Даже если были обнаружены изменения, программа продолжает выполняться, но со значениями, которые выяснены из применимых корреляций. На этапе 940 также заканчивается первое разделение, опять с помощью функции совмещения. На этапе 950 программа продолжает выполняться в виде двух потоков, например, над переменными состояния и длинными переменными. В конечном счете на этапе 960 имеется другая функция совмещения, и программа снова выполняется в единой последовательности выполнения.
На Фиг. 5 показано вычислительное устройство 500, имеющее запоминающее устройство 510. Устройство, показанное на фиг. 5, может использоваться с табличными сетями, проиллюстрированными на фиг. 1, 2, 3, 4, 8a, 8b и 9; в частности, как вычислительные устройства 100, 204, 202, 300 и 800.
Запоминающее устройство 510 обычно является одним или более энергонезависимыми запоминающими устройствами, но также может быть жестким диском, оптическим диском и т.д. Запоминающее устройство 510 также может быть энергозависимым запоминающим устройством, содержащим загруженные или принятые иным образом данные. Вычислительное устройство 500 содержит процессор 550. Процессор обычно исполняет код 555, сохраненный в запоминающем устройстве. Для удобства код может храниться в запоминающем устройстве 510. Код предписывает процессору исполнить некое вычисление. Устройство 500 может содержать необязательное устройство 560 ввода/вывода для приема входных значений и/или передачи результатов. Устройство 560 ввода/вывода может быть сетевым соединением, съемным запоминающим устройством и т.д.
Запоминающее устройство 510 содержит одну или более табличных сетей в соответствии с одной из фиг. 1-3.
Согласно варианту осуществления вычислительное устройство в ходе операции может работать следующим образом: вычислительное устройство 500 принимает входные значения. Входные значения кодируются, например, с использованием таблицы 541 кодирования, например таблицы 110. Таким образом входные значения получаются в виде закодированных входных значений. Заметим, что входные значения можно сразу получить в виде закодированных входных значений, например, посредством устройства 560. Кодирование входного значения в закодированное входное значение подразумевает, что нужно выбрать вход состояния. Это можно осуществлять по-разному, например, вход состояния можно выбирать случайным образом, например, с помощью генератора случайных чисел. Вход состояния можно выбирать в соответствии с неким алгоритмом; алгоритм может быть сложным и увеличивать обфускацию. Входное значение состояния также может быть постоянным или выбираться последовательно из последовательности чисел, например, последовательности целых чисел, имеющих постоянное приращение, например 1, и начинающихся в некоторой начальной точке; начальная точка может быть нулем, случайным числом и т.д. Выбор входов состояния в виде случайного числа и увеличение с 1 для каждого следующего выбора входа состояния является конкретным преимущественным выбором. Если входы состояния выбираются вне устройства, то нарушитель лишается возможности отследить, где выбираются входные значения состояния, и чем они являются.
Процессор 550 исполняет программу 555 в запоминающем устройстве 510. Программа предписывает процессору применить поисковые таблицы к закодированным входным значениям или к результирующим выходным значениям. Поисковые таблицы можно создать для любой логической или арифметической функции, таким образом, любое вычисление может выполняться с использованием последовательности поисковых таблиц. Это помогает осуществлять обфускацию программы. В этом случае поисковые таблицы кодируются для обфускации, и то же самое происходит с промежуточными значениями. В этом случае обфускация особенно выгодна, поскольку единое входное значение функции можно представить множественными закодированными входными значениями. Кроме того, некоторые или все таблицы и/или табличные сети обладают свойством множественных функций, из табличных сетей, которые обладают свойством множественных функций, некоторые или все образуют пару со второй табличной сетью для проверки результатов.
В некоторый момент времени обнаруживается значение результата. При необходимости результат можно декодировать, например с использованием таблицы 542 декодирования, например таблицы 170, проиллюстрированной на фиг. 1. Но результат также можно экспортировать в закодированной форме. Входные значения также можно получать от устройства ввода, а выходные значения могут использоваться для показа на экране.
Вычисление осуществляется над словами закодированных данных. Вычисление осуществляется путем применения последовательности обращений для поиска в таблице. Используемые входные значения могут быть входными значениями, принятыми извне вычислительного устройства, но также их можно получить путем предыдущего обращения к поисковой таблице. Таким образом, получаются промежуточные результаты, которые затем можно использовать для новых обращений к поисковой таблице. В некоторый момент времени один из промежуточных результатов является закодированным результатом функции.
Вычислительное устройство 500 может содержать генератор случайных чисел для присвоения входных значений состояния входам функции данных.
Фиг. 6 иллюстрирует в виде блок-схемы алгоритма способ 600 компиляции. На этапе 610 приемником принимается первая компьютерная программа. На этапе 620 лексическим анализатором осуществляется лексический анализ, например, чтобы идентифицировать лексемы. Возможно, также выполняется обработка, например макрорасширение. На этапе 630 программа анализируется анализатором. Например, анализатор формирует дерево грамматического разбора в соответствии с формальной грамматикой языка программирования первой программы. Анализатор идентифицирует разные языковые конструкции в программе и вызывает надлежащие процедуры генерации кода. В частности, идентифицируется оператор или множественные операторы. В этом случае на этапе 640 генератором кода осуществляется генерация кода. В ходе генерации кода генерируется некоторый код и, при необходимости, сопутствующие таблицы. Сопутствующие таблицы включают в себя таблицы, которые сконфигурированы для двух функций: одна для нужного оператора и для функции состояния, т.е. первые таблицы или первые табличные сети. Некоторые из первых табличных сетей образуют пару с соответствующей второй табличной сетью. Существуют различные способы решения, какие первые табличные сети поставить в пару со второй табличной сетью. Компилятор может конфигурироваться для образования пар из всех первых табличных сетей со второй табличной сетью. Компилятор может конфигурироваться для обнаружения меток начала и конца в принятой компьютерной программе, указывающих компилятору начать формирование вторых табличных сетей и соответствующего кода для применения их к выходу первых табличных сетей. Компилятор может формировать вторые табличные сети для случайной выборки первых табличных сетей.
Сгенерированный код не должен и, в целом, не будет содержать оператор, так как он заменяется одной или более поисковыми таблицами. Функция состояния может выбираться случайным образом. Функция состояния также может выбираться как результат программы, например, функция состояния может быть другим нужным оператором, который позволит повторно использовать таблицу. Например, анализатор идентифицирует и добавит операцию, и транслирует это в поисковую таблицу для добавленной инструкции и в сгенерированный код для применения поисковой таблицы к правильным значениям. В качестве функции состояния компилятор может выбирать случайную функцию. Компилятор также может выбирать случайным образом функцию из множества функций, например сложение, вычитание, умножение и т.п.
На этапе 655 сгенерированные таблицы объединяются в некую табличную базу, поскольку вполне может произойти, что некоторые таблицы генерируются несколько раз, в этом случае не нужно сохранять их несколько раз. Например, таблица сложения может быть нужна и сгенерирована только один раз. Когда объединен весь код, и объединены все таблицы, компиляция завершается. При желании может иметь место этап оптимизации.
Обычно компилятор использует закодированные области, т.е. части программы, в которых все значения или по меньшей мере все значения, соответствующие некоторым критериям, кодируются, т.е. имеют битовый размер кодового слова (n). В закодированной области операции могут исполняться путем выполнения поисковой таблицы. Когда входят в закодированную область, все значения кодируются, когда выходят из закодированной области, значения декодируются. Критерием может быть то, что значение связано или зависит от чувствительной к безопасности информации, например, криптографического ключа.
Любопытным способом создания компилятора является следующий. На этапе 630 осуществляется промежуточная компиляция. Она может осуществляться на промежуточный язык, например язык межрегистровых пересылок и т.п., но также может быть компиляцией в код машинного языка. Это означает, что для этапов 610-630 из фиг. 6 может использоваться традиционный компилятор, который не создает табличные сети. Однако на этапе 640 генерация кода осуществляется на основе промежуточной компиляции. Например, если использовался код машинного языка, то каждая инструкция заменяется соответствующей безоператорной реализацией той инструкции, т.е. табличной реализацией той инструкции. Это представляет конкретный прямой путь для создания компилятора. Фиг. 6 также может использоваться для формирования компилятора, который создает не машинный язык, а второй язык программирования.
Согласно варианту осуществления компилятор является компилятором для компиляции первой компьютерной программы, написанной на первом компьютерном языке программирования, во вторую компьютерную программу, компилятор содержит генератор кода для формирования второй компьютерной программы путем формирования таблиц и кода машинного языка, при этом сгенерированные таблицы и сгенерированный код машинного языка совместно образуют вторую компьютерную программу, сгенерированный код машинного языка обращается к таблицам, где компилятор выполнен с возможностью идентификации арифметического или логического выражения в первой компьютерной программе, причем выражение зависит от по меньшей мере одной переменной, и генератор кода выполнен с возможностью формирования одной или более таблиц, представляющих заранее вычисленные результаты идентифицированного выражения для множественных значений переменной и представляющих по меньшей мере одно другое выражение, и формирования кода машинного языка, чтобы реализовать идентифицированное выражение во второй компьютерной программе путем обращения к одной или более сгенерированным таблицам, представляющим заранее вычисленные результаты. В идеале код машинного языка, сгенерированный для реализации идентифицированного выражения, не содержит самих арифметических или логических машинных инструкций, по меньшей мере, никаких арифметических или логических машинных инструкций, связанных с конфиденциальной информацией. Нарушитель, который реверсивно проектирует таблицы, может обнаружить, что они могут представлять идентифицированное выражение, но они также могут представлять и другое выражение.
Это увеличивает устойчивость к реверсивному проектированию и уменьшает утечку по стороннему каналу второй компьютерной программы, поскольку она содержит меньше арифметических или логических операций. В идеале все арифметические и логические выражения и подвыражения заменяются обращениями к таблице. Поскольку отсутствуют те инструкции, которые составляют арифметическое или логическое выражение или подвыражения, они не могут раскрыть никакой информации. Таблица вычисляется заранее; энергия, потребленная для осуществления арифметического или логического поведения, заключенного в таблице, невидима в ходе выполнения программы.
Ниже приводятся дополнительные подробности и дополнительные варианты осуществления преимущественных табличных сетей.
Как и раньше, под W подразумевается множество операндов (входные и выходные значения операции), которые нужно кодировать, и конечное множество ∑ “состояний” и конечное множество V с кардинальным числом, равным произведению кардинальных чисел W и σ. Расширение тракта данных, описанное выше, является более выгодным, если нет простого способа его исключения. Если бы нарушитель был способен найти или выделить каждое Ω(w), можно было бы говорить, что расширение тракта данных нарушает безопасность. Опишем две связанные атаки, направленные на обнаружение классов Ω эквивалентности.
Первая атака состоит в расширенной настройке, где виртуальная машина (VM) и программа предоставляют выход пользователю, где выход не зависит от состояния (фактически, подойдет одна, возможно зашифрованная, переменная, которая не зависит состояния). Например: Подсистема дешифрования, предоставляющая изображения на экране. При такой настройке нарушитель может выполнить следующее: Для каждой переменной v в программе, от которой он ожидает информацию о состоянии. Нарушитель записывает значение исходной v, начинает замену этой переменной другими значениями t. Для всех значений t, которые создают правильные изображения, нарушитель знает, что t принадлежит множеству Ωv(w), экземпляром которого является v. Даже для изображений, которые не отображаются правильно, нарушитель мог бы сравнить результирующие ошибочные изображения и заключить, что значения s и t, используемые вместо v, приводящие к одинаковым ошибкам, будут представлять равные значения. Вторая аналогичная атака направлена на выход функциональных элементов типа операторов, которые, вероятно, представлены в табличной форме, допустим - в таблице T. Если выход T[i] таблицы используется программой, то нарушитель мог бы менять значение в ячейке i таблицы. Если алгоритм имеет успех, то нарушитель знает, что новая запись в положении i (скорее всего) находится в множестве Ω(T[i]).
В программу добавляется избыточность. В результате в ходе выполнения программы можно обнаружить ошибки и принять надлежащие меры. В одном из вариантов осуществления реакция на проверку ошибок выглядит следующим образом: если обнаруживается ошибка в переменной, то значение переменной изменяется (скорее всего, приводя к неправильному выходу программы), тогда как в противном случае изменяется состояние переменной, но ее значение остается таким же.
Можно использовать три компонента:
- добавление избыточности в программу, например, состояния помимо операндов, т.е. значения функции;
- использование избыточности в ходе (или после) выполнения программы, чтобы обнаружить неожиданные ситуации;
- принятие мер в результате использования избыточности для обнаружения неожиданных ситуаций.
Например, разные версии программы могут выполняться параллельно, например, чередуясь. Разные версии могут иметь разные операции E кодирования и/или разные начальные значения для состояний переменных в программах. Точнее говоря, предположим, что имеется программа P, и запустим m версий параллельно. Версия i использует кодирование Ei и имеет σi в качестве вектора начального состояния для всех (или некоторых) переменных. Обозначим i-ую версию P в виде Ei(P,σi). Предпочтительно, чтобы операции E1, E2, …, Em кодирования отличались.
Все версии выполняются параллельно, и в любой точке выполнения программы можно проверить, совпадает ли одна или более соответствующих переменных в программах. Заметим, что можно пропустить проверку совпадения одной или более переменных, и не все проверенные переменные нужно проверять во всех программах. Например, при наличии трех версий программы P с тремя переменными x, y, z, то можно проверить переменную x на совпадение во всех трех версиях, проверить на совпадение переменную y между версиями 1 и 3 и вообще не проверять переменную z. В случае несовпадения можно принять различные меры, например, окончание выполнения программы, продолжение выполнения с модифицированными значениями и т.д.
Параллельное выполнение нескольких программ может быть довольно затратным. Теперь опишем второй вариант осуществления, более экономный и нацеленный на пресечение атак, связанных с изменением таблиц. В качестве пояснительного примера рассмотрим защиту от изменения записей в таблице, реализующей функцию f двух переменных.
Будем использовать следующую систему обозначений. Задаем функции w:V→W и σ:V→∑ путем требования, что для каждого v∈V имеем E(w(v),σ(v))=v. Рассмотрим секретную перестановку P для ∑. Функция F:V×V→V реализует функцию f:W→W, которая объяснена выше, поэтому для каждого x,y∈W и σ,τ∈∑, F(E(x,σ),E(y,τ))=E(f(x,y),g(σ,τ)), где g:∑×∑→∑
Всякий раз, когда нужно вычислить функцию f с входами x и y, можно выполнять процедуру, которая выражена следующим псевдокодом.
p:=σ(x);q:=σ(y);u:=F(x,y); v:=E(z(u,p,q),P(σ(u));
Функция z:V×∑×∑→W такова, что z(u,p,q)=w(u), если σ(u)=g(p,q), и другому значению, например случайному значению в противном случае. Например, если W=∑, то можем принять z=w(u)-σ(u)+g(p,q). Оценка v может выполняться с использованием таблицы T с записями, помеченными элементами из V×∑∑, чтобы для u∈V,p,q∈∑, T[u,p,q]=E(z(u,p,q),P(σ(u)). В вышеприведенном псевдокоде значения состояния для x и y появляются в открытом виде. Этого можно избежать, если использовать следующую процедуру: u:=F(x,y); v:=E(Z(u,x,y),P(σ(u))); последнее реализовано в виде единичной таблицы. Функция Z:V×V×V→W такова, что Z(u,x,y)=w(u) тогда и только тогда, когда σ(u)=g(σ(x),σ(y)). Оценка v может выполняться с использованием таблицы T с записями, помеченными элементами в V×V×V таким образом, что T[u,x,y]=E(Z(u,x,y),P(σ(u)) для всех u,x,y∈V.
В качестве третьей альтернативы можно использовать следующую процедуру. a:=g(σ(x),σ(y)); u:=F(x,y); v:=E(z(u,a),P(σ(u)), где функция z:V×∑→W такова, что z(u,a)=w(u) тогда и только тогда, когда a=σ(u). Оценка a может выполняться с использованием таблицы T с записями, помеченными элементами в V×V таким образом, что T[x,y]=g(σ(x),σ(y)) для всех x,y∈V, или помеченными записями в ∑×∑, если σ(x),σ(y) появляются в программе; в последнем случае T[p,q]=a[p,q] для всех p,q∈∑. Оценка v может выполняться с использованием таблицы U с записями, помеченными элементами из V×∑ таким образом, что U[u,a]=E (z(u,a),P(σ(u))) для всех u∈V, a∈∑.
В качестве четвертой альтернативы можно использовать следующую процедуру, очень похожую на третью. a :=g(σ(x),σ(y)); u :=F(x,y); v :=E(z(u,a),P(a)), где функция z: V×∑→W такова, что z(u,a)=w(u) тогда и только тогда, когда a=σ(u). Оценка a может выполняться с использованием таблицы T с записями, помеченными элементами в V×V таким образом, что T[x,y]=g(σ(x),σ(y)) для всех x,y∈V, или помеченными записями в ∑×∑, если σ(x),σ(y) появляются в программе; в последнем случае T[p,q]=a[p,q] для всех p,q∈∑. Оценка v может выполняться с использованием таблицы U с записями, помеченными элементами из V×∑ таким образом, что U [u,a]=E(z(u,a),P(a)) для всех u∈V, a∈∑.
Ниже иллюстрируется логическое обоснование для первой из вышеупомянутых процедур (аналогичные рассуждения справедливы для других вариантов). Предположим, что нарушитель модифицировал запись [x,y] в таблице T, реализующую F из a в a’. Применяем вышеупомянутую процедуру с входами x и y. Таким образом, имеем u=T[x,y]=a’, и v=E(z(a’,σ(x),σ(y)),P((σ(a’)))). Теперь рассматриваем два случая.
Сначала предполагаем, что w(a)=w(a’). Так как a≠a’, имеем σ(a’)≠σ(a). Так как σ(a)=g(σ(x),σ(y)), из свойства z следует, что w(u’)≠w(u)=w(a), и поэтому, в соответствии с предположением, что w(a)=w(a’), имеем w(v)≠w(a’), то есть w(v)≠w(a’)=w(a)=w(F(x,y)). Другими словами: значение v не равно значению F(x,y). Таким образом: программа продолжится с переменной с неправильным значением, и нарушитель будет думать, что w(a)=w(a’). Если w(a)≠w(a’), то значение v может быть равно или не равно значению F(x,y). В первом случае нарушитель думает, что w(a)=w(a’), что, очевидно, помогает защитнику. Во втором случае нарушитель будет думать, что w(a)=w(a’), что является для него не очень полезной информацией.
В вышеприведенных вариантах можно видеть, что в преобразовании переменной u в v w(u)=w(v) тогда и только тогда, когда состояние u совпадает с состоянием, предполагаемым на основании x и y. При обобщении вместо совпадения значений состояния сопоставляется функция значений состояния. Например, w(u)=w(v) тогда и только тогда, когда состояние и предполагаемое состояние согласуются в заданном количестве их старших битов (MSB), или в заданном количестве их младших битов (LSB), или если согласуются контрольные суммы по символам состояния и предполагаемого состояния.
Разновидности второго варианта осуществления защищают от атаки, в которой изменяются записи таблицы. Далее рассмотрим третий вариант осуществления, который предлагает защиту от атаки, в которой изменяется переменная. С этой целью, для каждой переменной x∈V, которую нужно защитить, отслеживается соответствующая переменная τx∈∑ (которая в обычных обстоятельствах должна быть равна σ(x)). Всякий раз при обновлении x, обновляется и τx. Следовательно, части программ для обновления x и τx обязаны быть синхронизированы. При обновлении τx предпочтительно не использовать переменные, используемые для обновления x, а только квазипеременные состояния, соответствующие этим переменным. Например, исходя из того, что имеются переменные x,y∈V с соответствующими квазипеременными состояния τx, τy, заменим x на F(x,y). Затем также обновим τx до g(τx,τy), где g:∑×∑→∑ такова, что F(E(w1,σ1),E(w2,σ2))=E(f(w1,w2),g(σ1,σ2)). (Квазипеременные состояния представляют собой переменные со значениями в ∑ вместо V).
Функция g смешивания состояния может быть разной для разных функций F. Таким образом, способ обновления τx может зависеть от преобразования, применяемого к x. В более общем смысле способ обновления τx мог бы зависеть от x перед обновлением и/или функции (способа, процедуры?), которая использовалась для обновления x. Значения τx и σ(x) можно проверять каждый раз, когда обновляются значения x и τx, но это не обязательно. Всякий раз, когда происходит проверка, может применяться следующая процедура: x:=E(ζ(x,τx),P(τx)); τx:=P(τx); (A). Здесь P является перестановкой ∑, а функция ζ:V×∑→W такова, что ζ(x,τ)=w(x) тогда и только тогда, когда σ(x)=τ.
Другими словами: если состояние и предполагаемое состояние совпадают, то значение x остается таким же, но его состояние изменяется; если состояние и предполагаемое состояние не совпадают, то значение x изменяется. Оценка x может выполняться с использованием таблицы T с записями, помеченными элементами из V×∑ таким образом, что T[x,τ]=E(ζ(x,τ),P(τ)) для всех x∈V, τ∈∑.
Заметим, что после процедуры имеем τ=σ(x). Если нарушитель ухитряется отключить в процедуре либо обновление x, либо обновление τ (но не оба), то при последующей проверке τ и σ(x), скорее всего, не равны, и значение x будет изменено (если нарушитель также не ухитряется отключить обновление x в вышеупомянутой процедуре).
Порядок назначений в (A) равносильно можно изменить на τx:=P(τx); x:=E(ζ(x,τx),τx) (A’), где ζ:V×∑→W такова, что ζ(x,τ)=w(x) тогда и только тогда, когда σ(x)=P-1(τ), или то же самое, что тогда и только тогда, когда P(σ(x))=τ. Снова оценку x можно провести с использованием таблицы с записями, помеченными элементами из V×∑.
Альтернативной процедурой является следующая:
x:=E(ζ(x,τ),P(σ(x))); τ:=P(σ(x)); (B)
Оценка x может выполняться с использованием таблицы с записями, помеченными элементами из V×∑ таким образом, что T[x,τ]=E(ζ(x,τ),P(σ(x))) для всех x∈V, τ∈∑. Заметим, что в этой альтернативе обновление для τ можно выполнить с помощью таблицы U с записями, помеченными элементами из V таким образом, что U[x]=P(σ(x)), или, если явное появление σ(x) не повредит, то сначала можно найти p:=σ(x) с помощью таблицы для σ, а потом найти τ:=Y[p] с использованием таблицы Y с записями, помеченными элементами из W. Таблица Y имеет меньше записей, нежели таблица U.
При более общей настройке новое состояние x после проверки зависит не только от σ(x), но и от x. Тогда вместо (B) будем использовать
x:=E(ζ(x,τ),Q(x)); τ:=Q(x)
где Q:V→∑ такова, что Q(v) ≠ σ(v) для всех v∈V. Оценка x может выполняться с использованием таблицы с записями, помеченными элементами из V×∑ таким образом, что T[x,τ]=E(ζ(x,τ),Q(x))) для всех x∈V, τ∈∑.
Фиг. 7 иллюстрирует способ 700 в виде блок-схемы алгоритма. На этапе 710 множественные входы первой таблицы получаются для первой табличной сети, сохраненной в электронном хранилище. Например, их можно принять из предшествующей таблицы. На этапе 720 первая табличная сеть применяется к множественным входам первой таблицы для вычисления функции данных. Например, код компьютерной программы может дать процессору инструкцию искать конкретную запись таблицы в таблице первой табличной сети, которая указана множественными входами. Даже если используются множественные входы, это можно скрыть путем совместного кодирования некоторых или всех из них. На этапе 730 множественные входы второй таблицы получаются для второй табличной сети, сохраненной в электронном хранилище, причем входы второй таблицы включают в себя выход первой табличной сети и по меньшей мере один из множественных входов первой таблицы. На этапе 740 эта вторая табличная сеть затем применяется к множественным входам второй таблицы для создания выходов второй таблицы, включающих в себя защищенный выход функции.
Также вторая табличная сеть может быть единичной таблицей, в которой осуществляется единичный поиск в таблице, однако эта таблица построена так, чтобы несколько вещей происходило совместно, включая этапы 744, 748 и 749; это проиллюстрировано пунктирными стрелками. На этапе 740 создаются выходы второй таблицы, включающие в себя защищенный выход функции. На этапе 744 по меньшей мере для конкретного одного из множественных выходов первой таблицы проверяется, может ли немодифицированная первая табличная сеть получить конкретный из множественных выходов первой таблицы из данного по меньшей мере одного из множественных входов первой таблицы. В зависимости от этой проверки выбирается либо этап 748, либо 749. На этапе 748 (т.е. в случае неуспешной проверки, т.е. нельзя было получить значение) защищенный выход функции не равен выходу функции. На этапе 749 (т.е. в случае успешной проверки, т.е. значение можно получать) защищенный выход функции равен выходу функции.
Защищенный выход может использоваться при следующих вычислениях. Заметим, что защищенный выход можно кодировать совместно со значением состояния, т.е. значением состояния, полученным из выходов первой таблицы. Значение состояния предпочтительно переставляется. Поскольку значения функции и состояния кодируются совместно, это приводит к тому, что все закодированное значение выглядит измененным. В предпочтительных вариантах осуществления защищенный выход объединяется со значением состояния, и значение состояния всегда переставляется, чтобы нарушитель не мог понять, применен ли этап 748 или 749.
Возможны многие разные пути исполнения способа, что будет очевидно специалисту в данной области техники. Например, может меняться порядок этапов, либо некоторые этапы могут исполняться параллельно. Кроме того, между этапами можно вставить этапы другого способа. Вставленные этапы могут представлять уточнения способа, например, описанного в этом документе, или могут быть не связаны с этим способом. Например, этапы 744, 748 и/или 749 предпочтительно исполняются путем единичного поиска в таблице или, в другом компромиссе предпочтительности, путем последовательности поисков в таблице в единичной табличной сети. Кроме того, заданный этап может быть завершен не полностью перед тем, как начинается следующий этап.
Способ согласно изобретению может исполняться с использованием программного обеспечения, которое содержит инструкции для побуждения процессорной системы осуществить способ 700. Программное обеспечение может включать в себя только те этапы, выполняемые конкретным подобъектом системы. Программное обеспечение может храниться на подходящем носителе данных, например жестком диске, дискете, запоминающем устройстве и т.д. Программное обеспечение можно отправить в виде сигнала по проводу, или беспроводным способом, или с использованием сети передачи данных, например, Интернета. Программное обеспечение можно сделать доступным для загрузки и/или для удаленного использования на сервере.
Нужно будет принять во внимание, что изобретение также распространяется на компьютерные программы, особенно компьютерные программы на некотором носителе, приспособленном для осуществления изобретения. Программа может быть в виде исходного кода, объектного кода, переходного кода между исходным и объектным кодом, например в частично скомпилированном виде, или в любом другом виде, подходящем для использования при реализации способа согласно изобретению. Вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером инструкции, соответствующие каждому из этапов обработки в по меньшей мере одном из изложенных способов. Эти инструкции можно подразделить на подпрограммы и/или сохранить в одном или более файлах, которые можно связать статически или динамически. Другой вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером инструкции, соответствующие каждому из средств в по меньшей мере одной из изложенных систем и/или изделий.
Следует отметить, что вышеупомянутые варианты осуществления иллюстрируют, а не ограничивают изобретение, и что специалисты в данной области техники смогут спроектировать многие альтернативные варианты осуществления.
В формуле изобретения никакие ссылочные позиции, заключенные в скобки, не следует рассматривать в порядке ограничения формулы изобретения. Использование глагола "содержать" и его производных не исключает наличия элементов или этапов помимо заявленных в формуле изобретения. Употребление наименования элемента в единственном числе, не исключает наличия множества таких элементов. Изобретение можно реализовать аппаратными средствами, содержащими несколько отдельных элементов, и посредством соответствующим образом запрограммированного компьютера. В пункте устройства, где перечислено несколько средств, некоторые из этих средств могут быть реализованы посредством одного и того же элемента оборудования. Лишь тот факт, что определенные меры упомянуты во взаимно различных зависимых пунктах, не говорит о том, что нельзя выгодно использовать комбинацию этих мер.
Список ссылочных позиций из фиг. 1, 2, 3, 4, 5, 8a и 8b:
100 табличная сеть
102, 104 входное значение функции
110 кодер
112, 114 входное значение состояния
122, 124 закодированное входное значение
130 таблица для функции данных и функции состояния
160 закодированное выходное значение
162 выходное значение функции
164 выходное значение состояния
170 декодер
180 табличная сеть
202, 204 вычислительные устройства
210, 220 входы первой таблицы A
212, 222 первая табличная сеть A
214, 224 первая табличная сеть B
216, 226 выходы первой таблицы A
232 вторая табличная сеть A
234 вторая табличная сеть B
236 выходы второй таблицы A
300 вычислительное устройство
305 вход x=E(w,p)
307 выход u
310 первая табличная сеть
312 функция f данных
314 функция g состояния
320 таблица средства извлечения состояния
322 выход таблицы 320°(x)=p
330 таблица совмещения
332 функция z
334 перестановка
340 вторая табличная сеть
410 входная таблица
420 промежуточная таблица
430 выходная таблица
500 вычислительное устройство
510 запоминающее устройство
521, 522 поисковые таблицы с единичным входом
531, 532 поисковые таблицы с множественными входами
5311-5323 поисковые таблицы с единичным входом
541 поисковая таблица кодирования
542 поисковая таблица декодирования
550 компьютерный процессор
555 код машинного языка
560 устройство ввода/вывода
800 вычислительное устройство
805, 806, 816 вход состояния
807, 817 выход состояния
810, 820 таблица функции состояния
830 таблица функции данных
836 вход функции
837 выход функции
| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, СОДЕРЖАЩЕЕ СЕТЬ ТАБЛИЦ | 2013 |
|
RU2676454C2 |
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО И КОДИРУЮЩЕЕ УСТРОЙСТВО | 2016 |
|
RU2692419C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, ХРАНЯЩЕЕ ТАБЛИЦЫ СООТВЕТСТВИЯ ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИИ | 2013 |
|
RU2657178C2 |
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ АРИФМЕТИКИ С ОБФУСКАЦИЕЙ | 2015 |
|
RU2701716C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО И СПОСОБ | 2016 |
|
RU2708439C1 |
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО, ПРИСПОСОБЛЕННОЕ ДЛЯ ВЫЧИСЛЕНИЯ ЦЕЛЕВОГО БЛОЧНОГО ШИФРА | 2016 |
|
RU2711193C2 |
| СКРЫТИЕ ИСПОЛНЕНИЯ ПРОГРАММЫ | 2015 |
|
RU2715021C2 |
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ЗАМАСКИРОВАННЫХ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ | 2015 |
|
RU2698764C2 |
| УСТРОЙСТВО ВИРТУАЛЬНОЙ МАШИНЫ, ИМЕЮЩЕЕ УПРАВЛЯЕМУЮ КЛЮЧОМ ОБФУСКАЦИЮ, И СПОСОБ | 2012 |
|
RU2620712C2 |
| ЭЛЕКТРОННОЕ УСТРОЙСТВО ФОРМИРОВАНИЯ | 2015 |
|
RU2710310C2 |
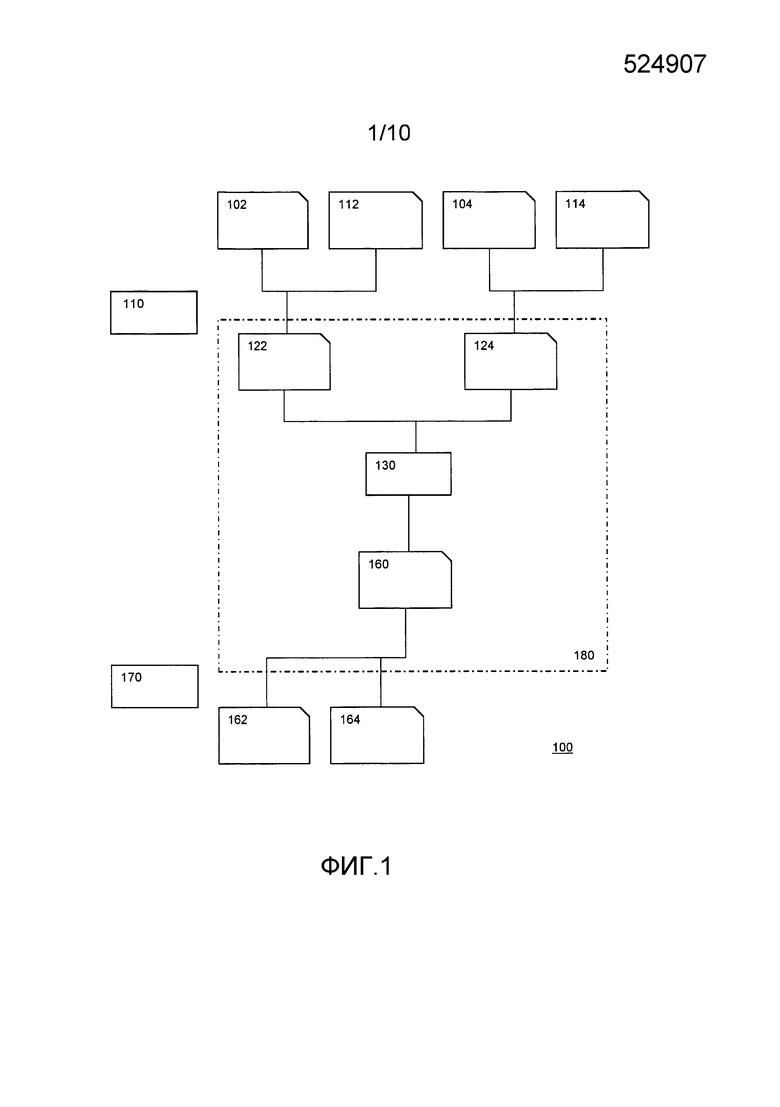
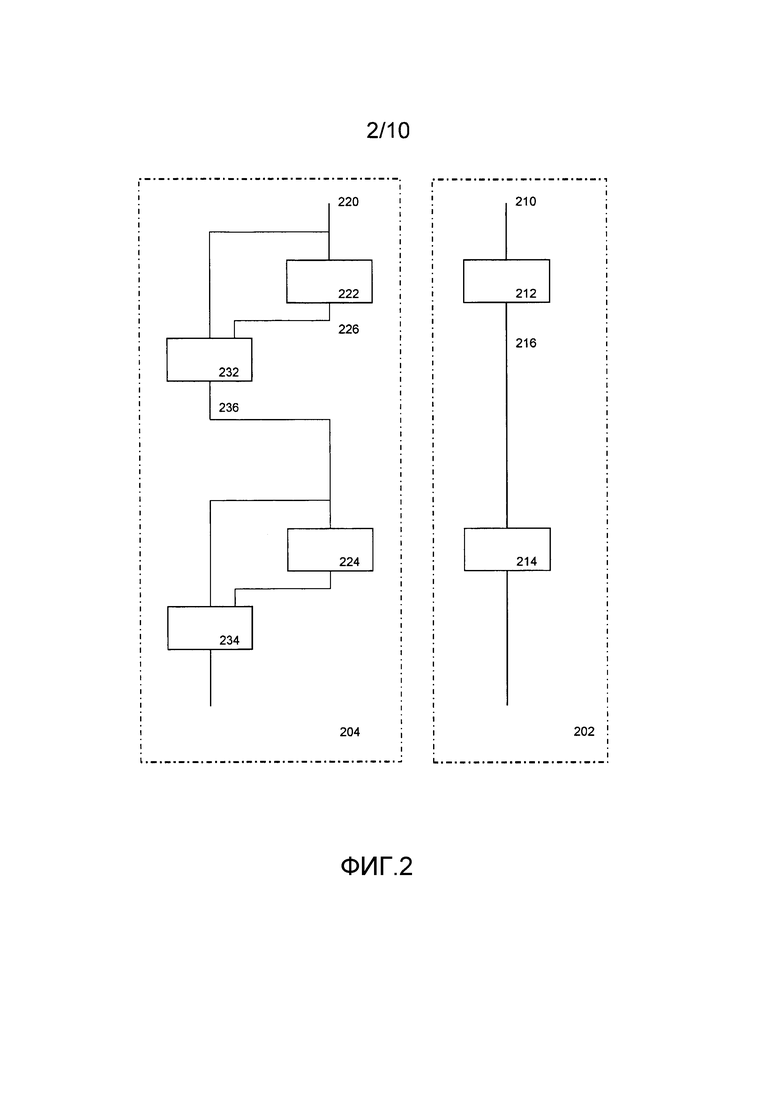
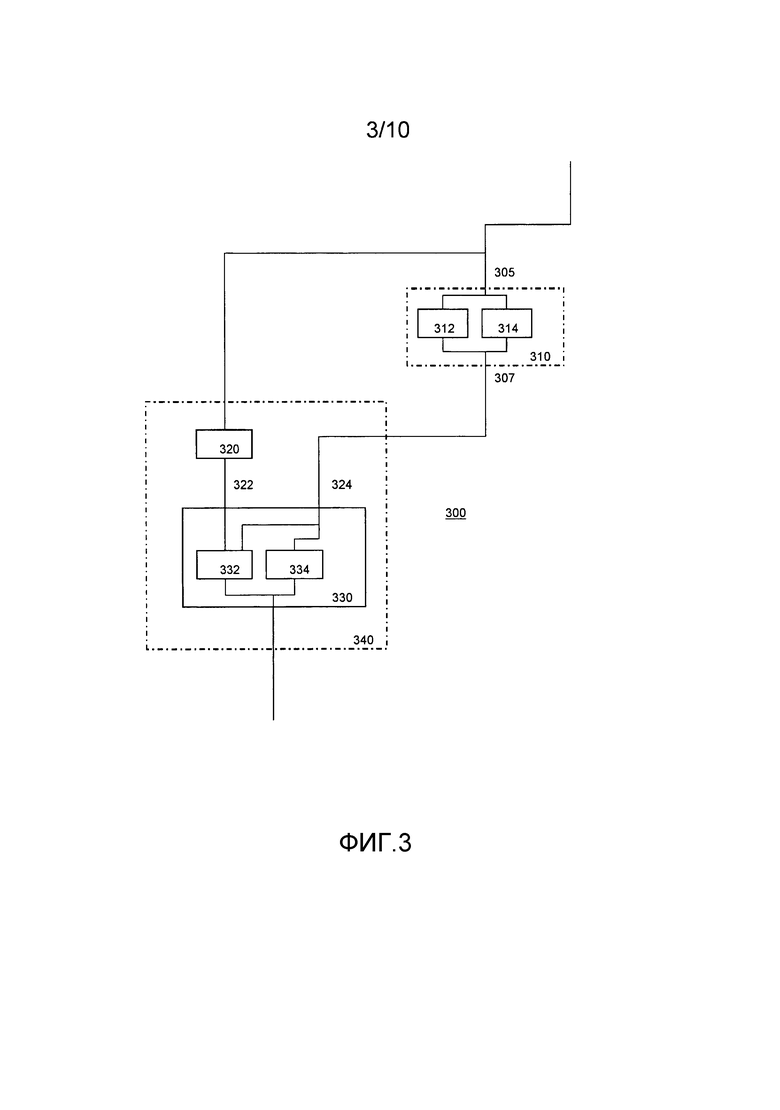
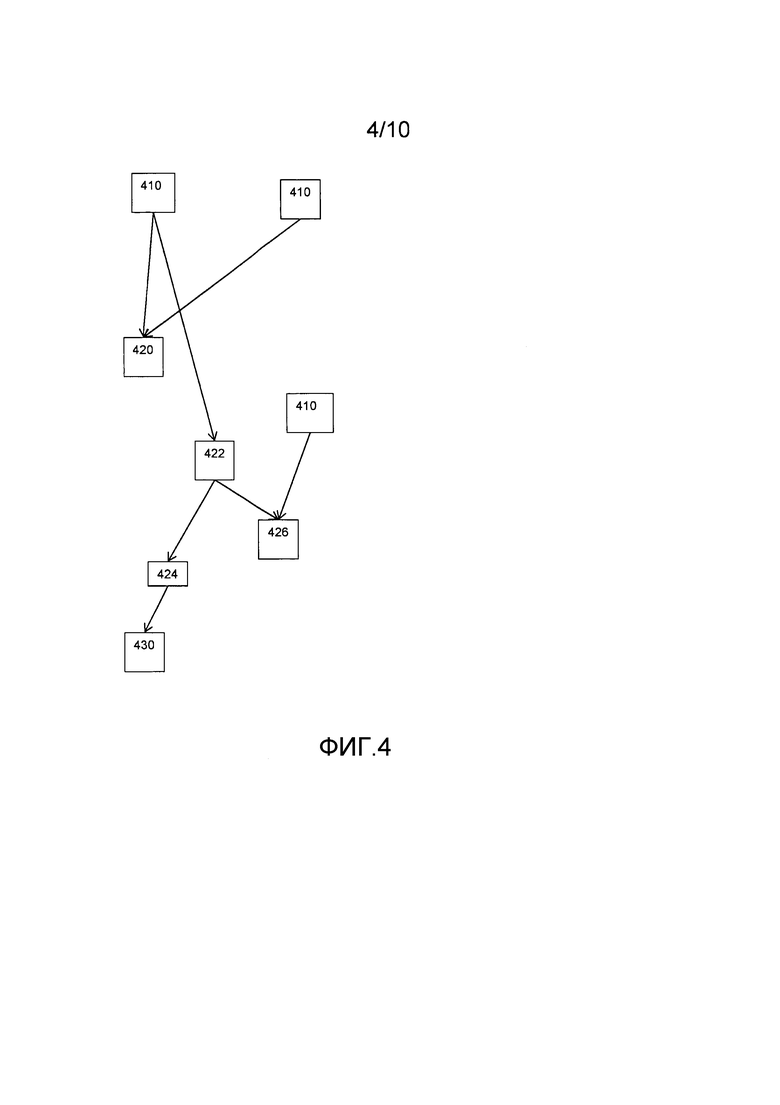
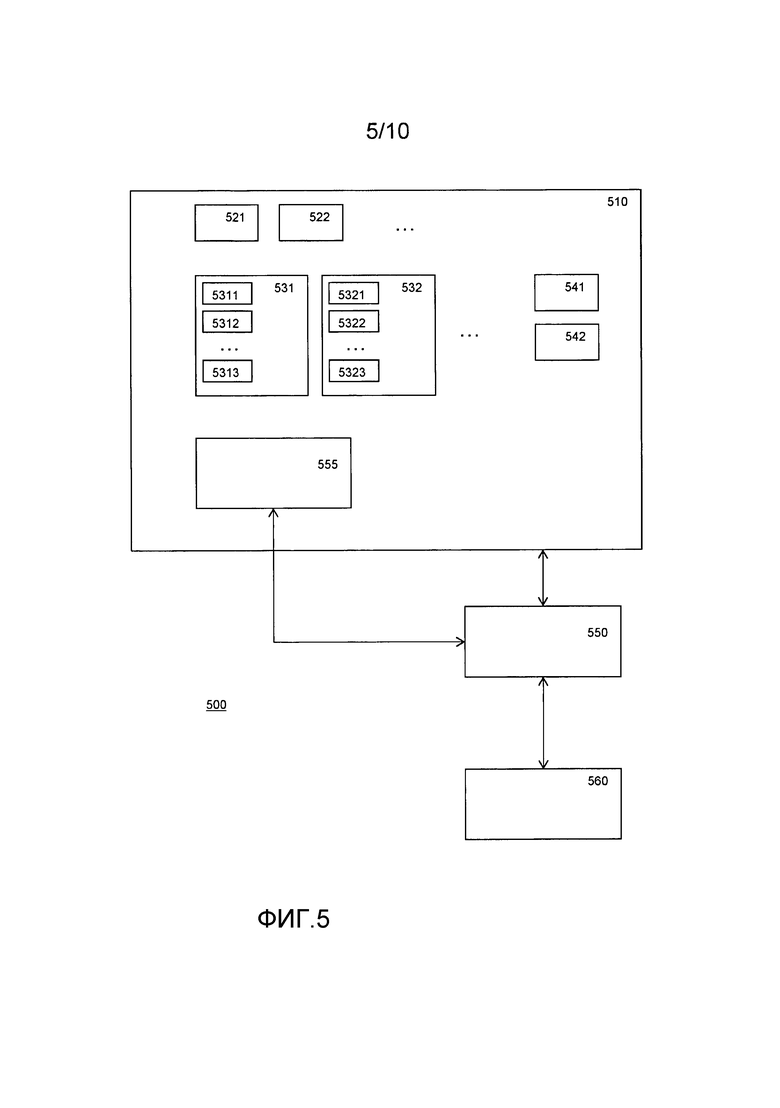
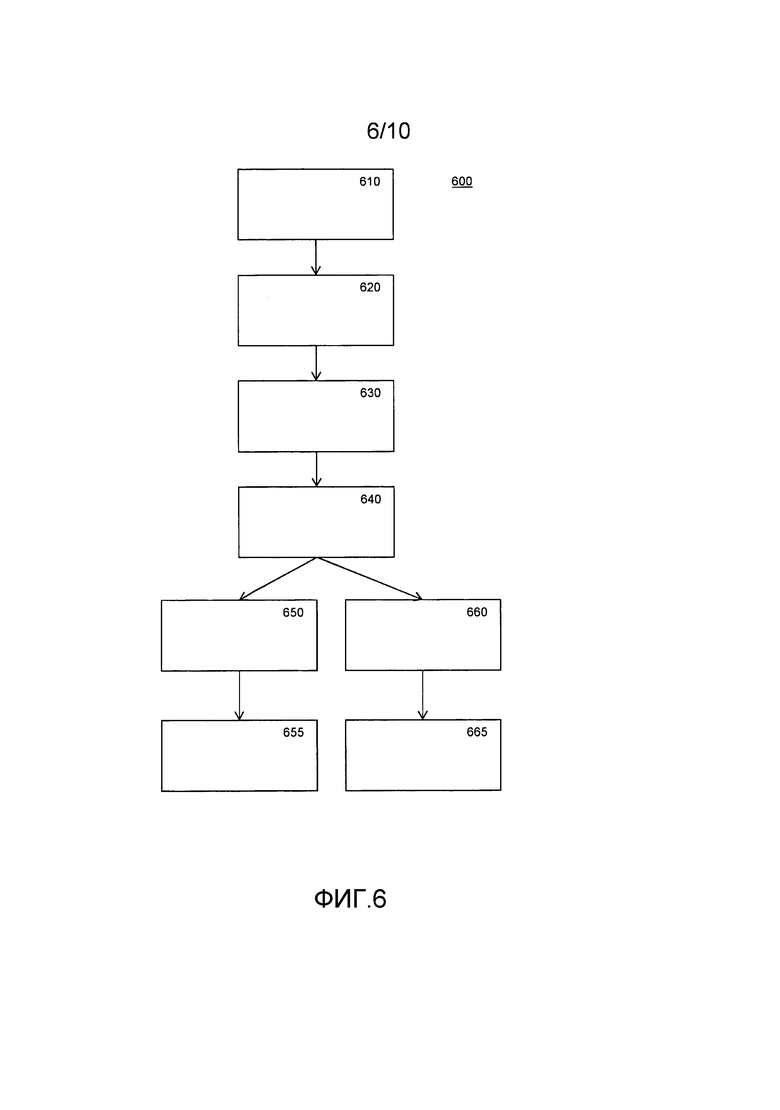
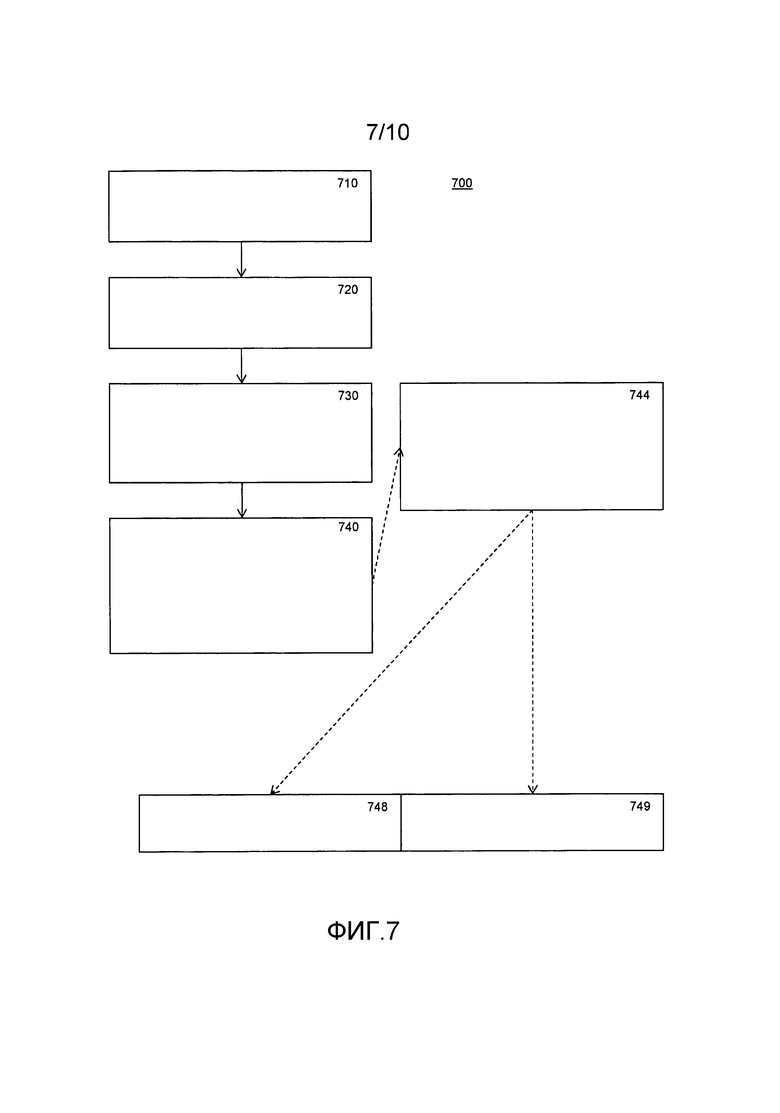
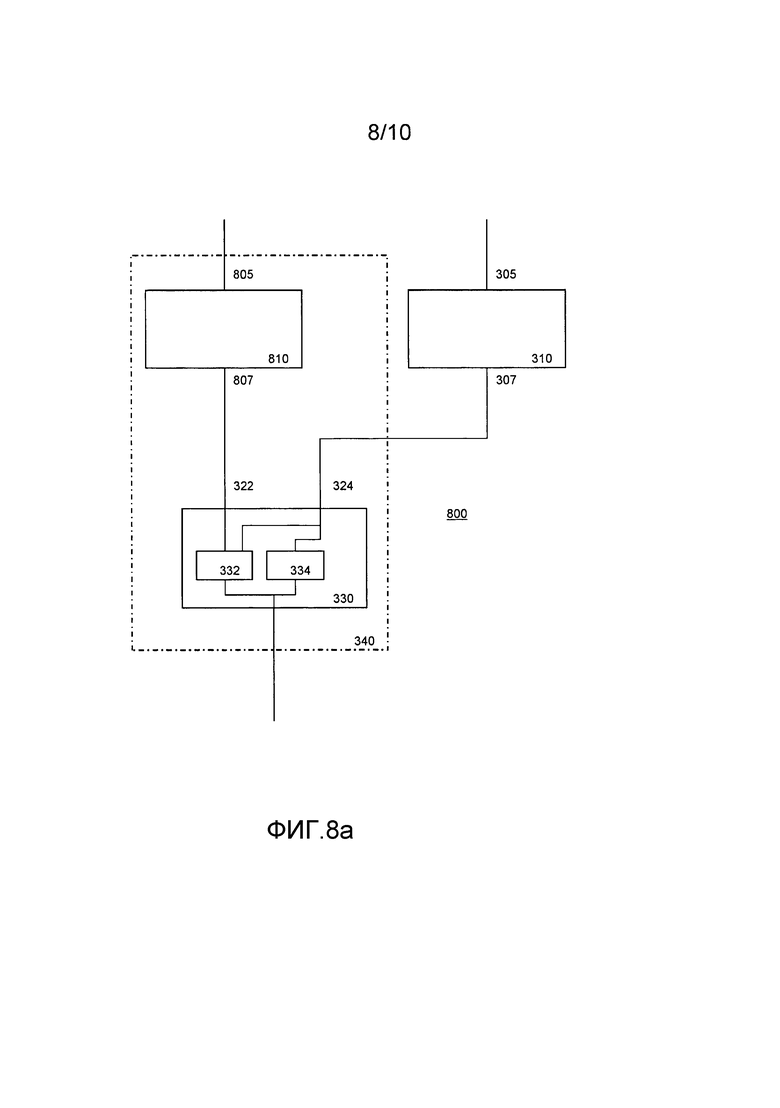
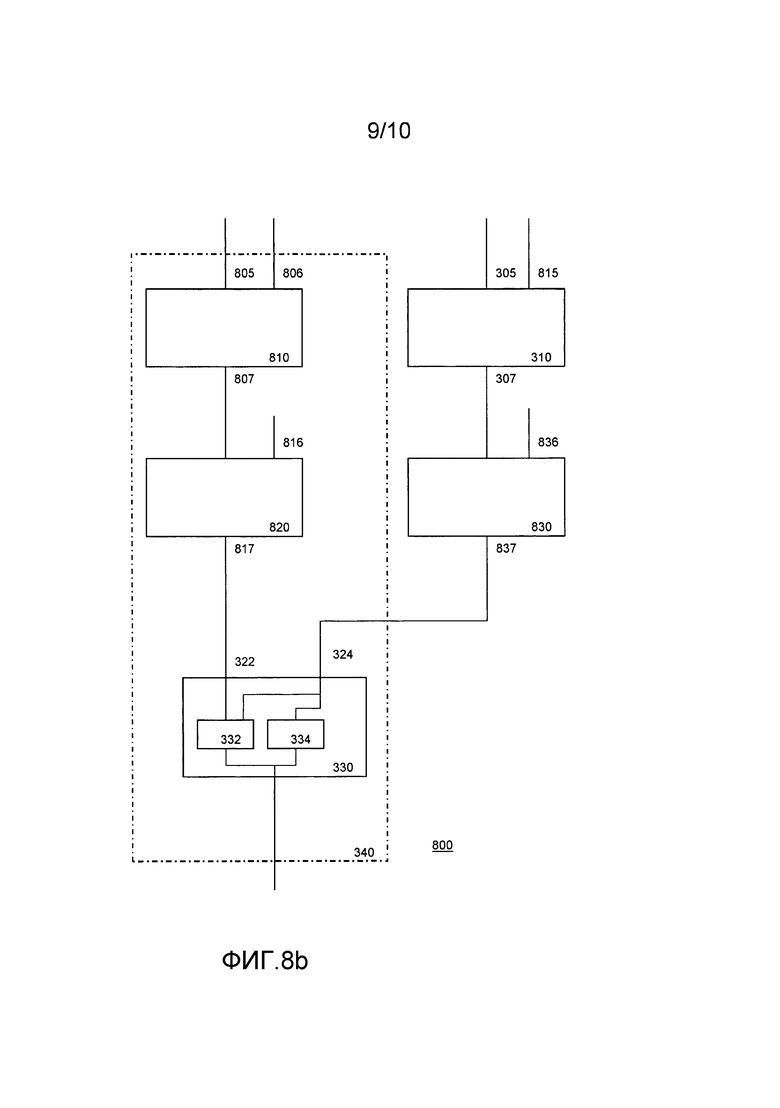
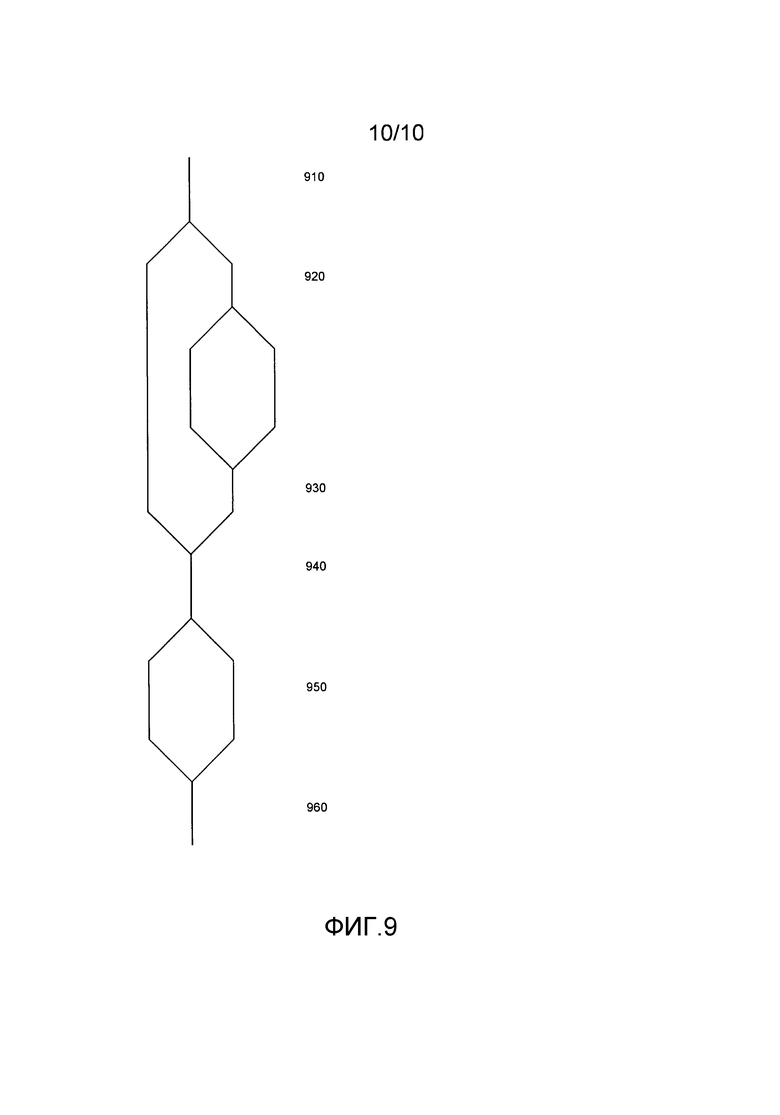
Изобретение относится к вычислительному устройству. Технический результат заключается в обеспечении защиты от атак компьютерных систем по сторонним каналам. Вычислительное устройство выполнено с возможностью вычисления функции (f) данных на входном значении (w) функции, причем вычислительное устройство содержит электронное хранилище, хранящее первую табличную сеть, сконфигурированную для функции (f) данных, а также содержит электронный процессор, подключенный к хранилищу и выполненный с возможностью получения множественных входов первой таблицы для первой табличной сети. При этом электронное хранилище дополнительно хранит вторую табличную сеть, выполненную с возможностью взаимодействия с первой табличной сетью для противодействия модификациям, вносимым в первую табличную сеть, причем электронный процессор выполнен с возможностью получения множественных входов второй таблицы для второй табличной сети. 3 н. и 7 з.п. ф-лы, 10 ил.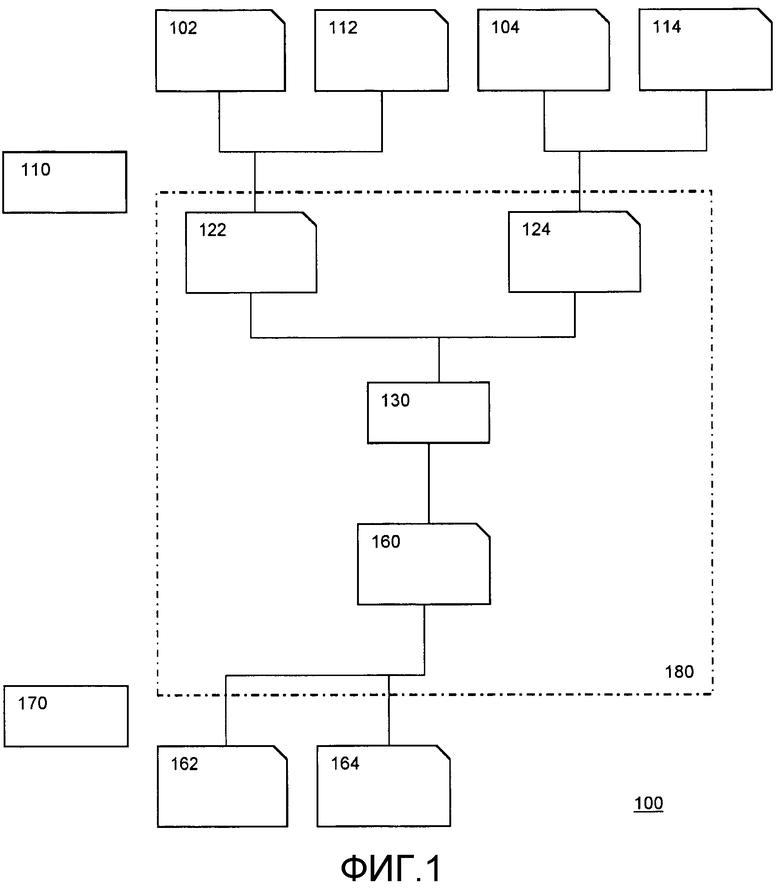
1. Вычислительное устройство, выполненное с возможностью вычисления функции (f) данных на входном значении (w) функции, причем устройство содержит электронное хранилище, хранящее первую табличную сеть, сконфигурированную для функции (f) данных,
причем вычислительное устройство содержит электронный процессор, подключенный к хранилищу и выполненный с возможностью получения множественных входов первой таблицы для первой табличной сети, причем множественные входы (x=E(w,s)) первой таблицы включают в себя входное значение (w) функции, и вычисления функции (f) данных путем применения первой табличной сети к множественным входам (x) первой таблицы для создания множественных выходов (u=E(f(w), g(w,s)) первой таблицы, причем множественные выходы (u) первой таблицы включают в себя выходное значение (f(w)) функции, причем выходное значение (f(w)) функции соответствует результату применения функции (f) данных к входному значению (w) функции, в котором
электронное хранилище дополнительно хранит вторую табличную сеть, выполненную с возможностью взаимодействия с первой табличной сетью для противодействия модификациям, вносимым в первую табличную сеть, причем электронный процессор выполнен с возможностью получения множественных входов второй таблицы для второй табличной сети, причем входы второй таблицы включают в себя множественные выходы (u) первой таблицы, и входы второй таблицы совместно используют по меньшей мере один вход с множественными входами (w; s) первой таблицы, и применения второй табличной сети к множественным входам второй таблицы, причем вторая табличная сеть выполнена с возможностью проверки для по меньшей мере конкретного одного (f(w) или g(w,s)) из множественных выходов первой таблицы, могла ли немодифицированная первая табличная сеть получить упомянутый конкретный один из множественных выходов (f(w); g(w,s)) первой таблицы из данного по меньшей мере одного из множественных входов (w; s) первой таблицы,
вторая табличная сеть создает выходы (v=E(w’,s’)) второй таблицы, включающие в себя защищенный выход (w’) функции, причем защищенный выход функции равен выходу (f(w)) функции в случае успешной проверки, и защищенный выход (w’) функции не равен выходу функции в случае неуспешной проверки для по меньшей мере некоторых значений множественных входов первой таблицы.
2. Вычислительное устройство по п. 1, в котором
множественные входы первой таблицы включают в себя входное значение состояния, и множественные выходы первой таблицы включают в себя выходное значение состояния, причем выходное значение состояния равно результату применения функции (g) состояния к входному значению состояния, и
вторая табличная сеть выполнена таким образом, что входы второй таблицы, совместно используемые с множественными входами первой таблицы, включают в себя входное значение состояния, вторая табличная сеть выполнена таким образом, что защищенный выход функции равен выходу (f(w)) функции в случае, когда результат применения функции (g) состояния к входному значению состояния равен значению состояния, включенному во множественные выходы первой таблицы, вводимые во вторую табличную сеть.
3. Вычислительное устройство по п. 1, в котором
первая табличная сеть выполнена с возможностью использовать в качестве входа закодированное входное значение (x), причем закодированное входное значение объединяет входное значение функции с входным значением состояния, совместно зашифрованные в единое значение (x), и
первая табличная сеть выполнена с возможностью создания, в качестве выхода, первого закодированного выходного значения (u=F(x)), причем первое закодированное выходное значение объединяет выходное значение функции с выходным значением состояния, совместно зашифрованные в единое значение, причем выходное значение состояния равно результату применения функции (g) состояния к входному значению состояния,
вторая табличная сеть выполнена с возможностью использовать в качестве входа первое закодированное выходное значение (u) первой табличной сети и по меньшей мере одно из входного значения состояния и входного значения функции, причем вторая табличная сеть выполнена с возможностью создания, в качестве выхода, второго закодированного выходного значения (v), причем закодированное выходное значение содержит защищенный выход функции.
4. Вычислительное устройство по п. 3, в котором вторая табличная сеть выполнена с возможностью создания, в качестве выхода, второго закодированного выходного значения (v), причем закодированное выходное значение объединяет защищенное выходное значение функции с защищенным выходным значением состояния, совместно зашифрованные в единое значение, причем защищенное выходное значение состояния равно результату применения перестановки состояний к выходному значению состояния.
5. Вычислительное устройство по п. 2, в котором вторая табличная сеть содержит сеть таблиц состояний и сеть таблиц совмещения, причем таблица состояний сконфигурирована для функции состояния, процессор выполнен с возможностью применения таблицы состояний к входному значению состояния для получения параллельного выходного значения состояния, сеть таблиц совмещения выполнена с возможностью принимать в качестве входа по меньшей мере параллельное выходное значение состояния и выходное значение состояния, принятое от первой табличной сети.
6. Вычислительное устройство по п. 2, в котором вторая табличная сеть содержит модифицированную таблицу состояний и сеть таблиц совмещения, таблица состояний выполнена с возможностью принимать в качестве входа входное значение состояния и вычислять модифицированное значение состояния, причем модифицированное значение состояния равно результату применения функции состояния к входному значению состояния, а затем дополнительной функции состояния, сеть таблиц совмещения выполнена с возможностью использовать в качестве входа выходное значение состояния и модифицированное выходное значение состояния и проверять, что дополнительная функция состояния, применяемая к выходному значению состояния, дает модифицированное выходное значение состояния.
7. Вычислительное устройство по п. 5, в котором параллельно поддерживаются закодированная переменная, содержащая в закодированной форме значение функции и значение состояния, и переменная состояния.
8. Вычислительное устройство по п. 1, в котором
вторая табличная сеть выполнена с возможностью использовать в качестве входа входное значение функции, вторая табличная сеть выполнена таким образом, что защищенный выход функции равен выходу (f(w)) функции в случае, когда результат применения функции (f) данных к входному значению функции равен выходному значению функции, закодированному в первом закодированном выходном значении (u).
9. Компилятор, выполненный с возможностью приема функции данных и создания первой и второй табличной сети, в котором
первая табличная сеть выполнена с возможностью принимать множественные входы первой таблицы для первой табличной сети, причем множественные входы (x=E(w,s)) первой таблицы включают в себя входное значение (w) функции, и создавать множественные выходы (u=E(f(w), g(w,s))) первой таблицы, причем множественные выходы (u) первой таблицы включают в себя выходное значение (f(w)) функции, причем выходное значение (f(w)) функции соответствует результату применения функции (f) данных к входному значению (w) функции, в котором
вторая табличная сеть выполнена с возможностью взаимодействия с первой табличной сетью для противодействия модификациям, вносимым в первую табличную сеть, вторая табличная сеть выполнена с возможностью принимать множественные входы второй таблицы, причем входы второй таблицы включают в себя множественные выходы (u) первой таблицы, и входы второй таблицы совместно используют по меньшей мере один вход с множественными входами (w или s) первой таблицы, причем вторая табличная сеть выполнена с возможностью проверки для по меньшей мере конкретного одного (f(w) или g(w,s)) из множественных выходов первой таблицы, могла ли немодифицированная первая табличная сеть получить упомянутый конкретный один из множественных выходов (f(w) или g(w,s)) первой таблицы из данного по меньшей мере одного из множественных входов (w или s) первой таблицы,
вторая табличная сеть создает выходы (v=E(w’,s’)) второй таблицы, включающие в себя защищенный выход (w’) функции, причем защищенный выход функции равен выходу (f(w)) функции в случае успешной проверки, и защищенный выход (w’) функции не равен выходу функции в случае неуспешной проверки для по меньшей мере некоторых значений множественных входов первой таблицы.
10. Электронный способ вычисления функции (f) данных на входном значении (w) функции, содержащий этапы, на которых
сохраняют в электронном хранилище первую табличную сеть, сконфигурированную для функции (f) данных,
получают множественные входы первой таблицы для первой табличной сети, причем множественные входы (x=E(w,s)) первой таблицы включают в себя входное значение (w) функции,
вычисляют функцию (f) данных путем применения первой табличной сети к множественным входам (x) первой таблицы для создания множественных выходов (u=E(f(w), g(w,s))) первой таблицы, причем множественные выходы (u) первой таблицы включают в себя выходное значение (f(w)) функции, причем выходное значение (f(w)) функции соответствует результату применения функции (f) данных к входному значению (w) функции,
сохраняют вторую табличную сеть, выполненную с возможностью взаимодействия с первой табличной сетью для противодействия модификациям, вносимым в первую табличную сеть,
получают множественные входы второй таблицы для второй табличной сети, причем входы второй таблицы включают в себя множественные выходы (u) первой таблицы, и входы второй таблицы совместно используют по меньшей мере один вход с множественными входами (w или s) первой таблицы, и применяют вторую табличную сеть к множественным входам второй таблицы, причем вторая табличная сеть выполнена с возможностью проверки для по меньшей мере конкретного одного (f(w) или g(w,s)) из множественных выходов первой таблицы, могла ли немодифицированная первая табличная сеть получить упомянутый конкретный один из множественных выходов (f(w) или g(w,s)) первой таблицы из данного по меньшей мере одного из множественных входов (w или s) первой таблицы, вторая табличная сеть создает выходы (v=E(w’,s’)) второй таблицы, включающие в себя защищенный выход (w’) функции, причем защищенный выход функции равен выходу (f(w)) функции в случае успешной проверки, и защищенный выход (w’) функции не равен выходу функции в случае неуспешной проверки для по меньшей мере некоторых значений множественных входов первой таблицы.
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| JOYE M et al., "Strengthening hardware AES implementations against fault attacks", IET Information Security, 2007, vol | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| СПОСОБ ЗАЩИТЫ ТЕКСТОВОЙ ИНФОРМАЦИИ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА | 2010 |
|
RU2439693C1 |
Авторы
Даты
2018-07-13—Публикация
2013-12-19—Подача