Изобретение относится к области исследования азотсодержащих алмазов и может использоваться в геммологии, при осуществлении геолого-поисковых работ методом поиска «алмазов по алмазам», для сравнения кристаллов из россыпей с алмазами из известных коренных и россыпных источников, а также при экспертных оценках партий кристаллов, включая обработанные камни, на предмет их принадлежности известным алмазоносным источникам.
Известен способ идентификации источника коллекции кристаллов алмаза, включающий облучение кристаллов электромагнитным излучением инфракрасного диапазона, регистрацию значений оптической плотности кристаллов в инфракрасном диапазоне, определение усредненных концентраций дефектов кристаллической структуры и сравнение их со значениями концентраций дефектов эталонной коллекции в диапазоне полосы поглощения 1350-1390 см-1 (Пат. 2413931 Российская Федерация, МПК G01N 21/87, Способ идентификации источника коллекции кристаллов алмаза / Е.А. Васильев. - №2009124872/28, заявл. 29.06.2009, опубл. 10.03.11, Бюл. №7) [1].
Недостатком способа является недостаточная обусловленность значений усредненных концентраций отдельных дефектов кристаллической структуры температурно-временными условиями генезиса алмаза. Это приводит к недостоверным корреляциям при разбраковке выборок алмазов из россыпных объектов посредством статистического сравнения частот встречаемости концентраций дефектов в этих объектах с объектами кимберлитового поля, содержащего несколько коренных источников, и ограничивает надежность локального прогноза на наличие новых коренных тел.
Известен способ восстановления температурно-временной истории генезиса алмаза, принятый за прототип, включающий регистрацию изменений Δ(Knt) интегрального параметра агрегации азотных С, либо А-центров от генетического центра кристалла к его периферии, путем измерения локальных концентраций азотных центров, например, в тонкой пластине, пересекающей ростовые слои. При этом определение температуры Т и времени Δt событий генезиса алмаза в изотермической модели проводят по математической формуле (1) (Пат. 2539904 Российская Федерация, МПК G01N 21/35, G01V 9/00, Способ восстановления температурно-временных условий генезиса алмаза / С.В. Софронеев. №2013122237/28, заявл. 14.05.2013, опубл. 27.01.2015, Бюл. №3) [2].

где Kn - константа скорости реакции агрегации азотных С, либо А-центров для кинетики n-го порядка, равная

Здесь Ar и Ea - определяемые экспериментально [3] постоянная Аррениуса и энергия активации процесса агрегации соответствующих азотных центров для выбранного порядка кинетики агрегации, n, kB - постоянная Больцмана, Т - абсолютная температура. Численное значение интегрального параметра агрегации азотных центров Knt для локальной области алмаза представляет собой функционал от температурной истории T(t) данной локальной области от момента времени начала ее кристаллизации tнач до момента измерения в ней концентрации азота tкон.
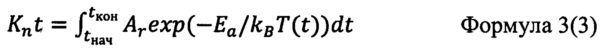
Вычисление локальных численных значений интегрального параметра агрегации осуществляется по формулам (4)÷(7).
Недостатком данного метода при статистическом анализе представительных алмазных выборок является необходимость вырезания из алмазов алмазных пластин, что приводит к необратимой трансформации исходного материала и к резкому увеличению трудоемкости и удорожанию данного метода. Невозможность осуществления измерений на достаточно большом количестве образцов приводит к нерепрезентативности анализируемой выборки и, соответственно, к низкой статистической достоверности полученных результатов.
Целью настоящего изобретения является повышение достоверности определения степени статистического подобия выборок азотсодержащих алмазов из разных источников.
Поставленная цель достигается тем, что в способе сравнения выборок азотсодержащих алмазов из различных источников с представительностью N, основанном на измерении, например, методом ИК-Фурье спектроскопии, усредненных концентраций азота [А] - в форме А и [В] - в форме В, или [С] - в форме С и определении для выбранного порядка кинетики агрегации n усредненных численных значений интегрального параметра агрегации KnCt азотных С-центров, либо интегрального параметра агрегации KnAt азотных А-центров, приобретенных кристаллами за время их генезиса, дополнительно вычисляют логарифмы усредненных значений интегральных параметров агрегации (lgKnt), строят сглаженную функцию плотности вероятности распределения кристаллов из выборок по логарифму интегрального параметра агрегации и определяют степень статистического подобия двух выборок путем сравнения пары дискретных числовых массивов значений логарифмов интегрального параметра агрегации кристаллов или сглаженных функций плотности, например, по критерию Пирсона.
Причем измерения, например методом ИК-Фурье спектроскопии, проводят на целых кристаллах выборки алмазов.
Усредненные численные значения интегрального параметра агрегации азотных С-центров KnCt, либо А-центров KnAt при n≠1 рассчитывают по формулам:
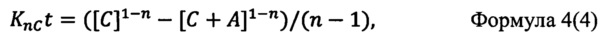
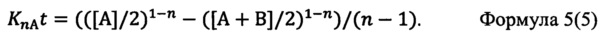
А при n=1, рассчитывают по формулам:


Построение сглаженных функций плотности вероятности распределения кристаллов из выборок с представительностью N по логарифму интегрального параметра Knt, осуществляют по точкам, определяющим гистограмму эмпирической функции плотности [4] алмазов из данной выборки и вычисляемым в соответствии с формулой (8):

где ΔN - это число алмазов выборки, со значениями логарифма интегрального параметра агрегации, попавшими в интервал Δlg(Knt).
А определение степени статистического подобия выборок по критерию Пирсона осуществляют, например, при помощи программного средства «Pearson Analyzer of Density Functions (PADF)» [5].
По данным ИК-измерений концентраций азота на алмазных пластинах, локальные значения интегрального параметра агрегации Knt в алмазе обладают максимальной величиной в генетическом центре кристалла, уменьшаются в промежуточной области и принимают свои минимальные значения в периферийной области вблизи поверхности кристалла [2, 6].
Значения интегрального параметра агрегации азотных центров в генетическом центре кристалла обусловлены суммарным отжигом в верхней мантии за весь период генезиса природного алмаза (формула (3). Величина интегрального параметра агрегации азотных центров природного алмаза у поверхности кристалла обусловлена его отжигом в верхней мантии в постростовой период, продолжительность которого также имеет геологический масштаб времени порядка сотен миллионов лет.
Поскольку значения интегрального параметра в центральной и промежуточной области кристалла, как правило, значительно (на ~1÷3 порядка) превышают его значения у поверхности и часто содержат участки непрерывного роста алмаза, на которых плавное уменьшение интегрального параметра составляет величину одного порядка с его значением у поверхности кристалла [2], то естественно предположить, что основной вклад в величину интегрального параметра в центре и промежуточной области кристалла связан с периодами непрерывного роста, растворения и возобновления роста алмаза, проходящими при существенно более высоких температурах, чем средняя равновесная температура материнской среды, в которой пребывал алмаз. Это обусловлено тем, что периоды непрерывного роста алмаза имеют нулевую, то есть на 6÷10 порядков меньшую, продолжительность по сравнению с геологическим (~1 млрд лет) масштабом времени, а константа скорости реакции агрегации (формула (2) имеет очень резкую зависимость от температуры. На фиг. 1 представлена номограмма рассчитанных из формул (1) и (2) изохронных зависимостей изменения величины интегрального параметра агрегации А-центров Δ(K2At)×105 от температуры по шкале Цельсия при различных продолжительностях процесса отжига алмаза типа IaAB от 0,5 часа (0.5 hour) до 5 млрд лет (5 Ga). Согласно этой номограмме, можно сделать вывод о том, что рост алмазов осуществлялся в результате кратковременных высокотемпературных событий в истории генезиса алмаза, температура которых существенно (на несколько сотен градусов) выше, чем средняя равновесная температура материнской среды, в которой пребывал алмаз. Например, значение интегрального параметра агрегации K2At×105 у поверхности кристалла, равное 100 ppm-1, дает в изотермической модели для времени пребывания 1 млрд лет температуру приблизительно 1100°C. Значение интегрального параметра K2At×105 в центральной области кристалла, равное ~500 ppm-1, дает для суммарной продолжительности событий роста, растворения, возобновления роста ~100 лет, среднюю температуру ~1745°C, а для 10 лет ~1877°C. Если из значения интегрального параметра K2At×105 в центре кристалла, равного 500 ppm-1, вычесть удвоенное значение интегрального параметра на краю кристалла, оценочно исключив таким способом из истории генезиса алмаза периоды его пребывания при равновесной температуре материнской среды, то для полученного нового значения K2At×105, равного 300 ppm-1, мы получим для суммарной продолжительности событий роста, растворения, возобновления роста ~100 лет, среднюю температуру ~1718°C, а для 10 лет ~1846°C, то есть температуры, близкие к исходным оценкам для K2At×105 в центре кристалла, равного 500 ppm-1. Как видно из приведенных численных оценок, основной вклад в величину интегрального параметра в центральной части кристалла вносят кратковременные высокотемпературные события генезиса, сопровождающие процессы роста, растворения и возобновления роста кристалла.
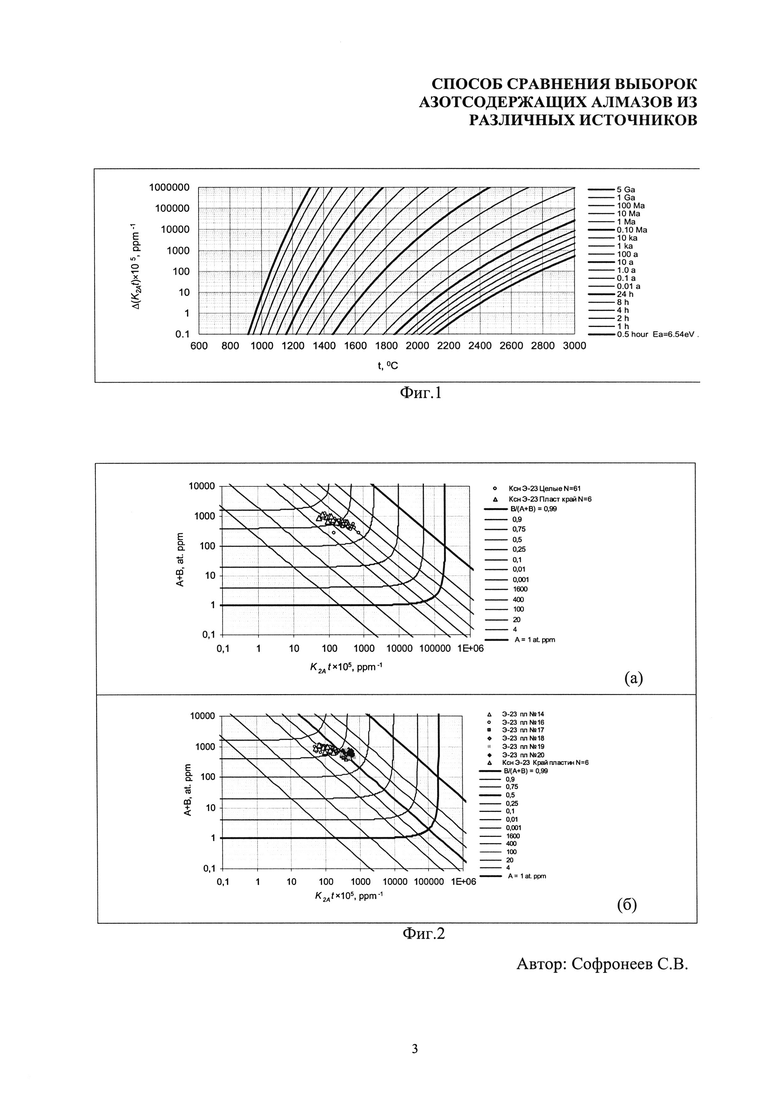
В предлагаемом способе сравнения выборок используется тот факт, что величины усредненных значений интегрального параметра агрегации азотных центров, вычисленные из измеренных значений усредненных концентраций азота на целых кристаллах, близки к локальным значениям интегрального параметра в вырезанных из этих кристаллов пластинах в области их генетического центра и промежуточной области. Для иллюстрации этого на номограмме, представленной на фиг. 2, приведены значения усредненных концентраций азота и интегральных параметров K2At×105 для 61-го целого кристалла, извлеченного из ксенолита Э-23 тр. Удачная, и локальные значения концентраций азота и интегральных параметров в 6 тонких пластинах, вырезанных из 6 алмазов этого ксенолита, и измеренных в 12÷14 эквидистантных локальных областях на прямолинейных траверсах, проходящих через генетический центр этих кристаллов. Значения усредненного интегрального параметра K2At×105 для большинства целых кристаллов из ксенолита Э-23 лежат в диапазоне 200÷400 ppm-1 (фиг. 2а). Локальные значения интегрального параметра агрегации с прямолинейных траверс, соответствующие центральной и промежуточной алмазных пластин, находятся в близком диапазоне 300÷500 ppm-1 (фиг. 2б). Таким образом, вычисленные из измерений концентраций азота на целых кристаллах, усредненные значения интегрального параметра агрегации азотных центров в алмазах отражают высокотемпературную часть тепловой истории кристаллов T(t), связанную с событиями роста, растворения и возобновления роста кристаллов. То есть именно высокие температуры, при которых пребывал алмаз за время своего генезиса, определяют значения усредненного интегрального параметра агрегации для целого кристалла.
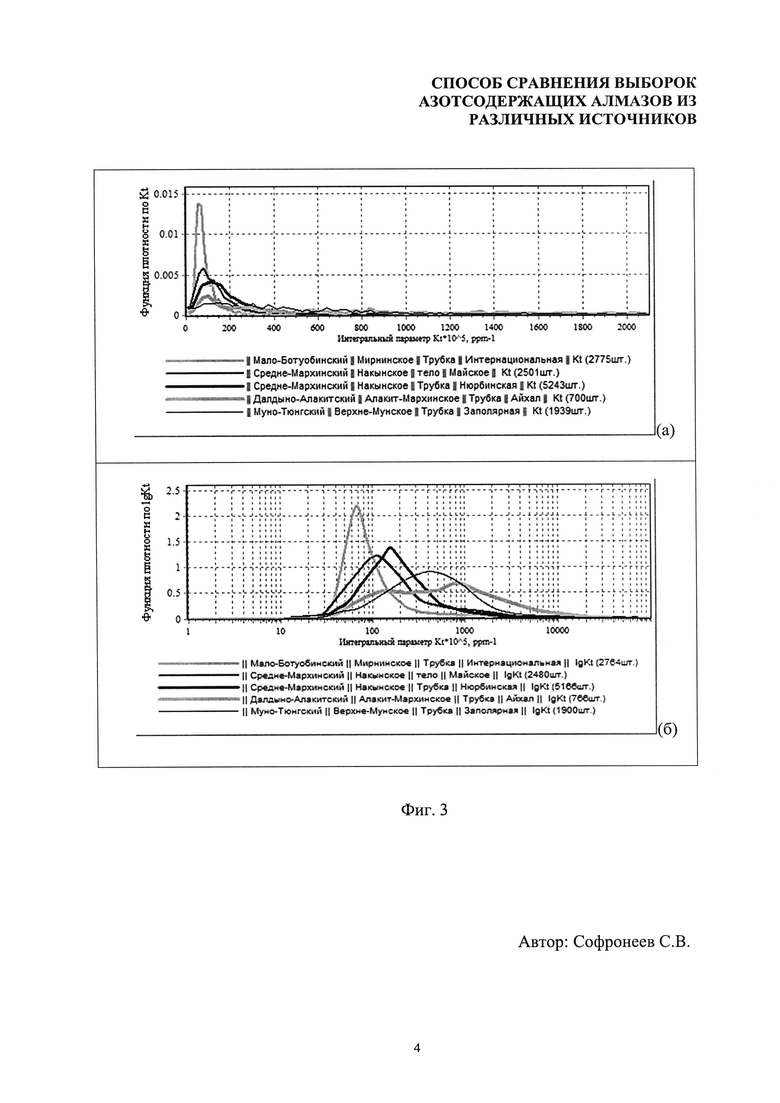
Поскольку в формуле (1) для вычисления изменения интегрального параметра агрегации температура находится под знаком экспоненты (формула (2)), то генетически значимой характеристикой выборки алмазов из данного источника должна быть функция плотности вероятности распределения кристаллов выборки по логарифму интегрального параметра агрегации. Это наглядно демонстрируют представленные на фиг. 3 функции плотности пяти коренных источников из различных кимберлитовых полей Якутской алмазоносной провинции (ЯАП) - Мирнинского, Накынского, Алакит-Мархинского и Верхне-Мунского. Функции плотности по параметру K2At×105 (фиг. 3а) и по логарифму параметра K2At×105 (фиг. 3б) построены для одних и тех же наборов значений интегральных параметров агрегации алмазов из представленных коренных источников (представительности выборок указаны в скобках). Построение сглаженной функции плотности по параметру Knt осуществляются по точкам, определяемым по формуле (9):

Как видно из графиков, переход от функций плотности по параметру K2At к функциям плотности по логарифму интегрального параметра производит «логнормализацию» распределения. При рассмотрении достаточно представительных выборок (>~1000 шт.), вероятности распределения кристаллов алмаза из некоторого коренного источника по различным диапазонам значений логарифма интегрального параметра агрегации азотных А-центров, являются уникальными и однозначно определенными. Этим определяется генетическая значимость функции плотности по логарифму параметра Knt. Данная функция отображает распределение кристаллов коренного источника по высокотемпературно-временным отрезкам событий в истории генезиса алмазов, а ее форма определяется совокупностью тепловых историй генезиса всех алмазов, присутствующих в данной трубке.
Предлагаемый способ поясняется на фиг. 1÷6, где:
- фиг. 1. Номограмма изохрон зависимости Δ(K2At)×105 от t°C для процесса агрегации А-дефектов в алмазе типа IaAB при длительностях процесса агрегации от 0,5 часа (0.5 hour) до 5 млрд лет (5 Ga). Расчет сделан из формулы (1), значения Еа и Ar взяты из [3];
- фиг. 2. Номограмма содержания азота в алмазе в координатах «Интегральный параметр агрегации K2At×105 - Общий азот [А+В]». На номограмме также нанесены изолинии степени агрегации азота из формы А в форму В ([В]/[А+В]) и изолинии содержания азота в форме А;
(а) - точки, соответствующие усредненным параметрам агрегации азотных центров, рассчитанным из ИК-измерений содержания азота в форме А и В на неразрезанных алмазах (61 шт.) из ксенолита Э-23 тр. Удачная;
(б) - точки, соответствующие локальным значениям интегрального параметра агрегации для 6 пластин, вырезанных из 6 алмазов ксенолита Э-23. Значения рассчитаны из локальных концентраций азота в форме А и В в 12÷14 точках прямолинейных траверс, проходящих через генетический центр пластин; треугольниками на обоих рисунках отмечены значения для точек, измеренных вблизи края пластин;
- фиг. 3. Функции плотности вероятности алмазов пяти коренных источников ЯАП по интегральному параметру и логарифму интегрального параметра для одних и тех же наборов значений интегрального параметра агрегации азотных центров;
(а) - функции плотности вероятности ƒp(K2At) распределения алмазов по интегральному параметру агрегации K2At×105;
(б) - функции плотности вероятности ƒp(lgK2At) распределения алмазов этих же источников по логарифму интегрального параметра агрегации;
- фиг. 4. Функции плотности вероятности распределения алмазов из четырех коренных и россыпных объектов Накынского кимберлитового поля по логарифму интегрального параметра K2At×105. В скобках указаны представительности выборок;
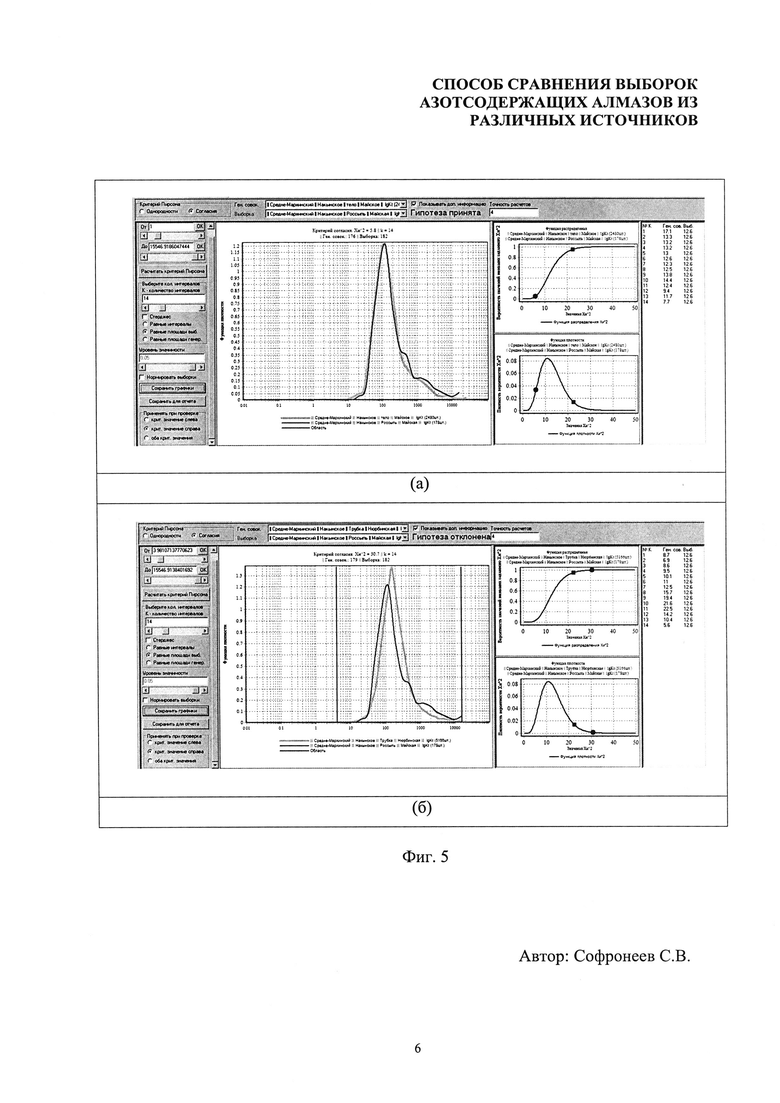
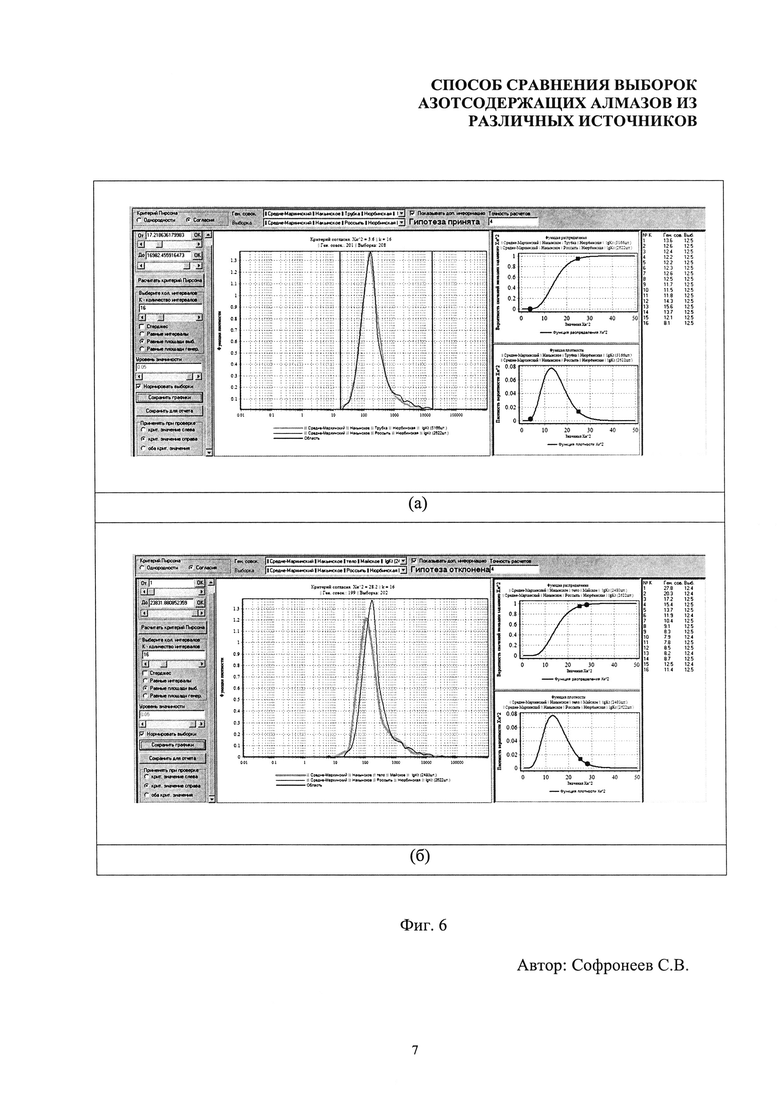
- фиг. 5. Принтскрины рабочей панели программного средства «PADF» с результатами попарного сравнения массивов значений логарифма параметра агрегации по критерию согласия Пирсона россыпи Майская (178 шт.) с коренными источниками (а) - тело Майское (2480 шт.) и (б) - тр. Нюрбинская (5166 шт.). Число интервалов k=14;
- фиг. 6. Принтскрины рабочей панели программного средства «PADF» с результатами попарного сравнения массивов значений логарифма параметра агрегации по критерию согласия Пирсона россыпи Нюрбинская (2622 шт.) с коренными источниками (а) - тр. Нюрбинская (5166 шт.) и (б) - тело Майское (2480 шт.). Представительность выборки из россыпи Нюрбинская при вычислении критической статистики по функциям плотности нормирована на N=200. Число интервалов k=16.
Пример конкретной реализации осуществлен на представительных выборках алмазов Накынского кимберлитового поля Средне-Мархинского района ЯАП из двух коренных источников и двух россыпных, генетическая принадлежность которых к коренным источникам однозначно установлена из геологического расположения объектов (тр. Нюрбинская (5166) - россыпь Нюрбинская (2622) и тело Майское (2480) - россыпь Майская (178)).
Способ реализуется следующим образом. Определяют на целых кристаллах алмаза, например методом ИК-Фурье спектроскопии, значения усредненных по кристаллу концентраций [С] и [А] примесного азота в форме С и А - для алмазов смешанного типа Ib-IaA, или концентраций [А] и [В] примесного азота в форме А и В - для алмазов типа IaAB и вычисляют по формулам (4)-(7) соответствующие усредненные значения интегрального параметра агрегации, приобретенные кристаллами за время их генезиса, для выбираемого пользователем значения порядка кинетики агрегации n. В нашем случае выбираем значение n=2, соответствующее модели процесса агрегации азотных центров по диффузионному механизму [3]. Алмазы исследуемых объектов принадлежат типу IaAB, поэтому вычисление значений интегрального параметра K2At кристаллов анализируемых выборок осуществляется по формуле (5). Для удобства анализа и представления численных данных используются численные значения интегрального параметра агрегации K2At, умноженные на 105.
Статистическое сравнение двух выборок по критерию согласия или критерию однородности Пирсона осуществляют путем вычисления для пары дискретных массивов из логарифмов интегрального параметра, численного значения критической статистики Хи-квадрат для выбранного критерия, представляющей собой интегральную меру расхождения выборочных относительных частот попадания алмазов из сравниваемых массивов в соответствующие интервалы Δlg(Knt). Для статистического сравнения N алмазов из россыпи, с относительными (ΔNi/N) частотами попадания μi в заданные интервалы логарифма интегрального параметра агрегации, с алмазами из коренного источника, с вероятностями попадания в эти же интервалы pi, применяется критерий согласия Пирсона, используемый для проверки гипотезы принадлежности выборки к данной генеральной совокупности. В этом случае вычисляется численное значение критической статистики χ2(k-1) для k интервалов, для Хи-квадрат распределения с (k-1) степенями свободы по формуле (10):
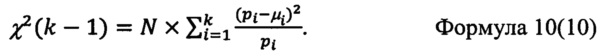
При сравнении алмазов в количестве N1 и N2 из двух россыпей с относительными частотами попадания μ1i и μ2i в соответствующие интервалы логарифма интегрального параметра для проверки гипотезы их принадлежности общему коренному источнику применяют критерий однородности Пирсона, используемый для проверки гипотезы принадлежности двух выборок одной генеральной совокупности. В этом случае вычисляется численное значение критической статистики χ2(k-1) для k интервалов по формуле (11):
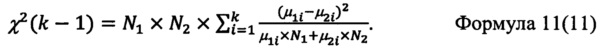
Выбираемое число интервалов k и количество попаданий ΔN в интервал подчиняются определенным правилам [4]. Число интервалов k для массива N должно быть не менее 8, либо не менее числа, определяемого правилом Стерджеса N=2k-1. Число попаданий в интервал должно быть не менее 7-10, интервалы не обязательно должны иметь одинаковую длину, желательно, чтобы в разные интервалы попадало примерно одинаковое число точек. Оптимальная представительность выборки N составляет ~200 единиц. Увеличение представительности выборок до тысяч единиц вызывает значительное (до 60 и более) увеличение числа интервалов, по сравнению с задаваемым правилом Стерджеса, так как при числах попаданий в интервал ~100 аномально возрастает значение критической статистики Хи-квадрат.
Принятие или отвержение гипотезы осуществляется по положению вычисленного значения Хи-квадрат по отношению к его граничному значению, определяемому выбранным уровнем значимости, который задает максимальную вероятность ошибки при отвержении гипотезы.
В силу очень высокой представительности исследуемых выборок, процедура вычисления значений интегрального параметра агрегации азотных центров и его логарифма, построения сглаженной функции плотности вероятности распределения кристаллов из выборок по логарифму интегрального параметра агрегации и статистическое сравнение полученных массивов числовых данных по критерию Пирсона осуществляется при помощи программного средства «Pearson Analyzer of Density Functions (PADF)». Входными данными для программы PADF являются занесенные в базу данных программы массивы полученных методом ИК-спектроскопии численных значений концентраций азота в форме А и В, выраженных в at. ppm. Программа осуществляет формирование числовых массивов логарифмов значений параметра агрегации и осуществляет построение сглаженных функций плотности вероятности распределения кристаллов выборок по логарифму интегрального параметра (формула (8)). Расчет значений критической статистики Хи-квадрат по формулам (10) и (11) осуществляется путем разбиения областей изменения логарифма интегрального параметра сравниваемых выборок на k идентичных для двух выборок интервалов, вычисления относительных (ΔNi/N) частот попадания в соответствующие интервалы алмазов из сравниваемых выборок, определяемых как площади под кривыми их функций плотности в границах соответствующих интервалов, и дальнейшего вычисления численного значения критической статистики Хи-квадрат для выбранного критерия. Разбиение на интервалы программой PADF может осуществляться тремя способами - одинаковые по длине интервалы, одинаковые относительные частоты (площади) в интервалах выборки, одинаковые относительные частоты (площади) в интервалах генеральной совокупности, либо второй выборки (для критерия однородности).
Построенные программой PADF сглаженные функции плотности вероятности по логарифму интегрального параметра K2At×105 для четырех исследуемых объектов (россыпь Нюрбинская, россыпь Майская, трубка Нюрбинская и тело Майское) приведены на фиг. 4.
На фиг. 5 и фиг. 6 представлены принтскрины рабочей панели программы PADF с результатами попарного сравнения по критерию согласия Пирсона дискретных массивов значений логарифмов интегрального параметра агрегации посредством сравнения их сглаженных функций плотности по логарифму интегрального параметра. Вычисление численного значения критической статистики Хи-квадрат осуществлено по формуле (10), где число N означает представительность выборки алмазов из россыпи. Разбиение на интервалы осуществлено для реализации одинаковых относительных частот в интервалах для выборки. Частоты попаданий ΔNi в соответственные интервалы для двух сравниваемых объектов, рассчитанные из функций плотности, представлены на принтскринах в колонках справа. Полученные значения критической статистики Хи-квадрат равны: для пары россыпь Майская - тело Майское k=14, χ2(k-1)=5.8 (фиг. 5а); для пары россыпь Майская - тр. Нюрбинская k=14, χ2(k-1)=30.7 (фиг. 5б); для пары россыпь Нюрбинская - тр. Нюрбинская k=16, χ2(k-1)=3.6 (фиг. 6а); для пары россыпь Нюрбинская - тело Майское k=16, χ2(k-1)=28.2 (фиг. 6б). Представительность выборки из россыпи Нюрбинская при вычислении критической статистики по функциям плотности нормирована на N=200.
Для иллюстрации полученных результатов и степени статистического подобия пар выборок на принтскринах (фиг. 5, 6) представлены также графики функции распределения (верхний график) и функции плотности (нижний график) распределения Хи-квадрат для (k-1) степеней свободы, где k - выбранное нами число интервалов. По оси абсцисс этих графиков откладываются значения параметра Хи-квадрат, по оси ординат у функции распределения - вероятность иметь значение параметра Хи-квадрат меньше выбранного значения (верхний график), а по оси ординат у функции плотности - плотность вероятности для выбранного значения (нижний график).
Положение маленького квадрата на этих кривых фиксирует значение выбранного уровня значимости (в нашем случае 0,05). Уровень значимости задает максимальную вероятность ошибки при отвержении гипотезы принадлежности выборки (в нашем случае - россыпи) к данной генеральной совокупности (в нашем случае - коренному телу). Вычисленное значение критической статистики отображается на графиках функции распределения и функции плотности в виде маленького кружка. Гипотеза отвергается, если вычисленное значение критической статистики χ2(k-1), положение которого фиксирует кружок, оказывается больше значения, определяемого уровнем значимости, положение которого фиксирует квадрат, т.е. кружок оказывается справа от квадрата. При заданном k, для выбранного уровня значимости 0,05, в эту область справа от квадрата будут попадать 5% случайных выборок из данной генеральной совокупности, следовательно, вероятность ошибочного отвержения гипотезы будет составлять 5%.
Соответственно, гипотеза принимается, если кружок оказывается слева от красного квадрата. Чем левее находится кружок, тем меньше вычисленное значение χ2(k-1), представляющее собой интегральную меру расхождения выборочных относительных частот попадания алмазов из сравниваемых массивов в соответствующие интервалы Δlg(Knt), и, следовательно, тем меньше статистическое расхождение сравниваемых массивов.
Как видно из положения вычисленных значений χ2(k-1) для сравниваемых пар функций плотности на графике функции распределения Хи-квадрат, россыпные источники демонстрируют очень высокую вероятность статистического подобия к своим коренным источникам: россыпь Майская - тело Майское (фиг. 5а) и россыпь Нюрбинская - тр. Нюрбинская (фиг. 6а) и дают отрицательный результат экспертизы при сравнении с «чужим» коренным источником: россыпь Майская - тр. Нюрбинская (фиг. 5б) и россыпь Нюрбинская - тело Майское (фиг. 6б).
Список использованной информации
[1] Васильев Е.А. (2011) / Пат. 2413931 Российская Федерация, МПК G01N 21/87, Способ идентификации источника коллекции кристаллов алмаза / Е.А. Васильев. - №2009124872/28, заявл. 29.06.2009, опубл. 10.03.11, Бюл. №7. - 5 с.
[2] Софронеев С.В. (2015) / Пат. 2539904 Российская Федерация, МПК G01N 21/35, G01V 9/00, Способ восстановления температурно-временных условий генезиса алмаза / С.В. Софронеев. - №2013122237/28, заявл. 14.05.2013, опубл. 27.01.2015, Бюл. №3. - 25 с.
[3] Evans Т. Aggregation of nitrogen in diamond // In: Field J.E. (ed.) The properties of natural and synthetic diamond. London: 1992, p. 259-290.
[4] Айвазян C.A., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. - М.: Финансы и статистика, 1983. - 472 с.
[5] Софронеев С.В., Забелин А.В. (2016) / Свидетельство о регистрации программы для ЭВМ №2016617075 Российская Федерация, «Реагеоп Analyzer of Density Functions (PADF)» / С.В. Софронеев, А.В. Забелин. - №2016614264, заявл. 28.04.2016, опубл. 24.06.2016.
[6] Софронеев С.В. Температурно-временные характеристики генезиса алмаза / Материалы VII Всеросс. науч.-практ. конф. «Геология и минерально-сырьевые ресурсы северо-востока России», Якутск, 5-7 апреля 2017. - Т. 1. - С. 444-450.

Изобретение относится к области исследования и экспертизы алмазов и может использоваться в геммологии, при осуществлении геолого-поисковых работ методом поиска «алмазов по алмазам», для сравнения кристаллов из россыпей с алмазами из известных коренных и россыпных источников, а также при экспертных оценках партий кристаллов, включая обработанные камни, на предмет их принадлежности известным алмазоносным источникам. Заявлен способ сравнения выборок азотсодержащих алмазов с представительностью N, основанный на измерении, например, методом ИК-Фурье спектроскопии на целых кристаллах выборки усредненных концентраций азота в форме А и В или С и определении для выбранного порядка кинетики агрегации n, усредненных численных значений интегрального параметра агрегации Knt азотных А-центров либо С-центров, приобретенных кристаллами за время их генезиса. При этом дополнительно вычисляют логарифмы усредненных значений интегральных параметров агрегации (lgKnt), строят сглаженную функцию плотности вероятности распределения кристаллов из выборок по логарифму интегрального параметра агрегации и определяют степень статистического подобия двух выборок путем сравнения пары дискретных числовых массивов значений логарифмов интегрального параметра агрегации кристаллов или сглаженных функций плотности, например, по критерию Пирсона, а определение степени статистического подобия выборок по критерию Пирсона осуществляют, например, при помощи программного средства «Pearson Analyzer of Density Functions (PADF)». Технический результат - повышение достоверности определения степени статистического подобия выборок азотсодержащих алмазов из разных источников. 3 з.п. ф-лы, 6 ил.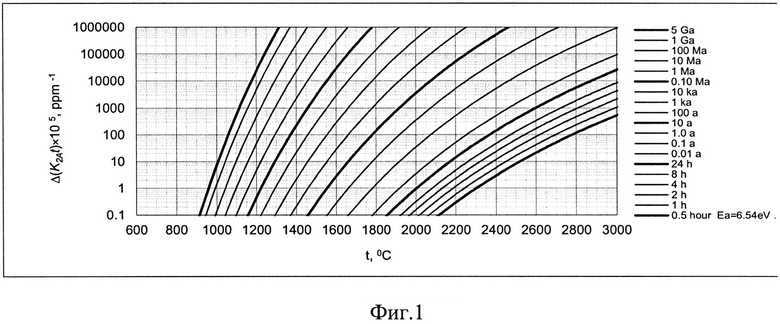
1. Способ сравнения выборок азотсодержащих алмазов из различных источников с представительностью N, основанный на измерении, например, методом ИК-Фурье спектроскопии усредненных концентраций азота [А] - в форме А и [В] - в форме В или [С] - в форме С и определении для выбранного порядка кинетики агрегации n усредненных численных значений интегрального параметра агрегации KnCt азотных С-центров либо интегрального параметра агрегации KnAt азотных А-центров, приобретенных кристаллами за время их генезиса, отличающийся тем, что измерения проводят на целых кристаллах, дополнительно вычисляют логарифмы усредненных значений интегральных параметров агрегации (lgKnt), строят сглаженную функцию плотности вероятности распределения кристаллов из выборок по логарифму интегрального параметра агрегации и определяют степень статистического подобия двух выборок путем сравнения пары дискретных числовых массивов значений логарифмов интегрального параметра агрегации кристаллов или сглаженных функций плотности, например, по критерию Пирсона.
2. Способ по п. 1, отличающийся тем, что усредненные численные значения интегрального параметра агрегации азотных С-центров KnCt либо А-центров KnAt рассчитывают при n≠1 по формулам
KnCt=([С]1-n-[С+А]1-n)/(n-1),
KnAt=(([А]/2)1-n-([А+B]/2)1-n)/(n-1).
3. Способ по п. 1, отличающийся тем, что усредненные численные значения интегрального параметра агрегации азотных С-центров KnCt либо А-центров KnAt при n=1 рассчитывают по формулам
KnCt=ln([С+А]/[С]),
KnAt=ln([A+В]/[А]).
4. Способ по п. 1, отличающийся тем, что определение степени статистического подобия выборок по критерию Пирсона осуществляют, например, при помощи программного средства «Pearson Analyzer of Density Functions (PADF)».
| СПОСОБ ВОССТАНОВЛЕНИЯ ТЕМПЕРАТУРНО-ВРЕМЕННЫХ УСЛОВИЙ ГЕНЕЗИСА АЛМАЗА | 2013 |
|
RU2539904C2 |
| SU 1603588 A1, 20.08.1999 | |||
| Способ определения содержания алмазов в пробах сырья | 1988 |
|
SU1589777A1 |
| СПОСОБ ИДЕНТИФИКАЦИИ АЛМАЗОВ И ИХ ФРАГМЕНТОВ | 1990 |
|
SU1797336A1 |
Авторы
Даты
2018-08-07—Публикация
2017-08-30—Подача