Описание изобретения
Предлагаемый способ относится к области моделирования процессов тепломассопереноса, в частности к области моделирования процессов лучистого теплообмена.
Известен зональный метод моделирования процессов тепломассопереноса, в основе которого лежит деление излучающей объемной среды и ограничивающих поверхностей на ряд зон, теплофизические параметры в пределах каждой из которых считаются постоянными. Каждая из зон связана с другими через обобщенные угловые коэффициенты излучения, показывающие, какая доля энергии, излученной в одной зоне, достигает другой зоны и поглощается ею.
Основы прикладного зонального метода расчета радиационного и сложного теплообмена были заложены в работах Г.Л. Поляка, Ю.А. Суринова, А.С. Невского, В.Н. Адрианова, X. Хоттеля. Дальнейшее развитие методы расчета топок получили в работах В.М. Седелкина, В.Г. Лисиенко, Ю.А. Журавлева и др.
В зональных методах расчетная область делится на n поверхностных и m объемных зон. В пределах каждой зоны температура и радиационные характеристики считаются постоянными. Представление излучающей системы в виде совокупности изотермичных зон, обменивающихся радиационной энергией, позволяет получить распределение потоков излучения как функции средне-зональных температур. В математическом плане применение зональных методов позволяет перейти от интегро-дифференциальных уравнений, которыми описываются процессы сложного теплообмена, к аппроксимирующей конечной системе нелинейных алгебраических уравнений относительно среднезональных температур.
Было разработано несколько схем расчета с целью эффективного применения зонального метода к различным теплотехническим задачам. Эти схемы характеризуются различием математической записи выражений, аппроксимирующих интегральные уравнения излучения, последовательностью и способами их решения [1-4]. При определении лучистой составляющей зональных уравнений теплового баланса в нашей стране распространена расчетная схема, использующая введенные Ю.А. Суриновым разрешающие угловые коэффициенты излучения [5]. В общем виде, для каждой из n поверхностных и т объемных зон можно записать соответствующее нелинейное уравнение теплового баланса и теплопередачи:

В такой форме запись уравнения впервые была предложена В.Г. Лисиенко [6]. В этом уравнении первые два слагаемых представляют собой результирующий радиационный тепловой поток для зоны j, равный разности между теплом, поглощенным данной зоной j вследствие лучистого переноса из других зон i, и собственным излучением 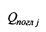 . Третье и четвертое слагаемые представляют собой величину результирующего теплообмена данной зоны j с соседними зонами i в результате переноса тепла с движущейся средой, конвективного теплопереноса и теплопередачи через поверхностные зоны; последнее слагаемое - количество тепла подводимое извне.
. Третье и четвертое слагаемые представляют собой величину результирующего теплообмена данной зоны j с соседними зонами i в результате переноса тепла с движущейся средой, конвективного теплопереноса и теплопередачи через поверхностные зоны; последнее слагаемое - количество тепла подводимое извне.
Угловой коэффициент излучения - это величина, характеризующая поток излучения, который попадает с одной площадки изучаемой системы на другую. Если i-тая излучающая поверхность (источник излучения) системы излучает на j-тую излучающую поверхность системы (приемник излучения), то ϕi,j определяет, какая часть от общего излучения i-той поверхности попадает на j-тую. В литературе часто приводится формула (2), которая, однако плохо работает при переходе к алгебраическим уравнениям, в случае если площади поверхностей сопоставимы с квадратом расстояния между ними (рисунок 1):
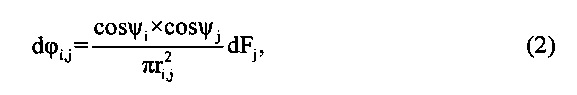
где, ψi, ψj - углы между нормалями излучающих поверхностей и прямой, соединяющей их центры,
ri,j - расстояние между излучающими поверхностями.
dFj - площадь поверхности-приемника.
Особенностью системы уравнений с разрешающими угловыми коэффициентами излучения является простота формы записи и универсальность уравнений. Взаимный баланс лучистых и конвективных членов в выражении (1) позволяет учесть совместное тепловое взаимодействие конвекции и излучения.
Точность такого подхода исследовалась относительно точной постановки задачи радиационно-конвективного теплообмена [7], где было показано, что погрешность зонального расчета на участках, где наиболее сильно проявляется взаимодействие конвекции и излучения, не превышает 7% при определении результирующих потоков и 2% при нахождении распределений температуры.
Известные способы нахождения обобщенных угловых коэффициентов - метод Монте-Карло, метод квадратур Гаусса и другие, имеют ряд недостатков, в числе которых огромная вычислительная мощность аппаратных средств, требуемых для расчета сложной системы взаимодействующих тел (большое количество нагревателей в печном агрегате, большое число обрабатываемых изделий в рабочем объеме, сложная геометрия печного пространства). Расчет коэффициента согласно формуле 2 применимо только в случае, когда квадрат расстояния между исследуемыми элементами значительно больше их площади.
Графический процессор это отдельное устройство в составе компьютера, которое выполняет обработку графической информации для вывода на экран (рендеринг). Благодаря специализированной конвейерной архитектуре он справляется с этой задачей намного лучше центрального процессора. Видеоадаптеры (видеокарты) имеют в своем составе до нескольких тысяч ядер и собственную оперативную память, их архитектура оптимизирована для массивных параллельных вычислений, что и определяет их большую эффективность в рендеринге.
Графический конвейер - это аппаратно-программный комплекс визуализации трехмерной графики, последовательность стадий (функций), выполняющихся в фиксированном порядке и параллельно. Каждая стадия принимает информацию из предыдущей стадии и отправляет в следующую. В современном графическом конвейере поддерживаемом существует пять программируемых стадий: вершинный шейдер (Vertex Shader), шейдер поверхности (Hull Shader), шейдер домена (Domain Shader), геометрический шейдер (Geometry Shader) и пиксельный шейдер (Pixel Shader). Каждая из стадий служит этапом в выводе изображения на экран. Если принять излучение полностью диффузионным (независящим от направления), то угловой коэффициент отражает, какая часть излучения источника, распространяемого по полусфере, попадает на проекцию приемника на эту сферу. Используя термины трехмерной компьютерной графики, получается, что если поставить наблюдателя в точку источника излучения, и направить взгляд по направлению нормали в данной точки и отобразить полученное изображение в сферической системе координат (зенитные и азимутные углы откладываются по осям x и y, r выполняет роль глубины изображения - координаты z), то отношение полученной площади приемника к полной площади изображения, есть угловой коэффициент излучения.
Техническая задача, решаемая предлагаемым способом, состоит в использовании аппаратных средств графических ускорителей (графического конвейера) для расчета обобщенных угловых коэффициентов.
Суть предложенного способа заключается в представлении источника излучения в виде «камеры», прорисовки видимом ей изображении средствами графического ускорителя и обработке этого изображения. Обработка изображения имеет целью рассчитать степень «видимости» остальных элементов системы из точки «камеры».
Из этого следует, что для расчета углового коэффициента излучения необходимо:
1) Поставить наблюдателя (камеру) в точку, принимаемую как локальный источник излучения, таких точек на одной поверхности может быть сколько угодно, для увеличения точности расчета, при этом интенсивность каждой отдельной точки обратно пропорциональна их количеству.
2) Направлением камеры выбрать нормаль к излучающей поверхности в данной точке.
3) Произвести рендеринг изображения, переведя перед этим все координаты в сферическую систему координат. В цвете поступающих на отрисовку примитивов закодирован номер изотермической зоны и номер излучающей поверхности этой зоны.
4) Определить на полученном изображении отношение площадей видимых поверхностей к площади изображения (точнее круговой центральной его части, так как координаты точек будут иметь разброс по первым двум координатам от -π/2 до π/2).
Для реализации алгоритма предлагается использовать стандартные средства для работы с графическими процессорами, а именно DirectX 11 фирмы Microsoft. Программа, реализующая данный алгоритм имеет свидетельство о государственной регистрации программы для ЭВМ №2015619364.
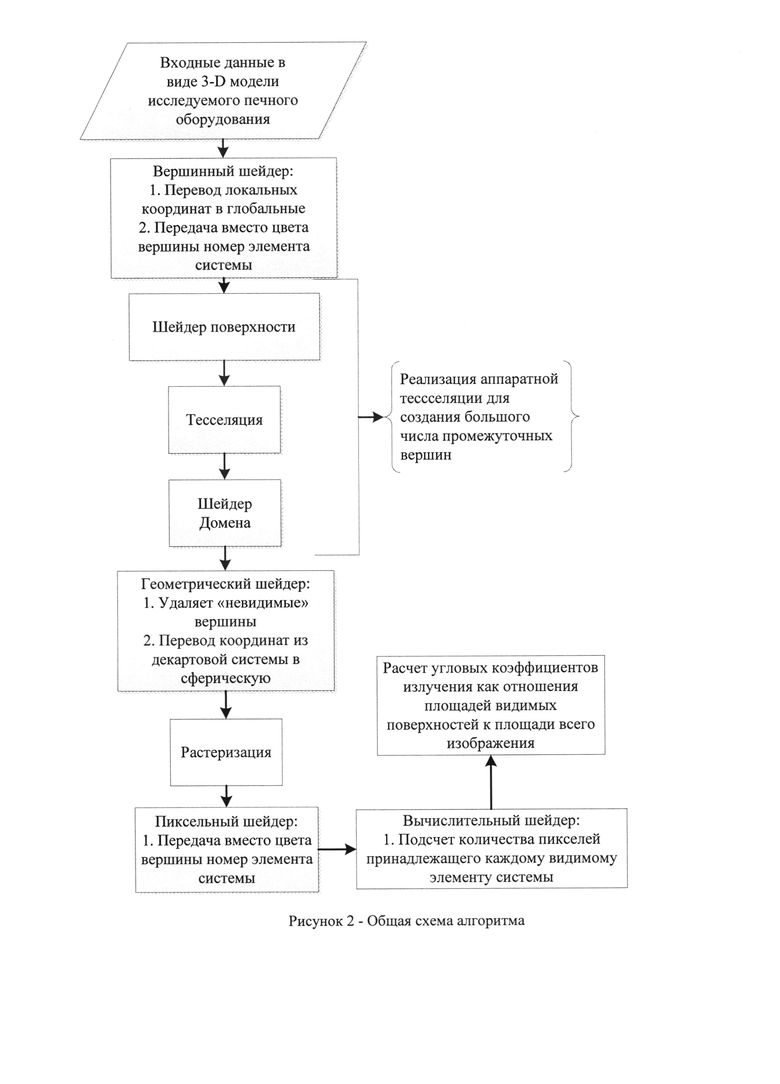
В современном графическом конвейере, поддерживаемом в DirectX 11 пять программируемых стадий (рисунок 2): вершинный шейдер (Vertex Shader), шейдер поверхности (Hull Shader), шейдер домена (Domain Shader), геометрический шейдер (Geometry Shader) и пиксельный шейдер (Pixel Shader).
Каждая из этих стадий необходима для реализации алгоритма. Прежде чем запускать графический конвейер в видеокарты необходимо загрузить текстуры (с точки зрения программирования это обычный массив) и буфер вершин. В буфере трехмерная модель, которую необходимо отрисовать, представлена в виде последовательности точек (вершин), объединенных в треугольники. Получив данные видеокарта запускает графический конвейер, в котором каждая из стадий выполняется параллельно на всех имеющихся ядрах (шейдерных процессорах).
Вершинный шейдер вызывается для каждой вершины. В данной реализации служит для перевода локальных координат примитивов (треугольников) в глобальные, а затем из глобальных в координаты камеры. В итоге координата z отвечает за глубину изображения, то есть, направлена вглубь экрана. Вместо цвета, для дальнейшей обработки передается номер элемента системы, к которому принадлежит вершина (в данном случае это два числа - номер изотермической зоны и номер излучающей поверхности этой зоны).
Так как графический конвейер способен работать только с вершинами в декартовой системе координат, то он будет некорректно проводить растеризацию, то есть заполнения пространства внутри треугольника. Прямые, соединяющие вершины в декартовой системе координат, не являются таковыми в сферической, вырождаясь в дуги, что вызывает погрешности, вплоть до полного искажения результатов. Решением данной проблемы в рамках графического конвейера может быть увеличение числа треугольников, то есть уменьшение их размеров. Но задавать заранее большее количество вершин накладно с точки зрения ресурсов и отнимает у алгоритма гибкость (необходимо загружать разные модели для разной точности расчетов). Более правильным является использование двух следующих стадий конвейера, появившихся в 11 версии DirectX: шейдер поверхности и шейдер домена. Их совокупная работа позволяет организовать так называемую тесселяцию - разделение поступающих на вход треугольников на более мелкие треугольники «на лету», т.е. генерируемые вершины не присутствуют в исходной модели, а появляются на этой стадии. Это позволяет резко повысить детализацию трехмерной модели, в том числе и в сферической системе координат, и следственно точность расчета угловых коэффициентов. Чем больше уровень тесселяци, тем точнее грани первичного треугольника соответствуют их реальному виду в сферической системе координат. Данный способ позволяет организовать изменение уровня тесселяции в зависимости от расстояния до объекта и его углового размера, так как нет смысла тратить ресурсы графического процессора на деление далеких от камеры треугольников, они и так отобразятся близко к истине, в то время как близкие объекты будут искажены, и требуют более высокого уровня тесселяции. Так же теселяция позволяет «на лету» округлять поверхности, что удобно при прорисовке сфер, цилиндров и других сферических объектов, так как они при разбиении на излучающие поверхности заменяются правильными многоугольниками и многогранниками.
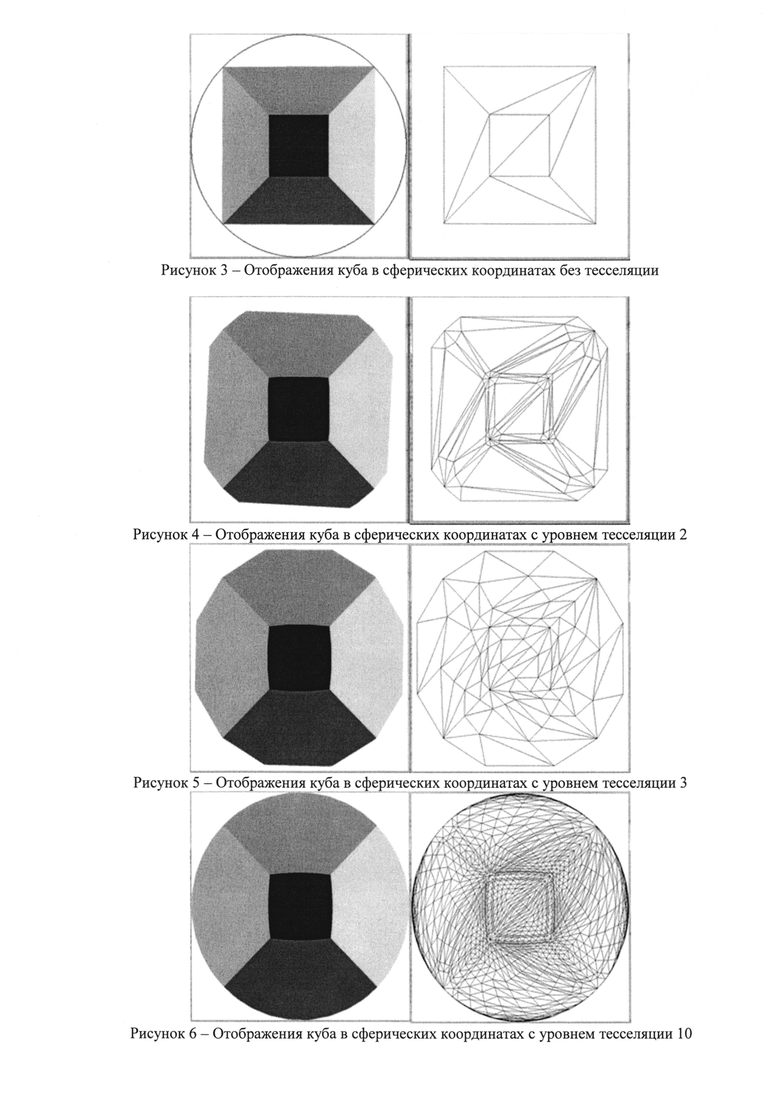
В качестве примера необходимости применения тесселяции рассмотрим простейший случай - куб, каждая из граней которого состоит из двух треугольников и является излучающей поверхностью. Если поставить камеру в центр одной их граней и смотреть внутрь куба то в сферических координатах получится картинка, представленная на рисунке 3. Каждая грань для удобства раскрашена своим цветом. Рядом для наглядности каркасное изображение.
Как видно из представленного рисунка, получившееся изображение сильно искажено слишком малым количеством вершин. Соединяя их по прямой при рендеринге графический процессор не учитывает что это сферическая система координат, в результате мы получим сильно заниженные угловые коэффициенты и часть излучения будет просто «улетать в пустоту» (в случае куба очевидно что излучение изнутри никуда не может исчезнуть и должна быть заполнена вся центральная круговая зона). При тесселяции каждая из сторон исходного треугольника и его внутренняя область разбивается на несколько отрезков, которые становятся сторонами новых более мелких треугольников. Назовем количество делений уровнем тесселяции. На рисунках 4-7 представлены изображения при уровнях тесселяции 2, 3, 10 и 20 соотвественно (рендеринг производился в текстуру 3000×3000 точек).
Полученные вершины поступают на следующую стадию - геометрический шейдер. В отличие от вершинного, он обрабатывает весь примитив целиком, т.е. на его вход приходит сразу три вершины, принадлежащие одному треугольнику. Так же этот шейдер способен генерировать новые произвольные (по заданному пользователем алгоритму) вершины и удалять старые. На этом этапе необходимо сначала проверить вершины на видимость камерой, и если необходимо пересчитать некоторые их них. Видимой для камеры вершиной в данном случае считается вершина с неотрицательной координатой z (вся полусфера). В случае если в треугольнике нет неотрицательных вершин, он не отправляется на дальнейшую отрисовку (вершины удаляются).
На этапе растеризации (рисунок 2) графический процессор закрашивает все пиксели, принадлежащие треугольнику, но при стандартном использовании графического конвейера применяется матрица проекций, трансформирующая координаты примитивов в проекционные. Координата z (глубина изображения) приводится к диапазону (0.0,1.0), а координаты x и y приводятся к виду, в котором видимая часть изображения имеет координаты (-0.5, 0.5).
В сферической системе координат по оси x откладываем θcos(ϕ), по оси y - θsin(ϕ), r - выступает в роли глубины изображения, где θ - зенитный угол, ϕ - азимутный угол, r - кратчайшее расстояние до начала координат (камеры). Для компенсации отсутствия проекционной матрицы необходимо разделить r на некоторую, заранее большую максимального расстояния в исследуемой модели величину (таким образом, приведя к нужному диапазону); в 4 компоненту координаты вершины в сферической системе координат вписать π/2 (так как диапазон сферических координат (-π/2, π/2)). На рисунке 8 приводится пример прорисовки треугольников. Красный квадрат определяет зону выводимую на экран (кадр), черный круг показывает разброс сферических координат. В случае зеленого треугольника имеется одна неотрицательная вершина, при перерасчете в сферические координаты будет закрашена сверх необходимого серая зона, что приведет к неправильному расчету площади. Необходимо заменить каждую из двух точек за границей обзора на точки пересечения с окружностью (в декартовой системе это точки пересечения с плоскостью XY). В случае наличие двух неотрицательных точек (синий треугольник) заменяется только одна из точек, но количество треугольников удваивается.
Белый участок между отрисованным треугольником и окружностью обзора появляется из-за погрешности приведения к сферической системе, и исправляется тесселяцией (желтый треугольник). После выполнения геометрического шейдера треугольник отобразиться внутри зоны ограниченной кругом, площадью π/4 от общей площади квадратного изображения. Ниже приведен код перевода из декартовых в сферические координаты. Если треугольник полностью лежит в неотрицательной области z, то он отрисовывается без изменений. В полученной системе точки, лежащие на одной прямой, если смотреть из начала координат (камеры) имеют одни и те же координаты x и y, но разную составляющую z, что позволяет применить стандартный буфер глубины (z-буфер), для определения перекрываемости точек поверхностей для корректного отображения.
Пиксельный шейдер возвращает в качестве цвета пикселя номер излучающей поверхности к которой принадлежит. Так как он вызывается уже после проверки буфера глубины, то это значит, что точка видна из камеры (источника) и на нее попадает излучение, равное излучению источника деленной на полное число пикселей в центральной круговой части изображения.
Полученное изображение обрисовывается не на экран, а в текстуру, и подсчитывается количества пикселей, принадлежащих каждой попавшей в кадр поверхности, и делению этой величины на полное число пикселей в круговой части изображения. Полученные числа аддитивно вносятся в таблицу угловых коэффициентов излучения для дальней обработки [8-10].
Для подсчета угловых коэффициентов на основе изображения выгодно так же использовать ресурсы графического процессора, чтобы, во-первых, не тратить время на выгрузку каждой картинки из видеопамяти в память компьютера (разрешение изображения оптимально делать не менее 2000 на 2000 пикселе), во-вторых, графическое ядро справится с задачей обработки изображения значительно быстрей. Для решения поставленной задачи предлагается использовать новшество DirectX 11 - вычислительный шейдер (Compute Shader). Вычислительный шейдер это программа, заменяющая собой весь графический конвейер, позволяя использовать графическое ядро для общих задач. В данной задаче, вычислительный шейдер обрабатывает полученное изображение, и возвращает массив элементов системы, на которые излучает исследуемая излучающая поверхность и количество пикселей попавших в кадр.
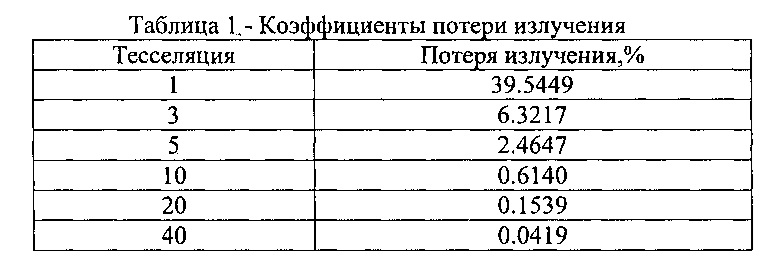
Как видно из рисунков 3-7, переход к сферической системе координат приводит к не полному заполнению круговой зоны (полусфера излучения). Число «потерянных» пикселей (разница между числом закрашенных пикселей и полным их числом во внутренней круговой зоне) уменьшается с увеличением уровня тесселяции. Назовем отношение числа потерянных пикселей к общему их числу в круговой зоне коэффициентом потери излучения модели (Таблица 1).
Частично данный эффект можно компенсировать последующим распределением «недостающих пикселей» среди всех пограничных элементов.
В модели [8-10], разработанной на основе зонального метода, применяется рекурсивный учет отражения и одним из критериев корректности матрицы излучения является нулевая сумма элементов каждой строки (иначе замкнутая система не стремиться к выравниванию температуры при прекращении подачи энергии извне). Назовем дефицитом излучения модели отношение отклонения суммы элементов строки от нуля к величине диагонального элемента. По сути дефицит излучения отражает количество излучения «потерянного» излучающей ячейкой из-за принятых в модели допущений. Ниже представлены таблицы коэффициентов дефицита излучения (в процентах) для куба при различных уровнях тесселяции и глубине отражения (в случае куба все 6 граней равнозначны).
Как видно из таблиц 2 и 3 при тесселяции больше 10 основную погрешность вносит недостаточное количество отражений, особенно при низком коэффициенте поглощения (при последнем вызове рекурсивной функции отраженная часть излучения теряется). Если при последнем вызове не учитывать отражение, то коэффициент дефицита резко уменьшится.
Предложен принципиально новый способ расчета угловых коэффициентов излучения основанный на использовании ресурсов графического процессора и средств Microsoft DirectX 11, разработано программное обеспечение и проведены экспериментальные исследования. Данный способ позволяет рассчитывать угловые коэффициенты в системе произвольной сложности с любой необходимой точностью. Средства DirectX позволяют автоматизировать и скрыть от программиста большую часть расчетов, значительно упростив написание и снизив время работы программы. Использование вычислительного шейдера позволяет избежать потерь времени на копирование данных из памяти видеокарты в память персонального компьютера.
Краткое описание чертежей:
Рисунок 1 - графическое пояснение к формуле 2,
Рисунок 2 - схема работы графического конвейера,
Рисунок 3-7 - изображения куба в сферической системе координат с различными уровнями тесселяции,
Рисунок 8 - пример прорисовки треугольников в сферической системе координат с учетом видимости его вершин для наблюдателя,
Таблица 1-3 - влияние тесселяции на потерю излучения.
1. Невский А.С. Лучистый теплообмен в печах и топках. 2-е изд., испр. и доп. М.: Металлургия, 1971. 440 с.
2. Спэрроу Э.М., Сесс Р.Д. Теплообмен излучением. Л.: Энергия, 1971. 296 с.
3. Зигель Р., Хауэлл Дж. Теплообмен излучением. М.: Мир, 1975. 936 с.
4. Юдаев Б.Н. Теплопередача. - Москва: Высшая школа, 1973. - 360 с.
21. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. - Москва: Энергия, 1975. - 480 с.
5. Суринов Ю.А. Об итерационно зональном методе исследования и расчета локальных характеристик лучистого теплообмена. - Теплофизика высоких температур, 1972. Т. 10. №4. С. 844-852.
6. Лисиенко В.Г., Волков В.В., Гончаров А.Л. Математическое моделирование теплообмена в печах и агрегатах. Киев: Наук, думка, 1984. 232 с.
7. Щербинин В.И., Боковикова А.Х., Шкляр Ф.Р. Взаимодействие излучения и конвекция при сложном теплообмене в коротком канале // Инженерно-физический журнал, 1974. Т. 26. №2. С. 238-244.
8. Лебедев, И.А. Модель термообработки металлических изделий в вакууме / И.А. Лебедев, А.П. Пономарев // VII Международная научно-практическая конференция «Энергосберегающие технологии в промышленности. Печные агрегаты. Экология»: сб. материалов. - Москва: МИСиС, 2014. - С. 270-280.
9. Лебедев, И.А. Управление равномерностью нагрева изделий в вакуумных электрических печных агрегатах / И.А. Лебедев, Д.В. Шатов // XII Всероссийское совещание по проблемам управления: сб. трудов. - Москва: ИПУ РАН, 2014. - С. 4315-4324.
10. Лебедев, И.А. Компьютерная модель нагрева теплозащитного контейнера в вакуумных печах / И.А. Лебедев, А.П. Пономарев // VI Международная научно-практическая конференция «Печные агрегаты и энергосберегающие технологии в промышленности. Экология»: сб. трудов. - Москва: МИСиС, 2012. - С. 319-320.




Изобретение относится к области моделирования процессов тепломассопереноса. Технический результат – обеспечение расчета обобщенных угловых коэффициентов излучения посредством использования средств графического процессора. Способ расчета обобщенных угловых коэффициентов излучения, применимый для вакуумных печных агрегатов, выполняется посредством использования графического конвейера, включающего в себя вершинный шейдер для перевода локальных координат примитивов в глобальные, а затем из глобальных в координаты камеры, шейдер поверхности и шейдер домена для выполнения аппаратной тесселяции, геометрический шейдер для преобразования координат вершин трехмерной модели исследуемого объекта из декартовой системы координат в сферическую и удаления невидимых излучателем поверхностей, пиксельный шейдер для возврата в качестве цвета пикселя номера излучающей поверхности и вычислительный шейдер для обработки полученного изображения и возврата массива элементов системы, на которые излучает исследуемая излучающая поверхность, и количества пикселей, попавших в кадр, и для подсчета угловых коэффициентов излучения на основе изображения. 2 з.п. ф-лы, 8 ил., 3 табл.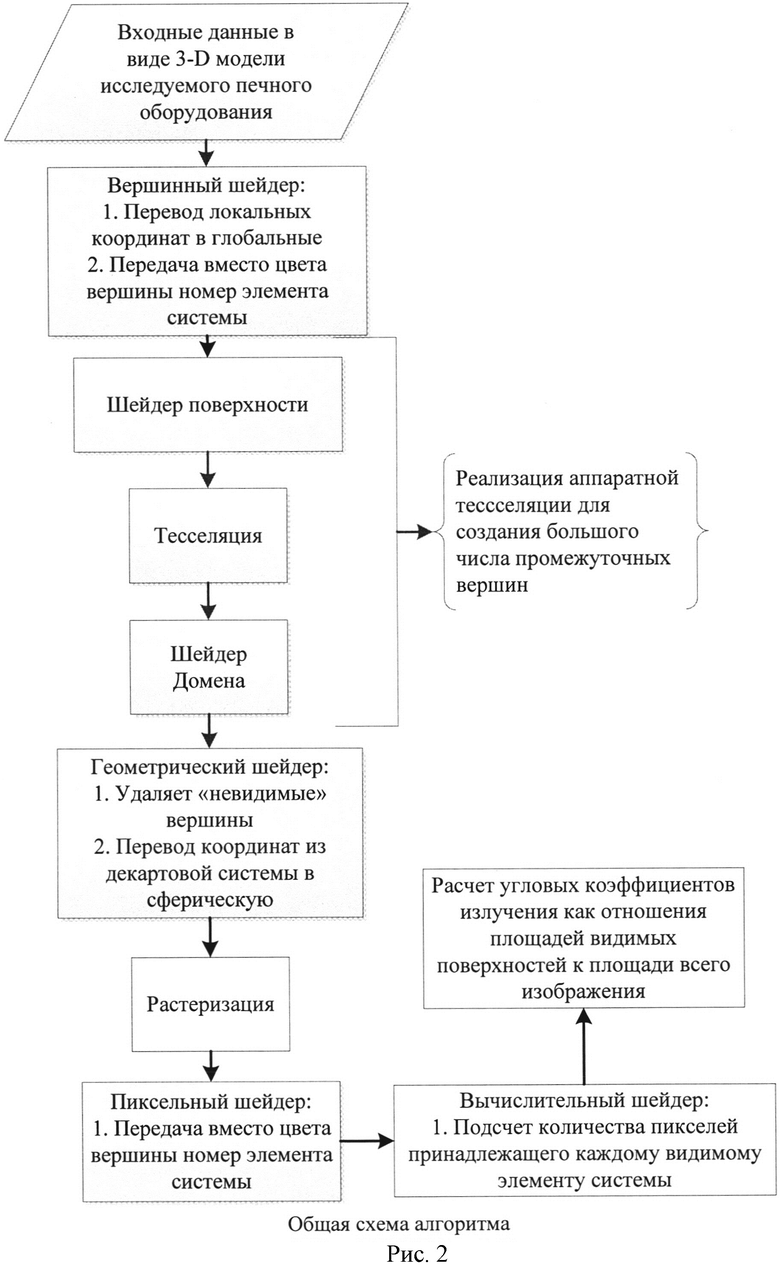
1. Способ расчета обобщенных угловых коэффициентов излучения, применимый для вакуумных печных агрегатов, выполняемый посредством использования графического конвейера, исполняемого на графическом процессоре, причем указанный графический конвейер включает в себя вершинный шейдер для перевода локальных координат примитивов в глобальные, а затем из глобальных в координаты камеры, шейдер поверхности и шейдер домена для выполнения аппаратной тесселяции, геометрический шейдер для преобразования координат вершин трехмерной модели исследуемого объекта из декартовой системы координат в сферическую и удаления невидимых излучателем поверхностей, пиксельный шейдер для возврата в качестве цвета пикселя номера излучающей поверхности и вычислительный шейдер для обработки полученного изображения и возврата массива элементов системы, на которые излучает исследуемая излучающая поверхность, и количества пикселей, попавших в кадр, и для подсчета угловых коэффициентов излучения на основе изображения.
2. Способ по п. 1, в котором вершинный шейдер дополнительно используется для передачи номера излучающей поверхности вместо цвета на следующий этап графического конвейера - шейдер поверхности.
3. Способ по п. 1, в котором геометрический шейдер дополнительно используется для преобразования координат из декартовой в сферическую систему координат, с последующим удалением вершин трехмерной модели, имеющих отрицательную координату z.
| CN 103544356 A, 29.01.2014 | |||
| US 7570267 B2, 04.08.2009 | |||
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ИЗЛУЧАТЕЛЬНОЙ СПОСОБНОСТИ ВНУТРЕННИХ ПОВЕРХНОСТЕЙ НЕОДНОРОДНО НАГРЕТОЙ ПОЛОСТИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2247339C2 |
| БУХМИРОВ В.В | |||
| и др | |||
| Зональные методы расчета радиационного и сложного теплообмена/ФГБОУВПО "Ивановский государственный энергетический университет имени В.И | |||
| Ленина", Иваново, 2012, 96 с. | |||
Авторы
Даты
2018-08-14—Публикация
2015-12-14—Подача