Изобретение относится к области информационных технологий, предназначенных для специализированной обработки данных, в частности к способу вычислительного моделирования процессов в подземной гидродинамике и к разработке аппаратно-программных средств предсказательного моделирования в подземной гидродинамике.
Существуют коммерческие гидродинамические симуляторы, не включающие в себя возможность учета мелкомасштабной (подсеточной) неустойчивости:
1) ECLIPSE, https://www.software.slb.com/products/eclipse.
2) STARS CMG, http://www.cmgl.ca/stars.
3) Техсхема, http://tecscheme.org/.
4) Т-навигатор, http://rfdyn.ru/technology/.
Программного пакета, позволяющего проводить моделирование нелинейных процессов вытеснения углеводородов с учетом возникающей неустойчивости фронта на мелком масштабе, на данный момент нет.
Методы математического моделирования процессов фильтрации на основе параметров, полученных из геологических исследований в скважинах и лабораторных исследований свойств жидкостей и породы, описываются во многих патентах (RU 2148169 С1, 17.09.1998; RU 2166619 С1, 03.09.1999; RU 2166630 С1, 03.09.1999; RU 2183268 С2, 14.07.2000; RU 2522494 С1, 10.05.2013).
Одним из недостатков известных методов является то, что моделирование происходит на макроуровне без учета возможных процессов на микроуровне, а именно, неустойчивости, возникающей на фронте вытеснения углеводорода из пласта, что оказывает существенное влияние на результат моделирования. Впоследствии это может привести к выбору неправильной стратегии разработки месторождения и к существенным финансовым потерям организации, использующей представленные методы моделирования.
Учет физических свойств на микроуровне производится в методе, описанном в патенте RU 2428739 С2, 16.05.2007. Суть метода заключается в разбиении исследуемой геологической структуры на крупномасштабные блоки (КМБ), а затем разбиение КМБ на более мелкомасштабные блоки (ММБ) и вычисление значения физических свойств для ММБ после чего путем ремасштабирования осуществляют вычисление значения физических свойств для КМБ.
Недостатком известного метода является то, что неустойчивость, возникающая на фронте вытеснения, в данной модели не учитывается как на макроуровне, так и на микроуровне, из-за чего снижается точность расчетов и увеличивается время их проведения при построении реальной модели прогнозирования протекания процессов в нефтесодержащих пластах.
Задачей является повышение точности расчетов и сокращение времени их проведения при построении реальной модели прогнозирования протекания процессов в нефтесодержащих пластах.
Технический результат заключается в изменении модели на макроуровне за счет дополнительных потоков в уравнениях в зависимости от физических свойств, полученных при исследовании процесса на микроуровне.
Указанные задача и технический результат достигаются использованием способа многомасштабного моделирования нелинейных процессов подземной гидродинамики, включающим разбиение исследуемой геологической структуры на крупномасштабные блоки (КМБ), разбиение КМБ на более мелкомасштабные блоки (ММБ), вычисление значения физических свойств для ММБ после чего вычисление значения физических свойств для КМБ, при этом, вычисления значений физических свойств для КМБ осуществляют с учетом дополнительных корректирующих членов уравнений, коэффициенты для которых получены из вычислений для ММБ, а в качестве физического свойства, определяемого на ММБ, определяют неустойчивость на фронте вытеснения углеводорода из пласта.
А также тем, что для вычисления физических свойств для ММБ формируют диапазон возможных безразмерных параметров и контрольных точек в фазовом пространстве этих параметров внутри этого диапазона, проводят различные варианты расчетов на основе указанных параметров и формируют интерполяционные зависимости результатов от введенных параметров, с помощью которых определяют коэффициенты дополнительных корректирующих членов уравнений для определения значений физических свойств для КМБ.
А также тем, что вычисление физических свойств для ММБ осуществляют из соотношений:
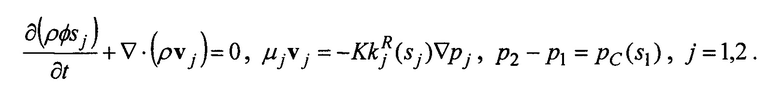
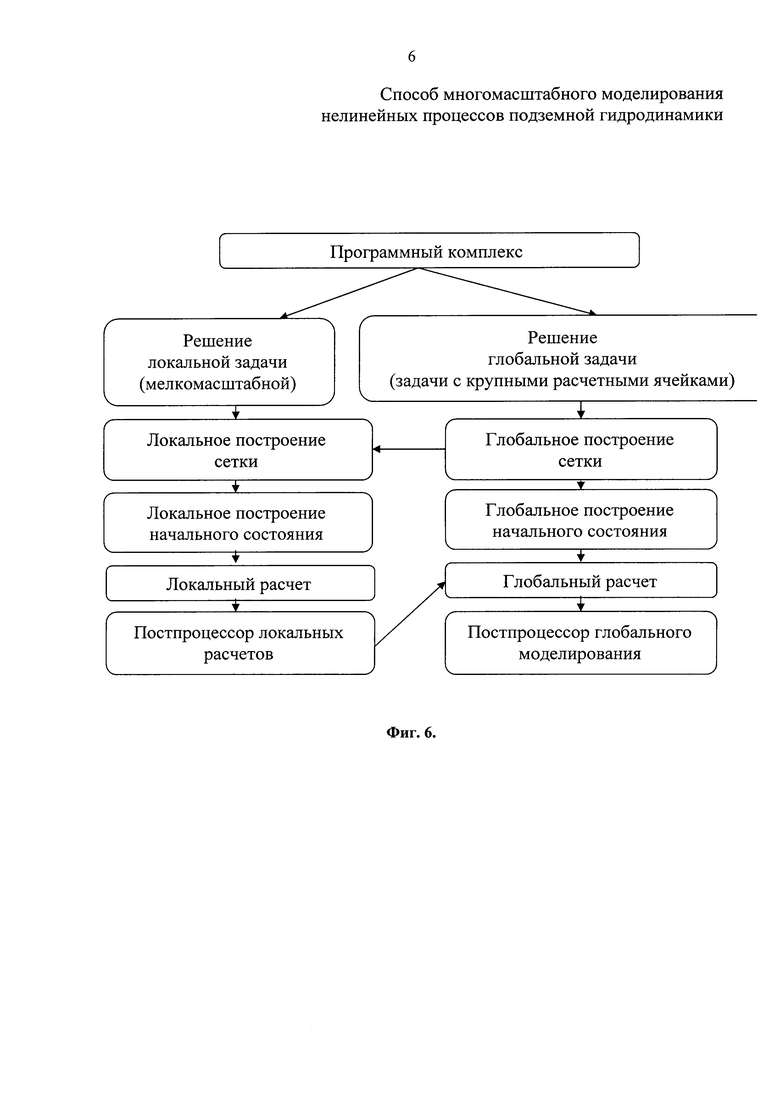
где ρ - плотность, φ - пористость, s1, s2 - насыщенности фаз, 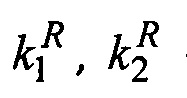 - относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, K - абсолютная проницаемость, v1, v2 - вектора скорости фильтрации фаз, р1, р2 - давление в фазах, рC - капиллярное давление.
- относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, K - абсолютная проницаемость, v1, v2 - вектора скорости фильтрации фаз, р1, р2 - давление в фазах, рC - капиллярное давление.
А также тем, что вычисление физических свойств для КМБ осуществляют из соотношений:
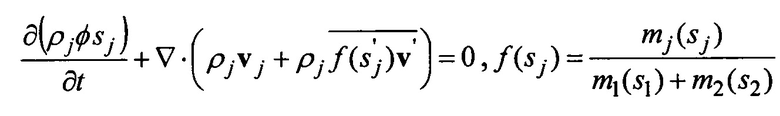
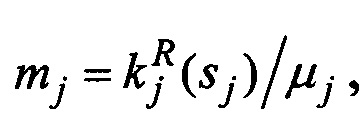
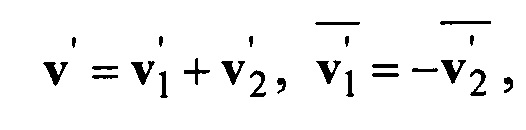 j=1, 2, где m1, m2 - относительные мобильности фаз, v - суммарная объемная скорость фильтрации, ρ1, ρ2 - плотности фаз, φ - пористость, s1, s2 - насыщенности фаз,
j=1, 2, где m1, m2 - относительные мобильности фаз, v - суммарная объемная скорость фильтрации, ρ1, ρ2 - плотности фаз, φ - пористость, s1, s2 - насыщенности фаз, 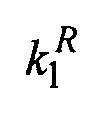 ,
, 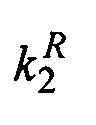 - относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, v1, v2 - вектора скорости фильтрации фаз; штрихом обозначены пульсационные составляющие переменных, чертой сверху обозначены средние величины.
- относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, v1, v2 - вектора скорости фильтрации фаз; штрихом обозначены пульсационные составляющие переменных, чертой сверху обозначены средние величины.
А также тем, что дополнительные корректирующие члены уравнений определяют из соотношений:
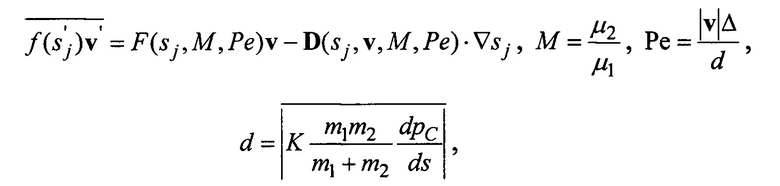
где М - отношение вязкостей, Ре - число Пекле, Δ - характерный размер расчетной ячейки глобальной задачи, d - характерная дисперсия фаз, возникающая за счет капиллярных эффектов, m1, m2 - относительные мобильности фаз, K - абсолютная проницаемость, v - суммарная объемная скорость фильтрации, рC - капиллярное давление, μ1, μ2 - динамические вязкости фаз, s1, s2 - насыщенности фаз.
Все существующие методы объединяет то, что для моделирования на макро- и микро- уровнях используются одинаковые системы уравнений. Значительным отличием изобретения от известных существующих методов является то, что в патентуемом способе для проведения апскейлинга в дифференциальные уравнения на макроуровне добавляются дополнительные корректирующие члены, коэффициенты для которых получены из исследований на микроуровне. В зависимости от физических свойств, полученных при исследовании процесса на микроуровне, меняется модель на макроуровне за счет учета дополнительных потоков в уравнениях. Такой подход дает возможность учесть неустойчивость, не прибегая к мелкому разбиению, что также сопровождается экономией расчетного времени.
Коэффициент извлечения нефти по большинству отечественных месторождений не превосходит 30%, а в большом числе случаев опускается ниже 20%, при этом, трудно извлекаемые запасы нефти в России составляют 60-70%. Один из методов нефтедобычи предполагает вытеснение углеводорода, при этом, на фронте вытеснения развивается неустойчивость, существенно сказывающаяся на качестве нефтедобычи.
Изобретение позволяет создать специализированный программный комплекс для предсказательного моделирования неустойчивого вытеснения нефти из природных коллекторов на малом масштабе, работающего как самостоятельно, так и допускающего интегрирование в любой коммерческий симулятор подземной гидродинамики.
Особенностью специализированного программного комплекса является то, что он позволит осуществлять многомасштабное моделирование нелинейных процессов вытеснения углеводородов с учетом возникающей неустойчивости фронта и даст возможность оценки качества вытеснения в условиях неустойчивых режимов с разрешением на уровне 1 см, и в то же время без уменьшения общей области моделирования, а также без увеличения времени вычислений. Полученные результаты могут привести к увеличению нефтеотдачи на 3-10%.
Патентуемый способ позволит учитывать эффекты с разрешением на несколько порядков выше, но без увеличения времени расчета.
Фиг. 1 иллюстрирует двумерную картину развития неустойчивости фронта вытеснения жидкости при перепаде вязкостей 1:100 (вытесняющей к вытесняемой жидкости). Изображена насыщенность вытесняющей фазы (минимальная - синий, максимальная - пурпурный). Под каждой картинкой подписано безразмерное время; единице в этой шкале соответствует время, за которое бы при устойчивом фронте вытеснения вся жидкость в области была бы замещена. Видно, что при неустойчивом фронте прорыв вытесняющей жидкости осуществляется в 5 раз раньше этого момента, но объем вытеснения значительно уменьшен.
Фиг. 2 иллюстрирует вид поверхности, разделяющей вытесняемую и вытесняющую жидкости, с двух точек зрения в последовательные моменты времени при трехмерном моделировании. Соотношение вязкостей вытесняющей и вытесняемой жидкости 1:100. Под каждой картинкой подписано безразмерное время; единице в этой шкале соответствует время, за которое бы при устойчивом фронте вытеснения вся жидкость в области была бы замещена. Прорыв происходит раньше, чем при двумерном моделировании, результаты которого показаны на предыдущей фигуре.
Фиг. 3 иллюстрирует общий вид уравнений глобальной модели вытеснения. Обозначено: ρ - плотность, φ - пористость, s1, s2 - насыщености фаз, 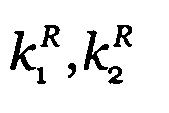 - относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, K - абсолютная проницаемость, мобильности фаз, v1, v2 - вектора скорости фильтрации фаз, р1, р2 - давление в фазах, рС - капиллярное давление.
- относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, K - абсолютная проницаемость, мобильности фаз, v1, v2 - вектора скорости фильтрации фаз, р1, р2 - давление в фазах, рС - капиллярное давление.
Фиг. 4 иллюстрирует дополнительный член, возникающий при осреднении модели вытеснения в уравнении динамики массы фаз, и его структура. Обозначено: mj - относительная мобильность фазы, v - суммарная объемная скорость фильтрации, штрихом обозначены пульсационные составляющие переменных, чертой сверху обозначены средние величины.
Фиг. 5 иллюстрирует моделирование дополнительного потока фазы, возникающего за счет неустойчивости вытеснения на микроуровне. Обозначено: М - отношение вязкостей, Ре - число Пекле, Δ - характерный размер расчетной ячейки глобальной задачи, d - характерная дисперсия фаз, возникающая за счет капиллярных эффектов.
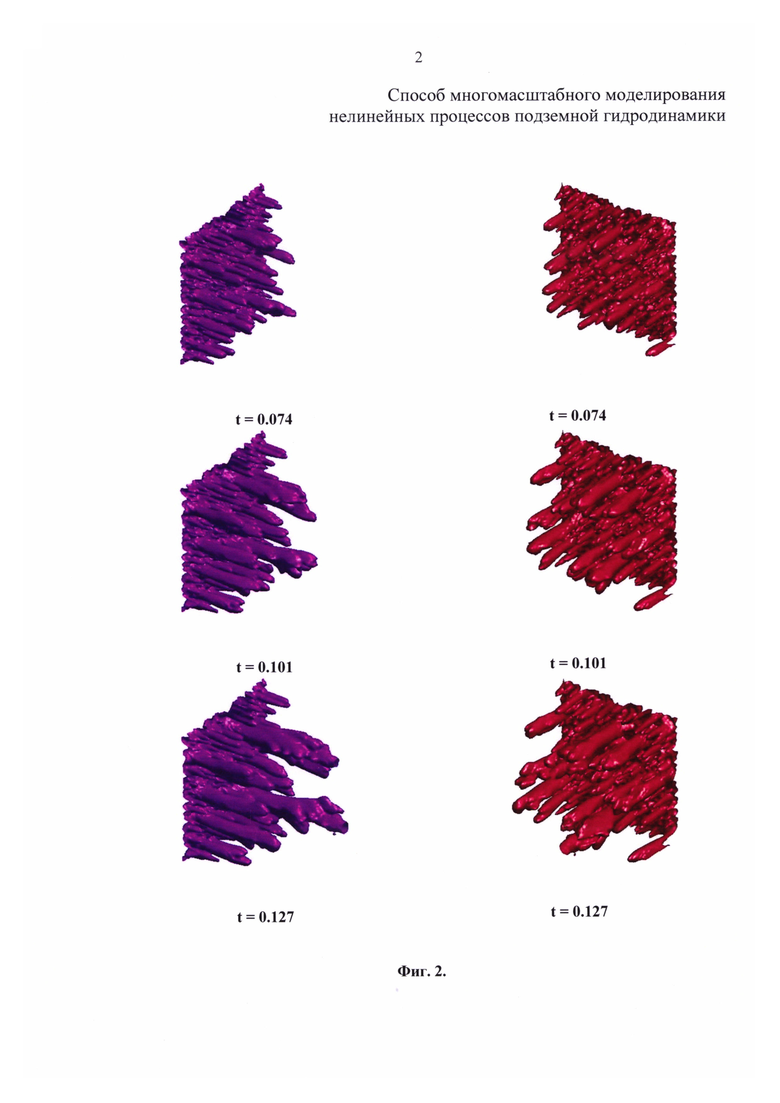
Фиг. 6 иллюстрирует блок-схему работы алгоритма, с включением расчета на двух уровнях, глобальном и локальном.
Один из основных методов нефтедобычи предполагает вытеснение углеводорода менее вязкой жидкостью (водой), при этом, на фронте вытеснения развивается неустойчивость, существенно сказывающаяся на качестве нефтедобычи.
Задача вытеснения углеводородов осложняется тем, что в практических случаях ее приходится решать на значительном пространственном масштабе. В то же время из-за использования менее вязкой воды для вытеснения более вязкой смеси углеводородов (пластовой нефти) этот процесс является неустойчивым: фронт вытеснения, даже если он был вначале прямым, искажается за счет пальцеобразных выступов, по которым менее вязкая вода прорывается к добывающей скважине, оставляя позади себя невытесненную нефть. После достижение одним из таких выступов добывающей скважины картина вытеснения резко меняется - большая часть подаваемой воды будет направляться в канал, созданный лидирующим пальцем. В скважину начинает закачиваться уже не нефть, а ее смесь с вытесняющей водой, причем процент воды будет быстро увеличиваться. Оставшаяся же в пласте нефть после такого прорыва будет практически неподвижна. На фиг. 1 приведена картина развития неустойчивости фронта вытеснения жидкости при перепаде вязкостей 1:100; маловязкая жидкость вытесняет более вязкую, видно образование каналов, по которым в основном и течет вытесняющая жидкость, оставляя позади вытесняемую.
Такая неустойчивость многомасштабна, и дело ее моделирования осложняется тем, что наиболее быстро растут мелкомасштабные «пальцы». Основная проблема прямого моделирования неустойчивости в том, что разрешение мелкомасштабных потоков на практической сетке нереальна даже с использованием современной вычислительной техники. Например, при обработке малого участка месторождения размером 10×10×1 км с ячейками размером 1×1×1 м потребуется 100 млрд. ячеек. Такая крупная задача находится на пределе возможности современных вычислительных комплексов. Но разрешить неустойчивости размером по ширине менее 3 ячеек численная схема не способна. Тем самым пальцеобразные выступы вытесняющего агента шириной менее 3 м, проникающие в вытесняемую нефть, на такой сетке не только не будут обнаружены, но решение вообще не будет учитывать их влияние, хотя бы и скрытое, на процесс вытеснения. Уменьшение же линейного размера ячейки в 10 раз увеличивает число ячеек двумерной сетки в 100, а трехмерной в 1000 раз. В то же время опыт показывает, что значение имеет пальцеобразная неустойчивость фронта вытеснения для размеров порядка 1 см. Весьма важно и то, что реальный фронт вытеснения имеет существенно трехмерную структуру, что видно из развития трехмерной картины вытеснения, изображенной на фиг. 2, где в двух проекциях изображен вид поверхности, разделяющей вытесняемую и вытесняющую жидкости. Картина эта показывает, что прорыв маловязкой жидкости в случае неустойчивости фронта вытеснения проходит по каналам, имеющим форму, близкую к цилиндрической, и тем самым объем невытесненной жидкости при трехмерном моделировании выше, чем при двумерном. Это говорит о том, что для решения задачи, позволяющей учитывать мелкую структуру вытеснения, требуется именно трехмерное моделирование с мелким разрешением. Измельчение исходной сетки до такого масштаба делает решение задачи вытеснения если и не невозможным, то не применимым на практике.
В то же время учесть влияние мелкомасштабной (подсеточной) неустойчивости при решении глобальной задачи на грубой сетке возможно. Для этого с уравнениями глобальной задачи поступают так же, как поступают с уравнениями Навье-Стокса при моделировании эффектов подсеточной турбулентности: вводится временной масштаб осреднения параметров (в данном случае насыщенности фаз, их скорости и давления). Затем решение представляется как сумма среднего на этом временном масштабе и осциллирующего, после чего уравнения осредняются.
В случае уравнений Навье-Стокса такое осреднение называется осреднением по Рейнольдсу, оно приводит к тому, что в осредненных уравнениях появляются новые члены, прежде всего в конвективных составляющих уравнений импульса. Эти новые члены, дополнительные потоки импульса, требуют дополнительного эмпирического моделирования, которое в различных моделях турбулентности проводится различным способом, но самым простым и, тем не менее, результативным во многих случаях является способ алгебраический.
Уравнения динамики вытеснения приведены на фиг. 3. Система содержит уравнение динамики массы каждой фазы (3.1), закон Дарси для каждой фазы (3.2), связь между давлениями в фазах через капиллярное давление (3.3) и дополнительные алгебраические соотношения (3.4). Уравнения глобальной системы приведены в размерном виде.
В случае подобной обработки уравнений динамики насыщенности новые члены также возникнут, и они будут соответствовать дополнительным потокам массы фаз. Эти потоки учитывают влияние мелкомасштабной неустойчивости, которая в данной модели скрыта на фоне среднего решения, и, тем не менее, выражается в резком усилении фактических фильтрационных потоков фаз. Собственно, именно эти потоки и ответственны за возможный преждевременный прорыв воды к добывающей скважине; преждевременным он будет относительно времени прорыва, полученного на грубой (глобальной) сетке без учета дополнительных членов. Возникающий в результате осреднения член содержится в уравнениях динамики массы потоков, и его структура приведена на фиг. 4. Уравнение (4.1) - это уравнение динамики массы фаз после осреднения, содержащее дополнительный член, выражение (4.2) определяет структуру зависимости потока от насыщенности, которая подвергается дополнительному осреднению, выражения (4.3) и (4.4) определяют относительную мобильность фаз и суммарную скорость фильтрации, соответственно.
Данные потоки моделируются алгебраически, будучи частично разделены на конвективную и диффузионную составляющие. Дополнительные потоковые члены должны обнуляться в том случае, когда вытеснение устойчиво на микроуровне, и тогда, когда насыщенность какой-либо фазы уменьшается до остаточной. Они зависят алгебраически от небольшого набора безразмерных параметров, регулирующих неустойчивость вытеснения. В частности, члены, усиливающие неустойчивость, должны в общем случае увеличиваться с ростом отношения вязкости вытесняемой жидкости к вязкости вытесняющей, и уменьшаться с ростом диффузии, возникающей вследствие капиллярных эффектов, и формирующей вместе с характерной скоростью фильтрации жидких фаз безразмерное число Пекле. На фиг. 5 приведена форма моделирования дополнительных потоков (5.1) и перечислены основные безразмерные параметры (5.2), от которых в большей или меньшей степени зависят дополнительные фильтрационные потоки фаз. Выражение (5.3) показывает, каким образом оценивается характерная диффузия, возникающая за счет капиллярных эффектов; черта сверху означает осреднение этих данных по глобальной ячейке. Форма самой зависимости дополнительного скаляра F в конвективном члене и тензора D в дисперсионном члене, моделирующих дополнительны поток, от указанных параметров, определяется характером неустойчивости и подлежит нахождению путем решения локальной задачи.
Патентуемый способ предполагает создание программного комплекса, предназначенного прежде всего для определения параметров алгебраической модели эффектов мелкомасштабной неустойчивости. Это достигается путем решения двух задач - локальной (мелкомасштабной) и глобальной (задачи с крупными расчетными ячейками). Алгоритм состоит из нескольких блоков: локальное построение сетки, локальное построение начального состояния, локальный расчет (последовательность шагов по времени), постпроцессор локальных расчетов (собственно формирование потоков, моделирующих неустойчивость на микроуровне); глобального построения сетки, глобального построения начального состояния, глобального расчета (шагов по времени). Дополнительный блок - постпроцессор, обрабатывающий данные глобального моделирования. Все расчетные блоки можно подразделить на две крупных группы: локальную (расчет на микроуровне и получение дополнительных потоков) и глобальную (расчет на макроуровне с применением членов, моделирующих особенности течения на микроуровне).
Последовательность работы алгоритма, в том случае, когда решение локальной задачи интегрировано в глобальную, изображена в виде блок-схемы на фиг. 6.
Подробности работы таковы.
Вначале строится глобальная сетка под цели расчета крупномасштабной задачи вытеснения.
Затем для работы локального блока строится сетка, моделирующая типичную ячейку глобальной сетки как рабочую область.
Формируется диапазон возможных безразмерных параметров локальной задачи и контрольные точки в фазовом пространстве этих параметров внутри этого диапазона. Параллельно на локальной сетке проводятся расчеты для различных вариантов (строятся начальные условия, проводятся шаги по времени, формируется результат в виде профиля насыщенности и потоков компонент на входе и выходе). Для этого используются модуль построения начального состояния локальной задачи и модуль ее решения.
Затем модуль постпроцессора локальной задачи обрабатывает полученные результаты, формируя интерполяционную зависимость результатов локальной задачи от введенных параметров. В зависимости от полученных данных такая зависимость представляется либо простым алгебраическим соотношением, в котором следует лишь определить коэффициенты, либо (в общем случае) табличными данными, которые могут быть интерполированы локально различными методами: сплайн с привязкой к точным значениям (для регулярного расположения полученных данных), сплайн без таковой привязки с минимальным средне-квадратичным отклонением (для менее регулярного их расположения), использование функций радиального базиса (для случая хаотично или неравномерно расположенных данных в фазовом пространстве большой размерности).
Затем полученные данные используются при решении глобальной задачи, в модулях которой - построения начального состояния и решения - вводятся дополнительные потоки, сформированные моделированием неустойчивости на микроуровне.
В качестве решателя глобальной задачи может быть использован как собственный решатель, так и любой существующий решатель для задач подземной гидродинамики.
Применение изобретения позволит:
1. Создать программное обеспечение для предсказательного моделирования неустойчивого вытеснения нефти из природных коллекторов;
2. Провести компьютерный анализ и автоматизированную обработку результатов численных экспериментов;
3. Разработать функциональные формы и таблицы коэффициентов для описания динамики эволюции зоны взаимного проникновения жидкостей и ее структуры;
4. Создать приложение, совместимое с коммерческими гидродинамическими симуляторами и улучшающего качество моделирования вытеснения;
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ГИДРОРАЗРЫВА УГЛЕВОДОРОДНОГО ПЛАСТА | 2016 |
|
RU2655513C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ | 1994 |
|
RU2097740C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ В ПОРИСТОЙ СРЕДЕ | 2010 |
|
RU2442133C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ С НЕОДНОРОДНЫМИ ВЫСОКО- И НИЗКОПРОНИЦАЕМЫМИ КОЛЛЕКТОРАМИ | 1991 |
|
RU2030566C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДИФИЦИРОВАННЫХ ФУНКЦИЙ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ ДЛЯ СЛОИСТО-НЕОДНОРОДНЫХ ПОРИСТЫХ СРЕД | 1994 |
|
RU2061221C1 |
| ИТЕРАТИВНАЯ ИНВЕРСИЯ ДАННЫХ ОТ ОДНОВРЕМЕННЫХ ГЕОФИЗИЧЕСКИХ ИСТОЧНИКОВ | 2007 |
|
RU2435215C2 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОЙ ЗАЛЕЖИ | 2000 |
|
RU2193649C2 |
| УКРУПНЕНИЕ СЕТКИ ДЛЯ МОДЕЛЕЙ КОЛЛЕКТОРОВ ПУТЕМ ПОВТОРНОГО ИСПОЛЬЗОВАНИЯ РАСЧЕТОВ ПОТОКА, ПОЛУЧЕННЫХ НА ОСНОВЕ ГЕОЛОГИЧЕСКИХ МОДЕЛЕЙ | 2007 |
|
RU2428739C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕКУЩИХ НЕФТЕНАСЫЩЕННОСТЕЙ ОТДЕЛЬНЫХ ПРОПЛАСТКОВ СЛОИСТО-НЕОДНОРОДНОГО ПЛАСТА ПО ОБВОДНЕННОСТИ ПРОДУКЦИИ | 1994 |
|
RU2061220C1 |
| СПОСОБ ИССЛЕДОВАНИЯ И ИНТЕРПРЕТАЦИИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ СКВАЖИНЫ | 2014 |
|
RU2558549C1 |




Изобретение относится к способам многомасштабного моделирования нелинейных процессов подземной гидродинамики. Сущность: разбивают исследуемую геологическую структуру на крупномасштабные блоки (КМБ). Разбивают КМБ на более мелкомасштабные блоки (ММБ). Вычисляют значения физических свойств для ММБ. Вычисляют значения физических свойств для КМБ с учетом дополнительных корректирующих членов уравнений, коэффициенты для которых получают из вычислений для ММБ. При этом в качестве физического свойства, определяемого на ММБ, определяют неустойчивость на фронте вытеснения углеводорода из пласта. Технический результат: повышение точности расчетов и сокращение времени их проведения. 4 з.п. ф-лы, 6 ил.
1. Способ многомасштабного моделирования нелинейных процессов подземной гидродинамики, включающий разбиение исследуемой геологической структуры на крупномасштабные блоки (КМБ), разбиение КМБ на более мелкомасштабные блоки (ММБ), вычисление значения физических свойств для ММБ, последующее вычисление значения физических свойств для КМБ, отличающийся тем, что вычисления значений физических свойств для КМБ осуществляют с учетом дополнительных корректирующих членов уравнений, коэффициенты для которых получены из вычислений для ММБ, а в качестве физического свойства, определяемого на ММБ, определяют неустойчивость на фронте вытеснения углеводорода из пласта.
2. Способ многомасштабного моделирования по п.1, отличающийся тем, что для вычисления физических свойств для ММБ формируют диапазон возможных безразмерных параметров и контрольных точек в фазовом пространстве этих параметров внутри этого диапазона, проводят различные варианты расчетов на основе указанных параметров и формируют интерполяционные зависимости результатов от введенных параметров, с помощью которых определяют коэффициенты дополнительных корректирующих членов уравнений для определения значений физических свойств для КМБ.
3. Способ многомасштабного моделирования по п.1, отличающийся тем, что вычисление физических свойств для ММБ осуществляется из соотношений
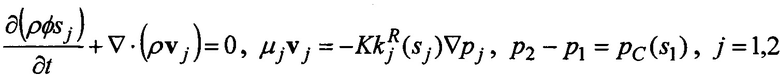 ,
,
где ρ - плотность, φ - пористость, s1, s2 - насыщенности фаз, 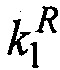 ,
, 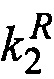 - относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, К - абсолютная проницаемость, v1, v2 - векторы скорости фильтрации фаз, р1, р2 - давление в фазах, рC - капиллярное давление.
- относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, К - абсолютная проницаемость, v1, v2 - векторы скорости фильтрации фаз, р1, р2 - давление в фазах, рC - капиллярное давление.
4. Способ многомасштабного моделирования по п.1, отличающийся тем, что вычисление физических свойств для КМБ осуществляется из соотношений
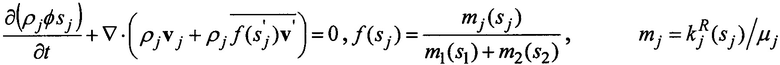 ,
, 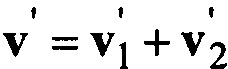 ,
,  , j=1, 2, где m1, m2 - относительные мобильности фаз, v - суммарная объемная скорость фильтрации, ρ1, ρ2 - плотности фаз, φ - пористость, s1, s2 - насыщенности фаз,
, j=1, 2, где m1, m2 - относительные мобильности фаз, v - суммарная объемная скорость фильтрации, ρ1, ρ2 - плотности фаз, φ - пористость, s1, s2 - насыщенности фаз,  ,
, 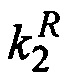 - относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, v1, v2 - векторы скорости фильтрации фаз; штрихом обозначены пульсационные составляющие переменных, чертой сверху обозначены средние величины.
- относительные проницаемости фаз, μ1, μ2 - динамические вязкости фаз, v1, v2 - векторы скорости фильтрации фаз; штрихом обозначены пульсационные составляющие переменных, чертой сверху обозначены средние величины.
5. Способ многомасштабного моделирования по п.1, отличающийся тем, что дополнительные корректирующие члены уравнений определяются из соотношений
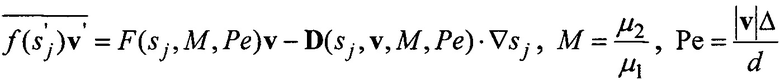
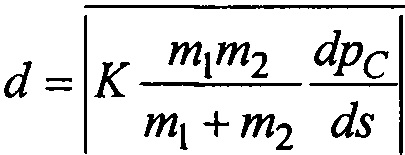 ,
,
где М - отношение вязкостей, Ре - число Пекле, Δ - характерный размер расчетной ячейки глобальной задачи, d - характерная дисперсия фаз, возникающая за счет капиллярных эффектов, m1, m2 - относительные мобильности фаз, K - абсолютная проницаемость, v - суммарная объемная скорость фильтрации, рC - капиллярное давление, μ1, μ2 - динамические вязкости фаз, s1, s2 - насыщенности фаз.
| УКРУПНЕНИЕ СЕТКИ ДЛЯ МОДЕЛЕЙ КОЛЛЕКТОРОВ ПУТЕМ ПОВТОРНОГО ИСПОЛЬЗОВАНИЯ РАСЧЕТОВ ПОТОКА, ПОЛУЧЕННЫХ НА ОСНОВЕ ГЕОЛОГИЧЕСКИХ МОДЕЛЕЙ | 2007 |
|
RU2428739C2 |
| МНОГОМАСШТАБНОЕ ЦИФРОВОЕ МОДЕЛИРОВАНИЕ ПОРОДЫ ДЛЯ МОДЕЛИРОВАНИЯ ПЛАСТА | 2012 |
|
RU2573739C2 |
| WO 2015153506 A1, 08.10.2015. | |||
Авторы
Даты
2018-10-18—Публикация
2017-12-18—Подача