Эта заявка истребует приоритет предварительной заявки на патент США № 60/819,186, зарегистрированной 7 июля 2006 года.
Область техники
Это изобретение, в общем, относится к области создания числовых моделей для имитационного моделирования на компьютере диффузных процессов (процессов, математически описываемых уравнением диффузии), таких как поток текучих веществ в пористых средах. В частности, предлагается способ укрупнения сетки ("апскейлинга") с переходом от мелкомасштабной геологической модели подземного образования к набору сеток, пригодных для имитационного моделирования на компьютере.
Уровень техники
Имитационное моделирование на компьютере потока текучих веществ в пористых средах широко применяется в нефтедобывающей промышленности, в гидрологии, а также при изучении состояния окружающей среды с целью ремедиации (удаления плавающих загрязнений) загрязненных грунтовых вод. Прогнозы, полученные на основе имитационного моделирования, часто оказывают значительное влияние на экономическую оценку ресурсов, планирование, связанное с истощением запасов углеводородов, и политику правительства.
Залежи углеводородного сырья, такого как нефть и газ, в природе обычно существуют в виде комплексных подземных структур, известных как "коллекторы". Коллекторы состоят из разных типов пористых сред (горных пород) с различающимися физическими свойствами, такими как пористость и проницаемость. Эти свойства могут изменяться в широком диапазоне на небольших расстояниях. Упомянутыми физическими свойствами определяются характеристики потока текучих веществ.
Развитие геологами методик стохастического моделирования геологических свойств позволило специалистам, занимающимся построением моделей, создавать модели приповерхностных областей с огромным объемом данных, которые представлены в трехмерной "сетке", охватывающей весь объем таких областей. Создание имитационных моделей коллектора для различных ситуаций, которые представляют интерес, в масштабе геологической модели является нецелесообразным из-за большого количества ячеек в сетке такой модели. Кроме того, сложное распределение свойств сделало несоответствующими современному уровню методики простого усреднения проницаемости. В результате создание сеток с более крупным масштабом (апскейлинг) для вычисления характеристик потока стало неотъемлемой частью имитационного моделирования коллекторов.
Объединение данных, описывающих свойства горных пород и геологические структуры, представляет собой решающий этап на пути к созданию точных имитационных моделей потока текучих веществ в коллекторах. Геологические модели ячеечного типа, с помощью которых происходит объединение данных, учитывают свойства горных пород (например, пористость и проницаемость), заданные в каждой ячейке. Геологические ячейки формируют неперекрывающуюся (элементарную) часть коллектора.
Геологическая модель ячеечного типа для описания коллектора может включать миллионы геологических ячеек, поэтому непосредственное имитационное моделирование движения текучих веществ в коллекторе во многих случаях, которые представляют интерес, является непомерно дорогим. Таким образом, с экономической точки зрения, необходимо трансформировать детализированную геологическую модель в грубую имитационную модель с меньшим числом степеней свободы, что позволяет выполнять имитационное моделирование коллекторов на приемлемом стоимостном уровне. Эта трансформация названа "ремасштабированием" или "укрупнением сетки" ("апскейлингом"). Последние статьи по ремасштабированию опубликованы Д. Штерн (D. Stern) ("Practical Aspects of Scaleup of Simulation Models", "Практические аспекты укрупнения сетки имитационных моделей", J. Pet. Tech., Sept. 2005, pp. 74-82) и Л.Дж. Дурлофски (L.J. Durlofsky ("Upscaling and Gridding of Fine Scale Geological Models for Flow Simulation", "Укрупнение и построение сетки для геологических моделей с мелким масштабом при имитационном моделировании потока", доклад на 8-м Международном форуме по имитационному моделированию коллекторов, г. Стреса, Италия, июнь 2005 года) (см. http://ekofisk.stanford.edu/faculty/durlofskypub12.html).
Апскейлинг включает создание сетки имитационной модели, которая крупнее геологической сетки, и преобразование свойств, заданных в геологической сетке, для сетки имитационной модели. После того, как задана сетка имитационной модели, для преобразования геологических свойств в типичном случае требуется вычислить определенные средние значения геологических свойств для наполнения сетки имитационной модели. Для некоторых из этих свойств, таких как пористость, достаточно простого усреднения с подходящими весами. Доказано, что для ремасштабирования проницаемости наилучшим путем являются процедуры усреднения на основе потоков. Такие процедуры описаны Дурлофски (2005), а последние данные по математическому анализу ремасштабирования проницаемости на основе потоков приведены Ву (Wu) и др. ("Analysis of Upscaling Absolute Permeability", "Анализ апскейлинга абсолютной проницаемости", Discrete and Continuous Dynamical Systems-Series B (Дискретные и непрерывные динамические системы - Серия В), Vol. 2, No. 2, 2002).
Ремасштабирование на основе потоков требует решения уравнений для однофазных ламинарных потоков применительно к сетке мелкого масштаба. В большинстве из существующих способов требуется, чтобы мелкая сетка была согласована с крупной сеткой имитационной модели. К настоящему времени Хе (C. He, "Structured Flow-based Gridding and Upscaling for Reservoir Simulation", "Структурирование при построении и укрупнении сетки для имитационного моделирования коллекторов" PhD Thesis (Докторская диссертация), Стэнфордский университет, г. Стэнфорд, штат Калифорния, декабрь 2004 года) описан способ апскейлинга проводимости для сетки имитационной модели с использованием расчетов потока для мелкой сетки, которая не согласована с сеткой имитационной модели. Уайт (White) и Хорн (Horne) представили алгоритм для вычисления значений проводимости при ремасштабировании, если в масштабе мелкой сетки имеет место неоднородность и анизотропия проницаемости ("Computing Absolute Transmissibility in the Presence of Fine-Scale Heterogeneity", "Вычисление абсолютной проводимости при наличии неоднородности в масштабе мелкой сетки", доклад SPE 16011, Девятый симпозиум SPE по имитационному моделированию коллекторов, Society of Petroleum Engineers (Общество инженеров-нефтяников Американского института горных инженеров), 209-220 (1987)).
Как рассмотрено Штерн (2005) и Дурлофски (2005), для успешного ремасштабирования часто требуется, чтобы сетка имитационной модели позволяла напрямую учитывать коррелированные неоднородности. Часто необходимо выполнять итерационный процесс, который включает построение нескольких сеток имитационной модели, чтобы определить "оптимальную" сетку. Этот процесс назван оптимизацией сетки. При построении нескольких сеток имитационной модели требуется неоднократное ремасштабирование геологической модели. При ремасштабировании проницаемости наиболее затратным с точки зрения времени и стоимости является этап расчетов потока в сетке мелкого масштаба. Из-за высокой стоимости не представляется возможной автоматическая оптимизация сетки; на практике, фактически, редко осуществляют даже модификацию сеток имитационной модели вручную. В результате имитационные модели часто не обладают наивысшей точностью, и прогнозирование на их основе не согласуется с геологическими моделями. Необходим способ, который сделал бы возможной более быструю и менее дорогую оптимизацию сетки.
Сущность изобретения
Данным изобретением предлагается способ более быстрой и менее дорогой оптимизации сетки при ремасштабировании. Основной отличительной особенностью этого изобретения является повторное использование расчетов потока, проведенных непосредственно для геологических моделей, и за счет этого устранение необходимости повторения этой наиболее трудоемкой с точки зрения вычислений части процесса ремасштабирования. При помощи повторного использования расчетов потока ремасштабирование различных сеток имитационной модели можно выполнить более эффективным образом. В результате модификация сеток имитационной модели вручную перестает быть чересчур трудоемкой с точки зрения затрат времени, и может стать реальностью выполнение автоматической оптимизации сетки. Данный способ может применяться, если физическая модель описана линейными дифференциальными уравнениями с частными производными, либо если решение физической проблемы может потребовать математической модели на основе нелинейных уравнений, как в случае многофазного потока текучих веществ в пористых средах.
Предлагается компьютеризованный способ ремасштабирования физического свойства в интересующей области с переходом от мелкомасштабной сетки, где известны значения этого свойства, к нескольким крупным сеткам, причем упомянутое свойство связано с диффузным процессом в упомянутой интересующей области, и этот способ содержит следующие этапы:
- выбирают объем в интересующей области, причем упомянутый объем составляет, по меньшей мере, часть этой интересующей области;
- разделяют упомянутый объем на множество ячеек мелкой сетки, чтобы создать мелкомасштабную сетку для этого объема, и получают значение физического свойства для каждой из множества ячеек мелкой сетки;
- решают уравнение диффузии, отражающее диффузный процесс для мелкомасштабной сетки в выбранном объеме, используя значения физического свойства для мелкого масштаба, таким образом генерируя глобальное решение;
- сохраняют глобальное решение;
- разделяют выбранный объем с использованием первой крупной сетки, содержащей, по меньшей мере, одну ячейку крупной сетки, причем число ячеек в упомянутом множестве ячеек мелкой сетки превышает число ячеек, состоящих из упомянутой, по меньшей мере, одной ячейки крупной сетки;
- выбирают ячейку крупной сетки и определяют, какие из множества ячеек мелкой сетки заключены в выбранной ячейке крупной сетки полностью или частично, используя предварительно выбранный критерий частичного включения;
- вычисляют ремасштабированное значение физического свойства для выбранной ячейки крупной сетки, извлекая и используя глобальное решение для ячеек мелкой сетки, заключенных внутри выбранной ячейки крупной сетки;
- повторяют упомянутые этапы с этапа выбора и определения по этап вычисления, чтобы вычислить ремасштабированные значения физического свойства для, по меньшей мере, одной другой ячейки крупной сетки, выбранной из числа ячеек, состоящих из упомянутой, по меньшей мере, одной ячейки крупной сетки, в выбранном объеме интересующей области; и
- повторяют упомянутые этапы с этапа разделения выбранного объема по предыдущий этап повторения для, по меньшей мере, еще одной крупной сетки, используя глобальное решение для каждой крупной сетки.
В некоторых вариантах осуществления настоящего изобретения глобальное решение генерируют путем разделения выбранного объема на две или более частей, которые могут перекрываться, и решения уравнения диффузии отдельно в каждом субобъеме, причем решения для субобъемов совместимы. Кроме того, представленный способ, обладающий признаками изобретения, необязательно использовать для ремасштабирования с переходом к крупной сетке, вместо этого его можно использовать для ремасштабирования с получением двух или более объемов ремасштабирования любого вида.
Согласно другому варианту осуществления настоящего изобретения предлагается компьютеризованный способ масштабирования физического свойства приповерхностной области с переходом от значений, известных для ячеек мелкой сетки, к нескольким отличающимся ячейкам, причем упомянутое свойство связано с диффузным процессом в упомянутой области. Данный способ масштабирования включает следующие этапы: выбирают объем в приповерхностной области, причем упомянутый объем составляет, по меньшей мере, часть этой приповерхностной области; разделяют упомянутый объем на ячейки мелкого масштаба, чтобы создать мелкомасштабную сетку для этого объема, и получают значение физического свойства для каждой ячейки мелкого масштаба; решают уравнение диффузии для мелкомасштабной сетки в выбранном объеме, таким образом генерируя глобальное решение, причем упомянутое глобальное решение создано в результате разделения упомянутого объема на два или более субобъемов, решения уравнения диффузии отдельно в каждом субобъеме и сопоставления решений на границах субобъемов; сохраняют глобальное решение в памяти компьютера или устройстве хранения данных; задают отличающуюся ячейку внутри одного из упомянутых двух или более субобъемов, причем упомянутая отличающаяся ячейка отличается по размеру или форме от упомянутых ячеек мелкого масштаба; определяют, какие из ячеек мелкого масштаба заключены в упомянутой отличающейся ячейке полностью или частично, используя предварительно выбранный критерий частичного включения; вычисляют масштабированное значение физического свойства для упомянутой отличающейся ячейки, извлекая и используя глобальное решение для ячеек мелкого масштаба, заключенных внутри этой отличающейся ячейки; и повторяют упомянутые этапы с этапа задания по этап вычисления, чтобы вычислить масштабированное значение физического свойства для, по меньшей мере, еще одной отличающейся ячейки, расположенной в выбранном объеме приповерхностной области, используя глобальное решение, взятое из памяти компьютера или устройства хранения данных для каждой отличающейся ячейки.
Согласно следующему, альтернативному, варианту осуществления настоящего изобретения предлагается способ добычи углеводородов из приповерхностного образования. Данный способ включает следующие этапы: получают геологическую модель приповерхностной области, причем упомянутая модель предоставляет дискретные значения физического свойства среды для мелкомасштабной сетки, охватывающей выбранный объем, составляющий, по меньшей мере, часть упомянутой приповерхностной области; и получают ремасштабированную модель физического свойства, подходящую для использования в программе имитационного моделирования коллектора. Упомянутую ремасштабированную модель создают следующим образом: решают уравнение диффузии, отражающее диффузный процесс для мелкой сетки в выбранном объеме, используя значения физического свойства, полученные для мелкого масштаба, таким образом генерируя глобальное решение; сохраняют глобальное решение в памяти компьютера или устройстве хранения данных; разделяют упомянутый объем с использованием первой крупной сетки, причем эта крупная сетка содержит меньше ячеек, чем мелкомасштабная сетка; выбирают ячейку крупной сетки и определяют, какие из ячеек мелкой сетки заключены в выбранной ячейке крупной сетки полностью или частично, используя предварительно выбранный критерий частичного включения; вычисляют ремасштабированное значение физического свойства для выбранной ячейки крупной сетки, извлекая и используя глобальное решение для ячеек мелкой сетки, заключенных внутри выбранной ячейки крупной сетки; повторяют упомянутые этапы с этапа выбора и определения по предыдущий этап повторения, чтобы вычислить ремасштабированные значения физического свойства для других выбранных ячеек крупной сетки в выбранном объеме приповерхностной области; повторяют упомянутые этапы с этапа разделения объема по этап вычисления для, по меньшей мере, еще одной крупной сетки, используя глобальное решение, извлеченное из памяти компьютера или устройства хранения данных, для каждой крупной сетки; и выбирают предпочтительную крупную сетку на основе предварительно определенного критерия оптимизации сетки. Этот способ добычи дополнительно включает этап, на котором добывают углеводороды из приповерхностной области, основываясь, по меньшей мере, частично на результатах имитационного моделирования коллектора, полученных с использованием ремасштабированной модели физического свойства для предпочтительной крупной сетки.
Согласно еще одному варианту осуществления настоящего изобретения предлагается способ ремасштабирования физического свойства. Этот способ включает следующие этапы: получают в условиях мелкого масштаба решения для, по меньшей мере, одного уравнения, описывающего физику диффузного процесса в интересующей среде, причем упомянутые решения в условиях мелкого масштаба существуют для каждой ячейки мелкого масштаба из мелкомасштабной сетки и эти решения хранятся в памяти; строят крупную сетку для, по меньшей мере, части интересующей среды, причем крупная сетка содержит множество ячеек; создают, по меньшей мере, один объем ремасштабирования в интересующей среде, причем этот объем используют, чтобы определить физику диффузного процесса в интересующей среде для крупной сетки; устанавливают соответствие между набором решений в условиях мелкого масштаба и упомянутой, по меньшей мере, одной крупной сеткой, причем это соответствие содержит отнесение, по меньшей мере, одной ячейки мелкого масштаба к одной из множества ячеек крупной сетки; извлекают из памяти упомянутые решения в условиях мелкого масштаба для каждой ячейки мелкого масштаба, относящейся к ячейке крупной сетки; вычисляют ремасштабированное физическое свойство для крупной сетки, используя упомянутые решения в условиях мелкого масштаба; строят, по меньшей мере, одну дополнительную крупную сетку для дополнительной части интересующей среды, причем эта дополнительная крупная сетка содержит множество ячеек; в режиме итерации повторяют упомянутые этапы с этапа создания, по меньшей мере, одного объема ремасштабирования по этап вычисления ремасштабированного физического свойства для упомянутой, по меньшей мере, одной дополнительной крупной сетки, используя решения, созданные на упомянутом этапе получения решений в условиях мелкого масштаба.
Краткое описание чертежей
Настоящее изобретение и его преимущества станут более понятными при рассмотрении приведенного ниже подробного описания и приложенных чертежей, из которых:
на фиг.1 показана блок-схема примерного способа ремасштабирования физических свойств;
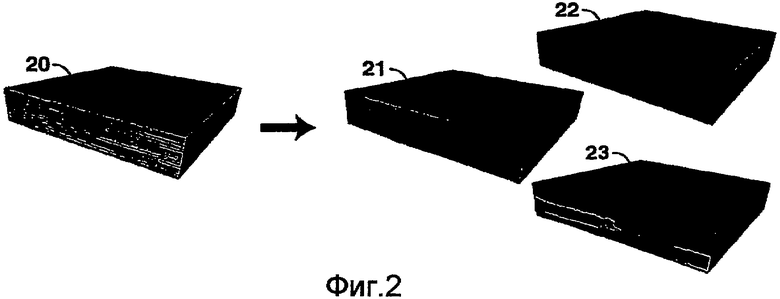
фиг.2 иллюстрирует геологическую модель мелкого масштаба, предназначенную для выполнения расчетов потока;
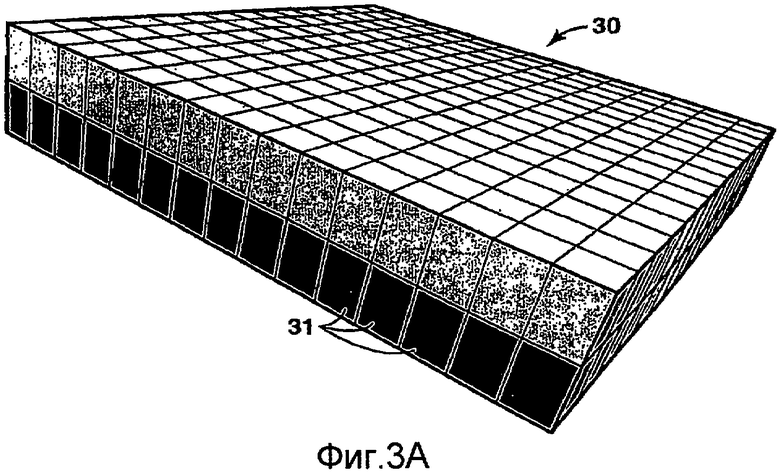
на фиг.3А изображена крупная структурированная сетка, имеющая два слоя;
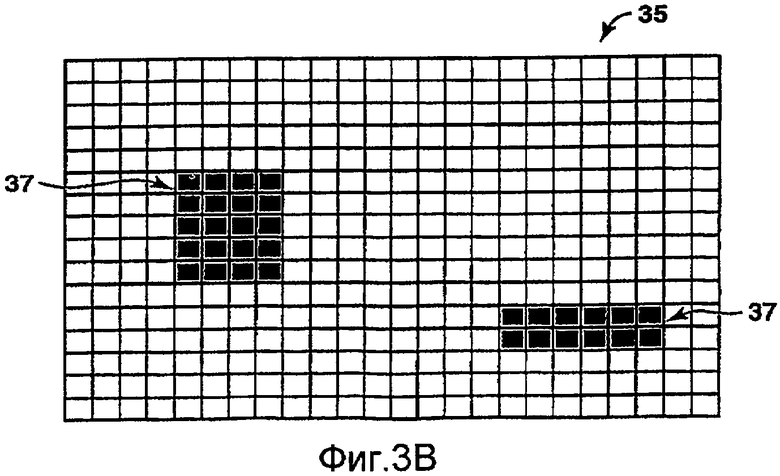
на фиг.3В показана структурированная, ортогональная мелкая сетка и ячейки крупной сетки, согласованной с этой мелкой сеткой;
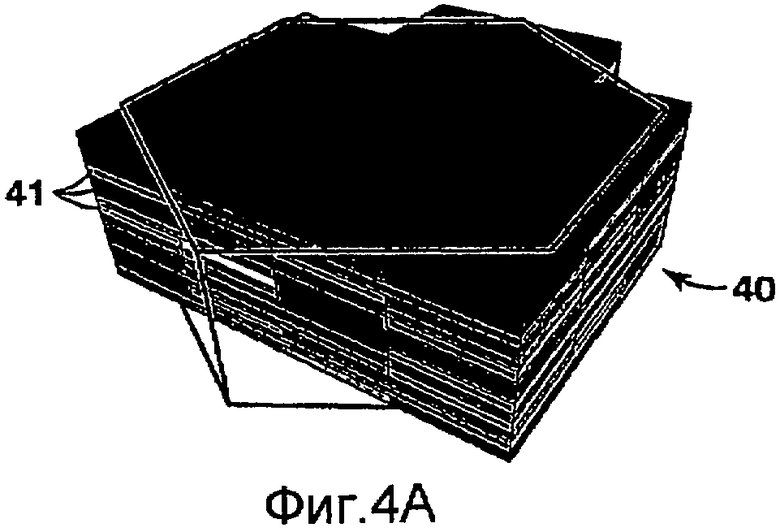
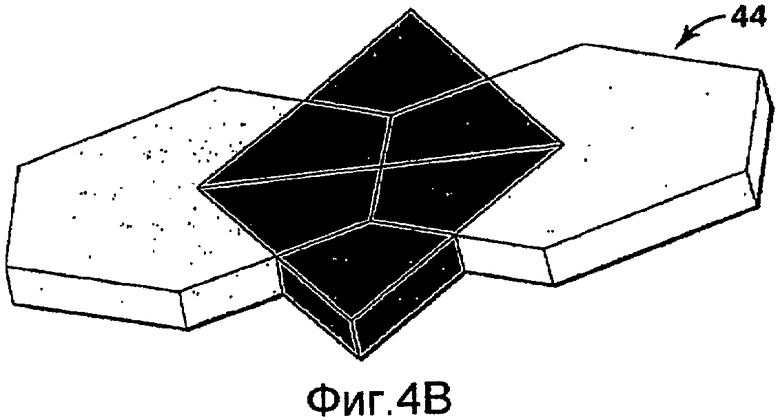
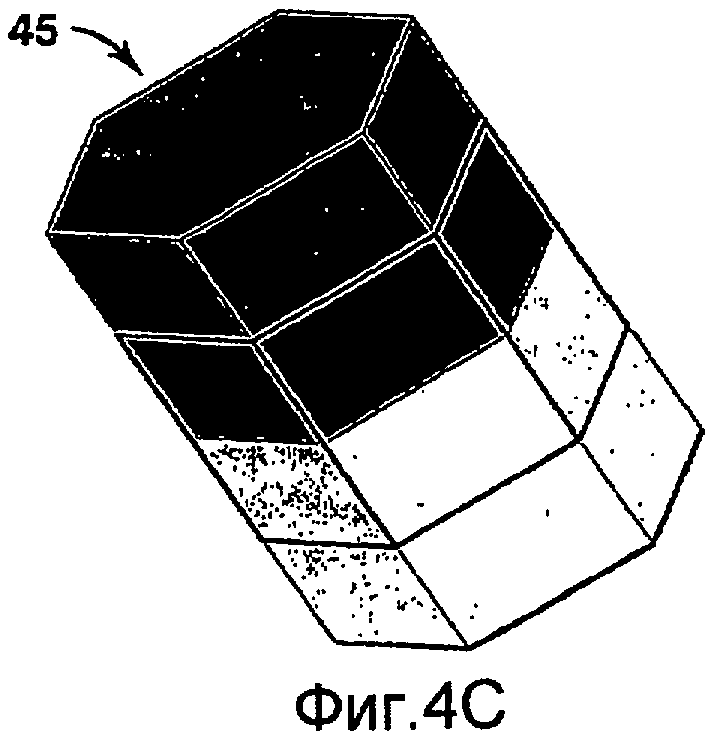
на фиг.4А-4С изображены неструктурированные объемы ремасштабирования;
на фиг.4А показаны традиционно используемые объемы ремасштабирования на основе ячеек, где объемы ремасштабирования представляют собой просто ячейки крупной сетки;
на фиг.4В показан объем ремасштабирования в форме кристалла алмаза для горизонтального соединения, предназначенный для моделирования соединения между двумя ячейками;
на фиг.4С показан объем ремасштабирования для вертикального соединения, в котором заключено соединение между двумя соседними ячейками;
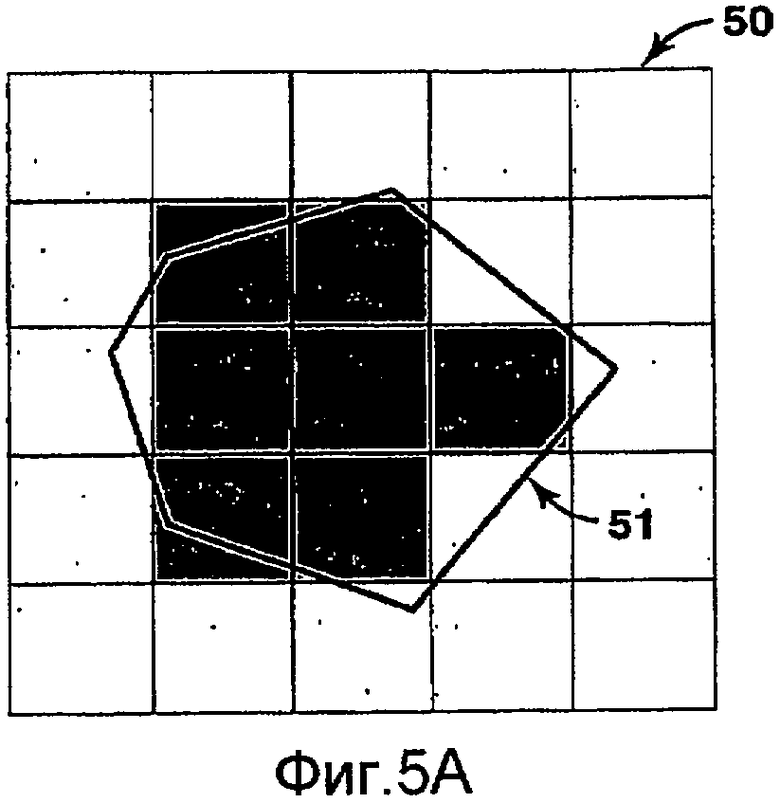
на фиг.5А изображен крупный объем ремасштабирования неправильной формы, наложенный на мелкую сетку; и
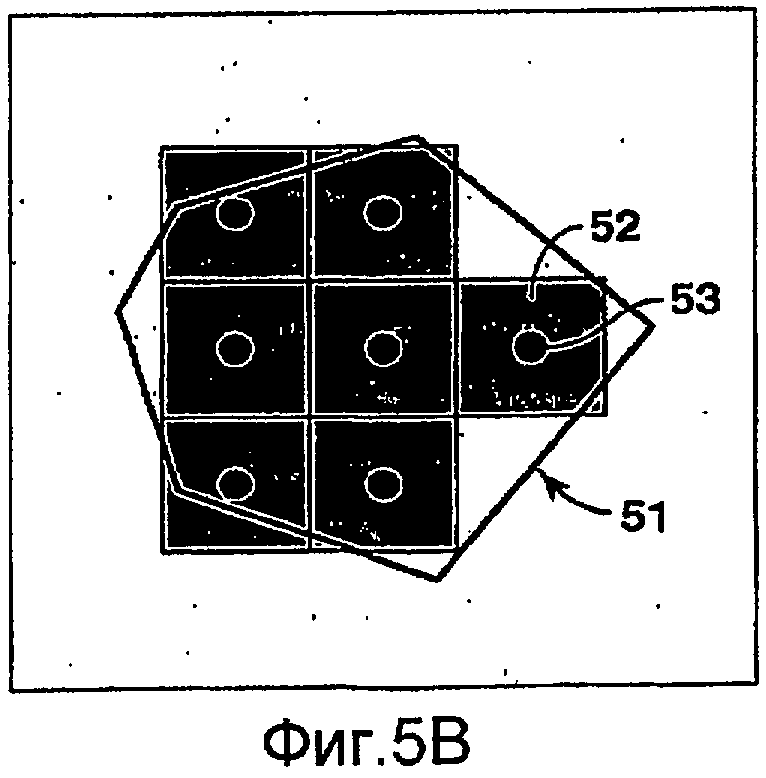
фиг.5В иллюстрирует то, каким образом можно использовать центры ячеек мелкой сетки, чтобы связать ячейку мелкой сетки с конкретным объемом ремасштабирования.
Подробное описание предпочтительных вариантов осуществления
Это изобретение будет описано применительно к предпочтительным вариантам осуществления. Однако если в приведенном ниже подробном описании рассмотрен конкретный вариант осуществления или конкретный вариант применения изобретения, то подразумевается, что этот вариант является всего лишь иллюстративным и не должен восприниматься с точки зрения ограничения объема этого изобретения. Наоборот, предполагается охват всех альтернативных вариантов, модификаций и эквивалентов, не выходящих за пределы сущности и объема настоящего изобретения, которые определены в пунктах приложенной формулы изобретения.
Описанное здесь изобретение представляет собой новый способ ремасштабирования, обеспечивающий возможность повторного использования выполненных в мелком масштабе (глобальных) решений для множества крупномасштабных сеток. Как показано на фиг.1, этот способ включает следующие этапы:
Этап 1. Получение набора выполненных в мелком масштабе решений для соответствующих уравнений, описывающих физику диффузного процесса в интересующей области. Для генерации расчетов потока могут быть использованы граничные условия с линейным изменением давления. Могут быть использованы и другие граничные условия, как рассмотрено Ву и др. (2002).
Этап 2. Построение крупной сетки, подходящей для каждой интересующей области.
Этап 3. Создание на основе этой крупной сетки объемов ремасштабирования для вычисления конкретных интересующих физических свойств в крупной сетке.
Этап 4. Установление соответствия между мелкомасштабной моделью и объемами ремасштабирования.
Этап 5. Извлечение для каждого объема ремасштабирования решений в мелком масштабе для каждой мелкомасштабной ячейки, которая связана с объемом ремасштабирования посредством упомянутого соответствия.
Этап 6. Использование этих решений в мелком масштабе для вычисления ремасштабированного свойства для каждого объема ремасштабирования.
Этап 7. Повторение этапов с 2 по 6 для новой крупной сетки. Для выполнения ремасштабирования в новой крупной сетке, решение в мелком масштабе повторно не вычисляется. Вместо этого оно извлекается из устройства хранения данных, например памяти компьютера или с диска.
Одним из различий между описанным здесь подходом и уже существующими является возможность повторного использования выполненных в мелком масштабе (глобальных) решений для различных крупных сеток. При применении существующих подходов решение в мелком масштабе вычисляется для каждой новой крупной сетки.
Для одного из примерных вариантов реализации настоящего изобретения рассмотрим ремасштабирование проницаемости в модели ламинарного потока через пористую среду. Необходимо понимать, что, хотя этот способ применен к проницаемости и потоку текучих веществ, он в равной степени применим к другим физическим процессам, описываемым следующим уравнением диффузии:
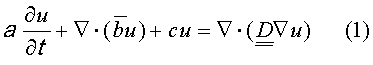
где a,
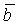 , c и
, c и 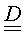 - известные функции пространства и времени. Физический смысл коэффициентов зависит от условий, в которых используется уравнение. Для ламинарных потоков a относится к сжимаемости и пористости горных пород, а
- известные функции пространства и времени. Физический смысл коэффициентов зависит от условий, в которых используется уравнение. Для ламинарных потоков a относится к сжимаемости и пористости горных пород, а 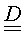 представляет собой тензор проницаемости. Переменная u в уравнении 1 - это неизвестная величина, которую необходимо найти при решении уравнения; она соответствует давлению, насыщению или концентрации в потоках через пористую среду.
представляет собой тензор проницаемости. Переменная u в уравнении 1 - это неизвестная величина, которую необходимо найти при решении уравнения; она соответствует давлению, насыщению или концентрации в потоках через пористую среду.
Фиг.2 демонстрирует Этап 1 - вычисление решений в мелком масштабе для модели потока текучих веществ через пористые среды в трех измерениях. Мелкая сетка или геологическая модель 20 ячеечного типа учитывает свойства пористости и проницаемости горных пород для каждой ячейки. Результаты вычислений потока для трех измерений изображены под номерами 21, 22 и 23. Для трехмерной (3D) модели ламинарного потока необходимо три решения, чтобы вычислить ремасштабированную проницаемость. Эти три расчета потока могут быть выполнены при помощи любого желаемого метода, хотя часто используются такие численные методы, как метод конечных разностей или метод конечных элементов, оба из которых хорошо известны в области имитационного моделирования коллекторов. В этом случае интересующей областью является вся модель в целом, но может оказаться желательным разделить модель на несколько областей, чтобы сделать вычисления возможными. Решения для частей объема объединяются путем использования соответствующих граничных условий, чтобы создать глобальное решение, охватывающее весь объем, т.е. модель или интересующую область. Решения в мелком масштабе затем сохраняются для использования в дальнейшем.
Описанный здесь способ будет работать наиболее эффективным образом, если мелкая сетка является структурированной и ортогональной. Структурированные сетки позволяют более простым и эффективным путем работать с информацией по сравнению с неструктурированными сетками. В частности, алгоритм установления соответствия, использованный на Этапе 4, может быть упрощен и сделан более эффективным. Если мелкая сетка является как структурированной, так и ортогональной, появляется выгодная возможность применить более простые и эффективные способы решения физической проблемы. Важность этих соображений быстро возрастает с ростом числа ячеек (т.е. разрешением) мелкой сетки, особенно в 3D-приложениях.
Как указано ранее, если размер представления физического процесса в мелкой сетке настолько велик, что становится нецелесообразным получать решение для всей модели в целом, то эту модель можно подразделить на несколько областей, и решения могут быть получены для каждой области в отдельности. В предпочтительном случае области перекрываются, и размер областей будет выбираться значительно больше размера ячейки крупной сетки. Такой выбор поможет уменьшить влияние граничных условий на локальные (для областей) решения, а также позволит этим областям охватить элементы большего масштаба (Ву и др., 2002). Крупная сетка также может быть неструктурированной.
Фиг.3А-3В иллюстрируют один из вариантов Этапа 2 - построения крупной структурированной сетки для мелкомасштабной геологической модели, показанной на фиг.2. Как видно на фиг.3А, крупная сетка 30 состоит из ячеек 31, которые могут быть заданы просто как блок из конкретного набора структурированных и ортогональных ячеек мелкой сетки.
На фиг.3В показана структурированная мелкая сетка 35 прямоугольной формы и две ячейки 37 крупной сетки, которые согласованы с мелкой сеткой 35. Для этого простого случая существует эффективный путь дискретизации, а именно двухточечная аппроксимация потока методом конечных объемов (two-point flux finite volume approximation). Кроме того, благодаря сетчатой структуре, решающая программа будет работать более эффективно. Так как ячейки крупной сетки согласованы с мелкой сеткой, то установление соответствия между крупной и мелкой сетками является тривиальным и не приведет к появлению ошибок выборки.
На Этапе 3 для крупной сетки вычисляют объемы ремасштабирования. Объемы ремасштабирования представляют собой конкретный интересующий объем для решаемой проблемы. При имитационном моделировании коллекторов эти объемы в типичном случае связаны с ячейками крупной сетки или соединениями.
Способы, соответствующие настоящему изобретению, работают одинаково хорошо как для структурированных, так и для неструктурированных сеток. Фиг.4А-4С иллюстрируют примерные варианты Этапа 3 - создания объемов ремасштабирования в крупной неструктурированной сетке. На фиг.4А показан традиционный объем 40 ремасштабирования на основе ячеек и ячейки 41 мелкой сетки внутри него. Крупный объем 40, внутри которого вычисляют ремасштабированное свойство, представляет собой аппроксимацию ячеек крупной сетки. Для крупной неструктурированной сетки с неструктурированными многоугольниками или полигонами Вороного (Voronoi) в плоскости, но с многослойной структурой в вертикальном направлении, если для получения расчетов потока в крупной сетке используется метод конечных разностей, то предпочтительными являются объем 44 ремасштабирования, показанный на фиг.4В, и объем 45 ремасштабирования, показанный на фиг.4С. Однако при выполнении метода конечных разностей для обычных неструктурированных сеток можно использовать объемы ремасштабирования на основе ячеек или блоков из двух соседних ячеек. Объем ремасштабирования делает возможным прямое вычисление проводимости - ключевого параметра метода конечных разностей. Для вычисления проводимости может быть применен подход, описанный в патенте США № 6826520. Специалистам в данной области техники будут очевидны и другие подходы. Для других схем числовой дискретизации могут потребоваться отличающиеся объемы ремасштабирования.
Фиг.5А-5В иллюстрируют примерный вариант Этапа 4 - установление соответствия, чтобы определить, какие ячейки мелкой сетки связаны с каждым объемом ремасштабирования. На фиг.5А показан крупный объем 51 ремасштабирования, наложенный на мелкомасштабную сетку 50. На фиг.5В изображен предпочтительный способ определения того, связана ли (т.е. будет считаться заключенной внутри), например, ячейка 52 мелкой сетки с крупным объемом 51 ремасштабирования. При выполнении этого способа ячейка 52 мелкой сетки связана с объемом 51 ремасштабирования, если ее центр 53 лежит внутри этого объема. Этот способ или критерий частичного включения ячейки рассмотрен в работе Дурлофски (2005) и патенте США № 6826520. Как известно в данной области техники, могут применяться и другие способы. Соответствие между мелкой и крупной сетками может устанавливаться множеством различных путей. Например, можно применить геометрические алгоритмы, которые хорошо известны в области вычислительной геометрии и генерации сеток.
Подходящий способ создания сетки рассмотрен в патенте США № 6106561. Могут применяться и другие способы построения сеток, что хорошо известно в данной области техники. Существует много литературы по данному вопросу, например, "Handbook of Grid Generation" (Руководство по генерации сеток) (Дж. Ф. Томпсон (J.F. Thompson) и др., CRC Press, 1999).
В качестве примера Этапа 6, показанного на фиг.1, можно рассмотреть случай проницаемости пористой среды, что так важно при имитационном моделировании нефтяных коллекторов с точки зрения облегчения добычи из них углеводородного сырья. В этом случае компонентами решения в мелком масштабе (т.е. глобального) для ламинарного потока в пористой среде являются как скорость, так и градиент давления. Поэтому из устройства хранения данных извлекают (Этап 5) как информацию по градиенту давления, так и по скорости для каждого из трех решений, полученных на Этапе 1. Для проницаемости в уравнениях ламинарного потока Уэн (Wen) и Гомез-Эрнандез (Gomez-Hernandez) ("Upscaling Hydraulic Conductivity in Heterogeneous Media" (Апскейлинг гидравлической проводимости в гетерогенных средах), J. Hydrology 183, 9-32 (1996)) показали, что свойство проницаемости для крупной сетки может быть представлено следующим образом:
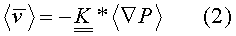
где 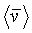 - взвешенное по объему среднее значение скорости, определенной для мелкого масштаба, в объеме ремасштабирования,
- взвешенное по объему среднее значение скорости, определенной для мелкого масштаба, в объеме ремасштабирования, 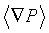 - взвешенное по объему среднее значение градиента давления, определенного для мелкого масштаба, и
- взвешенное по объему среднее значение градиента давления, определенного для мелкого масштаба, и 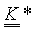 - проницаемость, определенная для крупного масштаба. Эти средние значения вычисляют для каждого расчета потока. Необходимо отметить, что скорость и градиент давления являются векторами, а проницаемость представлена тензором. Это объясняет то, почему предпочтительны три разных решения; три решения и три уравнения на одно решение (по одному для каждого компонента вектора) позволяют вычислить девять компонентов тензора проницаемости для крупного масштаба.
- проницаемость, определенная для крупного масштаба. Эти средние значения вычисляют для каждого расчета потока. Необходимо отметить, что скорость и градиент давления являются векторами, а проницаемость представлена тензором. Это объясняет то, почему предпочтительны три разных решения; три решения и три уравнения на одно решение (по одному для каждого компонента вектора) позволяют вычислить девять компонентов тензора проницаемости для крупного масштаба.
Существует несколько способов вычисления свойства, действующего в крупной сетке, после того, как стало доступным решение для мелкой сетки. Эти способы рассмотрены Дурлофски (2005). Предпочтительным способом является использование подхода с усреднением по объему и уравнения 2.
Если желательно использовать новую крупную сетку для улучшения результативности, то при выполнении представленного способа, обладающего признаками изобретения, решение в мелком масштабе повторно не вычисляется. Как показано на фиг.1, необходимо повторно построить объемы ремасштабирования и установить их соответствие мелкой сетке, после чего решение в мелком масштабе просто повторно используется при помощи выборки для новых объемов ремасштабирования, заданных на основе новой крупной сетки. Результаты вычислений с использованием новой крупной сетки затем могут сравниваться с результатами вычислений с использованием первой крупной сетки. Результаты расчетов для линейного или однофазного потока, полученные для различных крупных сеток, могут сравниваться с глобальными расчетами потока, полученными для геологической модели ячеечного типа, чтобы выбрать предпочтительную крупную сетку. Этот процесс может повторяться до тех пор, пока не будет найдена наиболее предпочтительная крупная сетка. Предпочтительная крупная сетка, полученная на основе этих сравнений, может затем быть использована в математической модели, основанной на нелинейных уравнениях, как в случае многофазного потока текучих веществ в пористых средах.
Пример 1
Вычисление для мелкой сетки было выполнено с использованием геологической модели, содержащей 14 миллионов ячеек, из которых 580.000 были активными ячейками. Глобальное решение для скорости и давления было получено для однофазного ламинарного потока внутри модели. При использовании одного из вариантов представленного способа, обладающего признаками изобретения, первоначальное ремасштабирование до крупной сетки потребовало 60 минут времени вычислений, а за счет извлечения и повторного использования результатов решения в мелком масштабе, потребовалось всего лишь 7 минут, чтобы провести ремасштабирование для получения модели с повторно построенной сеткой. В противоположность этому, при использовании типичного существующего способа потребовалось 125 минут для ремасштабирования как первоначальной модели, так и модели с повторно построенной сеткой. Обе крупные сетки содержали 40.500 активных ячеек.
Пример 2
Вычисление для мелкой сетки было выполнено с использованием геологической модели, содержащей 7,5 миллионов ячеек, почти все из которых были активными. Глобальное решение для скорости и давления было получено для однофазного ламинарного потока внутри модели. При использовании представленного способа, обладающего признаками изобретения, первоначальное ремасштабирование до крупной сетки потребовало 390 минут времени вычислений, а за счет извлечения и повторного использования результатов решения в мелком масштабе, потребовалось всего лишь 20 минут, чтобы провести ремасштабирование для получения модели с повторно построенной сеткой. В противоположность этому, при использовании существующих способов потребовалось 150 минут для ремасштабирования как первоначальной модели, так и модели с повторно построенной сеткой. Обе крупные сетки содержали 87.000 активных ячеек.
Размер модели Примера 1 более часто встречается в современной практике. Для модели любого из двух указанных размеров оптимизация рассмотренных здесь способов позволит дополнительно увеличить преимущества, заключающиеся в уменьшении времени и снижении стоимости, по сравнению с существующими способами. Очевидно, что при использовании рассмотренных способов значительное уменьшение времени, требующегося для решений с повторным построением сетки, делает осуществимым получение набора решений с повторным построением сетки вручную или применение решений с автоматическим повторным построением сетки.
Хотя это изобретение описано применительно к ремасштабированию сеток имитационных моделей, необходимо понимать, что описанные здесь способы с таким же успехом применимы к наборам простых объемов, которые не формируют сеток, т.е. эти объемы не формируют неперекрывающуюся (элементарную) часть приповерхностной области. Объемы для дискретизации могут выбираться случайным образом или в соответствии с определенной схемой. Это изобретение делает возможным более быстрое и имеющее меньшую стоимость получение статистических данных от различных наборов объемов для дискретизации. Нужно также отметить, что для представленного способа, обладающего признаками изобретения, не требуется, чтобы объем для дискретизации был больше ячеек мелкомасштабной сетки. Это изобретение в равной степени применимо к ячейкам крупной сетки (объемам ремасштабирования), которые меньше ячеек мелкомасштабной сетки.
Хотя это изобретение описано применительно к потоку текучих веществ в пористых средах, необходимо понимать, что с использованием описанных здесь способов может быть реализовано на практике имитационное моделирование других физических явлений, описываемых уравнением диффузии. Например, с использованием этого способа, обладающего признаками изобретения, можно моделировать тепловую диффузию в твердых веществах и молекулярную диффузию в жидкостях. В этих случаях с использованием указанных выше этапов может быть выполнено ремасштабирование физического свойства, аналогичного проницаемости, с переходом от вычисления для мелкой сетки к вычислению для крупной сетки.
В приведенном выше описании рассмотрены конкретные варианты реализации настоящего изобретения, что имеет целью проиллюстрировать это изобретение. Однако для специалиста в данной области техники будет очевидным, что для описанных здесь вариантов возможно внесение множества модификаций и изменений. Предполагается, что все такие модификации и изменения не выходят за пределы объема настоящего изобретения, который определен в пунктах приложенной формулы изобретения.
Литература
1. D. Stern, "Practical Aspects of Scaleup of Simulation Models", JPT (September, 2005),74.
- Д. Штерн, "Практические аспекты укрупнения сетки имитационных моделей", Журнал по технологиям нефтяной промышленности, (сентябрь 2005),74.
2. L.J. Durlofsky, "Upscaling and Gridding of Fine Scale Geologic Models for Flow Simulation", Proceedings of the 8 th International Forum on Reservoir Simulation (June 20-25, 2005), Stresa, Italy.
- Л.Дж. Дурлофски, "Укрупнение и построение сетки для геологических моделей с мелким масштабом при имитационном моделировании потока", Материалы 8-го Международного форума по имитационному моделированию коллекторов, 20-25 июня 2005 года, г. Стреса, Италия.
3. Ph. Renard and G. de Marily, "Calculating Effective Permeability: A Review," Advances in Water Resources, 20 (1997), 253-278.
- Ф. Ренар и Г. де Марили, "Вычисление эффективной проницаемости: Обзор", Журнал "Достижения в области водохозяйственных систем", 20 (1997), 253 - 278.
4. X.H. Wen and J.J. Gomez-Hernandez, "Upscaling Hydraulic Conductivity in Heterogeneous Media," Journal of Hydrology, 183 (1996), 9-32.
- К.Х. Уэн и Дж.Дж. Гомез-Эрнандез, "Апскейлинг гидравлической проводимости в гетерогенных средах", Журнал гидрологии, 183 (1996), 9-32.
5. X.H. Wu, Y. Efendiev and T.Y. Hou, "Analysis of Upscaling Absolute Permeability", Discrete and Continuous Dynamical Systems-Series B, 2 (2002), 185-204.
- К.Х. Ву, Ю. Эфендиев и Т.Ю. Хоу, "Анализ апскейлинга абсолютной проницаемости", Дискретные и непрерывные динамические системы - Серия В, 2 (2002), 185-204.
6. S.A. Khan and A.G. Dawson, "Method of Upscaling Permeability for Unstructured Grids," U.S. Patent № 6,826,520, В1 (30 November 2004).
- С.А. Хан и А.Г. Доусон, "Способ апскейлинга проницаемости для неструктурированных сеток", патент США № 6,826,520, В1 (30 ноября 2004).
7. C. He, "Structured Flow-based Gridding and Upscaling for Reservoir Simulation", Ph.D. Thesis (2004), Stanford University, Stanford, CA.
- Ц. Хе, "Структурирование при построении и укрупнении сетки для имитационного моделирования коллекторов", Докторская диссертация, Стэнфордский университет, г. Стэнфорд, штат Калифорния.
8. M. de Berg, M. van Kreveld, M. Overmans and O. Schwarzkopf, "Computational Geometry: Algorithms and Applications," Springer, 1997.
- М. де Берг, М. ван Кревельд, М. Оверманс и О. Шварцкопф, "Вычислительная геометрия: алгоритмы и применение", изд-во Springer, 1997.
9. P.G. Ciarlet, "The Finite Element Method for Elliptic Problems," North-Holland, 1978.
- П.Г. Царлет, "Метод конечных элементов для проблем эллиптичности", изд-во North-Holland, 1978.
10. K. Aziz and A. Settari, "Petroleum Reservoir Simulation," Elsevier, 1979.
- К. Азиз и А. Сеттари, "Имитационное моделирование нефтяных коллекторов", изд-во Elsevier, 1979.
11. C.L. Farmer, "Simulation Gridding Method and Apparatus Including a Structured Areal Gridder Adapted for Use by a Reservoir Simulator," U.S. Patent № 6106561 (22 August 2000).
- К.Л. Фармер, "Способ и устройство для построения сетки при имитационном моделировании, использующие построитель сеток для структурированных площадей, предназначенный для использования средством имитационного моделирования коллекторов", патент США № 6106561 (22 августа 2000).
12. J.F. Thompson, B.K. Soni and N.P. Weatherill. "Handbook of Grid Generation." CRC Press, 1999.
- Дж. Ф. Томпсон, Б.К. Сони и Н.П. Везерилл. " Руководство по генерации сеток", изд-во CRC Press, 1999.
13. C.D. White and R.N. Horne, "Computing Absolute Transmissibility in the Presence of Fine-Scale Heterogeneity," paper SPE 16011, Ninth SPE Symposium on Reservoir Simulation, Society of Petroleum Engineers, 209-220 (1987).
- К.Д. Уайт и Р.Н. Хорн, "Вычисление абсолютной проводимости при наличии неоднородности в масштабе мелкой сетки", доклад SPE 16011, Девятый симпозиум SPE по имитационному моделированию коллекторов, Общество инженеров-нефтяников Американского института горных инженеров, 209-220 (1987).
Изобретение относится к области создания числовых моделей для имитационного моделирования на компьютере диффузных процессов. Техническим результатом является увеличение скорости оптимизации сетки при ремасштабировании за счет повторного использования расчетов потока, проведенных для геологических моделей. Способ имитационного моделирования физического процесса, например, потока текучих веществ в пористых средах путем выполнения вычислений для этого процесса в среде в условиях мелкой сетки и повторного использования решения для мелкой сетки в последующих вычислениях для крупной сетки. В случае потока текучих веществ в приповерхностных образованиях данный способ может быть применен для оптимизации созданных на основе геологических моделей крупных сеток, которые для проведения вычислений получены путем ремасштабирования. При использовании этого способа уменьшается стоимость оптимизации сетки при имитационном моделировании физического процесса, который математически описывается уравнением диффузии. 4 н. и 23 з.п. ф-лы. 9 ил.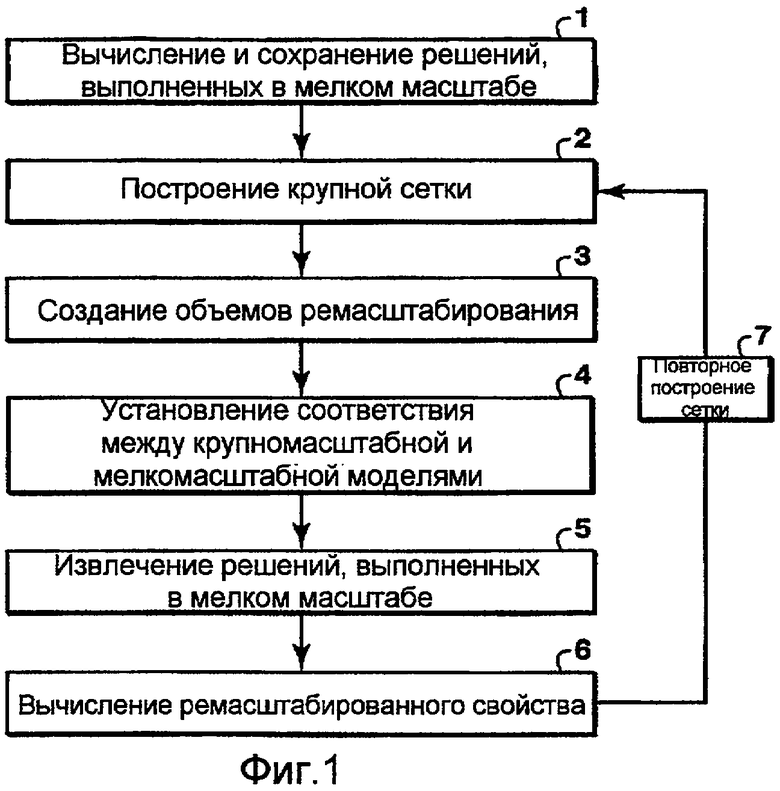
1. Реализуемый с помощью компьютера способ ремасштабирования физического свойства в интересующей области с переходом от мелкомасштабной сетки, где известны значения этого свойства, к нескольким крупным сеткам, причем упомянутое свойство связано с диффузным процессом в упомянутой интересующей области, и этот способ содержит следующие этапы:
a) выбирают объем в интересующей области, причем упомянутый объем составляет, по меньшей мере, часть этой интересующей области;
b) разделяют упомянутый объем на множество ячеек мелкой сетки, чтобы создать мелкомасштабную сетку для этого объема, и получают значение физического свойства для каждой из множества ячеек мелкой сетки;
c) решают уравнение диффузии, отражающее диффузный процесс для мелкомасштабной сетки в выбранном объеме, используя значения физического свойства для мелкого масштаба, таким образом генерируя глобальное решение;
d) сохраняют глобальное решение;
e) разделяют выбранный объем с использованием первой крупной сетки, содержащей, по меньшей мере, одну ячейку крупной сетки, причем число ячеек в упомянутом множестве ячеек мелкой сетки превышает число ячеек, состоящих из упомянутой, по меньшей мере, одной ячейки крупной сетки;
f) выбирают ячейку крупной сетки и определяют, какие из множества ячеек мелкой сетки заключены в выбранной ячейке крупной сетки полностью или частично, используя предварительно выбранный критерий частичного включения;
g) вычисляют ремасштабированное значение физического свойства для выбранной ячейки крупной сетки, извлекая и используя глобальное решение для ячеек мелкой сетки, заключенных внутри выбранной ячейки крупной сетки;
h) повторяют этапы f)-g), чтобы вычислить ремасштабированные значения физического свойства для, по меньшей мере, одной другой ячейки крупной сетки, выбранной из числа ячеек, состоящих из упомянутой, по меньшей мере, одной ячейки крупной сетки, в выбранном объеме интересующей области; и
- повторяют этапы e)-h) для, по меньшей мере, еще одной крупной сетки, используя глобальное решение для каждой крупной сетки.
2. Способ по п.1, в котором для глобального решения получают три независимых расчета потока по уравнению диффузии, что позволяет на основе глобального решения вычислять одну или более векторных величин для мелкомасштабной сетки.
3. Способ по п.2, в котором упомянутые одна или более векторных величин представляют собой градиент давления и скорость.
4. Способ по п.3, в котором физическим свойством является проницаемость пористой среды, а диффузным процессом является поток текучих веществ в пористой среде.
5. Способ по п.4, в котором ремасштабированное значение тензора проницаемости получают путем вычисления среднего значения для каждого компонента градиента давления и скорости в выбранной ячейке крупной сетки, причем упомянутые средние значения взвешены по объему ячейки мелкой сетки, а затем определяют тензор 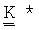 проницаемости для крупного масштаба из соотношения
проницаемости для крупного масштаба из соотношения
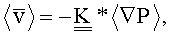
где 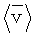 - взвешенное по объему среднее значение скорости в выбранной ячейке крупной сетки, а
- взвешенное по объему среднее значение скорости в выбранной ячейке крупной сетки, а 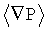 - взвешенное по объему среднее значение градиента давления.
- взвешенное по объему среднее значение градиента давления.
6. Способ по п.1, в котором определение того, какие из множества ячеек мелкой сетки заключены в выбранной ячейке крупной сетки полностью или частично, выполняют, устанавливая соответствие между мелкой сеткой и крупной сеткой, с последующим использованием полученной в результате функции соответствия.
7. Способ по п.1, в котором критерий частичного включения содержит включение ячейки мелкой сетки в ячейку крупной сетки, если центр упомянутой ячейки мелкой сетки лежит внутри упомянутой ячейки крупной сетки.
8. Способ по п.1, в котором глобальное решение генерируют путем разделения выбранного объема на два или более субобъемов и решения уравнения диффузии отдельно в каждом субобъеме, причем эти решения совместимы для упомянутых субобъемов.
9. Способ по п.4, в котором упомянутое множество ячеек мелкого масштаба и соответствующие значения физического свойства определяют геологическую модель пористой среды.
10. Способ по п.1, в котором упомянутое множество ячеек крупной сетки образует структурированную сетку.
11. Способ по п.1, в котором упомянутое множество ячеек крупной сетки образует неструктурированную сетку.
12. Способ по п.1, дополнительно содержащий этап, на котором выбирают предпочтительную крупную сетку на основе предварительно определенного критерия оптимизации сетки.
13. Способ по п.1, в котором интересующей областью является приповерхностная область.
14. Способ по п.1, в котором глобальное решение сохраняют в памяти компьютера или устройстве хранения данных.
15. Реализуемый с помощью компьютера способ масштабирования физического свойства приповерхностной области с переходом от значений, известных для ячеек мелкой сетки, к нескольким отличающимся ячейкам, причем упомянутое свойство связано с диффузным процессом в упомянутой области, и этот способ содержит следующие этапы:
a) выбирают объем в приповерхностной области, причем упомянутый объем составляет, по меньшей мере, часть этой приповерхностной области;
b) разделяют упомянутый объем на ячейки мелкого масштаба, чтобы создать мелкомасштабную сетку для этого объема, и получают значение физического свойства для каждой ячейки мелкого масштаба;
c) решают уравнение диффузии для мелкомасштабной сетки в выбранном объеме, таким образом генерируя глобальное решение, причем упомянутое глобальное решение создано в результате разделения упомянутого объема на два или более субобъемов, решения уравнения диффузии отдельно в каждом субобъеме и сопоставления решений на границах субобъемов;
d) сохраняют глобальное решение в памяти компьютера или устройстве хранения данных;
e) задают отличающуюся ячейку внутри одного из упомянутых двух или более субобъемов, причем упомянутая отличающаяся ячейка отличается по размеру или форме от упомянутых ячеек мелкого масштаба;
f) определяют, какие из ячеек мелкого масштаба заключены в упомянутой отличающейся ячейке полностью или частично, используя предварительно выбранный критерий частичного включения;
g) вычисляют масштабированное значение физического свойства для упомянутой отличающейся ячейки, извлекая и используя глобальное решение для ячеек мелкого масштаба, заключенных внутри этой отличающейся ячейки; и
h) повторяют этапы e)-g), чтобы вычислить масштабированное значение физического свойства для, по меньшей мере, еще одной отличающейся ячейки, расположенной в выбранном объеме приповерхностной области, используя глобальное решение, взятое из памяти компьютера или устройства хранения данных для каждой отличающейся ячейки.
16. Способ по п.15, в котором упомянутые, по меньшей мере, две отличающиеся ячейки больше ячеек мелкого масштаба.
17. Способ по п.15, в котором упомянутые два или более субобъемов перекрываются.
18. Способ по п.15, в котором для глобального решения получают три независимых расчета потока по уравнению диффузии, что позволяет на основе значений глобального решения вычислять одну или более векторных величин для мелкомасштабной сетки.
19. Способ по п.18, в котором упомянутые одна или более векторных величин представляют собой градиент давления и скорость.
20. Способ по п.19, в котором физическим свойством является проницаемость пористой среды, а диффузным процессом является поток текучих веществ в пористой среде.
21. Способ по п.15, в котором определение того, какие ячейки мелкой сетки заключены в упомянутой отличающейся ячейке, выполняют, устанавливая соответствие между мелкомасштабной сеткой и субобъемом, разделенным на множество отличающихся ячеек, с последующим использованием полученной в результате функции соответствия.
22. Способ по п.15, в котором критерий частичного включения содержит включение одной из ячеек мелкой сетки в одну из упомянутых отличающихся ячеек, если центр этой ячейки мелкой сетки лежит внутри упомянутой отличающейся ячейки.
23. Способ добычи углеводородов из приповерхностной области, содержащий следующие этапы:
a) получают геологическую модель приповерхностной области, причем упомянутая модель предоставляет дискретные значения физического свойства среды для мелкомасштабной сетки, охватывающей выбранный объем, составляющий, по меньшей мере, часть упомянутой приповерхностной области;
b) получают ремасштабированную модель физического свойства, подходящую для использования в программе имитационного моделирования коллектора, причем упомянутую ремасштабированную модель создают следующим образом:
(i) решают уравнение диффузии, отражающее диффузный процесс для мелкой сетки в выбранном объеме, используя значения физического свойства, полученные для мелкого масштаба, таким образом генерируя глобальное решение;
(ii) сохраняют глобальное решение в памяти компьютера или устройстве хранения данных;
(iii) разделяют упомянутый объем с использованием первой крупной сетки, причем эта крупная сетка содержит меньше ячеек, чем мелкомасштабная сетка;
(iv) выбирают ячейку крупной сетки и определяют, какие из ячеек мелкой сетки заключены в выбранной ячейке крупной сетки полностью или частично, используя предварительно выбранный критерий частичного включения;
(v) вычисляют ремасштабированное значение физического свойства для выбранной ячейки крупной сетки, извлекая и используя глобальное решение для ячеек мелкой сетки, заключенных внутри выбранной ячейки крупной сетки;
(vi) повторяют этапы (iv)-(v), чтобы вычислить ремасштабированные значения физического свойства для других выбранных ячеек крупной сетки в выбранном объеме приповерхностной области;
(vii) повторяют этапы (iii)-(vi) для, по меньшей мере, еще одной крупной сетки, используя глобальное решение, извлеченное из памяти компьютера или устройства хранения данных, для каждой крупной сетки; и
(viii) выбирают предпочтительную крупную сетку на основе предварительно определенного критерия оптимизации сетки; и
с) добывают углеводороды из приповерхностной области, основываясь, по меньшей мере, частично на результатах имитационного моделирования коллектора, полученных с использованием ремасштабированной модели физического свойства для предпочтительной крупной сетки.
24. Способ по п.23, в котором физическим свойством является проницаемость, глобальное решение состоит из трех независимых расчетов потока по уравнению диффузии и средние значения по ячейкам мелкой сетки для скорости и градиента давления, являющихся векторными величинами, вычисляют для каждого расчета потока, на основе чего получают девять компонентов тензора проницаемости для крупного масштаба.
25. Способ ремасштабирования физического свойства, содержащий следующие этапы:
a) получают в условиях мелкого масштаба решения для, по меньшей мере, одного уравнения, описывающего физику диффузного процесса в интересующей среде, причем упомянутые решения в условиях мелкого масштаба существуют для каждой ячейки мелкого масштаба из мелкомасштабной сетки, и эти решения хранятся в памяти;
b) строят крупную сетку для, по меньшей мере, части интересующей среды, причем крупная сетка содержит множество ячеек;
c) создают, по меньшей мере, один объем ремасштабирования в интересующей среде, причем этот объем используют, чтобы определить физику диффузного процесса в интересующей среде для крупной сетки;
d) устанавливают соответствие между набором решений в условиях мелкого масштаба и упомянутой, по меньшей мере, одной крупной сеткой, причем это соответствие содержит отнесение, по меньшей мере, одной ячейки мелкого масштаба к одной из множества ячеек крупной сетки;
e) извлекают из памяти упомянутые решения в условиях мелкого масштаба для каждой ячейки мелкого масштаба, относящейся к ячейке крупной сетки;
f) вычисляют ремасштабированное физическое свойство для крупной сетки, используя упомянутые решения в условиях мелкого масштаба;
g) строят, по меньшей мере, одну дополнительную крупную сетку для дополнительной части интересующей среды, причем эта дополнительная крупная сетка содержит множество ячеек;
h) в режиме итерации повторяют этапы c)-f) для, по меньшей мере, одной дополнительной крупной сетки, используя решения, созданные на упомянутом этапе получения решений в условиях мелкого масштаба.
26. Способ по п.25, в котором интересующей средой является пористая среда.
27. Способ по п.25, в котором физическим свойством является проницаемость пористой среды, а диффузным процессом является поток текучих веществ в пористой среде.
| RU 94040861 А1, 10.07.1996 | |||
| US 20050020210 А1, 27.01.2005 | |||
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ С НЕОДНОРОДНЫМИ КОЛЛЕКТОРАМИ И ТРУДНОИЗВЛЕКАЕМЫМИ ЗАПАСАМИ НЕФТИ | 2002 |
|
RU2215128C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ | 2004 |
|
RU2277630C1 |
| СПОСОБ ПРЕДСКАЗАНИЯ КОЛИЧЕСТВЕННЫХ ЗНАЧЕНИЙ СВОЙСТВА СКАЛЬНОЙ ПОРОДЫ ИЛИ ТЕКУЧЕЙ СРЕДЫ В ПРОДУКТИВНОМ ПЛАСТЕ С ПОМОЩЬЮ СЕЙСМИЧЕСКИХ ДАННЫХ | 2001 |
|
RU2271023C2 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| US 2005234690 А1, 20.10.2005 | |||
| US 2005228623 A1, 13.10.2005 | |||
| УСТРОЙСТВО ДЛЯ УМЕНЬШЕНИЯ РАДИОАКТИВНОГО ЗАГРЯЗНЕНИЯ И ИНДИКАЦИЯ РАДИОАКТИВНОСТИ | 2006 |
|
RU2328048C1 |
Авторы
Даты
2011-09-10—Публикация
2007-05-16—Подача