Область техники, к которой относится изобретение
Изобретение относится к механическим передачам для преобразования вращательного движения, использующим зубчатое зацепление колес с профилем зубьев, содержащим в комбинации две эквидистанты трохоидальных участков, и может найти применение в различных передачах, в которых ранее использовалось зубчатое зацепление с эвольвентными и другими профилями зубьев.
В описании изобретения под термином «удлиненная трохоида» следует понимать циклоидальные кривые, не имеющие самопересечений, а под термином «укороченная трохоида» - кривые, имеющие самопересечение в виде петель при вершинах.
Уровень техники
Известен профиль зуба зубчатого колеса, который искривлен в противоположных направлениях на противоположных концах от его центральной части и около корня зуба профиль вогнут. При этом в районе входа и выхода зубьев из контакта, контакт выпукло-вогнутый, что обеспечивает самую большую поверхностную прочность там, где самое большое скольжение профилей и где необходима повышенная поверхностная прочность, в то время как эвольвентные зубья имеют самую малую поверхностную прочность в этих местах профиля. (Ernest Wildhaber, патент США 3,251,236 от 17.05.1966 г.).
Недостатком этой передачи является то, что форма профиля зуба создана кривой линией, которая не обеспечивает точное выполнение основного закона зацепления, а только приближается к строго корректной.
Известно циклоидальное зацепление двух колес обычного вида, в котором профиль ножки зуба очерчен циклоидальной кривой, полученной при внутренней обкатке центроиды колеса первой вспомогательной центроидой, а профиль головки зуба этого колеса очерчен циклоидальной кривой, полученной при внешней обкатке центроиды этого колеса второй вспомогательной центроидой. Эти две циклоидальные кривые соединены в точке, расположенной на центроиде колеса и образуют, одна, вогнутую ножку зуба, а вторая выпуклую головку. Преимуществом такого зацепления является то, что оно имеет во всех точках контакта зуба выпукло-вогнутый контакт.(Книга: Литвин Ф.Л. Теория зубчатых зацеплений. М., «Наука», 1968, стр. 267).
Недостатком этого зацепления является то, что в точке соединения профилей ножки и головки радиус кривизны каждой кривой равен нулю, что при отклонении межосевого расстояния от теоретически заданного приводит к неравномерности вращения и к вибрациям.
Наиболее близким является двухстороннее цевочно-циклоидальное зацепление двух колес, в котором головки зубьев каждого колеса имеют круговой выпуклый профиль, а ножки зубьев каждого колеса имеют эквидистантный трохоидальный, большей частью вогнутый профиль, касательно соединенный с профилем головок. Преимуществом этого зацепления является то, что оно позволяет обеспечить выпукло-вогнутый контакт на входе и выходе зубьев из зацепления, что повышает нагрузочную способность передачи и уменьшает шум при работе. (Токарь А.С, международная заявка WO 2017/030471 от 23.02.2017) (Прототип).
Недостатком этого зацепления является то, что инструментальная рейка для каждого колеса должна быть индивидуальная и что пара колес с таким профилем зубьев может работать только друг с другом, т.е. невозможно заменить какое либо из колес колесом другого размера.
Раскрытие сущности изобретения
Задачей изобретения является создание нового зубчатого зацепления, в котором профиль зубьев каждого колеса состоит из двух касательно соединенных между собой эквидистант трохоидальных кривых, образующих, одна частично или полностью вогнутую ножку зуба, а вторая выпуклую головку зуба. Точка соединения этих кривых расположена на центроидах каждого колеса. При работе зацепления частично или полностью вогнутая ножка зуба первого колеса входит в контакт с выпуклой головкой зуба второго колеса, и этот контакт продолжается до прохода полюса зацепления. При проходе точки контакта полюс зацепления, точки соединения ножек и головок обоих колес совпадают друг с другом и с точкой контакта, и после полюса зацепления контакт сразу переходит на вторую пару кривых: выпуклую головку зуба первого колеса и ножку зуба второго колеса. Таким образом, на протяжении всего цикла зацепления или на большей его части сохраняется выпукло-вогнутый контакт. При переходе контакта с первой пары кривых на вторую пару, в полюсе зацепления, при равных вспомогательных центроидах, приведенный радиус кривизны для одной и второй пары, при определенных исходных параметрах, имеет одно и то же значение, т.е. нет скачкообразного изменения приведенного радиуса кривизны на всей линии зацепления. Таким образом, решена проблема, присущая почти во всех неэвольвентных зацеплениях.
Технический результат. При таком профилировании зубьев можно получить повышенную нагрузочную способность зубчатой передачи, по сравнению с эвольвентным зацеплением за счет увеличения приведенного радиуса кривизны контактирующих поверхностей в начале и конце зацепления.
Профиль зубьев для этого зацепления строится следующим образом. Задают центроиды колес, количество зубьев на каждом колесе, две вспомогательные центроиды и расположение чертящих точек на них. При помощи этих двух вспомогательных центроид получают две трохоидальные кривые для каждого колеса, первая, полученная при внутренней обкатке центроиды колеса - для построения профиля головки зуба, а вторая, полученная при внешней обкатке центроиды этого же колеса - для построения профиля ножки зуба. Эти две трохоиды привязывают к системе координат колеса со сдвигом в половину углового шага и, взяв от них эквидистанты, от первой во внешнюю сторону колеса, для получения профиля головки зуба, а от второй во внутреннюю, для получения профиля ножки зуба. Для получения конечного профиля зуба, производят выбор величины эквидистант для профилей головки и ножки, при которых будут выполнены следующие условия: обе эквидистантные кривые будут соединены по касательной и точки их соединения будут лежать на центроиде колеса. Делается это следующим образом. В более простом случае, когда первая и вторая вспомогательные центроиды равны между собой и имеют одно и то же расположение чертящей точки, поворачивают колесо так, чтобы начальная точка трохоиды головки (точка начала качения вспомогательной центроиды) находилась на расстоянии четверти углового шага от горизонтальной оси (межосевой линии колес, на которой расположен полюс зацепления) и в этом положении через точку полюса проводят нормаль к трохоиде головки зуба. В этом угловом положении колеса, на центроиде колеса, в точке, совпадающей с полюсом, будет находиться точка начала эквидистанты, очерчивающей профиль головки зуба, а расстояние от полюса до точки пересечения нормали с трохоидой головки будет равно величине необходимой эквидистанты, удовлетворяющей заданным условиям: соединение по касательной, и точка соединения находится на центроиде. Профиль головки зуба получают, проведя эквидистанту от трохоиды головки с этим значением величины эквидистанты, начиная ее от вышеупомянутой начальной точки на центроиде колеса, во внешнюю сторону, и до пересечения ее с центроидой колеса с другой стороны. Профиль ножки зуба получают, проведя эквидистанту от трохоиды ножки, начиная ее от начальной точки профиля головки на центроиде колеса, во внутреннюю сторону, и до пересечения ее с центроидой колеса с другой стороны. Величина эквидистанты профиля ножки в этом случае будет равна величине эквидистанты профиля головки. Нормаль к трохоиде ножки в этом положении, проведенная через точку полюса, будет находиться на одной прямой с вышеупомянутой нормалью к трохоиде головки, что подтверждает соединение двух кривых по касательной.
В более сложном, общем случае, когда первая и вторая вспомогательные центроиды не равны друг другу, профили головки и ножки строятся подобным вышеописанному способом, за исключением того, что колесо поворачивают не на четверть углового шага (как в предыдущем случае), а на угол, при котором нормали, проведенные через полюс к трохоидам головки и ножки, окажутся на одной прямой. После этого профили головки и ножки строятся от точки на центроиде, совпадающей с полюсом аналогичным способом, только величины эквидистант для головки и ножки в этом случае будут разными.
Для построения профиля зубьев второго колеса, как при равных первой и второй вспомогательных центроидах, так и в общем случае, для построения головок и ножек зубьев, описанный выше процесс повторяется с использованием этих же вспомогательных центроид и центроиды второго колеса. Второе колесо может быть как внешнего зацепления, так и внутреннего. Профили зубьев всех колес, построенных на разных центроидах (т.е. с разным количеством зубьев) с использованием одних и тех же вспомогательных центроид будут сопряжены с профилем зубьев первого колеса, а если первая и вторая вспомогательные центроиды равны и расположение чертящей точки на них одинаково, то и взаимно сопряжены между собой.
Трохоиды, используемые для получения эквидистантных профилей головок и ножек зубьев каждого колеса в настоящем изобретении строятся с использованием одной общей математической формулы. Основными и достаточными исходными параметрами, которые вводятся в эту формулу являются:
Aw - межосевое расстояние между центроидой колеса и вспомогательной;
r - радиус центроиды колеса;
Rroll - радиус вспомогательной центроиды (для расчета Aw и коэффициента «k»);
Rdr - расстояние чертящей точки от центра вспомогательной центроиды.
Эта математическая формула (уравнение трохоидальной кривой в прямоугольных координатах) имеет вид:

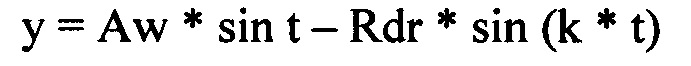
где:
«+/-» - означает, что для получения гипотрохоиды нужно брать знак «+», а для получения эпитрохоиды нужно брать знак «-»;
«*» - знак умножения;
х, у - декартовы координаты точек эпи- или гипотрохоиды;
t - переменная (аргумент) - угол поворота центра катящейся вспомогательной центроиды (центроиды, перекатываемой без скольжения по центроиде колеса);
k - коэффициент при угле поворота, который является однозначной функцией радиуса вспомогательной центроиды «Rroll» и радиуса центроиды колеса «r».
Для получения значения коэффициента «k» используется три различных варианта уравнений:
1) Для эпитрохоиды ножек зубьев колеса при внешней обкатке центроиды колеса вспомогательной центроидой:
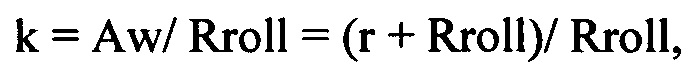
2) Для гипотрохоиды головок зубьев колеса при «Rroll» меньше «r» при внутренней обкатке центроиды колеса вспомогательной центроидой:
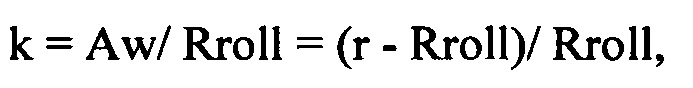
3) Для эпитрохоиды головок зубьев колеса при «Rroll» больше «г» при внутренней обкатке большой вспомогательной центроидой «Rroll» по меньшей центроиде колеса «r»:

Для получения реальных профилей головок и ножек зубьев, как было описано выше, берутся эквидистанты от этих полученных трохоидальных кривых, если первая и вторая вспомогательные центроиды равны друг другу, то с одним значением Eq, а если разные, то со значением Eq1 для головки зуба и Eq2 для ножки.
Для построения профиля зубьев зубчатой рейки (профиля исходного контура), сопряженной с зубчатым колесом по настоящему изобретению, используется другая математическая формула для получения двух трохоидальных кривых, необходимых для построения профиля головки и ножки зубьев зубчатой рейки:


Порядок построения зубьев зубчатой рейки такой же, как описанный выше для зубьев колес, за исключением того, что две трохоиды привязываем к системе координат рейки со сдвигом не в половину углового шага, а со сдвигом вдоль центроиды рейки (прямой линии) на половину линейного шага, который равен: 2*π*r/z.
Где «r» - радиус центроиды колеса, а «z» - число зубьев колеса.
Если зубья всех колес построены с использованием одной и той же (первой и второй) вспомогательной центроиды и зубчатая рейка построена с использованием этой
же вспомогательной центроиды, то она будет сопряжена с первым и со всеми любыми вторыми колесами.
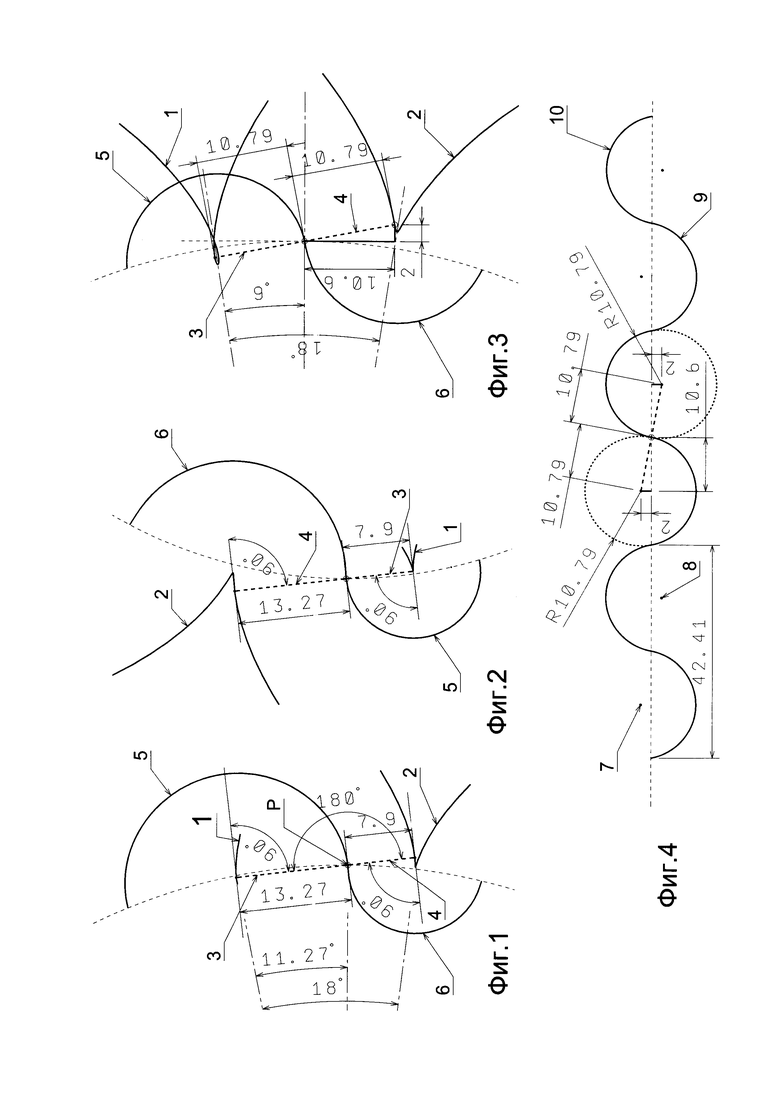
Еще одним важным аспектом настоящего изобретения является то, что оно позволяет построить на таком же принципе профили зубьев колес, когда вспомогательная центроида прямая линия. В этом случае необходимые укороченная и удлиненная трохоиды вырождаются в укороченную и удлиненную эвольвенты, для построения которых используется следующая математическая формула:
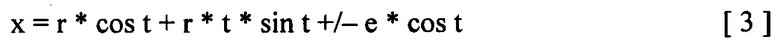
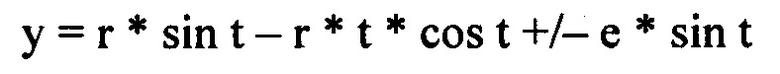
где:
«+/-» - означает, что для получения удлиненной эвольвенты ножки, нужно брать знак «+», а для получения укороченной эвольвенты головки нужно брать знак «-»;
«е» - расстояние чертящей точки от линии вспомогательной центроиды.
Главным преимуществом этого варианта является то, что профиль зубьев инструментальной рейки для изготовления таких зубчатых колес не имеет сложных математических кривых, а состоит из двух соединенных по касательной дуг окружностей.
Краткое описание чертежей
На Фиг. 1 показан принцип построения профиля зуба первого колеса при разных вспомогательных центроидах.
На Фиг. 2 то же что и на Фиг. 1 для второго колеса.
На Фиг. 3 показан принцип построения профиля зуба любого колеса с обоими вспомогательными центроидами в виде прямых линий.
На Фиг. 4 показан принцип построения не размноженного (т.е. до размножения числа зубьев) профиля зубчатой рейки при вспомогательных центроидах в виде прямых линий.
На Фиг. 5 показан вид не размноженных (т.е. до размножения числа зубьев) профилей зубчатых колес с зубьями на Фиг. 1 и Фиг. 2, рейки и колеса внутреннего зацепления.
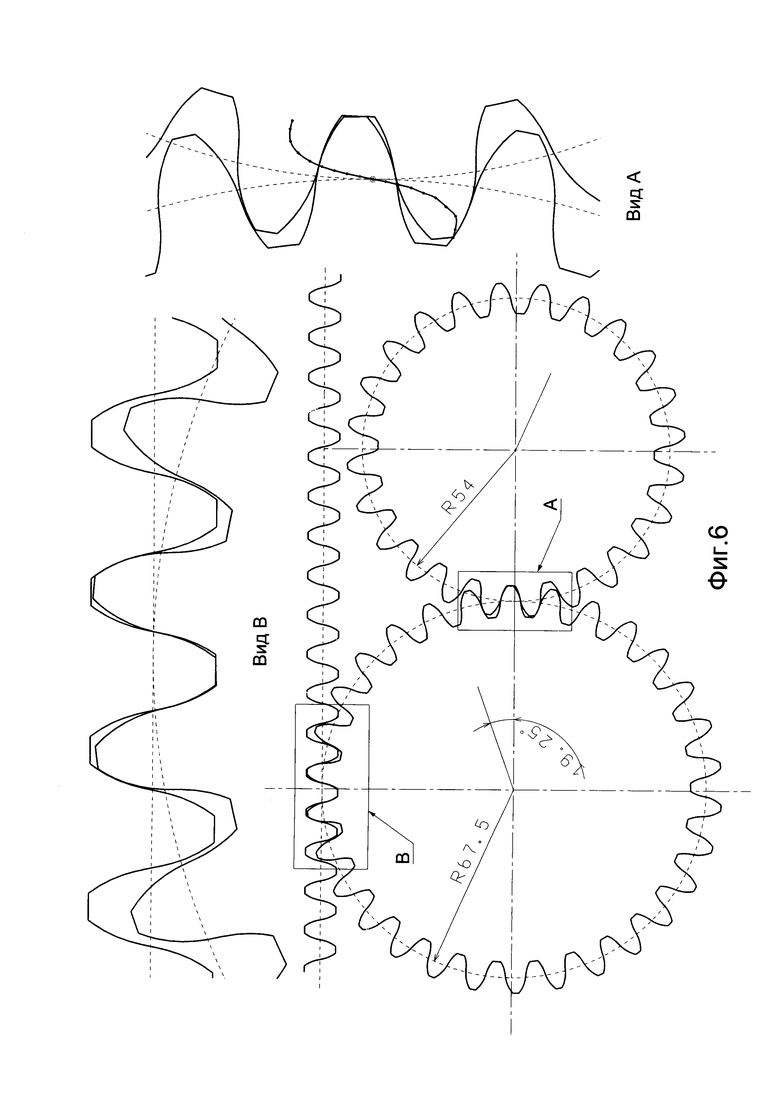
На Фиг. 6 показан вид профилей зубчатых колес внешнего зацепления и рейки, построенных с использованием одинаковых круговых вспомогательных центроид и размноженных в три раза по числу зубьев относительно не размноженных.
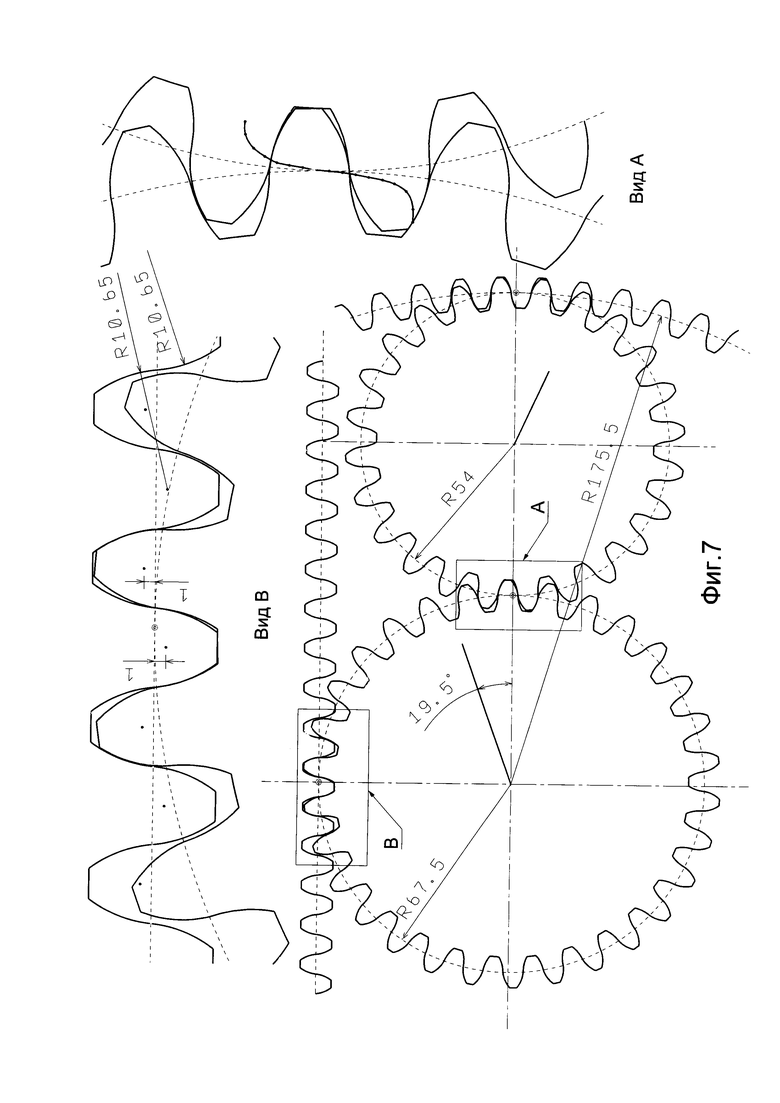
На Фиг. 7 то же, что на Фиг. 6, и колеса внутреннего зацепления, но с использованием прямолинейных вспомогательных центроид.
На Фиг. 8 показан вид профилей зубчатых колес внутреннего зацепления для сравнения трохоидального зацепления с эвольвентным.
Осуществление изобретения
На Фиг. 1 показан принцип построения профиля зуба первого колеса при разных вспомогательных центроидах. Исходные данные: Z=10, r=67,5 мм, Rroll-1=167,5 мм, Rroll-2=47,5 мм, Rdr-1=166,5 мм (e1=-1 мм), Rdr-2=47,25 мм (е2=-0,25 мм). Подставив эти значения в формулу [1], получаем от первой вспомогательной центроиды укороченную трохоиду головки зуба (1), (показана только верхняя полу ветвь петли трохоиды) и закрепляем эту трохоиду на первом колесе, а от второй вспомогательной центроиды получаем удлиненную трохоиду ножки зуба (2) и закрепляем ее на первом колесе со сдвигом вниз на полшага, т.е. на 18°. Поворачиваем колесо влево на угол больше чем четверть шага, например, на 11° и проводим через точку полюса (Р) нормаль (3) к трохоиде головки (1). В этом же угловом положении колеса, через точку полюса (Р) проводим нормаль (4) к трохоиде ножки (2). При этом угловом положении нормаль (4) не дошла до продолжения вниз линии нормали (3). Поворачиваем еще колесо до угла 12°, повторяем построение нормалей (3) и (4) и видим, что нормаль (4) прошла за линию продолжения нормали (3). Подбираем угол, при котором нормаль (4) будет на одной линии с нормалью (3). Этот угол оказался равен 11,269°. Величина эквидистант оказалась равна Eq1=13,27055549 мм, a Eq2=7,90365106 мм. Взяв эквидистанты от трохоид головки и ножки с этими величинами, получаем профиль головки (5) и профиль ножки (6).
На Фиг. 2 показан построенный аналогичным способом профиль зуба второго колеса. Исходные данные: Z=8, r=54 мм, Rroll-1=47,5 мм, Rroll-2=167,5 мм, Rdr-1=47,25 мм, Rdr-2=166,5 мм. Подбор величины эквидистант не требуется, все вторые колеса, сопряженные с первым колесом будут иметь Eq1=7.90365106 мм, а Eq2=l3,27055549 мм.
На Фиг. 3 показан принцип построения профиля зуба колеса с обоими вспомогательными центроидами в виде прямых линий. Исходные данные: Z=10 и r=67,5 мм, e1=е2=2 мм. Так как вспомогательные центроиды прямые линии, расчет трохоид головки и ножки производим по формуле [3], в результате для головки получаем укороченную эвольвенту (1), а для ножки удлиненную эвольвенту (2). При равных вспомогательных центроидах поворачиваем колесо влево на четверть шага, т.е. на 9°. В этом случае всегда Eq1=Eq2=Eq. Из рисунка видно, что величину этой эквидистанты можно рассчитать по теореме Пифагора. Один катет равен расстоянию чертящей точки от линии вспомогательной центроиды: «е»=2 мм, а второй, четверти линейного шага колеса: 2*π*67,5 мм /10/4=10,602875206 мм. В результате Eq=10,789854616 мм. Взяв эквидистанты от этих укороченной и удлиненной эвольвент, получим профиль головки зуба (5) и профиль ножки зуба (6).
На Фиг. 4 показан принцип построения исходного (т.е. до размножения числа зубьев) профиля зубьев зубчатой рейки при вспомогательных центроидах в виде прямых линий. Величина эквидистанты для профиля головок и ножек зубьев зубчатой рейки, сопряженной с колесом, имеющим зубья на Фиг. 3, такая же, как и у всех, сопряженных с этим колесом колес, и равна Eq как для Фиг. 3. Когда центроида рейки прямая линия и вспомогательная центроида прямая линия, трохоиды головки и ножки зубьев рейки вырождаются в неподвижные относительно центроиды рейки точки (7) и (8), расположенные на расстоянии «е»=2 мм, для головки зуба рейки, выше центроиды рейки, а для ножки - ниже. Законченный профиль зубьев рейки состоит из частей окружностей с центрами в упомянутых точках, соединенных по касательной на центроиде рейки, и с радиусами Eq=10,789854616 мм. Головкой зуба рейки является дуга окружности (9), а ножкой зуба рейки - дуга окружности (10).
На Фиг. 5 показаны законченные исходные профили первого колеса (11) с зубьями, построенными на Фиг. 1 и второго колеса (12), с зубьями, построенными на Фиг. 2. На увеличенном виде «А» показана линия зацепления (13) для колес (11) и (12).
Зубчатая рейка (14), сопряженная с колесом (11), построена таким способом: трохоида головки (15) и трохоида ножки (16) построены с использованием уравнений [2]. Исходными данными для трохоиды головки (15) являются: Rroll=47,5 мм, Rdr=47,25 мм, а для трохоиды ножки (16): Rroll=167,5 мм, Rdr=166,5 мм. Величины эквидистант для профилей головки (17) и ножки (18) зубчатой рейки (14) такие же, как для профиля зубьев второго колеса на Фиг. 2. Зубчатой рейкой, сопряженной со вторым колесом (12), будет зеркальное отражение рейки (14), как показано в позиции (19).
На этой фигуре также показан исходный профиль зубчатого колеса внутреннего зацепления (20), построенный таким же способом, как и колес (11) и (12), с использованием уравнений [1]. Исходные данные для построения профиля (20) колеса внутреннего зацепления следующие: Z=26, г=175,5 мм, a Rroll-1, Rroll-2, Rdr-1, Rdr-2, Eql и Eq2 - такие же как для второго колеса на Фиг. 2.
На Фиг. 6 показаны профили зубчатых колес и рейки, построенных с использованием одинаковых круговых вспомогательных центроид с Rroll=47,5 мм и Rdr=46,5 мм, размноженных в три раза по числу зубьев относительно исходных и с обрезанием зубьев по окружностям вершин и впадин. (Исходные профили не показаны).
На Фиг. 7 показаны профили зубчатых колес и рейки, построенных с использованием прямолинейных вспомогательных центроид и размноженных в три раза по числу зубьев относительно исходных и с обрезанием зубьев по окружностям вершин и впадин. Исходные профили зубьев колес и рейки показаны на Фиг. 3 и Фиг. 4 с разницей только в том, что на Фиг. 7 взято расстояние чертящей точки от линии вспомогательной центроиды «е»=1 мм, а на Фиг. 3 и 4 для большей наглядности было взято «е»=2 мм.
При сравнении колес на Фиг. 6 и Фиг. 7 можно заметить, что они очень подобны, разница только в том, что крутизна зуба на Фиг. 6 меньше. При уменьшении радиуса вспомогательной центроиды крутизна зуба и линии зацепления уменьшаются, а при увеличении, увеличиваются и быстро стремятся к пределу, как на Фиг. 7.
На Фиг. 8 показаны профили колес внутреннего зацепления с малой разностью зубьев. В позиции (21) показана, для сравнения, известная из уровня техники пара колес с эвольвентным зацеплением, разработанная J.R. Colbourne и опубликованная в журнале «Gear Technology)), May/June 1990, статья "The Geometric Design of Internal Gear Pairs". Исходные параметры для этой передачи были следующие: Z1=29, Z2=34, r1=90,306 мм, r2=105,876 мм, Aw=15,57 мм, основные окружности: Rb1=81,753 мм, Rb2=95,894 мм. В этих размерах и с этими же параметрами (основные окружности не требуются) были построены зубчатые профили колес по изобретению, поз. (22). Необходимые дополнительные параметры: число зубьев до размножения: Z1=5,8; Z2=6,8; размножение в 5 раз. Расположение чертящей точки: «е»=10 мм, вспомогательная центроида - прямая линия.
Для сравнительной оценки преимуществ изобретенного профиля зубьев по сравнению с эвольвентным зацеплением был произведен расчет приведенного радиуса кривизны во всех точках линии зацепления.
Для внешнего зацепления была взята пара колес с эвольвентным зацеплением в тех же размерах и с тем же количеством зубьев, что и на Фиг. 6 и Фиг. 7. Результаты расчета занесены в следующую таблицу:

В вышеприведенной таблице при угле поворота 9° точка контакта находится строго в полюсе зацепления. Для Фиг. 7 при этом угле поворота был выполнен математический расчет, который показал равенство приведенных радиусов кривизны в полюсе зацепления для первой пары кривых (ножка-головка) и для второй пары кривых (головка-ножка).
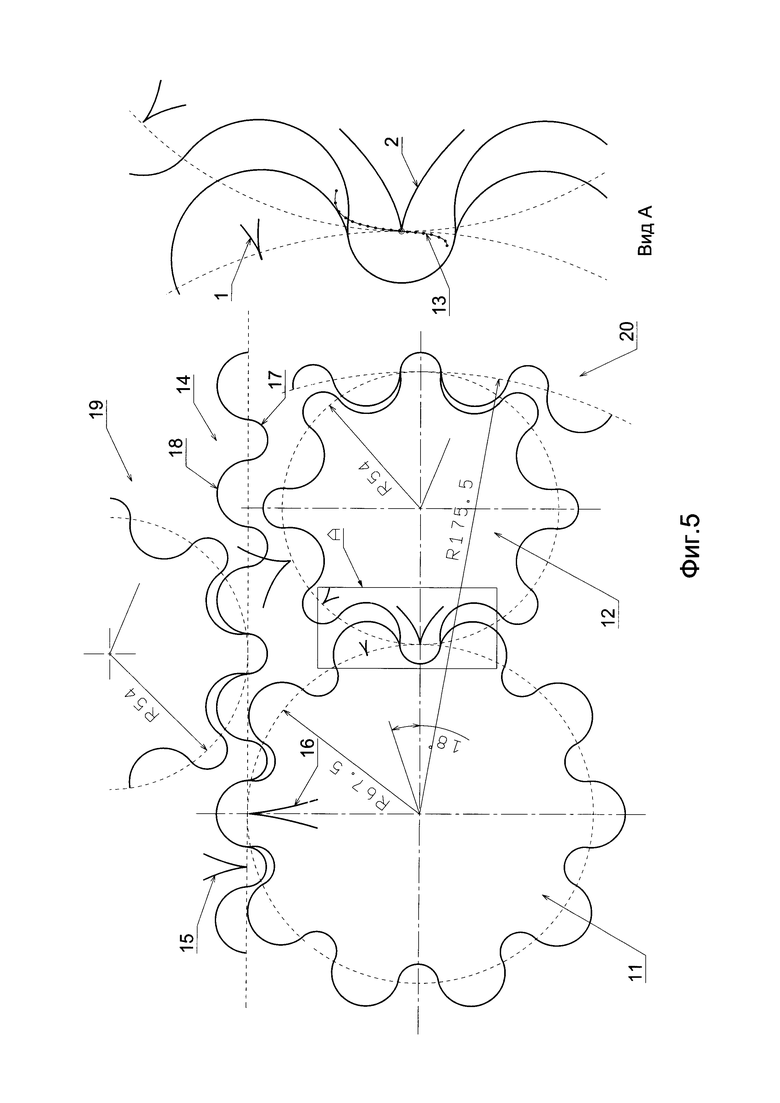
Результат для «е»=2 и 3 соответственно равен: 5,56077929 мм и 8,16762281 мм. Расчет радиуса кривизны эвольвенты в точке для угла поворота «t» производился по формуле:
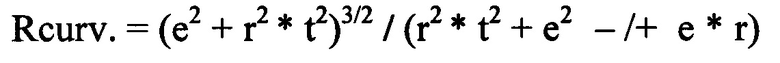
где: «-/+» означает, что верхний знак «-» берется для удлиненной эвольвенты (без петли), а нижний знак «+» для укороченной (с петлей).
Для колес внутреннего зацепления, показанных на Фиг. 8, результаты расчета занесены в следующую таблицу:

Для колес (22) на Фиг. 8 точка контакта будет находиться в полюсе зацепления при угле поворота первого колеса равном четверти шага: 15,51724138°, математический расчет, выполненный по вышеуказанной формуле, показал равенство приведенных радиусов кривизны в полюсе зацепления для обоих пар кривых, равных: 232,406464 мм
| название | год | авторы | номер документа |
|---|---|---|---|
| ЗУБЧАТАЯ ПАРА | 1944 |
|
SU67425A1 |
| ПЛАНЕТАРНАЯ ПЕРЕДАЧА С УСТРОЙСТВОМ НЕЙТРАЛИЗАЦИИ РАДИАЛЬНОЙ НАГРУЗКИ ОТ КОНТАКТИРУЮЩИХ ЗУБЬЕВ | 2017 |
|
RU2668451C1 |
| Циклоидное зубчатое зацепление | 1990 |
|
SU1772470A1 |
| УСТРОЙСТВО для ОБРАБОТКИ ТРОХОИДАЛЬНЫХ ПОВЕРХНОСТЕЙ | 1969 |
|
SU248446A1 |
| Цилиндрическая эвольвентная зубчатая передача | 1982 |
|
SU1096415A1 |
| ПЛАНЕТАРНЫЙ РЕДУКТОР С ДВУМЯ СООСНЫМИ ВЫХОДНЫМИ ВАЛАМИ ПРОТИВОПОЛОЖНОГО ВРАЩЕНИЯ | 2016 |
|
RU2729324C2 |
| ЗУБЧАТОЕ ЗАЦЕПЛЕНИЕ ВАХРУШЕВЫХ | 2009 |
|
RU2396473C1 |
| ПРЯМОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160403C1 |
| Цилиндрическая зубчатая передача | 1981 |
|
SU992863A1 |
| Зубчатая передача | 1979 |
|
SU870805A1 |

Изобретение относится к зубчатым передачам. Трохоидальное зубчатое зацепление двух колес, в котором профиль зубьев каждого колеса состоит из двух касательно соединенных между собой эквидистант трохоидальных кривых, образующих одна частично или полностью вогнутую ножку зуба, а вторая выпуклую головку зуба. В результате, на входе и выходе зубьев из зацепления образуется выпукло-вогнутый контакт с приведенным радиусом кривизны существенно большим, чем в эвольвентном зацеплении. В точке перехода контакта с ножки на головку в полюсе зацепления, в отличие от других неэвольвентных зацеплений, приведенный радиус кривизны не имеет скачкообразного изменения, а имеет конечное плавно изменяющееся значение, как в эвольвентном зацеплении. В наиболее преимущественном варианте этого зацепления, когда трохоидальными кривыми являются укороченная и удлиненная эвольвенты, профиль зубьев инструментальной рейки не имеет сложных кривых, а состоит из двух соединенных по касательной дуг окружностей. Одной и той же рейкой можно нарезать колеса с различным количеством зубьев. Обеспечивается повышение нагрузочной способности зубчатой передачи. 4 з.п. ф-лы, 8 ил.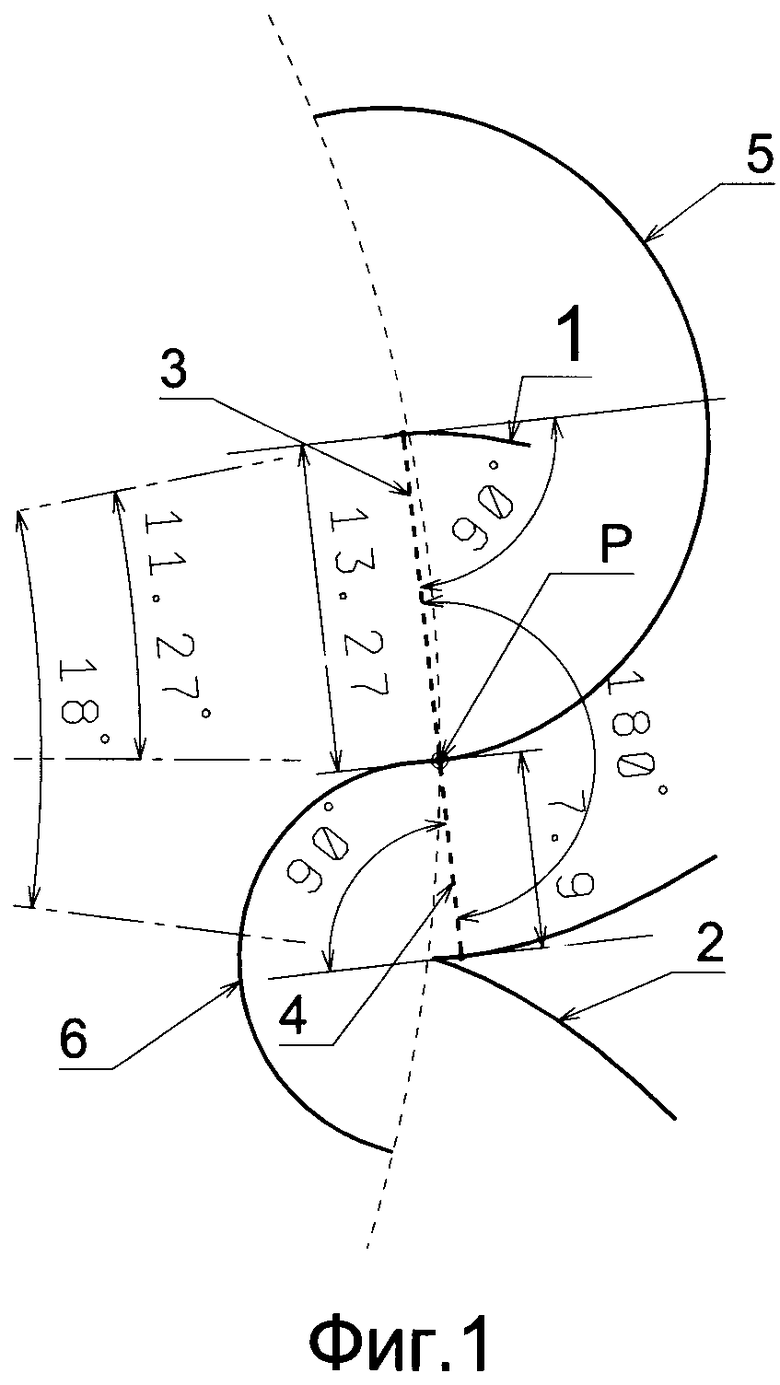
1. Трохоидальное зубчатое зацепление двух колес, в котором профиль зубьев каждого колеса состоит из двух касательно соединенных между собой кривых, образующих одна частично или полностью вогнутую ножку зуба, а вторая выпуклую головку зуба, профиль ножки зубьев первого колеса очерчен эквидистантой участка трохоиды, полученной при обкатке центроиды первого колеса второй вспомогательной центроидой, а профиль ножки зубьев второго колеса очерчен эквидистантой участка трохоиды, полученной при обкатке центроиды второго колеса первой вспомогательной центроидой, отличающееся тем, что профиль головки зубьев первого колеса очерчен эквидистантой участка трохоиды, полученной при обкатке центроиды первого колеса первой вспомогательной центроидой, а профиль головки зубьев второго колеса очерчен эквидистантой участка трохоиды, полученной при обкатке центроиды второго колеса второй вспомогательной центроидой, при этом величины эквидистант для профилей ножек и головок зубьев каждого колеса выбраны такими, что они обеспечивают соединение профилей ножек и профилей головок по касательной, а также обеспечивают расположение точек соединения профилей ножек и головок на центроидах каждого колеса.
2. Зацепление по п. 1, отличающееся тем, что первая и вторая вспомогательные центроиды равны между собой и имеют одно и то же расположение чертящей точки, а величина эквидистанты для профилей ножек и головок зубьев на каждом колесе имеет одно и то же значение.
3. Зацепление по п. 1, отличающееся тем, что первая и вторая вспомогательные центроиды или одна из них являются прямыми линиями.
4. Зацепление по п. 2, отличающееся тем, что первая и вторая вспомогательные центроиды являются прямыми линиями.
5. Зацепление по любому из пп. 1-4, отличающееся тем, что ценртоида второго колеса имеет бесконечно большой радиус и является прямой линией, а второе колесо при этом представляет собой зубчатую рейку, профилем зубьев которой является исходный контур.
| RU 2015136203 A, 20.02.2017 | |||
| US 7086304 B2, 08.08.2006 | |||
| US 6540637 B2, 01.04.2003 | |||
| US 20130112028 A1, 09.05.2013. |
Авторы
Даты
2018-11-28—Публикация
2017-06-21—Подача