Настоящее изобретение относится к области измерения, в части определения физических свойств материалов, и может быть использовано преимущественно для определения упругих и диссипативных постоянных полимерных композиционных материалов (ПКМ) неразрушающим способом в любых отраслях промышленности.
Динамическое поведение ПКМ, характеризующихся анизотропией упругих и диссипативных характеристик в плоскости укладки армирующих материалов, привлекает внимание исследователей в связи с возрастающим применением в конструкциях, испытывающих вибрационные воздействия. Поскольку реакция таких конструкций на действие вибрации зависит, главным образом, от жесткостных и диссипативных свойств, то оптимальное конструирование состоит в варьировании этих свойств с целью достижения соответствия тем или иным критериям качества, например, минимизации смещений, запасенной энергии и т.д. Подбор упругих и диссипативных характеристик конструкций может осуществляться посредством варьирования ориентацией и последовательностью укладки слоев армирующего материала по толщине композита. Такая задача может быть решена на основе методов механики слоистых композитов при наличии полного набора упругих и диссипативных характеристик всех компонуемых монослоев ПКМ.
Учитывая, что практически все конструкции из ПКМ являются тонкостенными (в этом случае свойства материалов реализуются наилучшим образом), в теории слоистых композитов, как правило, пренебрегают поперечными нормальными напряжениями (σ33=0, см. фиг. 1, где представлена геометрия стержня, вырезанного из пластины ортотропного материала под углом θ к направлению оси симметрии 3).
Таким образом, для описания динамического поведения конструкций из ортотропного ПКМ с армирующими волокнами, расположенными параллельно его срединной плоскости, необходимо знать численные значения главных комплексных динамических модулей упругости E11, Е22, комплексных динамических модулей сдвига G12, G13, G23 и коэффициента Пуассона ν12:
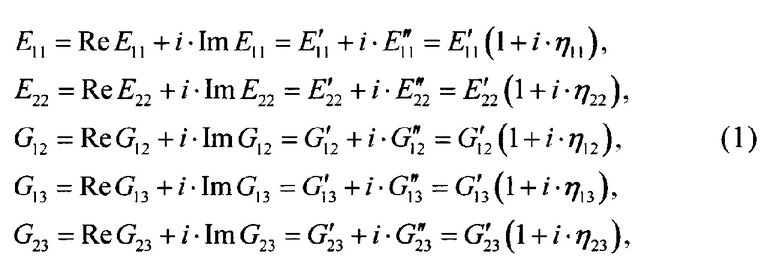
где
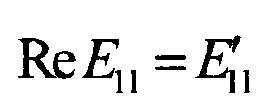 - вещественная часть комплексного модуля упругости ПКМ в направлении основы армирующего материала (θ=0°);
- вещественная часть комплексного модуля упругости ПКМ в направлении основы армирующего материала (θ=0°);
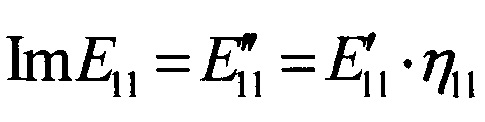 - мнимая часть комплексного модуля упругости ПКМ в направлении основы армирующего материала (θ=0°);
- мнимая часть комплексного модуля упругости ПКМ в направлении основы армирующего материала (θ=0°);
η11 - коэффициент механических потерь при изгибе образца в направлении основы армирующего материала (θ=0°);
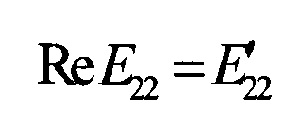 - вещественная часть комплексного модуля упругости ПКМ в направлении утка армирующего материала (θ=90°);
- вещественная часть комплексного модуля упругости ПКМ в направлении утка армирующего материала (θ=90°);
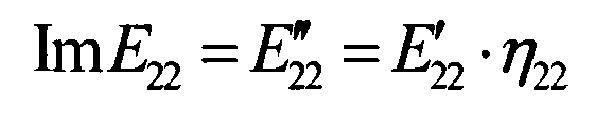 - мнимая часть комплексного модуля упругости ПКМ в направлении утка армирующего материала (θ=90°);
- мнимая часть комплексного модуля упругости ПКМ в направлении утка армирующего материала (θ=90°);
η22 - коэффициент механических потерь при изгибе образца в направлении утка армирующего материала (θ=90°);
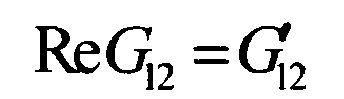 - вещественная часть комплексного модуля сдвига в плоскости армирования ПКМ;
- вещественная часть комплексного модуля сдвига в плоскости армирования ПКМ;
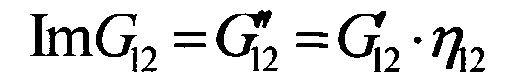 - мнимая часть комплексного модуля сдвига в плоскости армирования ПКМ;
- мнимая часть комплексного модуля сдвига в плоскости армирования ПКМ;
η12 - коэффициент механических потерь при сдвиге ПКМ в плоскости армирования;
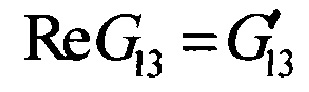 - вещественная часть комплексного модуля межслойного сдвига ПКМ в направлении основы армирующего материала (θ=0°);
- вещественная часть комплексного модуля межслойного сдвига ПКМ в направлении основы армирующего материала (θ=0°);
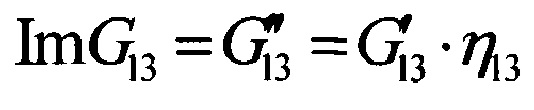 - мнимая часть комплексного модуля межслойного сдвига ПКМ в направлении основы армирующего материала (θ=0°);
- мнимая часть комплексного модуля межслойного сдвига ПКМ в направлении основы армирующего материала (θ=0°);
η13 - коэффициент механических потерь при межслойном сдвиге ПКМ в направлении основы армирующего материала (θ=0°);
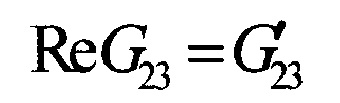 - вещественная часть комплексного модуля межслойного сдвига ПКМ в направлении утка армирующего материала (θ=90°);
- вещественная часть комплексного модуля межслойного сдвига ПКМ в направлении утка армирующего материала (θ=90°);
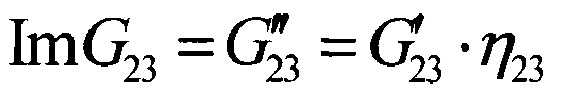 - мнимая часть комплексного модуля межслойного сдвига ПКМ в направлении утка армирующего материала (θ=90°);
- мнимая часть комплексного модуля межслойного сдвига ПКМ в направлении утка армирующего материала (θ=90°);
η23 - коэффициент механических потерь при межслойном сдвиге ПКМ в направлении утка армирующего материала (θ=90°).
Известен способ определения упругих свойств ПКМ [Патент на изобретение RU 2517989 С1, Опубликовано: 10.06.2014 Бюл. №16]. Способ заключается в возбуждении колебаний образца ПКМ в виде прямоугольной пластины со свободными краями и определении ее частот и форм собственных колебаний. Упругие характеристики ПКМ определяются путем перебора значений модулей упругости, модулей сдвига и коэффициентов Пуассона, подставляя их в математическую модель пластины и сравнивая каждый раз вычисленную частоту колебаний для каждой формы колебаний с частотами и формами колебаний, полученными экспериментально. В итоге определяются девять упругих постоянных. Недостатком указанного способа является высокая трудоемкость, а также необходимость определять большое кол-во собственных частот и форм колебаний образцов с высокой точностью. Кроме того, указанный способ имеет узкую область применения, а именно не позволяет определять диссипативные характеристики ПКМ.
Известен также способ определения механических свойств материалов [ASTM Standard Е1876-01, Standard test method for dynamic Young's modulus, shearmodulus, and Poisson's ratio by impulse excitation of vibration, Book of Standards, Volume 03]. Способ заключается в возбуждении колебаний образца материалов и определении, как правило, его собственных частот первого тона колебаний. Полученные собственные частоты подставляются в частотное уравнение, из которого, определяют упругие постоянные. Образцы, как правило, имеют простую геометрическую форму в виде балок. Данный способ может быть использован для изотропных материалов, но неприемлем для образцов ортотропных ПКМ. Кроме того, указанный способ имеет узкую область применения, а именно не позволяет определять диссипативные характеристики ПКМ.
Известен также способ определения механических свойств материалов [ГОСТ 23813-79 «Стеклопластики конструкционные для судостроения. Метод определения модуля упругости»]. Указанный подход основан на экспериментальном определении изгибных собственных частот призматических образцов с углами вырезки θ=0,90°. Способ дает возможность определять только главные динамические модули упругости ReE11, ReE22 и имеет узкую область применения, а именно не позволяет определять диссипативные характеристики ПКМ.
Наиболее близким к предлагаемому техническому решению является способ [ГОСТ 23814-79 «Стеклопластики конструкционные для судостроения. Метод определения модулей сдвига»]. Указанный подход основан на экспериментальном определении крутильных собственных частот призматических образцов в виде безопорных балок с углами вырезки θ=0, 90° с высотой сечения а и 2а. При определении модулей сдвига ReG12, ReG13, ReG23 используются зависимости, связывающие частоты собственных крутильных колебаний ортотропного стержня с модулями сдвига. Для нахождения этих зависимостей решается статическая задача о кручении ортотропного прямоугольного стержня, которая сводится к интегрированию уравнения Пуассона. Указанный метод не обеспечивает точного определения упругих характеристик. Кроме того, указанный способ имеет узкую область применения, а именно не позволяет определять диссипативные характеристики ПКМ.
Техническим результатом настоящего изобретения является возможность определения комплексных модулей упругости Е11, E22 и сдвига G12, G13, G23, необходимых для полного описания динамического поведения тонкостенных конструкций, включающие в себя жесткостные и диссипативные характеристики ортотропного ПКМ, имеющие высокую точностью и достоверность.
Технический результат достигается следующим образом. Способ определения упругих и диссипативных характеристик композиционного материала, заключающийся в обработке экспериментальных значений собственных частот и соответствующих этим частотам коэффициентов механических потерь низших тонов изгибных и крутильных колебаний безопорных балок, вырезанных из пластины ортотропного полимерного композиционного материала под углом 0, 45, 90°. В способе реализована возможность определять диссипативные характеристики полимерных композиционных материалов, при этом используется в своей основе процедура последовательных приближений, в соответствии с которой начальные значения динамических модулей упругости в направлении основы и утка армирующего материала, модуля сдвига в плоскости армирования и межслойных модулей сдвига в направлении основы и утка, определенными при помощи собственных частот первого тона изгибных и крутильных колебаний, а также соответствующим им коэффициентов потерь, уточняются при помощи зависимостей, основанных на теории колебаний балки Тимошенко, используя значения собственных частот и соответствующих коэффициентов потерь изгибных колебаний безопорных балок полимерных композиционных материалов более высоких тонов.
Количество образцов равно трем.
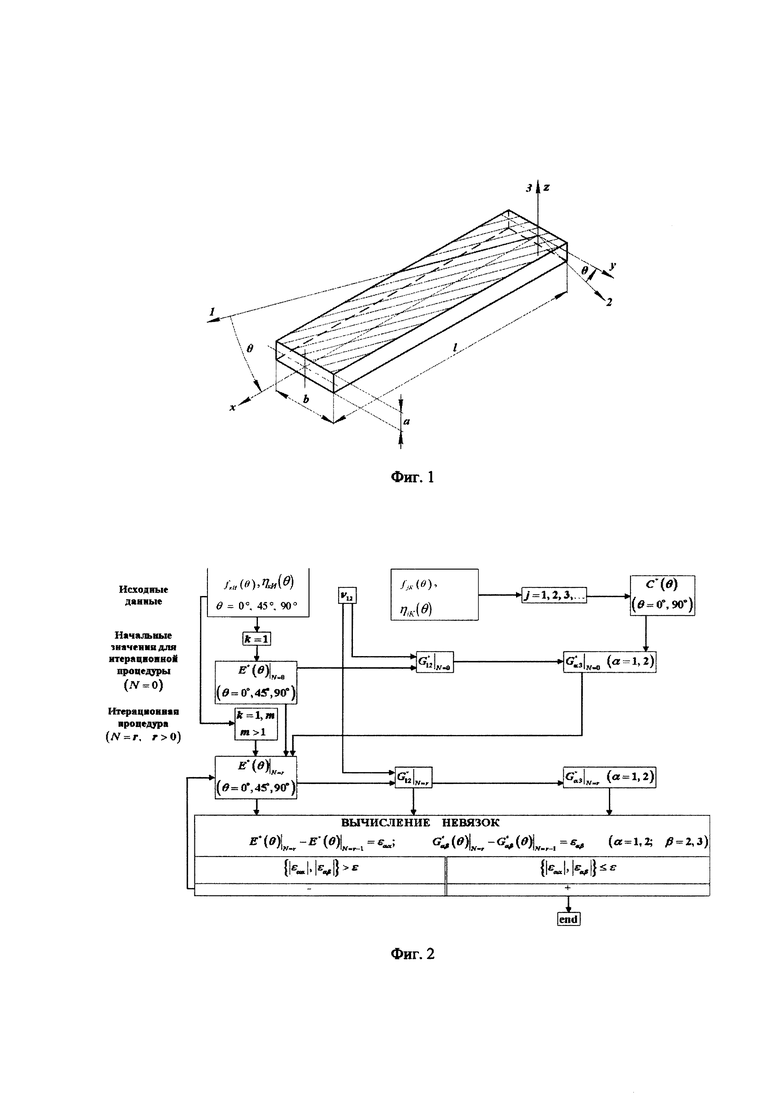
Указанные существенные признаки способа обеспечивают решение поставленной задачи с достижением заявленного технического результата. Блок-схема итерационной процедуры уточнения вещественных и мнимых частей комплексных модулей упругости и сдвига, раскрывающая сущность изобретения приведена на фиг. 2.
На фиг. 2 показано, что на первом шаге по первой собственной частоте ƒ1И(θ) изгибных колебаний, а также соответствующем коэффициенте потерь η1И(θ) определяются начальные значения динамических модулей упругости Е'(θ) стержневых образцов ПКМ (θ=0, 45, 90°). Далее при помощи коэффициента Пуассона ν12, а также полученных комплексных модулей упругости E11=E(0°), E(45°), E22=E(90°) определяется начальное значение комплексного модуля сдвига в плоскости укладки слоев армирующих волокон G12. При помощи зависимостей, связывающих частоты собственных крутильный колебаний ƒ1К(θ), а также соответствующих коэффициентов потерь η1К(θ) образцов ПКМ (θ=0°, 90°) с модулями сдвига, определяются начальные значения комплексных модулей межслойного сдвига G13, G23. На следующем шаге начальные значения E11=Е(0°), E(45°), Е22=E(90°) уточняются с учетом известных G13, G23 по значениям собственных частот ƒ2И(θ), ƒ3И(θ) и соответствующих коэффициентов потерь η2И(θ), η3И(θ) второго и третьего тонов изгибных колебаний. Указанная процедура повторяется до тех пор, пока две следующие друг за другом последовательности вещественных и мнимых частей комплексных модулей упругости и комплексных модулей сдвига не станут практически неизменны.
Способ определения модулей упругости и диссипативных характеристик ПКМ осуществляется следующим образом. Из исследуемого материала под углом θ=0, 45, 90° к направлению основного армирования материала вырезают балки постоянного по длине поперечного сечения с размерами L×a×b (см. рис. 1). С целью минимизации экспериментальных погрешностей рекомендуется использовать образцы со следующими геометрическими характеристиками для углепластиков: 1.5≤a/b≤3, L/a≥30 и для стеклопластиков 1/3≤a/b≤2/3, L/a≥15. Перед началом испытаний производят измерения длины, ширины, высоты сечения образцов, а также их массы. Производят возбуждения колебаний образцов ПКМ импульсной силой и определяют их частотные характеристики. По полученным частотным характеристикам путем анализа форм колебаний определяются собственные частоты первых трех тонов ƒ1И(θ), ƒ2И(θ), ƒ3И(θ) изгибных колебаний образцов ПКМ, вырезанных под углами θ=0, 45, 90° и первого тона крутильных ƒ1К(θ) колебаний образцов, вырезанных под углами θ=0,90°, а также соответствующие этим частотам коэффициенты потерь η1И(θ), η2И(θ), η3И(θ), η1К(θ) (см. формулу 3).

где ƒ0 - резонансная частота; ƒ2, ƒ1 - частоты, соответствующие уровню 0.707 от максимальной амплитуды виброускорений на резонансной частоте.
Начальные значения вещественных частей комплексных модулей упругости ReE(θ) в направлениях θ=0, 45, 90° (ReE(0°)=ReE11, ReE(45°)=E'(45°), ReE(90°)=ReE22) определяются по полученным из эксперимента величинам резонансных частот 1-го тона изгибных колебаний образцов ПКМ ƒ1И(θ) по формуле:
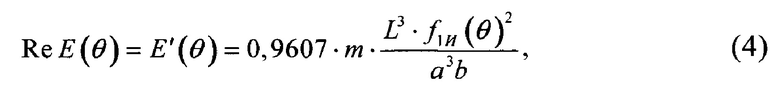
Начальные значения коэффициентов механических потерь η(θ) при изгибе образцов в направлениях θ=0, 45, 90° определяются по формуле (3) как наименьшая из экспериментально определенных величин коэффициентов механических потерь, соответствующих двум первым резонансным частотам изгибных колебаний образцов ПКМ.
Начальное значение комплексного модуля сдвига в плоскости армирования G12 вычисляется из соотношения:
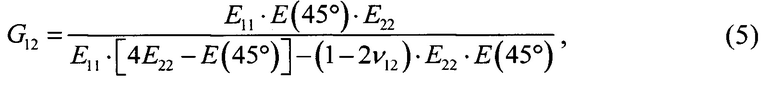
где E(45°)=E'(45°)(1+i⋅η(45°)), ν12 - коэффициент Пуассона, определяемый из статических испытаний на одноосное растяжение.
Значения комплексной крутильной жесткости С(θ) образцов, вырезанных в направлениях θ=0,90°, определяются по полученным из эксперимента величинам собственных частот 1-ого тона крутильных колебаний ƒ1К(θ) образцов ПКМ, а также соответствующим им коэффициентам механических потерь η1К(θ), по формуле:
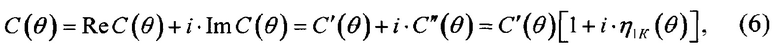
где
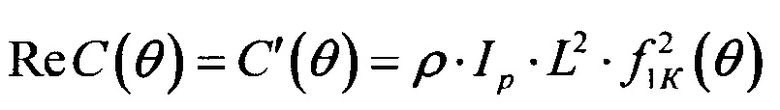 - вещественная часть комплексной крутильной жесткости;
- вещественная часть комплексной крутильной жесткости;
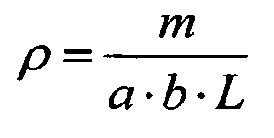 - плотность материала;
- плотность материала;
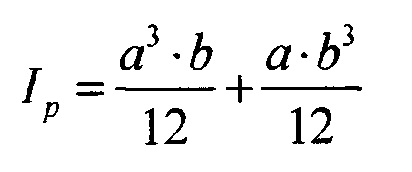 - полярный момент инерции прямоугольного поперечного сечения;
- полярный момент инерции прямоугольного поперечного сечения;
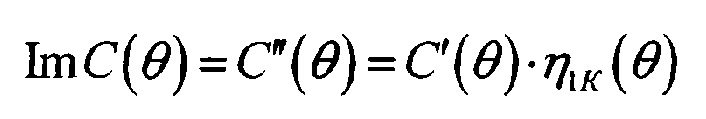 - мнимая часть комплексной крутильной жесткости;
- мнимая часть комплексной крутильной жесткости;
η1К(θ) - коэффициент механических потерь при кручении образца ПКМ вычисляемый по формуле (3).
По вычисленным начальным значениям комплексного модуля сдвига G12 в плоскости армирования и комплексной крутильной жесткости С(θ) образцов ПКМ, вырезанных в направлениях θ=0,90° определяются начальные значения комплексных модулей межслойного сдвига G13, G23 в направлениях основы и утка армирующего материала из соотношений:

где z0, z90 определяются из решения задачи минимизации |Ψ(z)| →min выражения:
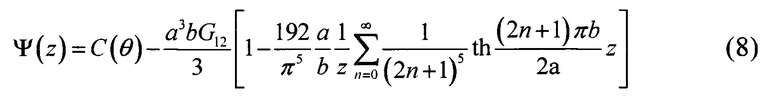
При численной реализации задачи минимизации рекомендуется использовать алгоритм №178 прямого поиска точки минимума [5], для которого требуются лишь начальное приближение к искомому решению Z и значения функции Ψ(z) в соответствующих точках. В качестве начального приближения берется точка:

Начальное значение комплексного модуля межслойного сдвига G(45°) по вычисленным начальным значениям комплексных модулей межслойного сдвига G13, G23 определяется из соотношения:

Полученные начальные значения комплексных модулей упругости E11=E(0°), E(45°), Е22=E(90°) и комплексных модулей сдвига G12, G13, G23 подвергаются итерационной процедуре уточнения (см. фиг. 2).
Уточнение начальных значений ReE(θ)=E'(θ) и ImE(θ)=Е''(θ) θ=0, 45, 90° выполняется на основе теории затухающих колебаний балки Тимошенко. Для этого используются экспериментально определенные величины собственных частот изгибных колебаний второго ƒ2И(θ) и третьего ƒ3И(θ) тонов, а также соответствующие этим частотам величины коэффициентов механических потерь η2И(θ), η3И(θ).
Уточненные комплексные модули упругости определяются из решения задачи минимизации ⎪Ψ(Eii, Gij)⎪→min выражения:
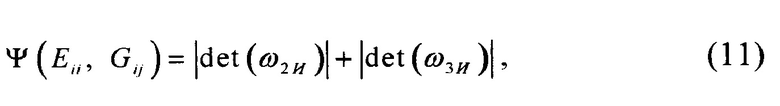
где
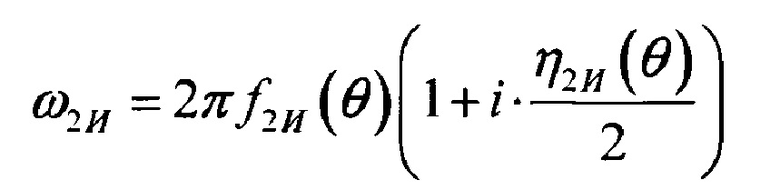 - круговая частота 2-го тона изгибных колебаний;
- круговая частота 2-го тона изгибных колебаний;
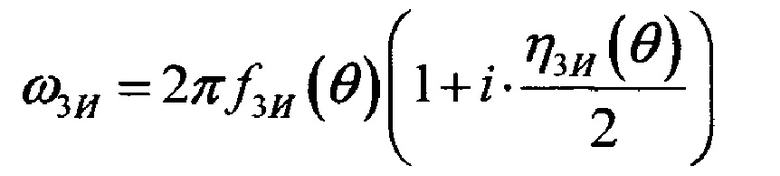 - круговая частота 3-го тона изгибных колебаний;
- круговая частота 3-го тона изгибных колебаний;
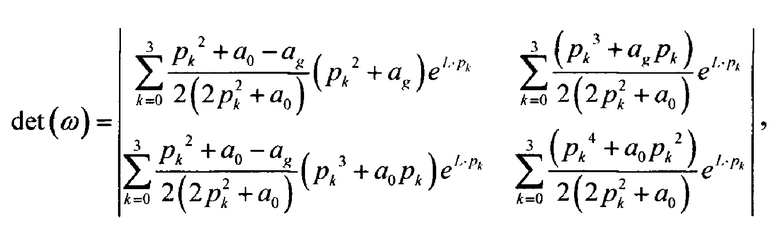
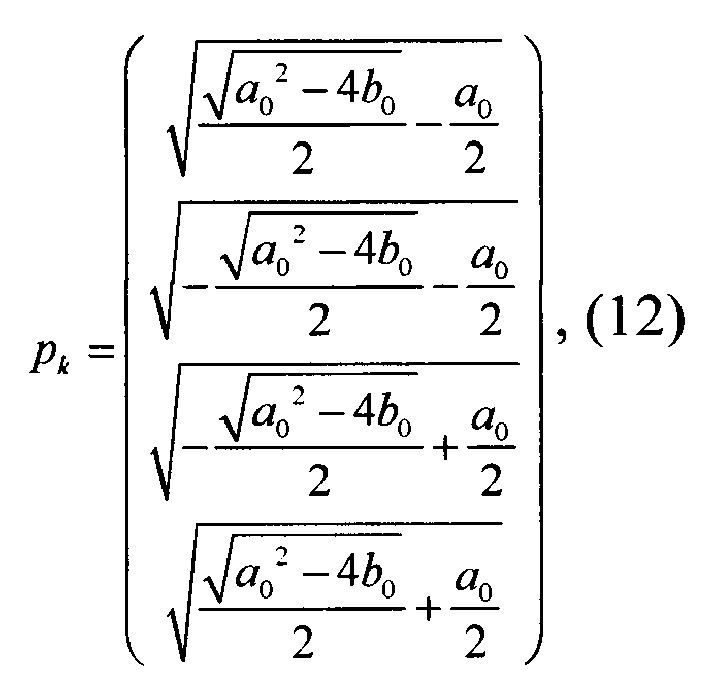
где 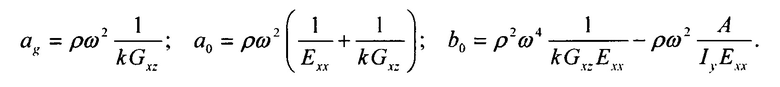
При численной реализации задачи минимизации рекомендуется воспользоваться процедурой прямого поиска точки глобального минимума [Библиотека алгоритмов 1516 - 2006 // Под ред. Агеева М.И. М.: Радио и связь. 1981, 184 с.] функции (11).
Уточненные значения ReE(θ)=Е'(θ) и ImE(θ)=Е''(θ) θ=0, 45, 90° влекут за собой новые значения вещественной 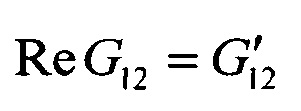 и мнимой
и мнимой 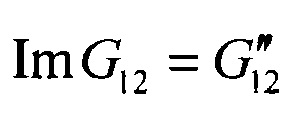 частей комплексного модуля сдвига в плоскости армирования G12 (в соответствии с формулой 2), а также новые значения вещественных
частей комплексного модуля сдвига в плоскости армирования G12 (в соответствии с формулой 2), а также новые значения вещественных 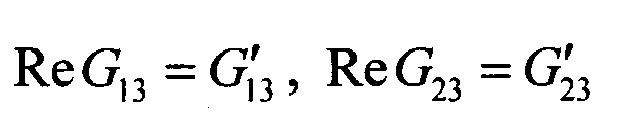 и мнимых
и мнимых 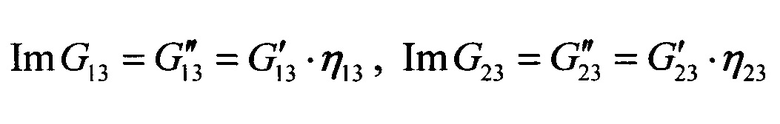 частей комплексных модулей межслойного сдвига в направлениях основы G13 и утка G23 армирующего материала (в соответствии с формулой 7);
частей комплексных модулей межслойного сдвига в направлениях основы G13 и утка G23 армирующего материала (в соответствии с формулой 7);
Указанная процедура повторяется до тех пор, пока две следующие друг за другом последовательности вещественных и мнимых частей комплексных модулей упругости Е11=E(0°), E(45°), Е22=E(90°) и комплексных модулей сдвига G12, G13, G23 не станут практически неизменны (рекомендуемое отличие 1%).
Таким образом, предложенный способ определения упругих и диссипативных характеристик полимерного композиционного материала дает возможность определять диссипативные свойства, а также позволяет повысить точность и достоверность определения жесткостных постоянных ортотропного ПКМ.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения модулей сдвига ортотропных материалов | 1978 |
|
SU697874A1 |
| ТРУБА ГРЕБНОГО ВАЛА ИЗ КОМПОЗИЦИОННОГО МАТЕРИАЛА | 1992 |
|
RU2011605C1 |
| Способ определения динамического модуля сдвига и динамического модуля упругости ортотропного материала | 1981 |
|
SU983508A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК И СОСТАВА ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ В КОНСТРУКЦИЯХ УЛЬТРАЗВУКОВЫМ МЕТОДОМ | 2001 |
|
RU2196982C2 |
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ФРИКЦИОННЫХ МОБИЛЬНЫХ СИСТЕМ | 2012 |
|
RU2517946C2 |
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| Способ определения динамического модуля сдвига | 1988 |
|
SU1525549A1 |
| РЕССОРА ОСНОВНОЙ ОПОРЫ ШАССИ ЛЕГКОГО САМОЛЕТА | 2014 |
|
RU2582591C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ВЯЗКОУПРУГИХ ЖИДКИХ СРЕД И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2411500C1 |
| ИЗМЕРИТЕЛЬНОЕ УСТРОЙСТВО КОРИОЛИСОВА ТИПА | 2012 |
|
RU2526898C1 |
Настоящее изобретение относится к области измерения, в части определения физических свойств материалов, и может быть использовано преимущественно для определения упругих и диссипативных постоянных полимерных композиционных материалов (ПКМ) неразрушающим способом в любых отраслях промышленности. Сущность: осуществляют обработку экспериментальных значений собственных частот и соответствующих этим частотам коэффициентов механических потерь низших тонов изгибных и крутильных колебаний безопорных балок, вырезанных из пластины ортотропного полимерного композиционного материала под углом 0, 45, 90°. В способе реализована возможность определять диссипативные характеристики полимерных композиционных материалов, при этом используется в своей основе процедура последовательных приближений, в соответствии с которой начальные значения динамических модулей упругости в направлении основы и утка армирующего материала, модуля сдвига в плоскости армирования и межслойных модулей сдвига в направлении основы и утка, определенными при помощи собственных частот первого тона изгибных и крутильных колебаний, а также соответствующим им коэффициентов потерь, уточняются при помощи зависимостей, основанных на теории колебаний балки Тимошенко, используя значения собственных частот и соответствующих коэффициентов потерь изгибных колебаний безопорных балок полимерных композиционных материалов более высоких тонов. Технический результат: возможность определения комплексных модулей упругости E11, Е22 и сдвига G12, G13, G23, необходимых для полного описания динамического поведения тонкостенных конструкций, включающие в себя жесткостных и диссипативные характеристики ортотропного ПКМ, имеющие высокую точностью и достоверность. 1 з.п. ф-лы, 2 ил.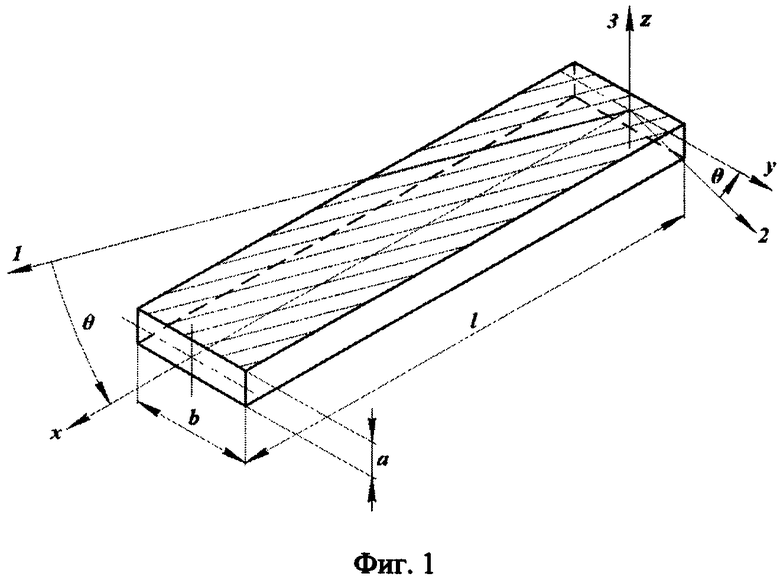
1. Способ определения упругих и диссипативных характеристик композиционного материала, заключающийся в обработке экспериментальных значений собственных частот и соответствующих этим частотам коэффициентов механических потерь низших тонов изгибных и крутильных колебаний безопорных балок, вырезанных из пластины ортотропного полимерного композиционного материала под углом 0, 45, 90°, отличающийся тем, что в способе реализована возможность определять диссипативные характеристики полимерных композиционных материалов, при этом используется в своей основе процедура последовательных приближений, в соответствии с которой начальные значения динамических модулей упругости в направлении основы и утка армирующего материала, модуля сдвига в плоскости армирования и межслойных модулей сдвига в направлении основы и утка, определенными при помощи собственных частот первого тона изгибных и крутильных колебаний, а также соответствующим им коэффициентов потерь, уточняются при помощи зависимостей, основанных на теории колебаний балки Тимошенко, используя значения собственных частот и соответствующих коэффициентов потерь изгибных колебаний безопорных балок полимерных композиционных материалов более высоких тонов.
2. Способ по п. 1, отличающийся тем, что количество безопорных балок равно трем.
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК КОМПОЗИЦИОННОГО МАТЕРИАЛА | 2012 |
|
RU2517989C1 |
| Способ определения динамического модуля сдвига и динамического модуля упругости ортотропного материала | 1981 |
|
SU983508A1 |
| Способ определения физико-механических характеристик ортотропных материалов | 1984 |
|
SU1366912A1 |
| Способ определения модулей сдвига ортотропных материалов | 1978 |
|
SU697874A1 |
| US 4321981 A1, 30.03.1982. | |||
Авторы
Даты
2019-05-14—Публикация
2018-08-22—Подача