Может быть использовано для автоматической (без участия оператора) обработки ионограмм вертикального и наклонного зондирования для определения параметров ионосферы, в первую очередь критических частот и высот слоев F2, F1 и E.
1. Общее описание
Ионосферные слои над заданной точкой земной поверхности традиционно описываются набором параметров, которые необходимы для решения связанных с ионосферой задач коротковолновой связи, спутниковой навигации и других областей. В качестве этих параметров используются максимальные значения плотностей (или плазменных частот) каждого слоя, высоты, на которых достигаются эти максимальные значения и толщины (или полутолщины) слоев [1]. Для мониторинга состояния ионосферы используются различные типы коротковолновых ионозондов - наземные вертикального и наклонного зондирования, а также спутниковые. Выходной информацией ионозондов являются ионограммы, то есть изображения в координатном пространстве «частота - время радиолокационной задержки». Ионосферные параметры определяются по ионограмме либо оператором-обработчиком, либо программным обеспечением, которое распознает характерные черты ионограммы и определяет числовые характеристики, описывающие ионосферные слои.
Ниже описывается новый способ автоматической обработки ионограмм для определения параметров, основанный на оптимизационном подходе [2], широко применяемом для решения задач распознавания образов. Идеальная ионосфера, состоящая из отчетливых слоев математически заданной формы, однозначно описывается набором числовых параметров. Поэтому эти же параметры однозначно задают и ионограмму, которая была бы получена при радиозондировании такой идеальной ионосферы. Распознавание ионограммы заключается в подгонке ионосферных параметров таким образом, чтобы вычисленная по ним модельная ионограмма максимально совпала с экспериментально полученной на ионозонде. Кроме максимальных частот, высот и полутолщин ионосферных слоев E, F1, F2 для более реалистического описания ионосферы можно добавить в набор и другие параметры, например, высоту и максимальную частоту слоя спорадического слоя E и частотное уширение при F-рассеянии.
Для решения оптимизационной задачи используется алгоритм Нельдера-Мида (симплекс-метод) [3]. Если требуется найти набор из n параметров, наиболее точным образом описывающих ионограмму, для входа в алгоритм задается n+1 начальных наборов этих параметров. С математической точки зрения эти наборы параметров представляют собой n+1 точку в n-мерном пространстве параметров. Эти точки представляют собой вершины симплекса (тетраэдра в n-мерном пространстве). В ходе исполнения алгоритма первоначальные вершины сближаются таким образом, что симплекс сжимается к точке, где результат сравнения модельной и реальной ионограмм является наилучшим (оптимизационная функция достигает максимума). Когда расстояние между вершинами по всем осям становится меньше, чем заданная точность определения параметров, происходит выход из цикла алгоритма.
Алгоритм Нельдера-Мида имеет тенденцию ошибочно сходится к локальным минимумам вместо глобального. Для полученных таким образом наборов параметров совпадение модельной и реальной ионограмм будет плохим, однако любое малое изменение любого из параметров приводит к еще большему ухудшению совпадения. Чтобы решить эту проблему, вся область, в которой ищется оптимальный набор параметров, разбивается на подобласти, в каждой из которых создается свой первоначальный симплекс. Для каждого из этих симплексов (их количество может составлять сотни и более) следует выполнить всю последовательность алгоритма. Полученные результаты сравниваются между собой, и наибольший из найденных максимумов считается глобальным. Именно он выдается как конечный результат.
Такой подход является весьма надежным, но требует значительной вычислительной мощности. Для эффективной работы алгоритма требуется организация параллельных вычислений, на современных многопроцессорных серверах или на видеопроцессорах.
Для более эффективной работы алгоритма возможно производить распознавание ионограммы по частям. Например, на первом этапе определяются параметры слоя F2 по высокочастотной части, на втором - проверяется наличие уширения следа из-за F-рассеяния, на третьем - определяется наличие слоя F1 и определяются его параметры по области средних частот, на четвертом - определяются параметры слоев E и Es по нижней части ионограммы. Такой подход позволяет экономить время обработки, если, например, известно заранее, что слои E и F1 отсутствуют.
2. Модификация ионограммы
При использовании алгоритма Нельдера-Мида важнейшее значение имеет правильный выбор оптимизационной функции, в данном случае, численной оценки степени совпадения ионограмм. Можно выбрать в качестве такой функции площадь пересечения следов реальной и модельной ионограммы, но возникает проблема оценки совпадения ионограмм с непересекающимися следами. Даже близко лежащий, но непересекающийся с реальным шаблон, даст такое же нулевое совпадение, как и удалeнный.
Для решения этой проблемы производится модификация реальной ионограммы. При модификации ионограммы след искусственно уширяется, сначала по частоте, потом по высоте, за счет добавления широких крыльев малой интенсивности по частоте и высоте, убывающих при удалении от следа. Пример модифицированной ионограммы (только обыкновенный след) показан на Фигуре 1. Цветовыми оттенками показано добавочное уширение, красный - наибольшая интенсивность, синий - наименьшая.
3. Инициализация симплекса
Для инициализации начального набора симплексов можно использовать климатические ионосферные модели, которые позволяют дать предварительную оценку критических частот, высот и полутолщин следов. Область поиска оптимизационного максимума строится, исходя из этих предварительных оценок, начиная от значений, в несколько раз меньше модельных средних, до значений, в несколько раз больших. Затем область поиска разбивается на ячейки, в которые вписываются первоначальные симплексы. Пределы области поиска, количество ячеек и первоначальных симплексов должны быть подобраны для конкретной реализации алгоритма в зависимости от решаемой и имеющейся вычислительной мощности.
4. Моделирование профиля плазменной частоты
Вертикальный профиль плазменной частоты в ионосфере рассчитывается исходя из заданных параметров как наложение нескольких слоев, имеющих форму параболы, косинуса или любой другой математической функции с выраженным максимумом. Например, в случае косинусоидальных слоев, каждый из слоев будет описываться функцией
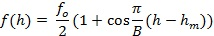
Здесь 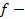 плазменная частота, зависящая от высоты h, и ионосферные параметры, задающие слой:
плазменная частота, зависящая от высоты h, и ионосферные параметры, задающие слой: 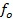 - плазменная частота в максимуме данного слоя,
- плазменная частота в максимуме данного слоя, 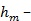 высота максимума электронной концентрации слоя,
высота максимума электронной концентрации слоя, 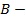 полутолщина слоя.
полутолщина слоя.
5. Моделирование ионограммы
На следующем этапе по заданному профилю рассчитывается ионограмма. Для каждой из заданных частот ионограммы производится пошаговое интегрирование действующей высоты, которая представляет собой время распространения импульса радиоволн t через плазменную среду, умноженное на скорость света c [4]:
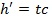 . (6)
. (6)
Импульс распространяется в плазме медленнее скорости в 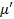 раз, где
раз, где 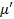 – групповой показатель преломления. Поэтому действующую высоту можно определить как:
– групповой показатель преломления. Поэтому действующую высоту можно определить как:
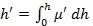 (7)
(7)
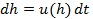 , (8)
, (8)
где 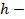 истинная высота,
истинная высота, 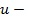 групповая скорость. При численном интегрировании шаг по времени и действующей высоте является равномерным, а по истинной высоте - неравномерным (меньшим в областях меньшей групповой скорости).
групповая скорость. При численном интегрировании шаг по времени и действующей высоте является равномерным, а по истинной высоте - неравномерным (меньшим в областях меньшей групповой скорости).
Для расчета показателя преломления, кроме профиля 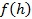 плазменной частоты, определенного в предыдущем параграфе, требуются данные о магнитном поле, которые рассчитываются по модели геомагнитного поля, такой как IGRF.
плазменной частоты, определенного в предыдущем параграфе, требуются данные о магнитном поле, которые рассчитываются по модели геомагнитного поля, такой как IGRF.
Вначале определяется фазовый показатель преломления 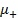 для обыкновенной волны и
для обыкновенной волны и 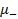 для необыкновенной:
для необыкновенной:
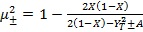 , (9)
, (9)
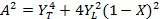 , (10)
, (10)
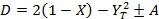 , (11)
, (11)
где 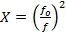 – квадрат отношения плазменной частоты к частоте радиоволны,
– квадрат отношения плазменной частоты к частоте радиоволны, 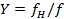 – отношение гирочастоты геомагнитного поля к частоте радиоволны,
– отношение гирочастоты геомагнитного поля к частоте радиоволны, 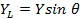 ,
, 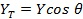 , θ – наклонение геомагнитного поля.
, θ – наклонение геомагнитного поля.
Затем определяется групповой показатель преломления 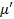 с помощью следующей формулы:
с помощью следующей формулы:
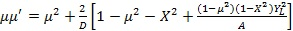 , (12)
, (12)
где 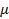 - фазовый показатель преломления.
- фазовый показатель преломления.
Теперь можно определить групповую скорость радиоимпульса
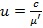 (13)
(13)
и, исходя из шага времени 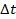 , определить приращения действующей высоты
, определить приращения действующей высоты 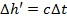 и истинной высоты
и истинной высоты 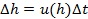 .
.
Прибавив значение приращения истинной высоты к текущему значению, получаем возможность определить по ионосферному профилю значение плазменной частоты на новой высоте, вычислить групповую скорость и снова повторить цикл. Интегрирование происходит до тех пор, пока фазовый показатель преломления 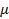 не станет мнимым, т.е., не выполнится условие отражения
не станет мнимым, т.е., не выполнится условие отражения 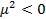 , что дает истинную и действующую высоту отражения радиоволны от ионосферы.
, что дает истинную и действующую высоту отражения радиоволны от ионосферы.
Все действия производятся дважды, для обыкновенной и необыкновенной волн. Зная высоты отражений, можно заполнить матрицы ионограмм, содержащие нули и единицы, для обыкновенной и необыкновенной компонент. Единицами заполняется след, находящийся на действующей высоте отражения и имеющий толщину, которая определяется заданной длительностью радиолокационного импульса ионозонда.
6. Сравнение реальной и модельной ионограмм
Для успешного нахождения модельной ионограммы, наиболее близкой к реальной, необходимо выбрать подходящую функцию сравнения, которая будет выполнять роль оптимизационной функции в алгоритме Нельдера-Мида. Поскольку подбор ионограмм осуществляется в несколько этапов, можно увеличить эффективность алгоритма, выбрав разные функции сравнения для разных этапов. В зависимости от этапа распознавания используется либо метрика заполнения, либо кросс-метрика.
Метрика заполнения определяется, как доля заполнения модельного следа (шаблона) реальным.
Кросс-метрика определяет долю заполнения модельного следа реальным, а затем наоборот - долю заполнения реальной ионограммы модельными следами, после чего полученные значения перемножаются.
На разных этапах целесообразно использовать разные метрики. Например, метрику дополнения можно использовать для определения точного значения критической частоты слоя F по высокочастотной части ионограммы. Во всех остальных случаях, т.е. при определении частотного рассеяния и параметров слоя F1 используется кросс-метрика. При определении критических частот вводится весовой множитель, увеличивающийся с ростом высоты для более точного совпадения асимптотического хвоста следа с шаблоном.
7. Алгоритм Нельдера-Мида
Для поиска минимума функции сравнения был выбран метод Нельдера-Мида прежде всего из-за его эффективности и простоты реализации, а также из-за отсутствия необходимости считать градиенты оптимизационной функции, что позволяет экономить машинное время.
Как описано выше, выбирается 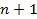 точка
точка 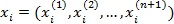 в заданной области поиска. Эти точки являются вершинами симплекса в n-мерном пространстве. В этих точках вычисляются значения функции:
в заданной области поиска. Эти точки являются вершинами симплекса в n-мерном пространстве. В этих точках вычисляются значения функции:
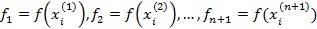 .
.
После этого, применяется алгоритм Нельдера-Мида в следующей форме:
1) Вершины сортируются по значениям функции 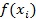 . Выбираются три вершины: наихудшая
. Выбираются три вершины: наихудшая 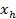 с наименьшим значением функции
с наименьшим значением функции 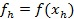 ,
, 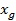 со следующим по величине значением
со следующим по величине значением 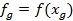 и наилучшая
и наилучшая 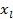 с наибольшим значением функции
с наибольшим значением функции 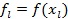 .
.
2) Вычисляется центр тяжести 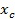 всех вершин симплекса, за исключением вершины
всех вершин симплекса, за исключением вершины 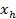 :
: 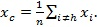
3) Точка 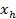 отражается относительно
отражается относительно 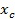 с коэффициентом α=1 в точку
с коэффициентом α=1 в точку 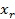 , в которой вычисляется функция:
, в которой вычисляется функция: 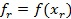 . Координаты новой точки вычисляются по формуле
. Координаты новой точки вычисляются по формуле 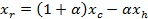 .
.
4) Далее сравнивается значение 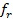 со значениями
со значениями 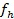 ,
, 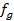 ,
, 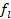 :
:
a) Если 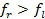 , то производится растяжение. Новая точка
, то производится растяжение. Новая точка 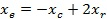 и значение функции
и значение функции 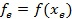 .
.
b) Если 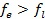 , то точка
, то точка 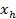 заменяется на
заменяется на 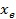 , итерация заканчивается.
, итерация заканчивается.
c) Если 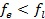 , то точка
, то точка 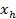 заменяется на
заменяется на 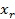 , итерация заканчивается.
, итерация заканчивается.
d) Если 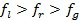 , то точка
, то точка 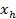 заменяется на
заменяется на 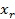 , итерация заканчивается.
, итерация заканчивается.
e) Если 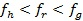 , то обозначения
, то обозначения 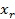 ,
, 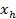 (и соответствующие значения функции) меняются местами, и производится сжатие (шаг 5).
(и соответствующие значения функции) меняются местами, и производится сжатие (шаг 5).
f) Если 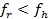 , то производится сжатие (шаг 5).
, то производится сжатие (шаг 5).
5) Производится сжатие: строится точка 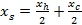 , в которой вычисляется значение
, в которой вычисляется значение 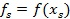 .
.
6) Если 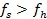 , то точка
, то точка 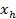 заменяется на
заменяется на 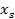 , итерация заканчивается.
, итерация заканчивается.
7) Если 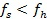 , то производится гомотетическое равномерное сжатие к точке с наименьшим значением
, то производится гомотетическое равномерное сжатие к точке с наименьшим значением 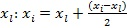 для всех требуемых точек
для всех требуемых точек 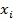 .
.
8) Проверка условия выхода из цикла, выход или переход к новой итерации.
Выход из алгоритма Нельдера-Мида осуществляется в трех случаях:
1) если совершено более заданного максимального числа итераций, но результат не найден;
2) если разница метрик в наилучшей и наихудшей точке меньше заданной;
3) если достигнута заданная точность определения всех параметров, т.е. разница параметров для вершин симплекса Δ не превышает указанной.
В случае успешного поиска, выход производится по условию 3. Остальные условия нужны для более быстрого прекращения расчетов по неудачно выбранным симплексам, которые отнимают процессорное время.
Если ни одна модельная ионограмма не сошлась с реальной или сошлась недостаточно точно (с низкими значениями метрик сравнения), то реальная ионограмма помечается как нераспознанная.
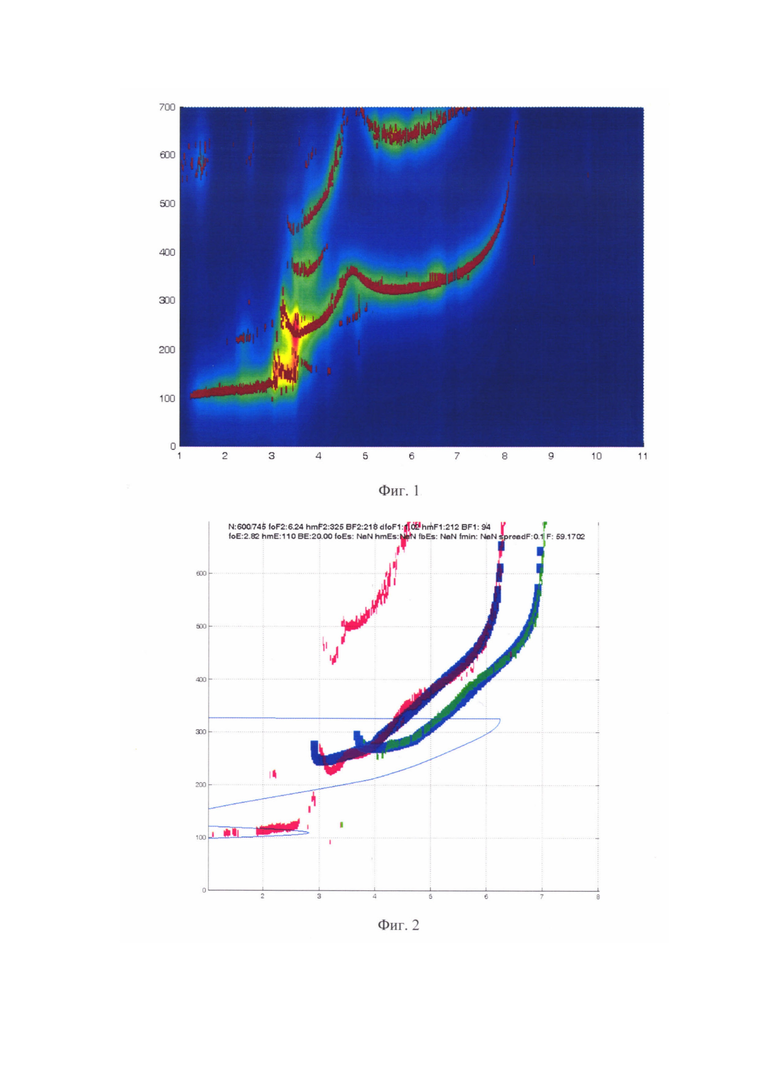
Для иллюстрации на Фигуре 2 показан промежуточный этап подгонки шаблона. Красный - экспериментально полученный след обыкновенной компоненты, зеленый - необыкновенной компоненты, синий прозрачный - ионограмма-шаблон, тонкая синяя линия - вертикальный профиль плазменной частоты, исходя из которого, рассчитана ионограмма.
Литература
1. Руководство URSI по интерпретации и обработке ионограмм / М.: Наука, 1978. - 342°с.
2. R.O. Duda, P.E. Hart, and D.G. Stork. Pattern Classification. John Wiley & Sons, second edition, 1999.
3. Nelder J.A. and Mead R.A Simplex Method for Function Minimization. Computer Journal, 1965, V. 7, p. 308-313.
4. Davies K. Ionospheric radio waves. Blaisdell Publishing Company, 1969.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения критической частоты слоя ионосферной плазмы | 1979 |
|
SU782486A1 |
| Способ однопозиционного определения координат источников радиоизлучений коротковолнового диапазона радиоволн при ионосферном распространении | 2019 |
|
RU2713188C1 |
| Способ местоопределения источников декаметрового радиоизлучения | 2022 |
|
RU2798776C1 |
| Способ радиозондирования ионосферы спиральными электромагнитными волнами | 2017 |
|
RU2662014C1 |
| СПОСОБ ПОЛУЧЕНИЯ ИОНОГРАММ | 2013 |
|
RU2552530C2 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ПАРАМЕТРОВ ЗЕМЛЕТРЯСЕНИЯ | 2003 |
|
RU2256199C2 |
| Способ краткосрочного прогноза землетрясений по данным вертикального зондирования ионосферы с ионозонда | 2017 |
|
RU2676235C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ИОНОСФЕРНЫХ НЕОДНОРОДНОСТЕЙ | 2013 |
|
RU2529355C2 |
| СПОСОБ ЗОНДИРОВАНИЯ ИОНОСФЕРЫ, ТРОПОСФЕРЫ, ГЕОДВИЖЕНИЙ И КОМПЛЕКС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2502080C2 |
| СПОСОБ МЕСТООПРЕДЕЛЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ | 1999 |
|
RU2154281C1 |
Изобретение относится к области ионосферных исследований и может быть использовано для определения параметров ионосферных слоев. Сущность: выполняют подгонку ионограммы-шаблона, определяемой искомыми параметрами, под экспериментально полученную ионограмму путем поиска максимума перекрытия этих двух ионограмм. В качестве шаблона используют ионограмму, полученную решением прямой задачи распространения радиоволн в ионосферной плазме. Максимальное перекрытие находят с помощью оптимизационного алгоритма Нелдера-Мида. Причем подгонка шаблона может быть произведена поэтапно для разных частей ионограммы и слоев ионосферы. Экспериментально полученную ионограмму предварительно модифицируют для облегчения поиска с целью ликвидации резких краев следа, и область параметров разбивают на части, в каждой из которых подгонку выполняют параллельно с целью нахождения глобального максимума. Технический результат: обеспечение оперативного круглосуточного мониторинга параметров ионосферы без вмешательства оператора. 2 ил.
Способ определения параметров ионосферных слоев по ионограммам спутникового, наземного вертикального и наземного наклонного зондирования, заключающийся в подгонке определяемой данными параметрами ионограммы-шаблона под экспериментально полученную ионограмму путем поиска максимума перекрытия этих двух ионограмм, отличающийся тем, что в качестве шаблона используется ионограмма, полученная решением прямой задачи распространения радиоволн в ионосферной плазме, максимальное перекрытие находится с помощью оптимизационного алгоритма Нелдера–Мида, причем подгонка шаблона может производится поэтапно для разных частей ионограммы и слоев ионосферы, экспериментально полученная ионограмма предварительно модифицируется для облегчения поиска с целью ликвидации резких краев следа, и область параметров разбивается на части, в каждой из которых подгонка производится параллельно с целью нахождения глобального максимума.
| К.Г.Цыбуля | |||
| Метод распознавания спутниковых ионограмм на основе алгоритма Нелдера-Мида / Гелиогеофизические исследования, 2016, N15, стр.59-70 | |||
| Способ измерения критической частоты слоя ионосферной плазмы | 1979 |
|
SU782486A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ИОНОСФЕРНЫХ НЕОДНОРОДНОСТЕЙ | 2013 |
|
RU2529355C2 |
Авторы
Даты
2019-08-14—Публикация
2018-10-26—Подача