Область техники
Изобретение относится к способам формирования систем магнитного управления формой и током плазмы с обратной связью в токамаках, а именно к способам, позволяющим имитировать замкнутые системы управления положением, током и формой плазмы с кодом восстановления равновесия плазмы в обратной связи по результатам экспериментальных данных, и может быть применено для стабилизации положения сепаратрисы плазмы при отражении действия возмущений типа малого срыва в токамаках.
Уровень техники
Конструкция токамака (тороидальная камера с магнитными катушками) представляет собой трансформатор, в первичную обмотку которого поступает импульс тока от внешнего источника энергии, а плазменный виток является вторичным витком трансформатора, в котором протекает ток, нагревающий плазму (см. фиг. 1). Также для дополнительного нагрева плазмы используются инжекторы нейтральных атомов и СВЧ электромагнитные колебания. Разного сорта неустойчивости плазмы подавляются сильным тороидальным полем, создаваемой обмоткой тороидального поля.
Установлено, что при достижении соответствия критерию Лоусона [2], когда произведение времени удержания плазмы τ на ее плотность n и температуру T достигает определенного уровня:

начинается реакция синтеза ядер легких элементов с выделением большого количества энергии. Когда происходит слияние ядер дейтерия и трития:

то образуется ядро гелия-4 и нейтрон, который на себе несет 80% энергии синтеза. Ядра гелия-4 остаются в плазме и вносят свою энергию для поддержания термоядерной реакции. Нейтроны поглощаются внешней оболочкой (первой стенкой в реакторе-токамаке), нагревают ее, а затем тепло отводится для дальнейшего превращения его в электроэнергию. Дейтерий-тритиевая смесь (DT) обладает чрезвычайно большой энергоемкостью: 1 грамм DT смеси эквивалентен 10000 литрам нефти.
Наиболее популярными и прогрессивными являются токамаки, имеющие тороидальные аксиально симметричные магнитные конфигурации. Токамаки были предложены в СССР, в Институте атомной энергии им. И.В. Курчатова [1], затем распространились по всему миру [2]. Первый токамак был построен в 1954 г.
В 2009 г. международным сообществом (Европа, Япония, Россия, США, Южная Корея, Китай и Индия) начато строительство первого в мире токамака-реактора ИТЭР (ITER, International Thermonuclear Experimental Reactor) во Франции (г. Кадараш).
Для управления формой плазмы, т.е. расположением в пространстве границы плазмы, необходимо по магнитным измерениям вне плазмы восстанавливать распределение плотности тороидального тока плазмы, полоидального магнитного потока и положение сепаратрисы плазмы. При этом настоящая ситуация такова, что не существует определенного сложившегося стандарта на системы управления плазмой, хотя эти системы и развивались в течение пятидесяти лет. Это связано с тем, что все токамаки имеют различные полоидальные системы, различные параметры и различные коллективы, разрабатывающие системы управления плазмой в конкретных токамаках с различными представлениями и степенью квалификации в этой области. Плазма (ионизованный газ) представляет собой многосвязный нелинейный объект с распределенными и переменными во времени параметрами, подверженный различного вида неконтролируемым возмущениям, динамика которого не изучена в полной мере в виду его чрезвычайной сложности. По этой причине данный объект можно отнести к сверхсложным объектам, так как требуется управлять супербольшим количеством заряженных частиц (ионов и электронов) в ограниченном объеме с плотностью порядка 1014 частиц/см3.
Более того, в вытянутых по вертикали токамаках, в частности, в ИТЭР, из-за неустойчивости плазмы по вертикали и ограниченности управляющих воздействий область управляемости в пространстве состояний модели плазмы ограничена и относительно невелика. Из-за этого неконтролируемые возмущения могут в любой момент вывести систему из области управляемости, что приведет к потере системой управления устойчивости.
В токамаке-реакторе типа ITER (Франция) или термоядерной электростанции типа DEMO (Япония) потеря устойчивости системой управления плазмой ведет к аварии: прожиганию камеры токамака и выбросу энергии высокотемпературной плазмы наружу. Выходом из этой ситуации является разработка таких систем управления плазмой, которые бы могли надежно противостоять плазменным возмущениям и гарантированно удерживать плазму в области управляемости, обеспечивая необходимую точность управления.
На основании сказанного, изучение плазмы в токамаках как объекта управления сложной физической природы, построение ее моделей по экспериментальным данным и с использованием законов физики плазмы, разработка методов достоверной диагностики плазмы по магнитным измерениям вне плазмы, разработка, исследование и применение в физическом эксперименте эффективных систем автоматического управления плазмой в условиях наличия неконтролируемых внешних воздействий, наличия неполной возможной информации, ограниченности ресурсов управления и множественности критериев оценки управления, развитие методики изучения плазмы, методики построения и моделирования систем диагностики и управления плазмой представляет собой важную и актуальную задачу.
Все вышеуказанные токамаки имеют общее сходство, состоящее в том, что они являются вытянутыми по вертикали, но все они отличаются друг от друга полоидальными системами, т.е. выполнением конструкций систем обмоток, создающих полоидальные поля. При этом известны обобщенные схемы магнитного управления положением, током и формой плазмы в токамаках.
Для моделирования таких систем применяют полные модели плазмы в токамаке, основанные на нелинейных плазмо-физических кодах типа TSC, CORSICA (США), TOSCA (Япония), MAXFEA (Италия), PET, DINA (Россия). Данные коды для получения равновесия плазмы решают уравнение Града-Шафранова [6, 7]. Это дифференциальное уравнение в частных производных второго порядка в цилиндрических координатах с учетом аксиальной симметрии плазмы, связывающее распределение плотности тороидального тока плазмы Jϕ с распределением создаваемого им полоидального потока ψ, которое выглядит следующим образом:

Здесь плотность тороидального тока плазмы Jϕ выражена через газокинетическое давление плазмы р и функцию F, пропорциональную полоидальному току плазмы:

На действующих токамаках для определения положения плазмы в контуре его стабилизации используется довольно простая магнитная диагностика, основанная на изменении внешнего измеряемого магнитного потока при смещении плазменного шнура. Для определения же сигналов формы плазмы применяются коды восстановления равновесия плазмы, которые могут определять распределение полоидального потока, тороидального тока и положение сепаратрисы.
Равновесие плазмы в токамаке описывается распределением полоидального магнитного потока ψ(r,z) в цилиндрической системе координат (r,ϕ,z) с учетом аксиальной симметрии плазмы. Полоидальный поток ψ в точке Р определяется как магнитный поток на радиан горизонтальной окружности с центром на оси токамака, проходящей через точку Р и ограничивающей площадь S (фиг. 2) [8]:

где  - вектор индукции магнитного поля,
- вектор индукции магнитного поля, 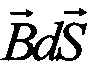 - скалярное произведение индукции и нормали элемента поверхности. Из определения полоидального потока следует, что он должен обращаться в ноль на аксиальной оси и на бесконечности (граничные условия).
- скалярное произведение индукции и нормали элемента поверхности. Из определения полоидального потока следует, что он должен обращаться в ноль на аксиальной оси и на бесконечности (граничные условия).
Граница плазмы (сепаратриса) в полоидальной плоскости (вертикальной плоскости, проходящей через ось z) может быть найдена как наибольшая замкнутая линия уровня полоидального потока. В случае, если сепаратриса касается камеры токамака, конфигурацию плазмы называют лимитерной. Если плазма не касается стенок токамака, то говорят, что плазма находится в диверторной фазе. Диверторная фаза также характеризуется наличием на сепаратрисе Х-точки, в которой магнитное поле обращается в ноль. Сепаратриса имеет ветви, которые «входят» в первую стенку токамака или диверторные пластины. Вдоль этих ветвей из плазмы выходят примеси и поглощаются диверторными пластинами. Таким образом, для определения формы плазмы необходимо найти распределение полоидального потока.
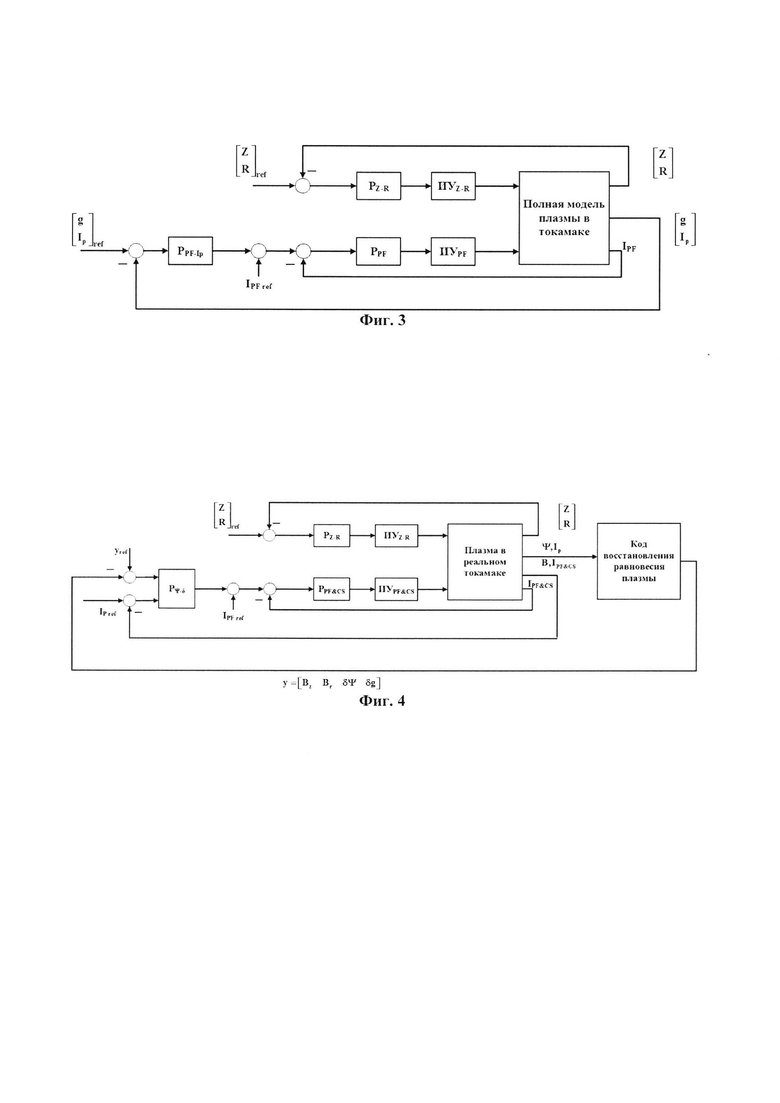
Из уровня техники известен способ моделирования систем магнитного управления плазмой в токамаках, в котором сигналы для управления формой плазмы берут непосредственно из полных нелинейных моделей плазмы в токамаках, поскольку коды моделирования плазмы позволяют это сделать при моделировании равновесия плазмы по уравнению Града-Шафранова (Докука В.Н., Кавин А.А., В.Э. Лукаш, М.М. Соколов, P.P. Хайрутдинов, В.А. Хайрутдинова, «Численное моделирование управления плазмой в модернизированном токамаке Т-15», «ВАНТ», Сер. «Термоядерный синтез», 2014, т. 37, вып. 3, с. 56-70). Для удержания плазмы в магнитном поле токамака применяются обмотки полоидального поля, каждую из которых подключают к исполнительному устройству, представляющему собой либо управляемый многофазный тиристорный выпрямитель, либо инвертор напряжения, либо инвертор тока [3] (фиг. 3). Ко входам исполнительных устройств подключают регуляторы PZ-R, PPF, через которые замыкают обратную связь для управления вертикальным Z и R горизонтальным положением плазмы или токами в обмотках полоидального поля и центрального соленоида (внутренний каскад управления). Под обратной связью понимают в терминах настоящей заявки поступление выходного сигнала объекта управления на его вход с некоторым преобразованием, осуществляемым регулятором и исполнительным устройством. Внешний каскад обратной связи образует регулятор для управления током плазмы Ip и зазорами g между сепаратрисой плазмы (магнитной поверхностью, внутри которой удерживается плазма) и первой стенкой токамака.
В данном способе не используют реконструкцию формы плазмы, а именно, восстановление распределения полоидального потока плазмы, плотности тороидального тока плазмы и расположения сепаратрисы. Данный способ реализуют в отсутствие кода восстановления равновесия плазмы в обратной связи, что приводит к недостаточной полноте систем моделирования магнитного управления плазмой в токамаке и отсутствию полной точности восстановления сепаратрисы плазмы.
Известен способ использования кода восстановления непосредственно на самом токамаке, отраженный на блок-схеме, представленной на фиг. 4. (Q.P. Yuan, B.J. Xiao, «Plasma current, position and shape feedback control on EAST», «Nuclear Fusion», №53, 2013, http://dx.doi.org/10.1088/0029-5515/53/4/043009).
При управлении током и формой плазмы в реальном времени на действующих токамаках с вытянутой по вертикали плазмой для определения положения сепаратрисы плазмы применяют коды восстановления равновесия плазмы в реальном времени в замкнутых системах управления (фиг. 4) (см., например, [9-11]). В этих системах на вход кода восстановления поступают сигналы с магнитной диагностики токамака: интегрированные сигналы с магнитных петель, пропорциональные магнитному потоку в заданных точках Ψ, сигналы о магнитном поле В с магнитных зондов (датчиков Мирнова), сигналы с поясов Роговского о токе плазмы Ip, токах в центральном соленоиде ICS и в обмотках полоидального поля IPF. С кода восстановления равновесия на регулятор тока и формы плазмы подаются сигналы о составляющих поля в предполагаемом расположении Х-точки Bz и Br, полоидального потока Ψ и смещении сепаратрисы δg.
На основании уравнения (1) задачу стационарной идентификации (восстановления) равновесия плазмы можно сформулировать, в частности, следующим образом при условии, что в токамаке имеются только магнитные петли [8].
Требуется найти область плазмы S, распределение тороидального тока Jϕ в ней и создаваемое им распределение полоидального потока, удовлетворяющие уравнению (1) и ограничениям вида:




где Ip и Ψi - измеренные значения полного тока плазмы и полоидального потока на магнитных петлях, М - количество измеряющих поток петель.
Функции р и F в (1) неизвестны, но зависят только от полоидального потока. Ввиду этого, составляющие плотности тороидального тока плазмы Jϕ могут быть аппроксимированы функциями полоидального потока:


Для решения задачи идентификации равновесия используется итерационный метод Пикара. На каждой итерации плотность тока плазмы аппроксимируется линейной комбинацией базисных функций ƒ(ψ) от полоидального потока, полученного на предыдущей итерации. Полоидальный поток в этом случае вычисляется как сумма, определяемая выбранными базисными функциями:
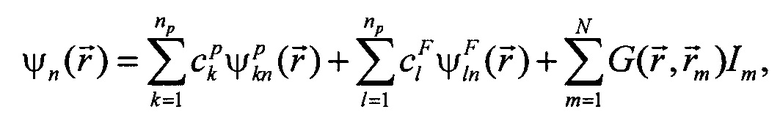
где
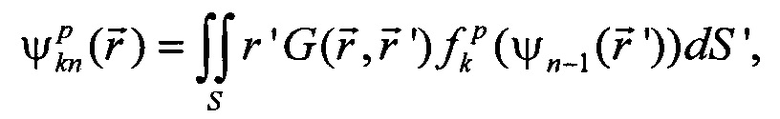

Здесь G - функция Грина для уравнения (1), имеющая физический смысл полоидального потока в точке  , создаваемого единичным бесконечно тонким кольцевым током с координатами
, создаваемого единичным бесконечно тонким кольцевым током с координатами 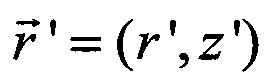 , распределение плотности тока которого имеет вид дельта функции
, распределение плотности тока которого имеет вид дельта функции 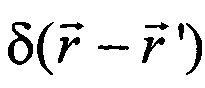 , и выражаемая через эллиптические интегралы первого K и второго рода Е [12]:
, и выражаемая через эллиптические интегралы первого K и второго рода Е [12]:
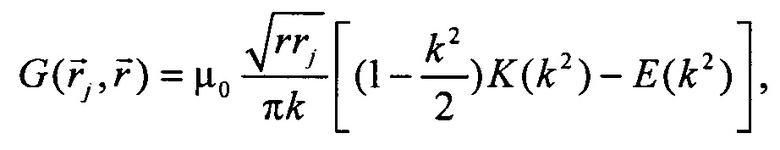

Коэффициенты  ,
, 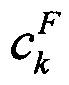 и токи в катушках Im подбираются на каждой итерации через минимизацию суммы квадратов разностей между рассчитанными и измеренными токами и потоками:
и токи в катушках Im подбираются на каждой итерации через минимизацию суммы квадратов разностей между рассчитанными и измеренными токами и потоками:

Здесь  и
и 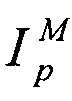 - рассчитанный и измеренный полные токи плазмы,
- рассчитанный и измеренный полные токи плазмы,  - измеренные токи в обмотках токамака,
- измеренные токи в обмотках токамака,  - погрешности измерений полоидального потока, тока плазмы и тока в обмотках соответственно.
- погрешности измерений полоидального потока, тока плазмы и тока в обмотках соответственно.
Наиболее близким способом к заявленному изобретению является способ создания модели систем магнитного управления плазмой в токамаках (фиг. 3) (Митришкин Ю.В., Коростелев А.Я., Докука В.Н., Хайрутдинов P.P. «Синтез и моделирование двухуровневой системы магнитного управления плазмой токамака-реактора», «Физика плазмы», 2011, том 37. №4. с. 307-349). Модель, полученная в соответствии с указанным способом, не использует кода восстановления равновесия плазмы в обратной связи. Сигналы для управления формой плазмы берутся непосредственно из полных нелинейных моделей плазмы в токамаках, поскольку коды моделирования плазмы позволяют это сделать при моделировании равновесия плазмы по уравнению Града-Шафранова.
Недостатком такого способа является недостаточная полнота моделирования за счет отсутствия кода восстановления распределения полоидального потока плазмы, плотности тороидального тока плазмы и расположения сепаратрисы, в результате чего при моделировании не учитывается диагностика формы плазмы. Это не дает возможности получить детальное представление о работе полной системы управления формой и током плазмы с кодом восстановления равновесия плазмы в обратной связи.
Раскрытие изобретения
Технической проблемой заявленного изобретения является преодоление технических недостатков, присущих аналогам, что ведет к необходимости создания способа содания модели магнитного управления плазмой в токамаке обратной связью, реализуемой при помощи кода восстановления, обеспечивающей максимально достоверное распределение полоидального потока плазмы.
Техническим результатом заявленного изобретения является повышение достоверности имитации процессов магнитного управления в токамаке, что позволяет, проводя эксперименты на созданной модели, избежать необходимости неоправданной корректировки положения плазмы в реальных токамаках и, как следствие, способствует повышению надежности эксплуатации реальных токамаков за счет использования результатов изобретения.
Заявляемый способ может быть применен для стабилизации положения сепаратрисы плазмы при отражении действия возмущений типа малого срыва в токамаках.
Поставленная задача решается тем, что способ формирования модели магнитного управления формой и током плазмы с обратной связью в токамаке, включающий имитацию плазмы в токамаке, с исполнительными устройствами, контурами управления положением плазмы и токами в обмотках полоидального поля, моделирование изменения положения сепаратрисы плазмы на диверторной фазе плазменного разряда с использованием многомерного регулятора формы и тока плазмы, включенного в обратную связь, в процессе которого осуществляют изменение значений выходных сигналов регулятора формы и тока плазмы в каждый момент времени в пределах, соответствующих относительно малому отклонению положения сепаратрисы плазмы от заданного, а также измеряют векторы токов в обмотках полоидального поля и центрального соленоида токамака, сигналов на магнитных петлях и зондах, тока плазмы, по полученным значениям которых формируют восстановление равновесия плазмы в токамаке с использованием кода восстановления, для применения его в обратной связи, согласно техническому решению, при формировании обратной связи используют переменные входные и выходные параметры плазмы в токамаке,
при этом входными параметрами являются значения векторов напряжения на обмотках полоидального поля и центрального соленоида токамака, обеспечивающих магнитную связь с плазмой, а
выходные параметры в каждый момент времени представляют собой одномерный массив значений изменения векторов тока плазмы, токов в обмотках полоидального поля и центрального соленоида, сигналы на магнитных петлях и зондах, сигналы, пропорциональные вертикальному и горизонтальному смещению магнитной оси плазмы или центра тока плазменного шнура,
полученный одномерный массив значений суммируют с аналогичными значениями массива сценарных сигналов, соответствующих заданному расположению сепаратрисы плазмы на диверторной фазе плазменного разряда в каждый момент времени, в результате чего формируют входные сигналы кода восстановления равновесия плазмы, основанного на решении нелинейной обратной краевой задачи, а на выходе кода восстановления получают сигналы, пропорциональные входным сигналам регулятора формы и тока плазмы, которые подают на вход регулятора и тем самым замыкают обратную связь, в результате чего получают полную модель управления формой плазмы в каждый момент времени. Выходные сигналы регулятора тока и формы плазмы соответствуют значениям токов в обмотках полоидального поля и центрального соленоида. Выходные сигналы регулятора формы и тока плазмы подают на вход каскадов управления токами в обмотках полоидального поля и центрального соленоида токамака.
Заявляемое изобретение, а также технические решения, являющиеся аналогами, поясняются следующими чертежами. При этом
На фиг. 1 - схема токамака с управляющими катушками полоидальных магнитных полей и центрального соленоида (первичная секционированная обмотка),
на фиг. 2 - схема расположения полоидального потока в токамаке,
на фиг. 3 - блок-схема, известная из аналога (Докука В.Н., Кавин А.А., В.Э. Лукаш, М.М. Соколов, P.P. Хайрутдинов, В.А. Хайрутдинова, «Численное моделирование управления плазмой в модернизированном токамаке Т-15», «ВАНТ», Сер. «Термоядерный синтез», 2014, т. 37, вып. 3, с. 56-70),
на фиг. 4 - блок-схема системы магнитного управления плазмой в токамаках, известная из наиболее близкого аналога, связанного с реальным физическим экспериментом,
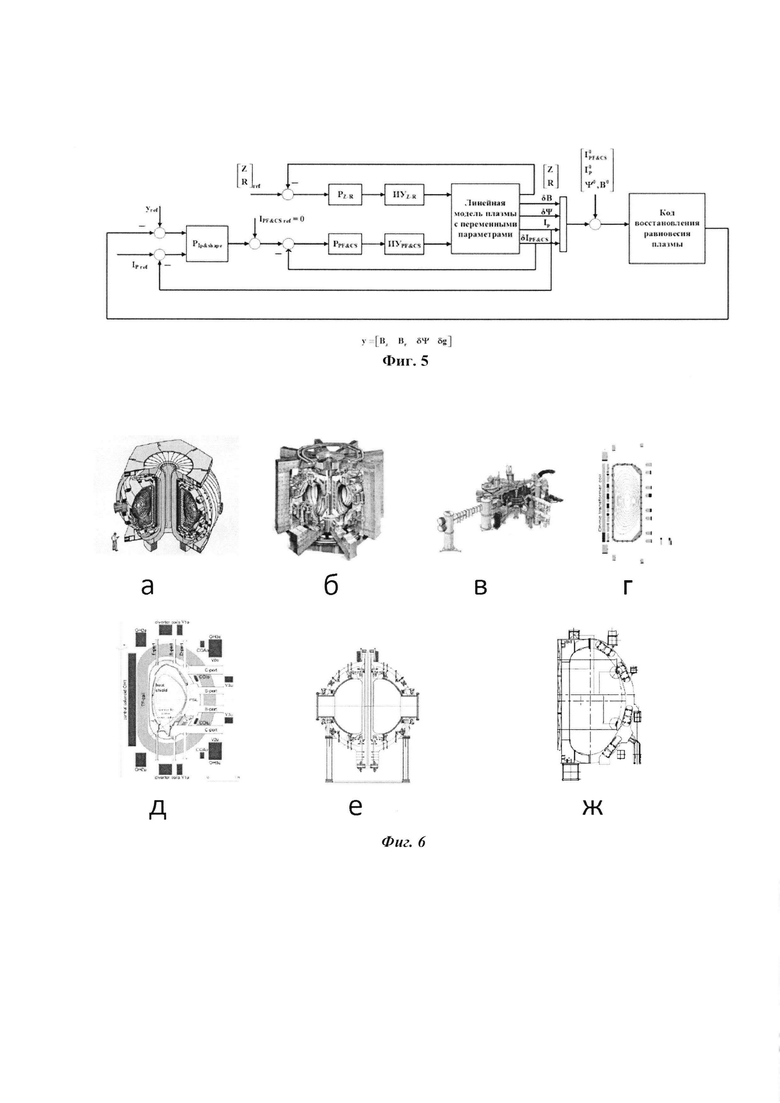
на фиг. 5 - блок-схема способа согласно заявленному изобретению, на фиг. 6 - вертикальные разрезы и поперечные сечения наиболее адаптированных в решении задач управления плазмой зарубежных токамаков, где а) - DIII-D (1.66 м, 0.67 м, 1986, США), б) - JET (3.00 м, 1.25-2.1 м, 1992, Англия), в) - JT-60U (3.40 м, 1.00 м, 1991, Япония), г) - TCV (0.88 м, 0.25-0.7 м, 1992, Швейцария), д) - ASDEX Upgrade (1.65 м, 0.5-0.8 м, 1991, Германия), е) - Глобус-М (0.36 м, 0.24 м, 1999, Россия), ж) Т-15 (1.48 м, 0.67 м, 2018, Россия). В маркировках токамаков указаны год их пуска (или планируемый год пуска), большой и малый радиусы.
На фиг. 7 - вертикальные сечения действующих токамаков, где а) - сечение конструкции токамака EAST (копия ITER, 1.75 м, 0.43 м, 2006, Китай), б) - сечение сооружаемого токамака-реактора ITER (6.20 м, 2.00 м, планируемый год пуска 2025, Франция). В маркировках токамаков указаны год их пуска, большой и малый радиусы.
На фиг. 8 - линии уровня восстановленного распределения полоидального потока в токамаке ГЛОБУС-М и точки измерения: а - полоидального потока на сепаратрисе; 6 -зазоров между первой стенкой и сепаратрисой,
На фиг. 9 - эволюция формы и положения плазмы, восстановленные для разряда №31648 токамака Глобус-М,
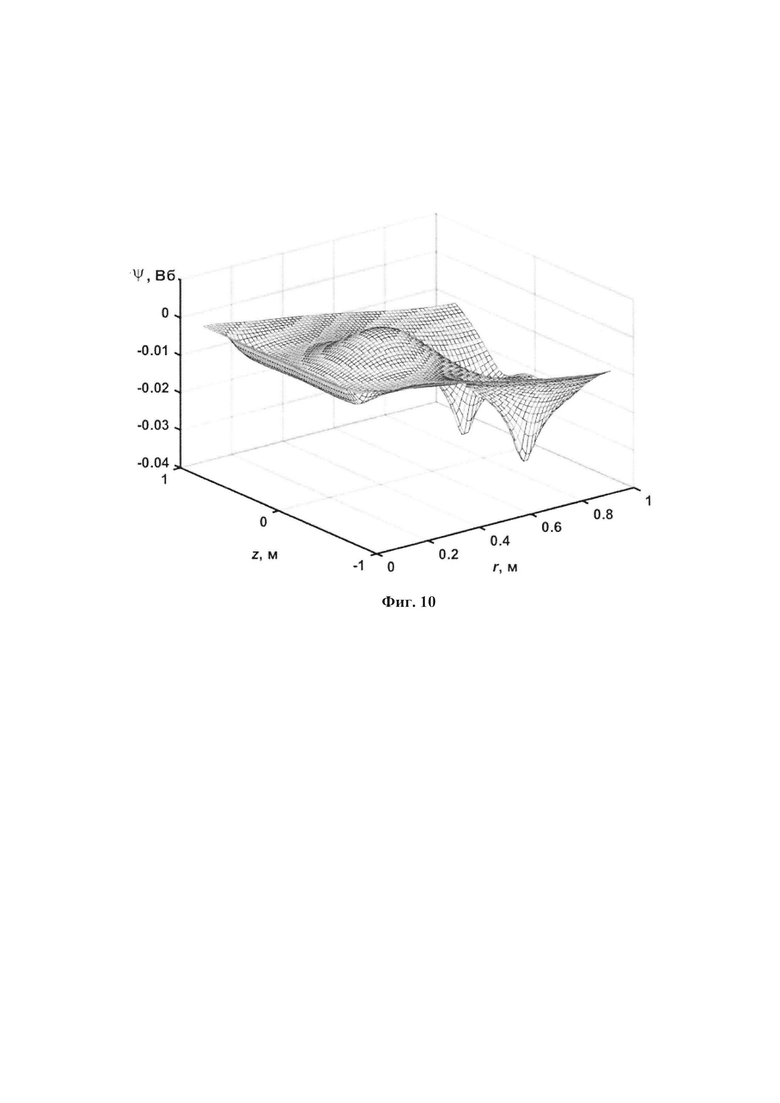
На фиг. 10 - Восстановленное распределение полоидального потока для момента времени t=180 мс разряда №31648 токамака Глобус-М,
На фиг. 11 - восстановленное распределение плотности тороидального тока плазмы для момента времени t=180 мс разряда №31648 токамака Глобус-М,
На фиг. 12 - Граница плазмы для разряда №31648 (t=0,19),
На фиг. 13 - сравнение сепаратрис, полученных методом филаментов и кодом DINA на модельном разряде,
На фиг. 14 - блок-схема системы управления полоидальными потоками для диверторной фазы разряда,
На фиг. 15 - Результат работы системы управления: а - отклонение компонент магнитного поля в X точке от нуля; 6 - разность полоидального потока в Х-точке от полоидального потока в точках желаемого расположения границы плазмы,
На фиг. 16 - эволюция границы плазмы: а - 0.18 с; б - 0.185 с; в - 0.19 с; г - 0.195 с и желаемое расположение границы плазмы.
Позициями на фиг. 1, где представлена известная конструкция токамака, обозначены:
1 - первичная обмотка;
2 - магнитопровод,
3 - обмотка тороидального поля;
4 - тороидальное поле;
5 - обмотка полоидального поля;
6 - полоидальное поле;
7 - винтовое магнитное поле;
8 - плазменный виток.
Заявленное изобретение основано на использовании динамической модели плазмы с переменными входными параметрами, при этом соответствующим образом обработанные выходные сигналы данной модели используют в качестве входных сигналов для кода восстановления равновесия.
Все расчеты для обоснования предложенного способа выполнены с использованием системы численно-математического моделирования MatLab и системы моделирования динамических систем Simulink.
В отсутствии плазмы в токамаке динамика вектора токов I в катушках полоидального поля и элементах вакуумной камеры токамака (горизонтальных кольцах) описывается векторно-матричным дифференциальным уравнением Кирхгофа, связывающим изменение вектора-столбца магнитного потока Ψс через контура проводников с диагональной матрицей активных сопротивлений проводников R и вектором приложенных к ним напряжений U:
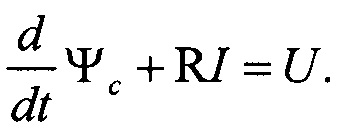
При этом вектор потоков Ψс определяется произведением постоянной матрицы индуктивностей проводников

и вектора токов I, и поэтому дифференциальное уравнение Кирхгофа является линейным:

При добавлении в систему подвижного контура плазмы с током Ip, вектор магнитных потоков Ψс нелинейно зависит от положения магнитной оси плазмы  и формы плазмы, определяемых распределениями полоидального потока ψ и плотности тока плазмы Jϕ, реконструкции которых посвящены предыдущие разделы.
и формы плазмы, определяемых распределениями полоидального потока ψ и плотности тока плазмы Jϕ, реконструкции которых посвящены предыдущие разделы.
От формы и положения плазмы также зависит магнитный поток

через контур плазмы, определяемый собственной индуктивностью плазмы Mpp и током через плазму, а также матрицей взаимных индуктивностей между плазмой и катушками управления (катушками полоидального поля) 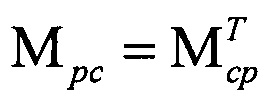 и токами через эти катушки. Матрицы индуктивностей, связанных с плазмой, выражаются из восстановленных распределения плотности тока, формы и положения плазмы при помощи функций Грина, например, для Mpc так:
и токами через эти катушки. Матрицы индуктивностей, связанных с плазмой, выражаются из восстановленных распределения плотности тока, формы и положения плазмы при помощи функций Грина, например, для Mpc так:

Эти формулы определяют связь линейных моделей с восстановленными распределениями потока и тока плазмы и приводят к решению полной согласованной задачи идентификации плазмы.
Для получения линейной модели приняты следующие физические допущения:
 масса и сопротивление плазмы пренебрежимо малы, поэтому они полагаются равными нулю,
масса и сопротивление плазмы пренебрежимо малы, поэтому они полагаются равными нулю,
 считается, что плазма не меняет свою форму при смещении по вертикали и горизонтали (концепция «жесткой модели» [15]),
считается, что плазма не меняет свою форму при смещении по вертикали и горизонтали (концепция «жесткой модели» [15]),
 изменение полного тока плазмы не сопровождается изменением профиля распределения плотности тока.
изменение полного тока плазмы не сопровождается изменением профиля распределения плотности тока.
Запишем теперь линеаризованные уравнения Кирхгофа в отклонениях от равновесных распределений ψ и Jϕ. Первое уравнение описывает контуры катушек и элементов камеры токамака, а второе - контур плазмы:

Поскольку масса плазмы принимается равной нулю, действующая на плазму сила в полоидальной плоскости
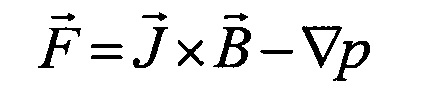
или в координатном виде

в любой момент должна быть равна нулю. Это равенство должно выполняться и при отклонениях от равновесных распределений ψ и J по положению магнитной оси плазмы и по токам в проводящих элементах:

Выразим из (3) отклонение  через вектор изменения токов в катушках и элементах камеры
через вектор изменения токов в катушках и элементах камеры 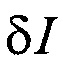 , подставим
, подставим  в уравнение (2), выразим из второго уравнения полученной системы скорость изменения тока плазмы
в уравнение (2), выразим из второго уравнения полученной системы скорость изменения тока плазмы 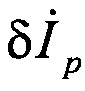 и подставим ее в первое уравнение. В итоге уравнение линейной модели примет вид:
и подставим ее в первое уравнение. В итоге уравнение линейной модели примет вид:
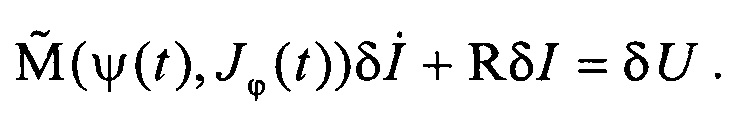
Матрица эффективных индуктивностей  в этой формуле зависит от равновесия плазмы и находится по формуле
в этой формуле зависит от равновесия плазмы и находится по формуле

В конечном виде линейная модель плазмы в пространстве состояний запишется в виде


Матрицы А и В выражаются через матрицы индуктивностей и сопротивлений по формулам

где Е - единичная матрица, N - количество обмоток токамака, V - количество горизонтальных кольцевых элементов, на которые разбита вакуумная камера.
В качестве выходных сигналов у модели используются отклонения токов в 8-и катушках управления от равновесных значений, горизонтальное и вертикальное смещения положения магнитной оси плазмы, изменение тока плазмы, приращения полоидального потока  в наборе из 10-ти точек Р1-Р10 на границе плазмы (фиг. 8а) и приращения δg 6-ти зазоров между границей плазмы и вакуумной камерой (фиг. 8б). Выходы модели как отклонения от восстановленного равновесия токов в активных и пассивных структурах, положения магнитной оси плазмы, тока плазмы, потоков и расстояний сепаратрисы и первой стенки представляются в одном векторе:
в наборе из 10-ти точек Р1-Р10 на границе плазмы (фиг. 8а) и приращения δg 6-ти зазоров между границей плазмы и вакуумной камерой (фиг. 8б). Выходы модели как отклонения от восстановленного равновесия токов в активных и пассивных структурах, положения магнитной оси плазмы, тока плазмы, потоков и расстояний сепаратрисы и первой стенки представляются в одном векторе:

и связаны с состояниями δI матрицей С:

Здесь  - вектор-столбец магнитного потока, создаваемого в горизонтальных контурах, проходящих через точки Р1-Р10 (фиг. 8а),
- вектор-столбец магнитного потока, создаваемого в горизонтальных контурах, проходящих через точки Р1-Р10 (фиг. 8а),  - матрица взаимных индуктивностей между данными контурами, катушками полоидального поля и элементами камеры, а
- матрица взаимных индуктивностей между данными контурами, катушками полоидального поля и элементами камеры, а  - вектор-столбец взаимных индуктивностей между рассматриваемыми контурами и плазмой.
- вектор-столбец взаимных индуктивностей между рассматриваемыми контурами и плазмой.
Сущность изобретения состоит в использовании кода восстановления равновесия плазмы в обратную связь системы управления током и формой плазмы токамака.
Для получения разряда в вакуумной камере токамака заранее определяется сценарий, представляющий собой программные изменения токов в центральном соленоиде ICS и обмотках полоидального тока IPS, чтобы они давали желаемую магнитную конфигурацию плазмы в токамаке. Когда производится восстановление равновесия плазмы по экспериментальным данным, то используются также сигналы с магнитных петель и зондов, которые были в разряде и которые также можно отнести к сценарным сигналам (фиг. 5). Поскольку линейная модель, как описано выше, получается при малых отклонениях от сценарных сигналов, то тогда, если на линейную модель подавать входные сигналы, как и в эксперименте, формируемые такими же каскадами обратной связи (фиг. 5), а выходные сигналы модели 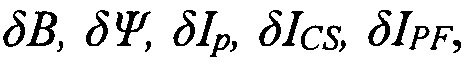 соответствующие малым отклонениям от сценарных сигналов, складывать с соответствующими сценарными сигналами
соответствующие малым отклонениям от сценарных сигналов, складывать с соответствующими сценарными сигналами 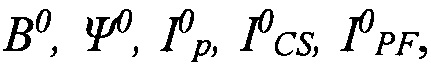 то получится полная имитация работы объекта управления в эксперименте.
то получится полная имитация работы объекта управления в эксперименте.
Полученная сумма выходных сигналов модели и сценарных сигналов будет соответствовать выходным сигналам эксперимента, по которым можно восстановить равновесие плазмы в токамаке. Код восстановления равновесия рассчитывает распределение полоидального потока, по которому можно получить вариации сигналов потока в нужных точках δΨ, отклонения зазоров δg в заданных точках на сепаратрисе, горизонтальную и вертикальную составляющую поля Br, Bz в Х-точке. Эти сигналы подаются на вход регулятора формы и тока плазмы 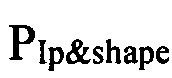 . Таким образом происходит замыкание обратной связи в системе управления током и формой плазмы с кодом восстановления равновесия плазмы внутри замкнутого контура управления. Это является новым предложением по сравнению с известными техническими решениями систем магнитного управления плазмой в токамаках при их компьютерном моделировании (фиг. 3).
. Таким образом происходит замыкание обратной связи в системе управления током и формой плазмы с кодом восстановления равновесия плазмы внутри замкнутого контура управления. Это является новым предложением по сравнению с известными техническими решениями систем магнитного управления плазмой в токамаках при их компьютерном моделировании (фиг. 3).
В частном случае реализации заявленного изобретения способ применяют в токамаках, вытянутых по вертикали.
Выходные сигналы регулятора могут соответствовать значениям токов в обмотках полоидального поля и центрального соленоида.
Выходные сигналы регулятора формы и тока плазмы возможно подавать на вход каскадов управления токами в обмотках полоидального поля и центрального соленоида токамака.
В качестве выходных переменных величин линейной модели устанавливают, например, ток плазмы, ток в обмотках полоидального поля и центральном соленоиде, сигналы на магнитных петлях и зондах.
Используют код восстановления равновесия плазмы, основанный, например, на уравнении Града-Шафранова
Согласно фиг. 1, токамак содержит первичную обмотку 1, внутри которой расположен магнитопровод 2, обмотка (катушка) 3 тороидального поля 4, обмотки (катушки) 5 полоидального поля 6 для управления положением и формой плазменного шнура. В первичную обмотку 1 поступает импульс тока от внешнего источника энергии, образуется результирующее винтовое магнитное поле 7, а плазменный виток 8 является вторичным витком трансформатора, в котором протекает ток, нагревающий плазму. Для дополнительного нагрева плазмы используются инжекторы нейтральных атомов и СВЧ электромагнитные колебания. Неустойчивости плазмы подавляются сильным тороидальным полем 4, создаваемым обмоткой 3.
На фиг. 3-4 представлены блок-схемы, иллюстрирующие аналоги заявленного изобретения (описаны в разделе описания «уровень техники»).
На фиг. 5 представлена блок-схема, иллюстрирующая заявленный способ. Блок-схема, согласно заявленному изобретению, содержит многомерный регулятор  для управления током плазмы Ip и зазорами g между сепаратрисой плазмы (магнитной поверхностью, внутри которой удерживается плазма) и первой стенкой токамака, соединенный с регулятором токов в обмотках полоидального поля и центрального соленоида токамака
для управления током плазмы Ip и зазорами g между сепаратрисой плазмы (магнитной поверхностью, внутри которой удерживается плазма) и первой стенкой токамака, соединенный с регулятором токов в обмотках полоидального поля и центрального соленоида токамака  , выход которого соединен с исполнительным устройством, охваченным отрицательной обратной связью, и регулятор положения магнитной оси плазмы PZ-R (для управления вертикальным Z и R горизонтальным положением плазмы), выход которого соединен с исполнительным устройством ИУz-r, также охваченными отрицательной обратной связью. Выходы исполнительных устройств соединены со входами линейной модели.
, выход которого соединен с исполнительным устройством, охваченным отрицательной обратной связью, и регулятор положения магнитной оси плазмы PZ-R (для управления вертикальным Z и R горизонтальным положением плазмы), выход которого соединен с исполнительным устройством ИУz-r, также охваченными отрицательной обратной связью. Выходы исполнительных устройств соединены со входами линейной модели.
А именно, выходы исполнительных устройств соединены со входами блока вычисления линейной модели, один векторный выход которого последовательно соединен с регулятором PZ-R через сумматор с отрицательным входом, при этом на другой вход сумматора подаются задающие воздействия Z и R, определяющие требуемое положение плазмы.
другой векторный выход - последовательно соединен со входом блока кода восстановления,
один скалярный выход соединен через отрицательный вход сумматора с регулятором тока и формы плазмы 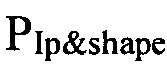 , выходы которого являются задающими воздействиями для каскада управления токами в обмотках полоидального поля и центрального соленоида,
, выходы которого являются задающими воздействиями для каскада управления токами в обмотках полоидального поля и центрального соленоида,
векторный выход, являющийся подвектором общего векторного выхода линейной модели, последовательно соединен через отрицательный вход сумматора со входом многомерного регулятора 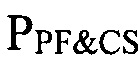 , выход которого подключен ко входу исполнительного устройства ИУPF, а на другой вход данного сумматора подаются задающие воздействия по токам в обмотках полоидального поля и центрального соленоида,
, выход которого подключен ко входу исполнительного устройства ИУPF, а на другой вход данного сумматора подаются задающие воздействия по токам в обмотках полоидального поля и центрального соленоида,
полный вход блока восстановления равновесия состоит из суммы выходного векторного сигнала линейной модели и соответствующих сценарных сигналов, представляющих собой вектор токов в обмотках полоидального поля и центрального соленоида, тока плазмы, сигналов с магнитных петель и зондов.
а третий выход - последовательно соединен с регулятором 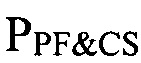 .
.
Выходы блока кода восстановления соединены со входом многомерного регулятора  тока и формы плазмы через отрицательный вход сумматора, на другой вход которого подаются задающие воздействия по зазорам между сепаратрисой плазмы и первой стенкой.
тока и формы плазмы через отрицательный вход сумматора, на другой вход которого подаются задающие воздействия по зазорам между сепаратрисой плазмы и первой стенкой.
Блок-схема включает в себя контур управления положением плазмы, который содержит исполнительное устройство ИУZ-R и регулятор положения плазмы PZ-R, контур управления токами в обмотках полоидального поля, который содержит исполнительное устройство ИУPF и регулятор  , являющийся внутренним каскадом управления током и формой плазмы, контур управления формой плазмы, включающий в себя код восстановления равновесия плазмы и регулятор управления током и формой плазмы
, являющийся внутренним каскадом управления током и формой плазмы, контур управления формой плазмы, включающий в себя код восстановления равновесия плазмы и регулятор управления током и формой плазмы 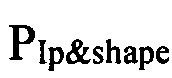 , причем все перечисленные контуры включают в себя линейную модель плазмы в токамаке с переменными выходными сигналами, что представляет взаимодействие данных замкнутых контуров между собой через линейную модель плазмы.
, причем все перечисленные контуры включают в себя линейную модель плазмы в токамаке с переменными выходными сигналами, что представляет взаимодействие данных замкнутых контуров между собой через линейную модель плазмы.
Для измерения сигналов тока плазмы, токов в обмотках полоидального поля и центральном соленоиде в эксперименте используются пояса Роговского, сигналы на магнитных петлях интегрируются для получения значений магнитного потока в местах их расположения.
Осуществление изобретения
На вход многомерного регулятора  подают значения задающих референсных сигналов
подают значения задающих референсных сигналов 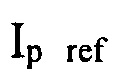 и
и 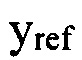 , заранее определенных в соответствии с выбранным сценарием плазменного разряда.
, заранее определенных в соответствии с выбранным сценарием плазменного разряда.
В качестве выходных сигналов регулятора получают значения токов в обмотках полоидального поля и центрального соленоида, которые направляют на регулятор  , выходные сигналы с которого подают на исполнительное устройство, где вычисляют векторы напряжения на обмотках полоидального поля и центрального соленоида токамака в каждый момент времени и подают полученные сигналы на вход линейной модели плазмы, причем указанные обмотки входят в линейную модель плазмы в токамаке, поскольку они магнитно связаны с плазмой и воздействуют на ее размещение в пространстве путем изменения магнитной конфигурации.
, выходные сигналы с которого подают на исполнительное устройство, где вычисляют векторы напряжения на обмотках полоидального поля и центрального соленоида токамака в каждый момент времени и подают полученные сигналы на вход линейной модели плазмы, причем указанные обмотки входят в линейную модель плазмы в токамаке, поскольку они магнитно связаны с плазмой и воздействуют на ее размещение в пространстве путем изменения магнитной конфигурации.
При этом задают значения выходных и выходных сигналов регулятора  в пределах малого отклонения положения сепаратрисы плазмы от заданного положения, соответствующего плазменному разряду диверторной фазы в каждый момент времени.
в пределах малого отклонения положения сепаратрисы плазмы от заданного положения, соответствующего плазменному разряду диверторной фазы в каждый момент времени.
По полученным входным сигналам с использованием динамической линейной модели плазмы вычисляют значения изменения векторов токов в обмотках полоидального поля и центрального соленоида токамака  сигналов на магнитных петлях, пропорциональных изменению магнитного потока в заданных точках δΨ, сигналы об изменении магнитного поля δB с магнитных зондов, значение тока плазмы Ip. Затем полученный на выходе линейной модели одномерный массив значений сигналов в данный момент времени
сигналов на магнитных петлях, пропорциональных изменению магнитного потока в заданных точках δΨ, сигналы об изменении магнитного поля δB с магнитных зондов, значение тока плазмы Ip. Затем полученный на выходе линейной модели одномерный массив значений сигналов в данный момент времени  суммируют с массивом аналогичных значений сценарных сигналов
суммируют с массивом аналогичных значений сценарных сигналов  соответствующих заданному расположению сепаратрисы плазмы на диверторной фазе плазменного разряда в каждый момент времени. После чего, полученный массив сигналов, соответствующий суммированным значениям, подают на вход кода восстановления равновесия плазмы. На выходе кода восстановления получают значения сигналов, пропорциональных входным сигналам регулятора формы и тока плазмы и соответствующие положению равновесия плазмы, которые подают на вход многомерного регулятора
соответствующих заданному расположению сепаратрисы плазмы на диверторной фазе плазменного разряда в каждый момент времени. После чего, полученный массив сигналов, соответствующий суммированным значениям, подают на вход кода восстановления равновесия плазмы. На выходе кода восстановления получают значения сигналов, пропорциональных входным сигналам регулятора формы и тока плазмы и соответствующие положению равновесия плазмы, которые подают на вход многомерного регулятора 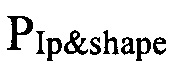 , цикл замыкается.
, цикл замыкается.
Таким образом реализуют обратную связь с внедренным в нее кодом восстановления равновесия плазмы по значениям сигналов, получаемых в каждый момент времени на выходе линейной модели плазмы, суммированных с соответствующими сценарными сигналами, причем полученная сумма является входным многомерным сигналом кода восстановления равновесия плазмы, выход которого, представляющий собой смещение выбранных точек сепаратрисы относительно заданных значений, замыкает обратную связь, поступая на вход регулятора тока и формы плазмы.
Примеры конкретного выполнения
Пример 1
На фиг. 9 приведены изображения положения и магнитной конфигурации плазмы в разные моменты времени, иллюстрирующие изменение формы и положения плазмы, восстановленной для разряда №31648 токамака Глобус-М. Магнитные конфигурации получены через каждые 10 мс, начиная со 150-й сек разряда. В моменты времени 150, 160, 170 сек в плазме существует лимитерная конфигурация, а в моменты времени 180, 190, 200 мс - диверторная конфигурация с одной верхней Х-точкой. Таким образом, использование в обратной связи кода восстановления равновесия плазмы позволяет проследить в течение всего разряда эволюцию магнитной конфигурации при восстановлении ее в дискретные моменты времени.
Пример 2
На фиг. 10 и 11 показаны восстановленное распределение полоидального потока и соответствующее ему распределение плотности тока плазмы в трехмерном масштабе в координатах  и
и  . При численном моделировании использовалась квадратная сетка размером 64×64. Эти трехмерные изображения восстановленных равновесий иллюстрируют работоспособность созданного авторами изобретения кода восстановления равновесия плазмы методом итераций Пикара по экспериментальным данным токамака Глобус-М. Код использовался в обратной связи для моделирования системы управления формой и током плазмы.
. При численном моделировании использовалась квадратная сетка размером 64×64. Эти трехмерные изображения восстановленных равновесий иллюстрируют работоспособность созданного авторами изобретения кода восстановления равновесия плазмы методом итераций Пикара по экспериментальным данным токамака Глобус-М. Код использовался в обратной связи для моделирования системы управления формой и током плазмы.
Пример 3
Ниже приведен частный пример создания системы управления формой и током плазмы с кодом восстановления равновесия плазмы методом подвижных филаментов с использованием заявленного изобретения.
Для описания физических процессов в токамаке обычно используется цилиндрическая система координат (r, ϕ, z) в предположении, что любая физическая величина не зависит от угла ϕ при аксиальной симметрии токамака. Для описания электромагнитных явлений в камере токамака вводится функция полоидального потока как полоидального потока на один радиан, проходящего через круг, на границе которого лежит точка Р:

Основной идеей метода филаментов (англ. filament - нить, волосок, волокно) является аппроксимация распределенного тока плазмы суммой токов от точечных источников (бесконечно тонких кольцевых витков, лежащих в горизонтальной плоскости) [16]:

где Jϕ (r) - тороидальная плотность тока плазмы, r - радиус-вектор на плоскости (r, z), Im - ток в m-ом филаменте, rm - координата m-го филамента, М - число филаментов, δ(r-rm) - дельта-функция.
В результате такой замены распределение полоидального потока от плазмы на плоскости (r, z), может быть найдено как сумма распределений полоидального потока от точечных источников:

где 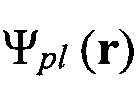 - распределение полоидального потока от плазмы, Im - ток в m-ом филаменте, G(rm, r) - функция Грина, [7] явный вид которой имеет вид:
- распределение полоидального потока от плазмы, Im - ток в m-ом филаменте, G(rm, r) - функция Грина, [7] явный вид которой имеет вид:

где μ0 - магнитная постоянная, K, Е - эллиптические интегралы первого и второго рода,  .
.
Аналогично выписываются распределения полоидального потока, создаваемые катушками управления и пассивными структурами - элементами вакуумной камеры:

где 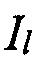 ,
,  - токи в катушках и элементах камеры, L - число катушек, V - число элементов вакуумной камеры.
- токи в катушках и элементах камеры, L - число катушек, V - число элементов вакуумной камеры.
В итоге суммарное распределение полоидального потока на плоскости (r, z) включает в себя три суммы:

Метод филаментов подразумевает определение расположений филаментов и токов, протекающих в них, таким образом, чтобы норма отклонения созданного филаментами магнитного сигнала (магнитная индукция или магнитный поток) и значения тока в филаментах от измеренных величин была минимальной.
На действующей установке Глобус-М во время сценария измеряются значения магнитного потока в 21-й точке расположения магнитных петель, закрепленных по периметру вакуумной камеры. Также во время плазменного разряда определяются ток плазмы и ток плазмы в сумме с током по вакуумной камере с помощью поясов Роговского.
Исходя из перечисленных данных, составляется функционал:
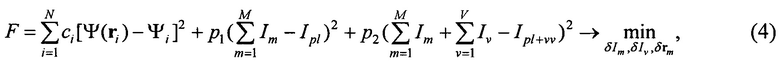
который необходимо минимизировать по значениям координат филаментов, токов, протекающих в них, а также токов в элементах вакуумной камеры, т.к. при произвольном разбиении камеры на кольцевые элементы, токи, протекающие в этих элементах, неизвестны. В функционале F величины ci, p1, p2 - нормирующие коэффициенты, N=21 - число магнитных петель, Ψi - измеренное значение потока i-ой магнитной петлей,  - измеренные значения тока плазмы и тока плазмы в сумме с током по вакуумной камере. Все измеряемые величины зависят от времени и в эксперименте регистрируются с некоторым дискретным шагом, поэтому равновесие плазмы восстанавливается для какого-то выбранного момента времени, т.к. для каждого момента времени будет иметься свое восстановленное равновесие.
- измеренные значения тока плазмы и тока плазмы в сумме с током по вакуумной камере. Все измеряемые величины зависят от времени и в эксперименте регистрируются с некоторым дискретным шагом, поэтому равновесие плазмы восстанавливается для какого-то выбранного момента времени, т.к. для каждого момента времени будет иметься свое восстановленное равновесие.
Для упрощения процедуры минимизации токи и функция Грина линеаризуются:
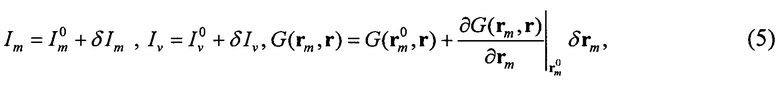
где  - начальные значения токов в филаментах и элементах камеры, определяемые как соответствующий полный ток, деленный на количество элементов,
- начальные значения токов в филаментах и элементах камеры, определяемые как соответствующий полный ток, деленный на количество элементов,  - начальные положения филаментов. Минимизация функционала теперь проводится по отклонениям токов
- начальные положения филаментов. Минимизация функционала теперь проводится по отклонениям токов  и
и 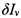 и отклонениям координат
и отклонениям координат  .
.
При использовании (5) формулу (4) при отбрасывании величин второго порядка малости можно привести к виду:
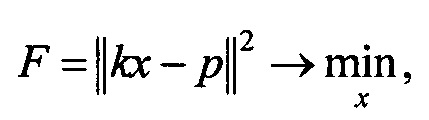
где 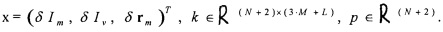
Нормальное псевдорешение системы kx=p находится посредством сингулярного разложения. Результат решения системы представлен на фиг. 12. Корректность восстановления равновесия была подтверждена на плазмо-физическом коде DINA (разработка ГНЦ РФ ТРИНИТИ) (Лукаш В.Э., Докука В.Н., Хайрутдинов P.P. Программно-вычислительный комплекс ДИНА в системе MATLAB для решения задач управления плазмой токамака. ВАНТ, серия: Термоядерный синтез, вып. 1, 2004, с. 40-49). На фиг. 13 представлено сравнение границ плазмы, полученных с помощью метода филаментов и с помощью кода DINA.
По аналогии с известной методикой получения линейных моделей (известной, например, из источников Mitrishkin Y.V., Korenev P.S., Kartsev N.M., and Patrov M.I. Plasma shape control with a linear model for Globus-M tokamak. 41st Conference on Plasma Physics, Berlin, Germany, June 23-27, 2014, P4.054. Walker M., Humphreys D. Valid coordinate systems for linearized plasma shape response models in tokamaks, Fusion Science and Technology, 2006, vol. 50, no. 4, pp. 473-489) были получены линейные динамические модели с учетом плазмы и вакуумной камеры следующего вида:

где

L, V - число катушек и элементов вакуумной камеры,

 - вектор-столбец, состоящий из приращений токов в катушках и элементах камеры,
- вектор-столбец, состоящий из приращений токов в катушках и элементах камеры,

- вектор-столбец, состоящий из приращений напряжений в управляющих катушках.
Вектор выхода

включает в себя сдвиги плазмы по вертикали и горизонтали, приращение полного тока плазмы и приращения тока в L управляющих катушках, а также 21 значение приращений полоидального тока в местах расположения магнитных петель. В соответствии с этим, матрица С имеет размерность (2+1+L+21)×(L+V).
На действующей установке Глобус-М уже имеется разработанная и внедренная система стабилизации положения плазмы токамака Глобус-М. Для целей управления положением плазмы зарезервированы катушки HFC (Horizontal Field Coils), VFC (Vertical Field Coils). Разрабатываемые блоки выделены на фиг. 14 серым цветом. В первую очередь это И-регулятор тока плазмы, который необходим для поддержания тока плазмы на определенном уровне во время квазистационарной стадии разряда в токамаке. Данный регулятор получает измеряемые данные о токе плазмы и через отрицательную обратную связь подключается к каскаду многофазного тиристорного выпрямителя напряжения катушки CS (Central Solenoid), так как именно эта катушка фактически управляет током плазмы по трансформаторному принципу.
Для управления формой плазмы предлагается следующий алгоритм. По выходным данным с линейной модели (значения полоидального потока в 21-ой точке расположения магнитных петель, ток плазмы, ток по вакуумной камере, ток в катушках) алгоритм восстановления рассчитывает r-,z-компоненты магнитного поля в месте желаемого расположения Х-точки, а также разность в полоидальном потоке между Х-точкой и точками желаемого расположения границы плазмы. Задачей многомерного регулятора KMIMO(s) является сведение данных величин к нулю, поскольку известно, что магнитное поле в Х-точке для любого разряда равно нулю, а граница плазмы определяется линей равного уровня полоидального потока. Данный регулятор синтезирован методом Н∞ оптимизации (loop shaping), и обеспечивает запас робастной устойчивости ε=0.485. Результат моделирования приведен на фиг. 15, 16.
Использованная литература
1. Artsimovich L.A. Tokamak devices // Nuclear Fusion, Vol. 12. 1972. P. 215-252.
2. Wesson J. Tokamaks. Oxford: Clarendon Press, 1997.
3. Под ред. Чиженко И.М. Справочник по преобразовательной технике. - Киев: «Техника», 1978. - 447 с.
4. Митришкин Ю.В., Коростелев А.Я., Докука В.Н., Хайрутдинов P.P. Синтез и моделирование двухуровневой системы магнитного управления плазмой токамака-реактора // Физика плазмы. 2011. Том 37. №4. С. 307-349 (прототип).
5. Докука В.Н., Кавин А.А., В.Э. Лукаш, М.М. Соколов, P.P. Хайрутдинов, В.А. Хайрутдинова. Численное моделирование управления плазмой в модернизированном токамаке Т-15. ВАНТ. Сер. Термоядерный синтез, 2014, т. 37, вып. 3, с. 56-70 (аналог).
6. Шафранов В.Д. Равновесие плазмы в магнитном поле // Вопросы теории плазмы. 1963. Вып.2. С. 92-131.
7. Ariola М., Pironti A. Magnetic control of tokamak plasmas. Springer-Verlag, 2008.
8. Коренев П.С., Митришкин Ю.В., Патров М.И. Реконструкция равновесного распределения параметров плазмы токамака по внешним магнитным измерениям и построение линейных плазменных моделей. Мехатроника, автоматизация и управление. Том 17, №4, 2016, с. 254-265. DOI: 10.17587/mau.17.254-266.
9. M.L. WALKER, D.A. HUMPHREYS, J.A. LEUER, J.R. FERRON, and B.G. PENAFLOR. Implementation of model-based multivariable control on DIII-D, GA-A23468, 2000 (аналог).
10. V. Mertens, G. Raupp, and W. Treutterer. Chapter 3: Plasma Control in ASDEX Upgrade. Fusion Science and Technology, Vol.44, Nov. 2003, pp.593-604 (аналог).
11. Q.P. Yuan, B.J. Xiao, Z.P. Luo, M.L.Walker, A.S. Welander, A. Hyatt, J.P. Qian1, R.R. Zhang, D.A. Humphreys, J.A. Leuer, R.D. Johnson, B.G. Penaflor and D. Mueller. Plasma current, position and shape feedback control on EAST. Nucl. Fusion 53, 2013, 043009, 10pp (аналог).
12. Абрамовиц M., Стиган И. Справочник по специальным функциям. - М.: Наука, 1979. 832 с.
13. Hofmann F., Tonetti G. Fast identification of plasma boundary and X-points in elongated tokamaks, Nuclear Fusion, 1988, vol. 28, no. 3, pp. 519-522.
14. Mitrishkin Y.V., Korenev P.S., Kartsev N.M., and Patrov M.I. Plasma shape control with a linear model for Globus-M tokamak. 41st Conference on Plasma Physics, Berlin, Germany, June 23-27, 2014, P4.054.
15. Walker M., Humphreys D. Valid coordinate systems for linearized plasma shape response models in tokamaks, Fusion Science and Technology, 2006, vol. 50, no. 4, pp. 473-489.
16. Зотов И., Персиянов И., Сычугов Д. Контроль границы плазмы в токамаке в режиме реального времени // Вопросы атомной науки и техники серия Термоядерный синтез. - 2004. - №4. - С. 44-54.
17. Лукаш В.Э., Докука В.Н., Хайрутдинов P.P. Программно-вычислительный комплекс ДИНА в системе MATLAB для решения задач управления плазмой токамака. ВАНТ, серия: Термоядерный синтез, вып.1, 2004, с. 40-49.
McFarlane D. and Glover K., Robust Controller Design Using Normalized Coprime Factor Plant Description. Lecture Notes in Control and Information Sciences, no 138, 1989. Springer-Verlag.







Изобретение относится к способу формирования систем магнитного управления формой и током плазмы с обратной связью в токамаках и может быть применено для стабилизации положения сепаратрисы плазмы при отражении действия возмущений типа малого срыва в токамаках. При формировании обратной связи используют переменные входные и выходные параметры плазмы в токамаке. Входными параметрами являются значения векторов напряжения на обмотках полоидального поля и центрального соленоида токамака, обеспечивающих магнитную связь с плазмой. Выходные параметры в каждый момент времени представляют собой одномерный массив значений изменения векторов тока плазмы, токов в обмотках полоидального поля и центрального соленоида, сигналы на магнитных петлях и зондах, сигналы, пропорциональные вертикальному и горизонтальному смещению магнитной оси плазмы или центра тока плазменного шнура. На основании указанных параметров получают полную модель управления формой плазмы в каждый момент времени. Техническим результатом является создание модели управления плазмой с кодом восстановления, сокращение времени отладки системы управления на токамаке, термоядерном реакторе-токамаке или термоядерной электростанции на основе токамака, а также сокращение времени эксперимента. 2 з.п. ф-лы, 16 ил.
1. Способ формирования модели магнитного управления формой и током плазмы с обратной связью в токамаке, включающий
имитацию плазмы в токамаке с исполнительными устройствами, контурами управления положением плазмы и токами в обмотках полоидального поля,
моделирование изменения положения сепаратрисы плазмы на диверторной фазе плазменного разряда с использованием многомерного регулятора формы и тока плазмы, включенного в обратную связь, в процессе которого
осуществляют изменение значений выходных сигналов регулятора формы и тока плазмы в каждый момент времени в пределах, соответствующих относительно малому отклонению положения сепаратрисы плазмы от заданного, а также
измеряют векторы токов в обмотках полоидального поля и центрального соленоида токамака, сигналов на магнитных петлях и зондах, тока плазмы, по полученным значениям которых формируют восстановление равновесия плазмы в токамаке с использованием кода восстановления, для применения его в обратной связи,
отличающийся тем, что при формировании обратной связи используют переменные входные и выходные параметры плазмы в токамаке,
при этом входными параметрами являются значения векторов напряжения на обмотках полоидального поля и центрального соленоида токамака, обеспечивающих магнитную связь с плазмой, а
выходные параметры в каждый момент времени представляют собой одномерный массив значений изменения векторов тока плазмы, токов в обмотках полоидального поля и центрального соленоида, сигналы на магнитных петлях и зондах, сигналы, пропорциональные вертикальному и горизонтальному смещению магнитной оси плазмы или центра тока плазменного шнура,
полученный одномерный массив значений суммируют с аналогичными значениями массива сценарных сигналов, соответствующих заданному расположению сепаратрисы плазмы на диверторной фазе плазменного разряда в каждый момент времени, в результате чего формируют входные сигналы кода восстановления равновесия плазмы, основанного на решении нелинейной обратной краевой задачи, а на выходе кода восстановления получают сигналы, пропорциональные входным сигналам регулятора формы и тока плазмы, которые подают на вход регулятора и тем самым замыкают обратную связь, в результате чего получают полную модель управления формой плазмы в каждый момент времени.
2. Способ моделирования по п. 1, отличающийся тем, что выходные сигналы регулятора тока и формы плазмы соответствуют значениям токов в обмотках полоидального поля и центрального соленоида.
3. Способ моделирования по п. 2, отличающийся тем, что выходные сигналы регулятора формы и тока плазмы подают на вход каскадов управления токами в обмотках полоидального поля и центрального соленоида токамака.
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ХАРАКТЕРИСТИК СПЕКТРАЛЬНЫХ ЛИНИЙ ПЛАЗМЫ В РЕАКТОРЕ-ТОКАМАКЕ | 2016 |
|
RU2633517C1 |
| СИСТЕМА УПРАВЛЕНИЯ ЭЛЕКТРОННОЙ ПЛОТНОСТЬЮ ПЛАЗМЫ НА УСТАНОВКАХ ТИПА ТОКАМАК | 2017 |
|
RU2654518C1 |
| Способ очистки от пыли и охлаждения горячих газов | 1961 |
|
SU144824A1 |
| WO 2012064767 A1, 18.05.2012. | |||
Авторы
Даты
2019-10-04—Публикация
2018-09-17—Подача