Область техники
Настоящее изобретение относится к быстродействующему способу выполнения булевых операций для построения трехмерных геометрических моделей из первичных геометрических объектов для системы автоматизированного проектирования, компьютерной графики, системы объемного моделирования и системе поверхностного моделирования, которые широко применяются в проектировании изделий, производстве и моделировании. Машиностроение, отрасли культуры и спорта - везде, где существуют геометрические формы, могут обладать приложениями CAD/CG.
Уровень техники
Компьютерное аппаратное обеспечение является настолько высокоразвитым, что даже обычный персональный компьютер можно применять для установки и запуска системы CAD/CG, причем это аппаратное обеспечение обычно обладает функциями осуществления булевых операций, включающих И, ИЛИ и НЕ. Персональные компьютеры включают устройства ввода, такие как мышь и клавиатура, системный блок, монитор и принтер. Программное обеспечение включает геометрические и не геометрические функции. На фиг. 1 показаны основные компоненты PC и на фиг. 2A-2D изображена обычная архитектура системы программного обеспечения CAD/CG.
Булевы операции обеспечивают процесс построения сложных объемных геометрических объектов из различных первичных геометрических форм в CAD/CG или объемных моделирующих системах. Ли применил булевы операции для деления поверхности (Lee US Patent No. 6,07,555).
Булевы операции могут базироваться на конструктивной блочной геометрии (CSG) для записи первичных геометрических объектов и последовательности операций с иерархической структурой данных, в то время как граничное представление (B-REP), которое рассматривают как более гибкий способ, поддерживающий больше типов геометрических объектов подобно расширенным геометриям (Gursoz, 1991).
Настоящее изобретение представляет пять (5) команд выполнения булевой операции: объединение, пересечение, исключение, вычитание и деление, которые оказывают непосредственное влияние на треугольники, полученные из геометрических граней, применяемых для функций визуализации, и не требуют конструктивной блочной геометрии и граничного представления для структуры данных. Структуры данных, заданные в настоящем изобретении, представляют собой несколько простых классов, алгоритмы, включенные в настоящее изобретение, лаконичны и просты для воплощения и пять (5) команд предоставляют возможность пользователю создавать различные геометрические модели не только выбором типов геометрических объектов, но также заданием их граней. На фиг. 3 представлены параллелепипед с 6 гранями и сфера с разными гранями, дающие хорошие результаты.
Хотя пять (5) команд предназначены для объемного моделирования и поверхностного моделирования, команда отсечения поверхности представляет альтернативу для поверхностного моделирования и она опознает, скрыта ли грань, другим способом.
Настоящее изобретение представляет структуры данных и алгоритмы, отличающиеся от CSG и B-REP, и алгоритмы, включенные в настоящее изобретение, содержат пересечения треугольник-треугольник, разбиение треугольников разделительными линиями, определение, является ли грань скрытой, и перестройку треугольников для формирования трехмерной геометрической модели.
Описание изобретения
Настоящее изобретение предоставляет набор шагов, составляющих способ для выполнения булевых операций, которые применяются для построения сложных геометрических моделей и непосредственно влияют на треугольники, полученные в результате разбиения геометрических граней, применяемых в качестве данных визуализации, посредством аппаратного обеспечения компьютера и функций визуализации подобно библиотекам OpenGL. Геометрическая форма, например сфера, конус, цилиндр, параллелепипед, треугольные грани, экструдированный или изогнутый объект и участок поверхности, разбивается на треугольники с целью составления набора, обозначенного как TriangleSet, для вывода на экран. Когда для выполнения булевой операции выбирают две геометрические формы, смежные треугольники добавляются к каждому треугольнику в TriangleSet для образования другого набора для каждого из форм, BlOpTriangleSet.
Вторым шагом булевой операции, описанной в настоящем изобретении, является поиск и построение линий пересечения между наборами треугольников. Это начинается с нахождения пары пересекающихся треугольников: эта система строит наименьший ограничивающий параллелепипед, ориентированный по координатным осям, для каждого треугольника и проверяет, пересекаются ли два ограничивающих параллелепипеда, чтобы принять решение, если необходимо вычислить пересечение ребро-треугольник. Как только точка(и) пересечения ребро-треугольник попадает во внутрь треугольника, эта система завершает поисковую задачу и сохраняет координаты точки в наборе линий пересечения.
Чтобы продолжить текущую линию пересечения, в этом способе прочерчиваются смежные треугольники и вычисляются точки пересечения ребро-треугольник, пока линия пересечения не замкнется.
Третьим шагом булевой операции, которая описана в настоящем изобретении, является разбиение треугольников. Каждый сегмент линий пересечения ссылается на два (2) треугольника, каждый из которых имеет по меньшей мере одну разделительную линию, которая содержит один или несколько сегментов, делящих треугольник на три (3) или несколько более мелких треугольников. После разбиения треугольников исходные треугольники удаляют, а те более мелкие треугольники добавляют в BlOpTriangleSet.
На четвертом шаге булевой операции по настоящему изобретению принимается решение о том, является ли каждый треугольник скрытым или видимым. Если треугольник загораживается другими треугольниками, то он скрывается. Треугольник видимый означает, что он находится вне другой фигуры.
На пятом шаге булевой операции по настоящему изобретению происходит перестроение треугольников: некоторые из них должны быть удалены, а некоторые нужно собрать вместе, при этом существует пять (5) вариантов перестроения.
На последнем шаге булевой операции по настоящему изобретению BlOpTriangleSet отображается на TriangleSet.
Продвижение упомянутой команды отсечения поверхности также содержит шесть (6) шагов. Сначала данная система отображает поверхность на BlOpTriangleSet и один из ее контуров отсечения на экструдированную форму для формирования BlOpTriangleSet. Шаги второй (2), третий (3), шестой (6) такие же, как и в булевых операциях. На шаге четвертом осуществляется проверка, находится ли треугольник слева или справа от контура отсечения, чтобы принять решение о необходимости его сохранения. Функция перестроения, шаг пятый (5), уничтожает только левую сторону или правую сторону треугольников, когда система отсекает поверхность.
Краткое описание чертежей
На фиг. 1 показаны основные компоненты персонального компьютера, который в основном содержит системный блок, входные устройства, включающие мышь и клавиатуру, монитор и принтер. На персональном компьютере может быть запущена высокоразвитая система CAD/CG.
На фиг. 2А-2D описана структура программного обеспечения, в котором система CAD/CG/Geometric Modeling применяет булевы операции и отсечение поверхности для построения геометрических моделей.
На фиг. 3 показано, что разные грани могут давать разные результаты, даже когда типы и размеры исходной геометрической фигуры одни и те же: пример слева имеет меньше граней, а справа - больше граней. На этих примерах операции булево пересечение воздействует на параллелепипед и сферу.
На фиг. 4 представлена блок-схема быстродействующих булевых операций, выполняемых посредством геометрических граней.
На фиг. 5 показано наличие у треугольника трех (3) соседей. Задан треугольник и две его вершины, в объемных моделях существует один и только один смежный треугольник.
На фиг. 6А и 6В показаны два наименьших ограничивающих непересекающихся параллелепипеда и два пересекающихся параллелепипеда. Каждый треугольник фактически имеет наименьший ограничивающий параллелепипед. Если два параллелепипеда не пересекаются, треугольники, содержащиеся в этих двух параллелепипедах, не пересекаются. Если параллелепипеды пересекаются, то необходимо вычислять пересечение грань-треугольник.
На фиг. 7А-7С изображены три (3) варианта пересечения ребро-треугольник: точка пересечения попадает вовнутрь треугольника, точка пересечения располагается на ребре треугольника, точка пересечения находится на вершине треугольника.
На фиг. 8А-8D показан поиск подходящего набора, который предоставляет возможность системе пересечь следующий треугольник для продолжения линий пересечения путем проведения вычисления ребро-треугольник. Треугольники, залитые цветом, являются последней парой треугольников, которые пересекаются, на не залитые треугольники ссылаются посредством элементов m_NeigTri структуры данных Triangle3dEx, которые сопровождают систему поиском минимального набора треугольников при построении линий пересечения. Набор содержит один треугольник, два треугольника или нуль треугольников.
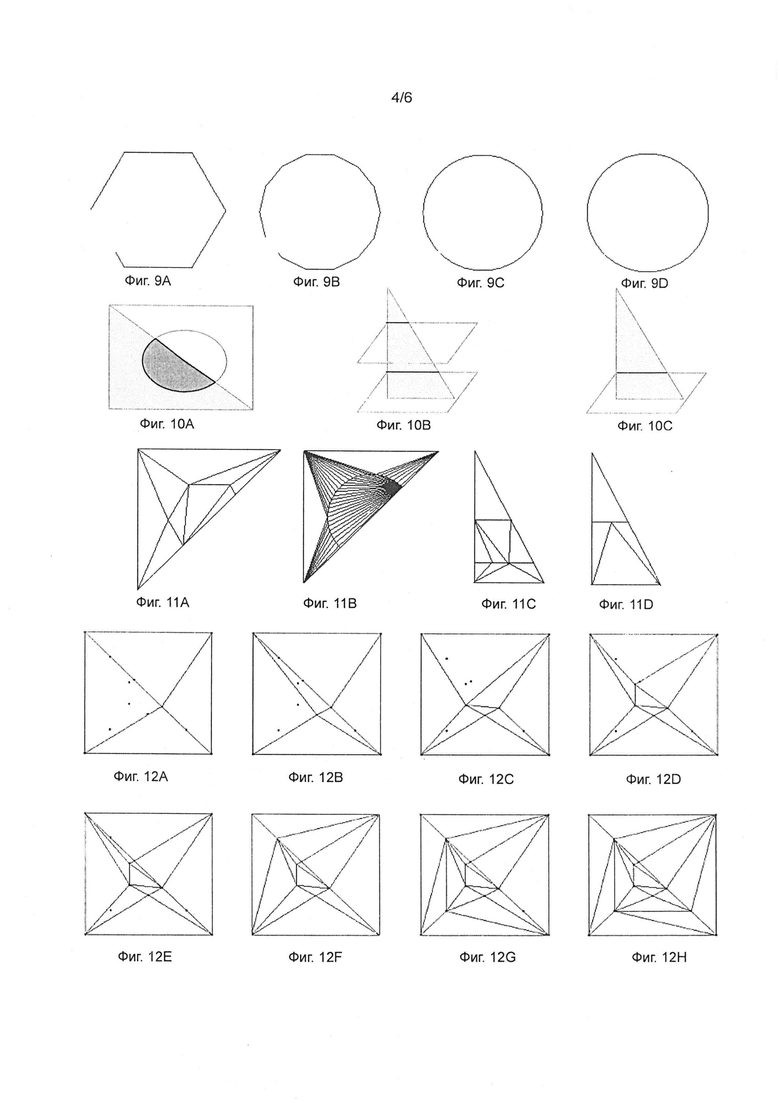
На фиг. 9А-9D показаны четыре (4) примера линий пересечения. Параллелепипед пересекает сферу, которая имеет разное число граней.
На фиг. 10А-10С даны три (3) примера разделительных линий в темном цвете. На фиг. 10А одна (1) разделительная линия, 10В - две (2), 10С одна (1).
На фиг. 11А-11D показаны четыре (4) примера, где разделительные линии делят треугольник на множество треугольников.
На фиг. 12А-12Н показана последовательность сеток Делоне, в которой каждая точка пересечения вставлена в сетку пошагово.
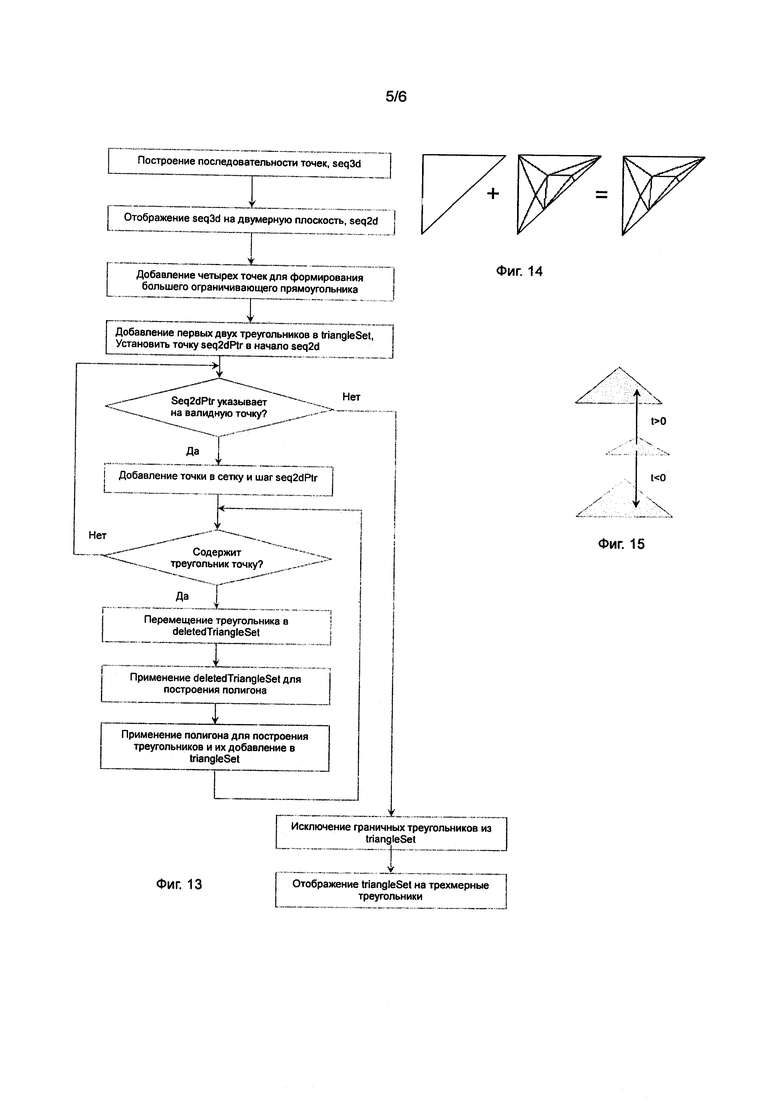
На фиг. 13 представлена блок-схема модифицированного метода Уотсона для построения последовательности сеток Делоне по фиг. 12А-12Н.
На фиг. 14 показан треугольник и его сетка Делоне. Исходный треугольник удален и только сетка Делоне сохранена для дальнейших вычислений.
На фиг. 15 показан t-Buffer, где t может быть отрицательным или положительным. Если размер отрицательного t и положительного t сбалансирован в t-Buffer, то рассматриваемый треугольник закрыт другой фигурой и скрыт.
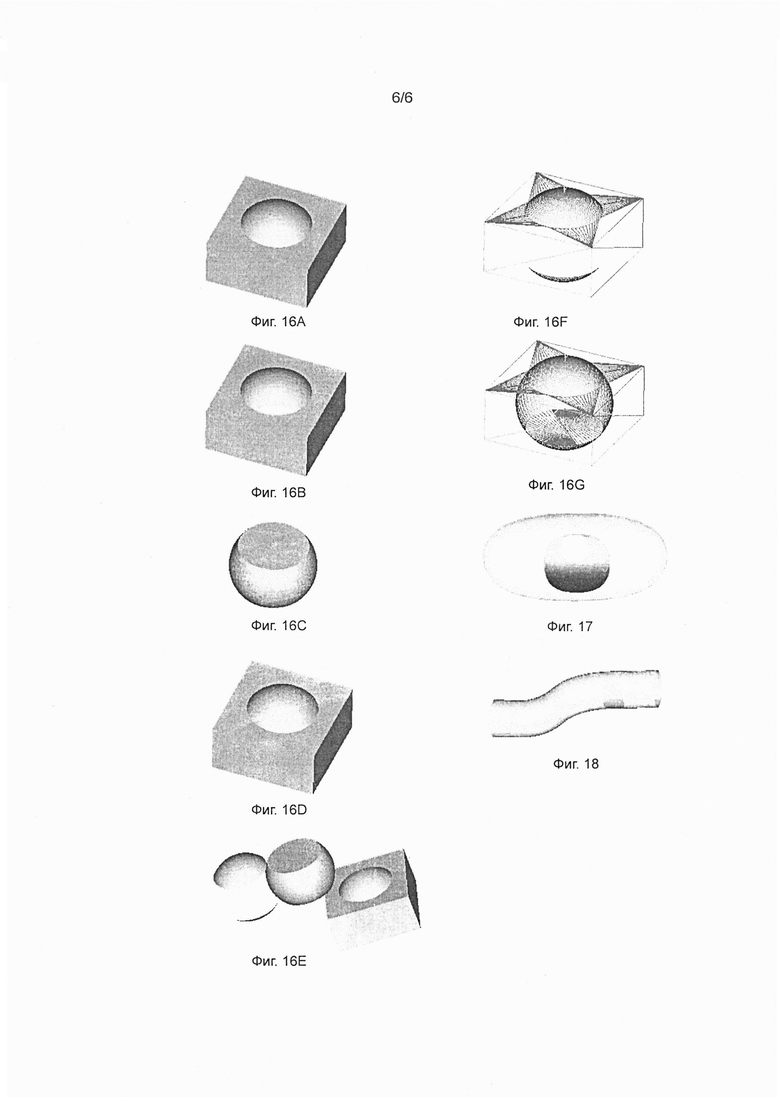
На фиг. 16А-16Е показаны пять (5) примеров булевых операций, проведенных с кубом и сферой. На фиг. 16F и 16G показана внутренняя сетка двух булевых операций: объединения и исключения.
На фиг. 17 показано, как контурная линия отсекает закрытую поверхность, деформированную сферу и образует два (2) отверстия.
На фиг. 18 представлен пример, в котором экструдированная поверхность, трубка, отсечена контурной линией и образует отверстие.
Подробное описание
Настоящее изобретение задает следующие структуры данных: Point3dEx, Triangle3dEx и BlOpTriangle3dSet, которые наследуют Point3d, Triangle3d, Triangle3dSet, хранящие грани для визуализации геометрических фигур. При выполнении булевой операции система отображает грани визуализации на BlOpTriangle3dSet и все последующие процессы рассматриваются с точки зрения элементов и атрибутов BlOpTriangle3dSet. На фиг. 4 представлена блок-схема, описывающая основную процедуру булевых операций, проводимых по настоящему изобретению. После завершения булевой операции система отображает полученный результат, сохраненный в BlOpTriangle3dSet, на грани визуализации.
Геометрические грани для визуализации
Система CAD визуализирует грани для представления геометрического объекта, такого как сфера, конус, параллелепипед, цилиндр, экструдированный или вогнутый объект. Грань можно составить из трех (3) или более точек и грани обычно разбивают на треугольники для упрощения расчетов. Параллелепипед имеет шесть (6) граней, разбитых на двенадцать (12) треугольников. Сфера может иметь восемнадцать (18) граней, составляющих двадцать четыре (24) треугольника. Сфера может быть также визуализирована посредством более чем тысячи (1000) граней и треугольников. На фиг. 3 показана сфера, визуализированная разным количеством граней. В этом способе применяется Triangle3dSet для обозначения структуры данных по набору треугольников и для визуализации геометрического объекта, при этом эта структура содержит два (2) атрибута: набор трехмерных точек и набор трехмерных треугольников, где Triangle3d ссылается на Point3d.

Треугольники для булевых операций.
В методе булевых операций, описываемом в настоящем изобретении, заданы три (3) ключевых класса: BlOpTriangleSet, Triangle3dEx, and Point3dEx.
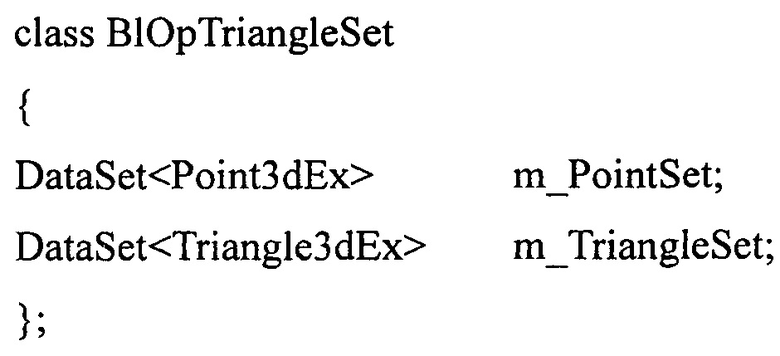

DataTypeII могут быть целыми, длинными целыми, беззнаковыми длинными целыми или другими целыми типами. DataTypeIII представляет собой тип данных с плавающей запятой.
Класс Triangle3dEx указывает на то, что каждый треугольник может иметь три (3) смежных треугольника и каждый треугольник хранится в BlOpTriangleSet только в одном (1) экземпляре. В примере с параллелепипедом, в простейшем варианте, когда он имеет двенадцать (12) треугольников, даже если каждый из них имеет трех (3) соседей, тем не менее BlOpTriangleSet хранит в сумме двенадцать (12) треугольников.
Технически Triangle3d может иметь атрибут m_Normal. Если DataTypeI и DataTypeIV одинакового типа, например двойной точности, атрибут m_Normal может быть унаследован.
Отображение данных.
В процессе отображения Triangle3dSet на BlOpTriangleSet копируется набор точек и набор треугольников из состояния визуализации и загружаются атрибуты по умолчанию. Отображение данных включает следующие процедуры:
1) Копирование точек из Triangle3dSet в BlOpTriangleSet и обеспечение отсутствия одинаковых точек.
2) Копирование треугольников из Triangle3dSet в BlOpTriangleSet.
3) Для каждого треугольника в BlOpTriangleSet установление его смежных треугольников.
4) Вычисление нормали и составление уравнения плоскости для каждого треугольника в BlOpTriangleSet.
Примечание 1: заданы две (2) точки а и b, если |ха-xb|<ε и |ya-yb|<ε и |za-zb|<ε, где ε - положительное число с плавающей запятой, например 5.0е-16, то b равно а.
Примечание 2: Когда отображаются точки из данных визуализации на BlOpTriangleSet, система проверяет, есть ли одинаковые точки в BlOpTriangleSet.
Примечание 3: Треугольник с тремя (3) точками задает плоскость, описываемую математической формулой ax+by+cz+d=0, и класс Plane записывает это во внутреннюю память как массив из четырех (4) элементов, такой как m_ABCD [4].
Примечание 4: Если три (3) точки треугольника не одинаковы, всегда есть валидная нормаль. Хотя это связано с m_ABCD, отдельная копия делает многое яснее и проще для последующей обработки.
Примечание 5: Каждый треугольник имеет три (3) ребра, когда нет повторяющихся точек, он имеет три (3) смежных треугольника в объемных моделях. На фиг. 5 показан пример: треугольник, залитый темным цветом и его три (3) соседа. Что касается участка поверхности для отсечения, то один или два смежных треугольника могут быть исключены.
Первая точка пересечения
Каждый треугольник имеет три (3) вершины, которые задают наименьший ограничивающий параллелепипед. В этом способе принята концепция ориентированного по осям ограничивающего параллелепипеда.
Дана пара треугольников, если их ограничивающие параллелепипеды не перекрываются, то два треугольника не имеют точку пересечения; в противном случае в этом способе выполняется вычисление пересечения ребро-треугольник.
Если ребро треугольника Та пересекается с плоскостью, задаваемой треугольником Tb, и точка пересечения pet попадает вовнутрь Tb, то pet является первой точкой пересечения. Если pet находится вне Tb, то следует поменять положение треугольников в паре (Та, Tb), изменив на (Tb, Та), и провести вычисление пересечения ребро-треугольник.
Формула вычисления для i-ого ребра треугольника Та, i∈[0, 2] такова: p=pi+t*(p(i+1)%3-pi) г а формула для плоскости, задаваемой треугольником Tb, ax+by+cz+d=0. Если эти две формулы имеют решение, то ребро пересекается с плоскостью. Если точка пересечения ребро-треугольник попадает вовнутрь Tb, то эта точка является точкой пересечения ребро-треугольник.
Продолжение линии пересечения.
Этот метод задает структуру данных для записи точки пересечения как PntEgTri:

В зависимости от местоположения точки пересечения на треугольнике структура PntEgTri, а проще говоря pet, может быть разбита на три (3) типа, показанных на фиг. 7А-7С.
1) Наиболее распространенным случаем является пересечение ребро-треугольник, где pet расположена на ребре треугольника Та и внутри треугольника Tb.
2) При пересечении ребро-ребро pet расположена на ребре треугольника Та и на ребре треугольника Tb.
3) При пересечении ребро-вершина pet расположена на ребре треугольника Та и на вершине треугольника Tb.
Для продолжения линии пересечения система захватывает следующий смежный треугольник(и) и проверяет пересечение ребро-треугольник до тех пор, пока линия пересечения не замкнется или все треугольники не будут пройдены.
Разделительная линия
Линия пересечения проходит через набор треугольников и делит каждый треугольник на множество частей. Сегменты линии пересечения внутри треугольника образуют разделительную линию. На фиг. 10А-10С показаны три (3) примера, в которых темные линии это разделительные линии. Практически треугольник может иметь нуль (0), одну (1), две(2) или три (3) разделительные линии.
Следующая процедура показывает как получить валидную ссылку на треугольник, который имеет по меньшей мере одну разделительную линию:

Заданы валидный треугольник и разделительная линия, чтобы решить, принадлежит ли pet разделительной линии треугольника, в этом методе проверяют:
1) расположен ли pet на ребре треугольника,
2) расположен ли pet внутри треугольника,
3) совпадает ли pet с вершиной треугольника.
Разбиение треугольника
Задан набор разделительных линий, чтобы разбить треугольник, данный метод предусматривает:
1) Удаление повторяющихся pet-ов. Если соседние pet-ы одинаковы, данный метод сохраняет только одну копию.
2) Определение положения конечных pet-ов: проверяется на каком ребре треугольника расположена каждая pet.
3) Разбиение верхней части, нижней части и средней части треугольника, где это применимо.
Задан набор точек на плоскости, которая представляет часть треугольника, чтобы разделить плоскость на группы треугольников, в данном изобретении модифицирован метод Уотсона применительно к двумерной сетке Делоне, который опубликован в 1981 году (Watson, 1981).
Двумерная сетка Делоне имеет три (3) набора данных: набор треугольников, который содержит созданные треугольники, набор удаленных треугольников, которые хранят только удаленные треугольники и полигон, который фиксирует контур набора удаленных треугольников.
Модифицированный метод для двумерной сетки Делоне содержит следующие шаги:
1) Построение последовательности эскизных линий, которые соединяют разделительные линии и вершины треугольника, где это применимо.
2) Отображение последовательности трехмерных точек на двумерные точки в соответствии с аспектом плоскости.
3) Добавление четырех (4) точек для формирования большего ограничивающего прямоугольника, который огораживает все двумерные точки.
4) Принятие факта, что одна диагональ ограничивающего прямоугольника делит этот прямоугольник на два (2) треугольника, и добавление их в набор треугольников.
5) Внесение каждой точки, кроме граничных, в набор треугольников.
a) Осуществление проверки для каждой точки и для каждого треугольника в наборе треугольников, содержит ли окружность, описанная вокруг указанного треугольника, указанную точку или проходит ли последний сегмент через указанный треугольник. Исключение, если условие выполнено, этого треугольника из набора треугольников и добавление его в набор исключенных треугольников.
b) Применение набора исключенных треугольников для расширения полигона и немедленная очистка набора исключенных треугольников.
c) Применение полигона для создания набора треугольников и добавления их в набор треугольников.
На фиг. 12А-12Н показана последовательность двумерных сеток Делоне.
Исключение разделенных треугольников.
На предыдущем шаге разделенный треугольник был помечен. В этом методе после того, как все треугольники пройдены, помеченные треугольники исключаются. На фиг. 14 показан результат исключения.
Скрытые грани.
Даны два набора треугольников А и В, если А ограничивает треугольник из В (Tb), то Tb скрыт; если В ограничивает треугольник из А (Та), то Та скрыт.
Чтобы определить, ограничивается ли треугольник Т фигурой О, в настоящем изобретении задействованы следующие шаги.
1) Вычисление центра тяжести (с) треугольника Т.
2) Построение линии 1: p=c+t*N, которая проходит через центр тяжести по нормали N треугольника Т.
3) Для каждого треугольника To объекта О вычисляется точка пересечения линии с плоскостью. Если существует валидная точка пересечения pet, которая попадает вовнутрь треугольника To, то вычисляют t, который определяется центром тяжести и pet, и добавляют t в буфер глубины, butterT.
4) Проверяют размер отрицательного t и положительного t, сохраненного в butterT. Если оба размера равны, то треугольник Т ограничен и скрыт.
При отсечении поверхности, данная система вызывает следующую процедуру для определения того, скрыт ли треугольник.
1) Установление номера m_ID каждой Point3dEx из BlOpTriangleSet рассматриваемой части поверхности в 0.
2). Пометка m_ID Point3dEx линий пересечения упомянутой части в порядке возрастания или убывания в зависимости от того, направлены ли упомянутая линия и контур отсечения в одну сторону, например оба против часовой стрелки.
3) Принятие решения согласно m_ID элемента m_Points каждого треугольника, является ли он граничным треугольником.
4) Определение для каждого граничного треугольника, находится ли он слева или справа от контура отсечения, и установление, находятся ли его соседи, которые не являются граничными треугольниками, слева или справа.
Перестройка граней.
В настоящем изобретении определены пять (5) типов булевых операций, каждая из которых имеет отличающуюся процедуру перестройки.
Операция объединения, логическое ИЛИ, объединяет два стереометрических объекта и создает новый объект, обычно отбрасывает скрытые разделы и сохраняет видимые разделы и представляет следующую процедуру.
1) Исключение скрытых треугольников объекта А.
2) Исключение скрытых треугольников объекта В.
3) Объединение треугольников объектов А и В.
Операция пересечения, логическое И, создает стереометрический объект, используя общие части двух геометрических объектов и отбрасывая любые части А и В, находящиеся вне этих общих частей, и представляет следующую процедуру.
1) Исключение НЕ скрытых треугольников объекта А.
2) Исключение НЕ скрытых треугольников.
3) Объединение треугольников объектов А и В.
Операция исключения, которая строит стереометрический объект посредством удаления общих частей двух геометрических объектов и сохранения необщих разделов, и представляет следующую процедуру.
1) Копирование скрытых треугольников объекта А в буфер, bufferA.
2) Исключение скрытых треугольников из объекта А.
3) Копирование скрытых треугольников объекта B в объект А.
4) Исключение скрытых треугольников из объекта В.
5) Копирование треугольников из bufferA в объект В.
6) Переворот нормали каждого скрытого треугольника из А и В.
7) Объединение треугольников двух объектов.
Операция вычитания, которая вырезает геометрический объект А из другого объекта В путем удаления всех частей А, находящихся внутри В, и представляет следующую процедуру.
1) Исключение скрытых треугольников из объекта А.
2) Исключение НЕ скрытых треугольников объекта В.
3) Переворот нормали каждого треугольника из В.
4) Объединение треугольников объектов А и В.
Операция деления, которая делит два стереометрических объекта А и В на три (3) объекта, общие части двух геометрических объектов, НЕ общие разделы А и разделы В, и представляет следующую процедуру.
1) Копирование скрытых треугольников объекта А в буфер, bufferA.
2) Копирование скрытых треугольников объекта B в bufferA.
3) Копирование скрытых треугольников объекта А в другой буфер, bufferB.
4) Исключение скрытых треугольников из объекта А.
5) Копирование скрытых треугольников объекта B в объект А.
6) Исключение скрытых треугольников объекта В.
7) Копирование скрытых треугольников объекта А, хранимых в bufferA в объект В.
8) Переворот нормали каждого треугольника из А и В.
Отображение на грани визуализации.
Как только выполнение булевых операций завершается, этот метод отображает BlOpTriangleSet на треугольники визуализации.
1) Каждая Point3dEx из BlOpTriangleSet отображается на Point3d из TriangleSet;
2) каждый Triangle3dEx of BlOpTriangleSet отображается на Triangle3d из TriangleSet.
ПАТЕНТНЫЕ ДОКУМЕНТЫ
6,307,555 10/2001 Lee 345/423
ДРУГИЕ ПУБЛИКАЦИИ
"Boolean Set Operations on Non-Manifold bounding Representation Objects", E. Gursoz и др., Computer-Aided Design 23 (1991) Jan./Feb. No. 1 London, GB. "Computing the n-dimensional Delaunay tessellation with application to Voronoi polytopest", D.F. Watson, The Computer Journal 24 (2) 1981.
| название | год | авторы | номер документа |
|---|---|---|---|
| СОЗДАНИЕ ОГРАНИЧЕННОЙ СЕТКИ ВОРОНОГО НА ПЛОСКОСТИ | 2008 |
|
RU2444788C2 |
| СПОСОБ И СИСТЕМА УДАЛЕНИЯ НЕВИДИМЫХ ПОВЕРХНОСТЕЙ ТРЁХМЕРНОЙ СЦЕНЫ | 2017 |
|
RU2680355C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕХМЕРНОЙ ГЕОЛОГИЧЕСКОЙ МОДЕЛИ ГРУНТА НА ОСНОВЕ ДАННЫХ ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИХ СКВАЖИН | 2015 |
|
RU2589457C1 |
| СПОСОБ И СИСТЕМА РЕНДЕРИНГА 3D МОДЕЛЕЙ В БРАУЗЕРЕ С ИСПОЛЬЗОВАНИЕМ РАСПРЕДЕЛЕННЫХ РЕСУРСОВ | 2020 |
|
RU2736628C1 |
| СПОСОБ ТРЕХМЕРНОГО МОДЕЛИРОВАНИЯ ЗАДАННОГО ГИДРОГЕОЛОГИЧЕСКОГО ОБЪЕКТА, РЕАЛИЗУЕМЫЙ В ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЕ | 2015 |
|
RU2611892C1 |
| ТРЕХМЕРНЫЙ ТЕКСТ В ИГРОВОЙ МАШИНЕ | 2003 |
|
RU2344483C9 |
| СПОСОБ ОТОБРАЖЕНИЯ ТРЕХМЕРНОГО ЛИЦА ОБЪЕКТА И УСТРОЙСТВО ДЛЯ НЕГО | 2017 |
|
RU2671990C1 |
| СПОСОБ СЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ И УСТРОЙСТВО ДЛЯ СЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ | 2012 |
|
RU2519269C1 |
| Программно-аппаратный комплекс, предназначенный для обработки аэрокосмических изображений местности с целью обнаружения, локализации и классификации до типа авиационной и сухопутной техники | 2021 |
|
RU2811357C2 |
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУХМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2011 |
|
RU2484427C1 |
Изобретение относится к вычислительной технике. Технический результат заключается в обеспечении возможности создания геометрических моделей из первичных и добавленных геометрических объектов, сформированных посредством различных граней. Такой результат достигается тем, что отображают грани визуализации геометрических объектов на добавленные треугольники, вычисляют линии пересечения граней, разделяют грани, через которые проходят линии пересечения, определяют, видима ли каждая грань или скрыта, и перестраивают грани для формирования одного или нескольких геометрических объектов. 2 н. и 18 з.п. ф-лы, 48 ил.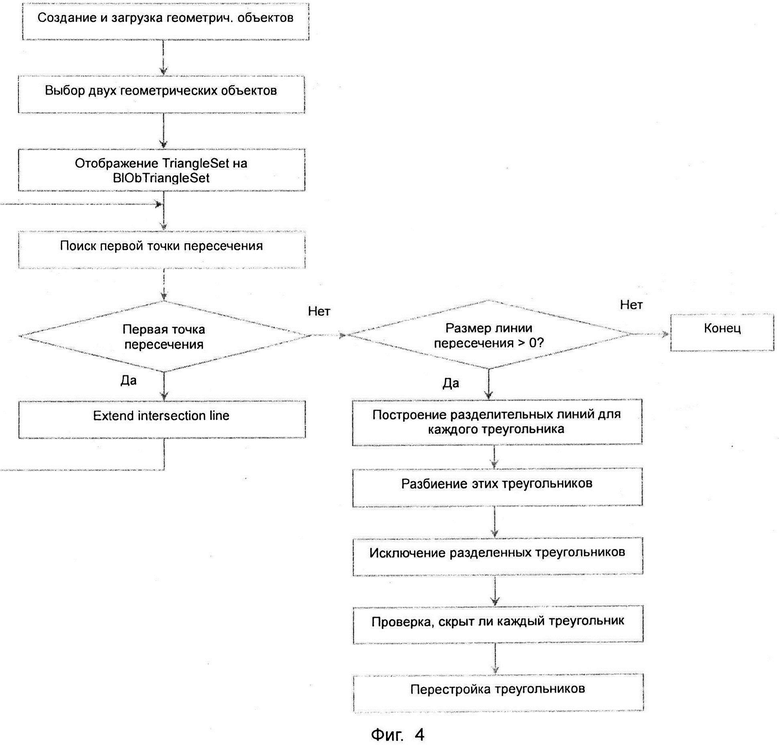
1. Способ выполнения быстродействующих булевых операций посредством геометрических граней, внедренный в вычислительную систему и функционирующий с компьютером, включающий: отображение граней визуализации геометрических объектов на добавленные треугольники, которые содержат смежные треугольники; поиск первой пары треугольников, которые содержат начальную точку линии пересечения путем определения, перекрываются ли два наименьших ориентированных по осям ограничивающих параллелепипеда, и осуществление пересечения ребро-треугольник; продолжение линий пересечения пока они не замкнутся путем поиска смежных треугольников или пока все треугольники не будут пройдены; разбиение треугольников, через которые линии пересечения проходят; перестройка граней, уничтожение и сохранение треугольников в соответствии с типами булевой операции; и отображение добавленных треугольников на грани визуализации.
2. Способ по п. 1, в котором в любых булевых операциях, включающих объединение, пересечение, исключение, вычитание и деление, используются грани визуализации геометрических объектов для создания новых геометрических объектов и полученные результаты сразу отображаются на треугольники визуализации без структуры данных конструктивной блочной геометрии (CSG) и граничного представления (B-REP).
3. Способ по п. 1, в котором в любых булевых операциях, включающих объединение, пересечение, исключение, вычитание и деление, используются грани визуализации геометрических объектов для создания новых геометрических объектов и полученные результаты сразу отображаются на треугольники визуализации со структурой данных CSG и B-REP.
4. Способ по п. 1, в котором при построении линий пересечения применяются наименьшие ограничивающие параллелепипеды для определения, не перекрываются ли два треугольника, и выполняется вычисление точки пересечения ребро-треугольник, так чтобы точки пересечения были точными и линии пересечения не были аппроксимированными искривленными линиями ребер.
5. Способ по п. 1, в котором поиск точки пересечения осуществляется вычислением пересечения ребро-треугольник с привлечением смежных граней, так что прямое вычисление точки пересечения ребро-ребро заменяется проверкой, расположена ли точка на ребре треугольника.
6. Способ по п. 1, в котором при разбиении треугольника каждые трехмерные треугольники проектируются на двумерную плоскость и строится двумерная сетка Делоне посредством измененного метода Уотсона, в котором треугольник делится на разные части, даже когда разделительные линии не выпуклы.
7. Способ по п. 1, в котором шаг проверки, принадлежит ли треугольник Та к А, ограниченному геометрическим объектом В, использует t-Buffer и дополнительно включает: вычисление центра тяжести (с) треугольника Та; построение линии 1: p=c+t*N, проходящей через центр тяжести (с) и вдоль нормали треугольника Та; для каждого треугольника Tb объекта В осуществление проверки, пересекается ли 1 с Tb во внутренней точке р, и добавление t в t-Buffer; установление Та в «скрытое», когда размер отрицательного t равен размеру положительного t в t-Buffer.
8. Способ по п. 1, в котором шаг проверки, является ли треугольник «скрытым» при отсечении участка поверхности, дополнительно включает: установление m_ID регулярных точек BlOpTriangleSet рассматриваемого участка в 0, a m_ID точек линии пересечения упомянутого участка в порядке возрастания или убывания в зависимости от того, направлены ли упомянутая линия и контур отсечения в одну сторону; принятие решения в соответствии с m_ID элемента m_Points каждого треугольника, является ли он граничным треугольником; определение для каждого граничного треугольника, находится ли он слева или справа от контура отсечения и установление, находятся ли его соседи, которые не являются граничными треугольниками, слева или справа.
9. Способ по п. 1, в котором булева операция, такая как объединение, пересечение, исключение, вычитание или деление, сохраняет видимые или скрытые грани, или сочетание видимых и скрытых граней для получения результата этой операции.
10. Способ по п. 1, в котором результат булевой операции непосредственно отображается на данные визуализации для вывода на дисплей и получения данных для следующих булевых операций.
11. Вычислительная система, состоящая из аппаратного и программного обеспечения, которая выполняет быстродействующие булевы операции посредством граней визуализации геометрических объектов, включающая: компьютер с входными устройствами для ввода данных и команд и монитором, показывающим пользовательский интерфейс, геометрические объекты и дополнительные данные, содержащий носитель, хранящий геометрические данные и инструкции, образующие систему программного обеспечения, или содержащий микрочип или интегральную схему с вшитыми частично или полностью инструкциями, и процессор, который исполняет следующие действия: создание, модификация или загрузка первичных геометрических объектов, включающих вогнутые и экструдированные объекты и перевод их на другие позиции и направления при помощи входных устройств компьютера; выбор двух геометрических объектов; отображение граней визуализации геометрических объектов на добавленные треугольники, которые содержат смежные треугольники; поиск первой пары треугольников, которая содержит начальную точку линии пересечения путем определения, перекрываются ли два наименьших ориентированных по осям ограничивающих параллелепипеда, и осуществление пересечения ребро-треугольник; продолжение линий пересечения пока они не замкнутся путем поиска смежных треугольников или пока все треугольники не будут пройдены; разбиение граней, через которые линии пересечения проходят; перестройка граней, уничтожение, сохранение и объединение граней в соответствии с типами булевой операции; и отображение добавленных треугольников на грани визуализации.
12. Система по п. 11, в которой в любых булевых операциях, включающих объединение, пересечение, исключение, вычитание и деление, используются грани визуализации геометрических объектов для создания новых геометрических объектов и полученные результаты сразу отображаются на треугольники визуализации без структуры данных конструктивной блочной геометрии (CSG) и граничного представления (B-REP).
13. Система по п. 11, в которой в любых булевых операциях, включающих объединение, пересечение, исключение, вычитание и деление, используются грани визуализации геометрических объектов для создания новых геометрических объектов и полученные результаты сразу отображаются на треугольники визуализации со структурой данных CSG и B-REP.
14. Система по п. 11, в которой при построении линий пересечения применяются наименьшие ограничивающие параллелепипеды для определения, не перекрываются ли два треугольника, и выполняется вычисление точки пересечения ребро-треугольник, так чтобы точки пересечения были точными и линии пересечения не были аппроксимированными искривленными линиями ребер.
15. Система по п. 11, в которой поиск точки пересечения осуществляется вычислением пересечения ребро-треугольник с привлечением смежных граней, так что прямое вычисление точки пересечения ребро-ребро заменяется проверкой, расположена ли точка на ребре треугольника.
16. Система по п. 11, в которой при разбиении треугольника каждые трехмерные треугольники проектируются на двумерную плоскость и строится двумерная сетка Делоне посредством измененного метода Уотсона, в котором треугольник делится на разные части, даже когда разделительные линии не выпуклы.
17. Система по п. 11, в которой шаг проверки, принадлежит ли треугольник Та к А, ограниченному геометрическим объектом В, использует t-Buffer и дополнительно включает: вычисление центра тяжести (с) треугольника Та; построение линии 1: p=c+t*N, проходящей через центр тяжести (с) и вдоль нормали треугольника Та; для каждого треугольника Tb объекта В осуществление проверки, пересекается ли 1 с Tb во внутренней точке р, и добавление t в t-Buffer; установление Та в «скрытое», когда размер отрицательного t равен размеру положительного t в t-Buffer.
18. Система по п. 11, в которой шаг проверки, является ли треугольник «скрытым» при отсечении участка поверхности, дополнительно включает: установление m_ID регулярных точек BlOpTriangleSet рассматриваемого участка в 0, a m_ID точек линии пересечения упомянутого участка в порядке возрастания или убывания в зависимости от того, направлены ли упомянутая линия и контур отсечения в одну сторону; принятие решения в соответствии с m_ID элемента m_Points каждого треугольника, является ли он граничным треугольником; определение для каждого граничного треугольника, находится ли он слева или справа от контура отсечения, и установление, находятся ли его соседи, которые не являются граничными треугольниками, слева или справа.
19. Система по п. 11, в которой булева операция, такая как объединение, пересечение, исключение, вычитание или деление, сохраняет видимые или скрытые грани, или сочетание видимых и скрытых граней для получения результата этой операции.
20. Система по п. 11, в которой результат булевой операции непосредственно отображается на данные визуализации для вывода на дисплей и получения данных для следующих булевых операций.
| US 7324105 B1, 29.01.2008 | |||
| US 6172679 B1, 09.01.2001 | |||
| US 6348921 B1, 19.02.2002 | |||
| Двоичный счетчик с параллельным входом и последовательно параллельным переносом | 1974 |
|
SU630755A1 |
| СПОСОБ СОЗДАНИЯ ИЗОБРАЖЕНИЙ ТРЕХМЕРНЫХ ОБЪЕКТОВ ДЛЯ СИСТЕМ РЕАЛЬНОГО ВРЕМЕНИ | 2011 |
|
RU2467395C1 |
Авторы
Даты
2019-11-19—Публикация
2017-02-03—Подача