Данная заявка претендует на приоритет предварительной заявки США №60/932705, поданной 1 июня 2007 года.
Область техники, к которой относится изобретение
Последующее описание относится к созданию двумерных сеток Вороного в ограниченных зонах с внутренними разломами. В частности, это описание относится к использованию сеток Вороного в численном моделировании и имитационных экспериментах.
Уровень техники
Клетку Вороного определяют как зону в пространстве, находящуюся ближе к ее узлу, чем к любому другому узлу, причем сетка Вороного составлена из указанных клеток. Каждая клетка связана с одним узлом и рядом соседних клеток. Сетка Вороного является локально ортогональной в геометрическом смысле, то есть границы клетки перпендикулярны линиям, соединяющим узлы, лежащие по двум сторонам каждой границы. По этой причине сетки Вороного также называют сетками с перпендикулярной бисекцией (PEBI). Особым случаем сетки Вороного является прямоугольный сеточный блок (декартова сетка). Сетка Вороного обладает гибкостью, позволяющей представлять геометрию с сильно изменяющимися областями, поскольку дает возможность свободного выбора местоположения узлов. Сетки Вороного создают присваиванием местоположений узлов данной области с последующим созданием границ клеток, так чтобы каждая клетка содержала все точки, находящиеся ближе к месту расположения ее узла, чем к месту расположения любого другого узла.
Сеть, сформированную путем соединения смежных узлов клеток Вороного, обычно называют сетью Делоне, если она образована только треугольниками. В двумерной сети Делоне упомянутая область разделена на треугольники с сеточными узлами при вершинах треугольников, так чтобы эти треугольники заполняли некоторый резервуар. Такая триангуляция является триангуляцией Делоне, если окружность, проходящая через вершины треугольника (то есть, описанная окружность), не содержит внутри себя какого-либо другого узла. Известно несколько способов триангуляции Делоне (см., например, A.Bowyer, Computing Dirichlet tessellations, The Computer Journal, vol.24, No2, pp.162-166, 1981). Сетки Вороного также можно создать на основе сети Делоне, то есть триангуляции Делоне.
Сетки Вороного широко используются в технических приложениях (например, томография, геологическое моделирование, вычислительная механика, сверхпроводники и динамика жидкости) для численного моделирования и имитационных экспериментов. В частности, сетки Вороного можно использовать при геологическом моделировании для запоминания информации о структуре и свойствах породы геологического месторождения, а также при компьютерном моделировании потока жидкости в месторождениях углеводородов для создания основы для численной дискретизации уравнений, моделирующих поток. На практике сетки Вороного создают в областях со сложной геометрией, содержащих внутренние и граничные геометрические особенности, которые должны быть представлены сеткой Вороного с высокоточным разрешением. Такую согласующую сетку называют ограниченной сеткой Вороного, которая играет важную роль для обеспечения точных результатов моделирования или имитации.
Одним из недостатков существующих способов создания сетки Вороного является их неспособность точно учитывать эффекты внутренних разломов (особенностей) и, в частности, пересечений указанных внутренних разломов. Имеются другие запатентованные способы, пытающиеся решить проблему создания ограниченных сеток Вороного применительно к имитационному моделированию нефтяных месторождений. В этой прикладной области сетки Вороного часто называют сетками с перпендикулярной бисекцией (PEBI). Один из указанных известных способов предложен Kocerber (патент США №5740342). В этом способе сочетаются два типа способов создания сетки. В нем используют треугольники и тетраэдры для выравнивания вдоль разломов, представленных ломаными линиями, а также структурированные тетрагональные/шестигранные сетки в остальной части области. В этом запатентованном способе решение проблемы моделирования потока жидкости по указанной сетке включает в себя объединение методов решения при конечном объеме и конечном количестве элементов. Численные решения, использующие указанный способ, могут оказаться неустойчивыми и неточными (например, при решении проблем многофазного потока жидкости).
В способе Heinemann и др. (Z.E.Heinemann & G.F.Heinemann, Gridding Techniques for Reservoir Simulation, Proceedings of the 7-th International Forum on Reservoir Simulation, June 23-27, 2003) предпринята попытка создания сетки, которая точно следует ломаным линиям, но этот способ не может создать сетку Вороного в окрестности ломаной линии. Ребра (на ломаной линии) блока сетки Вороного не делят пополам ребра треугольников. Для упрощения вычислений потока между блоками сетки в этом способе используют псевдоточки с любой стороны дефектного участка. Такое упрощение снижает точность вычислений параметров потока.
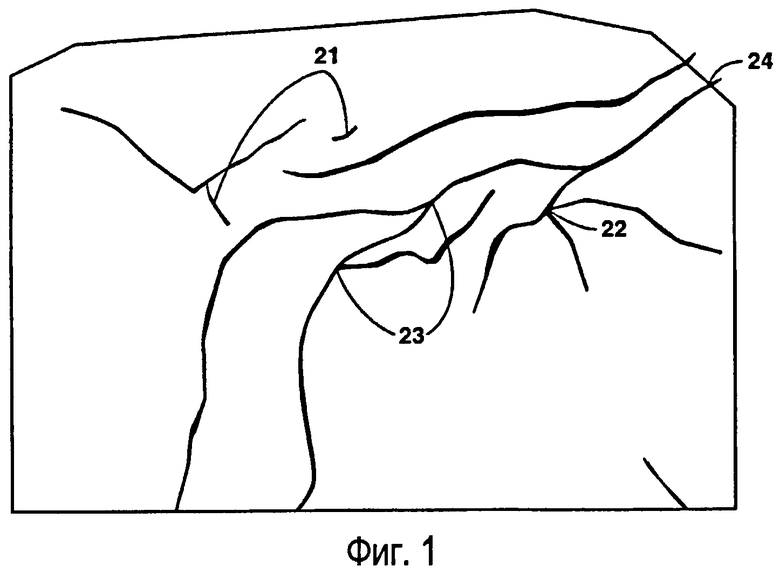
На фиг.1 показана область с ломаной границей и внутренними линейными разломами. Она взята из геологического структурного строения, то есть каркасного представления геологической структуры и дефектов углеводородного месторождения. На фиг.1 показан вид сверху на структурное строение с проекциями границы модели и следами дефектов на плоскости при виде сверху. Из фиг.1 становится очевидным ряд проблем, возникающих при создании ограниченной сетки Вороного. К этим проблемам относится создание сетки, которая точно соответствует небольшим дефектам 21, пересечению множества дефектов 22, пересечению дефектов под острыми углами 23 и пересечениям 24 дефекта с границей. В точной ограниченной сетке Вороного разломы точно согласованы с границами клеток Вороного.
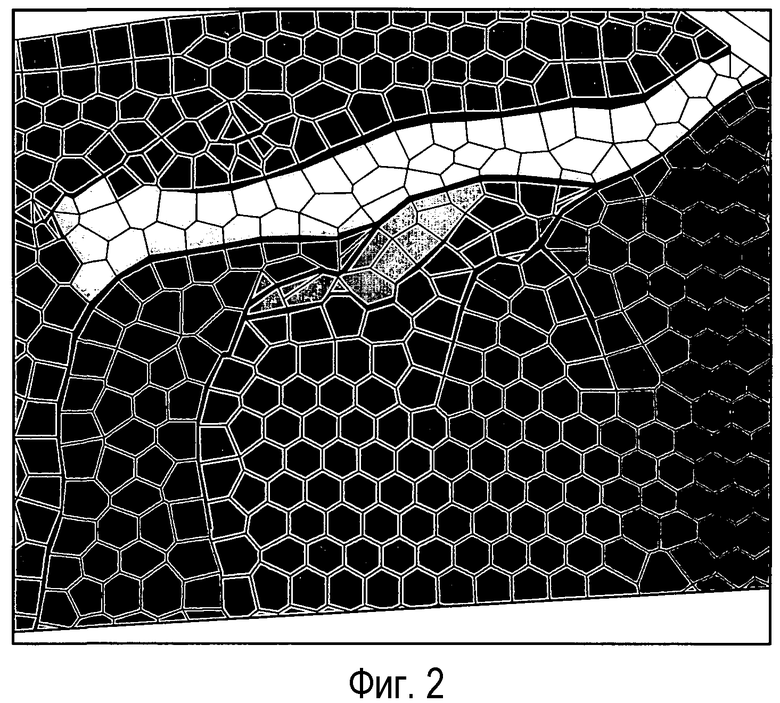
На фиг.2 показан пример сетки Вороного, созданной для структурного строения по фиг.1. Эта сетка была создана с использованием известного типового способа (например, D.L.Gunasekera, патент США №6078869). Многоугольники сетки не точно выровнены по внутренним разломам, поскольку метод согласно известному уровню техники не может адекватно отразить проблемные разломы на фиг.1. Таким образом, существует потребность в способе создания сеток Вороного, который обеспечивает более точное соответствие с внутренними разломами.
Сущность изобретения
Настоящее изобретение направлено на решение проблемы создания двумерных ограниченных сеток Вороного, которые обеспечивают соответствие с высокоточным разрешением ломаных внутренних или граничных разломов с ребрами клеток Вороного. Ограниченные сетки Вороного могут иметь адаптивные размеры клеток на основе заданного критерия плотности. Если разломы в имеющемся геометрическом описании не являются ломаными линиями, то создают ломаные линии, которые отслеживают их местоположение. Для ограничения сетки Вороного используют защитные области, которые образуются защитными ломаными линиями или точками вокруг указанных ломаных линий. Для повышения качества и точности конечной сетки Вороного и модели на ее основе можно использовать дополнительные шаги, такие как выравнивание сетки.
Согласно одному общему аспекту способ создания ограниченной триангуляции Делоне для плоской области с границами и внутренними разломами включает в себя аппроксимацию границ и внутренних разломов области ломаными линиями. Для упомянутой области строят неограниченную триангуляцию Делоне. Неограниченную триангуляцию Делоне модифицируют для согласования сторон треугольника с ломаными линиями. Строят модифицированную ограниченную триангуляцию для ее превращения в ограниченную триангуляцию Делоне.
Варианты реализации этого аспекта могут включать в себя один или несколько из следующих признаков. Например, модификация неограниченной триангуляции Делоне для согласования сторон треугольника с ломаными линиями может включать в себя замену ребер всех треугольников, пересекающих внутренний разлом. Коррекция модифицированной ограниченной триангуляции для получения ограниченной триангуляции (ограниченной триангуляции Делоне) может включать в себя выравнивание сетки и фиксирование разломов. Коррекция модифицированной ограниченной триангуляции для получения ограниченной триангуляции Делоне может включать в себя привязку внутренней точки к сегменту разлома, перемещение точки из сегмента разлома внутрь, перестановку всех точек в сторону центров масс зон Вороного и рекурсивное применение локальной замены ребер на ребра, не относящиеся к разлому, пока все ребра триангуляции, не относящиеся к разломам, не окажутся оптимальными. При выравнивании сетки можно использовать заданное распределение плотности точек.
Согласно другому общему аспекту способ создания ограниченной сетки Вороного для плоской области с границами и внутренними разломами включает в себя аппроксимацию границ и внутренних разломов указанной области ломаными линиями. Вокруг ломаных линий строят защищенные многоугольники. Ограниченную триангуляцию Делоне строят с защищенными сторонами многоугольников в качестве ограничений в дополнение к защищенным многоугольникам в отношении указанной области. Ограниченную сетку Вороного строят на основе ограниченной триангуляции Делоне.
Варианты реализации этого аспекта могут включать в себя один или несколько следующих признаков. Ломаные линии, например, могут базироваться на геометрии внутренних разломов и заданном распределении плотности точек. Построение защищенных многоугольников может включать в себя: построение многоугольников разломов из ломаных линий; построение многоугольников из перекрывающихся окружностей с центрами на пересечениях сегментов ломаной линии и разделение многоугольников с получением триангуляции Делоне. Ломаные линии можно детализировать для согласования с заданным распределением плотности точек. Радиусы окружностей можно определять на основе заданного распределения плотности точек и/или локальных геометрических особенностей. Можно выполнить сеточное выравнивание триангуляции Делоне, причем такое сеточное выравнивание может быть основано на центроидальных двухмерных сотах Вороного. Триангуляцию Делоне можно адаптировать к распределению плотности точек.
Согласно еще одному общему аспекту способ создания ограниченной сетки Вороного для плоской области с границами и внутренними разломами включает в себя аппроксимацию границ и внутренних разломов указанной области ломаными линиями. Ограниченную триангуляцию Делоне строят с ограничениями по ломаным линиям. Вокруг ломаных линий из вершин ограниченной триангуляции Делоне, лежащей на ломаных линиях, строят защищенные точки. Из набора защищенных точек и внутренних вершин защищенной триангуляции Делоне строят новую неограниченную триангуляцию Делоне. Исходя из новой неограниченной триангуляцию Делоне строят ограниченную сетку Вороного.
Варианты реализации этого аспекта могут включать в себя один или несколько следующих признаков. Ломаные линии, например, могут базироваться на геометрии внутренних разломов и заданном распределении плотности точек. Построение защищенных точек может включать в себя: замену каждой точки, лежащей на разломе, парой зеркальных отображений защищенных точек и замену каждой точки, лежащей на пересечении разломов, набором точек, расположенных на окружности с центром на указанном пересечении. Построение защищенных точек может включать в себя упорядочение путем оценки проекций на ограниченные ребра ограниченной триангуляции Делоне, всякий раз когда защитное ребро, взятое из ограниченного ребра, не удовлетворяет условию Делоне, и добавление защищенных точек, образованных из проекционных точек. Ломаные линии можно детализировать для согласования с заданным распределением плотности точек. Радиусы окружностей можно определять на основе размера ребра в ограниченной триангуляции Делоне. Можно выполнить сеточное выравнивание триангуляции Делоне, причем такое сеточное выравнивание может быть основано на центроидальных двухмерных сотах Вороного. Триангуляцию Делоне можно адаптировать к распределению плотности точек.
Краткое описание чертежей
Фиг.1 - вид сверху на структурное строение с разломами;
фиг.2 - сетка Вороного, созданная для структурного строения по фиг.1 с использованием известного способа;
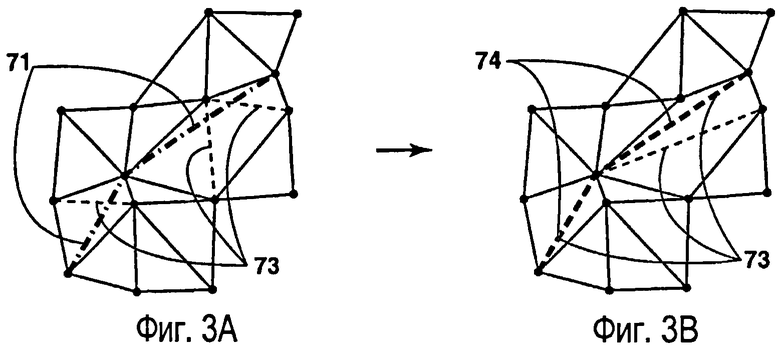
фиг.3А-3В - иллюстрация одного варианта способа создания триангуляции Делоне, которая соответствует внутреннему разлому, с использованием замены ребер, как это показано пунктирными линиями;
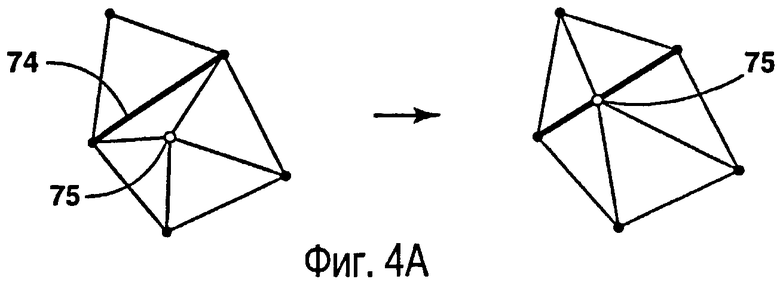
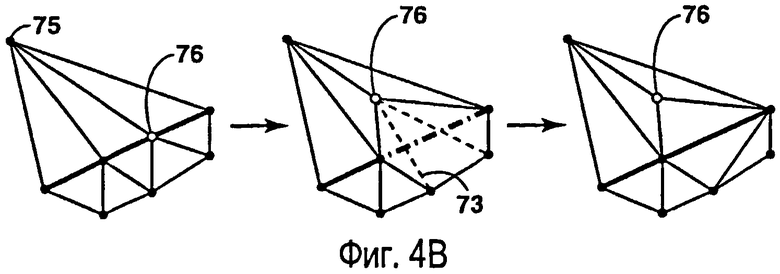
фиг.4А-4В - иллюстрация способа фиксации разломов, который является частью варианта способа создания триангуляции Делоне, согласованной с внутренними разломами;
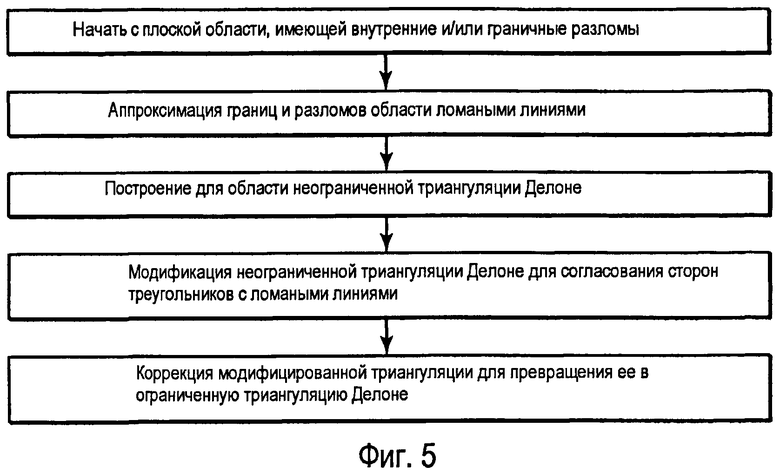
фиг.5 - блок-схема, иллюстрирующая способ создания ограниченной триангуляции Делоне;
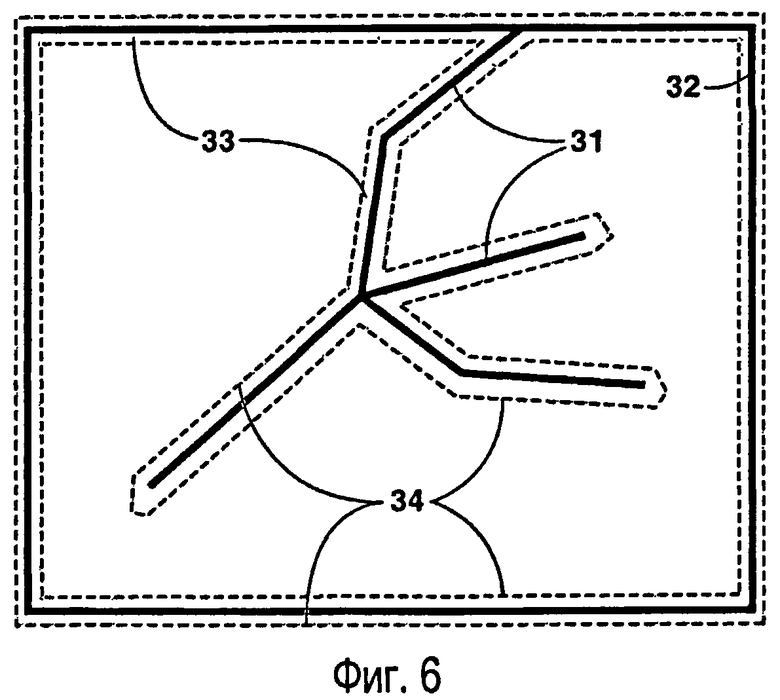
фиг.6 - вид сверху на структурное строение, показывающее внутренние разломы и границы двумерной области, а также защитные границы вокруг разломов;
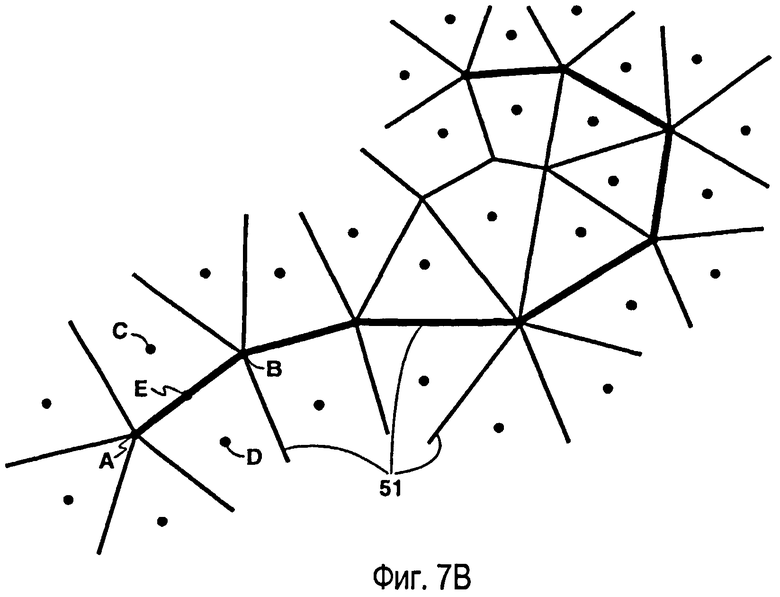
фиг.7А - вид сверху на внутренний разлом, иллюстрирующий один вариант способа формирования сетки Вороного, согласованной с внутренним разломом. На фиг.7В показаны сетки Вороного, созданные для внутренних разломов по фиг.7А;
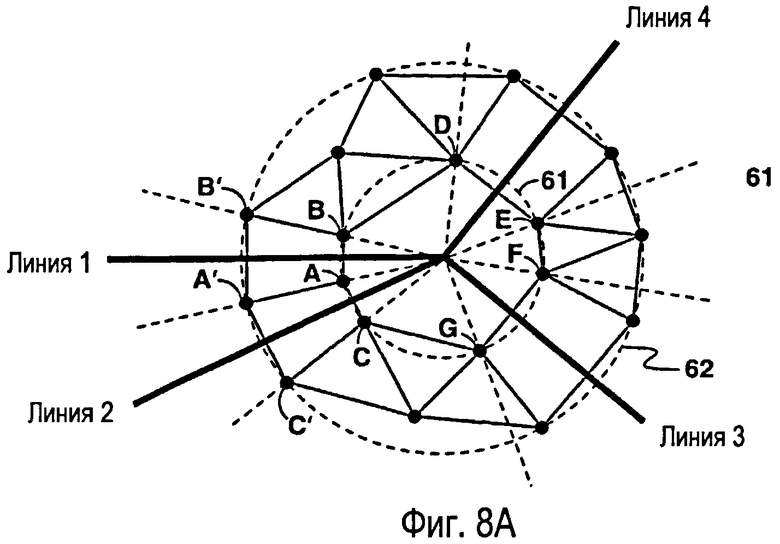
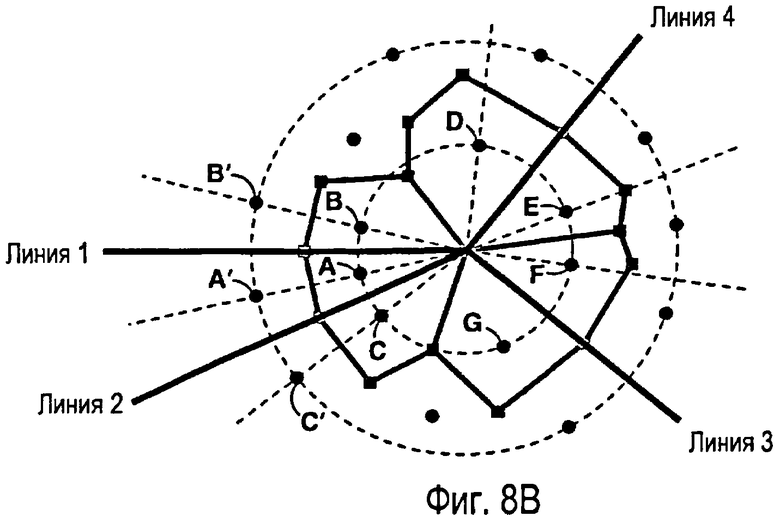
фиг.8А - иллюстрация одного варианта способа формирования сетки Вороного вокруг точки пересечения множества внутренних разломов. На фиг.8В показана сетка Вороного, созданная вокруг точки пересечения на фиг.8А;
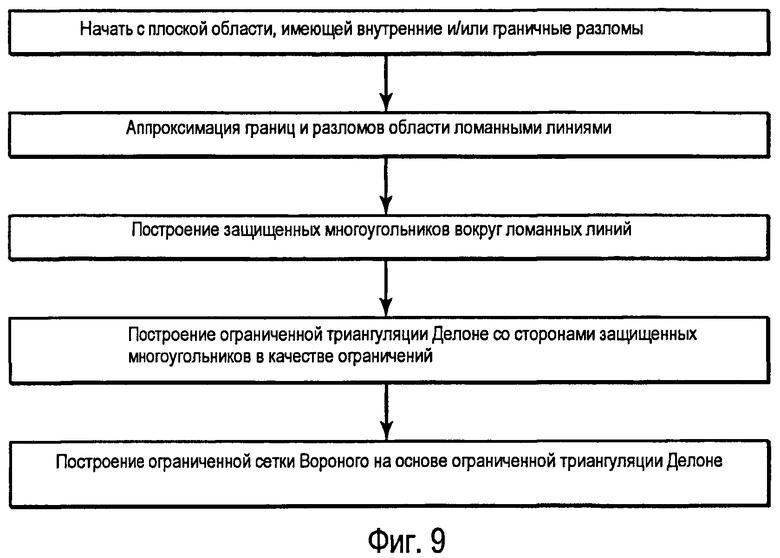
фиг.9 - блок-схема, иллюстрирующая способ создания ограниченной сетки Вороного;
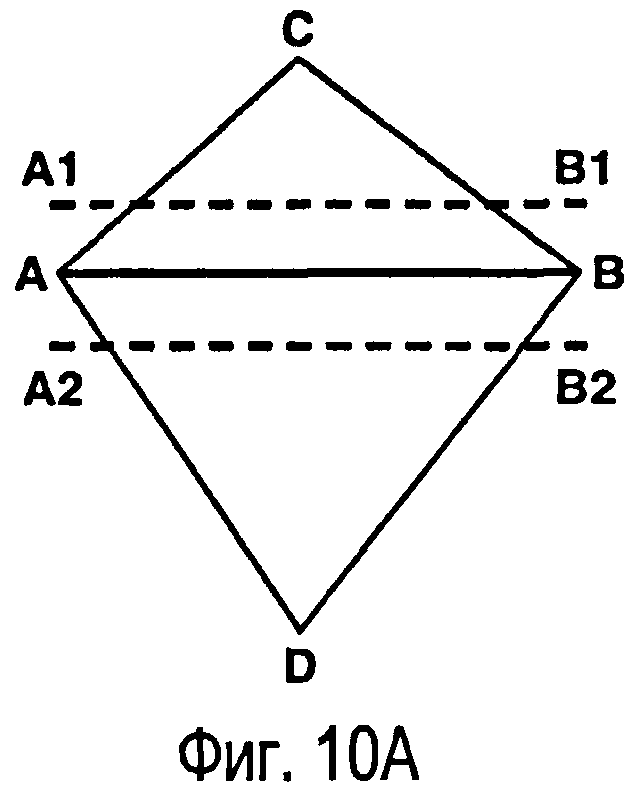
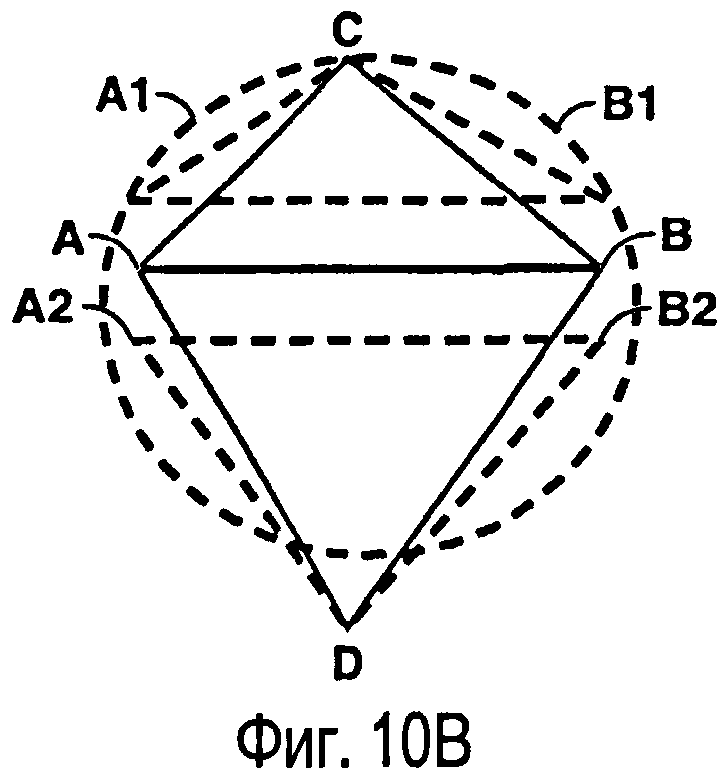
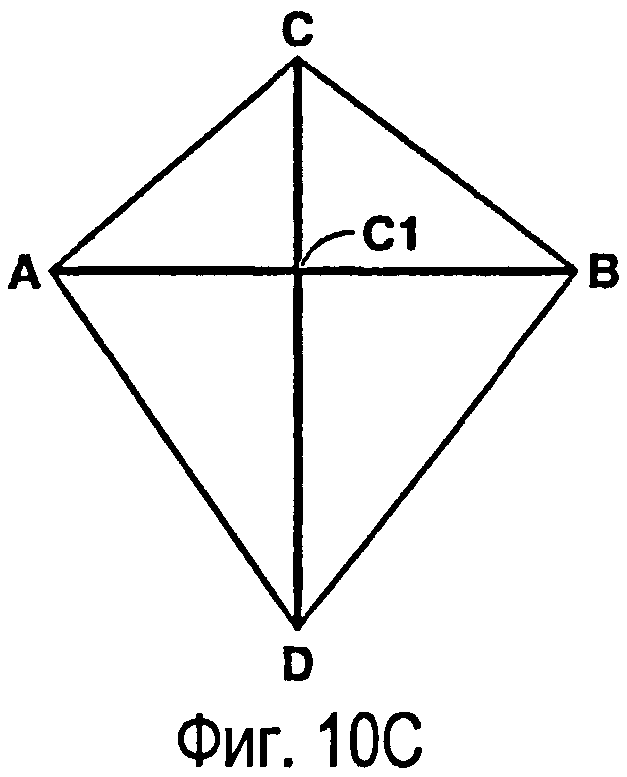
фигуры 10А-10С - виды, иллюстрирующие упорядочение набора защищенных точек в одном варианте способа создания ограниченных сеток Вороного;
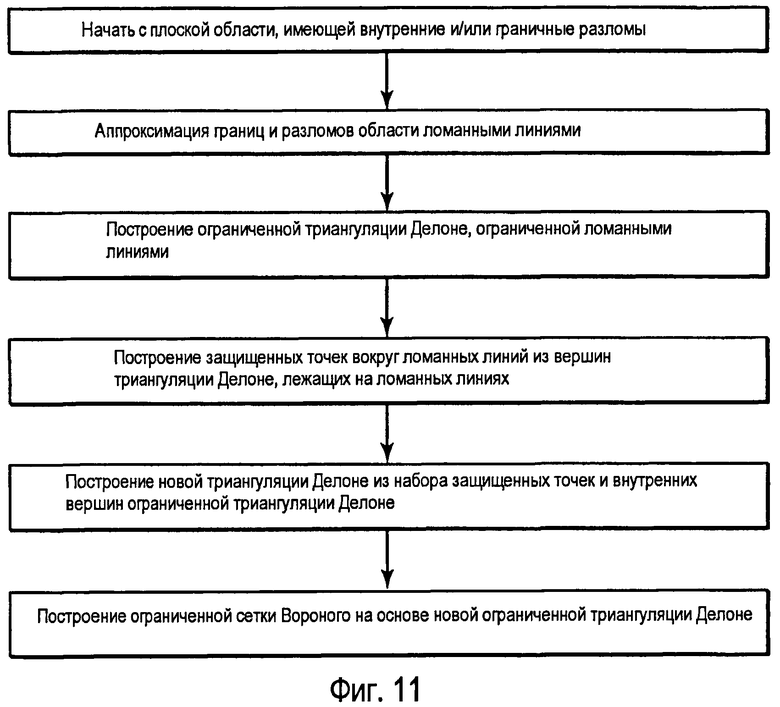
фиг.11 - блок-схема, иллюстрирующая альтернативный способ создания ограниченной сетки Вороного;
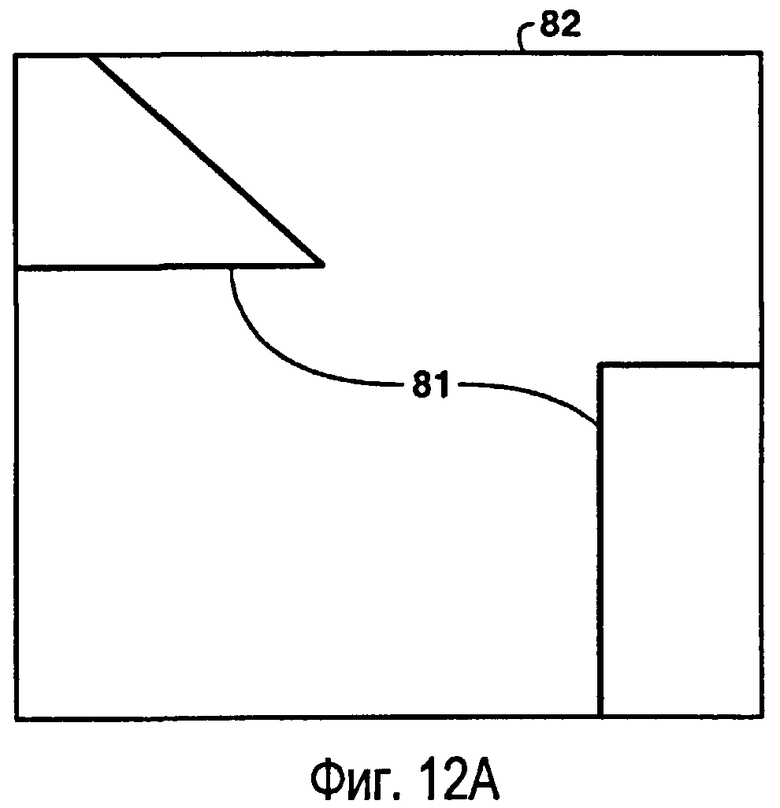
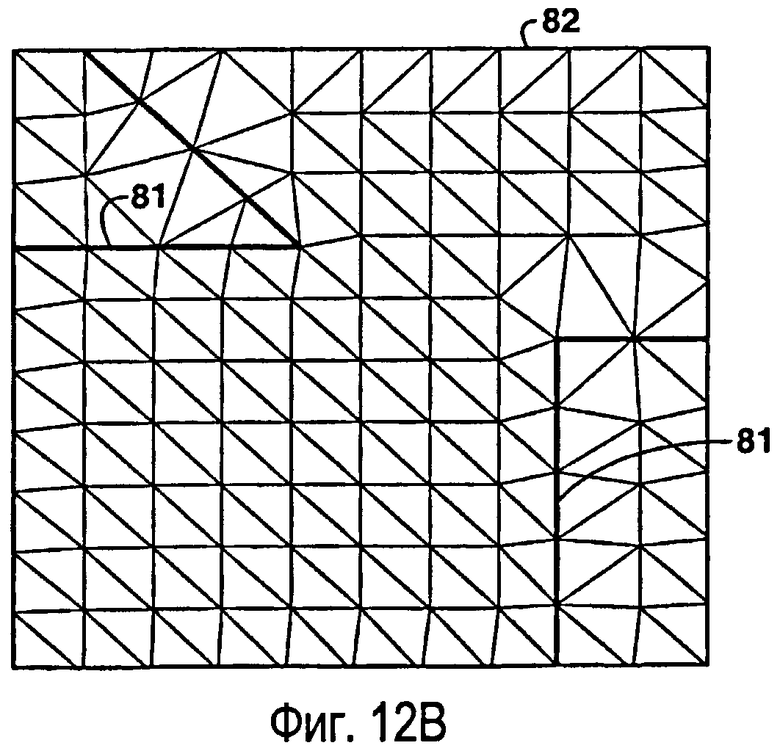
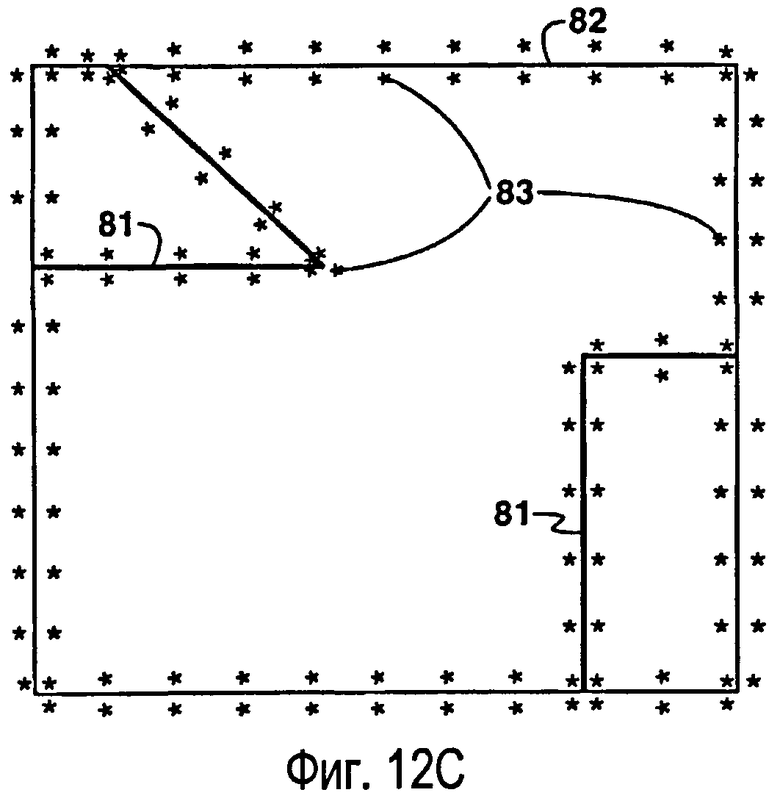
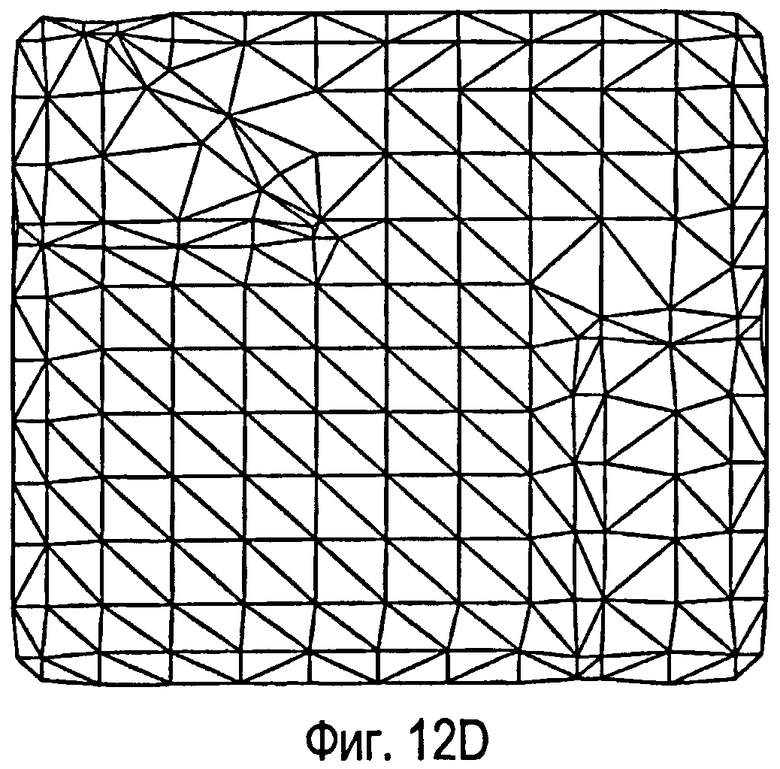
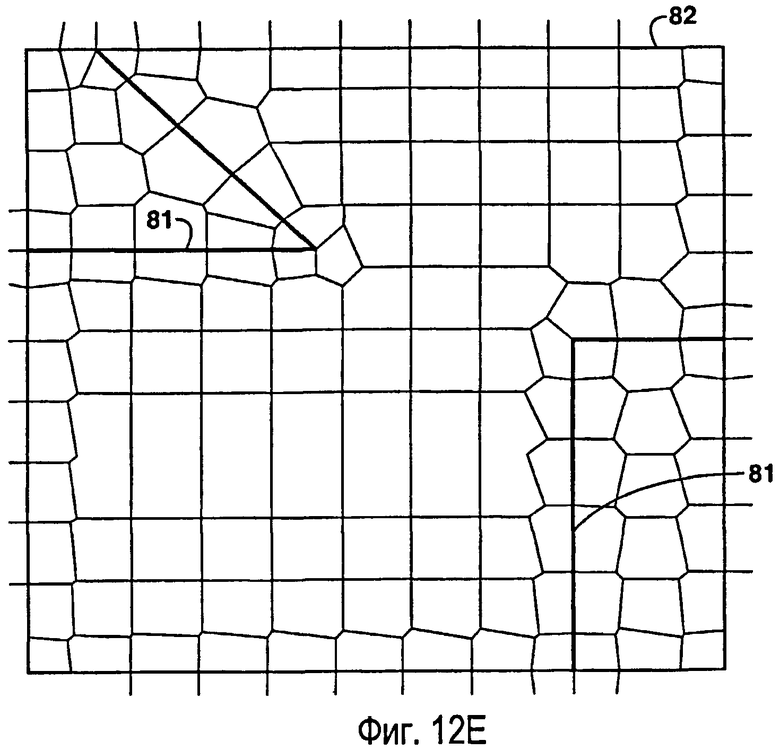
фиг.12 - пример одного варианта способа создания ограниченной сетки Вороного. На фиг.12А показана плоскость с аппроксимированными внутренними разломами и границами области. На фиг.12В показана триангуляция Делоне, соответствующая внутренним разломам и границам. На фиг.12С показаны защищенные точки, находящиеся вокруг разломов и границ. На фиг.12D показано создание новой триангуляции Делоне с использованием защищенных точек, показанных на фиг.12С. На фиг.12Е показана сетка Вороного, созданная исходя из триангуляции Делоне по фиг.12D;
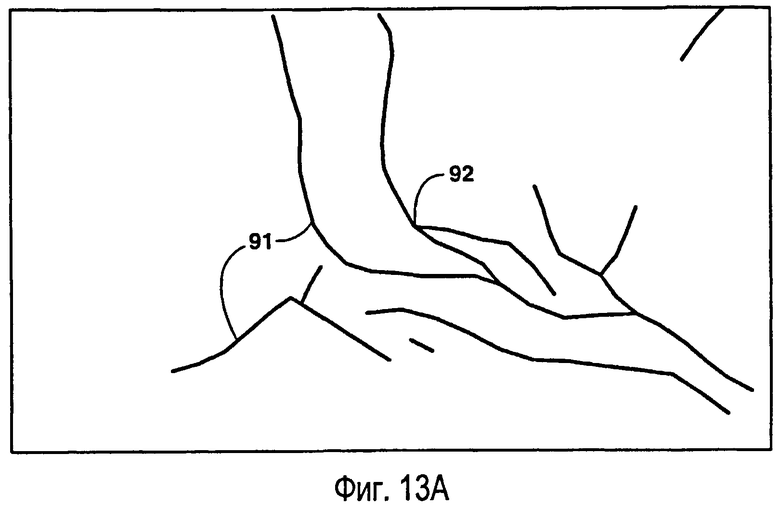
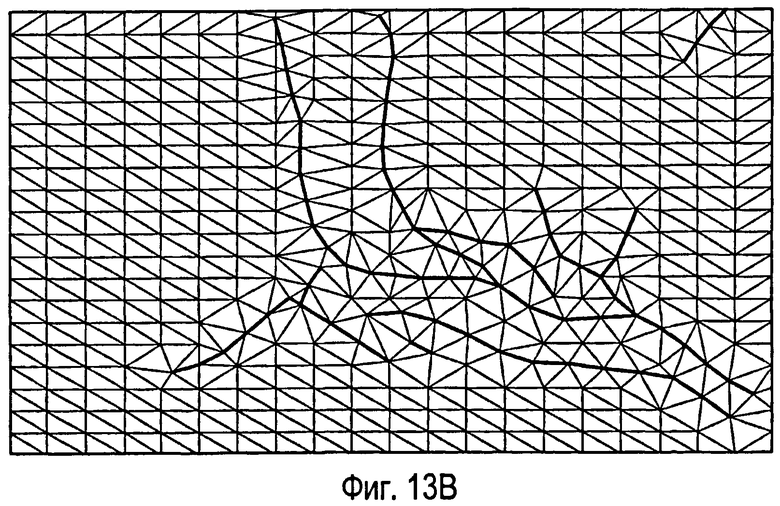
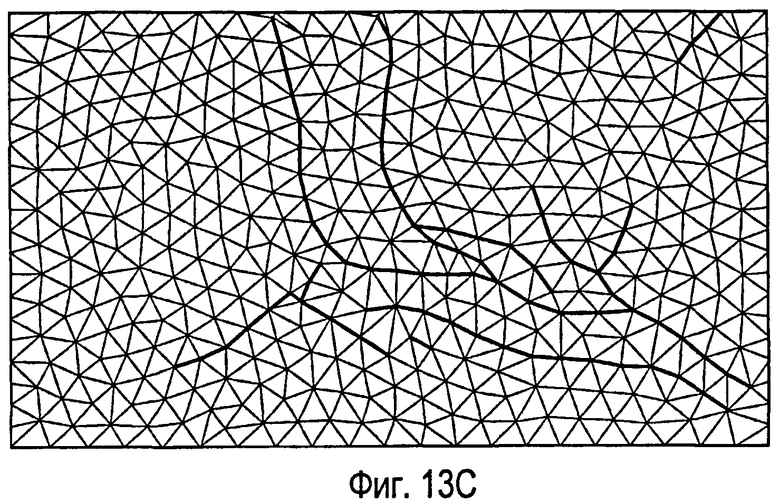
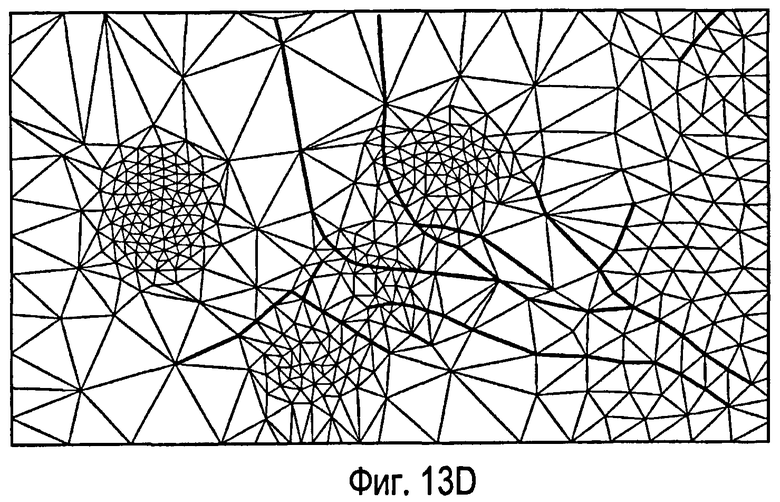
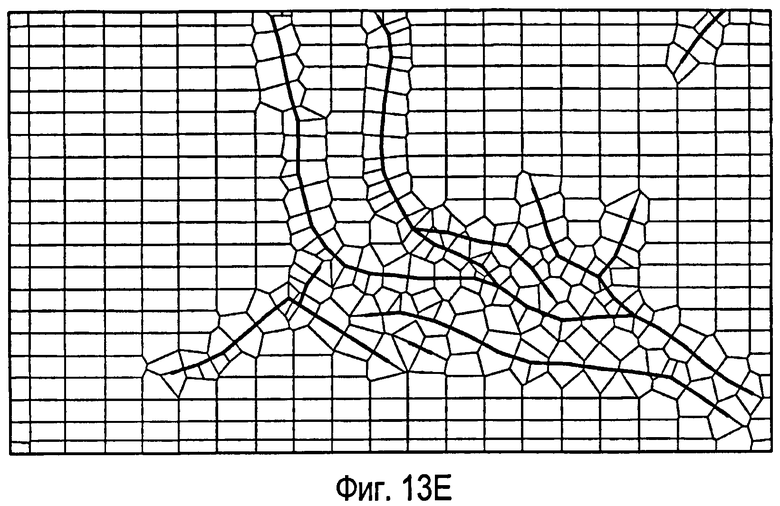
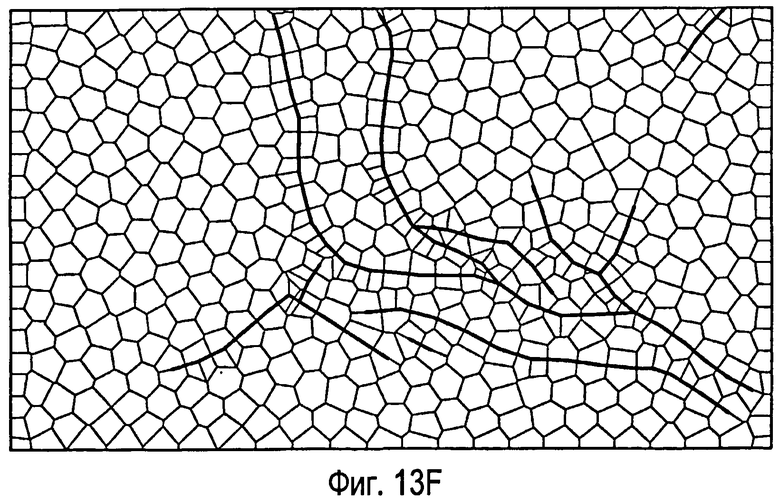
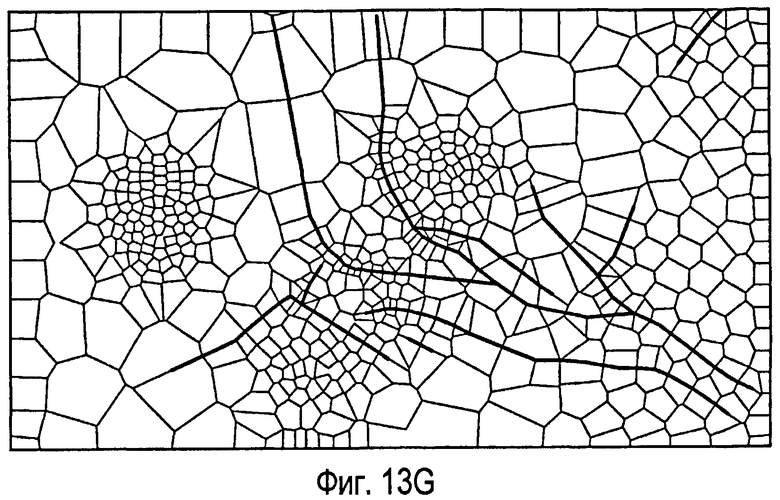
фиг.13 - пример одного варианта способа создания ограниченной сетки Вороного. На фиг.13А показана плоскость со сложными внутренними разломами. На фиг.13В показана ограниченная триангуляция Делоне, созданная согласно раскрытому способу для плоскости на фиг.13А. На фиг.13С показана выровненная триангуляция Делоне для плоскости на фиг.13А. На фиг.13D показана триангуляция Делоне, адаптированная к распределению плотности точек для плоскости на фиг.13А. На фиг.13Е показана ограниченная сетка Вороного, созданная на основе фиг.13В. На фиг.13F показана выровненная ограниченная сетка Вороного, созданная на основе фиг.13С. На фиг.13G показана ограниченная сетка Вороного, адаптированная к распределению плотности точек, созданному на основе фиг.13D.
Подробное описание изобретения
Данное изобретение решает проблему создания двумерных сеток Вороного в ограниченных зонах с внутренними разломами, которые представляют непрерывными линиями, оставленными из одной или нескольких отрезков прямых линий (называемых ломаными линиями). На практике желательно, чтобы сетки Вороного точно соответствовали границам и разломам в виде ломаных линий (то есть, чтобы границы сеточного многоугольника (клетки) точно соответствовали границам зон и разломам. В предпочтительных вариантах некоторые или все шаги реализуются на компьютере. При использовании компьютера программное обеспечение для выполнения любого шага в способе может находиться на считываемом компьютером носителе, который может, но не обязательно, быть съемным носителем.
В последующем описании термин «область» используется для ссылки на ограниченную зону, которую представляют и моделируют в виде сетки. Триангуляцию Делоне считают «ограниченной», если она обеспечивает разрешение внутренних линейных разломов и границ в области с помощью ребер клеток. Триангуляцию Делоне, построенную на заданном наборе точек и не ограниченную необходимостью соблюдения разломов, называют здесь «неограниченной» триангуляцией Делоне. Известные алгоритмы для создания ограниченных триангуляций Делоне (см., например, J.R.Shewchuk, Delaunay refinement algorithms for triangular mesh generation, Computational Geometry: Theory and Applications, v.22, pp.21-74, 2002; J.Ruppert, A Delaunay refinement algorithm for quality 2-dimensional mesh generation, J. Algorithms, vol.18, no.3, pp.548-585, 1995; L.P.Chew, Constrained Delaunay triangulation, Algorithmica, vol.4, pp.97-108, 1989; and G.L.Miller, S.E.Pav, & N.J.Walkington, When and why Ruppert 's algorithm works, Proceedings of the 12th International Meshing Roundtable, pp.91-102, 2003) и неограниченных триангуляций Делоне (см., например, работу Bowyer, упомянутую ранее) отличаются по реализации, сложности и вычислительным затратам. Триангуляцию Делоне или сетку Вороного называют «адаптивной», когда плотность точек предпочтительно регулируется так, что, чем больше имеется точек, тем требуется более высокая точность.
Раскрытые способы создания ограниченной триангуляции Делоне и сеток Вороного позволяют обеспечить разрешение внутренних разломов в точном соответствии с краями сетки Вороного при обеспечении адаптации размеров сеточной клетки к заданному распределению плотности точек. Эти способы обеспечивают преодоление таких трудностей, как присутствие небольших разломов, множество пересечений разломов, пересечения разломов под малыми углами и разломы с высокой кривизной, которые нельзя удовлетворительно обработать существующими алгоритмами.
1. Способ адаптивной ограниченной триангуляции Делоне
Последующее описание относится к способу создания ограниченной триангуляции Делоне, согласующейся с внутренними и граничными разломами и имеющей адаптивные размеры, на основе заданного критерия плотности.
Шаг 1
Строят ломаные линии разломов на основе их оцифрованного вида (см., например, A.Cunha, S.Canann, & S.Saigal, Automatic boundary sizing for 2D and 3D meshes, AMD-VoI.220 Trends in Unstructured Mesh Generation, ASME, pp.65-72, 1997) или вводят их в зависимости от имеющегося геометрического описания. Для обеспечения соответствия заданным требованиям по плотности иногда необходимо детализировать заданные ломаные линии (то есть, укоротить сегменты ломаных линий путем вставки в них дополнительных точек).
Шаг 2
Строят неограниченную триангуляцию Делоне с помощью любого известного алгоритма (например, Bowyer, упомянутый ранее) на основе точек, образующих конечные отрезки полиномиальных разломов и/или границ, полученных на шаге 1, и набора точек с заданным или равномерным распределением плотности по всей области (точки, совпадающие в пределах заданного допуска, обрабатываются как одна точка). Результирующая триангуляция оказывается не согласованной с разломами.
Шаг 3
Модифицируют начальную триангуляцию, чтобы обеспечить ее согласование с разломами и/или границами путем замены всех тех ребер в триангуляции, которые пересекают отрезки разломов, и коррекции результирующей сети с использованием известной стратегии рекурсивного применения локальной замены ребер, пока все внутренние (то есть, не лежащие на разломах) ребра триангуляции не станут локально оптимальными (см., например, C.L.Lawson, Surface for C1 surface interpolation, JPL Publication pp. 77-30, 1977). Это показано на фиг.3А и 3В. На фиг.3А сегменты 71 разлома пересечены ребрами 73 триангуляции. Ребра 73 триангуляции помечены для замены, которая наглядно обозначается штрихпунктирными линиями, а их положения после замены показаны на фиг.3В, в результате чего ребро 73 оказывается идентичным сегментам 71 разлома. Внутренние сегменты 71 разлома стали теперь на фиг.3В ребрами 74 триангуляции. Результирующая сеть соответствует разломам, но ее качество может быть неудовлетворительным в окрестности разломов.
Шаг 4
Применяем процедуру коррекции сетки, содержащую алгоритмы выравнивания сетки и фиксации разломов. Можно использовать алгоритм выравнивания (см., например, Q.Du and M.Gunzburger, Grid generation and optimization based on centroidal Voronoi tessellations, Appl. Math. Comput, v. 133, pp. 591-607, 2002) с использованием распределения плотности. Алгоритм выравнивания итеративно перемещает точки сетки, например, к центрам масс зон Вороного. Таким образом, количество точек остается неизменным, но их положения меняются. Триангуляция должна корректироваться после каждой итерации выравнивания, чтобы она оставалась триангуляцией Делоне, что может быть обеспечено многократной рекурсивной локальной заменой ребер, пока все ребра триангуляции не станут локально оптимальными (см., например, работу Lawson, упомянутую выше). Выравнивание заканчивается, когда будет удовлетворен некоторый критерий допустимости, например малое кумулятивное изменение в положении точек сетки во время последней итерации.
При итерации процедуры коррекции сетки (здесь это шаг 4) объединяют итерацию выравнивания с процедурой фиксации разлома на основе следующих двух локальных операций:
i. Выполняют привязку внутренней точки к сегменту разлома, как показано на фиг.4А. Когда внутренняя точка 75 является вершиной треугольника напротив ребра 74 границы/разлома и угол при этой вершине является тупым, внутренняя точка 75 проецируется на ребро разлома, после чего следует замена ребра 74.
ii. Перемещают точку 76 разлома из сегмента разлома внутрь, как показано на фиг.4В. Выполнение этой операции, когда внутренняя точка 75 находится напротив ребер разлома на том же сегменте разлома, предпочтительно по меньшей мере в трех треугольниках, причем сумма углов в этой точке соответствует острому углу. Во время этой операции одно из ребер, соединяющих внутреннюю точку 75 и точку 76 разлома, являющуюся общей для двух сегментов разлома, лежащих против точки 75, укорачивается (предпочтительно наполовину) путем перемещения внутрь точки 76 разлома. Это перемещение приводит к пересечению ребер, соединяющихся с точкой 76 разлома, с сегментом разлома. Указанные ребра 73 заменяются, как на вышеописанном шаге 2.
Итерация процедуры коррекции сети выполняется следующим образом:
i. Выполняют итеративный цикл по всем точкам в триангуляции и привязку подходящих точек к разлому, пока не останется ни одной подходящей точки, удовлетворяющей сформулированному выше условию; в результате перед ребрами разлома оказываются только острые углы.
ii. Аналогичным образом выполняют итеративный цикл по всем точкам с удалением подходящих точек из разломов.
iii. Корректируют триангуляцию путем рекурсивной замены ребер (см., например, работу Lawson, упомянутую выше) внутренних ребер.
iv. Переставляют все точки к центру масс их зон Вороного (точки на разломах перемещают только вдоль разломов, как, например, в работе Du и др., упомянутой выше).
v. Корректируют триангуляцию путем рекурсивной замены внутренних ребер.
Результирующая выровненная ограниченная триангуляция Делоне будет характеризоваться хорошим качеством и в основном соответствовать распределению плотности точек как внутри области, так и на разломах и/или границах. На фиг.5 показаны базовые шаги этого способа в виде блок-схемы.
Способ создания ограниченных сеток Вороного
Последующее описание относится к способу создания ограниченных сеток Вороного, которые соответствуют внутренним и граничным разломам и имеют адаптивные размеры, основанные на заданном критерии плотности.
Шаг 1
Строят ломаные линии разломов исходя из оцифрованного вида (например, работа Cunha и др., упомянутая выше) или интерактивно вводят их в зависимости от имеющегося геометрического описания. Для обеспечения соответствия заданным требованиям по плотности иногда необходимо детализировать заданные ломаные линии (то есть, укоротить отрезки ломаных путем вставки дополнительных точек на ломаных линиях).
Шаг 2
Строят защищенные многоугольники вокруг ломаных линий. Защищенные многоугольники окружают ломаные линии разломов защитной зоной и строятся для обеспечения точного представления разломов на конечной сетке Вороного. Эта концепция показана на фиг.6, где внутренние разломы 31 и граница 32 модели вложены в защитную зону 33. Защитная зона 33 ограничена ребрами защищенных многоугольников 34, которые становятся ребрами триангуляции Делоне.
Точки, используемые для формирования защищенных многоугольников, создают следующим образом. Рассмотрим ломаную линию 41 на фиг.7А и положим, что все сегменты этой ломаной линии станут ребрами многоугольников (клеток) в конечной сетке Вороного. Таким образом, вершины 42 многоугольника являются вершинами конечной сетки Вороного. Вокруг этих вершин формируют пересекающиеся окружности - диски 43. Эти окружности могут иметь радиус, изменяющийся в широком диапазоне в зависимости от геометрии разлома. Появление слишком больших окружностей можно избежать путем дополнительного разделения сегментов линии на более мелкие отрезки. Вершинами защищенного многоугольника будут две точки 44 пересечения двух соседних окружностей. Заметим, что линейный сегмент AB перпендикулярен линейному сегменту CD и делит его пополам. На границе соединения окружностей могут находиться дополнительные точки, но внутри этой границы не допускается ни одна точка. С помощью этих точек вокруг ломаной линии образуется защищенный многоугольник 45. Ребра защищенного многоугольника сохраняются в ограниченной триангуляции Делоне. Все точки на защищенном многоугольнике являются центрами клеток конечной сетки Вороного, показанной на фиг.7В, с ребрами из клеток 51 Вороного.
Предпочтительно, чтобы линейный сегмент, образованный пересечениями двух соседних окружностей (например, CD), пересекал сегмент с конечными точками, являющимися центрами этих окружностей (например, AB). Это не всегда возможно, если длинный сегмент на ломаной линии соседствует с двумя значительно более короткими сегментами. В этом случае длинный сегмент можно разбить на два или больше более коротких сегментов путем вставки дополнительных точек в длинный сегмент.
Внутри защищенного многоугольника 45 триангуляция Делоне не является уникальной, поскольку треугольники, образованные точками на одной и той же окружности, имеют один и тот же центр окружности (например, точка А). Поскольку защитная зона, ограниченная защищенным многоугольником, не содержит ни одной точки, отличной от точек на ее границе (вершины на ломаной линии разлома в триангуляции не используются), любая триангуляция Делоне внутри защитной зоны приводит к диаграмме Вороного, чьи ребра включают в себя линейные сегменты на ломаной линии. Результирующая диаграмма Вороного является уникальной.
Применительно к случаю, когда множество ломаных линий пересекаются в одной точке, можно использовать упрощенный способ, показанный на фиг.8. В этом примере четыре ломаные линии (обозначенные как линии с 1 по 4) пересекаются в одной точке. Точки размещают по окружности с центром в точке пересечения (то есть, внутренняя окружность 61 на фиг.8А и 8В). Таким образом, любая триангуляция Делоне многоугольника порождает треугольники с одним и тем же центром окружности, то есть упомянутой точкой пересечения.
Для учета пересекающихся ломаных линий для формирования зеркальных отображений по отношению к ломаной линии (например, пары А-В, А-С, D-E и F-G на фиг.8) необходима пара точек на двух сторонах ломаной линии. Для острых углов, таких как угол, образованный между линией 1 и линией 2, предпочтительно разместить только одну точку на пунктирной линии, делящей этот угол пополам. В результате получится триангуляционная клетка Вороного, согласованная с острым углом. Опять же, внутри внутренней окружности не находится ни одной точки.
Для дополнительного управления размещением клеток Вороного вблизи пересечения можно использовать еще одну окружность, например 62 на фиг.8А, особенно при наличии острых углов. Точки размещаются на этой внешней окружности таким же образом, как точки на внутренней окружности. Однако допустимо расположение точек внутри внешней окружности. Эти точки используют для упорядочения размеров и форм клеток Вороного. Способ, показанный на фиг.7А и 7В, следует использовать для размещения точек вокруг ломаных линий вдали от пересечений.
Радиусы окружностей, расположенных вокруг ломаных линий и точек пересечения, определяют на основе заданного распределения плотности точек и локальных геометрических особенностей.
Шаг 3
Используют алгоритм триангуляции Делоне, например триангуляцию Делоне (см., работу Shevchuk, упомянутую ранее), алгоритм Ruppert's (Ruppert, упомянутый ранее) или их модификации (например, в работе Chew, упомянутой ранее; Miller, упомянутый ранее) для нанесения на сетку дополнения к защитным зонам по отношению к сеточной области, которая учитывает защитные зоны в качестве ограничений. Дополнением защитной зоны является зона, лежащая вне защитной зоны, но не выходящая за границы области. То есть создают ограниченную триангуляцию Делоне со сторонами защищенных многоугольников в качестве ограничений, в дополнение к защищенным многоугольникам по отношению к исходной области. Например, алгоритм Ruppert's применим в двухмерной области с заданным плоским прямолинейным графом, состоящим из набора линейных сегментов и набора точек, которые в нашем случае представлены границами защитных зон и, но не обязательно, дополнительными точками вблизи пересечений разломов.
Алгоритмы, раскрытые в работах Shevchuk, Du и др., Ruppert, Chew, и Miller и др., упомянутых ранее, основаны на вставке новых точек и детализации, причем плотность сеточных точек и соответственно размер треугольников определяется размером и формой геометрических разломов. Вставку точек можно модифицировать с учетом заданного распределения плотности точек, так чтобы в областях с большим значением функции распределения плотности точек вставлять больше точек, то есть усилить детализацию. Для этой цели можно использовать ряд известных способов (например, R.Lohner, & J.Cebral, Generation of non-isotropic unstructured grids via directional enrichment, International Journal for Numerical Methods in Engineering, vol 49, pp.219-232, 2000). Результирующая триангуляция в основном адаптирована к геометрии разломов (то есть имеет меньше клеток в зонах с высокой кривизной разлома или с пересечением нескольких разломов под малыми углами), а также подчиняется распределению размера, определенному заданным распределением плотности точек.
Применительно к этой триангуляции можно использовать сеточное выравнивание, например, как в работе Du и др., упомянутой ранее, которое дополнительно повышает ее качество и согласованность с распределением плотности точек вдали от разломов и границ, в то время как защищенные точки не должны изменяться во время выравнивания. Сеточное выравнивание предпочтительно, но не обязательно.
Шаг 4
В стандартной процедуре строят клетки дуальной сетки Вороного путем соединения центров окружностей треугольников Делоне. То есть клетка Вороного строится путем перемещения всех треугольников Делоне, имеющих общую вершину, по часовой или против часовой стрелки вокруг этой вершины и соединения центров окружностей этих треугольников Делоне ребрами. Таким образом, указанная вершина становится центром заново построенной клетки Вороного; ребра, соединяющие центры окружностей треугольников, становятся ребрами клеток Вороного, а центры окружностей треугольников становятся вершинами клетки Вороного. Вершины триангуляции вне границ сеточной области для формирования центров клеток Вороного в этой процедуре не используются. На фиг.9 показаны основные шаги этого способа в виде блок-схемы.
3. Альтернативный способ создания ограниченных сеток Вороного
Еще в одном варианте ограниченные сетки Вороного, которые согласованы с внутренними и граничными разломами и имеют адаптивные размеры на основе заданного критерии плотности, можно создать, выполнив следующие шаги.
Шаг 1
Строят ломаные линии P1 разломов исходя из оцифрованного вида (см., например, работу Cunha и др., упомянутую выше) или вводят их интерактивным образом в зависимости от имеющегося геометрического описания. Для обеспечения соответствия заданным требованиям по плотности иногда необходимо детализировать заданные ломаные линии (то есть, вставить токи в ломаные линии).
Шаг 2
Строят ограниченную триангуляцию (Т) Делоне, согласованную с разломами и/или границами многоугольников, с использованием алгоритмов, описанных в работах Shewchuk, Ruppert, Chew, Miller и др., упомянутых ранее, или нового вышеописанного здесь способа. Во время триангуляции и/или выполнения выравнивания можно, но не обязательно, использовать распределение плотности точек (например, как было описано на шаге 4 в первом подходе к созданию сетки Вороного).
Шаг 3
Вокруг ломаных линий строят защищенные точки из вершин треугольников Делоне, лежащих на этих ломаных линиях; то есть преобразуют точки на разломах/границах в защищенные точки. Каждую точку на границе, лежащую на прямолинейном сегменте, заменяют парой защищенных точек, образующих зеркальное отображение друг против друга относительно этого сегмента (например, точки С и D, образованные из точки Е на границе на фигурах 7А и 7В). Каждую точку на границе, лежащую на пересечении нескольких сегментов, заменяют набором точек, расположенных на окружности вокруг пересечения, например точки от А до В на фиг.8А и 8В. Радиус окружности, то есть расстояние между старой точкой на границе и любой образованной из нее защищенной точкой, определяют в качестве доли минимальной длины ребра (предпочтительно 0,25) для всех ребер треугольников, соединенных с этой точкой на границе.
Многоугольные границы Р2 защитных зон формируют путем объединения защищенных точек. Для обеспечения того, чтобы триангуляция Делоне из нового набора точек S, состоящего из всех внутренних (не лежащих на границах) вершин из триангуляции Т на шаге 2, и новые защищенные точки на шаге 3 содержали все ребра границ Р2, может потребоваться дополнительное упорядочение набора точек S. С этой целью до построения защитных зон (показанных на фиг.10) выполняют дополнительный шаг, состоящий в добавлении к начальной триангуляции Т проекций точек на ограничения. Сначала оценивают текущее положение защитной зоны путем определения защищенных точек и формирования пары зеркально отображенных защитных ребер А1В1 и А2В2 на фиг.10А из каждого ограниченного ребра АВ триангуляции Т (здесь ребро триангуляции Т, лежащее на ограничивающем сегменте Р1, называют «ограниченным ребром», а ребра, образующие защитный многоугольник Р2, «защитными ребрами»). Затем ищут защитные ребра, которые нарушают условие Делоне, среди модифицированных треугольников А1В1С на фиг.10В в триангуляции Т с ограниченными ребрами АВ, замененными соответствующими оцененными защитными ребрами А1В1 (любые, которые ближе к противоположной вершине треугольника). Проверяют, находятся ли конечные точки зеркально отображенного защитного ребра А2В2, образованного из того же ограничительного ребра АВ, внутри окружности модифицированного треугольника А1В1С. Если это подтверждается, то соответствующие ограниченные ребра AB делят на части путем добавления проекции С1 противолежащей вершины С треугольника на ребро АВ к вершинам триангуляции Т (см. фиг.10С). Затем обновляют набор защищенных точек S путем восстановления защищенных точек из новых граничных точек А, В и С1 триангуляции Т. Такое упорядочение итеративно повторяется, пока не останется ни одного защитного ребра, не соответствующего триангуляции Делоне.
Шаг 4
Строят триангуляцию Делоне из набора точек S, полученных на шаге 3. Эту триангуляцию создают с использованием любого алгоритма неограниченной триангуляции Делоне (например, алгоритм Bowyer, упомянутый выше). Поскольку набор точек задан, алгоритм триангуляции не должен учитывать распределение плотности точек или ограничения. Кроме того, выполнение триангуляции необходимо только для зон вокруг заново вставленных защищенных точек; остальная часть триангуляции Делоне остается такой же, как после шага 2. Можно, но не обязательно, выполнить выравнивание, которое поддерживает защищенные точки неизменными.
Шаг 5
В стандартной процедуре строят клетки дуальной сетки Вороного путем соединения центров окружностей треугольников Делоне. То есть клетка Вороного строится путем перемещения всех треугольников Делоне, имеющих общую вершину, по часовой или против часовой стрелки вокруг этой вершины и соединения центров окружностей этих треугольников Делоне ребрами. Таким образом, указанная вершина становится центром заново построенной клетки Вороного; ребра, соединяющие центры окружностей треугольников, становятся ребрами клеток Вороного, а центры окружностей треугольников становятся вершинами клетки Вороного. Вершины триангуляции вне границ сеточной области в этой процедуре не используют для формирования центров клеток Вороного. На фиг.11 показаны основные шаги этого альтернативного способа в виде блок-схемы.
4. Примеры
Пример 1
Обратимся к фигурам 12А-12Е, где показан вариант, описанный выше как «альтернативный способ создания ограниченных сеток Вороного». Для данной плоскости выполняют аппроксимацию внутренних разломов 81 и границ 82, как показано на фиг.12А. Строят ограниченную триангуляцию Делоне для этой плоскости, как показано на фиг.12В. Как показано на фиг.12С, вводят защищенные точки 83 около внутренних разломов 81 и границ 82. Строят новую ограниченную триангуляцию Делоне с использованием нового набора точек, как показано на фиг.12D. На фиг.12Е показана конечная сетка Вороного, ограниченная внутренними разломами и границами. Количество клеток/точек сетки определяется заданным требованием равномерной плотности.
Пример 2
Обратимся к фигурам 13А-13F, где показаны варианты, описанные выше как «альтернативный способ создания ограниченных сеток Вороного» и «новый подход к адаптивной ограниченной триангуляции Делоне». На фиг.13А показана плоскость с многочисленными внутренними разломами, включая пересечения 92 между разломами. В этом примере внутренние разломы, полученные из следов сбросов в геологическом описании месторождения углеводородов, нарушенного сбросами, аппроксимированы набором ломаных линий 91, показанных на фигурах 13А-13F, иллюстрирующих этот пример. На фиг.13В показана ограниченная триангуляция Делоне согласно раскрытому способу. На фиг.13С показана триангуляция Делоне после сеточного выравнивания. На фиг.13D показана ограниченная триангуляция Делоне, адаптированная к распределению плотности точек.
На фиг.13Е показана ограниченная сетка Вороного согласно настоящему изобретению для плоскости на фиг.13А. Сетку Вороного можно получить исходя из выровненной триангуляции Делоне, как показано на фиг.13F, и/или адаптировать к распределению плотности точек, как показано на фиг.13G.
Хотя настоящее изобретение было описано достаточно подробно, следует понимать, что в него могут быть внесены различные изменения, замены и модификации, не выходящие за рамки объема и существа изобретения, определенные в прилагаемой формуле изобретения.
Изобретение относится к созданию двумерных сеток Вороного в ограниченных зонах с внутренними разломами. Технический результат заключается в повышении качества и точности конечной сетки Вороного и модели на ее основе за счет выравнивания сетки. Способ создания ограниченных триангуляций Делоне на плоскости с внутренними разломами и границами включает в себя аппроксимацию внутренних разломов и границ ломаными линиями на основе геометрии плоскости. Вокруг ломаных линий создают защищенные многоугольники или точки, а затем строят триангуляцию Делоне из защищенных точек и вершин защищенных многоугольников. В остальной части сеточной области создают триангуляцию Делоне, которая учитывает защищенные многоугольники или точки. Затем из этой триангуляции Делоне создают ограниченную сетку Вороного, которая обеспечивает разрешение всех аппроксимированных разломов и границ с помощью ребер клеток Вороного. Ограниченные сетки Вороного можно создать с адаптивными размерами клеток на основе заданного критерия плотности. 3 н. и 19 з.п. ф-лы, 29 ил.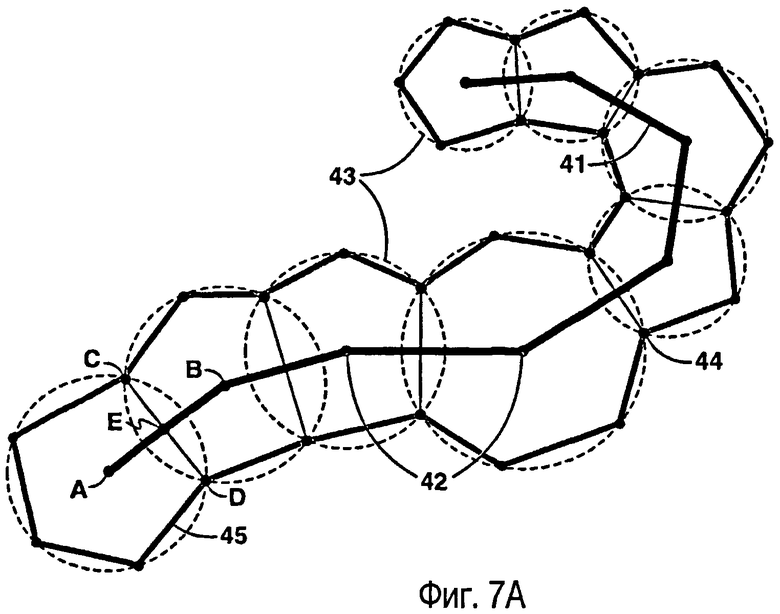
1. Способ создания ограниченной триангуляции Делоне для плоской области с границами и внутренними разломами, содержащий:
аппроксимацию границ и внутренних разломов области ломаными линиями;
построение для упомянутой области неограниченной триангуляции Делоне;
модификацию неограниченной триангуляции Делоне для согласования сторон треугольников с ломаными линиями;
коррекцию модифицированной ограниченной триангуляции для превращения ее в ограниченную триангуляцию Делоне.
2. Способ по п.1, в котором модификация неограниченной триангуляции Делоне для согласования сторон треугольников с ломаными линиями содержит замену ребер всех треугольников, пересекающих внутренний разлом.
3. Способ по п.1, в котором коррекция модифицированной ограниченной триангуляции для превращения ее в ограниченную триангуляцию Делоне содержит сеточное выравнивание и фиксацию разлома.
4. Способ по п.1, в котором коррекция модифицированной ограниченной триангуляции для превращения ее в ограниченную триангуляцию Делоне содержит:
привязку внутренней точки к сегменту разлома;
перемещение точки из сегмента разлома вовнутрь;
перестановку всех точек к центрам масс их зон Вороного и
рекурсивное применение локальной замены ребер на ребра, не относящиеся к разлому, пока все ребра триангуляции, не относящиеся к разлому, не окажутся оптимальными.
5. Способ по п.3, в котором при выравнивании сетки используют заданное распределение плотности точек.
6. Способ создания ограниченной сетки Вороного для плоской области с границами и внутренними разломами, содержащий:
аппроксимацию границ и внутренних разломов области ломаными линиями;
построение защищенных многоугольников вокруг ломаных линий;
построение ограниченной триангуляции Делоне со сторонами защищенных многоугольников в качестве ограничений в дополнение к защищенным многоугольникам в отношении указанной области;
построение ограниченной сетки Вороного на основе ограниченной триангуляции Делоне.
7. Способ по п.6, в котором ломаные линии основаны на геометрии внутренних разломов и заданном распределении плотности точек.
8. Способ по п.6, в котором построение защищенных многоугольников содержит:
построение многоугольников разломов из ломаных линий;
построение многоугольников из перекрывающихся окружностей с центрами на пересечениях сегментов ломаных линий и
разделение многоугольников с получением триангуляции Делоне.
9. Способ по п.8, дополнительно содержащий детализацию ломаных линий для согласования с заданным распределением плотности точек.
10. Способ по п.8, в котором радиусы указанных окружностей определяют на основе заданного распределения плотности точек и/или локальных геометрических особенностей.
11. Способ по п.6, дополнительно содержащий сеточное выравнивание триангуляции Делоне.
12. Способ по п.11, в котором сеточное выравнивание основано на цетроидальных двумерных сотах Вороного.
13. Способ по п.6, дополнительно содержащий адаптацию триангуляции Делоне к распределению плотности точек.
14. Способ создания ограниченной сетки Вороного для плоской области с границами и внутренними разломами, содержащий:
аппроксимацию границ и внутренних разломов области ломаными линиями;
построение ограниченной триангуляции Делоне, ограниченной ломаными линиями;
построение защищенных точек вокруг ломаных линий из вершин ограниченной триангуляции Делоне, лежащих на ломаных линиях;
построение новой неограниченной триангуляции Делоне из набора защищенных точек и внутренних вершин ограниченной триангуляции Делоне и построение ограниченной сетки Вороного на основе новой неограниченной триангуляции Делоне.
15. Способ по п.14, в котором ломаные линии основаны на геометрии внутренних разломов и заданном распределении плотности точек.
16. Способ по п.14, в котором построение защищенных точек содержит:
замену каждой точки, лежащей на разломе, парой зеркальных отображений защищенных точек; и
замену каждой точки, лежащей на пересечении разломов, набором точек, находящихся на окружности с центром на указанном пересечении.
17. Способ по п.16, в котором построение защищенных точек содержит:
упорядочение путем оценки проекций на ограниченные ребра ограниченной триангуляции Делоне всякий раз, когда защитное ребро, оцененное исходя из ограниченного ребра, не удовлетворяет условию Делоне; и
добавление защищенных точек, образованных из точек проекции.
18. Способ по п.14, дополнительно содержащий детализацию ломаных линий для согласования с заданным распределением плотности точек.
19. Способ по п.16, в котором радиусы указанных окружностей определяют на основе размера ребра в ограниченной триангуляции Делоне.
20. Способ по п.14, дополнительно содержащий сеточное выравнивание триангуляции Делоне.
21. Способ по п.20, в котором сеточное выравнивание основано на цетроидальных двумерных сотах Вороного.
22. Способ по п.14, дополнительно содержащий адаптацию триангуляции Делоне к распределению плотности точек.
| US 20040246249 A1, 09.12.2004 | |||
| US 20060173338 A1, 03.08.2006 | |||
| US 20050099415 A1, 12.05.2005 | |||
| RU 2003110175 A, 27.08.2004 | |||
| RU 2004126667 A, 10.02.2006. |
Авторы
Даты
2012-03-10—Публикация
2008-04-02—Подача