ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к материаловедению и может быть использовано для создания изделий с заданными свойствами, в частности для изготовления материалов и устройств с низкими, высокими или сверхвысокими физическими свойствами и характеристиками.
УРОВЕНЬ ТЕХНИКИ
В уровне техники известны так называемые пучковые материалы и устройства, изготовленные по пучковой технологии [1-7]. Пучковая технология (ПТ) - это физическая модификация материалов и устройств без перестройки их химической структуры с целью изготовления изделий с заданными физическими свойствами и характеристиками.
ПТ - это физическая модификация материалов и свойств без перестройки химического строения тел с целью получения изделий с заданными низкими, высокими, или сверхвысокими физическими свойствами и характеристиками.
Прототипы пучковых материалов и устройств ПТ изначально реализованы в натуральной природе, к примеру, в тонких паутинках и волокнах шелкопряда, кератина шерсти, джута и льна, в бамбуке или тростнике, в стволах деревьев и т.д. Тонкие волокна из числа N составляющих, собранные в пучок, т.е. в ствол растения противостоят погодным стихиям, высоким и низким температурам, агрессивным средам, высоким и сверхвысоким силовым и энергетическим нагрузкам. Эти природные феномены подсознательно использовались нашими далекими предками в шелковых и хлопковых нитях, в морских корабельных канатах, в такелажных тросах и в веревках, в дамасских саблях, в японских мечах и булатных сталях древней Руси.
Под пучком (или стопой) в уровне техники (см., к примеру, патенты [1-4]) и ряд др. понимается многоэлементная (многослойная) структура, выполненная из числа N>1 (где N - целое число) отдельных однотипных тонких составляющих элементов (волокон или пленок, или фольги), расположенных параллельно друг с другом (или друг над другом) и объединенных общим контактом. А сам способ выполнения материалов и устройств путем объединения отдельных тонких однотипных составляющих элементов в пучок был назван ПТ.
К наиболее близким к заявленному изобретению относится материал для компонентов радиоэлектронных приборов (патент [1, 4]), выполняемый по ПТ. Материал для компонентов радиоэлектронных приборов, имеющий многослойную структуру, выполненную из N>1 слоев пленок или волокон, причем слои выполнены из отдельных однотипных тонких пленок или волокон с толщиной, равной d<80 мкм.
В указанных изобретениях в качестве составляющих элементов пучка (пленок, волокон, проволок) использованы полиимид, или кварц, или слюда, или медь, или серебро, или германий, или галлий, алюминий, или нихром и т.д.
Известен из той же серии изобретений этих авторов пучковый материал для защиты от ударных воздействий [5], фактически являющийся одновременно по функциональному назначению устройством. Этот материал или устройство для защиты от ударных воздействий, согласно описанию изобретения, имеет многослойную (многоэлементную) или пучковую структуру, выполненную из N>1 отдельных однотипных тонких пленок, по существу, равной толщины d<70 мкм, объединенных в стопу (или в пучок). В качестве составляющих однотипных элементов-пленок пучка (или стопы) использованы полимерные и металлические пленки. Это изобретение направлено на расширение функциональных возможностей, повышение значений механической и электрической прочности, механической и электрической долговечности материала или устройства для защиты от ударных воздействий.
Близким к заявленному являются изобретения на пучковые электроизоляционные материалы [5, 6]. Тесно по свойствам примыкает изобретение «Диэлектрический материал для изделий, работающих в СВЧ-диапазоне» [3].
Не менее близким к настоящему изобретению является изобретение «Проводник электрического тока и способ его изготовления» [7], где предлагается пучковый материал-проводник, по которому протекает электрический ток большой плотности без выделения Джоулева тепла, т.е. без его нагревания. Недостатком этого проводника является его малая протяженность. В реальных условиях нужен достаточно длинномерный по протяженности проводник. Для этого авторами предлагаются дополнительные усложняющие приемы их изготовления. В настоящем изобретении устранен этот недостаток.
Все эти изобретения относятся к пучковым материалам и устройствам, т.е. к материалам и устройствам, имеющим однотипные отдельные составляющие элементы, выполненные по ПТ. Однако фактически во всех изобретениях пучковый материал одновременно является и пучковым устройством. Например, в [5] электроизоляционный материал одновременно, без какой-либо переделки может служить изолятором электрического тока, т.е. защитным устройством. Или, к примеру, «Проводник электрического тока и способ его изготовления» [7] является пучковым материалом-проводником и одновременно устройством для протекания сверхвысоких плотностей тока.
Если от классического одноэлементного материала до устройства лежит более или менее длительный технологический путь перестройки (переделки) материала в какое-то устройство или изделие, то от пучкового материала до пучкового устройства такого практически нет, либо требуется перестройка по минимуму.
Указанные выше изобретения из уровня техники посвящены созданию материалов и устройств с низкими или сверхнизкими, высокими или сверхвысокими значениями физических свойств и характеристик. Их осуществление основано на более или менее корректном использовании явления дискретности физических свойств твердых тел, применении универсальных общих природных закономерностей изменения структурно-чувствительных физических свойств (СЧФС) и характеристик (СЧФХ) одноэлементных и многоэлементных структур, явлении одноэлементного и многоэлементного масштабного фактора или «эффект пучка», а также применении общих закономерностей экспериментального разброса данных при физических измерениях [8].
СЧФС и СЧФХ - структурно-чувствительные физические свойства и характеристики - это свойства и характеристики чувствительные и зависимые от структуры и изменений в структуре тела. Например, механическая прочность на разрыв σ - это свойство тела, а характеристикой прочности является ее долговечность под нагрузкой τ. Или, к примеру, электрическая прочность - это свойство тела, а его долговечность - это характеристика прочности. К структурно-чувствительным относятся: электрическое сопротивление и емкость, индуктивность, механические и диэлектрические потери, теплофизические характеристики тел, деформационные характеристики, коэффициенты газопроницаемости и т.д.
Согласно этим феноменам при снижении линейных размеров одноэлементных структур (пленок и волокон) происходит эффект высокого увеличения СЧФС и характеристик (СЧФХ) полимеров и твердых тел. При объединении в пучок (стопу) этих тонких одноэлементных структур (с высокими характеристиками) происходит эффект сверхвысокого увеличения (эффект пучка) физических характеристик или свойств и снижение дисперсии пропорционально числу элементов N в пучке. Это означает, что разброс данных эксперимента при увеличении числа N отдельных однотипных тонких элементов в пучке устраняется. В пучке физические характеристики и свойства тел имеют не только сверхвысокие, но прецизионные значения.
Таким образом, объединение в пучок при его корректном исполнении может явиться не только универсальным способом улучшения и повышения физических свойств и характеристик, но и способом устранения разброса экспериментальных данных.
В изобретениях материалов и устройств, из уровня техники, модифицируются те или иные физические свойства или характеристики, например, электрические, диэлектрические, механические и т.д. Однако для того чтобы использовать модифицируемые физические свойства и характеристики в реальных условиях, эти материалы должны, прежде всего, обладать минимальной, высокой или даже сверхвысокой долговечностью и прочностью, а также стойкостью к факторам внешнего воздействия. Такому требованию отвечают, при ее корректном исполнении, предлагаемые авторами пучковые материалы и устройства, выполненные ПТ.
ПТ позволяет изготовить материалы и устройства физической модификацией структуры тел, путем простого изменения масштаба и числа N составляющих элементов и их последующего складывания (объединения) в стопу (или пучок) без химической перестройки структуры этих тел.
Физические свойства и характеристики предлагаемого пучкового материала или устройства увеличиваются как минимум на два десятичных порядка. Это наглядно демонстрируется на фиг. 1, где на примере долговечности пленок полиметилметакрилата (ПММА) показан эффект пучка в многоэлементной (пучковой) структуре.
Объединение тонких элементов в стопку или пучок, а также снижение масштаба составляющего элемента пучка, одновременно улучшают структуру материала и существенно усиливают (повышают) его физические свойства и характеристики. При этом, поскольку пучки являются многоэлементными структурами, которые состоят из множества N индивидуальных однотипных отдельных тонких составляющих элементов пучка, то они являются, фактически, математическими выборками или статистическими ансамблями, подчиняющиеся математическому закону больших чисел.
Согласно математическому закону больших чисел, в статистическом ансамбле, выборке или пучке число однотипных отдельных составляющих элементов N должно стремиться к бесконечно большой величине (N→∞), а размер этих индивидуальных составляющих элементов пучка должен стремиться к бесконечно малой величине (d→Δ). На практике величина N→∞ не достижима, но приблизиться к достаточно большим значениям, для получения материалов с предельными физическими свойствами, например, при заданном минимальном масштабе, например, толщине d возможно.
Согласно настоящему изобретению бесконечно малая величина составляет в идеале Δ=1 нм. В уровне техники в пучковых материалах или устройствах бесконечно малая величина Δ не заявлена, по крайней мере, для использования в пучковой технологии изготовления материалов и устройств. Это минимальный поперечный размер тела, при котором оно существует как вещество, т.е. это размер атома вещества в поперечнике.
В указанных выше изобретениях из уровня техники авторы выставили в формулах изобретения требования, что число составляющих элементов N должно быть больше 1 (N>1, где N - целое число). Толщина d составляющего элемента-пучка в этих изобретениях составляет: в изобретении [5] менее 25 мкм, а в [1] и [2] менее 80 и 70 мкм. Из математического закона больших чисел следует, что N должно стремиться к бесконечно большому числу (N→∞), а толщина d должна стремиться к бесконечно малому значению Δ (d→Δ), т.е. N должно быть достаточно большим числом, a d - достаточно малым, обеспечивающим эффект усиления физических свойств. Однако в этих формулах изобретения требование N>1 недостаточно для толщины d=70-80 мкм. N должен при таких значениях толщины быть намного больше 1 (т.е. N>>1). По крайней мере, для получения предельных значений физических свойств и характеристик проведенные эксперименты показывают и подтверждают, что должно быть выполнено условие N>>1, или даже намного больше 10 (N>>10), 100 и т.д.
Известно, что для числа N больше 1 (N>1), например, N=2 эффект усиления может быть выполненным, а может быть и не выполнимым. Вероятность Pm получения усиления (увеличения) физической характеристики в таком пучке из двух элементов очень низкая. А для числа N>>1, например, N=11 вероятность Pm увеличится. Однако это, прежде всего, зависит не только от числа N, но и от масштаба (размера) образца, в частности, от толщины d волокна или пленки. Кроме того, известно, что при меньших значениях чем 70 мкм и 80 мкм, например, при 69,99999 мкм или 69,9 мкм и 79,99999 или 79,9 мкм и т.д. эффекта увеличения значений физических характеристик или свойств не будет.
Чем больше N и тоньше составляющий элемент, тем больше вероятность Pm того, что эффект усиления свойств проявится. Если, например, толщину составляющих элементов в [1, 4] взять меньше 80 мкм, как это сказано в формуле, например, в 79 мкм, то Pm=0, а эффект пучка технически будет нереализуем и изобретение при таком d технически не выполнимо! Кроме того, если в изобретении [2] размер d взять равным, как там сказано, меньше 70 мкм (d<70 мкм), т.е., например, в 69 мкм, то это изобретение также технически не реализуемо.
В другом изобретении [2] в формуле предлагается толщина пленки не d<80 мкм, а толщина d<70 мкм, которая для значений достаточно близких к 70 мкм (хоть и меньших 70 мкм), также фактически не является тонкой, следовательно, это изобретение при таком значении толщины не реализуемо. При выполнении пучковых материалов выбор пленок и волокон толщиной d≤50-60 мкм можно считать более корректным.
Поэтому выбор в изобретении [5] толщины составляющего элемента d<25 мкм можно считать более корректным. Следовательно, при толщине d=50 мкм и N=2 эффект пучка также реализуется. Все это говорит о том, что в каждом конкретном случае, в уровне техники, для выполнения пучка необходимо было провести дополнительные эксперименты для корректного и точного выбора размеров составляющего элемента пучка, что было вполне возможно для того уровня развития техники, когда эти изобретения были заявлены.
С другой стороны, во всех изобретениях, приведенных выше, в формулах изобретения, вводятся ограничения по геометрическому размеру только в отношении толщины d, а ширина h и длина l составляющего элемента пучка не принимаются во внимание. Если бы в этих изобретениях рассматривались только волокна (т.е. длинномерные протяженные тела с малым поперечным размером), то даже в этих случаях надо учитывать ограничения не только по толщине d, но и по длине l составляющего элемента пучка. Но поскольку во многих изобретениях рассматриваются плоские тела, т.е. пленки, тела, имеющие большую поверхность, но малый поперечный размер (толщину), то в общем виде надо ограничения в формулах вводить не только по толщине d, но и по ширине h и длине l составляющего элемента пучка исходя из геометрических особенностей конструкции многоэлементного изделия, поскольку явление масштабного фактора возникает как по толщине, так и по ширине и длине пленочных образцов.
Таким образом, в уровне техники в формулах изобретений требования по ширине и длине составляющих элементов пучка, учитывающие геометрические особенности конструкции многоэлементного изделия, ни в одном из изобретений не заявлены.
В предлагаемом изобретении для расчета оптимального числа N в пучке авторами предложены формулы расчета, учитывающие толщину d, ширину h, длину l составляющего элемента пучка. Кроме того, учитывается и внешняя физическая нагрузка F на образец.
Общая схема определения, при каких оптимальных линейных размерах одного составляющего элемента надо начинать формировать пучковый материал, состоит в том, что для этого предварительно необходимо провести статистические измерения искомых физических характеристик или свойств в зависимости от его линейных размеров (толщины d, ширины h и длины l) с учетом геометрических особенностей конструкции многоэлементного изделия (пучка), исходя из которых нужно менять один, два или сразу все три линейных размера d, h, l.
По результатам этих измерений d, h, l строится функция распределения плотности вероятности ρ физической характеристики или свойства σ для образцов разных линейных размеров d, h, l до появления полимодальности этой функции распределения. При этом согласно методике (см. главу 1 в [9]), каждому зафиксированному линейному размеру одного элемента (образца) должна соответствовать статистическая выборка или ансамбль из не менее 100 образцов.
В процессе указанных измерений постепенно прекращается изменение сначала одного, затем другого линейных размеров по достижении ими нужных геометрических размеров и остается определение оптимального последнего линейного размера. Для пленок и волокон таким линейным размеров является толщина d.
Таким образом, практически для того, чтобы определить при какой оптимальной толщине d волокна или пленки, надо начинать компоновку (формирование) пучкового материала, необходимо предварительно провести статистические измерения искомых физических характеристик или свойств пленок и волокон различного масштаба, например, толщины d. При этом, согласно методике (см. главу 1 в [9]), каждой толщине di (где i=1, 2, 3, …, n) должна соответствовать статистическая выборка или ансамбль из не менее 100 членов (образцов). Практически члены статистического ансамбля располагают в последовательный ряд в порядке возрастания номера n и получают таким путем интегральную кривую или функцию распределения физической характеристики или свойства (см. к примеру, фиг. 2 и фиг. 3В).
По результатам этих измерений строится дифференциальная кривая, т.е. функция распределения плотности вероятности ρ(σ) физической характеристики или свойства σ для образцов разных толщин, начиная, например, с d=80 мкм. При этом функция ρ(σ) вычисляется по формуле [9-10, 19]:

где N - число образцов данной серии (не меньше 100); n - число образцов из этой серии со значением физической характеристики или свойства σ, находящейся в некотором интервале Δσ, причем все возможные значения σ от нуля до ∞ разбиваются на эти интервалы и каждому интервалу Δσ соответствует свое значение ρ(σ) (здесь σ - среднее значение σ в интервале Δσ). Интервалы Δσ для расчета плотности вероятности ρ(σ) выбираются произвольно, но так, чтобы в интервалах, где ρ(σ) не близко к нулю, число образцов, попадающих в эти интервалы, было существенно больше единицы (N>>1). Площадь, ограниченная кривой распределения, всегда равна по условию нормировки единице:

На основании таких измерений строятся графические зависимости функции распределения плотности вероятности физических характеристик и свойств (см. далее, примеры на фиг. 2б, 3-4).
Если при снижении толщины d, будет обнаружена полимодальность функции распределения, т.е. несколько максимумов на дифференциальных кривых распределения, то эта пленка считается тонкой и эта толщина и будет оптимальным значением толщины d, с которого надо начинать формировать (компоновать) пучок из N составляющих элементов.
Как показали систематические теоретические и экспериментальные исследования [9-10], тонкие пленки и волокна имеют полимодальные функции распределения физических характеристик. К тонким относятся пленки и волокна толщиной d≤50-60 мкм. Пленки и волокна толщиной d более 60 мкм имеют унимодальные функции распределения и они, как правило, являются массивными. Следовательно, при толщине d=80 мкм, как заявлено в уровне техники, и гораздо меньших значениях d, а также при значениях N≥1 эффекта пучка не будет, т.е. физические свойства и характеристики в таких пучках не будут усиливаться (увеличиваться).
Практически, для получения сверхвысоких физических свойств и характеристик, согласно закону больших чисел надо число элементов N брать не больше 1, а намного больше 1 или даже больше 10, или больше 100 и т.д. Желательно (необходимо), чтобы в пучке было N>>1, N>>10, N>>100 и т.д., т.е. число N должно стремиться к бесконечности ∞, а толщину d пленки (волокна) надо, фактически, брать меньше 50-60 мкм (d≤50-60 мкм) или намного меньше 50-60 (d<<50-60) мкм. Соблюдение этих требований не ведет к непроизводительным материальным затратам, как при изготовлении пучковых материалов и устройств по вышеуказанным изобретениям из уровня техники.
Снижение толщины волокна или пленки d ведет к снижению числа N в пучке и снижению в итоге материалоемкости конечного изделия. Однако в любом случае требование в формуле этих изобретений о выборе толщины d<70-80 мкм, а не d≤50 мкм является некорректным, хоть увеличивает правовую область защиты изобретения.
Таким образом, выше установлена верхняя граница корректного выбора толщины d составляющего элемента пучка исходя из данных в уровне техники, выше которой пленка или волокно являются массивными, а нижнюю границу не уточняли, считая всю область пленки меньше 80 мкм тонкой. В настоящем изобретении этот признак определен и уточнен. Ниже показано, что тонкой пленку или волокно можно считать условно до d=0,1 мкм. При толщине d≤0,1 мкм пленка или волокно имеют принципиально иные физические свойства. Это нижняя граница толщины, до которой волокно или пленку можно считать тонкой. Но это уже новый уровень развития техники. Это принципиально другая область. Функция распределения плотности вероятности физических характеристик и свойств в ней переходит в унимодальную форму с одним максимумом. Поэтому в формулах изобретений из уровня техники требуются принципиальные уточнения и дополнения.
В указанных выше известных из уровня техники технических решениях для получения материалов и устройств с заведомо высокими или сверхвысокими значениями физических свойств и характеристик требуется также соблюдение ряда других условий, при которых в пучке возникал бы эффект сверхвысокого увеличения характеристик и свойств. К примеру, для реализации эффекта пучка в соответствии с законом больших чисел требуется соблюдение признаков однотипности, отдельности тонких индивидуальных составляющих элементов пучка.
Признаки однотипности и отдельности и требования большого числа тонких составляющих элементов N и малой толщины d пленок и волокон являются фундаментальными и основополагающими требованиями математического закона больших чисел, без выполнения которых у пучковых материалов и устройств эффекты усиления свойств будут выражены очень слабо, или их вовсе не будет.
Однотипность в перечисленных выше изобретениях обеспечивается одинаковыми массогабаритными размерами составляющих элементов пучка, например, одинаковой толщиной, шириной и длиной, весом и конфигурацией образцов в статистическом ансамбле.
Однако, и это естественно, кроме однотипности составляющие элементы в пучке должны выполнять и однотипную (одинаковую) функцию, иметь одинаковое функциональное назначение, о котором ни в одном изобретении из уровня техники не заявлялось. Это фактически приведет к промышленной неосуществимости изобретения. Что также необходимо отнести как к существенным неточностям в заявленных изобретениях, так и недостаткам в изобретениях из уровня техники.
Описания приемов обеспечения другого фундаментального признака, отдельности, например, в изобретениях [1, 4] не заявлено, что является в них скорее их недостатком. Хотя в другом изобретении этих авторов [2] в качестве способа отделения пленок или волокон друг от друга предлагается послойное напыление составляющих элементов пучка. Однако послойное, обычно вакуумное напыление, ограничено малыми площадями и объемами, технологической трудоемкостью. В настоящем изобретении предлагается более простой и технологичный способ: для этого необходимо использовать готовые однотипные отдельные пленки, изготовленные любым известным способом или обеспечивать между слоями небольшой воздушный зазор.
В уровне техники в вышеуказанных изобретениях пучковых материалов и устройств есть еще один существенный недостаток. В зависимости от функционального назначения составляющих элементов пучка, отделитель несет определенную нагрузку (например, механическую или электрическую). Поэтому для обеспечения принципа отдельности отделитель надо выполнять пучковым из числа N≥1 составляющих элементов.
Кроме того, в самом определении пучка [1] сказано, что для выполнения пучка требуется объединение тонких составляющих элементов общим контактом. Однако этого недостаточно. Требования наличия контактов в пучке не менее фундаментальны при изготовлении пучкового материала или устройства. Это требование не может быть достаточным, например, при рассмотрении пучкового проводника из волокон или пленок. Скорее, пучок, например, проводник, с одним объединяющим контактом не будет функционировать. Такое изобретение, фактически, неосуществимо. Для функционирования пучкового проводника, по крайней мере, должно быть минимум два объединяющих противоположных токовых электродов-контактов (один на входе, а другой на выходе) пучка. При одном общем объединяющем контакте в пучке, скорее всего, будет реализовываться не эффект пучка, а обратный эффект - эффект делокализации физических свойств и характеристик или «эффект веника».
При выполнении электроизоляционного материала (устройства) или материала для защиты от ударных воздействий требуется стопа из N слоев пленок, закрепленных по краям и концам пленки (если составляющие элементы, например, круговой или прямоугольной конфигурации). Затем такая многослойная стопа заключается (размешается) как минимум между двумя противоположными токовыми электродами-контактами, хотя об этом в описаниях патентов в уровне техники ничего не упоминается.
Для функционирования пучка, следовательно, изготовления пучкового материала или устройства необходимо наличие как минимум двух противоположных (пар контактов), объединяющих (сходящихся в узел составляющих элементов пучка, а не расходящихся) в пучок контактов. При этом составляющие элементы пучка, т.е. сам пучок, для функционирования, должен быть заключен между противоположными контактами. Контакты - неотъемлемая часть пучкового материала или устройства для его функционирования. Противоположных пар контактов может быть гораздо больше двух. Все зависит от конкретной конфигурации и конструкции пучкового материала. Все эти соображения свидетельствуют о том, что предлагаемые в уровне техники пучковые материалы и способы их изготовления нуждаются как в уточняющих определениях, так и в дальнейшей диверсификации в соответствии с новым уровнем развития техники.
Из закона больших чисел следует, что осуществить эффект пучка возможно несколькими способами. В частности, чтобы получить материал со сверхвысокими свойствами и характеристиками необходимо варьировать число N однотипных элементов и их толщину d. Если снижать толщину d пленки, его ширину d и длину l (или для волокна толщину и длину), то число N соответственно снижается. При меньших геометрических размерах требуется меньшее число N составляющих элементов и наоборот.
Это связано с тем, что при снижении геометрического масштаба волокон или пленок увеличивается экспериментальный разброс физических характеристик и свойств. Проявляется весь дискретный спектр больших и малых дефектов и соответствующих им уровней физических свойств (см. далее текст описания изобретения). Снижение масштаба, например, толщины d ведет к переходу образцов, содержащих дефекты, с низких уровней свойств, на более высокие уровни свойств и в результате такого перераспределения среднее значение физических характеристик и свойств увеличивается. Поэтому в пучке тонких составляющих все образцы находятся на высоких уровнях свойств. В результате среднее значение физических характеристик в пучке тонких пленок (волокон) существенно увеличивается.
Следовательно, при снижении масштаба, например, толщины d для достижения сверхвысоких характеристик требуется меньшее число N составляющих элементов в пучке. Если d увеличивается, то надо увеличивать соответственно и число N составляющих пленок или волокон. Однако d можно увеличивать до определенной толщины - до d=50-60 мкм, выше которого уже наступит массивное (низкомодовое) состояние и эффекта усиления в пучке не будет.
Число N можно увеличивать до достаточно большого значения в идеале до ∞, что практически не достижимо. При снижении числа составляющих элементов N до 2 (N=2) максимальная толщина d должна составлять 50-60 мкм, при которой еще возможен эффект усиления в пучке. При снижении N до 1 (N=1) пучок вырождается. Эти структуры нами названы соответственно вырожденными пучками, являющимися фактически одноэлементными сверхтонкими структурами. Примерами вырожденных пучков являются паутинки, пленки мыльных пузырей и нефтяных пятен на воде. В вырожденных (одноэлементных) пучках эффект сверхвысокого увеличения характеристик реализуется при толщине d от 1,0 нм до 100 нм. В уровне техники выдвинуты требования к исполнению пучка: число N>1, d<25 мкм (для электроизоляционных материалов [5]), число N>1, d<70 мкм (материал для защиты от ударных воздействий [2]) и N>1, d<80 мкм (материал для компонентов радиоэлектронных приборов [1]). В то время как закон больших чисел требует, независимо от того, с какими физическими свойствами мы имеем дело, чтобы N→∞, a d→Δ (где Δ - бесконечно малая величина).
Если учитывать вышеизложенное, то на данном этапе развития уровня техники будет более корректным выдвигать в формулах пучкового материала и устройств, следующие требования: N>1, N>>1, N>>10, N>>100 и т.д., d≤50 мкм; N>1, N>>1, N>>10 и т.д, d<<50 мкм; N>1, N>>1, N>>10 и т.д., d≤100 нм. как варианты корректного исполнения в пучке должно быть: N≥1, d≤100 нм; N≥1, d=1 нм.
Таким образом, из уровня техники известен целый ряд пучковых материалов, имеющих существенные недостатки. Кроме того, не известны, в частности в патентной литературе, материалы на основе сверхтонких элементов, являющихся вырожденными пучками, хотя они могли бы дать принципиально новые результаты, как по улучшению свойств материалов, так и по способам их изготовления, так и по их экономике. Использование в пучковых материалах сверхтонких пленок или волокон требует меньшего количества составляющих элементов N, следовательно, это приведет к снижению материалоемкости, компактности и большей технологичности. В любом случае ценность ПТ в том, что она позволяет гарантированно, без изменения гетерогенности структуры тел, без энергозатрат на изменение его химического строения, получать материалы и устройства с предельными (со сверхвысокими) прецизионными характеристиками.
Кроме того, в пучковых материалах и устройствах на порядок и более снижается материалоемкость по сравнению с одноэлементными материалами-монолитами такого же суммарного размера, например, толщины, как и пучок тонких. Использование ПТ посему сулит огромные экономические выгоды.
Поэтому необходимо и дальше развивать и совершенствовать как сами изобретения по пучковым материалам и устройствам, так и способы их изготовления в соответствии с новым уровнем развития техники.
В настоящем изобретении предлагаются пучковые материалы и устройства с учетом новых требований, замечаний и уточнений к ним. Причем их выполнение технологичнее и экономически выгоднее, чем это было до сих пор в уровне техники.
Сущности изобретения, его более осмысленному пониманию, описанию и обоснованию посвящено дальнейшее обсуждение.
Открытие явления дискретности физических свойств и характеристик тел, обусловленной дискретностью их строения, стимулировало появление серии изобретений пучковых материалов [1-7] и устройств со сверхвысокими физическими свойствами и характеристиками. Это, прежде всего, материалы или устройства для защиты от ударных воздействий, материалы для компонентов радиоэлектронных приборов, проводники и диэлектрики, длинномерные витые изделия, преобразователи электромагнитного излучения, диоды и транзисторы и т.д. Феномен универсальности дискретности физических свойств впервые обнаружен в 1982 г. (см. [8] и [10-11]).
Явление дискретности строения тел приводит к образованию дискретно распределенных по размерам дефектов, а это в свою очередь - к дискретности физических свойств и характеристик тел. Универсальность дискретности физических свойств подтвердилось для всех исследованных твердых полимеров и тел [9-16], что позволило авторам пересмотреть старые и предложить новые, более совершенные и обобщенные универсальные изобретения по пучковым материалам и устройствам, касающиеся модифицирования любых структурно-чувствительных физических свойств (СЧФС) и характеристик (СЧФХ) тел.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Пучковый материал, содержащий число N≥1 (где N - целое число) индивидуальных однотипных отдельных, не связанных между собой составляющих элементов, объединенных в стопу или пучок, причем каждый из однотипных элементов имеет одинаковое функциональное назначение и заключен между противоположными контактами из числа K≥2, а число N рассчитывается по формуле

где F - внешнее воздействие на образец; σр,м - есть значение σр структурно-чувствительной физической характеристики или свойства, реагирующей на внешнее воздействие F, которое определяет нижнюю границу значений σp, с которой образцы отбираются в пучковый материал или устройство; s - площадь поперечного сечения одного составляющего элемента пучка; р - вероятность попадания элемента с уровнем структурно-чувствительной характеристики σр>σр,м, в многоэлементный образец-пучок, определяемая из кривых распределений структурно-чувствительной характеристики или свойства.
Между стопами или пучками располагаются отделители.
Отделитель выполняется из числа N≥1 отдельных однотипных тонких или сверхтонких составляющих элементов-пленок.
Число составляющих элементов пучка N может быть рассчитано по формуле
N≥ln(1-P0)/ln(1-P).
где Р есть экспериментально установленная доля образцов с эффектом сверхмодового состояния в их выборке из числа составляющих элементов, подготовленных к компоновке (изготовлению) многоэлементного пучка; Р0 - есть доверительная вероятность, с которой в многоэлементном пучке должен быть хотя бы один элемент, не содержащий дефект, разрушающий сверхмодовое состояние.
Число составляющих элементов пучка N может быть рассчитано по формуле
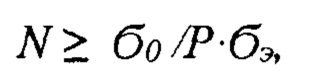
где Р - экспериментально установленная доля материалов со значением структурно-чувствительного свойства или характеристики σ≤σ0 , σ0 - нижняя граница структурно-чувствительного свойства или характеристики, σэ - требуемое или заданное значение структурно-чувствительного свойства или характеристики пучка.
Пучок составлен из сверхтонких элементов-волокон или пленок толщиной d≤100 нм.
Однотипные отдельные составляющие элементы пучка по функциональному назначению представляют диэлектрик, проводник, полупроводник, пьезоэлектрик, сегнетоэлектрик, металл, полимер, металлоид, композит, керамику, pn переход, гетеропереход или переход Шоттки.
Согласно первому варианту способа изготовления пучкового материала, материал выполняется из числа N≥1 (где N - целое число) тонких однотипных отдельных, не связанных между собой индивидуальных составляющих элементов, объединенных в пучок или стопу, причем, каждый из составляющих элементов имеет одинаковое функциональное назначение и заключается между противоположными контактами из числа K≥2, а число N рассчитывается по каждой из формул, приведенных выше.
Пучок составлен из сверхтонких элементов-волокон или пленок толщиной d≤100 нм.
Составляющие элементы пучка представляют диэлектрик, проводник, полупроводник, пьезоэлектрик, сегнетоэлектрик, металл, полимер, металлоид, композит, керамику, pn переход, гетеропереход или переход Шоттки.
Согласно второму варианту способа изготовления пучкового материала, производят М серий измерений структурно-чувствительных физических характеристик или свойств, М - натуральное число, причем в каждой i-й серии (i=1…M) составляющие элементы являются отдельными однотипными, и их число равно Ni, по результатам измерений отбирают j-ю выборку из Nj однотипных элементов, в которой зафиксировано наибольшее значение структурно-чувствительной физической характеристики или свойства среди всех испытанных элементов, далее R≥Nj составляющих элементов, отличающихся тем, что каждый из них имеет толщину D≤dj, где dj - толщина элементов в j-й выборке, соединяют параллельно.
Согласно еще одному варианту способа изготовления пучкового материала, производят М серий измерений физических характеристик или свойств материала, М - натуральное число, причем в каждой i-й серии (i=1…M) составляющие элементы пучка являются отдельными однотипными, а их число равно Ni, по результатам измерений отбирают j-ю выборку из Nj однотипных элементов, в которой зафиксировано наименьшее значение требуемой физической характеристики или свойства среди всех испытанных элементов, далее R≥Nj составляющих элементов пучка, отличающихся тем, что каждый из них имеет толщину D≤dj, где dj - толщина элементов в j-й выборке, соединяют параллельно.
Толщину d составляющего элемента пучка определяют по размеру наименьшего дефекта в его структуре.
Сущность заявленного изобретения, решение задач и достижение заявленных результатов по получению материалов и устройств с низкими, высокими и сверхвысокими значениями физических свойств и характеристик основана на использовании принципа температурно-временной эквивалентности (ТВЭ) [9-10], явлениях универсальности дискретности физических свойств и характеристик твердых тел, закономерностей одноэлементного и многоэлементного масштабного факторов и статистических методов, разработанных авторами изобретений [11-16].
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
На фигурах и в таблицах приняты следующие обозначения.
Таблица 1. Характеристики прочности волокон НШ при испытании на разрыв при температуре 293 K; толщина волокна шелка d=18 мкм размеры дефектов оценены методом механики разрушения на основе математической теории трещин.
Таблица 2. Характеристики прочности волокон α-кератина толщиной 60 мкм. Обозначения: σi уровни прочности; l0i - размеры дефектов; σп=5820 МПа - предельная прочность α-кератина; βi=σп/σI - коэффициент концентрации напряжения в вершине трещины. Примечание: σmax - наивысший прогнозируемый уровень прочности; σп - предельная прочность.
Таблица 3. Характеристики уровней прочности σi, напряжения U, дефектности l0 монокристалла кварца (предельная прочность σп=14500 МПа). Образцы в виде диска диаметром 6 мм и толщиной d=40 мкм. Обозначения: σi - уровни прочности; l0i - размеры дефектов; βi=σп/σ1 - коэффициент концентрации напряжения в вершине трещины.
Таблица 4. Характеристики прочности пленок ПЭТФ (длина рабочей части 22 мм, ширина 1,9 мм) при различных значениях толщины образца-полоски (мкм), степени кристалличности (%) и среднего разрывного напряжения (МПа). Образцы в виде двойных лопаток испытаны на воздухе при 293 K.
Фиг. 1. Полная изотерма долговечности пленки ПММА при Т=293 K (кривая 1), время гарантированной работоспособности одноэлементной (кривая 3) и многоэлементной (кривая 2) пленки ПММА. Вероятность Pm=0,99.
Фиг. 2. Пример низкомодового состояния. Функции распределения плотности вероятности долговечности массивных одноэлементных пленок ПММА марки СО-95 при 293 K и различных растягивающих напряжениях: 1 - 90 МПа; 2 - 75; 3 - 60; 4 - 40; 5 - 35. Обозначения: а - интегральная кривая, б - дифференциальная кривая. Толщина пленок ПММА d=100 мкм.
Фиг. 3. Примеры высокомодовго состояния. Уровни физических свойств.
A. Функция распределения плотности вероятности логарифма долговечности некоторых одноэлементных (одиночных N=1) пленок при Т=293 K (дифференциальные кривые распределения долговечности): 1 - ПЭТФ + железо (магнитная лента), d0=46 мкм, σ=340 МПа; 2 - алюминиевая фольга, d0=34 мкм, σ=77 МПа; 3 - пленка ПМ-4 (полиамидная), d0=18 мкм; σ=110 МПа; 4 - пленка ПМ-1, d0=42 мкм; 5 - шелковое волокно (пучок из трех волокон), d0=54 мкм. Во всех измерениях число членов выборки n=100.
B. Вариационная диаграмма и кривая распределения прочности пленок ПЭТФ при 293 K для серии (объема выборки) из 700 образцов; d0=22 мкм;  σ1-σ7 - дискретные уровни прочности.
σ1-σ7 - дискретные уровни прочности.
Фиг. 4. Пример высокомодового состояния. Функция распределения плотности вероятности механической прочности (а), деформации разрыва (b) и электрической прочности (с) тонкой одиночной (N=1) пленки ПЭТФ при 293 K; число образцов в выборке n=100; d0=18 мкм.
Фиг. 5. Пример сверхмодового состояния. Функция распределения плотности вероятности прочности волокон НШ: А - пучок из N волокон натурального шелка НШ, N=50, d=18 мкм, L=10 мм; В - сверхтонкое одиночное (одноэлементное) волокно натурального шелка НШ, d=18 мкм, L=1 нм. Число образцов в выборке - 100. Предельная, наиболее вероятное и среднее значение прочности волокон НШ совпадают  Предельная прочность волокна НШ, рассчитанная по данным механики разрушения и теории трещин равна 3590 МПа.
Предельная прочность волокна НШ, рассчитанная по данным механики разрушения и теории трещин равна 3590 МПа.
Фиг. 6. Три физических состояния вещества (твердых тел) по масштабному фактору; влияние масштабного фактора (L0 - длина волокна) на среднюю прочность волокон α-кератина (1) и волокон натурального шелка (2). Температура опыта 293 K. Толщина волокон НШ d=18 мкм, а альфа-кератина d=60 мкм. Обозначения: σ1 … σn - уровни прочности σП=5820 МПа - предельная прочность волокна альфа-кератина.
Фиг. 7. Диаграмма распределения (разброса) электрической прочности стопы (пучка) тонких (А) пленок полиэтилентерефталата (ПЭТФ) толщиной d=12,5 мкм) и массивных (В) пленок ПЭТФ толщиной d=200 мкм пленок; N - число пленок-слоев в образце.
Фиг. 8. Кривые распределения (разброса) прочности ПЭТФ: 1 - массивные пленки ПЭТФ толщиной 150 мкм; 2 - тонкие пленки толщиной 18 мкм; 3 - стопа (N>>1) из тонких пленок толщиной 18 мкм. Температура опыта 293 K.
Фиг. 9. Пример экспериментального разброса сопротивления электрическому току образцов медного проводника толщиной 50 мкм; данные измерений сопротивления 500 образцов медной проволоки расположены в последовательный ряд в порядке возрастания номера n (интегральная функция распределения сопротивления).
Обозначения: RO, R1, R2, R3, R4, R5 - уровни электрического сопротивления или уровни диссипации энергии (E1, Е2, Е3, Е4, Е5); n - порядковый номер образца; 1 - одноэлементный образец из медной проволоки длиной 3 мм; 2 - многоэлементные пучковые образцы медной проволоки (в пучке N=100 образцов-элементов).
Фиг. 10. Интегральные кривые распределения значений электросопротивлений для медных проводников различной длины (длина lo=3 мм, 30 мм, 110 мм, 200 мм) толщиной d=120 мкм. N=100. В ансамбле с lo=3 мм два члена выборки имеют нулевые значения электрического сопротивления.
Фиг. 11. Интегральные кривые распределения значений электросопротивлений пучковых медных проводников с числом проводников N=1, 4, 8 и 100; длина образца 3 мм; толщина d=120 мкм.
Фиг. 12. Диаграмма распределения отдельных измерений долговечности при 293 K пленок ПЭТФ толщиной 16 мкм, при различных растягивающих напряжениях: 1 - 352 МПа; 2 - 386 МПа; 3 - 405 МПа; 4 - 415 МПа; 5 - 436 МПа; 6 - 456 МПа.
Фиг. 13. Интегральные кривые распределения тангенса угла диэлектрических потерь tgδ полиимидной пленки толщиной 35 мкм; tgδ1, tgδ2, …, tgδ7 - дискретные уровни тангенса угла диэлектрических потерь (уровни диссипации). 1 - одноэлэментная кривая распределения, число пленок в пучке (стопе) N=1; 2 - многоэлементная кривая распределения, число пленок в пучке (стопе) N>>10. n - порядковый номер образца.
Фиг 14. Интегральные кривые распределения электрической емкости С полиимидных пленок ПМ-4 (1 - монопленка, 2 - пучок) и индуктивности L медной проволоки (3-монопроволока, 4 - пучок).
Фиг. 15. Фрагмент структуры простейшего стандартного фотоэлектрического преобразователя (ФЭП) с одним большим сплошным pn переходом и оптическим окном закрытым n слоем и Т-образные линии тока, иллюстрирующие наличие слоевого сопротивления. Число переходов N=1.
Фиг. 17. Зависимости внутреннего последовательного сопротивления Rs пучкового многопереходного ФЭП (фигура слева) и стандартного однопереходного ФЭП (фигура справа) от падающей мощности Pinp галогеновой лампы-фары Osram.
Фиг. 18. Зависимости максимальной выходной мощности пучковых ФЭП различной модификации от падающей мощности Pinp в спектре галогенной лампы-фары и монохроматического ИК излучения лазера на длине 0,808 мкм.
Обсудим эти подходы и представления, использованные в настоящем изобретении для получения заявленных результатов. Для получения материалов с заданными СЧФС и СЧФХ в изобретении широко применен принцип ТВЭ.
Принцип ТВЭ заключается в том, что действие на образец температуры, масштаба, силовой (энергетической) нагрузки или частоты (или одно и то же - времени воздействия) приводят к эквивалентным изменениям СЧФС или СЧФХ образца. Поэтому низкие, высокие или сверхвысокие значения СЧФС или СЧФХ изделий можно получить воздействием (изменением) на тело любого фактора: температуры, масштаба, величиной воздействующей нагрузки или величиной воздействующей частоты при неизменности какого-либо параметра, например, температуры, т.е. Т=const на образец.
Для исследователя с точки зрения принципа ТВЭ безразлично, какой из этих воздействующих факторов использовать для получения эквивалентных результатов. Использование любого фактора приводит к идентичному эквивалентному результату.
Однако выбор (использование) масштабного фактора более предпочтителен, поскольку он является более простым и дешевым способом модифицирования материалов. Он не требует бездефектности от образцов, а также не требует перестройки их химической структуры. Поэтому в настоящем изобретении для достижения заявленных результатов использован феномен и закономерности изменения масштабного фактора. Хотя для модификации свойств можно использовать комбинированные факторы или их раздельное, т.е. поочередное влияние.
Масштабный (размерный) фактор V, геометрический размер тела (толщина, ширина, длина, т.е. его объем), влияют, прежде всего, на наличие в них больших и малых по размеру дефектов в их структуре. В зависимости от масштаба образца в них могут находиться (расселиться) дефекты того или иного размера, той или иной степени опасности. Дефекты, как правило, имеют произвольную форму, конфигурацию и размеры, которые расположены на крае, поверхности и в объеме образца, распределенные статистически случайно и хаотично. Под дефектами в уровне техники [9-10, 15] понимаются всякого рода примеси, разрывы сплошности с разрывами химических и межмолекулярных связей, или неоднородности структуры и их границы, или любые дислокации, вакансии и несовершенства структуры, связанные, к примеру, с искажением кристаллической решетки материала и т.д.
При увеличении масштаба образца V происходит перераспределение образцов в ансамбле однотипных изделий (образцов) с высоких на низкие уровни; а при уменьшении - имеет место обратный процесс перераспределения образцов - с низких на высокие уровни свойств. В результате такого перераспределения происходит снижение (или увеличение) величины разброса и среднего значения прочности, долговечности и других СЧФС и характеристик (СЧФХ). Указанное перераспределение составляет суть явления масштабного фактора.
Наши многолетние систематические теоретические и экспериментальные исследования статистических свойств материалов свидетельствуют, о том, что по масштабному фактору твердое тело (вещество) условно находится в трех физических состояниях:
a) Низкомодовое состояние
- массивные тела (объемные тела, пленки и волокна толщиной d>50-60 мкм) - это состояние с низкими значениями физических характеристик и свойств тела, образцы имеют низкие значения с дефектами размером от 1000 нм до 10000 нм и выше (макродефекты или макротрещины); функция распределения плотности вероятностей физической характеристики имеет унимодальный (нормальный Гауссовый) вид с одним максимумом (фиг. 2, 7, 8);
b) Высокомодовое состояние
- тонкие тела (волокна и пленки толщиной 0,1 мкм <d ≤ 50-60 мкм) - это состояние с высокими средними значениями физических характеристик и свойств тела; образцы имеют высокие средние значения с размерами дефектов от 100 нм до 1000 нм (микродефекты или микротрещины); функция распределения плотности вероятностей физической характеристики имеет полимодальный вид с несколькими максимумами (см. фиг. 3-4, 7-8);
c) Сверхмодовое состояние
- пучки из N тонких тел (волокна и пленки толщиной 0,1 мкм <d ≤ 50-60 мкм, собранные в пучок) с размерностью дефектов от 0,1 мкм до 1 мкм (микродефекты или микротрещины);
- сверхтонкие тела (одиночные волокна и пленки толщиной от 1 нм до 100 нм) с размерностью дефектов от 3 нм до 90 нм (СМТ или нанотрещины НТ).
Обе модификации тел - это суть сверхмодовые состояния со сверхвысокими значениями физических характеристик и свойств вещества, достигающие в этом состоянии теоретических или предельных значений; образцы имеют сверхвысокие значения; функция распределения плотности вероятностей физической характеристики в обоих случаях становятся унимодальными с узко-симметричным видом (см. фиг. 5, 8).
Пучок с тонкими волокнами (пленками) при N→∞ и сверхтонкая пленка (или волокно) при N=1 находятся в состоянии сверхвысоких характеристик, но с разными группами (типами) размерных дефектов; одиночное сверхтонкое волокно (пленка) - это фактически, тот же пучок, но возникший при вырождении (снижении) числа составляющих элементов N до 1 и толщине элементов (волокон и пленок) до d<0,1 мкм (100 нм).
В соответствии с этими представлениями предлагаемый авторами пучковый материал или пучковое устройство и способ его изготовления - это объединение трех технологических подходов в уровне техники: субмикронной или нанотехнологии (размерность рассматриваемых дефектов 1 нм - 100 нм), микронной технологии (размерность дефектов 100 нм - 1000 нм) и макротехнологии (размерность дефектов 1000 нм - 10000 нм и более). Чтобы реализовать пучок необходима корректная (пучковая) упаковка нано- и микро-составляющих в реальное макроскопическое изделие, которое в итоге предстоит эксплуатировать в реальных условиях. При неправильной упаковке в пучке эффект усиления свойств не возникнет.
Таким образом, для выполнения пучковых материалов в уровне техники используются тонкие волокна (проволоки) или пленки, т.е. тела, имеющие большую протяженность по длине 1 и малый поперечный размер по толщине d. К тонким волокнам и пленкам относится область с толщиной d<50-60 мкм, но больше 0,1 мкм с размерностью дефектов в них от 100 нм до 1000 нм, т.е. уровень техники - это область микронной технологии. В уровне техники число тонких однотипных отдельных пленок или волокон в пучковых материалах составляет N>1.
Волокна и пленки толщиной d<0,1 мкм - это уже сверхтонкие тела, которые относятся к области субмикронной или нанотехнологии с унимодальной функцией распределения физических характеристик и свойств. Изобретения пучковых материалов с субмикронной размерностью составляющих элементов на данный момент еще не заявлены.
В настоящем изобретении учитывается сверхмодовое состояние, возникающее при толщине пленок и волокон d≤100 нм (0,1 мкм). Представления о трех состояниях вещества являются основой физического модифицирования материалов с предельными структурно-чувствительными свойствами СЧФС и характеристиками (СЧФХ) без изменения химического строения тел.
Из уровня техники известно, что дефекты в виде субмикротрещин (СМТ) в тонких пленках и волокнах возникают под нагрузкой F (например, механической или электрической) в слабых местах структуры. СМТ затем в результате роста и слияния они перерастают в микротрещины и в обычные магистральные трещины разрушения образца. Образующиеся под нагрузкой дефекты имеют дискретное распределение по размерам и типам n [17, 15, 20]. Образованные таким путем дефекты имеют некоторое распределение по размерам (длинам) 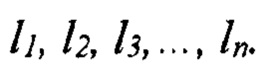
Как оказалось, этому дискретному распределению (спектру) дефектов по их размерам (длинам) li (где i=1, 2, 3, …, n - целое число) и типам соответствуют дискретный спектр (набор) значений разрывных (механических и электрических) напряжений в виде ряда а, σ1, σ2, σ3, …, σn или долговечности в виде ряда τ1, τ2, τ3, …, τn (см. фиг. 3), обусловленных дискретностью строения материи, которые были названы уровнями прочности и долговечности, а впоследствии - уровнями физических свойств и характеристик.
Явление дискретности физических свойств и характеристик, обусловленное дискретностью строения тел носит универсальный характер: дискретному спектру дефектов по размерам соответствует не только дискретный спектр уровней механической и электрической прочности, но и дискретный спектр уровней электрических сопротивлений R1, R2, R3, …, Rn (фиг. 9) и дискретный спектр физических свойств в целом. В общем случае дискретному строению тел соответствует дискретный спектр дефектов структуры, которым в свою очередь соответствуют дискретные уровни или дискретный спектр физических свойств Ф1, Ф2, Ф3, …, Фn. Дискретный спектр уровней свойств включают в себе все наблюдаемые ранее уровни СЧФС или СЧФХ - долговечности, прочности, уровни сопротивлений R1, R2, R3, …, Rn или уровни диссипации энергии E1, Е2, Е3, …, En, уровни диэлектрических потерь [9-11, 15, 18] (фиг. 5, 7, 8-9) и т.д.
Такая структурная иерархия дефектов и физических свойств проявляется во всех твердых телах, независимо от природы и сложности строения: в металлах, полимерах, стеклах, композитах и в керамике, в проводниках, диэлектриках, и полупроводниках органического и неорганического происхождения, и т.д. [9-11, 15].
В таблице 1-4 приведены уровни прочности σi и дефекты в волокнах шелкопряда, альфа-кератина (нормальный человеческий волос), пленках монокристалла кварца и поли-этидентерефталата (ПЭТФ), распределенные по трем группам (типам) и размерам дефектов l0i. Под уровнями прочности или уровнями физических свойств, таким образом, понимаются выделенные значения прочностных или других физических свойств на их дифференциальных (в виде максимумов) и интегральных (в виде горизонтальных площадок) функциях распределения свойств (см. фиг. 3, 4, 7-8). Уровням физических свойств, как отмечено выше, соответствуют структурные дефекты определенной степени опасности и размеров [9-10, 15]. Дефекты соответствуют трем состояниям вещества по масштабному фактору.
Размеры дефектов в настоящем описании изобретения рассчитаны авторами методом математической теории трещин по результатам механики разрушения волокон натурального шелка и кератина шерсти с различной длиной образцов. Размеры дефектов рассчитаны по уровням прочности σi и коэффициенту концентрации напряжения в вершинах трещин βi [9-10], которые контролировались дополнительно методами рентгенофазового анализа.
Из таблиц видно:
Группа (тип) 1 - это макротрещины с поперечным размером 1000-10000 нм (1-10 мкм), обнаруженные в образцах волокон натурального шелка (НШ) длиной L=50-90 мм);
Группа (тип) 2 - это микротрещины МТ размером 100-1000 нм (0,1-1 мкм), обнаруженные в образцах волокон НШ длиной L=10-50 мм;
Группа (тип) 3 - это СМТ или нанотрещины размером 10-90 нм (0,01-0,09 мкм), обнаруженные в образцах волокон НШ длиной L=5-22 мкм. Наименьший размер СМТ в этой группе составляет в 10 нм (0,01 мкм).
В классическом твердом теле монокристалле кварца (табл. 3), обнаружены дефекты, относящиеся к макротрещинам группы 1 и субмикротрещинам с группы 3. Наименьший дискретный размер СМТ обнаружен в кварце, который составляет 2,8-5,0 нм (0,003-0,005 мкм). Наибольший размер дефектов наблюдается в плоских (пленочных) образцах ПЭТФ (табл. 4), составивший 12570 нм (12,6 мкм), относящийся к грубым дефектам края образцов-полосок.
Как оказалось, в твердых полимерах, например, в ПММА размеры дефектов, образовавшихся под нагрузкой, соответствуют (совпадают) с размерами в поперечнике микро-фибрилл, фибрилл и макрофибрилл (или размерам микропачек, пачек и макропачек в ПЭТФ и т.д.), а в классическом твердом теле, монокристалле кварца, - размерам микро-неоднородностей структуры [9, 15, 19]. Образование дефектов под нагрузкой объясняется по С.Н. Журкову и В.А. Закревскому [17] механохимическими реакциями цепи в слабых местах структуры, где химические связи находятся в перенапряженном состоянии.
Зная размеры дефектов, можно более корректно рассчитать толщину составляющих элементов пучка d. Как следует из таблиц 1-4, наиболее корректным будет, если выбирать толщину d составляющего элемента пучка по наибольшему поперечному размеру дефектов структуры пленок и волокон. Например, для кварца наибольший размер дефекта составляет 29 мкм, а для пленок ПЭТФ - 12,6 мкм. То есть для пучкового материала или устройства из монокристалла кварца толщина однотипного отдельного составляющего элемента пучка d должна быть менее 29 мкм (d≤29 мкм), а для пленок ПЭТФ - менее 12.6 мкм (d≤12,6 мкм). В этом случае дефектные элементы с дефектами размером 12.6 мкм и 29 мкм исключаются из пучков и для получения материала с предельными свойствами требуется меньшая материалоемкость. Поэтому расчет числа однотипных отдельных составляющих элементов N должен быть в [2] не по толщине d<70 мкм, а по толщине d<12 мкм.
На фиг. 6 приведена диаграмма физических состояний вещества по масштабному фактору, построенная авторами по данным испытаний прочности волокон альфа-кератина (нормальный человеческий волос) и натурального шелка. Как видно из этой диаграммы, группы (типы) размерности дефектов из таблиц 1-4 соответствуют на диаграмме трем физическим состояниям вещества по масштабному фактору.
Зависимость от масштаба, как видно из фиг. 6, ступенчатая, т.е. не линейная, как принято, было в различных подходах 20-го века [19]. Как видно на диаграмме, в тонких волокнах масштабный эффект наблюдается при увеличении длины образца l до 70 мм. При дальнейшем увеличении длины масштабного эффекта нет. В то время как в пленках [9-10] масштабный эффект наблюдается до толщины d=60-70 мкм.
Уровни прочности σ1-σ11 на диаграмме расположены ступеньками, которые обусловлены дефектами структуры определенного размера и степени опасности, приведенные в таблице 2. Самый низкий уровень σ1 расположен в низкомодовой области, которому соответствуют дефекты размером 220 нм (0,22 мкм), а наивысший уровень σП, соответствующий предельному значению находится в сверхмодовой области и соответствует бездефектному состоянию.
Из этой диаграммы видно, что в низкомодовом состоянии прочность кератина имеет небольшие значения, порядка 200 МПа. В высокомодовом состоянии она достигает до 850 МПа, а сверхмодовом - прочность волокна альфа-кератина достигает предельных значений, составляющего σп=5820 МПа.
Сверхмодовое состояние по данным диаграммы возникает в одиночных (одноэлементных) образцах волокон кератина длиной L0<10 мм (при толщине d=60 мкм); высокомодовое - возникает в образцах волокон длиной L0<60-70 мм; низкомодовое - возникает в образцах волокон длиной L0≥60-70 мм.
В пучке тонких пленок (волокон), в соответствии с эффектом пучка и законом больших чисел, сверхмодовое состояние возникает при числе N→∞ и размере, например, толщины d составляющих элементов стремящемся к бесконечно малой величине Δ (d→Δ). Для достижения сверхвысокого состояния в пучке не требуется наличие или отсутствие дефектных иди бездефектных составляющих элементов. Дефектные составляющие в пучке шунтируются большим количеством бездефектных элементов.
При N=1 получаем вырожденный пучок. Многоэлементный масштабный эффект не реализуется. Он переходит в одноэлементный размерный эффект. При снижении толщины к d=1-100 нм, а в идеале к d=1 нм мы получаем сверхтонкое тело, в котором в результате одноэлементного эффекта возникает сверхмодовое состояние, т.е. эффект сверхвысокого увеличения структурно-чувствительных физических характеристик (СЧФХ) тела.
При снижении толщины пленок или волокон микродефекты испаряются (вытесняются) с поверхности и объема тела, поскольку из-за своей большой размерности они не могут разместиться (реализоваться) в пленке или волокне, у которой толщина меньше, чем, например, сам поперечный размер микротрещины.
При толщине d=1 нм, мы получаем протяженную бездефектную структуру, поскольку СМТ даже с минимальным поперечным размером в l0=2,8-10 нм не могут разместиться по всей протяженности длины и ширины пленки и длины волокна из-за большего своего поперечного размера в меньшей по размеру толщине d пленки или волокна. В такой пленке (или волокне) структурно-чувствительные физические характеристики и свойства достигают теоретических или предельных значений.
Таким образом, при толщине волокна (пленки) d=1 нм получаются протяженные длинномерные бездефектные (по всей протяженности или длине) волокна или пленки.
Такой результат следует также из более строгих теоретических соображений. В работах [15, 20] показано, что закон распределения наиболее опасного дефекта структуры материала, определяющего его соответствующую структурно-чувствительную физическую характеристику (СЧФХ) или свойство (СЧФС) σ, определяется выражением

Здесь pi есть вероятность (доля) образцов имеющих значение СЧФС (или СЧФХ) σi, i=1, 2, …n, n - число типов (групп) дефектов структуры материала; V есть объем или площадь поверхности одного составляющего элемента пучка; ci есть концентрация дефектов, то есть среднее число дефектов структуры материала в единице объема материала, определяемое технологией его изготовления, с характерным размером дефекта структуры di (например, размера дефекта в поперечнике), определяющим значение СЧФХ или СЧФС σi, i=1, 2, …n,; здесь σ1<σ2<…<σn.
Как видно из приведенной формулы, при уменьшении объема (поверхности) материала V множитель (1-exp(-ci⋅V)) стремится к нулю, а множитель 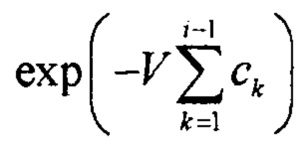 стремится к единице. Уменьшение объема материала V должно производиться с учетом геометрии дефектов структуры, то есть ее характерного размера дефекта di, которые определяют соответствующую СЧФХ или СЧФС. При этом в силу неравенства n1<n2<…<nn в первую очередь становятся исчезающе малыми величины pi c меньшими номерами, то есть соответствующие более низким значениям СЧФХ или СЧФС σi. При дальнейшем уменьшении V последними исчезнут pi с номером пив пределе мы получим протяженный (длинномерный) бездефектный материал с предельным значением СЧФС иди СЧФХ σmax с существенным снижением и устранением разброса свойств и характеристик.
стремится к единице. Уменьшение объема материала V должно производиться с учетом геометрии дефектов структуры, то есть ее характерного размера дефекта di, которые определяют соответствующую СЧФХ или СЧФС. При этом в силу неравенства n1<n2<…<nn в первую очередь становятся исчезающе малыми величины pi c меньшими номерами, то есть соответствующие более низким значениям СЧФХ или СЧФС σi. При дальнейшем уменьшении V последними исчезнут pi с номером пив пределе мы получим протяженный (длинномерный) бездефектный материал с предельным значением СЧФС иди СЧФХ σmax с существенным снижением и устранением разброса свойств и характеристик.
Таким образом, в формуле изобретения, учитывающей новый уровень развития техники, необходимы принципиальные добавления и уточнения, следующие из рассмотрения таблиц 1-4 и диаграммы на фиг. 6.
Вернемся снова к рассмотрению трех состояний вещества по масштабному фактору.
Низкомодовое состояние вещества - это обычное объемное (или массивное) состояние тел в окружающем нас мире: в быту, промышленности, в природе и т.д.
Высокомодовое состояние вещества по масштабному фактору возникает при одноэлементном масштабном эффекте физических свойств и характеристик. Возникает это состояние при снижении линейных размеров массивных тел до размеров тонких и вытеснении макродефектов с поверхности и объема тела. Толщина волокон в этом состоянии d≤50-60 мкм. Оно реализуется в натуральной природе, например, в виде тонких высокопрочных волокон шелкопряда, хлопка, льна, джута и т.д. В промышленности делают разнообразные текстильные искусственные и синтетические высокопрочные ориентированные волокна (например, из полиамидных смол, полиэтилентерефталата и т.д.) для производства тканых материалов, делают волокна для кордов шин автомобилей, волокна для производства нитей, веревок, канатов, такелажных тросов и т.д.
Сверхмодовое состояние вещества возникает в пучках из N→∞ тонких пленок (волокон) при многоэлементном масштабном эффекте физических характеристик и свойств. Оно также возникает в одноэлементном масштабном эффекте физических характеристик при снижении линейных размеров тонких тел до размеров сверхтонких. В промышленных масштабах пучковые материалы реализованы, например, в автомобильных кордах, нитях, такелажных тросах, тканях. В натуральной природе пучки реализованы в стволах растений, например, бамбука, тростника, камыша, льна, деревьев и т.д.
Сверхтонкие свободные пленки в настоящее время реализованы в графеновых пленках, их можно увидеть в паутинках, в мыльных пузырях, нефтяных пятнах на воде и т.д.
В уровне техники пучковые материалы из таких свободных пленок толщиной d≤100 нм (0,1 мкм) пока не заявлены. При снижении толщины d тонких однотипных составляющих элементов пучка и ее стремлении к минимальному значению (d→1 нм), сверхмодовое состояние наступает при существенно меньшем значении N и меньшей материалоемкости. Поэтому пучковые материалы и устройства из таких сверхтонких волокон и пленок представляют существенный интерес.
Для достижения сверхвысоких значений требуется существенно меньшее число N элементов пучка, а при достижении d=1 нм требуется всего одно значение N=1. Кроме того, понятно, что, если формировать пучок не с тонкими, а сверхтонкими элементами, или близкими к такому состоянию, то можно получить более высокие результаты. Это как по абсолютным значениям физических характеристик и свойств, так по их материалоемкости.
Поэтому для выполнения пучкового материала или устройства с предельными структурно-чувствительными свойствами и характеристиками, как вариант, нужно формировать его не только из N>>1 тонких, а из N≥1 сверхтонких однотипных отдельных пленок или волокон толщиной d меньше 100 нм (d<100 нм). Следовательно, при формировании пучка из тонких пленок, чтобы добиться получения сверхмодового состояния, требуется использовать большее количество составляющих элементов N, чем при формировании его из пленок или волокон близких по толщине к сверхтонким.
Для практики имеет большое значение насколько сложнее или проще производить сверхтонкую или тонкую пленку, или волокно. Если сверхтонкую пленку или волокно экономически и технически производить сложнее, чем тонкую, то необходимо обойтись тонкими, поскольку в любом случае тонкие пленки и волокна позволяют создать сверхмодовое состояние путем их составления (объединения) в пучок и увеличения числа N однотипных отдельных составляющих элементов. Поэтому надо исходить из реальной целесообразности использования сверхтонкой или тонкой пленок и волокон. Например, в микроэлектронике для микросхем целесообразней использовать сверхтонкую пленку.
С другой стороны, одиночная (одноэлементная) сверхтонкая пленка или волокно, имея сверхвысокие удельные характеристики, имеет низкую суммарную долговечность и прочность в абсолютном выражении. С другой стороны, как показано в главе 5 авторами [9] многоэлементная (пучковая) структура имеет более высокие СЧФХ, чем одноэлементная, выполненная изменением ее гетерогенности. Поэтому выходом из этой ситуации является формирование пучка из N тонких пленок или волокон.
Далее, понятно, что в любой материальной субстанции есть локальные зоны (ЛЗ) или участки, или кластеры не только с дефектами или примесями, но и чистые или сверхчистые зоны, где нет дефектов, в силу которого они являются свободными (бездиссипативными) зонами. Этим сверхчистым локальным зонам соответствуют сверхвысокие физические свойства и характеристики. ЛЗ, как и зоны с дефектами расположены в материале хаотично, имеют произвольную форму и конфигурацию.
Расположение и распределение ЛЗ на крае, поверхности и в объеме образца статистически случайное и хаотичное. Причем, чем меньше геометрический размер V тела, тем меньше вероятность присутствия в нем грубого дефекта [8-10, 15-19]. Отсюда следует, что, начиная с некоторых размеров образцов, грубые дефекты вообще не будут наблюдаться ни в одном образце, размер которого меньший в данной серии. И тогда тем выше будет степень его чистоты, поскольку в них не могут разместиться грубые дефекты. К примеру, при толщинах волокон в 1 нм ни один дефект, имея минимальный размер 2,8 нм, вообще не сможет в них разместиться. С локальными зонами получается аналогично. Чем меньше ЛЗ по своему масштабу V, тем степень ее чистоты выше. Это потому, что большие по размерам дефекты или примеси в маленьких по геометрическим размерам ЛЗ (или кластерах) образца, не могут поместиться (реализоваться).
Физические свойства тел зависят от степени его чистоты, т.е. от количества и концентрации содержащихся в нем инородных включений или примесей, являющихся дефектами структуры материала. В целом, содержание дефектов в образце зависит от технологических особенностей формирования и предыстории его изготовления.
Локальные чистые зоны в зависимости от технологической предыстории, как и дефекты, имеют определенные геометрические размеры, произвольную форму и конфигурацию.
В массивных образцах твердых тел имеется целый спектр или набор дефектов структуры (больших и малых размеров), влияющих на его СЧФС и характеристики (СЧФХ), в частности, механические или электрические, или другие.
Локальные бездефектные зоны ЛЗ в телах разрознены и не связаны между собой в одну непрерывную цепь и, таким образом, они маскируются наличием зон с грубыми дефектами и не проявляются при измерениях. Поэтому в массивных образцах нет большого экспериментального разброса значений физических характеристик и свойств образцов (см. фиг. 7, кривая В и фиг. 8, кривая 1). По отсутствию или наличию экспериментального разброса данных измерений в этих образцах можно судить о том, массивные они, тонкие или сверхтонкие.
Массивные образцы, как выше отмечено, характеризуются нормальными унимодальными статистическими распределениями дефектов и соответствующих им физических свойств и характеристик (фиг. 2, фиг. 8, кривая 1). Тонкие образцы характеризуются большим экспериментальным разбросом и полимодальными кривыми распределениями (фиг. 3-4, фиг. 7, фиг. 8, фиг. 12). В пучке экспериментальный разброс устраняется, кривая распределения приобретает унимодальную форму (фиг. 5, фиг. 8, фиг. 9).
У сверхтонкой пленки или волокна функция распределения вырождается в узкосимметричную (колоколообразную) унимодальную форму и сдвигается по оси абсцисс к предельному значению (см. фиг. 5В).
В тонких пленках и волокнах, т.е. малых по толщине или диаметру, грубые дефекты структуры, например, макротрещины, влияющие на физические свойства, отсутствуют (из-за большого поперечного размера дефектов, например, превышающих толщину или диаметр образцов). Их там быть не может потому, что они там не могут поместиться (реализоваться) и потому проявляется только весь спектр (набор) тонких дефектов структуры, влияющих на физические свойства и характеристики, например, прочность или их проводимость, включая локальные зоны различной степени чистоты и поперечных размеров. Поэтому разброс структурно-чувствительных физических характеристик (СЧФХ) и других свойств в тонких образцах существенный. Тонкие пленки и волокна поэтому характеризуются полимодальными статистическими распределениями дефектов и соответствующих им физических свойств и характеристик.
Чем меньше будет масштаб (размер) образца V, тем больше будет экспериментальный разброс физической характеристики или свойства σi. Поэтому в серии малых по масштабу однотипных (одинаковых) тонких образцов будут значения с как угодно малыми значениями характеристик (свойств), так и со значениями как угодно большими (см. к примеру, данные по разбросу в тонких образцах на фиг. 7, 9-14).
В отличие от тонких пленок и волокон, сверхтонкие пленки и волокна имеют идеальную бездефектную структуру. Бездефектные зоны в сверхтонких пленках и волокнах имеют большую протяженность по длине по сравнению с бездефектными зонами в тонких образцах. Это потому, что дефекты, имея даже минимальный поперечный размер от 2,8 до 10 нм, в сверхтонких бездефектных пленках (волокнах), например, толщиной 1 нм не могут в них поселиться (поместиться) по всей их длине (протяженности).
В тонких пленках реализуются дефекты размерностью от 100 нм до 1000 нм, в промежутках между дефектами располагаются бездефектные локальные зоны. Потому локальные зоны в тонких пленках имеют меньшую протяженность, чем в сверхтонких или пленках или волокнах близких по толщине к сверхтонким. Поскольку бездефектные зоны встречаются не только в сверхтонких, но и в тонких и в массивных пленках (и волокнах), то они различаются между собой протяженностью. В массивных пленках и волокнах, таким образом, они менее протяженны, чем в тонких и сверхтонких, из-за наличия в структуре пленок и волокон грубых дефектов больших размеров.
Местонахождение в образцах локальных зон с дефектами и без дефектов, как и распределение их по объему в том или ином месте материала статистически случайное.
Случайные величины определяются, как известно, их статистической функцией распределения или плотностью распределения вероятностей. Поэтому методы поисков и определения, а также исследования этих зон, также как и методы исследования самих дефектов, должны быть статистическими.
Для исследования локальных зон и доказательства их реального существования, на большой статистике, на основании большого количества измерений, авторами строились статистические функции распределения электрических сопротивлений. Это подобно тому, как для изучения дефектности материалов, авторами строились функции распределения прочности и долговечности в [9, 18]. В частности, для исследования ЛЗ и определения размеров дефектов находились дискретные значения уровней долговечности прочности, по которым затем согласно математической теории трещин рассчитывались дефекты [9-10]. Под дискретными уровнями прочности и долговечности, а также дискретных уровней физических свойств и характеристик, в уровне техники [9, 10] понимаются более или менее выделенные их значения в виде максимумов на функциях распределения плотности вероятности или в виде горизонтальных площадок на интегральных функциях распределения этих физических свойств (см., к примеру, фиг. 3, 4, 7, 8, 9).
Аналогично этому уровнями электрического сопротивления, или просто уровнями сопротивления, понимаются более или менее выделенные значения сопротивления на кривых распределениях (дифференциальных или интегральных) электрического сопротивления. В зависимости от степени чистоты материала электрическое сопротивление может быть сверхнизким, низким или высоким, т.е. обратная величина, электрическая проводимость, может быть сверхвысокой (сверхмодовой), высокой (высокомодовой) или низкой (низкомодовой).
В целом, в любом проводнике имеются Q локальных участков (зон или кластеров) не только с дефектами, но и без дефектов, расположенных в материале проводника хаотично и статистически случайно. Кроме того, конфигурация этих зон произвольная, а их поперечные размеры являются также произвольными, которые зависят в общем случае от концентрации дефектов и степени очистки материала проводника. Участки (или кластеры) с дефектами - это зоны или кластеры, где в результате столкновения электронов происходит рассеяние (или диссипация) электрической энергии Ed. Поэтому уровни сопротивления названы авторами еще уровнями диссипации энергии Ed.
В бездефектных локальных зонах электроны двигаются без потерь. Поэтому бездефектные зоны были названы свободными или бездиссипативными. В них сопротивление близко к нулю или равно нулю. Чтобы локальные зоны были бездиссипативными необходимо, чтобы они были максимально бездефектными вдоль направления течения тока [21].
На фиг. 9 представлены интегральные функции распределения электрического сопротивления медной проволоки, построенной по данным измерений электрического сопротивления из 500 однотипных отдельных образцов. Для нахождения вида и построения интегральной функции распределения сопротивления, результаты измерений сопротивлений R (см. фиг. 9) располагались в порядке возрастания по номерам последовательности n, т.е. строилась последовательная функция.
Локальным зонам различной степени чистоты с дискретным набором дефектов соответствуют дискретные уровни электрического сопротивления R0, R1, R2, R3, …, Rn (поскольку значение сопротивления равно нулю, то для удобства он назван нулевым уровнем сопротивления, а не первым уровнем) или уровни диссипации энергии E0, E1, Е2, Е3, …, En (поскольку диссипация имеет нулевое значение, то для удобства он назван нулевым уровнем диссипации, а не первым уровнем.) (см. фиг. 9).
Среднее значение сопротивления R изменяется при переходе от массивных пленок (волокон или проволок) к тонким пленкам (волокнам или проволокам) в результате того, что образцы, содержащие дефекты переходят с низких уровней Ri на более высокие уровни электрического сопротивления и наоборот.
Методика статистических исследований, нахождение вида статистических функций распределений подробно описаны в главе 1 документа [9].
Для определения размеров локальных бездефектных и дефектных зон варьировалась рабочая длина образцов - от 200 мм до 3 мм (при толщине 120 мкм. Результаты этих измерений сопротивлений R (см. фиг. 10) располагались в порядке возрастания по номерам последовательности n, т.е. представлены в виде интегральной функции распределения электрического сопротивления. Видно, что при снижении масштаба проводника от 200 мм до 3 мм обнаруживается огромный разброс значений сопротивления, составившего от нуля до обычного - в 1,55⋅10-8 Ом⋅м и выше. Большой экспериментальный разброс обусловлен наличием в серии проводников образцов локальных бездефектных (бездиссипативных) зон как с нулевым сопротивлением, так и проводников с дефектными зонами с различным значением электрического сопротивления, соответствующих различным степеням чистоты материала и наличием в структуре материалов различных типов дефектов. Нулевое сопротивление, как видно из фиг. 10, имеется только в выборке, где размер образца составляет lo=3 мм и N=100. Причем, нулевым сопротивлением обладают всего два члена выборки. Следовательно, это значение соответствует поперечному размеру локальной бездефектной зоны. При этом эти локальные зоны пропускают при комнатной температуре 293 K через себя без нагревания (без выделения Джоулева тепла) плотности тока до 5000 А/мм2 и более, свидетельствуя, что измеренные выборки медных проволок имеют локальные зоны со сверхпроводящими свойствами. Бездефектные локальные зоны, как выше отмечено, являются бездиссипативными со сверхпроводящими свойствами, где электроны движутся без потерь и которым соответствует нулевой уровень сопротивления R0 или нулевой уровень диссипации энергии Е0 (см. фиг. 9-10).
На статистических кривых распределения уровни R1 и R2 относятся к дефектам структуры поверхности пленок и волокон (проволок) проводника, а уровни R3 - Rn - к более глубоко пролегающим дефектам структуры объема. Поэтому, чтобы вся токопроводящая пленка проводника стала бездиссипативной и сверхпроводящей, необходимо удалить уровни сопротивления R1 - Rn, т.е. необходимо снизить толщину до критического наноразмера Dc, т,е. до сверхтонкого состояния. Критическая толщина Dc, при которой в нанопленке (нановолокне или нанопроволоке) появится протяженная бездиссипативная зона или кластер составляет нанометровый диапазон порядка менее 2,8 нм, хотя отдельные бездефектные зоны будут проявляться и высокомодовом состоянии, как это показано на фиг. 10.
При критической толщине нанопленки или нанопроволоки Dc<2,8 нм все образцы (вся выборка) переходят в бездефектное бездиссипативное состояние.
В экспериментах с увеличением толщины проволок до 270 мкм были обнаружены локальные зоны с поперечным размером в 1000 мкм, также пропускающие через себя без нагревания огромные плотности тока. В то время как в проволоках толщиной 120 мкм были найдены более протяженные локальные зоны - с поперечным размером в 3000 мкм. Следовательно, для изготовления протяженных бездефектных образцов предпочтительней снижать рабочую толщину пленок или волокон, а не их длину, как это было сделано в документе [7].
Далее, в зависимости от степени концентрации дефектов той или иной локальной зоны, эти участки проводника будут иметь разную проводимость, т.е. будут иметь высокое, низкое, сверхнизкое или нулевое электрическое сопротивление. Это явление может контролироваться и быть использованным на практике. При необходимости, можно выбирать локальные зоны с той или иной проводимостью и выполнять из них проводники с требуемым значением сопротивления R. Практически это осуществляется изменением масштаба образцов и составлением (подборкой) пучка с различным числом N составляющих элементов.
Как видно из фиг. 9, если составить пучок между двумя токовыми электродами-контактами, т.е. параллельную цепь, из 500 медных образцов, расположенных в последовательном ряду от первого, сопротивление которого равно нулю, до 500-го (последнего в ряду), имеющего наибольшее значение сопротивления, то расчеты в соответствии с законом Ома и измерения, показывают нулевое суммарное сопротивление, соответствующее нулевому уровню R0.
Токи через такие пучки проходят плотностью свыше 5000 А/мм2, свидетельствующие о сверхпроводящих свойствах испытуемого пучка. Если составим пучок из последовательного ряда, начиная, например, с 175 члена выборки (номера образца), соответствующего уровню R3 до 500-го, то суммарное значение сопротивления такого пучка составит согласно закону параллельного соединения Ома значению равного меньше значения уровня R3. Далее, если составим пучок, начиная со значения уровня R4 до 500-го, то получим сопротивление, соответствующее значению меньше уровня R4 и т.д. Эти значения суммарного сопротивления пучков согласно закону Ома легко рассчитываются по формуле 1/R=1/R1+1/R2+1/R3+…+1/Rn. При этом, если есть необходимость получить пучковый проводник с более низким сопротивлением, то расчет суммарного сопротивления надо делать не со значения R3, а со значения равного R2 или R1. Если делать расчет с наименьшего значения сопротивления с R0 до R500, то мы получим проводник с нулевым значением сопротивления. Таким путем мы получаем пучковые проводники с заданным значением электрического сопротивления.
Аналогично можно изготовить не только проводники со сверхвысокой или любой заданной проводимостью (или сопротивлением), но и любой материал с заданными структурно-чувствительными физическими свойствами или характеристиками, например, если необходимо получить материал или устройство со сверхмодовым значением.
Практически, для того, чтобы получить бездефектный длинномерный образец одноэлементного материала-проводника со сверхмодовым значением прочности или со сверхвысокой долговечностью, то необходимо любым известным способом снизить толщину до размера 1 нм.
Для изготовления пучкового материала необходимо предварительно построить кривые распределения (разброса) значений прочности и долговечности для пленок или волокон разных толщин di, например, для толщин 90, 80, 75, 70, 60, 50 мкм. Для каждой толщины готовится серия из 100 (не менее) однотипных отдельных образцов. Затем проводятся измерения СЧФС или СЧФХ, например, прочности и долговечности или электропроводимости. Данные измерений характеристик или свойств располагают в ряд в порядке возрастания номера последовательности n. Эти данные заносят в таблицу, либо графически строят интегральную функцию распределения. Интегральные функции распределения перестраивают в дифференциальные функции, т.е. в плотность вероятности СЧФС или СЧФХ. Если в какой-либо серии по толщине di обнаруживается полимодальность, наибольшее значение СЧФС ил СЧФХ, то эта толщина выбирается в качестве оптимальной толщины, с которой необходимо компоновать пучковый материал или устройство со сверхвысокими СЧФС или СЧФХ. При формировании пучка с низкими или сверхнизкими значениями СЧФС или СЧФХ необходимо выбирать ту толщину di, в серии которой будет наименьшее значение СЧФС или СЧФХ.
Таким образом, как при снижении масштаба одноэлементного образца, так и при увеличении масштаба (путем увеличения числа составляющих элементов N) образца-пучка происходит усиление и улучшение СЧФС и СЧФХ. В обоих случаях возникают сверхмодовые особые физические состояния, когда физические свойства и характеристики катастрофически усиливаются - становятся предельными (сверхвысокими).
Рассмотрим эти явления, одноэлементный и многоэлементный масштабный фактор, подробней в целях более рационального использования их на практике и понимания сущности заявленного изобретения.
В пучке тонких пленок или волокон, в соответствии с эффектом пучка, сверхмодовое состояние возникает, когда число N→∞, а толщина d составляющих элементов стремится к бесконечно малой величине Δ (d→Δ).
При числе N=1 пучок вырождается (многоэлементный масштабный эффект переходит в одноэлементный), а при стремлении толщины элемента d→1 нм мы получаем сверхтонкое тело, в котором уже в результате одноэлементного масштабного фактора, возникает сверхмодовое состояние, т.е. эффект сверхвысокого увеличения СЧФХ.
При снижении толщины d волокон (пленок) до размеров меньших, чем поперечные размеры микродефектов l0 (2,8 нм - 10 нм), последние испаряются (вытесняются) с объема тела, поскольку они из-за своей большой размерности не помещаются в объеме волокна или пленки.
Если учесть, что наименьшие по размерам дефекты согласно таблицам 1-4 составляют 2,8-10 нм, то при толщине d=1 нм, мы получаем бездефектную структуру, в котором физические характеристики и свойства достигают предельных значений.
Феномен одноэлементного масштабного фактора - это эффект необычайно высокого роста значений СЧФС и характеристик (СЧФХ) одиночных (одноэлементных) образцов при снижении их линейных размеров, например, толщины пленки или волокна [14].
В одноэлементном эффекте при снижении масштаба образца происходит вытеснение дефектов с поперечными размерами больше толщины образца (например, пленки или волокна) с объема образца и увеличение его средних значений физических свойств и характеристик: например, прочности (механической и электрической), долговечности (механической и электрической), электропроводимости и т.д. При этом изменяется дискретность или гетерогенность структуры образца, но его химическая структура неизменна.
По существу, свойства тонких пленок и волокон - это свойства поверхности, поскольку она во многом превышает объем. Решающую роль здесь играет дефектная структура и процессы перераспределения дефектов с одного уровня на другой, изменяющие среднее значение физических характеристик и свойств тела. В массивных образцах пленок (при увеличении толщины до значений более чем 50-60 мкм, или в длинных волокнах более чем 60-70 мм все образцы будут находиться на низких уровнях свойств и дальнейшее изменение масштаба не приведет к изменениям значений СЧФС и СЧФХ (см. фиг. 6). Потому в массивных образцах при увеличении его размеров масштабный эффект не возникает. В существующих статистических теориях такого ограничения нет [19].
Различие СЧФС и СЧФХ образцов малых и больших размеров согласно полученным результатов объясняется процессом перераспределения образцов (содержащих дефекты) между уровнями свойств, в результате, которого меняется среднее значение их свойств. Эти выводы имеют, большое научно-прикладное значение. Проведенные исследования четко доказали, что в природе существует более общее явление одноэлементного масштабного эффекта любых СЧФС и характеристик (СЧФХ) твердых тел и закономерность их изменения. Частным случаем этого феномена является известный масштабный эффект механической прочности и долговечности.
Массивные образцы, таким образом, при снижении толщины, становятся тонкими и переходят в высокомодовое состояние из-за отсутствия в них грубых макроскопических дефектов структуры. Это особое физическое состояние характеризуется высокими СЧФС и характеристиками (СЧФХ): высокой механической и электрической прочностью, высокой механической и электрической долговечностью, высокой электрической проводимостью и т.д.
В высокомодовом состоянии образцов твердого тела начальные микротрещины и макротрещины отсутствуют. В них под нагрузкой, в серии одинаковых образцов, возникает (образуются), как отмечено выше, весь спектр тонких дефектов структуры, которые соответствуют субмикротрещинам, перерастающие в микротрещины в результате их слияния и роста. Эти дефекты обнаруживаются методами рентгенофазового анализа и механики разрушения.
Соответственно СЧФС и СЧФХ тонких пленок и волокон, например, прочности, долговечности, электрического сопротивления и т.д., имея дискретный набор дефектов l0i (например, см. табл. 1-4), имеют большой экспериментальный разброс [(фиг. 7 (кривая 1), фиг. 8 (кривая 2), фиг. 9 (кривая 1), фиг. 12)].
Практически это означает, что если один образец под нагрузкой может, например, не разрушаясь просуществовать 1 секунду, а другой точно такой же (однотипный, одинаковый) разрушится в течение 10 секунд, третий - за 2 месяца или более (см. на фиг. 12 диаграмму распределения долговечности под нагрузкой для пленок ПЭТФ). Изделие или устройство с такого материала, который ведет себя, таким образом, затруднительно выполнять, хотя средние значения СЧФС и СЧФХ, например, прочности и долговечности имеют высокие значения. Или, к примеру, один образец проводника из внешне однотипной (одинаковой) серии может иметь нулевое электрическое сопротивление, а другой может иметь 0, 0,2, 0,8 или 1,0 Ом или более (см. фиг. 9, кривая 1). Изделия, например, резисторы, изготовленные из материала с таким экспериментальным разбросом физических характеристик, естественно, использовать на практике для прецизионных целей смысла нет.
Разброс данных эксперимента можно устранить изменением масштаба образца, а также изменением его температуры и величиной приложенной нагрузки на него.
Экспериментальный разброс данных можно устранить и другими технологическими приемами воздействия на образцы, включая химические методы обработки, которые кратко и разрозненно рассмотрены в работах [9-10, 15-16]. Однако химические методы, например, требуют использования агрессивных сред. Что с одной стороны, нарушает экологию, а с другой - это более дорогое и трудоемкое и материалоемкое занятие. С точки зрения так называемого принципа температурно-временной эквивалентности ТВЭ [10] безразлично каким из этих методов устранять разброс данных эксперимента. Однако не каждый из этих методов устранения разброса пригоден для улучшения свойств материалов и устройств из них, которые можно было бы безопасно использовать на практике.
В каждом конкретном случае требуется выбирать самые надежные, оптимальные, экономически и экологически целесообразные методы. Но как бы там ни было, сам факт экспериментального разброса дает возможность спрогнозировать свойства и поведение конструкций из того или иного материала. Изменяя (контролируя) экспериментальный разброс данных, можно обеспечить реальному изделию низкие или высокие, или сверхвысокие эксплуатационные свойства и характеристики без изменения химической структуры материала.
В настоящем изобретении обсуждаются предлагаемые нами универсальные способы не только устранения разброса данных эксперимента, но и способы одновременного (вместе с устранением разброса) существенного улучшения физических свойств и характеристик материалов и конструкций из них.
В этой связи, выше было показано, что массивные образцы характеризуются низкомодовым состоянием, которому соответствуют нормальные Гауссовые распределения свойств. Образцы малых размеров, тонкие пленки и волокна характеризуются высокомодовым состоянием с полимодальными функциями распределения. При этом вид функции распределения зависит не только от размеров образца, когда каждый образец данного материала имеет свой случайный набор дефектов, но и от заданных внешних условий испытания (температуры, напряжения, наличия или отсутствия контакта со средой и т.д.). Однако в целом, чем меньше образец, тем меньше вероятность присутствия в нем грубого дефекта [9].
Отсюда следует, что, начиная с некоторых размеров образцов, грубые дефекты вообще не будут наблюдаться ни в одном образце, размер которого меньший в данной серии. Это, в свою очередь, ведет к существенному различию разброса данных образцов больших и малых размеров (в смысле наличия или отсутствия в них грубых дефектов). Эти соображения имеют принципиальное значение для прогнозирования свойств тонких пленок и волокон и создания на их основе материалов и устройств с низкими, высокими или сверхвысокими значениями физических характеристик и свойств.
Универсальным способом устранения разброса, одновременно и способом улучшения свойств и выходом из создавшегося положения является, как это видно, из фиг. 9 (кривая 2) объединение в пучок тонких однотипных отдельных составляющих элементов-проводников между двумя противоположными токовыми контактами. В этом случае сопротивление гарантировано снижается, а разброс полностью устраняется. Резистор становится прецизионным без химической очистки резистивного материала.
Другой пример устранения разброса и улучшения физических свойств приведен на фиг. 8 (кривая 2 и 3). Как видно из этой фигуры, тонкая пленка ПЭТФ толщиной 18 мкм имеет значительный разброс и полимодальную функцию распределения плотности вероятности прочности, а объединение в пучок этих пленок с числом составляющих элементов N>>1 существенно приводит к сужению функции распределения и снижению разброса с одновременным сверхвысоким увеличением прочности пленок ПЭТФ. Используя этот эффект сверхнизкого снижения электрического сопротивления (т.е. сверхвысокой проводимости) в пучке, можно сделать высокоэффективные пучковые полупроводниковые приборы, солнечные элементы, пьезоэлектрические преобразователи, холодильники Пельтье и т.д.
С другой стороны, для того чтобы каждый n-й испытуемый образец в пучке (выборке) материала в гарантировано имел низкое электрическое сопротивление, снижают, к примеру, толщину токопроводящих пленок и волокон d до размера меньше поперечного размера наименьших СМТ в этом проводящем материале. Если наименьший размер дефекта считать равным l0=lmin=2,8 нм (как в таблице 3), тогда все испытуемые образцы перейдут в бездефектное сверхмодовое состояние, поскольку при толщине пленки или проволоки d0<2,8 нм дефекты, имея поперечный размер l0>2,8 нм, в них не могут разместиться. И тогда мы получаем гарантированное сверхнизкое сопротивление без экспериментального разброса. Однако наименьший размер дефекта в проводнике, в каждом конкретном случае необходимо определять рентгенофазовыми и методами механики разрушения.
В бездефектном сверхмодовом состоянии тела устраняется экспериментальный разброс данных, существенно увеличиваются все макроскопические СЧФС и СЧФХ: механическая и электрическая прочность и долговечность, обратная величина электрического сопротивления (т.е. проводимость), обратная величина добротности и (т.е. тангенс угла диэлектрических потерь) и т.д. Все СЧФС и СЧФХ материалов в этом состоянии приближаются к предельным или близким к теоретическим значениям. Функция распределения этих характеристик вырождается в этом состоянии из полимодального распределения (для тонких высокопрочных пленок или волокон, фиг. 4) в узко-симметричную унимодальную форму (см. фиг. 5).
На практике таким путем были получены свободные бездефектные пленки графена. Применительно к проводникам - это бездефектное состояние будет бездиссипативным для движения электронов и проводник в этом случае катастрофически теряет электрическое сопротивление до сверхнизких значений.
Сверхмодовое состояние, таким образом, для проводников является бездиссипативным сверхпроводящим состоянием. Поэтому одиночные бездиссипативные проводники с успехом могут использованы для токопроводящих цепей, например, в микросхемах.
Однако, свободные одиночные одноатомные пленки, имея сверхвысокие удельные физические характеристики, а также сверхвысокую удельную прочность, они имеют низкую суммарную прочность и долговечность. И там, где требуются выдерживать большие суммарные силовые нагрузки необходимо это учитывать.
Выходом из этого положения поэтому является использование пучков (стопок) с большим числом N>>1, N>>10 или даже N>>100 сверхтонких составляющих элементов. Как уже показано, на фиг. 9 (кривая 2) и фиг. 11, в пучке при N>>1 полностью устраняется экспериментальный разброс, а электрическое сопротивление катастрофически падает до нуля, а проводник переходит в сверхмодовое состояние со сверхвысокой проводимостью и сверхвысокой прочностью. Эксперименты показали, что такие проводники, например, из меди пропускают через себя сверхвысокие плотности тока - в 5000 А/мм2 и более, подтверждая тем самым, что они имеют сверхпроводящие свойства и являются без диссипативными. На практике в любом случае надо использовать пучковые материалы и устройства. В связи с этим ниже более подробно рассмотрим феномен пучка.
Явлением многоэлементного масштабного фактора назван феномен сверхвысокого увеличения СЧФС и СЧФХ тел, возникающий в структуре, которая состоит не из одиночного монолита, а из множества тонких отдельных индивидуальных однотипных составляющих моноэлементов [13].
Возникает этот эффект при увеличении числа N однотипных отдельных одиночных тонких (не массивных!) элементов при объединении их в пучок, стопу, трос и т.д. Возникает эффект пучка не за счет вытеснения дефектов из объема и поверхности и края тонких составляющих элементов пучка. Он возникает за счет шунтирования дефектных составляющих элементов пучка бездефектными элементами при росте масштаба образца-пучка при увеличении числа N элементов пучка.
Многоэлементные структуры или пучки, как и сверхтонкие моноэлементы (пленки и волокна) находятся в особом физическом состоянии. При объединении тонких индивидуальных отдельных составляющих элементов из числа N в пучок минимум между двумя противоположными контактами, возникает совершенно новое необычное особое физическое (сверхмодовое) состояние. Теория пучка в кратком виде приведена нами в [8-9, 16].
Таким образом, наряду с закономерностями одноэлементного масштабного (размерного) эффекта физических свойств, существует более общее природное явление многоэлементного масштабного (размерного) фактора физических свойств и характеристик. Частным случаем является известный с древнейших времен механический эффект троса или пучка. Статистические свойства, наблюдаемые в явлении пучка, реализуется не только с механическими свойствами, но и с любыми СЧФС и СЧФХ, например, электрической прочностью (фиг. 7, сравнить кривую. А N=1 и кривую А N=20), электрическим сопротивлением (фиг. 9), с тангенсом угла диэлектрических потерь (фиг. 13), электрической емкостью и индуктиверстью (фиг. 14) и т.д.
Как видно, с приведенных фиг. 7, 9, 13-14, независимо от рассматриваемого физического свойства или характеристики, в пучке при увеличении числа N наблюдается многоэлементный масштабный эффект СЧФС и СЧФХ: физические свойства и характеристики пропорционально увеличиваются, а экспериментальный разброс снижается.
При увеличении числа отдельных тонких элементов N в образце-пучке доля составляющих элементов пучка на высоких уровнях физических свойств увеличивается прямо пропорционально числу элементов, а разброс данных эксперимента снижается. Поэтому среднее значение СЧФС и СЧФХ многоэлементного пучка (или стопки) намного больше среднего значения отдельного индивидуального составляющего элемента стопки (пучка) - этим и объясняется явление сверхмодового состояния пучков, стопок, жгутов и т.д. Теория многоэлементного масштабного фактора приводит к идентичным результатам (см главу 5 в [9].
Если составлять многоэлементный образец (пучок) не из тонких, а массивных элементов, то многоэлементный масштабный эффект проявляться не будет - поскольку, как бы мы не увеличивали число элементов N, все составляющие элементы пучка будут находиться на одном и том же (самом низком) уровне свойств. Однако, в многоэлементной структуре ситуация с разбросом СЧФС или СЧФХ имеет обратную картину по сравнению с одноэлементной пленкой или волокном.
С увеличением числа тонких отдельных однотипных составляющих элементов N, т.е. увеличении масштаба пучка, грубые дефекты в них будут маскироваться (подавляться) наличием тонких дефектов. То есть составляющие элементы с грубыми дефектами в пучке шунтируются элементами с тонкими дефектами. При этом постепенно при достижении N некоторого Ni-го значения полимодальная кривая распределения перейдет в унимодальную кривую с большим значением прочности (если мы имеем дело с прочностными свойствами или характеристиками), близкой или совпадающей с предельным значением. Это связано с тем, что при нагружении пучка наиболее слабые его элементы (звенья) с грубыми дефектами будут разрушаться в первую очередь и выходить из зоны напряжения. Нагрузку будут воспринимать оставшиеся не разрушенные элементы (звенья пучка или стопки), если их число N при заданной степени нагрузки и многоэлементности достаточно велико. Т.е. многоэлементные структуры, как и тонкие пленки и волокна, находятся в особом физическом состоянии на высоких уровнях физических свойств и характеристик.
Таким образом, эффект сверхвысокого усиления физических свойств в пучках достигается без изменения гетерогенности структуры отдельных составляющих элементов, что имеет большое практическое значение. Следовательно, для достижения сверхмодовости или сверхвысоких значений тел не является обязательным требование бездефектности и идеальности структуры всех составляющих моноэлементов пучка. Это один из важнейших итогов рассмотрения многоэлементого масштабного эффекта физических свойств и характеристик тел. Это позволяет использовать эффект пучка в технологических целях для формирования материалов и устройств со сверхвысокими свойствами и характеристиками не на сверхчистых или особо чистых материалах, а на материалах невысокой степени очистки. Поэтому объединение тонких элементов в пучок эквивалентно химической очистке материала от примесей без изменения химической структуры материала и нарушения гетерогенности. При этом, не только объединение в пучок, а сам по себе процесс снижения масштаба одиночных элементов пучка также является эквивалентным химической очистке. Это потому, что при снижении, например, толщины пленки или волокна, вначале уходят из структуры объема образца, самые грубые дефекты группы 1 (см. табл. 1-3), а затем микродефекты группы II, поскольку из-за малого масштаба образца они (дефекты) в них просто не могут разместиться.
Важнейшей практической задачей в этой связи является нахождение числа N, при котором пучок будет иметь значения, равные или близкие к предельному значению или значению теоретической СЧФХ или СЧФС.
Ниже нами предлагается формулы для оптимального выбора (расчета) числа отдельных однотипных составляющих элементов N в пучке, учитывающего как дефектность и бездефектность составляющих элементов пучка, так и внешнюю нагрузку F, масштаб составляющих элементов V пучка (толщину d, ширину h и длину l). Рассмотрим эти два варианта.
Вариант 1.
Пусть  есть объем дефекта, разрушающий сверхмодовое состояние (CMC); ld - длина дефекта, sd - площадь его поперечного сечения.
есть объем дефекта, разрушающий сверхмодовое состояние (CMC); ld - длина дефекта, sd - площадь его поперечного сечения.
Пусть V - объем материала, из которого изготовляются составляющие элементы пучка. Далее пусть 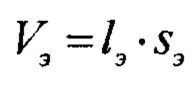 - объем составляющего элемента пучка, lэ - длина составляющего элемента пучка, sэ - площадь поперечного сечения составляющего элемента пучка.
- объем составляющего элемента пучка, lэ - длина составляющего элемента пучка, sэ - площадь поперечного сечения составляющего элемента пучка.
Изготавливаем из исходного материала число Nэ=V/Vэ элементов пучка, из которых далее составляются многоэлементные пучки, каждый из которых состоит из N элементов. Тогда, если Р0 есть доверительная вероятность, с которой в многоэлементном пучке должен быть хотя бы один элемент, не содержащий дефект, разрушающий CMC, то есть элемент, находящийся в CMC, то число элементов, находящихся в CMC в каждом многоэлементном образце-пучке должно удовлетворять условию

где Р есть экспериментально установленная доля многоэлементных пучков с эффектом CMC в их выборке (пучке, жгуте) из числа составляющих элементов, подготовленных к изготовлению многоэлементного пучка, с приведенными выше геометрическими характеристиками.
Теоретическая формулировка выражения (1) имеет следующий вид
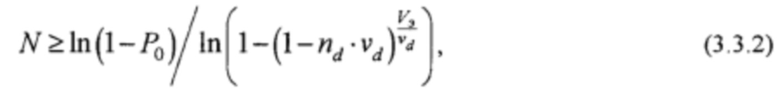
где nd есть среднее число дефектов, разрушающих CMC, в единице объема исходного материала.
Соотношение (3.3.1), таким образом, учитывает наличие в статистической выборке хоть одного образца, находящегося в CMC. При требовании изготовления материала с заданным значением СЧФС или СЧФХ, т.е. в случае, если в статистической выборке отсутствует хоть один элемент, находящийся в СМС, соотношение выглядит так:

где Р - экспериментально установленная доля материалов со значением СЧФС и СЧФХ σ≤σ0 , σ0 - нижняя граница СЧФС или СЧФХ, σэ - требуемое или заданное значение СЧФС или СЧФХ пучка.
Вариант 2.
Пусть задан уровень внешнего воздействия F, который должен выдерживать образец при сохранении своей работоспособности, а σр,м есть значение СЧФХ или СЧФС σр, реагирующей на указанное внешнее воздействие, соответствующее выбранному ее уровню (моде) на дифференциальных кривых распределения СЧФС (СЧФХ) или соответствующей горизонтальной площадке на интегральной кривой распределения СЧФХ или СЧФС материала с заданными геометрическими размерами длиной l, толщиной d и шириной h [9], так что все образцы со значением σp≥σр,м являются высокомодовым. То есть σр,м определяет нижнюю границу σр, принимаемой по технологии изготовления многоэлементного образца-пучка, области высокомодовости образца (материала) и является функцией указанных геометрических размеров 
Критическое число Nk высокомодовых элементов определяется уравнением

где 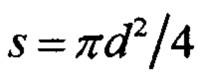 есть площадь поперечного сечения одного составляющего элемента пучка, если образец имеет круговое сечение, или s=d⋅h, если образец имеет прямоугольное сечение. Каждый многоэлементный образец-пучок, состоящий из N элементов можно рассматривать как результат N повторных испытаний, в которых успехом является попадание элемента с уровнем структурно-чувствительной характеристики или свойства σр>σр,м в многоэлементный образец (пучок). Вероятность успеха равна р. Она определяется из кривых распределения СЧФХ (СЧФС), или по вариационной диаграмме СЧФХ (СЧФС) материала с заданными геометрическими размерами как доля элементов с уровнем структурно-чувствительной характеристики или свойства σр>σр,м. Вероятность неуспеха q=1-p, таким образом, есть доля одноэлементных образцов со значением СЧФХ (СЧФС), σр<σр,м, то есть ниже σр,м. Так как N>>1, то для определения Nk можно применить интегральную теорему Лапласа для распределения Бернулли, в соответствии с которой вероятность модуля отклонения случайной величины N от ее математического ожидания Np на величину меньше, чем ε>0, то есть
есть площадь поперечного сечения одного составляющего элемента пучка, если образец имеет круговое сечение, или s=d⋅h, если образец имеет прямоугольное сечение. Каждый многоэлементный образец-пучок, состоящий из N элементов можно рассматривать как результат N повторных испытаний, в которых успехом является попадание элемента с уровнем структурно-чувствительной характеристики или свойства σр>σр,м в многоэлементный образец (пучок). Вероятность успеха равна р. Она определяется из кривых распределения СЧФХ (СЧФС), или по вариационной диаграмме СЧФХ (СЧФС) материала с заданными геометрическими размерами как доля элементов с уровнем структурно-чувствительной характеристики или свойства σр>σр,м. Вероятность неуспеха q=1-p, таким образом, есть доля одноэлементных образцов со значением СЧФХ (СЧФС), σр<σр,м, то есть ниже σр,м. Так как N>>1, то для определения Nk можно применить интегральную теорему Лапласа для распределения Бернулли, в соответствии с которой вероятность модуля отклонения случайной величины N от ее математического ожидания Np на величину меньше, чем ε>0, то есть  определяется уравнением
определяется уравнением

где  есть функция Лапласа, 1-α есть доверительная вероятность. Так как распределение Бернулли в рассматриваемом случае, когда N>>1, Nk>>1 и р является не очень малым, имеет асимптотический вид нормального распределения, то выполняется правило трех сигма, то есть трех среднеквадратичных отклонений σБ, которое в асимптотике распределения Бернулли равно
есть функция Лапласа, 1-α есть доверительная вероятность. Так как распределение Бернулли в рассматриваемом случае, когда N>>1, Nk>>1 и р является не очень малым, имеет асимптотический вид нормального распределения, то выполняется правило трех сигма, то есть трех среднеквадратичных отклонений σБ, которое в асимптотике распределения Бернулли равно  и означающее, что все отклонения величины N от величины Np сосредоточены на интервале определяемым неравенством
и означающее, что все отклонения величины N от величины Np сосредоточены на интервале определяемым неравенством  с доверительной вероятностью 1-α=0,9974. Раскрывая это неравенство, получим
с доверительной вероятностью 1-α=0,9974. Раскрывая это неравенство, получим 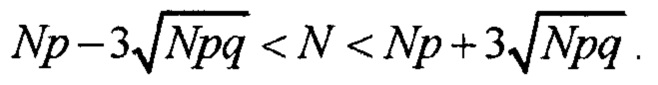 Потребуем, чтобы выполнялось неравенство
Потребуем, чтобы выполнялось неравенство 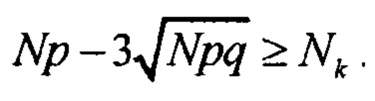 В этом случае выбранное в соответствии с этим неравенством число элементов в многоэлементном образце с доверительной вероятностью 0,9974 гарантирует работоспособность многоэлементного образца под внешним воздействием F после разрушения всех элементов с и σр ниже σр,м. Решая это неравенство, получим условие выбора числа элементов в многоэлементном образце (пучке)
В этом случае выбранное в соответствии с этим неравенством число элементов в многоэлементном образце с доверительной вероятностью 0,9974 гарантирует работоспособность многоэлементного образца под внешним воздействием F после разрушения всех элементов с и σр ниже σр,м. Решая это неравенство, получим условие выбора числа элементов в многоэлементном образце (пучке)
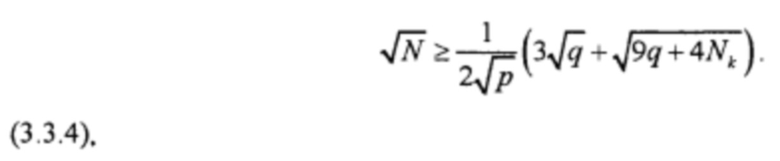
Отсюда, с учетом того, что Nk>>1, получим следующий критерий отбора числа составляющих элементов для многоэлементного образца (пучка) с заданной доверительной вероятностью 1-α=0,9974
 F.
F.
Обе величины, р и σр,м являются экспериментально определяемыми до компоновки многоэлементного образца (пучка), функциями геометрических размеров его элементов длины l, толщины d и ширины h, в соответствии со схемой описанной выше.
Пример оценки. Оценим N на примере внешнего воздействия на ПММА (полиметилметакрилата) в виде внешнего растягивающего напряжения σ.
Имеем при р=10-1, d=10-3 М, S=πd2/4~7,5⋅10-5 М2 F=108 H, σр,м=8⋅108 МПа.

Необходимо отметить, что свойства пучка принципиально отличаются от свойств моноэлемента (монолита), т.е. одноэлементного образца, соответствующего по геометрическому размеру многоэлементному пучку. С увеличением в пучке числа однотипных тонких элементов, несмотря на увеличение масштаба, среднее значение СЧФС и СЧФХ увеличиваются до значений близких к предельному, в то время как у монолита при увеличении масштаба среднее значение прочности (если рассматриваем прочностные СЧФС) снижается до достижения толщины d0>50-60 мкм и длины d0>60-70 мм. Поскольку при достижении некоторого Ni-го значения подавляющее число образцов-элементов будут находиться на самом высоком уровне прочности σi (т.е. совпадающем с предельным значением прочности σп), то разброс экспериментальных значений будет незначительным, а материал будет находиться в сверхпрочном (сверхмодовом) состоянии. Следовательно, на практике для достижения сверхвысокого состояния («эффекта пучка» необходимым условием является как снижение диаметра (толщины) волокон или пленок, составляющих конструкцию пучка (стопки), так и многоэлементность. Чем больше будет число элементов N в пучке и будут тоньше составляющие элементы, тем выше будет эффект усиления.
Таким образом, из вышеизложенного следует, что статистическое распределение в пучках вырождается в узко-симметричное унимодальное распределение подобно тому, как это в феномене одноэлементного масштабного фактора. Это особое физическое состояние возникает, как в одноэлементном масштабном факторе, без изменения химической структуры пленок или волокон. Если в одноэлементном факторе это происходит за счет вытеснения дефектов и изменения дискретности и гетерогенности структуры, то в многоэлементном масштабном факторе происходит за счет шунтирования грубых дефектов, причем без изменения гетерогенности структуры составляющих элементов при простом увеличении числа N отдельных тонких составляющих элементов (без энергозатрат на изменение их химического строения). При этом концентрация и степень опасности дефектов в пучке не изменяется. Как были в пучке дефекты, так и они остались там.
Дефекты с дефектными составляющими элементами пучка шунтируются (блокируются) большим количеством бездефектных элементов. В пучке можно достичь прочности химической связи и получить материалы со сверхнизкими электрическими и сверхвысокими прочностными свойствами, а также обладающими рядом других предельных физических свойств и характеристик.
Таким образом, из вышеизложенного следует, что если мы изменяем не толщину тонких индивидуальных составляющих элементов (они остаются тонкими и постоянными по длине и толщине), неизменна здесь и структура волокна или пленки, а изменяем число N тонких индивидуальных составляющих элементов-волокон или пленок, то мы тем самым изменяем, масштаб (суммарную толщину) образца-пучка и достигаем эффекта сверхвысокого усиления физических свойств.
В эффекте одноэлементного масштабного фактора высокий рост и усиление свойств происходит не за счет увеличения, а за счет снижения масштаба одиночного одноэлементного образца, вытесняющего таким путем дефекты структуры поверхности и объема образца, изменяющего этим гетерогенность структуры образца.
В многоэлементном размерном эффекте одновременно происходит: эффект шунтирования дефектов, и устранение разброса данных со сверхвысоким увеличением и усилением СЧФС и СЧФХ при увеличении в пучке или стопе числа N тонких индивидуальных отдельных однотипных составляющих элементов.
Эффект пучка возникает, таким образом, не за счет вытеснения дефектов из тонких составляющих элементов пучка, а за счет шунтирования в пучке дефектных элементов бездефектными. При этом масштаб образца-пучка увеличивается за счет увеличения числа N тонких индивидуальных составляющих элементов в пучке.
Таким образом, из вышеизложенного следует, что, изменяя масштаб образца-пучка за счет увеличения числа N тонких или сверхтонких однотипных образцов (пленок или волокон), затем складывая или собирая их в стопу или пучок между двумя противоположными контактами можно получить пучковые материалы или устройства с любыми заданными физическими свойствами: низкими, высокими или сверхвысокими значениями.
Такой многоэлементный способ в изготовлении материалов и устройств в патентной литературе [1-18] назван пучковым, а концепция технологии - пучковой технологией материалов и устройств.
Ниже более подробно рассмотрена концепция пучковой технологии. Даны определения, обозначения и основополагающие принципы пучковой технологии материалов и устройств.
Предлагаемые способы изготовления пучковых материалов основаны на структурно-статистическом кинетическом подходе и представлениях о масштабном (размерном) эффекте физических свойств и характеристик тел, объединившие три современные технологические концепции: субмикронную (или нанотехнологию), микронную технологию и макротехнологию.
Каждой из составляющих технологий соответствуют (см. раздел 3.1) три типа размерностей дефектов в образцах, условно разделенные на три типа: 1 - субмикро - или нанотрещины (1-99 нм); 2 - микротрещины (100-1000 нм); 3 - макротрещины (1000-10000 нм и более). В соответствии с такой классификацией твердые тела по масштабному фактору могут находиться в трех физических состояниях: низкомодовое, всокомодовое и сверхмодовое.
Эти три физических состояния являются методологической основой и предметом пучковой технологии.
Под пучком (стопой) понимается многоэлементная структура, образованная из числа N→∞ (где N - целое число) однотипных отдельных индивидуальных составляющих элементов, имеющих одинаковое функциональное назначение, стремящихся своим размером  к бесконечно малой величине Δ, но так, чтобы величина V⋅N оставалась конечной, равной заданному объему многоэлементной структуры, расположенных параллельно друг с другом (или друг над другом) на поверхности (крае) и в объеме (или промежутке) и объединенных противоположными контактами из числа K≥2.
к бесконечно малой величине Δ, но так, чтобы величина V⋅N оставалась конечной, равной заданному объему многоэлементной структуры, расположенных параллельно друг с другом (или друг над другом) на поверхности (крае) и в объеме (или промежутке) и объединенных противоположными контактами из числа K≥2.
Составляющий элемент пучка (многоэлементной структуры) - это пленки, волокна, проволоки, гетеропереходы, переходы Шоттки, pn переходы с областями проводимости в полупроводниках и т.д. То есть может быть использована любая тонкая материальная субстанция, имеющая ограниченный размер по толщине d и достаточную протяженность по ширине h и длине L.
Волокно - линейное длинномерное протяженное тело с малым поперечным размером (толщиной) по сравнению с длиной. Волокна - это двумерные тела, имеющие два измерения: толщину d и длину L (протяженность).
Пленка - плоское тело, имеющее малый поперечный размер (т.е. толщину) и большую площадь поверхности по ширине и протяженности (длине). Пленки - это трехмерные тела, имеющие толщину d, ширину h и протяженность L (длину).
Если пучок или стопа составлена из N монопленок, то такая многоэлементная структура имеет плоскопараллельное расположение элементов-пленок, имеющих поверхностные (краевые) и промежуточные (внутри объемные) слои. А если пучок или стопа составлена объединением N моноволокон, то такая многоэлементная структура имеет линейно-параллельное расположение элементов-волокон, находящихся на поверхности (крае) и в объеме (промежутке).
Многоэлементные структуры и изделия, выполненные параллельным объединением составляющих элементов (волокон, пленок) между двумя (или более противоположными контактами названы пучковыми.
Это пучковый резистор, полученный параллельным объединением, например, из числа N>>1 резистивных пленочных или волоконных элементов.
Это пучковый полупроводниковый прибор, полученный объединением в пучок из N>>1, или N>>10, или 10000 или более, например, точечных pn переходов между противоположными контактами.
Это может быть пучковый транзистор, полученный объединением N>>10000 или более pn переходов с геометрически малыми размерами в пучок на коллекторе, эмиттере, базе в биполярных транзисторах и стоке, истоке, затворе (в полевых транзисторах), подчеркивая этим самым способ их изготовления.
Это может быть пучковый диэлектрик, полученный, например, объединением N>1 тонких или сверхтонких диэлектрических пленок между противоположными контактами из числа K≥2.
Или это может пучковый проводник электрического тока, полученный объединением N>1 тонких или сверхтонких проволок (или токопроводящих пленок) между противоположными контактами из числа K≥2.
Или это материалы для защиты от ударных (механических, электронных, лазерных) или агрессивных внешних воздействий, полученные объединением в пучок N>1 тонких и сверхтонких пленок между противоположными контактами из числа K≥2.
Это может быть сверхпротяженный сверхпрочный канат или трос, полученный свивкой тонких или сверхтонких проволок с числом N>1 с шагом свивки длиной менее 60 мм.
И наконец, это могут быть любые материалы или устройства, полученные объединением в пучок N>1 тонких или сверхтонких составляющих элементов между противоположными контактами из числа K≥2.
Составляющие элементы в пучке могут иметь органическое или неорганическое происхождение, могут быть металлами, металлоидами или полимерами, диэлектриками или проводниками, или полупроводниками, металополимерами или любой другой материальной субстанцией. При этом основополагающим и фундаментальным для выполнения пучкового материала является требование большого количества составляющих элементов пучка (N→∞) и их малый размер, вплоть до микроразмеров, а в идеальном случае составляющие элементы должны быть наноразмерными, т.е. должны быть от 1 нм до 100 нм.
Признаки однотипный и отдельный (вместе с требованием множества N→∞ и малого размера толщины волокон или пленок) являются основополагающими и фундаментальными, без которых эффект сверхвысоких свойств и значений физических характеристик в пучке не реализуется.
Под однотипными элементами следует понимать такие, которые получены из одного и того же вида, и строения материи, одинаковым способом, имеющие одинаковые геометрические размеры, массу, форму и конфигурацию, а также одинаковые структурно-чувствительные физические (механические, электромагнитные и др.) характеристики и свойства.
Под признаком «отдельный» или отделенный друг от друга, не связанный друг с другом подразумевают наличие границы между элементами и его обособленность. Отделителем может быть воздух, нейтральная среда, диэлектрик, полимерная или металлическая пленка, фольга и т.д.
Дискретные уровни физических свойств и характеристик. Это выделенные значения физических свойств и характеристик в виде максимумов на их дифференциальных функциях и в виде горизонтальных площадок на их интегральных функциях распределений. Например, уровни прочности σi (см. фиг. 8, кривая 2), уровни долговечности (см. фиг. 3) или уровень электрического сопротивления Ri (см. фиг. 9, кривая 1), уровни диссипации энергии Ei, уровни напряжения ионизации Ui и т.д.
Низкомодовое состояние - физическое состояние тел по масштабному фактору, в котором находятся (пребывают) массивные тела (волокна, пленки толщиной более 60-70 мкм с размерностью дефектов 1000-10000 нм и более), имеющее низкие значения СЧФС и СЧФХ с нормальной унимодальной функцией распределения характеристик.
Высокомодовое состояние - физическое состояние тел по масштабному фактору, в котором находятся (пребывают) тонкие тела (волокна, пленки толщиной менее 50-60 мкм с размерностью дефектов 100-1000 нм), имеющее высокие средние значения СЧФС и СЧФХ с полимодальной функцией распределения характеристик.
Сверхмодовое состояние - физическое состояние тел по масштабному фактору, в котором находятся (пребывают) пучки из тонких тел (волокна, пленки толщиной менее 50-60 мкм с размерностью дефектов 100-1000 нм), имеющие сверхвысокие СЧФС и СЧФХ с унимодальной узко-симметричной функцией распределения характеристик и свойств,
- это также сверхтонкие тела (волокна и пленки толщиной 1-100 нм с размерностью дефектов 2,8-90 нм), имеющее сверхвысокие СЧФС и СЧФХ с унимодальной узкосимметричной функцией распределения характеристик.
Суть ПТ материалов и устройств заключается в том, что материал или устройство выполняются из числа N→∞ однотипных отдельных, не связанных между собой индивидуальных составляющих элементов (волокон, проволок, пленок, фольги, переходов и т.п.) размер (толщина) которых стремится к бесконечно малой величине Δ, объединенных в пучок или стопу, причем каждый из составляющих элементов имеет одинаковое функциональное назначение и заключен между противоположными контактами из числа K≥2.
В основе создания пучковой технологии материалов и устройств со сверхвысокими физическими свойствами и характеристиками лежат простые, но фундаментальные природные закономерности, свойства и явления.
Это прежде всего свойства и явления, связанные со снижением масштаба образцов до микро- и нано- (т.е. субмикронных) размеров и увеличением масштаба в пучке за счет увеличения числа микро- и наносоставляющих отдельных однотипных моноэлементов.
Пучковая технология состоит из трех составных частей: субмикро- (или нано-), микро- и макротехнологии. Представляет из себя физический, а не химический способ модификации структуры материалов и устройств без изменения их дискретноти и гетерогенности. Пучковые технологии относятся к масштабам выше 1 нм, т.е. к чисто физическим процессам.
Физическая природа масштабного эффекта была раскрыта еще в первой половине 20 века, однако, до недавнего времени это связывали в основном с механической прочностью твердых тел больших и малых объемов и присутствием в них дефектов различной степени опасности.
Систематические экспериментальные и теоретические исследования авторов с сотр. с 70-х годов прошлого столетия позволили установить универсальность структурной иерархии твердых тел и полимеров. Открыты были явления дискретности физических свойств и характеристик. Это позволило в свою очередь установить, что масштабный эффект механической прочности является всего лишь частным случаем проявления более общих природных закономерностей - феноменов одноэлементного и многоэлементного масштабного эффектов физических свойств и характеристик физических объектов, связанных с дискретностью строения материи, воспетых еще античным философом Лукрецием в трактате «О природе вещей».
В одноэлементном масштабном или размерном эффекте (см. вышеизложенные разделы) изменение масштаба происходит за счет изменения геометрических размеров одноэлементного образца; в многоэлементном масштабном эффекте изменение масштаба происходит за счет изменения числа N тонких элементов в стопе или пучке одноэлементных (одиночных) образцов.
Явление одноэлементного масштабного фактора в наиболее общем виде - это эффект необычайно высокого роста значений СЧФХ и СЧФС тел при снижении их геометрических размеров, вплоть до микро- и наноразмеров. Это явление обусловлено тем, что в массивных по объему образцах существует дискретный спектр или набор дефектов структуры различной степени опасности: больших и малых по размеру, в которых малые по размеру дефекты замаскированы присутствием больших. Поэтому массивные образцы имеют низкие физические свойства и характеристики. В малых по объему образцах могут быть только малые по размеру дефекты, которые находятся на высоких уровнях. Поэтому изначально тонкие пленки и волокна имеют высокие физические свойства и характеристики.
Явление многоэлементного масштабного фактора (или эффекта пучка или троса) - это эффект сверхвысокого роста значений структурно-чувствительных свойств и характеристик физических объектов, возникающий при объединении в пучок одиночных однотипных элементов, имеющих субмикро- (или нано-) и микроразмерность, и уже достигших высоких значений физических характеристик. В обоих эффектах с ростом значений структурно-чувствительных свойств и характеристик физических объектов их химическая структура остается без изменения. При этом, чем будут меньше линейные размеры одноэлементных составляющих, тем больше будет эффект усиления в пучке или стопе. Идеальным будет случай, когда одноэлементные составляющие пучка будут иметь наноразмерный масштаб. В наноразмерном элементе дефекты с большими размерами не могут поместиться. Потому их там нет. С точки зрения эффекта пучка в пучковой технологии нет требования к чистоте составляющего элемента. Каким бы не был по чистоте материал, пучковая технология, для своей реализации, требует отдельность, однотипность, геометрически малый микро-, предпочтительно, наноразмер (в которых нет больших дефектов или включений) составляющих элементов и число составляющих элементов N→∞. Это замечание имеет существенное значение. Только на стоимости материала изделий можно получить значительную экономическую выгоду, поскольку, чем чище исходный материал для изделия, тем он дороже. Например, стоимость кремния от чистоты имеет экспоненциальную зависимость. К примеру, не очищенный технический кремний на порядок и более дешевле чистого кремния.
Для пучковой технологии необходима реализация всех трех составляющих - сверхмодового, высокомодового и низкомодового (нано-, микро- и макро). Особенно важна микро- и субмикронная или наноразмерная составляющая отдельного однотипного элемента, которые формируют высокие значения физических характеристик. В связи с этим надо особо подчеркнуть важность правильной упаковки наноразмерных или микроразмерных элементов в макроупаковку реального изделия. Некорректная упаковка элементов, пусть даже наноразмерных, в макроизделие не даст желаемого эффекта сверхвысокого увеличения прочности и др. физических характеристик и свойств.
Многолетние систематические и детальные исследования показали, что для получения эффекта сверхвысокого увеличения свойств и характеристик в макроизделиях должна быть пучковая упаковка большого множества, в идеале наноразмерных, отдельных индивидуальных и однотипных элементов.
Для реализации эффекта пучка, в соответствии с математическим законом больших чисел, число однотипных элементов N в пучке должно стремиться к бесконечно большой величине, а его размер - к бесконечно малому числу. Условию бесконечно малой величины соответствует наноразмерный однотипный отдельный элемент. В полупроводниковой технологии этому условию соответствуют точечные р-n переходы. Снижение толщины составляющих элементов-пленок (или волокон) в пучке до микро-, субмикроразмеров (или наноразмеров) при стремлении их числа N→∞ (при отдельности и однотипности индивидуальных тонких составляющих элементов) приводит к сверхвысокому увеличению физических свойств и характеристик. В этом суть эффекта пучка.
Пучковые материалы и устройства формируются из тонких или сверхтонких тел, волокон, пленок (органического и неорганического происхождения), носителей зарядов, областей проводимости, или р-n переходов и.т.д. Составляющие элементы пучка могут быть выполнены из металла, металлоида, полимера, диэлектрика или проводника электрического тока, или тепла, или полупроводника. Функциональное назначение пучкового материала и устройства зависит от функционального назначения составляющих элементов. Ниже приведем несколько вариантов пучковых материалов по функциональному назначению составляющих элементов.
Пример 1.
Пучковый материал или устройство для защиты от механического, электрического и СВЧ удара.
Пучковый материал или устройство для защиты от механического, электрического и СВЧ удара по изобретению может быть получен следующим образом. Выбирается заданное число N тонких или сверхтонких отдельных однотипных пленок для формирования стопы (пучка), например, из полиэтилентерефталата (ПЭТФ). Эти однотипные пленки являются составляющими элементами стопы и имеют конфигурацию задуманного изделия, например, их можно нарезать (вырубить) виде прямоугольных полосок или круга из одной и той же партии материала (рулона), изготовленных в пределах партии в идентичных технологических условиях. Таким образом, все они имеют одинаковую технологическую предысторию изготовления, массогабаритные размеры, состав и т.п. Поэтому каждый из этих индивидуальных отдельных однотипных полосок также имеют одинаковое функциональное назначение.
Число элементов-слоев может быть определено экспериментально путем измерения механической и электрической прочности статистических выборок, содержащих не менее 100 образцов. Либо для расчета числа N составляющих элементов стопы (пучка) при заданной толщине пленок d принята полуэмпирическая формула Nэ≥f/p⋅fp,max, где р - доля элементов имеющих максимальное ударное разрывное усилие fp,max, f - ударная нагрузка, которую должна выдержать стопа, Nэ - число элементов-слоев в стопе. Значение р для выбранных пленок (заданной толщины и из определенного материала) может быть установлено экспериментальным путем (испытанием определенного количества образцов, например пятидесяти или ста) в лабораторных условиях.
Далее, однотипные отдельные пленки-слои складываются в стопу (пучок) в многослойную (многоэлементную) структуру. Стопа - это структура, имеющая нижний слой, верхний слой и промежуточные слои, каждый из которых размещен любым известным способом на ближайшем к нему снизу слое.
В целях соблюдения принципа отдельности, в промежутке между составляющими элементами (слоями), оставляется воздушный зазор. Для обеспечения отдельности можно использовать любую другую нейтральную среду. Затем при необходимости края стопы закрепляются любым известным способом, например, ламинированием, или посредством зажимов, или клеевых соединений и т.п. Сверху слоя стопы и снизу напылением (либо любым другим способом, обеспечивающим высокое сцепление со слоем стопы) выполняются контактные площадки для электродов, количество которых должно быть не менее двух - минимум по одному контакту с каждой из противоположных сторон.
Однотипные отдельные составляющие элементы (слои) стопы (пучка) согласно заявленному изобретению, должны быть тонкими или сверхтонкими.
Тонкими элементами, согласно изобретению, являются пленки толщиной d≤50 мкм, имеющие полимодальную функцию распределения физических характеристик и свойств, в котором при механическом или электрическом нагружении, возникают дискретно распределенные по размерам дефекты. Возникающее в тонких пленках и волокнах субмикротрещины (размерностью от 1 нм до 100 нм) и микротрещины (размерностью от 100 нм до 1000 нм) в результате роста и слияния перерастают в макроскопические магистральные трещины разрушения.
Сверхтонкими, согласно изобретению, являются одиночные пленки или волокна толщиной от 1 нм до 100 нм с размерностью дефектов от 3 нм до 90 нм (субмикротрещины СМТ или нанотрещины НТ).
Методика оценки дефектов отработана и подробно изложена монографии авторов изобретения [9]. Имея данные о размерах дефектов можно использовать более корректные данные по толщине составляющих элементов d.
Поэтому, в нашем случае, толщина составляющего элемента (слоя стопы) d взята из расчета не больше поперечного размера наибольшего дефекта, образующегося при нагружении в пленках толщиной 50-60 мкм. В таблицах 1-4 приведены данные о размерах дефектов в волокнах кератина и шелка, в пленках монокристалла кварца и ПЭТФ. Как видно из таблицы 4, в пленках ПЭТФ наибольший поперечный размер дефекта составляет 12,6 мкм. Поэтому для изготовления пучкового материала был выбран размер 12,5 мкм (d≤12,6 мкм) за толщину составляющего элемента. При такой толщине пленки дефекты размером 12,6 мкм в них отсутствуют. Дефекты меньшего размера в пучке блокируются большим количеством бездефектных элементов (см. раздел 3.3). Если в качестве однотипного отдельного составляющего элемента использовать пленки кварца, то в нем наибольший поперечный размер дефекта составляет 29 мкм. Тогда за толщину d надо принять d≤25 мкм, как это было принято в изобретении [5].
Однако, для формирования стопы (пучка) предпочтительно использовать пленки толщиной соответствующих размерам наименьших структурных дефектов, например, можно использовать пленки ПЭТФ толщиной d=3 мкм. Такие пленки в промышленности выпускаются серийно. В этом случае, как видно с таблицы 4, микротрещины размером более 3 мкм выходят из зоны нагрузки. И в этом случае требуется меньшее число N элементов в пучке, ведущее к существенному (в разы) снижению материалоемкости конечного изделия. Поэтому формировать стопу пучкового материала необходимо из сверхтонких пленок, в них образуются СМТ меньшего размера. Как уже известно, для достижения сверхмодового состояния в стопе требуется существенно меньшее количество однотипных составляющих элементов-слоев. Поэтому пучок из сверхтонких пленок имеет меньшую материалоемкость.
В реальных условиях, несмотря на очевидную выгодность сверхтонких пленок, технологически их сложнее изготовить, чем тонкую пленку. Например, сверхтонкие одноатомные пленки промышленность в настоящее время не в состоянии производить серийно. Они производятся пока только в лабораториях. В то время как тонкие пленки промышленностью производятся серийно и крупномасштабно.
Но с другой стороны, если в пучке увеличивать число N составляющих элементов-слоев, то при достижении определенного значения мы также получим сверхмодовое состояние и сверхвысокие значения физических свойств пучка. При этом, как отмечено выше, в пучке тонких пленок или волокон можно получить более высокие значения СЧФС или СЧФХ, чем в одноэлементной структуре путем изменения ее гетерогенности.
Пучок или стопа из пленок ПЭТФ, выполненная вышеуказанным способом (см. фиг. 7-8) имеет сверхвысокую электрическую и механическую прочность. Она может выполнять защитные функции от механического удара и электрического пробоя. Она выдерживает предельные нагрузки. Такая стопа, кроме того, имеет сверхнизкое значение тангенса угла диэлектрических потерь, составляющая tgΔ=10-6. Имея такое значение тангенса угла диэлектрических потерь, стопа может служить защитой от СВЧ воздействия. Такую стопу можно использовать, например, в преобразователях и усилителях параболических антенн СВЧ-диапазона, спутниковых и наземных мобильных телефонах, в радиолокации и т.д. Низкие значения тангенса угла диэлектрических потерь были получены не только для пучковых материалов из ПЭТФ, но и других, например, на полиимидных, результаты измерений которых представлены на фиг. 13.
Если, к примеру, необходимо получить защитный экран от механического удара, например, для защиты автомобиля от пуль, из такой стопки-книжки вырубаются заготовки под размеры и конфигурацию автомобильных стекол (лобового или боковых), после чего заготовки-книжки прикрепляют (например, приклеивают) по посадочному месту.
Для изготовления пучкового защитного материала можно использовать любые другие, например, полиимидные, фторопластовые, полистирольные пленки или из кварца, слюды и других материалов и т.п. Выбор полимерной или металлической пленки, или любой иной зависит от функционального назначения защитного материала. Например, если защита необходима от электрического поражения, то нужно использовать для этого диэлектрические полимерные пленки; если нужна защита от механического удара необходимо использовать, например, титановые пленки; для защиты автомобильных стекол - необходимо также использовать тонкие полимерные пленки и т.д. Следует заметить, что подобные пленки производятся в настоящее время промышленным способом, что гарантирует их доступность и обеспечивает существенное упрощение технологии изготовления конечного защитного материала в сравнении с известным уровнем техники.
Пример 2.
Пучковый пьезоэлектрический материал или устройство.
Пучковый пьезоэлектрический материал или устройство выполняется следующим образом. Для этого используются диэлектрические материалы (вещества), обладающие пьезоэлектрическими свойствами. К ним относятся, к примеру, кварц, турмалин, сегнетовая соль, титанат бария, фторопласт, керамики и т.д. Из них любым известным способом изготавливаются тонкие или сверхтонкие пластины (пленки), из которых вырезаются заданное число N однотипных отдельных заготовок, например, прямоугольной или круговой конфигурации. На гранях таких пластин-пленок напыляют токопроводящие контактные площадки для напайки электродов. Из таких фактически уже готовых элементарных пластин-пьезоэлектриков собирается стопа. В стопе элементарные пьезоэлектрики посредством контактных площадок соединяются параллельно в токовую цепь, т.е. объединяются в пучок. Из таких пучков, состоящих из N элементарных пьезоэлектриков, в зависимости от их функционального назначения, выполняются пучковые пьезоэлектрические преобразователи: генераторы, трансформаторы, усилители и т.п.
Толщину d составляющего однотипного элемента можно априори приять значение d≤50 мкм. Однако, более корректным будет, если рассчитаем его из данных по поперечному размеру дефектов, распределенных в том или ином пьезоэлектрике. Если для выполнения пучкового диэлектрика, используем кварц, то данные на него представлены в таблице 3.
Как видно из таблицы 3, наибольший поперечный размер дефекта в кварцевой пластине толщиной 40 мкм составляет 29000 нм (29 мкм), а наименьший - 2,8 нм. Пленку из кварца толщиной d=29 мкм, выполнить промышленными способами вполне возможно, а толщиной 2,8 нм гораздо сложнее. Поэтому за толщину составляющего элемента пучка, для изготовления пучкового пьезоэлектрика из кварца, надо принять d=29 мкм.
Число N можно подобрать экспериментально - в зависимости от того, какой хотим получить коэффициент электромеханической связи (ЭМС).
Пьезоэлектрический преобразователь из массивных пластин кварца, являющегося «слабым» пьезоэлектриком, имеет коэффициент ЭМС порядка 5%. Однако, если выполнить из этого «слабого» пьезоэлектрика пластины толщиной всего в 29 мкм и собрать из них стопу всего из 10 пластин и сделать из него преобразователь, например, трансформатор или усилитель напряжения, то коэффициент ЭМС составит не менее 95%.
Пример 3.
Пучковый фотоэлектрический преобразователь (ФЭП) на полупроводнике.
Для изготовления фотоэлектрического преобразователя (ФЭП) использовали полупроводниковую подложу на монокристаллический кремний типа p-CZ-Si и n-CZ-Si, на котором методами стандартной промышленной полупроводниковой технологии формировали pn переходы.
Стандартные из уровня техники фотоэлектрические преобразователи (ФЭП) с одним большим сплошным pn переходом, составляющие основу современной солнечной электроэнергетики, имеют ключевые недостатки: высокое внутреннее (последовательное) сопротивление и сравнительно низкое КПД преобразования излучения (до 22%), а в модулях они снижаются до 15-16%. Высокое внутреннее сопротивление не позволяет эксплуатировать ФЭП при высоких интенсивностях падающего излучения. Причем в обычных стандартных ФЭП диодные и оптические свойства взаимосвязаны так, что улучшение одного из параметров неизбежно приводит к ухудшению другого.
Для того чтобы получить преобразователь с низким внутренним сопротивлением и с высокими как диодными, так и оптическими свойствами, диод и оптическое окно нужно разделить. Проблема снижения сопротивления в обозримом будущем считается непреодолимой, хотя, например, для кремниевых ФЭП все, что можно оптимизировать, уже сделано, кроме внутреннего сопротивления. Более того, эта проблема явилась камнем преткновения современной кремниевой фотовольтаики, из-за которой не поднимается уровень эффективности солнечной электроэнергетики. С другой стороны, из-за проблемы с внутренним сопротивлением ФЭП, до сих пор не могут сделать кремниевые концентраторные элементы, удовлетворяющие как техническим, так экономическим требованиям.
Однако эта проблема решена в настоящем изобретении путем выполнения в ФЭП пучковых pn переходов. В пучковых ФЭП составляющими и нагрузочными элементами пучка являются отдельные однотипные точечные pn переходы. Для изготовления обычного стандартного ФЭП, в кремниевых пластинах толщиной d=200 мкм и размером 156 мм × 156 мм формируется один большой монолитный pn переход (N=1) на всей его лицевой поверхности с площадью 156 мм × 156 мм и глубиной в 0,004 мм. В примере пучкового ФЭП, размер pn перехода локализуется до 0.004 мм × 0,004 мм × 0,004 мм, а число переходов в таком образце достигает N>10000/см2 в зависимости от дизайна преобразователя. При таком геометрическом размере переходов в них могут разместиться согласно нашей классификации (см. таблицы 1-3) структурные дефекты группы 3, т.е. СМТ размером от 2,8 нм до 100 нм.
Сам элементарный пучковый ФЭП, фактически, представляет из себя статистическую выборку или ансамбль, состоящий из N>10000/см2 отдельных однотипных индивидуальных геометрически малого размера элементов, т.е. pn переходов, являющихся по структуре обычным диодом. Наглядная принципиальная схема стандартного и пучкового ФЭП приведены на фиг. 15-16.
Для геометрически малых размеров тел реализуется весь дискретный спектр дефектов. И такому статистическому ансамблю из N>>10000/см2 элементов соответствует огромное распределение (разброс) значений внутреннего сопротивления переходов R. И этот огромный по величине разброс еще более усилится, если этот статистический ансамбль окажется в условиях воздействия температур и нагрузок.
В таком ансамбле могут быть элементы с как угодно большими значениями сопротивления Rmax, так и с как угодно малыми значениями Rmin, близких к нулевому значению R0. Тогда, поскольку в таком ФЭП pn переходы объединяются в пучок между большим количеством противоположных контактов, т.е. в параллельную электрическую цепь, то разброс значений сопротивлений в таком пучке подавлен, а суммарное значение электрического сопротивления всего пучка в целом, несмотря на громадный разброс отдельных индивидуальных составляющих элементов, будет минимальным и иметь значение согласно закону Ома меньше значения сопротивления Rmin элемента с как угодно малым значением (близким к нулю), имеющемся в статистическом ансамбле из числа N>>10000 образцов. Поэтому внутреннее сопротивление пучковых фотоэлектрических преобразователей (ФЭП) существенно (в разы) ниже, чем у стандартного (см. фиг. 17). При воздействии на такой пучковый образец приложенной нагрузки, например, мощности падающего излучения и температуры, этот разброс может оказаться еще более внушительным. Соответственно этому внутреннее сопротивление ФЭП снизится более существенно, а удельный энергосьем с такого пучкового ФЭП будет еще выше.
Чтобы в этом убедиться, надо сравнить данные фиг. 17, на которых приведены значения последовательного сопротивления пучкового и стандартного однопереходного ФЭП в условиях воздействия малых и больших интенсивностей падающего излучения от фары-лампы Osram.
В этих экспериментах надо иметь ввиду то, что с увеличением мощности падающего излучения от галогенной лампы-фары одновременно происходит нагрев лампы и повышение температуры образца ФЭП до +90°С и более.
Локализация и дискретизация pn переходов при переходе от сплошного стандартного ФЭП к многопереходным пучковым ФЭП, в дополнение к масштабно-статистическому эффекту снижения сопротивления, приводит к открытию оптических окон и устранению слоевого внутреннего сопротивления (см. фиг. 15-17), расширению спектрального диапазона преобразования, а также развязыванию их диодных и оптических свойств.
Кроме того, локализация pn переходов с разрывом сплошного монолитного перехода в пучковых полупроводниковых приборах увеличивает суммарную поверхность pn переходов. Это подобно тому, как при дроблении монолитного булыжника в песок, свободная суммарная площадь поверхности образованных песчинок гораздо больше площади поверхности самого монолита-булыжника. В итоге локализация и увеличение числа переходов N в пучковом ФЭП, ведет к существенному увеличению площади токособирающих элементов и самого токосбора в пучковом ФЭП.
Кроме того, сам процесс локализации pn переходов введет к делокализации или к перераспределению, приложенных на такое многопереходное устройство энергетических, силовых, радиационных, световых и т.д. нагрузок по отдельным геометрически маленького размера N однотипным pn переходам. Эффект делокализации позволяет пропускать большие энергетические нагрузки, позволяет использовать пучковые ФЭП в концентрированном излучении (см. фиг. 17-18).
В целом, такой многоэлементный (или многопереходный) пучковый образец позволяет пропускать через себя огромные по величине энергетические и силовые нагрузки. При этом повышается его стойкость и надежность к воздействию факторов внешней среды, шунтируются дефектные pn переходы, устраняется внутреннее слоевое сопротивление по сравнению со стандартными элементами с большим сплошным монолитным переходом (см. фиг. 17). К примеру, изготовленный нами с вышеуказанными локализованными переходами пучковый кремниевый ФЭП, выдерживает без деградации огромные температуры: вплоть до +90°С и более его электрические характеристики стабильны. В настоящее время в уровне техники нет ни одного кремниевого ФЭП, который способен был бы выдерживать такие температуры.
В целом, во всех многоэлементных (многопереходных), по нашей классификации пучковых, полупроводниковых приборах с локализованными отдельными и однотипными переходами (например, в диодах, фотодиодах, светодиодах, транзисторах, тиристорах, в солнечных элементах и т.д.) существенно выше будет их стойкость к таким факторам как температура и нагрузка (радиационная, силовая, энергетическая, световая и т.д.), воздействующих в реальных условиях как раздельно, так и комбинировано.
При этом снижение геометрических размеров pn переходов до субмикро- или наноразмеров и увеличение числа переходов до N→β (где β - бесконечно большая величина) существенно увеличит стойкость пучковых приборов к факторам воздействия внешней среды. Снижая размер переходов, можно получить пучковые одноатомные полупроводниковые приборы аналогично графеновым приборам.
В заключении следует отметить, что приведенные примеры представлены лишь для лучшего понимания сущности изобретения, а также его преимуществ и ни в коей мере не претендуют на полноту представлений. Специалисту в данной области техники ясно, что возможны и другие конкретные варианты его исполнения, например, в материалах для защиты от агрессивных воздействий среды, в холодильниках Пельтье, в пьезоэлектрических генераторах, в полупроводниковых приборах, в различных токопроводящих цепях, в колебательных контурах, катушках индуктивности, в обмотках двигателей и т.д. Таким образом, все эти варианты будут находиться в рамках объема притязаний, определяемого исключительно прилагаемой формулой.
Результаты экспериментальных статистических измерений СЧФС и СЧФХ по доказательству осуществимости заявленного изобретения представлены в таблицах 1-4, на фигурах 1-18.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Патент RU 2284267. Приоритет от 10.11.2004 г.
2. Патент RU 2295692. Приоритет от 22.08.2005.
3. Патент RU 2273969. Приоритет 26.10.2004 г.
4. Патент ЕР 1818168. Приоритет от 10.11.2004 г.
5. Патент RU 2284593. Приоритет от 26.10.2004 г.
6. Цой В.Э., Цой Б., Шерматов Д. и Абдуллаев Х.М. / Пучковый диэлектрический материал // ДАН Республики Таджикистан, 2016, том 59, №3-4, С. 133-137.
7. Патент RU 2336585. Приоритет от 10.07.2007 г.
8. Tsoi Bronya. // Three scientific Inventions concerning the Phenomenon of Dicreteness. M.: - Khimya, 2004. 208 p.
9. Карташов Э.М., Цой Б. и Шевелев В.В. Разрушение пленок и волокон. Структурно-статистические аспекты. Изд. 2, испр. и доп. Москва: URSS. 2015.784 с.
10. Цой Б. Дискретные уровни прочности и долговечности полимерных пленок и волокон (динамика, прогноз // Дисс. докт. хим. наук, М., 2000 г. - 368 с.
11. Цой Б., Карташов Э.М., Шевелев В.В. Явление дискретности физических характеристик полимеров и твердых тел. Москва. Диплом №203 на открытие от 18.04.2002 г., рег. №23.
12. Цой Б., Карташов Э.М., Шевелев В.В., Бартенев Г.М. Закономерность распределения значений физических характеристик полимеров и твердых тел при внешнем многофакторном воздействии. Москва. Диплом на открытие №209 от 02 октября 2002 г Рег. №248.
13. Б. Цой, Э.М. Карташов, В.В. Шевелев. Явление многоэлементного масштабного эффекта характеристик физических объектов (эффект Цоя-Карташова-Шевелева). Москва. Диплом на открытие №243 от 16 декабря 2003 г. Рег. №287.
14 Цой Б., Закономерность изменения физических характеристик одноэлементных структур полимеров и твердых тел при изменении масштаба (эффект Б. Цоя. Москва. Диплом на открытие №247 от 02 марта 2004 г. Рег. №293.
15. Карташов Э.М., Цой Б., Шевелев В.В. Структурно-статистическая кинетика разрушения полимеров. Москва: Химия, 2002. 736 с.
16. Цой Б. и Лаврентьев В.В. // Основы создания материалов со сверхвысокими характеристиками. Москва: Энергоатомиздат, 2004. 400 с.
17. Регель В.Р., Слуцкер А.И. и Томашевский Э.Е. Кинетическая природа прочности твердых тел. Москва: Наука, 1974. 560 с.
18. Tsoi В., Kartashov E.M. and Shevelev V.V. // The Statistical Nature of Strength and Lifetime in Polimer Films and Fibers. Utrecht-Boston. Brill Academic Publishers. VSP. 2004. 522 p.).
19. Бартенев Г.М. // Сверхпрочные высокопрочные неорганические стекла. М.: Стройиздат, 1974. 240 с.
20. Шевелев В.В., Карташов Э.М. Некоторые статистические аспекты хрупкого разрушения и долговечности полимеров. Материалы с трещинами. // Высокомолекулярные соединения. 1997. т. Б, 39, №2, с. 371-381.
21. Yugay K.N. On the possible Nature of "Room-Temperature Superconductivity". Russia-Korea Science Conference, Present collected articles, Ekaterinburg, Jul. 4-5, 2014.


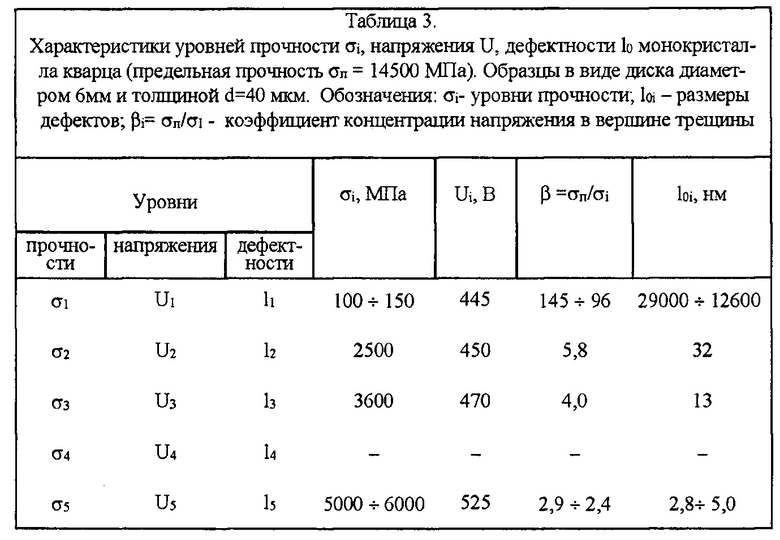
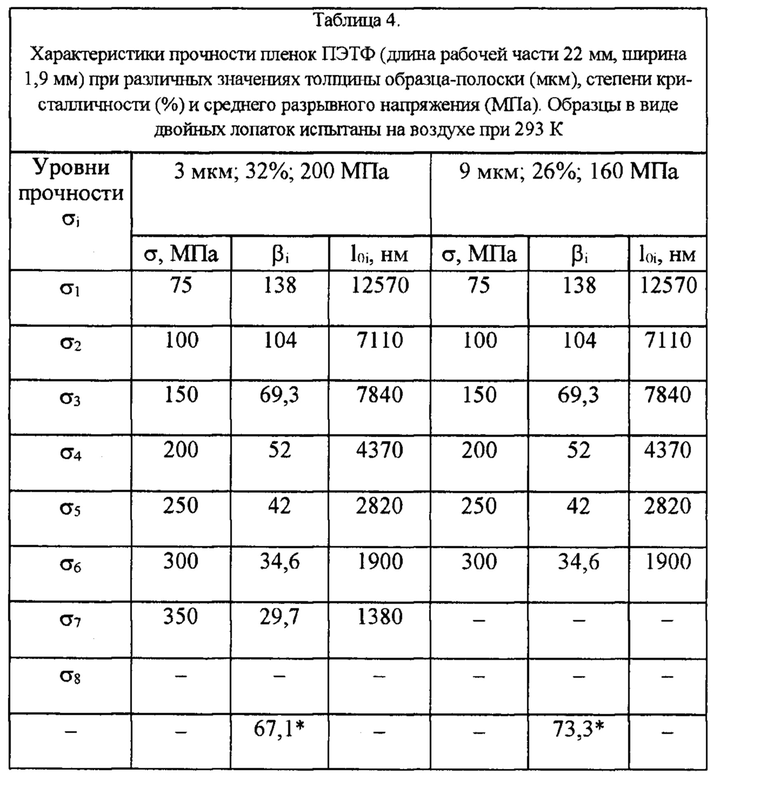
* Значения  без учета дискретности структуры.
без учета дискретности структуры.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПУЧКОВЫЙ ПРОВОДНИК ЭЛЕКТРИЧЕСКОГО ТОКА И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2019 |
|
RU2709824C1 |
| МАТЕРИАЛ ДЛЯ КОМПОНЕНТОВ РАДИОЭЛЕКТРОННЫХ ПРИБОРОВ | 2004 |
|
RU2284267C2 |
| МАТЕРИАЛ ДЛЯ ЗАЩИТЫ ОТ УДАРНЫХ ВОЗДЕЙСТВИЙ | 2005 |
|
RU2295692C1 |
| ПРОВОДНИК ЭЛЕКТРИЧЕСКОГО ТОКА И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2007 |
|
RU2336585C1 |
| ЭЛЕКТРОИЗОЛЯЦИОННЫЙ МАТЕРИАЛ | 2004 |
|
RU2284593C2 |
| ДЛИННОМЕРНОЕ ВИТОЕ ИЗДЕЛИЕ | 2005 |
|
RU2352699C2 |
| ДИЭЛЕКТРИЧЕСКИЙ МАТЕРИАЛ ДЛЯ ИЗДЕЛИЙ, РАБОТАЮЩИХ В СВЧ-ДИАПАЗОНЕ | 2004 |
|
RU2273969C1 |
| ЯЧЕЙКА ПАМЯТИ | 2004 |
|
RU2287206C2 |
| ТРАНЗИСТОР И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2006 |
|
RU2364008C2 |
| СПОСОБ ЗАПИСИ И СЧИТЫВАНИЯ КОДИРОВАННОЙ ИНФОРМАЦИИ | 2004 |
|
RU2256239C1 |
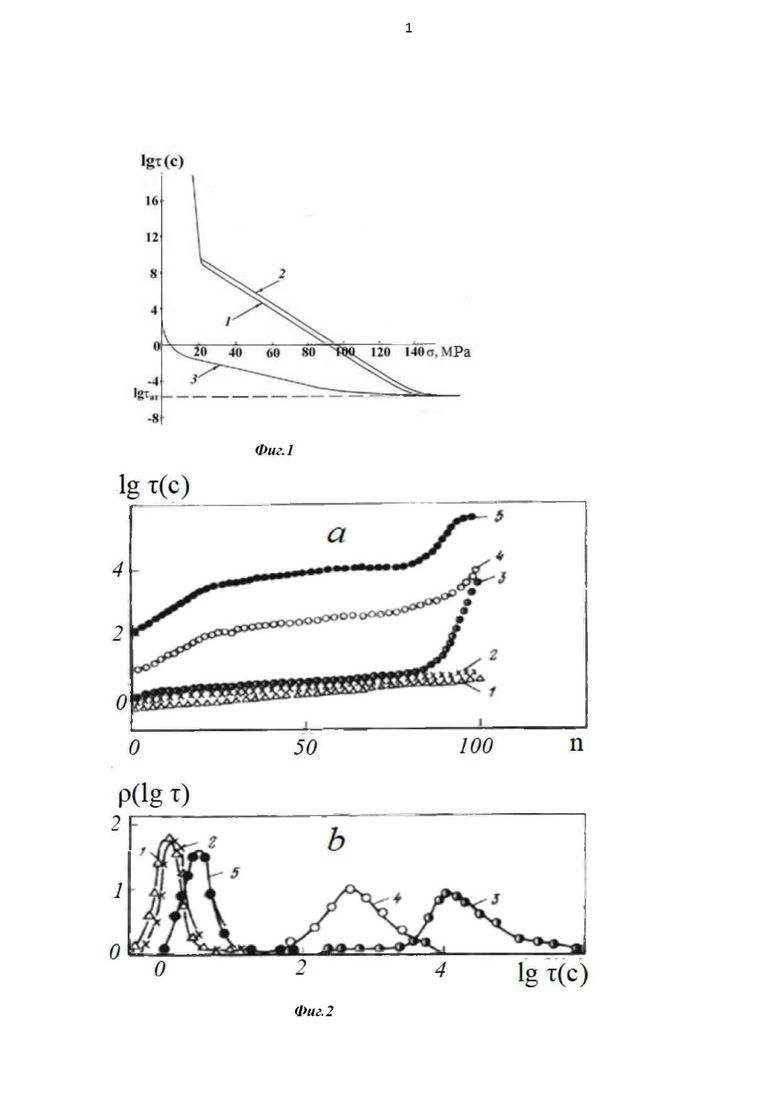









Изобретение относится к материаловедению и может быть использовано для создания изделий с заданными свойствами, в частности, для изготовления материалов и устройств с низкими, высокими или сверхвысокими физическими свойствами и характеристиками. Технический результат заключается в повышении стойкости материала к таким факторам как температура и нагрузка, воздействующих в реальных условиях как раздельно, так и комбинированно. Пучковый материал, содержащий число N ≥ 1 (где N – целое число) индивидуальных однотипных отдельных, не связанных между собой составляющих элементов, объединенных в стопу или пучок, причем каждый из однотипных элементов имеет одинаковое функциональное назначение и заключен между противоположными контактами из числа K≥2, а число N рассчитывается по формуле

где F - внешнее воздействие на образец; σр,м - есть значение σр структурно-чувствительной физической характеристики или свойства, реагирующей на внешнее воздействие F, которое определяет нижнюю границу значений σр, с которой образцы отбираются в пучковый материал или устройство; s - площадь поперечного сечения одного составляющего элемента пучка; p - вероятность попадания элемента с уровнем структурно-чувствительной характеристики σр>σр,м, в многоэлементный образец-пучок, определяемая из кривых распределений структурно-чувствительной характеристики или свойства. 6 н. и 13 з.п. ф-лы, 4 табл., 16 ил.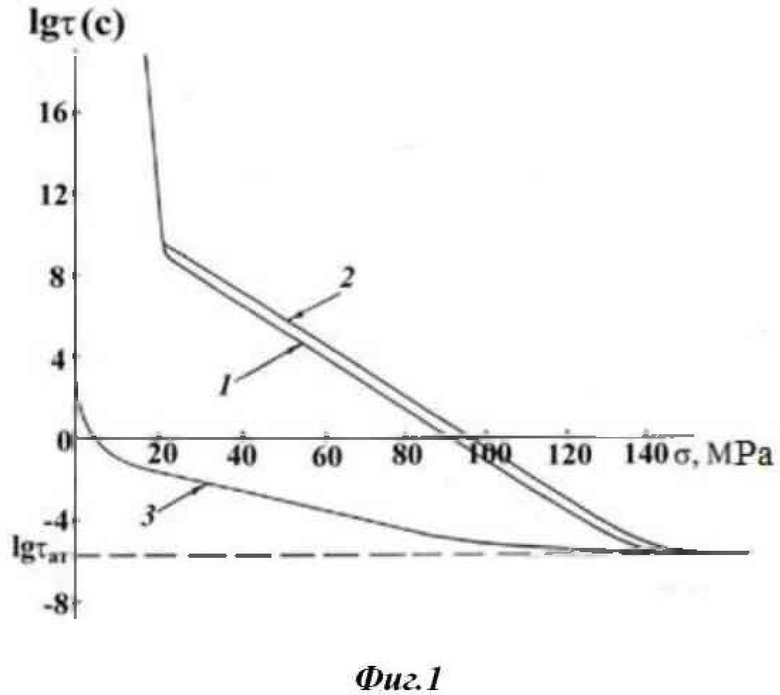
1. Пучковый материал, содержащий число N≥1 (где N - целое число) индивидуальных тонких однотипных отдельных, не связанных между собой составляющих элементов, объединенных в стопу или пучок, причем каждый из составляющих элементов имеет одинаковое функциональное назначение и заключен между противоположными контактами из числа K≥2, а число N рассчитывается по формуле
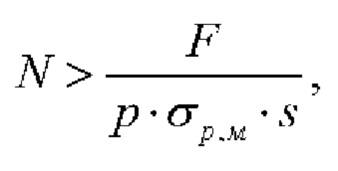
где F - внешнее воздействие на образец; σр,м - есть значение σр структурно-чувствительной физической характеристики или свойства, реагирующей на внешнее воздействие F, которое определяет нижнюю границу значений σр, с которой образцы отбираются в пучковый материал или устройство; s - площадь поперечного сечения одного составляющего элемента пучка; р - вероятность попадания элемента с уровнем структурно-чувствительной характеристики σр>σр,м, в многоэлементный образец-пучок, определяемая из кривых распределений структурно-чувствительной характеристики или свойства.
2. Пучковый материал по п. 1, отличающийся тем, что между составляющими элементами стопы или пучка располагаются отделители.
3. Пучковый материал по п. 2, отличающийся тем, что отделитель выполняется из числа N≥1 отдельных однотипных тонких или сверхтонких составляющих элементов-пленок.
4. Пучковый материал по пп. 1-3, отличающийся тем, что пучок составлен из сверхтонких элементов-волокон или пленок толщиной d≤100 нм.
5. Пучковый материал по пп. 1-4, отличающийся тем, что однотипные отдельные составляющие элементы пучка по функциональному назначению представляют диэлектрик, проводник, полупроводник, пьезоэлектрик, сегнетоэлектрик, металл, полимер, металлоид, композит, керамику, pn переход, гетеропереход или переход Шоттки.
6. Способ изготовления пучкового материала, заключающийся в том, что материал выполняется из числа N≥1 (где N - целое число) тонких однотипных отдельных, не связанных между собой индивидуальных составляющих элементов, объединенных в пучок или стопу, причем каждый из составляющих элементов имеет одинаковое функциональное назначение и заключается между противоположными контактами из числа K≥2, а число N рассчитывается по формуле из п. 1.
7. Пучковый материал, содержащий число N≥1 (где N - целое число) индивидуальных тонких однотипных отдельных, не связанных между собой составляющих элементов, объединенных в стопу или пучок, причем каждый из однотипных элементов имеет одинаковое функциональное назначение и заключен между противоположными контактами из числа K≥2, а число N рассчитывается по формуле

где Р - есть экспериментально установленная доля образцов с эффектом сверхмодового состояния в их выборке из числа составляющих элементов, подготовленных к компоновке (изготовлению) многоэлементного пучка; Р0 - есть доверительная вероятность, с которой в многоэлементном пучке должен быть хотя бы один элемент, не содержащий дефект, разрушающий сверхмодовое состояние.
8. Пучковый материал, содержащий число N≥1 (где N - целое число) индивидуальных тонких однотипных отдельных, не связанных между собой составляющих элементов, объединенных в стопу или пучок, причем каждый из однотипных элементов имеет одинаковое функциональное назначение и заключен между противоположными контактами из числа K≥2, а число N рассчитывается по формуле

где Р - экспериментально установленная доля материалов со значением структурно-чувствительного свойства или характеристики σ≤σ0 , σ0 - нижняя граница структурно-чувствительного свойства или характеристики, σэ - требуемое или заданное значение структурно-чувствительного свойства или характеристики пучка.
9. Способ изготовления пучкового материала, заключающийся в том, что материал выполняется из числа N≥1 (где N - целое число) тонких однотипных отдельных, не связанных между собой индивидуальных составляющих элементов, объединенных в пучок или стопу, причем каждый из составляющих элементов имеет одинаковое функциональное назначение и заключается между противоположными контактами из числа K≥2, а число N рассчитывается по формуле из п. 7.
10. Способ изготовления пучкового материала, заключающийся в том, что материал выполняется из числа N≥1 (где N - целое число) тонких однотипных отдельных, не связанных между собой индивидуальных составляющих элементов, объединенных в пучок или стопу, причем каждый из составляющих элементов имеет одинаковое функциональное назначение и заключается между противоположными контактами из числа K≥2, а число N рассчитывается по формуле из п. 8.
11. Способ изготовления пучкового материала по п. 6, отличающийся тем, что пучок составлен из сверхтонких элементов-волокон или пленок толщиной d≤100 нм.
12. Способ изготовления пучкового материала по п. 6, отличающийся тем, что составляющие элементы пучка представляют диэлектрик, проводник, полупроводник, пьезоэлектрик, сегнетоэлектрик, металл, полимер, металлоид, композит, керамику, pn переход, гетеропереход или переход Шоттки.
13. Способ изготовления пучкового материала по п. 6, отличающийся тем, что производят М серий измерений структурно-чувствительных физических характеристик или свойств, М - натуральное число, причем в каждой i-й серии (i=1…M) составляющие элементы являются отдельными однотипными, и их число равно Ni, по результатам измерений отбирают j-ю выборку из Nj однотипных элементов, в которой зафиксировано наибольшее значение структурно-чувствительной физической характеристики или свойства среди всех испытанных элементов, далее R≥Nj составляющих элементов, отличающихся тем, что каждый из них имеет толщину D≤dj, где dj - толщина элементов в j-й выборке, соединяют параллельно.
14. Способ изготовления пучкового материала по п. 6, отличающийся тем, что производят М серий измерений физических характеристик или свойств материала, М - натуральное число, причем в каждой i-й серии (i=1…M) составляющие элементы пучка являются отдельными однотипными, а их число равно Ni, по результатам измерений отбирают j-ю выборку из Nj однотипных элементов, в которой зафиксировано наименьшее значение требуемой физической характеристики или свойства среди всех испытанных элементов, далее R≥Nj составляющих элементов пучка, отличающихся тем, что каждый из них имеет толщину D≤dj, где dj - толщина элементов в j-й выборке, соединяют параллельно.
15. Способ изготовления пучкового материала по п. 6, отличающийся тем, что толщину d составляющего элемента пучка определяют по размеру наименьшего дефекта в его структуре.
16. Пучковый материал по п. 7, отличающийся тем, что пучок составляется из сверхтонких пленок, волокон или проволок, или переходов толщиной d≤100 нм.
17. Пучковый материал по п. 7, отличающийся тем, что однотипные отдельные составляющие элементы по функциональному назначению представляют диэлектрик, проводник, полупроводник, пьезоэлектрик, сегнетоэлектрик, pn переход, гетеропереход или переход Шоттки.
18. Пучковый материал по п. 8, отличающийся тем, что пучок составляется из сверхтонких пленок, волокон или проволок, или переходов толщиной d≤100 нм.
19. Пучковый материал по п. 8, отличающийся тем, что однотипные отдельные составляющие элементы по функциональному назначению представляют диэлектрик, проводник, полупроводник, пьезоэлектрик, сегнетоэлектрик, pn переход, гетеропереход или переход Шоттки.
| ПРОВОДНИК ЭЛЕКТРИЧЕСКОГО ТОКА И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2007 |
|
RU2336585C1 |
| МНОГОСЛОЙНЫЙ МАТЕРИАЛ | 1994 |
|
RU2131157C1 |
| ЭЛЕКТРОИЗОЛЯЦИОННЫЙ МАТЕРИАЛ | 2004 |
|
RU2284593C2 |
| МАТЕРИАЛ ДЛЯ КОМПОНЕНТОВ РАДИОЭЛЕКТРОННЫХ ПРИБОРОВ | 2004 |
|
RU2284267C2 |
| СПОСОБ ИОННО-ЛУЧЕВОГО ЛЕГИРОВАНИЯ КРИСТАЛЛОВ | 2003 |
|
RU2258977C1 |
Авторы
Даты
2019-12-23—Публикация
2019-01-22—Подача