Область техники, к которой относится изобретение
Изобретение относится к электронному устройству формирования, электронному способу формирования, компьютерной программе и машиночитаемому носителю.
Уровень техники
В криптографии принципа "белый ящик" и, если обобщать, в запутывании программного обеспечения, вычисления зачастую выполняются для кодированных значений вместо простых значений. Декомпиляция на исходные коды запутанного программного обеспечения является более сложной, если вычисления выполняются для кодированных значений, а не непосредственно для простых значений.
После кодирования, регулярные операции, такие как суммирование или умножение, более не могут выполняться с использованием встроенных примитивов компьютера. Прямое суммирование кодированных значений нормально не приводит к кодированию суммирования значений. То же применимо для умножения. В формуле: E(x)+E(y)≠E(x+y), для большинства x и y; E обозначает функцию кодирования.
Решение этой проблемы состоит в том, чтобы вводить таблицы суммирования (A) и умножения (M). Таблицы принимают два кодированных значения в качестве ввода и формируют кодированное значение в качестве вывода, который соответствует кодированию операции суммирования или умножения. Таблицы могут задаваться следующим образом: A(E(x),E(y))= E(x+y);M(E(x),E(y))= E(xy). Эти таблицы обеспечивают возможность выполнения арифметических действий непосредственно для кодированных значений.
Запутанное суммирование и умножение с использованием таблиц страдает, по меньшей мере, от двух недостатков. Во-первых, таблицы могут становиться довольно большими. Если x и y представляются как l битов, каждой таблице требуется 22ll бит.
Во-вторых, такие большие таблицы могут легко обнаруживаться в программном обеспечении. Что еще хуже, таблицы по-прежнему могут идентифицироваться в качестве операций суммирования или умножения, даже если они кодируются; например, через свойства этих функций, которые сохраняются при кодировании. Например, таблица умножения удовлетворяет M(E(0),E(x))= E(0). Взломщик может использовать это и аналогичные свойства, чтобы предполагать, какую операцию представляют таблицы.
Сущность изобретения
В предшествующей заявке от того же заявителя, представлен улучшенный способ выполнения запутанных арифметических действий. Предшествующая заявка подана в Европейское патентное ведомство (EPO) под заголовком "Electronic calculating device for performing obfuscated arithmetic", дата подачи: 30.09.2014, номер заявки: 14186951.1. Предшествующая заявка полностью включается в данный документ по ссылке и, в частности, также в части описания вычислительного устройства с использованием гомогенного запутывания по целочисленному кольцу.
Авторы изобретения обнаружили, что в некоторых случаях умножение и суммирование для кодированных значений может выполняться с использованием сводной таблицы без необходимости кодировать несколько значений в одно кодированное значение. Поскольку идентичная таблица используется для суммирования и умножения, в ходе декомпиляции на исходные коды затруднительно видеть, выполняется суммирование или умножение. Поскольку суммирование и умножение кажется идентичной операцией при просмотре снаружи, авторы изобретения назвали этот способ "гомогенным запутыванием". Даже если взломщик имеет возможность находить таблицу, которая используется, и даже если он имеет возможность выяснить тем или иным образом ее функцию в качестве таблицы приращений, он по-прежнему не знает, выполняются операции суммирования или умножения. Способ, которым таблица осуществляет действия с элементом списка целых чисел, должен отличаться для суммирования и умножения, тем не менее, это может легко маскироваться с использованием традиционного запутывания.
Помимо этого, сводная таблица, которая используется, также меньше сводной таблицы, предложенной в разделе "Уровень техники": требуется приблизительно 2ll битов. Даже если используется только суммирование, таблица, необходимая для запутанного суммирования, меньше таблицы, предлагаемой в разделе "Уровень техники".
Например, кольцевой элемент может быть кодирован как два целых числа(a,b). Арифметические действия могут выполняться непосредственно для кодирования с использованием таблицы приращений, которая преобразует кодированный кольцевой элемент в кодированный кольцевой элемент плюс значение приращения. Например, таблица может преобразовывать (a,b) в (c,d), если uc-ud=ua-ub+1. Суммирование и умножение выполняются посредством повторных применений таблицы приращений.
Запутанные арифметические действия применяются к множеству различных коммутативных колец R, хотя не каждое кольцо обеспечивает кодирование в качестве списков целых чисел. Коммутативные кольца являются математическим понятием, которое включает в себя множество различных знакомых математических структур, например, целые числа по модулю число (Zn). Устройство формирования согласно формуле изобретения может использоваться для того, чтобы формировать параметры для цифровых запутанных арифметических действий, причем параметры задают коммутативное кольцо (Zn), имеющее конечное число кольцевых элементов, причем базовый элемент (u) содержится в кольцевых элементах, так что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента (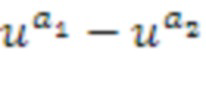 ). Модуль n задает коммутативное кольцо в качестве целого числа по модулю модуль n.
). Модуль n задает коммутативное кольцо в качестве целого числа по модулю модуль n.
Эффективное формирование целочисленных колец, которые обеспечивают гомогенное запутывание, обеспечивает возможность использования различных типов колец в вычислительном устройстве, в силу этого увеличивая запутывание.
Способ согласно изобретению может реализовываться на компьютере в качестве машинореализованного способа или в выделенных аппаратных средствах либо в комбинации вышеозначенного. Исполняемый код для способа согласно изобретению может быть сохранен на компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя запоминающие устройства, оптические устройства хранения данных, интегральные схемы, серверы, онлайновое программное обеспечение и т.д. Предпочтительно, компьютерный программный продукт содержит средство энергонезависимого программного кода, сохраненное на машиночитаемом носителе для осуществления способа согласно изобретению, когда упомянутый программный продукт выполняется на компьютере.
В предпочтительном варианте осуществления, компьютерная программа содержит средство компьютерного программного кода, выполненное с возможностью осуществлять все этапы способа согласно изобретению, когда компьютерная программа выполняется на компьютере. Предпочтительно, компьютерная программа осуществляется на машиночитаемом носителе.
Краткое описание чертежей
Эти и другие аспекты изобретения являются очевидными и должны истолковываться со ссылкой на описанные ниже варианты осуществления. На чертежах:
Фиг. 1a схематично показывает пример варианта осуществления электронного устройства формирования,
Фиг. 1b схематично показывает пример варианта осуществления электронного устройства формирования,
Фиг. 2 схематично показывает пример варианта осуществления электронного способа 200 формирования,
Фиг. 3 схематично показывает пример варианта осуществления электронного способа 300, верифицирующего, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента,
Фиг. 4 схематично показывает пример варианта осуществления электронного способа 400 формирования,
Фиг. 5a показывает машиночитаемый носитель, имеющий записываемую часть, содержащую компьютерную программу согласно варианту осуществления,
Фиг. 5b показывает схематичное представление процессорной системы согласно варианту осуществления.
Элементы, которые имеют идентичные ссылки с номерами на различных чертежах, имеют идентичные структурные признаки и идентичные функции либо представляют собой идентичные сигналы. Если функция и/или структура такого элемента пояснена, нет необходимости ее повторного пояснения в подробном описании.
Подробное описание вариантов осуществления
Хотя это изобретение допускает вариант осуществления во многих различных формах, показаны на чертежах и подробно описываются в данном документе один или более конкретных вариантов осуществления с пониманием того, что настоящее раскрытие должно рассматриваться в качестве примера принципов изобретения, и не имеет намерение ограничивать изобретение конкретными показанными и описанными вариантами осуществления.
Далее, для понимания, элементы вариантов осуществления описываются при работе. Тем не менее, должно быть очевидным, что соответствующие элементы выполнены с возможностью осуществлять функции, описанные как выполняемые посредством них.
В предшествующей заявке, процитированной выше, приводятся примеры варианта осуществления вычислительного устройства для выполнения запутанных арифметических действий в коммутативном кольце. Вычислительное устройство представляет собой электронное устройство для выполнения запутанных арифметических действий в конечном коммутативном кольце. Один пример, который приведен для таких колец, представляет собой целые числа по модулю число (Zn). Устройство формирования согласно варианту осуществления находит модуль таким образом, что кольцо, сформированное посредством целых чисел по модулю этот модуль (Zn), обеспечивает запутанные арифметические действия. Также формируется базовый элемент, требуемый для того, чтобы кодировать и декодировать кольцевые элементы, например, целые числа, в/из запутанного домена.
Гомогенное запутывание, например, представляющее кольцевые элементы, в частности, целые числа по модулю модуль, представляет собой тип зашифрованной арифметических действий; иногда также называется гомоморфным шифрованием. С использованием запутывания, например, компьютерный программный код защищен от декомпиляции на исходные коды. Запутывание здесь представляет собой часть кода, который выполняет арифметические действия. В варианте осуществления цифровых запутанных арифметических действий, вычисления могут выполняться для шифрованного текста и формировать зашифрованный результат, который, после дешифрования, совпадает с результатом операций, выполняемых для простого текста. Другими словами, если выйти за пределы некоторого традиционного запутывания программного обеспечения, арифметические действия могут выполняться для зашифрованных значений. Тем не менее, арифметическая реализация с использованием гомогенного запутывания может быть функционально идентичной арифметическим действиям, выполняемым для простых значений.
Элементы кольца могут задаваться как целые числа по модулю модуль. Элементы кольца упоминаются в качестве кольцевых элементов. Кольцевые элементы также могут называться вычетами. Кольцевой элемент может представляться в цифровой форме в качестве целого числа между 0 и модуль минус 1; причем 0 и модуль минус 1 включены. Для кольцевых элементов, задается суммирование и умножение, причем они упоминаются в качестве кольцевого суммирования и кольцевого умножения.
Кольцевые элементы могут представляться в любой подходящей форме, в случае необходимости. Например, элементы Zn могут представляться как целые числа. Тем не менее, в вычислительном устройстве, кольцевые элементы представляются как списки целых чисел. Например, кольцевой элемент a может представляться в вычислительном устройстве посредством списка(a1,a2). Списки целых чисел кодируют кольцевой элемент согласно некоторому преобразованию между кольцевыми элементами и списком целых чисел; касательно любого кольцевого элемента, предусмотрен, по меньшей мере, один список целых чисел, который представляет кольцевой элемент, и касательно любого списка целых чисел, предусмотрен точно один кольцевой элемент, который он представляет. В вариантах осуществления, любой кольцевой элемент может представляться как список целых чисел.
Списки целых чисел имеют, по меньшей мере, два элемента. Как вытекает, операции суммирования и умножения требуют меньшего числа этапов, если список целых чисел короче. Соответственно, в варианте осуществления, списки целых чисел всегда имеют два элемента. В основном описании предполагается, что списки целых чисел являются целочисленными парами, тем не менее, предоставляются примеры списков целых чисел, имеющих более двух элементов. В качестве примера, (a1,a2)может преобразовываться в кольцевой элемент (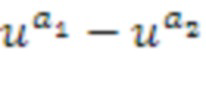 ), при этом u представляет собой специальный кольцевой элемент, называемый в качестве базового кольцевого элемента. В предшествующей заявке пояснено множество разновидностей, включающих в себя использование нескольких базовых элементов. Тем не менее, в основном пояснении в качестве "примерного кодирования" предполагается то, что данный список (a1,a2) целых чисел преобразуется в кольцевой элемент (
), при этом u представляет собой специальный кольцевой элемент, называемый в качестве базового кольцевого элемента. В предшествующей заявке пояснено множество разновидностей, включающих в себя использование нескольких базовых элементов. Тем не менее, в основном пояснении в качестве "примерного кодирования" предполагается то, что данный список (a1,a2) целых чисел преобразуется в кольцевой элемент (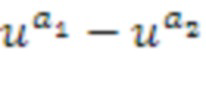 ). Каждый кольцевой элемент в силу этого может выражаться как разность между двумя степенями базового элемента u.
). Каждый кольцевой элемент в силу этого может выражаться как разность между двумя степенями базового элемента u.
Ниже представлен ряд примеров запутанных арифметических действий с использованием модуля и базового элемента, например, сформированных посредством устройства формирования согласно варианту осуществления. Приводятся примеры кодирований, таблиц приращений, способов кольцевого суммирования и способов кольцевого умножения. Блоки отрицания, суммирования и умножения вычислительного устройства могут быть выполнены для любого из этих вариантов осуществления. Все примеры применяются к коммутативному кольцу Zn. В данном документе n является положительным целочисленным модулем. Любой элемент коммутативного кольца может представляться в выбранном кодировании. Не все коммутативные кольца обеспечивают представление всех элементов в данном кодировании, например, в качестве данного типа представления в виде списка целых чисел. Касательно коммутативного кольца R, можно сказать, что оно обеспечивает (полное) гомогенное запутывание, если какой-либо элемент в R может представляться как список целых чисел с использованием данного типа кодирования. Специалисты в данной области техники могут верифицировать то, обеспечивает или нет данное коммутативное кольцо полное гомогенное запутывание касательно кодирования, например, посредством формирования всех допустимых кодирований и верификации того, что совместно они представляют все элементы данного кольца.
Ниже сначала приводится описание примерного кодирования. Предусмотрено множество типов кодирований, общее между которыми то, что кольцевые элементы могут представляться как списки целых чисел. Эти целые числа не представляют собой кольцевые элементы, например, даже если кольцо не представляет собой целочисленное кольцо, скажем, полиномиальное кольцо, то несмотря на это, элементы могут представляться как списки целых чисел. Кодирование, используемое в отношении того, как данный список целых чисел преобразуется в кольцевой элемент, упоминается в качестве кодирования. Типично, списки целых чисел всегда должны иметь идентичную длину, тем не менее, это не является обязательным. Обычно, поскольку кодирование обеспечивает возможность большего числа типов списков целых чисел, например, более длинных списков, возникает большая вероятность того, что данный кольцевой элемент может быть кодирован как список целых чисел различными способами.
Касательно коммутативного кольца R с примерным кодированием, предусмотрен специальный кольцевой элемент u, так что любой элемент a R может записываться в качестве 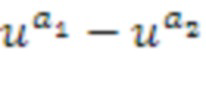 для некоторых целых чисел a1 и a2. Такой специальный кольцевой элемент упоминается в качестве базового кольцевого элемента. Не все коммутативные кольца могут кодироваться таким образом, но достаточно большое число из них должны быть полезными для кодирования. Целые числа a1 и a2 не представляют собой непосредственно кольцевые элементы кольца R; они представляют собой целые числа, с которыми выполняются операции по модулю порядок базового элемента. Следует отметить, что кольцевой элемент a равен линейной комбинации степеней базового элемента u, а именно,
для некоторых целых чисел a1 и a2. Такой специальный кольцевой элемент упоминается в качестве базового кольцевого элемента. Не все коммутативные кольца могут кодироваться таким образом, но достаточно большое число из них должны быть полезными для кодирования. Целые числа a1 и a2 не представляют собой непосредственно кольцевые элементы кольца R; они представляют собой целые числа, с которыми выполняются операции по модулю порядок базового элемента. Следует отметить, что кольцевой элемент a равен линейной комбинации степеней базового элемента u, а именно, 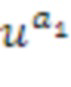 и
и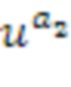 ; в этом случае линейная комбинация получается посредством умножения степеней на +1 или -1 и их суммирования, более конкретно, посредством вычитания второй степени из первой степени. Вычислительное устройство управляет кольцевыми элементами, кодированными вышеуказанным способом. Блоки суммирования, отрицания и умножения могут управлять кольцевыми элементами в этом кодировании.
; в этом случае линейная комбинация получается посредством умножения степеней на +1 или -1 и их суммирования, более конкретно, посредством вычитания второй степени из первой степени. Вычислительное устройство управляет кольцевыми элементами, кодированными вышеуказанным способом. Блоки суммирования, отрицания и умножения могут управлять кольцевыми элементами в этом кодировании.
Таблица T приращений играет центральную роль в операции суммирования и умножения. Таблица приращений преобразует входной кольцевой элемент, и в этом случае входной кольцевой элемент может представляться как список целых чисел. Например, касательно входного списка (k1,k2) целых чисел, представляющего входной кольцевой элемент 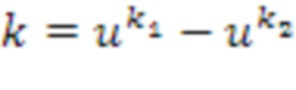 , таблица T преобразует его в выходной список целых чисел, например, T((k1,k2))=(l1,l2), кодирующий выходной кольцевой элемент
, таблица T преобразует его в выходной список целых чисел, например, T((k1,k2))=(l1,l2), кодирующий выходной кольцевой элемент 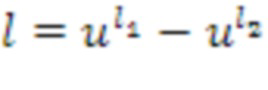 . Выходной кольцевой элемент равен кольцевому элементу приращения после кольцевого суммирования с входным кольцевым элементом. В этом примере, элемент приращения может рассматриваться как 1, т.е. кольцевой элемент, который представляет собой единичный элемент для кольцевого умножения; в этом случае l=k+1. Удобно, что таблица может применяться непосредственно к кольцевым элементам, которые используют идентичное кодирование, и которое в силу этого может применяться к кольцевым элементам, имеющим представление в виде списка целых чисел. Тем не менее, предусмотрены варианты осуществления, в которых таблица применяется к кольцевым элементам в альтернативном кодировании. Альтернативное кодирование также может представлять собой список целых чисел, но альтернативного типа. Также кольцевой элемент приращения не должен обязательно быть равен 1.
. Выходной кольцевой элемент равен кольцевому элементу приращения после кольцевого суммирования с входным кольцевым элементом. В этом примере, элемент приращения может рассматриваться как 1, т.е. кольцевой элемент, который представляет собой единичный элемент для кольцевого умножения; в этом случае l=k+1. Удобно, что таблица может применяться непосредственно к кольцевым элементам, которые используют идентичное кодирование, и которое в силу этого может применяться к кольцевым элементам, имеющим представление в виде списка целых чисел. Тем не менее, предусмотрены варианты осуществления, в которых таблица применяется к кольцевым элементам в альтернативном кодировании. Альтернативное кодирование также может представлять собой список целых чисел, но альтернативного типа. Также кольцевой элемент приращения не должен обязательно быть равен 1.
Ниже описываются операции отрицания, суммирования и умножения.
Отрицание. Касательно входного списка (a1,a2) целых чисел отрицания, представляющего входной кольцевой элемент 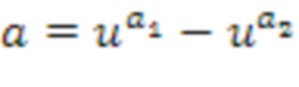 отрицания, выходной список целых чисел отрицания может получаться посредством перестановки списка целых чисел, в этом случае посредством изменения порядка на противоположный. Выходной список целых чисел отрицания может представлять собой(a2,a1). При условии, что существует m, так что um=-1, что дает базовые элементы с четным порядком, отрицание альтернативно может получаться посредством суммирования константы, например, m, с каждым целым числом из списка целых чисел. Во втором случае, выходной список целых чисел отрицания может представлять собой (a1+m,a2+m). Это работает, поскольку
отрицания, выходной список целых чисел отрицания может получаться посредством перестановки списка целых чисел, в этом случае посредством изменения порядка на противоположный. Выходной список целых чисел отрицания может представлять собой(a2,a1). При условии, что существует m, так что um=-1, что дает базовые элементы с четным порядком, отрицание альтернативно может получаться посредством суммирования константы, например, m, с каждым целым числом из списка целых чисел. Во втором случае, выходной список целых чисел отрицания может представлять собой (a1+m,a2+m). Это работает, поскольку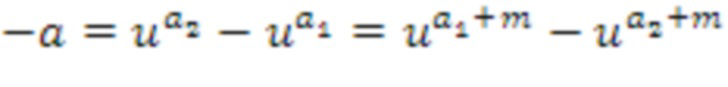 . Арифметические действия в списке целых чисел предпочтительно выполняются по модулю порядок базового элемента. Здесь, целое число списков целых чисел соответствует экспоненте базового элемента, так что целые числа, которые являются идентичным модулем порядок базового элемента, кодируют идентичный кольцевой элемент.
. Арифметические действия в списке целых чисел предпочтительно выполняются по модулю порядок базового элемента. Здесь, целое число списков целых чисел соответствует экспоненте базового элемента, так что целые числа, которые являются идентичным модулем порядок базового элемента, кодируют идентичный кольцевой элемент.
Суммирование. Чтобы суммировать принимаемый первый входной список (a1,a2) целых чисел суммирования, кодирующий первый входной кольцевой элемент 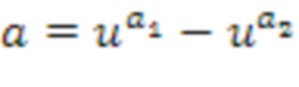 суммирования, и второй входной список (b1,b2) целых чисел суммирования, кодирующий второй входной кольцевой элемент
суммирования, и второй входной список (b1,b2) целых чисел суммирования, кодирующий второй входной кольцевой элемент 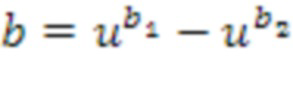 суммирования, определяется первый промежуточный список ((c1,c2)) целых чисел суммирования, кодирующий промежуточный кольцевой элемент c суммирования.
суммирования, определяется первый промежуточный список ((c1,c2)) целых чисел суммирования, кодирующий промежуточный кольцевой элемент c суммирования.
Кольцевой элемент c может представлять собой первый входной кольцевой элемент a суммирования плюс базовый элемент u в степень, определенную из второго входного списка целых чисел суммирования, в частности, первое целое число второго входного списка целых чисел суммирования. В этом примере, можно иметь 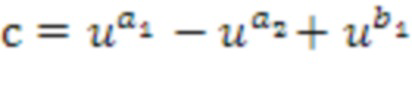 . Чтобы вычислять последнее, следует отметить, что
. Чтобы вычислять последнее, следует отметить, что 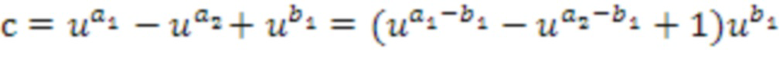 . Член в скобках может перезаписываться при кодировании с использованием таблицы приращений. Через первое применение таблицы приращений к кольцевому элементу
. Член в скобках может перезаписываться при кодировании с использованием таблицы приращений. Через первое применение таблицы приращений к кольцевому элементу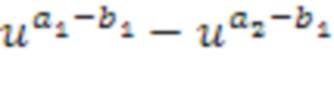 , получается элемент
, получается элемент 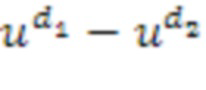 =
=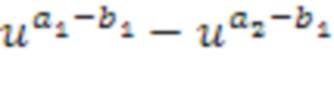 +1. Например, посредством T((a1-b1,a2-b1))=(d1,d2). В таком случае можно иметь, что c1=d1+b1 и c2=d2+b1, за счет этого определяя то, что промежуточный список ((c1,c2)) целых чисел суммирования дополнительно может содержать суммирование целого числа, определенного из вторых входных списков целых чисел суммирования, с целыми числами в списке целых чисел, получающемся в результате первого применения. Суммирование
+1. Например, посредством T((a1-b1,a2-b1))=(d1,d2). В таком случае можно иметь, что c1=d1+b1 и c2=d2+b1, за счет этого определяя то, что промежуточный список ((c1,c2)) целых чисел суммирования дополнительно может содержать суммирование целого числа, определенного из вторых входных списков целых чисел суммирования, с целыми числами в списке целых чисел, получающемся в результате первого применения. Суммирование 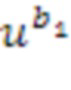 с кольцевым элементом в представлении в виде списка целых чисел, в этом случае, с a, иногда упоминается в качестве этапа положительного уменьшения.
с кольцевым элементом в представлении в виде списка целых чисел, в этом случае, с a, иногда упоминается в качестве этапа положительного уменьшения.
Таким образом, блок суммирования получает промежуточный кольцевой элемент 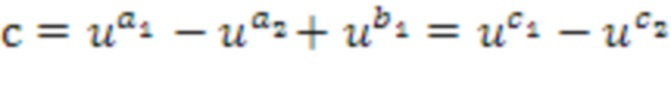 суммирования, в качестве списка (c1,c2) целых чисел. Промежуточный кольцевой элемент суммирования в силу этого представляет собой линейную комбинацию степеней одного или более базовых элементов, при этом степени определяются из первых входных списков целых чисел суммирования и вторых входных списков целых чисел суммирования. В этом случае, таблица приращений применяется к кольцевому элементу
суммирования, в качестве списка (c1,c2) целых чисел. Промежуточный кольцевой элемент суммирования в силу этого представляет собой линейную комбинацию степеней одного или более базовых элементов, при этом степени определяются из первых входных списков целых чисел суммирования и вторых входных списков целых чисел суммирования. В этом случае, таблица приращений применяется к кольцевому элементу 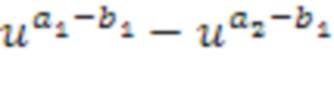 , сформированному посредством одного или более базовых кольцевых элементов (u), возведенных в степень первого целого числа из первого списка (a1) целых чисел минус первое целое число из второго списка (b1) целых чисел, минус базовый кольцевой элемент (u), возведенный в степень второго целого числа из первого списка (a2) целых чисел минус первое целое число из второго списка (b1) целых чисел.
, сформированному посредством одного или более базовых кольцевых элементов (u), возведенных в степень первого целого числа из первого списка (a1) целых чисел минус первое целое число из второго списка (b1) целых чисел, минус базовый кольцевой элемент (u), возведенный в степень второго целого числа из первого списка (a2) целых чисел минус первое целое число из второго списка (b1) целых чисел.
В этом примере, выходной список целых чисел суммирования может определяться через второе применение таблицы приращений к кольцевым элементам, определенным из промежуточного списка целых чисел суммирования и второго входного списка целых чисел суммирования. Это может содержать вычисление суммы промежуточного кольцевого элемента c суммирования и минус базовый элемент, возведенный в степень, определенную из второго входного списка целых чисел суммирования, например, второе целое число второго входного списка b2 целых чисел суммирования: 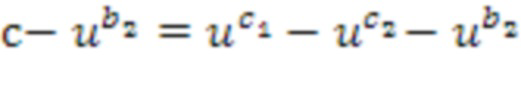 . Это может быть выполнено посредством отрицания промежуточного кольцевого элемента суммирования, представленного посредством промежуточного списка целых чисел суммирования, перед вторым применением таблицы приращений. Отрицание c может выполняться так, как указано выше. В качестве примера используется перестановка, но идентичная операция может выполняться посредством суммирования константы с экспонентой. После отрицания, сумма может использовать плюс (вместо минуса) базовый элемент, возведенный в степень, определенную из второго входного списка целых чисел суммирования:
. Это может быть выполнено посредством отрицания промежуточного кольцевого элемента суммирования, представленного посредством промежуточного списка целых чисел суммирования, перед вторым применением таблицы приращений. Отрицание c может выполняться так, как указано выше. В качестве примера используется перестановка, но идентичная операция может выполняться посредством суммирования константы с экспонентой. После отрицания, сумма может использовать плюс (вместо минуса) базовый элемент, возведенный в степень, определенную из второго входного списка целых чисел суммирования: 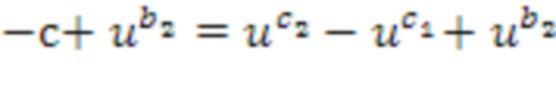 . Вторая операция имеет идентичный тип, как описано выше, и может выполняться через применение таблицы, идентично суммированию
. Вторая операция имеет идентичный тип, как описано выше, и может выполняться через применение таблицы, идентично суммированию 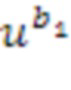 . После этого результат отрицается снова. Полное суммирование может использовать два отрицания и два применения таблицы, для идентичной таблицы T приращений.
. После этого результат отрицается снова. Полное суммирование может использовать два отрицания и два применения таблицы, для идентичной таблицы T приращений.
Вычитание 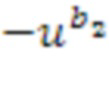 из кольцевого элемента в представлении в виде списка целых чисел, в этом случае из c, иногда упоминается в качестве этапа отрицательного уменьшения. Этап отрицательного уменьшения может выполняться посредством отрицания, выполнения этапа положительного уменьшения и повторного отрицания.
из кольцевого элемента в представлении в виде списка целых чисел, в этом случае из c, иногда упоминается в качестве этапа отрицательного уменьшения. Этап отрицательного уменьшения может выполняться посредством отрицания, выполнения этапа положительного уменьшения и повторного отрицания.
Умножение. Чтобы умножать принимаемый первый входной список (r1,r2) целых чисел умножения, кодирующий первый входной кольцевой элемент 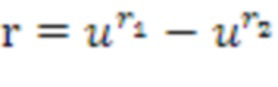 умножения, и второй входной список ((s1,s2)) целых чисел умножения, кодирующий второй входной кольцевой элемент
умножения, и второй входной список ((s1,s2)) целых чисел умножения, кодирующий второй входной кольцевой элемент 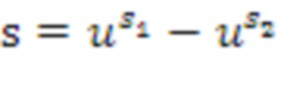 умножения, определяются первый промежуточный список (t1,t2) целых чисел умножения и второй промежуточный список (u1,u2) целых чисел умножения. Выходной список целых чисел умножения, кодирующий выходной кольцевой элемент умножения, определяется из первого и второго промежуточного элемента. В других вариантах осуществления, может быть предусмотрено более двух промежуточных списков целых чисел умножения. Имеется то, что
умножения, определяются первый промежуточный список (t1,t2) целых чисел умножения и второй промежуточный список (u1,u2) целых чисел умножения. Выходной список целых чисел умножения, кодирующий выходной кольцевой элемент умножения, определяется из первого и второго промежуточного элемента. В других вариантах осуществления, может быть предусмотрено более двух промежуточных списков целых чисел умножения. Имеется то, что
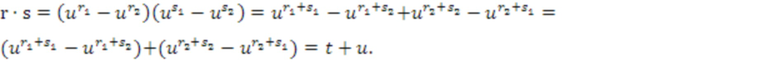
Сегментация членов в развернутых произведениях по двум членам t и u может выполняться различными способами, например, в качестве 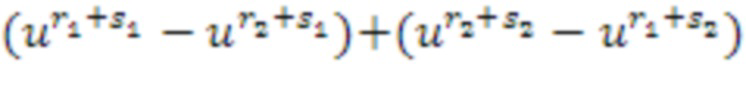 .
.
Таким образом, чтобы умножать два кольцевых элемента, представленные в качестве списков целых чисел, они могут преобразовываться в два новых списка целых чисел, которые могут суммироваться, чтобы получать ответ на умножение. Суммирование может выполняться так, как описано выше. Например, блок умножения может вычислять промежуточные списки целых чисел и отправлять их в блок умножения.
Например, первое целое число t1 из первого промежуточного списка целых чисел умножения может содержать первое целое число r1 из первого входного списка целых чисел умножения плюс первое целое число s1 из второго входного списка целых чисел умножения, и второе целое число t2 из первого промежуточного списка целых чисел умножения может содержать первое целое число r1 из первого входного списка целых чисел умножения плюс второе целое число s2 из второго входного списка t1=r1+s1,t2=r1+s2 целых чисел умножения. Первое целое число u1 из второго промежуточного списка целых чисел умножения может содержать второе целое число r2 из первого входного списка целых чисел умножения плюс второе целое число s2 из второго входного списка целых чисел умножения, и второе целое число u2 из второго промежуточного списка целых чисел умножения может содержать второе целое число r2 из первого входного списка целых чисел умножения плюс первое целое число s1 из второго входного списка u1=r2+s2,u2=r2+s1 целых чисел умножения.
В варианте осуществления, например, в примере, раскрытом выше, арифметические действия выполняется для списков целых чисел, кольцевые элементы не должны вычисляться как кольцевые элементы в некотором естественном представлении. Далее пояснен ряд разновидностей. Многие разновидности являются независимыми, например, кодирование разновидностей может комбинироваться с разновидностью, чтобы выполнять суммирование.
Через запутанные арифметические действия, когда вычисления выполняются в списке целых чисел, соответствующем, например, 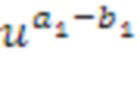 и т.д., значение может уменьшаться по модулю порядок u. Например, если порядок u равен 30, все вычисления могут выполняться mod 30.
и т.д., значение может уменьшаться по модулю порядок u. Например, если порядок u равен 30, все вычисления могут выполняться mod 30.
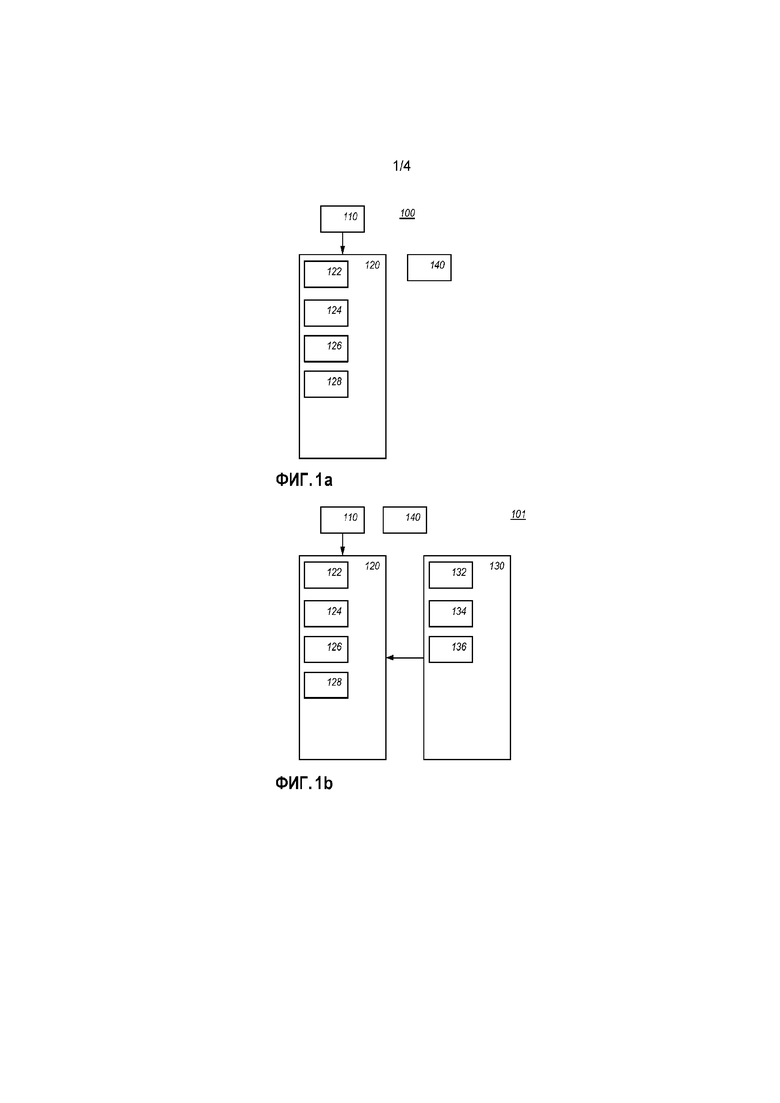
Фиг. 1a схематично показывает пример варианта осуществления электронного устройства 100 формирования. Электронное устройство 100 формирования выполнено с возможностью формировать параметры для цифровых запутанных арифметических действий. Параметры могут содержать модуль и базовый элемент.
Модуль задает коммутативное кольцо (Zn), имеющее конечное число кольцевых элементов. Базовый элемент (u) содержится в кольцевых элементах, так что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента (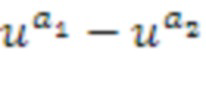 ). Вычеты по модулю модуль представляют собой кольцевые элементы. Например, кольцевой элемент может представлять целые числа от 0 вплоть до и включая модуль минус 1.
). Вычеты по модулю модуль представляют собой кольцевые элементы. Например, кольцевой элемент может представлять целые числа от 0 вплоть до и включая модуль минус 1.
Устройство 100 формирования формирует модуль и базовый элемент таким образом, что базовый элемент имеет требуемый порядок k по модулю модуль n. Например, устройство 100 может иметь интерфейс, например, ввод, для получения требуемого порядка, либо требуемый порядок может быть предварительно определен в устройстве формирования и т.д. Порядок определяет размер так называемой таблицы приращений и в силу этого представляет собой важный параметр, который зачастую выбирается посредством разработчика криптосистемы заранее. С использованием варианта осуществления разработчик может выяснять то, существуют или нет соответствующие модули и базовый элемент для требуемого порядка. Например, интерфейс может представлять собой API (интерфейс прикладного программирования). В варианте осуществления, требуемый порядок выбирается до выбора простого модуля.
Устройство 100 формирования содержит блок 110 формирования простых чисел, выполненный с возможностью формировать простой модуль p. Простой модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>p). Может быть предусмотрено самое большее k2 различных списков целых чисел двух степеней базового элемента. Если все кольцевые элементы должны представляться таким образом, должно быть предусмотрено, что (k2>p). С другой стороны, простое число должно быть больше порядка.
Формирование простых чисел может выполняться рядом способов. Например, случайное число формироваться и тестироваться на предмет простоты чисел. Тестирование на предмет простоты чисел может выполняться рядом способов, например, посредством пробного деления, теста простоты чисел Агравала-Каяла-Саксены и т.д. Альтернативно, способы просеивания могут совместно использоваться для того, чтобы формировать число простых чисел. Например, просеивание может использоваться для того, чтобы формировать все простые числа, меньшие k2. Способы просеивания включают в себя решето Эратосфена и разновидности, например, решето Аткина и т.д. Способ просеивания может быть выполнен с возможностью формировать простые числа только в интервале[k,k2].
В варианте осуществления, блок формирования простых чисел выполнен с возможностью формировать простое число (p) таким образом, что требуемый порядок (k) делит простое число минус один (k|(p-1)). Например, блок формирования простых чисел может тестировать сформированное простое число на предмет этого условия, и если оно не удовлетворяется, формировать новый простой модуль до тех пор, пока каждый действительно не будет удовлетворять ему. Альтернативно, блок 110 формирования простых чисел может формировать целые числа в форме p=λk+1 и тестировать их на предмет простоты чисел. Такое простое число должно автоматически удовлетворять условию. Условие может считаться истинным посредством оценки мультипликативной группы, сформированной посредством базового элемента, которая имеет размер k, но которая представляет собой подгруппу мультипликативной группы по модулю p (все ненулевые элементы) и которая имеет p-1 элементов. Верификация этого условия отбрасывает простые числа p, для которых требуемый базовый элемент не существует, без необходимости выполнять поиск базового элемента. Вертикальная черта (|) указывает делимость.
Устройство 100 формирования содержит блок 120 формирования базовых элементов. После того, как обнаружено подходящее простое число p, блок 120 формирования базовых элементов выполняет поиск соответствующего базового элемента.
Блок 120 формирования базовых элементов выполнен с возможностью выбирать потенциальный базовый элемент (u), больший единицы и меньший простого модуля минус один(p-1). Эта функция блока 120 формирования базовых элементов проиллюстрирована с помощью ссылки с номером 122. Например, потенциальный базовый элемент может выбираться случайно. Потенциальный базовый элемент также может выбираться систематически, например, начиная с потенциального базового элемента 2.
Блок 120 формирования базовых элементов выполнен с возможностью формировать различные степени потенциального базового элемента (u0,u1,u2,u3,…uk-1). Эта функция блока 120 формирования базовых элементов проиллюстрирована с помощью ссылки с номером 124. Формирование различной степени может выполняться посредством формирования всех степеней базового элемента, начиная с экспоненты 1 и до тех пор, пока экспонента не равна требуемому порядку k. Формирование степеней включает в себя вычисление операции по модулю по модулю простой модуль. Например, можно использовать следующую формулу ui+1=ui*u mod p, чтобы итеративно формировать степени.
Блок 120 формирования базовых элементов выполнен с возможностью определять то, имеет или нет потенциальный базовый элемент (u) порядок, равный требуемому порядку. Эта функция блока 120 формирования базовых элементов проиллюстрирована с помощью ссылки с номером 126. Например, блок 120 формирования базовых элементов может верифицировать то, удовлетворяется или нет uk=1 mod p. Определение может использовать сформированную степень, вычисленную с использованием функции 124. Тем не менее, можно вычислять порядок быстрее, приблизительно за log2(k) модульных умножений. В варианте осуществления, сначала вычисляется порядок u. Например, только если порядок равен требуемому порядку, формируются степени базового элемента. Последнее требует примерно k модульных умножений.
Блок 120 формирования базовых элементов выполнен с возможностью определять, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента. Эта функция блока 120 формирования базовых элементов проиллюстрирована с помощью ссылки с номером 128.
Например, функция 128 может реализовываться следующим образом. Формируется список целых чисел по модулю простой модуль. С каждым целым числом ассоциируется флаг. Флаг указывает то, может или нет целое число, ассоциированное с флагом, представляться в качестве разности между степенями потенциального базового элемента. Первоначально, все флаги сбрасываются, т.е. указывают, что целое число не может представляться в качестве разности между степенями потенциального базового элемента.
Затем формируются разности между двумя степенями потенциального базового элемента, и для каждой сформированной разности, задается флаг, ассоциированный с упомянутой разностью. Разности оцениваются по модулю простой модуль. Формирование разностей может формировать все разности из сформированных различных степеней потенциального базового элемента. Например, блок формирования базовых элементов может оценивать все формулы ui-uj по модулю простой модуль.
Последнее может быть оптимизировано. В варианте осуществления, список состоит из целых чисел от 1 до половины простого модуля минус один. В варианте осуществления, список содержит самое большее половину целых чисел от 1 до простого модуля минус один. Это может достигаться, поскольку если целое число x может выражаться как ui-uj, то -x также может выражаться таким образом, а именно, как uj-ui.
Если блок 120 формирования базовых элементов находит, что каждый кольцевой элемент может выражаться как разность между двумя степенями потенциального базового элемента, находятся подходящий кольцевой и соответствующий базовый элемент. Например, устройство 100 может переходить к конфигурированию вычислительного устройства с помощью модуля и базового элемента.
В случае если базовый элемент не проходит тест согласно 128, он может попытаться еще раз с новым простым числом и/или потенциальным базовым элементом. Например, устройство 100 может быть выполнено с возможностью итеративно формировать простое число и/или потенциальный базовый элемент, по меньшей мере, до положительного определения, может ли каждый кольцевой элемент выражаться как разность между двумя степенями базового элемента.
Например, устройство 100 может выбирать новый потенциальный базовый элемент из целых чисел между 2 и p-1, которые еще не сформированы, в качестве степени предыдущего потенциального базового элемента для идентичного модуля. Если все целые числа попробованы в качестве потенциального базового элемента или сформированы в качестве степени потенциального базового элемента затем, новый модуль может пробоваться.
В предпочтительном варианте осуществления, устройство 100 формирует полную таблицу, содержащую все простые числа и базовые элементы порядка k по модулю упомянутое простое число, которые обеспечивают запутанные арифметические действия, т.е. которые обеспечивают возможность записи всех кольцевых элементов по модулю простое число в качестве разности между степенями базового элемента.
Наличие таблицы допустимых простых чисел значительно ускоряет формирование непростых модулей.
Фиг. 1b схематично показывает пример варианта осуществления электронного устройства 101 формирования. Варианты осуществления, проиллюстрированные посредством фиг. 1b, расширяют варианты осуществления, проиллюстрированные посредством фиг. 1a, в том, что также могут формироваться непростые модули.
Устройство 101 содержит блок 110 формирования простых чисел и блок 120 формирования базовых элементов и дополнительно блок 130 формирования целых чисел. Аналогично устройству 100, устройство 101 формирует модуль и базовый элемент, так что базовый элемент имеет данный требуемый порядок k. Например, устройство 101 может содержать ввод для приема требуемого порядка. Например, устройство 101 может быть сконфигурировано для одного или более конкретных порядков.
Блок 130 формирования целых чисел выполнен с возможностью формировать целочисленный модуль (n) таким образом, что целочисленный модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>n). Блок 130 формирования целых чисел также может быть скомпонован таким образом, что целочисленный модуль (n) имеет, по меньшей мере, требуемый порядок базового элемента (n≥k). Эта функция проиллюстрирована на фиг. 1b с помощью ссылки с номером 132.
Блок 130 формирования целых чисел выполнен с возможностью определять (134) то, что для делителя целочисленного модуля, существует базовый элемент (u) таким образом, что каждый кольцевой элемент по модулю делитель может выражаться как разность между двумя степенями базового элемента. Например, в варианте осуществления, блок 130 формирования целых чисел выполнен с возможностью определять с использованием блока формирования базовых элементов то, что для каждого простого делителя целочисленного модуля, существует базовый элемент (u) таким образом, что каждый кольцевой элемент по модулю простой делитель может выражаться как разность между двумя степенями базового элемента. Эта функция проиллюстрирована на фиг. 1b с помощью ссылки с номером 134. В этой заявке, если первое целое число представляет собой делитель второго целого числа, это подразумевает то, что первое целое число представляет собой надлежащий делитель.
Можно подтверждать, что если u представляет собой допустимый базовый элемент для модуля n, то u mod p представляет собой допустимый базовый элемент по модулю p для любого простого делителя для n (p|n). Соответственно, если блок 130 формирования целых чисел определяет то, что для некоторого простого делителя модуля n, базовых элементов не существует, в таком случае, следовательно, также не может существовать базовый элемент по модулю n. На самом деле этот аргумент является справедливым также для непростых делителей, больших 1 и меньших модуля n.
Если установлено то, что каждый простой делитель для n обеспечивает базовый элемент и гомогенное запутывание, то можно верифицировать, что непосредственно модуль n обеспечивает возможность каждому кольцевому элементу по модулю целочисленный модуль (n) выражаться как разность между двумя степенями потенциального базового элемента. Эта операция может использовать процедуру, идентичную процедуре, описанной для функции, отличной от использования целочисленного модуля n вместо простого модуля p.
Например, последняя может содержать следующее:
- выбор потенциального базового элемента (u), большего единицы и меньшего целочисленного модуля минус один,
- формирование различных степеней потенциального базового элемента (u0,u1,u2,u3,…uk-1),
- определение, имеет ли потенциальный базовый элемент (u) порядок, равный требуемому порядку, и если да,
- определение, может ли каждый кольцевой элемент по модулю целочисленный модуль выражаться как разность между двумя степенями потенциального базового элемента. Если потенциальный базовый элемент не удовлетворяет последнему условию, новый потенциальный базовый элемент может выбираться, например, до тех пор, пока все модули целочисленный модуль не попробованы, либо до тех пор, пока все не попробованы или сформированы в качестве степени потенциального базового элемента.
Таким образом, в варианте осуществления устройства 101, формируются не только простые модули, но также и непростые целочисленные модули. Устройство 101 может использовать устройство 100 для простых делителей для n.
В варианте осуществления устройства 100 или 101, блок 120 формирования простых чисел выполнен с возможностью формировать простые числа (p), меньшие квадрата требуемого порядка (k2), и определять с использованием блока формирования базовых элементов то, может или нет каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента. Наличие доступной таблицы простых чисел, которые обеспечивают гомогенное запутывание с использованием базового элемента порядка k, значительно ускоряет поиск целочисленных модулей, которые обеспечивают гомогенное запутывание с использованием базового элемента порядка k.
Вариант осуществления с использованием способа просеивания, чтобы формировать целочисленные модули, обеспечивающие гомогенное запутывание с использованием базового элемента порядка k, заключается в следующем:
- Блок 110 формирования простых чисел и блок 120 формирования базовых элементов формируют наименьшее простое число p1, большее k, которое обеспечивает гомогенное запутывание с использованием базового элемента порядка k.
- Блок 130 формирования целых чисел формирует список целых чисел, больших или равных p1 и меньших k2, причем каждое из них имеет ассоциированный флаг. Флаги первоначально задаются с возможностью указывать то, что они могут обеспечивать гомогенное запутывание с использованием базового элемента порядка k. Задание индекса в списке равным наименьшему целому числу, превышающему p1.
- Формирование простых чисел, меньших p1, и сброс флагов, ассоциированных с целыми числами в списке, которые являются кратным числом упомянутых меньших простых чисел.
- (A) определение наименьшего целого числа m в списке с индексом, большим или равным индексу, для которого задается флаг. Определение, например, с использованием функции 136, обеспечивает ли целое число m, рассматриваемое в качестве модуля, гомогенное запутывание для порядка k.
- Если не сброшен флаг, ассоциированный с m, и сброшены все флаги целых чисел в списке, которые являются кратным числом m, приращение индекса. Если индекс по-прежнему указывает внутрь списка, продолжение с (A).
После того, как обнаружены подходящий модуль и базовый элемент, электронное устройство 100 или 101 формирования может продолжать вычисление таблицы приращений для использования в вычислительном устройстве для выполнения запутанных арифметических действий в коммутативном кольце (Zn), например, с использованием необязательного модуля 140 создания таблиц.
Блок создания таблиц выполнен с возможностью составлять таблицу приращений. Например, блок 140 создания таблиц может быть выполнен с возможностью:
- многократно выбирать входной кольцевой элемент, например, класс вычетов по модулю модуль,
- определять выходной кольцевой элемент, который равен кольцевому элементу приращения после кольцевого суммирования с входным кольцевым элементом,
- определять кодирование выходного списка целых чисел для выходного кольцевого элемента,
- добавлять запись в таблицу приращений, преобразующую входной кольцевой элемент в выходной список целых чисел.
Дополнительные сведения относительно составления таблицы приведены в упомянутой предшествующей заявке.
Устройство 100 или 101 формирования может быть выполнено с возможностью формировать таблицу, например, полную таблицу, с учетом некоторых или всех простых чисел и/или всех целых чисел, которые обеспечивают гомогенное запутывание для порядка k, но это необязательно. Вместо этого устройство 100 или 101 формирования может быть выполнено с возможностью формировать, итеративно формировать модули и/или потенциальный базовый элемент до положительного определения, может ли каждый кольцевой элемент выражаться как разность между двумя степенями базового элемента.
Типично, устройства 100 и 101 содержат микропроцессор (не показан), который выполняет надлежащее программное обеспечение, сохраненное в устройствах 100 и 101; например, это программное обеспечение, возможно, загружено и/или сохранено в соответствующем запоминающем устройстве, например, в энергозависимом запоминающем устройстве, к примеру, в RAM, или в энергонезависимом запоминающем устройстве, к примеру, во флэш-памяти (не показана). Альтернативно, устройства 100 и 101 могут, полностью или частично, реализовываться в программируемой логике, например, в качестве программируемой пользователем вентильной матрицы (FPGA). Устройства 100 и 101 могут реализовываться, полностью или частично, в качестве так называемой специализированной интегральной схемы (ASIC), т.е. интегральной схемы (IC), специально разработанной для конкретного использования.
Функции 122, 124, 126, 128, 132, 134, 136 могут реализовываться как соответствующие функциональные блоки.
В варианте осуществления, электронное устройство формирования содержит схему формирования простых чисел, схему формирования базовых элементов и необязательно схему формирования целых чисел. Электронное устройство формирования может содержать функциональные схемы, соответствующие функциональным блокам. Схемы скомпонованы для соответствующей функции блока. Схемы могут представлять собой процессорную схему и запоминающую схему, причем процессорная схема выполняет инструкции, представленные электронно в запоминающих схемах. Схемы также могут представлять собой FPGA, ASIC и т.п.
Электронное устройство формирования выполнено с возможностью формировать параметры для цифровых запутанных арифметических действий, причем параметры задают коммутативное кольцо, имеющее конечное число кольцевых элементов, причем базовый элемент содержится в кольцевых элементах, так что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента, причем устройство формирования выполнено с возможностью формировать модуль, меньший квадрата требуемого порядка базового элемента, выбирать потенциальный базовый элемент, больший единицы и меньший модуля минус один, формировать различные степени потенциального базового элемента, определять то, имеет или нет потенциальный базовый элемент порядок, равный требуемому порядку, и если да, определять то, может или нет каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента.
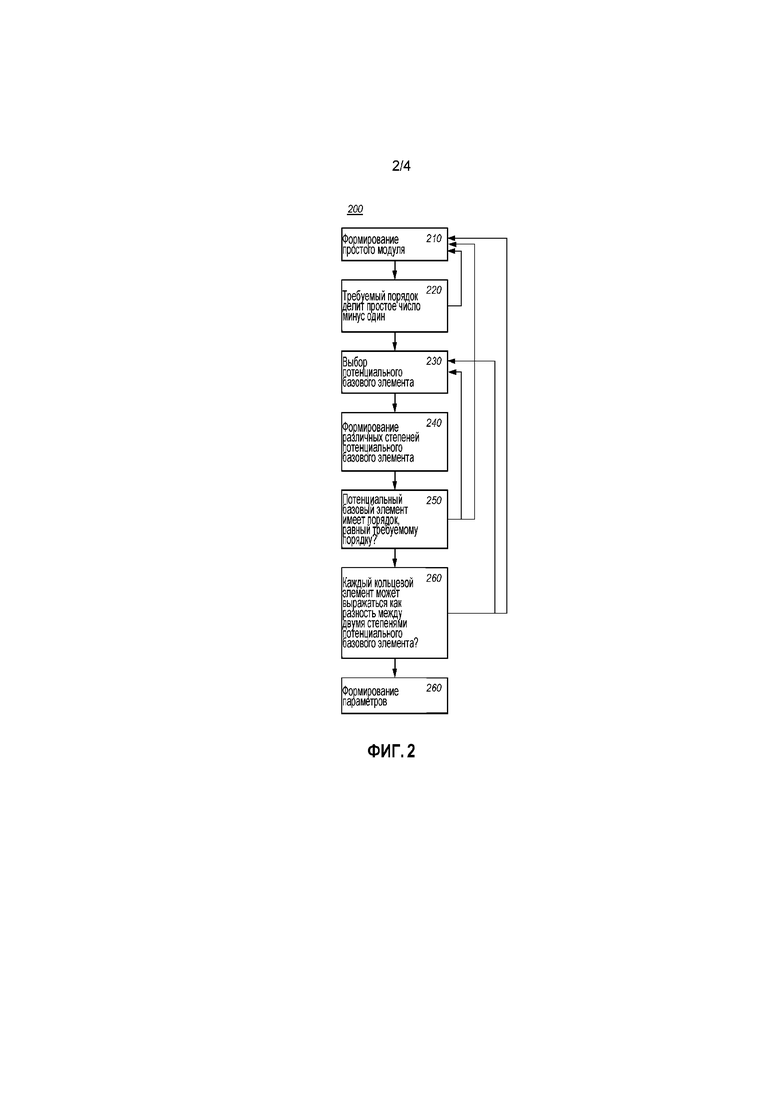
Фиг. 2 схематично показывает пример варианта осуществления электронного способа 200 формирования. Электронный способ 200 формирования выполнен с возможностью формировать параметры для цифровых запутанных арифметических действий. Параметры задают коммутативное кольцо, имеющее конечное число кольцевых элементов. Базовый элемент (u) содержится в кольцевых элементах, так что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента.
Способ 200 формирования содержит:
- формирование 210 простого модуля (p) таким образом, что простой модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>p), и
- верификацию 220, что требуемый порядок (k) делит простое число минус один (k|(p-1)).
- выбор 230 потенциального базового элемента (u), большего единицы и меньшего модуля минус один,
- формирование 240 различных степеней потенциального базового элемента (u0,u1,u2,u3,…uk-1),
- определение 250, имеет ли потенциальный базовый элемент (u) порядок, равный требуемому порядку, и если да,
- определение 260, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента.
После того, как обнаружены модуль и базовый элемент, способ 200 может формировать 270 параметры, включающие в себя простое число и базовый элемент, если определено то, что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента.
Способ 200 итеративно формирует простое число и/или потенциальный базовый элемент, по меньшей мере, до положительного определения, может ли каждый кольцевой элемент выражаться как разность между двумя степенями базового элемента. Это указано на фиг. 2 посредством стрелок, указывающих назад на блок-схеме последовательности операций способа. Например, если тест 220, 250 или 260 завершается ошибкой, способ может продолжать формирование, например, поиск при формировании простого модуля или выбора базового элемента.
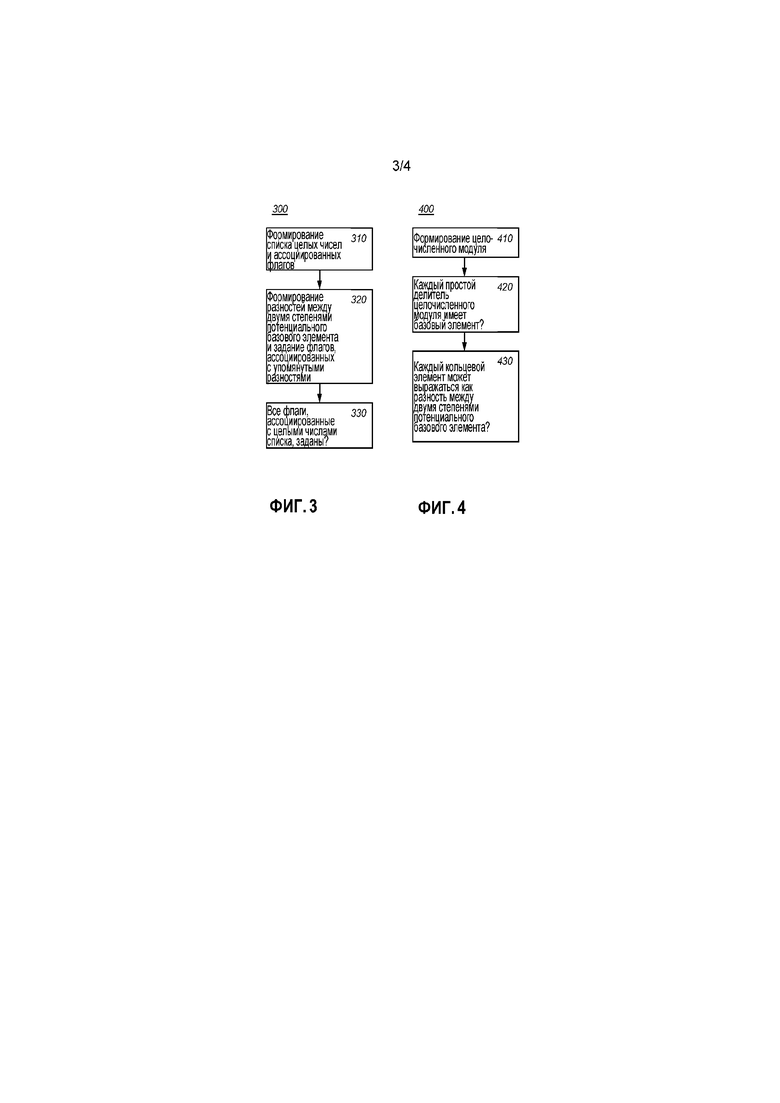
Фиг. 3 схематично показывает пример варианта осуществления электронного способа 300, верифицирующего, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента. Способ может использоваться для кольцевого элемента по модулю целочисленный модуль, в частности, по модулю простой модуль.
Способ 300 содержит:
- формирование 310 списка целых чисел и ассоциированных флагов,
- формирование 320 разностей между двумя степенями потенциального базового элемента и задание флагов, ассоциированных с упомянутыми разностями,
- определение 330, что каждый кольцевой элемент может выражаться как разность между двумя степенями потенциального базового элемента, если задаются все флаги, ассоциированные с целыми числами списка.
Фиг. 4 схематично показывает пример варианта осуществления электронного способа 400 формирования. Способ 400 содержит:
- формирование 410 целочисленного модуля (n) таким образом, что модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>n),
- определение 420 с использованием блока формирования базовых элементов, что для каждого простого делителя модуля, существует базовый элемент (u) таким образом, что каждый кольцевой элемент по модулю простой делитель может выражаться как разность между двумя степенями базового элемента,
- определение 430, может ли каждый кольцевой элемент по модулю целочисленный модуль (n) выражаться как разность между двумя степенями потенциального базового элемента.
Специалистам в данной области техники должно быть очевидным, что возможно множество различных вариантов осуществления способа. Например, порядок этапов может варьироваться, либо некоторые этапы могут выполняться параллельно. Кроме того, между этапами могут вставляться другие этапы способа. Вставленные этапы могут представлять уточнения способа, к примеру, описанного в данном документе, или могут быть не связаны со способом. Например, этапы 240 и 260 могут выполняться, по меньшей мере, частично, параллельно. Например, этап 250 может выполняться перед этапом 240. Кроме того, данный этап может не заканчиваться полностью до того, как начинается следующий этап.
Способ согласно варианту осуществления может осуществляться с использованием программного обеспечения, которое содержит инструкции для инструктирования процессорной системе осуществлять способ 200, 300 или 400. Программное обеспечение может включать в себя только этапы, выполняемые посредством конкретного подобъекта системы. Программное обеспечение может быть сохранено на подходящем носителе хранения данных, к примеру, на жестком диске, дискете, в запоминающем устройстве и т.д. Программное обеспечение может отправляться в качестве сигнала проводным или беспроводным способом либо с использованием сети передачи данных, например, по Интернету. Программное обеспечение может становиться доступным для скачивания и/или для удаленного использования на сервере. Способ может выполняться с использованием потока битов, выполненного с возможностью конфигурировать программируемую логику, например, программируемую пользователем вентильную матрицу (FPGA), чтобы осуществлять способ.
Следует принимать во внимание, что вариант осуществления также применим к компьютерным программам, в частности, к компьютерным программам на носителе, приспособленном для осуществления варианта осуществления на практике. Программа может иметь форму исходного кода, объектного кода, кода, промежуточного между исходным и объектным кодом, к примеру, частично компилированную форму, либо любую другую форму, подходящую для использования при реализации способа согласно варианту осуществления. Вариант осуществления, связанный с компьютерным программным продуктом, содержит машиноисполняемые инструкции, соответствующие каждому из этапов обработки, по меньшей мере, одного из изложенных способов. Эти инструкции могут быть подразделены на подпрограммы и/или сохранены в одном или более файлов, которые могут быть связаны статически или динамически. Другой вариант осуществления, связанный с компьютерным программным продуктом, содержит машиноисполняемые инструкции, соответствующие каждому из средств, по меньшей мере, одной из изложенных систем и/или продуктов.
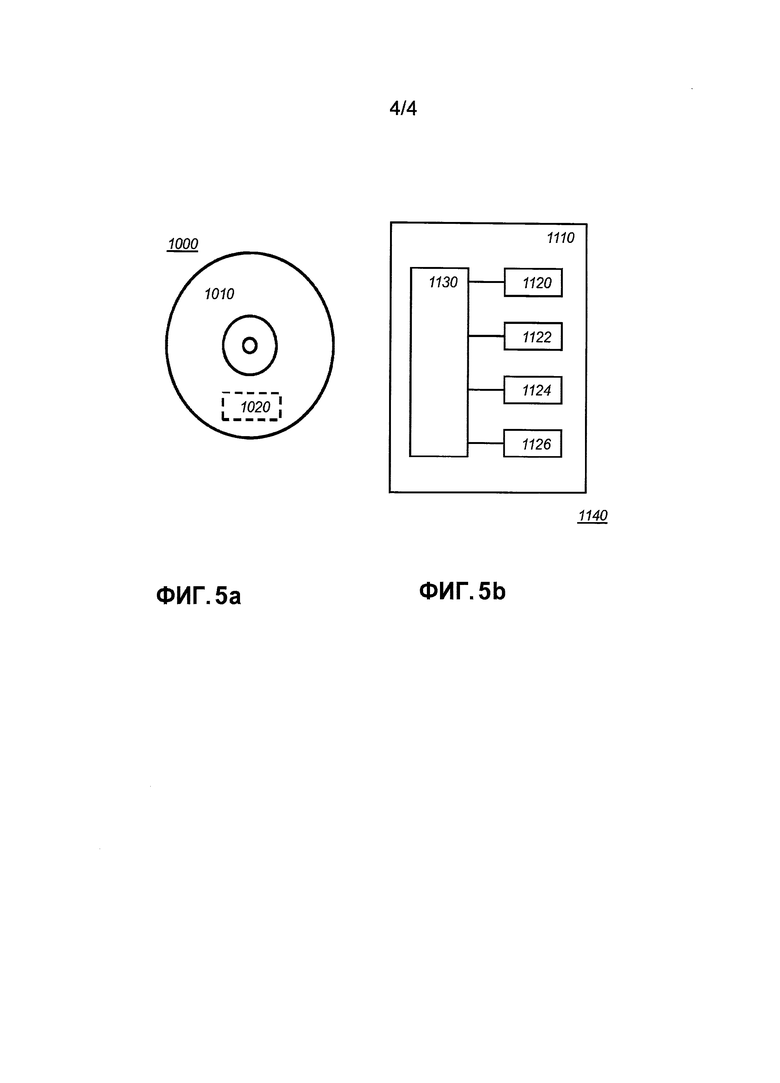
Фиг. 5a показывает машиночитаемый носитель 1000, имеющий записываемую часть 1010, содержащую компьютерную программу 1020, причем компьютерная программа 1020 содержит инструкции для инструктирования процессорной системе осуществлять способ формирования параметров для цифровых запутанных арифметических действий, согласно варианту осуществления. Компьютерная программа 1020 может быть осуществлена на машиночитаемом носителе 1000 в качестве физических меток либо посредством намагничивания машиночитаемого носителя 1000. Тем не менее, также возможен любой другой подходящий вариант осуществления. Кроме того, следует принимать во внимание, что хотя машиночитаемый носитель 1000 показан здесь в качестве оптического диска, машиночитаемый носитель 1000 может представлять собой любой подходящий машиночитаемый носитель, такой как жесткий диск, полупроводниковое запоминающее устройство, флэш-память и т.д., и может быть незаписываемым или записываемым. Компьютерная программа 1020 содержит инструкции для инструктирования процессорной системе осуществлять упомянутый способ.
Фиг. 5b показывает схематичное представление процессорной системы 1100 согласно варианту осуществления. Процессорная система содержит одну или более интегральных схем 1110. Архитектура одной или более интегральных схем 1110 схематично показана на фиг. 7b. Схема 1110 содержит блок 1120 обработки, например, CPU, для выполнения компьютерных программных компонентов, чтобы осуществлять способ согласно варианту осуществления и/или реализовывать его модули или блоки. Схема 1110 содержит запоминающее устройство 1122 для сохранения программного кода, данных и т.д. Часть запоминающего устройства 1122 может быть неперезаписываемой. Схема 1110 может содержать элемент 1126 связи, например, антенну, разъемы либо и то, и другое и т.п. Схема 1110 может содержать специализированную интегральную схему 1124 для выполнения части или всей обработки, заданной в способе. Процессор 1120, запоминающее устройство 1122, специализированная IC 1124 и элемент 1126 связи могут соединяться между собой через межкомпонентное соединение 1130, скажем, шину. Процессорная система 1110 может быть выполнена с возможностью контактной и/или бесконтактной связи, с использованием антенны и/или разъемов, соответственно.
Следует отметить, что вышеуказанные варианты осуществления иллюстрируют, а не ограничивают изобретение, и что специалисты в данной области техники должны иметь возможность разрабатывать множество альтернативных вариантов осуществления.
В формуле изобретения все ссылки с номерами, помещенные в круглые скобки, не должны рассматриваться как ограничивающие формулу изобретения. Использование глагола "содержит" и его спряжений не исключает наличия элементов или этапов, отличных от элементов или этапов, изложенных в формуле изобретения. Артикль "a" или "an" перед элементом не исключает наличия множества таких элементов. Изобретение может быть осуществлено посредством аппаратных средств, содержащих несколько отдельных элементов, и посредством надлежащим образом запрограммированного компьютера. В пункте формулы изобретения на устройство, перечисляющем несколько средств, некоторые из этих средств могут быть осуществлены посредством идентичного элемента аппаратных средств. Простой факт того, что определенные меры упомянуты в различных зависимых пунктах формулы изобретения, не означает того, что комбинация этих мер не может быть использована с выгодой.
В формуле изобретения, ссылки в круглых скобках означают ссылки с номерами на чертежах вариантов осуществления либо формулы вариантов осуществления, за счет этого повышая ясность требования. Эти ссылки не должны истолковываться как ограничивающиеся формулу изобретения.
Группа изобретений относится к области вычислительной техники и может быть использована для выполнения запутанных арифметических действий. Техническим результатом является повышение защищенности. Устройство содержит блок (110) формирования простых чисел, выполненный с возможностью формировать простой модуль (p), блок (120) формирования базовых элементов, выполненный с возможностью формировать простой модуль и базовый элемент таким образом, что каждый кольцевой элемент по модулю простой модуль может выражаться как разность между двумя степенями потенциального базового элемента. 3 н. и 10 з.п. ф-лы, 7 ил.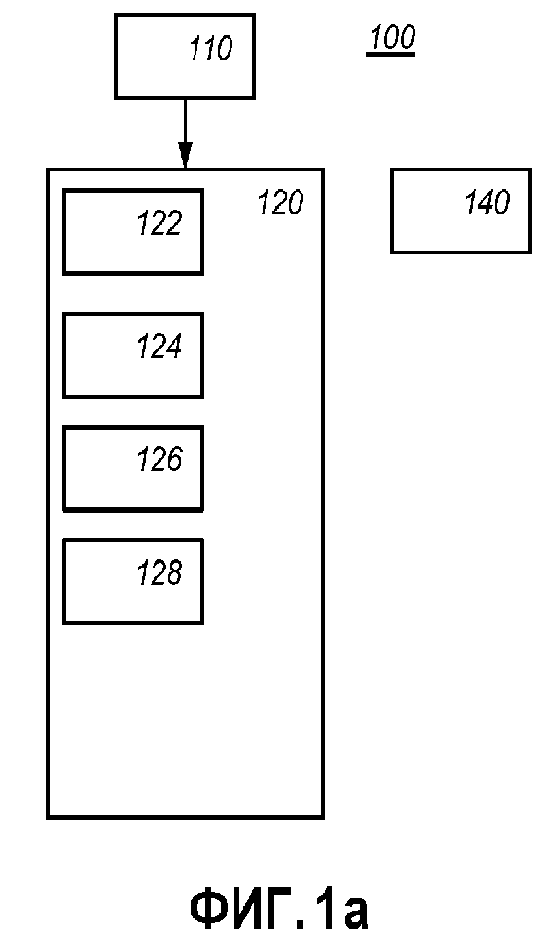
1. Электронное устройство (100) формирования, выполненное с возможностью формировать параметры для цифровых запутанных арифметических действий, причем параметры задают коммутативное кольцо (Zn), имеющее конечное число кольцевых элементов, причем базовый элемент (u) содержится в кольцевых элементах, так что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента (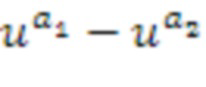 ), причем устройство формирования содержит:
), причем устройство формирования содержит:
- блок (110) формирования простых чисел, выполненный с возможностью формировать простой модуль (p) таким образом, что простой модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>p), и
- блок (120) формирования базовых элементов, выполненный с возможностью:
- выбирать (122) потенциальный базовый элемент (u), больший единицы и меньший простого модуля минус один,
- формировать (124) различные степени потенциального базового элемента (u0,u1,u2,u3,…uk-1),
- определять (126), имеет ли потенциальный базовый элемент (u) порядок, равный требуемому порядку, и если да,
- определять (128), может ли каждый кольцевой элемент по модулю простого модуля выражаться как разность между двумя степенями потенциального базового элемента.
2. Электронное устройство формирования по п. 1, в котором блок формирования простых чисел выполнен с возможностью формировать простое число (p) таким образом, что требуемый порядок (k) делит простое число минус один (k|(p-1)).
3. Электронное устройство формирования по любому из предшествующих пунктов, выполненное с возможностью формировать параметры, включающие в себя простое число и базовый элемент, если определено, что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента.
4. Электронное устройство формирования по п. 1, в котором блок формирования простых чисел выполнен с возможностью формировать все простые числа (p), меньшие квадрата требуемого порядка, и определять с использованием блока формирования базовых элементов, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента.
5. Электронное устройство формирования по п. 1, выполненное с возможностью итеративно формировать простое число и/или потенциальный базовый элемент, по меньшей мере, до положительного определения, может ли каждый кольцевой элемент выражаться как разность между двумя степенями базового элемента.
6. Электронное устройство формирования по п. 1, в котором определение, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента, содержит:
- формирование списка целых чисел по модулю простого модуля и ассоциированных флагов,
- формирование разностей между двумя степенями потенциального базового элемента и задание флагов, ассоциированных с упомянутыми разностями,
- определение, что каждый кольцевой элемент может выражаться как разность между двумя степенями потенциального базового элемента, если задаются все флаги, ассоциированные с целыми числами списка.
7. Электронное устройство формирования по п. 6, в котором список состоит из целых чисел от 1 до половины простого модуля минус один.
8. Электронное устройство формирования по п. 1, в котором блок (130) формирования целых чисел выполнен с возможностью:
- формировать (132) целочисленный модуль (n) таким образом, что целочисленный модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>n),
- определять (134), что для делителя целочисленного модуля существует базовый элемент (u') таким образом, что каждый кольцевой элемент по модулю делитель может выражаться как разность между двумя степенями базового элемента (u'), и
- если да, определять (136) то, может или нет каждый кольцевой элемент по модулю целочисленного модуля (n) выражаться как разность между двумя степенями потенциального базового элемента (u).
9. Электронное устройство формирования по п. 1, выполненное с возможностью вычислять таблицу приращений для использования в вычислительном устройстве для выполнения запутанных арифметических действий в коммутативном кольце (Zn), причем устройство формирования содержит:
- блок (140) создания таблиц, выполненный с возможностью составлять таблицу приращений, причем блок создания таблиц выполнен с возможностью:
- многократно выбирать входной кольцевой элемент,
- определять выходной кольцевой элемент, который равен кольцевому элементу приращения после кольцевого суммирования с входным кольцевым элементом,
- определять кодирование выходного списка целых чисел для выходного кольцевого элемента,
- добавлять запись в таблицу приращений, преобразующую входной кольцевой элемент в выходной список целых чисел.
10. Электронное устройство формирования по п. 1, содержащее интерфейс, выполненный с возможностью принимать требуемый порядок перед формированием упомянутого простого модуля или целочисленного модуля.
11. Электронный способ формирования, выполненный с возможностью формировать параметры для цифровых запутанных арифметических действий, причем параметры задают коммутативное кольцо, имеющее конечное число кольцевых элементов, причем базовый элемент (u) содержится в кольцевых элементах, так что каждый кольцевой элемент может выражаться как разность между двумя степенями базового элемента, причем способ формирования содержит этапы, на которых:
- формируют простой модуль (p) таким образом, что простой модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>p),
- выбирают потенциальный базовый элемент (u), больший единицы и меньший модуля минус один,
- формируют различные степени потенциального базового элемента (u0,u1,u2,u3,…uk-1),
- определяют, имеет ли потенциальный базовый элемент (u) порядок, равный требуемому порядку, и если да,
- определяют, может ли каждый кольцевой элемент выражаться как разность между двумя степенями потенциального базового элемента.
12. Способ по п. 11, содержащий этапы, на которых:
- формируют целочисленный модуль (n) таким образом, что целочисленный модуль меньше квадрата требуемого порядка (k; order(u)=k) базового элемента (k2>n),
- определяют, что для делителя целочисленного модуля существует базовый элемент (u') таким образом, что каждый кольцевой элемент по модулю делитель может выражаться как разность между двумя степенями базового элемента (u'), и
- если да, определяют, может ли каждый кольцевой элемент по модулю целочисленного модуля (n) выражаться как разность между двумя степенями потенциального базового элемента (u).
13. Машиночитаемый носитель, содержащий средство компьютерного программного кода, выполненное с возможностью осуществлять все этапы по п. 11 или 12, когда компьютерная программа выполняется на компьютере.
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| СПОСОБ ЗАЩИТЫ ПРОГРАММНО-ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ОТ НЕСАНКЦИОНИРОВАННОГО ИСПОЛЬЗОВАНИЯ | 2011 |
|
RU2467389C1 |
| Устройство для умножения двух чисел | 1989 |
|
SU1667059A2 |
Авторы
Даты
2019-12-25—Публикация
2015-12-11—Подача