Область техники
Изобретение относится к электронному вычислительному устройству, устройству для кодирования в кольце, устройству для декодирования в кольце, устройству для вычисления таблицы, способу электронных вычислений, компьютерной программе и машиночитаемому носителю.
Уровень техники
В криптографии типа "белый ящик" и в целом при маскировании программного обеспечения вычисления часто выполняются над закодированными значениями вместо явных значений. Вскрытие технологии замаскированного программного обеспечения является более трудной, если вычисления выполняются над закодированными значениями, а не над самими явными значениями.
После кодирования регулярные операции, такие как сложение или умножение, больше не могут выполняться с использованием встроенных примитивов компьютера. Прямое сложение закодированных значений обычно не приводит к кодированию сложения значений. То же самое относится к умножению. В формуле: 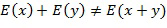 для большинства x и y; E обозначает функцию кодирования.
для большинства x и y; E обозначает функцию кодирования.
Решение этой проблемы состоит в том, чтобы ввести таблицы сложения (A) и умножения (M). Таблицы берут два закодированных значения в качестве входных данных и производят закодированное значение в качестве выходных данных, которые соответствуют кодированию операции сложения или умножения. Таблицы могут быть определены как 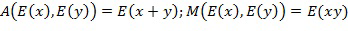 . Эти таблицы позволяют выполнять арифметические действия непосредственно над закодированными значениями.
. Эти таблицы позволяют выполнять арифметические действия непосредственно над закодированными значениями.
Замаскированное сложение и умножение с использованием таблиц страдают по меньшей мере от двух недостатков. Во-первых, таблицы могут стать довольно большими. Если x и y представлены как l битов, то каждой таблице нужны  битов.
битов.
Во-вторых, такие большие таблицы могут быть легко найдены в программном обеспечении. Еще хуже, таблицы по-прежнему могут быть идентифицированы как операции сложения или умножению даже при том, что они закодированы; например, через свойства этих функций, которые сохраняются при кодировании. Например, таблица умножения удовлетворяет выражению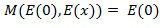 . Взломщик может использовать это и подобные свойства, чтобы предположить, какую операцию представляют таблицы.
. Взломщик может использовать это и подобные свойства, чтобы предположить, какую операцию представляют таблицы.
Сущность изобретения
Было бы полезно иметь улучшенный способ выполнения замаскированных арифметических действий. Обеспечено вычислительное устройство, определенное в формуле изобретения.
Авторы изобретения обнаружили, что в некоторых случаях умножение и сложение закодированных значений могут быть выполнены с использованием единственной таблицы без необходимости кодировать несколько значений в единственное закодированное значение. Поскольку одна и та же таблица используется для сложения и умножения, во время вскрытия технологии будет трудно увидеть, выполнено ли сложение или умножение. Поскольку сложение и умножение кажутся одной и той же операцией при рассмотрении с внешней стороны, авторы изобретения назвали этот способ "однородной маскировкой". Даже если бы взломщик смог найти таблицу, которая используется, и даже если бы он мог выяснять каким-либо образом ее функцию как инкрементную таблицу, он по-прежнему не знал бы, выполняются ли операции сложения или умножения. Метод, которым таблица действует на элементы целочисленного списка, будет отличаться для сложения и умножения, однако это может быть легко скрыто с использованием традиционной маскировки.
Кроме того, единственная используемая таблица также меньше, чем таблица, описанная в разделе "Уровень техники": требуется приблизительно 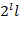 битов. Даже если используется только сложение, таблица, необходимая для замаскированного сложения, меньше, чем таблица, предложенная в разделе "Уровень техники".
битов. Даже если используется только сложение, таблица, необходимая для замаскированного сложения, меньше, чем таблица, предложенная в разделе "Уровень техники".
Изобретение применяется ко многим разным коммутативным кольцам 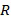 , хотя не каждое кольцо позволяет выполнять кодирование как целочисленные списки. Коммутативные кольца представляют собой математическое понятие, которое включает в себя много разных знакомых математических структур, например, целые числа по модулю числа (
, хотя не каждое кольцо позволяет выполнять кодирование как целочисленные списки. Коммутативные кольца представляют собой математическое понятие, которое включает в себя много разных знакомых математических структур, например, целые числа по модулю числа (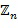 ) или полиномы по модулю числа и полинома (
) или полиномы по модулю числа и полинома (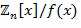 ). Поля представляют собой особый случай коммутативных колец. Как будет описано в настоящем документе, специалист может проверить, допускает ли данное кольцо маскировку.
). Поля представляют собой особый случай коммутативных колец. Как будет описано в настоящем документе, специалист может проверить, допускает ли данное кольцо маскировку.
Например, элемент кольца может быть закодирован как два целых числа 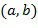 . Арифметические действия могут быть выполнены непосредственно над кодированием с использованием инкрементной таблицы, которая отображает закодированный элемент кольца на закодированный элемент кольца плюс инкрементное значение. Например, таблица может отобразить
. Арифметические действия могут быть выполнены непосредственно над кодированием с использованием инкрементной таблицы, которая отображает закодированный элемент кольца на закодированный элемент кольца плюс инкрементное значение. Например, таблица может отобразить 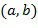 на
на 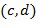 , если
, если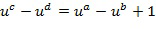 . Как сложение, так и умножение выполняются посредством повторяющихся применений инкрементной таблицы.
. Как сложение, так и умножение выполняются посредством повторяющихся применений инкрементной таблицы.
Использование инкрементной таблицы для выполнения сложения и умножения одновременно улучшает маскировку, поскольку одна и та же таблица может использоваться для сложения и умножения, и сокращает размер, поскольку операция инкремента является унарной, а не бинарной; эта таблица может действовать на единственный элемент кольца вместо двух элементов кольца. Однако имеется желание дополнительно сократить размер инкрементной таблицы.
Авторы изобретения обнаружили, что инкрементная таблица может быть дополнительно сокращена посредством установления ограничения на экспоненты основного элемента и косвенно на целые числа в целочисленных списках, которые представляют элементы кольца. В частности, разность между целыми числами в целочисленном списке может быть ограничена конкретным списком разрешенных разностей. Размер этого списка меньше, чем порядок основного элемента кольца (или одного из основных элементов кольца, если существует более одного).
Как будет пояснено более полно в настоящем документе, существует много других возможностей и вариаций. Взломщику обычно будет неизвестно, какая из многих вариаций была выбрана в любой данной реализации.
Вычислительное устройство представляет собой электронное устройство и может являться мобильным электронным устройством, например, мобильным телефоном, телеприставкой, компьютером, смарт-картой и т.д.
Замаскированные арифметические вычисления согласно настоящему описанию могут быть применены в широком спектре практических применений. Такое практическое применение включает в себя защищенные приложения, работающие на частных аппаратных средствах, например, банковские приложения и т.д., в которых должно быть предотвращено вскрытие технологии. Другие применения включают в себя применения, в которых должна быть предотвращена непреднамеренная утечка данных. Если программа взломана и раскрыты частные данные, это принесет меньше беспокойства, если упущенные данные закодированы. Замаскированные арифметические действия также могут быть применены к работающим на серверах приложениям. Конфиденциальность увеличивается, если пользователи отправляют и принимают данные в закодированной форме.
Способ в соответствии с изобретением может быть реализован на компьютере как реализованный на компьютере метод, или в специализированном аппаратном оборудовании, или в их комбинации. Исполняемый код или его части для способа в соответствии с изобретением могут быть сохранены в компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя запоминающие устройства, оптические запоминающие устройства, интегральные схемы, серверы, онлайновое программное обеспечение и т.д. Предпочтительно компьютерный программный продукт содержит энергонезависимое средство программного кода, сохраненное на машиночитаемом носителе, для выполнения способа в соответствии с изобретением, когда упомянутый программный продукт исполняется на компьютере.
В предпочтительном варианте осуществления компьютерная программа содержит средство компьютерного программного кода, выполненное с возможностью выполнять все этапы способа в соответствии с изобретением, когда компьютерная программа выполняется на компьютере. Предпочтительно компьютерная программа воплощена на машиночитаемом носителе.
Краткое описание чертежей
Эти и другие аспекты изобретения являются очевидными и будут объяснены со ссылкой на описанные далее варианты осуществления.
Фиг. 1a схематично показывает пример варианта осуществления вычислительного устройства 100,
Фиг. 1b схематично показывает пример варианта осуществления блока 130 сложения в кольце,
Фиг. 1c схематично показывает пример варианта осуществления блока 140 умножения в кольце,
Фиг. 2 схематично показывает пример варианта осуществления вычислительного устройства 101,
Фиг. 3 схематично показывает пример варианта осуществления устройства 200 вычисления таблицы для вычисления инкрементной таблицы для использования в вычислительном устройстве,
Фиг. 4 схематично показывает пример варианта осуществления способа 30 вычислений для выполнения замаскированных арифметических действий,
Фиг. 5 схематично показывает пример варианта осуществления способа 400 сложения,
Фиг. 6 схематично показывает пример варианта осуществления способа 500 умножения,
Фиг. 7a показывает машиночитаемый носитель, имеющий записываемую часть, содержащую компьютерную программу в соответствии с вариантом осуществления,
Фиг. 7b показывает схематическое представление системы процессора в соответствии с вариантом осуществления.
Элементы, которые имеют одинаковые номера для ссылок на разных фигурах, имеют одинаковые структурные признаки и одинаковые функции или являются одинаковыми сигналами. Когда функция и/или структура такого элемента были описаны, нет необходимости их повторного объяснения в подробном описании.
Список номеров для ссылок на фиг. 1:
100 вычислительное устройство
110 запоминающее устройство, выполненное с возможностью хранить инкрементную таблицу
120 блок отрицания в кольце
130 блок сложения в кольце
140 блок умножения в кольце
150 хранилище операндов
160 блок декодирования
170 блок кодирования
172 запоминающее устройство, выполненное с возможностью хранить таблицу кодирования
Подробное описание вариантов осуществления
Хотя это изобретение допускает варианты осуществления во многих разных формах, на чертежах показаны и в настоящем документе будут подробно описаны один или несколько конкретных вариантов осуществления с пониманием того, что настоящее раскрытие должно рассматриваться как иллюстративное для принципов изобретения и не предназначено для ограничения изобретения конкретными показанными и описанными вариантами осуществления.
Далее ради понимания элементы вариантов осуществления описываются в работе. Однако будет очевидно, что соответствующие элементы выполнены с возможностью выполнять функции, описываемые, как выполняемые ими.
Варианты осуществления позволяют выполнять операции умножения и сложения с использованием одной и той же таблицы. Ниже сначала обсуждаются несколько возможных архитектур вариантов осуществления вычислительных устройств. Затем обсуждаются несколько альтернативных способов выполнения замаскированных арифметических действий.
Фиг. 1 схематично показывает пример варианта осуществления вычислительного устройства 100. Вычислительное устройства 100 является электронным устройством для выполнения замаскированных арифметических действий в конечном коммутативном кольце. Известно много примеров коммутативных колец. Ниже даны примеры для двух таких колец: целые числа по модулю числа (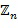 ) и полиномы по модулю числа и полинома (
) и полиномы по модулю числа и полинома (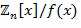 ). Другой вариант осуществления может использовать другие коммутативные кольца.
). Другой вариант осуществления может использовать другие коммутативные кольца.
Элементы кольца упоминаются как элементы кольца. На элементах кольца определены сложение и умножение, последние упоминаются как сложение в кольце и умножение в кольце.
При необходимости элементы кольца могут быть представлены в любой подходящей форме. Например, элементы 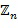 могут быть представлены как целые числа; элементы
могут быть представлены как целые числа; элементы 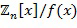 - как полиномы. Однако в вычислительном устройстве 100 элементы кольца представлены как целочисленные списки. Например, элемент кольца
- как полиномы. Однако в вычислительном устройстве 100 элементы кольца представлены как целочисленные списки. Например, элемент кольца  может быть представлен в вычислительном устройстве 100 посредством списка
может быть представлен в вычислительном устройстве 100 посредством списка 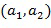 . Последнее относится даже для нецелочисленных колец, то есть полиномиальных колец. Целочисленный список кодирует элемент кольца в соответствии с некоторым отображением между целочисленными списками и элементами кольца; для заданного любого элемента кольца существует по меньшей мере один целочисленный список, который представляет элемент кольца, и для заданного любого целочисленного списка существует точно один элемент кольца, который он представляет. В вариантах осуществления любой элемент кольца может быть представлен как целочисленный список.
. Последнее относится даже для нецелочисленных колец, то есть полиномиальных колец. Целочисленный список кодирует элемент кольца в соответствии с некоторым отображением между целочисленными списками и элементами кольца; для заданного любого элемента кольца существует по меньшей мере один целочисленный список, который представляет элемент кольца, и для заданного любого целочисленного списка существует точно один элемент кольца, который он представляет. В вариантах осуществления любой элемент кольца может быть представлен как целочисленный список.
Целочисленные списки содержат по меньшей мере два целых числа и кодируют элемент кольца, в результате чего элемент кольца равен линейной комбинации степеней основного элемента кольца, причем степени имеют экспоненты, определенные целочисленным списком. Например, целочисленный список 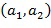 может закодировать элемент кольца α, в результате чего элемент кольца равен линейной комбинации степеней, например,
может закодировать элемент кольца α, в результате чего элемент кольца равен линейной комбинации степеней, например, 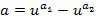 с использованием основного элемента кольца
с использованием основного элемента кольца 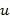 .
.
Основной элемент кольца имеет порядок в кольце. Порядок основного элемента кольца 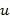 определяется как самое малое положительное целое число
определяется как самое малое положительное целое число 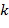 такое, что
такое, что 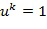 в кольце. Иногда порядок обозначается как
в кольце. Иногда порядок обозначается как  .
.
Разность между экспонентами содержится в списке разрешенных разностей. Если сами экспоненты находятся в целочисленном списке, тогда первое целое число, например, 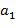 , из целочисленного списка и второе целое число, например,
, из целочисленного списка и второе целое число, например, 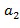 , из целочисленного списка содержатся в списке разрешенных разностей. С другой стороны, это не является необходимым. Например, целочисленный список
, из целочисленного списка содержатся в списке разрешенных разностей. С другой стороны, это не является необходимым. Например, целочисленный список 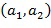 может также отображаться на
может также отображаться на 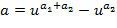 ,
, 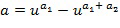 и т.д. В этом случае требуется только, чтобы один элемент из целочисленного списка содержался в списке разрешенных разностей. Возможны другие отображения из целочисленного списка на экспоненты.
и т.д. В этом случае требуется только, чтобы один элемент из целочисленного списка содержался в списке разрешенных разностей. Возможны другие отображения из целочисленного списка на экспоненты.
Размер списка разрешенных разностей меньше, чем порядок основного элемента. Это означает, что количество выборов для целочисленного списка сокращено. Например, для заданного единственного основного элемента кольца 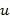 с порядком
с порядком 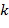 общее количество разных представлений будет равно
общее количество разных представлений будет равно 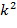 . Однако требуется, чтобы разность находилась в списке разрешенных разностей размера
. Однако требуется, чтобы разность находилась в списке разрешенных разностей размера 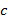 , общее количество представлений становится равным
, общее количество представлений становится равным 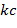 , и это меньше, чем
, и это меньше, чем 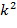 . Мы будем использовать букву
. Мы будем использовать букву 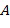 для обозначения списка разрешенных разностей.
для обозначения списка разрешенных разностей.
Целочисленные списки имеют по меньшей мере два элемента. Как оказалось, операции сложения и умножению требуют меньшего количества шагов, если целочисленный список короче. В соответствии с этим в варианте осуществления целочисленные списки всегда имеют два элемента. В основном описании мы предположим, что целочисленные списки представляют собой пары целых чисел, однако, обеспечены примеры целочисленных списков, имеющих более двух элементов.
В качестве примера целочисленный список 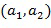 может отображаться на элемент кольца (
может отображаться на элемент кольца (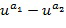 ), где
), где 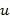 - специальный элемент кольца, называемый основным элементом кольца. Кроме того, мы предположим, что в качестве единственного основного элемента кольца используется
- специальный элемент кольца, называемый основным элементом кольца. Кроме того, мы предположим, что в качестве единственного основного элемента кольца используется 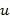 . Ниже обсуждаются многие варианты, включающие в себя использование нескольких основных элементов. Однако, в основном обсуждении мы примем в качестве "иллюстративного кодирования", в котором данный целочисленный список
. Ниже обсуждаются многие варианты, включающие в себя использование нескольких основных элементов. Однако, в основном обсуждении мы примем в качестве "иллюстративного кодирования", в котором данный целочисленный список 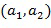 отображается на элемент кольца (
отображается на элемент кольца (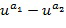 ), и в котором
), и в котором 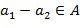 , где A представляет список разрешенных разностей; следует отметить, что существуют другие варианты.
, где A представляет список разрешенных разностей; следует отметить, что существуют другие варианты.
Список разрешенных разностей 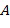 может рассматриваться как подмножество
может рассматриваться как подмножество 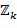 . Список разрешенных разностей может быть представлен как список, например, массив, или положительные целые числа. Подтверждение, находится ли разность в списке, может потребовать выполнения операции по модулю
. Список разрешенных разностей может быть представлен как список, например, массив, или положительные целые числа. Подтверждение, находится ли разность в списке, может потребовать выполнения операции по модулю 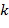 . Однако в практической реализации использование списка разрешенных разностей будет неявным; операции кодирования производят целочисленные списки, удовлетворяющие условию, операции над целочисленными списками производят выходные целочисленные списки, которые удовлетворяют условию.
. Однако в практической реализации использование списка разрешенных разностей будет неявным; операции кодирования производят целочисленные списки, удовлетворяющие условию, операции над целочисленными списками производят выходные целочисленные списки, которые удовлетворяют условию.
В варианте осуществления целые числа в целочисленном списке являются неотрицательными. Это упрощает вычисление, но не является необходимым. Кроме того, в варианте осуществления целые числа в целочисленном списке берутся по модулю порядка основного элемента. Порядок основного элемента 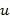 является таким наименьшим целым числом
является таким наименьшим целым числом 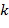 , что
, что 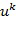 =1. Удобно поддерживать значения в целочисленном списке в диапазоне
=1. Удобно поддерживать значения в целочисленном списке в диапазоне 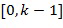 , например, выполняя операцию деления по модулю k.
, например, выполняя операцию деления по модулю k.
Вычислительное устройство 100 может содержать хранилище 150 операндов. Операнды хранятся как целочисленные списки в хранилище 150 операндов. Над операндами, хранящимися в хранилище 150 операндов, могут выполняться арифметические действия. Результаты упомянутых арифметических действий могут быть сохранены в хранилище 150 операндов, причем они могут использоваться в новых операциях или могут являться выходными данными для другого устройства и т.д.
Целочисленные списки, например, операнды в хранилище 150 операндов, могут быть представлены несколькими разными способами. Целочисленный список может быть представлен как целочисленный список, например, массив. Например, арифметическая разность между первым целым числом из целочисленных списков и вторым целым числом из целочисленного списка содержится в списке разрешенных разностей. Например, если взять предпочтительный случай целочисленных списков, имеющих два элемента, целочисленный список может быть представлен как упорядоченный список 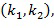 причем
причем  . В этом примере оба параметра
. В этом примере оба параметра 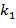 и
и 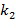 могут быть выбраны по модулю k, т.е., по модулю порядка основного элемента кольца. Это не является строго необходимым, параметры могут являться любым целым числом, в этом случае требование может быть реализовано, например, как
могут быть выбраны по модулю k, т.е., по модулю порядка основного элемента кольца. Это не является строго необходимым, параметры могут являться любым целым числом, в этом случае требование может быть реализовано, например, как 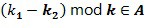 .
.
В качестве другого примера инкрементный список может быть представлен посредством выбора одного из целых чисел в целочисленном списке из списка разрешенных разностей. Например, это представление может взять целочисленный список ( , где
, где 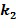 содержится в списке разрешенных разностей, другое целое число или целые числа могут быть взяты по модулю порядка
содержится в списке разрешенных разностей, другое целое число или целые числа могут быть взяты по модулю порядка 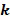 основного элемента кольца
основного элемента кольца  . Список разрешенных разностей может быть значительно меньше, чем порядок, в этом представлении может потребоваться меньше битов для представления элементов
. Список разрешенных разностей может быть значительно меньше, чем порядок, в этом представлении может потребоваться меньше битов для представления элементов 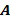 , тем самым сокращаются требования к объему. В варианте осуществления целое число в целочисленном списке, для которого требуется, чтобы оно являлось элементом списка разрешенных разностей
, тем самым сокращаются требования к объему. В варианте осуществления целое число в целочисленном списке, для которого требуется, чтобы оно являлось элементом списка разрешенных разностей 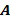 , находится в фиксированной позиции, например, в первой или второй позиции. Но последнее не является необходимым; позиция может изменяться как дополнительная мера маскировки.
, находится в фиксированной позиции, например, в первой или второй позиции. Но последнее не является необходимым; позиция может изменяться как дополнительная мера маскировки.
Вычислительное устройство 100 содержит запоминающее устройство 110, выполненное с возможностью хранить инкрементную таблицу 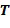 , определенную для инкрементного элемента кольца. Инкрементная таблица отображает входной элемент кольца на выходной целочисленный список, кодирующий выходной элемент кольца, в результате чего выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца. В варианте осуществления входной элемент кольца представлен как целочисленный список. Таким образом, таблица
, определенную для инкрементного элемента кольца. Инкрементная таблица отображает входной элемент кольца на выходной целочисленный список, кодирующий выходной элемент кольца, в результате чего выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца. В варианте осуществления входной элемент кольца представлен как целочисленный список. Таким образом, таблица 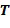 отображает целочисленные списки на целочисленные списки; и те, и другие в соответствии с одинаковым кодированием, например, с одинаковым отображением. Однако существуют варианты осуществления, в которых входной элемент кольца представлен как целочисленный список в альтернативном кодировании. В любом случае входной элемент кольца представлен в цифровой форме, позволяя таблице отображать входной элемент кольца на выходной элемент кольца.
отображает целочисленные списки на целочисленные списки; и те, и другие в соответствии с одинаковым кодированием, например, с одинаковым отображением. Однако существуют варианты осуществления, в которых входной элемент кольца представлен как целочисленный список в альтернативном кодировании. В любом случае входной элемент кольца представлен в цифровой форме, позволяя таблице отображать входной элемент кольца на выходной элемент кольца.
Выходной целочисленный список инкрементной таблицы удовлетворяет требованию, чтобы выходной элемент кольца, который представляет выходной целочисленный список, был равен линейной комбинации степеней основного элемента кольца ( ), причем степени имеют экспоненты, определенные посредством выходного целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенные посредством выходного целочисленного списка, разность между первой экспонентой ( ) и второй экспонентой (
) и второй экспонентой ( ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (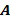 ). Это будет упоминаться как требование ограниченных разностей. В вариантах осуществления требования ограниченных разностей переводятся в требование к целым числам в целочисленном списке, например, чтобы функция целых чисел в целочисленном списке содержалась в списке разрешенных разностей.
). Это будет упоминаться как требование ограниченных разностей. В вариантах осуществления требования ограниченных разностей переводятся в требование к целым числам в целочисленном списке, например, чтобы функция целых чисел в целочисленном списке содержалась в списке разрешенных разностей.
Таблица может перечислять входные элементы кольца в некотором формате вместе со связанным выходным целочисленным списком. Таблица также может быть представлена в запоминающем устройстве посредством опускания входного кольца и перечисления только выходных целочисленных списков. Например, это может быть сделано, если входное кольцо представлено в каноническом формате.
Например, в предположении иллюстративного кодирования входной элемент кольца 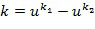 может быть отображен посредством таблицы
может быть отображен посредством таблицы 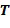 на выходной целочисленный список. В этом случае входной элемент кольца может быть представлен как целочисленный список, в результате чего мы можем иметь
на выходной целочисленный список. В этом случае входной элемент кольца может быть представлен как целочисленный список, в результате чего мы можем иметь 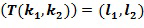 . Последнее кодирует выходной элемент кольца
. Последнее кодирует выходной элемент кольца 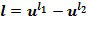 . Выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца. Например, если инкрементный элемент кольца равен 1, то
. Выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца. Например, если инкрементный элемент кольца равен 1, то 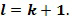 В варианте осуществления инкрементный элемент может быть равен 1, однако это не является необходимым. Например, с использованием иллюстративного кодирования инкрементный элемент может быть выбран как
В варианте осуществления инкрементный элемент может быть равен 1, однако это не является необходимым. Например, с использованием иллюстративного кодирования инкрементный элемент может быть выбран как 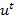 для некоторого значения t, например, любого значения
для некоторого значения t, например, любого значения 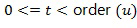 .
.
Не все возможные комбинации входного целочисленного списка обязательно должны быть представлены в таблице, поскольку многие целочисленные списки не представляют элементы кольца в соответствии с требованием ограниченных разностей.
Инкрементная таблица намного меньше, чем таблицы, описанные в разделе "Уровень техники". Последние таблицы берут два элемента входных данных, например, два закодированных числа, чтобы произвести закодированные выходные данные. Однако таблица 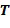 берет только одни закодированные входные данные, чтобы произвести одни закодированные выходные данные; инкрементный элемент кольца является фиксированным. В предположении, что кодирование занимает такой же объем, входной объем таблицы T сокращается приблизительно как квадратный корень. Это является значительным улучшением по размеру.
берет только одни закодированные входные данные, чтобы произвести одни закодированные выходные данные; инкрементный элемент кольца является фиксированным. В предположении, что кодирование занимает такой же объем, входной объем таблицы T сокращается приблизительно как квадратный корень. Это является значительным улучшением по размеру.
С помощью только инкрементной таблицы вычислительное устройство может представлять элементы кольца замаскированным образом и может добавлять инкрементные элементы к такому закодированному элементу кольца. Это может быть использовано, например, для реализации счетчика.
В варианте осуществления вычислительное устройство 100 содержит блок 130 сложения в кольце и блок 140 умножения в кольце. Вычислительное устройство 100 также может содержать блок 120 отрицания в кольце. В варианте осуществления блок 140 умножения в кольце может использовать блок 130 сложения для выполнения сложения; блок 130 сложения может использовать блок 120 отрицания. Это обозначено на фигуре 1 линиями между блоками 120, 130 и 140. Однако блоки могут быть дублированы; например, блок 130 сложения может выполнять свое собственное отрицание, и блок 140 умножения может выполнять свое собственное сложение. Отрицание также упоминается как "изменение знака".
Блок 120 отрицания может принимать входной для отрицания целочисленный список 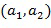 , кодирующий входной для отрицания элемент кольца α. Блок 120 отрицания выполнен с возможностью определять выходной для отрицания целочисленный список
, кодирующий входной для отрицания элемент кольца α. Блок 120 отрицания выполнен с возможностью определять выходной для отрицания целочисленный список 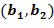 , кодирующий выходной для отрицания элемент кольца
, кодирующий выходной для отрицания элемент кольца 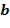 . Выходной для отрицания элемент кольца представляет собой отрицание входного для отрицания элемента кольца, например, выходной для отрицания элемент кольца равен нейтральному элементу кольца для сложения (0) минус входной для отрицания элемент кольца. Таким образом,
. Выходной для отрицания элемент кольца представляет собой отрицание входного для отрицания элемента кольца, например, выходной для отрицания элемент кольца равен нейтральному элементу кольца для сложения (0) минус входной для отрицания элемент кольца. Таким образом,  .
.
В варианте осуществления блок отрицания может вычислять выходной целочисленный список посредством перестановки входного для отрицания целочисленного списка. С использованием иллюстративного кодирования  выходной целочисленный список может представлять собой
выходной целочисленный список может представлять собой 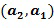 . Отрицание посредством перестановки может быть эффективно реализовано в коде посредством изменения адреса, из которого считывается элемент, и это не обязательно изменяет фактический порядок в памяти. Это возможно, если списки разрешенных разностей удовлетворяют требованию, в котором
. Отрицание посредством перестановки может быть эффективно реализовано в коде посредством изменения адреса, из которого считывается элемент, и это не обязательно изменяет фактический порядок в памяти. Это возможно, если списки разрешенных разностей удовлетворяют требованию, в котором 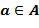 подразумевает
подразумевает  .
.
В варианте осуществления блок отрицания может вычислять выходной целочисленный список посредством добавления константы к каждому целому числу из целочисленного списка. Например, в приведенном в качестве примера кодировании с использованием целого числа 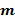 , такого что
, такого что 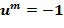 ; например, выходной целочисленный список может представлять собой
; например, выходной целочисленный список может представлять собой  .
.
В варианте осуществления блок отрицания содержит таблицу отрицания. Таблица отрицания выполнена с возможностью принимать входной для отрицания целочисленный список ( ), кодирующий входной для отрицания элемент кольца
), кодирующий входной для отрицания элемент кольца 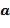 , и производить выходной для отрицания целочисленный список (
, и производить выходной для отрицания целочисленный список (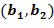 ), кодирующий выходной для отрицания элемент кольца
), кодирующий выходной для отрицания элемент кольца 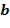 , в результате чего
, в результате чего  . Таблица отрицания не является очень большой, поскольку она унарная, кроме того, таблица отрицания должна содержать только выходной для отрицания целочисленный список для входных данных, которые удовлетворяют требованию ограниченных разностей на целочисленных списках. Таблица отрицания используется таким же образом во время операций сложения и умножения.
. Таблица отрицания не является очень большой, поскольку она унарная, кроме того, таблица отрицания должна содержать только выходной для отрицания целочисленный список для входных данных, которые удовлетворяют требованию ограниченных разностей на целочисленных списках. Таблица отрицания используется таким же образом во время операций сложения и умножения.
Блок 130 сложения в кольце выполнен с возможностью принимать первый входной для сложения целочисленный список  , кодирующий первый входной для сложения элемент кольца, и второй входной для сложения целочисленный список
, кодирующий первый входной для сложения элемент кольца, и второй входной для сложения целочисленный список 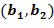 , кодирующий второй входной для сложения элемент кольца. Например, блок 130 сложения в кольце может принимать два операнда из хранилища 150 операндов. Блок 130 сложения в кольце выполнен с возможностью определять выходной для сложения целочисленный список, кодирующий выходной для сложения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для сложения целочисленных списков, выходной для сложения элемент кольца является равным сложению в кольце первого входного для сложения элемента кольца и второго входного для сложения элемента кольца.
, кодирующий второй входной для сложения элемент кольца. Например, блок 130 сложения в кольце может принимать два операнда из хранилища 150 операндов. Блок 130 сложения в кольце выполнен с возможностью определять выходной для сложения целочисленный список, кодирующий выходной для сложения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для сложения целочисленных списков, выходной для сложения элемент кольца является равным сложению в кольце первого входного для сложения элемента кольца и второго входного для сложения элемента кольца.
В варианте осуществления отображение целочисленного списка на конкретный элемент кольца содержит несколько частичных отображений, каждое частичное отображение связано с целым числом из целочисленного списка, частичное отображение отображает целое число на элемент кольца. Отображение представляет собой линейную комбинацию, например, сумму частичных отображений, примененных к соответствующим целым числам. Частичное отображение может возводить в степень основной элемент, определенный посредством соответствующего целого числа. Например, в иллюстративном кодировании 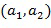 может рассматриваться как сумма частичных отображений
может рассматриваться как сумма частичных отображений 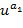 и
и 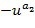 .
.
Фиг. 1b иллюстрирует вариант осуществления блока 130 сложения. Блок 130 сложения принимает первый входной для сложения целочисленный список 131 и второй входной для сложения целочисленный список 132. Блок 130 сложения содержит промежуточный блок 134 сложения, выполненный с возможностью итерационно добавлять элемент кольца, полученный из целого числа из второго входного для сложения целочисленного списка 132, к первому входному для сложения элементу кольца. Например, промежуточный блок 134 сложения может выполнять сложение с промежуточной суммой 133, которая инициализируется как первый элемент целочисленного списка. Сложение включает в себя применение инкрементной таблицы из запоминающего устройства 110.
Блок 140 умножения в кольце выполнен с возможностью принимать первый входной для умножения целочисленный список 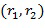 , кодирующий первый входной для умножения элемент кольца, и второй входной для умножения целочисленный список
, кодирующий первый входной для умножения элемент кольца, и второй входной для умножения целочисленный список 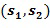 , кодирующий второй входной для умножения элемент кольца. Например, блок 140 умножения может принять два операнда из хранилища 150 операндов. Блок 140 умножения в кольце выполнен с возможностью определять выходной для умножения целочисленный список, кодирующий выходной для умножения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для умножения целочисленных списков, выходной для умножения элемент кольца равен умножению в кольце первого входного для умножения элемента кольца и второго входного для умножения элемента кольца.
, кодирующий второй входной для умножения элемент кольца. Например, блок 140 умножения может принять два операнда из хранилища 150 операндов. Блок 140 умножения в кольце выполнен с возможностью определять выходной для умножения целочисленный список, кодирующий выходной для умножения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для умножения целочисленных списков, выходной для умножения элемент кольца равен умножению в кольце первого входного для умножения элемента кольца и второго входного для умножения элемента кольца.
Фиг. 1c показывает возможный вариант осуществления блока 140 умножения. Блок 140 умножения принимает первые входные для умножения целочисленные списки 141 и вторые входные для умножения целочисленные списки 142. Блок 140 умножения содержит промежуточный блок 144 умножения, выполненный с возможностью определять из первых и вторых входных для умножения целочисленных списков 141, 142 первый целочисленный список 145 промежуточного умножения 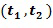 и второй целочисленный список 146 промежуточного умножения
и второй целочисленный список 146 промежуточного умножения  , кодируя первый и второй элемент кольца промежуточного умножения соответственно. Блок 140 умножения выполнен с возможностью складывать первый список 145 и второй целочисленный список 146 промежуточного умножения через блок 130 сложения в кольце. Определение промежуточного целочисленного списка может включать в себя арифметические операции над целыми числами в целочисленном списке, но не требует инкрементной таблицы.
, кодируя первый и второй элемент кольца промежуточного умножения соответственно. Блок 140 умножения выполнен с возможностью складывать первый список 145 и второй целочисленный список 146 промежуточного умножения через блок 130 сложения в кольце. Определение промежуточного целочисленного списка может включать в себя арифметические операции над целыми числами в целочисленном списке, но не требует инкрементной таблицы.
Вычислительное устройство 100 факультативно содержит блок 170 кодирования в кольце для кодирования элемента кольца коммутативного кольца как целочисленного списка и модуль 160 декодирования в кольце для декодирования целочисленного списка  в элемент кольца (
в элемент кольца ( ) коммутативного кольца. Блок 170 кодирования и/или блок 160 декодирования может отсутствовать, например, когда вычислительное устройство 100 принимает закодированные входные данные и/или сообщает закодированные выходные данные. Блок 170 кодирования и/или блок 160 декодирования могут быть реализованы как автономный блок, например, как устройство кодирования и/или устройство 160 декодирования.
) коммутативного кольца. Блок 170 кодирования и/или блок 160 декодирования может отсутствовать, например, когда вычислительное устройство 100 принимает закодированные входные данные и/или сообщает закодированные выходные данные. Блок 170 кодирования и/или блок 160 декодирования могут быть реализованы как автономный блок, например, как устройство кодирования и/или устройство 160 декодирования.
Блок 170 кодирования в кольце может содержать запоминающее устройство 172, выполненное с возможностью хранить таблицу кодирования, определенную для основного элемента кольца ( ), таблица кодирования отображает элемент кольца (
), таблица кодирования отображает элемент кольца ( ) на целочисленный список (
) на целочисленный список ( ), в результате чего элемент кольца равен линейной комбинации степеней основного элемента кольца (
), в результате чего элемент кольца равен линейной комбинации степеней основного элемента кольца (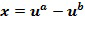 ), причем степени имеют экспоненты, определенные посредством целочисленного списка. Блок 170 кодирование может сохранять закодированный элемент кольца в хранилище 150 операндов. Блок 170 кодирования позволяет системе работать с простой информацией.
), причем степени имеют экспоненты, определенные посредством целочисленного списка. Блок 170 кодирование может сохранять закодированный элемент кольца в хранилище 150 операндов. Блок 170 кодирования позволяет системе работать с простой информацией.
Таблица кодирования отображает элемент кольца ( ) на целочисленный список (
) на целочисленный список ( ) таким образом, что элемент кольца равен линейной комбинации степеней основного элемента кольца (
) таким образом, что элемент кольца равен линейной комбинации степеней основного элемента кольца ( ), причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (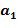 ) и второй экспонентой (
) и второй экспонентой (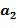 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (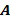 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (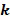 ).
).
Блок 160 декодирования в кольце выполнен с возможностью определять для одного или более основных элементов кольца ( ) такой элемент кольца (
) такой элемент кольца ( ), что элемент кольца равен линейной комбинации степеней одного или более основных элементов кольца (
), что элемент кольца равен линейной комбинации степеней одного или более основных элементов кольца (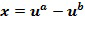 ), причем степени имеют экспоненты, определенные посредством целочисленного списка. Например, блок 160 декодирования может содержать хранилище, хранящее таблицу декодирования, отображающую целочисленные списки на элементы кольца. Например, блок 160 декодирования может содержать блок вычисления для вычисления степеней и их линейной комбинации.
), причем степени имеют экспоненты, определенные посредством целочисленного списка. Например, блок 160 декодирования может содержать хранилище, хранящее таблицу декодирования, отображающую целочисленные списки на элементы кольца. Например, блок 160 декодирования может содержать блок вычисления для вычисления степеней и их линейной комбинации.
Таблица декодирования должна отображать только целочисленный список, которые удовлетворяют требованию ограниченных разностей, с тем чтобы таблица декодирования имела меньший размер, чем таблица декодирования, которой требуется отображать все возможные разности.
Многие интересные варианты осуществления опускают один или оба из блоков 160 и 170 кодирования и декодирования. Например, вычислительное устройство 100 может быть выполнено с возможностью принимать закодированную информацию по компьютерной сети, например, Интернет. Владелец системы, на которой работает замаскированное вычислительное устройство 100, например, компьютер, исполняющий программное обеспечение для замаскированных вычислений, может не знать о кодировании, используемом ни для входной информации, ни для информации, выдаваемой системой 100, например, передаваемой обратно по компьютерной сети. В соответствии с этим, даже если вычисления выполняются в облаке, владелец информации имеет некоторую гарантию, что его информация находится в безопасности. Работа над информацией в закодированной форме, как правило, невозможна с использованием криптографии, например, шифрования. Даже если используется система таблиц, как описано в общих чертах в разделе "Уровень техники", для этого требуются двойные таблицы.
Как правило, вычислительное устройство 100 содержит микропроцессор (не показан), который исполняет подходящее программное обеспечение, сохраненное в устройстве 100; например, это программное обеспечение, возможно, было загружено и/или сохранено в соответствующей памяти, например, в энергозависимой памяти, такой как оперативное запоминающее устройство (ОЗУ; RAM), или в энергонезависимой памяти, такой как флэш-память (не показана). В качестве альтернативы устройство 100 может быть реализовано полностью или частично в программируемой логической схеме, например, как программируемая пользователем вентильная матрица (FPGA). Устройство 100 может быть реализовано полностью или частично как так называемая специализированная интегральная схема (ASIC), т.е. интегральная схема (IC), приспособленная для ее конкретного использования.
В варианте осуществления электронное вычислительное устройство содержит схему сложения в кольце и схему умножения в кольце, выполненные с возможностью исполнять функцию соответствующего блока. Вычислительное устройство также может содержать схему отрицания. Схема может представлять собой интегральные схемы, такие как комплементарный металло-оксидный полупроводник (КМОП; CMOS), например, полученные посредством описания функций на языке описания аппаратных средств, таком как Verilog и VHDL. Схемы могут представлять собой схему процессора и запоминающую схему, схема процессора исполняет инструкции, представленные в электронном виде в запоминающих схемах. Схемы также могут представлять собой программируемую пользователем вентильную матрицу (FPGA), специализированную интегральную схему (ASIC) и т.п.
Хранилище 110 таблиц и хранилище 150 операндов могут быть реализованы как электронное запоминающее устройство, например, память. Оба хранилища могут являться частью одной и той же памяти, но они могут являться различными запоминающими устройствами. Хранилище 110 таблиц может являться энергонезависимым, не записываемым, например, постоянным запоминающим устройством (ПЗУ; ROM) или запоминающим устройством с однократной записью и многократным считыванием (WORM). Хранилище 150 операндов может являться энергозависимой или энергонезависимой записываемой памятью, например, флэш-памятью или оперативным запоминающим устройством (ОЗУ; RAM).
Фиг. 2 схематично показывает пример варианта осуществления вычислительного устройства 101. Вычислительное устройство 101 представляет собой усовершенствованный вариант вычислительного устройства 100. В варианте осуществления вычислительное устройство 101 содержит несколько блоков сложения в кольце, несколько блоков умножения в кольце и факультативно несколько блоков отрицания. Например, фиг. 2 показывает три блока 1401.1, 140.2 и 140,3 умножения и два блока 130.1 и 130.2 сложения. Эти блоки могут иметь такую же конструкцию, как блоки 140 и 130 соответственно. Блоки умножения и сложения занимают относительно мало места, например, при реализации в программном обеспечении этим блокам требуется не более чем несколько сотен компьютерных инструкций низкого уровня. В частности, копия блока сложения и/или умножения может использоваться для каждого умножения или сложения, которое требуется в компьютерной программе. Это дает возможность традиционных методик маскирования. В качестве примера фиг. 2 показывает, как может быть вычислен полином с использованием замаскированных арифметических действий.
с использованием замаскированных арифметических действий.
Операции нескольких арифметических блоков, например, сложение, умножение, отрицание, могут быть выполнены в любом порядке, позволяемом их зависимостями данных. Например, операция 140.3 может быть вставлена в порядок 140.1, 140.2, 130.1 и 130.2 в любой точке перед 130.1. Кроме того, порядок последующих умножений или сложений может быть заменен на обратный. Таким образом, такая схема, как схема 2, может быть переведена в линейный порядок для программы многими разными способами. Не является необходимым, чтобы блоки были строго разделены; инструкции для первого блока могут быть вставлены между инструкций для другого блока.
Фиг. 3 схематично показывает пример варианта осуществления устройства 200 вычисления таблицы для вычисления инкрементной таблицы для использования в вычислительном устройстве. Инкрементная таблица может использоваться в таком устройстве, как вычислительное устройство 100. Инкрементная таблица может быть сохранена на непереходном запоминающем устройстве, например, жестком диске, микросхеме энергонезависимой памяти и т.д.
Устройство 200 вычисления таблицы содержит блок 210 создания таблицы, выполненный с возможностью строить инкрементную таблицу. Например, блок создания таблицы может быть выполнен с возможностью
- многократно выбирать входной элемент кольца, например, 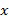 ,
,
- определять выходной элемент кольца, который равен инкрементному элементу кольца, добавленному с помощью сложения в кольце ко входному элементу кольца. Например, 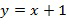 , если инкрементное значение равно 1.
, если инкрементное значение равно 1.
- определять кодирование выходного целочисленного списка для выходного элемента кольца. Например, устройство 200 вычисления таблицы может содержать блок кодирования, такой как блок 170 кодирования.
- добавлять запись в инкрементную таблицу, отображающую входной элемент кольца на выходной целочисленный список, удовлетворяющий требованию ограниченных разностей.
Эти этапы могут выполняться, пока все элементы кольца не будут отображены на целочисленный список. В некоторых вариантах осуществления элементы могут быть пропущены с построением частичной инкрементной таблицы; например, может быть известно из контекста, что некоторые элементы кольца не возникнут.
Пусть задано кольцо 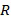 , потенциальный основной элемент кольца
, потенциальный основной элемент кольца 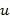 , кодирование, например, иллюстративное кодирование, и длина целочисленного списка, например, составляет 2, таблица декодирования может быть сгенерирована, как задано ниже. Пусть
, кодирование, например, иллюстративное кодирование, и длина целочисленного списка, например, составляет 2, таблица декодирования может быть сгенерирована, как задано ниже. Пусть 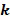 является порядком элемента
является порядком элемента  .
.
- генерировать все целочисленные списки, удовлетворяющие требованию ограниченных разностей, например, посредством генерации всех целочисленных списков с длиной целочисленного списка, имеющих целые числа по модулю k, и первое целое число из целочисленного списка и целое число из выходного целочисленного списка содержатся в списке разрешенных разностей 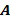 .
.
Например, для целочисленного списка длины 2 может использоваться следующий иллюстративный алгоритм: для k1 от 0 до (k-1); для всех d в A; генерировать (k1, k1+d mod k). Например, для списка разностей A={0, 1, 4, 5, 902, 903, 906} можно сгенерировать: (0,0), (0,1), (0, 4),..., (1, 1), (1, 5),... и т.д. В этом примере список разностей может использоваться с кольцом 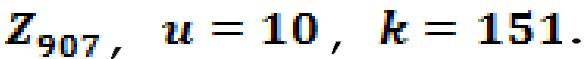
- для каждого сгенерированного целочисленного списка вычислять элемент кольца, закодированный посредством целочисленного списка, и добавлять запись в таблицу декодирования, связанную со целочисленным списком для декодирования. Например, продолжая упомянутый выше пример, можно вычислить . Таким образом таблица декодирования может принять запись, которая (1,5) декодируется в 76.
. Таким образом таблица декодирования может принять запись, которая (1,5) декодируется в 76.
Хотя декодирование может использовать или не использовать таблицу декодирования, такая таблица также является полезной, поскольку таблица кодирования может быть сгенерирована из таблицы декодирования, например, посредством сортировки таблицы для элементов кольца. Может случиться, что элемент кольца имеет несколько кодирований. Например, элемент кольца 0 (нейтральный элемент для сложения) может быть представлен как (a, a) в приведенном в качестве примера кодировании для любого a. Такие множественные кодирования могут быть удалены из таблицы, например, посредством удаления всех кроме одной из нескольких записей для данного элемента кольца; или посредством оставления нескольких кодирований в таблице и использования таблицы кодирования, чтобы закодировать в одну случайную запись из нескольких записей.
Построение таблицы декодирования или кодирования также может использоваться, чтобы обнаружить, является ли элемент кольца u основным элементом кольца. Если построение таблицы кодирования терпит неудачу, поскольку оказывается, что некоторые элементы кольца не имеют кодирования, тогда u не является основным элементом кольца.
Ниже представлены несколько вариантов осуществления кодирований, инкрементных таблиц, способов сложения в кольце и способов умножения в кольце. Блоки отрицания, сложения и умножения вычислительного устройства 100 могут быть сконфигурированы для любого из этих вариантов осуществления. Все примеры относятся к любому коммутативному кольцу, в частности, 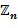 и
и 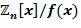 . Где
. Где 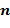 - положительное целое число. Кроме того, очень предпочтительно, что любой элемент коммутативного кольца может быть представлен в выбранном кодировании. Не все коммутативные кольца позволяют представить все элементы в данном кодировании, например, как данный тип представления целочисленного списка. Пусть задано коммутативное кольцо R, мы будет говорить, что оно допускает полную однородную маскировку, если любой элемент в R может быть представлен как целочисленный список с использованием данного типа кодировки. Специалист в области техники может проверить, допускает ли данное коммутативное кольцо полную однородную маскировку при данном кодировании, например, посредством генерации всех допустимых кодирований и проверки, что вместе они представляют все элементы данного кольца. Для некоторых применений может допускаться, чтобы кодирование имело некоторые промежутки. Это может иметь как следствие, что арифметические действия не могут быть выполнены на этих промежутках, по меньшей мере без использования замаскированного кодирования целочисленного списка. Конкретные примеры коммутативных колец, допускающих определенные типы кодирований, представлены ниже.
- положительное целое число. Кроме того, очень предпочтительно, что любой элемент коммутативного кольца может быть представлен в выбранном кодировании. Не все коммутативные кольца позволяют представить все элементы в данном кодировании, например, как данный тип представления целочисленного списка. Пусть задано коммутативное кольцо R, мы будет говорить, что оно допускает полную однородную маскировку, если любой элемент в R может быть представлен как целочисленный список с использованием данного типа кодировки. Специалист в области техники может проверить, допускает ли данное коммутативное кольцо полную однородную маскировку при данном кодировании, например, посредством генерации всех допустимых кодирований и проверки, что вместе они представляют все элементы данного кольца. Для некоторых применений может допускаться, чтобы кодирование имело некоторые промежутки. Это может иметь как следствие, что арифметические действия не могут быть выполнены на этих промежутках, по меньшей мере без использования замаскированного кодирования целочисленного списка. Конкретные примеры коммутативных колец, допускающих определенные типы кодирований, представлены ниже.
Ниже сначала дано описание приведенного в качестве примера кодирования, в котором параметры ограничены тем, что находятся в списке разрешенных разностей. Существует много типов кодирований, которые имеют то общее, что элементы кольца могут быть представлены как целочисленные списки. Эти целые числа не являются элементами кольца, например, даже если кольцо является не целочисленным кольцом, а, например, полиномиальным кольцом, то, тем не менее, элементы могут быть представлены как целочисленные списки. Используемое кодирование, каким образом данный целочисленный список отображается на элемент кольца, называется кодированием. Как правило, целочисленные списки будут всегда иметь одинаковую длину, однако это не является необходимым. Обычно, поскольку кодирование допускает больше типов целочисленных списков, например, более длинные списки, становится более вероятно, что данный элемент кольца может быть по-разному закодирован как целочисленный список.
Пусть задано коммутативное кольцо 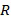 , которое имеет основной элемент кольца
, которое имеет основной элемент кольца 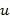 , такой что любой элемент
, такой что любой элемент  кольца
кольца 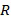 может быть записан как
может быть записан как 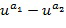 , для некоторых целых чисел
, для некоторых целых чисел 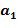 и
и 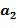 , таких что
, таких что 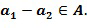 Не все коммутативные кольца могут быть закодированы таким образом, но достаточно многие из них будут полезны для кодирования. Целые числа
Не все коммутативные кольца могут быть закодированы таким образом, но достаточно многие из них будут полезны для кодирования. Целые числа 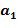 и
и 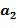 сами не являются элементами кольца R; они являются целыми числами, управляемыми по модулю порядка основного элемента. Следует отметить, что элемент кольца
сами не являются элементами кольца R; они являются целыми числами, управляемыми по модулю порядка основного элемента. Следует отметить, что элемент кольца 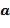 равен линейной комбинации степеней основного элемента
равен линейной комбинации степеней основного элемента  , а именно,
, а именно,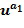 и
и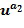 ; в этом случае линейная комбинация получается посредством умножения степеней на +1 или -1 и их суммирования, больше подробно посредством вычитания второй степени из первой степени. Вычислительное устройство воздействует на элементы кольца, закодированные упомянутым выше образом. Блоки сложения, отрицания и умножения могут воздействовать на элементы кольца при этом кодировании.
; в этом случае линейная комбинация получается посредством умножения степеней на +1 или -1 и их суммирования, больше подробно посредством вычитания второй степени из первой степени. Вычислительное устройство воздействует на элементы кольца, закодированные упомянутым выше образом. Блоки сложения, отрицания и умножения могут воздействовать на элементы кольца при этом кодировании.
Инкрементная таблица 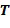 играет центральную роль и в операции сложения, и в операции умножения. Инкрементная таблица отображает входной элемент кольца, в этом случае входной элемент кольца может быть представлен как целочисленный список. Например, пусть задан входной целочисленный список
играет центральную роль и в операции сложения, и в операции умножения. Инкрементная таблица отображает входной элемент кольца, в этом случае входной элемент кольца может быть представлен как целочисленный список. Например, пусть задан входной целочисленный список  , представляющий входной элемент кольца
, представляющий входной элемент кольца 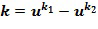 , таблица
, таблица 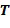 отображает его на выходной целочисленный список, например,
отображает его на выходной целочисленный список, например, 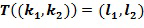 , кодирующий выходной элемент кольца
, кодирующий выходной элемент кольца 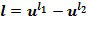 . Выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца. В этом примере инкрементный элемент может быть взят как 1, т.е., элемент кольца, который является идентичностью для умножения в кольце; в этом случае
. Выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца. В этом примере инкрементный элемент может быть взят как 1, т.е., элемент кольца, который является идентичностью для умножения в кольце; в этом случае 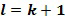 . Удобно, что таблица может быть применена непосредственно к элементам кольца, которые используют одно и то самое кодирование, и, таким образом, может быть применена к элементам кольца, имеющим представление целочисленного списка. Тем не менее, существуют варианты осуществления, в которых таблица применяется к элементам кольца в альтернативном кодировании. Альтернативное кодирование также может являться целочисленным списком, но альтернативного типа. Также инкрементный элемент кольца не обязательно должен быть равен 1.
. Удобно, что таблица может быть применена непосредственно к элементам кольца, которые используют одно и то самое кодирование, и, таким образом, может быть применена к элементам кольца, имеющим представление целочисленного списка. Тем не менее, существуют варианты осуществления, в которых таблица применяется к элементам кольца в альтернативном кодировании. Альтернативное кодирование также может являться целочисленным списком, но альтернативного типа. Также инкрементный элемент кольца не обязательно должен быть равен 1.
Ниже описаны операции отрицания, сложения и умножения.
Отрицание. Пусть задан входной для отрицания целочисленный список  , представляющий входной для отрицания элемент кольца
, представляющий входной для отрицания элемент кольца  , выходной для отрицания целочисленный список может быть получен посредством перестановки целочисленного списка, в этом случае посредством изменения порядка на обратный. Выходной для отрицания целочисленный список может представлять собой
, выходной для отрицания целочисленный список может быть получен посредством перестановки целочисленного списка, в этом случае посредством изменения порядка на обратный. Выходной для отрицания целочисленный список может представлять собой 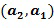 . Отрицание посредством перестановки, чтобы
. Отрицание посредством перестановки, чтобы 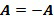 . В предположении, что существует такое
. В предположении, что существует такое 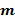 , что
, что 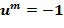 , и имеет место для многих колец R, отрицание в качестве альтернативы может быть получено посредством добавления константы, например,
, и имеет место для многих колец R, отрицание в качестве альтернативы может быть получено посредством добавления константы, например, 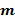 , к каждому целому числу целочисленного списка. В последнем случае выходной для отрицания целочисленный список может представлять собой
, к каждому целому числу целочисленного списка. В последнем случае выходной для отрицания целочисленный список может представлять собой  . Это работает, поскольку
. Это работает, поскольку  . Арифметические действия в целочисленном списке предпочтительно выполняются по модулю порядка основного элемента. При этом целое число из целочисленных списков соответствует экспоненте основного элемента, таким образом, целые числа, которые являются одинаковыми по модулю порядка основного элемента, кодируют один и тот же элемент кольца. В любом случае отрицание может быть выполнено посредством таблицы отрицания, которая отображает первый целочисленный список, представляющий первый элемент кольца, на второй целочисленный список, представляющий минус первый элемент кольца. Когда для отрицания используется таблица, не требуется какого-либо фиксированного отношения между параметрами, описывающими элемент кольца, и параметрами, описывающими минус элемент кольца.
. Арифметические действия в целочисленном списке предпочтительно выполняются по модулю порядка основного элемента. При этом целое число из целочисленных списков соответствует экспоненте основного элемента, таким образом, целые числа, которые являются одинаковыми по модулю порядка основного элемента, кодируют один и тот же элемент кольца. В любом случае отрицание может быть выполнено посредством таблицы отрицания, которая отображает первый целочисленный список, представляющий первый элемент кольца, на второй целочисленный список, представляющий минус первый элемент кольца. Когда для отрицания используется таблица, не требуется какого-либо фиксированного отношения между параметрами, описывающими элемент кольца, и параметрами, описывающими минус элемент кольца.
Сложение. Чтобы добавить принятый первый входной для сложения целочисленный список  , кодирующий первый входной для сложения элемент кольца
, кодирующий первый входной для сложения элемент кольца  , и второй входной для сложения целочисленный список
, и второй входной для сложения целочисленный список 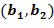 , кодирующий второй входной для сложения элемент кольца
, кодирующий второй входной для сложения элемент кольца 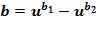 , сначала определяется целочисленный список промежуточного сложения (
, сначала определяется целочисленный список промежуточного сложения (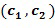 ), кодирующий элемент кольца промежуточного сложения
), кодирующий элемент кольца промежуточного сложения 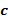 .
.
Элемент кольца 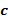 может представлять собой первый входной для сложения элемент кольца
может представлять собой первый входной для сложения элемент кольца 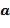 плюс основной элемент
плюс основной элемент  в степени, определенной из второго входного для сложения целочисленного списка, в частности, первым целым числом из второго входного для сложения целочисленного списка. В этом примере мы можем иметь
в степени, определенной из второго входного для сложения целочисленного списка, в частности, первым целым числом из второго входного для сложения целочисленного списка. В этом примере мы можем иметь 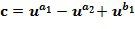 . Чтобы вычислить последний, мы замечаем, что
. Чтобы вычислить последний, мы замечаем, что  . Член в скобках может быть переписан в кодировании с использованием инкрементной таблицы. Следует отметить, что целочисленный список
. Член в скобках может быть переписан в кодировании с использованием инкрементной таблицы. Следует отметить, что целочисленный список 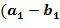 ,
,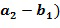 по-прежнему удовлетворяет требованию ограниченных разностей, если удовлетворяет список
по-прежнему удовлетворяет требованию ограниченных разностей, если удовлетворяет список 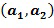 .
.
Через первое применение инкрементной таблицы к элементу кольца 
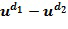
 получается элемент
получается элемент 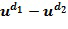 =
= +1. Например, посредством
+1. Например, посредством 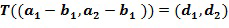 . Тогда мы имеем, что
. Тогда мы имеем, что 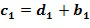 и
и 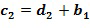 , тем самым определяя, что целочисленный список промежуточного сложения (
, тем самым определяя, что целочисленный список промежуточного сложения (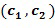 ) может далее содержать добавление целого числа, определенного из вторых входных для сложения целочисленных списков, к целым числам в целочисленном списке, полученным в результате из первого применения. Добавление
) может далее содержать добавление целого числа, определенного из вторых входных для сложения целочисленных списков, к целым числам в целочисленном списке, полученным в результате из первого применения. Добавление 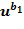 к элементу кольца в представлении целочисленного списка, в этом случае к
к элементу кольца в представлении целочисленного списка, в этом случае к 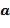 , иногда упоминается как этап положительного сокращения.
, иногда упоминается как этап положительного сокращения.
Таким образом, блок сложения получил элемент кольца промежуточного сложения  как целочисленный список
как целочисленный список  . Элемент кольца промежуточного сложения, таким образом, является линейной комбинацией степеней одного или более основных элементов, причем степени определяются из первого и второго входных для сложения целочисленных списков. В этом случае инкрементная таблица применяется к элементу кольца
. Элемент кольца промежуточного сложения, таким образом, является линейной комбинацией степеней одного или более основных элементов, причем степени определяются из первого и второго входных для сложения целочисленных списков. В этом случае инкрементная таблица применяется к элементу кольца  , сформированному посредством основного элемента кольца (
, сформированному посредством основного элемента кольца ( ), возведенного в степень первого целого числа из первого целочисленного списка (
), возведенного в степень первого целого числа из первого целочисленного списка (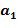 ) минус первое целое число из второго целочисленного списка (
) минус первое целое число из второго целочисленного списка (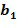 ), минус основной элемент кольца (
), минус основной элемент кольца ( ), возведенный в степень второго целого числа из первого целочисленного списка (
), возведенный в степень второго целого числа из первого целочисленного списка (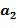 ) минус первое целое число из второго целочисленного списка (
) минус первое целое число из второго целочисленного списка (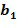 ).
).
В этом примере выходной для сложения целочисленный список может быть определен через второе применение инкрементной таблицы к элементам кольца, определенным из целочисленного списка промежуточного умножения и второго входного для сложения целочисленного списка. Это может содержать вычисление суммы элемента кольца промежуточного сложения 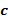 и минус основного элемента, возведенного в степень, определенную из второго входного для сложения целочисленного списка, например, второго целого числа из второго входного для сложения целочисленного списка
и минус основного элемента, возведенного в степень, определенную из второго входного для сложения целочисленного списка, например, второго целого числа из второго входного для сложения целочисленного списка 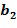 :
: 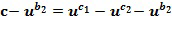 . Это может быть достигнуто посредством отрицания элемента кольца промежуточного сложения, представленного целочисленным списком промежуточного сложения, перед вторым применением инкрементной таблицы. Отрицание
. Это может быть достигнуто посредством отрицания элемента кольца промежуточного сложения, представленного целочисленным списком промежуточного сложения, перед вторым применением инкрементной таблицы. Отрицание 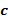 может быть выполнено, как указано выше. В качестве примера мы используем перестановку, но такая же операция может быть выполнена посредством добавления константы к экспоненте. После отрицания сумма может использовать плюс (вместо минуса) основной элемент, возведенный в степень, определенную из второго входного для сложения целочисленного списка:
может быть выполнено, как указано выше. В качестве примера мы используем перестановку, но такая же операция может быть выполнена посредством добавления константы к экспоненте. После отрицания сумма может использовать плюс (вместо минуса) основной элемент, возведенный в степень, определенную из второго входного для сложения целочисленного списка: 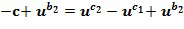 . Последняя операция имеет такой же тип, как выше, и может быть выполнена через применение таблицы таким же образом, как добавление
. Последняя операция имеет такой же тип, как выше, и может быть выполнена через применение таблицы таким же образом, как добавление 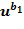 . После этого результат снова подвергается отрицанию. Полное сложение может использовать два отрицания и два применения одной и той же инкрементной таблицы
. После этого результат снова подвергается отрицанию. Полное сложение может использовать два отрицания и два применения одной и той же инкрементной таблицы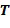 .
.
Вычитание 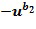 из элемента кольца в представлении целочисленного списка, в этом случае из
из элемента кольца в представлении целочисленного списка, в этом случае из 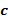 , иногда упоминается как этап отрицательного сокращения. Этап отрицательного сокращения может быть выполнен посредством отрицания, выполнения этапа положительного сокращения и снова отрицания.
, иногда упоминается как этап отрицательного сокращения. Этап отрицательного сокращения может быть выполнен посредством отрицания, выполнения этапа положительного сокращения и снова отрицания.
Посредством индексирования инкрементной таблицы через первый параметр 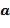 и разность
и разность 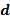 , например, посредством представления элемента кольца
, например, посредством представления элемента кольца 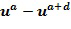 , достигается сокращение времени вычисления. В этом случае инкрементная таблица может быть индексирована посредством
, достигается сокращение времени вычисления. В этом случае инкрементная таблица может быть индексирована посредством  . Рассмотрим этап положительного сокращения для добавления
. Рассмотрим этап положительного сокращения для добавления 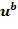 . Он может быть сделан посредством
. Он может быть сделан посредством , в этом случае таблица индексирована как
, в этом случае таблица индексирована как 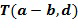 . Таким образом, требуется только одна операция вычитания по модулю k.
. Таким образом, требуется только одна операция вычитания по модулю k.
Умножение. Чтобы умножить принятый первый входной для умножения целочисленный список  , кодирующий первый входной для умножения элемент кольца
, кодирующий первый входной для умножения элемент кольца 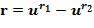 , и второй входной для умножения целочисленный список (
, и второй входной для умножения целочисленный список (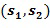 ), кодирующий второй входной для умножения элемента кольца
), кодирующий второй входной для умножения элемента кольца 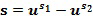 , определяются первый целочисленный список промежуточного умножения
, определяются первый целочисленный список промежуточного умножения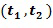 и второй целочисленный список промежуточного умножения
и второй целочисленный список промежуточного умножения . Выходной для умножения целочисленный список, кодирующий выходной для умножения элемент кольца, определяется из первого и второго промежуточных элементов. В других вариантах осуществления может иметься более двух целочисленных списков промежуточного умножения. У имеем, что
. Выходной для умножения целочисленный список, кодирующий выходной для умножения элемент кольца, определяется из первого и второго промежуточных элементов. В других вариантах осуществления может иметься более двух целочисленных списков промежуточного умножения. У имеем, что  Разбиение членов в развернутых произведениях на два члена t и u могут быть сделаны по-разному, например, как
Разбиение членов в развернутых произведениях на два члена t и u могут быть сделаны по-разному, например, как 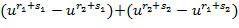 .
.
Таким образом, чтобы умножить два элемента кольца, представленные как целочисленные списки, они могут быть преобразованы в два новых целочисленных списка, которые могут быть сложены, чтобы получить ответ для умножения. Сложение может быть выполнено, как описано выше. Например, блок умножения может вычислить промежуточные целочисленные списки и отправить их блоку умножения.
Например, первое целое число 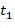 из первого целочисленного списка промежуточного умножения может содержать первое целое число
из первого целочисленного списка промежуточного умножения может содержать первое целое число 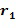 из первого входного для умножения целочисленного списка плюс первое целое число
из первого входного для умножения целочисленного списка плюс первое целое число 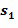 из второго входного для умножения целочисленного списка, и второе целое число
из второго входного для умножения целочисленного списка, и второе целое число 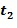 из первого целочисленного списка промежуточного умножения может содержать первое целое число
из первого целочисленного списка промежуточного умножения может содержать первое целое число 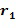 из первого входного для умножения целочисленного списка плюс второе целое число
из первого входного для умножения целочисленного списка плюс второе целое число 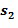 из второго входного для умножения целочисленного списка
из второго входного для умножения целочисленного списка 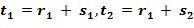 ; первое целое число
; первое целое число 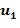 из второго целочисленного списка промежуточного умножения может содержать второе целое число
из второго целочисленного списка промежуточного умножения может содержать второе целое число 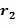 из первого входного для умножения целочисленного списка плюс второе целое число
из первого входного для умножения целочисленного списка плюс второе целое число  из второго входного для умножения целочисленного списка, и второе целое число
из второго входного для умножения целочисленного списка, и второе целое число 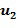 из второго целочисленного списка промежуточного умножения может содержать второе целое число
из второго целочисленного списка промежуточного умножения может содержать второе целое число 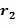 из первого входного для умножения целочисленного списка плюс первое целое число
из первого входного для умножения целочисленного списка плюс первое целое число 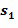 из второго входного для умножения целочисленного списка
из второго входного для умножения целочисленного списка 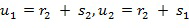 ,
,
В варианте осуществления, например, в только что раскрытом примере, арифметические действия выполняются над целочисленными списками, элементы кольца не обязательно должны вычисляться как элементы кольца в некотором естественном представлении. Теперь поясняются несколько вариаций. Несколько вариаций являются независимыми, например, различное кодирование может быть объединено с вариацией для выполнения сложения.
Через замаскированные арифметические действия, когда вычисления выполняются в целочисленном списке, соответствующем, например, 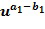 , и т.д., значение может быть сокращено по модулю порядка u. Например, если порядок
, и т.д., значение может быть сокращено по модулю порядка u. Например, если порядок  равен 30, все вычисления могут выполняться по модулю 30 (mod 30).
равен 30, все вычисления могут выполняться по модулю 30 (mod 30).
Инкрементное значение. Инкрементное значение не обязательно должно быть равно 1. Существует по меньшей мере два способа использовать другое инкрементное значение. Во-первых, уравнение  может быть модифицировано в
может быть модифицировано в 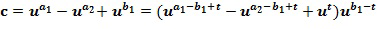 . Это означает, что может быть построена инкрементная таблица, которая добавляет значение
. Это означает, что может быть построена инкрементная таблица, которая добавляет значение 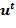 . Эта инкрементная таблица применяется к тем же самым целочисленным спискам, кроме того, что добавляется целое число
. Эта инкрементная таблица применяется к тем же самым целочисленным спискам, кроме того, что добавляется целое число 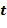 . После первого применения инкрементной таблицы вместо
. После первого применения инкрементной таблицы вместо 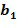 добавляется число
добавляется число 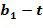 .
.
Другой способ изменить инкрементное значение состоит в том, чтобы взять такие два элемента 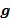 и
и 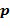 кольца R, чтобы повторное добавление
кольца R, чтобы повторное добавление 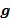 в кольце давало
в кольце давало 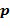 . Например, имеется такое целое число
. Например, имеется такое целое число 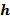 , что
, что 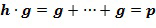 . Предположим, что существует инкрементная таблица
. Предположим, что существует инкрементная таблица 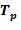 с инкрементным значением
с инкрементным значением 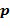 , например,
, например,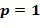 или
или 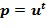 . Инкрементная таблица
. Инкрементная таблица 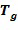 может быть построена для
может быть построена для 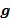 как инкрементного значения. Таблица
как инкрементного значения. Таблица 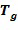 может быть применена
может быть применена 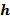 раз, чтобы получить тот же самый эффект, как и применение
раз, чтобы получить тот же самый эффект, как и применение  непосредственно. Использование разных инкрементных таблиц с различными инкрементными значениями даже может быть объединено в единственном варианте осуществления, например, для увеличения маскировки. Последнее построение имеет преимущество в том, что несколько инкрементных значений могут быть объединены без изменения последующего вычисления сложения.
непосредственно. Использование разных инкрементных таблиц с различными инкрементными значениями даже может быть объединено в единственном варианте осуществления, например, для увеличения маскировки. Последнее построение имеет преимущество в том, что несколько инкрементных значений могут быть объединены без изменения последующего вычисления сложения.
Принципы, проиллюстрированные для иллюстративного кодирования, могут быть применены к нескольким альтернативным кодированиям. Первое альтернативное кодирование состоит в кодировании элемента кольца 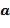 как целочисленного списка
как целочисленного списка  с использованием кодирования
с использованием кодирования  , с прежним требованием, что
, с прежним требованием, что 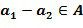 . Кольцо, которое имеет основной элемент кольца
. Кольцо, которое имеет основной элемент кольца  , такой что любой элемент кольца может быть закодирован таким образом, как говорят, допускает положительную замаскированную арифметику. Иллюстративное кодирование будет упоминаться как отрицательная замаскированная арифметика. Можно доказать математически, что для любого кольца, которое допускает положительную замаскированную арифметику с основным элементом кольца
, такой что любой элемент кольца может быть закодирован таким образом, как говорят, допускает положительную замаскированную арифметику. Иллюстративное кодирование будет упоминаться как отрицательная замаскированная арифметика. Можно доказать математически, что для любого кольца, которое допускает положительную замаскированную арифметику с основным элементом кольца  , существует такое целое число
, существует такое целое число 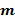 , что
, что 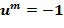 . Кроме того, кольцо, которое допускает отрицательную замаскированную арифметику, допускает положительную замаскированную арифметику, если и только если существует такое значение
. Кроме того, кольцо, которое допускает отрицательную замаскированную арифметику, допускает положительную замаскированную арифметику, если и только если существует такое значение 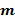 . Любое кольцо, которое допускает положительную замаскированную арифметику, также допускает отрицательную замаскированную арифметику, хотя обратное не верно.
. Любое кольцо, которое допускает положительную замаскированную арифметику, также допускает отрицательную замаскированную арифметику, хотя обратное не верно.
Положительная замаскированная арифметика в основном повторяет отрицательную замаскированную арифметику, описанную в общих чертах выше. Вкратце, изменение знака целочисленного списка может быть выполнено посредством добавления значения 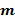 ко всем целым числам в целочисленном списке. Пусть заданы входные для сложения данные
ко всем целым числам в целочисленном списке. Пусть заданы входные для сложения данные  и
и 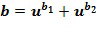 , сложение может быть выполнено посредством вычисления промежуточного
, сложение может быть выполнено посредством вычисления промежуточного 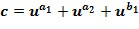 , например, через
, например, через 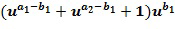 . Инкрементная таблица применяется к
. Инкрементная таблица применяется к 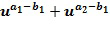 с инкрементным значением 1. В предположении, что целочисленный список
с инкрементным значением 1. В предположении, что целочисленный список  удовлетворяет требованию, это последнее число также удовлетворяет.
удовлетворяет требованию, это последнее число также удовлетворяет.
Положительное сокращение может быть применено дважды, и для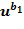 , и бля
, и бля 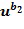 , никакое отрицательное сокращение не требуется. Это упрощает сложение. Построение инкрементной таблицы может быть различным, как указано выше, посредством разложения по разным степеням u. Инкрементное значение может быть различным, как указано выше. Положительная замаскированная арифметика имеет преимущество в том, что инкрементная таблица всегда симметрична и может быть сохранена в сжатой форме. Недостаток положительной маскировки состоит в том, что меньше колец допускают этот тип кодирования.
, никакое отрицательное сокращение не требуется. Это упрощает сложение. Построение инкрементной таблицы может быть различным, как указано выше, посредством разложения по разным степеням u. Инкрементное значение может быть различным, как указано выше. Положительная замаскированная арифметика имеет преимущество в том, что инкрементная таблица всегда симметрична и может быть сохранена в сжатой форме. Недостаток положительной маскировки состоит в том, что меньше колец допускают этот тип кодирования.
Представленные кодирования могут быть факультативно умножены на постоянный элемент кольца 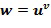 для некоторых
для некоторых 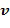 . Тем самым целочисленный список
. Тем самым целочисленный список  может представлять элемент кольца
может представлять элемент кольца 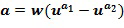 . Этап отрицания не изменяется. Этап положительного сокращения становится
. Этап отрицания не изменяется. Этап положительного сокращения становится  . Инкрементная таблица может использовать в качестве инкрементного значения
. Инкрементная таблица может использовать в качестве инкрементного значения 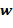 и применяется к
и применяется к 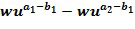 , и это имеет такой же тип кодировки. Этап отрицательного сокращения может быть получен из этапа положительного сокращения, как указано выше. Умножение может перемножить
, и это имеет такой же тип кодировки. Этап отрицательного сокращения может быть получен из этапа положительного сокращения, как указано выше. Умножение может перемножить 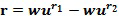 и
и 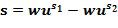 , представленные как целочисленные списки
, представленные как целочисленные списки 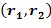 и целочисленные списки
и целочисленные списки 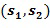 , с использованием
, с использованием 
Количество целых чисел в целочисленном списке. В поясняемом примере количество элементов в целочисленном списке всегда равнялось двум. Это количество имеет преимущества, т.е., оно сокращает количество этапов вычисления. С другой стороны, допущение большего количества элементов в целочисленном списке увеличивает количество колец, которые допускают маскировку. Приведенный ниже пример рассматривает три целых числа на список, но возможно большее количество, и это действует аналогично.
Рассмотрим первый целочисленный список  и второй целочисленный список
и второй целочисленный список 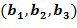 , кодирующие элементы
, кодирующие элементы 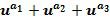 и
и 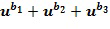 соответственно. Может быть выполнено отрицание посредством добавления константы
соответственно. Может быть выполнено отрицание посредством добавления константы 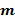 к целым числам в списке. Сложение может быть выполнено посредством применения инкрементной таблицы для каждого целого числа во втором целочисленном списке, в этом случае три раза. Первый целочисленный список промежуточного сложения может быть вычислен из
к целым числам в списке. Сложение может быть выполнено посредством применения инкрементной таблицы для каждого целого числа во втором целочисленном списке, в этом случае три раза. Первый целочисленный список промежуточного сложения может быть вычислен из  . В этом случае инкрементное значение равно 1, и инкрементная таблица применяется к
. В этом случае инкрементное значение равно 1, и инкрементная таблица применяется к 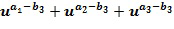 . Для умножения делается такое же количество целочисленных списков промежуточного умножения, как во втором целочисленном списке, например:
. Для умножения делается такое же количество целочисленных списков промежуточного умножения, как во втором целочисленном списке, например: 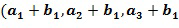 ),
), 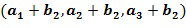 ,
,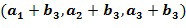 .
.
Если целочисленный список  удовлетворяет тому, что два конкретных числа из списка имеют разность в списке разрешенных разностей, например,
удовлетворяет тому, что два конкретных числа из списка имеют разность в списке разрешенных разностей, например, 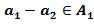 , то
, то 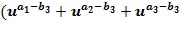 ) также удовлетворяет, поскольку
) также удовлетворяет, поскольку  . Для целочисленного списка с длиной больше 2 можно также ввести дополнительное ограничение, например, что еще одно первое целое число из целочисленного списка и еще одно второе целое число из целочисленного списка содержатся в еще одном списке разрешенных разностей, например, дополнительное ограничение, что
. Для целочисленного списка с длиной больше 2 можно также ввести дополнительное ограничение, например, что еще одно первое целое число из целочисленного списка и еще одно второе целое число из целочисленного списка содержатся в еще одном списке разрешенных разностей, например, дополнительное ограничение, что 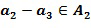 . Может быть, что
. Может быть, что 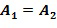 .
.
Ниже приведены примеры для колец, допускающих отрицательную и/или положительную маскировку, и того, как найти список разрешенных разностей. Кольцо R может являться целочисленным кольцом 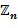 для модуля
для модуля 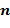 . Кольцо R также являться полиномиальным кольцом
. Кольцо R также являться полиномиальным кольцом 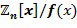 для некоторого модуля
для некоторого модуля 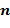 и полинома сведения
и полинома сведения 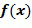 .
.
Пусть 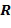 - кольцом с маскируемой арифметикой и основным элементом
- кольцом с маскируемой арифметикой и основным элементом  , и пусть
, и пусть  . Два элемента
. Два элемента 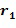 и
и 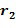 , оба в
, оба в 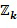 , будут называться эквивалентными, если
, будут называться эквивалентными, если
существует такое 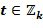 , что
, что 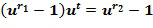 . Следует отметить, что это условие подразумевает, что
. Следует отметить, что это условие подразумевает, что 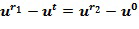 . Неформально можно сказать, что два целых числа эквивалентны при том условии, что добавление одного из них к списку разрешенных разностей дает такой же эффект, как добавление другого. Например, возьмем
. Неформально можно сказать, что два целых числа эквивалентны при том условии, что добавление одного из них к списку разрешенных разностей дает такой же эффект, как добавление другого. Например, возьмем 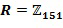 , основной элемент
, основной элемент 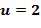 , имеющий порядок
, имеющий порядок 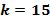 . Элементы 2 и 8 эквивалентны, поскольку
. Элементы 2 и 8 эквивалентны, поскольку 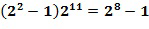 . Аналогичным образом, элементы 4 и 10 эквивалентны, поскольку
. Аналогичным образом, элементы 4 и 10 эквивалентны, поскольку 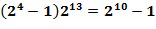 .
.
Можно доказать математически, что если 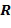 является таким кольцом, что
является таким кольцом, что 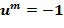 , то
, то 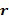 и
и 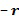 всегда эквивалентны.
всегда эквивалентны.
Это отношение эквивалентности порождает классы эквивалентности на 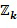 , например, множества, в которых все элементы эквивалентны друг другу. Список разрешенных разностей теперь может быть определен посредством выбора одинакового количества элементов каждого класса эквивалентности, кроме класса эквивалентности, содержащего 0. Элемент 0 также будет включен в множество разрешенных разностей, если будет необходимо представить элемент кольца 0. Этот способ конфигурации электронного вычислительного устройства (100) для выполнения замаскированных арифметических действий в коммутативном кольце может быть исполнен посредством электронного устройства конфигурации, например, содержащего микропроцессор и программное обеспечение для исполнения программного обеспечения.
, например, множества, в которых все элементы эквивалентны друг другу. Список разрешенных разностей теперь может быть определен посредством выбора одинакового количества элементов каждого класса эквивалентности, кроме класса эквивалентности, содержащего 0. Элемент 0 также будет включен в множество разрешенных разностей, если будет необходимо представить элемент кольца 0. Этот способ конфигурации электронного вычислительного устройства (100) для выполнения замаскированных арифметических действий в коммутативном кольце может быть исполнен посредством электронного устройства конфигурации, например, содержащего микропроцессор и программное обеспечение для исполнения программного обеспечения.
Мы предоставляем следующие примеры:
Пусть  , поле с 256 элементами, сгенерированными как
, поле с 256 элементами, сгенерированными как 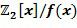 , где
, где 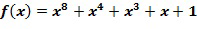 , и с основным элементом кольца
, и с основным элементом кольца 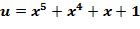 , имеющим порядок 51, и который является основным элементом для замаскированной арифметики в поле
, имеющим порядок 51, и который является основным элементом для замаскированной арифметики в поле 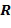 . Следует отметить, что поскольку R имеет характеристику 2, положительная и отрицательная маскировка являются одним и тем же. Классы эквивалентности:
. Следует отметить, что поскольку R имеет характеристику 2, положительная и отрицательная маскировка являются одним и тем же. Классы эквивалентности:
[0]
[1; 3; 11; 16; 21; 23; 28; 30; 35; 40; 48; 50]
[2; 5; 6; 9; 19; 22; 29; 32; 42; 45; 46; 49]
[4; 7; 10; 12; 13; 18; 33; 38; 39; 41; 44; 47]
[8; 14; 15; 20; 24; 25; 26; 27; 31; 36; 37; 43]
[17; 34]
Множество разрешенных разностей может быть получено посредством выбора по меньшей мере одного элемента из каждого класса, например, A={0, 1, 2, 4, 8, 17}.
Пусть 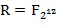 , поле с
, поле с 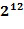 элементами, сгенерированными как
элементами, сгенерированными как 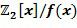 , где
, где 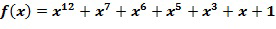 , и с основным элементом кольца
, и с основным элементом кольца  , имеющим порядок 195, и который является основным элементом для замаскированной арифметики в поле
, имеющим порядок 195, и который является основным элементом для замаскированной арифметики в поле 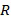 . Классы эквивалентности:
. Классы эквивалентности:
[0]
[13; 26; 39; 52; 65; 78; 91; 104; 117; 130; 143; 156; 169; 182]
[1; 8; 64; 73; 84; 87; 108; 111; 122; 131; 187; 194]
[2; 16; 21; 27; 49; 67; 128; 146; 168; 174; 179; 193]
[4; 32; 42; 54; 61; 97; 98; 134; 141; 153; 163; 191]
[3; 47; 72; 83; 112; 123; 148; 192]
[6; 29; 51; 94; 101; 144; 166; 189]
[7; 12; 58; 93; 102; 137; 183; 188]
[9; 14; 24; 79; 116; 171; 181; 186]
[18; 28; 37; 48; 147; 158; 167; 177]
[36; 56; 74; 96; 99; 121; 139; 159]
[5; 25; 40; 70; 125; 155; 170; 190]
[10; 50; 55; 80; 115; 140; 145; 185]
[20; 35; 85; 95; 100; 110; 160; 175]
[11; 69; 76; 90; 105; 119; 126; 184]
[15; 22; 43; 57; 138; 152; 173; 180]
[30; 44; 81; 86; 109; 114; 151; 165]
[23; 33; 60; 88; 107; 135; 162; 172]
[19; 46; 66; 75; 120; 129; 149; 176]
[38; 45; 63; 92; 103; 132; 150; 157]
[17; 53; 62; 68; 77; 82; 113; 118; 127; 133; 142; 178]
[31; 34; 41; 59; 71; 89; 106; 124; 136; 154; 161; 164]
Снова множество разрешенных разностей может быть получено посредством выбора по меньшей мере одного элемента из каждого класса эквивалентности. Выбор может быть случайным.
Пусть 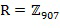 с основным элементом кольца
с основным элементом кольца 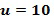 , имеющим порядок 151, и которое является основным элементом для замаскированной арифметики в поле
, имеющим порядок 151, и которое является основным элементом для замаскированной арифметики в поле 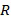 . Семь классов эквивалентности:
. Семь классов эквивалентности:
[0]
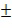 [1; 3; 8; 16; 18; 30; 31; 32; 33; 43; 53; 56; 62; 75; 78; 79; 101; 102; 113; 116; 124; 126; 128; 140; 149]
[1; 3; 8; 16; 18; 30; 31; 32; 33; 43; 53; 56; 62; 75; 78; 79; 101; 102; 113; 116; 124; 126; 128; 140; 149]
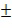 [4; 9; 12; 15; 28; 44; 45; 47; 55; 57; 66; 67; 69; 71; 81; 83; 92; 99; 112; 114; 115; 127; 137; 138]
[4; 9; 12; 15; 28; 44; 45; 47; 55; 57; 66; 67; 69; 71; 81; 83; 92; 99; 112; 114; 115; 127; 137; 138]
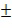 [5; 6; 7; 21; 26; 29; 34; 40; 41; 51; 54; 61; 63; 64; 74; 86; 91; 93; 103; 105; 109; 129; 131; 132; 134; 141]
[5; 6; 7; 21; 26; 29; 34; 40; 41; 51; 54; 61; 63; 64; 74; 86; 91; 93; 103; 105; 109; 129; 131; 132; 134; 141]
Следует отметить, что классы эквивалентности имеют симметрию, которая используется для обозначения классов в сокращенной форме.
Пусть  с основным элементом кольца
с основным элементом кольца 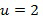 , имеющим порядок 100. Следует отметить, что это кольцо не является полем. 17 классов эквивалентности:
, имеющим порядок 100. Следует отметить, что это кольцо не является полем. 17 классов эквивалентности:
[0]
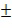 [1; 23; 25; 27; 42; 49; 94]
[1; 23; 25; 27; 42; 49; 94]
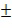 [2; 34; 54; 55; 57; 67; 74; 83; 93; 95]
[2; 34; 54; 55; 57; 67; 74; 83; 93; 95]
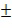 [3; 11; 39; 47; 82; 90]
[3; 11; 39; 47; 82; 90]
[4; 16; 24; 48; 52; 76; 84; 96]
[8; 44; 56; 92]
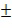 [9; 19; 31; 38; 41; 70; 78]
[9; 19; 31; 38; 41; 70; 78]
[12; 20; 28; 72; 80; 88]
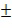 [13; 14; 21; 29; 37; 65; 85]
[13; 14; 21; 29; 37; 65; 85]
[32; 40; 60; 68]
[36; 64]
[50]
Можно доказать, что в поле, для заданного  мы имеем, что
мы имеем, что 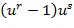 является разным для всех значений
является разным для всех значений  . Таким образом, каждый класс может представлять точно
. Таким образом, каждый класс может представлять точно 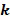 элементов. Таким образом, мы имеем формулу
элементов. Таким образом, мы имеем формулу 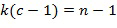 для полей. Числовые эксперименты показывают, что для коммутативных колец, которые не являются полями, отношение
для полей. Числовые эксперименты показывают, что для коммутативных колец, которые не являются полями, отношение 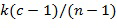 является близким к 1, особенно по мере роста
является близким к 1, особенно по мере роста 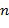 .
.
Это также подразумевает, что если задано поле, и список разрешенных разностей, который был получен посредством выбора точно одного элемента из каждого класса эквивалентности, и целочисленные списки длины 2, это дает уникальное представление каждого элемента поля. Посредством выбора большего количества элементов из каждого класса эквивалентности элементы кольца получают множественные представления.
Ниже обобщены несколько примеров и даны дополнительные примеры. Для полиномиальных колец подробные сведения об основном элементе кольца и генераторе даны выше. Следует отметить, что 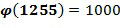 (функция сумм Эйлера), поэтому кольцо
(функция сумм Эйлера), поэтому кольцо  имеет только 1000 элементов.
имеет только 1000 элементов.
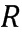
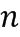
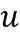
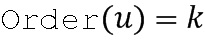
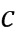
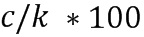
Также, как можно заметить из приведенной выше таблицы, кольца с разными размерами списка разрешенных разностей могут быть получены посредством генерации колец с маскирующей арифметикой и вычисления классов эквивалентности.
Наличие меньших списков разрешенных разностей имеет преимущество в том, что это сокращает размер инкрементной таблицы. В варианте осуществления инкрементная таблица не отображает входной элемент кольца, представленный входным целочисленным списком как линейная комбинация степеней (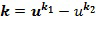 ) основного элемента кольца (
) основного элемента кольца ( ), если степени не имеют экспонент, которые удовлетворяют требованию ограниченных разностей, например, определенных целочисленным списком, для которого разность в списке разрешенных разностей (
), если степени не имеют экспонент, которые удовлетворяют требованию ограниченных разностей, например, определенных целочисленным списком, для которого разность в списке разрешенных разностей (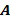 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (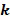 ).
).
Посредством поиска большего количества колец размер списка разрешенных разностей может быть выбран малым относительно порядка 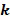 . Список разрешенных разностей может быть сокращен в размере посредством выбора только одного элемента из каждого класса эквивалентности; список разрешенных разностей может быть расширен в размере посредством выбора более одного элемента каждого класса эквивалентности. Предпочтительно, если размер списка разрешенных разностей составляет менее 50% порядка, более предпочтительно менее 20% порядка, еще более предпочтительно менее 10% порядка, еще более предпочтительно менее 5% порядка. В случае уникального представления в полях желательно, чтобы
. Список разрешенных разностей может быть сокращен в размере посредством выбора только одного элемента из каждого класса эквивалентности; список разрешенных разностей может быть расширен в размере посредством выбора более одного элемента каждого класса эквивалентности. Предпочтительно, если размер списка разрешенных разностей составляет менее 50% порядка, более предпочтительно менее 20% порядка, еще более предпочтительно менее 10% порядка, еще более предпочтительно менее 5% порядка. В случае уникального представления в полях желательно, чтобы 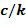 было меньше 0,5, 0,2, 0,1 и 0,05.
было меньше 0,5, 0,2, 0,1 и 0,05.
Посредством выбора только одного элемента каждого класса эквивалентности получается, что (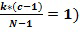 , это обеспечивает большее сокращение для таблицы. (Здесь c представляет количество элементов в списке разрешенных разностей.) Для колец, которые не являются полями, значение быть несколько больше 1, например, меньше 2. В последнем случае представление иногда является уникальным, но не всегда. С другой стороны, может быть желательно иметь несколько разных представлений для элементов кольца. Это может быть достигнуто посредством увеличения списка разрешенных разностей таким образом, чтобы (
, это обеспечивает большее сокращение для таблицы. (Здесь c представляет количество элементов в списке разрешенных разностей.) Для колец, которые не являются полями, значение быть несколько больше 1, например, меньше 2. В последнем случае представление иногда является уникальным, но не всегда. С другой стороны, может быть желательно иметь несколько разных представлений для элементов кольца. Это может быть достигнуто посредством увеличения списка разрешенных разностей таким образом, чтобы (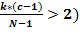 .
.
Фиг. 4 схематично показывает пример варианта осуществления способа 300 вычислений для выполнения замаскированных арифметических действий в коммутативном кольце (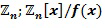 ), кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, способ вычислений обрабатывает целочисленные списки (
), кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, способ вычислений обрабатывает целочисленные списки ( ), кодирующие элементы кольца (
), кодирующие элементы кольца (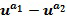 ), целочисленные списки содержат по меньшей мере два целых числа, причем целочисленный список (
), целочисленные списки содержат по меньшей мере два целых числа, причем целочисленный список ( ) кодирует элемент кольца (
) кодирует элемент кольца (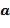 ) таким образом, что элемент кольца равен линейной комбинации степеней (
) таким образом, что элемент кольца равен линейной комбинации степеней ( ;
; 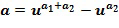 ;
;  ) основного элемента кольца (
) основного элемента кольца ( ), основной элемент кольца имеет порядок (
), основной элемент кольца имеет порядок (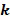 ) в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
) в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (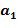 ) и второй экспонентой (
) и второй экспонентой (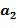 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (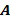 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (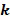 ). Способ вычислений содержит
). Способ вычислений содержит
- сохранение 305 инкрементной таблицы (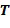 ), заданной для инкрементного элемента кольца (1;
), заданной для инкрементного элемента кольца (1;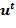 ), инкрементная таблица отображает входной элемент кольца (
), инкрементная таблица отображает входной элемент кольца (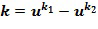 ) на выходной целочисленный список (
) на выходной целочисленный список (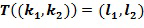 ), кодирующий выходной элемент кольца (
), кодирующий выходной элемент кольца (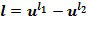 ) таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца (
) таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца (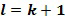 ), выходной элемент кольца равен линейной комбинации степеней основного элемента кольца (
), выходной элемент кольца равен линейной комбинации степеней основного элемента кольца ( ), причем степени имеют экспоненты, определенные посредством выходного целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенные посредством выходного целочисленного списка, разность между первой экспонентой (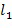 ) и второй экспонентой (
) и второй экспонентой (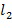 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (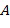 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (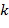 ).
).
Способ дополнительно может содержать сложение в кольце:
- прием 310 первого входного для сложения целочисленного списка (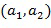 ), кодирующего первый входной для сложения элемент кольца, и второго входного для сложения целочисленного списка (
), кодирующего первый входной для сложения элемент кольца, и второго входного для сложения целочисленного списка (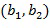 ), кодирующего второй входного для сложения элемент кольца,
), кодирующего второй входного для сложения элемент кольца,
- определение 320 выходного для сложения целочисленного списка, кодирующего выходной для сложения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для сложения целочисленных списков, выходной для сложения элемент кольца равен сложению в кольце первого входного для сложения элемента кольца и второго входного для сложения элемента кольца.
Способ дополнительно может содержать умножение в кольце:
- прием 330 первого входного для умножения целочисленного списка (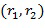 ), кодирующего первый входной для умножения элемент кольца, и второго входного для умножения целочисленного списка (
), кодирующего первый входной для умножения элемент кольца, и второго входного для умножения целочисленного списка (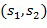 ), кодирующего второй входной для умножения элемент кольца,
), кодирующего второй входной для умножения элемент кольца,
- определение 340 выходного для умножения целочисленного списка, кодирующего выходной для умножения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для умножения целочисленных списков, выходной для умножения элемент кольца равен умножению в кольце первого входного для умножения элемента кольца и второго входного для умножения элемента кольца.
Фиг. 5 схематично показывает пример варианта осуществления способа 400 сложения, который может использоваться в устройстве 100 или в способе 300 и т.д. Этот пример использует иллюстративное кодирование. Способ может быть адаптирован к другим кодированиям. Все вариации, описанные в настоящем документе, могут быть применены; этот пример использует инкрементное значение 1, и инкрементная таблица строится посредством разложения 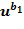 .
.
Способ 400 содержит прием операндов 410 сложения. Это может содержать прием 410 первого входного для сложения целочисленного списка, например, 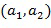 , и прием 420 второго входного для сложения целочисленного списка, например,
, и прием 420 второго входного для сложения целочисленного списка, например, 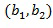 .
.
Каждый из входных для сложения целочисленных списков кодирует элемент кольца таким образом, что элемент кольца равен линейной комбинации степеней основного элемента кольца, основной элемент кольца имеет порядок в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка. Экспоненты удовлетворяют требованию, чтобы разность между первой экспонентой и второй экспонентой содержалась в списке разрешенных разностей.
Способ 400 дополнительно содержит определение 420 целочисленного списка промежуточного сложения, например, 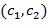 . Например, это может содержать применение инкрементной таблицы к элементу кольца, определенному из первого и второго входных для сложения целочисленных списков. В частности, инкрементная таблица может быть применена к целочисленному списку, элементы в целом числе произведены из элементов во входных целочисленных списках. Выходные данные таблицы удовлетворяет требованию.
. Например, это может содержать применение инкрементной таблицы к элементу кольца, определенному из первого и второго входных для сложения целочисленных списков. В частности, инкрементная таблица может быть применена к целочисленному списку, элементы в целом числе произведены из элементов во входных целочисленных списках. Выходные данные таблицы удовлетворяет требованию.
Например, определение 420 может содержать применение 422 инкрементной таблицы к 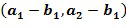 , например, получение
, например, получение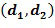 ; и добавление 424 целого числа
; и добавление 424 целого числа 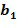 , определенного из вторых входных для сложения целочисленных списков, к целым числам в целочисленном списке, полученном в результате их первого применения, например,
, определенного из вторых входных для сложения целочисленных списков, к целым числам в целочисленном списке, полученном в результате их первого применения, например, 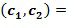
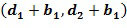 .
.
Способ 400 дополнительно содержит определение 430 выходного для сложения целочисленного списка через второе применение инкрементной таблицы к элементу кольца, определенному из целочисленного списка промежуточного сложения и второго входного для сложения целочисленного списка. Для более длинных целочисленных списков это может включать в себя дополнительные применения инкрементной таблицы. Например, это может содержать отрицание 431 целочисленного списка промежуточного сложения, например, перестановку в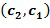 . Применение 432 инкрементной таблицы и добавление 434 совпадают с применением 422 и добавлением 424 за исключением того, что входные для сложения целочисленные списки
. Применение 432 инкрементной таблицы и добавление 434 совпадают с применением 422 и добавлением 424 за исключением того, что входные для сложения целочисленные списки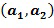 заменены промежуточным целочисленным списком
заменены промежуточным целочисленным списком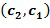 и
и 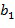 заменено на
заменено на 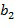 . Наконец, результат 434 подвергается отрицанию 453, чтобы получить результат замаскированного сложения.
. Наконец, результат 434 подвергается отрицанию 453, чтобы получить результат замаскированного сложения.
Если вместо отрицательного маскирования, как было здесь, используется положительное маскирование, то отрицание 431, 435 может быть опущено.
Фигура 6 схематично показывает пример варианта осуществления способа 500 умножения, который может использоваться в устройстве 100 или в способе 300 и т.д. Этот пример использует такое же кодирование и инкрементные таблицы, как способ 400. Что касается сложения, входные данные и выходные данные умножения удовлетворяют требованию.
Способ 500 содержит прием операндов 510 умножения. Это может содержать прием 510 первого входного для умножения целочисленного списка, например,  , и прием 514 второго входного для умножения целочисленного списка
, и прием 514 второго входного для умножения целочисленного списка 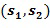 .
.
Способ 500 дополнительно содержит определение 520 первого и второго целочисленного списка промежуточного умножения. Например, 520 может содержать определение 522 первого целочисленного списка промежуточного умножения и определение 524 второго целочисленного списка промежуточного умножения. Они могут, например, быть выбраны как 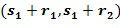 и
и 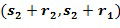 , соответственно, хотя существует другой выбор. Умножение продолжается посредством сложения этих чисел в способе 400 сложения.
, соответственно, хотя существует другой выбор. Умножение продолжается посредством сложения этих чисел в способе 400 сложения.
Следует отметить, что таблица используется только в применении 422 и применении 432 и больше нигде в способах 400 и 500. И сложение, и умножение используют одну и ту же таблицу, и оба используют таблицу одинаковое количество раз (2). Другие операции содержат малые арифметические операции над целыми числами в целочисленном списке, например, модуль по порядку основного элемента кольца
Возможны многие другие методы исполнения способов, как будет очевидно для специалиста в области техники. Например, порядок этапов может быть изменен, или некоторые этапы могут исполняться параллельно. Кроме того, между этапами могут быть вставлены другие этапы способа. Вставленные этапы могут представлять уточнения способа согласно настоящему описанию или могут не относиться к способу. Кроме того, заданный этап может не полностью закончиться перед началом следующего этапа.
Способ в соответствии с вариантом осуществления может быть исполнен с использованием программного обеспечения, которое содержит инструкции для того, чтобы побуждать систему процессора выполнить любой из способов 300, 400 и 500. Программное обеспечение может включить в себя только те этапы, которые выполняются конкретным подобъектом системы. Программное обеспечение может быть сохранено на подходящем запоминающем носителе, таком как жесткий диск, гибкий диск, память и т.д. Программное обеспечение может быть отправлено как сигнал по проводу или по радио, или с использованием сети передачи данных, например, Интернет. Программное обеспечение может быть сделано доступным для скачивания и/или для удаленного использования на сервере. Способ может быть исполнен с использованием битового потока, выполненного с возможностью конфигурировать программируемую логическую схему, например, программируемую пользователем вентильную матрицу (FPGA), для выполнения способа.
Очевидно, что вариант осуществления также распространяется на компьютерные программы, особенно компьютерные программы на носителе, приспособленном к проведению варианта осуществления на практике. Программа может быть в форме исходного кода, объектного кода, промежуточного исходного кода и объектного кода, такого как частично скомпилированный формат, или в любой другой форме, подходящей для использования в реализации способа в соответствии с вариантом осуществления. Вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером инструкции, соответствующие каждому из этапов обработки по меньшей мере одного из изложенных способов. Эти инструкции могут быть подразделены на подпрограммы и/или сохранены в одном или более файлах, которые могут быть соединены статически или динамически. Другой вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером инструкции, соответствующие каждому из средств по меньшей мере одной из изложенных систем и/или продуктов.
Фиг. 7a показывает машиночитаемый носитель 1000, имеющий записываемую часть, содержащую компьютерную программу 1020, компьютерная программа 1020 содержит инструкции для побуждения системы процессора выполнить способ вычислений для выполнения замаскированных арифметических действий в соответствии с вариантом осуществления. Записываемая часть может быть выполнена с возможностью многократной записи или только для однократной записи. Компьютерная программа 1020 может быть воплощена на машиночитаемом носителе 1000 как физические метки или посредством намагничивания машиночитаемого носителя 1000. Однако любой другой подходящий вариант осуществления также является возможным. Кроме того, очевидно, что хотя машиночитаемый носитель 1000 показан здесь как оптический диск, машиночитаемый носитель 1000 может представлять собой любой подходящий машиночитаемый носитель, такой как жесткий диск, твердотельная память, флэш-память и т.д., и может быть не позволять или позволять запись. Компьютерная программа 1020 содержит инструкции для побуждения системы процессора выполнить упомянутый способ вычислений для выполнения замаскированных арифметических действий.
Машиночитаемый носитель, например, машиночитаемый носитель 1000, может содержать инкрементную таблицу, и/или таблицу декодирования, и/или таблицу кодирования.
Фиг. 7b показывает схематическое представление системы 1100 процессора в соответствии с вариантом осуществления. Система процессора содержит одну или более интегральных схем 1110. Архитектура одной или более интегральных схем 1110 схематично показана на фиг. 7b. Схема 1110 содержит процессор 1120, например, центральный процессор, для выполнения компонентов компьютерной программы, чтобы исполнить способ в соответствии с вариантом осуществления и/или реализовать его модули или блоки. Схема 1110 содержит память 1122 для хранения программного кода, данных и т.д. Часть памяти 1122 может быть предназначена только для чтения. Схема 1110 может содержать элемент 1126 связи, например, антенну, соединители или и то, и другое, и т.п. Схема 1110 может содержать специализированную интегральную схему 1124 для выполнения части или всей обработки, определенной в способе. Процессор 1120, память 1122, специализированная ИС 1124 и элемент 1126 связи могут быть соединены друг с другом через взаимное соединение 1130, например, шину. Система 1110 процессора может быть выполнена с возможностью контактной и/или бесконтактной связи с использованием антенны и/или соединителей, соответственно.
Следует отметить, что упомянутые выше варианты осуществления иллюстрируют, а не ограничивают изобретение, и что специалисты в области техники смогут скомпоновать многие альтернативные варианты осуществления.
В формуле изобретения любые ссылочные позиции, помещенные между круглыми скобками, не должны быть истолкованы как ограничение пункта формулы изобретения. Использование глагола "содержит" и его форм спряжения не исключает присутствие элементов или этапов, кроме заявленных в пункте формулы изобретения. Использование формы единственного числа для элемента не исключают присутствие множества таких элементов. Изобретение может быть реализовано посредством аппаратных средств, содержащих несколько различных элементов, и посредством подходящим образом запрограммированного компьютера. В пункте формулы изобретения, описывающем устройство, перечисляющем несколько средств, несколько из этих средств могут быть воплощены посредством одного и того же элемента аппаратных средств. Тот лишь факт, что некоторые меры излагаются во взаимно различных зависимых пунктах формулы изобретения, не указывает, что комбинация этих мер не может успешно использоваться.
В формуле изобретения ссылки в круглых скобках относятся к ссылочным позициям на чертежах вариантов осуществления или к формулам вариантов осуществления, тем самым добавляя ясность пункту формулы изобретения. Эти ссылки не являются исчерпывающими и не должны быть истолкованы как ограничение пункта формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ АРИФМЕТИКИ С ОБФУСКАЦИЕЙ | 2015 |
|
RU2701716C2 |
| ЭЛЕКТРОННОЕ УСТРОЙСТВО ФОРМИРОВАНИЯ | 2015 |
|
RU2710310C2 |
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2015 |
|
RU2698763C2 |
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО И КОДИРУЮЩЕЕ УСТРОЙСТВО | 2016 |
|
RU2692419C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, СОДЕРЖАЩЕЕ СЕТЬ ТАБЛИЦ | 2013 |
|
RU2676454C2 |
| ВЫВЕДЕНИЕ ВЕСА ВЫБОРКИ ЦВЕТНОСТИ ДЛЯ ГЕОМЕТРИЧЕСКОГО РЕЖИМА РАЗДЕЛЕНИЯ | 2020 |
|
RU2814812C2 |
| УСТРОЙСТВО ВИРТУАЛЬНОЙ МАШИНЫ, ИМЕЮЩЕЕ УПРАВЛЯЕМУЮ КЛЮЧОМ ОБФУСКАЦИЮ, И СПОСОБ | 2012 |
|
RU2620712C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, КОНФИГУРИРУЕМОЕ С ПОМОЩЬЮ ТАБЛИЧНОЙ СЕТИ | 2013 |
|
RU2661308C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, ХРАНЯЩЕЕ ТАБЛИЦЫ СООТВЕТСТВИЯ ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИИ | 2013 |
|
RU2657178C2 |
| ВЫЧИСЛЕНИЕ РАССТОЯНИЯ ДО ВЫБОРКИ ДЛЯ РЕЖИМА ГЕОМЕТРИЧЕСКОГО ДЕЛЕНИЯ | 2020 |
|
RU2826830C2 |
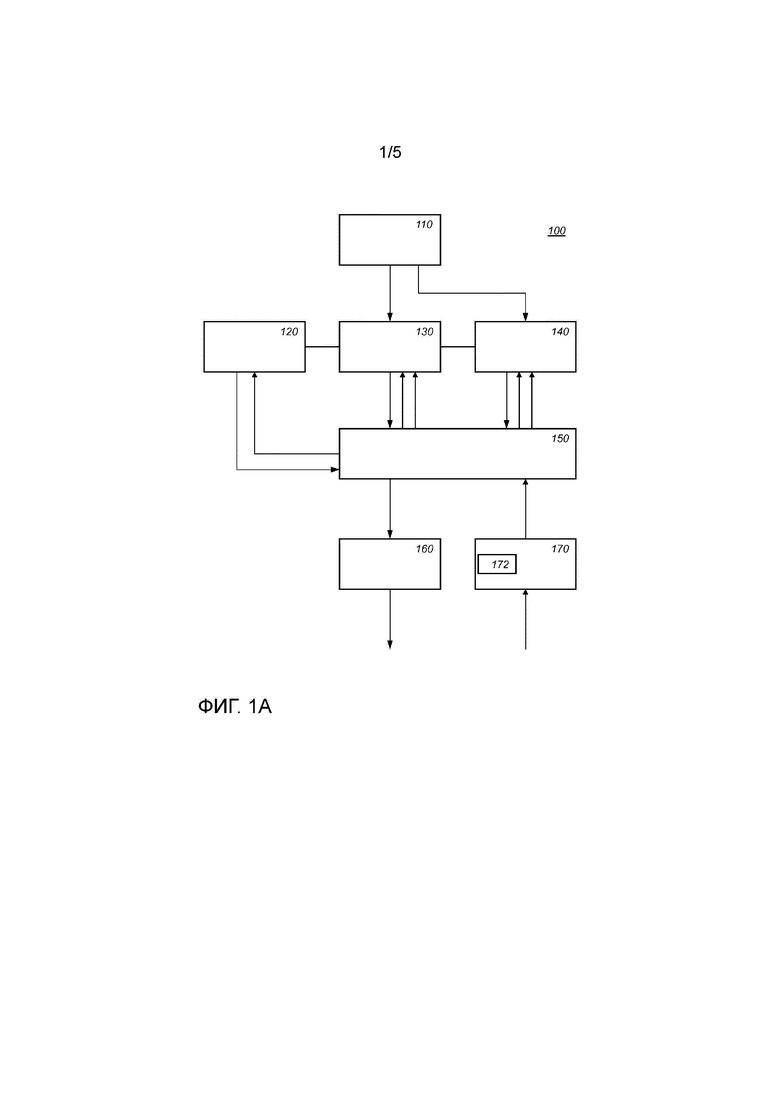
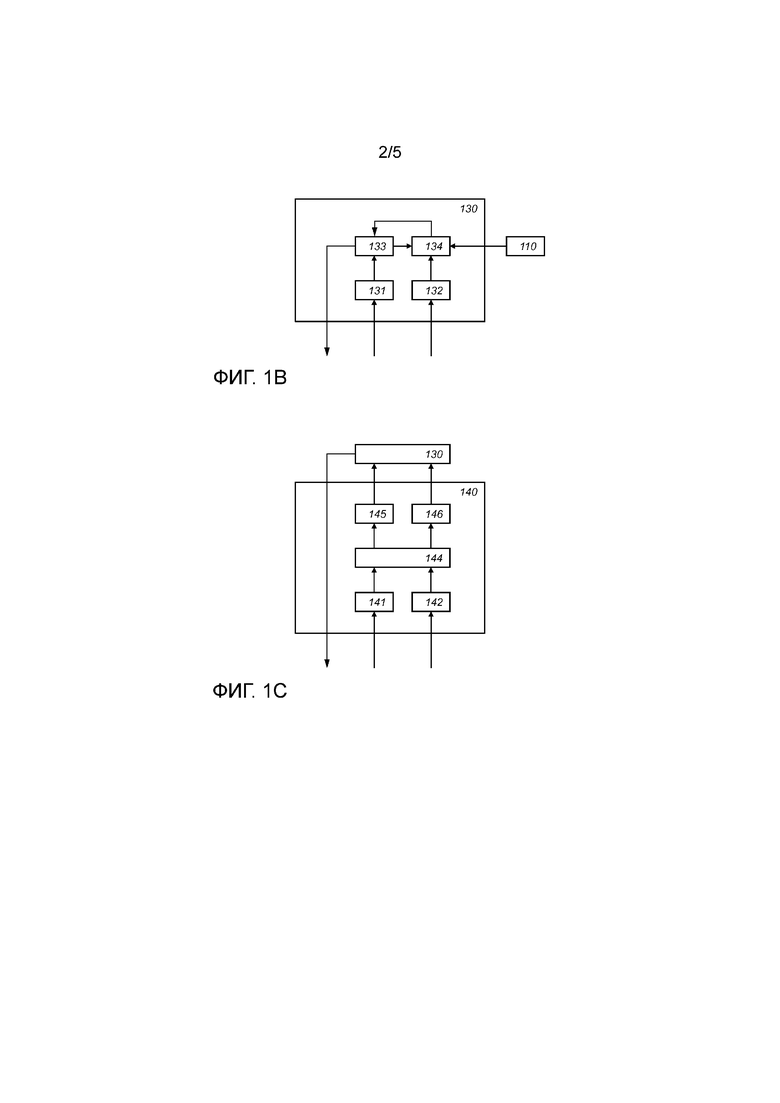
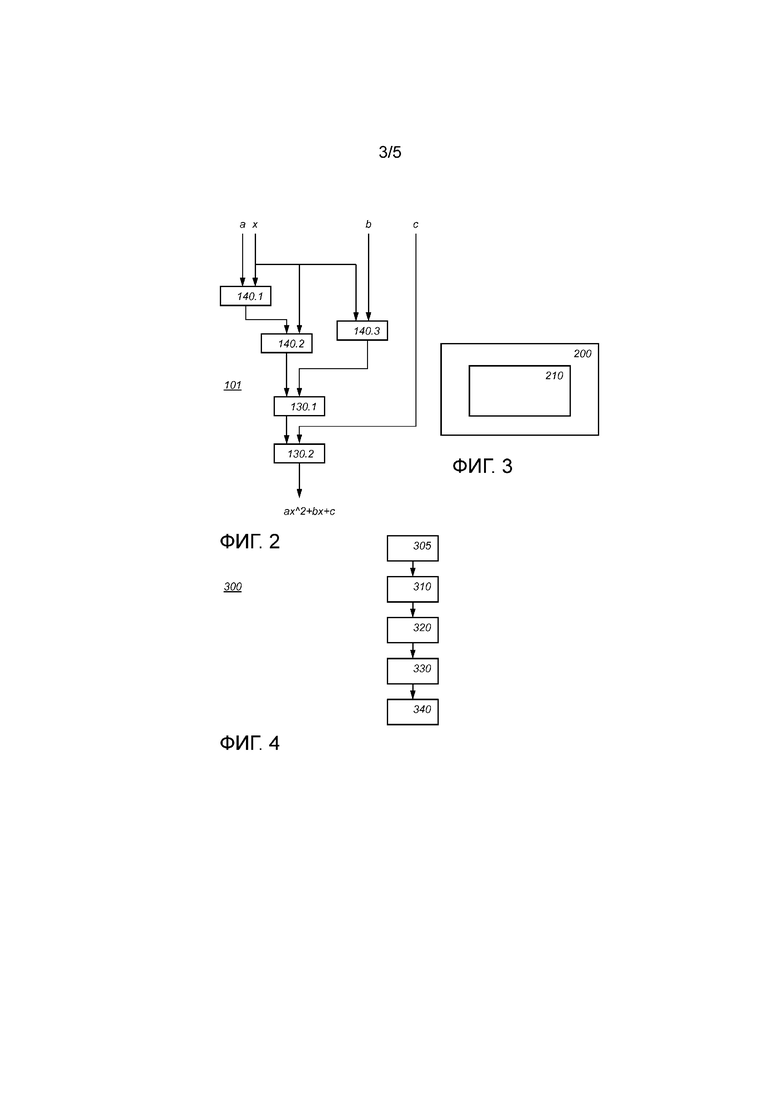
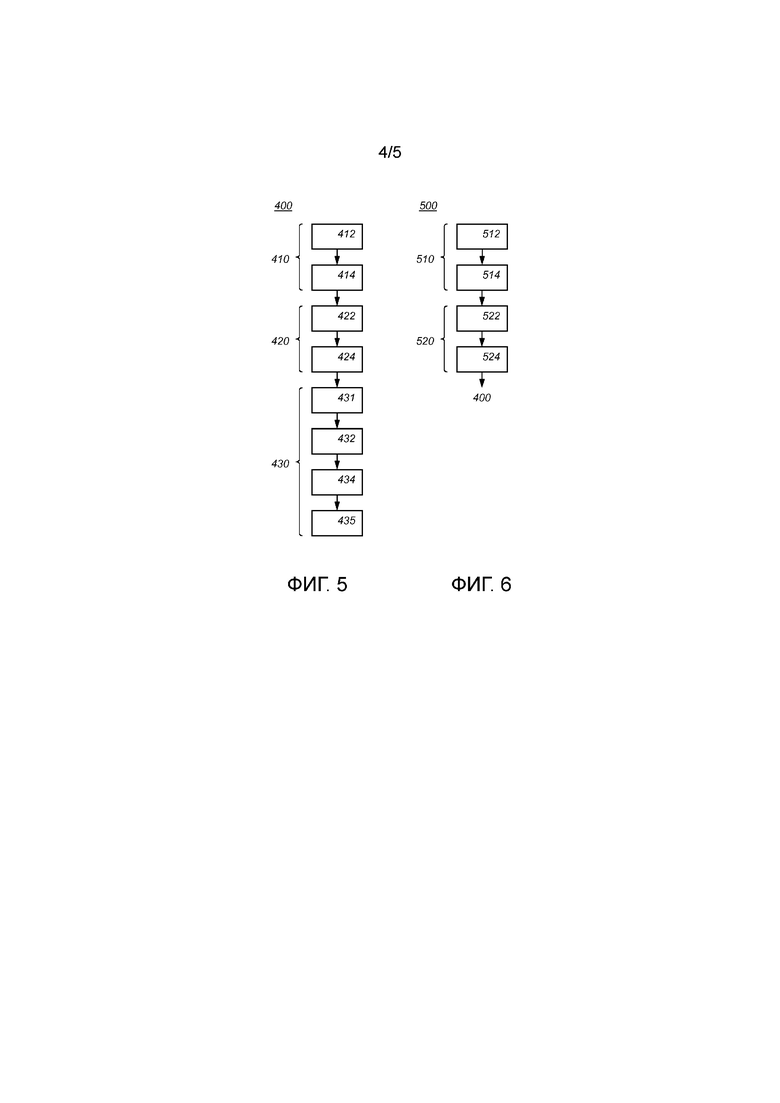
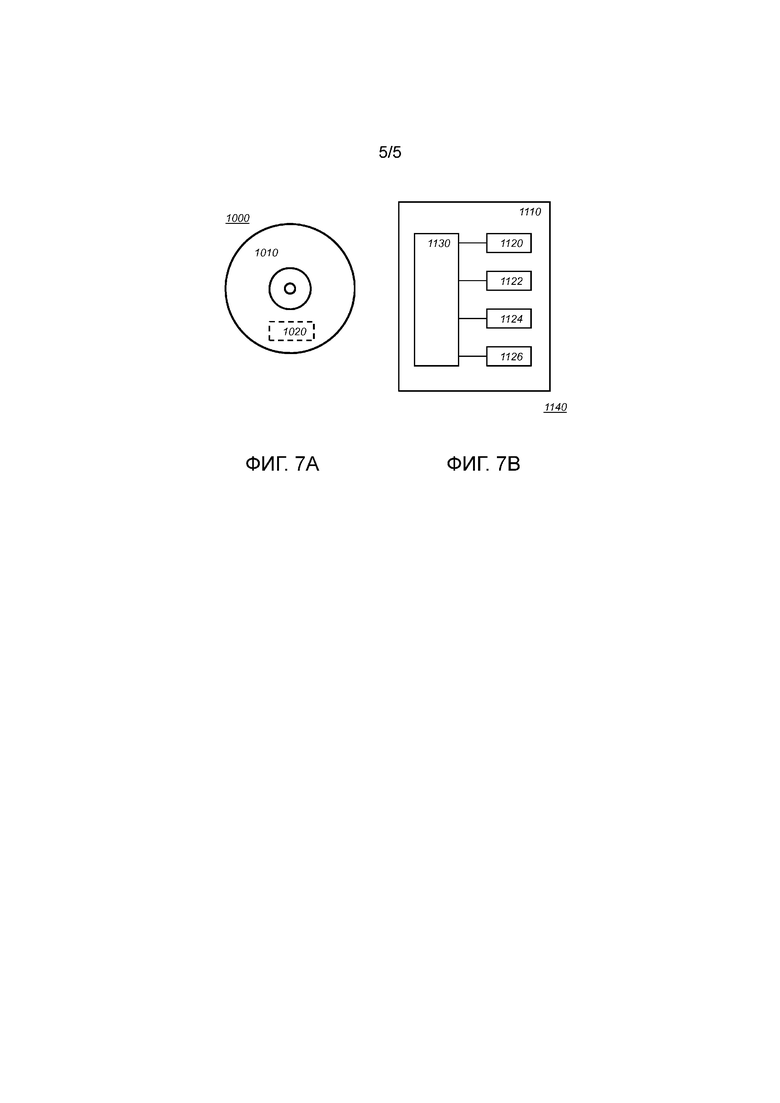
Изобретение относится к выполнению замаскированных арифметических действий в коммутативном кольце. Технический результат – повышение эффективности выполнения замаскированных арифметических действий. Электронное вычислительное устройство для выполнения замаскированных арифметических действий в коммутативном кольце, содержит запоминающее устройство, выполненное с возможностью хранить инкрементную таблицу, заданную для инкрементного элемента кольца, инкрементная таблица отображает входной элемент кольца на выходной целочисленный список, кодирующий выходной элемент кольца, таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца, выходной элемент кольца равен линейной комбинации степеней основного элемента кольца, причем степени имеют экспоненты, определенный посредством выходного целочисленного списка, разность между первой экспонентой и второй экспонентой содержится в списке разрешенных разностей. 6 н. и 9 з.п. ф-лы, 1 табл., 10 ил.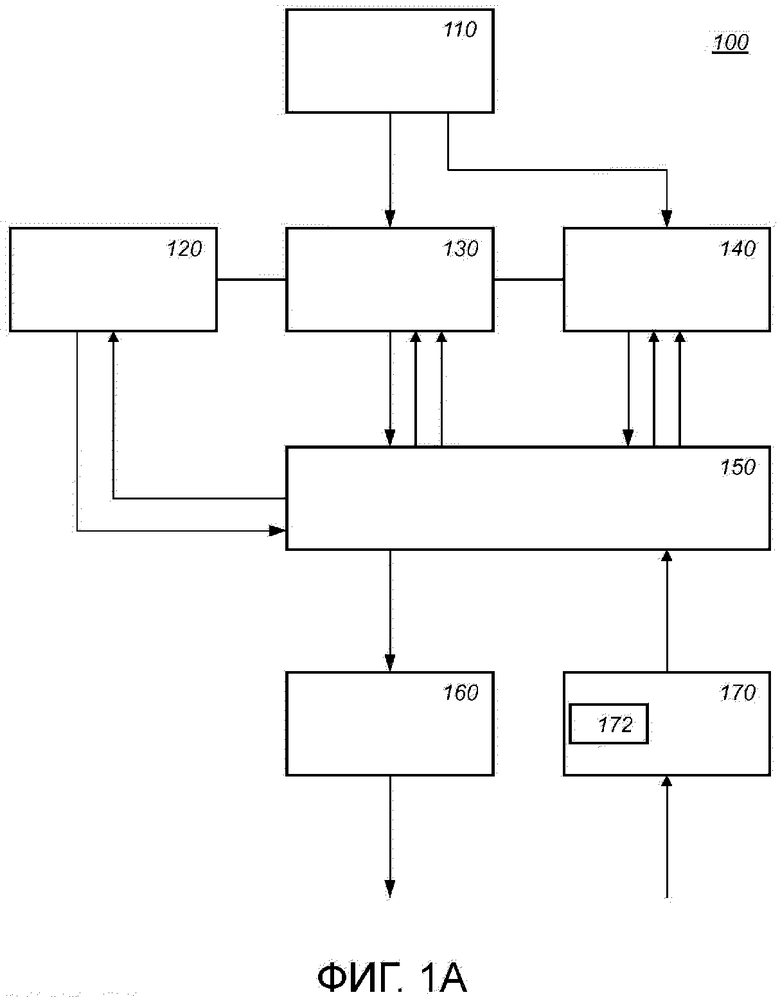
1. Электронное вычислительное устройство (100) для выполнения замаскированной арифметики в коммутативном кольце (
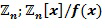 ), кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, вычислительное устройство обрабатывает целочисленные списки (
), кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, вычислительное устройство обрабатывает целочисленные списки (
 ), кодирующие элементы кольца (
), кодирующие элементы кольца (
 ), целочисленные списки содержат по меньшей мере два целых числа, причем целочисленный список (
), целочисленные списки содержат по меньшей мере два целых числа, причем целочисленный список (
 ) кодирует элемент кольца (
) кодирует элемент кольца (
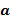 ) таким образом, что элемент кольца равен линейной комбинации степеней (
) таким образом, что элемент кольца равен линейной комбинации степеней (
 ;
;
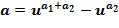 ;
;
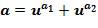 ) основного элемента кольца (
) основного элемента кольца (
 ), основной элемент кольца имеет порядок (
), основной элемент кольца имеет порядок (
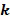 ) в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
) в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
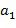 ) и второй экспонентой (
) и второй экспонентой (
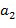 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (
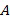 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (
 ),
),
вычислительное устройство содержит
- запоминающее устройство (110), выполненное с возможностью хранить инкрементную таблицу (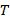 ), определенную для инкрементного элемента кольца (1;
), определенную для инкрементного элемента кольца (1; ),
),
- инкрементная таблица отображает целочисленный список, представляющий входной элемент кольца (
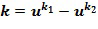 ) на выходной целочисленный список (
) на выходной целочисленный список (
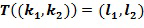 ), кодирующий выходной элемент кольца (
), кодирующий выходной элемент кольца (
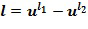 ), таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца (
), таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца (
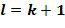 ), выходной элемент кольца равен линейной комбинации степеней основного элемента кольца (
), выходной элемент кольца равен линейной комбинации степеней основного элемента кольца (
 ), причем степени имеют экспоненты, определенный посредством выходного целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенный посредством выходного целочисленного списка, разность между первой экспонентой (
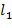 ) и второй экспонентой (
) и второй экспонентой (
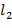 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (
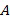 ).
).
2. Вычислительное устройство по п. 1, в котором размер списка разрешенных разностей составляет менее чем 50% порядка, более предпочтительно менее чем 20% порядка, еще более предпочтительно менее чем 10% порядка, еще более предпочтительно менее чем 5% порядка.
3. Вычислительное устройство по любому из предыдущих пп., в котором основной элемент кольца имеет порядок, причем порядок (
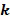 ), умноженный на размер списка разрешенных разностей минус один (
), умноженный на размер списка разрешенных разностей минус один (
 ), разделенный на размер кольца минус один (
), разделенный на размер кольца минус один (
 ), меньше 2, более предпочтительно равен 1 (
), меньше 2, более предпочтительно равен 1 (
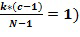 .
.
4. Вычислительное устройство по п. 1 или 2, в котором основной элемент кольца имеет порядок, причем порядок (
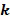 ), умноженный на размер списка разрешенных разностей минус один (
), умноженный на размер списка разрешенных разностей минус один (
 ), разделенный на размер кольца минус один (
), разделенный на размер кольца минус один (
 ), больше или равен двум (
), больше или равен двум (
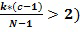 .
.
5. Вычислительное устройство по любому из предыдущих пунктов, в котором инкрементная таблица берет в качестве входных данных входные целочисленные списки (
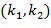 ), представляющие входной элемент кольца,
), представляющие входной элемент кольца,
в котором
- арифметическая разность между первым целым числом (
 ) из входных целочисленных списков (
) из входных целочисленных списков (
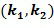 ) и вторым целым числом (
) и вторым целым числом (
 ) из целочисленного списка содержится в списке разрешенных разностей, или
) из целочисленного списка содержится в списке разрешенных разностей, или
- целое число (
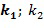 ) из входных целочисленных списков (
) из входных целочисленных списков (
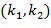 ) содержится в списке разрешенных разностей.
) содержится в списке разрешенных разностей.
6. Вычислительное устройство по любому из предыдущих пунктов, содержащее
- блок (130) сложения в кольце, выполненный с возможностью
- принимать первый входной для сложения целочисленный список (
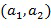 ), кодирующий первый входной для сложения элемент кольца, и второй входной для сложения целочисленный список (
), кодирующий первый входной для сложения элемент кольца, и второй входной для сложения целочисленный список (
 ), кодирующий второй входной для сложения элемента кольца,
), кодирующий второй входной для сложения элемента кольца,
- определять выходной для сложения целочисленный список, кодирующий выходной для сложения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для сложения целочисленных списков, выходной для сложения элемент кольца равен сложению в кольце первого входного для сложения элемента кольца и второго входного для сложения элемента кольца.
7. Вычислительное устройство по п. 6, в котором определение выходного для сложения целочисленного списка содержит
- определение целочисленного списка промежуточного сложения (
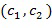 ), кодирующего элемент кольца промежуточного сложения, посредством первого применения инкрементной таблицы к элементу кольца (
), кодирующего элемент кольца промежуточного сложения, посредством первого применения инкрементной таблицы к элементу кольца (
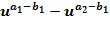 ), являющегося линейной комбинацией степеней одного или более основных элементов, причем степени определены из первого и второго входных для сложения целочисленных списков, (
), являющегося линейной комбинацией степеней одного или более основных элементов, причем степени определены из первого и второго входных для сложения целочисленных списков, (
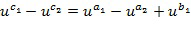 ),
),
- определение выходного для сложения целочисленного списка, содержащее второе применение инкрементной таблицы к элементам кольца, определенным из целочисленного списка промежуточного сложения и определенным из второго входного для сложения целочисленного списка.
8. Вычислительное устройство по любому из предыдущих пп., содержащее
- блок (140) умножения в кольце, выполненный с возможностью
- принимать первый входной для умножения целочисленный список (
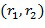 ), кодирующий первый входной для умножения элемент кольца, и второй входной для умножения целочисленный список (
), кодирующий первый входной для умножения элемент кольца, и второй входной для умножения целочисленный список (
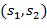 ), кодирующий второй входной для умножения элемент кольца,
), кодирующий второй входной для умножения элемент кольца,
- определять выходной для умножения целочисленный список, кодирующий выходной для умножения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для умножения целочисленных списков, выходной для умножения элемент кольца равен умножению в кольце первого входного для умножения элемента кольца и второго входного для умножения элемента кольца.
9. Вычислительное устройство по любому из предыдущих пп., в котором
- коммутативное кольцо представляет собой кольцо, сформированное целыми числами по модулю целого числа (
 ), и/или
), и/или
- коммутативное кольцо представляет собой кольцо, сформированное целочисленными полиномами по модулю целочисленного полинома (
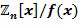 )
)
10. Устройство (170) кодирования в кольце для кодирования элемента кольца коммутативного кольца (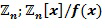 ) как целочисленного списка для использования с вычислительным устройством по п. 1, при этом устройство кодирования в кольце содержит
) как целочисленного списка для использования с вычислительным устройством по п. 1, при этом устройство кодирования в кольце содержит
- запоминающее устройство (172), выполненное с возможностью хранить таблицу кодирования, определенную для основного элемента кольца (
 ), причем таблица кодирования отображает элемент кольца (
), причем таблица кодирования отображает элемент кольца (
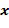 ) на целочисленный список (
) на целочисленный список (
 ) таким образом, что элемент кольца равен линейной комбинации степеней основного элемента кольца (
) таким образом, что элемент кольца равен линейной комбинации степеней основного элемента кольца (
 ), причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
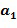 ) и второй экспонентой (
) и второй экспонентой (
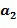 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (
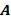 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (
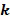 ).
).
11. Устройство (160) декодирования в кольце для декодирования целочисленного списка (
 ) в элемент кольца (
) в элемент кольца (
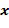 ) коммутативного кольца (
) коммутативного кольца (
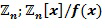 ) для использования с вычислительным устройством по п. 1, причем устройство декодирования в кольце выполнено с возможностью определять для одного или более основных элементов кольца (
) для использования с вычислительным устройством по п. 1, причем устройство декодирования в кольце выполнено с возможностью определять для одного или более основных элементов кольца (
 ) элемент кольца (
) элемент кольца (
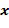 ) таким образом, что элемент кольца равен линейной комбинации степеней одного или более основных элементов кольца (
) таким образом, что элемент кольца равен линейной комбинации степеней одного или более основных элементов кольца (
 ), причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
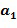 ) и второй экспонентой (
) и второй экспонентой (
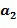 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (
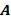 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (
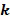 ).
).
12. Устройство (200) вычисления таблицы для вычисления инкрементной таблицы для использования в вычислительном устройстве для выполнения замаскированных арифметических действий в коммутативном кольце (
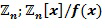 ), кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, вычислительное устройство обрабатывает целочисленные списки (
), кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, вычислительное устройство обрабатывает целочисленные списки (
 ), кодирующие элементы кольца (
), кодирующие элементы кольца (
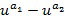 ), целочисленные списки содержат по меньшей мере два целых числа, при этом устройство вычисления таблицы содержит
), целочисленные списки содержат по меньшей мере два целых числа, при этом устройство вычисления таблицы содержит
- блок (210) создания таблицы, выполненный с возможностью строить инкрементную таблицу, причем блок создания таблицы выполнен с возможностью
- многократно выбирать входной элемент кольца,
- определять выходной элемент кольца, который равен инкрементному элементу кольца, добавленному с помощью сложения в кольце ко входному элементу кольца,
- определять кодирование выходного целочисленного списка для выходного элемента кольца как линейную комбинацию степеней (
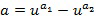 ;
;
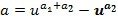 ;
;
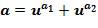 ) основного элемента кольца (
) основного элемента кольца (
 ), основной элемент кольца имеет порядок (
), основной элемент кольца имеет порядок (
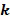 ) в кольце, причем степени имеют экспоненты, определенные посредством выходного целочисленного списка, разность между первой экспонентой (
) в кольце, причем степени имеют экспоненты, определенные посредством выходного целочисленного списка, разность между первой экспонентой (
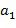 ) и второй экспонентой (
) и второй экспонентой (
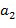 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (
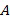 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (
 ),
),
- добавлять запись в инкрементную таблицу, отображающую входной элемент кольца на выходной целочисленный список.
13. Электронное устройство конфигурации для конфигурации электронного вычислительного устройства (100) для выполнения замаскированных арифметических действий в коммутативном кольце (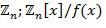 ) по п. 1,
) по п. 1,
- обеспечивающее кольцо, имеющее конечное количество элементов кольца,
- обеспечивающее основной элемент кольца
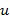 , имеющий порядок
, имеющий порядок
 ,
,
- определяющее такое отношение эквивалентности на
 , что два элемента
, что два элемента
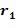 и
и
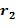 эквивалентны, если и только если
эквивалентны, если и только если
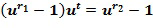 в кольце для некоторого элемента
в кольце для некоторого элемента

 , отношение эквивалентности порождает классы эквивалентности на
, отношение эквивалентности порождает классы эквивалентности на
 ,
,
- определяющее список разрешенных разностей посредством выбора по меньшей мере одного элемента из каждого класса эквивалентности.
14. Способ электронных вычислений для выполнения замаскированных арифметических действий в коммутативном кольце (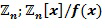 ), причем кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, при этом способ вычислений обрабатывает целочисленные списки (
), причем кольцо имеет конечное количество элементов кольца, сложение в кольце и умножение в кольце определены на элементах кольца, при этом способ вычислений обрабатывает целочисленные списки ( ), кодирующие элементы кольца (
), кодирующие элементы кольца ( ), целочисленные списки содержат по меньшей мере два целых числа, причем целочисленный список (
), целочисленные списки содержат по меньшей мере два целых числа, причем целочисленный список ( ) кодирует элемент кольца (
) кодирует элемент кольца (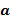 ) таким образом, что элемент кольца равен линейной комбинации степеней (
) таким образом, что элемент кольца равен линейной комбинации степеней ( ;
; 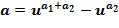 ;
; 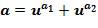 ) основного элемента кольца (
) основного элемента кольца ( ), основной элемент кольца имеет порядок (
), основной элемент кольца имеет порядок (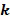 ) в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (
) в кольце, причем степени имеют экспоненты, определенные посредством целочисленного списка, разность между первой экспонентой (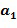 ) и второй экспонентой (
) и второй экспонентой (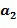 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (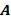 ), и причем размер списка разрешенных разностей меньше, чем порядок (
), и причем размер списка разрешенных разностей меньше, чем порядок (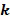 ), при этом способ вычислений содержит этапы, на которых
), при этом способ вычислений содержит этапы, на которых
- сохраняют инкрементную таблицу (
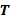 ), заданную для инкрементного элемента кольца (1;
), заданную для инкрементного элемента кольца (1;
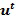 ), причем инкрементная таблица отображает целочисленный список, представляющий входной элемент кольца (
), причем инкрементная таблица отображает целочисленный список, представляющий входной элемент кольца (
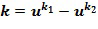 ) на выходной целочисленный список (
) на выходной целочисленный список (
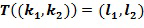 ), кодирующий выходной элемент кольца (
), кодирующий выходной элемент кольца (
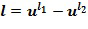 ), таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца (
), таким образом, что выходной элемент кольца равен инкрементному элементу кольца, добавленному посредством сложения в кольце к входному элементу кольца (
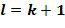 ), выходной элемент кольца равен линейной комбинации степеней основного элемента кольца (
), выходной элемент кольца равен линейной комбинации степеней основного элемента кольца (
 ), причем степени имеют экспоненты, определенный посредством выходного целочисленного списка, разность между первой экспонентой (
), причем степени имеют экспоненты, определенный посредством выходного целочисленного списка, разность между первой экспонентой (
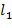 ) и второй экспонентой (
) и второй экспонентой (
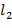 ) содержится в списке разрешенных разностей (
) содержится в списке разрешенных разностей (
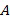 ).
).
15. Способ электронных вычислений по п. 14, содержащий этапы, на которых
- выполняют сложение в кольце, сложение в кольце содержит этапы, на которых
- принимают первый входной для сложения целочисленный список (
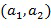 ), кодирующий первый входной для сложения элемент кольца, и второй входной для сложения целочисленный список (
), кодирующий первый входной для сложения элемент кольца, и второй входной для сложения целочисленный список (
 ), кодирующий второй входной для сложения элемент кольца,
), кодирующий второй входной для сложения элемент кольца,
- определяют выходной для сложения целочисленный список, кодирующий выходной для сложения элемент кольца, посредством применения инкрементной таблицы к элементам кольца, определенным из первого и второго входных для сложения целочисленных списков, выходной для сложения элемент кольца равен сложению в кольце первого входного для сложения элемента кольца и второго входного для сложения элемента кольца.
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| US 6298137 B1, 02.10.2001 | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| СПОСОБ ЗАЩИТЫ ТЕКСТОВОЙ ИНФОРМАЦИИ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА | 2010 |
|
RU2439693C1 |
Авторы
Даты
2019-08-29—Публикация
2015-11-25—Подача