ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Изобретение относится к электронному вычислительному устройству, выполненному с возможностью выполнения обфускационных арифметических операций в коммутативном кольце.
Изобретение дополнительно относится к способу электронного вычисления, компьютерной программе и машиночитаемому носителю.
УРОВЕНЬ ТЕХНИКИ
При использовании криптографии типа «белый ящик» и в более общем случае обфускации программного обеспечения вычисления часто выполняют с кодированными значениями вместо использования простых значений. Обратное проектирование обфускационного программного обеспечения затрудняется, если вычисления выполняются с кодированными значениями вместо использования самих простых значений.
После кодирования такие регулярные операции, как сложение или умножение, можно больше не выполнять с использованием встроенных компьютерных примитивов. Прямое сложение кодированных значений обычно не дает кодированный результат сложения этих значений. То же самое относится к умножению. В формуле 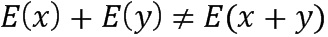 для большинства
для большинства 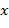 и
и 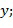 ; где
; где 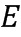 обозначает кодирующую функцию.
обозначает кодирующую функцию.
Решение этой проблемы состоит во введении таблиц сложения (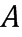 ) и умножения (
) и умножения (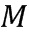 ). В этих таблицах берутся два кодированных значения в качестве входных данных, и создается кодированное значение в качестве выхода, которое соответствует кодированию операции сложения или умножения. Эти таблицы можно определить в виде
). В этих таблицах берутся два кодированных значения в качестве входных данных, и создается кодированное значение в качестве выхода, которое соответствует кодированию операции сложения или умножения. Эти таблицы можно определить в виде 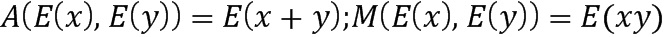 . Эти таблицы позволяют выполнять арифметические операции непосредственно над кодированными значениями.
. Эти таблицы позволяют выполнять арифметические операции непосредственно над кодированными значениями.
Использование таблиц обфускационного сложения и умножения связано по меньшей мере с двумя недостатками. Во-первых, таблицы могут оказаться слишком большими. Если 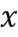 и
и 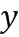 представлены в виде
представлены в виде 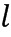 бит, то для каждой таблицы потребуется
бит, то для каждой таблицы потребуется 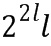 бит.
бит.
Во-вторых, такие большие таблицы можно без труда обнаружить программным путем. Хуже того, эти таблицы можно к тому же идентифицировать в качестве операций сложения или умножения даже в том случае, если они закодированы, например, через свойства этих функций, которые сохраняются в процессе кодирования. Например, таблица умножения удовлетворяет условию 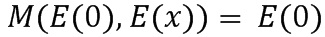 . Взломщик может использовать это обстоятельство и аналогичные свойства, чтобы догадаться, какую операцию представляют указанные таблицы.
. Взломщик может использовать это обстоятельство и аналогичные свойства, чтобы догадаться, какую операцию представляют указанные таблицы.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
В предшествующей заявке, поданной тем же заявителем, был представлен усовершенствованный подход к выполнению обфускационных арифметических операций. Эта предшествующая заявка была подана в Европейскую Патентную Службу (EPO) под названием ʺElectronic calculating device for performing obfuscated arithmeticʺ. Дата подачи: 30.09.2014. Номер заявки: 14186951.1. Указанная предшествующая заявка целиком включена сюда посредством ссылки, и, в частности, для описания вычислительных устройств, использующих гомогенную обфускацию на целочисленном кольце.
Авторы изобретения обнаружили, что в некоторых случаях умножение и сложение, выполняемые над кодированными значениями, можно выполнять, используя единую таблицу без необходимости кодирования множества значений с получением единого кодированного значения. Поскольку для сложения и умножения используют одну и ту же таблицу, трудно распознать в процессе обратного проектирования (reverse engineering), выполняется ли сложение или умножение. Поскольку сложение и умножение кажется одной и той же операцией при наблюдении со стороны, авторы изобретения назвали этот способ «гомогенной обфускацией». Даже в том случае, если взломщик смог бы обнаружить используемую таблицу, и даже в том случае, если он смог бы догадаться, какова ее функция в качестве таблицы приращений, он все же не смог бы понять, какая операция (сложение или умножение) выполняется. Алгоритм действия таблицы над элементом целочисленного списка будет отличаться для сложения и умножения; однако, это можно легко скрыть, используя традиционную обфускацию. Вдобавок, единая таблица, которую используют, также имеет меньший размер, чем таблица, обсужденная в разделе «Уровень техники», а именно, в данном случае для нее потребуется примерно 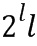 бит. Даже в том случае, если используется только сложение, таблица, необходимая для обфускационного сложения, будет меньше, чем таблица, предложенная в разделе «Уровень техники».
бит. Даже в том случае, если используется только сложение, таблица, необходимая для обфускационного сложения, будет меньше, чем таблица, предложенная в разделе «Уровень техники».
Например, элемент кольца можно закодировать в виде двух целых чисел 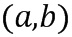 . Арифметические операции можно выполнять непосредственно при кодировании, используя таблицу приращений, которая отображает кодированный элемент кольца в кодированный элемент кольца плюс значение приращения. Например, эта таблица может отобразить
. Арифметические операции можно выполнять непосредственно при кодировании, используя таблицу приращений, которая отображает кодированный элемент кольца в кодированный элемент кольца плюс значение приращения. Например, эта таблица может отобразить 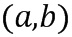 в
в 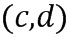 , если
, если 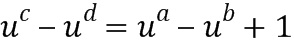 . Как сложение, так и умножение выполняют путем повторных применений таблицы приращений.
. Как сложение, так и умножение выполняют путем повторных применений таблицы приращений.
Обфускационные арифметические операции применяются к множеству различных коммутативных колец 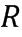 , хотя не каждое кольцо можно закодировать в виде целочисленного списка. Коммутативные кольца представляют собой математическую концепцию, которая включает в себя множество различных хорошо известных математических структур, например, остатки от деления целого на число (
, хотя не каждое кольцо можно закодировать в виде целочисленного списка. Коммутативные кольца представляют собой математическую концепцию, которая включает в себя множество различных хорошо известных математических структур, например, остатки от деления целого на число (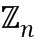 ) или остаток от деления многочлена на число и многочлен (
) или остаток от деления многочлена на число и многочлен (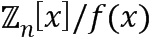 ). Особым случаем коммутативных колец являются поля.
). Особым случаем коммутативных колец являются поля.
Заметим, что два последних типа коммутативных колец обычно определяются операцией по модулю. Например, остаток от деления целых чисел на целое число (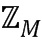 ) полностью определяются целочисленным модулем (
) полностью определяются целочисленным модулем (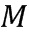 ). Аналогичным образом, кольца (
). Аналогичным образом, кольца (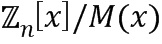 ) многочленов определяются модулем (
) многочленов определяются модулем (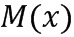 ). Коэффициенты многочленов являются модулярными коэффициентами, то есть, остатками от деления целых чисел на целое число (
). Коэффициенты многочленов являются модулярными коэффициентами, то есть, остатками от деления целых чисел на целое число (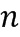 ).
).
Хотя гомогенная обфускация имеет преимущества по сравнению с традиционными видами обфускации, например, из-за меньшего размера таблиц, имеется потребность расширения диапазона гомогенной обфускации для больших целых чисел. Размер таблиц растет быстрее, чем по линейному закону, с увеличением размера основного кольца.
Преимущественным путем выполнения такой обфускации является вычисление в коммутативном кольце, определенном комбинированным модулем (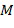 ) в системе остаточных классов, причем систему остаточных классов определяют для ряда модулей (
) в системе остаточных классов, причем систему остаточных классов определяют для ряда модулей (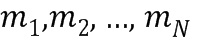 ).Область хранения операндов выполнена с возможностью хранения одного или более остатков от деления операндов на комбинированный модуль (
).Область хранения операндов выполнена с возможностью хранения одного или более остатков от деления операндов на комбинированный модуль (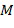 ), в виде одного или более рядов остатков от деления элементов кольца на упомянутые модули, причем каждый элемент кольца ряда связан с соответствующим модулем из указанного ряда модулей. Вычислительный блок выполнен с возможностью сложения и/или умножения первого и второго операнда из области хранения операндов согласно системе счисления элементов кольца. Преимуществом является то, что по меньшей мере один элемент кольца ряда, с которым вычислительный блок выполняет действие, закодирован в виде целочисленного списка. Это позволяет выполнить обфускацию для системы остаточных классов, используя гомогенную обфускацию.
), в виде одного или более рядов остатков от деления элементов кольца на упомянутые модули, причем каждый элемент кольца ряда связан с соответствующим модулем из указанного ряда модулей. Вычислительный блок выполнен с возможностью сложения и/или умножения первого и второго операнда из области хранения операндов согласно системе счисления элементов кольца. Преимуществом является то, что по меньшей мере один элемент кольца ряда, с которым вычислительный блок выполняет действие, закодирован в виде целочисленного списка. Это позволяет выполнить обфускацию для системы остаточных классов, используя гомогенную обфускацию.
В одном варианте осуществления вычислительный блок производит действия над упомянутым целочисленным списком, причем эти действия содержат операции нахождения остатка от деления на порядок базовых элементов, причем порядок по меньшей мере двух базовых элементов, связанных с двумя разными модулями из упомянутого ряда модулей, одинаков. Операции гомогенной обфускации включают в себя операцию нахождения остатка от деления, где модуль представляет собой порядок базового элемента. Таким образом, если даже модули разные, реальные операции нахождения остатка от деления могут оказаться одинаковыми. Это сокращает размер кода и улучшает обфускацию; то есть из операции по модулю невозможно понять, для какого модуля она была выполнена. Например, вычислительный блок может быть выполнен с возможностью извлечения обоих целых числе из целочисленных списков для выполнения операции сложения и/или умножения.
Способ согласно настоящему изобретению можно реализовать на компьютере в виде компьютерно-реализуемого способа, в виде специализированного аппаратного обеспечения, или в виде комбинации того и другого. Исполняемый код для способа согласно настоящему изобретению может храниться в компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя устройства памяти, оптические запоминающие устройства, интегральные схемы, серверы, онлайновое программное обеспечение и т.д. Предпочтительно, чтобы компьютерный программный продукт содержал средство долговременного хранения программного кода на машиночитаемом носителе для выполнения способа согласно изобретению, при выполнении на компьютере указанного программного продукта.
В предпочтительном варианте осуществления компьютерная программа содержит средство компьютерного программного кода, выполненное с возможностью осуществления всех этапов способа согласно настоящему изобретению при выполнении упомянутой компьютерной программы на компьютере. Предпочтительно, чтобы компьютерная программа была воплощена на машиночитаемом носителе.
Электронное вычислительное устройство может представлять собой мобильное электронное устройство, например, мобильный телефон, или телевизионную приставку, компьютер и т.д.
Способ согласно изобретению можно реализовать на компьютере в качестве компьютерно-реализуемого способа, специализированными аппаратными средствами, или в виде комбинации того и другого. Исполняемый код для способа согласно настоящему изобретению может храниться в компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя устройства памяти, оптические запоминающие устройства, интегральные схемы, серверы, онлайновое программное обеспечение и т.д. Предпочтительно, чтобы компьютерный программный продукт содержал средство долговременного хранения программного кода на машиночитаемом носителе для выполнения способа согласно изобретению, при выполнении на компьютере указанного программного продукта.
В предпочтительном варианте осуществления компьютерная программа содержит средство компьютерного программного кода, приспособленное выполнять все этапы способа согласно настоящему изобретению, при выполнении упомянутой компьютерной программы на компьютере. Предпочтительно, чтобы компьютерная программа была воплощена на машиночитаемом носителе.
Другой аспект изобретения обеспечивает способ создания компьютерной программы доступной для загрузки (скачивания). Этот аспект используют, когда компьютерная программа выгружается, например, в магазины Apple's App Store, Google's Play Store, или Microsoft's Windows Store, и когда эта компьютерная программа доступна для скачивания из указанного магазина.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Дополнительные подробности, аспекты и варианты осуществления изобретения описываются ниже исключительно в качестве примеров со ссылками на чертежи. Для упрощения и ясности изложения элементы на фигурах не обязательно представлены в масштабе. На этих фигурах элементы, соответствующие уже обсужденным элементам, могут иметь одинаковые ссылочные позиции. На чертежах:
фиг. 1а схематично показывает пример варианта осуществления электронного вычислительного устройства;
фиг. 1b схематично показывает пример остатка от деления остатка на первый модуль;
фиг. 2 схематично показывает пример варианта осуществления электронного вычислительного устройства;
фиг. 3 схематично показывает пример варианта осуществления способа электронного вычисления;
фиг. 4а показывает машиночитаемый носитель, имеющий доступную для записи часть, содержащую компьютерную программу согласно одному варианту осуществления;
фиг. 4b показывает схематическое представление обрабатывающей системы согласно одному варианту осуществления.
Список ссылочных позиций на фигурах 1-2
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Хотя данное изобретение допускает возможность его реализации во множестве различных видов, на чертежах показаны и подробно описываются один или более конкретных вариантов его осуществления, причем необходимо понимать, что настоящее раскрытие следует рассматривать в качестве примера реализации принципов изобретения, а не как ограничение изобретения показанными и описанными конкретными вариантами осуществления.
Далее для понимания сути изобретения описаны в действии элементы вариантов его осуществления. Однако следует понимать, что соответствующие элементы выполнены с возможностью реализации функций, описанных как подлежащих выполнению ими.
На фиг. 1а схематически показан пример варианта осуществления электронного вычислительного устройства 100.
Вычислительное устройство 100 содержит область 110 хранения операндов. Область 110 хранения операндов выполнена с возможностью хранения одного или более операндов, над которыми должны выполняться вычисления. Вычисления включают в себя операции сложения. Вычисления также могут включать в себя операции умножения. Путем комбинирования операций сложения и/или умножения с управляющей логикой можно сформировать дополнительные операции, например, операции вычитания и деления.
На фиг. 1а показано два операнда, хранящихся в области 110 хранения операндов: операнд 101 и операнд 106. Хотя на фиг. 1а показано только два операнда, возможно большее количество операндов. Операнды представляют остаток от деления остатка на комбинированный модуль (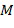 ). Операнды представлены в виде, подходящем для системы остаточных классов. Система остаточных классов определяется рядом модулей (
). Операнды представлены в виде, подходящем для системы остаточных классов. Система остаточных классов определяется рядом модулей (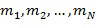 ). Каждый модуль определяет одно коммутативное кольцо. В одном варианте осуществления все модули являются целыми числами, или все они представляют собой многочлены. В последнем случае многочлены имеют коэффициенты, которые берутся из одного и того же кольца для всех многочленов. Коэффициенты этих многочленов могут представлять собой модулярные коэффициенты, то есть, остатки от деления целых чисел на модуль. Модуль, используемый для определения кольца для коэффициентов, одинаков для всех модулей.
). Каждый модуль определяет одно коммутативное кольцо. В одном варианте осуществления все модули являются целыми числами, или все они представляют собой многочлены. В последнем случае многочлены имеют коэффициенты, которые берутся из одного и того же кольца для всех многочленов. Коэффициенты этих многочленов могут представлять собой модулярные коэффициенты, то есть, остатки от деления целых чисел на модуль. Модуль, используемый для определения кольца для коэффициентов, одинаков для всех модулей.
В том случае, когда модуль 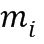 из ряда модулей является целым числом, соответствующее кольцо обозначается как
из ряда модулей является целым числом, соответствующее кольцо обозначается как 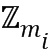 . В том случае, когда модуль
. В том случае, когда модуль 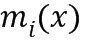 из ряда модулей является многочленом, соответствующее кольцо обозначается как
из ряда модулей является многочленом, соответствующее кольцо обозначается как 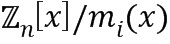 . В последнем примере общий модуль для коэффициентов многочленов обозначен как
. В последнем примере общий модуль для коэффициентов многочленов обозначен как 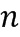 .
.
В качестве комбинированного модуля можно взять наименьшее общее кратное модулей (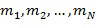 ) в ряде модулей. В том случае, когда модули являются парными простыми числами, комбинированный модуль можно взять в виде произведения модулей. Для представления остатка от деления числа
) в ряде модулей. В том случае, когда модули являются парными простыми числами, комбинированный модуль можно взять в виде произведения модулей. Для представления остатка от деления числа 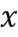 на комбинированный модуль в системе остаточных классов данное число отображают в ряд
на комбинированный модуль в системе остаточных классов данное число отображают в ряд 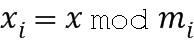 , где
, где 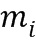 пробегает значения от модуля
пробегает значения от модуля 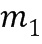 до модуля
до модуля 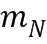 . В одном варианте осуществления комбинированный модуль является собственным делителем наименьшего общего кратного. Такой подход имеет недостаток, заключающийся в том, что пространство чисел, которые могут быть представлены, оказывается меньшим, но, с другой стороны, числа получают множество представлений, которые могут понадобиться в некоторых вариантах осуществления обфускационных вычислений.
. В одном варианте осуществления комбинированный модуль является собственным делителем наименьшего общего кратного. Такой подход имеет недостаток, заключающийся в том, что пространство чисел, которые могут быть представлены, оказывается меньшим, но, с другой стороны, числа получают множество представлений, которые могут понадобиться в некоторых вариантах осуществления обфускационных вычислений.
Операнд, хранящийся в области 110 хранения операндов, представлен в виде ряда остатков от деления элементов кольца на модули. Хотя каждый элемент кольца ряда связан с соответствующим модулем из ряда модулей, нет необходимости хранить данный ряд в упорядоченном виде. Например, ряд можно хранить в распределенном виде по всей области хранения операндов.
На фиг. 1а показан первый операнд 101, хранящийся в виде ряда из трех остатков: остатка 102 от деления на первый модуль, остатка 103 от деления на второй модуль и остатка 104 от деления на третий модуль. Аналогичным образом второй операнд 106 хранится в виде ряда из трех остатков: остатка 107 от деления на первый модуль, остатка 108 от деления на второй модуль и остатка 109 от деления на третий модуль. Первый, второй и третий остатки являются остатками от деления на модуль 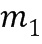 ,
, 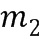 и
и 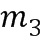 , соответственно. Возможно другое количество модулей, например, только два модуля или больше 3. Как правило, все модули разные. В одном варианте осуществления модули являются парными простыми числами. Для парных простых модулей комбинированный модуль можно взять в виде произведения модулей, что приводит к относительно большому значению комбинированного модуля.
, соответственно. Возможно другое количество модулей, например, только два модуля или больше 3. Как правило, все модули разные. В одном варианте осуществления модули являются парными простыми числами. Для парных простых модулей комбинированный модуль можно взять в виде произведения модулей, что приводит к относительно большому значению комбинированного модуля.
Вычислительное устройство 100 содержит вычислительный блок 130, выполненный с возможностью сложения и/или умножения первого и второго операнда из области хранения операндов в соответствии с системой остаточных классов. Рассмотрим, например, два операнда 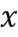 и
и 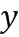 , например, операнды 101 и 106, представленные в виде двух рядов
, например, операнды 101 и 106, представленные в виде двух рядов 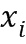 и
и 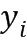 (в ряде операндов индекс пробегает значения для обращения ко всем модулям, например, от 1 до
(в ряде операндов индекс пробегает значения для обращения ко всем модулям, например, от 1 до 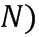 . Для сложения двух операндов вычислительное устройство может вычислить ряд
. Для сложения двух операндов вычислительное устройство может вычислить ряд 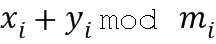 ; заметим, что каждый элемент ряда является вычисленным остатком от деления на соответствующий модуль из ряда модулей. Аналогичным образом, для умножения двух операндов вычислительное устройство может вычислить ряд
; заметим, что каждый элемент ряда является вычисленным остатком от деления на соответствующий модуль из ряда модулей. Аналогичным образом, для умножения двух операндов вычислительное устройство может вычислить ряд 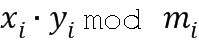 ; здесь также каждый элемент ряда представляет собой вычисленный остаток от деления на соответствующий модуль из ряда модулей. Результатом использования системы остаточных классов является то, что эти результаты в представлении сложения и умножения являются остатками от деления на комбинированный модуль. Последний случай подтверждается так называемой китайской теоремой об остатках.
; здесь также каждый элемент ряда представляет собой вычисленный остаток от деления на соответствующий модуль из ряда модулей. Результатом использования системы остаточных классов является то, что эти результаты в представлении сложения и умножения являются остатками от деления на комбинированный модуль. Последний случай подтверждается так называемой китайской теоремой об остатках.
По меньшей мере для одной из последних операций сложения или умножения используют гомогенную обфускацию. Из этого следует, что реальное вычисление, которое выполняется, включает в себя операцию вычисления остатка от деления для другого модуля, отличного от модуля 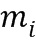 . Таким образом, хотя функционально выполняется нахождение остатка от деления сложения или умножения на конкретный модуль
. Таким образом, хотя функционально выполняется нахождение остатка от деления сложения или умножения на конкретный модуль 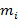 , реальное вычисление показывает только операцию нахождения остатка от деления для другого числа. Эта любопытная ситуация является одним из последствий гомогенной обфускации и дополнительно раскрывается ниже и в упомянутой предшествующей заявке.
, реальное вычисление показывает только операцию нахождения остатка от деления для другого числа. Эта любопытная ситуация является одним из последствий гомогенной обфускации и дополнительно раскрывается ниже и в упомянутой предшествующей заявке.
Модули 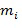 в этом варианте осуществления были специально выбраны так, чтобы они позволяли выполнение гомогенной обфускации. В частности, для каждого модуля (
в этом варианте осуществления были специально выбраны так, чтобы они позволяли выполнение гомогенной обфускации. В частности, для каждого модуля (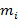 ) из ряда существует ассоциированный базовый элемент (
) из ряда существует ассоциированный базовый элемент (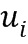 ), удовлетворяющий условию, заключающемуся в том, что остаток от деления каждого элемента (
), удовлетворяющий условию, заключающемуся в том, что остаток от деления каждого элемента (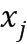 ) кольца на модуль (
) кольца на модуль (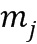 ) можно выразить в виде целочисленного списка
) можно выразить в виде целочисленного списка 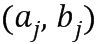 , так чтобы элементы кольца представляли линейную комбинацию степеней базового элемента, каковые степени имеют показатели, определенные целочисленным списком. Каноническим способом представления элемента
, так чтобы элементы кольца представляли линейную комбинацию степеней базового элемента, каковые степени имеют показатели, определенные целочисленным списком. Каноническим способом представления элемента 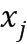 кольца в виде линейной комбинации степеней является представление элемента
кольца в виде линейной комбинации степеней является представление элемента 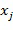 кольца в виде разности между двумя степеням базового элемента; при этом показатели степеней содержатся в целочисленном списке. Например, остаток от деления каждого элемента
кольца в виде разности между двумя степеням базового элемента; при этом показатели степеней содержатся в целочисленном списке. Например, остаток от деления каждого элемента 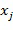 кольца на
кольца на 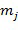 можно записать в виде
можно записать в виде 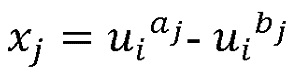 . Также будем обращаться к этому представлению как к примерному представлению. Имеются разные подходы к представлению элемента кольца, например,
. Также будем обращаться к этому представлению как к примерному представлению. Имеются разные подходы к представлению элемента кольца, например, 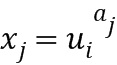 +
+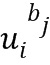 . Еще больше примеров представлено в предшествующей заявке.
. Еще больше примеров представлено в предшествующей заявке.
На фиг. 1b схематически показан пример остатка от деления на первый модуль. Показан список из целых чисел, содержащий целые числа 107.1 и 107.2. Например, остаток 107 можно представить двумя целыми числами 107.1 и 107.2, так чтобы представленный остаток представлял собой линейную комбинацию степеней базового элемента 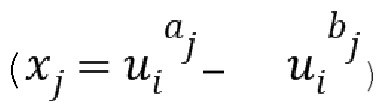 , где степени имеют показатели, определенные целочисленным списком. В этом примере целым числом 107.1 может быть
, где степени имеют показатели, определенные целочисленным списком. В этом примере целым числом 107.1 может быть 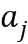 , а целым числом 107.2 может быть
, а целым числом 107.2 может быть 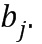 Остаток в операнде 102 для одного и того же модуля также представлен в виде целочисленного списка, использующего целые числа 102.1 и 102.2. В одном варианте осуществления целые числа в целочисленных списках находятся в диапазоне от 0 до порядка базового элемента минус 1 (включительно).
Остаток в операнде 102 для одного и того же модуля также представлен в виде целочисленного списка, использующего целые числа 102.1 и 102.2. В одном варианте осуществления целые числа в целочисленных списках находятся в диапазоне от 0 до порядка базового элемента минус 1 (включительно).
Аналогичным образом в области 110 хранения могут храниться другие остатки, например, 102, 103, 104, 108, 109. В одном варианте осуществления все элементы кольца в ряду, связанном с конкретным модулем, представлены в виде целочисленного списка. Например, если элемент 107 кольца представлен в виде целочисленного списка, то тогда соответствующий элемент кольца 102 также можно представить в виде целочисленного списка, используя один и тот же базовый элемент; это позволяет выполнять вычисления с обоими элементами 107 и 102, с использованием гомогенной обфускации.
Выполнение арифметических операций с остатками с использованием гомогенной обфускации обычно включает два типа операций: арифметические операции над остатками от деления целых чисел в целочисленном списке на порядок базового элемента, и применение таблицы. Эта последняя таблица называется таблицей приращений, поскольку она добавляет фиксированный элемент к элементу кольца, определенному из целых чисел в целочисленном списке. Существуют разные подходы к организации этих вычислений. Ниже объясняется, как они могут быть выполнены для примерного представления, больше примеров приведены в предыдущей заявке.
Обратимся к фиг. 1а, где вычислительное устройство 100 содержит область 120 хранения таблиц. Область 120 хранения таблиц выполнена с возможность хранения, для каждого из модулей в ряде, таблицы (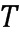 ) приращений, определенной для элемента (-1; 1;
) приращений, определенной для элемента (-1; 1; 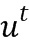 ) приращения, связанного с модулем из ряда модулей. В примере по фиг. 1 имеется три разных модуля, каждый из которых связан с одним из трех базовых элементов, и каждый из которых связан с таблицей приращений. В области 120 хранения таблиц хранится ряд таблиц 121 приращений. Ряд содержит таблицы 122, 123 и 124 приращений. Заметим, что таблицы
) приращения, связанного с модулем из ряда модулей. В примере по фиг. 1 имеется три разных модуля, каждый из которых связан с одним из трех базовых элементов, и каждый из которых связан с таблицей приращений. В области 120 хранения таблиц хранится ряд таблиц 121 приращений. Ряд содержит таблицы 122, 123 и 124 приращений. Заметим, что таблицы 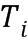 соответствуют модулям
соответствуют модулям 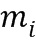 и базовым элементам
и базовым элементам 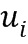 . Эти модули и базовые элементы во время вычисления не требуются, и также не требуется их хранение в явном виде в вычислительном устройстве 100; однако для выполнения вычисления потребуются таблицы приращений. Таблица приращений зависит от модуля, базового элемента, выбранного линейного отображения между степенями и элементами кольца и от значения приращения.
. Эти модули и базовые элементы во время вычисления не требуются, и также не требуется их хранение в явном виде в вычислительном устройстве 100; однако для выполнения вычисления потребуются таблицы приращений. Таблица приращений зависит от модуля, базового элемента, выбранного линейного отображения между степенями и элементами кольца и от значения приращения.
Таблица приращений отображает входной элемент (например, 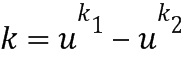 ) кольца в выходной целочисленный список (например,
) кольца в выходной целочисленный список (например, 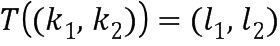 ), кодирующий выходной элемент (например,
), кодирующий выходной элемент (например, 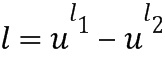 ) кольца, так что выходной элемент кольца равен элементу приращения, добавляемому к входному элементу (например,
) кольца, так что выходной элемент кольца равен элементу приращения, добавляемому к входному элементу (например, 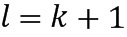 ) кольца, выходной элемент кольца равен линейной комбинации степеней базового элемента (
) кольца, выходной элемент кольца равен линейной комбинации степеней базового элемента (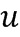 ), где степени имеют показатели, определенные выходным целочисленным списком.
), где степени имеют показатели, определенные выходным целочисленным списком.
Значение приращения может быть равным 1, но не обязательно; возможны также значения -1 или значение степени базового элемента, а также другие значения.
Вернемся к вычислительному блоку 130. Как было отмечено выше, используя систему остаточных классов, можно выполнять нахождение остатка от деления сложения и умножения на комбинированный модуль посредством выполнения ряда отдельных вычислений, каждый из которых является остатком от деления на один модуль из данного ряда модулей. Например, вычислительный блок 130 может содержать ряд блоков 131 сложения и ряд блоков 136 умножения. Если операции умножения не требуются, то блоки умножения можно опустить. Каждый из блоков сложения и/или умножения вычисляет остаток от деления на один из указанных модулей. На фиг. 1 показаны блоки 132, 133 и 134 сложения и блоки 135, 137 и 139 умножения.
Вычислительный блок 130 также содержит ряд операторов 141 нахождения остатка от деления, реализованных, например, в виде блоков нахождения остатка от деления. Операторы нахождения остатка от деления выполняют операцию нахождения остатка от деления на порядок базового элемента, ассоциированного с модулем из ряда модулей. Заметим, что сами по себе операторы 141 нахождения остатка от деления не предназначены для выполнения операций нахождения остатка от деления на модули в упомянутом ряду. Хотя функционально операции нахождения остатка от деления на модули в ряду вычисляются, при кодировании с использованием гомогенной обфускации фактическим вычислением, которое выполняется, является операция нахождения остатка от деления на порядок базового элемента. Эти операции нахождения остатка от деления на разные числа, то есть, разные порядки базового элемента, могут реализовать операцию нахождения остатка от деления в процессе кодирования, инициируемого гомогенной обфускацией. Операторы 141 нахождения остатка от деления используются соответствующими блоками 131 и 136 сложения и умножения.
Суммируя вышесказанное, можно констатировать, что операнды представляются в виде остатка от деления на некоторое число разных модулей. Базовый элемент и таблица ассоциированы с каждым модулем. По меньшей мере один, но возможно все из остатков представлены в виде целочисленных списков; причем это представление зависит от базового элемента, связанного с модулем остатка. Операция нахождения остатка от деления, использующая порядок базового элемента, ассоциированного с модулем, используется одним или более блоками сложения и блоками умножения. В примере по фиг. 1а остатки 102 и 107 ассоциированы с одним и тем же модулем, таблица 122 предназначена для базового элемента, ассоциированного с этим модулем, блок 132 сложения и блок 137 умножения выполняют операции нахождения остатка от деления на эти модули, используя оператор 142 нахождения остатка от деления. Аналогичным образом то же самое выполняется и для других модулей.
На фиг. 1а все элементы, связанные с одним и тем же модулем из ряда модулей, скомпонованы в вертикальном столбце. В этом примере были использованы три разных модуля. Также возможно использование двух модулей или более трех модулей.
Не обязательно, чтобы все остатки от деления на модули из ряда модулей кодировались с использованием гомогенной обфускации, то есть, были представлены в виде целочисленного списка. Например, некоторые могут быть представлены как простые значения, например, как остаток от деления целого числа на ассоциированный модуль. Например, некоторые могут быть закодированы по-другому, скажем, с использованием традиционной негомогенной таблицы на основе кодирования. Так как система остаточных классов оперирует каждым модулем в отдельности, такое разное кодирование можно использовать одновременно. В последующих примерах предполагается, что все остатки в ряду для операнда представлены с использованием гомогенной обфускации как в виде целочисленного списка.
В процессе функционирования вычислительный блок 130 может сложить операнды 101 и 106. Это можно сделать следующим образом. Блок 131 сложения или блок 136 умножения производит действия над целочисленными списками 102 и 107 для получения промежуточного целочисленного списка; операция нахождения остатка от деления применяется к каждому элементу в промежуточном целочисленном списке с использованием оператора 142 нахождения остатка от деления, то есть, остаток от деления на базу ассоциированного базового элемента. К результирующему промежуточному целочисленному списку применяется таблица 122. Блок сложения или умножения может продолжать работать с результатом, полученным путем применения таблицы, и целочисленными списками 102 или 107, выполнять вторую операцию нахождения остатка от деления, используя модулярный оператор 142, и вновь применять таблицу 122. Более подробные описания операций сложения и умножения можно найти в предшествующей заявке. Аналогичные операции выполняются и для других модулей.
В результате получают представление сложения или умножения в виде целочисленных списков. Этот результат можно сохранить в области 110 хранения операндов и использовать для будущих вычислений. Комбинируя операции сложения и умножения, можно реализовать и другие операции.
В предшествующей заявке дано множество примеров целочисленных колец (остаток от деления целого числа на целочисленный модуль) или колец многочленов (многочлены с остатком от деления модулярных коэффициентов на модуль многочлен).
На фиг. 2 схематически показан пример варианта осуществления электронного вычислительного устройства 200. Устройство 200 основано на устройстве 100. Область 110 хранения операндов и область 120 хранения таблиц в устройстве 200 могут быть такими же, как в устройстве 100. Устройство 200 отличается выбором модулей и базовых элементов и вычислительного устройства 230.
Для устройства 200 порядок по меньшей мере двух базовых элементов, ассоциированных с двумя разными модулями из указанного ряда модулей, одинаков. Предпочтительно, чтобы все порядки всех базовых элементов, ассоциированных с модулями ряда модулей, были одинаковы. Как и в устройстве 100, комбинированный модуль может быть равен наименьшему общему кратному модулей(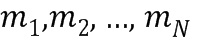 ) в ряду модулей. На фиг. 2 показан случай, когда все порядки одинаковы.
) в ряду модулей. На фиг. 2 показан случай, когда все порядки одинаковы.
Если два базовых элемента имеют одинаковый порядок, даже если эти базовые элементы ассоциированы с разными модулями, оператор нахождения остатка от деления может совместно использоваться для операций вычисления остатка от деления для этого модуля. Заметим, что каждый модуль продолжает иметь собственную таблицу приращений в области 120 хранения таблиц. Если порядок базового элемента разных модулей одинаков, все операции с целочисленными списками будут одинаковыми, включая операцию нахождения остатка от деления, а именно, остатка от деления на порядок базового элемента. Однако операция с таблицей остается уникальной для каждого отличающегося от других модуля. Таким образом, в высокой степени вычисления для разных модулей будут идентичными, но только с использованием разных таблиц приращений. Даже размер таблиц приращений может быть одинаков, так как размер таблицы приращений может зависеть от порядка базового элемента. (Заметим, что в особо сложных операциях различие между целыми числами в целочисленном списке ограничено допустимым разностным множеством. Это может привести к тому, что размер таблиц приращений будет отличаться для разных модулей).
Вычислительный блок 230, показанный на фиг. 2, содержит оператор 242 нахождения остатка от деления, блок 232 сложения и блок 237 умножения.
В процессе функционирования вычислительный блок 230 может складывать операнды 101 и 106. Это может выполняться следующим образом. Блок 232 сложения или блок 237 умножения производит действия над целочисленными списками 102 и 107 для получения промежуточного целочисленного списка; выполняется операция нахождения остатка от деления для каждого элемента в промежуточном целочисленном списке с использованием оператора 242 нахождения остатка от деления, то есть, остатка от деления на базу ассоциированного базового элемента. К результирующему промежуточному целочисленному списку применяется таблица 122. Блок сложения или умножения может продолжать работать с результатом, полученным путем применения этой таблицы, и целочисленными списками 232 и/или 237, выполнить вторую операцию нахождения остатка от деления, используя модулярный оператор 242, и вновь использовать таблицу 122.
Аналогичные операции выполняются для других модулей. Например, блок 232 сложения или 237 умножения выполняет действия с целочисленными списками 103 и 108 для получения промежуточного целочисленного списка, применяется операция нахождения остатка от деления к каждому элементу в промежуточном целочисленном списке с использованием оператора 242 нахождения остатка от деления, а именно, остатка от деления на базу ассоциированного базового элемента. К полученному в результате промежуточному целочисленному списку применяется таблица 123. Блок сложения или умножения может продолжать обработку результата, полученного путем применения таблицы, и целочисленных списков 232 и/или 237, выполнять вторую операцию нахождения остатка от деления, используя модулярный оператор 242, и вновь использовать таблицу 123, и т.д.
Блоки 232 сложения и блок 237 умножения выполнены с возможностью применения таблицы приращений, соответствующей модулям, для вычислений остатков от деления на модуль из ряда. В качестве альтернативы, блок 232 сложения и блок 237 умножения могут быть реализованы в виде ряда блоков сложения и умножения, как на фиг. 1. Каждый блок указанного ряда скомпонован для конкретной таблицы приращений, но с использованием оператора 242 нахождения остатка от деления.
Преимуществом использования одного оператора 242 нахождения остатка от деления является то, что из программного обеспечения вычислений невозможно определить, для какой операции нахождения остатка от деления выполняется вычисление.
Система остаточных классов (RNS) позволяет использовать небольшие модули для выполнения вычислений с модулями, имеющими большее значение. Все ниже перечисленные модули имеют базовый элемент порядка 30. Пример такого базового элемента порядка 30 представлен ниже для каждого модуля.
элемент
Эти модули можно использовать для создания системы счисления RNS. Например, из этих модулей можно отобрать два набора, которые имеют комбинированный модуль, превышающий 2^32=4294967296.
93 * 143 * 181 * 209 * 231=116213298201
99 * 151 * 183 * 211 * 241=139111402617
Заметим, что все модули в этих двух наборах являются взаимно-простыми. Таким образом, используя операции, где задействованы только те элементы, которые укладываются в один байт, можно выполнить вычислительную операцию с 32-битовыми словами. Полное описание системы RNS и Mixed Radix System можно найти, наример, в Omondi, A., Prekumar, B.: Residue Number Systems. Theory and Implementation. Imperial College Press.
Аналогичным образом можно построить систему остаточных классов многочленов. Например, выбрать несколько взаимно-простых многочленов, которые допускают применение гомогенной обфускации над одним и тем же базовым кольцом. Соответствующая система RNS позволяет реализовать обфускационные вычисления на гораздо больших многочленах, например, остаток от деления на произведение выбранных многочленов.
Область 110 хранения операндов и область 120 хранения таблиц могут быть реализованы в виде электронной памяти. Эти области могут быть объединены в единую область хранения, например, в виде единой электронной памяти. Таблицы приращений могут быть реализованы в виде просмотровых таблиц.
Как правило, устройства 100 и 200 содержат каждое микропроцессор (не показан), который исполняет соответствующее программное обеспечение, хранящееся в устройстве 100 и 200; например, это программное обеспечение может скачиваться или храниться в соответствующей памяти, например, энергозависимой памяти, такой как RAM, или энергонезависимой памяти, такой как флэш-память (не показана). В качестве альтернативы, устройства 100 и 200 могут быть в целом или частично реализованы в программируемой логике, например, в виде вентильной матрицы, программируемой пользователем (FPGA). Устройства 100 и 200 могут быть в целом или частично реализованы в виде так называемой прикладной специализированной интегральной схемы (ASIC), то есть, интегральной схемы (IC), разработанной для конкретного использования. Область хранения таблиц и операндов может быть реализована в виде электронной памяти, магнитного запоминающего устройства и т.п. Эта память может быть энергозависимой или энергонезависимой.
В одном варианте осуществления устройство содержит схему хранения операндов и вычислительную схему. Устройство может содержать дополнительные схемы, например, одну или более схем модулярных операций, схему сложения, схему умножения и схему хранения таблиц; причем указанные схемы реализуют соответствующие описанные здесь блоки. Указанные схемы могут представлять собой обрабатывающую схему и схему хранения, где обрабатывающая схема исполняет команды, представленные электронным путем в схемах хранения. Эти схемы также могут представлять собой FPGA, ASIC и т.п.
На фиг. 3 схематически показан пример варианта реализации способа 300 электронного вычисления. Способ электронного вычисления создан для выполнения обфускационных арифметических операций нахождения остатка от деления на комбинированный модуль (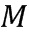 ) в системе остаточных классов. Система остаточных классов определена для ряда модулей (
) в системе остаточных классов. Система остаточных классов определена для ряда модулей (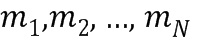 ), где каждый модуль определяет коммутативное кольцо (
), где каждый модуль определяет коммутативное кольцо (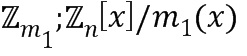 ). Для каждого модуля (
). Для каждого модуля (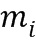 ) ряда существует соответствующий базовый элемент (
) ряда существует соответствующий базовый элемент (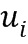 ), удовлетворяющий условию, заключающемуся в том, что остаток от деления каждого элемента (
), удовлетворяющий условию, заключающемуся в том, что остаток от деления каждого элемента (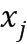 ) кольца на модуль (
) кольца на модуль (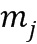 ) можно выразить в виде целочисленного списка (
) можно выразить в виде целочисленного списка (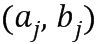 ), так что элементы кольца будут равны линейной комбинации степеней базового элемента (
), так что элементы кольца будут равны линейной комбинации степеней базового элемента (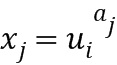 -
- 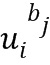 ), каковые степени имеют показатели, определенные упомянутым целочисленным списком. Способ содержит:
), каковые степени имеют показатели, определенные упомянутым целочисленным списком. Способ содержит:
запоминание 310 одного или более операндов нахождения остатка от деления на комбинированный модуль (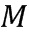 ) в виде одного или более рядов остатков от деления элементов кольца на модули, причем каждый элемент кольца из ряда ассоциирован с соответствующим модулем из ряда модулей, где по меньшей мере один элемент кольца из данного ряда кодируют в виде целочисленного списка,
) в виде одного или более рядов остатков от деления элементов кольца на модули, причем каждый элемент кольца из ряда ассоциирован с соответствующим модулем из ряда модулей, где по меньшей мере один элемент кольца из данного ряда кодируют в виде целочисленного списка,
сложение и/или умножение 320 первого и второго операнда из области хранения операндов согласно системе счисления элементов кольца.
Способ может быть расширен, например, как описано со ссылками на фигуры 1а, 1b и 2.
Возможно множество разных путей выполнения указанного способа, как очевидно специалистам в данной области техники. Например, может быть изменен порядок этапов, или некоторые этапы могут выполняться параллельно. Кроме того, между этапами могут выполняться этапы другого способа. Эти вставленные этапы могут представлять конкретные детали способа, как здесь было описано, или могут не иметь отношения к данному способу. Кроме того, заданный этап не обязательно должен полностью заканчиваться до начала следующего этапа.
Способ согласно изобретению можно выполнить, используя программное обеспечение, которое содержит команды, инициирующие выполнение обрабатывающей системой способа 300. Программное обеспечение может включать в себя только этапы, выполняемые конкретным составляющим субъектом системы. Программное обеспечение может храниться на подходящем носителе, таком как жесткий диск, гибкий диск, память и т.д. Программное обеспечение может быть передано в виде сигнала по проводам или беспроводным способом, либо с использованием сети передачи данных, например, Интернет. Программное обеспечение может быть выполнено в виде, доступном для скачивания и/или дистанционного использования на сервере. Способ согласно настоящему изобретению может выполняться с использованием битового потока предназначенного для конфигурирования программируемой логики, например, с использованием вентильной матрицы, программируемой пользователем (FPGA), для выполнения данного способа.
Очевидно, что изобретение также распространяется на компьютерные программы, в частности, на компьютерные программы, находящиеся на (или в) носителе, адаптированном для практической реализации изобретения. Программа может быть представлена в виде исходного кода, объектного кода, промежуточного исходного и объектного кода, такого как частично компилированная форма, или в любом другом виде, подходящем для использования при реализации способа согласно изобретению. Вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером команды, соответствующие каждому из этапов обработки по меньшей мере одного из изложенных здесь способов. Эти команды могут быть разделены на подпрограммы и/или храниться в одном или более файлах, которые могут иметь статическую или динамическую связь. Другой вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером команды, соответствующие каждому из средств по меньшей мере одной из описанных здесь систем и/или продуктов.
На фиг. 4а показан читаемый компьютером носитель 1000, имеющий доступную для записи часть 1010, содержащую компьютерную программу 1020, причем компьютерная программа 1020 содержит команды для инициирования выполнения обрабатывающей системой способа обфускационной арифметики согласно варианту осуществления изобретения. Компьютерная программа 1020 может быть воплощена на машиночитаемом носителе 1000 в виде физических меток или посредством намагничивания машиночитаемого носителя 1000. Однако может быть использован любой другой возможный вариант осуществления. Кроме того, следует иметь в виду, что, хотя машиночитаемый носитель 1000 показан здесь в виде оптического диска, машиночитаемый носитель 1000 может быть любым подходящим машиночитаемым носителем, таким как жесткий диск, твердотельная память, флэш-память и т.д., и может быть не перезаписываемым или перезаписываемым. Компьютерная программа 1020 содержит команды для инициирования выполнения обрабатывающей системой указанного способа обфускационной арифметики.
На фиг. 4b схематически показана обрабатывающая система 1100 согласно варианту осуществления изобретения. Обрабатывающая система содержит одну или более интегральных схем 1110. Архитектура одной или более интегральных схем 1110 схематически показана на фиг. 4b. Схема 1110 содержит обрабатывающий блок 1120, например, центральный процессор (CPU) для прогона компонентов компьютерной программы с целью выполнения способа согласно варианту осуществления изобретения или реализации ее модулей или блоков. Схема 1110 содержит память 1122 для хранения программирующего кода, данных и т.д. Часть памяти 1122 может быть предназначена только для считывания. Схема 1110 может содержать коммуникационный элемент 1126, например, антенну, соединители либо то и другое, и т.п. Схема 1110 может содержать специализированную интегральную схему 1124 для выполнения части или всей обработки, определенной в упомянутом способе. Процессор 1120, память 1122, специализированная интегральная схема 1124 и коммуникационный элемент 1126 могут быть соединены друг с другом через средство 1130 межсоединений, например, шину. Обрабатывающая система 1110 может быть выполнена с возможность контактной и/или бесконтактной связи с использованием антенны и/или соединителей соответственно.
В предшествующей заявке, на которую ссылались выше, приведены примеры варианта осуществления вычислительного устройства для выполнения обфускационной арифметики в коммутативном кольце. Здесь в вариантах осуществления изобретения применена гомогенная обфускация к отдельным модулям из ряда модулей.
Указанное вычислительное устройство может быть применено в устройстве 100 или 200, например, для реализации блока сложения и/или умножения. Вычислительное устройство и способ выполняют операции обфускационной арифметики в конечном коммутативном кольце. В одном приведенном примере, касающемся указанных колец, представлены остатки от деления целых чисел на число (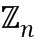 ). Согласно одному варианту осуществления устройство генерирования находит модуль таким образом, чтобы кольцо, сформированное остатками от деления целых чисел на этот модуль (
). Согласно одному варианту осуществления устройство генерирования находит модуль таким образом, чтобы кольцо, сформированное остатками от деления целых чисел на этот модуль (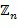 ), допускало использование обфускационной арифметики. Также создается базовый элемент, необходимый для кодирования и декодирования элементов кольца, например, целых чисел, в или вне обфускационной области.
), допускало использование обфускационной арифметики. Также создается базовый элемент, необходимый для кодирования и декодирования элементов кольца, например, целых чисел, в или вне обфускационной области.
Гомогенная обфускация, например, представление элементов кольца, в частности, остатки от деления целых чисел на модуль, относится к типу шифруемой арифметики, называемой также иногда гомоморфной криптографией. Используя обфускацию, например, защищают компьютерный программный код от попыток его обратного проектирования. Здесь обфускация является частью кода, который выполняет арифметические операции. В одном варианте осуществления цифровой обфускационной арифметики вычисления могут выполняться над зашифрованным текстом и создавать шифрованный результат, который при его расшифровке совпадает с результатом операций, выполненных над простым текстом. Другими словами, выходя за рамки традиционной обфускации программного обеспечения, арифметические операции можно выполнять над шифрованными значениями. Тем не менее, арифметика, реализованная с использованием гомогенной обфускации, функционально может быть идентична арифметике, выполняемой над простыми значениями.
Элементы кольца могут быть определены как остатки от деления целых чисел на модуль. Элементы кольца также могут называться кольцовыми элементами. Элементы кольца также могут называться остатками. Элемент кольца может быть представлен в цифровом виде как целое число в диапазоне от 0 до модуля минус 1; причем 0 и значение модуля минус 1 включены в этот список. На элементах кольца определено сложение и умножение, причем последние называется сложением в кольце и умножением в кольце.
Элементы кольца могут быть представлены в любой подходящей форме, если это необходимо. Например, элементы (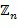 ) могут быть представлены целыми числами. Однако в вычислительном устройстве элементы кольца представлены в виде целочисленных списков. Например, элемент
) могут быть представлены целыми числами. Однако в вычислительном устройстве элементы кольца представлены в виде целочисленных списков. Например, элемент 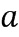 кольца может быть представлен в вычислительном устройстве списком
кольца может быть представлен в вычислительном устройстве списком 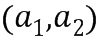 . Целочисленный список кодирует элемент кольца согласно некоторому отображению между элементами кольца и целочисленным списком, при каком-либо элементе кольца имеется по меньшей мере один целочисленный список, который представляет элемент кольца, и при заданном каком-либо целочисленном списке имеется ровно один элемент кольца, который он представляет. В вариантах осуществления любой элемент кольца может быть представлен в виде целочисленного списка.
. Целочисленный список кодирует элемент кольца согласно некоторому отображению между элементами кольца и целочисленным списком, при каком-либо элементе кольца имеется по меньшей мере один целочисленный список, который представляет элемент кольца, и при заданном каком-либо целочисленном списке имеется ровно один элемент кольца, который он представляет. В вариантах осуществления любой элемент кольца может быть представлен в виде целочисленного списка.
Целочисленные списки имеют по меньшей мере два элемента. Отсюда вытекает, что для операций сложения и умножения потребуется тем меньше этапов, чем короче целочисленный список. Соответственно, в варианте осуществления целочисленные списки всегда имеют два элемента. В основном описании предполагается, что целочисленные списки представляют собой целочисленные пары, однако в предшествующей заявке представлены целочисленные списки, имеющие более двух элементов. Например, 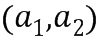 может отображаться в элемент (
может отображаться в элемент (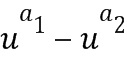 ) кольца, где
) кольца, где 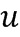 - особый элемент кольца, называемый базовым элементом кольца. В предшествующей заявке обсуждалось множество вариантов, включая использование множества базовых элементов. Однако в основном обсуждении предполагается в качестве примера кодирования, что данный целочисленный список
- особый элемент кольца, называемый базовым элементом кольца. В предшествующей заявке обсуждалось множество вариантов, включая использование множества базовых элементов. Однако в основном обсуждении предполагается в качестве примера кодирования, что данный целочисленный список 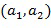 отображается в элемент (
отображается в элемент (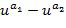 ) кольца. Таким образом, каждый элемент кольца можно выразить в виде разностями между двумя степенями базового элемента
) кольца. Таким образом, каждый элемент кольца можно выразить в виде разностями между двумя степенями базового элемента 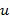 .
.
Далее представлено несколько примеров обфускационной арифметики, где используют модуль и базовый элемент, например, созданные генерирующим устройством согласно варианту осуществления. Представлены примеры кодирования, таблиц приращений, способов сложения в кольце и способов умножения в кольце. Блоки отрицания, сложения и умножения вычислительного устройства могут быть сконфигурированы для любого из указанных вариантов осуществления изобретения. Все примеры применимы к коммутативному кольцу 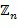 . Здесь
. Здесь 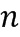 положительный целочисленный модуль. Любой элемент коммутативного кольца может быть представлен в выбранном варианте кодирования. Не все коммутативные кольца позволяют представить все элементы в данном варианте кодирования , например, в виде представления целочисленного списка заданного типа. Мы будем говорить, что данное коммутативное кольцо R позволяет (полную) гомогенную обфускацию, если любой элемент в R может быть представлен в виде целочисленного списка с использованием заданного типа кодирования. Специалисты в данной области техники могут проверить, позволяет ли заданное коммутативное кольцо полную гомогенную обфускацию при заданном варианте кодирования, например, путем создания всех возможных вариантов кодирования и подтверждения того, что они все вместе представляют все элементы заданного кольца.
положительный целочисленный модуль. Любой элемент коммутативного кольца может быть представлен в выбранном варианте кодирования. Не все коммутативные кольца позволяют представить все элементы в данном варианте кодирования , например, в виде представления целочисленного списка заданного типа. Мы будем говорить, что данное коммутативное кольцо R позволяет (полную) гомогенную обфускацию, если любой элемент в R может быть представлен в виде целочисленного списка с использованием заданного типа кодирования. Специалисты в данной области техники могут проверить, позволяет ли заданное коммутативное кольцо полную гомогенную обфускацию при заданном варианте кодирования, например, путем создания всех возможных вариантов кодирования и подтверждения того, что они все вместе представляют все элементы заданного кольца.
Далее сначала описывается заданный тип кодирования. Имеется много типов кодирования, которые в общем случае дают возможность представления элементов кольца в виде списка целых чисел. Эти целые числа не являются элементами кольца, например, если даже кольцо не является целочисленным кольцом, к примеру, кольцо многочлена, тем не менее элементы могут быть представлены в виде целочисленных списков. Используемый здесь термин «кодирование» раскрывает, каким образом данный целочисленный список отображается в элемент кольца. Как правило, целочисленные списки всегда будут иметь одинаковую длину, однако это не является обязательным. В общем случае, так как кодирование допускает несколько типов целочисленных списков, например, более длинные списки, оно скорее всего приведет к тому, что данный элемент кольца может быть закодирован в виде целочисленного списка разными способами. При заданном коммутативном кольце 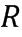 с примерным кодированием имеется особый элемент
с примерным кодированием имеется особый элемент 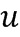 кольца, с использованием которого любой элемент
кольца, с использованием которого любой элемент 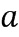 из
из 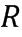 может быть записан в виде (
может быть записан в виде (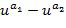 ) для некоторых целых чисел
) для некоторых целых чисел 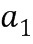 и
и 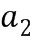 . На указанный особый элемент кольца ссылаются как на базовый элемент кольца. Не все коммутативные кольца могут быть закодированы таким образом, но достаточно много из них пригодны для данного типа кодирования. Целые числа
. На указанный особый элемент кольца ссылаются как на базовый элемент кольца. Не все коммутативные кольца могут быть закодированы таким образом, но достаточно много из них пригодны для данного типа кодирования. Целые числа 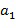 и
и 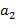 сами по себе не являются элементами кольца R; они представляют собой целые числа, над которыми выполняют операцию нахождения остатка от деления на порядок базового элемента. Заметим, что элемент
сами по себе не являются элементами кольца R; они представляют собой целые числа, над которыми выполняют операцию нахождения остатка от деления на порядок базового элемента. Заметим, что элемент 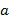 кольца равен линейной комбинации степеней базового элемента
кольца равен линейной комбинации степеней базового элемента 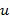 , а именно,
, а именно, 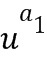 и
и 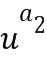 ; в этом случае линейную комбинацию получают путем умножения степеней на +1 или -1 и их сложения, а точнее, путем вычитания второй степени из первой степени. Вычислительное устройство производит операции над элементами кольца, закодированными вышеописанным образом. Блоки сложения, отрицания и умножения могут производить операции над элементами кольца при этом кодировании.
; в этом случае линейную комбинацию получают путем умножения степеней на +1 или -1 и их сложения, а точнее, путем вычитания второй степени из первой степени. Вычислительное устройство производит операции над элементами кольца, закодированными вышеописанным образом. Блоки сложения, отрицания и умножения могут производить операции над элементами кольца при этом кодировании.
Таблица 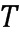 приращений играет центральную роль как в операции сложения, так и в операции умножения. Таблица приращений отображает входной элемент кольца, в этом случае входной элемент кольца может быть представлен в виде целочисленного списка. Например, при заданном входном целочисленном списке
приращений играет центральную роль как в операции сложения, так и в операции умножения. Таблица приращений отображает входной элемент кольца, в этом случае входной элемент кольца может быть представлен в виде целочисленного списка. Например, при заданном входном целочисленном списке 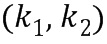 , представляющем входной элемент
, представляющем входной элемент 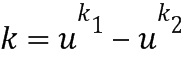 кольца, таблица
кольца, таблица 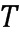 отображает его в выходной целочисленный список, например,
отображает его в выходной целочисленный список, например, 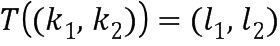 , кодирующую выходной элемент
, кодирующую выходной элемент 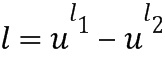 кольца. Выходной элемент кольца равен элементу кольца приращений, сложенному с входным элементом кольца. В этом примере элемент приращения может быть принят равным 1, то есть, элемент кольца, который является единичным для кольцевого умножения; в этом случае
кольца. Выходной элемент кольца равен элементу кольца приращений, сложенному с входным элементом кольца. В этом примере элемент приращения может быть принят равным 1, то есть, элемент кольца, который является единичным для кольцевого умножения; в этом случае 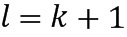 . Удобно, что эту таблицу можно применить непосредственно к элементам кольца, для которых используется один и тот же тип кодирования, и, следовательно, которая может быть применена к элементам кольца, представленным в виде целочисленного списка. Тем не менее, имеются варианты осуществления, в которых таблицу применяют к элементам кольца при альтернативном кодировании. Альтернативное кодирование также может представлять целочисленный список, но альтернативного типа. Также элемент кольца приращения не обязательно должен быть равен 1.
. Удобно, что эту таблицу можно применить непосредственно к элементам кольца, для которых используется один и тот же тип кодирования, и, следовательно, которая может быть применена к элементам кольца, представленным в виде целочисленного списка. Тем не менее, имеются варианты осуществления, в которых таблицу применяют к элементам кольца при альтернативном кодировании. Альтернативное кодирование также может представлять целочисленный список, но альтернативного типа. Также элемент кольца приращения не обязательно должен быть равен 1.
Ниже описываются операции отрицания, сложения и умножения.
Отрицание. При заданном целочисленном списке 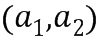 , являющимся вводом в отрицание, который представляет элемент
, являющимся вводом в отрицание, который представляет элемент 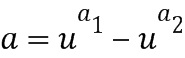 кольца ввода в отрицание, целочисленный список вывода из отрицания можно получить путем перестановки целочисленного списка, в данном случае, путем реверсирования порядка. Целочисленный список вывода из отрицания может представлять собой
кольца ввода в отрицание, целочисленный список вывода из отрицания можно получить путем перестановки целочисленного списка, в данном случае, путем реверсирования порядка. Целочисленный список вывода из отрицания может представлять собой 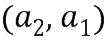 . Предположим, что существует
. Предположим, что существует 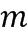 , такое что
, такое что 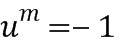 , что случается для базовых элементов с четным порядком, и тогда в альтернативном варианте отрицание можно получить путем прибавления константы, например,
, что случается для базовых элементов с четным порядком, и тогда в альтернативном варианте отрицание можно получить путем прибавления константы, например, 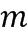 к каждому целому числу из целочисленного списка. В последнем случае целочисленный список вывода из отрицания может быть представлен в виде
к каждому целому числу из целочисленного списка. В последнем случае целочисленный список вывода из отрицания может быть представлен в виде 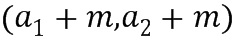 . Это получается потому, что
. Это получается потому, что 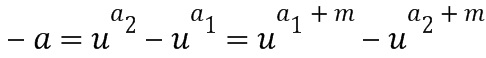 . Арифметические операции над целочисленным списком предпочтительно выполнять над остатками от деления на порядок базового элемента. Здесь целое число из целочисленных списков соответствует показателю степени базового элемента, так как целые числа, которые представляют собой одинаковый модуль порядка базового элемента, кодируют один и тот же элемент кольца.
. Арифметические операции над целочисленным списком предпочтительно выполнять над остатками от деления на порядок базового элемента. Здесь целое число из целочисленных списков соответствует показателю степени базового элемента, так как целые числа, которые представляют собой одинаковый модуль порядка базового элемента, кодируют один и тот же элемент кольца.
Сложение. Для сложения принятого первого целочисленного списка 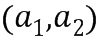 , являющегося вводом в сложение, кодирующего первый элемент
, являющегося вводом в сложение, кодирующего первый элемент 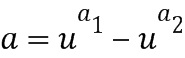 кольца ввода в сложение, со вторым целочисленным списком
кольца ввода в сложение, со вторым целочисленным списком 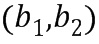 ввода в сложение, кодирующим второй элемент
ввода в сложение, кодирующим второй элемент 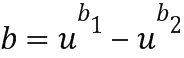 кольца ввода в сложение, сначала определяют промежуточный целочисленный список (
кольца ввода в сложение, сначала определяют промежуточный целочисленный список (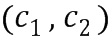 ) сложения, кодирующий промежуточный элемент
) сложения, кодирующий промежуточный элемент 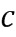 кольца сложения.
кольца сложения.
Элемент 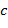 кольца может представлять собой первый элемент
кольца может представлять собой первый элемент 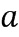 кольца ввода в сложение плюс базовый элемент
кольца ввода в сложение плюс базовый элемент 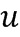 в степени, определенной из второго целочисленного списка ввода в сложение, в частности, первого целого числа из второго целочисленного списка ввода в сложение. В этом примере имеем, что
в степени, определенной из второго целочисленного списка ввода в сложение, в частности, первого целого числа из второго целочисленного списка ввода в сложение. В этом примере имеем, что 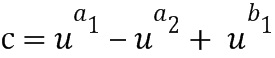 . Для вычисления последнего выражения имеем в виду, что
. Для вычисления последнего выражения имеем в виду, что 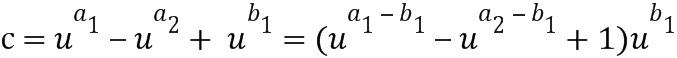 . Член в скобках можно перезаписать при кодировании, используя таблицу приращений. Посредством первого применения таблицы приращений к элементу
. Член в скобках можно перезаписать при кодировании, используя таблицу приращений. Посредством первого применения таблицы приращений к элементу 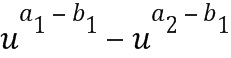 кольца получим элемент
кольца получим элемент 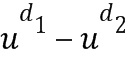 =
=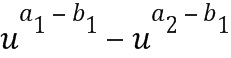 +1. Например, посредством
+1. Например, посредством 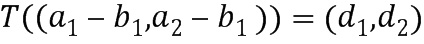 . Тогда имеем, что
. Тогда имеем, что 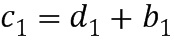 и
и 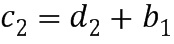 . Это показывает, что определение промежуточного целочисленного списка
. Это показывает, что определение промежуточного целочисленного списка 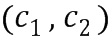 сложения дополнительно может содержать сложение целого числа, определенного из второго целочисленного списка ввода в сложение с целыми числами в целочисленном списке, являющемся результатом первого применения таблицы. Сложение
сложения дополнительно может содержать сложение целого числа, определенного из второго целочисленного списка ввода в сложение с целыми числами в целочисленном списке, являющемся результатом первого применения таблицы. Сложение 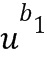 с элементом кольца в представлении целочисленного списка, в этом случае с
с элементом кольца в представлении целочисленного списка, в этом случае с 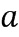 , иногда называют этапом положительной редукции.
, иногда называют этапом положительной редукции.
Блок сложения получил промежуточный элемент 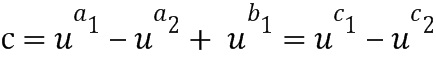 кольца сложения в виде целочисленного списка
кольца сложения в виде целочисленного списка 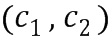 . Таким образом, промежуточный элемент кольца сложения представляет собой линейную комбинацию степеней одного или более базовых элементов, где степени определяют из первого и второго целочисленных списков ввода в сложение. В этом случае таблицу приращений применяют к элементу
. Таким образом, промежуточный элемент кольца сложения представляет собой линейную комбинацию степеней одного или более базовых элементов, где степени определяют из первого и второго целочисленных списков ввода в сложение. В этом случае таблицу приращений применяют к элементу 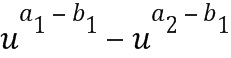 кольца, сформированному одним или более базовыми элементами (
кольца, сформированному одним или более базовыми элементами (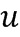 ) кольца, возведенными в степень первого целого числа из первого целочисленного списка (
) кольца, возведенными в степень первого целого числа из первого целочисленного списка (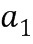 ) минус первое целое число из второго целочисленного списка (
) минус первое целое число из второго целочисленного списка (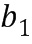 ) минус базовый элемент (
) минус базовый элемент (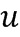 ) кольца, возведенный в степень второго целого числа из первого целочисленного списка (
) кольца, возведенный в степень второго целого числа из первого целочисленного списка (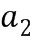 ) минус первое целое число из второго целочисленного списка (
) минус первое целое число из второго целочисленного списка (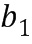 ).
).
В этом примере целочисленный список вывода из сложения можно определить посредством второго применения таблицы приращений к элементам кольца, определенным из промежуточного целочисленного списка сложения и второго целочисленных списков ввода в сложение. Это может содержать вычисление суммы промежуточного элемента 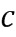 кольца сложения минус базовый элемент, возведенный в степень, определенную из второго целочисленного списка ввода в сложение, например, второго целого числа из второго целочисленного списка
кольца сложения минус базовый элемент, возведенный в степень, определенную из второго целочисленного списка ввода в сложение, например, второго целого числа из второго целочисленного списка 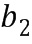 ввода в сложение:
ввода в сложение: 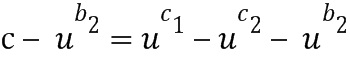 . Это может сопровождаться выполнением операции отрицания над промежуточным элементом кольца сложения, представленным промежуточным целочисленным списком сложения, перед вторым применением таблицы приращений. Операция отрицания над
. Это может сопровождаться выполнением операции отрицания над промежуточным элементом кольца сложения, представленным промежуточным целочисленным списком сложения, перед вторым применением таблицы приращений. Операция отрицания над 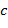 может быть выполнена, как указано выше. В качестве примера здесь используется перестановка, но аналогичная операция может быть выполнена путем прибавления константы к показателю степени. После выполнения операции отрицания в суммировании можно использовать плюс (вместо минуса) базовый элемент, возведенный в степень, определенную из второго целочисленного списка ввода в сложение:
может быть выполнена, как указано выше. В качестве примера здесь используется перестановка, но аналогичная операция может быть выполнена путем прибавления константы к показателю степени. После выполнения операции отрицания в суммировании можно использовать плюс (вместо минуса) базовый элемент, возведенный в степень, определенную из второго целочисленного списка ввода в сложение: 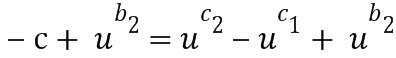 . Последняя операция относится к тому же типу, который был использован выше, и может быть выполнена посредством применения таблицы таким же образом в виде прибавления
. Последняя операция относится к тому же типу, который был использован выше, и может быть выполнена посредством применения таблицы таким же образом в виде прибавления 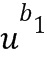 . После этого над полученным результатом снова выполняется операция отрицания. При полном сложении можно использовать две операции отрицания и два применения одной и той же таблицы
. После этого над полученным результатом снова выполняется операция отрицания. При полном сложении можно использовать две операции отрицания и два применения одной и той же таблицы 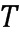 приращений.
приращений.
Вычитание 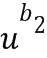 из элемента кольца в представлении целочисленного списка (например, добавление
из элемента кольца в представлении целочисленного списка (например, добавление 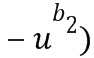 в этом случае из
в этом случае из 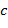 иногда называют этапом отрицательной свертки. Этап отрицательной свертки можно выполнить посредством операции отрицания, выполнения этапа положительной свертки и еще одной операции отрицания.
иногда называют этапом отрицательной свертки. Этап отрицательной свертки можно выполнить посредством операции отрицания, выполнения этапа положительной свертки и еще одной операции отрицания.
Имеется много вариантов, некоторые из которых описаны в предшествующей заявке. Например, вариант с использованием 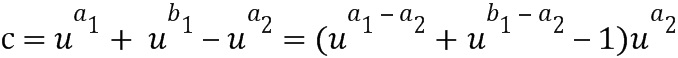 . В этом примере элемент приращения равен -1. Входами в таблицу приращений могут быть
. В этом примере элемент приращения равен -1. Входами в таблицу приращений могут быть 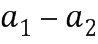 и
и 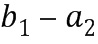 . Хотя последнее может быть записано в виде целочисленного списка, для целочисленного элемента, представленного ими, (
. Хотя последнее может быть записано в виде целочисленного списка, для целочисленного элемента, представленного ими, (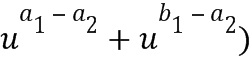 , используется кодирование, отличное от кодирования операндов (например,
, используется кодирование, отличное от кодирования операндов (например, 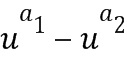 ).
).
Умножение. Для умножения полученного первого целочисленного списка 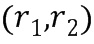 ввода в умножение, кодирующего первый элемент
ввода в умножение, кодирующего первый элемент 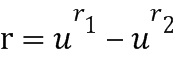 кольца ввода в умножение, на второй целочисленный список (
кольца ввода в умножение, на второй целочисленный список (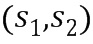 ) ввода в умножение, кодирующий второй элемент
) ввода в умножение, кодирующий второй элемент 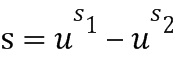 кольца ввода в умножение, определяют первый промежуточный целочисленный список
кольца ввода в умножение, определяют первый промежуточный целочисленный список 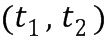 умножения и второй промежуточный целочисленный список
умножения и второй промежуточный целочисленный список 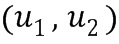 умножения. Целочисленный список вывода из умножения, кодирующий элемент кольца вывода из умножения, определяют из первого и второго промежуточного элемента. В других вариантах осуществления может быть более двух промежуточных целочисленных списков умножения. Получается, что
умножения. Целочисленный список вывода из умножения, кодирующий элемент кольца вывода из умножения, определяют из первого и второго промежуточного элемента. В других вариантах осуществления может быть более двух промежуточных целочисленных списков умножения. Получается, что
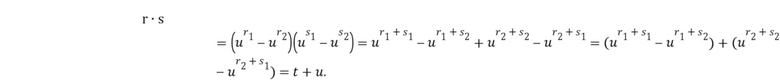 Подразделение членов в расширенных произведениях на два члена t и u можно выполнить разными путями, например, в виде
Подразделение членов в расширенных произведениях на два члена t и u можно выполнить разными путями, например, в виде 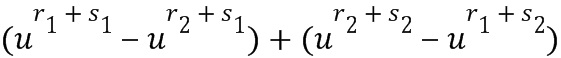 .
.
Это показывает, что для умножения двух элементов кольца, представленных в виде целочисленных списков, их можно преобразовать в два новых целочисленных списка, которые можно просуммировать для получения результата умножения. Сложение может быть выполнено, как это было описано выше. Например, блок умножения может вычислить промежуточные целочисленные списки и передать их в блок сложения.
Например, первое целое число 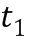 из первого промежуточного целочисленного списка умножения может содержать первое целое число
из первого промежуточного целочисленного списка умножения может содержать первое целое число 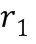 из первого целочисленного списка ввода в умножение плюс первое целое число
из первого целочисленного списка ввода в умножение плюс первое целое число 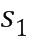 из второго целочисленного списка ввода в умножение, а второе целое число
из второго целочисленного списка ввода в умножение, а второе целое число 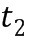 из первого промежуточного целочисленного списка умножения может содержать первое целое число
из первого промежуточного целочисленного списка умножения может содержать первое целое число 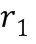 из первого целочисленного списка ввода в умножение плюс второе целое число
из первого целочисленного списка ввода в умножение плюс второе целое число 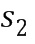 из второго целочисленного списка ввода в умножение
из второго целочисленного списка ввода в умножение 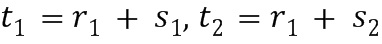 . Первое целое число
. Первое целое число 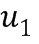 из второго промежуточного целочисленного списка умножения может содержать второе целое число
из второго промежуточного целочисленного списка умножения может содержать второе целое число 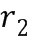 из первого целочисленного списка ввода в умножение плюс второе целое число
из первого целочисленного списка ввода в умножение плюс второе целое число 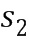 из второго целочисленного списка ввода в умножение, а второе целое число
из второго целочисленного списка ввода в умножение, а второе целое число 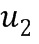 из второго промежуточного целочисленного списка умножения может содержать второе целое число
из второго промежуточного целочисленного списка умножения может содержать второе целое число 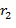 из первого целочисленного списка ввода в умножение плюс первое целое число
из первого целочисленного списка ввода в умножение плюс первое целое число 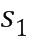 из второго целочисленного списка ввода в умножение
из второго целочисленного списка ввода в умножение 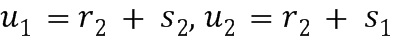 .
.
В одном варианте осуществления, например, в только что раскрытом примере, арифметические операции выполняются над целочисленными списками, и при этом нет необходимости вычислять элементы кольца как элементы кольца в их естественном представлении. Далее обсуждается ряд вариантов. Многие из этих вариантов являются независимыми; например, вариант кодирования может быть объединен с вариантом выполнения сложения.
Посредством обфускационных арифметических операций при выполнении вычислений в целочисленном списке, соответствующем, например, 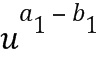 и т.д., соответствующее значение может быть остатком от деления на порядок
и т.д., соответствующее значение может быть остатком от деления на порядок 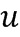 . Например, если порядок
. Например, если порядок 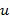 равен 30, то все вычисления могут выполняться по модулю 30. Следует отметить, что вышеупомянутые варианты осуществления являются лишь иллюстрациями, а не ограничениями изобретения, а специалисты в данной области техники способны разработать множество альтернативных вариантов осуществления изобретения.
равен 30, то все вычисления могут выполняться по модулю 30. Следует отметить, что вышеупомянутые варианты осуществления являются лишь иллюстрациями, а не ограничениями изобретения, а специалисты в данной области техники способны разработать множество альтернативных вариантов осуществления изобретения.
В формуле изобретения любые ссылочные позиции, помещенные в скобках, не следует трактовать как ограничение изобретения. Использование слова «содержит» и его спряжений не исключает присутствия элементов или этапов, отличных от установленных в формуле изобретения. Перечисление элементов в единственном числе не исключает присутствия множества указанных элементов. Изобретение можно реализовать аппаратными средствами, содержащими несколько отдельных элементов, а также с помощью компьютера, запрограммированного подходящим образом. В пункте формулы изобретения, относящемся к устройству, где перечислены несколько средств, некоторые из этих средств могут быть воплощены в одном и том же аппаратном изделии. Сам по себе факт, состоящий в том, что конкретные средства упомянуты во взаимно зависимых пунктах формулы изобретения, не указывают на то, что невозможно успешное использование комбинации этих средств.
В формуле изобретения ссылки в скобках относятся к ссылочным позициям на чертежах вариантов осуществления изобретения или к формулам в этих вариантах, что улучшает понимание формулы изобретения. Эти ссылки не следует трактовать как ограничение изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ АРИФМЕТИКИ С ОБФУСКАЦИЕЙ | 2015 |
|
RU2701716C2 |
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ЗАМАСКИРОВАННЫХ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ | 2015 |
|
RU2698764C2 |
| ЭЛЕКТРОННОЕ УСТРОЙСТВО ФОРМИРОВАНИЯ | 2015 |
|
RU2710310C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, КОНФИГУРИРУЕМОЕ С ПОМОЩЬЮ ТАБЛИЧНОЙ СЕТИ | 2013 |
|
RU2661308C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, ХРАНЯЩЕЕ ТАБЛИЦЫ СООТВЕТСТВИЯ ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИИ | 2013 |
|
RU2657178C2 |
| УСТРОЙСТВО ВИРТУАЛЬНОЙ МАШИНЫ, ИМЕЮЩЕЕ УПРАВЛЯЕМУЮ КЛЮЧОМ ОБФУСКАЦИЮ, И СПОСОБ | 2012 |
|
RU2620712C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, СОДЕРЖАЩЕЕ СЕТЬ ТАБЛИЦ | 2013 |
|
RU2676454C2 |
| Способ организации выполнения операции умножения двух чисел в модулярно-логарифмическом формате представления с плавающей точкой на гибридных многоядерных процессорах | 2017 |
|
RU2666285C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ЗАПИСЕЙ В ЗАПОМИНАЮЩЕМ УСТРОЙСТВЕ, СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ И МАШИНОЧИТАЕМЫЙ НОСИТЕЛЬ | 2010 |
|
RU2448361C2 |
| Способ организации выполнения операции умножения двух чисел в модулярно-индексном формате представления с плавающей точкой на универсальных многоядерных процессорах | 2017 |
|
RU2652460C1 |
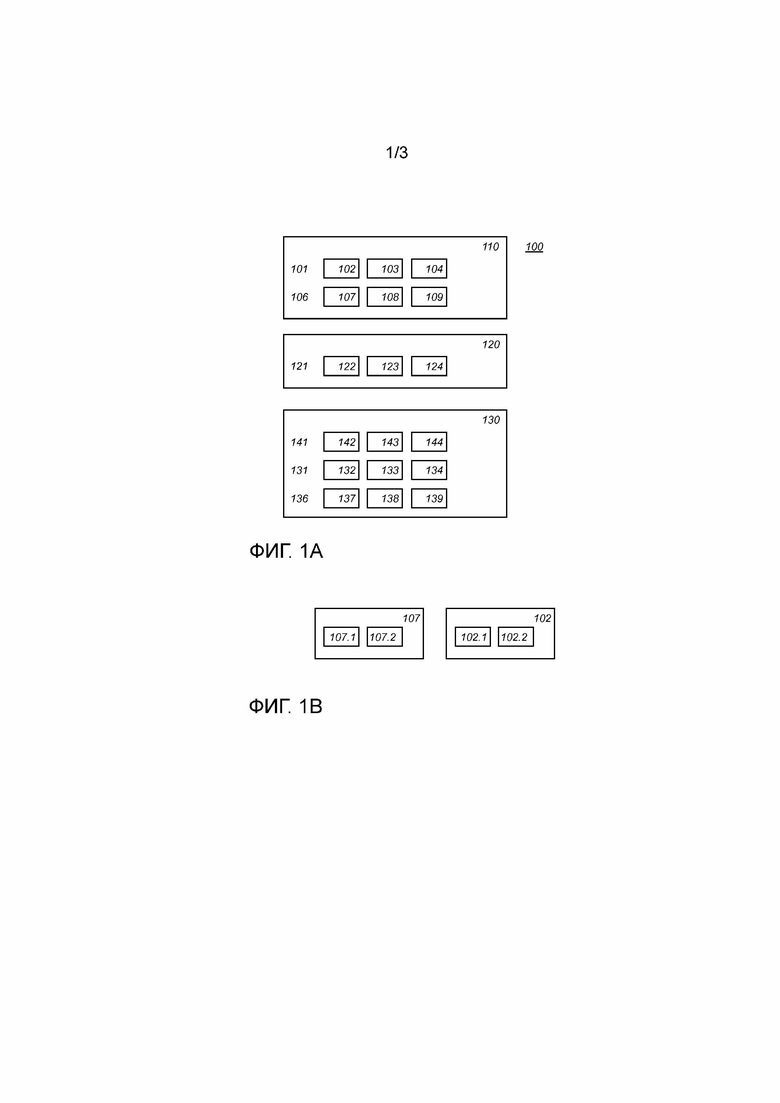
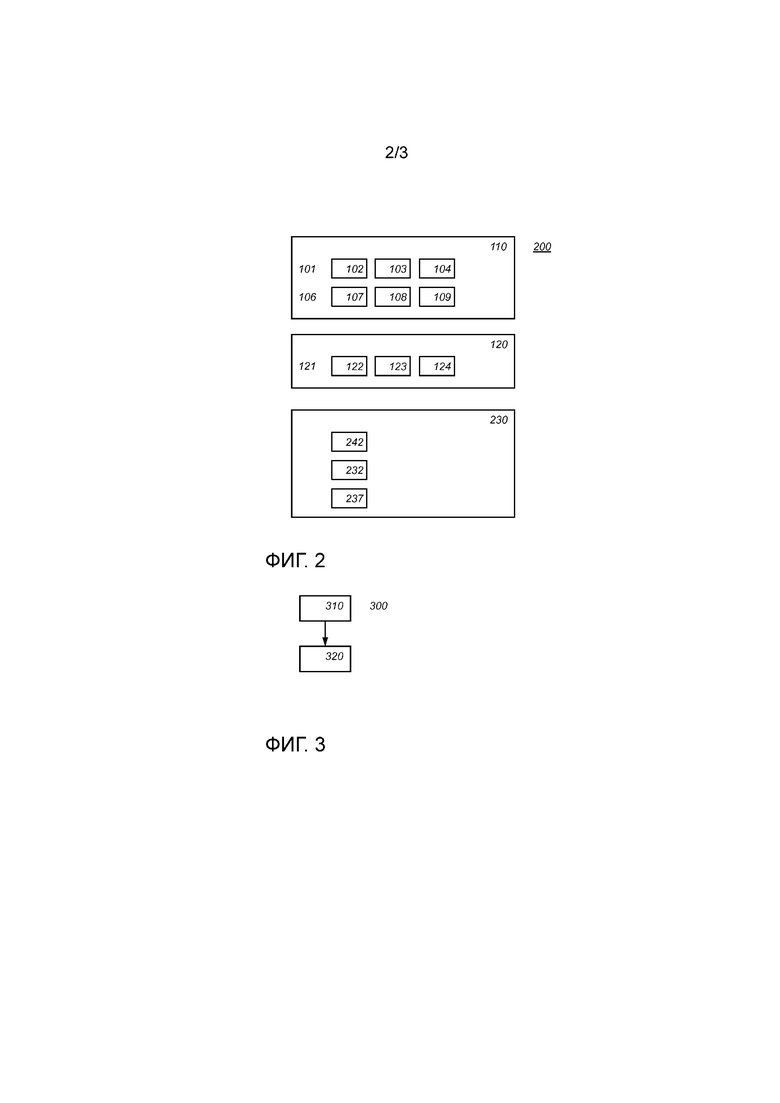
Группа изобретений относится к области вычислительной техники и может быть использована для выполнения обфускационных арифметических операций в коммутативном кольце. Техническим результатом является повышение защищенности. Устройство выполнено с возможностью осуществления обфускационных арифметических операций в коммутативном кольце 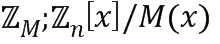 ), определенном комбинированным модулем (
), определенном комбинированным модулем (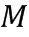 ;
; 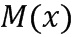 ) в системе остаточных классов, причем система остаточных классов определена для ряда модулей (
) в системе остаточных классов, причем система остаточных классов определена для ряда модулей (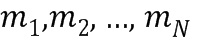 ), где каждый модуль определяет коммутативное кольцо (
), где каждый модуль определяет коммутативное кольцо (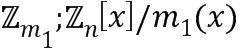 ), так что для каждого модуля (
), так что для каждого модуля (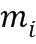 )ряда существует ассоциированный базовый элемент (
)ряда существует ассоциированный базовый элемент (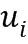 ), удовлетворяющий условию, заключающемуся в том, что каждый остаток от деления элемента (
), удовлетворяющий условию, заключающемуся в том, что каждый остаток от деления элемента (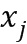 ) кольца на модуль (
) кольца на модуль (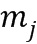 ) может быть выражен в виде целочисленного списка (
) может быть выражен в виде целочисленного списка (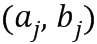 ), так что элементы кольца равны линейной комбинации степеней базового элемента (
), так что элементы кольца равны линейной комбинации степеней базового элемента (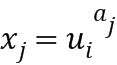 -
- 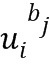 ), где степени имеют показатели, определяемые целочисленным списком. 3 н. и 12 з.п. ф-лы, 6 ил., 1 табл.
), где степени имеют показатели, определяемые целочисленным списком. 3 н. и 12 з.п. ф-лы, 6 ил., 1 табл.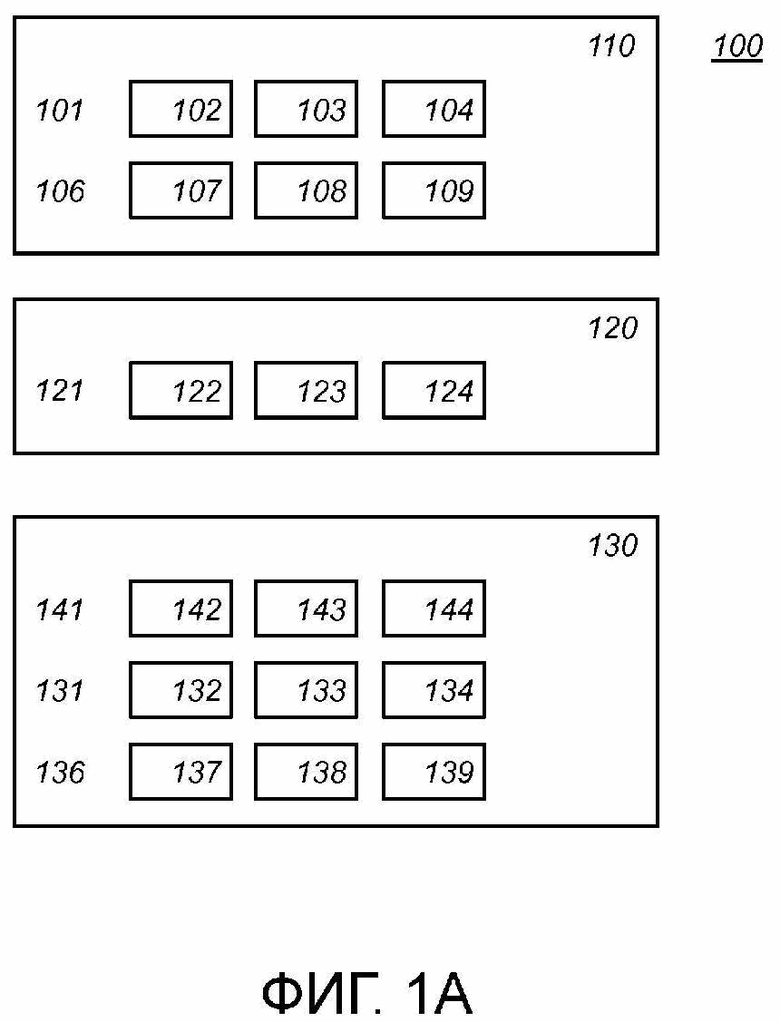
1. Электронное вычислительное устройство (100; 2 00), выполненное с возможностью выполнения обфускационных арифметических операций в коммутативном кольце 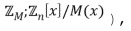 определенном комбинированным модулем (M; М(x)) в системе остаточных классов, причем система остаточных классов определена для ряда модулей (m1,m2, …, mN), где каждый модуль определяет коммутативное кольцо
определенном комбинированным модулем (M; М(x)) в системе остаточных классов, причем система остаточных классов определена для ряда модулей (m1,m2, …, mN), где каждый модуль определяет коммутативное кольцо 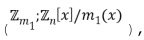 так что для каждого модуля (mi) данного ряда существует ассоциированный с ним базовый элемент (ui), удовлетворяющий условию, заключающемуся в том, что каждый остаток от деления элемента (xj) кольца на модуль (mj) может быть выражен в виде целочисленного списка ((aj, bj)), так что элементы кольца равны линейной комбинации степеней базового элемента (
так что для каждого модуля (mi) данного ряда существует ассоциированный с ним базовый элемент (ui), удовлетворяющий условию, заключающемуся в том, что каждый остаток от деления элемента (xj) кольца на модуль (mj) может быть выражен в виде целочисленного списка ((aj, bj)), так что элементы кольца равны линейной комбинации степеней базового элемента (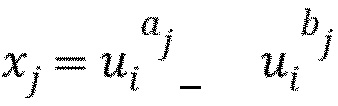 ), где каждая степень имеет показатель, определяемый целым числом в этом целочисленном списке, причем вычислительное устройство содержит
), где каждая степень имеет показатель, определяемый целым числом в этом целочисленном списке, причем вычислительное устройство содержит
хранилище (110) операндов, приспособленное для хранения одного или более остатков от деления операндов (101, 106) на комбинированный модуль (M) в виде одного или более рядов остатков от деления элементов кольца на модули, причем каждый элемент кольца ряда ассоциирован с соответствующим модулем из ряда модулей, где по меньшей мере один элемент кольца из упомянутого ряда закодирован в виде целочисленного списка,
вычислительный блок (130; 230), выполненный с возможностью сложения и/или умножения первого и второго операнда из хранилища операндов согласно системе остаточных классов.
2. Вычислительное устройство по п. 1, в котором комбинированный модуль и модули в ряде модулей являются целыми числами или многочленами с модулярными коэффициентами.
3. Вычислительное устройство по любому из предшествующих пунктов, в котором вычислительный блок производит действия над упомянутым целочисленным списком, каковые действия содержат операции нахождения остатка от деления на порядок базовых элементов, где порядок по меньшей мере двух базовых элементов, ассоциированных с двумя разными модулями ряда модулей, одинаков.
4. Вычислительное устройство по п. 3, в котором порядок всех базовых элементов, ассоциированных с модулями ряда модулей, одинаков.
5. Вычислительное устройство по п. 1, в котором комбинированный модуль равен наименьшему общему кратному модулей, (m1, m2, …, mN) в ряде модулей.
6. Вычислительное устройство по п. 1, содержащее хранилище (120) таблиц, приспособленное для хранения, для каждого из модулей в упомянутом ряде, таблицы (T) приращений, определенной для элемента (-1; 1; ut) приращения, ассоциированной с модулем из ряда модулей, при этом таблица приращений отображает входной элемент 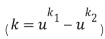 кольца на выходной целочисленный список
кольца на выходной целочисленный список 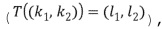 кодирующий выходной элемент
кодирующий выходной элемент 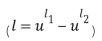 кольца, так что выходной элемент кольца равен элементу приращения, добавленному к входному элементу
кольца, так что выходной элемент кольца равен элементу приращения, добавленному к входному элементу 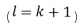 кольца, причем выходной элемент кольца равен линейной комбинации степеней базового элемента (u), каковые степени имеют показатели, определяемые выходным целочисленным списком.
кольца, причем выходной элемент кольца равен линейной комбинации степеней базового элемента (u), каковые степени имеют показатели, определяемые выходным целочисленным списком.
7. Вычислительное устройство по п. 6, в котором вычислительный блок (130; 230) выполнен с возможностью осуществления арифметических операций над первым и вторым элементом кольца в первом и втором операнде в качестве остатка от деления на один и тот же модуль и представленных в виде целочисленного списка, причем арифметические операции включают в себя операцию нахождения остатка от деления на порядок базового элемента, ассоциированного с упомянутым одним и тем же модулем, и выполнен с возможностью применения ассоциированной таблицы приращений, хранящейся для этого одного и того же модуля.
8. Вычислительное устройство по п. 6 или 7, в котором вычислительный блок содержит блок (130) сложения, выполненный с возможностью осуществления для каждого модуля из ряда:
приема первого целочисленного списка ((а1, а2)) ввода в сложение, кодирующего первый элемент кольца ввода в сложение, и второй целочисленный список ((b1, b2)) ввода в сложение, кодирующий второй элемент кольца ввода в сложение,
определения целочисленного списка вывода из сложения, кодирующего элемент кольца вывода из сложения, путем применения таблицы приращений к элементам кольца, определенным из первого и второго целочисленных списков ввода в сложение, причем элемент кольца вывода из сложения равен модулярному сложению первого элемента кольца ввода в сложение и второго элемента ввода в сложение.
9. Вычислительное устройство по п. 8, в котором определение целочисленного списка вывода из сложения содержит
определение промежуточного целочисленного списка ((c1, c2)) сложения, кодирующего промежуточный элемент кольца сложения, путем первого применения таблицы приращений к элементу 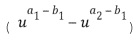 кольца, являющемуся линейной комбинацией степеней одного или более базовых элементов, каковые степени определяются из первого и второго целочисленных списков ввода в сложение,
кольца, являющемуся линейной комбинацией степеней одного или более базовых элементов, каковые степени определяются из первого и второго целочисленных списков ввода в сложение, 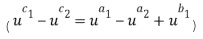 и операции нахождения остатка от деления на базовый элемент,
и операции нахождения остатка от деления на базовый элемент,
определение целочисленного списка вывода из сложения, содержащее второе применение таблицы приращений к элементам кольца, определенным из промежуточного целочисленного списка сложения и определенным из второго целочисленного списка ввода в сложение и операции нахождения остатка от деления на порядок базового элемента.
10. Вычислительное устройство по п. 9, в котором определение промежуточного целочисленного списка ((c1, c2)) сложения дополнительно содержит сложение целого числа, определенного из первого и второго целочисленных списков ввода в сложение, с целыми числами в целочисленном списке, получившемся в результате первого применения операции нахождения остатка от деления на порядок базового элемента.
11. Вычислительное устройство по п. 9 или 10, в котором
таблицу приращений применяют к элементу 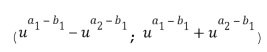 кольца, сформированному одним или более базовыми элементами (u) кольца, возведенными в степень первого целого числа из первого целочисленного списка (a1) минус первое целое число из второго целочисленного списка (b1) плюс или минус базовый элемент кольца (u), возведенный в степень второго целого числа из первого целочисленного списка (а2) минус первое целое число из второго целочисленного списка (b1); и/или
кольца, сформированному одним или более базовыми элементами (u) кольца, возведенными в степень первого целого числа из первого целочисленного списка (a1) минус первое целое число из второго целочисленного списка (b1) плюс или минус базовый элемент кольца (u), возведенный в степень второго целого числа из первого целочисленного списка (а2) минус первое целое число из второго целочисленного списка (b1); и/или
таблицу приращений применяют к элементу 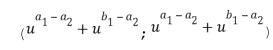 кольца, сформированному одним или более базовыми элементами (u) кольца, возведенными в степень первого целого числа из первого целочисленного списка (a1) минус второе целое число из первого целочисленного списка (а2) плюс или минус базовый элемент (u) кольца, возведенный в степень первого целого числа из второго целочисленного списка (b1) минус второе целое число из первого целочисленного списка (a2); и/или
кольца, сформированному одним или более базовыми элементами (u) кольца, возведенными в степень первого целого числа из первого целочисленного списка (a1) минус второе целое число из первого целочисленного списка (а2) плюс или минус базовый элемент (u) кольца, возведенный в степень первого целого числа из второго целочисленного списка (b1) минус второе целое число из первого целочисленного списка (a2); и/или
таблицу приращений применяют к элементу 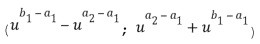 кольца, сформированному одним или более базовыми элементами (u) кольца, возведенными в степень второго целого числа из первого целочисленного списка (a2) минус первое целое число из первого целочисленного списка (a1) плюс или минус базовый элемент (u) кольца, возведенный в степень первого целого числа из второго целочисленного списка (b1) минус первое целое число из первого целочисленного списка (a1).
кольца, сформированному одним или более базовыми элементами (u) кольца, возведенными в степень второго целого числа из первого целочисленного списка (a2) минус первое целое число из первого целочисленного списка (a1) плюс или минус базовый элемент (u) кольца, возведенный в степень первого целого числа из второго целочисленного списка (b1) минус первое целое число из первого целочисленного списка (a1).
12. Вычислительное устройство по п. 9 или 10, в котором над промежуточным элементом кольца сложения, представленным промежуточным целочисленным списком сложения, выполняют операцию отрицания перед вторым применением таблицы приращений.
13. Вычислительное устройство по любому из пп. 6, 7, 9 и 10, в котором вычислительное устройство содержит блок (140) умножения, выполненный с возможностью
приема первого целочисленного списка ((r1, r2)) ввода в умножение, кодирующего первый элемент кольца ввода в умножение, и второго целочисленного списка ((s1, s2)) ввода в умножение, кодирующего второй элемент кольца ввода в умножение,
определения целочисленного списка вывода из умножения, кодирующего элемент кольца выхода умножения, путем применения таблицы приращений к элементам кольца, определенным из первого и второго целочисленных списков ввода в умножение, причем элемент кольца вывода из умножения равен модулярному умножению первого элемента кольца ввода в умножение и второго элемента кольца ввода в умножение.
14. Способ электронного вычисления для выполнения обфускационных арифметических операций нахождения остатка от деления на комбинированный модуль (M) в системе остаточных классов, причем система остаточных классов определена для ряда модулей (m1, m2, …, mN), где каждый модуль определяет коммутативное кольцо 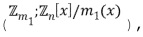 , так что для каждого модуля (mi) данного ряда существует ассоциированный с ним базовый элемент (ui), удовлетворяющий условию, заключающемуся в том, что каждый остаток от деления элемента (xj) кольца на модуль (mj) может быть выражен в виде целочисленного списка ((aj, bj)), так что элементы кольца равны линейной комбинации степеней базового элемента
, так что для каждого модуля (mi) данного ряда существует ассоциированный с ним базовый элемент (ui), удовлетворяющий условию, заключающемуся в том, что каждый остаток от деления элемента (xj) кольца на модуль (mj) может быть выражен в виде целочисленного списка ((aj, bj)), так что элементы кольца равны линейной комбинации степеней базового элемента 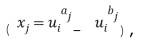 где каждая степень имеет показатель, определяемый целым числом в этом целочисленном списке, причем способ содержит этапы, на которых:
где каждая степень имеет показатель, определяемый целым числом в этом целочисленном списке, причем способ содержит этапы, на которых:
сохраняют один или более остатков от деления операндов на комбинированный модуль (M) в виде одного или более рядов остатков от деления элементов кольца на модули, причем каждый элемент кольца ряда ассоциирован с соответствующим модулем из ряда модулей, где по меньшей мере один элемент кольца из упомянутого ряда закодирован в виде целочисленного списка,
сложение и/или умножение первого и второго операнда из хранилища операндов согласно системе остаточных классов.
15. Машиночитаемый носитель, на котором сохранена компьютерная программа, содержащая команды компьютерной программы, которые при их исполнении на программируемом устройстве предписывают программируемому устройству осуществлять способ по п. 14.
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| СПОСОБ ЗАЩИТЫ ПРОГРАММНО-ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ОТ НЕСАНКЦИОНИРОВАННОГО ИСПОЛЬЗОВАНИЯ | 2011 |
|
RU2467389C1 |
| Устройство для умножения двух чисел | 1989 |
|
SU1667059A2 |
Авторы
Даты
2019-08-29—Публикация
2015-12-21—Подача