Заявляемое техническое решение относится к области антенной техники и может быть использовано для проектирования, моделирования и изготовления бифокальных линзовых антенн, имеющих две точки идеальной фокусировки, при помещении в которые получается плоский фазовый фронт, повернутый на некоторый угол.
Известен способ определения поверхности диэлектрической бифокальной линзовой антенны по методу Джента-Штернберга (Зелкин Е.Г., Петрова Р.А. Линзовые антенны - М.: Сов. Радио - 1974. - 280 с.). Он основан на определении положения краев линзы и углов наклона поверхностей линзы вблизи краев при помощи системы из четырех трансцендентных уравнений.
Недостатком способа является отсутствие аналитического решения системы уравнений. Кроме того, не для каждого набора параметров удается получить набор точек, аппроксимирующих поверхности бифокальной линзовой антенны. Способ определяет координаты точек лишь приближенно, что также является его недостатком.
Известен также способ определения поверхности по методу решетки (Зелкин Е.Г., Петрова Р.А. Линзовые антенны - М.: Сов. Радио - 1974. - 280 с.). Способ позволяет графоаналитическим способом определить координаты и наклон поверхности линзовой антенны при помощи системы рекуррентных уравнений. В отличие от предыдущего способа, эти точки выбираются точно, а не приближенно.
Недостатком способа является отсутствие аналитического решения. Кроме того, не для каждого набора параметров удается получить набор точек, аппроксимирующих поверхности бифокальной линзовой антенны, так как итерационная процедура не гарантирует результат.
Наиболее близким к заявляемому техническому решению является способ определения поверхности при помощи метода последовательных приближений (Жук М.С., Молочков Ю.Б. Проектирование линзовых, сканирующих, широкодиапазонных антенн и фидерных устройств. М.: Энергия, 1973. 440 с.). По сравнению с другими он требует меньшего объема вычислительных работ при достаточно высокой точности. В методе последовательных приближений уравнения поверхностей бифокальной линзы представляют в виде степенного ряда с четными степенями. Традиционно, ограничиваются двумя членами ряда и, соответственно, тремя коэффициентами [1]. Тогда уравнения освещенной и теневой поверхностей в полярной системе координат принимают вид

ρ1, ρ2 - коэффициенты, определяющие расстояние от оси, на которой расположены облучатели до освещенной и теневой поверхностей линзы соответственно;
А1, B1 - коэффициенты, определяющие форму освещенной поверхности линзы;
А2, В2- коэффициенты, определяющие форму теневой поверхности линзы.
Основные трудности при использовании этого способа заключаются в определении коэффициентов аппроксимирующих полиномов. Для определения коэффициентов решают две системы уравнений, состоящие из двух уравнений и дополненные двумя условиями каждая. Кроме того, усложняет задачу использование обратных тригонометрических функций и отсутствие выражения, определяющего эти коэффициенты, а также рекомендаций по выбору начальных параметров для системы уравнений.
Таким образом, решаемой технической проблемой (техническим результатом) является обеспечение однозначного определения поверхности линзовой антенны.
Технический результат (решаемая техническая проблема) достигается тем, что в известном способе, включающем аппроксимацию освещенной и теневой поверхности линзы степенными полиномами и определение коэффициентов, согласно изобретению, для каждого из лучей, претерпевающих преломление на поверхности линзы, записывают аналитическое выражение, определяющее его электрическую длину и зависящее от координат точек освещенной и теневой поверхностей линзы, затем последовательно, при помощи численных методов определяют по три точки, лежащие на теневой и освещенной поверхности, составляют по полученным координатам точек две системы уравнений, решением которых являются коэффициенты степенных полиномов, аппроксимирующие освещенную и теневую поверхности.
Суть заявляемых технических решений состоит в следующем.
На чертеже представлена геометрия бифокальной линзовой антенны.
Ось х - главная оптическая ось бифокальной линзовой антенны, относительно которой она является симметричной.
О1 и О2 - точки идеальной фокусировки с координатами (0;а) и (0;-а), соответственно. При размещении в этих точках облучателя, в раскрыве линзовой антенны получается плоский фазовый фронт, соответствующий прямой Р.
A1 и А2 - вершины линзы с координатами (XB;YB) и (XB;-YB), соответственно, которые принадлежат одновременно освещенной и теневой поверхностям.
а - расстояние от главной оптической оси х до точек фокуса О1 и O2;
α - угол наклона фазового фронта (прямая Р) в раскрыве линзы относительно апертуры исследуемой антенны NN1, которая устанавливается в точке с координатой М (с;0).
Лучи 1-4 (O1A1, О1В, O1C, O1D) - лучи, претерпевающие преломление на границе раздела сред воздух-материал линзы и направленные из облучателя О1 с координатой (0;а) к освещенной поверхности линзы.
Лучи 5-7 (BE, CG, DH) - лучи, преломленные на границе раздела сред воздух-материал линзы и претерпевающие преломление на теневой поверхности линзы, являющейся границей раздела сред,
Луч 8-11 (A1P1, ЕР2, GP3, НР4) - лучи, преломленные на теневой поверхности линзы и принадлежащие прямой, моделирующей фазовый фронт;
В (x1;y1), С (ρ1;0), D(x1;-y1) - точки освещенной поверхности линзы.
Е (х2;у2), F (ρ2;0), G (х2;-у2), Н (х'2; у'2) - точки теневой поверхности линзы.
Заявляемый способ основан на обеспечении равенства электрических длин лучей, проходящих из точек фокуса через края линзы и ее тело, в предположении, что в раскрыве линзовой антенны формируется плоский фазовый фронт, наклоненный на заданный угол относительно главной оптической оси. Для каждого из лучей записано уравнение, определяющее его электрическую длину. Электрическая длина лучей зависит от координат точек освещенной и теневой поверхностей линзы, в которых происходит его преломление. Полученные уравнения решают численными методами. Далее, последовательно определяют по три точки, лежащие на теневой и освещенной поверхности. По полученным координатам точек составляются системы уравнений, решением которых являются коэффициенты степенных полиномов, аппроксимирующие освещенную и теневую поверхности.
Зная три точки освещенной и три точки теневой поверхности, аналитически определяют коэффициенты, входящие в уравнения поверхностей.
В качестве одной из таких точек используется одна из вершин линзы с координатами А1(ХВ;YB). Данная точка принадлежит как освещенной, так и теневой поверхности.
Положение вершин определяют из уравнения эллипса равных краев (Жук М.С., Молочков Ю.Б. Проектирование линзовых, сканирующих, широкодиапазонных антенн и фидерных устройств. М.: Энергия, 1973. 440 с.)

Величины а и α задаются в начале вычислений и определяются размерами линзы и требуемым диапазоном сканирования облучателя. В силу симметрии линзы относительно главной оптической оси две ее вершины и два положения точек идеальной фокусировки полностью эквивалентны. Для определенности, в дальнейшем используется вершина с координатами (XB;YB) и считается, что облучатель расположен в точке (0;а).
Условие равенства электрических длин лучей, проходящих через одну из вершин линзы и центр линзы с координатой (ρ1;0) определяют как
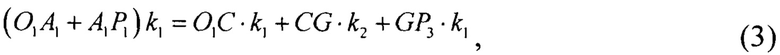
k1 - волновое число для воздуха;
k2 - волновое число материала линзы.
Определяют длины лучей, входящие в (3).
Длина луча 1 определяется как

Угол падения ∠OCO1 луча 3 на границу раздела сред в точке С (ρ1;0)

Угол преломления ∠FCG луча 3 определяется из закона Снеллиуса:
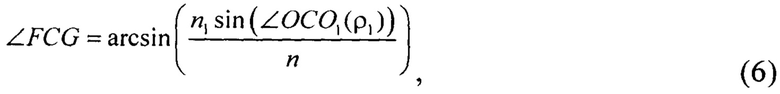
n1 - показатель преломления окружающей среды, в которой расположена линза (обычно эта среда - воздух, поэтому далее n1=1);
n - показатель преломления материала линзы.
Нормалью в точке падения луча на границу раздела сред (ρ1;0) является главная оптическая ось линзы х.
После подстановки (5) в (6) угол преломления:

Длина луча 6 определяется из геометрии линзы:

После математических преобразований получают:
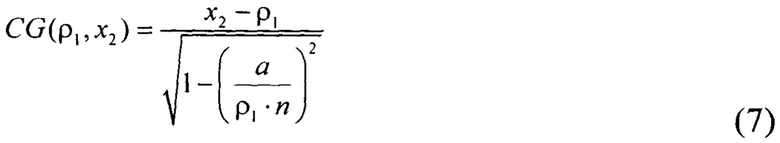
Определяют длину луча 10. Для этого находят значение модуля левой части нормального уравнения прямой, описывающей фазовый фронт в интересующей нас точке, в которой луч 10 пересекает теневую поверхность [5].
Записывается общее уравнение прямой Р:
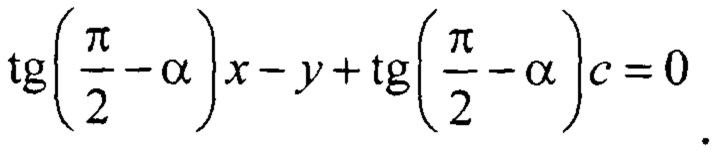
Преобразуется к нормальному уравнению прямой [5]:

После ряда преобразований
cos(α)(c-x)+sin(α)y=0.
После подстановки значений координат точки Е2, в которой преломляется луч 10 получают:
GP3(x2,y2)=|cos(α)(c-x2)+sin(α)y2|.
Так как по определению с>ρ2, то знак модуля опускается:

Длину луча 1, проходящего через край линзы с координатами (XB;YB), находят при помощи выражения, определяющего расстояния между двумя точками:

Длина луча 8
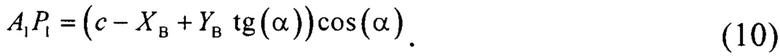
Подставив выражения (4), (7)-(10), определяющие длины лучей, в (3) получают уравнение с тремя неизвестными ρ1,х2 и у2:

Аналитически решить полученное уравнение с тремя неизвестными крайне сложно. Поэтому используются численные способы его решения. Для этого переносят все слагаемые по одну сторону знака равенства и получают целевую функцию трех переменных
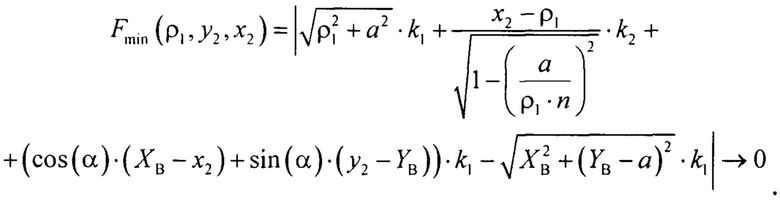
Поиск нулей функции проводят любым численным способом, например, градиентным поиском или покоординатным спуском.
Пределы изменения переменной у2 определяются геометрическими размерами бифокальной линзовой антенны, переменных ρ1 и х2 уравнением эллипса краев и требованием, чтобы ρ1 и х2 лежали по разные стороны от кривой эллипса:

После минимизации целевой функции определяют координаты второй точки освещенной поверхности (ρ1;0), и, соответственно, коэффициент ρ1 и координаты второй точки теневой поверхности (х2; -у2).
Так как линза симметрична относительно главной оптической оси, то найденной точке (х2; у2) соответствует симметричная ей точка с координатами (х2; -у2). Используется условие равенства электрических длин лучей для определения одной из точек освещенной поверхности с координатами (х1; y1)
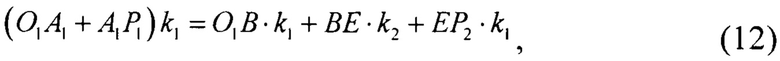
Длина луча 2

Длина луча 5
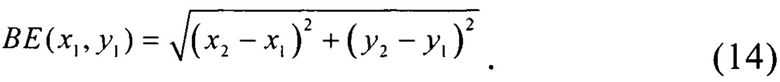
Определяют длину луча 9. Аналогично (8)
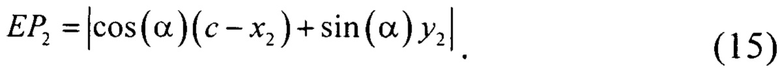
Подставив выражения (9), (10), (13)-(15), определяющие длины лучей, в (12) получают уравнение с двумя неизвестными х1 и y1
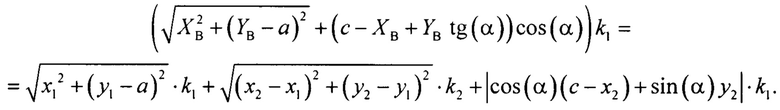
Аналогично получают целевую функцию, которую необходимо минимизировать:
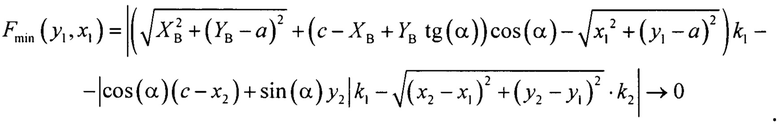
Пределы изменения переменной x1 определяются требованием, чтобы переменная лежала по левую сторону от кривой эллипса, переменной у1 - геометрией линзы:

После минимизации функции определяют координаты третьей точки освещенной поверхности (х1; y1).
Так как линза симметрична относительно главной оптической оси, то найденной точке (х1; y1) соответствует симметричная ей точка с координатами (х1; -y1). Используется условие равенства электрических длин лучей для определения третьей точки теневой поверхности с координатами (х'2; у'2):

Длина луча 4

Длина луча 7
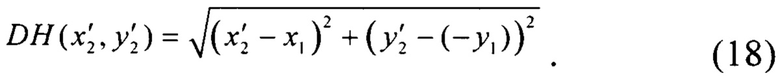
Определяют длину луча 11. Аналогично (8)

Подставляют выражения (9), (10), (17)-(19), определяющие длины лучей, в (16) и получают уравнение с двумя неизвестными х'2 и у'2.
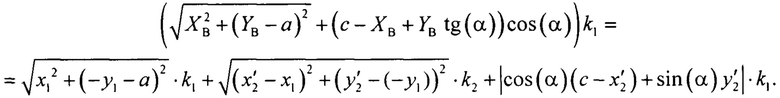
Аналогично получают целевую функцию, минимизация которой дает координаты еще одной точки теневой поверхности (х'2; у'2):
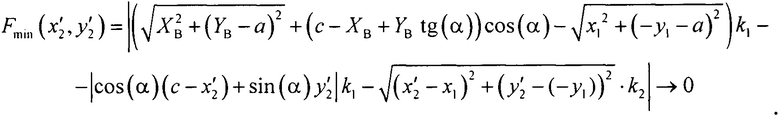
Пределы изменения переменной х'2 определяются требованием, чтобы переменная лежала по правую сторону от кривой эллипса, переменной у'2 - геометрией линзы:
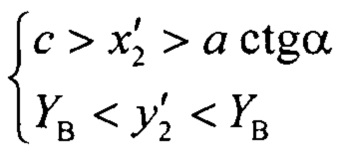
Таким образом, имеется 3 точки освещенной, 3 точки теневой поверхности. Предварительно переводят координаты точек из декартовой в полярную систему координат и составляют две системы линейных уравнений для определения искомых коэффициентов. Для освещенной поверхности:
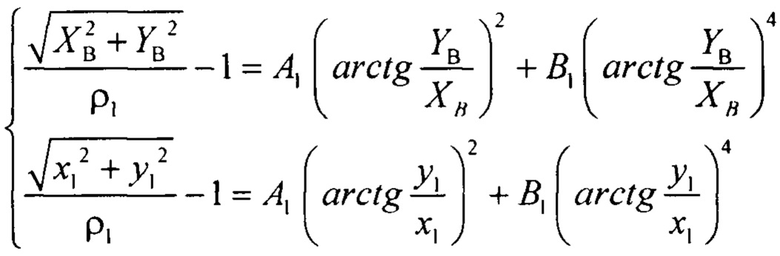
Для теневой поверхности:
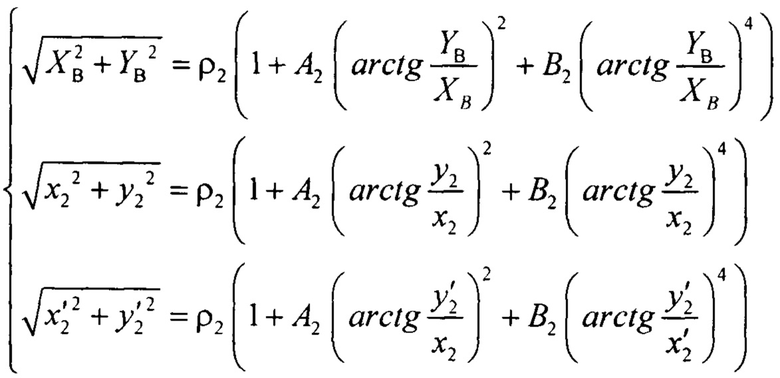
Искомые коэффициенты А1, B1 и ρ2, А2, В2 определяют при решении системы линейных алгебраических уравнений (например, по методу Крамера). Для освещенной поверхности:
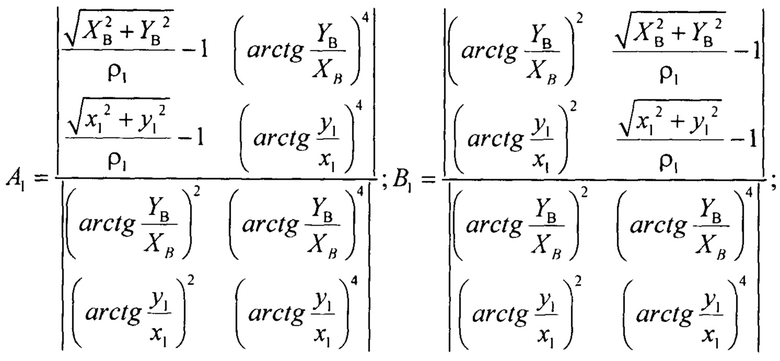
Для теневой поверхности:

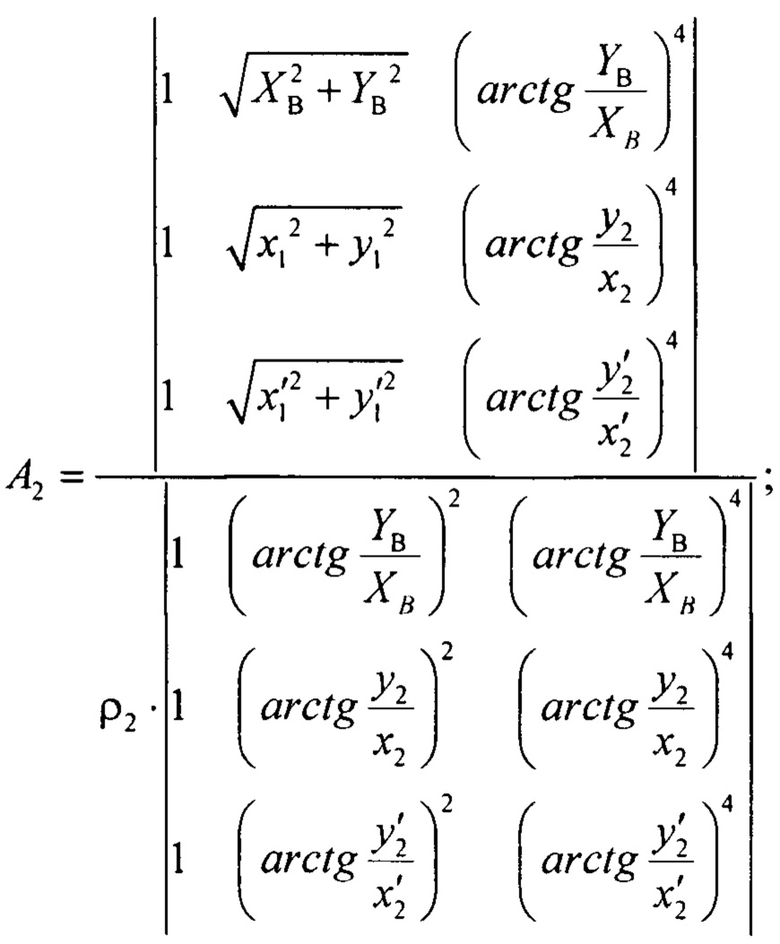
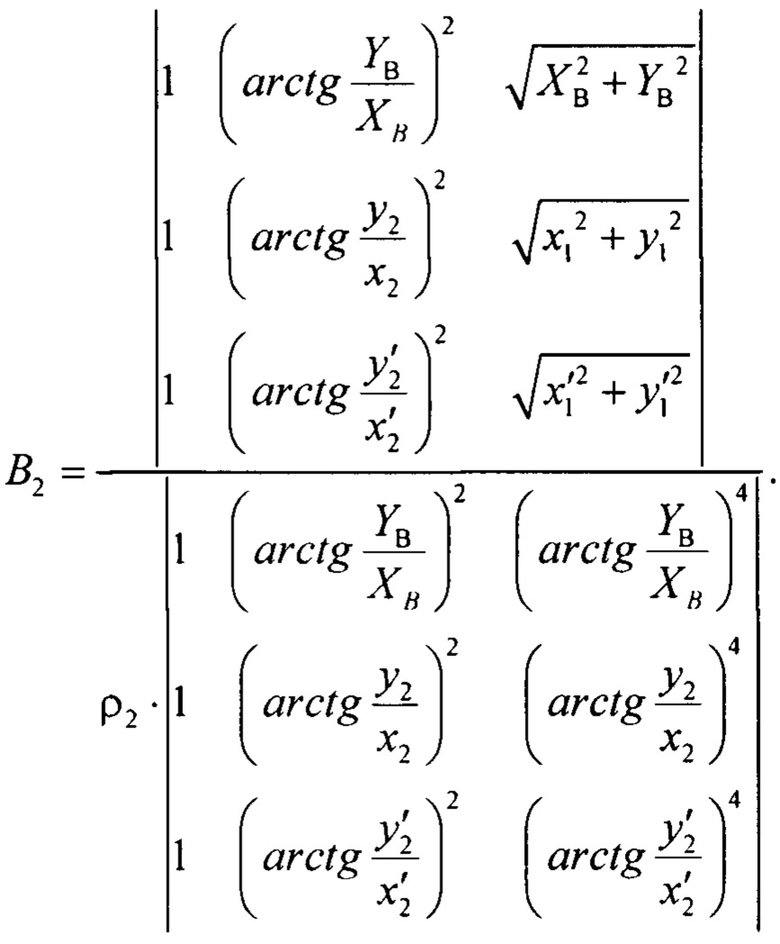
Таким образом, заявляемый способ позволяет рассчитать коэффициенты и определить поверхность бифокальной линзовой антенны, чем и обеспечивается заявленный технический результат.
| название | год | авторы | номер документа |
|---|---|---|---|
| МНОГОЛУЧЕВАЯ АНТЕННА СВЕРХВЫСОКИХ ЧАСТОТ | 1994 |
|
RU2084059C1 |
| ЗЕРКАЛЬНАЯ АНТЕННА | 2000 |
|
RU2173496C1 |
| СКАНИРУЮЩАЯ ТОРОИДАЛЬНАЯ ЛИНЗОВАЯ АНТЕННА | 1998 |
|
RU2147150C1 |
| Линзовая антенна | 1987 |
|
SU1427452A1 |
| СПОСОБ ОСВЕЩЕНИЯ ОБЪЕКТОВ | 1990 |
|
RU2024895C1 |
| Линзовая антенна | 1989 |
|
SU1771021A1 |
| Линзовая антенна | 1979 |
|
SU985864A1 |
| АПЛАНАТИЧЕСКАЯ ГРАДИЕНТНАЯ ЛИНЗА | 2005 |
|
RU2288490C1 |
| Сканирующая линзовая антенна | 2017 |
|
RU2660385C1 |
| ИНТЕРФЕРЕНЦИОННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ ХАРАКТЕРИСТИК ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (ВАРИАНТЫ) | 1993 |
|
RU2078307C1 |

Изобретение относится к области антенной техники и может быть использовано для проектирования, моделирования и изготовления бифокальных линзовых антенн. Технический результат заключается в возможности обеспечения однозначного определения поверхности линзовой антенны. Технический результат достигается тем, что для каждого из лучей, претерпевающих преломление на поверхности линзы, записывают аналитическое выражение, определяющее его электрическую длину и зависящее от координат точек освещенной и теневой поверхностей линзы. Затем последовательно при помощи численных методов определяют по три точки, лежащие на теневой и освещенной поверхностях, составляют по полученным координатам точек две системы уравнений, решением которых являются коэффициенты степенных полиномов, аппроксимирующие освещенную и теневую поверхности линзового коллиматора. 1 ил.
Способ определения поверхности диэлектрической бифокальной линзовой антенны, включающий аппроксимацию освещенной и теневой поверхностей линзы степенными полиномами и определение коэффициентов, отличающийся тем, что для каждого из лучей, претерпевающих преломление на поверхности линзы, записывают аналитическое выражение, определяющее его электрическую длину и зависящее от координат точек освещенной и теневой поверхностей линзы, затем последовательно при помощи численных методов определяют по три точки, лежащие на теневой и освещенной поверхностях, составляют по полученным координатам точек две системы уравнений, решением которых являются коэффициенты степенных полиномов, аппроксимирующие освещенную и теневую поверхности линзового коллиматора.
| ЛИНЗОВАЯ АНТЕННА, СПОСОБ ИЗГОТОВЛЕНИЯ И ИСПОЛЬЗОВАНИЯ ТАКОЙ АНТЕННЫ И АНТЕННАЯ СИСТЕМА | 2013 |
|
RU2622463C2 |
| Устройство для контроля канала связи | 1988 |
|
SU1536517A2 |
| WO 2005093905 A1, 06.10.2005 | |||
| WO 2004088793 A1, 14.10.2004. | |||
Авторы
Даты
2020-03-04—Публикация
2019-05-29—Подача