1. ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Предлагаемое изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении для создания объективов, конденсоров, эндоскопов, устройств согласования волоконно-оптических линий связи с источниками излучения и фотоприемниками и т.д.
2. УРОВЕНЬ ТЕХНИКИ
Известна апланатическая градиентная линза, ограниченная первой и второй преломляющими поверхностями вращения, имеющая толщину по оптической оси z, кратную удвоенному номинальному фокусному расстоянию линзы, выполненная из материала с радиальным распределением показателя преломления n(у), в которой образующая каждой преломляющей поверхности z(y) удовлетворяет уравнению [1]
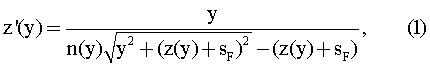
где у - координата, перпендикулярная оптической оси линзы;
z'(y) - первая производная от z(у);
sF - расстояние от предметной точки на оптической оси до вершины преломляющей поверхности линзы (передний отрезок).
В известной линзе задний отрезок s'F (расстояние от мнимого изображения предметной точки на оптической оси до вершины второй преломляющей поверхности линзы) равен по величине переднему отрезку sF.
Примечание. В [1] непосредственно в формуле изобретения приведено математическое выражение вида
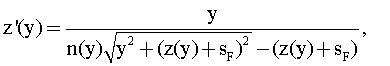
содержащее явную и досадную опечатку, не исправленную в свое время в силу ряда причин. Правильным является уравнение вида (1), приведенное в тексте описания изобретения.
Как указано в [1], перед изготовлением линзы форма поверхности может быть рассчитана для конкретного распределения показателя преломления (ПП) n(у) с любой наперед заданной точностью путем решения уравнения (1) одним из известных численных методов, например методом Рунге-Кутта. Получив этим методом координаты точек искомой образующей z(y), можно затем аппроксимировать образующую подходящей функцией, например параболой высшего порядка, с помощью метода наименьших квадратов или иным известным методом.
Аппроксимированная образующая затем может быть использована для формообразования преломляющих поверхностей. Соответственно, чем точней аппроксимация, тем ближе изготовляемая поверхность к расчетной и тем выше качество изображения, формируемое изготовленной линзой.
Однако указанный способ определения образующей сложен, требует значительного объема расчетных работ, высокой квалификации разработчика и имеет принципиально неустранимую суммарную погрешность, обусловленную как погрешностью численного интегрирования, так и погрешностью метода аппроксимации, причем при неизвестности точного аналитического выражения для образующей оценку погрешности получить весьма затруднительно. Наличие такой суммарной погрешности неизбежно ухудшает качество изображения после изготовления линзы и является недостатком известной линзы.
Использование искомой образующей в виде зависимости z(у) весьма неудобно, что также является недостатком известной линзы, в практике проще и легче оперировать зависимостью y(z).
Кроме того, несмотря на заявленную в [1] общность решения задачи, существует принципиальное ограничение на вид распределения ПП n(у), не упомянутое в [1] и сужающее выбор n(у) (это ограничение будет рассмотрено ниже).
3. РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Задача, на решение которой направлено изобретение, - повышение качества изображения и упрощение процесса изготовления апланатической градиентной линзы.
Решение поставленной задачи достигается путем определения аналитических выражений для образующих первой и второй преломляющих поверхностей и выбора единственно возможного распределения ПП для материала линзы.
Для этого в апланатической градиентной линзе, ограниченной первой и второй преломляющими поверхностями вращения, имеющей по оптической оси z толщину с, кратную удвоенному номинальному фокусному расстоянию, выполненной из материала с радиальным распределением показателя преломления n(у), имеющей форму преломляющих поверхностей, определяемую уравнением образующей z(y) вида
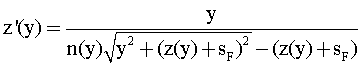
где z'(у) - первая производная от z(y)',
sF - передний отрезок;
распределение показателя преломления для материала линзы имеет вид
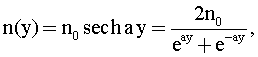
где n0 - значение показателя преломления на оси;
а - постоянная;
образующая первой поверхности определяется уравнением
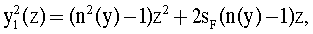
а образующая второй поверхности определяется уравнением
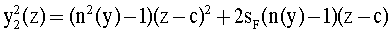
Для подтверждения правильности предложенных соотношений в заявляемой апланатической градиентной линзе рассмотрим сначала ход лучей в ней при преломлении на ее первой поверхности (фиг.1).
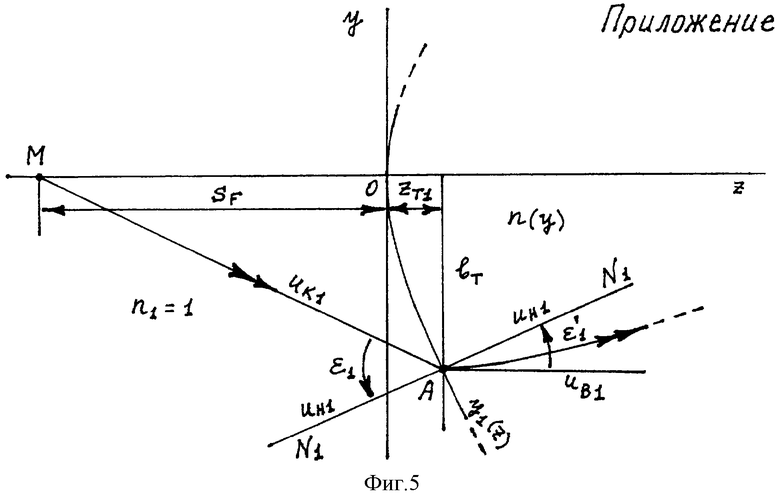
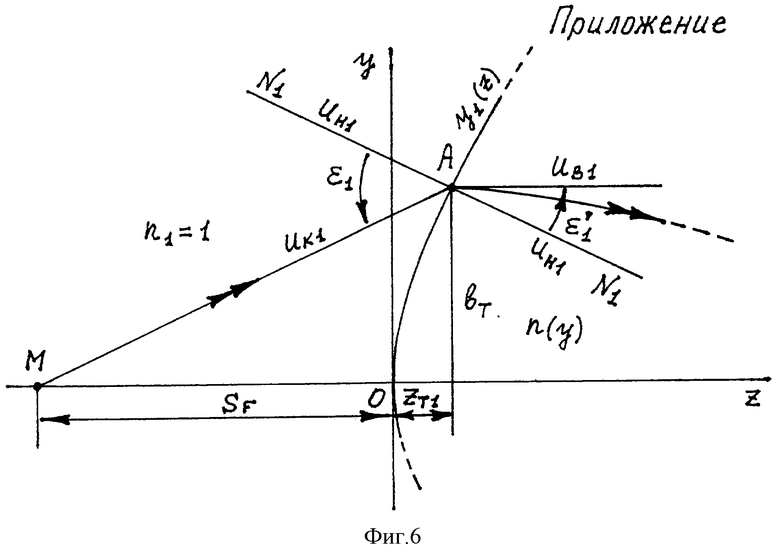
Линза толщиной с, выполненная из материала с зависящим от у распределением ПП n(у), известным для заданной длины волны, и ограниченная первой и второй преломляющими поверхностями вращения с образующими y1(z) и y2(z), расположена в однородной среде (примем ПП однородной среды n1=1 (воздух)). Отметим, что образующие y1(z) и y2(z) могут быть представлены также как z1(y) и z2(y) соответственно. Вершина первой поверхности расположена в начале координат. Ось z представляет собой оптическую ось линзы. Принимая, что линза обладает осевой симметрией, рассмотрение проводится в меридиональной плоскости.
Луч падающего на первую поверхность пучка, выходящего из точки М на оптической оси, имеет направляющий коэффициент uк1, преломляется в точке А с координатами zП1, yП1 и после преломления получает направление, параллельное оптической оси. Угол падения луча на первую поверхность обозначим как ε1, угол преломления - как 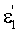 , а нормаль к первой поверхности в точке А - как N1.
, а нормаль к первой поверхности в точке А - как N1.
Направляющий коэффициент uн1 нормали N1 к первой поверхности в точке А можно выразить в виде
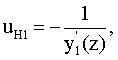
где 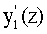 - первая производная от y1(z).
- первая производная от y1(z).
Значение uК1 определяется из выражения
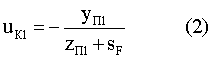
Угол падения луча можно определить по формуле [2]
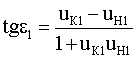
Соответственно, используя известное соотношение [2], можно вычислить
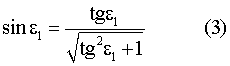
Тогда
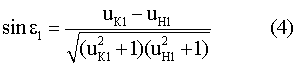
По закону преломления
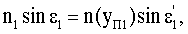
где n(yП1) - ПП в точке преломления А.
Тогда (с учетом того, что n1=1) угол преломления выразится в виде
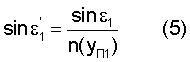
Подставив (4) в (5), получим
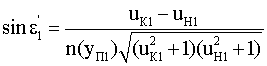
Пользуясь известным соотношением [2]
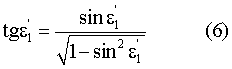
можно определить
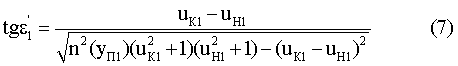
Угол преломления может быть также выражен следующим образом
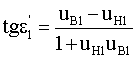
где uB1 - направляющий коэффициент преломленного на первой поверхности луча.
Учитывая, что в рассматриваемом случае после преломления направление луча должно быть параллельно оптической оси, принимаем uВ1=0. Тогда
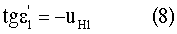
Приравняв (7) и (8), переходя к координатам и принимая n(yП1)=n(y), можно получить выражение
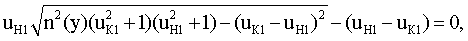
из которого после несложных преобразований можно получить уравнение для uН1
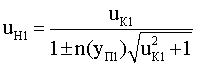
Нетрудно показать, что, подставив в полученное уравнение значение uК1 из (2), его можно преобразовать к виду
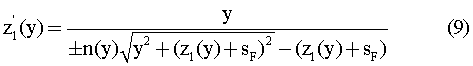
Учитывая, что первая поверхность выпуклая, и выбирая в (9) знак "плюс", получим приведенное в [1] уравнение (1)
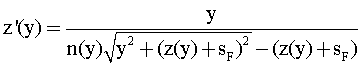
К сожалению, точное аналитическое решение для дифференциального уравнения (1) не известно и в [1] не указано, что ограничивает возможности изготовления линзы из-за необходимости аппроксимировать образующую подходящими кривыми.
Тем не менее найти в аналитическом виде вид образующей функции для первой поверхности можно. Для этого последовательно осуществим простые преобразования и запишем уравнение (1) следующим образом
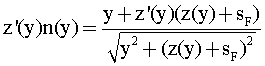
Нетрудно видеть, что правая часть полученного уравнения - полная производная
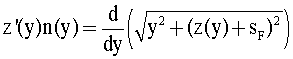
Соответственно, далее это уравнение можно записать в виде
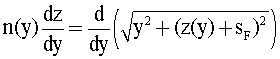
и окончательно получить пригодное для интегрирования выражение
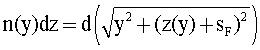
Отметим, что в левой части полученного выражения величина n(у) не зависит от z и ее можно вынести за пределы интегрирования. Переходя к координатам, можно записать
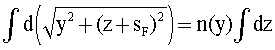
Проинтегрировав это выражение, получим общее решение в виде
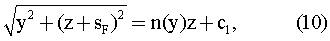
где c1 - постоянная интегрирования. Разрешив (10) относительно y1(z), получим
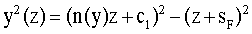
Для образующей y1(z) должно выполняться начальное условие
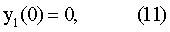
с учетом которого постоянная интегрирования
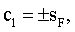
а образующая может быть представлена как
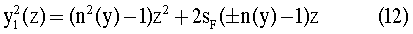
Разрешить неопределенность в отношении знака в уравнении (12) и проверить правильность полученного уравнения можно, если учесть, что при n(y)=n0=const должен получиться классический случай идеально фокусирующей линзы с первой поверхностью, имеющей форму гиперболы (вторая поверхность линзы должна при этом быть плоской), причем образующая первой поверхности определяется уравнением [3]
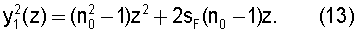
Сравнивая (12) и (13), можно придти к выводу о необходимости выбора в (12) знака "плюс". Таким образом с учетом (11), при наличии радиального градиента ПП уравнение образующей первой поверхности должно иметь вид
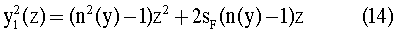
Полученное уравнение (14) определяет в аналитическом виде образующую, близкую к кривой второго порядка - гиперболе, но при этом усложненную наличием зависимости n(y), что позволяет ее условно считать гиперболой высшего порядка. В общем случае, из (14) можно, при заданном распределении n(у) и в соответствии с условиями фиг.1, выразить аналитически зависимость z1(у)=ƒ(y) в виде
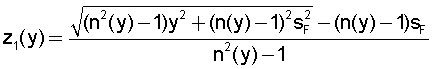
Заметим также, что уравнение (1) можно разрешить относительно y'(z), записав следующим образом
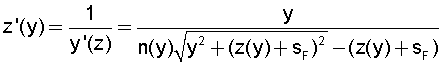
Соответственно, принимая за независимую координату z, получим
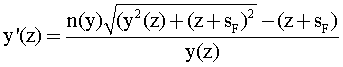
Перепишем это уравнение в виде
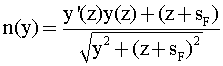
Правая часть здесь - также полная производная, а левая - не зависит от z
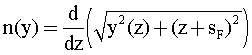
Получить пригодное для интегрирования выражение можно в следующем виде
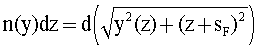
Интегрирование дает
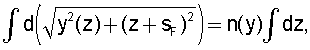
а общее решение совпадает с (10), и его можно найти аналогично описанному выше.
Для образования апланатической линзы необходимо, чтобы на выходе ее пучок оставался гомоцентрическим, в рассматриваемом случае - расходящимся.
Покажем, что, если форма второй поверхности линзы будет точно совпадать с формой первой поверхности, то после преломления на второй поверхности пучок на выходе линзы останется гомоцентрическим. Заметим, что для этого уравнение второй поверхности в выбранной системе координат должно иметь вид
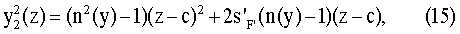
где 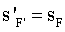 - задний отрезок.
- задний отрезок.
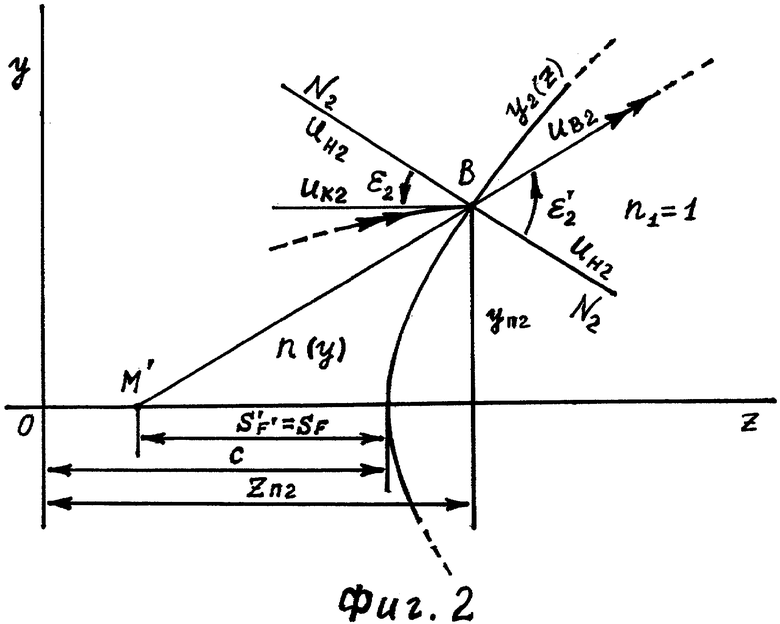
Рассмотрим преломление лучей на второй поверхности линзы (фиг.2).
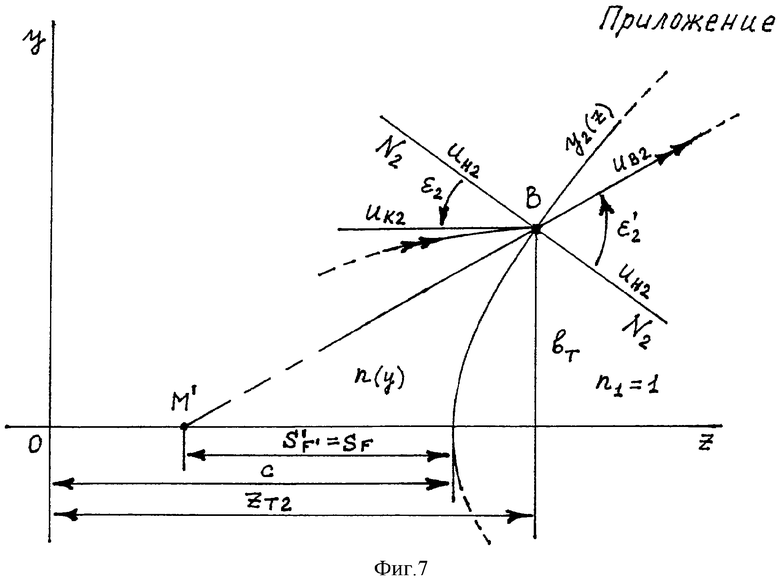
После распространения в материале линзы вдоль оптической оси луч попадает на вторую поверхность в точку В с координатами zП2, уП2, где вновь преломляется. При этом угол падения луча ε2, угол преломления - 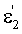 , направляющий коэффициент для луча в точке В должен быть равен uК2=0, а направляющий коэффициент uН2 нормали N2 ко второй поверхности в точке В 1
, направляющий коэффициент для луча в точке В должен быть равен uК2=0, а направляющий коэффициент uН2 нормали N2 ко второй поверхности в точке В 1
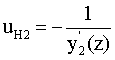
После преломления в точке В луч с направляющим коэффициентом uв2 распространяется в однородной среде с ПП n1=1, при этом мнимое продолжение луча пересекает оптическую ось в точке М' на расстоянии s'F' от вершины второй поверхности.
Направляющий коэффициент выходного луча
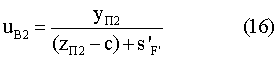
Угол падения луча на вторую поверхность
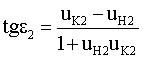
Учитывая, что в точке преломления должно выполняться условие uK2=0, получим
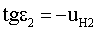
Соответственно, по известной формуле (3) можно вычислить
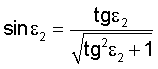
Тогда
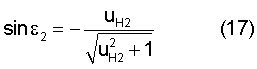
По закону преломления
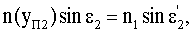
откуда
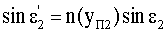
Тогда, подставляя (17), угол преломления выразим в виде
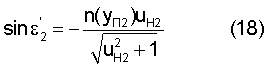
По известной формуле (6) определим
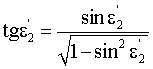
Тогда угол преломления можно с учетом (18) выразить в виде
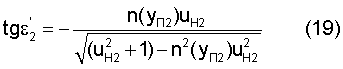
Угол преломления может быть также определен следующим образом
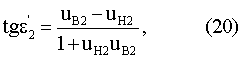
Переходя к координатам, приравняв (19) и (20), возведя обе части уравнения в квадрат и перенеся их в левую часть, получим
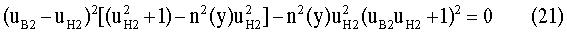
Раскроем выражение в квадратных скобках
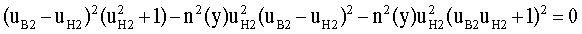
Сгруппируем второе и третье слагаемые
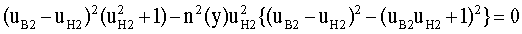
Учтем, что выражение в фигурных скобках преобразуется к виду
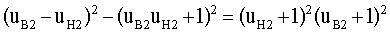
Тогда уравнение (21) можно записать в следующем виде
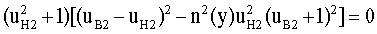
Далее будем рассматривать только выражение в квадратных скобках, поскольку левый сомножитель, очевидно, не имеет действительных решений. Получим выражение
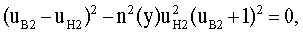
из которого нетрудно, после простых преобразований, выразить uн2
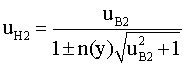
Подставив в это уравнение uB2 из (16) и переходя к
координатам, нетрудно получить уравнение, совпадающее по структуре с (9)
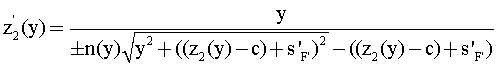
В полученном уравнении так же, как и в дифференциальном уравнении (1) для первой поверхности, должен быть выбран знак "плюс", в результате оно приобретет вид
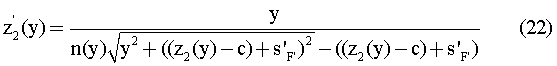
Это уравнение совпадает по структуре с (1), а отличия связаны с учетом смещения вершины по оптической оси в выбранной системе координат. Если же совместить начало координат с вершиной второй поверхности, то получим в точности уравнение (1).
Для интегрирования уравнения (22) можно применить описанную выше последовательность действий. Действительно, перепишем уравнение (22) в следующем виде
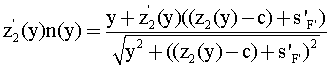
Здесь также правая часть полученного уравнения - полная производная
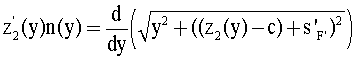
Далее это уравнение можно записать в виде
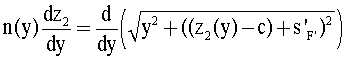
и окончательно получить пригодное для интегрирования выражение
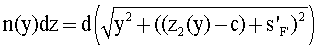
Отметим, что снова в левой части величина n(у) не зависит от z и ее можно вынести за пределы интегрирования. Переходя к координатам, получим выражение
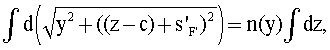
Проинтегрировав это выражение, получим
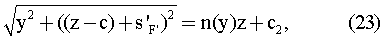
где с2 - постоянная интегрирования.
Разрешив (23) относительно у2(z), получим
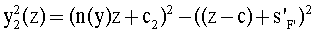
Для y2(z) должно выполняться начальное условие
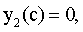
с учетом которого постоянная интегрирования
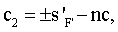
а образующая может быть представлена в виде
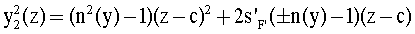
Выбирая в полученном уравнении знак "плюс", поскольку образующая рассматривается при z>с, получаем вид образующей, совпадающий с предсказанным выше видом уравнения (15). Учитывая, что передний и задний отрезки равны по величине, уравнение для второй поверхности можно записать в виде
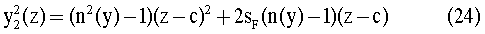
Сравнивая (14) и (24), можно видеть, что образующая y2(z) по форме повторяет y1(z), но сдвинута по оси z на толщину линзы с.
Из (24) также можно выразить z2(y)=ƒ(y) в виде
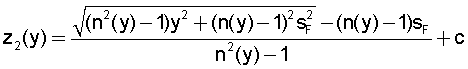
Важным условием достижения апланатической коррекции в предлагаемой линзе является постоянное значение длины периодичности линзы для любой начальной высоты луча. Тогда все лучи, преломленные на первой поверхности и распространяющиеся внутри материала с радиальным градиентом ПП вдоль оптической оси, будут формировать волновой фронт, точно повторяющий по форме первую поверхность, через расстояния, кратные половине длины периодичности (или удвоенному номинальному фокусному расстоянию). Это условие было в [1] указано как выполняющееся для любого распределения n(y) по умолчанию. Однако, к сожалению, условие постоянства значения длины периодичности для разных высот входа луча в градиентную среду выполняется не для всех распределений n(y).
Единственным распределением ПП, обеспечивающим это свойство градиентной среды, является так называемое идеально фокусирующее или гиперсекансное распределение ПП вида [4, 5]
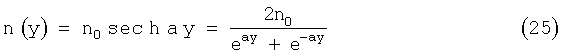
В связи с этим выбор среды для возможной реализации предлагаемой апланатической линзы оказывается, к сожалению, единственным, - только распределение ПП (25).
Длина периодичности L для гиперсекансного распределения ПП равна
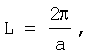
соответственно, половина длины периодичности
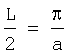
Номинальное фокусное расстояние линзы с гиперсекансным распределением ПП
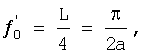
удвоенное номинальное фокусное расстояние будет равно половине длины периодичности

Как известно, две сопряженные точки в пространстве предметов и изображений называются апланатическими, если в изображении отсутствует сферическая аберрация и выполняется условие синусов (или закон синусов Аббе) [7]. Отсутствие сферической аберрации для точки М' было доказано выше. Покажем теперь, что для пары сопряженных точек М и М' выполняется закон синусов Аббе.
Закон синусов Аббе в общем случае имеет вид
n sinσ=βn'sinσ'
или
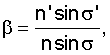
где n - показатель преломления среды, в которой расположен предмет;
n' - показатель преломления среды, в которой формируется изображение;
σ - угол между оптической осью и лучом, выходящим из осевой точки предмета;
σ' - угол между оптической осью и лучом, выходящим из оптической системы и проходящим через осевую точку изображения;
β - линейное увеличение оптической системы.
Для предложенной линзы уравнение примет вид (фиг.1, 2)
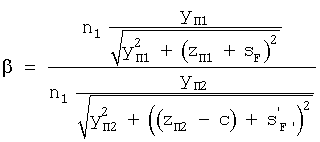
Поскольку в рассматриваемом случае yП1=yП2, sF=s' F' и образующие 1-й и 2-й поверхностей одинаковы, то стрелки прогиба поверхностей тоже равны, соответственно
zП1=(zП2-c)
В результате линейное увеличение линзы постоянно и равно β=1. В рассматриваемой линзе для пары сопряженных точек М и M' на оси отсутствует сферическая аберрация и выполняется закон синусов Аббе для любого луча. Точки М и М' являются парой апланатических точек, а саму линзу можно назвать апланатической.
Таким образом, знание аналитического вида уравнения (14) для первой преломляющей поверхности и уравнения (24) для второй преломляющей поверхности в совокупности с единственно возможным видом распределения n(у) в соответствии с (25) позволит в процессе изготовления линзы обойтись без этапов численного интегрирования и последующей аппроксимации, что упрощает процесс изготовления, повышает точность формообразования преломляющих поверхностей, облегчает контроль формы поверхностей и, в конечном итоге, повышает качество изображения, формируемое линзой.
4. КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
На фиг.1 показаны схема преломления луча на первой поверхности апланатической градиентной линзы в меридиональной плоскости и условные обозначения для расчета хода луча.
На фиг.2 показаны схема преломления луча на второй поверхности апланатической градиентной линзы в меридиональной плоскости и условные обозначения для расчета хода луча.
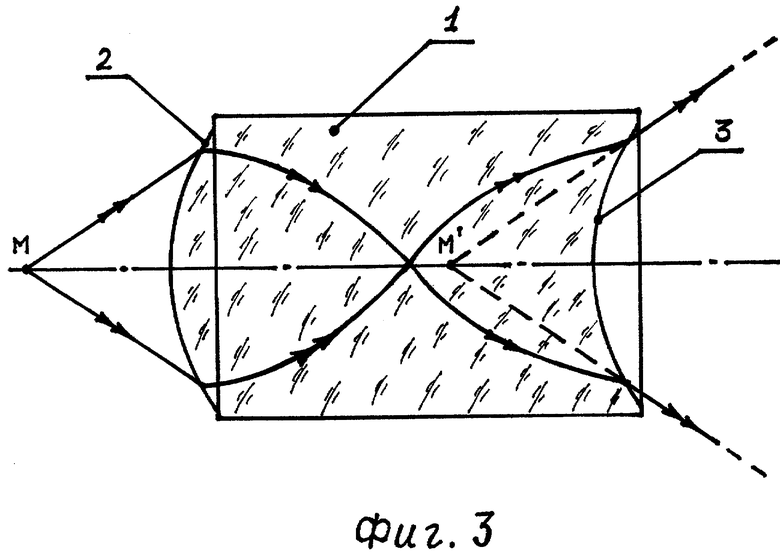
На фиг.3 показаны оптическая схема апланатической градиентной линзы в меридиональной плоскости и ход лучей в ней.
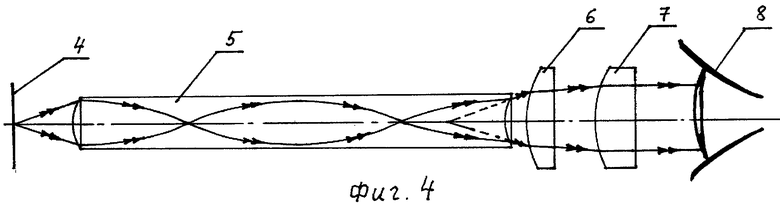
На фиг.4 показаны возможная оптическая схема эндоскопа с использованием апланатической градиентной линзы, в меридиональной плоскости, и ход лучей в ней.
Двойными стрелками на фиг.1-4 показан ход лучей.
5. ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Для реализации предложенной апланатической градиентной линзы из материала с гиперсекансным распределением ПП n(y) вида (25) и известными значениями n0 и а вначале, исходя из параметров распределения n{y}, зависящей от него толщины линзы с (кратной удвоенному номинальному фокусному расстоянию, согласно (26)) и переднего отрезка sF=s' F', определяется в соответствии с (14) форма образующей y1(z).
Затем берется заготовка для линзы необходимого диаметра из материала с известным распределением ПП n(y) и обрезается до рассчитанной толщины, кратной удвоенному номинальному фокусному расстоянию (с определенным технологическим припуском). Формообразование первой и второй преломляющих поверхностей на торцах заготовки производится по одной из известных оптических технологий, например, путем последовательной шлифовки и полировки или путем применения абразивной технологии с последующей ионной ретушью поверхностей [6], до достижения формы поверхностей согласно (14) и (24).
Поскольку стрелка прогиба требуемых поверхностей с образующими (14) и (24) больше, чем у обычных гиперболических поверхностей с образующими вида (13), то можно рекомендовать двухэтапный процесс формообразования преломляющих поверхностей - на первом этапе формируются обычные гиперболические поверхности, а на втором этапе их форма доводится до требуемой с помощью дополнительной полировки или ретуши.
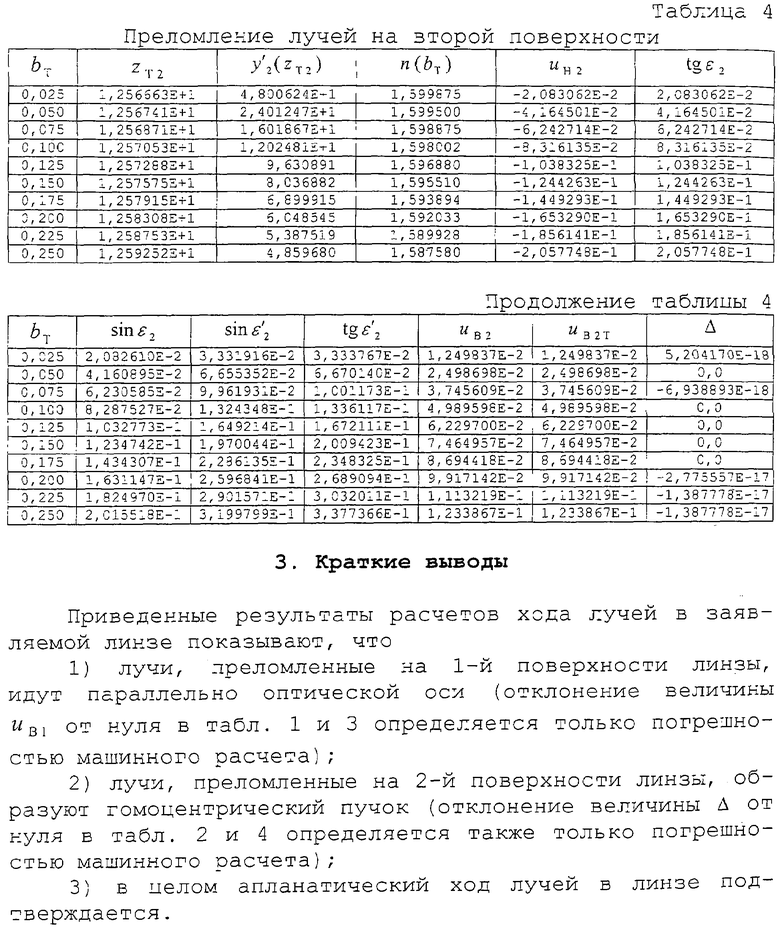
В Приложении приведены последовательность и результаты численных расчетов хода лучей в линзе толщиной L и 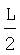 , подтверждающие апланатические свойства предлагаемой линзы.
, подтверждающие апланатические свойства предлагаемой линзы.
Используется предлагаемая градиентная линза обычным образом. В точку М перед первой поверхностью 2 линзы 1 (фиг.3) помещается точечный источник излучения. После преломления на первой поверхности и прохождения внутри линзы гомоцентрический пучок излучения, преломляясь на второй поверхности 3 линзы, выходит из нее, оставаясь гомоцентрическим (с центром в точке М').
Использование предложенной апланатической линзы возможно, например, в качестве градана в эндоскопах (фиг.4). В этом случае исследуемый объект 4 помещается в передний фокус апланатической линзы 5. Мнимое изображение объекта через окуляр 7 (с использованием компенсатора аберраций 6) попадает в глаз наблюдателя 8. В результате в эндоскопе можно обойтись без обычно применяемого входного объектива.
Другой возможностью использования линзы является применение ее как апланатического элемента в составе сложной оптической системы, например эндоскопа, объектива, конденсора и т.п.






6. ИСТОЧНИКИ ИНФОРМАЦИИ
1. Апланатическая градиентная линза - авторское свидетельство СССР №1569764, опубл. 07.06.1990 г., бюлл. №21.
2. Выгодский М.Я. Справочник по высшей математике. 1-е изд. - М.: Наука, 1972, 870 с.
3. Вычислительная оптика. Справочник/ Под ред. М.М.Русинова - М.: Машиностроение, 1984, 423 с.
4. Ильин В.Г. и др. Физические основы градиентной оптики/ Учебное пособие - Л., Ленингр. политех. институт, 1990, 55 с.
5. Микаэлян А.Л. Применение слоистой среды для фокусирования волн - Доклады Академии Наук СССР, 1951, т. 81, №4, стр.569-571.
6. Государственный оптический институт им. С. И. Вавилова. Официальный сайт в сети Интернет. Информация по адресу http://soi.srv.pu.ru/r_1251/developments/technology/ap_ktf.htm
7. Бегунов Б.Н., Заказнов Н.П. и др. Теория оптических систем. Учебник для вузов - М.: Машиностроение, 1981.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГРАДИЕНТНАЯ ЛИНЗА С АПЛАНАТИЧЕСКИМИ И ТЕЛЕСКОПИЧЕСКИМИ СВОЙСТВАМИ | 2013 |
|
RU2529775C1 |
| ГРАДИЕНТНАЯ ЛИНЗА | 2005 |
|
RU2289830C1 |
| ТЕЛЕСКОПИЧЕСКАЯ ГРАДИЕНТНАЯ ЛИНЗА | 1996 |
|
RU2114451C1 |
| Градиентная линза | 1987 |
|
SU1500964A1 |
| Апланатическая градиентная линза | 1988 |
|
SU1569764A1 |
| ГРАДИЕНТНАЯ ЛИНЗА (ВАРИАНТЫ) | 2002 |
|
RU2222819C2 |
| Градиентная линза | 1985 |
|
SU1337861A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ТРЕХМЕРНЫХ ОПТИЧЕСКИХ МИКРОСТРУКТУР С ГРАДИЕНТОМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ ДВУХФОТОННОЙ ЛИТОГРАФИИ | 2023 |
|
RU2826645C1 |
| ПЛАНАРНАЯ БИНАРНАЯ МИКРОЛИНЗА | 2010 |
|
RU2454760C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПЕРЕНАПРАВЛЯЮЩЕЙ СВЕТ ПОВЕРХНОСТИ КАУСТИЧЕСКОГО СЛОЯ, ОПТИЧЕСКИЙ ЗАЩИТНЫЙ ЭЛЕМЕНТ, СОДЕРЖАЩИЙ ИЗГОТОВЛЕННУЮ ПЕРЕНАПРАВЛЯЮЩУЮ СВЕТ ПОВЕРХНОСТЬ КАУСТИЧЕСКОГО СЛОЯ, МАРКИРОВАННЫЙ ОБЪЕКТ, ПРИМЕНЕНИЕ И СПОСОБ АУТЕНТИФИКАЦИИ ОБЪЕКТА | 2019 |
|
RU2794281C2 |
Изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении. Апланатическая градиентная линза ограничена первой и второй преломляющими поверхностями вращения, имеет по оптической оси z толщину с, кратную удвоенному номинальному фокусному расстоянию, и выполнена из материала с радиальным распределением показателя преломления n(у). Линза имеет форму преломляющих поверхностей, определяемую уравнением образующей z(y) вида 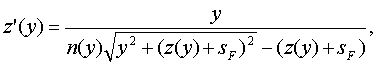 где z'(y) - первая производная от z(y); SF - передний отрезок. Распределение показателя преломления для материала линзы имеет вид
где z'(y) - первая производная от z(y); SF - передний отрезок. Распределение показателя преломления для материала линзы имеет вид 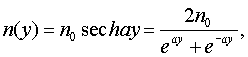 где n0 - значение показателя преломления на оси; а - постоянная. Образующие первой и второй поверхностей определяются следующими уравнениями y1 2(z)=(n2(y)-1)z2+2sF(n(y)-1)z, y2 2(z)=(n2(y)-1)(z-c)2+2sF(n(y)-1)(z-c). Технический результат - повышение качества изображения и упрощение процесса изготовления. 4 ил., 1 приложение с 3 ил.
где n0 - значение показателя преломления на оси; а - постоянная. Образующие первой и второй поверхностей определяются следующими уравнениями y1 2(z)=(n2(y)-1)z2+2sF(n(y)-1)z, y2 2(z)=(n2(y)-1)(z-c)2+2sF(n(y)-1)(z-c). Технический результат - повышение качества изображения и упрощение процесса изготовления. 4 ил., 1 приложение с 3 ил.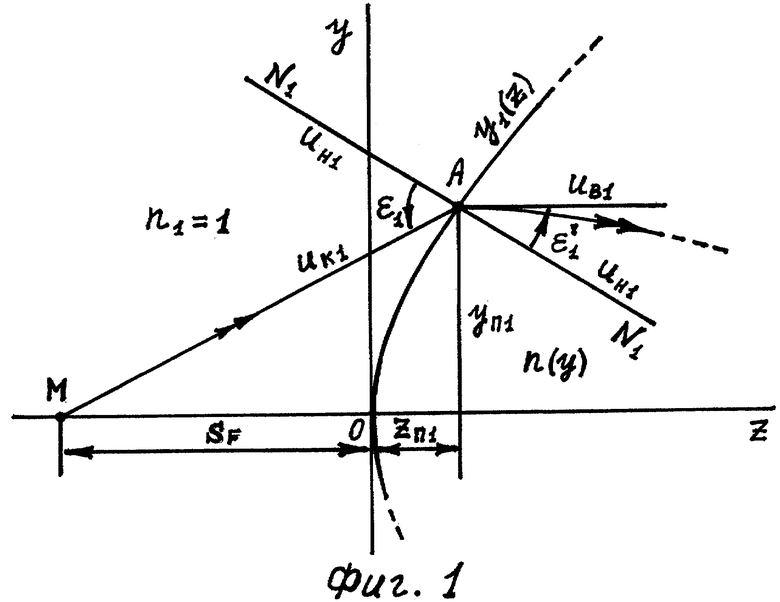
Апланатическая градиентная линза, ограниченная первой и второй преломляющими поверхностями вращения, имеющая по оптической оси z толщину с, кратную удвоенному номинальному фокусному расстоянию, выполненная из материала с радиальным распределением показателя преломления n(у), имеющая форму преломляющих поверхностей, определяемую уравнением образующей z(y) вида
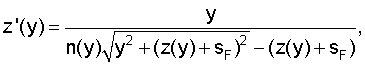
где z'(y) - первая производная от z(y);
sF - передний отрезок,
отличающаяся тем, что распределение показателя преломления для материала линзы имеет вид
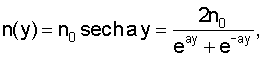
где n0 - значение показателя преломления на оси;
а - постоянная;
образующая первой поверхности определяется уравнением
y1 2(z)=(n2(y)-1)z2+2sF(n(y)-1)z,
а образующая второй поверхности определяется уравнением
y2 2(z)=(n2(y)-1)(z-c)2+2sF(n(y)-1)(z- с).
| Апланатическая градиентная линза | 1988 |
|
SU1569764A1 |
| ГРАДИЕНТНАЯ ЛИНЗА (ВАРИАНТЫ) | 2002 |
|
RU2222819C2 |
| ТЕЛЕСКОПИЧЕСКАЯ ГРАДИЕНТНАЯ ЛИНЗА | 1996 |
|
RU2114451C1 |
| US 5841586 A, 24.11.1994 | |||
| US 6057968 A, 02.05.2000. | |||
Авторы
Даты
2006-11-27—Публикация
2005-04-05—Подача