Изобретение относится к измерительной технике, а именно - к яркостной пирометрии, и может быть использовано для прецизионных измерений температуры нагретых тел и сред.
Известен способ измерения яркостной температуры объекта по методу исчезающей нити путем сравнения яркости нити накала эталонной лампы пирометра и объекта, в котором температуру объекта определяют по величине тока накала после уравнивания яркостей нити сравнения и объекта (Линевег Ф. Измерение температур в технике. - М.: Металлургия, 1980, с. 384).
Известен также способ измерения яркостной температуры объекта по методу исчезающей нити путем сравнения яркости нити накала эталонной лампы пирометра и объекта, температуру которого определяют после уравнивания яркостей нити накала и объекта, при этом яркость объекта регистрируют многоэлементным фотоприемником, а ток накала на эталонную лампу подают только в режиме калибровки пирометра, кроме того режим калибровки осуществляют по сигналу с устройства, чувствительного к изменению температуры, а изображение нити накала эталонной лампы проецируют на фоточувствительную поверхность фотоприемника только в режиме калибровки (патент РФ №2247338, МПК G01J 5/00, опубл. 27.02.2005).
Общим недостатком перечисленных выше способов является то, что сравнение яркостей нити и объекта осуществляется визуально оператором, выполняющим измерения, поэтому имеет место влияние субъективного фактора, зависящего от навыка оператора и светочувствительности рецепторов его глаза. Из-за этого результаты измерений, выполненные разными операторами, различаются - это снижает достоверность и воспроизводимость результатов измерений и не позволяет измерить температуру объекта с высокой точностью.
Известен способ и система коррекции на основе квантовой теории для повышения точности радиационного термометра, основанные на измерении энергии излучения объекта радиационным термометром, построении адаптированной эффективной физической модели системы и калибровке радиационного термометра (патент РФ №2523775, МПК G01J 5/00, G06F 17/17, опубл. 20.07.2014).
Недостаток способа заключается в том, что при его реализации используется операция подгонки значений параметров, отражающих структуру энергетических уровней объекта, что неизбежно влечет за собой существенное снижение метрологической точности. Кроме того, способ предполагает использование заранее откалиброванных стандартных средств измерений температуры - платинового термометра сопротивления, термопарного преобразователя или ртутного термометра, что дополнительно снижает точность получаемых результатов, так как на неопределенность конечного результата измерений накладывается неопределенность исходной калибровки указанных средств измерений.
Известен также пирометрический способ определения термодинамической температуры металлов, согласно которому при определении температуры используют поочередную подсветку анализируемого элемента поверхности металла тремя лазерами с известными мощностями и длинами волн излучения, при этом определяют возникающие при поочередной подсветке приращения сигналов фотоприемников, каждое из которых нормируют на мощность соответствующего лазера. По нормированным приращениям сигналов фотоприемников вычисляют отношения монохроматических коэффициентов отражения, учитывают отклонение излучательной способности поверхности металлов от константы и определяют термодинамическую температуру металлов при изменении их спектрального коэффициента излучения в процессе нагрева (патент РФ №2381463, МПК G01J 5/00, опубл. 10.02.2010).
Недостатки указанного способа заключаются в невысокой точности получаемых результатов, которая обусловлена тем, что для реализации способа требуется измерение спектральной чувствительности трех фотоприемников, из чего следует 3-х кратное увеличение неопределенности измерений в сравнении с одиночным фотоприемником. Кроме того использование способа для измерения температуры слабоотражающих объектов, например, таких как модели абсолютно черного тела, у которых коэффициент отражения лазерного излучения недостаточен для надежной и точной регистрации отраженного сигнала, - приводит к существенному повышению погрешности измерений.
Наиболее близким к предлагаемому способу по технической сущности является способ измерения термодинамической температуры (прототип) и реализующее его устройство, в котором для измерения термодинамической температуры используют калиброванные по спектру источник излучения и квантовый трап-детектор, измеряют сигнал трап-детектора, сформированный излучением от источника, по измеренному сигналу рассчитывают мощность излучения источника и по формуле М. Планка расчетным путем находят термодинамическую температуру, соответствующую данной яркости источника (заявка на изобретение №2018127133 от 23.07.2018, решение о выдаче патента от 19.06.2019, МПК G01K 15/00, G01N 21/41, G01J 5/00).
Главный недостаток способа заключается в том, что преимущественно он предназначен для измерений температуры моделей абсолютно черного тела. При измерениях температуры реальных тел, у которых спектр излучения отличен от спектра излучения абсолютно черного тела, в получаемый результат измерения вносится дополнительная неопределенность. В результате при использовании способа для измерения температуры реальных объектов достоверность результатов снижается, и в каждом конкретном случае она зависит от типа и вида исследуемого объекта.
Технический результат от применения способа - повышение точности измерения яркостной температуры.
Указанный результат достигается тем, что в способе измерения яркостной температуры объекта используют калиброванный по спектру опорный источник излучения, задают полосу излучения опорного источника, в заданной спектральной полосе излучения компарируют энергетические светимости объекта и опорного источника, регулируют мощность излучения опорного источника до достижения равенства энергетических светимостей источника и объекта, измеряют достигнутую энергетическую светимость опорного источника, рассчитывают коэффициент неэквивалентности спектра излучения опорного источника спектру идеального абсолютно черного тела, а искомую яркостную температуру объекта рассчитывают по соотношению
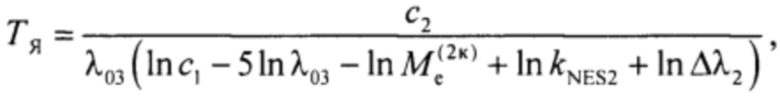
где
ТЯ - яркостная температура объекта,
с1, с2 - первый и второй коэффициенты в формуле М. Планка для спектральной энергетической яркости идеального абсолютно черного тела,
Δλ2 - эффективная ширина спектральной полосы излучения калиброванного опорного источника,
λ03 - центральная длина волны излучения идеального абсолютно черного тела,
Ме(2к) - измеренная энергетическая светимость калиброванного опорного источника,
kNES2 - коэффициент неэквивалентности спектра излучения калиброванного опорного источника спектру идеального абсолютно черного тела.
В другом варианте осуществления способа используют некалиброванный по спектру опорный источник, задают узкую спектральную полосу излучения опорного источника, в заданной спектральной полосе излучения компарируют энергетические светимости объекта и опорного источника, регулируют мощность излучения опорного источника до достижения равенства энергетических светимостей источника и объекта, измеряют достигнутую мощность излучения опорного источника и рассчитывают его энергетическую светимость, в заданной спектральной полосе измеряют спектральное распределение мощности излучения объекта, рассчитывают коэффициент неэквивалентности спектра излучения объекта спектру излучения идеального абсолютно черного тела, а искомую яркостную температуру объекта рассчитывают по соотношению
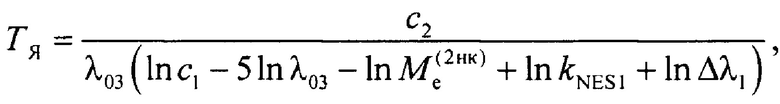
где
Δλ1 - эффективная ширина спектральной полосы излучения объекта,
Me(2нк) - энергетическая светимость некалиброванного опорного источника,
kNES1 - коэффициент неэквивалентности спектров излучения объекта и идеального абсолютно черного тела.
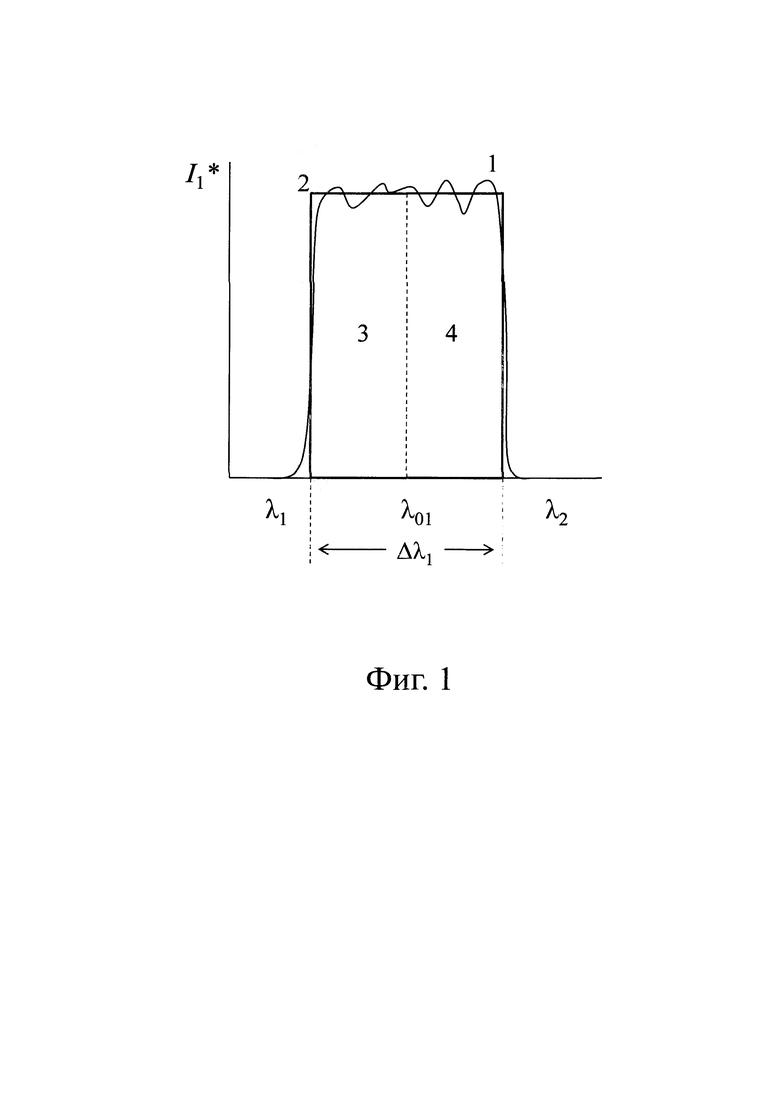
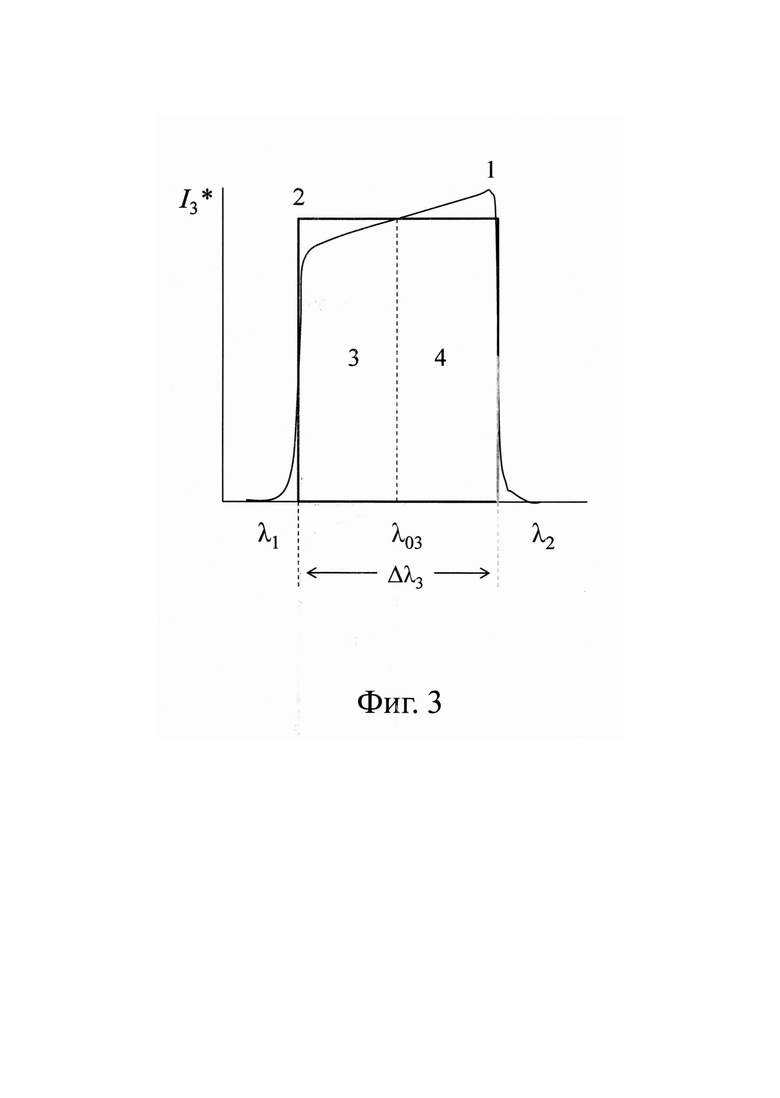
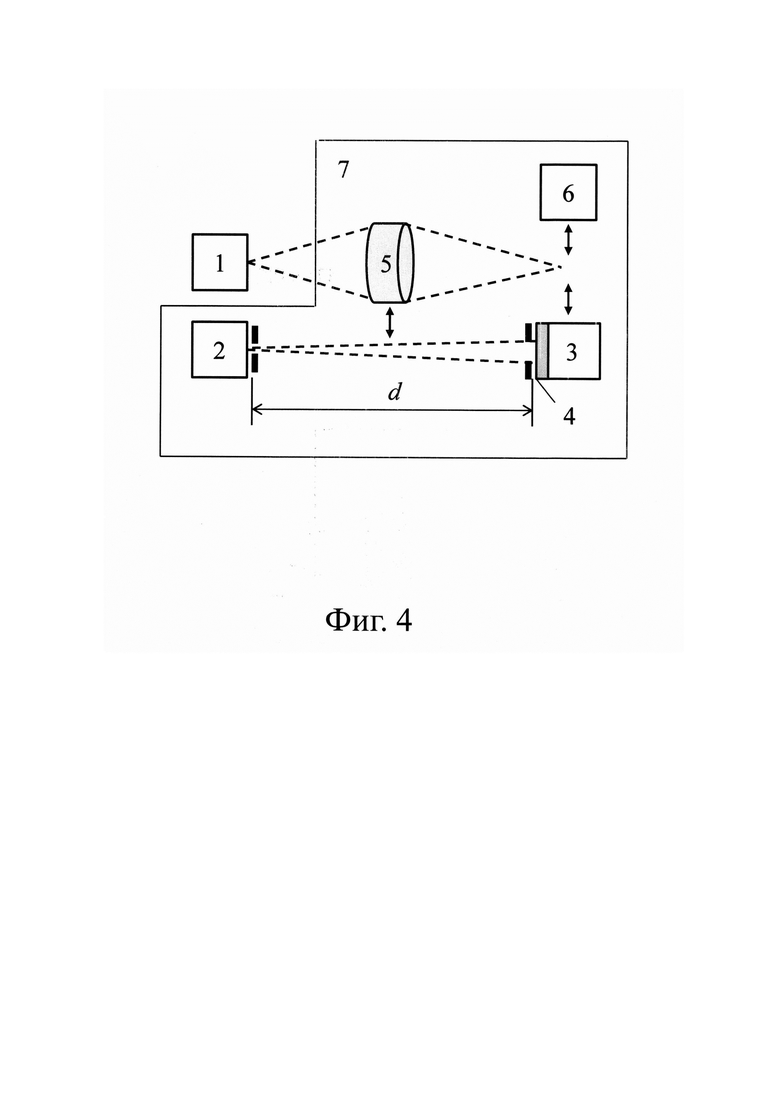
Сущность способа поясняется фиг. 1, 2, 3, 4, 5. На фиг. 1, 2, 3 для заданной спектральной полосы представлены графические примеры спектров излучения различных источников - объекта (фиг. 1), опорного источника (фиг. 2) и идеального абсолютно черного тела (фиг. 3), соответственно, в которых: линия 1 - спектральное распределение мощности излучения соответствующего источника, линия 2 - эквивалентное по площади спектрально-независимое распределение мощности излучения рассматриваемого источника. На фиг. 4 представлена структурная схема устройства 7, с помощью которого измеряется температура объекта 1, в котором: 2 - опорный источник излучения, 3 - фотодиодный приемник, 4 - полосовой оптический фильтр, 5 - оптическая фокусирующая система, 6 - анализатор оптического спектра. На фиг. 5 представлена зависимость абсолютной неопределенности измерений яркостной температуры от уровня измеряемой температуры (при коэффициенте охвата k=1).
Сущность заявленного способа заключается в следующем.
В основу уравнения измерения способа положен закон М. Планка, согласно которому зависимость спектральной энергетической яркости абсолютно черного тела от его термодинамической температуры имеет вид:

где
λ - длина волны, м;
c1=2πhc2=3,741771852⋅10-16 - первый коэффициент (первая радиационная постоянная) в законе Планка, Вт⋅м2;
с2=hc/k=1,438776877⋅10-2 - второй коэффициент (вторая радиационная постоянная) в законе Планка, м⋅К;
h=6,62607015⋅10-34 - постоянная М. Планка, Дж⋅с;
е=1,602176634⋅10-19 - элементарный заряд, Кл или (А⋅с);
с=2,99792458⋅108 - скорость света в вакууме, м/с;
k=1,380649⋅10-23 - постоянная Больцмана, Дж/К;
Т - термодинамическая температура, К.
Общеизвестно, что любое нагретое тело или среда, которые далее будем называть объект, излучает в окружающую среду некоторую энергию с мощностью, которую можно измерить, например, с помощью фотодиодного приемника. При таких измерениях фотодиод генерирует фототок, прямо пропорциональный указанной мощности. В общем случае уравнение для расчета мощности излучения по измеренному фототоку имеет вид:

где
Р - мощность излучения, Вт,
IFD - измеренный фототок фотодиода, А,
Sλ - спектральная чувствительность фотодиода, А/Вт.
В свою очередь, фототок, генерируемый фотодиодом от излучения объекта для спектральной полосы, задаваемой, например, с помощью полосового оптического фильтра, может быть рассчитан также по известному соотношению:

где
IFD(1) - фототок, генерируемый фотодиодом от излучения объекта, А,
Lλ(1) - спектральная энергетическая яркость объекта, Вт/м3,
λ1, λ2 - границы заданной спектральной полосы излучения, м,
τλ - спектральный коэффициент пропускания полосового оптического фильтра,
F - геометрический фактор, который рассчитывают по формуле:
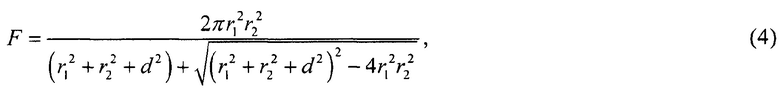
r1 - радиус выходного окна источника излучения, м,
r2 - радиус входного окна фотодиодного приемника, м,
d - расстояние между выходным окном источника излучения и входным окном фотодиодного приемника, м. В частном случае, когда фотодиод установлен вплотную к выходному окну источника излучения и r2>r1, геометрический фактор равен площади выходного окна источника излучения.
Подынтегральная функция в соотношении (3) 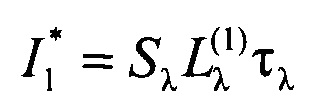 имеет спектральную зависимость, графический пример которой представлен на фиг. 1 (линия 1), при этом площадь под данной графической зависимостью - есть значение интеграла в соотношении (3), которое, в свою очередь, равно произведению энергетической светимости объекта Ме(1) на среднеинтегральную по заданной спектральной полосе чувствительность фотодиода Sλ, т.е.:
имеет спектральную зависимость, графический пример которой представлен на фиг. 1 (линия 1), при этом площадь под данной графической зависимостью - есть значение интеграла в соотношении (3), которое, в свою очередь, равно произведению энергетической светимости объекта Ме(1) на среднеинтегральную по заданной спектральной полосе чувствительность фотодиода Sλ, т.е.:

Для получения уравнения измерения способа заменим спектрально-зависимую подынтегральную функцию I* эквивалентной по площади спектрально-независимой функцией с эффективной шириной спектральной полосы, равной Δλ1, и симметричной относительно центральной длины волны λ01 (линия 2, фиг. 1). Равенство площадей под указанными спектральными зависимостями (линии 1, 2, фиг. 1) означает выполнение следующего условия:

в левой части которого значения спектральной чувствительности фотодиода (Sλ), спектральной энергетической яркости объекта (Lλ(1)) взяты для центральной длины волны λ01, а коэффициент пропускания полосового оптического фильтра (τλ) принят равным единице. При этом под центральной длиной волны λ01 понимается длина волны, для которой выполняется условие равенства следующих интегралов (равенство площадей участков 3,4 на фиг. 1):

С учетом условия (6) соотношение (3) принимает вид:

Рассуждения и математические операции, аналогичные представленным выше, полностью справедливы и могут быть применены для опорного источника излучения, например, построенного на основе лазерного излучателя. Подынтегральная функция 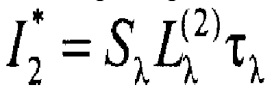 для опорного источника показана на фиг. 2 (линия 1), линия 2 - спектрально-независимая и эквивалентная по площади функция. Для такого опорного источника фототок, генерируемый фотодиодом от излучения источника, может быть рассчитан по соотношению, аналогичному полученному для объекта, и имеет вид:
для опорного источника показана на фиг. 2 (линия 1), линия 2 - спектрально-независимая и эквивалентная по площади функция. Для такого опорного источника фототок, генерируемый фотодиодом от излучения источника, может быть рассчитан по соотношению, аналогичному полученному для объекта, и имеет вид:

где
IFD(2) - фототок, генерируемый фотодиодом излучением, исходящим от опорного источника, А.
В соотношении (9) значение коэффициента пропускания полосового оптического фильтра (τλ) принято равным единице, а значения спектральной чувствительности фотодиода (Sλ) и спектральной энергетической яркости опорного источника (Lλ(2)) взяты для центральной длины волны λ02, которая рассчитывается по соотношению, аналогичному (7):

Применим рассуждения и математические операции, аналогичные представленным выше, для идеального абсолютно черного тела. Подынтегральная функция 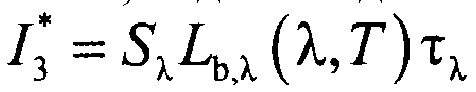 для идеального абсолютно черного тела показана на фиг. 3 (линия 1), линия 2 - спектрально-независимая и эквивалентная по площади функция. В этом случае фототок, генерируемый фотодиодом от АЧТ, может быть рассчитан по соотношению, аналогичному полученному для объекта и для опорного источника, и имеет вид:
для идеального абсолютно черного тела показана на фиг. 3 (линия 1), линия 2 - спектрально-независимая и эквивалентная по площади функция. В этом случае фототок, генерируемый фотодиодом от АЧТ, может быть рассчитан по соотношению, аналогичному полученному для объекта и для опорного источника, и имеет вид:

где
IFD(АЧТ) - фототок, генерируемый фотодиодом излучением от АЧТ,
Lb,λ(λ03,T) - энергетическая яркость идеального абсолютно черного тела на центральной длине волны λ03, описываемая формулой М. Планка (1).
В соотношении (11) значение коэффициента пропускания полосового оптического фильтра (τλ) принято равным единице, а значения спектральной чувствительности фотодиода (Sλ) и спектральной энергетической яркости АЧТ (Lb,λ) взяты для центральной длины волны λ03, которая рассчитывается по соотношению, аналогичному (7):
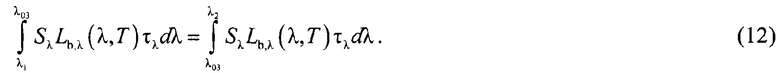
При равенстве энергетических светимостей исследуемого объекта и опорного источника для одной и той же заданной спектральной полосы равны и измеренные фототоки, т.е.:

Представим энергетическую яркость объекта L01(1) на центральной длине волны λ01 в виде произведения энергетической яркости идеального абсолютно черного тела (АЧТ) на центральной длине волны λ03 на коэффициент, учитывающий различие спектров излучения объекта и АЧТ, т.е.:

где
kNES1 - коэффициент приведения спектра излучения объекта к спектру излучения идеального абсолютно черного тела, который рассчитывается по соотношению:
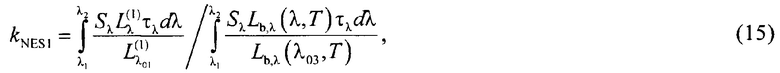
А с учетом условия (6), распространенного и на АЧТ, принимает вид:

Подставим соотношения (16), (14) в (8), получаем:

Аналогичные действия, выполненные по отношению к опорному источнику, дают следующие соотношения:
- для коэффициента приведения спектра излучения опорного источника к спектру излучения идеального абсолютно черного тела kNES2:
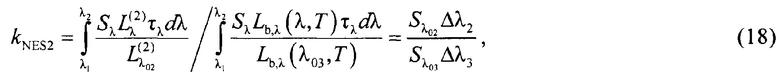
- для фототока:

Соотношения (17) и (19) можно равноправно брать за основу уравнения измерения способов. При этом, можно использовать заранее измеренный спектр излучения калиброванного опорного источника (соотношение (19)) - первый способ, либо измерять спектр излучения объекта (соотношение (17)) и при этом использовать некалиброванный опорный источник - второй способ.
Выберем соотношение (19) за основу уравнения измерения первого способа - это предполагает, что спектр излучения опорного источника заранее известен, т.е. опорный источник откалиброван. Для этого видоизменим данное уравнение, для чего используем известное расчетное соотношение для спектральной чувствительности фотодиода, которое имеет вид:

где
QED - квантовая эффективность фотодиода,
λ - длина волны,
h - постоянная М. Планка,
е - элементарный заряд,
с - скорость света.
Так как величины h, е, с - постоянные физические константы, а квантовая эффективность фотодиода в узкой спектральной полосе (которая обычно используется при пирометрических измерениях) - величина также постоянная, поэтому отношение спектральных чувствительностей одного и того же фотодиода для разных длин волн может быть записано в виде:

С учетом (21) соотношение (19) приобретает вид:
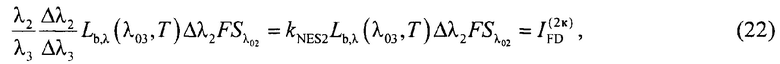
где
IFD(2к) - измеренный фототок, генерируемый от излучения калиброванного опорного источника.
Решая (22) совместно с формулой М. Планка (1), используя при этом приближение Вина и выполнив операцию логарифмирования, получаем искомое уравнение измерения для первого способа:
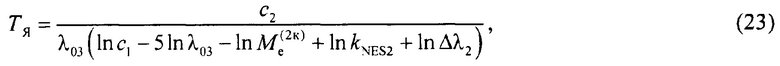
где
ТЯ - яркостная температура объекта,
с1, с2 - первый и второй коэффициенты в формуле М. Планка для спектральной энергетической яркости идеального абсолютно черного тела,
Δλ2 - эффективная ширина спектральной полосы излучения калиброванного опорного источника,
λ03 - центральная длина волны излучения идеального АЧТ,
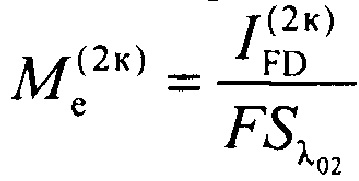 - энергетическая светимость калиброванного опорного источника,
- энергетическая светимость калиброванного опорного источника,
kNES2 - коэффициент неэквивалентности спектра излучения калиброванного опорного источника спектру излучения идеального АЧТ.
Из уравнения измерения (23) следует, что в случае, когда калиброванный опорный источник имеет спектр излучения, идентичный спектру АЧТ коэффициент неэквивалентности kNES2=1, а слагаемое в знаменателе уравнения измерения lnkNES2=0.
В случае, если в основу уравнения измерения положено соотношение (17) (используется некалиброванный опорный источник) уравнение измерения второго способа имеет вид:
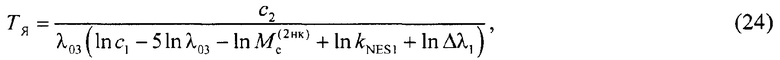
где
Δλ1 - эффективная ширина спектральной полосы излучения объекта,
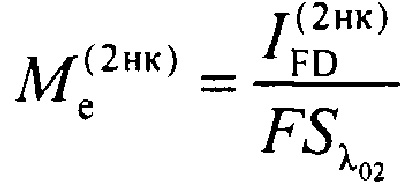 - энергетическая светимость некалиброванного опорного источника,
- энергетическая светимость некалиброванного опорного источника,
IFD(2нк) - измеренный фототок, сгенерированный от излучения некалиброванного опорного источника,
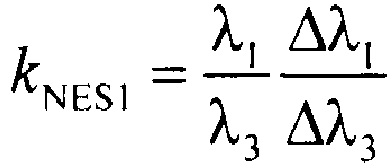 - коэффициент неэквивалентности спектра излучения объекта спектру идеального АЧТ.
- коэффициент неэквивалентности спектра излучения объекта спектру идеального АЧТ.
В частном случае, когда исследуемый объект является моделью АЧТ и его спектр идентичен идеальному АЧТ, то согласно уравнениям измерений обоих способов измеряется абсолютная термодинамическая температура. Во всех других случаях, когда спектр излучения объекта отличается от спектра идеального АЧТ, способы обеспечивают измерение яркостной температуры объекта.
В том случае, когда опорный источник имеет спектр излучения, близкий к спектрально-независимому, т.е. спектрально-независимую энергетическую яркость, или Lλ(2)=const, то, как следует из соотношения (10) центральная длина волны опорного источника λ02 будет целиком и полностью определяться спектром пропускания полосового оптического фильтра τλ. Реальные опорные источники излучения всегда имеют незначительную спектральную зависимость своей энергетической яркости. Однако, если использовать их совместно с полосовым оптическим фильтром, обладающим узкой полосой пропускания Гауссова вида, например, шириной 10 нм, то с высокой точностью энергетическую яркость такого источника можно считать спектрально-независимой. Для этого случая расчет спектральной чувствительности фотодиода Sλ02 выполняют по соотношению (20) для центральной длины волны полосового оптического фильтра λФ0, которую, в свою очередь рассчитывают исходя из соотношения:

Выбор ширины полосы пропускания полосового оптического фильтра зависит от вида конкретного опорного источника и заданной точности, поэтому для каждого конкретного случая выбор осуществляют индивидуально, а ее значение находят расчетным путем. Поэтому при использовании узкополосного фильтра и уравнения измерения (24) не требуется точно знать спектр излучения опорного источника и его измерять, достаточно лишь измерить спектр излучения объекта, т.е. можно использовать некалиброванный опорный источник.
Таким образом, для измерения яркостной температуры объекта согласно заявленным способам необходимо в заданной спектральной полосе излучения выполнить уравнивание энергетических светимостей объекта и опорного источника путем регулировки мощности опорного источника, затем при достигнутой мощности измерить энергетическую светимость опорного источника, при этом, в зависимости от выбранного способа и соответствующего ему уравнения измерения, использовать либо заранее измеренный спектр излучения калиброванного опорного источника, либо использовать некалиброванный опорный источник и измерять спектр излучения объекта, затем по формуле М. Планка рассчитать спектр излучения идеального абсолютного тела, на основании полученных данных рассчитать эффективную ширину спектральной полосы излучения опорного источника или объекта, центральную длину волны излучения идеального АЧТ, соответствующий коэффициент неэквивалентности спектра и на основании полученных результатов рассчитать искомую яркостную температуру.
В уравнениях измерения (23) и (24) заявленных способов приборно-измеряемой величиной является фототок фотодиода IFD(2к) либо IFD(2нк), а остальные параметры, входящие в уравнения, находятся расчетным путем. При этом, так как изначально температура объекта неизвестна и рассчитать спектр излучения АЧТ и его центральную длину волны не представляется возможным, поэтому необходимо использовать итерационный метод. Для этого на первом шаге итерации задают прогнозируемое значение температуры объекта и для нее выполняют расчет спектра излучения АЧТ и значения центральной длины волны АЧТ, по которым, используя уравнение измерения, рассчитывают температуру. Затем по полученному значению температуры объекта заново выполняют расчет спектра излучения АЧТ, центральной длины волны АЧТ и спектральной чувствительности фотодиода. Операцию итерации используют до тех пор, пока предшествующее и последующее расчетное значение температуры объекта не будут отличаться на заданную величину, например, на 0,1 К или 0,01 К. При этом последнее полученное значение температуры принимают равным искомой яркостной температуре объекта. Указанную итерацию проводят с использованием программных средств и компьютера.
Указанные способы реализуются при помощи устройства, структурная схема которого представлена на фиг. 4. Устройство 7 включает в себя: 2 - опорный источник излучения (либо калиброванный, либо некалиброванный), 3 - фотодиод, 4 - полосовой оптический фильтр, 5 - оптическую фокусирующую систему, 6 - анализатор оптического спектра. Полосу анализируемого излучения задает полосовой оптический фильтр 4, который устанавливается на входном окне фотодиода 3.
Измерение согласно заявленным способам осуществляется следующим образом.
В первом способе при помощи оптической фокусирующей системы 5 направляют излучение от объекта 1 на фотодиод 3 и измеряют фототок IFD(1)*, сгенерированный излучением от объекта. Затем при помощи оптической фокусирующей системы 5 направляют излучение от калиброванного опорного источника 2 на фотодиод 3 и регистрируют его фототок IFD(2к)*, далее регулируют мощность опорного источника 2 до достижения равенства фототоков IFD(1)* и IFD(2к)*, т.е. IFD(1)*=IFD(2к)*, после чего фиксируют достигнутую мощность. Далее перемещают оптическую фокусирующую систему 5 из зоны измерения и измеряют фототок IFD(2r) фототодиода 3, сгенерированный прямым излучением от калиброванного опорного источника 2, прошедшим через диафрагмы, которые установлены на опорном источнике и фотодиоде. По измеренному фототоку IFD(2к) рассчитывают энергетическую светимость калиброванного опорного источника Ме(2к), которая равна энергетической светимости объекта Ме(1), т.е.:
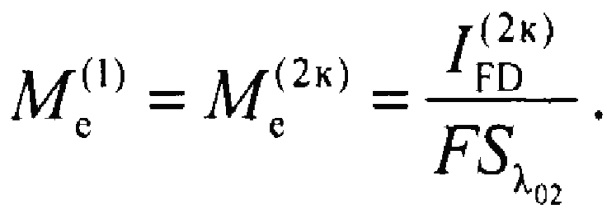
При этом, предварительно задают прогнозируемую температуру объекта, по соотношению (4) рассчитывают значение геометрического фактора F, а по соотношению (20) - рассчитывают значение спектральной чувствительности Sλ02 фотодиода на центральной длине волны калиброванного опорного источника λ02, которую, в свою очередь, рассчитывают по соотношению (10) исходя из известного точно спектра излучения калиброванного опорного источника 2 для заданной температуры. На первом шаге итерации рассчитывают эффективную ширину спектральной полосы излучения калиброванного опорного источника Δλ2, центральную длину волны излучения идеального АЧТ λ03 и коэффициент неэквивалентности kNES2 спектра излучения калиброванного опорного источника спектру излучения идеального АЧТ. По соотношению (23) рассчитывают первое значение яркостной температуры объекта. Затем по полученному значению температуры объекта заново выполняют расчет спектра излучения АЧТ, центральной длины волны АЧТ λ03 и спектральной чувствительности фотодиода Sλ02. Операцию итерации используют до тех пор, пока предшествующее и последующее расчетное значение температуры объекта не будут отличаться на заданную величину, например, на 0,1 К или 0,01 К. При этом последнее полученное значение температуры принимают равным искомой яркостной температуре объекта.
Во втором способе, в котором используется некалиброванный опорный источник излучения, задают узкую спектральную полосу, например, шириной 10 нм. При помощи оптической фокусирующей системы 5 направляют излучение от объекта 1 на фотодиод 3 и измеряют фототок IFD(1)*, сгенерированный излучением от объекта. Затем при помощи оптической фокусирующей системы 5 направляют излучение от некалиброванного опорного источника 2 на фотодиод 3 и регистрируют его фототок IFD(2нк)*, далее регулируют мощность некалиброванного опорного источника 2 до достижения равенства фототоков IFD(1)* и IFD(2нк)*, т.е. IFD(1)*=IFD(2нк)*, после чего фиксируют достигнутую мощность. Далее перемещают оптическую фокусирующую систему 5 из зоны измерения и измеряют фототок IFD(2нк) фототодиода 3, сгенерированный прямым излучением от некалиброванного опорного источника 2, прошедшим через диафрагмы, установленные на некалиброванном опорном источнике и фотодиоде. Затем с помощью анализатора оптического спектра 6 измеряют спектр излучения объекта 1. После этого выполняют следующие расчетные операции.
По измеренному фототоку IFD(2нк) рассчитывают энергетическую светимость некалиброванного опорного источника Ме(2нк), которая равна энергетической светимости объекта Ме(1), т.е.:
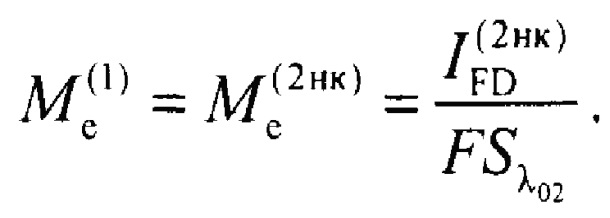
Далее предварительно задают прогнозируемую температуру объекта, по соотношению (4) рассчитывают значение геометрического фактора F, а по соотношению (20) - рассчитывают значение спектральной чувствительности Sλ02 фотодиода на центральной длине полосового оптического фильтра λФ0, которую рассчитывают по соотношению (25) исходя из спектра пропускания фильтра 4. На первом шаге итерации рассчитывают эффективную ширину спектральной полосы излучения объекта Δλ1, центральную длину волны излучения идеального АЧТ λ03 и коэффициент неэквивалентности kNES1 спектра излучения некалиброванного опорного источника спектру излучения идеального АЧТ. По соотношению (24) рассчитывают первое значение яркостной температуры объекта. Затем по полученному значению температуры объекта заново выполняют расчет спектра излучения АЧТ, центральной длины волны АЧТ λ03 и спектральной чувствительности фотодиода Sλ02. Операцию итерации используют до тех пор, пока предшествующее и последующее расчетное значение температуры объекта не будут отличаться на заданную величину, например, на 0,1 К или 0,01 К. При этом последнее полученное значение температуры принимают равным искомой яркостной температуре объекта.
Оценка неопределенности измерений способа.
Оценка ожидаемых значений неисключенной систематической погрешности (НСП) способов (для случая измерения температуры модели абсолютно черного тела) выполнена исходя из уравнений измерения по соотношению:
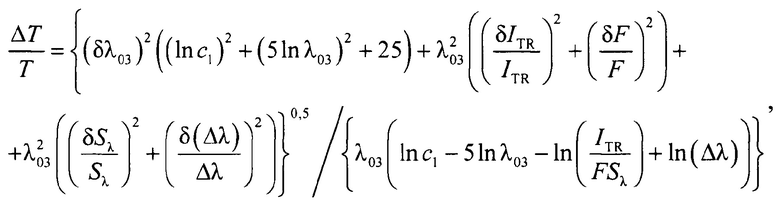
где использованы следующие численные значения параметров:
с1=3,741771852⋅10-16 Вт/м2; Sλ=0,5246 А/Вт; λ03=6,48⋅10-7 м; Δλ=1,542⋅10-8 м; F=2,8493⋅10-10 м2; ITR=6⋅10-10 - 3,9⋅10-6 А и неопределенности измерения параметров: δλ03=δ(Δλ)=0,02 нм = 2⋅10-11 м; δITR=0,0005ITR A; δF=0,0015F м2; δSλ=2⋅10-4Sλ А/Вт.
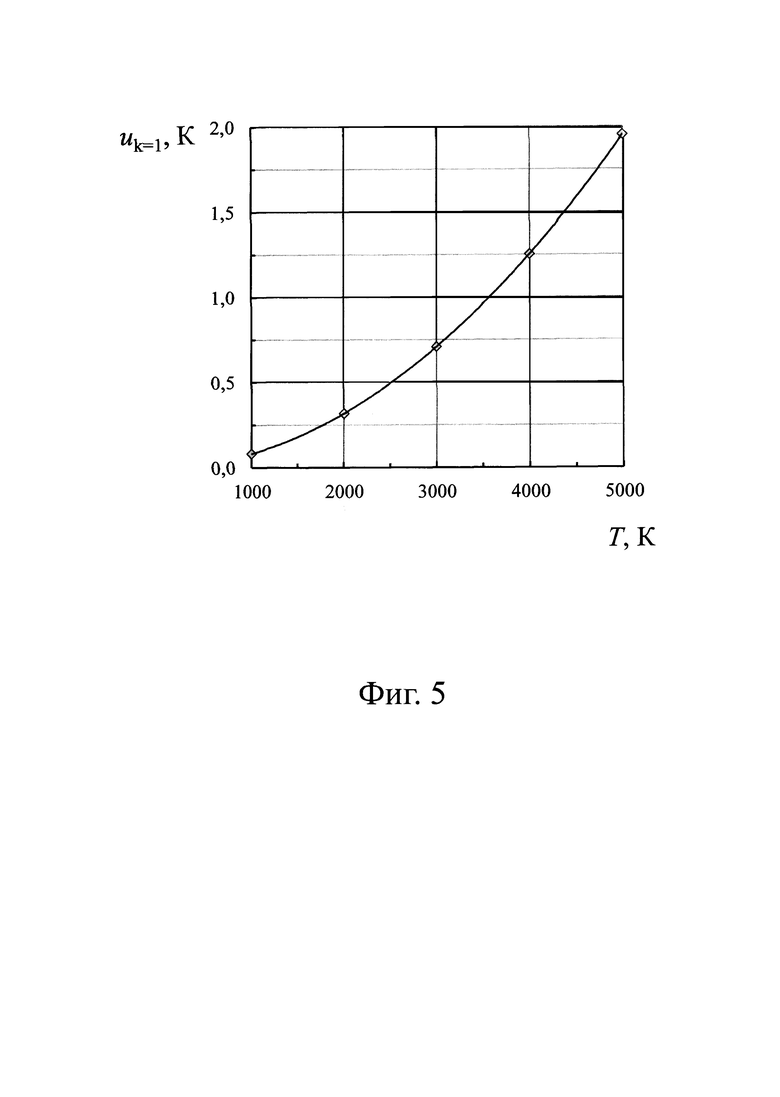
В результате получена следующая аппроксимирующая зависимость НСП (с коэффициентом охвата k=1) от уровня измеряемой температуры Т (фиг. 5): uk=1=1,991⋅10-11T3+1,967⋅10-7T2-2,214⋅10-4T+0,1362 [К]. Как следует из фиг. 5 даже при высоких температурах способ обеспечивает малую относительную НСП равную uk=1/T, которая, например, при температуре T=5000 К равна uk=1/T=1,95/5000≈4⋅10-4 отн. ед., или 100uk=1/T=100⋅1,95/5000≈0,04%.
Таким образом, по сравнению с известными способами заявленные способы обеспечивают существенно более высокую точность результатов измерений яркостной температуры объекта в широком температурном диапазоне вплоть до температуры 5000 К, при этом оценка относительной неопределенности результатов измерений дает значение не хуже 4⋅10-4.

Изобретение относится к области измерительной техники и касается способа измерения яркостной температуры объекта. Способ заключается в том, что используют опорный источник излучения, задают полосу излучения опорного источника, в заданной спектральной полосе излучения компарируют энергетические светимости объекта и опорного источника, регулируют мощность излучения опорного источника до достижения равенства энергетических светимостей источника и объекта, измеряют достигнутую мощность излучения опорного источника и рассчитывают его энергетическую светимость. Далее рассчитывают коэффициент неэквивалентности спектра излучения опорного источника или объекта спектру идеального абсолютно черного тела. Искомую яркостную температуру объекта рассчитывают с учетом энергетической светимости и эффективной ширины спектральной полосы опорного источника, центральной длины волны идеального абсолютно черного тела и коэффициента неэквивалентности. Технический результат заключается в повышении точности измерения яркостной температуры. 2 н.п. ф-лы, 5 ил.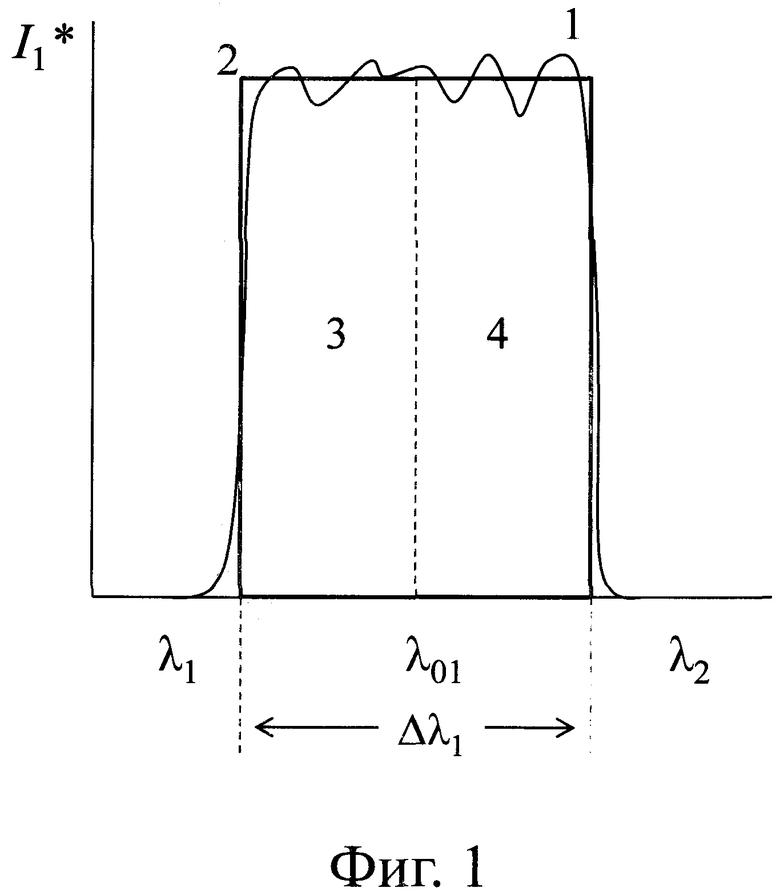
1. Способ измерения яркостной температуры объекта, заключающийся в том, что используют калиброванный по спектру опорный источник излучения, задают полосу излучения опорного источника, в заданной спектральной полосе излучения компарируют энергетические светимости объекта и опорного источника, регулируют мощность излучения опорного источника до достижения равенства энергетических светимостей источника и объекта, измеряют достигнутую мощность излучения опорного источника и рассчитывают его энергетическую светимость, рассчитывают коэффициент неэквивалентности спектра излучения опорного источника спектру идеального абсолютно черного тела, а искомую яркостную температуру объекта рассчитывают по соотношению
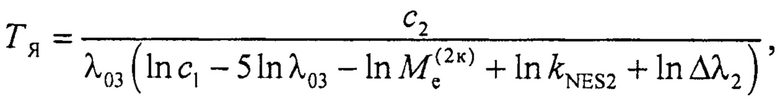
где
ТЯ - яркостная температура объекта,
с1, с2 - первый и второй коэффициенты в формуле М. Планка для спектральной энергетической яркости идеального абсолютно черного тела,
Δλ2 - эффективная ширина спектральной полосы излучения калиброванного опорного источника,
λ03 - центральная длина волны излучения идеального абсолютно черного тела,
Ме(2к) - энергетическая светимость калиброванного опорного источника,
kNES2 - коэффициент неэквивалентности спектров излучения калиброванного опорного источника и идеального абсолютно черного тела.
2. Способ измерения яркостной температуры объекта, заключающийся в том, используют некалиброванный по спектру опорный источник, задают узкую спектральную полосу излучения опорного источника, в заданной спектральной полосе излучения компарируют энергетические светимости объекта и опорного источника, регулируют мощность излучения опорного источника до достижения равенства энергетических светимостей источника и объекта, измеряют достигнутую мощность излучения опорного источника и рассчитывают его энергетическую светимость, в заданной спектральной полосе измеряют спектральное распределение мощности излучения объекта, рассчитывают коэффициент неэквивалентности спектра излучения объекта спектру излучения идеального абсолютно черного тела, а искомую яркостную температуру объекта рассчитывают по соотношению
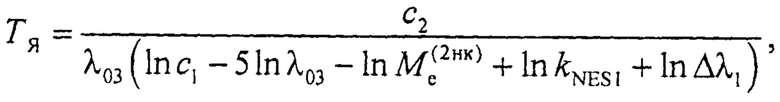
где
Δλ1 - эффективная ширина спектральной полосы излучения объекта,
Ме(2нк) - энергетическая светимость некалиброванного опорного источника,
kNES1 - коэффициент неэквивалентности спектров излучения объекта и идеального абсолютно черного тела.
| СПОСОБ ИЗМЕРЕНИЯ ЯРКОСТНОЙ ТЕМПЕРАТУРЫ ОБЪЕКТА | 2010 |
|
RU2439510C1 |
| СПОСОБ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ ЯРКОСТНОЙ ТЕМПЕРАТУРЫ ТЕПЛОВОГО ПОЛЯ ИССЛЕДУЕМОГО ОБЪЕКТА | 2014 |
|
RU2552599C1 |
| US 6585410 B1, 01.07.2003 | |||
| WO 2000054017 A1, 14.09.2000. | |||
Авторы
Даты
2020-04-14—Публикация
2019-08-05—Подача