Изобретение относится к способам испытаний узлов трения механических систем. Интенсивное развитие в XXI веке вычислительной техники, информационных технологий и инструментальных средств измерений способствует появлению новых, перспективных способов, методов и технологий для решения задач научного познания законов функционирования машин и механизмов. Практически любая машина или механизм являются фрикционными системами (ФС), состоящими из квазилинейных частей механических подсистем и существенно-нелинейных подсистем фрикционных контактов (ФК). С учетом специфики эксплуатации их можно выделить в особую группу - высокомобильные нелинейные технические системы (ВМНТС), к которым относятся железнодорожный, автомобильный, воздушный и водный транспорт.
Развивающиеся методы виброакустической диагностики ФС на базе виброакустического анализа колебательных состояний поверхностных слоев трущихся тел позволяют без изменения их конструкции обеспечить наблюдение за изменением состояния отображением свойств ФС в координатах состояния, доступных измерению. От их колебательных состояний зависит стабильность работы ФК и, в конечном счете, устойчивость всей ФС и безопасность эксплуатации. Однако до настоящего времени отсутствуют системы непрерывного динамического мониторинга ФС, имеющие высокую достоверность прогноза.
В качестве аналога выбран способ для контроля качества узлов трения [1], заключающийся в том, что осуществляют генерирование трибоакустического сигнала посредством относительного перемещения активных поверхностей узлов трения, происходящего с нагрузкой, измерение трибоакустического сигнала на контролируемом изделии и обработку преобразованного в электрическую форму сигнала, при этом процесс обработки состоит в последовательной фильтрации, разложении непрерывного сигнала в спектр, выделении информационных частот и соответствующих им амплитуд, перемножении получившегося вектора диагностических признаков на вектор взвешенных коэффициентов. и формировании интегральной регрессионной функции качества, значение которой однозначно характеризует узел трения и служит для сравнения с эталонными значениями интересующих диагнозов.
Недостатком аналога является то, что при данном способе не обеспечивается соответствие основных динамических характеристик квазилинейных (механических) подсистем натурной ВМНТС и модели.
В качестве прототипа выбран способ испытаний узлов трения [2], заключающийся в том что, механические системы объектной и модельной фрикционных механических систем (ВМНТС), состоящей из подсистемы механической и подсистемы или подсистем фрикционных, при этом механические подсистемы описываются системой аналогичных линеаризованных дифференциальных уравнений, а процессы, протекающие на фрикционном контакте (ФК) «объекта» и «модели», описываются аналогичными математическими моделями, уравнениями регрессии, получаемыми при натурном эксперименте, например, с применением математического планирования полного или дробного факторного эксперимента, при этом между параметрами «объекта» и «модели» обеспечивается следующее соотношение: отношение линейных размеров объекта (L) и модели (l) равно геометрическому масштабу подобия
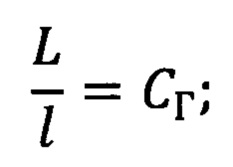
отношение времени протекания исследуемых процессов объекта (Т) и модели (t) равно
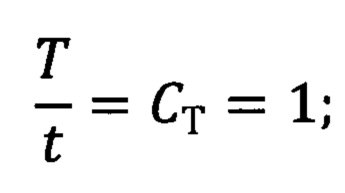
отношение физико-механических параметров материалов (модуля упругости, температуры объемной и ее градиента и т.д.) объекта (Ф) и модели (ф) равно
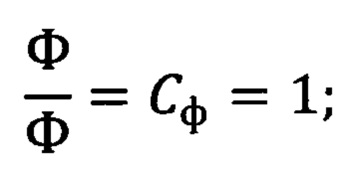
отношение внешних сил, действующих внутри системы, объекта (F) и модели (f) равно
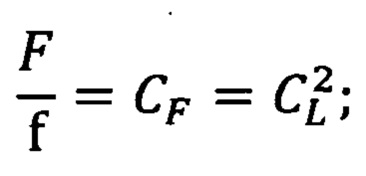
отношение площадей объекта (S) и модели (s) равно
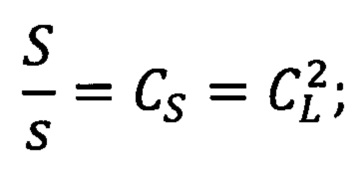
отношение амплитуд колебаний связей механических подсистем и деформаций микронеровностей объекта (А) и модели (а) равно
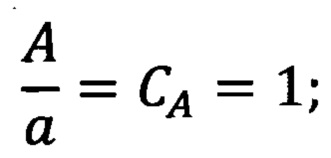
отношение параметров микрогеометрии фрикционных поверхностей объекта (Н) и модели (h) равно
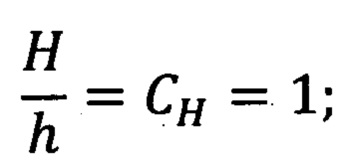
отношение контактного давления объекта (Q) и модели (q) равно
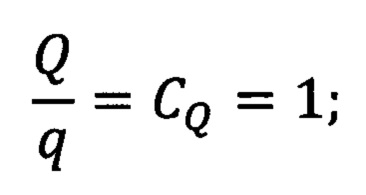
отношение линейных скоростей скольжения объекта (V) и модели (v) равно
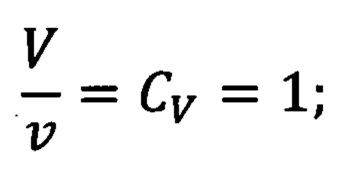
отношение масс объекта (М) и модели (m) равно
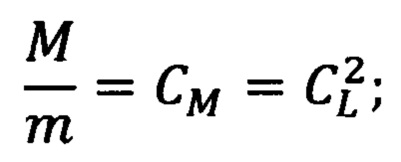
отношение жесткостей объекта (С) и модели (с) равно
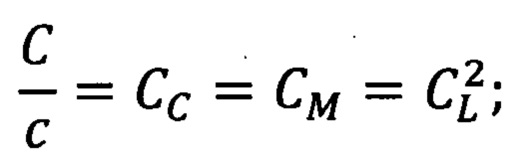
отношение частот колебаний объекта (Ω) и модели (ω) равно
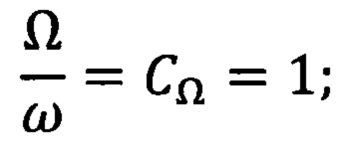
отношение удельных величин спектральных плотностей мощности
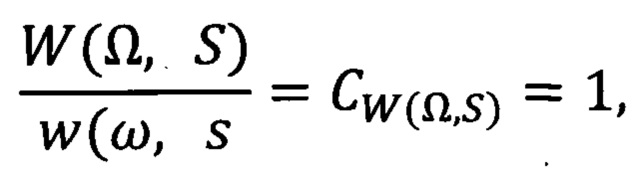
где
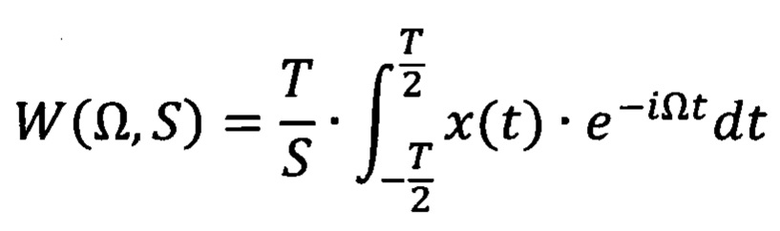
- спектральная плотность сигнала x(t) в единицу времени Т на частоте Ω, приходящаяся на единицу площади S поверхности), при этом правые части дифференциальных уравнений (внешние возмущающие воздействия математических моделей ВМНТС) обеспечивают выполнение констант подобия амплитуды колебаний
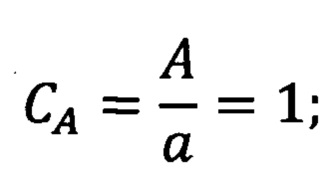
и частоты колебаний
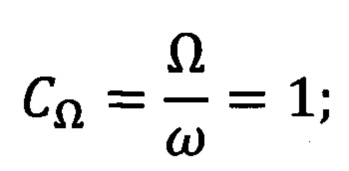
при этом измерение трибопараметров ВМНТС осуществляется во время проведения испытаний, коэффициент трения представляется в виде комплексной функции, т.е. в виде отношения взаимного трибоспектра в тангенциальном и нормальном направлениях к автотрибоспектру в нормальном направлении, действительная часть которого характеризует упругие, а мнимая - диссипативные свойства подсистемы фрикционного контакта, одновременно выполняется контроль и фиксирование удельной площади касания в реальном масштабе времени, например, методом проводимости в паре металл-металл или методом лазерного просвечивания в паре металл-полимер, а значение контактной температуры (максимальной объемной температуры, температуры на вершинах микронеровностей контакта) определяется формулой

где J - ток, проходящий через контакт;
Rk - сопротивление контакта;
αT - коэффициент внешней теплоотдачи;
ρ - удельное сопротивление,
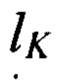 - «длина» контакта.
- «длина» контакта.
Недостатком этого способа является то, что не обеспечивается достаточное и необходимое соответствие основных динамических характеристик квазилинейных (механических) подсистем натурной ВМНТС и ее физической модели.
Сущность предлагаемого изобретения заключается в том, что с целью обеспечения равенства констант подобия в квазилинейной (механической) и существенно нелинейной (фрикционной) подсистемах высокомобильных нелинейных технических систем (ВМНТС) и в частности обеспечения константы подобия давления 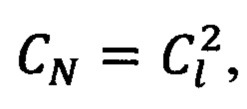 амплитуд колебания деформаций консервативных связей СΔA=1 и жесткости консервативных связей
амплитуд колебания деформаций консервативных связей СΔA=1 и жесткости консервативных связей 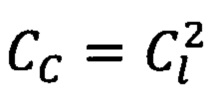 массы, совершающие плоскоколебательные движения в поле сил тяготения в натурной ВМНТС приводятся к вращающемуся центру приведения физико-математической модели ВМНТС, а упрощение эквивалентной динамической модели ВМНТС выполняется при соблюдении равенства суммарных кинематических и потенциальных энергий натурной ВМНТС и ее физико-математической модели, а также с использованием метода Рэлея, т.е. с учетом величины жесткости связей, соединяющих сосредоточенные и распределенные массы.
массы, совершающие плоскоколебательные движения в поле сил тяготения в натурной ВМНТС приводятся к вращающемуся центру приведения физико-математической модели ВМНТС, а упрощение эквивалентной динамической модели ВМНТС выполняется при соблюдении равенства суммарных кинематических и потенциальных энергий натурной ВМНТС и ее физико-математической модели, а также с использованием метода Рэлея, т.е. с учетом величины жесткости связей, соединяющих сосредоточенные и распределенные массы.
Пример:
Эксплуатационная эффективность и надежность тяжелонагруженных муфт привода вертолетов определяется как нагрузочно-скоростными условиями эксплуатации, так и физико-механическими, физико-химическими, трибологическими параметрами процессов трения во фрикционных подсистемах. С целью повышения надежности и долговечности тяжелонагруженных пар трения вертолетов в условиях низких температур Арктики и Антарктики в настояще примере предлагается способ оценки упруго-диссипативных характеристик фрикционного взаимодействия муфт шлицевых соединений хвостовой трансмиссии вертолета МИ-26 [3].
Схема привода хвостового винта показана на фиг. 1, из которой следует, что вращающий момент от главного редуктора передается винту через хвостовой вал, промежуточный и хвостовой редукторы. Хвостовой вал состоит из отдельных полых валов (труб 1 и 2), последовательно соединенных шлицевыми муфтами. Шлицевые муфты с фланцами вращаются в подшипниках промежуточных опор 3, на которых смонтированы также и температурные датчики 4.
Основное назначение хвостового вала - передача вращающего момента от главного редуктора хвостовому винту посредством последовательно соединенных упругих элементов, имеющих определенные массы и моменты инерции. Шлицевая муфта сконструирована так, что наконечник вращается в подшипнике, закрепленном на шпангоуте.
Установлено, что основными неисправностями шлицевых муфт трансмиссии вертолета являются: образование трещин и расслоений резиновой обоймы подшипника; подтекание смазочного материала из-под уплотнений шлицевых соединений и подшипника, в результате чего при высоких контактных напряжениях возрастают сопротивления, повышается коэффициент трения, способствующий перегреву подшипника, муфты и ее опоры, деформации и образованию продуктов износа деталей муфты; образованию бокового зазора в соединениях муфт, перекоса опоры хвостового вала, повышенного биения трубы вала, излома оси или скручиванию вала.
При запуске трансмиссии вертолета в условиях экстремально низких температур установленные в муфтах стационарные датчики контроля температуры 4 не в состоянии своевременно информировать пилотов о возникающих проблемах. Необходима более современная технология диагностики шлицевых соединений, позволяющая в реальном времени идентифицировать любые нештатные ситуации, что позволит повысить безопасность пилотирования на дальние расстояния.
Трибологическая система шлицевого соединения трансмиссии вертолета МИ-26 (Фиг. 2) рассмотрена на примере муфты (а), состоящей из шлицевого стакана (б) и шлицевого наконечника (в), на неподвижном шпангоуте фюзеляжа 5 установлены датчики виброускорения 6. Данное соединение относится к системам, характеризующимся нелинейными взаимосвязанными физико-механическими, теплофизическими, трибохимическими, нагрузочно-скоростными и другими факторами, факторами влияния окружающей среды. Она состоит из множества подсистем, которые взаимодействуют друг с другом. Особенностью данной трибосистемы муфты шлицевого соединения является то, что она эксплуатируется под влиянием значительных вибраций основного двигателя и всего вертолета в целом.
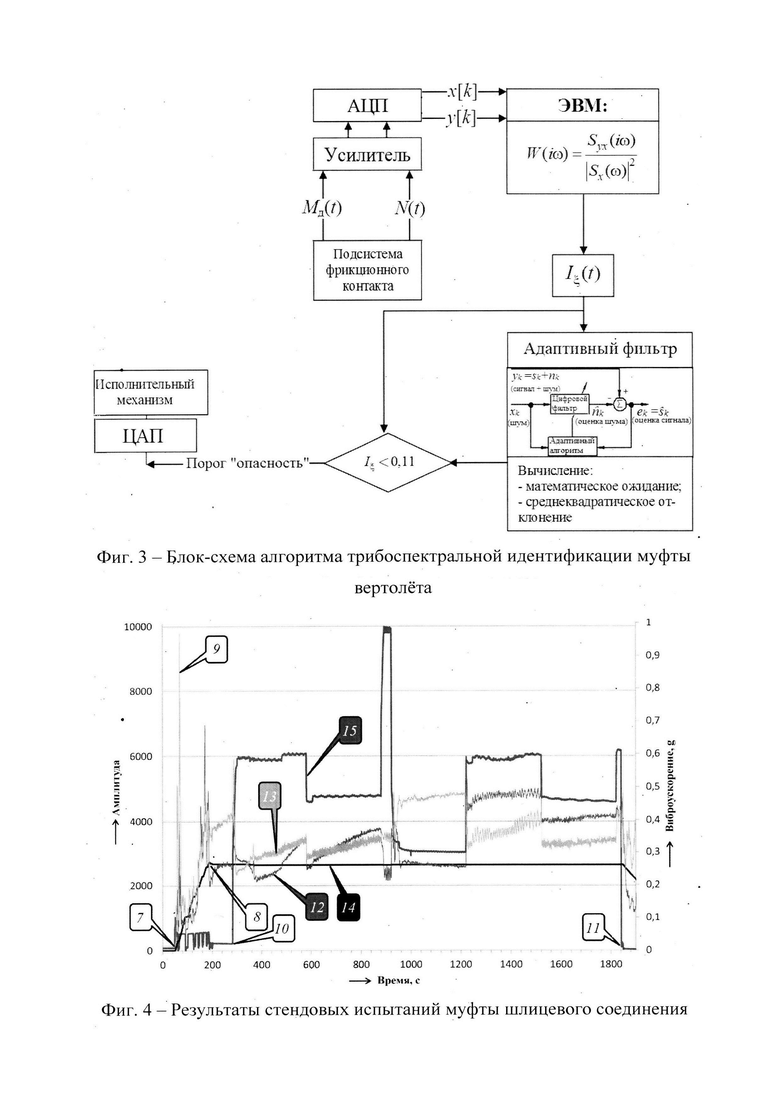
Для достижения поставленной цели следует использовать современные технические средства измерения физических величин, цифровой передачи и обработки сигналов. Наиболее эффективны измерительные схемы вибрации, включающие два измерительных сигнала о колебаниях входного воздействия (тягового момента двигателя) и колебаниях непосредственно муфты шлицевого соединения. Это позволяет использовать спектральный анализ данных, оценить соотношение когерентного спектра к спектру входного воздействия и устранить значительную часть случайных помех. Предлагается алгоритм трибоспектральной идентификации муфт шлицевых соединений трансмиссии вертолета МИ-26 (Фиг. 3) на основе использования датчиков крутящего момента Mд(t). Со стороны муфты шлицевого соединения отмечены ее вибронагруженности - N(t), Iξ(t) - интегральная оценка безразмерного коэффициента демпфирования, W(iω) - частотная передаточная функция. В схеме использованы аналого-цифровой преобразователь (АЦП) и Цифро-аналоговый преобразователь(ЦАП) (Фиг. 3).
Для идентификации процессов динамического нагружения муфт используем основы теории автоматического управления [6] путем анализа амплитудных фазовых, временных и интегральных критериев качества. На основе регистрируемых во времени измерительной подсистемой колебаний входного воздействия (момента тягового двигателя) и выходных координат смещений муфты оценивается комплексный коэффициент передачи на каждой частоте гармонического колебания.
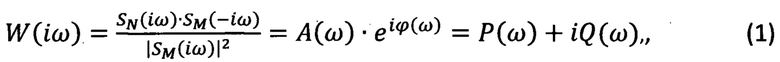
где SM(iω) - спектральная плотность мощности входного воздействия, тягового момента M(t); SN(iω) - спектральная плотность мощности силы нормального смещения N(t); А(ω) - амплитудный спектр; ϕ(ω) - фазовый спектр; Р(ω) - действительный спектр; Q(ω) - мнимый спектр.
Выражение (1) позволяет рассчитать комплексный коэффициент передачи [6] и амплитудную фазовую функцию, характеризующую соотношение упруго-инерционных и диссипативных составляющих фрикционного взаимодействия [5; 4]. Как известно, интегральные оценки позволяют оценить величины затухания колебаний и отклонений регулируемой величины в совокупности, без определения того и другого в отдельности [6]. Поэтому наряду с хорошо всем известными линейными и квадратичными интегральными критериями качества переходных характеристик нами предложено еще оценивать упруго-инерционные и диссипативные составляющие по амплитудным фазовым характеристикам для каждого момента времени в заданных октавных (1/3, 1/12 или 1/24-долеоктавных) диапазонах частот [5]. Это позволяет с более высокой степенью достоверности выбрать наиболее информативные диапазоны собственных частот, на которых проявляется влияние физико-механических характеристик смазочного материала (гипоидной смазки), а также износа поверхностей шлицев соединения муфты.
Для идентификации упруго-диссипативных и динамических характеристик муфт использованы следующие интегральные оценки:
- упруго-инерционных составляющих взаимодействия, способствующих сближению контактирующих поверхностей трения, повышению контактных напряжений и температур
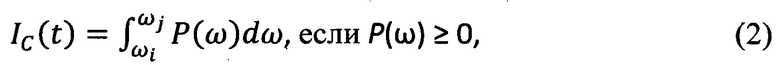
где t - регистрируемое время наработки;
ωi, ωj - граничные частоты при октавном (долеоктавном) спектральном анализе;
Р(ω) - действительная частотная характеристика, характеризующая упруго-инерционные составляющие комплексной величины (1)
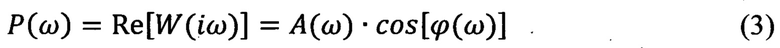
- инерционных составляющих взаимодействия, способствующих потере стабильности фрикционной связи
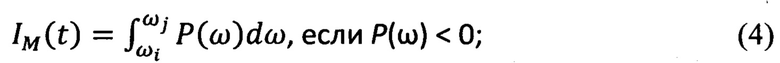
- диссипативных составляющих взаимодействия, характеризующих силы сопротивления, противоположно направленные вектору скорости относительного скольжения
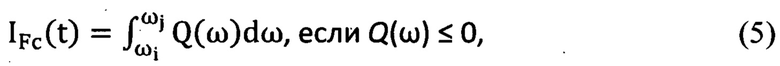
где Q(ω) - мнимая частотная характеристика комплексной величины (1), характеризующая диссипацию энергии при динамическом взаимодействии
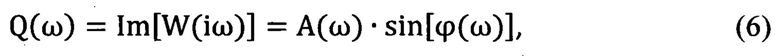
- диссипативных составляющих взаимодействия, характеризующих развитие во фрикционно-механической подсистеме фрикционных автоколебаний, то есть сил сопротивления, вектор которых сонаправлен с вектором скорости относительного скольжения
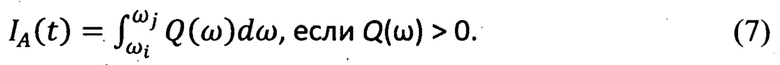
Известно, что демпфирующие свойства механических систем в линейной теории колебаний оценивается безразмерным коэффициентом демпфирования ξ, как отношение показателя экспоненты затухания амплитуд колебаний n к частоте свободных колебаний ω0. В существенно нелинейных фрикционных системах определить коэффициент сложно. Нами была предложена эмпирическое выражение для оценки коэффициента ξ в виде некоторой интегральной величины Iξ(t) для текущего момента времени t, позволяющее идентифицировать частотные диапазоны виброколебаний нелинейных систем, в которых диссипативные свойства оказывают наибольшее влияние на динамику системы
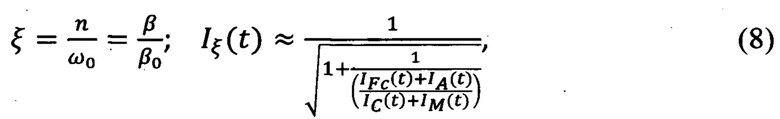
где n - коэффициент затухания колебаний, с-1; ω0 - частота собственных колебаний, с-1;
β - коэффициент сопротивления колебаниям, Н⋅с/м;
β0 - критическая величина коэффициента сопротивления колебаниям, при которой колебательный характер сменяется на монотонно затухающий (апериодический), Н⋅с/м;
IFc, IA, IC, Im - интегральные оценки качества [5], вычисленные на основе анализа амплитудно-фазовых характеристик и косвенно характеризующие соотношение сил сопротивления (5), фрикционных автоколебаний (7), сил упругости (2) и сил инерции (4).
Наблюдение за математическим ожиданием, среднеквадратичным отклонением и пик-фактором оценок (2)-(8) в реальном времени наблюдения t позволяет реализовать задачи идентификации и изменений во времени упруго-диссипативных характеристик.
Реализацию задачи динамического мониторинга шлицевых муфт удобнее. реализовать с помощью единого критерия, который бы реализовывал анализ обобщенных характеристик фрикционно-механической системы и позволял предсказывать с определенной вероятностью изменение тренда характеристик. В качестве такой характеристики нами предложен динамический критерий качества (9), предельно допустимое значение которого равно единице и соответствует порогу «предупреждения».

где Ik - интегральные оценки оцениваемых параметров стационарного коэффициента передачи (1); запаса устойчивости по амплитуде L и фазе ψ; частотного показателя колебательности М; частоты среза ωс, характеризующей длительность переходного процесса; частоты ω0 полосы пропускания; квадратичного критерия качества переходного процесса по смещению I и скорости I' [9], а также указанных ранее оценок (2)-(8) [5, 7]
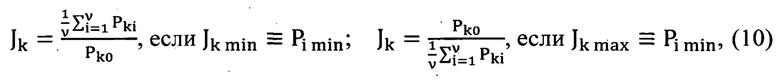
где ν - количество наблюдаемых значений; Pki - измеренная физическая величина; Pk0 - ее опорное значение, установленное по результатам предварительных испытаний.
Чем меньше уровень Iд(t), тем более стабильная и устойчивая фрикционная система муфты. Величины (9), превышающие единичное значение, соответствуют аномальным условиям эксплуатации в форме биений, резонанса и др. форм отклонений от стационарной траектории движения.. В соответствии с «правилом трех среднеквадратичных отклонений» был также установлен порог «опасности», когда значения Iд(t)≥1,15.
Наблюдение осредненных уровней, указанных выше оценок за длительный период эксплуатации, позволяет установить пороги «предупреждения» и «опасности», если точечные оценки математической статистики регистрируемых в данный момент времени величин превысят уровень соответственно в 2…3 среднеквадратичных отклонения. В этом случае бортовая система мониторинга трибоспектральной идентификации сигнализирует пилотам о возможных проблемах с трансмиссией вертолета и через ЦАП передает исполнительному механизму команды об уменьшении нагрузочно-скоростных режимов привода двигателя.
Изменение нагрузочно-скоростных условий эксплуатации, изменении температуры окружающего воздуха и значительное количество побочных факторов оказывают существенное влияние на динамику работы шлицевых муфт. К таким факторам можно отнести: высокочастотные колебания при образовании локальных металлических связей при фреттинг-коррозии; значительное изменение скорости относительного проскальзывания поверхностей трения; сближение или удаление контактирующих поверхностей трения под влиянием сил инерции; деформации активных объемов поверхностей трения, рост контактных напряжений. Совокупность неблагоприятных факторов, нагрузки и скорости скольжения может обусловливать изменение микрогеометрии поверхностей трения с последующим развитием пластических деформаций, фрикционных автоколебаний, что может приводить к увеличению нестабильности трибосистемы, атермическому или термическому схватыванию, высоким значениям динамического коэффициента трения (эффект Толстого - Пуша).
При возрастании передаваемого муфтой момента вследствие трения в соединениях шлицевой муфты в зависимости от соотношения физико-механических, триботехнических характеристик узла трения изменяется регистрируемое виброускорение шпангоута исследуемых муфт (Фиг. 4), где 7 - момент запуска тягового двигателя; 8 - достижение номинального числа оборотов; 9 - ряд резонансных колебаний; 10 - момент прикладывания тягового момента; 11 - момент остановки двигателя; 12 - виброускорение 5 опора, g; 13 - виброускорение 6 опора, g; 14 - скорость, об/мин; 15 - момент, Нм.
С момента запуска тягового двигателя 7 (см. Фиг. 4) до достижения. номинального числа оборотов 8 фрикционно-механическая система проходит через ряд резонансных колебаний Р. После некоторого прогрева трибосопряжений к механической системе прикладывается тяговый момент 10, обеспечивающий относительное вращение хвоста вертолета.
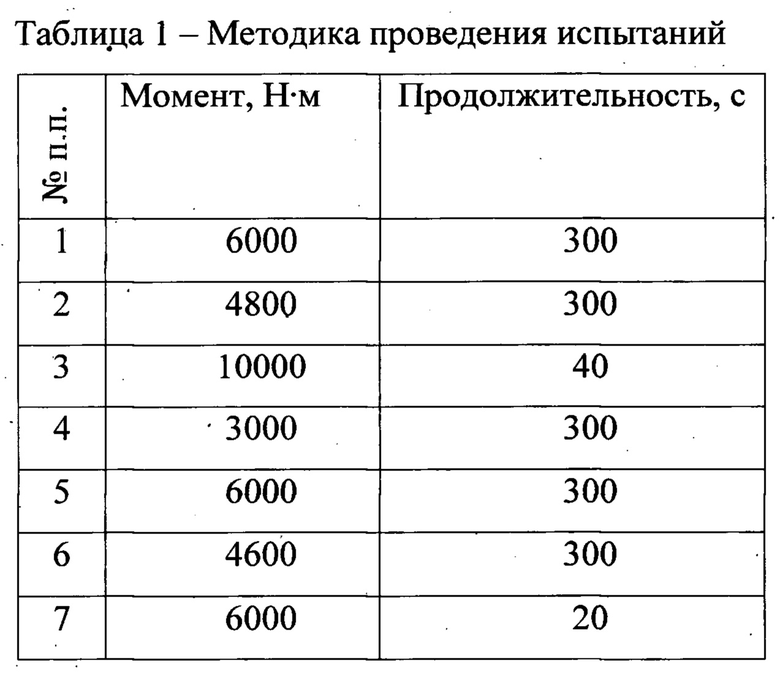
Испытания проводились в соответствии с утвержденной методикой испытаний (табл. 1). В момент времени 11 (Фиг. 4) производилась остановка двигателей. Видно, что регистрируемые виброускорения 12 и 13 (Фиг. 4) муфт шлицевых соединений вала трансмиссии вертолета по-разному откликаются на действие приложенного момента двигателя.
Это обусловлено как точностью сборки и установки муфт, внешними нагрузочно-скоростными внешними факторами, так и возникающими в трибосистеме шлицевого соединения сопротивлениями, связанными с неравномерностью попадания смазочного материала в зацепление шлицев, износом зубьев шлицевого соединения, инерционности зацепления и другими факторами.
Для возможности диагностики характеристик смазочного материала, предотвращения" заклинивания фрикционной связи, катастрофического износа шлицев соединения, повышения безопасности эксплуатаций вертолета были проведены экспериментальные исследования на испытательном комплексе.
Анализ полученных данных о вибрации двигателя и муфты проводился на базе методики трибоспектральной идентификации [7] путем вычисления для каждого момента времени t амплитудных и- фазовых частотных характеристик (АФЧХ) с помощью Выражения (1). Для оценки диссипативных характеристик муфты нами использован 1/3-долеоктавный анализ динамического коэффициента демпфирования (8), что позволило нам идентифицировать наиболее информативные частотные диапазоны, в которых наиболее выраженно проявляются влияние режимов нагружения и гипоидной смазки шлицевого соединения. Наиболее информативными оказались следующие диапазоны колебаний со среднегеометрическими частотами 80, 100, 127, 200, 253 и 400 Гц, однако для иллюстрации динамики муфты ограничимся двумя наиболее выраженными диапазонами частот (223,9-281,8 и 354,8-446,7 Гц со среднегеометрическими частотами 253 и 400 Гц соответственно) вынужденных колебаний, где влияние нагрузочно-скоростных характеристик наиболее ощутимо. Результаты вычислений представлены на фиг. 5, при этом 16 - постоянный коэффициент демпфирования; 17 - положительный градиент коэффициента демпфирования; 18 - отрицательный градиент коэффициента демпфирования; 19 и 20 - моменты времени ухудшения условий взаимодействия; 21 - 223,9 - 2281,8 Гц (5 опора); 22 - 223,9 - 281,8 Гц (6 опора); 23 - 354, 8 - 446,7 Гц (5 опора); 24 - 354, 8 - 446, 7 Гц (6 опора).
Видно, что с изменением передаваемого муфтой момента 15 (Фиг. 5) по заданной программе испытаний (с момента Времени 10 подачи крутящего момента до момента времени 11 - остановки) во фрикционных муфтах 12 и 13 опоры варьируются демпфирующие свойства. трибосистемы. При постоянном воздействии моментом двигателя регистрируемый коэффициент демпфирования (8) может быть как постоянным 16, так и иметь положительный 17 или отрицательный 18 градиент физико-механических свойств. В первом случае постоянный уровень ξ(t) соответствует стационарным условиям фрикционного взаимодействия, когда смазочный материал достаточно хорошо смазывает шлицевые зубчатые зацепления муфты. При отрицательном градиенте 18 регистрируемого коэффициента ξ(t) под влиянием нагрузочно-скоростных условий взаимодействия, действия инерционных воздействий и прочих физико-механических характеристик ухудшаются условия смазки шлицев муфты. Напротив, при положительном градиенте 17 анализируемого коэффициента ξ(t) значительное изменение инерционных воздействий в предшествующие моменты времени компенсируется обильным смазыванием шлицев, в результате чего регистрируемый коэффициент демпфирования в последующие моменты времени стабилизируется. Формируется новый стационарный режим работы муфты. Возможны также и такие моменты времени 19 и 20, когда ухудшение условий взаимодействия в одном частотном диапазоне (354,8-446,7 Гц) компенсируется смазкой в другом частотном диапазоне, обеспечивая работоспособность муфты.
В эксплуатации муфт реализовать предложенный на фиг. 5 метод диагностики и интерпретации физико-механических и трибологических характеристик не рационально, так как при эксплуатации необходим единый параметр, однозначно характеризующий состояния фрикционно-механической системы муфты. В этом случае удобно использовать динамический критерий качества (9), что позволит системе на основании анализа значительного количества критериев мониторинга сигнализировать о наступлении так называемых порогов «предупреждения» и «опасности». На фиг. 6, представлены результаты оценки работоспособности 5 и 6-й опор муфт шлицевых соединений трансмиссии вертолета МИ-26, где 25 - критерий качества (5 опора); 26 - критерий качества (6 опора); 27 - стационарно устойчивый режим смазки; 28 - регестрируемые тренды; 29 - импульсивные воздейтсвия; 30 - порог «предупреждения»; 31 - порог «опасности»), полученные при использовании стенда (фиг. 2).
Видно, что при запуске трансмиссии вертолета в диапазоне времени с 50-300 с эксперимента наблюдается тенденция роста динамического критерия (9), что связано с прохождением фрикционно-механической системы локальных резонансных частот (кривые 25 и 26 на фиг. 6). После выхода на стационарный режим вращения винтов вертолета (с момента 10 по момент времени 77) вариации тягового момента 75 не оказывают существенного влияния на критерий (9), так как реализуется стационарно устойчивый режим смазки трибосоединений шлицев муфты - тренд 27.
При остановке двигателей испытательного стенда в момент времени 77 регистрируемые тренды 28 динамического критерия Iд(t) возрастают как для 5, так и 6 опоры шпангоута. Это связано с уменьшением нагруженности муфт и возрастании инерционности их составляющих. Однако следует заметить, что в некоторые, моменты времени проявляются импульсные воздействия 29, когда критерий (9) достигает порога «предупреждения» 30 и даже порога «опасности» 31. Это может быть обусловлено тем, что под влиянием инерционности воздействия на муфты смазочный материал гипоидной смазки «уходит» из-под зацепления шлицев зубчатого соединения, что вызывает импульсный характер регистрируемых параметров, входящих в анализ критерия (9).
Оценить остаточный ресурс муфт можно только по результатам длительных испытаний или эксплуатации. Для этого может быть использован как метод долеоктавного анализа диссипации энергии, т.е. суммы вычисленных оценок (5) и (7), так и предложенный метод динамического критерия качества с установленными порогами «предупреждения» и «опасности». В первом случае характер изменений октавного спектра представлен на фиг. 7 в зависимости от наработки в часах. Наблюдая за величинами амплитуд октавных спектров в течение наработки муфты 5 опоры, можно идентифицировать с большей достоверностью периоды приработки (0-881 с.) и нормальной эксплуатации (992-1522 с.), когда диссипативные потери энергии на процессы трения максимальны, а фиксируемое значение коэффициента демпфирования ξ (15) достигает минимальных значений 0,11 (логарифмического декремента затуханий δ=0,69 и добротности колебательной системы Q=12,6). Кроме того, наблюдение за несколькими муфтами одновременно позволяет установить статистические уровни величины коэффициента демпфирования в каждом диапазоне частот долеоктавного спектра: базового уровня (32), а также порогов «предупреждения» (33) и опасности (34) (Фиг. 7).
Предложенная методика диагностики трибосопряжений муфт хвостового привода вертолетов МИ-26 в реальном времени позволяет по значениям долеоктавных спектров идентифицировать стабильность упруго-инерционных и диссипативных характеристик фрикционного взаимодействия, периоды времени приработки, нормальной эксплуатации и катастрофического изнашивания.
Использование разработанного динамического критерия упрощает технологический процесс диагностики, мониторинга и прогнозирования значительных изменений в упруго-диссипативных связях, предотвращая наступление аномальных условий эксплуатации путем информирования пилотов о фиксируемых пороговых значениях «предупреждения» или «опасности».
Предложенная методика трибоспектральной идентификации процессов трения и динамического мониторинга фрикционных систем повышает безопасность эксплуатации вертолетов и может быть распространена для любых узлов трения и позволит реализовать краткосрочный или долгосрочный прогноз в изменении динамических характеристик.
Проводить исследования и оптимизацию, набирать базу информационных данных в натурных условиях сложно, а в целом ряде случаев практически невозможно и не безопасно. Поэтому целый ряд исследований реальных механических систем воздушного транспорта выполняется на стендах, например, в аэродинамической трубе ФГУП ЦАГИ.
Предложен стенд (Фиг. 8), позволяющий смоделировать основные динамические колебания зубьев шлицевого соединения муфт валопровода вертолета МИ-26 при изменении характера нагружающего воздействия.
Система нагружения модели шлицевого соединения 35 (модельный узел трения) привода ходового винта вертолета представляет собой двойной рычаг 36 см. фиг. 8.
Данное конструктивное решение позволяет устранить существующее противоречие физико-математического моделирования, возникающее при реализации схем нагружения силой тяжести, в частности шлицевого соединения. А именно при соотношении масштабов подобия
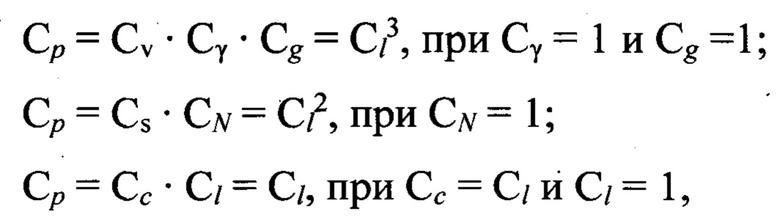
где Ср - масштаб силы;
Cν - масштаб объема, 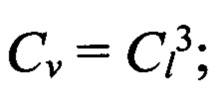
Сγ - масштаб плотности стали, Сγ=1;
Cg - масштаб ускорения свободного падения, Cg=1;
Cs - масштаб фактической площади касания, Cs=C12;
CN - масштаб нагрузки, условно примем CN=1;
Сс - масштаб жесткости связи, условно примем Cc=Cl;
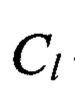 - геометрический масштаб.
- геометрический масштаб.
Применение схемы нагружения шлицевого зацепления уравновешивающим моментом М - 37 исключает из схемы нагружения силу тяжести, а применение в качестве меры инерционных масс m1 - 38 и m2 - 39 (Фиг. 8) устраняет вышеприведенное противоречие. Для этого в конструкции стенда обеспечена возможность ступенчатого регулирования момента нагружения шлицевого соединения путем перемещения планок 40, 41 с витка на виток нагружающих пружин 42.
Нагружение шлицевого соединения производится с помощью стопорных гаек 43, обеспечивая следующее соотношение
P1=C1⋅Δx1=С2⋅Δх2=P2,
где Р1, Р2 - упругие силы, действующие в пружинах 5;
C1, C2 - коэффициенты упругости пружин, Н/м;
Δx1, Δx2 - деформации пружин, м.
Изменением плечей рычагов, 44, 45 двойного рычага 36 (Фиг. 8) реализуется как плавное, так и ступенчатое регулирование нагрузки. Плавное регулирование момента нагружения шлицевого соединения осуществляется перемещением планок 40 и 41 (Фиг. 8). Модельный узел трения 35 приводится в движение возвратно-поступательными колебаниями малой амплитуды, под влиянием нагружающего момента 37 в зоне фрикционного контакта испытуемых образцов возникает нормальная нагрузка (Фиг. 8). За счет, возвратно-поступательных колебаний во фрикционном контакте формируется сила трения FT - 46 (Фиг. 8) величина которой определяется нагрузочно-скоростными параметрами, трибологическими свойствами смазочного материала и параметрами износа контактирующих тел.
Для проведения модельных испытаний шлицевого соединения при низких температурах предполагается использование криокамеры, вследствие чего, геометрические размеры узла трения шлицевого соединения выполнены в соответствии с размерами используемой криокамеры.
Модели зубьев стакана и наконечников муфты трансмиссии вертолета являются образцом и контробразцом. Для изготовления пазов используется сталь 38Х2МЮА-Ш, а для зубьев - сталь 12Х2Н4А. Для. ускорения трибологических испытаний и накопления статистических характеристик стенд предусматривает одновременное использование двух идентичных узлов трения.
Во всех работах по динамике фрикционных связей не учитывается важное влияние динамических процессов, протекающих во фрикционном контакте и в квазилинейной механической подсистеме. В свою очередь, данное взаимовлияние оказывает существенное влияние на выходные трибопараметры нелинейных фрикционных подсистем (узлов трения), включенных в квазилинейную подсистему. С динамическим взаимодействием процессов, протекающих в механической и фрикционной подсистеме связано явление изменения величины коэффициента трения от 0 до ∞ [8].
При исследовании фрикционных механических систем необходимо обеспечить идентичность протекания существенно - нелинейных процессов взаимодействия и контактирующих поверхностей трения и соответственно выходных триботехнических и трибоспектральных характеристик натурных фрикционных механических систем и их физикоматематических моделей. Для этого необходимо обеспечить ряд условий, среди которых ведущими является: обеспечение равенства параметра PV (Р - давление, V - скорость скольжения) при натурных и модельных испытаниях, а значит равенство масштабов моделирования давления CP=1 и скорости CV=1; масштаба сил 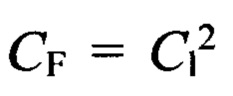 (C1 - геометрический масштаб); масштаба амплитуды деформации связей при линейном СΔA=1 или угловом СΔϕ=1 деформировании связей как в механической, так и в фрикционных подсистемах.
(C1 - геометрический масштаб); масштаба амплитуды деформации связей при линейном СΔA=1 или угловом СΔϕ=1 деформировании связей как в механической, так и в фрикционных подсистемах.
С целью обеспечения адекватности динамических свойств натурной 47 высокомобильной нелинейной технической системы (ВМНТС) и ее модели 48 (Фиг. 9), в частности обеспечения равенства амплитуд деформации фрикционных связей и связей механической системы поступательно-движущейся массы в квазилинейные подсистемы приводятся к вращающемуся центру приведения, где 49 - величина крутильных колебаний (Фиг. 9).
Противоречие приведения масс к вращающемуся центру. В том случае, когда задачей исследования является исследование процессов, происходящих на фрикционном контакте и обоснования их идентичности в натуре, возникает необходимость обеспечить равенство амплитуды. колебания деформации связей (СΔA). Главным условие идентичности процессов, протекающих во фрикционных контактах натуры и модели, является необходимость обеспечить постоянство равенства параметров PV. Отсюда следует, что масштаб подобия скорости CV=1, и масштаб подобия давления CP=1. В этом случае масштаб силы 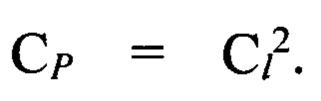 Сила изменяется пропорционально квадрату линейного масштаба. Для проведения исследования фрикционных механических систем масштабы подобия всех физических величин должны быть равны, как при моделировании процессов, протекающих на фрикционном контакте, так и в механической подсистеме. Исходя из этого должно быть обеспечено постоянство подобия амплитуды колебаний деформации связей СΔA=1 как при фрикционном взаимодействии микронеровностей, так и при деформации связи механической квазилинейной подсистемы.
Сила изменяется пропорционально квадрату линейного масштаба. Для проведения исследования фрикционных механических систем масштабы подобия всех физических величин должны быть равны, как при моделировании процессов, протекающих на фрикционном контакте, так и в механической подсистеме. Исходя из этого должно быть обеспечено постоянство подобия амплитуды колебаний деформации связей СΔA=1 как при фрикционном взаимодействии микронеровностей, так и при деформации связи механической квазилинейной подсистемы.
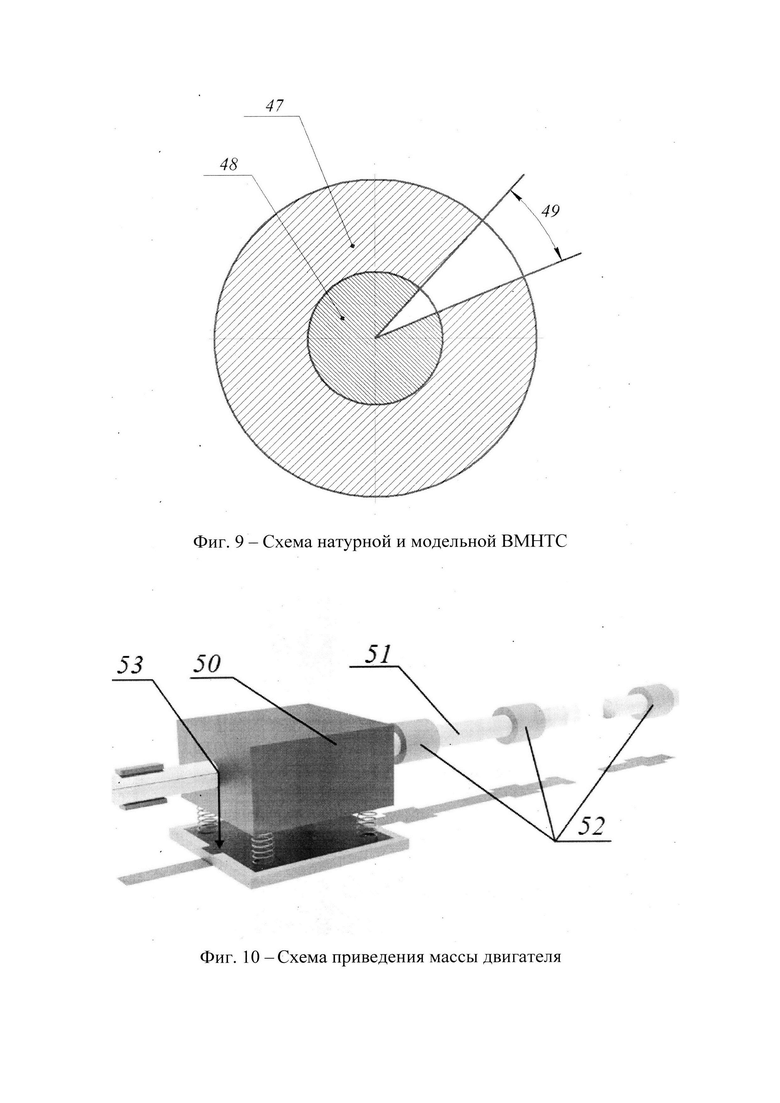
На схеме приведения массы двигателя (Фиг. 10) представлены: двигатель вертолета - 50; вал привода хвостового винта - 51; шлицевые муфты - 52; центр приведения - 53. Рассмотрим приведение масс на основе привода хвостового винта вертолета. Необходимо массу двигателя, совершающего поступательное движение привести к вращающемуся центру приведения 50, за который принят вал двигателя 51(Фиг 10).
Кинетические энергии определяются по формулам:

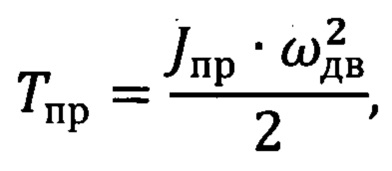
где ν - поступательная скорость движения массы m;
ωдв - угловая скорость двигателя, вал которого принят за центр приведения.
Из равенства кинетических энергий до и после приведения получим:
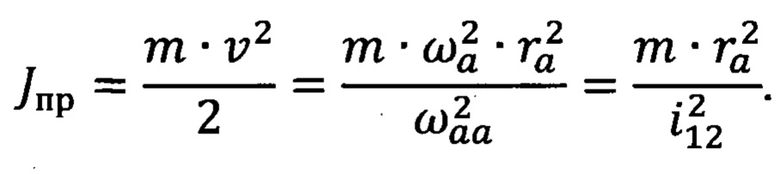
Таким образом, при приведении массы двигателя к валу величина массы умножается на квадрат передаточного отношения между валом двигателя и валом, принятым за центр приведения, в данном случае передаточное отношение равно i=1.
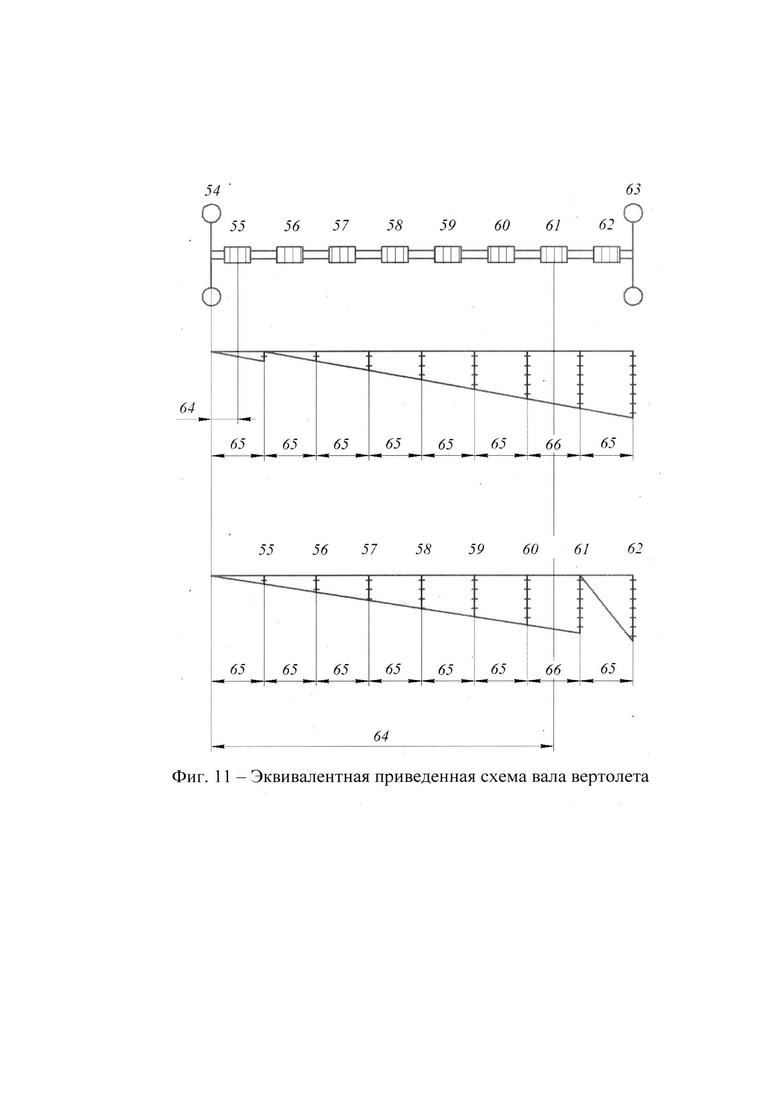
Упрощение эквивалентной динамической модели и построение эквивалентного вала и диаграммы масс, производится с помощью суммирования масс с использование принципа Рэлея (Фиг. 11), где 54 - суммарный момент инерции двигателя; 55-62 - шлицевые муфты; 63 - суммарный момент инерции винта и редуктора; 64 - текущая координата сечения по оси X; 65 - длина горизонтального участка вала; 66 - длина наклонного участка вала.
Для определения кинетической энергии распределенной массы шлицевой муфты 55 (Фиг. 11) воспользуемся формулой
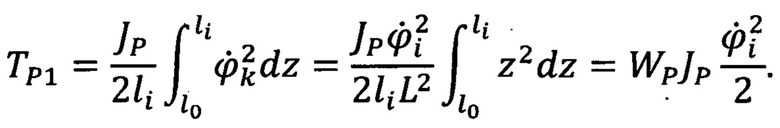
Для второй части
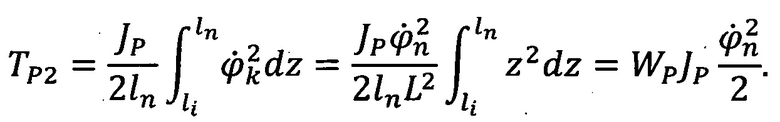
Для шлицевой муфты 61 (Фиг. 11) расчет производится аналогично.
ЛИТЕРАТУРА
1. Патент РФ №2344415, кл. G01N 29/14, 2006.
2. Патент РФ №2343450, кл. G01N 3/56, 2006.
3. Ми-26Т: Руководство по технической эксплуатации, Вертолет Ми-26Т. Стандартная спецификация, 2000. 342 с.
4. Озябкин, А.Л. Теоретические основы динамического мониторинга фрикционных мобильных систем // Трение и смазка в машинах и механизмах. - 2011. - №10. - С. 17-28.
5. Способ динамического мониторинга фрикционных мобильных систем [Текст]: пат. 2517946 РФ: МПК G01N 3/56 / В.В. Шаповалов [и др.]; заявитель и патентообладатель В.В. Шаповалов. №2012113329/28; заявл. 05.04.2012; опубл. 10.06.2014, Бюл. №16. 28 с.
6. Пупков К.А. Методы классической и современной теории автоматического управления: учебник. В 5 т. Т. 1: Математические модели, динамические характеристики и анализ систем автоматического управления / К.А. Пупков; под ред. К.А. Пупкова, Н.Д. Егупова. 2-е изд., перераб. и доп. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 656 с.
7. The Dynamic Monitoring of Friction Systems / V.V. Shapovalov, P.N. Scherbak, N.I. Boiko, A.C. Erkenov // International Journal of Applied Engineering Research ISSN 0973-4562 Volume 11, Number 23 (2016) pp. 11421-11427.
8. Заковоротный, В.Л. Исследование комплексного коэффициента трения / В.Л. Заковоротный, В.В. Шаповалов // Трение и износ. - 1987. - С. 22-24.
| название | год | авторы | номер документа |
|---|---|---|---|
| ДИНАМИЧЕСКИЙ МОНИТОРИНГ УЗЛОВ ТРЕНИЯ МОБИЛЬНЫХ ТЕХНИЧЕСКИХ СИСТЕМ | 2020 |
|
RU2748933C1 |
| ДИНАМИЧЕСКИЙ МОНИТОРИНГ МОБИЛЬНЫХ НЕЛИНЕЙНЫХ ТЕХНИЧЕСКИХ СИСТЕМ | 2020 |
|
RU2745984C1 |
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ФРИКЦИОННЫХ МОБИЛЬНЫХ СИСТЕМ | 2012 |
|
RU2517946C2 |
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| СПОСОБ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ФРИКЦИОННЫХ СИСТЕМ | 2016 |
|
RU2674899C1 |
| СПОСОБ ОЦЕНКИ ВНЕШНИХ И ВНУТРЕННИХ ПАРАМЕТРОВ УЗЛОВ ТРЕНИЯ ПРИ ИСПЫТАНИИ В СТЕНДОВЫХ УСЛОВИЯХ | 2015 |
|
RU2647338C2 |
| ТРАНСМИССИЯ ВЕРТОЛЕТА | 2013 |
|
RU2559676C2 |
| МОДИФИКАТОР ТРЕНИЯ И СИСТЕМА УПРАВЛЕНИЯ ПРИВОДОМ ЕГО ПОДАЧИ | 2005 |
|
RU2293677C2 |
| Способ определения оптимальных параметров узла трения механической системы | 1985 |
|
SU1307298A1 |
| СПОСОБ ПРОЕКТИРОВАНИЯ ЦЕНТРОБЕЖНЫХ НАСОСОВ | 2013 |
|
RU2542160C1 |



Изобретение относится к испытательной технике. Сущность: процессы, протекающие на фрикционном контакте (ФК) «объекта» и «модели», описываются аналогичными математическими моделями, уравнениями регрессии, получаемыми при натурном эксперименте, с применением математического планирования полного или дробного факторного эксперимента. Измерение трибопараметров ВМНТС осуществляется во время проведения испытаний. Коэффициент трения представляется в виде комплексной функции, т.е. в виде отношения взаимного трибоспектра в тангенциальном и нормальном направлениях к автотрибоспектру в нормальном направлении, действительная часть которого характеризует упругие, а мнимая - диссипативные свойства подсистемы фрикционного контакта. Выполняется контроль и фиксирование удельной площади касания в реальном масштабе времени методом проводимости в паре металл-металл или методом лазерного просвечивания в паре металл-полимер. Обеспечивается равенство констант подобия в квазилинейной (механической) и существенно нелинейной (фрикционной) подсистемах высокомобильных нелинейных механических систем (ВМНТС), в том числе константы подобия давления 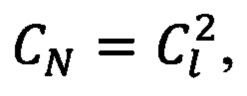 амплитуды колебания деформаций консервативных связей СΔА=1 и жесткости консервативных связей
амплитуды колебания деформаций консервативных связей СΔА=1 и жесткости консервативных связей 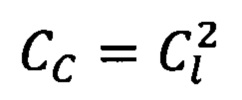 . Массы, совершающие плоскоколебательные движения в поле сил тяготения в натурной ВМНТС, приводятся к вращающемуся центру приведения физико-математической модели ВМНТС. Упрощение эквивалентной динамической модели ВМНТС выполняется при соблюдении равенства суммарных кинематических и потенциальных энергий натурной ВМНТС и ее физико-математической модели, с использованием метода Рэлея, учитывающего величины жесткости связей, соединяющих сосредоточенные и распределенные массы. Технический результат: обеспечение достаточного и необходимого соответствия основных динамических характеристик квазилинейных (механических) подсистем натурной ВМНТС и ее физической модели. 11 ил., 1 табл.
. Массы, совершающие плоскоколебательные движения в поле сил тяготения в натурной ВМНТС, приводятся к вращающемуся центру приведения физико-математической модели ВМНТС. Упрощение эквивалентной динамической модели ВМНТС выполняется при соблюдении равенства суммарных кинематических и потенциальных энергий натурной ВМНТС и ее физико-математической модели, с использованием метода Рэлея, учитывающего величины жесткости связей, соединяющих сосредоточенные и распределенные массы. Технический результат: обеспечение достаточного и необходимого соответствия основных динамических характеристик квазилинейных (механических) подсистем натурной ВМНТС и ее физической модели. 11 ил., 1 табл. 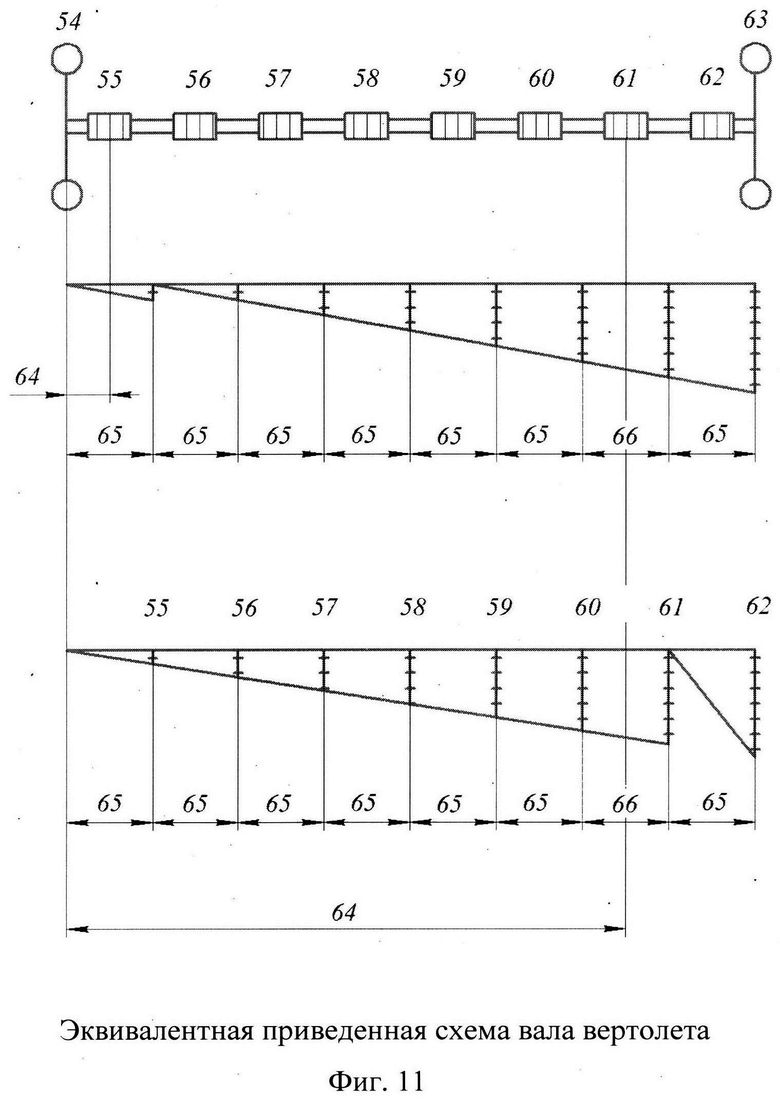
Способ динамического мониторинга высокомобильных нелинейных технических систем (ВМНТС), заключающийся в том, что механические системы объектной и модельной высокомобильных нелинейных технических систем (ВМНТС) состоят из подсистемы механической и подсистемы или подсистем фрикционных, при этом механические подсистемы описываются системой аналогичных линеаризованных дифференциальных уравнений, а процессы, протекающие на фрикционном контакте (ФК) «объекта» и «модели», описываются аналогичными математическими моделями, уравнениями регрессии, получаемыми при натурном эксперименте, например, с применением математического планирования полного или дробного факторного эксперимента, при этом измерение трибопараметров ВМНТС осуществляется во время проведения испытаний, коэффициент трения представляется в виде комплексной функции, т.е. в виде отношения взаимного трибоспектра в тангенциальном и нормальном направлениях к автотрибоспектру в нормальном направлении, действительная часть которого характеризует упругие, а мнимая - диссипативные свойства подсистемы фрикционного контакта, одновременно выполняется контроль и фиксирование удельной площади касания в реальном масштабе времени, например, методом проводимости в паре металл-металл или методом лазерного просвечивания в паре металл-полимер, отличающийся тем, что с целью обеспечения равенства констант подобия в квазилинейной (механической) и существенно нелинейной (фрикционной) подсистемах высокомобильных нелинейных механических систем (ВМНТС) и в частности обеспечения константы подобия давления  амплитуд колебаний деформаций консервативных связей СΔА=1 и жесткости консервативных связей
амплитуд колебаний деформаций консервативных связей СΔА=1 и жесткости консервативных связей 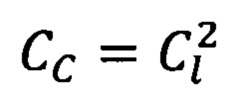 массы, совершающие плоскоколебательные движения в поле сил тяготения в натурной ВМНТС, приводятся к вращающемуся центру приведения физико-математической модели ВМНТС, а упрощение эквивалентной динамической модели ВМНТС выполняется при соблюдении равенства суммарных кинематических и потенциальных энергий натурной ВМНТС и ее физико-математической модели, а также с использованием метода Рэлея, т.е. с учетом величины жесткости связей, соединяющих сосредоточенные и распределенные массы.
массы, совершающие плоскоколебательные движения в поле сил тяготения в натурной ВМНТС, приводятся к вращающемуся центру приведения физико-математической модели ВМНТС, а упрощение эквивалентной динамической модели ВМНТС выполняется при соблюдении равенства суммарных кинематических и потенциальных энергий натурной ВМНТС и ее физико-математической модели, а также с использованием метода Рэлея, т.е. с учетом величины жесткости связей, соединяющих сосредоточенные и распределенные массы.
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| RU 2003126831 A, 20.02.2005 | |||
| СПОСОБ ОЦЕНКИ ВНЕШНИХ И ВНУТРЕННИХ ПАРАМЕТРОВ УЗЛОВ ТРЕНИЯ ПРИ ИСПЫТАНИИ В СТЕНДОВЫХ УСЛОВИЯХ | 2015 |
|
RU2647338C2 |
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ФРИКЦИОННЫХ МОБИЛЬНЫХ СИСТЕМ | 2012 |
|
RU2517946C2 |
| JP 6012323 B2, 16.02.1994. | |||
Авторы
Даты
2021-03-24—Публикация
2020-03-19—Подача