Настоящее изобретение относится к способам динамического мониторинга - мобильных нелинейных технических систем. Интенсивное развитие в XXI веке вычислительной техники, информационных технологий и инструментальных средств измерений способствует появлению новых, перспективных способов, методов и технологий для решения задач научного познания законов функционирования машин и механизмов. Практически любая машина или механизм являются фрикционными системами (ФС), состоящими из квазилинейных частей механических подсистем и существенно-нелинейных подсистем фрикционных контактов (ФК). С учетом специфики эксплуатации их можно выделить в особую группу -мобильные нелинейные технические системы (МНТС), к которым относятся железнодорожный, автомобильный, воздушный и водный транспорт.
Развивающиеся методы виброакустической диагностики ФС на базе виброакустического анализа колебательных состояний поверхностных слоев трущихся тел позволяют без изменения их конструкции обеспечить наблюдение за изменением состояния отображением свойств ФС в координатах состояния, доступных измерению. От их колебательных состояний зависит стабильность работы ФК и, в конечном счете, устойчивость всей ФС и безопасность эксплуатации. Однако до настоящего времени отсутствуют системы непрерывного динамического мониторинга ФС, имеющие высокую достоверность прогноза.
В качестве аналога выбран способ определения триботехнических характеристик пары трения [1], заключающийся в том, что по зарегистрированным переменным составляющих сил фрикционного взаимодействия пары трения и по их гармоническому анализу определяют текущие триботехнические характеристики пары трения, исключая влияние параметров мобильной технической системы на процессы трения и изнашивания.
В качестве ближайшего аналога выбран способ испытаний узлов трения [2]. Построение амплитудных и фазовых характеристик осуществляется на основе расчета частотного коэффициента передачи непараметрическим методом Уэлча:
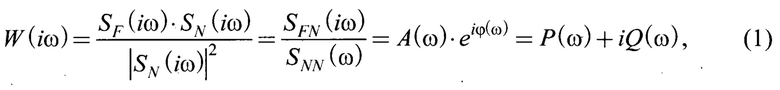
где SFN(iω) - взаимный спектр сил в тангенциальном (Fm=Сх⋅х, где Сх - жесткость, х - деформация связи) и нормальном (N=Су⋅у, где Су - жесткость связи, у - сближение поверхностей) направлениях, фрикционного взаимодействия;
SNN(iω) - энергетический спектр входного воздействия;
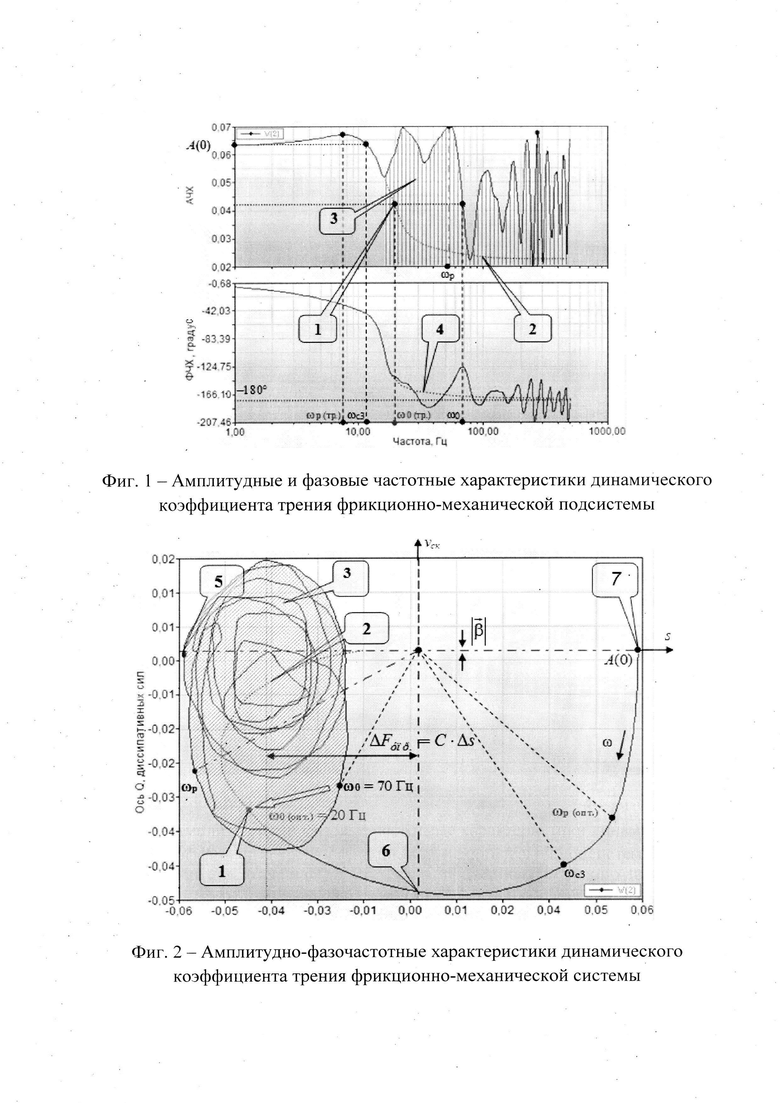
A(ω) - амплитудная частотная функция 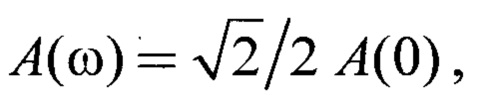 характеризующая коэффициент усиления или ослабления выходной координаты подсистемы на конкретной частоте ω гармонического воздействия амплитудно-частотных характеристик (АЧХ) (Фиг. 1)
характеризующая коэффициент усиления или ослабления выходной координаты подсистемы на конкретной частоте ω гармонического воздействия амплитудно-частотных характеристик (АЧХ) (Фиг. 1)
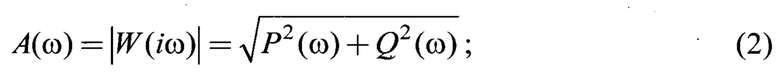
1 - требуемое значение частоты полосы пропускания; 2 - желаемая амплитудно-частотная характеристика; 3 - инерционно - диссипативная часть энергии динамического ƒmp; 4 - желаемая фазовая частотная характеристика; А(0) - коэффициент трения в стационарно-стабильном движении; ωр - резонансная частота колебаний; ωс3 - частота среза по условию А(ω)=А(0), определяющая время переходного процесса; ω0 - частота полосы пропускания А(ω)=0,707⋅А(0), Гц, определяющая высокочастотные помехи;
ϕ(ω) - фазовая частотная функция, характеризующая запаздывание выходной величины относительно входной в зависимости от частоты ω входного гармонического воздействия фазовых частотных характеристик (ФЧХ)(Фиг. 1)
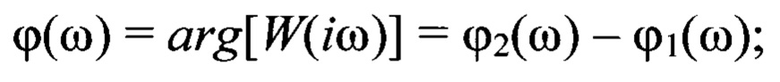
Р(ω) - вещественная частотная функция, характеризующая упруго-инерционные свойства подсистемы, или консервативную составляющую энергии системы (сумму потенциальной и кинетической энергий)

Q(ω) - мнимая частотная функция, характеризующая диссипативные свойства системы (потери на трение), или функцию рассеивания энергии

В качестве прототипа выбран способ динамического мониторинга фрикционных мобильных систем [3]. Динамический мониторинг МНТС - процесс непрерывного сбора информации об основных параметрах системы и ее преобразование в визуальную форму, выполняемый с целью диагностики ее текущего состояния, краткосрочного или долгосрочного прогнозирования его изменения и оперативного реагирования систем автоматического управления (САУ) или регулирования динамических параметров (САР). Наиболее эффективные направления реализации динамического мониторинга (исследование, диагностика, определение устойчивости, прогнозирование и оптимизация трибохарактеристик) МНТС осуществляются методами трибоспектральной идентификации (ТСИ). В отличие от коэффициента трения, предложенного в 1699 году Кулоном и Амонтоном, который вычисляется как отношение средних значений сил трения и нормального давления; от существующих подходов при определении устойчивости нелинейных систем, вместо релейных характеристик, условно моделирующих фрикционные звенья при определении их устойчивости, используются параметры комплексного коэффициента трения, статистически и достоверно отражающего свойства реального ФК, находящегося во МНТС. Во время проведения испытаний параллельно с фиксацией выходных триботехнических характеристик осуществляется «неразрушающий контроль» МНТС и ее подсистем путем регистрации и анализа их амплитудо-фазочастотных характеристик (АФЧХ) в требуемом частотном диапазоне, определяемом максимальной величиной одной из парциальных частот, параметрами микро- и макрошероховатостей поверхностей трущихся тел, аппаратно-программным обеспечением и классом решаемых задач. Комплексный коэффициент трения МНТС определяется комплексной функцией АФЧХ трибосистемы, отношения взаимного трибоспектра в тангенциальном и нормальном направлениях к автотрибоспектру в нормальном направлении, действительная часть которого характеризует упруго-инерционные, а мнимая - диссипативные свойства подсистемы фрикционного взаимодействия.
Недостатком приведенных изобретений является то, что они не обеспечивают достаточный уровень контроля МНТС на базе полученных результатов ее физической модели, также не обеспечивают необходимый уровень адекватности результатов модельных и натурных испытаний и определения выходных параметров натурной МНТС и ее физической модели.
Сущность предлагаемого изобретения заключается в том, что осуществление динамического мониторинга узлов трения мобильных нелинейных технических систем (МНТС), заключающегося в контроле процессов трения и изнашивания путем анализа нормальной и тангенциальной составляющих сил фрикционного взаимодействия, их взаимного спектра и автотрибоспектра нормальной составляющей, а также их отношения в форме комплексного коэффициента передачи или амплитудофазочастотной характеристики, с учетом того, что диагностика текущего состояния фрикционного контакта и краткосрочное или долгосрочное прогнозирование его изменения выполняется на основании информационно-диагностической базы интегральных) как на всем частотном диапазоне регистрации амплитудо-фазочастотных характеристик трибосистемы, так и на заданных октавных (1/3, 1/12, 1/24 - долеоктавных) диапазонах частот, либо заданных частотных диапазонах, охватывающих те или иные собственные частоты механической системы, полученных при испытаниях физико-механических моделей (ФММ) реального объекта исследования в лабораторных условиях, обеспечивающих идентичность динамических характеристик механических и фрикционных подсистем объекта и модели, а изменение указанных оценок на заданную величину пик-фактора (пикового значения отклонения оценки от математического ожидания к ее среднеквадратическому отклонению) определяет чувствительность систем автоматического управления (САУ) трибосистемой или систем автоматического регулирования (САР) параметрами трибосистемы и служит идентификационным признаком перехода из одного стационарного состояния в другое, в частности потери стабильности фрикционных связей, переходом от упругих деформаций к пластическим, к атермическому или термическому схватыванию активных микрообъемов поверхностей трения на фактической площади касания, отличающейся тем, что на основе критериев качества традиционной теории автоматического регулирования для каждого момента времени вычисляются предельно допустимые уровни физических величин параметров, а на их основе реализуются:
а) наблюдение за изменением тренда критерия диссипативных потерь энергии IQ во времени в октавных (долеоктавных) диапазонах частот по ГОСТу 17168-82 позволяет установить их корреляционную связь с заданным уровнем вероятности и характером изменения трибологических параметров (например, изменения градиента коэффициента трения) и на этой основе идентифицировать наиболее коррелируемые диапазоны частот, на которых проявляются трибологические свойства фрикционного контакта, а также изменение трибологических параметров и внешних факторов (например, изменений вязкости смазочного материала, понижения температуры окружающего воздуха, появления износа или атермических / термических, мостиков схватывания);
б) наблюдение за изменением тренда безразмерной интегральной величины коэффициента демпфирования Iξ в октавных (долеоктавных) диапазонах частот по ГОСТу 17168-82 и выделение наиболее коррелируемых k-информативных диапазонов частот трибоспектральных характеристик с k-трибологическими параметрами и внешними факторами фрикционного взаимодействия (например, изменением вязкости смазочного материала, понижением температуры окружающего воздуха, появлением износа, фреттинг-коррозии или атермических / термических мостиков схватывания), что позволяет с заданной вероятностью (0,95) идентифицировать моменты времени ухудшения упруго-диссипативных характеристик фрикционно-механической системы и на этой основе прогнозировать последующее поведение системы и остаточный ресурс работы модельного или натурного узла трения n-массной ФММ;
в) наблюдение за изменением тренда критерия энергетических потерь IE позволяет идентифицировать стабильность фрикционных связей в реальном времени функционирования узла трения;
г) мониторинг фрикционно-механической системы во времени по обобщенному критерию динамики IД фрикционно-механической системы, и его пороговым значением «предупреждения» - «1» и «опасности» - «1,15».
Более детально данный способ динамического мониторинга и идентификации упруго-диссипативных характеристик представлен в примере реализации.
Диаграмма Боде (Фиг. 1) позволяет получить информацию о том, как фрикционно-механическая система изменяет амплитуду гармонического сигнала и формирует запаздывающий аргумент на выходе по сравнению с входным сигналом на каждой частоте гармонического колебания.
Диаграмма Найквиста (Фиг. 2) представляет информацию аналогичную диаграмме Боде, но в фазовых координатах, где 1 - требуемое значение частоты полосы пропускания; 2 - желаемая амплитудно-частотная характеристика; 3 - Инерционно - диссипативная часть энергии динамического ƒmp; 5-Fин.=ms''; 6-Fсопр.=βs'; 7-Fупр.=Cs; s - обобщенная координата деформации связей (s=х/у); s' - ее скорость; sn - ее ускорение; νск - вектор скорости относительного скольжения; Δs - максимальное статическое смещение; С - жесткость связи, Н/м; β - коэффициент сопротивления связи, Н⋅с/м; m - масса поверхностных слоев, участвующих во взаимодействии.
Достоинством амплитудной фазовой характеристики является возможность идентификации упругих, диссипативных, инерционных и скоростных параметров фрикционно-механической системы.
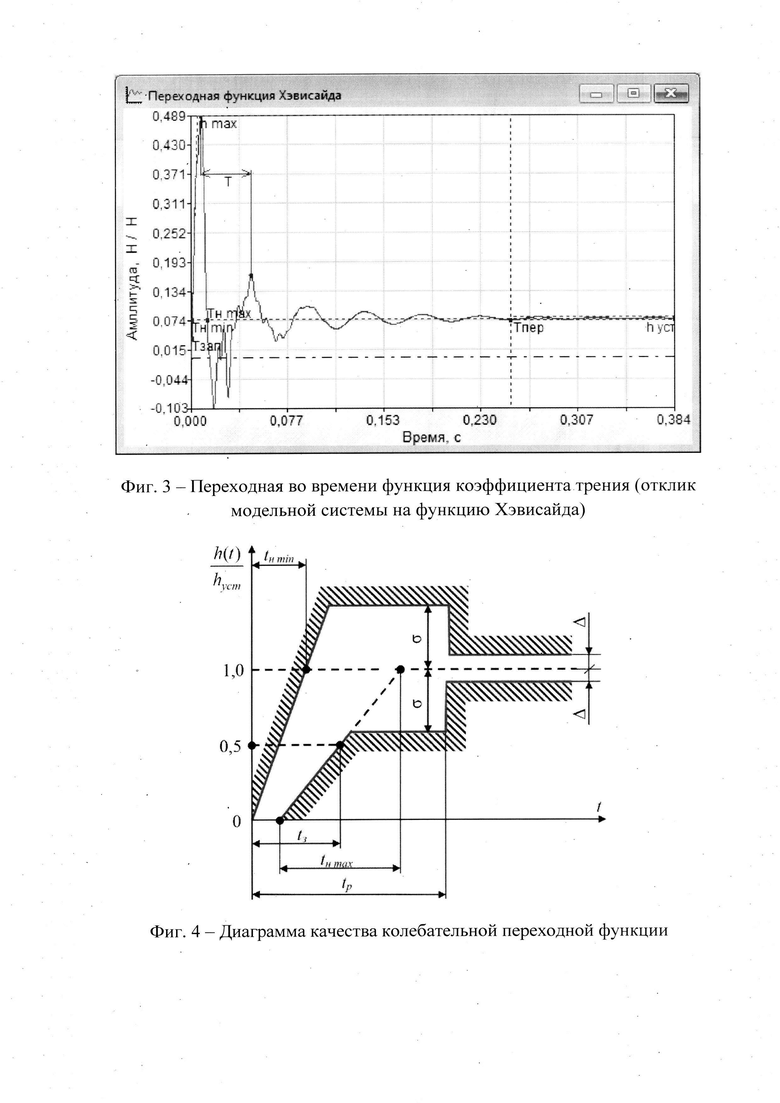
Как известно, колебательные состояния фрикционно-механических систем состоят из переходной и вынужденной составляющих (Фиг. 3) отклика модельной системы функции Хэвисайда, где Тзап.- время запаздывания; Тн min - минимальное время нарастания амплитуды; Тн max - максимальное время нарастания амплитуды; h max - максимальное отклонение от стационарной величины; Т - период низкочастотных колебаний; Тпер. - время регулирования; h уст. - установившееся (стационарное) значение.
Использование преобразования В.В. Солодовникова позволяет по значениям вещественно частотной функции (4) оценить функцию свободных (собственных) колебаний
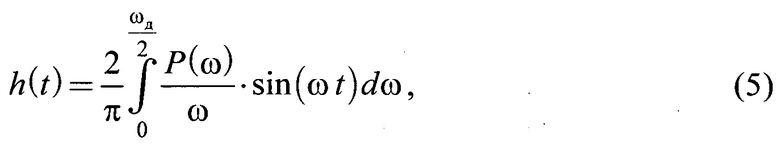
где ωд - максимальная частота дискретных данных, с-1;
Р(ω) - вещественная частотная функция (4);
ω - частота колебаний, с-1,
а по характеру ее изменений во времени - ряд критериев качества системы, таких как длительность переходного процесса, величину перерегулирования выходной координаты и др.
Совокупность анализируемых параметров позволяет реализовать мониторинг фрикционно-механической системы по наблюдаемым значениям частотных и временных критериев качества.
С целью идентификации диссипативных характеристик фрикционно-механической системы в программе предусмотрен октавный (треть-октавный или 12-октавный) спектральный анализ диссипативных потерь энергии и безразмерного коэффициента демпфирования.
Частотные характеристики не рассматривают вид переходного процесса, базируются на некоторых частотных свойствах системы и предназначены для оценки параметров, предназначенных для ограничения тех или иных параметров.
По частотным характеристикам (2) можно идентифицировать следующие характеристики фрикционно-механической системы:
1) Коэффициент трения в стационарном состоянии системы
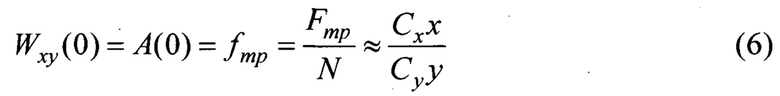
где Wxy(0) - значение комплексного коэффициента передачи при значении частоты колебаний ω, равной нулю, что соответствует коэффициенту передачи в стационарно устойчивом движении фрикционно-механической системы;
А(0) - значение амплитуды на графике амплитудной частотной характеристики (см. Фиг. 1);
ƒmp. - значение коэффициента трения в стационарно-устойчивом движении;
Fmp. - сила трения, Н;
N - нормальная нагрузка, Н;
Сх - коэффициент упругости фрикционных связей в направлении относительного смещения, Н/м;
Су - коэффициент упругости фрикционных связей в направлении относительного сближения контактирующих поверхностей трения, Н/м;
х - амплитуда тангенциального смещения (деформация активных объемов) поверхности трения;
у - амплитуда сближения контактирующих поверхностей трения.
2) Запас устойчивости по амплитуде, характеризующий возможность ограничения инерционных воздействий, способствующих разрыву фрикционной связи в трибоконтакте
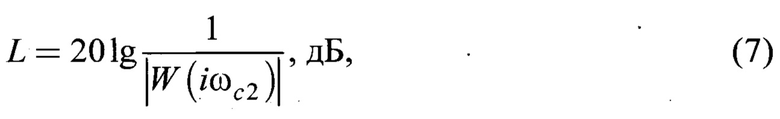
где ωc2 - частота среза, соответствующая точке пересечения годографом амплитудной фазовой функции W(iωc2) динамического коэффициента трения действительной оси, при котором частотный коэффициент передачи разомкнутой системы равен единице, а фазовый сдвиг составляет величину -180°;
W(iωc2) - амплитудная фазовая функция динамического коэффициента трения;
1 - критическое значение амплитуды, при котором амплитуда тангенциального смещения фрикционно-механической системы равна амплитуде нагрузки.
3) Запас устойчивости по фазе Ψ, позволяющий ограничить инерционные и диссипативные составляющие сил фрикционного взаимодействия, способствующие сближению контактирующих поверхностей трения, повышению контактных напряжений и температуры).
Запас устойчивости по фазе определяется на частоте, при которой комплексный коэффициент трения равен единице, т.е. |W(iω)|=1.
4) Частотный показатель колебательности М, характеризующий склонность фрикционно-механической системы к колебаниям. Его величину ограничивают в диапазоне от 1,1 до 1,5
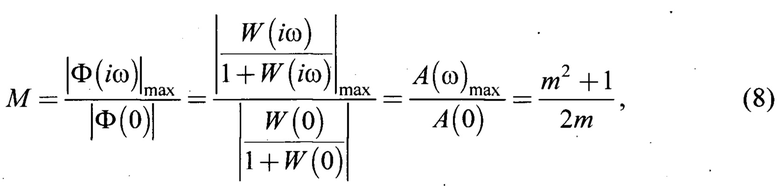
где Ф(iω) - амплитудная фазовая частотная характеристика замкнутой системы с помощью единичной обратной связи посредством трибоконтакта
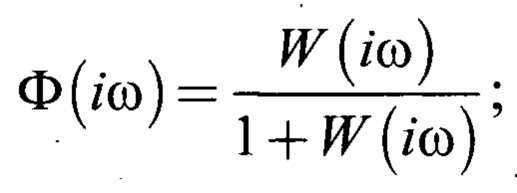
W(iω) - частотная передаточная функция исходно разомкнутой системы (7);
A(ω)max, А(0) - соответственно максимальная амплитуда самой низкочастотной гармоники и амплитуда установившегося стационарного состояния;
m - корневой показатель запаса устойчивости системы.
5) Частота среза ωс3 при А(ωс3)=А(0), косвенно определяющая длительность переходного процесса (см. Фиг. 1). Чем выше частота среза, тем меньше длительность переходного процесса и тем больше быстродействие

где (ω) - амплитудно-частотная функция;
А(0) - значение коэффициента трения в установившемся (стационарном) состоянии.
6) Частота полосы пропускания ω0 при А(ω0)=0,707⋅A(0), которая оценивает помехозащищенность фрикционно-механической системы. Полоса пропускания не должна быть слишком широкой

7) Резонансная частота, на которой гармонические колебания проходят через систему с наибольшим усилением. Желательно, чтобы резонансная частота ωр совпадала с частотой среза ωс3.
8) Квадратичный интегральный критерий качества I характеризует динамическую ошибку, возникающую при отклике системы на входное задающее воздействие типа функции Хэвисайда l(t). Оценка вычислена в частотной области на основе теоремы Парсеваля и формулы Рэлея. На базе указанных методов интегрирование квадрата временной функции в пределах от нуля до бесконечности заменяется интегрированием квадрата модуля комплексной амплитуды замкнутой системы, а изображение Фурье исследуемого отклонения определяет ошибку переходного динамического процесса ε
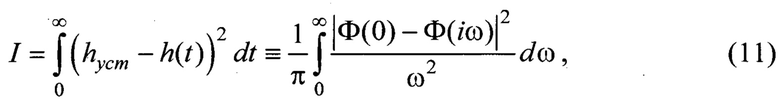
где hуст - установившееся (стационарное) значение переходной функции Хэвисайда (при значении времени t=∞).
9) Квадратичный интегральный критерий качества I' характеризует динамическую ошибку, возникающую при отклике системы на входное задающее воздействие типа функции Дирака δ(t), то есть импульсного воздействия. Оценка вычислена на основе теоремы Парсеваля и формулы Рэлея:
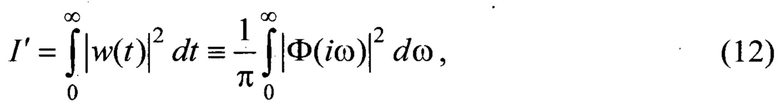
где w(t) - значения импульсной функции Дирака в момент времени t.
В прототипе [3] было показано, что интегральная оценка диссипативной составляющей АФЧХ определяется выражением (2) с учетом нелинейного коэффициента пропорциональности К. Нами было выполнено уточнение (2) с помощью следующих четырех критериев: IC, Im, Iсопр и Iфр.к.
10) Интегральная оценка IC характеризует упруго-инерционные свойства системы, способствующие возрастанию потенциальной энергии. Чем меньше величина IC, тем меньше инерционность системы оказывает на динамическое сближение контактирующих поверхностей трения друг к другу, повышение контактных напряжений и поверхностной температуры, развитию пластических деформаций, а также на стабильность динамики процессов трения
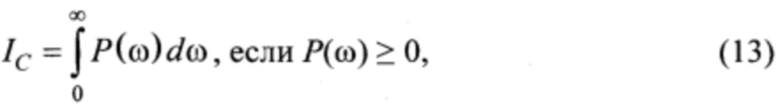
где Р(ω) - вещественная частотная функция.
11) Интегральная оценка инерционных сил Im характеризует инерционные свойства системы, способствующие возрастанию кинетической энергии, а также снижению устойчивости системы, стабильности фрикционных связей. Чем меньше величина Im, тем меньше инерционность системы и тем выше устойчивость, стабильность процессов трения
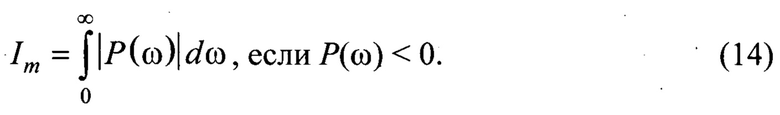
12) Интегральная оценка сил сопротивления перемещениям Icопр. характеризует сочетание инерционных воздействий на узел трения и ' диссипативных свойств трибологической среды. Чем больше интегральная оценка, тем выше амплитуда колебаний, вызванная сочетанием значительных инерционных и недостаточных диссипативных составляющих сил фрикционного взаимодействия. Чем меньше величина Iсопр., тем меньше кинетической энергии расходуется на процессы трения во фрикционных связях, меньше температурные колебания, выше диссипативные свойства и коэффициент сопротивления β (Н⋅с/м)
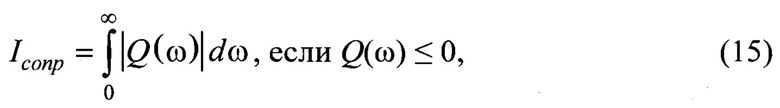
где Q(ω) - мнимая частотная функция.
13) Интегральная оценка сил, обусловленных сочетанием инерционных воздействий на узел трения, диссипативных свойств трибологической среды и скорости относительного скольжения, Iфp.к. также характеризует диссипативные свойства системы, однако когда вектор сил сопротивления движению сонаправлен с вектором скорости относительного скольжения. Значительное повышение оценки свидетельствует о значительном возрастании скоростей относительного скольжения поверхностей трения при преодолении местных или локальных сопротивлений,.вызванных процессами перехода от упругих к упругопластическим деформациям или от упругопластических к. пластическому деформированию контактирующих поверхностей, износу, термоповреждениям фрикционно-механической системы, снижению Стабильности и устойчивости, разрыву фрикционных связей и фрикционным автоколебаниям. Чем меньше величина Iфp.к., тем более устойчива и стабильна фрикционно-механическая система
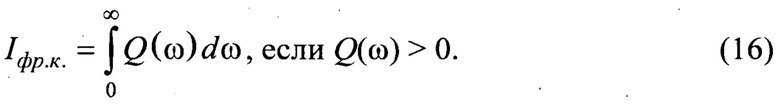
Аналогично, в прототипе [3] было показано, что интегральная оценка степени диссипации определяется выражением (3) с учетом нелинейного коэффициента пропорциональности К. Нами было выполнено уточнение (3) с помощью критерия: Iξ. Выполнив анализ регистрируемых АФЧХ показано, что амплитуда комплексного (динамического) коэффициента трения находится в обратной пропорциональности коэффициенту демпфирования |Qmax|=А(0)/(2ξmin) и пропорциональна величине корневого показателя колебательности. Следовательно, безразмерный коэффициент демпфирования ξ оценивается через корневой показатель колебательности как 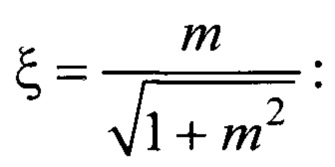 с увеличением амплитуды комплексного (динамического) коэффициента трения возрастает колебательность m, а безразмерный коэффициент демпфирования ξ и интегральная оценка Iξ снижаются.
с увеличением амплитуды комплексного (динамического) коэффициента трения возрастает колебательность m, а безразмерный коэффициент демпфирования ξ и интегральная оценка Iξ снижаются.
14) Интегральная оценка коэффициента демпфирования Iξ характеризует соотношение диссипативной и консервативной энергии фрикционно-механической системы и приблизительно соответствует его линейной величине ξ (34)
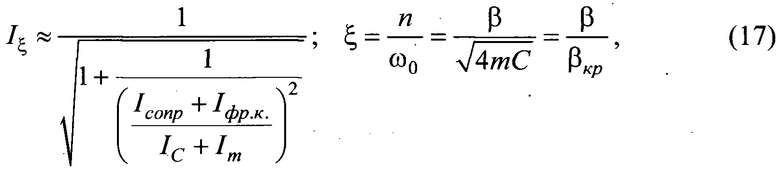
где Iсопр - интегральная оценка сопротивления колебаниям;
Iфp.к - интегральная оценка сил, вызванных фрикционными автоколебаниями;
IC - интегральная оценка упруго-инерционных составляющих;
Im - интегральная оценка инерционных составляющих;
n - коэффициент затухания колебаний, с-1;
ω0 - частота собственных колебаний, с-1;
m - приведенная масса контактирующих поверхностей, участвующих в трении, кг;
С - приведенный коэффициент упругости контактирующих поверхностей, Н/м;
β - эквивалентный коэффициент сопротивления колебаниям, Н⋅с/м;
β0 - эквивалентная критическая величина коэффициента сопротивления колебаниям,' при которой колебательный характер сменяется на монотонно затухающий (апериодический).
Временные характеристики в виде переходной функции (5) позволяют оценить характер изменения коэффициента трения во фрикционно-механической системе от воздействия на объект исследования (математическую модель) стандартной функции Хэвисайда l(t). Если система удовлетворяет заданным требованиям качества, то она будет удовлетворять этим требованиям и при любом другом произвольном воздействии. Функция Хэвисайда определяется выражением:
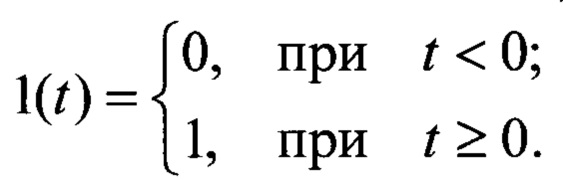
Требования качества к переходной функции следующие.
1) Время запаздывания tз (Фиг. 4) характеризует способность системы воспроизводить изменения входных координат без искажения, но с некоторым постоянным запаздыванием τ. Чем меньше время запаздывания, тем более быстродействующая система

где t - время переходного процесса;
h(t) - текущие значения амплитуд переходной характеристики;
hуст - установившаяся амплитуда h(t∞) переходной характеристики в стационарном состоянии (см. Фиг. 4).
2) Минимальное время нарастания амплитуды fн.min (Фиг. 4) - промежуток времени, по истечении которого управляемая величина в первый раз достигает своего установившегося значения hуст. Это время ограничивается допустимыми в системе ускорениями координат и предельными колебаниями. Чем меньше fн.min, тем более быстро система отрабатывает задающее воздействие
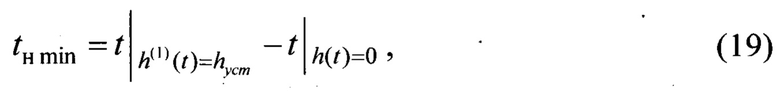
где t - время переходного процесса;
h(t) - текущие значения амплитуд переходной характеристики;
hуст - установившаяся амплитуда h(t∞) переходной характеристики (6) в стационарном состоянии (см. Фиг 3).
(1) - означает первое достижение условия.
3) Максимальное время нарастания амплитуды tн.max (см. Фиг. 3) характеризует длительность протекания переходного процесса. Чем меньше tн.max, тем выше быстродействие системы

где t - время переходного процесса;
tз - время запаздывания;
h(t) - текущие значения амплитуд переходной характеристики;
hуст - установившаяся амплитуда h(t∞) переходной характеристики (6) в стационарном состоянии (см. Фиг. 3).
tн min - минимальный период времени нарастания.
4) Время регулирования tp (Фиг. 4) - интервал времени, по истечении которого отклонение переходной характеристики от установившегося значения hуст не превышает некоторой заданной величины Δ и характеризует длительность переходного процесса (быстродействие системы) или, другими словами, быстроту реакции системы на изменение (появление) управляющих или возмущающих воздействий. Чем меньше время регулирования tp собственного переходного движения при отработке функции включения l(t), тем более быстродействующей является система

где Δ - отклонение управляемой величины от установившегося значения, по заданию.
Фактическая ошибка регулирования Δф, % определяет точность регулирования и время переходного процесса. Допускаемая ошибка Δ составляет 5; 2,5; 1,5; 1; 0,5; … % от установившегося значения h[t∞]
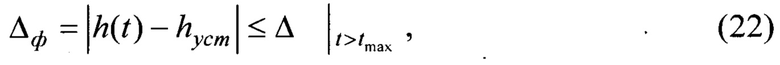
где h(t) - текущие значения амплитуд переходной характеристики;
hуст - установившаяся амплитуда h(t∞) переходной характеристики в стационарном состоянии (см. Фиг. 3).
tmax - время достижения первого максимума переходной функции hmax (см. Фиг. 3).
5) Время ty (Фиг. 3), соответствующее установившемуся значению, переходной функции hуст(ty) определяет статическую точность динамической системы. Чем меньше время установившегося значения переходной характеристики, тем более быстродействующая система.
6) Перерегулирование σ, % (Фиг. 4) характеризует склонность системы к колебаниям и запас устойчивости. Допустимое значение перерегулирования для той или иной системы может быть установлено на основе эксплуатационных исследований. В большинстве случаев считается, что запас устойчивости является достаточным, если величина перерегулирования не превышает 10…30%. Однако в некоторых случаях требуется, чтобы переходный процесс протекал вообще без перерегулирования, то есть был монотонным; в ряде других случаев может допускаться перерегулирование 50…70%.

где hmax - максимальное отклонение регулируемой величины (переходной функции) от ее установившегося значения в стационарном состоянии hуст.
Последующие оценки фрикционно-механической системы рассчитываются на основе частотных характеристик, линеаризованных с помощью весовых функций, для текущего момента времени и позволяют в некоторой степени их уточнить и определить функцию корреляции.
7) Добротность Q колебательной системы - мера относительной диссипации (рассеивания) энергии, характеризующая качество колебательной системы. Она определяет амплитуду и ширину амплитудно-частотной характеристики резонанса. Для системы с критическим затуханием. (ψ=1) добротность Q=2π. Добротность, меньшая или равная 2π соответствует не колебательному (апериодическому) характеру движения,. пересекающего положение равновесия не более одного раза. Чем меньше добротность колебательной системы, тем больше потери энергии за одно колебание и тем быстрее затухают колебания во фрикционно-механической системе
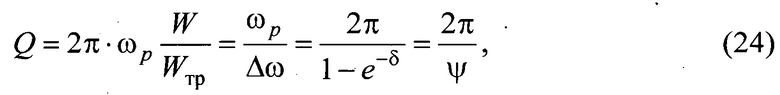
где ωр - резонансная частота колебаний, Гц

ω0 - собственная частота фрикционно-механической системы;
ξ - безразмерный коэффициент демпфирования;
n - коэффициент затухания колебаний, с-1;
W - энергия, запасенная в колебательной системе;
Wтр - рассеиваемая энергия;
Δω - ширина амплитудной частотной резонансной кривой по уровню 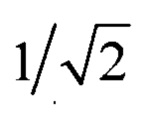 (минус 3 дБ) максимальной амплитуды на резонансной частоте ωр колебаний;
(минус 3 дБ) максимальной амплитуды на резонансной частоте ωр колебаний;
δ - логарифмический декремент затухания, характеризующий уменьшение амплитуды за один период колебаний
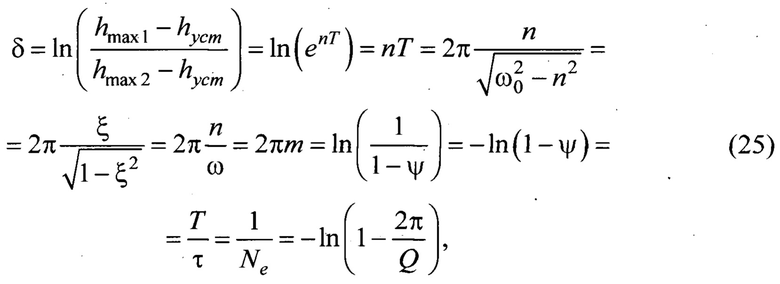
где hуст - установившаяся амплитуда h(ty) переходной характеристики (6) в стационарном состоянии (см. Фиг 3).
hmax1, hmax2 - максимальные отклонения амплитуд регулируемой величины от положения устойчивого стационарного состояния на. расстоянии одного периода Т колебаний;
Т - период затухающих колебаний, с (определяется по графику переходной характеристики);
τ - время релаксации фрикционной связи, с
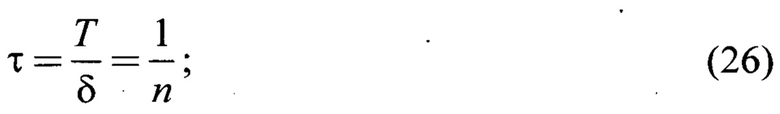
Ne - количество колебаний регулируемой величины за время релаксации
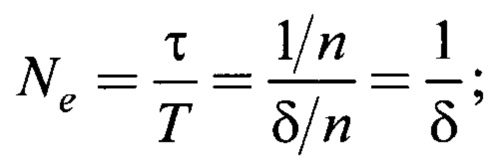
n - коэффициент затухания - количественная характеристика сопротивления системы относительному перемещению
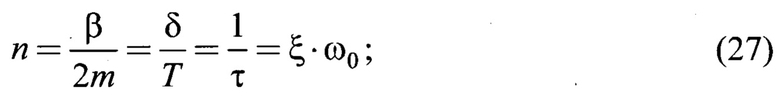
β - эквивалентный коэффициент сопротивления колебаниям, Н⋅с/м;
m - приведенная масса колеблющейся системы, кг;
ω0 - частота собственных колебаний
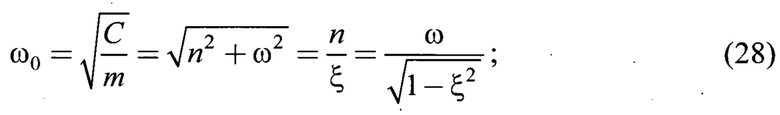
С - коэффициент жесткости упругой связи, Н/м;
ξ - безразмерный коэффициент демпфирования системы
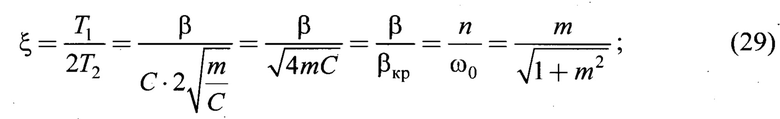
T1=β/С - постоянная времени, характеризующая затухание амплитуд колебаний;
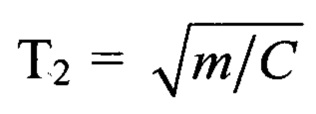 - постоянная времени, обратно пропорциональная частоте собственных колебаний ω0 системы;
- постоянная времени, обратно пропорциональная частоте собственных колебаний ω0 системы;
βкр. - критическая величина сопротивления колебаниям, Н⋅с/м, при которой период затухающих колебаний становится равным бесконечности, а характер колебаний - асимптотически затухающий;
ω - частота затухающих колебаний
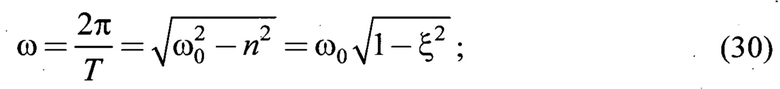
m - корневой показатель колебательности
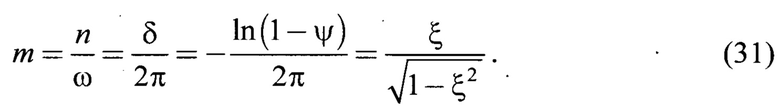
8) Степень затухания колебаний ψ, характеризующая уменьшение амплитуд в течение одного периода колебаний; чем выше его значение к единице, тем быстрее во фрикционно-механической системе завершаются переходные колебательные движения без существенного перерегулирования
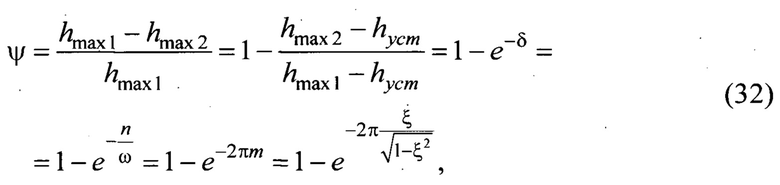
где hmax1, hmax2 - максимальные отклонения переходной функции от стационарной траектории движения на протяжении одного периода Т колебаний (Фиг. 3);
hуст - установившаяся амплитуда h(ty) переходной характеристики (6) в стационарном состоянии (Фиг. 3);
δ - логарифмический декремент затухания;
n - коэффициент затухания;
ω - частота затухающих колебаний;
m - корневой показатель колебательности;
ξ - безразмерный коэффициент демпфирования системы.
9) Число колебаний регулируемой величины N за время переходного процесса tp должно быть ограничено. По требованиям быстродействия системы обычно его принимают не более 2…3.
10) Линейный интегральный критерий качества I1 - простейшая интегральная оценка ошибки управления системой. В устойчивой системе при t→∞ ошибка управления ε=[h(t)-hycт]→0 имеет конечную величину. Отрицательная величина I1 при колебательном характере переходных процессов характеризует нежелательный эффект в процессе управления, а именно значительную долю разрыва фрикционных связей в переходных динамических режимах при ступенчатом воздействии на систему
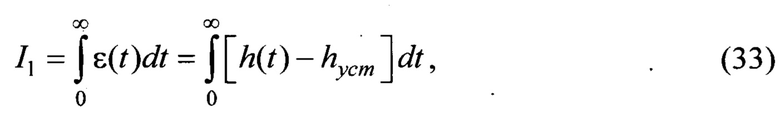
где ε - отклонения переходной характеристики h(t) от его установившегося значения.
Абсолютная' величина интеграла I1 будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения.
11) Линейный интегральный критерий качества по модулю I2 применяется в тех случаях, когда форма переходных процессов неизвестна. Величина интеграла I2 будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения
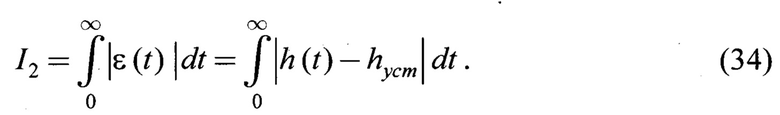
По указанным выше частотным и временным параметрам линеаризованной системы рассчитываются частные критерии качества фрикционно-механической системы в каждый момент времени, определяемые как отношение измеренной физической величины к его опорному значению:
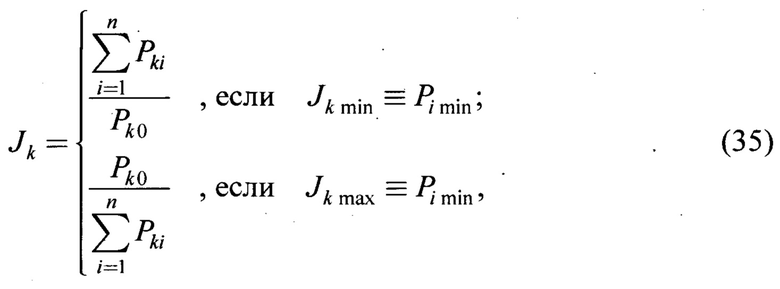
где Pki - измеренная физическая величина по результатам n циклов испытаний;
Pk0 - опорные значения физической величины, установленные по априорно достоверным источникам, либо экспериментально;
n - количество измерений во времени наблюдения.
Для реализации мониторинга динамических характеристик далее рассчитывается динамический критерий качества
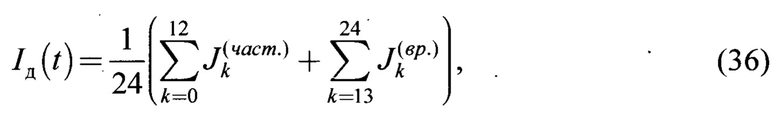
где 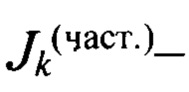 частные критериальные оценки частотных характеристик;
частные критериальные оценки частотных характеристик;
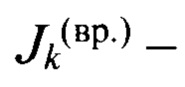 частные критериальные оценки временных характеристик;
частные критериальные оценки временных характеристик;
k - текущий номер критерия;
t - текущий момент времени анализа фрикционной механической системы,
таким образом, что предельно допустимое его значение при нормальной эксплуатации фрикционно-механической системы не должно превышать единицы.
Линейный уровень динамического критерия качества (36) фрикционно-механической системы может имеет 7 уровней, представленных в таблице 1.
Установлены следующие соотношения анализируемых параметров и их. частных критериев качества (35).
1) Опорные величины
• коэффициента передачи Wxy(0) (6), соответствующий значению стационарного коэффициента трения;
• частотного показателя колебательности М (8);
• частоты полосы пропускания ω0 при А(ω0)=0,707⋅A(0), которая оценивает помехозащищенность системы от высокочастотных колебаний (10), Гц;
• квадратичного критерия качества I(11) функции Хэвисайда;
• квадратичного критерия качества I'(12) функции Дирака;
• критерия упруго-инерционных составляющих IC (13);
• критерия инерционных составляющих Im (14);
• критерия сил сопротивления Iсопр (15);
• критерия фрикционных автоколебаний Iфр.к. (16)
должны иметь максимально предельные уровни значений, выше которых возможны аномальные условия эксплуатации фрикционно-механической системы.
2) Опорные величины
• минимально допустимого уровня запаса устойчивости по амплитуде, выбирается в соответствии с рекомендациями таблицы 2;
• минимально допустимая частота среза ωс3 при выполнении условия А(ωс3)=А(0)
частотных параметров должны иметь минимальные уровни значений, так как более низкие величины будут оказывать ухудшение динамики фрикционно-механической системы.

3) Опорная величина запаса устойчивости по фазе ψ частотных параметров, отличается от указанных ранее. Анализ осуществляется по заданной в таблице 1 предельно-допустимой величине. Если измеренная величина запаса устойчивости по фазе равна заданному предельному значению, то частному критерию присваивается весовой коэффициент, равный единице. Если же измеренная величина превышает предельную величину запаса устойчивости по фазе, то частный критерий варьируется от нуля до единицы, иначе - возрастает до двух.
4) Опорная величина критерия коэффициента демпфирования Iξ (17) устанавливается на основе рекомендаций таблицы 1 и следующего правила:
а) если коэффициент демпфирования фрикционно-механической системы меньше единицы, то значение его опорной величины следует принять минимально возможным, при котором еще быстродействие системы достаточно; в этом случае максимальным параметрам измеренного коэффициента демпфирования будет соответствовать минимальный критерий качества от нуля до единицы;
б) если коэффициент демпфирования больше или равен единице, то в этом случае минимальному измеренному коэффициенту демпфирования будет соответствовать минимальный критерий качества.

Для переходной функции (5) установлены следующие критерии:
1) опорные величины
• времени запаздывания tз;
• минимального времени нарастания tн.min;
• максимального времени нарастания tн.max;
• периода регулирования tp;
• времени устойчивого состояния ty, с;
• перерегулирования σ, %, таблица 2;
• линейного критерия качества I1;
• линейного критерия качества по модулю I2
должны иметь максимально допустимые предельные уровни значений, выше которых возможны аномальные условия эксплуатации системы.
2) Опорная величина добротности Q колебательной системы устанавливается в соответствии с таблицей 2 по максимально допустимой величине колебательного состояния системы, либо по минимальной - для апериодического характера движения. В этом случае если измеренное значение Q>2π, то минимальному значению Q будет соответствовать минимальный критерий качества; если Q≤2π, то максимальному значению Q будет соответствовать минимальный критерий качества.
3) Опорная величина степени затухания ψ выбирается аналогично параметру Iξ в соответствии с данными таблицы 3.
4) Опорная величина числа колебаний регулируемой величины N выбирается но максимально допустимому количеству колебаний регулируемой величины (см. таблицу 2). В этом случае при экспериментальном числе колебаний, меньшим установленной опорной величины, частный критерий качества будет минимальным. В противном случае - больше единицы.
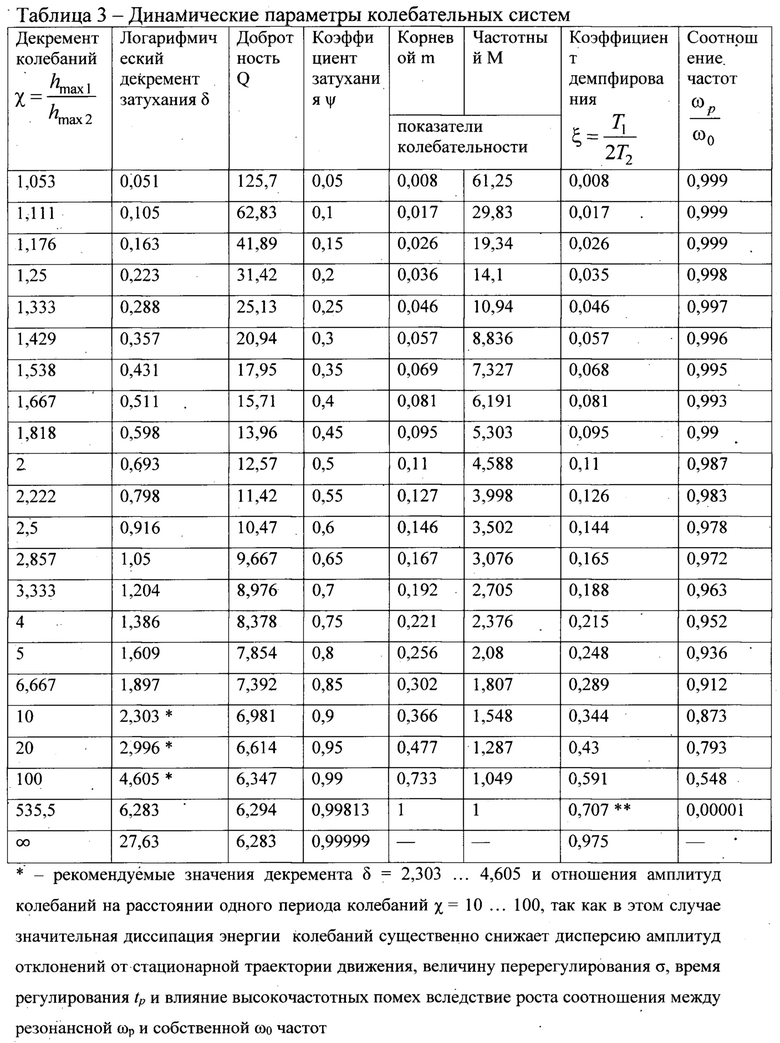
При вводе предельно допустимых значений параметров следует руководствоваться рекомендациями таблицы 3, позволяющей установить соответствие основных динамических параметров фрикционно-механической системы.
С целью идентификации трибологических характеристик смазочного материала, износа шлицев муфты трансмиссии привода хвостового винта вертолета (модели шлицевого соединения) в программе реализован октавный (треть-октавный или 1/12-ти октавный) спектральный анализ как интегральной оценки коэффициента демпфирования Iξ в стандартных диапазонах частот, так и интегральной оценки диссипативных потерь
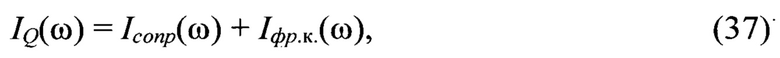
где Iсопр - интегральная оценка сопротивления колебаниям;
Iфр.к - интегральная оценка сил, вызванных фрикционными автоколебаниями;
ω - частота колебаний;
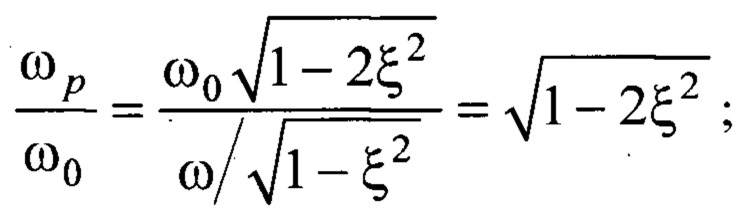
** - при 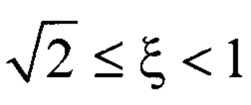 колебания приближаются к асимптотическим;
колебания приближаются к асимптотическим;
при ξ≥1 - движение лимитационное, пересекающее положение устойчивого равновесия не более одного раза.
Стабильность формируемых фрикционных связей можно определить по критерию энергетических потерь (8)
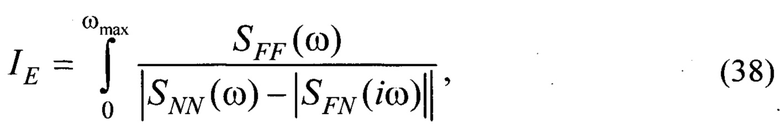
где SFF(ω) - спектральная плотность мощности выходного сигнала F(t) фрикционно-механической системы;
SNN(ω) - спектральная плотность мощности нагрузки N(t) - входного сигнала;
SFN(ω) - взаимная спектральная плотность мощности тангенциального смещения F(t) и нагрузки N(t);
Статистический анализ экспериментальных данных
После запуска файла Excel, содержащего результаты экспериментальных исследований, можно выполнить предварительный статистический анализ сформированных данных с помощью точечных " оценок математической статистики.
Для этого перейдите в одну из следующих вкладок
- Экспериментальные данные мониторинга;
- Диссипативные потери в октавных диапазонах частот;
- Коэффициент демпфирования в октавных диапазонах частот, нажмите сочетание клавиш Ctrl+s для вызова макроса;
при нажатой клавише Shift клавиатуры выделите указателем мыши диапазон ячеек выбором верхней левой ячейки и нижней правой ячейки, не трогая колонку А данных таблицы.
Примерный вид будет следующим: $B$2:$BF$546, где $В - наименование начальной колонки данных, $BF - наименование конечной колонки; $2 - начальная строка данных; $546 - конечный номер строки таблицы.
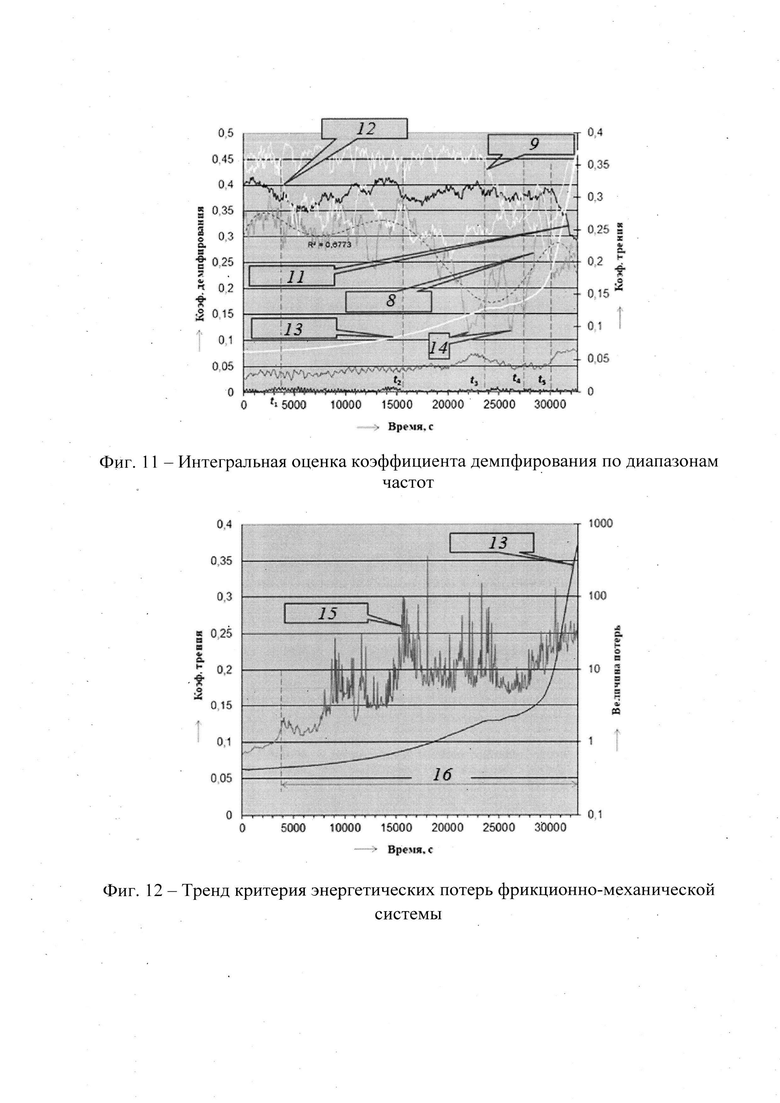
Подтвердив правильность ввода информации кнопкой «ОК», макрос выполнит статистический анализ и сформирует выходные данные в последующих строках так, как показано на Фиг. 5.
Здесь приняты следующие обозначения:
alpha - уровень статистической значимости α;
р - заданный уровень вероятности оценки параметра, р=1-α (95%);
ƒ - число степеней свободы, ƒ=n-1;
n - количество зафиксированных во времени значений параметров;
tT - табличное значение критерия Стьюдента, tт(α,ƒ);
minX - минимальное значение фиксируемого параметра;
maxX - максимальное значение фиксируемого параметра;
mX - математическое ожидание, μх;
dX - дисперсия, Dx;
sX - среднее квадратичное отклонение 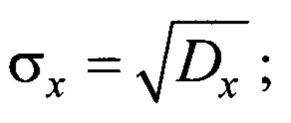
рХ - пик-фактор, 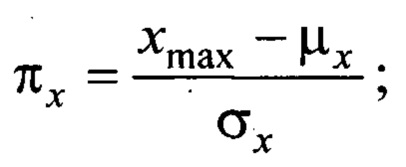
±sX - доверительный интервал
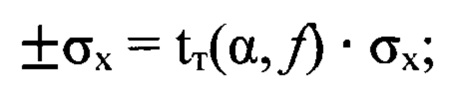
d - относительная ошибка параметра, характеризующая разброс измеренных величин параметра
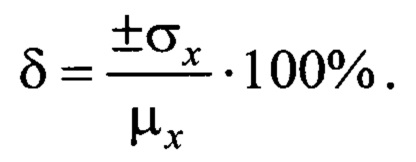
На основе полученных результатов вычислений можно сделать некоторые промежуточные выводы:
1) значения пик-фактора тангенциальной составляющей Y (πх=4,1) и относительная ошибка (δ=109%) высоки, следовательно, анализируемые данные характеризуют два или более трибологических процесса (трения со смазочным материалом, граничное трения и трения без смазочного материала);
2) в то же промежуток времени пик-фактор и статистическая оценка нормальной составляющей X значительно ниже (πх=3 и δ=0,2%), следовательно, характер нагружения узла трения стационарен, правило трех сигм выполняется.
Идентификация характерных диапазонов собственных частот
Идентификация характерных диапазонов собственных частот реализуется применением октавного (треть-октавного или 12-октавного) спектрального анализа диссипативных потерь (37) или безразмерного коэффициента демпфирования (17) фрикционно-механической системы.
Идентификация трибологических характеристик
Анализ экспериментальных данных диссипативных потерь во вкладке Microsoft Excel Октавный анализ диссипаивных потерь (Фиг. 6) позволяет идентифицировать диапазоны собственных частот, имеющих наибольший отклик и значение корреляционной функции на изменение трибологических характеристик фрикционного контакта.
В качестве единиц измерения шкалы Диссипативные потери.приняты единицы измерения коэффициента трения. Диссипативные потери характеризуют, какая часть механической энергии преобразуется в другие виды, в том числе тепловую.
Для расчета коэффициента корреляции Пирсона между значениями коэффициента трения и диссипативных потерь откроем вкладку Дис. потери в октавных диапазонах и выберем одну из свободных строк таблицы.
Например, табличные данные имеют число степеней свободы 544 (Фиг. 7); тогда на 548 строке в ячейке В548 вводим следующую команду
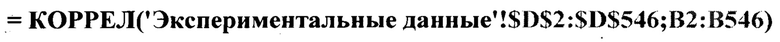
где 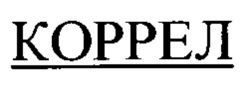 - встроенная в Excel функция расчета коэффициента корреляции Пирсона;
- встроенная в Excel функция расчета коэффициента корреляции Пирсона;
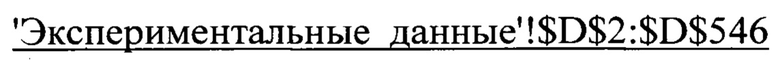 - ссылка на диапазон ячеек коэффициента трения, расположенных во вкладке 'Экспериментальные данные';
- ссылка на диапазон ячеек коэффициента трения, расположенных во вкладке 'Экспериментальные данные';
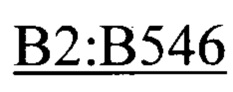 - ссылка на диапазон ячеек диссипативных потерь в диапазоне частот 0,35-0,71 Гц текущей вкладки
- ссылка на диапазон ячеек диссипативных потерь в диапазоне частот 0,35-0,71 Гц текущей вкладки
и нажимаем клавишу Enter. В указанной ячейке появится численное значение корреляции вектора данных коэффициента трения и диссипативных потерь энергии в диапазоне частот 0,35-0,71 Гц, равное 0,57.
Далее скопируем ячейку В548 для других диапазонов частот, потянув указатель мыши на ячейки таблицы, размещенные справа (Фиг. 7). При этом должна быть нажата левая кнопка мыши.
В результате копирования формул в каждом диапазоне частот диссипативных потерь энергии будет вычислена корреляционная функция. Анализ полученных результатов показал, что наиболее коррелированным со значением коэффициента трения является диапазон частот 44,7-89,1 Гц, так как коэффициент корреляции равен 0,99, а в диапазонах частот до 22,4 Гц изменение трибологических характеристик значительно слабее влияют на трибодинамику узла трения (Фиг. 8).
На основе выполненного анализа можно сформулировать вывод, что возрастание коэффициента трения в контактной области узла трения определяется динамическими процессами, протекающими в диапазонах частот 22,4-89,1 Гц (низкочастотные колебания) и 177,8-500 Гц (высокочастотные колебания), а наибольшее влияние на динамику фрикционно-механической системы оказывают трибологические процессы в диапазоне частот 44,7-89,1 Гц. Этот вывод хорошо иллюстрирован на Фиг. 6, где 8 - 89.1-177.8 Гц; 9 - 354.8-707.9 Гц; 10 - 22.4-44.7 Гц; 11 - 44.7-89.1 Гц; 12 - 177.8-354.8 Гц; 13 - коэффициент трения. Видно, что градиенты изменения коэффициента трения (кривая желтого цвета) и диссипативных потерь в диапазоне частот 44,7-89,1 Гц очень близки друг к другу.
Статистическую значимость коэффициента корреляции Пирсона можно оценить по критерию Стьюдента, рассчитав его расчетное значение и сравнив его с табличным. Расчетное значение критерия Стьюдента:
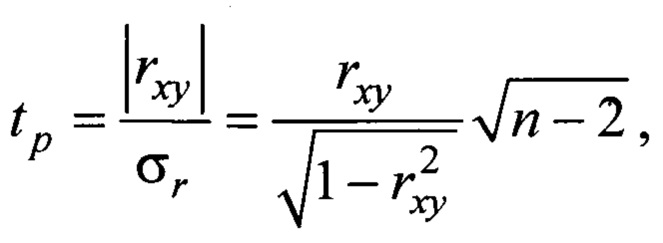
где rxy - значение коэффициента корреляции Пирсона;
σr - среднее квадратичное отклонение коэффициента корреляции;
n - количество значений статистической функции.
Коэффициент корреляции Пирсона rxy считается статистически значимым, если выполняется условие
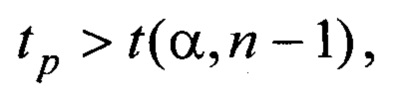
где t - табличное значение критерия Стьюдента;
α - статистический уровень значимости критерия (α=0,05);
n - количество значений статистической функции.
Табличное значение критерия Стьюдента берется по стандартным таблицам справочников или с помощью встроенной функции Excel.
Для вычисления расчетного критерия Стьюдента в Excel введем в. ячейку В549 команду (Фиг. 8)
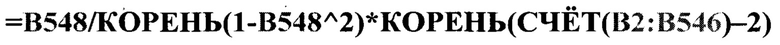
а в ячейку В550 - табличное значения критерия Стьюдента (Фиг. 7; 8)
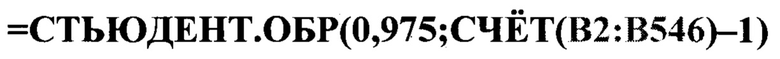
где  - встроенная в Excel функция расчета квадратного корня;
- встроенная в Excel функция расчета квадратного корня;
 - встроенная в Excel функция подсчета количества ячеек;
- встроенная в Excel функция подсчета количества ячеек;
 - встроенная в Excel функция, возвращающая левостороннее обратное t-распределение Стьюдента;
- встроенная в Excel функция, возвращающая левостороннее обратное t-распределение Стьюдента;
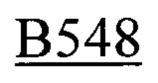 - ячейка, в которой вычислено значение коэффициента корреляции Пирсона;
- ячейка, в которой вычислено значение коэффициента корреляции Пирсона;
 - ссылка на диапазон ячеек;
- ссылка на диапазон ячеек;
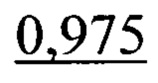 - вероятность, соответствующая t-распределению Стьюдента.
- вероятность, соответствующая t-распределению Стьюдента.
Результат проверки гипотезы статистической значимости коэффициента корреляции Пирсона введем в ячейку В551 (Фиг. 9)
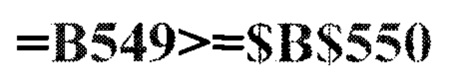
Размножим формулы ячейки В549 на диапазон ячеек C549…L549, а ячейки В551 - на диапазон С551…L551, потянув указателем мыши за черный квадратик (Фиг. 9). Результат копирования формул представлен на Фиг. 10.
Видим, что все полученные значения расчетного критерия Стьюдента выше табличного (в ячейке В550), следовательно принимается гипотеза о соответствии расчетных значений диссипативных потерь энергии в октавных диапазонах частот соответствующим значениям коэффициента трения. Все диапазоны частот статистически значимы для оценки трибологических характеристик исследуемой фрикционно-механической системы.
Кроме того, расчетное значение критерия Стьюдента в ячейке 1549 максимально. Приходим к выводу, что для исследуемой фрикционно-механической системы наиболее значимым является диапазон частот 44,7-89,1 Гц, так как корреляционная связь между коэффициентом трения и диссипацией энергии максимально (коэффициент корреляции Пирсона в ячейке 1548 также максимален).
Идентификация упруго-диссипативных характеристик
Не менее важным фактором идентификации трибосистем является установление связи упругих, инерционных и диссипативных составляющих фрикционного взаимодействия. Другими словами, соотношение кинетической и потенциальной энергии фрикционно-механической системы.
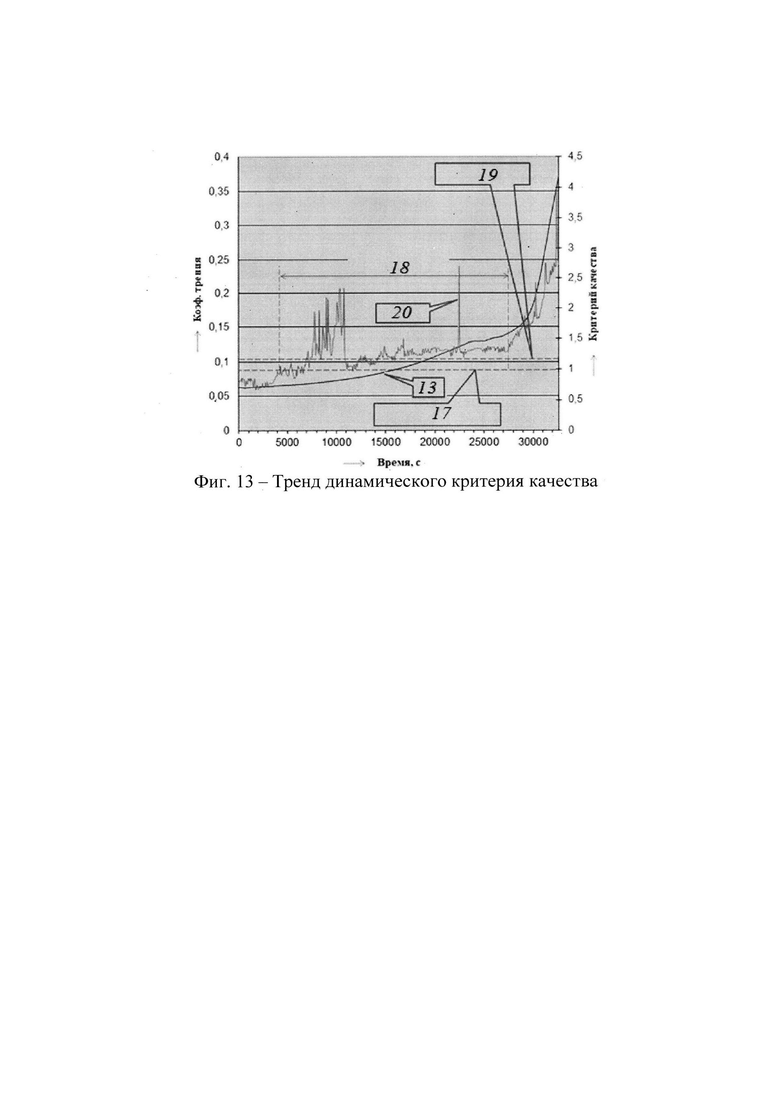
Для этого в программе «Трибоспектральная идентификация» выполнен октавный (треть-октавный или 12-октавный) анализ безразмерного коэффициента демпфирования, табличные данные сохранены во вкладке Коэффициент демпфирования в октавных диапазонах Microsoft Excel, а их графическое отображение - во вкладке Октавный анализ коэффициент демпфирования (Фиг. 11).
Как нами было показано ранее в п. 1.1, высокий уровень относительной ошибки (δ=109%) тангенциальной составляющей Y позволил нам установить, что исследуемые трибологические процессы характеризуются двумя или более временными периодами.
Действительно, в момент времени t1 наблюдаем переход от стационарных уровней коэффициента трения (малого изменения его градиента) к его динамическому возрастанию. Несмотря на довольно низкий уровень коэффициента трения 0,07 фиксируем в диапазоне частот 177,8-354,8 Гц значительное снижение безразмерного коэффициента демпфирования от 0,45 до 0,35. Во фрикционном контакте повышается колебательность контактирующих поверхностей, а логарифмический декремент колебаний δ (30) и коэффициента затухания n (32) снижаются.
В момент времени t2 наблюдаем в диапазоне частот 89,1-177,8 Гц аналогичное поведение фрикционно-механической системы: безразмерный коэффициент демпфирования ξ снижается с 0,35 до 0,12 (почти в три раза), что обусловливает значительное возрастание градиента коэффициента трения. Величина коэффициента трения достигает уровня 0,12 - граничного трения.
В зоне трения появляются ювенильные участки трения, что вызывает образование локальных мостиков схватывания поверхностей и повышение контактных температур (14 на Фиг. 11).
Динамическая нестабильность фрикционно-механической системы, значительный уровень контактных напряжений и температуры в момент времени t3 вызывает очередное снижение коэффициента демпфирования уже диапазоне высоких частот колебаний 354,8-500 Гц. За счет возрастания коэффициента трения в диапазоне низких частот 89,1-177,8 Гц коэффициент трения на не продолжительный период времени стабилизируется на стационарном уровне 0,13.
Однако, последующие моменты времени и повторного атермического схватывания (14 на Фиг. 11) вызывают значительные фрикционные автоколебания, а последующий резонанс активных объемов в момент времени t5 провоцирует уже термическое схватывание и лавинообразное возрастание коэффициента трения до 0,35.
Таким образом, наиболее информативными диапазонами частот оказались среднегеометрические частоты октавного анализа 66,9; 133,4; 266,3 и 531,4 Гц. Использование треть-октавного или 12-октавного анализа позволяет более точно идентифицировать указанные здесь диапазоны частот и, следовательно, с большей точностью идентифицировать:
- трибологические характеристики смазочного материала;
- износ зубьев шлицевого соединения;
- появление зазора в трибо-сопряжениях;
и огромное количество других причин, снижающих эксплуатационный ресурс и надежность системы.
Оценка стабильности фрикционных связей
Как было сказано ранее, стабильность фрикционных связей может быть оценена с помощью критерия энергетических потерь (38), который представлен на Фиг. 12, где 15 - энергетические потери; 16 - отсутствие стабильности фрикционной связи.
Видно, что после 4000 секунды наблюдений математическое ожидание критерия начинает меняться, а после 8000 с. среднее квадратичное отклонение критерия приобретает значительные выбросы, что обусловлено нестабильностью трибологических процессов, характеризуемых граничным трением.
Анализ динамического критерия качества
Аналогичные результаты мониторинга фрикционно-механической системы получены на основе анализа во времени динамического критерия качества. Результаты вычислений динамического критерия качества приводятся во вкладке Критерий качества Excel (Фиг 13), где 17 - порог, предупреждения; 18 - остаточный ресурс; 19 - порог опасности; 20 - критерий качества.
Как ранее нами было определено, порог «предупреждения» соответствует динамическому критерию качества, равным 1, а «опасности» - 1,15. Изобразим на графике пороги «предупреждения» и «опасности» горизонтальными линиями.
Сопоставляя момент времени t1 (см. Фиг 11) идентификации трибологических процессов во фрикционном контакте с тем же моментом времени тренда динамического критерия качества (Фиг. 13), видим, что стационарный процесс трения (до момента времени t1) характеризуется значениями динамического критерия качества в диапазоне 0,6…0,95.
На 4000 секунде наблюдений коэффициент демпфирования фрикционных связей в диапазоне частот 177,8-354,8 Гц снижается от 0,45 до 0,35 (см. Фиг. 6), а динамический критерий качества варьируется в диапазоне значений 1±0,05. Значительное снижение демпфирующих свойств гипоидной смазки до уровня ξ=0,35 вызывает на 7000 секунде наблюдений значительные вариации динамических характеристик; динамический критерий качества превышает порог «ОПАСНОСТИ» и варьируется в диапазоне значений от 1,15 до 2,2.
На 11000 секунде наблюдений наблюдаем некоторую стабилизацию динамического критерия (36) в районе 1,1±0,05, что обусловлено некоторым возрастанием коэффициента демпфирования в диапазоне частот 177,8-354,8 Гц с 0,3 до 0,4 за счет формирования некоторой равновесной шероховатости контактирующих поверхностей. Однако, этого улучшения не достаточно для стабилизации процессов трения.
На 14000 секунде наблюдений тренд динамического критерия качества очередной раз превышает порог «ОПАСНОСТИ» и больше не снижается.
Здесь мы также наблюдаем, что на 22500 секунде эксперимента фиксируется значительный пик-фактор πξ=(2,7-1,25)/(1,34-1,2)=10,4 динамического критерия качества до величины, что обусловлено значительным снижением коэффициента демпфирования до 0,09 (14 на Фиг. 11) и формированием атермического схватывания.
Проведя ряд исследований, мы установили, что мониторинг динамического критерия качества (36) фрикционно-механической системы совместно с анализом тренда безразмерного коэффициента демпфирования (17) позволяют идентифицировать не только трибологические характеристики смазочного материала, износ зубьев шлицевого соединения и др., но и приблизительно оценить остаточный ресурс работы (Фиг. 14) до наступления аномальных условий контактирования.
Литература
1. Авторское свидетельство СССР №1610402, кл. G01N 3/56, 1988.
2. Патент РФ №2343450, кл. G01N 3/56, 2006.
3. Патент РФ №2517946, кл. G01N 3/56, 2012.
4. Озябкин, А.Л. Теоретические основы динамического мониторинга фрикционных мобильных систем // Трение и смазка в машинах и механизмах. - 2011. - №10. - С. 17-28.
5. Сергиенко, А.Б. Цифровая обработка сигналов / А.Б. Сергиенко; - СПб.: Питер, 2003. - 604 с.
6. Колесников, В.И. Транспортная триботехника (трибомеханика): учеб. пособие / В.И. Колесников, В.Л. Заковоротный, В.В. Шаповалов. В 2-х томах. Т. II; Рост. гос. ун-т путей сообщения. - Ростов н/Д, 2006. - 478 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ВЫСОКОМОБИЛЬНЫХ НЕЛИНЕЙНЫХ ТЕХНИЧЕСКИХ СИСТЕМ | 2020 |
|
RU2745382C1 |
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ФРИКЦИОННЫХ МОБИЛЬНЫХ СИСТЕМ | 2012 |
|
RU2517946C2 |
| ДИНАМИЧЕСКИЙ МОНИТОРИНГ УЗЛОВ ТРЕНИЯ МОБИЛЬНЫХ ТЕХНИЧЕСКИХ СИСТЕМ | 2020 |
|
RU2748933C1 |
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| СПОСОБ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ФРИКЦИОННЫХ СИСТЕМ | 2016 |
|
RU2674899C1 |
| СПОСОБ ПОДБОРА СПОРТИВНОГО ИНВЕНТАРЯ С УЧЕТОМ РЕОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СНЕЖНОЙ ТРАССЫ | 2019 |
|
RU2706243C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ДИССИПАТИВНЫХ ХАРАКТЕРИСТИК ПОДШИПНИКОВ | 2005 |
|
RU2284019C1 |
| СПОСОБ ОЦЕНИВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ПОДШИПНИКОВ | 2009 |
|
RU2407999C1 |
| СПОСОБ ОЦЕНКИ ВНЕШНИХ И ВНУТРЕННИХ ПАРАМЕТРОВ УЗЛОВ ТРЕНИЯ ПРИ ИСПЫТАНИИ В СТЕНДОВЫХ УСЛОВИЯХ | 2015 |
|
RU2647338C2 |
| СПОСОБ УПРАВЛЕНИЯ И ИЗМЕНЕНИЯ ДИНАМИЧЕСКОГО СОСТОЯНИЯ ВИБРОЗАЩИТНОЙ СИСТЕМЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2018 |
|
RU2696062C1 |

Настоящее изобретение относится к способам динамического мониторинга мобильных нелинейных технических систем (МНТС). Способ заключается в контроле процессов трения и изнашивания путем анализа нормальной и тангенциальной составляющих сил фрикционного взаимодействия, их взаимного спектра и автотрибоспектра нормальной составляющей, а также их отношения в форме комплексного коэффициента передачи или амплитудофазочастотной характеристики. Отличительной особенностью способа является то, что основе критериев качества традиционной теории автоматического регулирования для каждого момента времени вычисляются предельно допустимые уровни физических величин параметров, а на их основе реализуются: а) наблюдение за изменением тренда критерия диссипативных потерь энергии IQ во времени в октавных (долеоктавных) диапазонах частот, что позволяет установить их корреляционную связь с заданным уровнем вероятности и характером изменения трибологических параметров (например, изменения градиента коэффициента трения) и на этой основе идентифицировать наиболее коррелируемые диапазоны частот, на которых проявляются трибологические свойства фрикционного контакта, а также изменение трибологических параметров и внешних факторов (например, изменений вязкости смазочного материала, понижения температуры окружающего воздуха, появления износа или атермических / термических мостиков схватывания); б) наблюдение за изменением тренда безразмерной интегральной величины коэффициента демпфирования Iξ в октавных (долеоктавных) диапазонах частот и выделение наиболее коррелируемых k-информативных диапазонов частот трибоспектральных характеристик с k-трибологическими параметрами и внешними факторами фрикционного взаимодействия (например, изменением вязкости смазочного материала, понижением температуры окружающего воздуха, появлением износа, фреттинг-коррозии или атермических / термических мостиков схватывания), что позволяет с заданной вероятностью (0,95) идентифицировать моменты времени ухудшения упруго-диссипативных характеристик фрикционно-механической системы и на этой основе прогнозировать последующее поведение системы и остаточный ресурс работы модельного или натурного узла трения n-массной ФММ; в) наблюдение за изменением тренда критерия энергетических потерь IE позволяет идентифицировать стабильность фрикционных связей в реальном времени функционирования узла трения; г) мониторинг фрикционно-механической системы во времени по обобщенному, критерию динамики Iд фрикционно-механической системы, и его пороговым значением «предупреждения» - величины «1» и «опасности» - «1,15». Технический результат - повышение точности результатов модельных и натурных испытаний и определения выходных параметров натурной МНТС и ее физической модели. 3 табл., 13 ил.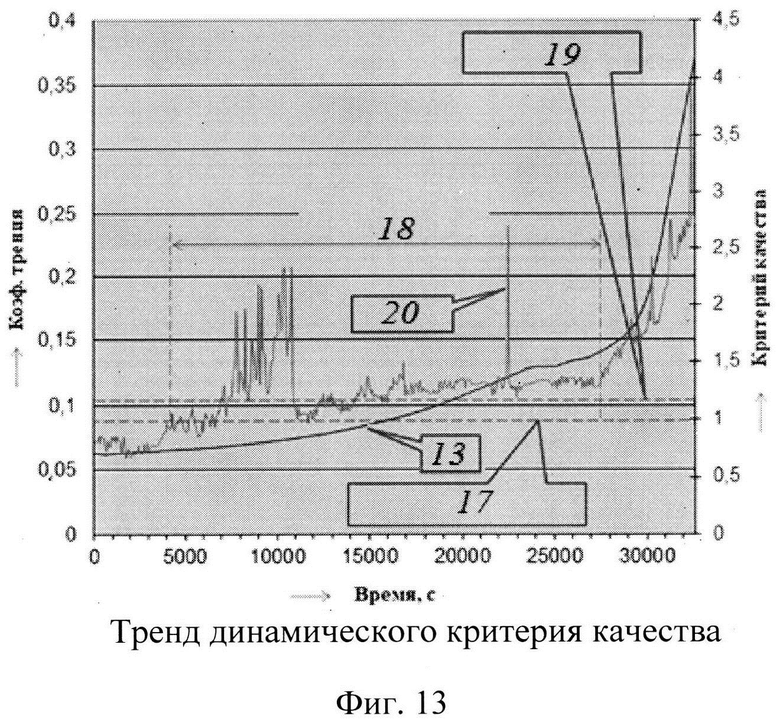
Способ динамического мониторинга мобильных нелинейных технических систем (МНТС), заключающийся в контроле процессов трения и изнашивания путем анализа нормальной и тангенциальной составляющих сил фрикционного взаимодействия, их взаимного спектра и автотрибоспектра нормальной составляющей, а также их отношения в форме комплексного коэффициента передачи или амплитудофазочастотной характеристики, с учетом, что диагностика текущего состояния фрикционного контакта и краткосрочное или долгосрочное прогнозирование его изменения выполняется на основании базы интегральных оценок как на всем частотном, диапазоне регистрации амплитудо-фазочастотных характеристик трибосистемы, так и на заданных октавных (1/3, 1/12, 1/24 - долеоктавных) диапазонах частот, либо заданных частотных диапазонах, охватывающих те или иные собственные частоты механической системы, полученных при испытаниях физико-механических моделей реального объекта исследования в лабораторных условиях, обеспечивающих идентичность динамических характеристик механических и фрикционных подсистем объекта и модели, а изменение указанных оценок на заданную величину пик-фактора (пикового значения отклонения оценки от математического ожидания к ее среднеквадратическому отклонению) определяет чувствительность систем автоматического управления (САУ) трибосистемой или систем автоматического регулирования (САР) параметрами трибосистемы и служит идентификационным признаком перехода из одного стационарного состояния в другое, в частности потери стабильности фрикционных связей, переходом от упругих деформаций к пластическим, к атермическому или термическому схватыванию активных микрообъемов поверхностей трения на фактической площади касания, отличающийся тем, что на основе критериев качества традиционной теории автоматического регулирования для каждого момента времени вычисляются предельно допустимые уровни физических величин параметров, а на их основе реализуются:
а) наблюдение за изменением тренда критерия диссипативных потерь энергии IQ во времени в октавных (долеоктавных) диапазонах частот, что позволяет установить их корреляционную связь с заданным уровнем вероятности и характером изменения трибологических параметров (например, изменения градиента коэффициента трения) и на этой основе идентифицировать наиболее коррелируемые диапазоны частот, на которых проявляются трибологические свойства фрикционного контакта, а также изменения трибологических параметров и внешних факторов (например, изменений вязкости смазочного материала, понижения температуры окружающего воздуха, появления износа или атермических / термических мостиков схватывания);
б) наблюдение за изменением тренда безразмерной интегральной величины коэффициента демпфирования Iξ в октавных (долеоктавных) диапазонах частот и выделение наиболее коррелируемых k-информативных диапазонов частот трибоспектральных характеристик с k-трибологическими параметрами и внешними факторами фрикционного взаимодействия (например, изменением вязкости смазочного материала, понижением температуры окружающего воздуха, появлением износа, фреттинг-коррозии или атермических / термических мостиков схватывания), что позволяет с заданной вероятностью (0,95) идентифицировать моменты времени ухудшения упруго-диссипативных характеристик фрикционно-механической системы и на этой основе прогнозировать последующее поведение системы и остаточный ресурс работы модельного или натурного узла трения n-массной. ФММ;
в) наблюдение за изменением тренда критерия энергетических потерь IE позволяет идентифицировать стабильность фрикционных связей в реальном времени функционирования узла трения;
г) мониторинг фрикционно-механической системы во времени по обобщенному критерию динамики Iд фрикционно-механической системы, и его пороговыми значениями «предупреждения» - величины «1» и «опасности» - «1,15».
| Озябкин, А.Л | |||
| Теоретические основы динамического мониторинга фрикционных мобильных систем // Трение и смазка в машинах и механизмах | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| - С | |||
| Печь для сжигания твердых и жидких нечистот | 1920 |
|
SU17A1 |
| СПОСОБ ДИНАМИЧЕСКОГО МОНИТОРИНГА ФРИКЦИОННЫХ МОБИЛЬНЫХ СИСТЕМ | 2012 |
|
RU2517946C2 |
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| Способ определения триботехнических характеристик пары трения | 1988 |
|
SU1610402A1 |
| US 5996395 A1, 07.12.1999. | |||
Авторы
Даты
2021-04-05—Публикация
2020-03-19—Подача