ПРЕДПОСЫЛКИ СОЗДАНИЯ ИЗОБРЕТЕНИЯ
Область техники
Настоящее изобретение относится к области технологий добычи угля и, в частности, к методу дискретных элементов для имитации развития разлома в породе, окружающей штрек.
Описание связанного уровня техники
Устойчивость угольного целика всегда находится в фокусе исследований безопасной и эффективной добычи. По мере увеличения глубины добычи и усложнения геологических условий, в ходе проходки штрека со стороны выработанной породы могут происходить сильные деформации и из выработанного участка может сочиться газ, ухудшая контроль породы, окружающей штрек. Ненадлежащая зарезервированная ширина угольного целика, а также неясное понимание механизмов разрушения угольного целика и окружающей породы, не позволяют предложить меру контроля, которая была бы эффективной для длительной, сильно воздействующей, безопасной и эффективной добычи угольных ресурсов.
Метод численного моделирования обладает очевидными преимуществами при решении проблем при инженерно-технических работах и в основном он включает метод конечных элементов и метод дискретных элементов. Численная модель конечных элементов может имитировать процесс разрушения породной массы и в явной форме имитировать расширение и развитие раскола, что делает ее широко применимой при решении подземных геотехнических проблем. Модель «UDEC Trigon», которая является непостоянной моделью, дополнительно усовершенствованной полигоном Вороного-Тиссена, формируется из блоков и сочленения. Повреждение сочленения между блоками возникает при различных нагрузках, и первичные разломы и вновь образованные разломы явным образом могут быть отличены друг от друга, так что имитация процесса развития разлома в породе, окружающей штрек, может быть реалистичной.
Существующие метод и технология численной имитации обладают следующими недостатками при имитации деформации штрека: Механические параметры, измеряемые в лабораторных условиях, выбираются непосредственно в качестве механических параметров породной массы для модели и применяются в численной модели. Однако образцы, используемые в лабораторных условиях, в целом являются малыми. Образцы, сформированные после использования и резки породной массы, меняют свое внутреннее напряжение и структуру в ходе этого процесса, и, следовательно, сильно отличаются от породной массы. Существующие метод и технология численной имитации оставляют без внимания разницу между породной массой и интактной породой, что приводит к сильному отклонению конечного результата от реальной ситуации на месторождении. Таким образом, существующие метод и технология не могут напрямую зависеть от работ на месторождении.
РАСКРЫТИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Задача настоящего изобретения заключается в представлении метода дискретных элементов для моделирования развития разлома в породе, окружающей штрек, который мог бы эффективно и реалистично воспроизводить условия на месторождении, а также получать реалистичные и достоверные результаты имитации.
Для решения указанной выше задачи, в настоящем изобретении используется метод дискретных элементов для имитации развития разлома в породе, окружающей штрек, включающий следующие этапы:
S1: в тестовом штреке, наблюдение за характеристиками деформации штрека и взятие колонок породы из угольного пласта и породной массы; запись характеристик деформации породы, окружающей штрек, и слежение за характеристиками распространения разломов в кровле и двух стенках штрека; и взятие колонок породы из кровли и угольного пласта, и запись значений RQD у колонок породы из кровли и колонок породы из угольного пласта;
S2: составление полученных по отдельности колонок породы из кровли и колонок породы из угольного пласта в стандартную интактную породу и выполнение экспериментов в отношении механических свойств для испытания интактных пород на прочность при одноосном сжатии, прочность на растяжение по бразильскому методу и модуль упругости; и, в соответствии с функциональной взаимосвязью между соотношением модуля упругости породной массы к таковому интактной породы и RQD, а также функциональной взаимосвязи между прочностью при одноосном сжатии породной массы и таковой интактной породы, определение прочности при одноосном сжатии и модуля упругости породной массы, причем прочность на растяжение породной массы по бразильскому методу составляет 0,1 от ее прочности при одноосном сжатии;
S3: создание калибровочной модели путем использования Trigon-логики в UDEC, причем среднее значение длин боковых сторон треугольных блоков в модели определяют в соответствии с характеристиками распространения разлома, статистически проанализированными на этапе S1; путем использования прочности при одноосном сжатии, прочности на растяжение по бразильскому методу и модуля упругости породной массы, вычисленных на этапе S2, в качестве известных характеристических значений, выполнение инверсии с калибровочной моделью для получения параметров треугольного блока и общих параметров в модели коррекции;
S4: создание численной модели с масштабом добычи рабочей поверхности месторождения путем использования UDEC, определение исследуемой области и разделение исследуемой области на треугольные блоки путем использования Trigon-логики, причем среднее значение длин краев треугольных блоков и параметры треугольного блока идентичны таковым в калибровочной модели на этапе S3; формирование прямоугольных блоков с постоянно возрастающей длиной путем разделения на области за пределами исследуемой области; и, основываясь на характеристиках деформации породы, окружающей штрек, и характеристиках распространения разлома, которые наблюдали на этапе S1, выполнение инверсии для получения механических параметров прямоугольных блоков в модели масштаба месторождения.
В соответствии с некоторыми вариантами реализации настоящего изобретения, параметры треугольного блока и общие параметры в калибровочной модели, которые получены посредством инверсии на этапе S3, соответственно, включают размер и модуль упругости треугольного блока, а также нормальную жесткость, жесткость на сдвиг, когезию, угол трения и прочность на растяжение сочленения; и способ инверсии, в частности, включает:
a) создание по отдельности прямоугольной калибровочной модели шириной 2 м и высотой 4 м, и круглой калибровочной модели с диаметром 2 м, причем среднее значение значений длины боковой стороны треугольных блоков гарантировано согласуется с длиной разлома на основе статистических данных месторождения;
b) настройку модуля упругости треугольных блоков в модели таким образом, чтобы они равнялись таковому у породной массы, вычисленному по формуле (II):
c) выведение нормальной жесткости Kn сочленения между треугольными блоками по формуле (IV), соотношение жесткости на сдвиг Ks к Kn составляет 0,2; и определение коэффициента Пуассона µ в соответствии с изменением Ks/Kn, причем формула (IV), в частности, является следующей:
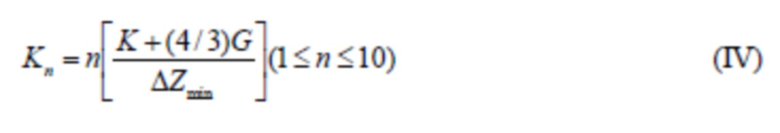
где K и G, соответственно, представляют собой объемный модуль и модуль сдвига треугольных блоков в ГПа и вычисляются согласно уравнениям K=E/3(l-2μ) и G=E/2(1+μ), μ представляет собой коэффициент Пуассона блока, а E представляет собой модуль упругости блока в ГПа; ΔZmin представляет собой минимальную ширину соседних блоков в вертикальном направлении в м; а n равняется 10; и
d) выполнение испытания прочности при одноосном сжатии и испытания раскалывания по бразильскому методу несколько раз путем использования калибровочной модели для получения кривых напряжение-деформация; применение средства итеративного метода проб и ошибок для обеспечения того, чтобы имитированные механические параметры соответствовали прочности при одноосном сжатии, прочности на растяжение по бразильскому методу и модулю упругости породной массы, вычисленным на этапе S2; и конечное выполнение инверсии для получения когезии, угла трения и прочности на растяжения сочленения в модели.
В соответствии с некоторыми вариантами реализации, на этапе S1 устанавливают станцию измерения смещения поверхности штрека посредством перекрестной схемы, характеристики деформации породы, окружающей штрек, записывают с помощью взрывоустойчивой камеры, характеристики распространения разломов в кровле и двух стенках штрека отслеживают с помощью инструмента для наблюдения за бурением, и характеристики распространения значений длины разломов в поверхности буровой скважины подвергают количественной оценке посредством прорисовки бурения.
В соответствии с некоторыми вариантами реализации настоящего изобретения, RQD на этапе S1 представляет собой показатель нарушенности породы, который выражается следующим специальным уравнением:

где l представляет собой совокупную длину колонок породы в м, которая больше или равна 10 см; а L представляет собой общую длину буровой скважины.
В соответствии с некоторыми вариантами реализации настоящего изобретения, на этапе S2 функциональная взаимосвязь между соотношением модуля упругости породной массы к таковой у блока породы и RQD выражается следующим специальным уравнением:

где Em представляет собой модуль упругости породной массы в ГПа; а Er представляет собой модуль упругости интактной породы в ГПа.
В соответствии с некоторыми вариантами реализации настоящего изобретения, на этапе S2 функциональная взаимосвязь между прочностью при одноосном сжатии породной массы и таковой у интактной породы выражается следующим специальным уравнением:

где σcm и σc представляют собой прочность при одноосном сжатии породной массы и таковой у интактной породы, соответственно, в МПа; а m равняется 0,63.
Полезный эффект
Настоящее изобретение имеет следующие преимущественные технические эффекты: Ввиду отличий между породной массы и интактной породой, механические параметры породной массы вычисляются в соответствии с функциональной взаимосвязью между показателем нарушенности породы RQD и соотношением модуля упругости породной массы к таковой у интактной породы, а также в соответствии с функциональной взаимосвязью между прочностью при одноосном сжатии породной массы и таковой у интактной породы, создается калибровочная модель путем использования Trigon-логики в UDEC и выполняется инверсия для получения параметров породной массы для численной вычислительной модели, что обеспечивает возможность реалистичной и достоверной имитации характеристик деформации штрека в месторождении. Таким образом, способ коррекции параметров для имитации деформации штрека методом дискретных элементов, предложенный в настоящем изобретении, преодолевает существующую проблему, заключающуюся в трудности определения параметров для численной имитации, а также может реалистично воспроизводить ситуации в месторождении, что обеспечивает реалистичность и достоверность результатов имитации. Таким образом, настоящее изобретение гарантирует в определенной степени безопасную и эффективную добычу и может быть использовано для обеспечения руководств при операциях в месторождении.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
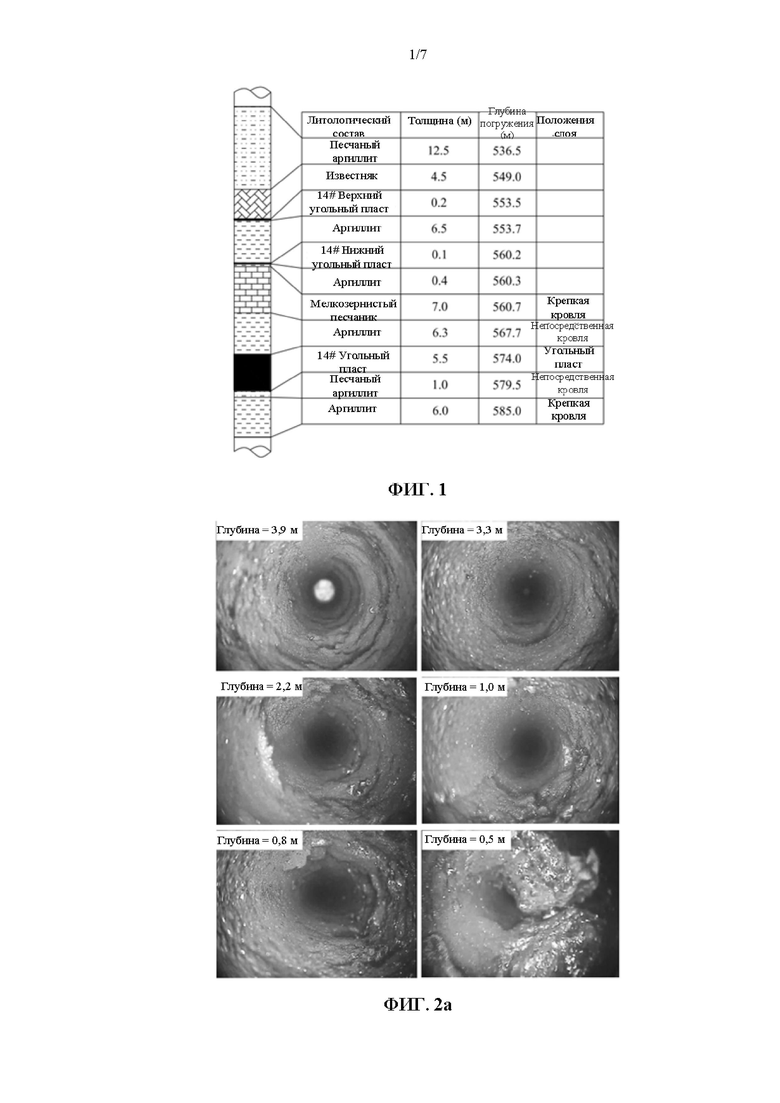
На ФИГ. 1 показана общая стратиграфическая колонка испытательной площадки;
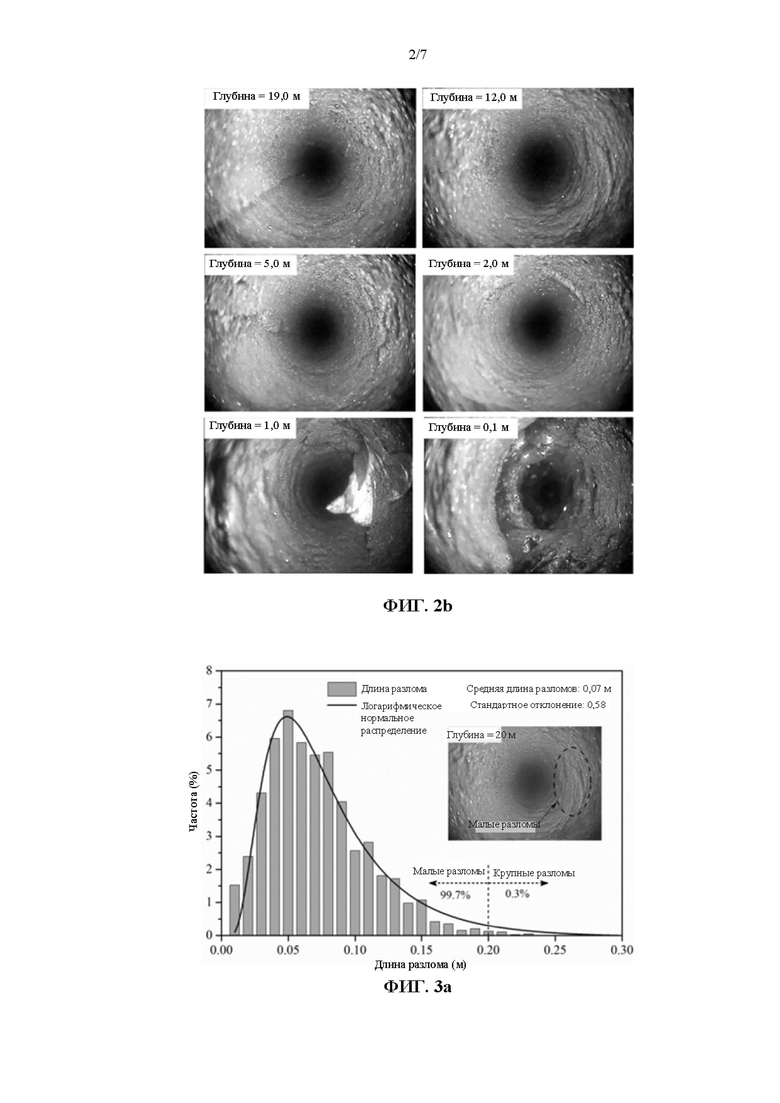
На ФИГ. 2a показаны характеристики распространения разлома на стенке угольного целика;
На ФИГ. 2b показаны характеристики распространения разлома на стенке неподработанного угольного пласта;
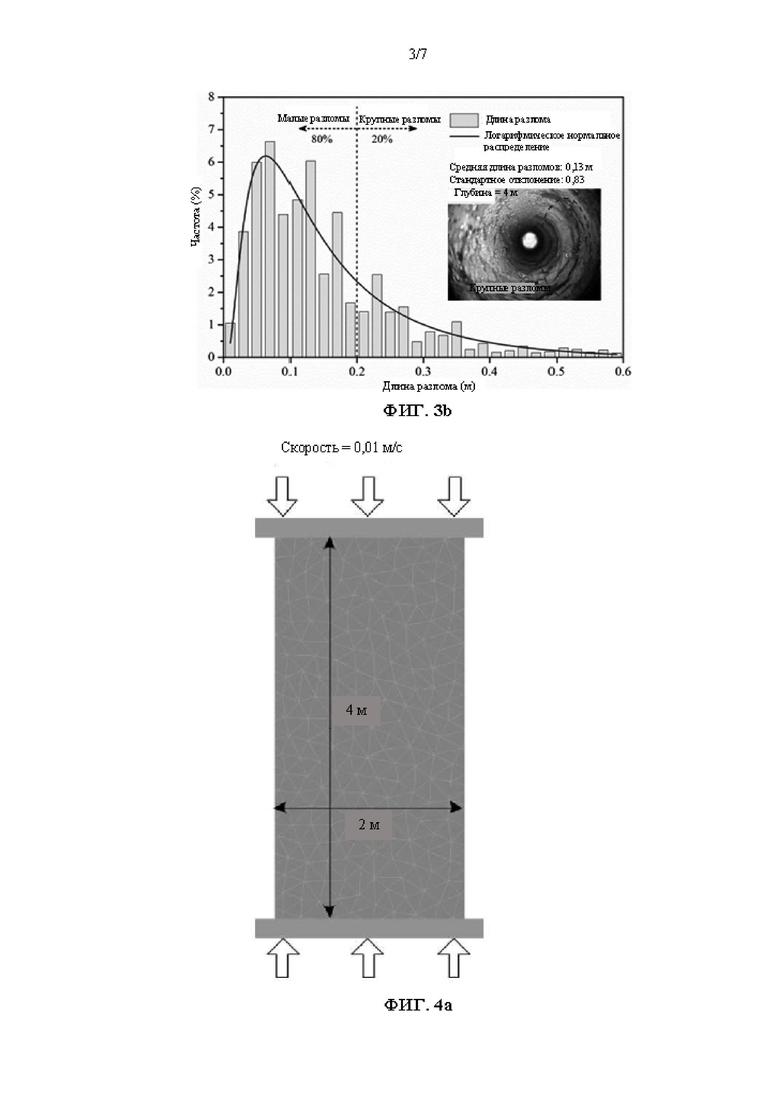
На ФИГ. 3a представлено вероятностное распределение длины разломов в угольном целике;
На ФИГ. 3b представлено вероятностное распределение длины разломов в неподработанном угольном пласте;
На ФИГ. 4a показана калибровочная модель для испытания прочности при одноосном сжатии;
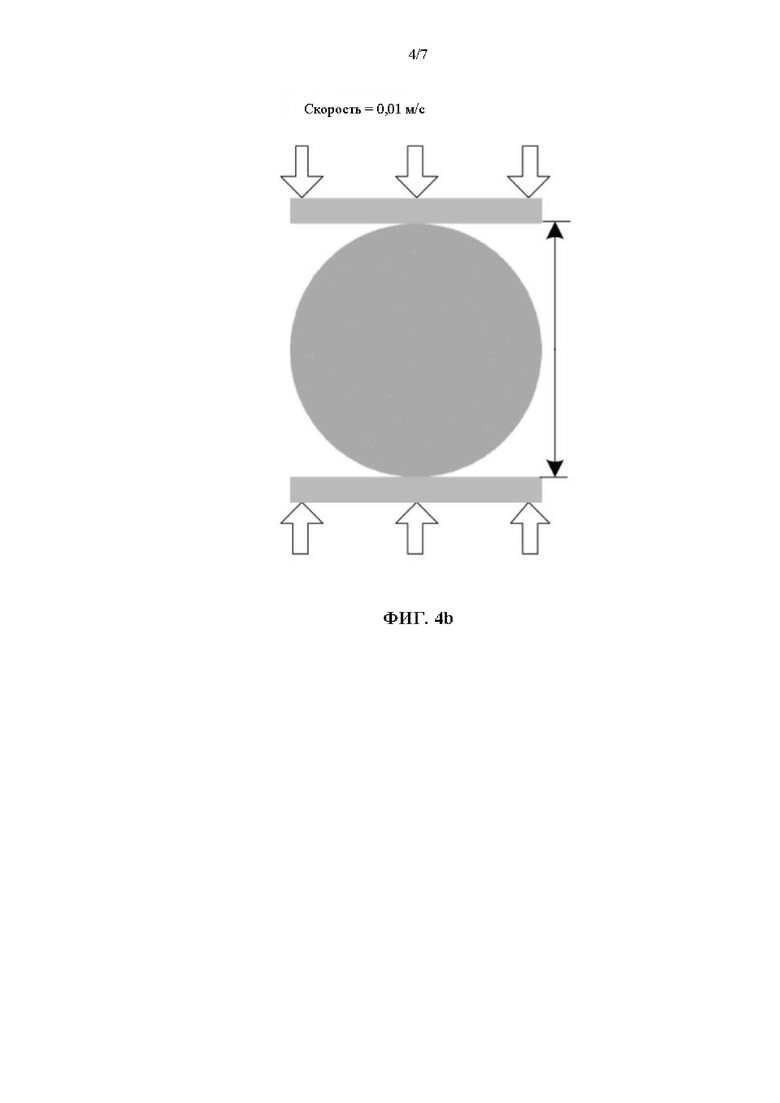
На ФИГ. 4b показана калибровочная модель для испытания прочности на растяжение по бразильскому методу;
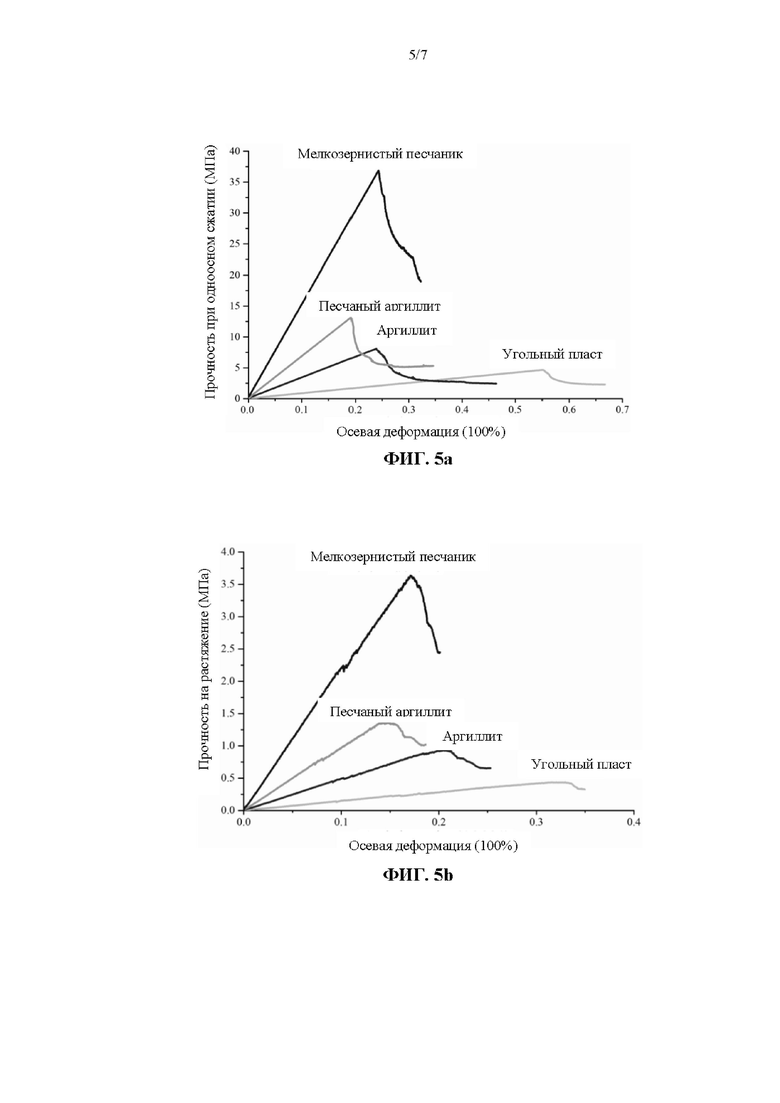
На ФИГ. 5a показана кривая напряжение-деформация в отношении одноосного сжатия по калибровочной модели;
На ФИГ. 5b показана кривая напряжение-деформация в отношении испытания раскалывания по бразильскому методу по калибровочной модели;
На ФИГ. 6 показана численная модель состояния месторождения;
На ФИГ. 7 представлена диаграмма, показывающая сравнение между деформацией штрека при численной имитации и наблюдениями на месторождении;
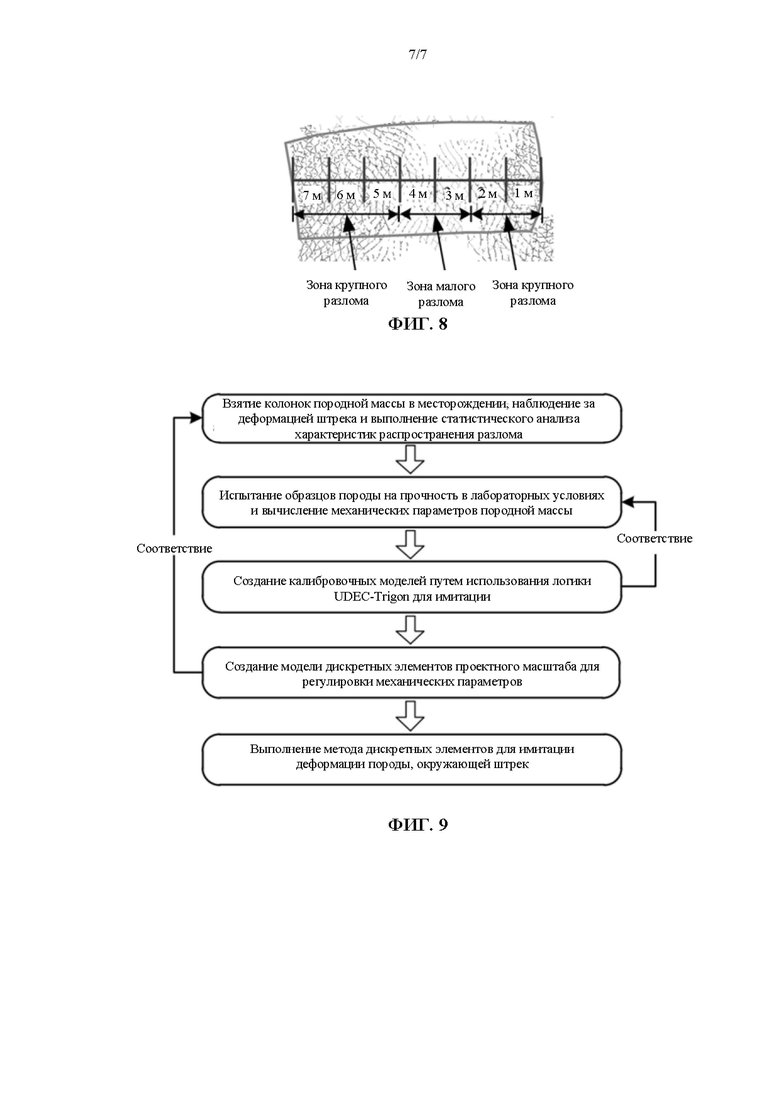
На ФИГ. 8 показано распространение разломов в угольном целике шириной 7 м после имитации; и
На ФИГ. 9 показана блок-схема метода дискретных элементов для моделирования развития разлома в породе, окружающей штрек, в настоящем изобретении.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
Настоящее изобретение далее подробно описано ниже со ссылкой на сопроводительные чертежи и конкретный вариант реализации. Следует отметить, что представленные далее варианты реализации используются лишь в целях описания настоящего изобретения и не предназначены для ограничения настоящего изобретения.
В варианте реализации предусмотрена проходка штрека со стороны выработанной породы в узком угольном целике шириной 7 м в хвостовом штреке 15106 шахты «Sijiazhuang», относящейся к «Yangquan Coal Group», в качестве основы для инженерных работ. В данном случае, угольный пласт имеет среднюю глубину погружения 574 м и среднюю толщину 5,5 м, и развивающиеся в нем совместные разломы. Хвостовой штрек 15106 имеет общую длину 1700 м. Выемку штрека проводят вдоль кровли угольного пласта, и секция выемки представляет собой прямоугольник шириной 4,8 м × высотой 4,0 м Статиграфический разрез буровой скважины угольного пласта показан на ФИГ. 1. Способ, в соответствии с настоящим изобретением, используется здесь для коррекции параметров в численной модели для моделирования имитации деформации штрека. Метод дискретных элементов для имитации развития разлома в породе, окружающей штрек, в данном варианте реализации включает следующие несколько этапов:
1) Взятие образцов из цельной кровли и грунта в хвостовом штреке 15106, и запись значений RQD, соответствующих другому литологическому составу. Для изучения стенки узкого угольного целика и стенки однородного угля используют инструмент для наблюдения за бурением модели YTJ20, разработанный и произведенный Китайским горно-технологическим институтом (China University of Mining and Technology). Горизонтальное разведочное отверстие диаметром 29 мм выполняют на расстоянии 2 м до грунта. Буровое отверстие на глубине 4 м выполняют в боковой стороне угольного целика, а буровое отверстие на глубине 20 м выполняют в боковой стороне однородного угля. Характеристики распространения разломов на двух стенках, полученные путем наблюдения, показаны на ФИГ. 2a и ФИГ. 2b соответственно. Из ФИГ. 2a и ФИГ. 2b можно увидеть, что на стороне угольного целика выполнено множество кольцевых сквозных разломов и вертикальных разломов в пределах наблюдаемого спектра 4 м. Уголь, находящийся вблизи части стенки угольного целика, уже поврежден, образуя разрушенную зону и приводя к обрушению отверстия. Выработанный участок находится на другой стороне угольного целика и его нельзя увидеть с помощью инструмента для наблюдения за бурением. Однако, в соответствии с результатом наблюдения за бурением, можно сделать вывод, что степень повреждения угольного целика вблизи стороны выработанной породы, вероятно, будет подобна таковой у штрека или являться более серьезной. Таким образом, может быть определено, что в хвостовом штреке 15106 разломы разрабатываются внутри угольного целика после выемки штрека и весь угольный целик уже выработан. На стороне однородного угля, угольный пласт на расстоянии в пределах 1 м до стенки угля серьезно разрушен; имеется несколько разломов в пределах диапазона от 1 м до 2 м; а угольный пласт, находящийся глубже чем 2 м, остался без воздействия со стороны процесса добычи и является почти полностью целым без относительно крупных разломов.
Посредством прорисовки бурения выполняют статистический анализ значений длины разломов в угольном целике и однородном угле для получения результатов, показанных на ФИГ. 3a и ФИГ. 3b соответственно. Из ФИГ. 3a и ФИГ. 3B можно увидеть, что длина разломов в угольном целике и однородном угле удовлетворяет правилу логарифмически нормального распределения. Длина разломов в однородном угле составляет от 0,01 м до 0,23 м и имеет среднее значение 0,07 м, при этом разломы длиной менее 0,2 м составляют 99,7% от общего количества, а крупные разломы (длиной более 0,2 м) практически отсутствуют. Длина разломов в угольном целике составляет от 0,03 м до 0,59 м и имеет среднее значение 0,13 м, при этом разломы длиной менее 0,2 м составляют 80% от общего количества, а крупные разломы составляют 20% от общего количества. Путем сравнения ФИГ. 3a с 3b можно увидеть, что в однородном угле, который не был подвержен воздействию процесса добычи, отсутствуют крупные разломы, а 20% крупных разломов в угольном целике не являются изначальными разломами в естественном угле, а получились в результате повреждения, нанесенного в ходе формирования угольного целика. Эти крупные разломы не могут представлять собой естественные изначальные разломы. Таким образом, изначальные разломы в угольном пласте должны иметь длину менее 0,2 м для того, чтобы обеспечить базовые данные для построения калибровочной модели.
2) Из колонок породы, полученных на этапе 1), делают стандартные образцы, представляющие собой цилиндры диаметром 50 мм и высотой 100 мм, а также малые цилиндры диаметром 50 мм и толщиной 25 мм, а затем эти цилиндры подвергают испытанию прочности при одноосном сжатии и испытанию раскалывания по бразильскому методу для испытания образцов породы на прочность при одноосном сжатии, прочность на растяжение и модуль упругости. Прочность и модуль упругости породной массы вычисляют по формулам (II) и (III), причем прочность породной массы на растяжение составляет 0,1 от ее прочности при одноосном сжатии. Результаты испытаний показаны в таблице 1.
Таблица 1. Свойства интактной породы и вычисленной породной массы в угольной шахте «Sijiazhuang»
Er/ГПа
σc/МПа
Em/ГПа
σcm/МПа
σtm/МПа
Результаты испытания показывают, что породная масса и мелкая интактная порода имеют явное отличие в части механических параметров, при котором модуль упругости и прочность при одноосном сжатии понижены до разных степеней. Результаты также показывают, что включать механические параметры мелкой породы, измеренные в лабораторных условиях, в численную модель для вычисления неправильно, и требуется дополнительная коррекция для обеспечения соответствия параметров породной массы.
Функциональная взаимосвязь между соотношением модуля упругости породной массы к таковой у блока породы и RQD выражается следующим специальным уравнением:

В уравнении, Em представляет собой модуль упругости породной массы в ГПа; а Er представляет собой модуль упругости интактной породы в ГПа.
Функциональная взаимосвязь между прочностью при одноосном сжатии породной массы и таковой у интактной породы выражается следующим специальным уравнением:

В уравнении, σcm и σc, соответственно, представляют собой прочность при одноосном сжатии породной массы и таковой у интактной породы, в МПа, где m равняется 0,63.
3) Как показано на ФИГ. 4a, прямоугольная модель коррекции малого размера шириной 2 м и высотой 4 м создается путем использования Trigon-модуля в UDEC и используется для испытания прочности приодноосном сжатии. Как показано на ФИГ. 4b, круговая модель коррекции с диаметром 2 м создается для испытания раскалывания по бразильскому методу. Треугольники в модели имеют среднюю длину стороны 0,2 м, которая может представлять размер начальных разломов в угольном пласте перед нарушением, тем самым легко отличая вновь образованные разломы от начальных разломов.
Модели создаются для коррекции, соответственно, для четырех породных толщ с разным литологическим составом. Блоки в моделях выполнены упругими, то есть, блоки могут быть деформированы, но не повреждены. Модель состояния, основанная на остаточной прочности Мора-Кулона, используется для сочленений. Породная масса повреждается только вдоль поверхности сочленения, а макроразломы постепенно формируются после образования, расширения и проникновения микроразломов.
Плотность блока идентична фактической плотности породной массы и измеряется в лабораторных условиях. Модуль упругости блока идентичен вычисленному модулю упругости породной массы. Жесткость поверхности сочленения определяется согласно размеру блока в модели и соотношению Ks/Kn. Инверсия выполняется посредством итеративного метода проб и ошибок для получения когезии, угла трения и прочности на растяжение сочленения модели.
Путем использования моделей выполняется ряд испытаний прочности при одноосном сжатии и раскалывания по бразильскому методу для получения кривых напряжение-деформация для всего процесса, как показано на ФИГ. 5a и 5b.
Результаты имитации соответствуют механическим параметрам породной массы (прочности при одноосном сжатии, прочности на растяжение и модулю упругости), и в конечном итоге выполняют инверсию для получения механических параметров, используемых для модели, как показано в таблице 2. Согласно совместному критерию остаточной прочности, когезия и угол внутреннего трения сочленения снижаются до 0 после повреждения, оставляя лишь некоторый остаточный угол внутреннего трения.
Таблица 2. Откалиброванные микросвойства в Trigon-модели для модели состояния месторождения
Кг/м3
ГПа
ГПа/м
ГПа/м
МПа
(°) (Пиковый/Остаточный)
Откалиброванные результаты механических параметров показаны в таблице 3. Как видно из таблицы 3, все ошибки между откорректированными механическими параметрами и целевыми значениями составляют менее 10%, что доказывает достоверность такого способа коррекции параметров.
Таблица 3. Откалиброванные результаты свойств породной массы в Trigon-модели
(100%)
(МПа)
(100%)
(100
%)
4) В соответствии с геологическими условиями панели 15106, создается численная модель путем использования программного обеспечения UDEC для метода дискретных элементов, где модель имеет длину 150 м и высоту 58 м. Для улучшения эффективности вычислений, ключевая область исследования делится на треугольные блоки с помощью Trigon-модуля, как показано на ФИГ. 6. Треугольные блоки в зоне угольного целика имеют длины боковых сторон 0,2 м, таковые в зоне, окружающей угольный пласт, имеют длины боковых сторон 0,4 м, а таковые непосредственно в зонах кровли и грунта угольного пласта имеют длины боковых сторон 0,5 м. Прямоугольные блоки с постоянно увеличивающейся длиной образуются путем деления на области за пределами исследуемой области и имеют меняющиеся значения длины 1,1 м, 2 м и 7 м. Такой способ настройки размера блока может эффективным образом имитировать механическое поведение угольного целика.
Левая и правая границы модели фиксированы по горизонтали, нижняя граница фиксирована по вертикали, давление, эквивалентное перегрузу, применяется к верхней границе, а поле напряжения, измеренное на месте, применяется внутри модели. Значения параметров для модели задаются в соответствии с откорректированными параметрами в таблице 2. План выемки осуществляется в соответствии с фактическим порядком добычи. Сначала производится выемка рабочей поверхности 15108, а затем производится выемка хвостового штрека 15106 после балансировки посредством вычисления модели. Резервная ширина угольного целика составляет 7 м. Способ поддержания штрека имитируется в соответствии с фактическими параметрами поддержания. Основываясь на характеристиках деформации породы, окружающей штрек, и правилу распространения разлома, которые наблюдались на этапе 1), выполняют инверсию для получения механических параметров прямоугольных блоков в крупной модели.
На ФИГ. 7 показано сравнение между имитированной деформацией штрека и результатом наблюдения за месторождением. Из ФИГ. 7 можно увидеть, что штрек был серьезно поврежден в ходе выемки, схождение кровли к грунту составляет приблизительно 592 мм, а схождение стенки к стенке составляет 696 мм. Эти показатели согласуются с показателями деформации штрека (где схождение кровли к грунту составляет 540 мм, а схождение стенки к стенке составляет 645 мм, как показано на ФИГ. 7b), которые наблюдаются на расстоянии 610 м до входа в штрек. На ФИГ. 7c-7g показано сравнение в отношении форм повреждения между численной имитацией и наблюдением в месторождении. Результат сравнения предполагает, что после влияния со стороны напряжения при добыче, кровля просевших сторон штрека месторождения, две стенки сжимаются в направлении пространства штрека и происходит вспучивание кровли, что приводит к разлому стальной полосы кровли и деформации реек, пролегающих по грунту. Угольный целик имеет максимальную степень деформации, которая в основном имеет место на ее нижней половине; и прочно прижимает ленту для доставки угля. Все указанные выше повреждения формы штрека, наблюдаемые в ходе выемки на месторождении, могут быть реально зарегистрированы в Trigon-модели UDEC, как показано на ФИГ. 7f.
Путем имитации с помощью Trigon-модели UDEC, можно изучить распространение разлома в угольном целике шириной 7 м после выемки воздушного вентиляционного штрека 15106, как показано на ФИГ. 8. Угольный целик делится на зоны крупного разлома и зоны малого разлома в соответствии с распространением разлома. Из ФИГ. 8 можно увидеть, что зоны крупного разлома находятся на двух сторонах угольного целика. Разломы при растяжении развиваются практически до разрушения в пределах расстояния 2 м от штрека и расстояния 3 м до выработанного участка с образованием зон крупного разлома. Разломы при сдвиге развиваются в пределах расстояния от 3 м до 4 м до штрека с образованием зон малого разлома. Результаты имитации в высокой степени соответствуют результатам наблюдения при бурении на месторождении (ФИГ. 2a).
Путем проверки с помощью большой модели масштаба месторождения, указывается, что деформация штрека в месторождении может быть реалистичным образом имитирована путем включения откалиброванных параметров в Trigon-модель UDEC, а поведение давления в шахте, активируемое последующей выемкой на рабочей поверхности, может быть дополнительно прогнозировано путем использования откалиброванных параметров. Более того, доказано, что метод, согласно настоящему изобретению, обладает высокой степенью достоверности и имеет практическую значимость.

Представлен метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, который включает: взятие колонок породы из угольного пласта в месторождении и запись значений RQD, наблюдение за деформацией штрека и выполнение статистического анализа характеристик распространения разломов в угольном пласте; испытание механических параметров образцов угольной породы в помещении и вычисление прочности породной массы в соответствии со значениями RQD; создание численной модели путем использования модуля UDEC-Trigon для регулировки параметров для обеспечения соответствия прочности породной массы и коррекцию параметров модели; и создание численной модели проектного масштаба для регулировки параметров для обеспечения соответствия характеристикам деформации в месторождении, и, в конечном итоге, имитация развития разлома в породе, окружающей штрек. Технический результат – в настоящем изобретении обеспечены точные и базовые механические параметры для численной имитации деформации штрека на основе дискретных элементов, гарантирующей реалистичные и достоверные результаты имитации. 5 з.п. ф-лы, 9 ил.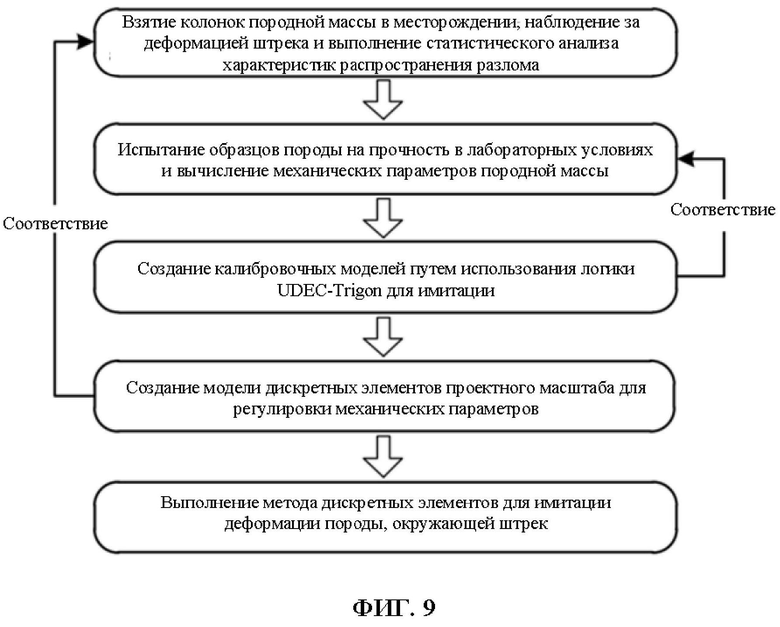
1. Метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, включающий следующие этапы:
S1: в тестовом штреке, наблюдение за характеристиками деформации штрека и взятие колонок породы из угольного пласта и породной массы; запись характеристик деформации породы, окружающей штрек, и слежение за характеристиками распространения разломов в кровле и двух стенках штрека; и взятие колонок породы из кровли и угольного пласта, и запись значений RQD у колонок породы из кровли и колонок породы из угольного пласта;
S2: составление полученных по отдельности колонок породы из кровли и колонок породы из угольного пласта в стандартную интактную породу и выполнение экспериментов в отношении механических свойств для испытания интактной породы на прочность при одноосном сжатии, прочность на растяжение и модуль упругости; и, в соответствии с функциональной взаимосвязью между соотношением модуля упругости породной массы к таковому интактной породы и RQD, а также функциональной взаимосвязи между прочностью при одноосном сжатии породной массы и таковой интактной породы, определение прочности при одноосном сжатии и модуля упругости породной массы, причем прочность на растяжение породной массы составляет 0,1 от ее прочности при одноосном сжатии;
S3: создание калибровочной модели путем использования Trigon-модуля в UDEC, причем среднее значение длин боковых сторон треугольных блоков в модели определяют в соответствии с характеристиками распространения разлома, статистически проанализированными на этапе S1; путем использования прочности при одноосном сжатии, прочности на растяжение и модуля упругости породной массы, вычисленных на этапе S2, в качестве известных характеристических значений, выполнение инверсии с калибровочной моделью для получения параметров треугольного блока и параметров поверхности сочленения в модели коррекции; и
S4: создание крупноразмерной численной модели с масштабом месторождения путем использования UDEC, определение исследуемой области и разделение исследуемой области на треугольные блоки путем использования Trigon-логики, причем среднее значение длин сторон треугольных блоков и параметры треугольного блока идентичны таковым в калибровочной модели на этапе S3; формирование прямоугольных блоков с постоянно возрастающей длиной путем разделения на области за пределами исследуемой области; и, основываясь на характеристиках деформации породы, окружающей штрек, и правиле распространения разлома, которые наблюдали на этапе S1, выполнение инверсии для получения механических параметров прямоугольных блоков в крупной модели.
2. Метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, по п. 1, отличающийся тем, что параметры треугольного блока и общие параметры в калибровочной модели, которые получены посредством инверсии на этапе S3, соответственно, содержат размер и модуль упругости треугольного блока, а также нормальную жесткость, жесткость на сдвиг, когезию, угол трения и прочность на растяжение сочленения; и способ инверсии, в частности, включает:
a) создание по отдельности прямоугольной калибровочной модели шириной 2 м и высотой 4 м, и круглой калибровочной модели с диаметром 2 м, причем среднее значение значений длины боковой стороны треугольных блоков гарантировано согласуется с длиной разлома на основе статистических данных месторождения;
b) настройку модуля упругости треугольных блоков в модели таким образом, чтобы они равнялись таковому у породной массы, вычисленному по формуле (II);
c) выведение нормальной жесткости Kn сочленения между треугольными блоками по формуле (IV), соотношение жесткости на сдвиг Ks к Kn составляет 0,2; и определение коэффициента Пуассона μ в соответствии с изменением Ks/Kn, причем формула (IV), в частности, является следующей:
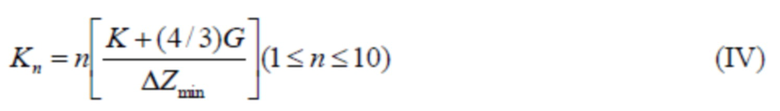
где K и G, соответственно, представляют собой объемный модуль и модуль сдвига треугольных блоков в ГПа и вычисляются согласно уравнениям K=E/3(l-2μ) и G=E/2(1+μ), μ представляет собой коэффициент Пуассона блока, а E представляет собой модуль упругости блока в ГПа; ΔZmin представляет собой минимальную ширину соседних блоков в вертикальном направлении в м; а n равняется 10; и
d) выполнение ряда испытаний прочности при одноосном сжатии и испытания раскалывания по бразильскому методу путем использования калибровочной модели для получения кривых напряжение-деформация; применение средства итеративного метода проб и ошибок для обеспечения того, чтобы имитированные механические параметры соответствовали прочности при одноосном сжатии, прочности на растяжение и модулю упругости породной массы, вычисленным на этапе S2; и конечное выполнение инверсии для получения когезии, угла внутреннего трения и прочности на растяжение сочленения в модели.
3. Метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, по п. 1 или 2, отличающийся тем, что на этапе S1 устанавливают станцию измерения смещения поверхности штрека посредством перекрестной схемы, характеристики деформации породы, окружающей штрек, записывают с помощью взрывоустойчивой камеры, характеристики распространения разломов в кровле и двух стенках штрека отслеживают с помощью инструмента для наблюдения за бурением, и правило распространения значений длины разломов в поверхности буровой скважины подвергают количественной оценке посредством прорисовки бурения.
4. Метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, по п. 3, отличающийся тем, что RQD на этапе S1 представляет собой показатель нарушенности породы, который выражается следующим специальным уравнением:

где l представляет собой совокупную длину колонок породы в м, которая больше или равна 10 см; а L представляет собой общую длину буровой скважины.
5. Метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, по п. 3, отличающийся тем, что на этапе S2 функциональная взаимосвязь между соотношением модуля упругости породной массы к таковой у интактной породы и RQD выражается следующим специальным уравнением:

где Em представляет собой модуль упругости породной массы в ГПа; а Er представляет собой модуль упругости интактной породы в ГПа.
6. Метод дискретных элементов для моделирования развития разлома в породе, окружающей штрек, по п. 3, отличающийся тем, что на этапе S2 функциональная взаимосвязь между прочностью породной массы при одноосном сжатии и таковой у интактной породы выражается следующим специальным уравнением:

где σcm и σc представляют собой прочность при одноосном сжатии породной массы и таковой у интактной породы, соответственно, в МПа; а m равняется 0,63.
| CN 109271738 A, 25.01.2019 | |||
| CN 105093349 A, 25.11.2015 | |||
| CN 106919770 A, 04.07.2017 | |||
| CN 108489809 A, 04.09.2018 | |||
| US 2017131192 A1, 11.05.2017. |
Авторы
Даты
2021-04-20—Публикация
2019-10-08—Подача