Область техники
Изобретение относится к области конструктивных элементов, сборных конструкций, состоящих из этих элементов. Более конкретно, к конструкциям, составленным из двух или более продолговатых элементов, скрепленных по кромкам, и предназначенных для прикрепления к подобным элементам в различных взаимных положениях. Изобретение может быть использовано в машиностроении, авиастроении, в строительстве и других отраслях промышленности.
Предшествующий уровень техники
Известна пространственная система структуры конструкции, описанная в патенте США №4,156,997, «Light weight tension-compression equilibrium structures)); МПК: F16S 3/00 (20060101); E04C 003/10; авторы: Decker, deceased; Bert J. (LATE OF Buffalo, NY), Decker, executrix; Jean S. (Buffalo, NY); приоритет: 14.07.1975, опубликовано 05.06.1979.
Легковесный, по существу плоский, структурный блок, который содержит не менее трех элементов сжатия в контакте друг с другом во внутренней части блока и множество натяжных элементов в контакте с такими элементами сжатия и оказывающими уравновешивание сил, действующих на элементы сжатия в плоскости структурного блока и удерживающих элементы сжатия в положении по отношению друг к другу укрепить их. Указанные участники напряженности производят силы сжатия в элементах сжатия, которые направлены в плоскости структурной единицы к точке контакта сжатия элементов во внутренней части плоскости структурного блока. Указанные силы, также сжимающие силы, приложенные к участникам сжатия, превышающие величину силы, обычно требуемой для скрепления указанных элементов сжатия. Элементы натяжения, распределены вдоль длины элементов сжатия таким образом, чтобы расстояния между растянутыми элементами вдоль элементов сжатия меньше длины, в которых одни только участники сжатия скрепили бы пряжкой под полными сжимающими силами.
Признаки, совпадающие с существенными признаками изобретения, структурный блок содержит не менее трех элементов в контакте друг с другом, уравновешивание сил, действующих на элементы.
Недостатком данного напряженно сжатого структурного блока можно считать зависимость целостности конструкции от целостности каждого единичного элемента. Разрушение любого из натяжных элементов или элементов сжатия приведет к разрушению структурного блока. Изготовление структурного блока требует предварительного изготовления натяжных элементов и элементов сжатия. Это усложняет и удорожает доставку элементов к месту сборки конструкции из структурных блоков.
В качестве прототипа для заявляемой плетёной пространственной конструкции был выбран легковесный напряженно сжатый структурный блок, описанный в патенте США №5,505,035, приоритет 24.06.1992; опубл. 09.04.1996 г.; МПК: Е04В 1/18; автор: Heresh Lalvani.
Пространственная система структуры конструкции заключается в том, что она содержит множество элементов соединенных множеством распорок, что узел вписан в неправильный - многогранник, многогранник включает интерьер и поверхность, указанная поверхность включает вершины, ребра и грани, где по крайней мере одна из сказанных граней - неправильный многоугольник, многоугольник имеющий по крайней мере два различных угла между указанными ребрами, и где сказано, что неправильный многогранник несимметричен правильному параллелепипеду и правильной призме, правильные параллелепипеды, и правильные призмы состоят только из правильных многоугольников, где узлы получены из указанных линий, линии соединены в точке, лежащей внутри многогранника, линии соединяют точку внутри многогранника и точки на гранях многогранника указанные линии являются распорками указанные ячейки соединены с распорками с возможностью сделать множество пространственных конфигураций.
Признаки, совпадающие с существенными признаками изобретения, пространственная система структуры содержит множество соединенных элементов, многогранник включает поверхность, поверхность включает вершины, ребра и грани, правильные призмы состоят только из правильных многоугольников.
Недостатком данной пространственной системы структуры конструкции является то обстоятельство, что единичные элементы выполнены только в прямолинейном виде. Сборка объемного тела из единичных элементов требует дополнительных крепежных узлов, материала и оборудования. Целостности конструкции зависит от целостности каждого единичного элемента. Разрушение любого из элементов приведет к разрушению структурного блока.
Раскрытие изобретения
Задачей, на решение которой направлено заявляемое изобретение, является повышение устойчивости пространственной конструкции, а при разрушении нескольких блоков в ее составе.
Технический результат, достигаемый при решении этой задачи, заключается в уравновешивании сил взаимодействия элементов в каждом структурном блоке пространственной конструкции.
Плетёная пространственная конструкция, содержащая узлы и линейные элементы, согласно изобретению, каждый линейный элемент выполнен конечной длины, и изогнут в пространстве с получением формы, соответствующей заранее рассчитанной математической модели с использованием теорий сплайнов. При этом изогнутый элемент представляет из себя кривой стержень. Кривые стержни переплетены друг с другом и связаны друг с другом с образованием плетёного многоугольника, с выходящими из него концами кривых стержней. Плетёные многоугольники соединены между собой связанными концами кривых стержней с образованием структурного блока в форме многогранника. Структурные блоки соединены между собой концами кривых стержней с образованием плетёной пространственной конструкции.
Во втором варианте плетёная пространственная конструкция содержащая узлы и линейные элементы, согласно изобретению, каждый линейный элемент выполнен конечной длины и изогнут в пространстве с получением формы, соответствующей заранее рассчитанной математической модели с использованием теорий сплайнов. При этом изогнутый элемент представляет из себя кривой стержень. Кривые стержни связаны друг с другом с образованием контура многоугольников, которые связаны между собой с образованием каркасного структурного блока. Каркасные структурные блоки связаны между собой концами кривых стержней с образованием плетёной пространственной конструкции.
Совокупность существенных признаков обеспечивает получение технического результата уравновешивание сил взаимодействия элементов в каждом структурном блоке и каркасном блоке, что позволяет решить задачу повышения устойчивости плетёной пространственной конструкции к разрушению при разрушении нескольких блоков в ее составе.
Каркасные структурные и структурные блоки могут быть соединены между собой концами кривых стержней, которые рассчитаны по математическим моделям на принципах тангенциального хода, «свободной геометрии» с использованием теорий сплайнов.
Каждый кривой стержень может быть рассчитан методами на принципах тангенциального хода, «свободной геометрии» с использованием теорий сплайнов.
Плетёные многоугольники могут быть соединены между собой концами кривых стержней, выходящими из вершин плетёных многоугольников, или выходящими из сторон плетёных многоугольников.
Структурные блоки и каркасные блоки могут быть соединены между собой концами кривых стержней, выходящими из смежных вершин структурных блоков, или выходящими из смежных ребер этих блоков, или выходящими из ребер одного блока и вершин смежного ему другого блока.
Структурные блоки могут быть соединены между собой концами кривых стержней, выходящими из смежных плетёных многоугольников образующих грани структурных блоков; или выходящими из плетёного многоугольника, образующего грань одного структурного блока, и из ребра смежного ему блока; или выходящими из плетёного многоугольника образующего грань одного структурного блока и из вершины смежного ему блока.
Это позволяет исключить крепежные элементы между соединяемыми линейными элементами, уравновешивать силы, возникающие в структурном блоке и в узлах соединения структурных блоков.
Таким образом, данное техническое решение обеспечивает отсутствие в конструкциях крепежных элементов и других конструктивных способов соединений внутри структурных блоков и в соединениях между структурными блоками конструкции. При этом силы взаимодействия элементов в каждом структурном блоке конструкции уравновешены. Это позволяет повысить устойчивость конструкции к разрушению при разрушении нескольких блоков в ее составе.
В приведенных аналогах, характеризующих уровень техники, отсутствует средство, которому присущи все признаки изобретения, выраженного предложенной формулой таким образом, чтобы все признаки известного ранее средства содержались в одном источнике информации. Это подтверждает соответствие заявленного изобретения условию «новизна».
Сведения, содержащиеся в уровне техники, путем объединения, изменения или совместного использования не могут создать предлагаемого изобретения. Из уровня техники не были выявлены решения, имеющие признаки, совпадающие с отличительными признаками рассматриваемого изобретения. Был сделан вывод, что изобретение явным образом не следует для специалиста из уровня техники. Это подтверждает соответствие заявленного изобретения условию «изобретательский уровень».
Краткое описание фигур чертежа
На фиг. 1 показан участок фундаментального сплайна r(t) между конечными точками pk и Pk+1.
На фиг. 2 показаны касательные векторы в конечных точках параллельные хордам 
На фиг. 3 показан график кривой на участке, ограниченном контрольными точками pk+1 и pk в плоскости OXZ.
На фиг. 4 показан график кривой между контрольными точками pk и pk-1 в плоскости OYZ.
На фиг. 5 показана математическая модель кривого стержня в проекциях OXY, OXZ, OYZ.
На фиг. 6 показан кривой стержень 1.
На фиг. 7 показан плетёный многоугольник 2 структурного блока 3.
На фиг. 8 показан панельный пустотелый структурный блок 3.
На фиг. 9 показана схема пустотелого панельного структурного блока 3.
На фиг. 10 показана схема каркасного структурного блока 5.
На фиг. 11 показана схема комбинированного пустотелого структурного блока 3.
На фиг. 12 показана схема связевого панельного структурного блока 3.
На фиг. 13 показана схема каркасного структурного блока 5.
На фиг. 14 показана схема связевого смешанного структурного блока 3.
На фиг. 15 показана схема соединения плетёных многоугольников 2 в вершинах структурного блока 3.
На фиг. 16 показана схема соединения плетёных многоугольников 2 структурных блоков 3 между ребрами.
На фиг. 17 показана схема соединения структурных блоков 3 между вершинами.
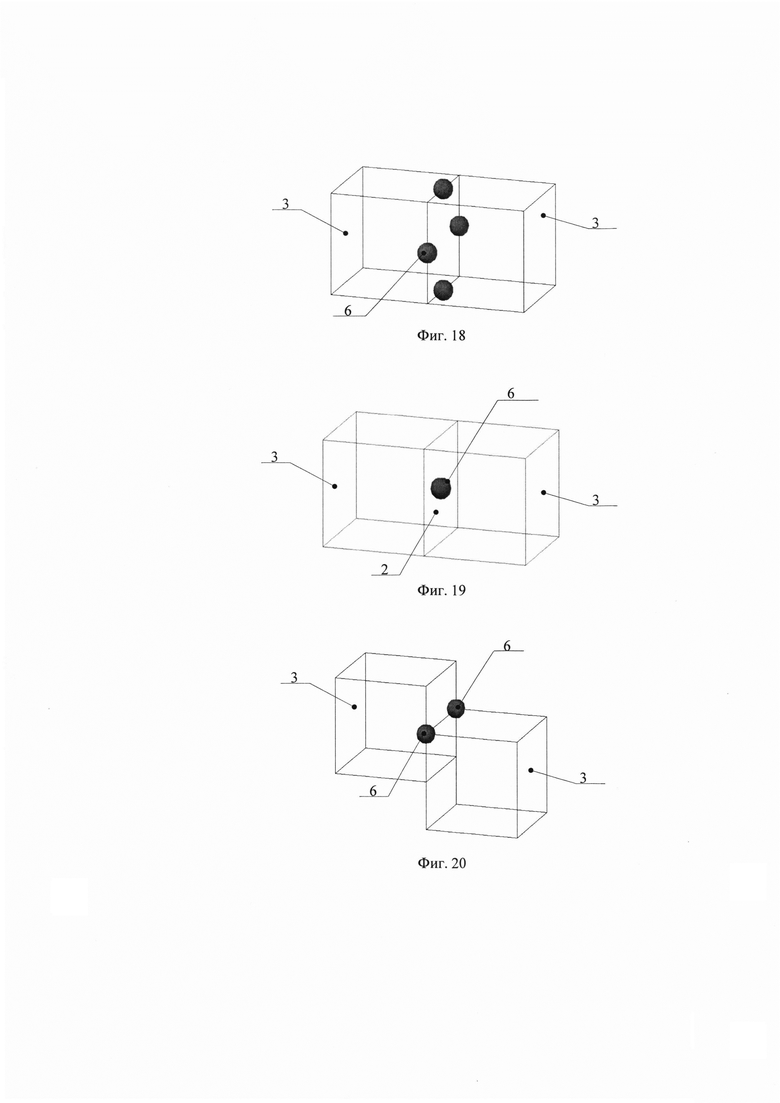
На фиг. 18 показана схема соединения структурных блоков 3 между ребрами.
На фиг. 19 показана схема соединения структурных блоков 3 между плетёными многоугольниками 2.
На фиг. 20 показана схема соединения структурных блоков 3 между ребрами одного структурного блока 3 и вершинами другого структурного блока 3.
На фиг. 21 показана схема соединения структурных блоков 3 между плетёным многоугольником 2 одного структурного блока 3 и ребром другого структурного блока 3.
На фиг. 22 показана схема соединения структурных блоков 3 между плетёным многоугольником 2 одного структурного блока 3 и вершиной другого структурного блока 3.
На фиг. 23 показана схема соединения структурных блоков 3 с образованием сферической оболочки из плетёной пространственной конструкции.
На фиг. 24 показана схема соединения каркасных структурных блоков 3 с образованием каркасной шестерни из плетёной пространственной конструкции.
Вариант осуществления изобретения
В патенте описана плетёная пространственная конструкция, которая универсально подходит для конструкций любых форм и размеров без применения дополнительных соединений и крепежных элементов.
Плетёная пространственная конструкция - система структурных блоков 3 и каркасных структурных блоков 5, каждый из которых сплетён из кривых стержней 1, скрепленных между собой выходящими из них концами 4 кривых стержней 1, с учетом расчета геометрии каждого кривого стержня 1 данной системы.
Кривой стержень 1 - протяженный элемент, у которого ось, проходящая через центры тяжести поперечных сечений, является кривой (фиг. 6).
Кривые стержни 1 могут быть металлическими и неметаллическими; сплошного сечения (проволока, пруток и т.п.) и не сплошного сечения (трубка и т.п.), криволинейными, описывающими траекторию двумерной или трехмерной кривой.
Плетёный многоугольник 2 - плетёная плоская фигура, выполненная из кривых стержней 1, имеющая форму многоугольника.
Структурный блок 3 - элементарная трехмерная ячейка плетёной пространственной конструкции, состоит из плетёных многоугольников 2 (фиг. 8), связанных друг с другом в узлах 6 (фиг. 12-16).
Правильные структурные блоки 3 могут иметь формы правильных многогранников (тетраэдр, октаэдр, икосаэдр, гексаэдр, додекаэдр и др.).
Каркасный структурный блок 5 (фиг. 10, 13) - элементарная трехмерная ячейка плетёной пространственной конструкции, состоящая из кривых стержней 1, которые связаны друг с другом в узлах 6 с образованием сторон каркаса. Кривые стержни 1 соединены друг с другом с образованием сторон многоугольников, соединение которых между собой образует каркасный структурный блок 5.
Структурные блоки 3 подразделяются: на панельные пустотелые (фиг. 9), комбинированные (фиг. 11); панельные связевые (фиг. 12), смешанные (фиг. 14).
Структурный блок 3 пустотелый (фиг. 9) - это структурный блок в форме многогранника, сформированный плетёными многоугольниками 2 в виде его граней. Плетёные многоугольники 2, сплетены из кривых стержней 1. Плетёные многоугольники 2 выполнены в форме в данном случае треугольника. Формирование плетёного многоугольника 2 полного заполнения осуществляют различными способами плетения кривых стержней 1, максимально заполняющих площадь формируемого плетёного многоугольника 2.
Структурный блок пустотелый комбинированный (фиг. 11) - это структурный блок 3, сформированный из совокупности плетёных многоугольников 2, и кривых стержней 1 в виде сторон многоугольников каркасного структурного блока 5. В данном случае плетёные многоугольники 2 выполнены в форме треугольника.
Структурный блок связевый панельный (фиг. 12) - это структурный блок, сформированный соединением плетёных многоугольников 2. В данном случае плетёные многоугольники 2 выполнены в форме треугольников, соединенных по двум сторонам 7 и 8. Остальные стороны плетёных многоугольников 2 образуют стороны структурного блока 3.
Структурный блок связевый смешанный (фиг. 14) - структурный блок 3 связевый, сформированный из плетёных многоугольников 2, связевого панельного блока и каркасного структурного блока 5.
При формировании структурных блоков 3 и каркасных структурных блоков 5 применяются комбинации кривых стержней 1 различные по материалу, сечению, толщине в зависимости от их назначения.
Из каждой стороны или плетёного многоугольника 2, которые являются гранями структурных блоков 3 и ребер каркасных структурных блоков 5 выходит как минимум по одному концу 4 кривого стержня 1 (фиг. 8). Они служат для соединения плетёных многоугольников 2 в узлах 6 (фиг. 9) известными способами плетения, скручиванием, завязыванием, загибом и т.п., с соседними вершинами, или ребрами или сторонами или гранями структурных блоков 3 для формирования структурных блоков 3 и каркасных структурных блоков 5.
Далее будет описан один из вариантов осуществления изобретения - создание панельного пустотелого структурного блока 3 кубической формы (фиг. 8). В качестве строительного элемента применяется кривой стержень 1.
Перед тем как выполнять структурный блок 3 проводят математический расчет методами на принципе тангенциального хода конечной формы кривого стержня 1 после его изгиба.
Геометрическое моделирование кривых стержней 1 может быть основано на известных и применяемых в практике проектирования методах, таких как методы на принципе тангенциального хода, методы «свободной геометрии» с использованием теорий сплайнов.
Принцип тангенциального хода заключается в том, что в трехмерном пространстве через набор координат точек проводится ломаная линия. Затем в ее изломы вписывают круговые кривые или круговые кривые, сопряженные с прямыми вставками - переходными кривыми, например клотоидными. Отрезки прямых представляют собой касательные к кривым, т.е. ломаная представляет собой тангенциальный ход. Ошибки, возможные при вписывании тех или иных кривых, не оказывают влияния на достоверность расчетов последующих кривых. Закругления, представленные круговыми кривыми с переходными кривыми могут быть симметричными (при равной длине входной и выходной кривой), несимметричными (если длины входной и выходной переходной не равны между собой), биклотоидой (если отсутствует круговая вставка между круговыми кривыми) симметричной и несимметричной соответственно.
Перспективными геометрическими элементами для проектирования закруглений кривых в составе тангенциального хода являются кривые Безье. Кривые Безье являются в общем случае пространственными функциями и способны обеспечивать пространственное моделирование кривых стержней.
Формула Безье для кубического многочлена (n=3) имеет следующий вид:
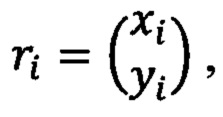
Пусть i=0, 1, 2, 3, тогда для 0<t<1
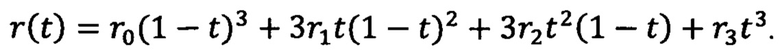
Помимо кривой Безье третьего порядка (кубической) для проектирования закруглений кривых стержней возможно применение кривых Безье второго, четвертого и пятого порядков.
Построение кривой Безье опирается на характеристическую ломаную, которая предопределяет ее свойства:
- кривая Безье является гладкой кривой;
- касательные в начале и в конце кривой совпадают по направлению с первым и последним отрезками ломаной;
- кривая Безье лежит в выпуклой оболочке, порожденной массивом точек (опорных вершин) ломаной;
- кривая симметрична (сохраняет свою форму при перемене порядка вершин ломаной);
- в случае если вершины ломаной лежат в одной плоскости, то кривая лежит в этой же плоскости;
- степень функциональных коэффициентов кривой на единицу меньше количества вершин ломаной;
- изменение положения хотя бы одной из вершин ломаной ведет к изменению очертаний кривой Безье.
Кривые стержни в составе структурного блока представляют собой нитевидные объекты, изогнутые в трехмерном пространстве. Математическая модель кривого стержня в пространстве представляет собой сплайн.
В условиях автоматизированного проектирования для формализованного представления информации о кривом стержне в числовом или аналитическом виде встает вопрос о выборе подходящих интерполирующих и аппроксимирующих функций. Наиболее подходящими функциями для этого являются сплайны как универсальный математический аппарат для описания, хранения, преобразования, анализа и представления геометрических форм элементов.
Физической моделью, называемой механической аналогией сплайна, является многоопорная балка, не испытывающая внешней нагрузки, а деформации которой вызваны внутренними реакциями на заданные реакции опор в фиксированные узлы. Математически данная модель описывается дифференциальным уравнением деформации балки и является многоточечной краевой задачей, для решения которой применяются сеточные методы, в результате которых получаются решения в виде сплайнов.
Сплайны имеют хорошие аппроксимативные свойства и в то же время просты и удобны для построения на ЭВМ вычислительных алгоритмов, полученных на их основе. При этом алгоритмы построения сплайнов совпадают с алгоритмом метода конечных элементов, который является основным промышленным методом прочностного анализа в системах автоматизированного проектирования.
Из всего многообразия сплайнов алгебраические сплайны первой и третьей степеней - интерполяционные и сглаживающие, наиболее экономичны с вычислительной точки зрения и обладают достаточными свойствами аппроксимации и гладкости.
Сплайны первой степени (линейные) служат, во-первых, хорошей и доступной иллюстрацией к пониманию процессов построения сплайновых алгоритмов, а во-вторых, достаточны для описания геометрических элементов конструкции, представляемых в виде ломаных линий.
Построению гладких кривых служат сплайны третьей степени (кубические), которые вместе со своими первой и второй производными несут проектировщику необходимую количественную и качественную информацию о проектируемой кривой.
Сплайны можно определить двумя способами:
Первый сеточный метод: исходя из взаимного согласования простых функций (многочленов невысокой степени);
Второй сеточный метод: из решения минимизации.
К сплайнам, определяемым по первому способу, можно отнести интерполяционные сплайны, которые необходимы для аналитического представления дискретно заданной информации.
Сглаживающие сплайны определяют чаще на основе второго способа. Именно сглаживающие сплайны находят самое широкое применение для оптимизации тех проектных решений, которые на начальной стадии рассмотрения носят, как правило, приближенный характер.
Интерполяция кубическими сплайнами может использоваться для получения элемента конструкции, а также применяться для разработки форм объектов (конструкций). Кубические сплайны предлагают разумный компромисс между гибкостью и скоростью вычислений. По сравнению с полиномами более высоких порядков кубические сплайны требуют меньше расчетов и памяти, они более устойчивы. Полиномы высших порядков могут не обеспечивать достаточной точности. Параметрические кубические кривые - это кривые самого низкого порядка, которые могут занимать произвольное положение (не лежать на плоскости) в трехмерном пространстве.
Построение кубических сплайнов сводится к решению системы линейных уравнений с диагональной матрицей, имеющей доминирующую главную диагональ. Решение таких систем легко реализуется численно.
Чтобы интерполировать заданный набор контрольных точек кубическими сплайнами, по входным данным подбирается кусочно-кубическая полиномиальная кривая, проходящая через все контрольные точки.
Пусть даны n+1 контрольные точки, заданные координатами.

Параметрический кубический полином, связывающий каждую пару контрольных точек, описывается системой уравнений:


а три производные задают координаты соответствующего касательного вектора в точке.
Например, для координаты х:

Задача построения полинома сводится к нахождению четырех коэффициентов 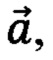


 для каждого из n участков кривой, при этом общее количество искомых коэффициентов полиномов будет 4n. Для этого задается достаточное число граничных условий в контрольных точках между участками кривой, на основе которых находятся численные значения всех коэффициентов.
для каждого из n участков кривой, при этом общее количество искомых коэффициентов полиномов будет 4n. Для этого задается достаточное число граничных условий в контрольных точках между участками кривой, на основе которых находятся численные значения всех коэффициентов.
Существует много способов задания параметрического сплайна. Это естественные кубические, эрмитовы, фундаментальные сплайны, сплайны Коханена-Бартелса, сплайны в форме Безье и β-сплайны и др.
Сплайн состоит из фрагментов одинакового вида, однако существуют комбинированные сплайны, состоящие из фрагментов различных сплайнов. Помимо фрагментов сплайнов в виде алгебраических полиномов могут быть использованы экспоненциальные сплайны, сплайны переменной жесткости, описанные в работах Снигирева В.Ф. и Павленко А.П., тригонометрические и рациональные сплайны.
Целесообразность применения фрагментов определенного вида основана на конкретных условиях задачи и ограничениях реализации. Основное требование - это достижение заданной точности интерполяции при приемлемых затратах времени и ресурсов на реализацию.
Известно, что интерполяционные сплайны не являются математическим аппаратом оптимального моделирования, а лишь удобным инструментом компьютерной обработки эскизно назначенных проектных решений. Таким образом, постановка задачи моделирования на основе сплайнов должна предполагать следующее: вершины интерполяции эскизной кривой кривого стержня назначают приближенно (с допуском) и точнее их местоположение нужно будет вычислить по определенным закономерностям.
В качестве математического аппарата для решения задачи генерации геометрической формы по их грубым (приближенным) описаниям необходимо рассмотреть применение сглаживающих сплайнов, которые минимизируют функционал И.Я. Шенберга:

S (х) - сплайн;
(х) - сплайн;
где q = 1, 2;
pi - весовой коэффициент узла интерполяции;
f0(xi) - функция начального приближения.
Ограничения могут быть по допустимому радиусу, направлению кривой, уклону в продольном профиле и т.д. При этом для сплайнов третьей степени (q=2) должны быть добавлены краевые условия в точках х0=а, xn=b, обеспечивающие единственность построения сплайна. Это могут быть условия заданного начального и конечного направления проектируемого участка кривой S'(xa), S'(xb).
Вышеприведенный функционал хорошо моделирует задачу построения кривой, которая состоит в том, чтобы добиться минимального отклонения проектируемой кривой от существующего (первоначального) эскиза, при одновременных условиях по уклону и кривизне в продольном профиле и по кривизне и скорости нарастания кривизны. Минимальное отклонение достигается за счет второго слагаемого функционала, а условие по кривизне - за счет первого слагаемого.
Вычисление сглаживающих сплайнов первой и третьей степени осуществляют покоординатного спуска, методом штрафных функций.
Трехмерное векторное представление точек на кривой относительно осей X, Y, Z математически описывается совокупностью параметрических сплайнов:
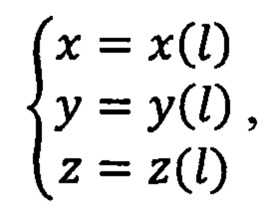
где параметр  - текущая длина кривой. Значение параметра
- текущая длина кривой. Значение параметра  задает координатный вектор точки на кривой.
задает координатный вектор точки на кривой.
Форма плоской кривой определяется функцией ее кривизны, форма пространственной кривой однозначно определяется совокупностью двух функций: кривизны и кручения.
Кривизна (r) и радиус кривизны (R=1/r) пространственной кривой имеют тот же геометрический смысл, что и для плоской кривой, но вычисляются по более сложной зависимости:


S(х) - сплайн;
где q = 1, 2;
pi - весовой коэффициент узла интерполяции
f0(xi) - функция начального приближения.
Ограничения могут быть по допустимому радиусу, направлению кривой, уклону в продольном профиле и т.д. При этом для сплайнов третьей степени (q=2) должны быть добавлены краевые условия в точках х0=а, xn=b, обеспечивающие единственность построения сплайна. Это могут быть условия заданного начального и конечного направления проектируемого участка кривой S'(xa), S'(xb).
Вышеприведенный функционал хорошо моделирует задачу построения кривой, которая состоит в том, чтобы добиться минимального отклонения проектируемой кривой от существующего (первоначального) эскиза, при одновременных условиях по уклону и кривизне в продольном профиле и по кривизне и скорости нарастания кривизны. Минимальное отклонение достигается за счет второго слагаемого функционала, а условие по кривизне - за счет первого слагаемого.
Вычисление сглаживающих сплайнов первой и третьей степени осуществляют покоординатного спуска, методом штрафных функций.
Трехмерное векторное представление точек на кривой относительно осей X, Y, Z математически описывается совокупностью параметрических сплайнов:
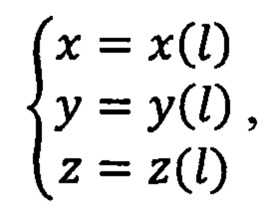
где параметр  - текущая длина кривой. Значение параметра
- текущая длина кривой. Значение параметра  задает координатный вектор точки на кривой.
задает координатный вектор точки на кривой.
Форма плоской кривой определяется функцией ее кривизны, форма пространственной кривой однозначно определяется совокупностью двух функций: кривизны и кручения.
Кривизна (r) и радиус кривизны (R=1/r) пространственной кривой имеют тот же геометрический смысл, что и для плоской кривой, но вычисляются по более сложной зависимости:
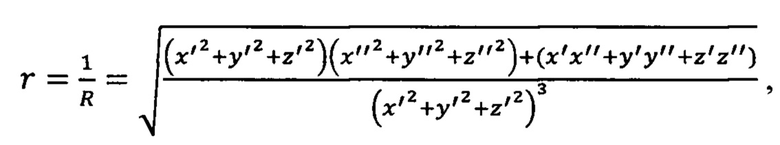
где х', х" - первая и вторая производная х по l.
Кручение (Т) пространственной кривой в точке соприкосновения определяется по формуле:
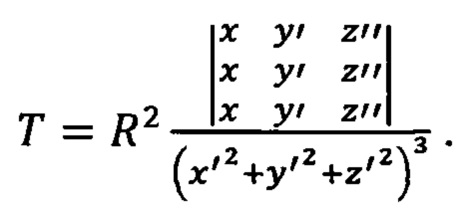
Пространственное моделирование кривых можно выполнять на основе тангенциального хода с вписанными закруглениями в виде кривых Безье. Опорные точки характеристической ломаной Безье (тангенциального хода), в общем случае, задаются точками трехмерного пространства Pi(xi, yi, xi), i=0, 1, …, m. Тогда пространственную кривую Безье определяют уравнением:
 - многочлены Бернштейна. Матричная запись параметрических уравнений, описывающих пространственную кривую Безье:
- многочлены Бернштейна. Матричная запись параметрических уравнений, описывающих пространственную кривую Безье:

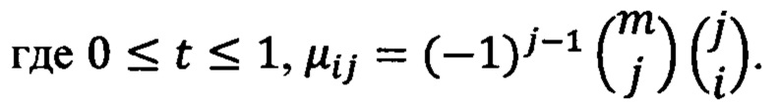
В случае, если промежуток измерения параметра произволен, а≤t≤b, уравнение кривой Безье имеет следующий вид:

Полученным представлением пользуются при задании единой параметризации составной кривой Безье как целого:
R=R(t),t0≤t≤ti, где
R=R(i)(t), ti-1≤t≤ti, i=1, 2, …, l - параметрическое векторное уравнение-й элементарной кривой Безье.
Таким образом, параметрические сплайны и кривые Безье позволяют осуществлять математическое моделирование кривого стержня в пространстве.
Пример геометрического моделирования участка кривого стержня. Для получения аналитического выражения, описывающего участок кривого стержня, используем фундаментальные сплайны.
Фундаментальные сплайны - это интерполирующие кусочно-кубические полиномы с заданными касательными в конечных точках. При этом значения касательных в конечных точках вводить не нужно. Постановка задачи:
Предположим, что даны n+1 контрольных точек, заданных координатами:



Необходимо определить значения четырех коэффициентов  для каждого из n участков кривой. Для этого задается достаточное количество граничных условий в контрольных точках между участками кривой, на основе которых находятся численные значения всех коэффициентов.
для каждого из n участков кривой. Для этого задается достаточное количество граничных условий в контрольных точках между участками кривой, на основе которых находятся численные значения всех коэффициентов.
Участок фундаментального сплайна r(t) плоскостью задается положениями четырех последовательных контрольных точек. Две средние контрольные точки pk и pk+1 являются конечными точками участка, другие две pk-1 и pk+2 используются при расчете касательных в конечных точках (на фиг. 1). Касательные векторы в конечных точках параллельны хордам 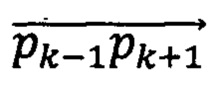 и
и  (на фиг. 2)
(на фиг. 2)
Пусть даны:


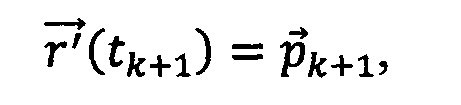


где 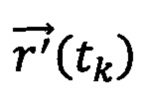 и
и  I - производные по параметру (наклон кривой) в контрольных точках pk и pk+1 соответственно.
I - производные по параметру (наклон кривой) в контрольных точках pk и pk+1 соответственно.
Запишем вид функций r(t) и r'(t) в матричном виде:
 Подставив вместо параметра t значения конечных точек tk и tk+1, фундаментальные граничные условия можно выразить в матричной форме:
Подставив вместо параметра t значения конечных точек tk и tk+1, фундаментальные граничные условия можно выразить в матричной форме:


Решая это уравнение относительно коэффициентов полиномов, при tk=0 и tk+1=1, получаем:
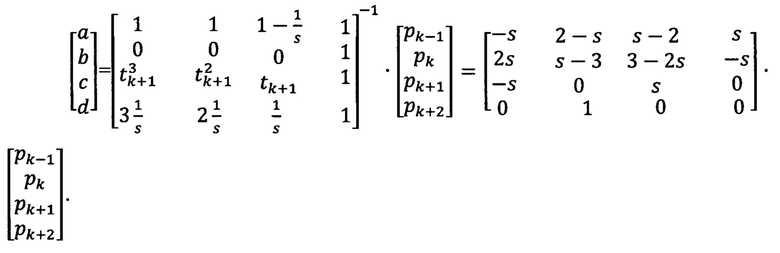
Получаем полиномиальную форму:
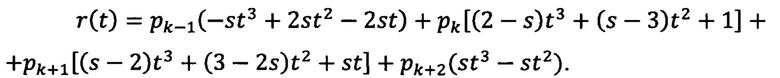
Пусть даны четыре контрольные точки, заданные с координатами:
p0=(x0, y0, z0), p1=(x1, y1, z1), p2=(x2, y2, z2), р3=(x3, y3, z3). Интерполируем заданный набор контрольных точек фундаментальными сплайнами.
Параметрический кубический полином, описывающий фундаментальный сплайн, связывающий каждую пару контрольных точек при u=0 (s=0,5) имеет вид:


Решением полученной системы уравнений на участке ограниченном контрольными точками pk+1 и pk являются координаты точек, приведенных в таблице 1.

По значениям координат в таблице 1 был построен график кривой на участке, ограниченном контрольными точками pk+1 и pk, приведенный на фиг. 3. Эта кривая соответствует изгибу кривого стержня на конкретном участке в плоскости OXZ.
Решением полученной системы уравнений на участке ограниченном контрольными точками pk и pk-1 являются координаты точек, приведенных в таблице 2.
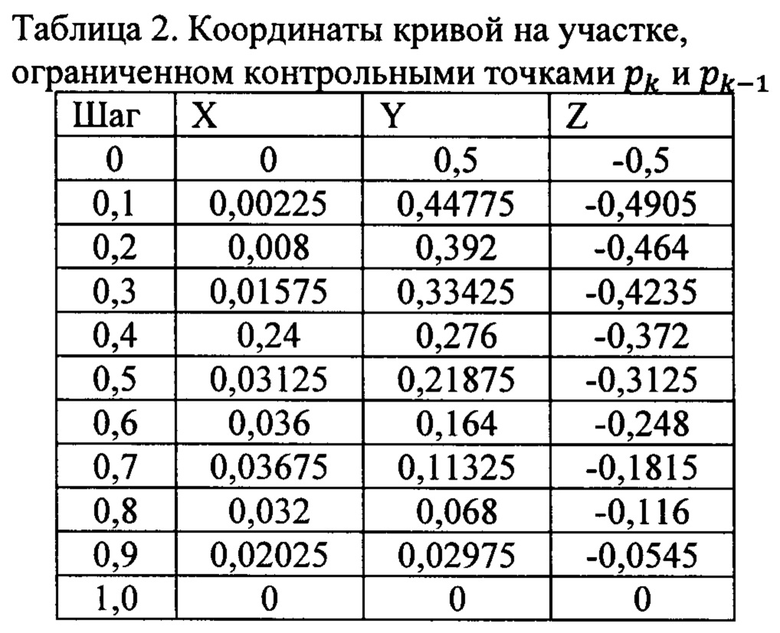
По значениям координат в таблице 2 был построен график кривой на участке, ограниченном контрольными точками pk и pk-1, приведенный на фиг. 4. Эта кривая соответствует изгибу кривого стержня 1 на конкретном участке в плоскости OYZ.
В результате расчетов получают решение в виде сплайна, который является математической моделью кривого стержня 1. Кривой стержень 1, изогнутый в соответствии с расчетом, представляет собой изогнутую в трехмерном пространстве проволоку (фиг. 6).
По рассчитанной математической модели кривого стержня 1 проволоке придают рассчитанную изогнутую в пространстве форму, показанную в проекциях OXY, OXZ, OYZ на фиг. 5.
На фиг. 6 показан кривой стержень 1, изогнутый в трехмерном пространстве по кривой, представляющей собой интерполяцию третьего порядка, проходящую через заданные рассчитанные координаты. В данном случае формирование кривого стержня 1 в пространстве осуществляют изгибом проволоки. Изображенный вариант изогнутого кривого стержня 1, не является единственно возможным, а является одним из многочисленных вариантов изгиба.
Кривые стержни 1 соединяют между собой путем переплетения, в результате чего образуется плетёный многоугольник 2 структурного блока 3. Плетёный многоугольник 2 на фиг. 7 представлен в виде четырехугольника и не является единственно возможной формой многоугольника, а одним из многочисленных вариантов. Эти варианты подробно не рассматриваются.
Плетёные многоугольники 2 соединяют между собой связанными концами 4 (фиг. 8) кривых стержней 1 в узлах 6 (фиг. 9) с образованием многогранника в виде структурного блока 3. Структурный блок 3 состоит из плетёных многоугольников 2, в виде граней, каждая из которых лежит в своей плоскости как показано на фиг. 8, 9.
Соединение плетёных многоугольников 2 структурного блока 3, осуществляют связыванием узлов 6 по рассчитанным изогнутым формам концов 4 кривых стержней 1. Соединение между собой всех плетёных многоугольников 2 концами 4 кривых стержней 1 образуют структурный блок 3.
Таким образом, уравновешиваются силы взаимодействия кривых стержней 1 внутри структурного блока 3 между собой. Структурный блок 3 - элементарная трехмерная плетёная ячейка плетёной пространственной конструкции.
Представление структурных блоков 3 плетёной пространственной конструкции в виде многогранника обеспечивает минимизацию вычислительных ресурсов ЭВМ, упрощение представления структурного блока 3 при дальнейшем проектировании плетёной пространственной конструкции.
Построение структурного блока 3 выполняют в следующей последовательности:
1. Определяют размер, форму, тип и назначение структурного блока 3;
2. Определяют форму каждого плетёного многоугольника 2 рассматриваемого структурного блока 3.
3. Определяют кривые стержни 1 для построения плетёного многоугольника 2 структурного блока 3.
4. Рассчитывают математическую модель каждого кривого стержня 1.
5. Строят плетёный многоугольник 2 структурного блока 3 путем сочленения кривых стержней 1.
6. Формируют структурный блок 3 соединением плетёных многоугольников 2, путем связывания в узлах 6 концами кривых стержней 1, выходящими из вершин плетёных многоугольников (фиг. 15), или концами кривых стержней 1, выходящими из сторон плетёных многоугольников (фиг. 16). Связывание концов кривых стержней 1, выходящих из соединяемых плетёных многоугольников 2 в виде граней, проводят по рассчитанной математической модели.
Как показано на фиг. 17, соединение структурных блоков 3 в узлах 6 можно осуществлять скручиванием, или переплетением, или связыванием концов кривых стержней 1, выходящих из вершин структурных блоков 3.
Как показано на фиг. 18, соединение структурных блоков 3 в узлах 6 можно осуществлять скручиванием, или переплетением, или связыванием концов 4 кривых стержней 1 (фиг. 8), выходящих из ребер структурных блоков 3.
Как показано на фиг. 19, соединение структурных блоков 3 в узлах 6 можно осуществлять скручиванием, или переплетением, или связыванием концов 4 кривых стержней 1 (фиг. 8), выходящих из сопрягаемых плетёных многоугольников 2 структурных блоков 3.
Соединение структурных блоков 3 в узлах 6 можно осуществлять скручиванием, или переплетением, или связыванием концов 4 кривых стержней 1, выходящих из сопрягаемых ребер одного структурного блока 3 с вершинами другого структурного блока 3 (фиг. 20); связыванием концов 4 кривых стержней 1, выходящих из сопрягаемых плетёного многоугольника 2 одного структурного блока 3 и ребра другого структурного блока 3 (фиг. 21); связыванием концов 4 кривых стержней 1, выходящих из сопрягаемых плетёного многоугольника 2 одного структурного блока 3 и вершины другого структурного блока 3 (фиг. 22).
Перечисленные соединения осуществляют плетением по рассчитанным математическим моделям концов 4 кривых стержней 1, выходящих из структурных блоков 3.
Здесь были рассмотрены способы соединения структурных блоков 3. Варианты соединения между собой каркасных структурных блоков 5 и соединения их со структурными блоками 3 основываются на тех же принципах.
На фиг. 23 показана плетёная пространственная конструкция в виде сферической оболочки из комбинированных структурных блоков. На фиг. 24 показана схема плетёной пространственной конструкции в виде шестерни из каркасных структурных блоков 5. Эти примеры не являются единственно возможными, а одними из многочисленных вариантов исполнения.
Формирование плетёных пространственных конструкций осуществляют соединением структурных блоков 3 и каркасных структурных блоков 5 таким образом, чтобы концы кривых стержней 1, выходящих из соединяемых между собой блоков 3 и 5, были изогнуты и сочленены между собой по их рассчитанным математическим моделям.
Плетёная пространственная конструкция может быть использована в производстве конструкций без применения дополнительных крепежных элементов. Строительный материал подают на место сборки конструкции в виде линейных материалов, таких как канат или проволока с бобины. Линейные материалы отрезают на линейные элементы необходимой длины. Из отрезанных линейных элементов формируют кривые стержни 1, затем плетут плетёные многоугольники 2 структурного блока 3 и стороны каркасного структурного блока 5. Плетёные многоугольники 2 соединяют между собой плетением концов 4 кривых стержней 1, выходящих из многоугольников 2, структурного блока 3, или сторон каркасного структурного блока 5. Изготовленные структурные блоки 3 и каркасные структурные блоки 5 соединяют между собой плетением концов 4 кривых стержней 1, выходящих из блоков 3 и 5.
Дополнительно к указанному техническому результату при изготовлении плетёной пространственной конструкции исключаются сварочные, клеевые и другие конструктивные соединения. Это удешевляет производство конструкций, и дает возможность Доставки строительного материала и создания конструкций любого размера в труднодоступных местах, таких как подземных, подводных, на большой высоте или при отсутствии земной атмосферы.
Промышленная применимость
Данное техническое решение может быть применено в бытовых и промышленных целях как способ формообразования конструкций, являющийся альтернативой литью, точению, формованию, аддитивным технологиям (трехмерная печать конструкций) и другим известным технологиям. Данная технология позволяет создавать функциональные конструкции широкого спектра применения.
Предлагаемое техническое решение может быть применено в конструкциях, к которым предъявляют высокие требования по независимости целостности структуры конструкции от целостности единичного элемента, упрощение и удешевление изготовления и доставки единичных элементов к месту сборки конструкции, также там, где в структуре конструкции присутствует необходимость соединения единичных элементов структуры конструкции из разнородных материалов при отсутствии элементов крепления.
В целом, рассмотренный вариант выполнения изобретения может быть реализован на существующем в настоящее время оборудовании с использованием имеющихся материалов. Это показывает его работоспособность и подтверждает промышленную применимость.
| название | год | авторы | номер документа |
|---|---|---|---|
| КАРКАСНОЕ ЗДАНИЕ НА ТРЕХ ОПОРАХ | 2018 |
|
RU2687691C1 |
| СГЛАЖИВАНИЕ И ВИЗУАЛИЗАЦИЯ ЦИФРОВОГО РУКОПИСНОГО ВВОДА С ПРИМЕНЕНИЕМ GPU | 2015 |
|
RU2701471C2 |
| Способ борьбы с беспилотными летательными аппаратами | 2018 |
|
RU2674392C1 |
| ПОКРЫТИЕ БЫСТРОВОЗВОДИМОГО ГЕОДЕЗИЧЕСКОГО КУПОЛА | 2024 |
|
RU2839516C1 |
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2010 |
|
RU2415381C1 |
| Способ профилирования элементов проточной части лопастной машины | 2019 |
|
RU2727223C1 |
| НАРУЖНЫЙ НЕСУЩИЙ КАРКАС ЗДАНИЯ НА ТРЕХ ОПОРАХ | 2019 |
|
RU2713054C1 |
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУХМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2011 |
|
RU2484427C1 |
| Способ образования стереометрических куполообразных оболочек | 1986 |
|
SU1370202A1 |
| СПОСОБ УПРАВЛЕНИЯ РАБОЧИМ ОРГАНОМ МНОГОСТЕПЕННОГО МАНИПУЛЯТОРА | 2021 |
|
RU2771456C1 |







Изобретение относится к области строительства, а именно к конструктивным элементам. Конструкция содержит линейные элементы конечной длины, изогнутые в пространстве, называемые кривыми стержнями. Кривые стержни изогнуты, переплетены и связаны между собой с образованием плетёного многоугольника в виде грани, с выходящими из него концами кривых стержней. Грани соединены между собой связанными концами кривых стержней с образованием структурного блока в форме многогранника. Кривые стержни связаны друг с другом с образованием сторон каркасного структурного блока. Структурные блоки и каркасные структурные блоки соединены между собой концами кривых стержней с образованием плетёной пространственной конструкции. Технический результат - повышение устойчивости конструкции. 2 н. и 10 з.п. ф-лы, 24 ил., 2 табл.
1. Плетёная пространственная конструкция, содержащая узлы и линейные элементы, отличающаяся тем, что каждый линейный элемент выполнен конечной длины и изогнут в пространстве с получением формы, соответствующей заранее рассчитанной математической модели с использованием теорий сплайнов, при этом изогнутый элемент представляет из себя кривой стержень, кривые стержни переплетены друг с другом и связаны друг с другом с образованием плетёного многоугольника, с выходящими из него концами кривых стержней, плетёные многоугольники соединены между собой связанными концами кривых стержней с образованием структурного блока в форме многогранника, структурные блоки связаны между собой концами кривых стержней с образованием плетёной пространственной конструкции.
2. Плетёная пространственная конструкция, содержащая узлы и линейные элементы, отличающаяся тем, что каждый линейный элемент выполнен конечной длины и изогнут в пространстве с получением формы, соответствующей заранее рассчитанной математической модели с использованием теорий сплайнов, при этом изогнутый элемент представляет из себя кривой стержень, кривые стержни связаны друг с другом с образованием контура многоугольников, которые связаны между собой с образованием каркасного структурного блока, каркасные структурные блоки связаны между собой концами кривых стержней с образованием плетёной пространственной конструкции.
3. Пространственная конструкция по пп. 1 и 2, отличающаяся тем, что каркасные структурные и структурные блоки связаны между собой концами кривых стержней, которые рассчитаны по математическим моделям на принципах тангенциального хода, «свободной геометрии» с использованием теорий сплайнов.
4. Пространственная конструкция по пп. 1 и 2, отличающаяся тем, что каждый кривой стержень рассчитан методами на принципах тангенциального хода, «свободной геометрии» с использованием теорий сплайнов.
5. Пространственная конструкция по п. 1, отличающаяся тем, что плетёные многоугольники соединены между собой концами кривых стержней, выходящими из вершин плетёных многоугольников.
6. Пространственная конструкция по п. 1, отличающаяся тем, что плетёные многоугольники соединены между собой концами кривых стержней, выходящими из сторон плетёных многоугольников.
7. Пространственная конструкция по пп. 1 и 2, отличающаяся тем, что структурные блоки и каркасные блоки соединены между собой концами кривых стержней, выходящими из смежных вершин этих блоков.
8. Пространственная конструкция по пп. 1 и 2, отличающаяся тем, что структурные блоки и каркасные блоки соединены между собой концами кривых стержней, выходящими из смежных ребер этих блоков.
9. Пространственная конструкция по пп. 1 и 2, отличающаяся тем, что структурные блоки и каркасные блоки соединены между собой концами кривых стержней, выходящими из ребер одного блока и вершин смежного ему другого блока.
10. Пространственная конструкция по п. 1, отличающаяся тем, что структурные блоки соединены между собой концами кривых стержней, выходящими из смежных плетёных многоугольников, образующих грани структурных блоков.
11. Пространственная конструкция по п. 1, отличающаяся тем, что структурные блоки соединены между собой концами кривых стержней, выходящими из плетёного многоугольника, образующего грань одного структурного блока и из ребра смежного ему структурного блока.
12. Пространственная конструкция по п. 1, отличающаяся тем, что структурные блоки соединены между собой концами кривых стержней, выходящими из плетёного многоугольника, образующего грань одного структурного блока и из вершины смежного ему структурного блока.
| US 5505035 A1, 09.04.1996 | |||
| US 20130180184 A1, 18.07.2013 | |||
| ЛЕГКАЯ ТРЕХМЕРНАЯ ПРОВОЛОЧНАЯ КОНСТРУКЦИЯ И СПОСОБ ЕЕ ИЗГОТОВЛЕНИЯ | 2009 |
|
RU2508175C2 |
| МНОГОСЛОЙНЫЕ ПЛЕТЕНЫЕ КОНСТРУКЦИИ ДЛЯ ОККЛЮЗИИ СОСУДИСТЫХ ДЕФЕКТОВ | 2007 |
|
RU2446773C2 |
| US 20130167462 A1, 04.07.2013. | |||
Авторы
Даты
2021-08-17—Публикация
2020-08-24—Подача