Предлагаемое техническое решение относится к устройствам определения характеристик случайных процессов и предназначено для оценки параметра распределения и проверки согласия экспериментальной функции распределения экспоненциальному закону. Устройство целесообразно использовать при исследовании временных характеристик газоразрядных матричных индикаторов.
Известны устройства для оценки числовых характеристик и закона распределения случайных процессов, содержащие блоки измерения и регистрации случайных значений, вычислительные, управляющие блоки, блоки представления результатов обработки. Например, Мирский Г.Я. Аппаратурное определение характеристик случайных процессов. М:, «Энергия», 1972 г.; Лаврентьев С.И., Шестеркин А.Н. Устройство для определения плотностей распределения времени запаздывания зажигания элементов отображения газоразрядных индикаторов. Электронная техника, серия 4, выпуск 3(98), 1983 г.; Заико А.И. Нагаев О.Н. Устройство для измерения распределений случайных процессов. Патент РФ №2 249 851; Толпарев Р.Г. и др. Устройство для определения характеристик случайного процесса. Патент РФ №2 253 147.
В этих устройствах реализованы различные методы оценки числовых характеристик и закона распределения вероятностей, устройства различаются по сложности, быстродействию, точности найденных значений. Конечной целью работы этих устройств является вычисление оценок параметров распределения и формирование самого распределения, при этом установление какому аналитическому описанию соответствует сформированное распределение и оценка достоверности (значимости) найденных характеристик и распределения в этих устройствах не производится. Это является недостатком аналогов.
Для практического применения методов теории вероятностей и математической статистики необходимо знание закона распределения (аналитического описания), устанавливающего связь между возможными значениями случайной величины и вероятностями, соответствующими этим случайным значениям. Математическая модель для описания экспериментальных данных в упомянутых устройствах принимается на основе «внешней схожести» экспериментального распределения с некоторым известным или на основе результатов предыдущих исследований. Однако, при определенных параметрах вид (график) некоторых распределений, в частности Эрланга, Вейбулла, Релея, Пирсона, гамма-распределения, логарифмически нормального распределения достаточно схож, поэтому такой выбор математической модели может привести к дальнейшим ошибочным выводам. Аналитическое описание экспериментального распределения на основе результатов предыдущих исследований используют в основном при проведении контрольных испытаний - статистическом приемочном контроле.
Для рационального выбора математической модели, характеризующей исследуемый процесс, выдвигают гипотезу: наблюдаемое распределение случайной величины описывается некоторым конкретным законом. Дальнейшая задача исследований - принять или отвергнуть предложенную гипотезу путем вычисления на основе измеренных случайных значений статистического критерия и сопоставления его для некоторого уровня значимости (достоверности) с критическим значением. Гипотеза на выбранном уровне значимости, как правило, принимается (конкретный закон можно использовать для описания исследуемых случайных значений), если значение статистики критерия, вычисленное по экспериментальным данным, не больше критического. В противном случае для данного критерия гипотеза признается противоречащей результатам наблюдений на выбранном уровне значимости.
Так как статистика критерия для проверки гипотезы вычисляется по выборочным данным, то и сама она является случайной величиной. Следовательно, решения по гипотезе на основе статистики носят вероятностный характер с возможными ошибками отклонения верной гипотезы (ошибки первого рода с вероятностью появления α) и принятия ложной (ошибки второго рода с вероятностью появления β). Эффективность статистического критерия проверки гипотезы оценивают его мощностью 1-β, которая равна вероятности отклонения ложной гипотезы.
Для описания времени запаздывания зажигания в газоразрядных элементах могут использоваться различные распределения. Запаздывание зажигания элемента в обычных режимах хорошо описывается экспоненциальным распределением. При возбуждении элементов импульсами малой длительности при сильной ионизации элементов время формирования разряда учитывают в виде сдвига. В условиях взаимоионизации, свойственной элементам отображения газоразрядных матричных индикаторов, используют гамма-распределение, более общее по сравнению с экспоненциальным. Суперпозиция экспоненциальных распределений позволяет учесть как «самостоятельное» зажигание элемента, так и его зажигание в результате «подсвета». Для каждого из распределений более целесообразно использовать специальные критерии согласия, формулирующие согласие только с определенным видом распределения. Такие критерии обладают большей эффективностью. В дальнейшем будем рассматривать согласие с экспоненциальным распределением, т.е. проверку экспоненциальности распределения.
Оценка экспоненциальности распределения возможна на основе большого числа различных критериев. Критерии различаются мощностью, простотой вычислений, анализируют разности плотностей или функций распределения, корреляционные функции, коэффициенты некоторых более общих распределений по отношению к экспоненциальному. Выдвигаемая гипотеза может быть простой (известны параметры теоретического распределения) или сложной (оценку параметров вычисляют по той же самой выборке). Эффективность применения того или иного критерия также зависит от числа случайных значений, на основе которых он вычисляется.
В литературе практически отсутствуют рекомендации по выбору числа элементов выборки N, необходимых для построения закона распределения. Ориентировочный объем выборки N можно вычислить, задавшись критическим значением некоторого распространенного критерия для определенного уровня значимости. Известно, что при проверке более часто встречающихся на практике сложных гипотез наиболее мощными являются непараметрические критерии (Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть И. Непараметрические критерии. М.: ИПК Издательство стандартов, 2002). Для критериев такого типа, в частности критерия Колмогорова, вычисляемого на основе максимальной разности DN между эмпирической FN(t) и теоретической 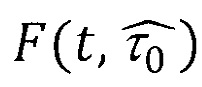 функцией распределения с оценкой среднего значения
функцией распределения с оценкой среднего значения  , найденного по самой выборке, с вероятностью 0,95 сложную гипотезу о согласии опытного распределения с экспоненциальным можно принять при числе элементов выборки около 400 элементов.
, найденного по самой выборке, с вероятностью 0,95 сложную гипотезу о согласии опытного распределения с экспоненциальным можно принять при числе элементов выборки около 400 элементов.
Если число измеренных случайных значений (объем выборки) N>50, то наибольшей мощностью экспоненциальности обладает критерий Фроцини (Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. М.: Физматлит, 2006). Критерий также основан на исследовании расстояния между теоретической и экспериментальной функциями распределения и предназначен для проверки сложных гипотез. Его статистика:

В этой формуле 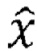 - оценка среднего значения, вычисленного на основе выборки; xi элементы упорядоченной (ранжированной) выборки, т.е. х1≤х2≤ … ≤ xN. Критическое значение критерия статистики BN зависит от доверительной вероятности и числа элементов выборки. В частности, для «инженерного» значения доверительной вероятности 0,95 и числе элементов выборки больше 20 критическое значение критерия экспоненциальности Фроцини 0,3840.
- оценка среднего значения, вычисленного на основе выборки; xi элементы упорядоченной (ранжированной) выборки, т.е. х1≤х2≤ … ≤ xN. Критическое значение критерия статистики BN зависит от доверительной вероятности и числа элементов выборки. В частности, для «инженерного» значения доверительной вероятности 0,95 и числе элементов выборки больше 20 критическое значение критерия экспоненциальности Фроцини 0,3840.
Проведенный патентный поиск показал, что наиболее близким по технической сущности и выполняемым операциям к предлагаемому устройству является второй вариант устройства для оценки среднего времени запаздывания возникновения разряда (патент РФ №2 678 646, кл. G06F 17/18).
Устройство для определения статистических характеристик времени запаздывания зажигания элементов матричного индикатора (второй вариант реализации патента РФ №2678646, прототип) содержит измерительный блок, информационный и синхронизирующий выходы которого подключены к информационному D и синхронизирующему С входам блока памяти и ранжирования, счетчик, первый счетный вход С1 которого соединен с синхронизирующим выходом измерительного блока. Выход блока выбора статистик соединен с первым адресным входом блока памяти и ранжирования. Первый выход блок управления подключен к входу «Старт» измерительного блока, входу установки в исходное состояние R блока памяти и ранжирования и первому входу R установки в исходное состояние счетчика. Второй выход блока управления подключен к входу разрешения сортировки блока памяти и ранжирования Sort. Третий выход блока управления подключен к входу разрешения блока выбора статистик. Выход заполнения счетчика соединен с входом блока управления и входом «Стоп» измерительного блока. Вход блока регистрации параметра распределения соединен с первым выходом блока памяти и ранжирования, управляющий вход блока выбора статистики, который обеспечивает реализацию выражения [0.632N], где N - объем выборки, […] - целая часть числа, ближайшая к целому, соединенный с входом установки коэффициента пересчета счетчика «Уст. N» и вход «Пуск» блока управления являются входами устройства.
В этом устройстве вычисление среднего значения распределения осуществляется на основе порядковой статистики с номером [0.632N]. Относительная эффективность такой оценки среднего значения по сравнению с оптимальной линейной оценкой превышает 0.90 (А.Е. Сархан, Б.Г. Гринберг. Ведение в теорию порядковых статистик. М:, Статистика, 1970 г. Раздел Б), т.е. оценка вычисляется достаточно точно. Однако столь простое и точное определение среднего значения обеспечивается только в том случае, если экспериментальное распределение является экспоненциальным.
В действительности, в некоторых случаях для описания времени запаздывания зажигания в элементах газоразрядных индикаторов может использоваться гамма распределение или суперпозиция экспоненциальных распределений (Орлов Ю.И., Шестеркин А.Н. Исследование функции распределения запаздывания пробоя в условиях взаимной ионизации разрядных промежутков. Электронная техника, Сер.4. 1978. Вып.5; Шестеркин А.Н. Определение надежности зажигания элемента отображения газоразрядного матричного индикатора. Вестник Рязанского государственного радиотехнического университета. 2017. №61). Очевидно, в этих случаях оценка среднего времени запаздывания зажигания устройством, принятым в качестве прототипа, будет вычисляться со значительной погрешностью.
Цель предлагаемого изобретения - повышение достоверности оценки среднего времени запаздывания зажигания элементов газоразрядного матричного индикатора. С этой целью в устройство дополнительно включен блок вычисления критерия Фроцини, выход которого подключен к входу разрешения блока регистрации параметра распределения. Входы блока вычисления критерия Фроцини подключены к выходу блока регистрации параметра распределения, второму выходу блока памяти и ранжирования, информационным выходам счетчика, входу установки коэффициента пересчета «Уст.N», входу установки «Критическое значения статистики» и четвертому выходу блока управления. Второй адресный вход блока памяти и ранжирования соединен с информационными выходам счетчика. Пятый и шестой выходы блока управления подключены, соответственно, к второму счетному входу С2 и второму входу установки в исходное состояние R счетчика. Включение дополнительного блока и дополнение связей в известном устройстве позволяет оценивать экспоненциальность экспериментального распределения и при подтверждении выдвинутой гипотезы воспроизводить вычисленное значение параметра распределения, а также свидетельствовать об экспоненциальном распределении результатов измерений.
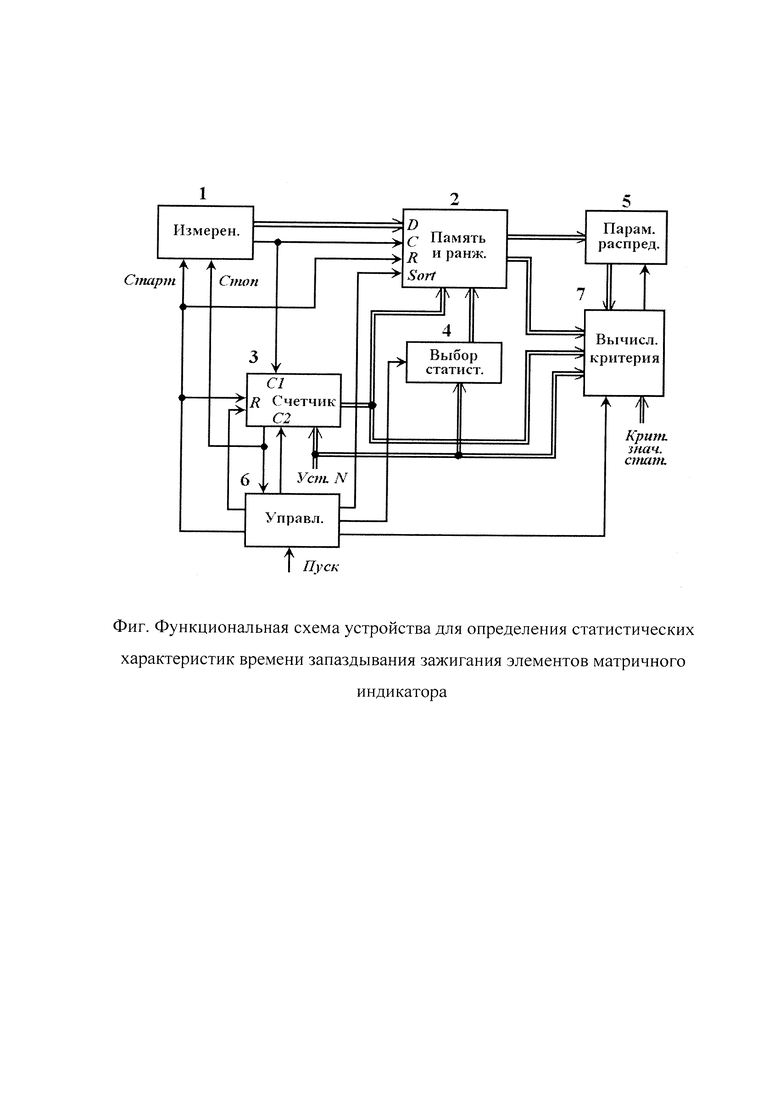
Функциональная схема устройства для определения статистических характеристик времени запаздывания зажигания элементов матричного индикатора изображена на фигуре. Устройство содержит измерительный блок 1, блок памяти и ранжирования 2, счетчик 3, блок выбора статистики 4, блок регистрации параметра распределения 5, блок управления 6 и блок вычисления критерия Фроцини 7.
Работу устройства можно разделить на четыре этапа: измерение времени запаздывания (случайных значений) и их сохранение, сортировка (ранжирование) зарегистрированных результатов измерений, вычисление на их основе оценки среднего значения и определение критерия экспоненциальности с последующим разрешением (запретом) воспроизведения вычисленной оценки среднего значения. Последовательность выполнения этапов определяется блоком управления.
Перед началом исследований на входе устройства «Уст.N» устанавливается число измерений случайной величины, т.е. объем выборки N. Это значение определяет коэффициент пересчета счетчика 3, выходной сигнал блока выбора статистик 4 - порядковый номер ранжированной выборки, которая является оценкой среднего значения исследуемой величины. В дальнейшем объем выборки N участвует в вычислении критерия экспоненциальности Фроцини блоком 7. Кроме того на входе устройства «Критическое значение статистики» блока 7 для определенного объема выборки и требуемой доверительной вероятности устанавливается критическое значение статистики.
Первый этап работы устройства начинается при поступлении сигнала «Пуск» на вход блока управления 6, который определяет последовательность функционирования блоков устройства. При этом на первом выходе блока управления 6 формируется сигнал «Старт», который устанавливает в исходное (нулевое) состояние блок памяти и ранжирования 2, счетчик 3, а также разрешает работу (измерение случайных значений) измерительного блока 1. Каждое измеренное значение случайной величины, сопровождаемое синхронизирующим сигналом, с выходов измерительного блока 1 записывается в блок памяти и ранжирования 2.
Одновременно синхронизирующим сигналом измерительного блока 1, поступающим на первый счетный вход О счетчика 3, увеличивается его содержимое. Очевидно, после измерения N случайных значений и записи их в блок памяти и ранжирования 2 состояние счетчика 3 станет равным коэффициенту пересчета. При этом на выходе заполнения счетчика 3 формируется сигнал «Стоп», который останавливает работу измерительного блока 1 и разрешает генерирование на втором выходе блока управления 6 сигнала, запускающего второй этап: сортировку результатов измерений, записанных в блоке памяти и ранжирования 2. После окончания сортировки по возрастанию зарегистрированных результатов измерений внутренние адресные шины блока памяти и ранжирования 2 отключаются.
Далее выполняется третий этап: определяется оценка среднего значения зарегистрированных случайных значений. Для этого на третьем выходе блока управления 6 формируется сигнал, поступающий на вход блока выбора статистик 4. Блок выбора статистики 4 в соответствии с формулой [0.632N] вычисляет номер порядковой статистики (адреса блока памяти и ранжирования 2, по которому записан результат измерения, соответствующий оценке среднего значения исследуемого процесса). По очередному сигналу на третьем выходе блока управления 6 на первом адресном входе блока памяти и ранжирования 2 устанавливается адрес, обеспечивающий вывод на выход блока памяти [0.632N]-й статистики, которая является оценкой среднего значения исследуемого случайного процесса. Эта оценка записывается в блок регистрации результатов параметров распределения 5, однако до завершения следующего (последнего) этапа результат вычислений не воспроизводится. Далее сигнал на первом адресном входе блока памяти и ранжирования 2 отключается.
На последнем этапе в блоке вычисления критерия 7 вычисляется значение критерия экспоненциальности Фроцини, сопоставление его с критическим значением и разрешение (запрет) воспроизведения ранее вычисленной оценки среднего значения исследуемого процесса, записанный в блок регистрации результатов параметров распределения 5. Вычисление критерия экспоненциальности производится при последовательном опросе ячеек блока памяти и ранжирования 2 информационными выходными сигналами счетчика 3, поступающими на второй адресный вход блока 2. Для этого счетчик 3 вначале устанавливается в исходное состояние (сигналом с шестого выхода блока управления 6 поступающим на второй вход R счетчика 3), а затем его состояние последовательно увеличивается до максимального сигналами с пятого выходов блока управления 6, поступающими на второй счетный вход счетчика 3. Таким образом, на входы блока вычисления критерия 8 с блока регистрации параметра распределения 5 поступает значение, соответствующее оценке среднего значения исследуемого процесса (в формуле критерия Фроцини 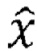 ), с выхода блока памяти и ранжирования 2 элементы упорядоченной выборки (xi). Синхронно с элементами упорядоченной выборки с информационного выхода счетчика 3 на вход блока вычисления критерия 8 поступает порядковый номер статистики (i), т.е. адрес соответствующий элементам упорядоченной выборки, а также значение объема выборки N, установленное на входе устройства. На основе этих значений последовательно вычисляется сумма разностей, которая по окончанию опроса всех ячеек блока памяти и ранжирования 2 уменьшается на величину
), с выхода блока памяти и ранжирования 2 элементы упорядоченной выборки (xi). Синхронно с элементами упорядоченной выборки с информационного выхода счетчика 3 на вход блока вычисления критерия 8 поступает порядковый номер статистики (i), т.е. адрес соответствующий элементам упорядоченной выборки, а также значение объема выборки N, установленное на входе устройства. На основе этих значений последовательно вычисляется сумма разностей, которая по окончанию опроса всех ячеек блока памяти и ранжирования 2 уменьшается на величину 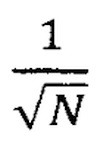 . Вычисленное значение критерия экспоненциальности Фроцини сравнивается с «Критическим значением статистики», установленном на входе устройства (блоке 7). Если вычисленное значение критерия оказывается меньше критического, то выходным сигналом блока вычисления критерия 7 разрешается воспроизведения ранее вычисленной оценки среднего значения исследуемого процесса, зарегистрированного в блоке 5.
. Вычисленное значение критерия экспоненциальности Фроцини сравнивается с «Критическим значением статистики», установленном на входе устройства (блоке 7). Если вычисленное значение критерия оказывается меньше критического, то выходным сигналом блока вычисления критерия 7 разрешается воспроизведения ранее вычисленной оценки среднего значения исследуемого процесса, зарегистрированного в блоке 5.
Таким образом, предлагаемое устройство обеспечивает воспроизведение оценки среднего значения на основе порядковой статистики только в том случае, если распределение зарегистрированных случайных значений соответствует экспоненциальному распределению. Устройство обеспечивает не только достоверное определение среднего значения, но и вычисляет соответствие исследуемого процесса экспоненциальному распределению.
Достоверность оценки среднего времени запаздывания зажигания элементов отображения матричного индикатора предлагаемым устройством проверялась путем статистического моделирования. Для этого генерировались массивы случайных значений, элементы которых соответствовали экспоненциальному распределению при автономном возбуждении и «подсвете» элемента отображения. На их основе формировался массив случайных значений, соответствующий суперпозиции двух экспоненциальных распределений. Для этих массивов определялись оценки средних значений на основе порядковой статистики, методом моментов, а также значение критерия Фроцини. Такая процедура повторялась многократно и на основе оценок, вычисленных в каждом цикле, определялась общая оценка среднего значения, максимальное и минимальное значение оценок средних значений. Исследования проводились при различных вероятностях зажигания (средних значениях времени запаздывания) для автономного возбуждения, «подсвечиваемого» элемента и при различных объемах выборки в среде MathCAD.
В таблице приведены результаты исследований для выборок, состоящих из 400 элементов. Такой объем выборки позволяет с высокой достоверностью определить оценку среднего значения и проверить сложную гипотезу о принадлежности исследуемой случайной величины экспоненциальному распределению непараметрическим критерием Фроцини. Приведенные в таблице результаты соответствуют типичным значениям вероятности автономного зажигания элемента Ра=0,2 и вероятности зажигания Рр=0,8 при его «подсвете», что соответствует равновероятному самостоятельному зажиганию и зажиганию элемента в результате «подсвета» (значения коэффициентов суперпозиции экспоненциальных распределений c1=c2=0,5). При времени возбуждения элементов в течение 80 мкс расчетные (идеальные) средние значения времени запаздывания при автономном зажигании 385,5 мкс, «подсвете» элемента 49,7 мкс и для суперпозиции распределений 204,1 мкс. Число циклов (повторений) 100. Доверительной вероятности 0,95 соответствует критическое значение критерия Фроцини 0,3840.
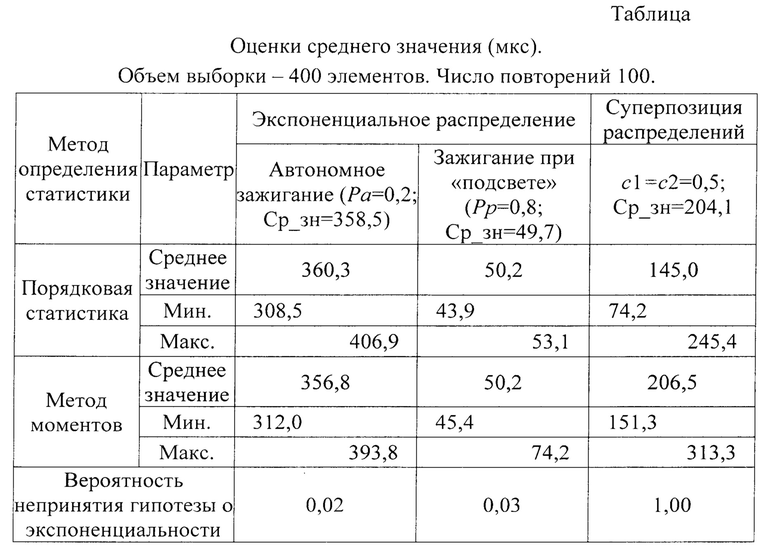
Анализ результатов исследований показывает, что для экспоненциальных распределений оценки средних значений, вычисленные на основе порядковой статистики и методом моментов, практически совпадают между собой и с расчетным значением. Общие оценки средних значений, вычисленные для экспоненциальных распределений, отличаются от идеальных на 0,5% для самостоятельного зажигания элемента и на 0,9% для подсвечиваемого элемента. При этом вероятность непринятия гипотезы о экспоненциальности для этих случаев меньше, чем допустимое значение (0,05) для доверительной вероятности 0,95.
Если случайная величина соответствует суперпозиции двух экспоненциальных распределений, то общая оценка среднего значения, вычисленная методом моментов, также отличается от реальной незначительно, лишь на 1,2%. Общая оценка среднего значения, вычисленная на основе порядковой статистики, меньше реальной на 59,3%. При этом во всех случаях вычисленное значение критерия экспоненциальности Фроцини превышает критическое значение критерия 0,3840, т.е. вероятность непринятия гипотезы о экспоненциальности равна 1. Таким образом, ни одна оценка среднего значения для суперпозиции экспоненциальных распределений, вычисленная на основе порядковой статистики, при использовании предлагаемого устройства не будет принята в качестве результата исследований.
Таким образом, предлагаемое устройство обеспечивает вычисление оценки среднего времени запаздывания возникновения разряда с высокой достоверностью, при этом устройство с большой мощностью позволяет подтвердить или отвергнуть гипотезу об экспоненциальности исследуемой случайной величины, т.е. обладает более широкими функциональными возможностями.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для оценки среднего времени запаздывания возникновения разряда (его варианты) | 2018 |
|
RU2678646C1 |
| Устройство для статистического приемочного контроля газоразрядных индикаторов | 2019 |
|
RU2714382C1 |
| Способ оценки параметров распределения времени запаздывания возникновения разряда и устройство для его осуществления | 2016 |
|
RU2646897C2 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И УСТРАНЕНИЯ АНОМАЛЬНЫХ ИЗМЕРЕНИЙ ПРИ ФИКСИРОВАННОМ ЗНАЧЕНИИ ВЕРОЯТНОСТИ ЛОЖНОЙ ТРЕВОГИ | 2007 |
|
RU2361268C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ И УСТРАНЕНИЯ АНОМАЛЬНЫХ ИЗМЕРЕНИЙ | 2016 |
|
RU2616568C1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И УСТРАНЕНИЯ АНОМАЛЬНЫХ ИЗМЕРЕНИЙ | 2005 |
|
RU2301445C1 |
| УСТРОЙСТВО ДЛЯ КЛАССИФИКАЦИИ ПОСЛЕДОВАТЕЛЬНОСТИ ЦИФРОВЫХ СИГНАЛОВ | 2003 |
|
RU2268485C2 |
| СПОСОБ ОЦЕНКИ ОТНОШЕНИЯ СИГНАЛ/ШУМ В УСТРОЙСТВАХ БЕСПРОВОДНОЙ СВЯЗИ | 2023 |
|
RU2809969C1 |
| Устройство для определения стационарности случайного процесса | 1981 |
|
SU1015394A1 |
| СПОСОБ ОБНАРУЖЕНИЯ АНОМАЛЬНЫХ ИЗМЕРЕНИЙ БЕЗ ОЦЕНКИ ФУНКЦИИ ТРЕНДА И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2005 |
|
RU2302655C1 |
Изобретение относится к области оценки среднего времени запаздывания зажигания элементов газоразрядного матричного индикатора. Техническим результатом является повышение достоверности оценки среднего времени запаздывания зажигания элементов газоразрядного матричного индикатора. Раскрыто устройство для определения статистических характеристик времени запаздывания зажигания элементов матричного индикатора, содержащее измерительный блок, блок памяти и ранжирования, счетчик, блок выбора статистик, блок управления, блок регистрации параметра распределения, блок вычисления критерия Фроцини. 1 ил., 1 табл.
Устройство для определения статистических характеристик времени запаздывания зажигания элементов матричного индикатора, содержащее измерительный блок, информационный и синхронизирующий выходы которого подключены к информационному D и синхронизирующему С входам блока памяти и ранжирования, счетчик, первый счетный вход С1 которого соединен с синхронизирующим выходом измерительного блока, блок выбора статистик, выход которого соединен с первым адресным входом блока памяти и ранжирования, блок управления, первый выход которого подключен к входу «Старт» измерительного блока, входу установки в исходное состояние R блока памяти и ранжирования и первому входу R установки в исходное состояние счетчика, второй выход блока управления подключен к входу разрешения сортировки блока памяти и ранжирования Sort, третий выход блока управления подключен к входу разрешения блока выбора статистик, выход заполнения счетчика соединен с входом блока управления и входом «Стоп» измерительного блока, блок регистрации параметра распределения, вход которого соединен с первым выходом блока памяти и ранжирования, управляющий вход блока выбора статистики, который обеспечивает реализацию выражения [0.632N], где N - объем выборки, [...] - целая часть числа, ближайшая к целому, соединенный с входом установки коэффициента пересчета счетчика «Уст. N» и вход «Пуск» блока управления являются входами устройства, отличающееся тем, что в устройство дополнительно включен блок вычисления критерия Фроцини, выход которого подключен к входу разрешения блока регистрации параметра распределения, входы блока вычисления критерия Фроцини подключены к выходу блока регистрации параметра распределения, второму выходу блока памяти и ранжирования, информационным выходам счетчика, входу установки коэффициента пересчета «Уст. N», входу «Критическое значение статистики» и четвертому выходу блока управления, второй адресный вход блока памяти и ранжирования соединен с информационными выходам счетчика, пятый и шестой выходы блока управления подключены, соответственно, ко второму счетному входу С2 и второму входу установки в исходное состояние R счетчика.
| Устройство для оценки среднего времени запаздывания возникновения разряда (его варианты) | 2018 |
|
RU2678646C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ПРОЦЕССОВ | 2003 |
|
RU2249851C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА | 2003 |
|
RU2253147C1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
Авторы
Даты
2022-03-17—Публикация
2020-09-29—Подача