Изобретение относится к расчетно-экспериментальным способам определения упругих объектов, в частности упругих свойств кузова пассажирского вагона.
Известен способ определения изгибной жесткости конструкции путем установки ее на опоры, замера прогибов под действием собственного веса, затем повторный замер прогибов при изменении положения опор и идентификация изгибной жесткости по разности показаний приборов для двух замеров [1]. Недостатком такого способа оценки изгибной жесткости транспортного средства является его трудоемкость, как следствие: необходимости конструирования и изготовления специальных средств в местах нового размещения опор; наличия трудностей с подкатыванием опорных устройств; понижения точности идентификации изгибной жесткости, вследствие вероятных трудно контролируемых локальных изменений жесткости опор; невозможностью, при наличии нескольких различных участков жесткости, идентификации изгибной жесткости.
Известен также способ определения характеристик изгибной жесткости протяженных объектов с помощью кривизномера Упадышева, заключающийся в замере кривизны на характерной осевой линии протяженного объекта, консольно закрепленного в специальной установке и последующей идентификации с введением расчетных поправок, основанных на сравнении номинальной средней кривизны участков с номинальной средней кривизной в середине участка [2]. Применительно к транспортным объектам недостатками такого способа является невозможность консольного закрепления, трудности с локализацией характерной осевой линии из-за значительных поперечных размеров объекта, а также то, что градуировка кривизномера основана на предположении о постоянстве кривизны на базе его измерений, что приводит к необходимости значительного увеличения количества замеров.
Известен способ идентификации изгибной жесткости, основанный на решении обратной коэффициентной задачи для конструкции, нагружаемой с помощью домкратов сосредоточенными силами в ряде точек, определении прогибов в ряде других точек и вычислении изгибной жесткости с помощью методов теории экстремального управления [3]. Недостатком этого метода является возможность нарушения контакта объекта с односторонними опорами при замере прогибов, невозможность уточненного определения прогибов в местах расположения домкратов из-за неизбежных локальных деформаций, а также вероятная неоднозначность результатов, возникающих из-за необходимости регуляризации решения многомерной экстремальной, некорректной по Адамару обратной коэффициентной задачи [4].
Прототип - способ определения изгибной жесткости объектов из композиционных материалов, применяемых для лопастей винтов в вертолетостроении. Известный способ основан на измерении прогибов под действием сосредоточенной силы, приложенной к свободному концу натурного объекта, консольно закрепленного в специальном приспособлении и последующей обработке измерений с учетом поправок, основанных на сравнении теоретических и экспериментальных результатов, так что фактическую изгибную жесткость в каждом сечении находят путем умножения расчетной жесткости на отношение вычисленной и измеренной деформации [5]. Недостатком этого способа применительно к транспортным средствам является невозможность консольного закрепления объекта, а также невозможность поточечной корректировки, основанной на нахождении отношения вычисленной и измеренной деформации, что связано с различной степенью сложности идентифицируемых объектов (относительная ширина лопасти вертолета значительно меньше относительной ширины поперечного сечения кузова пассажирского вагона).
Цель изобретения состоит в сокращении времени и трудоемкости определения изгибной жесткости за счет учета специфики транспортного объекта.
Поставленная цель достигается тем, что объект устанавливают на жесткие опоры, нагружают его поперечными распределенными и/или сосредоточенными усилиями, определяют величины прогибов в ряде сечений по длине объекта и оценивают фактическую изгибную жесткость, предполагая, что фактические моменты инерции редуцированных и геометрических поперечных сечений пропорциональны, т.е. для каждого сечения фактическая изгибная жесткость пропорциональна вычисляемой геометрической жесткости, и определяется по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта.
Кроме того, согласно заявляемого способа, производится идентификация объекта и определяются участки имеющие одинаковое значение изгибной жесткости, и за счет учета при проведении идентификации изгибной жесткости того факта, что участки одинаковой жесткости не следуют друг за другом, что фактическое число различных значений изгибной жесткости намного меньше количества перемен ее значений на длине объекта производится объединение таких участков в группы.
Технический результат заключается в: повышении точности определения значений тех динамических характеристик транспортного объекта, которые требуют для своей оценки определения значения изгибной жесткости; значительному сокращению, времени необходимого как на сами замеры, количество которых в случае динамического подхода к идентификации изгибной жесткости достигает многих тысяч, так и на их обработку, поскольку заявляемый способ требует небольшого количества, обычно достаточно десятка, значений прогибов в отдельных точках объекта, возникающих за счет действия статических распределенных и сосредоточенных весовых нагрузок.
Метод определения геометрических изгибных жесткостей, апробированная в ЗАО НО «ТИВ» на примере кузовов пассажирского вагона, предполагает представление кузова транспортного средства в виде балки Бернулли-Эйлера с кусочно-постоянной изгибной жесткостью 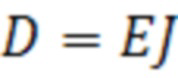 , где E - модуль Юнга, J - величина, имеющая смысл геометрического момента инерции поперечного сечения, но численно ему не равная, вследствие сложности реальной конструкции по сравнению с моделью (наличие вырезов, наличие подкреплений, деформация тонкостенного контура поперечного сечения и др.). Кроме того для достижения тождественности с кузовом транспортного средства, модель в виде балки Бернулли-Эйлера с кусочно-постоянной изгибной жесткостью выполняется с опорой на две жесткие шарнирные опоры Фиг. 1.
, где E - модуль Юнга, J - величина, имеющая смысл геометрического момента инерции поперечного сечения, но численно ему не равная, вследствие сложности реальной конструкции по сравнению с моделью (наличие вырезов, наличие подкреплений, деформация тонкостенного контура поперечного сечения и др.). Кроме того для достижения тождественности с кузовом транспортного средства, модель в виде балки Бернулли-Эйлера с кусочно-постоянной изгибной жесткостью выполняется с опорой на две жесткие шарнирные опоры Фиг. 1.
При испытаниях, имеющих целью определение изгибной жесткости, к кузову транспортного средства, прикладывают сосредоточенные вертикальные силы  и кусочно-постоянные распределенные нагрузки
и кусочно-постоянные распределенные нагрузки  Фиг. 2 и замеряют прогибы в расчетных сечениях. При этом изгибная жесткость на участке
Фиг. 2 и замеряют прогибы в расчетных сечениях. При этом изгибная жесткость на участке 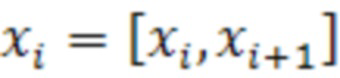 равна
равна 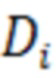 .
.
Следует отметить существенное свойство реальных транспортных средств, пассажирских вагонов в частности. Фактическое количество перемен жесткости обычно намного больше фактического количества значений изгибной жесткости. Например, для пассажирских вагонов в регулярной их части характерно чередование вида: оконный проем-простенок, т.е. чередуются в основном два значения изгибной жесткости. Наличие этого обстоятельства упрощает задачу идентификации за счет уменьшения количества расчетных сечений.
Также, определение изгибной жесткости кузова пассажирского вагона существенно упрощает предложение, что фактические моменты инерции редуцированных и геометрических поперечных сечений пропорциональны, и таким образом фактическая изгибная жесткость пропорциональна вычисляемой геометрической жесткости.
Допустимость этого предположения подтверждается ниже описанным математическим аппаратом.
Прогиб в любой точке 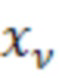 для схемы по Фиг. 1 при известных значениях
для схемы по Фиг. 1 при известных значениях 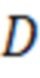 может быть вычислен по формуле:
может быть вычислен по формуле:
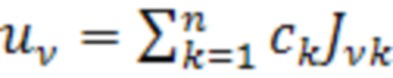 ,
,  . (1)
. (1)
 из формулы (1) в соответствии с теоремой Кастильяно может быть вычислен в виде интеграла:
из формулы (1) в соответствии с теоремой Кастильяно может быть вычислен в виде интеграла:
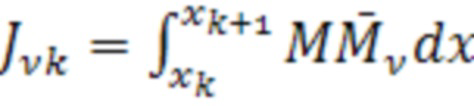 (2)
(2)
где 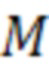 - изгибающий момент от внешней нагрузки, включая моменты от реакции опор
- изгибающий момент от внешней нагрузки, включая моменты от реакции опор 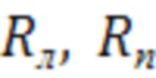 , которые находятся так:
, которые находятся так:
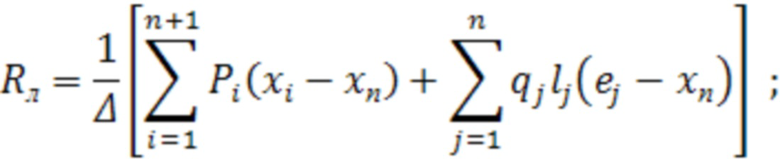
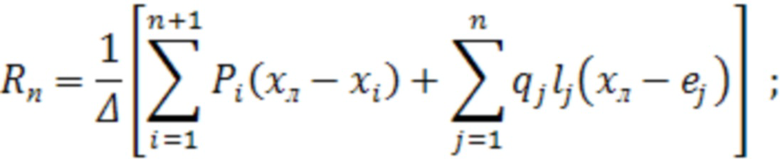
 (3)
(3)
Выражение для 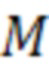 при этом имеет вид:
при этом имеет вид:
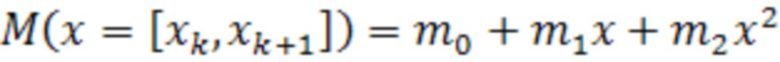 , (4)
, (4)
 ;
;
 ;
;
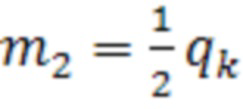 .
.
Момент 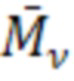 от единичной силы
от единичной силы  , приложенной в точке
, приложенной в точке 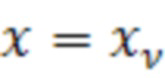 , строится в виде суммы трех линейных слагаемых:
, строится в виде суммы трех линейных слагаемых:
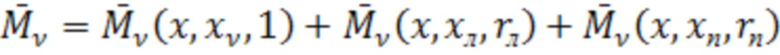 , (6)
, (6)
где 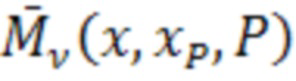 вычисляется по формуле:
вычисляется по формуле:
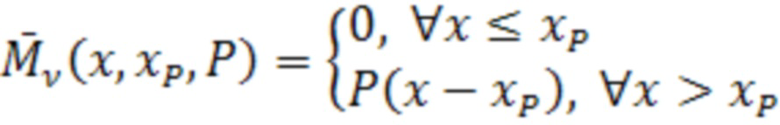 (7)
(7)
Реакции  из формулы 6 находятся так:
из формулы 6 находятся так:
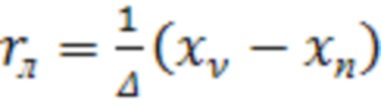 ,
, 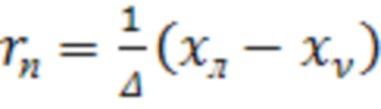 . (8)
. (8)
На основании этого интеграл из формулы (2) вычисляется следующим образом:
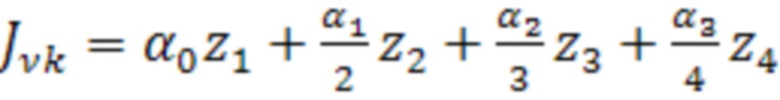 , (9)
, (9)
где 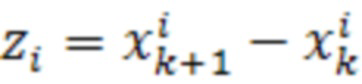
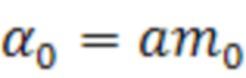 ;
;  ;
; 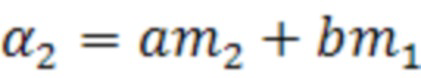 ;
; 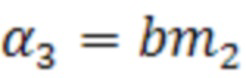 ;
;
 ;
; 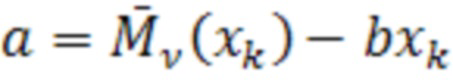 . (10)
. (10)
Если у нас фактически имеется (s) различных групп жесткости, то формула (1) приобретает вид
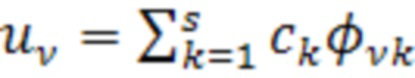 ,
, 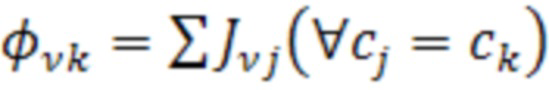 . (11)
. (11)
Сравнение вычисленных по формуле (11) перемещений  ,
, 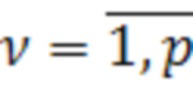 с экспериментальными (или полученными иным образом) значениями
с экспериментальными (или полученными иным образом) значениями  по методу наименьших квадратов приводит к системе линейных алгебраических уравнений, из которых вектор
по методу наименьших квадратов приводит к системе линейных алгебраических уравнений, из которых вектор 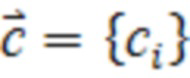 ,
, 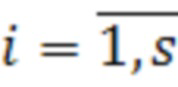 определяется по матричной формуле:
определяется по матричной формуле:
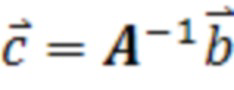 ,
, 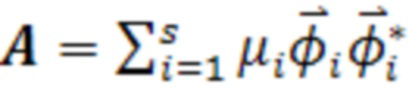 ,
, 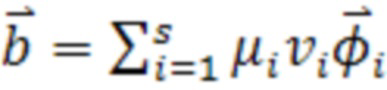 (12)
(12)
где  - неотрицательные весовые множители, вектор
- неотрицательные весовые множители, вектор 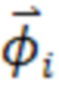 состоит из
состоит из 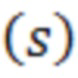 компонентов
компонентов 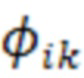 , вычисляемых по формуле (11), а значок
, вычисляемых по формуле (11), а значок  означает транспонирование.
означает транспонирование.
Решение s-мерной задачи в виде формулы (12) некорректно по Адамару, поэтому для получения физически разумных результатов проводится регуляризация. С учетом того, что формула (12) при 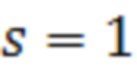 всегда дает качественно (но не количественно) физически обоснованные результаты и введя предположение о пропорциональности фактических - эффективных и геометрических изгибных жесткостей:
всегда дает качественно (но не количественно) физически обоснованные результаты и введя предположение о пропорциональности фактических - эффективных и геометрических изгибных жесткостей:
 , (13)
, (13)
где (баз) означает любой ненулевой элемент, принятый в качестве базового. после этого решение по формуле (12) заменяется на вычисление 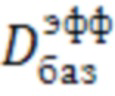 :
:
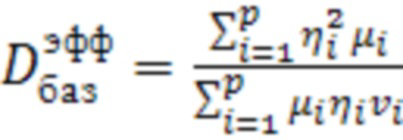 ,
,  , (14)
, (14)
после чего идентифицированные значения изгибных жесткостей 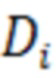 участков находятся по формуле:
участков находятся по формуле:
 . (15)
. (15)
Таким образом, идентифицированные значения изгибных жесткостей для фактического количества i значений изгибной жесткости могут быть рассчитаны на основании полученных расчетным путем, с использованием опробированных стандартных методов теоретической механики, геометрических изгибных жесткостей 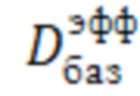 при использовании значений вертикальных сил
при использовании значений вертикальных сил 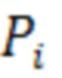 и кусочно-постоянных распределенных нагрузок
и кусочно-постоянных распределенных нагрузок 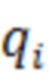 , прикладываемых при реализации расчетно-экспериментального способа определения упругих свойств объекта в виде кузова пассажирского вагона, используя предположение о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта.
, прикладываемых при реализации расчетно-экспериментального способа определения упругих свойств объекта в виде кузова пассажирского вагона, используя предположение о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта.
Способ иллюстрируется чертежами 1-3, таблицами 1-3.
Фиг. 1 - модель транспортного средства без нагрузки.
Фиг. 2 - модель транспортного средства под нагрузкой.
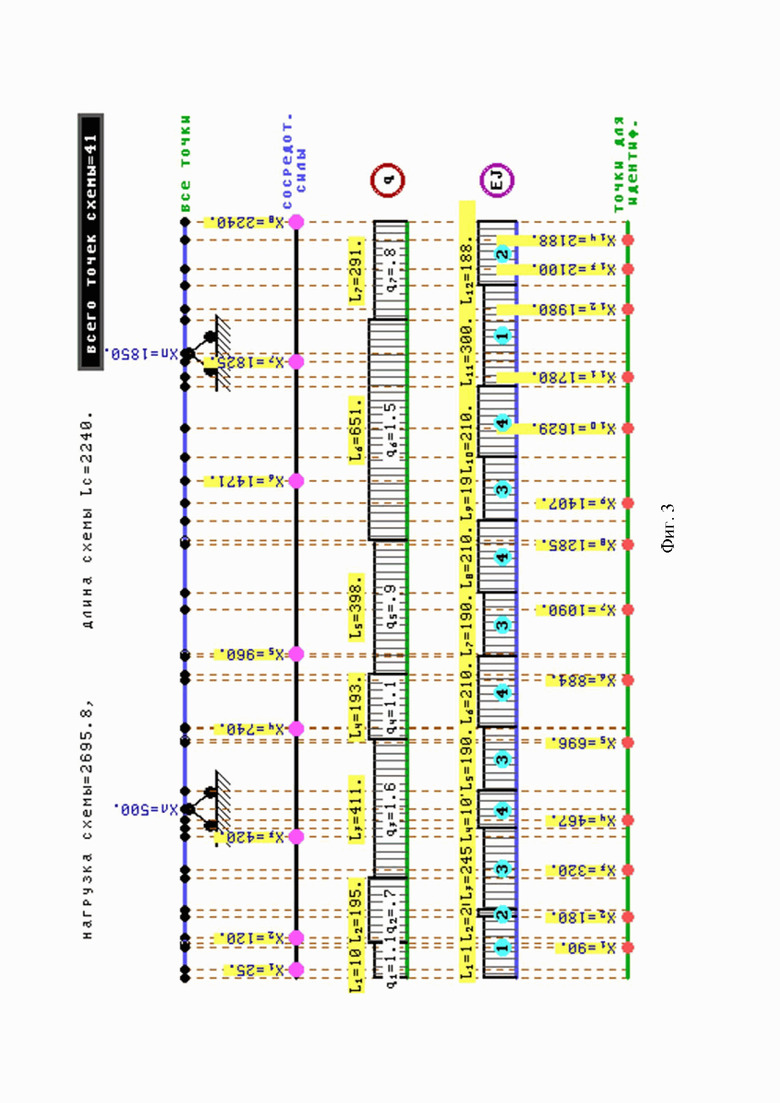
Фиг. 3 - схема и результат определения изгибной жесткости кузова вагона 61-4447.
Таблица 1 - длины участков li и номера групп жесткости ni кузова вагона 61-4447.
Таблица 2 - координаты точек xi и значения прогиба ui кузова вагона 61-4447.
Таблица 3 - значения Ji и изгибной жесткости Di вычисленные для кузова вагона 61-4447.
Способ осуществляется следующим образом.
Объект, представленный в виде балки Бернулли-Эйлера, с кусочно-постоянной изгибной жесткостью 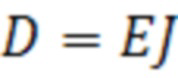 , где E - модуль Юнга, J - величина момента инерции редуцированного поперечного сечения, представленный в виде кузова пассажирского вагона, устанавливают на жесткие опоры, фиксируют начальное положение выбранных точек порожнего кузова, нагружают объект дополнительной нагрузкой, измеряют величины отклонений (прогибы) выбранных точек от начального положения и рассчитывают геометрических изгибные жесткости на каждом участке объекта. Далее определяют изгибную жесткость кузова пассажирского вагона, при использовании предположения о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта. По полученным значениям изгибной жесткости производится оценка пригодности объекта к эксплуатации.
, где E - модуль Юнга, J - величина момента инерции редуцированного поперечного сечения, представленный в виде кузова пассажирского вагона, устанавливают на жесткие опоры, фиксируют начальное положение выбранных точек порожнего кузова, нагружают объект дополнительной нагрузкой, измеряют величины отклонений (прогибы) выбранных точек от начального положения и рассчитывают геометрических изгибные жесткости на каждом участке объекта. Далее определяют изгибную жесткость кузова пассажирского вагона, при использовании предположения о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта. По полученным значениям изгибной жесткости производится оценка пригодности объекта к эксплуатации.
При практическом применении изгибная жесткость является искомой (неизвестной) величиной, что не позволяет напрямую оценить эффективность и точность предлагаемого способа. Для проверки адекватности и точности заявляемого способа вычислим значения геометрических изгибных жесткостей по известным испытательным нагрузкам. Фактическая изгибная жесткость кузова пассажирского вагона определяется, при использовании предположения о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта. По степени близости вычисленных по заявляемому способу и рассчитанных значений изгибной жесткости можно сделать вывод о точности и адекватности предлагаемого способа.
В качестве примера на Фиг. 3 показана модельная задача для балки Бернулли-Эйлера с 12 чередующимися участками изгибной жесткости, причем геометрическая изгибная жесткость рассчитывается по известной испытательной нагрузке Фиг. 3, которые объединены в 4 группы:
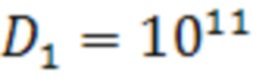 ,
, 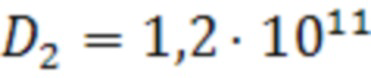 ,
, 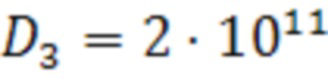 ,
, 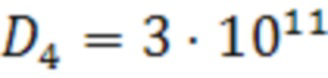 .
.
Значения 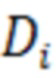 рассчитывались с использованием значений вертикальных прогибов в 14 точках, координаты которых указаны на фигуре, а сами прогибы равны следующим значениям:
рассчитывались с использованием значений вертикальных прогибов в 14 точках, координаты которых указаны на фигуре, а сами прогибы равны следующим значениям:
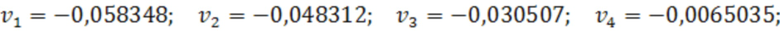
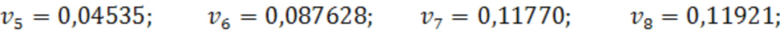


Вычисления проводились для весового множителя 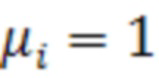 , и начальных значений
, и начальных значений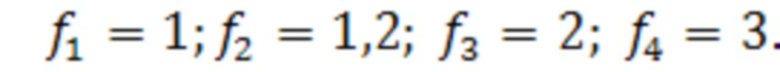
Значения Di рассчитывались при использовании предположения о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта.
В результате вычислений получены значения:
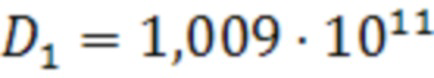 ,
, 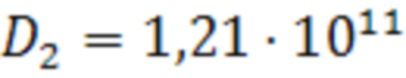 ,
,  ,
, 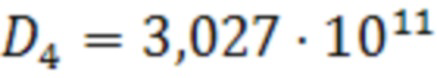
незначительно, менее, чем на 1 %, отличающиеся от заданных. Эта разница связана с небольшим количеством точек с заданными значениями прогибов и уменьшается при росте их количества.
Пример реализации заявляемого способа.
В качестве конкретного примера рассмотрена идентификация значений изгибной жесткости кузова вагона 61-4447, имеющего следующие характеристики: xл = 320 см, xп = 2040 см, l = 2360 см
Кузов нагружен равномерно распределенной нагрузкой с интенсивностью q = 193,25 Н/см и двумя сосредоточенными концевыми усилиями: P(0) = 8 кН, P(2360) = 16,5 кН.
Модель кузова состоит из 26 участков кусочно-постоянной изгибной жесткости, следующих друг за другом по порядку. Однако из анализа утверждения о том, что фактическое количество перемен жесткости обычно намного больше фактического количества значений изгибной жесткости, выявлено фактическое количество различных значений жесткости равное 9, т.е. все значения могут быть объединены в 9 групп. Значения длин участков li и номера групп жесткости ni для всех 26 участков, представленных в Таблице 1. Значения прогиба измерялись и в дальнейшем использовались для определения оптимального коэффициента пропорциональность геометрической и фактической изгибной жесткости пассажирского вагона в 9 точках Таблица 2. В Таблице 3 представлены значения геометрических моментов инерции Ji и фактические значения изгибной жесткости Di для всех 9 групп жесткости, вычисленные при использовании предположения о пропорциональности фактических - эффективных и геометрических изгибных жесткостей, по методу наименьших квадратов, с использованием значений прогибов в ряде расчетных сечений объекта.
Изобретение может быть использовано для получения динамических характеристик транспортного средства, в частности, для оценки низшей частоты изгибных колебаний в вертикальной плоскости, а также при моделировании динамического поведения конструкции в реальных условиях эксплуатации, где использование усложненных моделей оказывается невозможным по техническим и/или экономическим соображениям.
Список источников
1. SU 834428 А1 МПК G01M 5/00 Способ определения изгибной жесткости конструкции. Белоусов А.П. Обидин А.Д. Опубликовано 1981.05.30
2. RU 2535645 С1 МПК G01M 5/00, G0/N3/20 Способ определения характеристик изгибной жесткости протяженных объектов с помощью кривизномера. Шершавин В.В., Дорошенко Н.И., Мироненко Л.А., Иванов А.А. Опубликовано 20.12.2014
3. Василевский В.В., Скачков А.Н., Юхневский А.А. Идентификация изгибной жесткости кузова пассажирского вагона теоретико-экспериментальным методом / В кн.: Проблемы и перспективы развития вагоностроения: сборник научных трудов VIII Всероссийской научно-практической конференции (18-19 апреля 2019 г., г. Брянск), с. 36-39
4. Ватульян А.О. Обратные задачи в механике деформируемого твердого тела. - М.: Физматлит, 2007, 223 с.
5. RU 2120120 C1 G01N 3/20. G01B 7/16 Способ определения изгибной жесткости объектов из композиционных материалов. Афанасьев В.И., Балакирев А.И., Ершов Ю.М., Шатланов М.И. Опубликовано 1998.10.10
Таблица 1
Таблица 2
Таблица 3
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗГИБНОЙ ЖЕСТКОСТИ ОБЪЕКТОВ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ | 1991 |
|
RU2120120C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗГИБНОЙ ЖЕСТКОСТИ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ ПРИ РАЗЛИЧНЫХ ТЕМПЕРАТУРНЫХ УСЛОВИЯХ | 2020 |
|
RU2745947C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ СТРУКТУРНЫХ ПАРАМЕТРОВ РЕЛЬСОВОГО ПУТИ | 2015 |
|
RU2683137C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ИЗГИБНОЙ ЖЕСТКОСТИ ПРОТЯЖЕННЫХ ОБЪЕКТОВ С ПОМОЩЬЮ КРИВИЗНОМЕРА | 2013 |
|
RU2535645C1 |
| СПОСОБ УВЕЛИЧЕНИЯ ПЬЕЗОЧУВСТВИТЕЛЬНОСТИ БИМОРФА ИЗГИБНОГО ТИПА | 2022 |
|
RU2778161C1 |
| ГИДРАВЛИЧЕСКИЙ СТАБИЛИЗАТОР ПОПЕРЕЧНОЙ УСТОЙЧИВОСТИ ЖЕЛЕЗНОДОРОЖНОГО ВАГОНА | 2023 |
|
RU2807559C1 |
| ПАССАЖИРСКИЙ ВАГОН | 1997 |
|
RU2123948C1 |
| СПОСОБ ОЦЕНКИ СОСТОЯНИЯ ЖЕЛЕЗНОДОРОЖНОГО ПУТИ | 2008 |
|
RU2394120C2 |
| ВИБРОЗАЩИТНОЕ УСТРОЙСТВО ДЛЯ ПОДВИЖНОГО СОСТАВА ЖЕЛЕЗНЫХ ДОРОГ | 2015 |
|
RU2612227C2 |
| Кузов вагона надземной монорельсовой транспортной системы | 2018 |
|
RU2724201C2 |

Изобретение относится к расчетно-экспериментальным способам определения изгибной жесткости объекта, в частности к определению упругих свойств кузова пассажирского вагона. Способ включает установку объекта на жесткие опоры, нагружение его поперечными распределенными и/или сосредоточенными усилиями, определение величин в ряде расчетных сечений по длине объекта и оценку фактической изгибной жесткости. При этом нагружаемый объект представляют в виде балки Бернулли-Эйлера с кусочно-постоянной изгибной жесткостью и рассчитывают геометрическую изгибную жесткость при использовании значений вертикальных сил и кусочно-постоянных распределенных нагрузок, прикладываемых к объекту при реализации заявляемого способа. Затем производят вычисления фактической изгибной жесткости, пропорциональной вычисленной геометрической жесткости, по методу наименьших квадратов с использованием значений прогибов в ряде расчетных сечений объекта. Технический результат заключается в повышении точности определения значений динамических характеристик транспортного объекта, значительном сокращении времени, необходимого на замеры. 1 з.п. ф-лы, 3 ил. 
1. Способ определения изгибной жесткости объекта, заключающийся в том, что объект устанавливают на жесткие опоры, затем нагружают его поперечными распределенными и/или сосредоточенными усилиями, определяют величины прогибов в ряде расчетных сечений по длине объекта и оценивают фактическую изгибную жесткость, отличающийся тем, что оценка фактической изгибной жесткости определяется следующим образом: нагружаемый объект представляют в виде балки Бернулли-Эйлера с кусочно-постоянной изгибной жесткостью  , где E - модуль Юнга, J - величина момента инерции редуцированного поперечного сечения, и рассчитывают геометрическую изгибную жесткость при использовании значений вертикальных сил
, где E - модуль Юнга, J - величина момента инерции редуцированного поперечного сечения, и рассчитывают геометрическую изгибную жесткость при использовании значений вертикальных сил  и кусочно-постоянных распределенных нагрузок, прикладываемых к объекту при реализации заявляемого способа; вычисление фактической изгибной жесткости, пропорциональной вычисленной геометрической жесткости, по методу наименьших квадратов с использованием значений прогибов в ряде расчетных сечений объекта.
и кусочно-постоянных распределенных нагрузок, прикладываемых к объекту при реализации заявляемого способа; вычисление фактической изгибной жесткости, пропорциональной вычисленной геометрической жесткости, по методу наименьших квадратов с использованием значений прогибов в ряде расчетных сечений объекта.
2. Способ по п. 1, отличающийся тем, дополнительно учитывают то, что фактическое количество перемен изгибной жесткости намного меньше фактического количества различных ее значений, что позволяет производить объединение в группы участков, не следующих друг за другом, а расположенных в произвольных местах.
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗГИБНОЙ ЖЕСТКОСТИ ОБЪЕКТОВ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ | 1991 |
|
RU2120120C1 |
| Ватульян А.О | |||
| Обратные задачи в механике деформируемого твердого тела | |||
| - М.: Физматлит, 2007, 223 с | |||
| Василевский В.В., Скачков А.Н., Юхневский А.А | |||
| Идентификация изгибной жесткости кузова пассажирского вагона теоретико-экспериментальным методом / В кн.: Проблемы и перспективы развития вагоностроения: сборник научных | |||
Авторы
Даты
2022-05-16—Публикация
2020-07-30—Подача